Fast and Adaptive Sparse Precision Matrix Estimation in High Dimensions

Abstract

This paper proposes a new method for estimating sparse precision matrices in the high dimensional setting. It has been popular to study fast computation and adaptive procedures for this problem. We propose a novel approach, called Sparse Column-wise Inverse Operator, to address these two issues. We analyze an adaptive procedure based on cross validation, and establish its convergence rate under the Frobenius norm. The convergence rates under other matrix norms are also established. This method also enjoys the advantage of fast computation for large-scale problems, via a coordinate descent algorithm. Numerical merits are illustrated using both simulated and real datasets. In particular, it performs favorably on an HIV brain tissue dataset and an ADHD resting-state fMRI dataset.

1. Introduction

Estimating covariance matrices is fundamental in multivariate analysis. It has been popular to estimate the inverse covariance (or precision) matrix in the high dimensional setting, where the number of variables p goes to infinity with the sample size n (more precisely, in this paper, p ≫ n and (log p)/n = o(1)). Inverting the sample covariance matrix has been known to be unstable for estimating the precision matrix. Recent proposals usually formulate this objective as regularized/penalized optimization problems, where regularization is employed to control the sparsity of the precision matrix. Besides the challenge of solving such large optimization problems, there is an important issue on how to choose an appropriate regularization level that is adaptive to the data. To address these two challenges, we propose a fast and adaptive method, and establish the theoretical properties when the regularization level is chosen by cross validation.

Let X = (X₁,…, X_p)^T be a p-variate random vector with a covariance matrix Σ or its corresponding precision matrix Ω := Σ⁻¹. Suppose we observe independent and identically distributed random samples {X₁, …, X_n} from the distribution of X. To encourage a sparse and stable estimate for Ω, regularized/penalized likelihood approaches have been proposed. Here, sparsity means that most of the entries in Ω are exactly zero. Popular penalties include the ℓ₁ penalty [1] and its extensions, for example, [2], [3], [4], and [5]. In particular, [3] developed an efficient algorithm, glasso, to compute the penalized likelihood estimator, and its convergence rates were obtained under the Frobenius norm [5] and the elementwise ℓ_∞ norm and spectral norm [6]. Other penalties were also studied before. For example, the ℓ₁ penalty was replaced by the nonconvex SCAD penalty [7, 8, 9]. Due to the complexity of the penalized likelihood objective, theoretical analysis and computation are rather involved. Moreover, the theory usually relies on some theoretical assumptions of the penalty, and thus it provides limited guidance for applications.

Recently, column-wise or neighborhood based procedures have caught much attention, due to the advantages in both computation and analysis. [10] proposed to recover the support of Ω using ℓ₁ penalized regression, aka LASSO [1], in a row by row fashion. This can be computed efficiently via path-following coordinate descent [11] for example. A Dantzig selector proposal, replacing the LASSO approach, was proposed recently by [12], and the computation is based on standard solvers for linear programming. [13] proposed a procedure, CLIME, which seeks a sparse precision matrix under a matrix inversion constraint. Their procedure is also solved column by column via linear programming. Compared with the regularized likelihood approaches, their convergence rates were obtained under several matrix norms mentioned before, without imposing the mutual incoherence condition [6], and were improved when X follows polynomial tail distributions. However, all these procedures are computational expensive for very large p, and again these estimators were analyzed based on theoretical choices of the penalty.

Cross validation on the other hand has gained popularity for choosing the penalty levels or tuning parameters, because it is adaptive and usually yields superior performance in practice. Unfortunately, the theoretical understanding of cross validation is sparse. For a related problem on estimating sparse covariance matrices, [14] analyzed the performance of covariance thresholding where the threshold is based on cross validation. [15] provided a different approach using self-adaptive thresholding. However, these covariance estimation results cannot be extended to the inverse covariance setting, partly due to the problem complexity. This paper will provide theoretical justification for cross validation when estimating the precision matrix. This result is made possible because we propose a new column-wise procedure that is easy to compute and analyze. To the best of our knowledge, this paper is among the first to provide theoretical justification of cross validation for sparse precision matrix estimation.

The contributions of this paper are several folds. First, we propose a novel and penalized column-wise procedure, called Sparse Columnwise Inverse Operator (SCIO), for estimating the precision matrix Ω. Second, we establish the theoretical justification under mild conditions when its penalty is chosen by cross validation. The theory for cross validation is summarized as follows. A matrix is called s_p-sparse if there are at most s_p non-zero elements on each row. It is shown that the error between our cross validated estimator Ω̂ and Ω satisfies ${\Vert {\widehat{\mathbf{\Omega }}}^1-\mathbf{\Omega }\Vert }_F^2/p=O_P(s_p(logp)/n)$, where ||·||_F is the Frobenius norm. Third, theoretical guarantees for the SCIO estimator are also obtained under other matrix norms, for example the element-wise ℓ_∞ norm which achieves graphical model selection [16]. Fourth, we provide a fast and simple algorithm for computing the estimator. Because our algorithm exploits the advantages of conjugate gradient and coordinate descent, and thus it provides superior performance in computational speed and cost. In particular, we reduce two nested loops in glasso [3] to only one. An R package of our method, scio, has been developed, and is publicly available on CRAN.

The rest of the paper is organized as follows. In Section 2, after basic notations and definitions are introduced, we present the SCIO estimator. Finite sample convergence rates are established with the penalty level chosen both by theory in Section 3 and by cross validation in Section 4. The algorithm for solving SCIO is introduced in Section 5. Its numerical merits are illustrated using simulated and real datasets. Further discussions on the connections and differences of our results with other related work are given in Section 6. The supplementary material includes additional results for the numerical examples in Section 5 and the proof of the main results.

The notations in this paper are collected here. Throughout, for a vector a = (a₁, …, a_p)^T ∈ IR^p, define ${\mid \mathbf{a}\mid }_1={\sum }_{j=1}^p\mid a_j\mid$ and ${\mid \mathbf{a}\mid }_2=\sqrt{{\sum }_{j=1}^p{a}_j^2}$. All vectors are column vectors. For a matrix A = (a_ij) ∈ IR^p×q, we define the elementwise l_∞ norm |A|_∞ = max_{1≤i≤p,1≤j≤q} |a_ij |, the spectral norm ||A||₂ = sup_|x|2≤1 |Ax|₂, the matrix ℓ₁ norm ${\Vert \mathit{A}\Vert }_{L_1}={max}_{1\le j\le q}{\sum }_{i=1}^p\mid a_{ij}\mid$, the matrix ∞ norm ${\Vert \mathit{A}\Vert }_{\infty }={max}_{1\le i\le q}{\sum }_{j=1}^p\mid a_{ij}\mid$, the Frobenius norm ${\Vert \mathit{A}\Vert }_F=\sqrt{{\sum }_{i,j}{a}_{ij}^2}$, and the elementwise ℓ₁ norm ${\Vert \mathit{A}\Vert }_1={\sum }_{i=1}^p{\sum }_{j=1}^q\mid a_{ij}\mid$. A_i,· and A_·,j denote the ith row and jth column respectively. I denotes an identity matrix. 1 {·} is the indicator function. The transpose of A is denoted by A^T. For any two matrices A and B of proper sizes, 〈A, B〉 = Σ_i(A^T B). For any two index sets T and T′ and a matrix A, we use A_TT′ to denote the |T|×|T′| matrix with rows and columns of A indexed by T and T′ respectively. The notation A ≻ 0 means that A is positive definite. For two real sequences {a_n} and {b_n}, write a_n = O(b_n) if there exists a constant C such that |a_n| ≤ C|b_n| holds for large n, a_n = o(b_n) if lim_n→∞ a_n/b_n = 0, and a_n ≍ b_n if a_n = O(b_n) and b_n = O(a_n). Write a_n = O_P(b_n) if a_n = O(b_n) holds with the probability going to 1. The constants C, C₀, C₁, … may represent different values at each appearance.

2. Methodology

Our estimator is motivated by adding the ℓ₁ penalty [1] to a column loss function, which is related to conjugate descent and a constrained minimization approach CLIME [13]. The technical derivations that lead to the estimator is provided in the supplementary material. Denote the sample covariance matrix by Σ̂. Let a vector β̂_i be the solution to the following equation:

$${\widehat{\mathit{\beta }}}_i=\underset{\mathit{\beta }\in {IR}^p}{argmin}\left\{\frac{1}{2}{\mathit{\beta }}^T\widehat{\mathbf{\sum }}\mathit{\beta }-{\mathbf{e}}_i^T\mathit{\beta }+{\lambda }_{ni}{\mid \mathit{\beta }\mid }_1\right\},$$ (1)

where β̂_i = (β̂_i1, …, β̂_ip)^T, e_i is the ith column of a p × p identity matrix, and λ_ni > 0 is a tuning parameter. The tuning parameter could be different from column to column, adapting to different magnitude and sparsity of each column.

One can formulate a precision matrix estimate where each column is the corresponding β̂_i. However, the resulting matrix may not be symmetric. Similar to a symmetrization step employed in CLIME, we define the SCIO estimator Ω̂ = (ω̂_ij)_p×p, using the following symmetrization step,

$${\widehat{\omega }}_{ij}={\widehat{\omega }}_{ji}={\widehat{\beta }}_{ij}1\{\mid {\widehat{\beta }}_{ij}\mid <\mid {\widehat{\beta }}_{ji}\mid \}+{\widehat{\beta }}_{ji}1\{\mid {\widehat{\beta }}_{ij}\mid \ge \mid {\widehat{\beta }}_{ji}\mid \}.$$ (2)

As we will establish in Section 3, similar to the results of CLIME, the convergence rates shall not change if the diagonal of the sample covariance Σ̂ is added by a small positive amount, as long as in the order of n^−1/2 log^1/2 p. With this modification, (1) is then strictly convex and has a unique solution. In Section 5, we will present an efficient coordinate descent algorithm to solve it.

The SCIO estimator, like other penalized estimators, depends on the choice of λ_ni. We allow λ_ni to be different from column to column, so that it is possible to adapt to each column’s magnitude and sparsity, as we will illustrate in Section 4. More importantly, due to the simplified column loss function (1), we are able to establish, in Section 4, the theoretical guarantees when λ_ni is chosen by cross validation. In comparison, the theory of cross validation for glasso [3] and CLIME [13] has not been established before, to the best of our knowledge.

3. Theoretical guarantees

3.1. Conditions

Let be the support of Ω_·,i, the ith column of Ω = (ω_ij)_p×p. Define the s_p-sparse matrices class

$$\mathcal{U}=\left\{\mathbf{\Omega }\succ 0:\underset{1\le j\le p}{max}\sum _{i=1}^{p}1\{{\omega }_{ij}\ne 0\}\le s_p,{\Vert \mathbf{\Omega }\Vert }_{L_1}\le M_p,c_0^{-1}\le {\mathrm{\Lambda }}_{min}(\mathbf{\Omega })\le {\mathrm{\Lambda }}_{max}(\mathbf{\Omega })\le c_0\right\},$$

where c₀ is a positive constant, Λ_min(Ω) and Λ_max(Ω) are the minimum and maximum eigenvalues of Ω respectively. The sparsity s_p is allowed to grow with p, as long as it satisfies the following condition.

(C1). Suppose that Ω ∈ 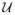with

$$s_p=o\left(\frac{\sqrt{n}}{logp}\right)$$ (3)

and

$$\underset{1\le i\le p}{max}{\Vert {\mathbf{\sum }}_{{\mathcal{S}}_i^c{\mathcal{S}}_i}{({\mathbf{\sum }}_{{\mathcal{S}}_i{\mathcal{S}}_i})}^{-1}\Vert }_{\infty }\le 1-\alpha$$ (4)

for some 0 < α < 1.

As we will see from Theorem 1, condition (3) is required for proving the consistency. Condition (4) is in the same spirit as the mutual incoherence or irrepresentable condition for glasso [6], but it is slightly relaxed, see Remark 2. In general, this type of conditions is believed to be almost necessary for penalization methods to recover support.

Let Y = (Y₁, …, Y_p)^T = ΩX − Ωμ where μ = EX. The covariance matrix of Y is thus Ω. The second condition is on the moments of X and Y.

(C2). (Exponential-type tails) Suppose that log p = o(n). There exist positive numbers η > 0 and K > 0 such that

$$⋿exp(\eta {(X_i-{\mu }_i)}^2)\le K,⋿exp(\eta Y_i^2)\le K\text{for}\text{all}1\le i\le p.$$

(C2*). (Polynomial-type tails) Suppose that for some γ, c₁ > 0, p ≤ c₁n^γ, and for some δ > 0

$$⋿{\mid X_i-{\mu }_i\mid }^{4\gamma +4+\delta }\le K,⋿{\mid Y_i\mid }^{4\gamma +4+\delta }\le K\text{for}\text{all}i.$$

We will assume either one of these two types of tails in our main analysis. These two conditions are standard for analyzing sparse precision matrix estimation, see [13] and references within.

3.2. Convergence rates of Ω̂ − Ω

The first theorem is on the convergence rate under the spectral norm. It implies the convergence rates of eigenvalues and eigenvectors, which are essential in principle component analysis for example. The convergence rate under the spectral norm may also be important for classification, for example linear/quadratic discriminant analysis as we illustrate in Section 5.

Theorem 1

Let ${\lambda }_{ni}=C_0\sqrt{logp/n}$ with C₀ being a sufficiently large number. Under (C1), and (C2) (or (C2^*)), we have

$${\Vert \widehat{\mathbf{\Omega }}-\mathbf{\Omega }\Vert }_2\le C{M}_p{s}_p\sqrt{\frac{logp}{n}}$$

with probability greater than 1 − O(p⁻¹) (or 1 − O(p⁻¹ + n^−δ/8) under (C2*)), where C > 0 depends only on c₀, η, C₀ and K (or c₀, c₁, γ, δ, C₀ and K under (C2*)).

Remark 1

If M_ps_pn^−1/2log^1/2 p = o(1), then Ω̂ is positive definite with probability tending to one. We can also revise Ω̂ to Ω̂_τ with

$${\widehat{\mathbf{\Omega }}}_{\tau }=\widehat{\mathbf{\Omega }}+\tau \mathbf{I},$$

where τ = (|Λ_min(Ω̂)| + n^−1/2)1{Λ_min(Ω̂) ≤ 0}. By Theorem 1, assuming τ ≤ CM_ps_pn^−1/2 log^1/2 p, we have with probability greater than 1 − O(p⁻¹) (or 1 − O(p⁻¹ + n^−δ/8)) that

$${\Vert {\widehat{\mathbf{\Omega }}}_{\tau }-\mathbf{\Omega }\Vert }_2\le C{M}_p{s}_p\sqrt{\frac{logp}{n}}.$$

Such a simple perturbation will make the revised estimator Ω̂_τ to have a larger minimal eigenvalue, for stability concerns. The later results on support recovery and other norms will also hold under such a small perturbation.

Remark 2

[6] imposed the following irrepresentable condition on glasso: for some 0 < α < 1,

$${\Vert {\mathbf{\Gamma }}_{{\mathrm{\Psi }}^c\mathrm{\Psi }}{({\mathbf{\Gamma }}_{\mathrm{\Psi }\mathrm{\Psi }})}^{-1}\Vert }_{\infty }\le 1-\alpha ,$$ (5)

where Ψ is the support of Ω, Γ = Σ ⊗ Σ, and ⊗ denotes the Kronecker matrix product. To make things concrete, we now compare our conditions using the examples given in [6]:

1. In the diamond graph, let p = 4, σ_ii = 1, σ₂₃ = 0, σ₁₄ = 2ρ² and σ_ij =ρ for all i ≠ j, (i, j) ≠ (2, 3) and (2, 4). For this matrix, (5) is reduced to 4|ρ|(|ρ| + 1) < 1 and so it requires ρ ∈ (−0.208, 0.208). Our relaxed condition (4) only needs ρ ∈ (−0.5, 0.5).

2. In the star graph, let p = 4, σ_ii = 1, σ_1,j = ρ for j = 2, 3, 4, σ_ij = ρ² for 1 < i < j ≤ 4. For this model, (5) requires |ρ|(| ρ| + 2) < 1 (i.e. ρ ∈ (−0.4142, 0.4142)), while our condition (4) holds for all ρ ∈ (−1, 1).

We have the following result on the convergence rates under the element-wise ℓ_∞ norm and the Frobenius norm.

Theorem 2

Under the conditions of Theorem 1, we have with probability greater than 1 − O(p⁻¹) under (C2) (or 1 − O(p⁻¹ + n^−δ/8) under (C2*))

$${\left|\widehat{\mathbf{\Omega }}-\mathbf{\Omega }\right|}_{\infty }\le C{M}_p\sqrt{\frac{logp}{n}}$$ (6)

and

$$\frac{1}{p}{\Vert \widehat{\mathbf{\Omega }}-\mathbf{\Omega }\Vert }_F^2\le C{s}_p\frac{logp}{n}.$$ (7)

Remark 3

The convergence rate under the Frobenius norm does not depend on M_p. In comparison, [17] obtained the minimax lower bound, when X ~ N (μ, Σ),

$$\frac{1}{p}\underset{\widehat{\mathbf{\Omega }}}{min}\underset{\mathbf{\Omega }\in \mathcal{U}}{max}⋿{\Vert \widehat{\mathbf{\Omega }}-\mathbf{\Omega }\Vert }_F^2\ge C{M}_p^2{s}_p\frac{logp}{n}.$$ (8)

They also showed that this rate is achieved by sequentially running two CLIME estimators, where the second CLIME estimator uses the first CLIME estimate as input. Though CLIME allows a weaker sparsity condition where our ℓ₀ ball bound s_p in 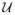is replaced by an ℓ_q ball bound (0 ≤ q < 1), our rate in (7) is faster than CLIME, because $M_p^2$ in (8) could grow with p. The faster rate is due to the fact that we consider the condition (4). Under a slightly stronger condition (5) (see Remark 2), [6] proved that the glasso estimator Ω̂_glasso has the following convergence rate

$$\frac{1}{p}{\Vert {\widehat{\mathbf{\Omega }}}_{\mathit{glasso}}-\mathbf{\Omega }\Vert }_F^2=O_P\left({\kappa }_{\mathrm{\Gamma }}^2{s}_p\frac{logp}{n}\right),$$ (9)

where κ_Γ = ||(&Gamma;_ΨΨ)⁻¹||_L1. Our convergence rate is also faster than theirs in (9) κ_Γ → ∞.

3.3. Support recovery

As discussed in the introduction, support recovery is related to Gaussian graphical models. The support of Ω is recovered by SCIO, with high probability by the following theorem. Recall Ψ = {(i, j) : ω_ij ≠ 0} be the support of Ω, and similarly

$$\widehat{\mathrm{\Psi }}=\{(i,j):{\widehat{\omega }}_{ij}\ne 0\}.$$

The next theorem gives the result on support recovery.

Theorem 3

(i). Under the conditions of Theorem 1, we have Ψ ⊆ Ψ with probability greater than 1 − O(p⁻¹) under (C2) (or 1 − O(p⁻¹ + n^−δ/8) under (C2*)). (ii). In addition, suppose that for a sufficiently large number C > 0,

$$\underset{(i,j)\in \mathrm{\Psi }}{min}\mid {\omega }_{ij}\mid \ge C{M}_p\sqrt{\frac{logp}{n}}.$$ (10)

Then under the conditions of Theorem 1, we have Ψ̂= Ψ with probability greater than 1 − O(p⁻¹) under (C2) (or 1 − O(p⁻¹ + n^−δ/8) under (C2*)).

The condition (10) on the signal strength is standard for support recovery, see [6], [13] for example. We also note that the CLIME method [13] requires an additional thresholding step for support recovery, while SCIO does not need this step.

4. Theory for data-driven penalty

This section analyzes a cross validation scheme for choosing the tuning parameter λ_ni, and we establish the theoretical justification of this data-driven procedure.

We consider the following cross validation method for simplicity, similar to the one analyzed in [14]. Divide the sample {X_k; 1 ≤ k ≤ n} into two subsamples at random. Let n₁ and n₂ = n − n₁ be the two sample sizes of the random splits satisfying n₁ ≍ n₂ ≍ n, and let ${\widehat{\mathbf{\sum }}}_1^l,{\widehat{\mathbf{\sum }}}_2^l$ be the sample covariance matrices from the two samples n₁ and n₂ respectively in the lth split, for l = 1,…, H, where H is a fixed integer. For each i, let ${\widehat{\mathit{\beta }}}_i^l(\lambda )$ be the estimator minimizing the average out-of-sample SCIO loss, over λ,

$${\widehat{R}}_i(\lambda )=\frac{1}{H}\sum _{v=1}^H\left[\frac{1}{2}{({\widehat{\mathit{\beta }}}_i^l(\lambda ))}^T{\widehat{\mathbf{\sum }}}_2^l{\widehat{\mathit{\beta }}}_i^l(\lambda )-{\mathbf{e}}_i^T{\widehat{\mathit{\beta }}}_i^l(\lambda )\right]$$ (11)

where ${\widehat{\mathit{\beta }}}_i^l(\lambda )$ is calculated from the n₁ samples with a tuning parameter λ to be determined. For implementation purposes, instead of searching for continuous λ, we will divide the interval [0, 4] by a grid λ₀ < λ₁ < ··· < λ_N, where ${\lambda }_i=\frac{4i}{N}$. The number 4 comes from the CLIME constraint, see the supplementary material. The tuning parameter on the grid is chosen by, for each i,

$${\widehat{\lambda }}_i=\underset{0\le j\le N}{argmin}{\widehat{R}}_i({\lambda }_j).$$ (12)

It is important to note that the size N should be sufficiently large but not too large, see the first two conditions on N in Theorem 4, and the convergence rate will then hold even if we only perform cross validation on a grid. The choice of λ̂_i could be different for estimating each column of the precision matrix using the column loss function (11). This allows the procedure to adapt to the magnitude and sparsity of each column, compared with the standard glasso estimator with a single choice of λ for the whole matrix. Though it is possible to specify different λ for each column (even each entry) in glasso, searching over all possible combinations of λ’s over high dimensional grids, using a non-column-wise loss (e.g. the likelihood), is computationally untrackable. Our column loss thus provides a simple and computationally trackable alternative for choosing adaptive λ.

As described before, the complexity of the likelihood function may make it difficult to analyze the glasso estimator using cross validation. Though CLIME uses a constrained approach for estimation, its constrained objective function cannot be directly used for cross validation. [13] proposed to use the likelihood function as the cross validation loss, which makes it difficult to establish the theory of cross validated CLIME. For a different setting of estimating the covariance matrix, [14] obtained the convergence rate under the Frobenius norm, using covariance thresholding. The threshold is also based on sample splitting like ours. However, to the best of our knowledge, it has been an open problem on establishing the theoretical justification of cross validation when estimating the precision matrix. Theorem 4 below fills the gap, showing that the estimator based on λ̂_i from (12) attains the optimal rate under the Frobenius norm. For simplicity, we set H = 1 as in [14].

Our theory adopts the following condition on the sub-Gaussian distribution, which was use in [18] for example.

(C3). There exist positive numbers η′ > 0 and K′ > 0 such that

$$\underset{{\mid \mathit{v}\mid }_2=1}{max}⋿exp({\eta }^{\prime }{({\mathit{v}}^T(\mathbf{X}-\mathit{\mu }))}^2)\le K^{\prime }$$

This condition is slightly stronger than (C2), because our next theorem adapts to unknown Ω using cross validation, instead of the theoretical choice λ_ni. It is easy to see that (C3) holds for the multivariate normal distribution as a special case.

Denote the unsymmetrized ${\widehat{\mathbf{\Omega }}}_1^1:=({\widehat{\omega }}_{ij1}^1)=({\widehat{\mathit{\beta }}}_1^1({\widehat{\lambda }}_1),\dots ,{\widehat{\mathit{\beta }}}_p^1({\widehat{\lambda }}_p))$ and recall the symmetrized matrix Ω̂¹ as

$${\widehat{\omega }}_{ij}^1={\widehat{\omega }}_{ji}^1={\widehat{\omega }}_{ij1}^{1}1\{\mid {\widehat{\omega }}_{ij1}^1\mid <\mid {\widehat{\omega }}_{ji1}^1\mid \}+{\widehat{\omega }}_{ji1}^{1}1\{\mid {\widehat{\omega }}_{ij1}^1\mid \ge \mid {\widehat{\omega }}_{ji1}^1\mid \}.$$

The following theorem shows that the estimator ${\widehat{\mathbf{\Omega }}}^1=({\widehat{\omega }}_{ij}^1)$ attains the minimax optimal rate under the Frobenius norm.

Theorem 4

Under the conditions log N = O(log p), $\sqrt{n/logp}=o(N)$, and (C3), we have as n, p → ∞,

$$\frac{1}{p}{\Vert {\widehat{\mathbf{\Omega }}}^1-\mathbf{\Omega }\Vert }_F^2=O_P\left(s_p\frac{logp}{n}\right).$$

The convergence rate using cross validation is the same as (7) in Theorem 2 with the theoretical choice of λ. Using similar arguments in Theorem 4 of [14], this result can be extended to multiple folds H > 1. To the best of our knowledge, Theorem 4 is the first result on the theoretical justification of cross validation when estimating the sparse precision matrix.

5. Numerical examples

5.1. Algorithm

Recall that the SCIO estimator is obtained by applying symmetrization (2) to the solution from (1), where each column β̂_i is given by the following

$${\widehat{\mathit{\beta }}}_i=\underset{{\mathit{\beta }}_i\in {IR}^p}{argmin}\left\{\frac{1}{2}{\mathit{\beta }}_i^T\widehat{\mathbf{\sum }}{\mathit{\beta }}_i-{\mathbf{e}}_i^T{\mathit{\beta }}_i+\lambda {\Vert {\mathit{\beta }}_i\Vert }_1\right\}$$ (13)

for any λ> 0. We propose to employ an iterative coordinate descent algorithm to solve (13) for each i. In contrast, the R package glasso employs an outside loop over the columns of the precision matrix, while having another inside loop over the coordinates of each column. Our algorithm does not need an outside loop because our loss function is column-wise.

The iterative coordinate descent algorithm for each i goes as follows. In each iteration, we fix all but one coordinate in β, and optimize over that fixed coordinate. Without loss of generality, we consider optimizing over the pth coordinate β_p while all other coordinates of β (denoted by β_−p) are fixed. The solution is in an explicit form by the following simple proposition. The solution when fixing other coordinates is similar, simply by permuting the matrix. We then loop through the coordinates until the updates are smaller than a user-specified threshold, say 10⁻⁴.

Proposition 1

Let the subvector partition β = (β_−p, β_p) and partition Σ̂ accordingly as follows

$$\widehat{\mathbf{\sum }}=\left(\begin{array}{cc}{\widehat{\mathbf{\sum }}}_{11}& {\widehat{\mathbf{\sum }}}_{12}^T\\ {\widehat{\mathbf{\sum }}}_{12}& {\widehat{\mathrm{\sum }}}_{22}\end{array}\right).$$

Fixing β_−p, the minimizer of (13) is

$${\beta }_p=\mathcal{T}\left(1\{p=i\}-{\mathit{\beta }}_{-p}^T{\widehat{\mathbf{\sum }}}_{12},\lambda \right)/{\widehat{\mathrm{\sum }}}_{22}$$

where the soft thresholding rule 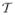(x, λ) = sign(x) max(|x| − λ, 0).

We implement this algorithm in an R package, scio, available on CRAN. All the following computation is performed using R on an AMD Opteron processor (2.6 GHz) with 32 Gb memory. The glasso and CLIME estimators are computed using its R packages glasso (version 1.7) and clime (version 0.4.1) respectively. The path-following strategy with warm-starts [11] is enabled in all methods.

5.2. Simulations

In this section, we compare the performance with glasso and CLIME on several measures using simulated data. In order to compare the adaptivity of the procedures, the covariance matrices that generate the data all contain two block diagonals of different magnitude, where the second block is 4 times the first one. Similar examples were used in [15] in comparing adaptive covariance estimation. The first block is generated from the following models respectively.

1. decay: ω_ij = 0.6^|i−j|.

2. sparse: Let the prototype Ω₀ = O + δI, where each off-diagonal entry in O is generated independently, and equals to 0.5 with probability 0.1 and 0 with probability 0.9. δ is chosen such that the conditional number (the ratio of maximal and minimal singular values of a matrix) equals to p. Finally, the block matrix is standardized to have unit diagonals.

3. block: A block diagonal matrix with block size 5 where each block has off-diagonal entries equal to 0.5 and diagonal 1. The resulting matrix is then randomly permuted.

100 independent and identically distributed observations constituting a training data set are generated from each multivariate Gaussian covariance model with mean zero, and 100 additional observations are generated from the same model as a validating data set. Using the training data alone, a series of penalized estimators with 50 different tuning parameters λ is computed. For a fair comparison, we first pick the tuning parameters in glasso, CLIME, and SCIO to produce the smallest Bregman loss on the validation sample. The Bregman loss is defined by

$$L(\mathbf{\sum },\mathbf{\Omega })=\langle \mathbf{\Omega },\mathbf{\sum }\rangle -logdet(\mathbf{\Omega }).$$

We also compare with our cross validation scheme in Section 4, where the cross validation loss is the column-wise adaptive loss (11). The resulting estimator is denoted by SCIOcv. We consider different values of p = 50, 100, 200, 400, 800, 1600, and replicate 100 times.

Table 1 compares the estimation performance of SCIO, SCIOcv, CLIME, and glasso under the spectral norm and the Frobenius norm. It shows that SCIO and SCIOcv almost uniformly outperform all other methods under both norms. SCIO has better performance when p ≤ 400, while SCIOcv has better performance when p ≥ 800. The glasso estimator has the worst performance overall, but it has slightly improved performance than other methods in the block model for p = 200 and 400. The CLIME estimator has slightly worse performance than our estimators overall, except for a few cases.

Table 1.

Comparison of average losses of SCIO, SCIOcv, CLIME, and glasso over 100 simulation runs. The best performance is highlighted in bold. All standard errors of the results are smaller than 0.1.

Spectral Norm
p	Decay				Sparse				Block
	SCIO	SCIOcv	CLIME	glasso	SCIO	SCIOcv	CLIME	glasso	SCIO	SCIOcv	CLIME	glasso
50	10.00	11.24	11.62	12.10	2.73	4.03	5.70	3.86	7.24	9.55	8.03	9.61
100	11.89	12.68	12.29	13.11	4.51	5.57	6.54	5.70	9.63	9.78	9.13	9.77
200	12.88	13.46	12.91	13.84	7.93	8.31	8.43	8.48	9.88	9.85	10.05	9.83
400	13.63	13.87	14.09	14.07	10.88	11.60	11.63	11.11	9.92	9.91	10.31	9.87
800	14.13	14.05	14.10	14.71	15.58	15.48	15.60	16.08	9.96	9.95	10.01	10.63
1600	14.15	14.12	14.12	14.83	20.94	20.90	20.94	21.61	9.97	9.96	10.15	10.68

Frobenius Norm
p	Decay				Sparse				Block
	SCIO	SCIOcv	CLIME	glasso	SCIO	SCIOcv	CLIME	glasso	SCIO	SCIOcv	CLIME	glasso
50	16.22	18.54	19.25	20.18	6.71	7.95	12.66	8.14	16.10	20.98	17.58	21.68
100	27.48	29.58	28.40	30.92	12.93	14.84	18.48	14.91	30.83	31.02	28.72	31.15
200	42.93	45.12	42.80	47.00	24.34	24.67	26.60	26.11	44.49	44.23	44.92	44.19
400	65.61	66.60	68.65	68.10	36.65	38.99	40.67	37.76	62.91	62.73	65.38	62.54
800	97.52	96.09	97.25	102.67	59.08	57.55	59.97	66.30	88.98	88.78	88.63	96.42
1600	138.09	136.90	137.74	147.11	83.85	82.87	84.50	96.90	125.85	125.64	125.41	137.27

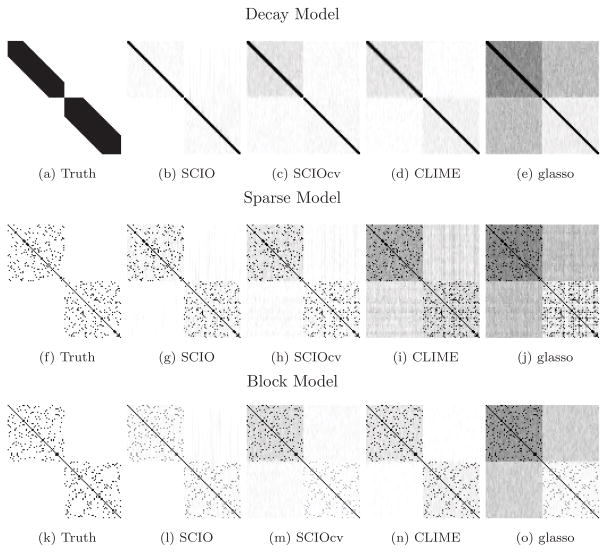
As discussed before, support recovery carries important consequences for graphical model estimation. The frequencies of correct zero/nonzero identification are summarized in Table 1 of the supplementary material. In there, the SCIO and SCIOcv estimates are sparser than the CLIME and glasso estimates in general. To further illustrate this, we plot the heatmaps of support recovery in Figure 1 using p = 100 as a representing example. These heatmaps confirm that the SCIO estimates usually contain less zeros than glasso and CLIME. By visual inspection, these SCIO estimates also tend to be closer to the truth, especially under the sparse model. In particular, they adapt to different magnitude. In contrast, glasso yields some interference patterns and artificial stripes, especially under the sparse model.

Figure 1.

Heatmaps of support recovery over 100 simulation runs (black is 100/100, white is 0/100).

5.3. A genetic dataset on HIV-1 associated neurocognitive disorders

Antiretroviral therapy (ART) has greatly reduced mortality and morbidity of HIV patients; however, HIV-1 associated neurocognitive disorders (HAND) are becoming common, which cause greatly degradation of life quality. We here apply our graphical models to a gene expression dataset [19] to study how their genetic interactions/pathways are altered between treated and untreated HAND patients, and compare with other methods using classification. The supplementary material includes the full description of the dataset, the modeling approach, and additional results.

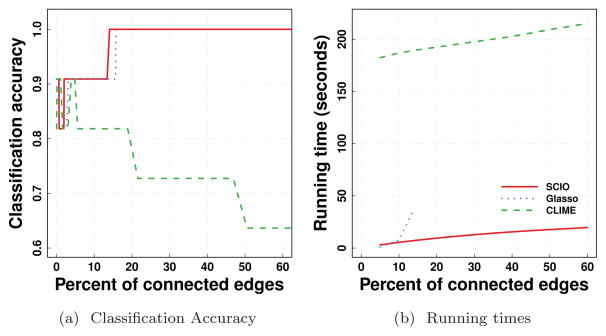
Figure 3a compares classification accuracy between treated and untreated HAND. The results comparing HAND and controls are not shown because all methods have a constant area-under-the-curve value 1. Because the number of nonzero off-diagonal elements may depend on the different scales of the penalization parameters in each method, we plot the classification accuracy against the average percentages of nonzero off-diagonals of these two classes (treated and untreated), i.e. the average percentages of connected edges in two recovered graphical models for the treated and untreated respectively. The SCIOcv estimators (not shown) only differs from SCIO on how to pick λ in a data-driven way, and thus it has the identical performance as SCIO under the same λ. This figure shows that in most cases SCIO outperforms glasso and CLIME when both methods use the same number of connected edges. The SCIO estimators are stable in classification performance even if the number of connected edges increases. We are not able to plot the performance of glasso with more than 14% connected edges (corresponding to small penalization parameters), because the glasso package does not converge within 120 hours. CLIME shows decreased performance when the number of connected edges increases. As a comparison with other classification algorithms, we use the same data to compare with a few other classification methods, including random forest [20], AIC penalized logistic regression, and ℓ₁ penalized logistic regression with 5-fold cross validation. Their classification accuracies are 78.6%, 90.9% and 45.6% respectively. Our classification rule compares favorably with these competing methods on this dataset.

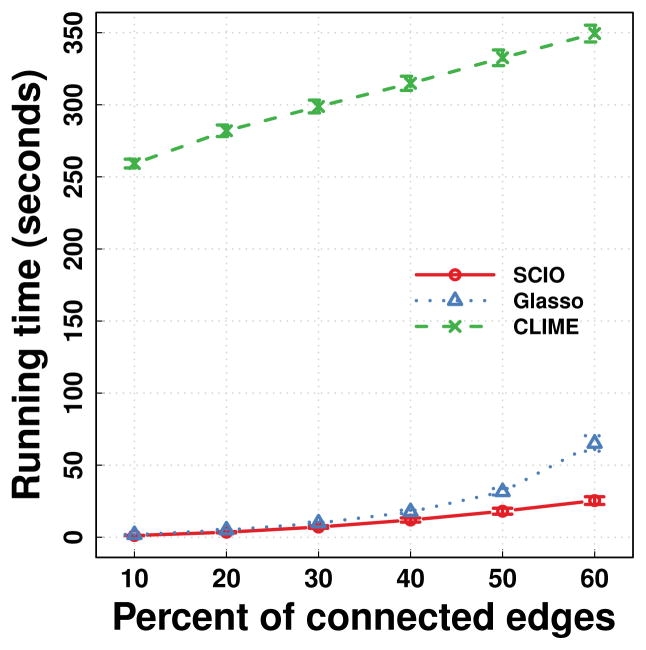
Figure 3.

Comparison of average (± 1 SE) running times for the ADHD dataset. The red solid line with circle marks is SCIO, the green dashed line with crosses is CLIME, and the blue dotted line with triangles is glasso.

Figure 3b compares the running times against the percentages of connected edges. Because it is known that path-following algorithms may compute a sequence of solutions much faster than for a single one, we use 50 log-spaced penalization parameters from the largest (0% edges) to the designated percentages of edges, including 5%, 10%, 14%, 20%, 30%, 40%, 50% and 60%. As reported before, we are unable to plot the running times for glasso beyond 14% due to nonconvergence. SCIO takes about 2 seconds more than glasso when computing for 5% edges, but is much faster than glasso for 10% and more. For example, it compares favorably in the 14% case where SCIO takes only a quarter of the time of glasso. In general, the running time of SCIO grows linearly with the number of connected edges, while glasso shows exponential growth in computation time. CLIME is the slowest among all methods.

Figure 1 of the supplementary material compares the performance of support recovery, and it shows similar advantages of SCIO as in the simulations.

5.4. An fMRI dataset on attention deficit hyperactivity disorders

Attention Deficit Hyperactivity Disorder (ADHD) causes substantial impairment among about 10% of school-age children in United States. A neuroimaging study showed that the correlations between brain regions are different between typically developed children and children with such disorders [21]. The description of the data and additional results are provided in the supplementary material. In there, we compare the performance of support recovery using the data from each subject, and the results suggest that SCIO has competitive performance with CLIME and glasso in recovering brain connectivities for both healthy and ADHD children.

Figure 3 compares the running times of SCIO, CLIME, and glasso. Similar to the procedure described before, for each subject, we use path following algorithms in all methods up to the designated edge percentages, including 10%, 20%, 30%, 40%, 50% and 60%. This plot shows that the running times of SCIO grows almost linearly, and it is about 2 times faster than glasso with 60% connected edges. CLIME again is the slowest among all methods.

6. Discussion

It is possible to achieve adaptive estimation via other approaches. During the preparation of this paper, it comes to our attention that recently [22] applied a new adaptive penalized regression procedure, Scale Lasso, to the inverse covariance matrix estimation. [17] proposed an improved CLIME estimator, which runs the CLIME estimation sequentially twice. We instead analyzed cross validation as an alternative approach for this goal because cross validation remains to be popular among practitioners. It would be interesting to study the theory of cross validation for these other estimators, and to study if these adaptive approaches can also be applied to our loss.

Choosing the tuning parameters is an important problem in the practice of penalization procedures, though most of the prior theoretical results are based on some theoretical assumptions of the tuning parameters. This paper is among the first to demonstrate that a cross validated estimator for the problem of precision matrix estimation achieves the n^−1/2 log^1/2 p rate under the Frobenius norm. This rate may not be improved in general, because it should be minimax optimal [17], though a rigorous justification is needed. We also note that the distribution condition (C3) in Theorem 4 is slightly stronger than (C2) and (C2^*). It is an interesting problem to study if the result in Theorem 4 can be extended to more general distributions. Moreover, it would be interesting to study whether minimax rates can also be achieved under other matrix norms, such as the operator norm, using cross validation.

The rate for support recovery in Theorem 3 also coincides with the minimax optimal rate in [17]. However, 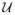together with (4) is actually a smaller class than theirs. It would be interesting to explore if their minimax rate can be improved in this important sub-class. It would also be interesting to study if our results can be extended to their general matrix class.

We employ the ℓ₁ norm to enforce sparsity due to computational concerns. It has been pointed out before that the ℓ₁ penalty inheritably introduces biases, and thus it would be interesting to replace the ℓ₁ norm by other penalty forms, such as Adaptive Lasso [23] or SCAD [9]. Such extensions should be easy to implement because our loss is column-wise, similar to penalized regression. We are currently implementing these variants for future releases of our R package.

There are several other interesting directions. It would be interesting to study the precision matrix estimation under the setting that the data are generated from statistical models, while the covariance estimation problem under this setting was studied by [24]. It is also of interest to consider extending SCIO to the nonparanormal family distributions [25].

Finally, this paper only considers the setting that all the data are observed. It is an interesting problem to study the inverse covariance matrix estimation when some observations are missing. It turns out that the SCIO procedure can also be applied to the missing data setting, with additional modifications. Due to the space limitation, we will report these results elsewhere.

Figure 2.

Comparison of classification accuracy and running times using SCIO, CLIME and glasso for the HIV dataset. Red solid lines are SCIO, green dash lines are CLIME, and blue dotted lines are glasso.

Highlights.

• We propose a new procedure for sparse precision matrix estimation.

• We are among the first to establish the theory of cross validation for this problem.

• The conditions are slightly weaker than an important penalized likelihood method.

• Improved numerical performance is observed in several examples.