The effects of transit time heterogeneity on brain oxygenation during rest and functional activation

Abstract

The interpretation of regional blood flow and blood oxygenation changes during functional activation has evolved from the concept of ‘neurovascular coupling', and hence the regulation of arteriolar tone to meet metabolic demands. The efficacy of oxygen extraction was recently shown to depend on the heterogeneity of capillary flow patterns downstream. Existing compartment models of the relation between tissue metabolism, blood flow, and blood oxygenation, however, typically assume homogenous microvascular flow patterns. To take capillary flow heterogeneity into account, we modeled the effect of capillary transit time heterogeneity (CTH) on the ‘oxygen conductance' used in compartment models. We show that the incorporation of realistic reductions in CTH during functional hyperemia improves model fits to dynamic blood flow and oxygenation changes acquired during functional activation in a literature animal study. Our results support earlier observations that oxygen diffusion properties seemingly change during various physiologic stimuli, and posit that this phenomenon is related to parallel changes in capillary flow patterns. Furthermore, our results suggest that CTH must be taken into account when inferring brain metabolism from changes in blood flow- or blood oxygenation-based signals .

Introduction

Brain function depends critically on a steady supply of oxygen. During rest, the central nervous system receives >20% of the cardiac output, and consciousness is lost within seconds after circulatory arrest. Although functional activation is typically associated with a modest 10% to 30% increase in local cerebral metabolic rate of oxygen (CMRO₂), regional cerebral blood flow (CBF) typically increases by 20% to 80%, with δCBF/δCMRO₂ coupling ratios consistently larger than unity.^{1, 2} This functional hyperemia permits the localization of brain activity by imaging techniques such as positron emission tomography and functional magnetic resonance imaging. Today, arterial spin labeling functional magnetic resonance imaging and blood oxygen level-dependent (BOLD) functional magnetic resonance imaging are the preferred tools in human brain mapping.^{3, 4} The interpretation of regional blood flow and blood oxygenation changes during functional activation has evolved from the concept of ‘neurovascular coupling': mechanisms that converge on cerebral arterioles to adjust CBF according to changing metabolic needs. The subsequent distribution of blood across the capillary bed, and the oxygen diffusion from the microcirculation to active cells, is extremely complex, and so far biophysical models have been unable to establish with certainty whether the increase in oxygen supply during functional hyperemia is matched to the increased metabolic demands.⁵

Buxton and Frank⁶ derived the so-called ‘oxygen limitation model', which relates CBF and CMRO₂ through the flow diffusion or Bohr–Kety–Crone–Renkin (BKCR) model.⁷ Based on the relation between blood flow velocity and solute extraction in single capillaries, this formalism assumes that all tissue capillaries display identical extraction properties. The model predicts that oxygen availability depends on blood flow and a rate parameter that describes oxygen diffusion from blood to tissue. In brain, opening of previously closed capillaries (‘capillary recruitment') is not observed under normal physiologic stimuli, and the rate parameter is therefore generally assumed to be constant. As oxygen extraction fraction (OEF) decreases with CBF according to the BKCR model, large CBF increases are required to support even modest increases in CMRO₂. Accordingly, the nonlinear relation between CBF and CMRO₂ could reflect tight coupling of CBF to CMRO₂ through an OEF that varies nonlinearly with CBF.

Hyder et al⁸ developed a model of the relation between CBF and CMRO₂ in which they permitted the ‘effective diffusivity' of oxygen to vary linearly with CBF—and hence relaxed the assumption of a constant rate or ‘oxygen conductance' parameter. The model yielded good fits to a wide range of positron emission tomography data. Vafaee and Gjedde⁹ also allowed oxygen conductance to vary, noting that their ‘oxygen diffusibility' varied with stimulus intensity in positron emission tomography measurements of CBF and CMRO₂ during functional activation. They speculated that such variations in oxygen conductance are linked to differences in CBF response, and possibly subject to local regulation.⁹

The models above assumed negligible oxygen tension (pO₂) in tissue, whereas measurements suggest that interstitial pO₂ in brain tissue is in fact roughly 25 mm Hg, albeit with high microregional heterogeneity.⁵ Tissue pO₂ affects the oxygen concentration gradient between blood and tissue, and therefore net oxygen extraction. Changes in tissue pO₂ during hyperemia could therefore contribute to the nonlinear relation between CBF and CMRO₂ observed during functional activation.¹ More recent models of the relation between CMRO₂ and CBF include tissue pO₂ as a variable,^{10, 11} and can account for a broad range of CBF/CMRO₂ coupling ratios without the need to introduce variation in oxygen diffusion properties, for which the biophysical rationale remains unclear.¹¹ These models have failed, however, to explain more recent dynamic recordings of CBF and tissue pO₂ obtained in the somatosensory cortex of rats during electrical forepaw stimulation by Vazquez et al.¹² Instead, these data could be explained if either arterial pO₂, capillary volume, or capillary oxygen permeability were allowed to vary.¹² Indeed, satisfactory fits to the observations of Vazquez et al,¹² and to more recent data that include blood oxygenation values¹³ by a multicompartment model could only be achieved if the capillary permeability/conductance to oxygen was allowed to vary.¹⁴ Again, the biophysical underpinnings of such a mechanism remain elusive.

Capillary flow patterns are very heterogeneous in resting brain,^{15, 16, 17} but tend to homogenize during functional activation¹⁷ in a manner that correlates with stimulus intensity.¹⁸ Figure 1 shows covariation between mean capillary transit time and capillary transit time heterogeneity (CTH) based on literature reports from in vivo animal experiments and numerical simulations in a vascular anatomic network (VAN) model. As the relation between flow velocity and oxygen extraction for individual capillaries is nonlinear, this heterogeneity implies that the relation between blood flow and oxygen extraction in tissue cannot be described by a unique, macroscopic oxygen conductance across physiological conditions as assumed by conventional compartment models.^{7, 19, 20, 21, 22, 23} The overall oxygen conductance of a microvascular system will be less than the sum of individual vessel conductances in presence of heterogeneity.²⁰ As a result, capillary flow heterogeneity may reveal itself as a need to adjust the oxygen conductance when fitting compartment models to clearance data obtained at different blood flow levels.^{8, 9, 12, 14}

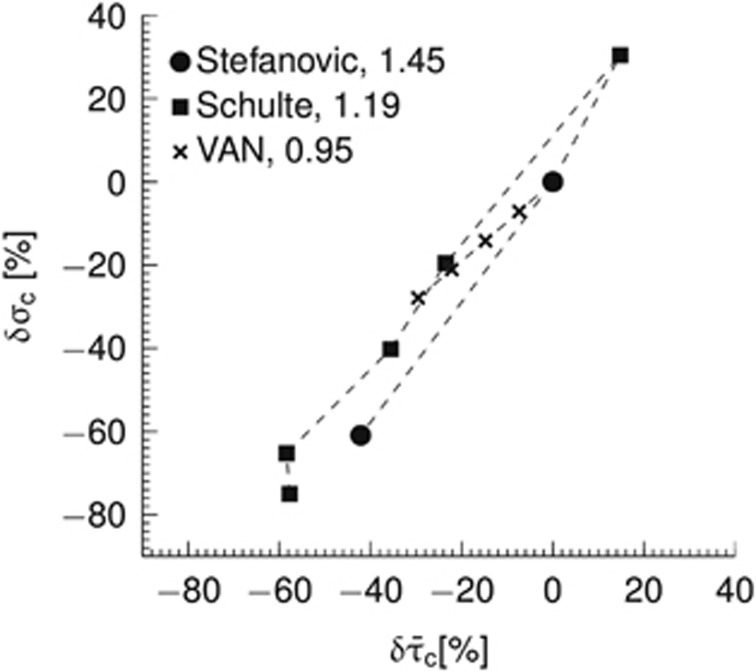
Figure 1.

Relationship between relative changes δ in average capillary transit time 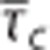and capillary transit time heterogeneity (CTH) as quantified by the standard deviation of the capillary transit time distribution σ_c. Pairs of 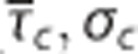from studies performed in rat by Stefanovic et al¹⁷ and Schulte et al,¹⁸ and simulation results from a vascular anatomic network (VAN) model.²⁶ A decrease in σ_c with decreasing 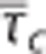is observed both in the estimates based on experimental data and in the simulation data. Note that the individual data sets have been normalized with respect to baseline value, that is, the baseline of all data sets is in (0%, 0%). Numbers next to references in the caption refer to a coupling parameter θ_σ of a linear model relating 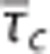and σ_c by 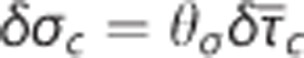. See Supplementary Material for details on the simulation and Jespersen and Østergaard²⁴ for details on estimates based on experimental data.

We recently extended the BKCR equation to take the effect of CTH into account.²⁴ This model predicts that presence of CTH leads to decreased oxygen extraction from blood into tissue as compared with a scenario with homogenous capillary transit times. Hence, the degree of CTH influences the overall oxygen transport capacity of the capillary bed. In this article, we model the effect of capillary flow or transit time heterogeneity on the apparent oxygen conductance of ‘conventional' compartment models. We validate our modeling framework by numerical simulations and comparison with experimental data of Vazquez et al.¹³

Materials and methods

Modeling Oxygen Transport

Compartment modeling

The concentration of oxygen in blood is modeled as a sum of oxygen bound to hemoglobin and oxygen dissolved in plasma^{11, 25}

where λ is the bound oxygen concentration at full hemoglobin saturation, s is oxygen saturation, α_p is oxygen solubility in plasma, and p is the partial pressure of oxygen in plasma. Under normal physiological conditions, the contribution from dissolved oxygen is relatively small (~2% to 3%), and the last term in equation (1) may be neglected. The relation between oxygen saturation and partial pressure of oxygen is modeled by the Hill equation

where p₅₀ is the oxygen partial pressure at which hemoglobin is 50% saturated, and the exponent h>1 defines the cooperative binding. The vascular bed is represented as a series of vascular compartments surrounded by a tissue compartment.²⁵ Change in oxygenation of the i'th vascular segment is derived from mass conservation and Fick's diffusion law

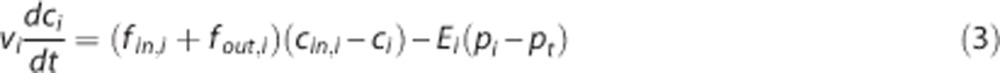where v_i is the volume of the vascular segment, f_in,i and f_out,i are inflow and outflow, respectively, c_i=(c_in,i+c_out,i)/2 is the average oxygen concentration,^{11, 25, 26} c_in,i and c_out,i are the inlet and outlet oxygen concentrations, respectively, E_i is an oxygen conductance coefficient,^{14, 27, 28, 29} whereas p_i and p_t are the average plasma pO₂ and tissue pO₂, respectively.^{11, 26} The oxygen conductance coefficient defines oxygen flux in relation to average intravascular and extravascular pO₂. Note that the ‘oxygen conductance' coefficient in equation (3) is mathematically equivalent to the ‘effective diffusivity',⁸ ‘oxygen diffusibility',⁹ ‘permeability-surface (PS) product',^{11, 12} and ‘vascular permeability rate'²⁵ coefficients. In the tissue compartment, the change in oxygenation is derived from mass conservation

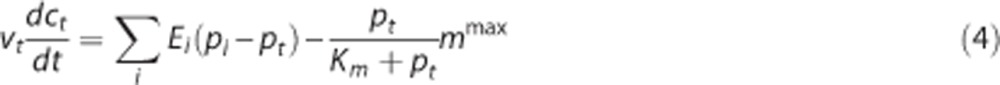where v_t is the volume of the tissue compartment. The last term represents the CMRO₂, termed m. m^max is the maximum rate at which oxygen is removed by tissue metabolism, and the product with p_t/(K_m+p_t) prevents p_t from becoming negative in case of insufficient oxygen delivery.¹¹ We follow previous work within the neuroimaging community and consider the metabolic response m^max to be driven in parallel with the hemodynamic response,^{2, 11, 14, 25, 30, 31} that is, m^max is a variable that is allowed to change. At steady state, equations 3 and 4 become

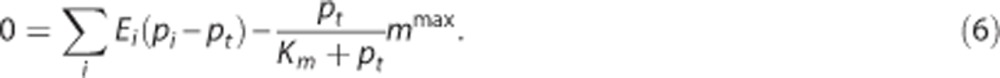Modeling capillary transit time heterogeneity

For the capillary compartment, the steady-state equation (5) can be rewritten as

where γ_c is the velocity at which an element of blood moves along the compartment representation with length l_c. The capillary transit time is related to flow through τ_c=v_c/f_c. Equation 9 shows that oxygen extraction depends on the compartment geometry, the velocity at which blood traverses the compartment, and on the oxygen conductance E_c.

A conventional oxygen transport model generalizes from individual capillaries to ensembles of capillaries in tissue by setting 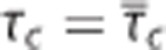the mean capillary transit time across capillary bed, in the equations above (Figures 2A and 2D). We refer to this model as Conv_ss below. It is important to note, however, that equations 7, 8, 9 only hold for tissue if blood indeed passes through individual capillaries with identical transit times, or if the flow velocities in individual capillaries are proportional to their oxygen conductance.²⁰

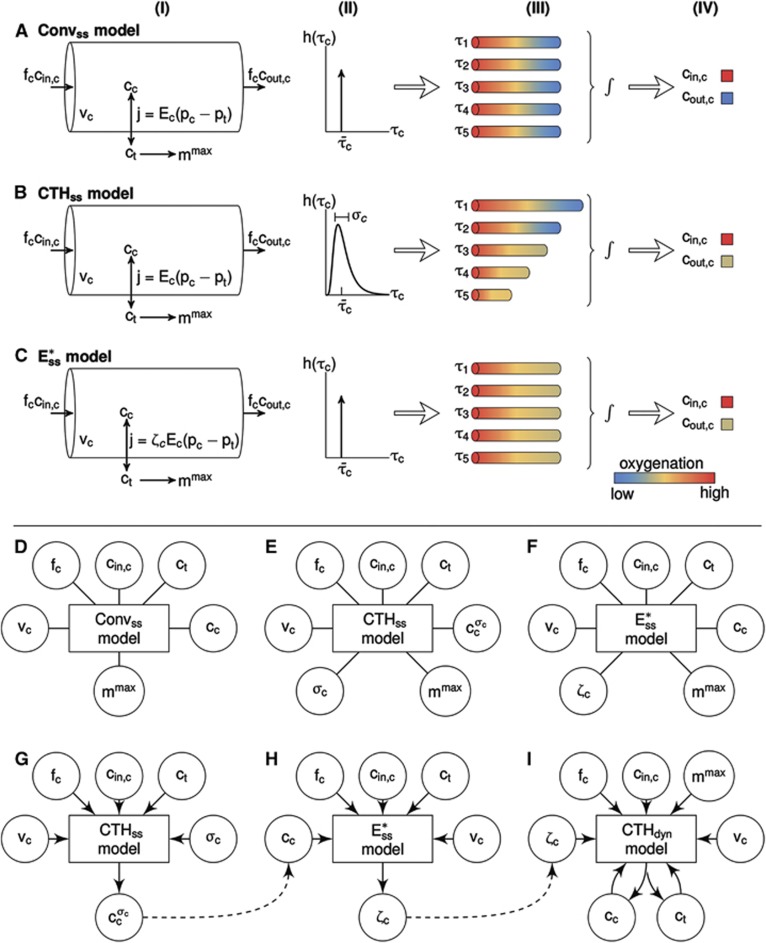
Figure 2.

(A–C) Three compartment models of brain oxygenation, (A) conventional steady-state model (Conv_ss model), (B) steady-state model incorporating the effect of capillary transit time heterogeneity (CTH; CTH_ss model), and (C) steady-state model incorporation the effect of changes in apparent oxygen conductance (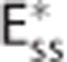 model). The cylinders in column (I) represent the capillary vascular compartment with volume v_c. Blood enters the capillary compartment with a flow rate of f_c with capillary inlet oxygen concentration c_in,c and leaves the capillary compartment with capillary outlet oxygen concentration c_out,c. The rate of oxygen exchange j between blood and tissue is assumed to be proportional to the difference between average oxygen tension in blood p_c and in tissue p_t with the proportionality constant E_c being an oxygen conductance parameter that describe oxygen exchange in relation to the averaged intravascular and extravascular oxygen tension. Oxygen flux in the model is described by an additional oxygen conductance scaling factor ζ_c defined by 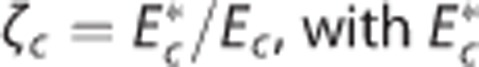being the apparent oxygen conductance and E_c being the underlying oxygen conductance (equations 11 and 12). Oxygen tensions in blood and tissue are calculated from average oxygen concentration in blood c_c and tissue c_t, respectively, by use of the Hill equation. Oxygen is removed from tissue by oxygen metabolism with a maximum rate of m^max. Column (II) shows distributions h(τ_c) of capillary transit times τ_c in the three models. The Conv_ss model and the 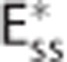model assume homogenous transit times, that is, all capillary transit times equal the average transit time . The CTH_ss model assumes a nonzero dispersion, and h(τ_c) is additionally parameterized by the standard deviation of transit times σ_c. Note that the three models have identical average transit times. The cylinders in column (III) represent oxygen extraction in five compartments that are parameterized according to samples from the respective transit time distributions shown in column (II). Differences in transit times are represented by cylinder length differences. Column (IV) shows inlet and outlet capillary oxygen concentration resulting from integration over the transit time distributions. A nonzero σ_c in the CTH_ss model results in decreased overall oxygen extraction in comparison with the Conv_ss model and hence a higher outlet oxygen concentration. The 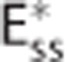model is capable in producing the same oxygen extraction as the CTH_ss model if the apparent oxygen conductance is calibrated by the scaling factor ζ_c. (D–I) Diagrams illustrating models, dynamical variables, and procedural steps that are used to incorporate the effect of CTH into conventional compartment models via changes in the apparent oxygen conductance scaling factor ζ_c. The models (D) Conv_ss model (equations 5 and 6), (E) CTH_ss model (equations 6, 8, and 10), and (F) 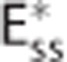model (equations 11 and 12) describe the relationship between the dynamical variables. Panels (G and H) illustrate how changes in ζ_c is calculated so that the 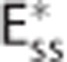model produces the same oxygen extraction as the CTH_ss model. Step (G) calculates the average capillary oxygen concentration of the CTH_ss model 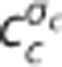(and hence oxygen extraction) based on numerical values of v_c,f_c,c_in,c,c_t,σ_c and the CTH_ss model. Note that the models are models of relationships rather than causal models; hence arrows do not imply claims about causality. This oxygen concentration is used together with the 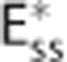model in step (H) to compute the required change in ζ_c. Panels (G–I) illustrate how the effect of CTH is incorporated into the dynamical CTH model (CTH_dyn) via changes in ζ_c (equations 13 and 14). The numerical value of ζ_c is computed, in a given time step, by feeding present values of v_c,f_c,c_in,c,c_t,σ_c into step (G) followed by computation of c_c in step (G) and ζ_c in step (H). Hence steps (G–I) are iterated as the temporal dynamics in c_c and c_t are evolved.

To model heterogeneous flow patterns across the capillary bed, we consider a distribution of capillary transit times h(τ_c),^{24, 32, 33} parameterized by a mean transit time 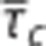and an s.d. σ_c, which operationally quantifies CTH.²⁴ The oxygen extraction is then modeled as the weighted contributions from multiple compartment representations with individual transit times τ_c, which are distributed according to h(τ_c) (Figures 2B and 2E). For simplicity, we consider compartment volume and oxygen conductance to be uniform across the capillary bed, so v_c can be lumped with E_c to yield the constant E_c/(2v_c) (equation 8). This allows us to model heterogeneity by assuming a distribution over transit times—a quantity with a straightforward interpretation. Note that heterogeneity could be modeled by considering the distribution of the quantity τ_cE_c/v_c instead, as also proposed by Renkin.⁷

The average capillary oxygen concentration across an ensemble of blood elements that traverse the capillary bed according to the transit time distribution h(τ_c) with s.d. σ_c can be determined as

where the capillary concentration c_c(τ_c) can be computed from equation 8. The model defined in terms of equations 6, 8, and 10 is referred to as CTH_ss below. It can be shown mathematically that 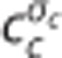is greater than or equal to the average capillary concentration of oxygen predicted by a conventional model that assumes identical transit times, that is, less oxygen can be extracted from a capillary bed with a heterogeneous transit time or flow distribution.

Modeling capillary transit time heterogeneity via the resulting changes in apparent oxygen conductance

The effect of CTH can be expressed in terms of an apparent oxygen conductance, E* (Jespersen and Østergaard²⁴). The apparent oxygen conductance is defined as the oxygen conductance of a conventional model that will lead to the same capillary compartment concentration (and oxygen extraction) as observed in a model that takes CTH into account (Figures 2C and 2F). E* is introduced into the steady-state equations 5 and 6 by

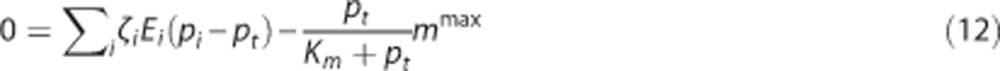where 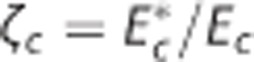and ζ_i≠c=1. The model defined by equations 11 and 12 is referred to as below. The value of the scaling factor ζ_i is computed by the following steps:

1. Compute 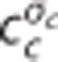of the CTH_ss model by equations 8 and 10 (Figure 2G).

2. Compute ζ _i of the 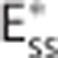model by equation 11 using 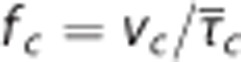so that 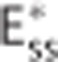produces the same oxygen extraction as the CTH_ss model (Figure 2H).

Modeling dynamic changes in the apparent oxygen conductance

As in steady state, we also use changes in the apparent oxygen conductance E* to model changes in the ability of the vascular bed to transport oxygen as hemodynamic variables evolve over time. E* is introduced as a dynamical variable into the dynamical equations (equations 3 and 4):

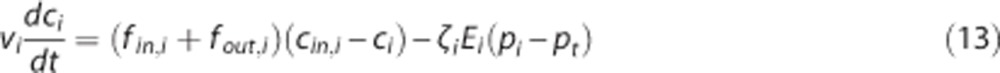where 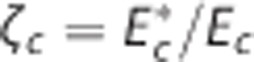and ζ_i≠c=1. The model defined by equations 13 and 14 is referred to as 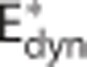below. To determine the effects of CTH on ζ_c during hyperemia, we developed a model that we refer to as CTH_dyn below, in which the steady-state procedure to compute ζ_c described in the previous section was used for every time point as hemodynamic variables evolve (Figures 2G–2I). That is, for a given average capillary compartment flow f_c=(f_in,c+f_out,c)/2, volume v_c, inlet concentration c_in,c, and tissue oxygen tension p_t we compute ζ_c. The scaling factor is subsequently used in the dynamical equations (equations 13 and 14) to compute the temporal dynamics of oxygen concentration (Figure 2I). In principle, transit time is only defined at steady state. To avoid abusive use of ‘transit time', one can instead model the distribution over τ_c=v_c/f_c (equation 7), or equally τ_c=γ_c/l_c (equation 9), rather than of transit times, with f_c=(f_in,c+f_out,c)/2 and γ_c=(γ_in,c+γ_out,c)/2 denoting the instantaneous mean flow and mean velocity, respectively. For notational simplicity, we let ‘CTH' refer to heterogeneity in these quantities and let σ_c refer to the s.d. of the distribution governing these quantities also in the dynamical modeling.

Simulations and Data Analysis

Modeling steady-state effects of capillary transit time heterogeneity

We examined the steady-state behavior of a compartment model in which the effects of CTH on oxygen transport are included (CTH_ss model). For simplicity, we considered a one-compartment model that describes oxygen exchange between a single-vascular compartment (capillaries) and tissue.^{2, 11} We assumed the volume of the capillary compartment to be constant, and capillary transit times to be distributed according to a gamma distribution.^{24, 32} The analysis was based on numerical simulations, using model parameters typical of rat brain as listed in Supplementary Material Table 1.

Modeling dynamical effects of capillary transit time heterogeneity

The dynamical behavior of our oxygen transport model was examined by numerical simulations and by modeling the data set of Vazques et al.¹³ We applied a multicompartment model comprising a tissue compartment and three vascular compartments connected in series: arteriolar, capillary, and venous. Arteriolar dilation drives volume and flow changes throughout the vascular compartments during activation.^{25, 26} The capillary and venous compartments were modeled as compliant elements that expand passively as pressure increases—see Huppert et al ²⁵ for further details. Oxygen transport from the vascular network was modeled as described above, and we again assumed capillary transit times to be described by a gamma distribution.

Modeling dynamical effects of capillary transit time heterogeneity—simulations

In our simulations, we defined the temporal development of a series of dynamical variables that serve as inputs to our model. These inputs include the dynamics of arteriolar volume, inlet arteriolar pO₂, maximum CMRO₂, and the s.d. of the transit time distribution. Time courses for these variables were constructed by convolving a stimulus block representing the experimental design with a gamma filter.³⁴ We considered two different versions of the oxygen transport model: (i) a conventional model in which neither the effect of CTH nor dynamical changes in the apparent oxygen conductance of the capillary compartment were modeled (Conv_dyn model), and (ii) a CTH model in which we modeled heterogeneity in terms of the dynamic changes in the apparent oxygen conductance of the capillary compartment (CTH_dyn). Parameters of the multicompartment models were set according to values in Supplementary Material Table 2.

Modeling dynamical effects of capillary transit time heterogeneity—comparison with in vivo data

The study of Vazquez et al¹³ reports a data set with dynamical measurements of blood flow, as well as arteriolar, venous, and tissue oxygenation from an experiment with somatosensory activation evoked by electrical forepaw stimulation in anesthetized rats.¹³ This data set was recently modeled with a multicompartment model by Barrett and Suresh.¹⁴ They showed that a model that incorporates dynamic changes in the capillary oxygen conductance was in better agreement with these data than a model with constant capillary conductance.

To model this data set, we considered three different versions of the oxygen transport model: (i) a conventional model in which neither the effect of CTH, nor changes in oxygen conductance were modeled (Conv_dyn model), (ii) an oxygen conductance model in which the apparent oxygen conductance was allowed to vary as proposed by Barrett and Suresh¹⁴ (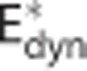 model), and (iii) our model in which the effect of CTH is assumed to drive dynamic changes in the apparent oxygen conductance of the capillary compartment (CTH_dyn model).

Similar to Vazquez et al,¹³ we modeled the vascular system from small surface arteries to small emerging surface veins, with the aim of representing the time series of corresponding laser Doppler flows, and oxygen concentrations in small arteries, small veins, and tissue. The reported value of baseline tissue pO₂ is rather high (38.0 mm Hg) relative to that of small veins (33.3 mm Hg). Similarly to Barrett and Suresh,¹⁴ we consider this observed tissue pO₂ to represent the average of a contribution from tissue and a contribution from the vascular segments. Specifically, we model the observed tissue tension 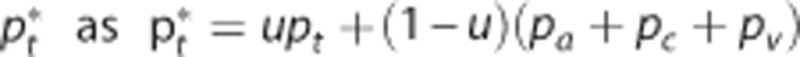with the weight u∈[0 1] being defined from baseline values of oxygen tensions in the compartments and kept constant during the dynamics. We modeled the temporal dynamics of arteriolar volume, inlet oxygen tension, and maximum CMRO₂ by parametric functions that are parameterized by relatively few parameters,^{14, 25} see Supplementary Material. We let the changes in the apparent oxygen conductance and in the s.d. of the transit time distribution σ_c be proportional to the changes in flow and transit time, respectively. A coupling between flow and oxygen conductance has been shown to be sufficient for modeling this particular data set.¹⁴ A more flexible approach is to model the temporal dynamics in the apparent oxygen conductance and in σ_c by individual parametric functions as in the simulations. We modeled the experimental data in two steps. By first making sure that the vascular submodel was identical in the three models, we could directly compare the three models of oxygen transport. Accordingly, we first fitted our vascular model to the time series of laser Doppler flow, that is, the response of the vascular submodel was identical in the three models. We also fitted the parametric function describing inlet oxygenation. We then fixed the parameters of these models to posterior median values in the second step (description of inference procedure follows below), where the oxygenation measurements was modeled by the three versions of the oxygen transport model (Conv_dyn model, 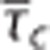model, CTH_dyn model). Model inference was performed using a Bayesian approach.^{25, 35} Based on a probability model of the measurement data (a likelihood function) and formulation of our prior knowledge on model parameters (prior distributions), the Bayesian paradigm provides the conditional distribution of the parameters given the measurement data (posterior distribution). Hence, the measurement data entered the analysis at the level of model inference rather than being used as either input or output of the hemodynamic models. We modeled the likelihood function in terms of Gaussian distributions and assumed uniform prior distributions over unknown parameters. Parameters were set according to values in Supplementary Material Table 2. For model inference, we used Markov Chain Monte Carlo sampling, where samples were drawn from the posterior distribution using the delayed rejection-adaptive metropolis algorithm.³⁶ Twenty thousand samples were drawn from each parameter chain, and the 5,000 first samples were discarded as burn-in samples.

Results

Modeling Steady-State Effects of Capillary Transit Time Heterogeneity

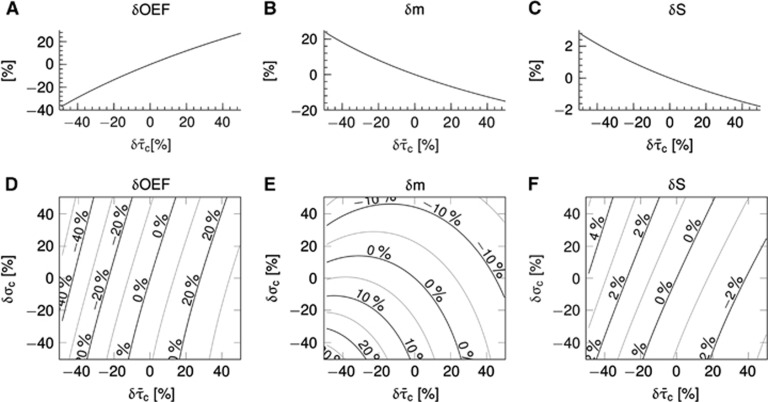
Figure 3 shows simulation results for a conventional version of the oxygen transport model without incorporating the effect of CTH (panels A–C) (Conv_ss model) and a version of the oxygen transport model that includes the effect of CTH (panels D–F) (CTH_ss model). Note that tissue pO₂ was fixed at 25 mm Hg in these simulations. The abscissae show relative changes in transit times, and the ordinate relative changes in the respective variables. The transit time range (−40% to 40%) corresponds to relative flow changes of (67% to −29%). In the Conv_ss model, the OEF increases as the transit time increases (panel A). The parallel reduction in CBF leads to a relative reduction in the metabolic rate of oxygen that can be supported (panel B). Panel C shows increased BOLD signal with increased flow (decreased transit time) and decreased BOLD signal with decreased flow. In the CTH_ss model, the efficacy at which oxygen can be extracted at a given tissue pO₂ depends not only on transit time but also on the level of transit time heterogeneity. The OEF increases if σ_c decreases for any fixed value of (panel D). Hence, the effect of CTH provides a mechanism by which the system can modulate oxygen extraction in addition to the well-known neurovascular coupling mechanisms, where changes in oxygen extraction are solely driven by changes in flow and tissue oxygenation. Panel E shows the metabolic rate of oxygen at a given 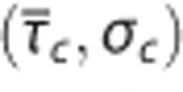pair. For low values of σ_c, increased metabolism can be supported as 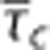decreases; a behavior also observed in the Conv_ss model (panel B). At high values of σ_c, the metabolism that can be supported decreases with low values of 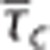. Hence, for a range of 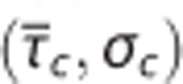pairs, a further decrease in (i.e., a flow increase) leads to a paradox reduction in oxygen availability. The region defined by such 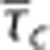pairs has been dubbed a region of ‘malignant CTH'.²⁴ Panel F shows increased BOLD signal with flow as in panel C but also increased BOLD signal with increased heterogeneity for a fixed average flow. This is the result of the lower oxygen extraction efficacy (at fixed flow and tissue pO₂) as CTH increases (panel D).

Figure 3.

Steady-state simulations in a conventional one-compartment model (Conv_ss model) (A–C) and an one-compartment model that includes the effect of capillary transit time heterogeneity (CTH; CTH_ss model) (D–F). Relative changes δ in the oxygen extraction fraction (OEF), cerebral metabolic rate of oxygen m, and the blood oxygenation level-dependent (BOLD) signal S versus changes in the average capillary transit time 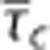assuming a constant tissue oxygen tension of 25 mm Hg. Note that OEF and m varies, not only as together with 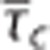but also as together with CTH as quantified by the standard deviation of the capillary transit time distribution σ_c. Note that a CTH model without homogenization is distinct from a conventional model with no modeled effect of heterogeneity, hence (E) does not reproduce (B) when δσ_c=0. The plots were constructed assuming baseline values: 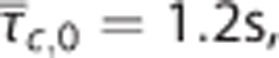and σ_c,0=0.94 s. The BOLD signal was calculated by use the ‘Davis' model 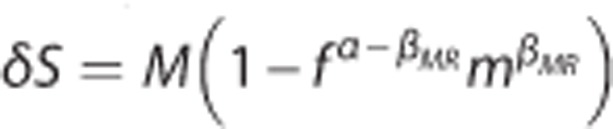with parameters M=0.08, β_MR=1.2, and α=0.4 (Buxton²and Davis et al⁴⁸).

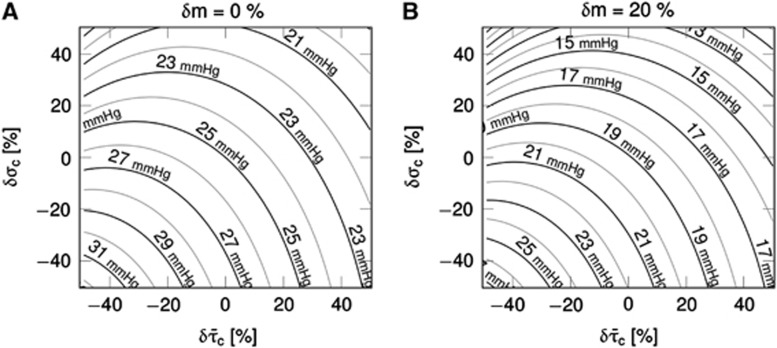
Figure 4 shows simulation results for the CTH_ss model with combinations of transit time, s.d. of the transit time distribution, and tissue pO₂ corresponding to a metabolic rate of oxygen at baseline level (panel A) and with a 20% increase in oxygen metabolism (panel B). The contour plots show the tissue pO₂ at a given 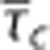pair. For example, increased oxygen metabolism causes a reduction in tissue oxygenation if hemodynamic variables are kept constant 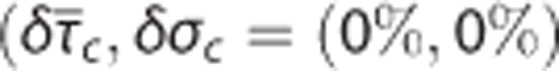(panel B). Accordingly, increased oxygen consumption can be supported by increasing blood–tissue oxygen concentration gradient, and thereby OEF. For a fixed flow response, changes in σ_c modulates the expected drop in tissue pO₂ caused by increased metabolism. Hence, the degree of heterogeneity in capillary flow patterns determines how tissue oxygenation is affected by the increased metabolic demand.

Figure 4.

Steady-state simulations in the one-compartment model incorporating the effect of capillary transit time heterogeneity (CTH; CTH_ss model). The model describe the relationship between the average capillary transit time 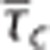the standard deviation of the capillary transit time distribution σ_c, the tissue oxygen tension, and the cerebral metabolic rate of oxygen m (equations 4 and 5). Hence, the model allows for computation of tissue oxygen tension for specified values of the variables 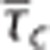σ_c, and m. The contours show tissue oxygen tension corresponding to 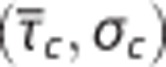pairs and m at baseline level in (A) and 20% increase in m in (B). The plots were constructed assuming baseline values: 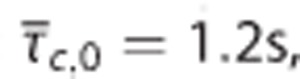and σ_c,0=0.94 s. δ denote relative changes about baseline value.

Modeling Dynamical Effects of Capillary Transit Time Heterogeneity—Simulations

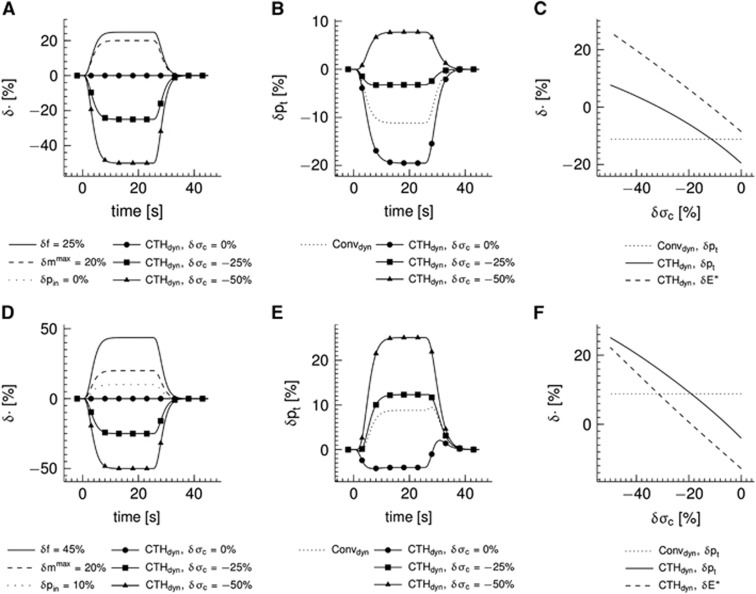
Figure 5 shows the effect of CTH as modeled by the multicompartment model (CTH_dyn model) in comparison with a conventional model (Conv_dyn model). The inlet pO₂ was fixed in panels (A–C), whereas the inlet pO₂ increased 10% in simulations presented in panels (D–F) representing decrease in upstream oxygen extraction because of flow increase. Panels A and D show the temporal dynamics of variables that served as inputs to the model. The ratio of flow/metabolism changes n was n=1.25 in panels (A–C) and n=2.25 in panels (D–F). Relative changes in tissue pO₂ are shown in panels B and E. The moderate flow response (panel A) results in a drop in tissue pO₂ of 11% for the conventional model (panel B), whereas the stronger flow response (panel D) together with increases in inlet pO₂ result in an increased tissue pO₂ in the conventional model (panel E). The tissue pO₂ is lower in the CTH model as compared with the Conv_dyn model, if σ_c is fixed at baseline value (panels B and E). However, if σ_c decreases in response to stimulation, the tissue pO₂ increases, approaches the level observed in the Conv_dyn model and finally exceeds this level (panels B and E). The solid curves in panels (C and F) show relative changes in tissue oxygenation for a range of plateau values of the σ_c response magnitude (the dotted lines mark the tissue pO₂ of the Conv_dyn model for reference). The point where the solid and the dotted curves intersect corresponds to the σ_c response magnitude at which the relative change in the apparent oxygen conductance for the capillary compartment equals zero (δE*=0%) in the CTH_dyn model. The dashed curves show relative changes in the apparent oxygen conductance of the capillary compartment in the CTH_dyn model over the range σ_c response magnitude values. A rather linear trend is observed, with the apparent oxygen conductance increasing as σ_c decreases.

Figure 5.

Simulations of temporal dynamics in the multicompartment model incorporating the effect of capillary ‘transit time' heterogeneity (CTH; CTH_dyn model) and a conventional multicompartment model for comparison (Conv_dyn model). (A, D) Temporal dynamics of dynamical variables that served as inputs to the model. Three CTH responses, characterized by different plateau values for relative changes δ in the standard deviation of the ‘transit time' distribution σ_c, are shown, whereas plateau values of the relative changes in flow f, maximum cerebral metabolic rate of oxygen m^max, and inlet oxygen tension p_in were identical for the three CTH responses. (B, E) Temporal dynamics of tissue oxygen tension p_t computed from models and the curves in (A, D). The dotted lines show tissue oxygenation response of the Conv_dyn model for reference. (C, F) Relationship observed in the CTH_dyn model between relative changes in σ_c and (i) p_t (solid line) and (ii) the apparent oxygen conductance E* (dashed line). The curves in (C, F) were constructed by tracing out plateau values (as seen in (B, E)) over a range of δσ_c. The dotted lines show p_t observed in the Conv_dyn model for reference.

Modeling Dynamical Effects of Capillary Transit Time Heterogeneity—Modeling In Vivo Data

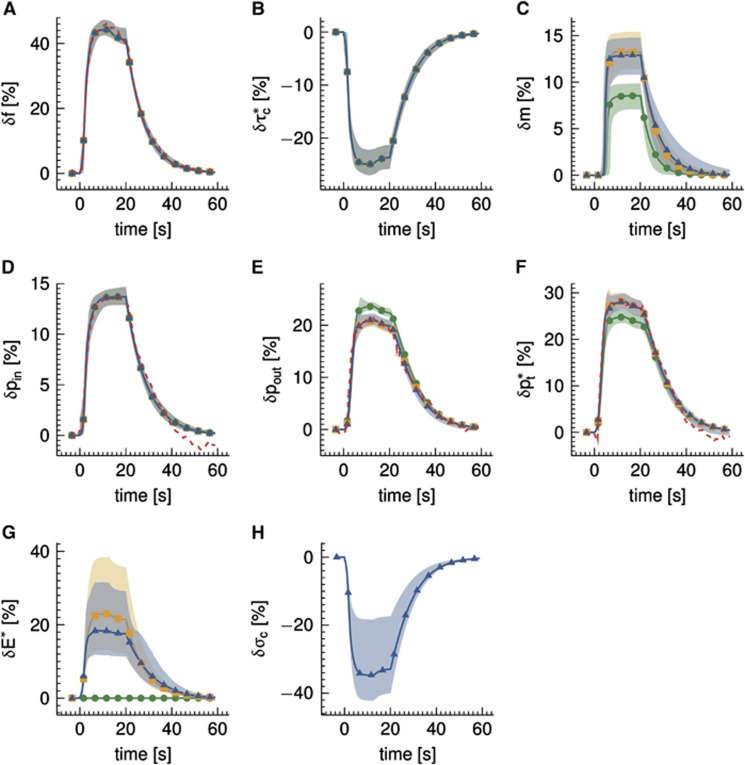
The analysis of the in vivo data set from Vazquez et al¹³ is presented in Figure 6. The data set was modeled by (i) a conventional model (Conv_dyn model), (ii) a model with dynamically varying apparent oxygen conductance (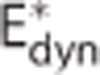 model), and (iii) a model that incorporates the effect of dynamic changes in CTH (CTH_dyn model). The dashed curves show measured data during and after an electrical stimulation epoch in the time interval (0, 20) seconds. The curves of the three models represent median model predictions based on 2,000 samples from the posterior distribution of the parameters, whereas the shaded areas show 95% credible intervals of model prediction reflecting model uncertainty. The vascular model, and hence vascular responses, was identical for all three models. The vascular model fitted the measured flow response well (panel A). Peak flow increase was 44%, the median transit time was 2.3 seconds, and the median capillary transit time 1.0 second. The dynamics of the arterial pO₂ was also identical for all oxygen transport models and in good agreement with measurements (panel D), whereas a poststimulus undershoot is observed in the measurements but not in the model because of limited model flexibility. Only the models that permitted oxygen conductance and CTH to vary fitted measured venous (panel E) and tissue (panel F) pO₂ well. The predicted changes in CMRO₂ is similar for the CTH_dyn and 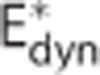models, with a relative increase of 13% (panel C), corresponding to a peak flow metabolism coupling ratio of n=3.4. The increase in CMRO₂ predicted by the Conv_dyn model was 8.8%, with n=5.0. Panel G shows the dynamic changes in E* for the model, and for the CTH_dyn model in which changes in E* are driven by underlying changes in CTH. Panel H shows the dynamics of CTH in terms of the changes in the s.d. of the ‘transit time' distribution σ_c. Note that larger model uncertainty (shaded regions) is seen for nonobserved dynamical variables (panels B, C, G and H) compared with dynamical variables where measurements are available (panels A, D, E and F). This reflects the fact that no direct additional cost is associated with this variability, as the parameter values leading to this variability conform with the prior specification. Furthermore, the models are still able to predict dynamics that comply well with the measurement data (panels A, D, E, and F).

Figure 6.

Analysis of experimental data from Vazquez et al¹³ acquired from rats with electrical forepaw stimulation in the interval (0, 20) seconds. Three multicompartment models were used to model the relative changes δ in (A) flow f, (B) ‘transit time' 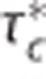defined by 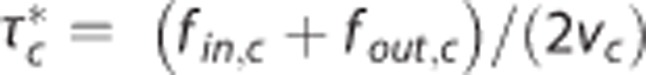(equals capillary transit time at steady state) with f_in,c and f_out,c being the inlet and outlet flow of the capillary compartment, respectively, and v_c being the volume of the capillary compartment, (C) cerebral metabolic rate of oxygen m, (D) arterial inlet oxygen tension p_in, (E) venous outlet oxygen tension p_out, (F) tissue oxygen tension 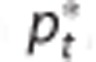, (G) apparent oxygen conductance of the capillary compartment 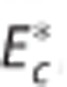, and (H) standard deviation of the ‘transit time' distribution σ_c. Conv_dyn is a conventional model (without changes in the oxygen conductance parameter), 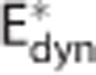is a model that includes a changing apparent oxygen conductance (E*) as an additional dynamical variable, and CTH_dyn is a model with a changing ‘transit time' heterogeneity (CTH) as an additional dynamical variable. In vivo data were available for variables in panels (A, D, E, F) only. Model curves show median simulations obtained by Markov Chain Monte Carlo (MCMC) analysis, and the shaded regions correspond to 95% credible regions reflecting model uncertainty. The vascular model and the dynamics in inlet arterial oxygen tension were held identical in all three models, hence model curves in panels (A, B, D) are identical.

Discussion

The extraction of solutes into tissue depends on the capillary distribution of blood flow.^{7, 22, 23, 24} The oxygen conductance coefficient used when describing the relation between solute extraction and blood flow in tissue by a macroscopic compartment model may therefore be interpreted as a variable that vary with transit time heterogeneity, rather than a physiologic constant for the solute and capillary bed in question. We have developed a framework for modeling the quantitative effect of transit time heterogeneity on the apparent oxygen conductance coefficient of compartment models, and found that the resulting change in oxygen extraction is consistent with dynamic recordings of CBF and oxygenation during functional activation in an animal model. Our results support earlier observations that oxygen diffusion properties seemingly change during various physiologic stimuli, and propose that this phenomenon is related in part to parallel changes in capillary flow patterns.

The Relation Between CBF and Capillary Transit Time Heterogeneity

The topology, morphology, and hemodynamics of the microvasculature are characterized by a large degree of heterogeneity.^{21, 22, 23} The heterogeneity of erythrocyte fluxes and velocities in capillaries is high, and this heterogeneity is reduced during functional activation.^{17, 18} Jespersen and Østergaard²⁴ compiled a table with estimates of mean and s.d. of transit times based on measurements of erythrocyte fluxes and velocities in rat brains. These estimates suggest that transit times homogenize as flow increases (Figure 1). To address this relation from the perspective of microvascular network properties, we extended a VAN model²⁶ to incorporate CTH. Details on this simulation are provided in the Supplementary Material. Similar to the literature reports, this extended VAN model exhibits a decrease in CTH as flow increases (Figure 1). Note that this reduced heterogeneity is ‘passive' in the sense that the capillary segments of the VAN model were not actively controlled to reduce heterogeneity. Note that Buxton and Frank⁶ observed a minor dependence of transit time heterogeneity on oxygen extraction. This may be explained by their parameterization of the transit time distribution (fixed shape parameter in gamma distribution), which entails a linear relationship between 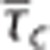and σ_c, that is, a transit times homogenization as flow increases.

Recently, advanced modeling and imaging methods have been combined to examine hemodynamic regulation within the cortical microvasculature. Microvascular network analysis has suggested that penetrating vessels may supply blood to multiple cortical columns, and that blood flow is controlled at the level of microvessels.³⁷ Two photon microscopy has shown that arteriolar vasodilation in response to functional activation propagates upstream toward the cortical surface, as well as downstream into local capillary beds.³⁸ Meanwhile, recent studies have shown that pericyte tone is actively regulated, causing capillaries to dilate approximately 1 second before the penetrating arterioles.³⁹ Indeed, it was speculated that the initial flow increase after functional activation is caused by a reduction in vascular resistance because of capillary dilation, rather than by the immediate relaxation of arteriolar smooth muscle cells.³⁹ In addition to the effects of pericyte dilation on CBF, we speculate that a flow regulation at the capillary level is part of a neurocapillary coupling that optimizes the microscopic distribution of blood during rest, and actively reduces flow pattern heterogeneity/CTH to optimize oxygen extraction during functional activation so that the metabolic needs of tissue can be met. Pries et al²³ proposed that transit time heterogeneity may facilitate a smooth modulation of solute exchange over a range of flow changes.

Capillary Oxygen Conductance: A Structural or a Physiological Property?

Previous studies have shown that conventional compartment models cannot be fitted to experimental data unless oxygen transport characteristics (dubbed ‘PS area product', ‘effective diffusivity', ‘diffusion capacity', or ‘conductance') are allowed to vary during physiologic stimuli.^{8, 9, 12, 14} It has been suggested that increased capillary oxygen tension, hematocrit, changes in blood volume, or capillary recruitment^{8, 9, 14} may explain these observations, but the existence of such mechanisms remains controversial.¹¹ Debates over whether the oxygen conductance/PS product, in this case for oxygen, can change during functional activation typically emerge from structural interpretations of this quantity.^{9, 12, 14} This misconception may date back to August Krogh who observed opening of previously closed capillaries (capillary recruitment) in tissue during stimulation. He correctly noted that this phenomenon would increase PS in proportion to the number of recruited capillaries. Since then, the reverse implication has prevailed, namely that changes in oxygen conductance/PS, as derived from the BKCR equation, are caused by changes in physical capillary surface area—that is, either opening or closing of capillaries, or diameter changes in already open capillaries. The absence of physical capillary recruitment in the brain has therefore been taken to imply that oxygen conductance for freely diffusible substances is constant despite speculations that capillary flow patterns across open capillaries may affect the efficacy of oxygen extraction.⁴⁰ Similar debates have dominated the study of other organs: in the heart it has been convincingly shown that the oxygen conductance/PS of oxygen must increase linearly with blood flow to yield satisfactory fits to experimental positron emission tomography oxygen uptake data,⁴¹ whereas no evidence of classical recruitment has been observed in heart muscle.

From the perspective of modeling, the misconception that the oxygen conductance/PS product one finds when fitting the clearance data to the BKCR equation is flow independent, originates from the generalization of single-capillary properties into models of tissue.^{7, 19, 20, 21, 22} Compartment models are convenient when we characterize tissue at a macroscopic scale, and generally apply averaged macroscopic parameters and variables such as volume flow rates, oxygen conductance/PS, and metabolic rates. In case of the BKCR equation, however, the relation between flow velocity and solute extraction in single capillaries is nonlinear, and our analysis clearly show that the distribution of flows or transit times at the capillary level must be considered when formulating compartment models, and when interpreting macroscopic parameters that were determined from fits to such models.^{21, 22} Indeed, Renkin realized that macroscopic solute clearance/extraction would be overestimated in the presence of any heterogeneity in microscopic parameters associated with vessel geometry, hemodynamics, and oxygen transport.^{7, 19, 20} In 1959, he thus pointed out that the overall PS product of a system's microvasculature would be less than the sum of single-capillary local PS products in the presence of microvascular heterogeneity.²⁰

Two topologically identical microvascular networks may yield different extraction of a diffusible substance such as oxygen depending on their capillary flow distributions.⁷ Instead of a ‘structural/physical' interpretation of the oxygen conductance/PS derived from compartment models, our analysis support the notion that oxygen conductance/PS varies, and suggest that changes in capillary flow patterns, either passively in response to increases in CBF (above), or actively, in response to pericyte dilations,³⁹ may influence this biophysical property.

Incorporating CTH into Models of Oxygenation-Based Signals

Our analysis suggests that knowledge of CTH may improve estimates of CMRO₂ based on measurements of CBF and pO₂ (Figure 3). Specifically, CTH affects the OEF and hence the estimates of CMRO₂ and the BOLD signal. Alternatively, if CBF, CMRO₂, and CTH are specified, the model allows the corresponding tissue pO₂ to be calculated (Figures 4 and 5). In existing models of neurovascular coupling, increased CMRO₂ is supported by increased CBF, and hence by an increase in the difference between blood and tissue oxygenation. In this framework, neurovascular coupling is associated with increased BOLD signals during functional activation, whereas reductions in BOLD signals, such as the initial dip, must result from either increased neuronal metabolism or an uncoupling/mismatch between CBF and CMRO₂, during which increased oxygen metabolism is accompanied by a reduction in tissue oxygenation, and a ‘passive' increase in blood–tissue pO₂ gradients. Homogenizations of capillary flow patterns provide a mechanism by which increases in oxygen metabolism can be supported by reductions in CTH—either alone or in combination increases in CBF (Figures 4 and 5). Hall et al³⁹ recently reported that pericyte dilations precede arteriolar dilation during functional activation. Meanwhile, lactate, which may form during functional activation, is also thought to relax pericytes.⁴² If we assume that capillary dilation gives rise to reduced CTH, the resulting changes in neurocapillary coupling would indeed be predicted to result in a brief, negative BOLD signal change at the onset of functional activation, and again during the washout of interstitial lactate, consistent with reports of an initial dip, and of poststimulus BOLD undershoots in relation to functional activations. We speculate that adjustment of local flow patterns may be an additional mechanism by which the vascular system can adjust oxygen availability to meet metabolic demands.

Limitations and Future Research Directions

In this study, we have developed a methodology for modeling the microscopic effect of flow pattern heterogeneity/CTH in macroscopic compartment models. By focusing on a macroscopic model, we aim at a rather simplistic description of an extremely complex underlying system. Compartment models may capture sufficient effects to account for experimental data despite their simplicity.² Future development of macroscopic compartment models may be guided by microscopic simulations and by evaluating the models' ability to describe experimental data.

Modeling oxygen transport has been a topic within microcirculatory research for many years. Model complexity range from compartment models, over Krogh cylinder models, to spatially distributed models with realistic geometry, see Goldman⁴³ for a comprehensive review. Significant gradients of pO₂ are present both within blood vessels and in tissue. Such effects are explicitly included in derivations of compartment models based on space averaging over parameters in distributed models incorporating ensembles of Krogh cylinders.^{27, 28, 44, 45} These compartment models are, similarly to the compartment model we consider, parameterized by compartment averages, that is, averaged intravascular and extravascular oxygen tensions. However, the numerical values of the oxygen conductance parameters in these models are derived in a ‘bottom up approach' from microscopic structural and functional parameters such as individual vessel diameters, radii of Krogh tissue cylinders, number of vessels, and the diffusion coefficient of oxygen. The macroscopic representation is obtained by summing contributions from identical microvessels.^{27, 28, 44, 45} This is in contrast to compartment models derived within the field of neuroimaging research, where oxygen conductance parameters are calibrated so that the models reproduce specified baseline OEFs.^{6, 25}

Although focusing on the distribution governing microscopic flow patterns, the present model only includes average tissue pO₂. Future research should address whether the assumption about average tissue pO₂ allows the macroscopic model to capture the main macroscopic effects or whether a more detailed description of tissue pO₂ including spatial heterogeneity and gradients of pO₂ is required.² The topological structure of the symmetrical VAN model used in the simulations of the CTH–mean transit time relation is relatively unrealistic. CTH was introduced in this model simply by manipulating the resistances associated with capillary segments. This is clearly a first approximation, and a rigorous approach is to consider realistic microvascular networks that naturally exhibit considerable heterogeneity in both geometry and flow rates.^{21, 22, 23} Recently, there has been an increased interest within the neuroimaging community to construct microscopic models of the brain microvascular system, where the model network topology is informed by microscopy.² Detailed analysis of such realistic microvascular networks provides estimates of the relevant microvascular parameters and their distributions. Such an analysis would also allow us to assess how realistic the distributional assumptions regarding the capillary transit time distribution are. Methods for measuring blood and tissue oxygenation and hemodynamics with high spatial and temporal resolution are also becoming increasingly available.^{46, 47} A combination of these advanced modeling and measurement techniques will allow for a detailed quantification of the distributions governing the relevant microscopic parameters and also provide insight into how these distributions change in response to activation. Such an analysis is highly relevant and is a topic for future research.

Conclusion

We modeled the effects of CTH on compartment models of the neurovascular coupling. Presence of heterogeneity influences oxygen availability and this effect mimics a change in the apparent oxygen conductance one finds by conventional compartment models. The modeling framework allows us to quantify how this oxygen conductance is affected by changes in CTH. Our results support the notion that the oxygen conductance/PS product of oxygen in compartment models may change during functional hyperemia, and ascribe this phenomenon to parallel reductions in CTH, which have been reported in the literature. Our analysis suggests that changes in CTH, either as a passive result of hyperemia, of active regulation at the capillary level, or disease are important when inferring brain function and metabolism from measurements of oxygenation-based signals.

The authors declare no conflict of interest.