Measuring Returns to Hospital Care: Evidence from Ambulance Referral Patterns

Abstract

Medicare spending exceeds 4% of GDP in the US each year, and there are concerns that moral hazard problems have led to overspending. This paper considers whether hospitals that treat patients more aggressively and receive higher payments from Medicare improve health outcomes for their patients. An innovation is a new lens to compare hospital performance for emergency patients: plausibly exogenous variation in ambulance-company assignment among patients who live near one another. Using Medicare data from 2002–2010, we show that ambulance company assignment importantly affects hospital choice for patients in the same ZIP code. Using data for New York State from 2000–2006 that matches exact patient addresses to hospital discharge records, we show that patients who live very near each other but on either side of ambulance service area boundaries go to different types of hospitals. Both identification strategies show that higher-cost hospitals achieve better patient outcomes for a variety of emergency conditions. Using our Medicare sample, the estimates imply that a one standard deviation increase in Medicare reimbursement leads to a 4 percentage point reduction in mortality (10% compared to the mean). Taking into account one-year spending after the health shock, the implied cost per at least one year of life saved is approximately $80,000. These results are found across different types of hospitals and patients, as well across both identification strategies.

Introduction

The US spends vastly more than other countries on healthcare at 18% of GDP, including close to 4% of GDP on Medicare: the public health insurance program for those over the age of 65 and the disabled (Hartman et al. 2013). Within the US, Medicare spending varies widely across hospitals, and a natural question is whether hospitals that provide more care and accrue higher Medicare spending levels actually achieve better health outcomes or whether the additional spending at high-cost hospitals is largely unnecessary due to moral hazard concerns (Baicker et al. 2012).

A main problem when estimating performance differences across hospitals is patient selection. Patients choose or are referred to hospitals based on the hospital’s capabilities: the highest-quality hospital in an area may treat the sickest patients. Alternatively, higher-educated or higher-income patients may be in better health and more likely to choose what is perceived to be a higher-quality hospital. Indeed, efforts to provide “report cards” for hospitals are often criticized for their inability to fully control for differences in patients across hospitals (Ryan et al. 2012).

This paper develops an empirical framework which allows us to compare hospital performance using plausibly exogenous variation in hospital assignment. The key ingredient of our approach is the recognition that the locus of treatment for emergency hospitalizations is, to a large extent, determined by pre-hospital factors: ambulance transport decisions and patient location. To the extent that ambulance companies are pseudo-randomly assigned to patients in an emergency, we can develop convincing measures of the impact of hospital differences on patient outcomes. In particular, we study differences in Medicare spending, which is directly related to policy and serves as a summary measure of treatment intensity.

We consider two complementary identification strategies to exploit variation in ambulance transports. The first uses the fact that in areas served by multiple ambulance companies, the company dispatched to the patient is effectively random due to rotational assignment or even direct competition between simultaneously dispatched competitors. Moreover, we demonstrate that ambulance companies serving the same small geographic area have preferences as to which hospital they take patients. These facts suggest that the ambulance company dispatched to emergency patients may serve as a random assignment mechanism across local hospitals. We can then exploit ambulance identifiers provided in national Medicare data to develop instruments for hospital choice based on patient ambulance assignment. Finally, an innovation in our approach is that we can also use these ambulance payment data to test and control for any pre-hospital differences in treatment which might independently impact outcomes.

Our second strategy considers contiguous areas on opposite sides of ambulance service area boundaries in the state of New York. In New York, each state-certified Emergency Medical Service (EMS) provider is assigned to a territory via a certificate of need process where they are allowed to be “first due” for response. Other areas may be entered when that area’s local provider is busy. We obtained the service-area boundaries for each EMS provider from the New York State Department of Emergency Medical Services, and we couple these data with a unique hospital discharge dataset that identifies each patient’s exact residential address. This combination allows us to compare those living on either side of an ambulance service area boundary. To the extent that these neighbors are similar to one another, the boundary can generate exogenous variation in the hospitals to which these patients are transported.

To carry out our primary analysis, we construct a universe of Medicare hospital claims for patients brought to the hospital for “non-deferrable” emergent conditions over the 2002–2008 period. We begin by showing that the observable characteristics of these patients are quite balanced across ambulance companies who take their patients to hospitals of very different spending levels, and that these ambulance company “preferences” are strongly associated with actual patient spending. We then show that higher-spending hospitals achieve better patient outcomes: we estimate that a one standard deviation increase in hospital reimbursement associated with an 11% reduction in emergency patient mortality compared to the mean. This finding is robust to a broad set of controls including detailed controls for treatment in the ambulance, as well as to other robustness tests. Our findings imply that the cost to the Medicare program of extending life by at least one year is approximately $80,000. These results are found across different types of patients and across different types of hospitals.

We then carry out a confirmatory analysis using the universe of elderly hospital inpatient admissions in New York State over the 2000–2006 period. Despite the fact that patient characteristics are balanced across bordering ambulance service areas with very different costs, we find that higher-cost hospitals are associated with better patient outcomes. Our estimates are similar to the Medicare analysis: a one standard deviation increase in costs is associated with a 9% reduction in mortality compared the mean.

Our paper proceeds as follows. Part I places our project in the context of the previous literature on measuring returns to hospital care and measuring hospital quality, and it describes the nature of pre-hospital care as it informs our approach. Part II discusses our empirical strategy and Part III describes the data sources. Part IV presents the basic results from Medicare data, and Part V presents comparable results from New York State. Part VI concludes.

I Background

I.1 Medicare Spending on Hospital Care

Before estimating whether high-spending hospitals achieve better health outcomes, it is useful to consider how some hospitals are able to bill Medicare more than others. The payments to hospitals are broken into two basic parts: a payment to the facility itself, and a separate payment for physician services.

Facility payments are largely determined by the well-studied Prospective Payment System (Cutler 1995, Gottlober 2001). Under this system, diagnoses and procedures performed during the hospital stay are coded by hospitals using the International Classification of Diseases (ICD) disease and procedure Classification codes.¹ An intermediary that administers the payments to hospitals from Medicare groups these Classifications into Diagnostic Related Groups (DRGs). Each DRG is assigned a weight that is associated with the level of resources associated with that DRG. This DRG weight is then multiplied by the hospitals payment rate, which is categorized as either “large urban” or “other.” These weights are further multiplied by factors that reflect (1) a wage index for the area, (2) indirect medical education costs for teaching hospitals, (3) a factor that further subsidizes hospitals that serve a “disproportionate share” of low-income patients, and (4) payments for patients whose costs are considered “outliers,” for which the hospital may appeal to CMS to be reimbursed.² We will compare patients who live near one another, so the sources of variation in spending come from the DRG, which is in turn a function of patient characteristics (illness severity, comorbidities) and provider treatment-intensity decisions (procedures performed). Smaller sources of variation come from the amount of medical education and care provided to low-income patients in the particular hospital and the extent to which there are outliers, which again is a function of patient characteristics and provider treatment intensity decisions. Controlling for the primary diagnosis and comorbidities, much of the variation should come from treatment intensity decisions, although these could be based on patient characteristics that are not fully captured by patient controls.³

The second source of variation in spending for patients admitted to the hospital comes from physician fees. These are paid on a fee-for-service basis: the more care is provided, the more physicians are paid by Medicare. In efforts to reduce Medicare spending, there is hope that by moving these payments to one that more closely resembles the prospective payment system through “bundled payments,” that Medicare can begin reimbursing hospitals for quality of care rather than volume of care (Colla et al. 2012).

In summary, within healthcare markets, hospitals can accrue higher Medicare spending by providing more intensive treatments through higher physician fees, higher DRG weights, and more outlier payments. These more intensive treatments could reflect supply or demand-side characteristics: provider preferences for treatment intensity on the supply side and underlying patient health on the demand side. Higher payments are also provided to teaching hospitals and hospitals that serve low-income populations.

I.2 Previous Literature

Our work is related to a number of cross-cutting literatures which speak to performance differences across hospitals.

I.2.1 Hospital Spending & Health Outcomes

There is a sizeable literature on spending and outcomes at the hospital level. This literature comes to mixed conclusions about the relationship between hospital spending and health outcomes (Joynt and Jha 2012). Several studies find significant returns to measures of hospital treatment intensity. Stukel et al. (2012) investigate variation in spending across hospitals in Ontario and find that higher spending due to costly interventions such as the use of specialists and more nursing care are associated with significantly lower mortality. Allison et al. (2000) find that those treated for Acute Myocardial Infarction (AMI) at teaching hospitals which tend to exhibit higher treatment intensity had roughly 10% lower mortality than non-teaching hospitals, and that this effect persisted for two years after the incident. Romley et al. (2011) document that those treated in California hospitals with the highest end-of-life spending have much lower inpatient mortality: inpatient mortality in hospitals at the highest quintile of spending is 10–37% lower than at the lowest quintile across a range of conditions. Skinner and Staiger (2009) show that hospitals that were early adopters of “home run” technologies had modestly better outcomes when they accrued higher costs, although slower-adopters did not.

Other studies suggest no returns to higher spending. Glance et al. (2010) study Nationwide Inpatient Sample (NIS) data from 2006 and find that hospitals with low risk-adjusted inpatient mortality rates are associated with lower costs. Rothberg et al. (2010) use these NIS data from 2000–2004 and find that the change in hospitals’ mortality rates and their growth in costs are uncorrelated. A middle ground is struck by Barnato et al. (2010), who find small positive returns to higher end-of-life spending in terms of lower mortality, but find that these effects fade quickly and are largely gone by 180 days after admission. These results suggest little long term benefit to higher spending.

Studies of regions within the US show large disparities in spending that are not associated with improvements in health outcomes (Fisher et al. 1994, Pilote et al. 1995, Kessler and McClellan 1996, Tu et al. 1997, O’Connor et al. 1999, Baicker and Chandra 2004, Fuchs 2004, Stukel et al. 2005, Sirovich et al. 2006, Cutler et al. 2013). Fisher et al. (2003) studied Medicare expenditure data and found that end-of-life spending levels are 60% higher in high-spending areas compared to low-spending ones in the U.S. Nevertheless, no difference is found across regions in 5-year mortality rates following a health event such as a heart attack or hip fracture. This wide variation in spending and similarity of mortality rates were again found when the sample was restricted to teaching hospitals (Fisher et al. 2004). The lack of a relationship between regional variation in spending and health outcomes has been cited in support of reducing Medicare spending by 20–30% without adversely affecting health outcomes (Fisher et al. 2009). Regional spending differences incorporate a variety of factors above and beyond the inpatient spending studied here; we return to this distinction in the conclusion.

I.2.2 Inference Problem: Patient Selection

A major issue that arises when comparing hospitals is that they may treat different types of patients. For example, greater treatment levels may be chosen for populations in worse health. At the individual level, higher spending is strongly associated with higher mortality rates, even after risk adjustment, which is consistent with more care provided to patients in (unobservably) worse health. At the hospital level, long-term investments in capital and labor may reflect the underlying health of the population as well. Differences in unobservable characteristics may therefore bias results toward finding no effect of greater spending.

Research on area- or hospital-level variation in costs recognizes the issue of patient selection. To address this concern, studies tend to focus on diagnoses where patients are likely to present with similar severity levels (e.g., heart attacks). They note that observable patient characteristics are similar across areas.⁴ For example, Cutler et al. 2013 find that demand-side factors do not explain regional variation in Medicare spending, but physician beliefs about treatment efficacy does. Further, these studies endeavor to control for patient mix with a variety of indicators of patient severity. But even the best controls based on diagnosis codes and patient characteristics are only imperfect proxies for underlying severity. Advanced risk-adjustment techniques explain less than 10% of the year-to-year variation in patient spending in the Medicare program (Garber et al. 1998). While some fraction of the unexplained variation is exogenous and therefore unpredictable, it is likely that patient decisions to seek medical treatment are driven by health factors unobservable to the researcher.

Zhang et al. (2010), for example, finds that the unadjusted correlation between pharmaceutical spending and medical (non-drug) spending across high- and low-spending Medicare regions is high (0.6), but that this finding is highly sensitive to patient controls; the correlation falls to just 0.1 when patient health status is taken into account. In addition, Doyle (2011) compared patients in Florida and again found that observable characteristics were similar across areas that had significant variation in hospital spending levels. When the analysis focused on tourists in similar destinations - a group of patients that is arguably more comparable across areas and is unlikely to affect the chosen level of treatment intensity in the area - higher-spending areas were associated with substantially lower mortality.

The use of claims-based diagnoses to control for underlying health may also be problematic because the diagnosis measures themselves could be endogenous. That is, a patient listed with many diagnoses could be in poor health or could have been treated by a provider that tends to diagnose (and record) more illnesses. For example, Song et al. (2010) find that Medicare patients who move to higher intensity regions experience a greater increase in the number of diagnoses over time compared to similar patients in the area from which they moved. Meanwhile, Welch et al. (2011) find an inverse relationship between regional diagnostic frequency rates and case fatality rates, suggesting that the marginal patient diagnosed in a high diagnosis-frequency (and high observation intensity) area may be less sick compared to patients diagnosed with the same condition in low-frequency areas. To control for underlying health differences, another direct measure is the patient’s lagged healthcare spending. Yet this too may be problematic when the goal is to describe healthcare systems as high vs. low intensity, as intensity is autocorrelated. Clearly, with the limitations of standard risk adjustment methods in mind, it is even more critical to develop a methodology that cleanly separates provider assignment from patient health.

One previous source of variation used in health economics is differential distance to the hospital as an exogenous instrument for determining hospital assignment. McClellan et al. (1994) and Cutler (2007) show that patients who live closer to (and are treated by) hospitals that perform cardiac catheterization, relative to hospitals that do not, have improved survival rates. They note that the mechanism for this improvement is likely due to “correlated beneficial care”’: superior care that is not due to the invasive procedures themselves. Geweke et al. (2003) used differential distance to study pneumonia patients in the Los Angeles area and found that large and small hospitals had better outcomes than medium-sized ones, and, related to the comparisons here, they found suggestive evidence that teaching hospitals had better outcomes than non-teaching hospitals. Chandra and Staiger (2007) employ a Roy model where physicians specialize in more intensive treatments over medical treatments if there are relatively high returns to doing so, and productivity spillovers further enhance the returns to intensive treatment. In this model, the spillover results in potentially worse outcomes for patients who would benefit most from the less-intensive treatment because the region has specialized in the intensive treatment to raise average outcomes. As a result, restricting the intensive hospitals to practice in the less-intensive style would result in worse health outcomes, despite the potential for little difference in outcomes across areas in the cross section. Using differential distance to estimate treatment effects, their empirical results support the model’s predictions.

While differential distance has proved useful, it also faces some key limitations. First, patients who live relatively close to “high tech” hospitals could be different than those who do not in ways that are difficult to control. For example, wealthier and healthier areas may demand the latest treatments, and hospitals may locate near certain types of patients. Indeed, Hadley and Cunningham (2004) find that safety net hospitals locate near the poorest patients. Additionally, hospitals may endogenously adopt technologies if they believe their patient population will benefit, and their patient population is primarily composed of those who live relatively close to the hospital. Third, exact distances are difficult to measure in most datasets, with researchers relying on distance from each patient’s ZIP code centroid to each hospital. This can affect the precision of the estimates. The current paper presents a new source of variation that is orthogonal to variation based on distance: patients who live near one another but are treated at different hospitals.

I.3 Background on Pre-Hospital Care

The key ingredient of our approach is the recognition that the locus of treatment for emergency hospitalizations is, to a large extent, determined by pre-hospital factors, including ambulance transport decisions and patient location. Among the emergency cases we consider, 61% are brought into the hospital via ambulance. In such cases, the level of care dispatched to the scene (e.g. Advanced Life Support (ALS) using paramedics vs. Basic Life Support (BLS) using Emergency Medical Technicians) may be chosen based on perceived severity (Curka et al. 1993, Athey and Stern 2002). Critically, however, in areas served by multiple ambulance companies, the company dispatched is usually chosen independent of the patient characteristics that can confound the hospital comparisons reviewed above.

Rotational assignment of competing ambulances services - as well as direct competition between simultaneously dispatched competitors - is increasingly common in the U.S. For example, two recent articles cite examples from North and South Carolina where the opportunity for ambulance transport is broadcast to multiple companies and whichever arrives there first gets the business.⁵ Similarly, large cities such as New York, Los Angeles and Chicago have adopted a hybrid approach under which private ambulance companies work in conjunction with fire departments to provide Emergency Medical Services (EMS) (Johnson 2001). Another report found that of the top 10 cities with the highest population over age 65, 5 contracted with both public and private ambulance carriers, while 2 others contracted exclusively with private carriers (Chiang et al. 2006). In a more recent 2010 survey covering 97 areas, 40 percent reported contracting with private ambulance companies and an additional 23 percent utilized hospital-based ambulance providers (Ragone 2012).

We are aware of no systematic evidence on the basis for rotational assignment of ambulances. To understand the dispatch process, we conducted a survey of 30 cities with more than one ambulance company serving the area in our Medicare data. The survey revealed that patients can be transported by different companies for two main reasons. First, in communities served by multiple ambulance services, 911 systems often use software that assigns units based on a rotational dispatch mechanism; alternatively, they may position ambulances throughout an area and dispatch whichever ambulance is closest, then reshuffle the other available units to respond to the next call. Second, in areas with a single ambulance company, neighboring companies provide service when the principal ambulance units are busy under so-called “mutual aid” agreements. Within a small area, then, the variation in the ambulance dispatched is either due to rotational assignment or one of the ambulance companies being engaged on another 911 call. Both sources appear plausibly exogenous with respect to the underlying health of a given patient.

There is some existing evidence that pre-hospital care is an important determinant of hospital choice due to the “preferences” of ambulance companies to take patients to particular hospitals. In the South Carolina example, the article explicitly points out that if an ambulance company associated with a particular hospital gets to the patient first, the patient is much more likely to be transported to that hospital.

Directly relevant to our approach is research by the New York State Comptroller’s Office in the wake of a major change in the rotational assignment of private and Fire Department of the City of New York (FDNY) ambulances in New York City. Skura (2001) found that patients living in the same ZIP code as public Health and Hospital Corporation (HHC) hospitals were less than half as likely to be taken there when assigned a private, non-profit ambulance (29%) compared to when the dispatch system assigned them to an FDNY ambulance (64%). In most cases, the private ambulances were operated by non-profit hospitals and stationed near or even within those facilities, so they tended to take their patients to their affiliated hospitals.⁶

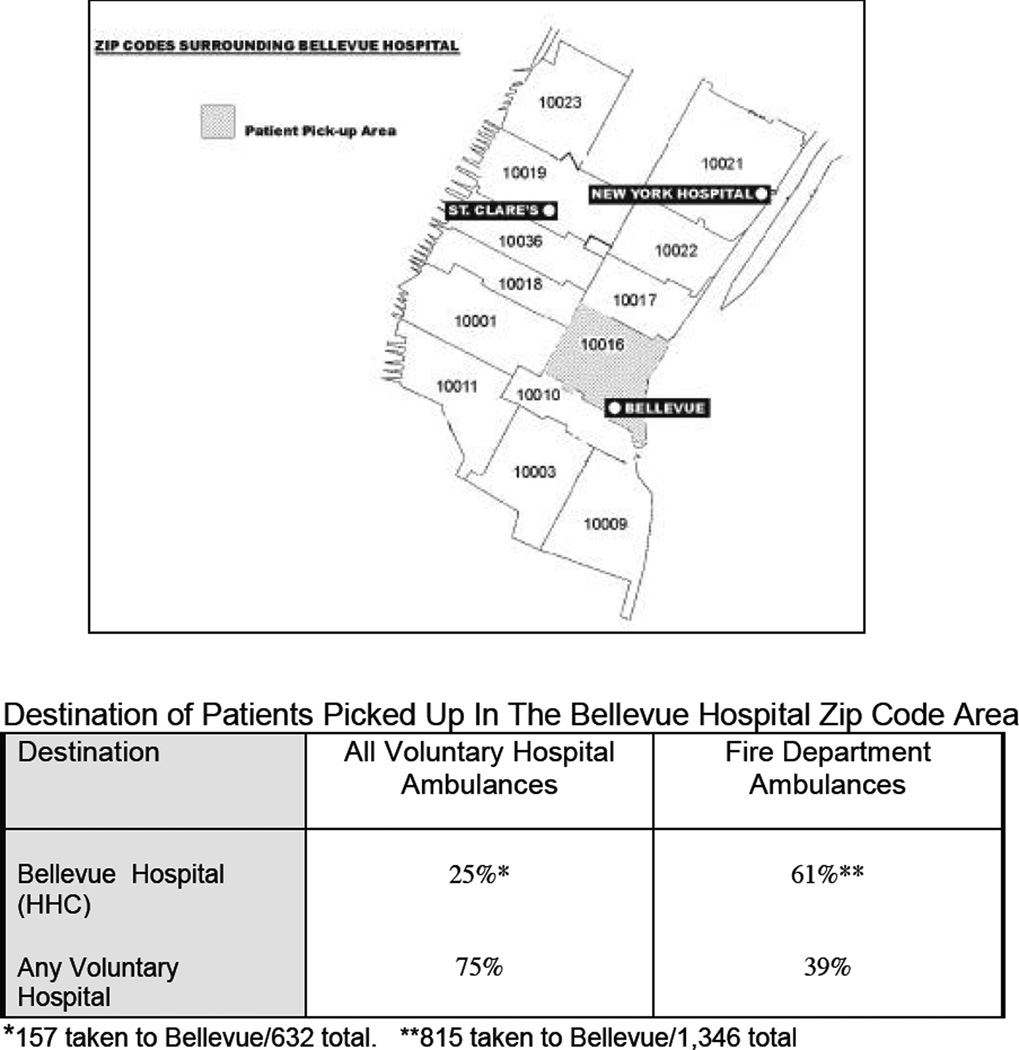
This point is illustrated in Figure 1, from Skura (2001). This figure shows the location of three hospitals, two of them private hospitals that operate ambulance service (St. Clare’s and New York Hospital) and one public (Bellevue hospital). The author examined the rate at which ambulances took patients residing in the Bellevue ZIP code to these hospitals. He found that for those picked up by FDNY ambulances, 61% were brought to Bellevue, and 39% brought to the more distant private hospitals. But for those picked up by private ambulance companies, only 25% were brought to Bellevue, and 75% to the other hospitals (Figure 1). Similar results were found for other ZIP codes within New York City as well.

Figure 1.

New York City Ambulance Referral Patterns: Skura (2001)

Source: Skura, Barry. ”Where do 911 System Ambulances Take Their Patients? Differences Between Voluntary Hospital Ambulances and Fire Department Ambulances.” City of New York, Office of the Comptroller, 2001.

In summary, ambulance dispatch rules appear to effectively randomize patients to ambulance companies. Previous case studies suggest that these ambulances have preferences about which hospital to choose. Our empirical strategy exploits this plausibly exogenous variation in the hospital choice, as described below.

II Empirical Strategy

II.1 Ambulance Referral Patterns within ZIP Code Areas

Our first approach relies on differences in ambulance referral patterns within ZIP code areas. Ambulance companies have some discretion over hospital choice, with a typical tradeoff between distance and the hospital with the most appropriate level of care. We compare patients picked up by ambulances with different tendencies to favor particular types of hospitals (characterized by their average Medicare spending) in these decisions. We then assess whether these different preferences lead to meaningful differences in the type of hospital where patient is treated.

We can illustrate that such “preferences” exist by essentially generalizing the New York City example above using variation in hospital shares across ambulance companies serving the same ZIP codes. Specifically, using observed ambulance-hospital frequencies within each ZIP code in our Medicare sample, we estimate a Chi-square test of homogeneity. Consider, for example, a ZIP code served by two hospitals in which we observe emergency patients taken to hospital h₁ 75% of the time when they are picked up by ambulance company a1, but only 33% of the time when they are picked up by company a₂. Since there are only two hospitals, it follows that we would observe 25% of a₁’s patients, and 66% of a₁’s patients, being taken to hospital h₂. Given these observed proportions, we can test whether there is statistical evidence that companies a₁ and a₂ have different patient transport patterns.

In our sample, we calculated test statistics for every ZIP code in our Medicare data with at least 5 ambulance transports by comparing observed ambulance-hospital cell frequencies to those expected under the null hypothesis, which is that ambulances distribute patients across nearby hospitals at the same rates.⁷ Among the 9,125 ZIP codes where we can calculate these statistics, 38% have test statistics with p < 0.1. This provides evidence that there appear to be differences in where patients are taken based on which ambulance company picks them up that well exceeds pure chance (which would result in less than 10% of ZIPs having test statistics with p < 0.1). This type of variation is the basis of our first-stage estimation, which we turn to next.

To operationalize ambulance preferences, we calculate an instrumental variable that measures the treatment intensity of hospitals where each ambulance company takes its patients. For patient i assigned to ambulance a(i), we calculate the average Medicare expenditure made for hospital care among the patients in our analysis sample for each ambulance company:⁸

$$Z_{a(i)}=\frac{1}{N_{a(i)}-1}\sum _{j\ne i}^{N_{a(i)}-1}{\mathit{\text{MedicareSpending}}}_j$$

This measure is essentially the ambulance company fixed effect in a model of hospital costs. We exclude the given patient from this measure to avoid a direct linkage between Z and the average spending in a given hospital – a Jackknife Instrumental Variables Estimator (JIVE) that is more robust to weak-instrument concerns when fixed effects are used to construct an instrument (Stock et al. 2002, Doyle 2007, Kolesar et al. 2011).⁹

We then use this measure to estimate the first-stage relationship between average hospital spending, H, and the instrument, Z: hospital costs associated with the ambulance assigned to patient i with principal diagnosis d(i)living in ZIP code z(i) in year t(i):

$$H_i={\alpha }_0+{\alpha }_1{Z}_{a(i)}+{\alpha }_2{X}_i+{\alpha }_3{A}_i+{\gamma }_{d(i)}+{\theta }_{z(i)}+{\lambda }_{t(i)}+{\nu }_i$$ (1)

where X_i is a vector of patient controls including indicators for each age, race, sex, miles from the ZIP code centroid, and indicators for fifteen common comorbidities; A_i represents a vector of ambulance characteristics including the payment to the company, which provides a useful summary of the treatment provided in the ambulance; indicators for distance traveled in miles; whether the transport utilized Advanced Life Support (e.g., paramedic) capabilities; whether intravenous therapy was administered; whether the transport was coded as emergency transport; and whether the ambulance was paid through the outpatient system rather than the carrier system.¹⁰ We cluster standard errors at the Hospital Service Area (HSA) level, as each local market may have its own assignment rules. This choice is relatively conservative compared to clustering at the ambulance company level instead.

We also include a full set of fixed effects for principal diagnosis, year and ZIP code.¹¹ This regression therefore compares individuals who live in the same ZIP code, but who are picked up by ambulance companies with different “preferences” across different types of hospitals (excluding the patient herself). A positive coefficient of 1 would indicate that ambulance company “preferences” are correlated with where the patient actually is admitted. Our main regression of interest is the relationship between hospital spending on mortality, M, for patient i:

$$M_i={\beta }_0+{\beta }_1{H}_i+{\beta }_2{X}_i+{\beta }_3{A}_i+{\gamma }_{d(i)}+{\theta }_{z(i)}+{\lambda }_{t(i)}+{\epsilon }_i$$ (2)

This OLS regression parallels the previous literature in modeling mortality of patient i who goes to hospital h, as a function of average hospital spending. Mortality can be measured at intervals such as 30 days, 90 days, or 1 year. As noted earlier, this regression suffers from the fact that patients may be selected into certain hospitals based on characteristics which affect their mortality. To address this, we estimate the model by instrumental variables, where the instrument is the ambulance measure discussed above. That is, we use equation (1) above as a first stage to estimate this model by instrumental variables.

II.2 Limitations

This empirical approach has four main limitations. The first is that ambulance company preferences could be correlated with underlying patient characteristics even within ZIP codes. For example, some ambulance companies could be expert at avoiding complicated cases that are likely to die, or ambulance companies may serve particular parts of a ZIP code. Our survey evidence gives us confidence that this is not the case among the relatively severe conditions considered here. Further, we investigate the extent to which observable patient characteristics differ across ambulance companies. We also address this concern to some extent in our specification checks by restricting our sample to particularly homogenous ZIP codes.

A second concern is that the approach interprets differences in spending and outcomes as stemming from different hospital assignment patterns across ambulance companies, but ambulance companies may have a direct impact on health. In particular, the companies provide treatment in the ambulance and may drive farther to reach their preferred hospital. An innovation in this project is that we study (and control for) differences in care provided by the ambulance company, including the distance traveled to the hospital, as described in detail below.

A third limitation is that results provide a local-average treatment effect for a subset of patients where the ambulance assignment matters. For example, we are unable to estimate effects for patients who always insist (and are taken to) high-spending hospitals, or for patients who would always be taken to the nearest hospital regardless of ambulance-company assignment. Related, when interpreting instrumental-variable results as a local-average treatment effect, a monotonicity assumption is also required. This could be violated if, for example, ambulance companies steer particular types of patients to different hospitals. Reassuringly, all patients considered here are relatively homogeneous: insured patients suffering from a severe emergency. The steering of uninsured patients to public hospitals, for example, is not a concern in this population.

Fourth, there could be concerns over sample selection. If high-spending hospitals are more likely to admit patients, these patients could be healthier on average. In addition, ambulance companies associated with high-spending hospitals could affect the likelihood of survival to the hospital, which would introduce its own sample-selection bias. To begin to address these concerns, we conduct a robustness check where we include all patients transported by ambulance and test whether admission rates are associated with our instrument.

II.3 Borders Approach

Our alternative approach compares patients along borders that define distinct ambulance service areas. The idea is that patients could live in the same neighborhood yet go to very different hospitals because they reside on opposite sides of a shared border. This parallels the analysis of Black (1999), who compared those living on either side of school district borders to study the impact of school quality on housing prices. For this analysis, we focus on New York State, where we have data on exact patient addresses coupled with a detailed service area grid we obtained from the New York State Department of Emergency Medical Services.

Each state-certified Emergency Medical Service (EMS) provider in New York is assigned to a territory where they are allowed to be “first due” for response via a certificate of need process, subject to the terms of New York Public Health Law (Article 30). These territories are typically delineated using county, city, town, village and fire district boundaries. Other areas may be entered when the provider is requested for mutual aid.

Using these data, we can identify census block groups in New York State on either side of an ambulance service area boundary. Census block groups are the smallest geographical units defined by the U.S. Census Bureau for which demographic information is publicly available. These block groups have an average population of 1,300 residents. Using the latitude and longitude coordinates of each patient’s residential address as recorded in our hospital discharge data, we map each patient to a unique census block group. We then identify individuals whose block group centroid is located within a defined distance of its nearest ambulance service territory border.

Specifically, we include patients residing in block groups located within 1-mile, 2-miles, and 5-miles of an ambulance service area border. The smaller distance criteria allows us to compare patients who live very near to one another and are likely a better matched comparison. The 5-mile criterion allows us to retain more rural areas, however, as block groups are constructed based on population counts and the centroid in these areas may lie outside the 1- or 2-mile restrictions.

The estimating equations parallel the earlier analysis, but now the instrument is constructed across service areas rather than ambulance companies. Rather than ZIP code fixed effects, we include matched-pair fixed effects that allow us to compare patients who live on either side of the same boundary. For patient i living in ambulance service area a(i), the first-stage model takes the form:

$$H_i={\varphi }_0+{\varphi }_1{Z}_{a(i)}+{\varphi }_2{X}_i+{\gamma }_{d(i)}+{\theta }_{p(i)}+{\lambda }_{t(i)}+{\omega }_i$$ (3)

where H_i represents the average costs in the hospital where the patient is treated, d(i) represents the patients principal diagnosis, Z_a(i) is the average hospital cost for patients living in the ambulance service area where the patient resides, and θ_p(i) is a set of dummies for each matched pair of census block groups. So this regression asks: are patients who live near a border but within an ambulance service area serviced by relatively high-cost hospitals more likely to be treated at high-cost hospitals themselves compared to those who live close to that same border but in a separate ambulance service area? Standard errors in these models are clustered at the ambulance service area level.

We can then once again estimate a mortality-cost model of the form:

$$M_i={\gamma }_0+{\gamma }_1{H}_i+{\gamma }_2{X}_i+{\gamma }_{d(i)}+{\theta }_{p(i)}+{\lambda }_{t(i)}+{\epsilon }_i$$ (4)

where we instrument for hospital costs using the first stage relationship in (3).

The borders approach augments the ambulance preference approach because differences in hospital patterns within these small areas are plausibly due to differences in ambulance dispatch patterns and not patient tastes. At the same time, there may be other factors that change at borders that could bias our findings. For example, in New York a common border used to delineate ambulance service areas is the county, and counties may differ in other factors that impact the choice of residence, such as the quality of public services.¹² Our analysis will control for differences in resident characteristics at the boundary using U.S. Census SF3 data. Of course, differences in unobserved characteristics of patients across a border from one another remain a concern.

In summary, we consider two different identification strategies using two different data sets. Each has advantages and weaknesses, but taken together they can provide insights into whether different types of hospitals achieve better outcomes.

III Data

III.1 Medicare Claims Data

Our national data are Medicare claims between 2002 and 2010. The use of these data was previously authorized under a data use agreement with the Centers for Medicare and Medicaid Services (CMS). In particular, the Carrier file includes a 20% random sample of beneficiaries, and from this file we observe the ambulance claim. We then link these claims to inpatient claims, which include standard measures of treatment, such as procedures performed, and up to 10 diagnosis codes. Patient characteristics are also recorded, such as age, race, and sex. The claims data also include the ZIP code of the beneficiary, where official correspondence is sent. In principle, this could differ from the patient’s home ZIP code. In addition, vital statistics data that record when a patient dies are linked to these claims. This allows us to measure our primary outcome measure: one-year mortality.

In addition to these usual controls in claims data, we discovered that the ambulance claims offer a new set of control variables. These data include detailed information on the mode and method of transport (Advanced Life Support vs. Basic Life Support; emergency vs. non-emergency¹³) and on specific pre-hospital interventions administered by ambulance personnel (e.g., intravenous therapy and administered drugs). While previous studies using Medicare data have been limited by their inability to control for patient location (beyond using distance from the centroid of the patient’s ZIP code), an innovation of our approach is that we also control for “loaded miles”: a billing term referring to the exact distance the ambulance traveled to the hospital with the patient on board. Finally, our Medicare claims also include an ambulance company identifier.¹⁴ This allows us to construct empirical referral pattern measures that serve as the basis for our analytic strategy.

III.2 Medicare Spending

Our key treatment measure is the level of reimbursement that Medicare pays for the hospital stay. This includes the amount paid to the hospital under the prospective inpatient payment system (the DRG price), plus any outlier and graduate medical education payments. In addition, as noted above our hospital reimbursement measure also includes Medicare Part B payments that reimburse for the physician component of patient care inside the hospital, as well as any outpatient facility provided concurrent with the inpatient stay.

In addition to our measure of reimbursement for the hospital stay, to investigate the cost per at-least one life-year saved we also use the Medicare claims to construct a measure of total Medicare spending over a one-year period that begins with the index admission. This measure is designed to capture the range of services provided to each patient that are reimbursed by the Medicare program in the year following their initial admission (e.g., inpatient and outpatient care). Due to data access limitations we were unable to include certain services (e.g., drugs covered under Medicare Part D) in either our admission-based or one-year spending measure. Finally, given the skewness of the data, we transform spending using the natural logarithm.

III.3 New York State Data

Our other major data source is the universe of inpatient hospital discharges from New York State, made available from the New York State Department of Health through the Statewide Planning and Research Cooperative System (SPARCS). These data include detailed information on patient demographic characteristics, diagnoses, and treatments, as well as a unique patient identifier that allows for longitudinal linking across facilities. A unique feature of these data is an address field that allows us to identify the exact patient residence location for 90% of the discharge records in our 2000–2006 sample (approx. 20.6 million records for all patients). These data are matched to vital statistics databases from the entire state of New York, enabling the construction of our 1-year mortality outcome measure.

The SPARCS data complement our analysis in three ways. First, because the SPARCS data include a residential address for each hospital patient, we can use narrowly defined geographic areas such as census block groups for our analysis. These smaller areas are likely to be even more homogeneous than the larger ZIP code areas. Second, these addresses allow us to match patients to narrowly defined areas located near ambulance service area boundaries. Third, the New York data allow us to compare patients throughout the age distribution and study patients not insured under Medicare.

One limitation is that Medicare reimbursement information are not available in the New York data. As a substitute, we use total hospital charges, deflated by a hospital-specific cost-to-charge ratio published each year by CMS, to form average hospital costs.¹⁵ Our inferences are similar in the Medicare data when we use this alternative measure.

III.4 Sample Construction

In both data sets, our primary sample consists of patients admitted to the hospital through the emergency room with 29 “nondeferrable” conditions where selection into the healthcare system is largely unavoidable. Discretionary admissions see a marked decline on the weekend, but particularly serious emergencies do not. Following Dobkin (2003) and Card et al. (2009), diagnoses whose weekend admission rates are closest to 2/7ths reflect a lack of discretion as to the timing of the hospital admission. Using our Medicare sample, we chose a cutoff of all conditions with a weekend admission rate that was as close or closer to 2/7ths as hip fracture, a condition commonly thought to require immediate care. Appendix Table A1 shows the distribution of admissions across these diagnostic categories. These conditions represent 39% of the hospital admissions via the emergency room, 61% of which arrived by ambulance. The reliance on ambulance transports allows us to focus on patients who are less likely to decide whether or not to go to the hospital. Table A2 reports summary statistics, and this sample is slightly older with a higher 1-year mortality rate (37%) compared to all Medicare patients who enter the hospital via the emergency room (20%). These are relatively severe health shocks, and the estimates of the effects of hospital types on mortality apply to these types of episodes. We caution against applying the results to more chronic conditions.

For our analysis of the Medicare data, we are unable to consider beneficiaries who are part of Medicare Advantage programs, as their claims are not available. These beneficiaries constitute 17% of the Medicare population in 2000 and 22% in 2008 (Kaiser Family Foundation 2010). We further limit the sample to patients during their first hospitalization under the Medicare program, in order to study outcomes after an initial health shock, and in an effort to exclude patients who may have preferences for particular hospitals due to previous hospitalizations. The patient’s hospital is recorded as the first hospital where the patient was treated even if they were subsequently transferred, as the initial hospital is more likely to be exogenous. By necessity of the empirical strategy, we limit the analysis to those patients who are brought to the emergency room by ambulance. We further remove a small number of observations with missing ZIP code information, missing ambulance company information, as well as ambulance companies, ZIP codes, or hospitals with fewer than 10 observations. One concern is that our controls for ZIP code do not well capture homogenous areas when the ZIP code is too large. We therefore restrict our sample to ZIP codes with an area of less than 100 square miles. This does not meaningfully impact the results. Last, we restrict the sample to hospitals that are within 50 miles of the patient’s ZIP code centroid. This results in a sample of 351,701 patients.

For our analysis of the New York SPARCS data, pre-hospital care is not collected so we cannot identify ambulance transports. To facilitate comparison of results using these data to the Medicare sample, we restrict the analysis to patients who enter inpatient care via the emergency room and have a principal diagnosis considered nondeferrable. Our main results will also focus on the first hospitalization in our data, as well as a restriction to Medicare patients. We also remove a small number of observations with missing address information, patients whose residence is located outside of New York State, and patients whose address could not be matched to a block group. We again restrict the sample to patients receiving care at a hospital located within 50 miles of their residential address. This results in a sample of 142,809 patients within 1 mile of an ambulance service area boundary, 213,968 patients within 2 miles of an ambulance service area boundary, and 281,036 patients within 5 miles of an ambulance service area boundary.

IV Ambulance Company Preference Results

IV.1 Balance

The key underlying assumption of our approaches is that the sources of variation in the hospital type have been purged of patient-specific factors which impact costs or outcomes. To assess whether this is true at least along observable dimensions, Table 1 shows the balance of patient characteristics across those whose ambulances tend to transport patients to relatively high-spending or low-spending hospitals available to a ZIP code area. In particular, we divide the data by quartiles of the distribution of our instrument, ambulance-level average spending levels, relative to the mean for the ZIP code to mirror the identifying variation.

Table 1.

Balance: Demographics and Comorbidities

	1st Quartile	2nd Quartile	3rd Quartile	4th Quartile
Ambulance Avg log(Hospital Spending)	8.830	8.914	8.938	9.017**
Predicted One-Year Mortality	0.333	0.332	0.332	0.333
One-Year Mortality	0.380	0.366	0.351	0.362**
Patient Age	81.461	81.277	81.330	81.394
Male	0.376	0.383	0.377	0.379
Race: White	0.888	0.885	0.885	0.880**
Race: Black	0.076	0.078	0.077	0.080**
Race: Other	0.035	0.036	0.037	0.038**
Miles Transported with Patient	7.088	6.915	6.861	7.066
Ambulance: Emergency Transport	0.655	0.673	0.673	0.656
Ambulance: Advanced Life Support	0.867	0.870	0.871	0.860
Ambulance IV Fluids Administered	0.059	0.057	0.061	0.056
Ambulance: Intubation Performed	0.002	0.002	0.002	0.002
Patient Origin: Home or Nursing Home	0.792	0.812	0.813	0.784
Comorbidity: Hypertension	0.184	0.182	0.173	0.182
Comorbidity: Stroke	0.022	0.019	0.018	0.020
Comorbidity: Cerebrovascular Disease	0.031	0.029	0.028	0.030
Comorbidity: Renal Failure Disease	0.049	0.048	0.045	0.049
Comorbidity: Dialysis	0.004	0.004	0.004	0.005
Comorbidity: COPD	0.089	0.087	0.085	0.086
Comorbidity: Pneumonia	0.060	0.056	0.055	0.057**
Comorbidity: Diabetes	0.083	0.080	0.078	0.080
Comorbidity: Protein Caloria Malnutrition	0.019	0.016	0.015	0.017
Comorbidity: Dementia	0.059	0.050	0.048	0.055**
Comorbidity: Paralysis	0.025	0.022	0.020	0.023**
Comorbidity: Peripheral Vascular Disease	0.048	0.046	0.044	0.046
Comorbidity: Metastatic Cancer	0.026	0.026	0.025	0.025
Comorbidity: Trauma	0.036	0.032	0.030	0.034**
Comorbidity: Substance Abuse	0.023	0.024	0.022	0.023
Comorbidity: Major Psych. Disorder	0.015	0.013	0.012	0.014
Comorbidity: Chronic Liver Disease	0.003	0.004	0.004	0.004

Note: N=351,701. Some ambulance measures have smaller sample sizes, largely because they are not recorded in the in the outpatient reimbursement system. N=330,607 for Ambulance measures for Advanced Life Support, IV administration and distance travelled. Columns correspond to quartiles based on the difference in ambulance company average hospital spending relative to average hospital spending in the ZIP, mirroring our estimation strategy. The last column reports significance test for difference between 1st and 4th Quartile means

^*p < 0.05;

^**p < 0.01

Source: 2002–2010 Medicare Part A Claims Data

The first row of the table lists the value of our instrument in each of the quartiles, and the top quartile shows that ambulance companies’ average hospital spending is about 20 log points higher compared to the lowest quartile. The next two rows show that while predicted mortality using all of our covariates is nearly identical across the quartiles, actual mortality declines across the quartiles, especially comparing the bottom quartile and the top three. The remaining rows shows that these four groups of patients are similar in terms of their overall health and demographic characteristics. While differences can be statistically significant given the large sample size, they are arguably not economically significant. The patient demographics are similar across the quartiles, as are the recorded comorbidities. The travel distances are particularly similar, suggesting that ambulances do not drive farther to get to hospitals that tend to spend more. Meanwhile, the distribution of principal diagnoses is similar across these categories (Table A3). At least in terms of observable characteristics, our sample appears well balanced.

IV.2 First Stage Relationship: Ambulance Company Affects Hospital Choice

Table 2 shows the first-stage results for our ambulance company preference instrument, equation (1) above. We begin by estimating the relationship between average hospital spending at the patient’s hospital and the average hospital spending associated with the ambulance company assigned to the patient, controlling only for year and ZIP code fixed effects. There is a very strong correlation between the two, suggesting that if the ambulance company that tends to take other patients to 10% more expensive hospitals, the hospital where the patient is taken has 1.7 higher average hospital spending, and this difference is highly statistically significant. The subsequent columns add controls for patient and ambulance characteristics. The result is remarkably robust to these additional controls.

Table 2.

Ambulance Strategy: First Stage

Dependent Variable: Avg. log(Hospital Spending)	(1)	(2)	(3)	(4)
Ambulance Average log(Hospital Spending)	0.169	0.168	0.166	0.166
	(0.008)**	(0.008)**	(0.008)**	(0.008)**
Observations	351,701	351,701	351,701	351,701
Diagnosis Controls	Yes	Yes	Yes	Yes
Demographic Controls	No	Yes	Yes	Yes
Ambulance Controls	No	No	Yes	Yes
Comorbidity Controls	No	No	No	Yes
ZIP Code Fixed Effects	Yes	Yes	Yes	Yes

Note: Estimates reported for Equation (1) in the text. All models include ZIP code and year fixed effects. Patient controls include indicators for year of age, race, sex, miles from the ZIP code centroid, and comorbidities. Ambulance controls are listed in Table 1. Standard errors in parentheses, clustered at the HSA level.

^*significant at 5%;

^**significant at 1%

Source: 2002–2010 Medicare Part A Claims Data

The first stage coefficient yields insights into the source of variation employed by this empirical strategy. Consider variation from mutual-aid agreements: when the “main” ambulance company is busy, another ambulance company (either a private ambulance possibly coming from a hospital or an ambulance from a nearby area) is called in to help. The instrument measures the spending level of the hospitals where that ambulance company takes other patients, and most of these will be from the company’s usual area, by definition. A positive first-stage coefficient that is less than one says that these ambulances are significantly more likely than the main ambulance company to take the patient back to their usual hospital, but not as often as they take their usual patients: the mutual aid area likely has other nearby hospitals in the choice set.

IV.3 Hospital Spending and Patient Mortality

Table 3 shows the results of estimating equation (2) by OLS. We find a significant negative correlation between hospital spending and mortality. The results suggest that raising spending 10% (or $800) would lower one-year mortality by 0.2 percentage points (or about 0.5% of baseline mortality) in our richest specification. As noted earlier, patient selection could result in an upward or downward bias. This may explain the sensitivity of the results to include demographic controls; the coefficient falls by half between columns (1) and (2), and then again in half when we control for ambulance characteristics. This suggests that higher spending hospitals treat healthier patients in terms of age, sex, and recorded comorbidities and whose ambulance characteristics are associated with lower mortality.

Table 3.

Ambulance Strategy: One Year Mortality & Hospital Spending

Dependent Variable: 1-Year Mortality	(1)	(2)	(3)	(4)
Panel A: OLS
Avg. log(Hospital Spending)	−0.069	−0.034	−0.018	−0.020
	(0.007)**	(0.007)**	(0.007)*	(0.007)**
Observations	351,701	351,701	351,701	351,701
Outcome Mean	.364	.364	.364	.364
Panel B: 2SLS
Avg. log(Hospital Spending)	−0.235	−0.210	−0.188	−0.187
	(0.063)**	(0.059)**	(0.059)**	(0.056)**
Observations	351,701	351,701	351,701	351,701
Outcome Mean	.364	.364	.364	.364
Diagnosis Controls	Yes	Yes	Yes	Yes
Demographic Controls	No	Yes	Yes	Yes
Ambulance Controls	No	No	Yes	Yes
Comorbidity Controls	No	No	No	Yes
ZIP Code Fixed Effects	Yes	Yes	Yes	Yes

Note: Estimates reported for Equation (2) in the text. All models include ZIP code and year fixed effects. Patient controls include indicators for year of age, race, sex, miles from the ZIP code centroid, and comorbidities. Ambulance controls are listed in Table 1. Standard errors in parentheses, clustered at the HSA level.

^*significant at 5%;

^**significant at 1%

Source: 2002–2010 Medicare Part A Claims Data

The next set of rows report the 2SLS estimates and the point estimates are much larger in magnitude: a 10% rise in spending is associated with a 2.4 percentage-point lower mortality rate, or about 6% of baseline mortality. Unlike the OLS results, these 2SLS results are more robust to the inclusion of controls; the estimates fall by only 20% from the first to the last column, and are statistically indistinguishable, albeit partly due to larger 2SLS standard errors.

To put the estimate in context, this result implies that a one standard deviation increase in average hospital spending, an increase of 0.2 log points or approximately $1800, is associated with a 3.7 percentage-point reduction in mortality, or 10% of the sample mortality rate. Thus, we find compelling evidence that higher-spending hospitals have significantly lower patient mortality, at least for emergency admissions. We consider the cost per life year saved below.

IV.4 Robustness & Specification Checks

IV.4.1 Sample Selection

We next explore tests designed to address our key identifying assumptions. One concern is that we are only considering patients who have been admitted to the hospital, and not other patients picked up by the ambulance company. If, for example, the most expensive hospitals admit more patients who are healthier on average, such selection could bias the results.¹⁶

To address this concern, we extend our analysis to consider every patient picked up by an ambulance, regardless of whether or not they are admitted. In particular, we divide all ambulance pickups into those who are admitted, those who leave after visiting the ER, and those who are brought into the hospital on “observation status”.¹⁷ Figure A1 displays the odds of each discharge status against the percentiles of our ambulance instrument. For most of the range of our instrument, there is no meaningful correlation between the instrument and being admitted inpatient.¹⁸

IV.4.2 ZIP Code Characteristics

A related concern is ZIP code heterogeneity: some ambulance companies may serve only a certain part of a ZIP code, and these ambulance companies may disproportionately take their patients to particular hospitals. For example, an ambulance company that serves a higher-income part of a ZIP code could be more likely to take patients to high-spending hospitals. In that case, comparisons of outcomes across ambulance companies would include differences in the patients they serve. We can address this concern to some extent in our specification checks by restricting our sample to particularly homogenous ZIP codes using the Summary File 3 (SF3) file issued by the U.S. Census. By restricting our analysis to ZIP codes with little within-ZIP code variation in demographic characteristics such as household income and racial composition, we hope to minimize the potential for ambulance selection within a ZIP code.

The results of doing so are shown in the Panel A of Table 4. We divide ZIP codes into quartiles based on the standard deviation of income (so a higher value implies a more heterogeneous ZIP code) and the Herfindahl index for racial composition (so a higher value implies a more homogenous ZIP code). In both cases we find no systematic pattern of results across types of ZIP codes. Indeed, in both cases it appears that the effects are largest in ZIP codes that are neither the most heterogeneous nor the most homogenous. This suggests that ambulance-company sorting to neighborhoods within heterogeneous ZIP codes is not driving the main results.

Table 4.

Ambulance Strategy: 2SLS Results for Subgroups

Dependent Variable: 1-Year Mortality	Coefficient	S.E.	Obs.	Mean 1-Year Mortality
A. ZIP Code Characteristics
Income: Standard Deviation
Bottom Quartile	−0.145	(0.104)	86,377	0.370
2nd	−0.206	(0.11)	86,684	0.364
3rd	−0.287	(0.106) **	86,056	0.362
Top Quartile	−0.089	(0.095)	86,036	0.360
Race HHI
Bottom Quartile	−0.118
2nd	−0.216	(0.098)	86,052	0.372
3rd	−0.407	(0.106) *	86,980	0.365
Top Quartile	−0.131	(0.126) **	86,974	0.363
B. Patient Characteristics		(0.106)	85,145	0.358
Age
65–74	−0.091	(0.098)	75,288	0.274
75–84	−0.312	(0.093) **	147,891	0.334
85–94	−0.192	(0.097)	114,243	0.436
95+	−0.07	(0.324)	14,362	0.589
Diagnosis Mortality Rate Quartile
Bottom Quartile	−0.196	(0.077) *	129,381	0.204
2nd	−0.286	(0.133) *	80,550	0.359
3rd	−0.409	(0.15) **	65,022	0.393
Top Quartile	−0.014	(0.118)	76,901	0.618
Diagnosis Category
Circulatory	−0.331	(0.113) **	87,431	0.372
Respiratory	−0.177	(0.134)	74,053	0.490
Digestive	−0.208	(0.233)	25,488	0.255
Injury	−0.17	(0.133)	67,633	0.239
All Other	−0.178	(0.102)	97,219	0.377
C. Hospital Characteristics
Teaching	−0.299	(0.117) *	158,872	0.357
Non-Teaching	−0.207	(0.121)	140,325	0.372
For Profit	−0.189	(0.105)	175,047	0.368
Not For Profit	−0.239	(0.101) *	176,633	0.361
High Process Quality	−0.274	(0.132) *	183,385	0.369
Low Process Quality	−0.223	(0.461)	59,983	0.351
High Tech (Top 10%)	−0.652	(0.387)	50,344	0.377
Not High Tech	−0.199	(0.073) **	271,486	0.362
D. Ambulance Characteristics
Patient at Home or Nursing Home	−0.223	(0.085) *	281,577	0.381
Patient Not at Home or Nursing Home	−0.144	(0.067) *	70,130	0.301
E. Instrument Calculation
Varies at Ambulance Co. × Disease Level	−0.217	(0.194)	294,200	0.365

Note: Total sample N= 351,701, though sample sizes for each subgroup set may not add to 351,701 due to some sample loss from small ZIPs without sufficient subgroup sample sizes to fit ZIP fixed effects. Each cell represents a separate model. All models include full controls. Standard errors in parentheses, clustered at the HSA level. ZIP code characteristic cells are for ZIP codes with available 2000 US Census data.

^*significant at 5%;

^**significant at 1%.

Source: 2002–2010 Medicare Part A Claims Data

IV.4.3 Heterogeneity Across Patients & Hospitals

Table 4 reports further estimates across patient and hospital characteristics. This allows us to consider whether hospital spending has heterogeneous treatment effects and also serves to consider the robustness of the results.

Panel B shows heterogeneity of results by patient age and disease category. The results are not monotonic by either age or predicted mortality rate of the diagnosis. The effects are largest for the third quartile of predicted mortality, before dropping to zero for the fourth quartile. This top quartile is dominated by septicemia, an indication of a serious infection anywhere in the body where there may not be returns to higher spending. In terms of disease categories defined in Table A1, the results are particularly large for circulatory diseases, and relative constant across the other categories.

Panel C considers different hospital characteristics. To do so, we rerun our regressions within alternative selected sets of hospitals: teaching hospitals (as defined by the Council on Teaching Hospitals) vs. non-teaching hospitals; for-profit vs. non-profit; hospitals which are measured by the Centers for Medicare and Medicaid Services as having high process quality vs. not;¹⁹ and whether hospitals are or are not at the leading edge of technology adoption.²⁰ While the standard errors are fairly large, the estimates are strikingly similar across all of these types of hospitals. The largest estimates are for hospitals which are at the leading edge of technology adoption. This suggests that the marginal returns to spending may be higher in more technically advanced hospitals.

Panel D considers an alternative thought experiment. Consider someone who suffers a health shock when he is away from home and happens to be close to a high-spending hospital compared to a similar individual who happens to be close to a low-spending hospital. We observe patients who are picked up by an ambulance when they are away from home at the time when they may be subject to this natural experiment. Unfortunately, we do not observe the ZIP code where the patient experienced the health shock, however. As a result, we must use the residence ZIP code of the patient as a control in our models, adding noise to the estimates.

Nonetheless, as we show in the final panel of Table 4, there are strong impacts of hospital spending on mortality both for those picked up at home and for those picked up away from home. The results are stronger for those picked up at home, but that may reflect the fact that we have a more precise measure of the risk set of potential hospitals to which they might have been taken. The similarity of the results suggests that patients picked up away from home, who are less likely to be able to direct their hospital choice, have better outcomes if they are treated at higher-spending hospitals.

Finally, one issue that arises with this type of instrument is that the monotonicity assumption to interpret the results in a LATE framework need not be satisfied. In this context, ambulance companies could be more likely to take certain types of patients to high-spending hospitals, but less likely to take other types of patients to those hospitals. In speaking with EMS technicians, this did not seem to be the case for serious emergencies considered here. As noted above, this is an insured population, so there are fewer concerns with regard to “dumping” uninsured patients on other hospitals. To further investigate this issue, we calculated the instrument for each ambulance-company by disease-category cell rather than at the ambulance- company level. This estimation allows ambulances to direct patients differentially by type of illness but retain the LATE interpretation.²¹ Panel E of Table 4 shows that the results are similar when we allow the instrument to vary at the disease-type level. It is also reassuring that similar results are found across broad measures of disease categories as shown earlier in the Table.

IV.5 Mechanisms

The results show that when similar patients are treated at high-spending hospitals, they are more likely to survive to one year. To unpack this overall result, we investigated the sources of the overall spending differences. First, we find similar results when we consider the number of procedures typically performed by the hospital. This is not surprising given that Medicare pays hospitals more when they treat patients more aggressively through higher-paying diagnosis-related groups and higher physician fees. We also considered different payment categories that sum to the overall spending measure: payments stemming from the diagnosis-related group (DRG) paid to the hospital itself, outlier payments, physicians payments, and graduate medical-education payments. We find lower mortality rates at hospitals with higher physician payments and higher outlier payments, both of which are related to higher levels of treatment intensity. DRG payments do reflect differences in treatment intensity but also differences across diagnoses, and these diagnosis differences are largely soaked up by the diagnosis fixed effects in our specification. In the end, Medicare pays hospitals more when physicians treat patients more intensively, and these higher-intensity hospitals have lower mortality. The results of this analysis are shown in Appendix Table A4.

IV.6 Interpretation: Cost per Life Year Saved

One way to interpret the size of the estimates is to consider the cost per (at least) one year of life saved. High spending at the time of the initial health shock may lead to higher spending over the course of that year if initial spending is a complement to later spending (in part because patients are more likely to survive), or initial spending may lower costs over the course of the year as it substitutes for care later in the year: patients may be discharged healthier if they are treated in a high-spending hospital.

We first calculated one-year spending on inpatient and outpatient claims, including the spending on the initial episode.²² We then estimated the relationship between one-year spending and initial hospital spending analogous to the mortality models. Table 5 reports that a 10% increase in initial hospital spending leads to a 6% increase in one-year spending, or approximately $1500. The earlier results showed that this also leads to a 1.9 percentage-point reduction in one-year mortality. As a result, the cost per (at least) one life year saved is approximately $80,000.²³ As a comparison, similar estimates of the cost per life year have been found for cardiac catheterization ($62,500 in 1996 dollars by Chandra and Staiger (2007) and $70,000 in 1987 dollars by McClellan and Newhouse (1997). Thus, our estimates are consistent with previous literature with sizeable marginal returns to intensive medical interventions for emergency care relative to standard value of statistical life-year benchmarks of $100,000 to $200,000.

Table 5.

One-Year Spending

Dependent Variable: log(One-Year Spending)	(1)	(2)	(3)	(4)
Average log(Hospital Spending)	0.594	0.569	0.624	0.623
	(0.111)**	(0.112)**	(0.115)**	(0.114)**
Observations	351,701	351,701	351,701	351,701
Outcome Mean	10.1	10.1	10.1	10.1
Diagnosis Controls	Yes	Yes	Yes	Yes
Demographic Controls	No	Yes	Yes	Yes
Ambulance Controls	No	No	Yes	Yes
Comorbidity Controls	No	No	No	Yes
ZIP Code Fixed Effects	Yes	Yes	Yes	Yes

Note: Estimates reported for Equation (2) in the text. All models include ZIP code and year fixed effects. Patient controls include indicators for year of age, race, sex, miles from the ZIP code centroid, and comorbidities. Ambulance controls are listed in Table 1. Standard errors in parentheses, clustered at the HSA level.

^*significant at 5%;

^**significant at 1%

Source: 2002–2010 Medicare Part A Claims Data

V Border Results for New York State

V.1 Balance

In this section, we turn to the second empirical strategy, relying on comparisons of individuals living in close proximity but on either side of ambulance service territory borders in New York State. Once again, we begin by showing that these samples are similar in terms of observed characteristics. In Table 6 we divide each pair of census block groups in New York into those on the low-cost side of an ambulance border, and those on the high-cost side.²⁴ We find an 8 to 11 log point difference in hospital cost, on average between these two groups, depending on the sample. The remaining rows again show relatively well-balanced compositions of the groups in terms of our control variables. Little difference is found for age, sex, and demographics (see a more detailed set of comorbidity comparisons in Table A5), while the high-cost side is associated with a larger fraction of African American patients. Also, while it is notable that the distance from the patient’s home census block-group to the hospital, is 0.25 miles shorter for patients on the high-cost side in the 1-mile sample; this difference fades away, and is not seen in the sample of patients within 5 miles of a boundary. In summary, the predicted mortality rate using the observable characteristics are remarkably similar across these groups.

Table 6.

Patient Characteristics Across Borders (block groups)

Sample:	Census Block Groups within 1- mile of a Border		Census Block Groups within 2- miles of a Border		Census Block Groups within 5- miles of a Border
	Low Cost Side	High Cost Side	Low Cost Side	High Cost Side	Low Cost Side	High Cost Side
Mean Area log(Spending)	8.658	8.763**	8.657	8.757**	8.675	8.752**
Age	78.6	78.5	78.5	78.4	78.6	78.4*
Age < 65	0.060	0.064	0.062	0.066*	0.062	0.067**
Age >=65 & <70	0.116	0.117	0.118	0.120	0.117	0.120
Age >=70 & <75	0.144	0.144	0.145	0.145	0.142	0.144
Age >=75 & <80	0.186	0.189	0.187	0.188	0.185	0.187
Age >=80 & <90	0.372	0.364	0.370	0.359**	0.369	0.359**
Age >= 90	0.122	0.122	0.120	0.122	0.125	0.124
Share African American	0.063	0.108**	0.069	0.116**	0.081	0.119**
Share Asian	0.008	0.021**	0.011	0.018**	0.021	0.018
Share Hispanic	0.028	0.027	0.030	0.028	0.030	0.025*
Share Other Race	0.028	0.040	0.029	0.041*	0.025	0.037*
Share Nat. Amer	0.001	0.001	0.001	0.001	0.001	0.001
Share Male	0.383	0.385	0.385	0.384	0.383	0.382
Distance travelled	3.977	3.727	4.126	3.915	3.958	4.001
Predicted Mortality	0.235	0.237	0.236	0.237	0.236	0.237
Median Income	33293	32092	32061	30949	30680	29672
Share Owner Occ. Housing	0.866	0.861	0.864	0.871	0.856	0.879**
Share Urban	0.971	0.973	0.941	0.940	0.930	0.926
Number of Cross-border Pairs	336		482		583

Areas represented are distances from US Census Block Group centroids to an ambulance service-area boundary.

2000–2006 SPARCS Inpatient Data

^*significant at 5%;

^**significant at 1%

Since individuals may differ if they choose to live on one side of the boundary the other, we can also consider differences in characteristics of the block groups in which they reside. In the final rows of Table 6, we find that block groups on adjacent sides of these borders are similar in terms of characteristics such as income, share owner-occupied housing, and share urban, though we find slight differences in the share of owner occupied housing for the 5-mile sample.

V.2 Basic Results

Patients are more likely to attend a hospital located within their area. Specifically, for patients with a hospital located in their area: 72% of patients living within one mile of an ambulance service area border are treated at a hospital within this same area, and this rate increases to 75% and 78% for those living within 2 and 5 miles of a border, respectively. This is borne out in the first-stage relationship reported in Table 7. The point estimates range between 0.63 and 0.74, with F-statistics that range from 12.8 to 18.1. Table 7 also reports the OLS and 2SLS results for the relationship between one-year mortality and hospital costs. As for the national Medicare results, the NYS OLS results are sensitive to controls; indeed, adding controls moves the coefficients from an insignificant positive estimate to a significant negative estimate. These findings indicate substantial selection bias in OLS.

Table 7.

NYS First Stage, OLS and 2SLS (block groups)

A. Dependent Variable: Mean Area log(Spending)
	1 mile		2 miles		5 miles
	(1)	(2)	(3)	(4)	(5)	(6)
Ambulance Dispatch Area:	0.715	0.738	0.671	0.678	0.627	0.632
Mean Area log(Spending)	(0.207)**	(0.206)**	(0.181)**	(0.177)**	(0.153)**	(0.148)**
Year Controls	Yes	Yes	Yes	Yes	Yes	Yes
Demographic Controls	No	Yes	No	Yes	No	Yes
Diagnosis and Comorbidity Controls	No	Yes	No	Yes	No	Yes
Observations	142809	142809	213968	213968	281036	281036
Mean of Dep. Var.	8.700	8.700	8.701	8.701	8.715	8.715
B. Dependent Variable: 1-year Mortality
	1 mile		2 miles		5 miles
	OLS		OLS		OLS
	(1)	(2)	(3)	(4)	(5)	(6)
Mean Area log(Spending)	0.009	−0.015	0.014	−0.012	0.015	−0.016
	(0.010)	(0.008)*	(0.010)	(0.007)	(0.008)	(0.007)*
	2SLS		2SLS		2SLS
	(1)	(2)	(3)	(4)	(5)	(6)
Mean Area log(Spending)	−0.046	−0.054	−0.038	−0.047	−0.040	−0.047
	(0.031)	(0.023)*	(0.028)	(0.024)*	(0.024)*	(0.020)*
Year Controls	Yes	Yes	Yes	Yes	Yes	Yes
Demographic Controls	No	Yes	No	Yes	No	Yes
Diagnosis and Comorbidity Controls	No	Yes	No	Yes	No	Yes
Observations	142809	142809	213968	213968	281036	281036
Mean of Dep. Var.	0.236	0.236	0.236	0.236	0.236	0.236

Panel A reports estimates from Equation (3) in the text, and Panel B reports estimates from Equation (4). All models include boundary fixed effects. Demographic controls include indicators for age, race, sex, miles from the hospital to the block-group centroid, and US Census block-group characteristics. Diagnosis controls include the patient’s three-digit principal diagnosis code. Comorbidities included are those listed in Table A5 aggregated into 4 categories by diagnosis type. Standard errors in parentheses, clustered at the ambulance service-area level.

^*significant at 5%;

^**significant at 1%

2000–2006 SPARCS Inpatient Data

As with the national sample, however, the estimates increase in magnitude when we use a 2SLS approach. Using the border strategy, we find that a 10% increase in costs is associated with a 0.005 percentage point reduction in mortality, or about 2% of baseline mortality rate.²⁵ This result implies a one standard deviation increase in average hospital costs is associated with a 2.1 percentage point reduction in mortality, or 8.9% of the baseline mortality rate.²⁶ These results reinforce our findings from the ambulance company preference strategy, as we again find compelling evidence that higher-cost hospitals have lower mortality for emergency admissions.²⁷

One extension that is available in New York is our ability to look at the impacts of hospital costs on the non-elderly. To do so, we replicate our existing strategy for the non-elderly sample, ages 18–64, and the “near elderly,” ages 50–64 (see Appendix Tables A6 and A7). For both samples, we restrict analysis to the same non-deferrable conditions analyzed in the Medicare sample. We find similar first-stage estimates in these samples, and the OLS results are again sensitive to controls. In contrast to the results for the elderly, we find no statistically significant impacts on mortality using 2SLS. As with the elderly, however, point estimates for the 2SLS results are roughly twice as large in magnitude relative to the OLS estimates. In addition, the point estimates imply a substantial mortality-cost relationship. For both groups, a standard-deviation increase in hospital costs is associated with a 6–15% reduction in mortality compared to the sample mean mortality rate, magnitudes which are mostly within the range of the New York Medicare sample.²⁸

Third, we explored how the results differ by disease category. Table A8 shows sizable reductions in mortality for circulatory, respiratory, and injuries, with little effect found for digestive and other disorders. Further, when the principal diagnosis is used to construct predicted mortality quartiles, the point estimates suggest similar results across the top three quartiles.

VI Conclusions

As we move from compensating healthcare providers on the basis of the quantity of care to the quality of care, it is more important than ever to measure hospital performance. A key limitation is the potential for confounding due to patient selection, even after risk adjustment. We show that plausibly exogenous assignment of emergency patients to ambulance companies is related to hospital choice. This need not have been the case if, for example, ambulance companies always took patients to the nearest hospital. Further, we show that for patients who live near the boundary of an ambulance service area, their location relative to the boundary matters for the hospital choice, even for patients who live very close to those boundaries.

Our results suggest that hospital choice does matter for patient survival. Using a summary measure of treatment intensity, a one standard deviation increase in hospital spending is associated with a 10% reduction in mortality compared to the mean using both of our estimation strategies. This implies that the cost to Medicare per (at least one) life year saved for these emergency patients is in the range of $80,000. We show that these results are robust to a number of tests of our identifying assumptions, and are comparable with both identification strategies.

While our specification and robustness checks suggest that differences in hospital assignment drive the main result, there remain important limitations to the empirical approach. One particular limitation is that the results apply to patients whose the ambulance assignment matters for hospital choice: a local average treatment effect. We view the results as particularly relevant to hospital choice decisions, however, as they apply to cases where there is some discretion over where a patient may be treated. In addition, the results necessarily apply to emergency cases, and future research that extends this analysis to the non-emergent population would be particularly fruitful.

Finally, future work on the mechanisms that underlie these findings is critical. It may well be that high-spending hospitals could achieve similar mortality rates at lower costs as they become more efficient. The results here do suggest caution when considering a reduction in Medicare spending for patients receiving emergency care.