Significance
Hair bundles are the sensory antennae that detect different types of mechanical signals in diverse sensory systems of vertebrates. Here we design and use a mechanical-load clamp to show that the mechanical properties of hair bundles and their accessory structures dictate their sensory behaviors. By demonstrating how the same organelle can be used to detect a wide gamut of signals, this study reveals both the versatility and essential similarity of hair bundles across receptor organs. These observations reveal a general principle that may be used by both biological and artificial systems: by adjustment of only a few key parameters, a nonlinear system can be controlled to serve many different functions.
Keywords: auditory system, dynamical system, hair cell, Hopf bifurcation, vestibular system
Abstract
Hair cells, the sensory receptors of the internal ear, subserve different functions in various receptor organs: they detect oscillatory stimuli in the auditory system, but transduce constant and step stimuli in the vestibular and lateral-line systems. We show that a hair cell's function can be controlled experimentally by adjusting its mechanical load. By making bundles from a single organ operate as any of four distinct types of signal detector, we demonstrate that altering only a few key parameters can fundamentally change a sensory cell’s role. The motions of a single hair bundle can resemble those of a bundle from the amphibian vestibular system, the reptilian auditory system, or the mammalian auditory system, demonstrating an essential similarity of bundles across species and receptor organs.
The hair bundles of vertebrates are mechanosensory organelles responsible for detecting sounds in the auditory system, linear and angular accelerations in the vestibular system, and water movements and pressure gradients in the lateral-line system of fishes and amphibians (1, 2). In each instance an appropriate stimulus deflects the bundles, depolarizing the hair cells from which they emerge (3). Hair bundles are not simply passive detectors, however, for they actively amplify their responses to mechanical stimulation (4, 5). Hair-bundle motility contributes to an active process that endows the auditory system with the ability to detect stimuli with energies near that of thermal fluctuations (6), to distinguish tones that differ by less than 0.2% in frequency (7), and to accommodate inputs varying over a millionfold range in amplitude (4, 8–11).
Auditory, vestibular, and lateral-line organs respond to distinct patterns of mechanical input. The mechanical properties and environments of hair bundles differ correspondingly between different organisms, among receptor organs, and with the tonotopic position along individual auditory organs (12–15). A mathematical model predicts that the response of a hair bundle is regulated both by its intrinsic mechanical characteristics and by its mechanical load (16). Motivated by this proposition, we investigated how the load stiffness and constant force imposed on a bundle control its dynamics and response to external perturbations.
Results
Mapping the Hair Bundle’s Experimental State Diagram.
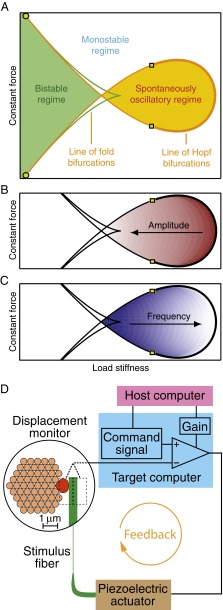
The hair bundle’s state diagram characterizes its behavior for different combinations of two control parameters: load stiffness, or force per unit displacement, and constant force. These control parameters describe the mechanical load imposed on a hair bundle within a sensory organ. A theoretical model of hair-bundle dynamics predicts the qualitative structure of the state diagram (Fig. 1 A–C). To test this prediction experimentally, we varied the mechanical load imposed on an individual hair bundle and monitored its displacement. The load was delivered to an individual hair bundle by attaching the tip of a flexible glass fiber to the bundle's top and using a piezoelectric actuator to displace the fiber's base. To control the load, we used a real-time processor that compared the bundle's actual position, measured by a photomicrometer system, with that specified by a command signal, and then provided feedback to the actuator to minimize the difference between the two (Fig. 1D). By adjusting the strength of the system’s feedback and the commanded position, we independently manipulated the load stiffness and the constant force, which allowed us to vary the bundle’s operating point to reveal its experimental state diagram (Fig. S1).
Fig. 1.
Measurement of experimental state diagrams with a mechanical-load clamp. (A) A theoretical state diagram depicts the qualitative behavior of a hair bundle for different values of the load stiffness and constant force. These parameters determine whether a bundle will oscillate spontaneously, remain quiescent, or manifest bistable switching. A region of spontaneous oscillation is enclosed within a line of Hopf bifurcations (orange). Two Bautin points (squares) separate the supercritical portion of the line (thick) from the subcritical parts (thin). The hair bundle has one stable state and remains quiescent within the monostable region. In the bistable region bounded by the line of fold bifurcations (green), a bundle may switch between two stable states. The line of Hopf bifurcations intersects the line of fold bifurcations at two Bogdanov–Takens points (circles). (B) The amplitude of spontaneous oscillations is expected to increase as the load stiffness decreases (arrow). The amplitude's dependence on the constant force is more complex. Smaller amplitudes are denoted by darker shades of red. (C) The frequency of spontaneous oscillations is theorized to rise as the load stiffness grows. The frequency's dependence on the constant force load is more complex. Lower frequencies are denoted by darker shades of blue. (D) As shown in the magnified circular inset, the tip of a flexible glass stimulus fiber exerts a force on the kinociliary bulb at the top of a hair bundle while an image of the fiber’s tip is projected onto a dual photodiode (dashed rectangles). Information from this displacement monitor is conveyed to a target computer, which compares the bundle’s position with the displacement commanded by the host computer and provides feedback with gain to a piezoelectric actuator that displaces the fiber’s base. The command signal and gain together define the stiffness and constant force confronting the hair bundle. Positive forces act toward the hair bundle's tall edge, to the right, and negative forces in the opposite direction.
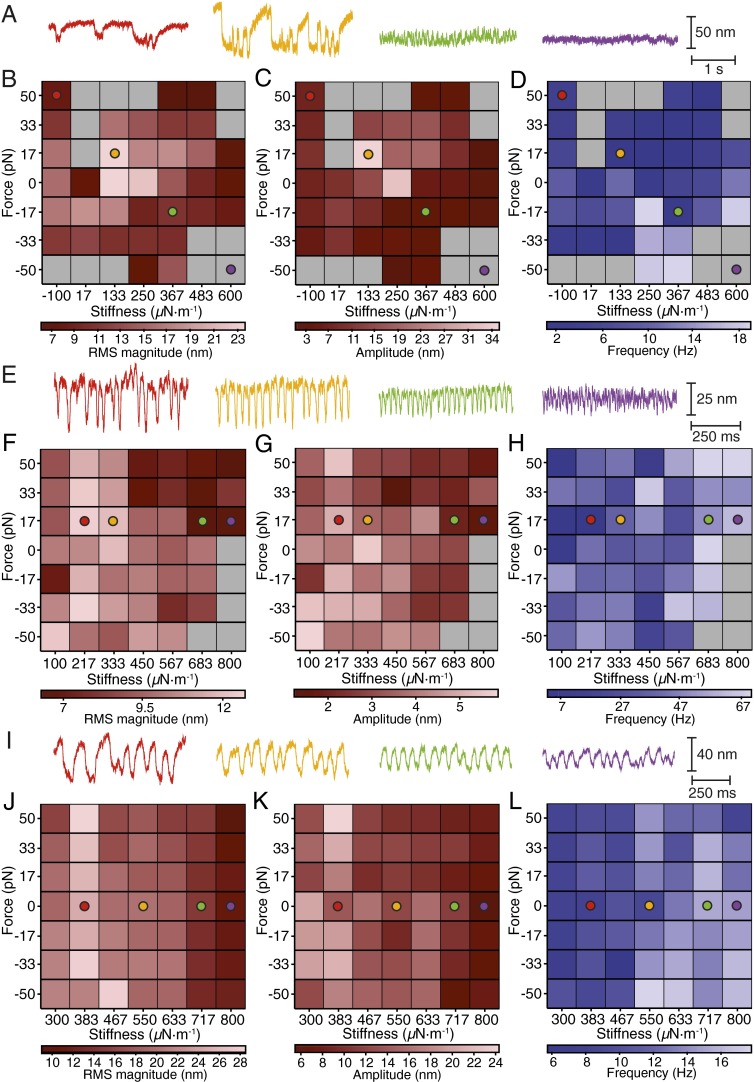
At each operating point we classified a hair bundle’s motion as oscillatory or quiescent based on the distribution of its displacement. In accord with previous manipulations of applied force (17), we found that hair bundles oscillated spontaneously for operating points in certain regions of the experimental state diagram but were quiescent for others. The activity and mechanical properties of hair bundles depended on their diameter, which resulted in oscillatory regions of varying extent (Fig. 2 and Fig. S2). For the lowest values of load stiffness, small bundles exhibited multimodal oscillations (Fig. 2A) (18). The limited range of operating points for which the clamp was stable permitted exploration of only the region of spontaneous oscillation for the largest hair bundles (Fig. 2 I–L and Figs. S2 G–I and S3C).
Fig. 2.
Experimental state diagrams of oscillatory hair bundles. (A) The oscillations of a small hair bundle changed in character as the effective stiffness of the stimulus fiber increased; a few operating points elicited complex oscillations whose multimodal nature is captured by the experimental records. (B) An experimental state diagram shows the behavior of the same hair bundle for various combinations of load stiffness and constant force encompassing most of the oval locus of spontaneous oscillation. The gray region corresponds to quiescent operating points. Within the ruddy locus of spontaneous oscillation, color intensity represents the RMS magnitude of oscillation. The colored circles in the associated panels mark the operating points in A. (C) In another representation of the experimental state diagram the color intensity encodes the amplitude of oscillation. (D) A third depiction of the experimental state diagram for the same bundle portrays the frequency of oscillation for various combinations of load stiffness and constant force. (E) Experimental records show the motions of a medium-sized hair bundle. (F–H) Both the RMS magnitude (F) and the amplitude (G) of oscillation were smallest along the high-stiffness border of the oscillatory region. The colored circles in these panels represent the transect along which the records in E were obtained. (H) The oscillation frequency for the same hair bundle was greatest along the high-stiffness boundary of the oscillatory region. (I) A large hair bundle oscillated spontaneously for all combinations of constant force and load stiffness. (J–L) As the load stiffness increased, both the RMS magnitude (J) and amplitude (K) of spontaneous oscillation decreased. Colored circles correspond to the operating points whose experimental records are shown in I. (L) Increasing the load stiffness evoked a corresponding increase in the frequency of oscillation. The actual stiffness and drag coefficient of the stimulus fiber were respectively KSF = 425 µN·m−1 and ξSF = 53 nN·s·m−1. Analysis parameters and statistics for each experimental state diagram can be found in Table S1. Additional experimental state diagrams may be found in Fig. S2.
In agreement with simulations, an increase in the stiffness was correlated with a rise in the frequency of oscillation for many bundles and with a decrease in the amplitude of oscillation in all but one case (Fig. 2, Figs. S2–S4, and Table S1) (16). The decrease in the amplitude of oscillation for a given bundle generally persisted for the duration of an experiment (Fig. S3 A and B). The region of spontaneous oscillation was abolished upon addition of gentamicin, a drug that blocks mechanoelectrical-transduction channels (Fig. S3 C–F). This result implies that the architecture of the experimental state diagram reflects active hair-bundle motility, which depends upon functional channels (17).
Response to Sinusoidal Stimulation.
The principal role of hair cells in the auditory system is the detection of periodic forces derived from sound. Although modeling suggests that a quiescent hair bundle should respond with maximal frequency tuning and nonlinearity at the boundary of the region of spontaneous oscillation (11, 19–22), no experimental study has systematically examined bundles near this critical locus. We therefore inquired how hair bundles situated at various positions in the experimental state diagram respond to sinusoidal stimulation over a range of amplitudes and frequencies.
The boundary between the regions of spontaneous activity and quiescence lay between operating points for which a bundle’s behavior could be clearly classified as either oscillatory or quiescent based on the distribution of its displacement. When poised near this border, a hair bundle exhibited resonant frequency tuning: the magnitude of its phase-locked response to sinusoidal stimulation—its average oscillation amplitude at the stimulus frequency—displayed a clear peak (Fig. 3A). As the bundle’s operating point was displaced into the quiescent region, the response at this resonant frequency progressively diminished. The sharpness of tuning, quantified by the quality factor of the resonance, was greatest on the oscillatory side of the boundary and in one instance approached that of auditory organs (10, 23) (Fig. 3A and Fig. S5 A and C).
Fig. 3.
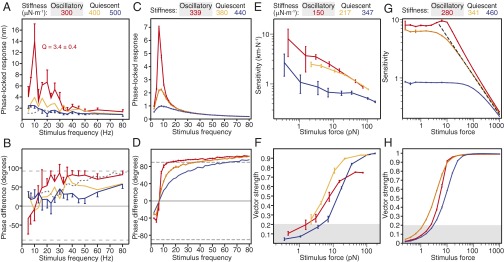
Hair-bundle responses to sinusoidal stimuli. (A) The behavior of a medium-sized hair bundle in the absence of stimulation was first classified for different operating points. The bundle’s response to sinusoidal stimulation was then analyzed as a function of stimulus frequency. Here the constant force was zero and the amplitude of the stimulus was 1.5 pN. The response peaked at 10 Hz for a stiffness of 300 µN·m−1, with the amplitude and quality of the resonant peak decreasing as the load stiffness increased. When the bundle was exposed to 500 µM gentamicin, the frequency response lost its peak for a load stiffness of 300 µN·m−1 (gray dashed line). (B) The phase of hair-bundle motion with respect to the corresponding stimuli is shown for the operating points defined in A. A negative angle corresponds to the bundle’s motion leading the stimulus. The dashed lines signify phase differences of ±90°. At a load stiffness of 300 µN·m−1, the bundle’s motion switched from a phase lead to a phase lag near the bundle’s resonant frequency. This pattern disappeared for higher stiffnesses (orange and blue) and upon application of gentamicin (gray dashed line). (C) In a model of hair-bundle responsiveness with an intermediate level of noise (SDs of the noise terms σx = 0.1 and σf = 0.1), a bundle yielded responses similar to those in A. The resonant peak was greatest for a stiffness of 339 near the boundary of the oscillatory region, which occurred for zero constant force and a load stiffness of 340 in the absence of noise. (D) In the same model, the phase of the bundle’s motion with respect to that of the stimulus displayed a pattern similar to that for the oscillatory point in B. The magnitudes of the maximal phase lead and phase lag peaked at a stiffness of 339. (E) The behavior of a small hair bundle in the absence of stimulation was first classified for different operating points. The sensitivity is portrayed as a function of stimulus force at 5 Hz, near the bundle’s frequency of spontaneous oscillation. (F) The vector strength of the bundle’s motion with respect to that of the stimulus is displayed for the same operating points as in E. (G) Using the model described for C, a virtual bundle’s sensitivity is portrayed as a function of stimulus force for stimulus frequencies 10% greater than the frequency of spontaneous oscillation. The pattern resembles that shown in E. The dashed line corresponds to a slope of −2/3. (H) The vector strength of the simulated bundle’s motion is plotted against stimulus force. The bundle was best entrained at a stiffness of 341 for a range of intermediate to large forces. The error bars for experiments represent SEMs for four observations; those that are not shown are similar in magnitude to those that are included. For all experiments, the stiffness and damping coefficient of the stimulus fiber were respectively 425 µN·m−1 and 53 nN·s·m−1. Additional examples appear in Figs. S5 and S6. For the panels resulting from simulations, the stiffness, frequency, and force have been rescaled by a factor of 100 to facilitate comparison with the experimental data. Because the model was rescaled, no units are displayed for simulated results. All simulations used the same values of a, b, and τ as the original description of the theoretical model (16). The error bars represent SEMs from three stochastic simulations. Values of the vector strength below 0.2 (shaded areas) correspond to regions with poor phase locking as quantified by the Rayleigh test.
When we exposed a hair cell's apical surface to gentamicin to abolish active hair-bundle motility, a hair bundle’s tuning diminished at all operating points; the response at the original resonant frequency collapsed to the noise floor (Fig. 3A and Fig. S5A). This result confirmed that the peak response and sharpness of tuning stem from active hair-bundle motility that augments the bundle's mechanical response. Indeed, the response of an untreated hair bundle exceeded that of a treated bundle for most stiffness values and stimulus frequencies. Unlike the response of a control bundle, that of a gentamicin-treated bundle was insensitive to the load stiffness and resembled that of a low-pass filter.
The phase of an active hair bundle’s response led that of the stimulus for frequencies below the bundle’s resonant frequency and lagged for frequencies exceeding that value (Fig. 3B and Fig. S5 B and D) (11). The phase lead diminished far from and on the quiescent side of the border of spontaneous oscillation and disappeared upon application of gentamicin, indicating that the lead was generated by active hair-bundle motility (Fig. 3B).
A hair bundle’s sensitivity—the magnitude of its phase-locked response divided by the stimulus force—decreased for forces of increasing amplitude (Fig. 3E and Fig. S6A) (11). This change in the sensitivity was greatest for spontaneously oscillating bundles and the sensitivity appeared to become independent of the operating point for large forcing. The sensitivity was largest for operating points at which the hair bundle oscillated, but the bundle was most strongly entrained when it operated on the quiescent side of and near the border of spontaneous oscillation for forces of intermediate magnitude (Fig. 3F and Fig. S6B). Unlike previous experimental and theoretical work that described a linear response for large-amplitude forcing (24), no such effect was found in the present observations owing to a technical limit on the maximal stimulus force.
To compare the experimental behavior of hair bundles with the predictions of a dynamical model of hair-bundle activity (16), we conducted simulations of the responses expected in the presence of thermal noise. The model's response agreed qualitatively with the experimental observations (Fig. 3 C, D, G, and H). Near the boundary of the oscillatory region, the entrained responses accorded with those predicted for a system operating at the edge of an oscillatory instability (21, 22, 25, 26), for which the sensitivity decreases as the magnitude of the force to the power of −2/3.
Far from the border of the oscillatory region, a hair bundle’s maximal response to weak stimulation was smaller and the response as a function of frequency was less sharply tuned than near the border (Fig. 4A). Hypothesizing that this observation reflected reduced entrainment to the stimulus, we assessed how well the responses followed the stimuli by computing the vector strength near the resonant frequency for a range of load stiffnesses. The vector strength peaked at the edge of and on the quiescent side of the boundary of spontaneous oscillations (Fig. 4B). To better characterize entrainment, we delivered stimuli of both increasing force and increasing frequency to oscillatory hair bundles subjected to three load stiffnesses. Entrainment to small stimulus forces was maximal for operating points nearest the boundary of oscillation (Fig. 4C). This dependence of vector strength on the operating point diminished for stimulation away from the bundle’s characteristic frequency (Fig. 4 D and E). In agreement with published observations (27, 28), entrainment was frequency-dependent for a range of stimulus forces. A map of vector strength computed across a range of stimulus forces and frequencies disclosed a phase-locked region or Arnol'd tongue that depended on load stiffness. Although experiments were limited by the bundle’s low resonant frequency, the entrainment region appeared to become more sharply tuned as the load stiffness increased (Fig. 4 F–H), an effect that was previously obscured by the use of different hair bundles for each load stiffness (27). The responses to periodic forcing together indicate that a hair bundle’s capacity to encode auditory stimuli depends upon its mechanical load.
Fig. 4.
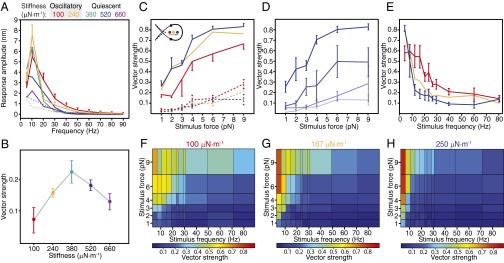
Hair-bundle entrainment by sinusoidal stimulation. (A) The behavior of a medium hair bundle was first classified for different operating points in the absence of stimulation. The bundle's frequency response to stimuli of 0.5 pN in amplitude peaked at 10 Hz for all operating points. When the bundle was exposed to 500 µM gentamicin, its frequency response lacked a peak for load stiffnesses from 300 to 800 µN·m−1 (dark and light dashed lines, respectively). (B) Quantified by the vector strength for each operating point in A, the degree of entrainment peaked at a stiffness of 380 µN·m−1. (C) A second hair bundle oscillated at all three load stiffnesses (Inset) of 100 (red), 167 (yellow), and 250 µN·m−1 (blue). The vector strengths for all operating points increased with stimulus force during stimulation at 5 Hz (solid lines). This stimulus frequency was selected to maximize the vector strength (Fig. S7). When stimulated at 80 Hz, away from the frequency of spontaneous oscillation, the bundle was entrained poorly by the stimulus (dashed lines). (D) For a load stiffness of 250 µN·m−1 the bundle displayed a gradual decrease in the slope of the relation of vector strength to stimulus force as the frequency increased (5, 9, 21, and 80 Hz; dark to light). (E) For a stimulus force of 6 pN, the same bundle achieved maximum entrainment at 5 Hz for a load stiffness of 250 µN·m−1. Additional data appear in Figs. S7–S9. (F–H) Heat maps display the vector strength as a function of stimulus force and stimulus frequency for stiffnesses of 100 (F), 167 (G), and 250 µN·m−1 (H). The error bars represent SEMs for three observations; those not shown resembled in magnitude those that are included. The stiffness and damping coefficient of the stimulus fiber were respectively 425 µN·m−1 and 53 nN·s·m−1.
Response to Pulsatile Stimulation.
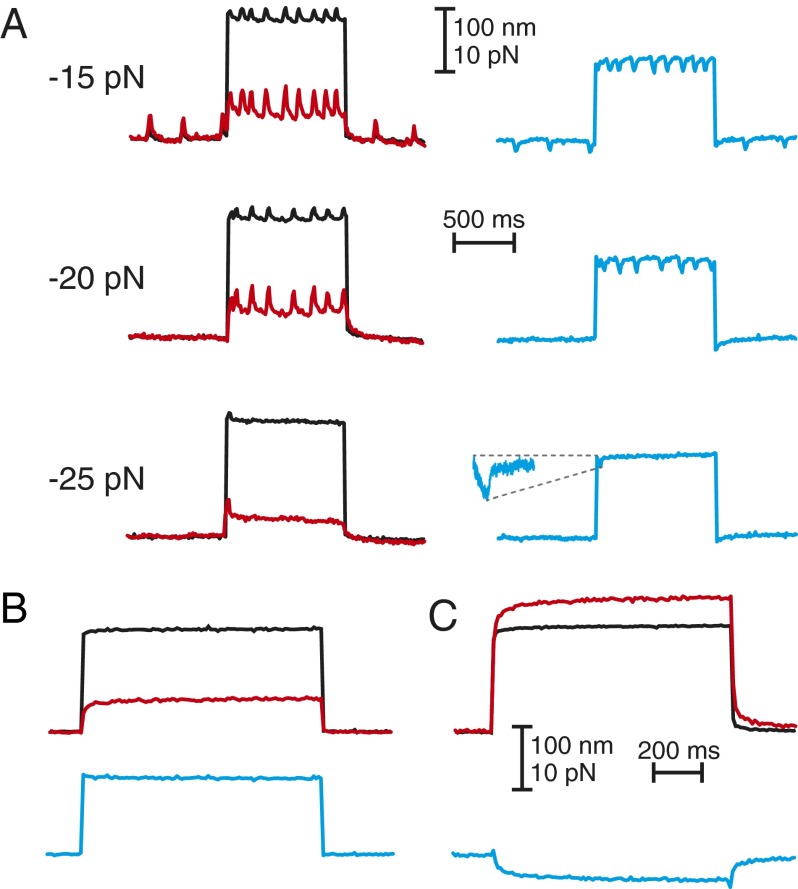
Hair bundles are often investigated in vitro with pulses of displacement or force (1, 8, 29) that additionally correspond to the stimulation of some vestibular organs in vivo (30). Because we expected a bundle’s response to such stimuli to depend upon its load (16), we recorded responses to force pulses from hair bundles subjected to mechanical loads representing operating points within and outside their regions of spontaneous oscillation.
As the constant force applied to a bundle became more negative, hair-bundle oscillations decreased in frequency but not in amplitude until they ceased altogether (Fig. 5A). This observation accords with the results of previous studies that used a low load stiffness (28). Positive force pulses delivered to a hair bundle subjected to successively more negative constant forces first induced oscillations and subsequently evoked twitches (1, 31), rapid movements that transiently exerted negative forces on the stimulus fiber (Fig. 5A). A second bundle held under a negative constant force responded to a positive pulse by moving less than the stimulus fiber’s base (Fig. 5B). When the bundle was subjected to a still more negative constant force, however, the bundle’s displacement in response to a pulse exceeded that of the stimulus fiber’s base (Fig. 5C). During this movement, the force delivered to the hair bundle was negative in sign, implying that the hair bundle exerted a positive force on the fiber. This phenomenon, which had previously been observed only once for an outer hair cell’s bundle in the rat's cochlea (29), demonstrates that amphibian vestibular hair bundles can be induced to respond qualitatively like mammalian auditory bundles despite their different morphologies. The behavior arises from the nonlinear stiffness of a bundle owing to channel gating, a feature conserved in bundles across receptor organs (1).
Fig. 5.
Responses to force pulses. (A) Movement of a stimulus fiber’s base (black) subjected a large hair bundle under a load stiffness of 40 µN·m−1 to a force pulse. For constant forces of −15 and −20 pN, the bundle’s response (red) to the force (blue) displayed an increase in the rate of spontaneous oscillation. For a constant force of −25 pN, the bundle responded to a positive force pulse with a twitch and a negative force transient of 1.2 pN that decayed with a time constant of 5 ms (Inset). (B) When a large hair bundle was subjected to a stiffness of 100 µN·m−1 and a constant force of −66 pN, a positive force pulse elicited a response (red) smaller than the displacement of the fiber’s base (black). The force applied by the fiber during the pulse (blue) was therefore positive. (C) When the constant force was increased to −100 pN, a positive force pulse (black) elicited a response (red) exceeding the displacement of the fiber’s base; the force applied by the fiber (blue) was accordingly negative. The stiffness and damping coefficient of the stimulus fiber were respectively 105 µN·m−1 and 71 nN·s·m−1 (A) or 425 µN·m−1 and 53 nN·s·m−1 (B and C).
Discussion
From the level of molecules to that of ecosystems, a cardinal feature of life is the detection of environmental perturbations by sensory systems. Owing to the complexity of cells and organisms, however, mathematical descriptions that make testable predictions about such systems are rare. Moreover, experimental tools are seldom available to test theoretical predictions about biological dynamics. The present work represents an exception to these generalizations. On the basis of a simple dynamical model of hair-bundle activity, we have predicted the effects of mechanical loading on bundles (16). The present experimental results accord with these predictions. For example, the experimental state diagram revealed by mechanical-load clamping displays a bounded locus of spontaneous activity. Within that area, the frequency of oscillation increases and the amplitude decreases as the boundary is approached by increasing the load stiffness. The changes in the hair bundle’s response to sinusoidal and pulsatile stimuli as its operating point varies are also in qualitative agreement with the model's predictions.
We observed that increasing the stiffness and constant force confronting a hair bundle drives it from the region of spontaneous oscillation into a domain of quiescence. The boundary between the two regimes represents a bifurcation, that is, a dramatic change in behavior in response to continuous variation of one or more control parameters. Several observations indicate that the boundary associated with large values of the load stiffness constitutes a line of supercritical Hopf bifurcations (11, 16, 20, 27, 32–34): both the tuning and degree of entrainment of a bundle are maximal near the bifurcation; the frequency of spontaneous oscillations on the active side matches the resonant frequency on the quiescent side; and the amplitude of spontaneous movement grows continuously from zero as the operating point progresses into the region of spontaneous oscillation. For low values of the load stiffness, however, the amplitude of spontaneous oscillation does not change as the bifurcation is approached, a behavior more consistent with a fold of limit cycles or an infinite-period bifurcation (35). The model for hair-bundle mechanics predicts this change in the type of bifurcation as the stiffness is varied (16).
The characteristic frequencies measured near the supercritical bifurcation accord with those of saccular afferent axons in vivo (36, 37), suggesting that hair bundles normally reside at operating points near the high-stiffness arc of bifurcations. Consistent with this idea, the elastic load imposed experimentally at the bifurcation resembles the stiffness of the otolithic membrane that ordinarily confronts a saccular hair bundle (38). This result reinforces the thesis that the behavior of hair bundles in vivo is dictated by their mechanical loads. We also predict that reduction of these elastic loads in vivo affects the oscillatory behavior of hair bundles, for example by increasing the prevalence and amplitude of otoacoustic emissions.
Although the sharpness of tuning that we measured was less than that of the mammalian cochlea (39), it largely accounts for frequency tuning in the amphibian auditory system (23). Moreover, the sharpness of tuning and the degree of nonlinearity found here represent lower estimates owing to the limited frequency resolution of the recordings. In agreement with theory (16), hair bundles situated at operating points distant from the oscillatory region lost their resonant character and behaved as low-pass filters.
Within a receptor organ, a hair bundle must counter viscous damping to minimize the loss of stimulus energy. Our results indicate that the bundle accomplishes this task when poised near its boundary of spontaneous activity. Although all bundles may potentially exhibit this behavior, mechanical loading by accessory structures controls their ability to amplify external signals. It remains to be determined how a hair bundle in vivo finds the operating conditions that foster optimal responsiveness (25).
Our results demonstrate an essential similarity of hair bundles, whose responsiveness in various receptor organs is controlled by mechanical loading. Although previous studies used different stimulus fibers to investigate the effects of stiffness and constant force on different hair bundles (27, 32), our approach revealed multiple mechanosensory modes in individual bundles. Depending upon its operating point, an individual bundle may twitch and oscillate like those in amphibian and reptilian receptor organs (31) or overshoot the stimulus like those in the mammalian cochlea (29). Although hair bundles in the mammalian cochlea detect frequencies extending two or three orders of magnitude higher than those detected by the bullfrog's sacculus, these results indicate that bundles from both organs rely on the same fundamental mechanisms. Adjustments to these mechanisms—the rate of adaptation and the degree of nonlinearity—regulate the speed and range of responsiveness. It is probable that the physical properties of hair bundles and their accessory structures have evolved to adjust the functions of different receptor organs in most organisms.
In contrast to a manufactured device that is designed to produce or respond to signals in a stereotypical fashion, a single hair bundle can function in various capacities. Here we show that an individual hair bundle can behave like any of four different devices. A bundle may generate spontaneous oscillations like an oscillator that produces repetitive square or sine waves. It can resonate with high-frequency resolution like a resonant circuit that responds to one frequency with a greater amplitude than to any other. By attenuating high-frequency stimuli, a bundle may serve as a low-pass filter that attenuates signals above a cutoff frequency. Finally, by twitching at the onset of a pulse displacement, a bundle can mimic a step detector that identifies discontinuities in incoming signals. These observations for a particular sensory organelle reveal a general principle that may be used by both biological and artificial systems: a nonlinear system can be controlled to serve many different functions by adjusting only a few key parameters.
Materials and Methods
Experimental Preparation.
All procedures were approved by the Institutional Animal Care and Use Committee of The Rockefeller University. Experiments were performed at 21 °C on hair cells from the saccular maculae of adult bullfrogs, Rana catesbeiana, of both sexes. Each dissected sacculus was placed in oxygenated artificial perilymph containing 114 mM Na+, 2 mM K+, 2 mM Ca2+, 118 mM Cl−, 5 mM Hepes, and 3 mM d-glucose. After isolation from the labyrinth and removal of otoconia, the saccular macula was sealed over a 1-mm hole in a 12-mm disk of aluminum foil with n-butyl cyanoacrylate (Vetbond; 3M) to form a partition in a two-compartment chamber. The apical surface was exposed to 67 mg·L−1 of protease (type XXIV; Sigma) for 35 min at 21 °C to loosen the otolithic membrane, which was then removed with an eyelash. During recordings the lower chamber contained oxygenated artificial perilymph and the upper chamber held oxygenated artificial endolymph containing 2 mM Na+, 118 mM K+, 250 µM Ca2+, 118 mM Cl−, 5 mM Hepes, and 3 mM d-glucose. Both solutions had a pH of 7.3 and an osmotic strength of 230 mOsmol·kg−1.
Microscopic Apparatus.
Hair bundles were visualized with differential–interference–contrast optics through a 60× water-immersion objective lens of numerical aperture 0.9 on an upright microscope (BX51WI; Olympus). To detect spontaneously active hair bundles, we directed the image through a 0.35× or 4.0× telescope to a charge-coupled-device camera and a video processor (Argus-20; Hamamatsu Photonics K. K.). Digital subtraction of each frame from the average of the previous one to five frames eased the detection of hair-bundle oscillations. An infrared-reflecting mirror (21002b; Chroma Technology) and a broadband interference filter (585 ± 30 nm; no. 220494; Chroma Technology) protected the tissue from photodamage. For experimental measurements, the polarizer and filter were removed from the light path and the sample was illuminated at 630 nm with a 900-mW light-emitting diode (UHP-Mic-LED-630; Prizmatix).
Mechanical Stimulation.
Mechanical stimuli were delivered by flexible glass fibers fabricated from borosilicate capillaries 1.2 mm in external diameter (TW120-3; World Precision Instruments). After a capillary had been narrowed by an electrode puller (P-2000; Sutter Instruments), a 120-V solenoid pulling at a right angle created a solid fiber no more than 100 µm in length and 0.5–0.8 µm in diameter. To enhance its optical contrast, each fiber was sputter coated with gold palladium (Hummer 6.2; Anatech). To improve its attachment to the kinociliary bulb, the fiber was treated for 15 min with 200 µg·L−1 concanavalin A (type IV; Sigma).
To determine a fiber’s stiffness and drag coefficient, we analyzed its thermal fluctuations while submerged in water. We fit the power spectrum SX as a function of frequency f from a 30-s record to the Lorentzian relation (40)
| [1] |
| [2] |
| [3] |
Here, a is a fitting parameter, f0 is the half-power frequency, kB is Boltzmann’s constant, T is the temperature, ξSF is the fiber’s drag coefficient, and KSF is the fiber’s stiffness. Fibers had stiffnesses of 50–600 µN·m−1 and drag coefficients of 25–80 nN·s·m−1.
The base of each stimulus fiber was secured to a high-frequency piezoelectric actuator (PA 4/12; Piezosystem Jena GmbH) driven by an 800-mA amplifier (ENV 800; Piezosystem Jena). The actuator was mounted on a micromanipulator (ROE-200; Sutter Instruments) for positioning of the fiber’s tip.
The tip of a horizontally mounted stimulus fiber was tightly coupled to the kinociliary bulb of an individual hair bundle. Each hair bundle was classified by its diameter at the insertion into the cuticular plate. A small bundle was estimated to have a diameter of less than 2 µm and about 20 stereocilia; a medium bundle was 2–4 µm in diameter and encompassed roughly 40 stereocilia, whereas a large bundle of more than 4 µm contained around 60 stereocilia.
Photometric Recording.
The motion of a hair bundle was tracked by imaging the stimulus fiber’s tip on a dual photodiode at a magnification of 1,350×. The output of the photodiode was then relayed through a low-pass filter with a cutoff frequency of 2 kHz (BM8; Kemo Limited). The sensitivity of the photodiode system was calibrated by independently translating the fiber’s image in 20-µm steps with a mirror coupled to a second piezoelectric actuator driven by a 300-mA amplifier (PA 120/14 SG and ENV 300 SG, Piezosystem Jena). This actuator was calibrated by a heterodyne interferometer (OFV 501; Polytec GmbH).
Mechanical-Load Clamp.
In most clamp systems, such as the venerable voltage clamp, a negative feedback loop holds one experimental variable fixed while the conjugate variable is measured. Under displacement-clamp conditions, for example, a hair bundle is maintained at a commanded position while the ensuing force is evaluated (41, 42). A force clamp inverts this relationship: feedback imposes a constant force while the displacement is determined.
In the present experiments we implemented a generalization of this procedure, load clamping, in which the feedback system simultaneously imposes on a hair bundle two conditions that mimic the bundle's environment in vivo. The system serves as a stiffness clamp that imposes a specified elastic load and at the same time acts as a force clamp that applies a commanded constant, sinusoidal, or pulsatile force. Load clamping is possible because contemporary computers can solve the necessary differential equations on a timescale shorter than the mechanical relaxation time of the stimulus fiber and attached hair bundle (43, 44). In a further generalization of the approach, we intend to examine the hypothesized effects on hair bundles of inertia and drag, two parameters that may play an important role in vestibular and auditory organs (16). An extension of the present system that includes additional mechanical control parameters is under development.
At the point of contact between a stimulus fiber and hair bundle, the elastic force produced by the flexion of the fiber is balanced by the sum of the elastic and drag forces associated with the fiber and bundle:
| [4] |
Here, KSF is the stiffness of the stimulus fiber and KHB is that of the hair bundle, Δ is the position of the fiber's base and X is that of the hair bundle, ξXX is the drag coefficient of the stimulus fiber owing to motion at the fiber’s tip and ξΔX is that owing to motion at the fiber’s base, and ξHB is the drag coefficient of the hair bundle. An overdot denotes a temporal derivative. FA represents any active or nonlinear force produced by the hair bundle. Note that all inertial effects of the bundle and fiber are assumed to be small.
The photodiode’s output voltage VD is linearly related to the hair bundle’s position by a coefficient α: VD = αX. If the clamp accomplishes a commanded displacement XC, the photodiode’s output voltage is VC = αXC. The error signal at the clamp's amplifier is therefore
| [5] |
This signal is amplified by the gain G to generate an output signal VO that is delivered to the piezoelectric stimulator,
| [6] |
The stimulator's displacement output is linearly related to its input signal by a coefficient β, Δ = βVO, so the resultant displacement of the stimulus fiber’s base is
| [7] |
| [8] |
When and , this relation becomes
| [9] |
in which KEFF = (1 + αβG)KSF is the effective load stiffness due to the clamp. The condition is met for sufficiently small values of ξΔX and G, in which αβ ∼ 1 and ξHB ≥ 100 nN·s·m−1. The experiments presented here satisfy this condition, with G typically less than 1 and never exceeding 2. For the fibers used here (45), ξXX = 50–70 nN·s·m−1 and ξΔX = 30–40 nN·s·m−1. When KSF = 100–350 μN·m−1, the condition is satisfied for timescales greater than ξΔX/KSF < 0.1–0.3 ms. Additional forces owing to the drag from the base of the fiber are not significant for times exceeding this bound.
The displacement command may be used to apply various types of stimuli to the bundle. We may choose , such that FC = αβGKSFXCC is a constant force, is a sinusoidal force of angular frequency ωS, and is a force pulse. Eq. 9 then yields
| [10] |
The clamp thus allows us to control the stiffness and various forms of stimulus force independently through adjustment of the proportional gain G and command displacement XC.
After poising a hair bundle at a particular operating point defined by the stiffness and offset force, we sometimes delivered sinusoidal force stimuli and recorded the bundle’s response. Before each set of stimuli, the hair bundle was held at its operating point for 3 s to allow it to reach a steady state; stimuli were subsequently delivered for 15–50 cycles, depending upon the frequencies chosen. In other experiments we used a similar protocol to deliver 1-s force pulses.
Clamp Verification.
To demonstrate robust independent control of the stiffness and constant force with a mechanical-load clamp, we applied stimuli to a vertically mounted glass fiber that served as a simulacrum of a hair bundle. This arrangement provided a system with a known, linear stiffness for calibration and controls. For calibration purposes, steps were delivered for a series of forces and stiffnesses. For each constant force, the steady-state position of the fibers' tip is given by
| [11] |
The validity of this relation is confirmed in Fig. S1.
Signal Production and Acquisition.
Stimuli were generated and data recorded by a host computer running programs written in LabVIEW (version 10.0; National Instruments) with a sampling interval of 100 μs. For mechanical load-clamp experiments, signals were relayed to a target computer running the LabVIEW Real-Time operating system (version 10.0; National Instruments). To set a defined stiffness and constant force, the host computer adjusted the proportional gain according to Eqs. 10 and 11 and adjusted the command displacement and transmitted those values to the target computer. The target computer then rapidly executed a short program that implemented Eq. 6 and provided an appropriate signal to the piezoelectric stimulator.
State-Diagram Mapping and Analysis.
To construct an experimental state diagram, we subjected a hair bundle to a set of load stiffnesses and constant forces, recording at each operating point for 2–8 s. The control parameters were specified for each operating point by a constant command displacement XC and proportional gain G. The duration of recording at each operating point was limited by the stability of the load clamp, which took 3 min to recalibrate after each 1 min of recording, and by the time of about 30 min during which the bundle’s dynamics was unchanged by cellular deterioration. Here we describe the procedure for classifying and analyzing the operating points that constituted the bundle’s experimental state diagram. The parameter values used for each diagram are listed in Table S1; the analysis was performed using MATLAB (R2014a, 8.3.0.532).
If a hair bundle was oscillating at a particular operating point, then the distribution of its displacements displayed more than one peak. To analyze this distribution, we first removed slow drift in the time trace of bundle displacement by subtracting the time trace smoothed by moving averages over a time window of a fixed length. We then used up to three statistical tests to determine whether the displacement distribution was multimodal. Hartigans’ dip statistic is larger for multimodal than for unimodal distributions (46). Using as the null distribution a normal distribution with the same mean and variance as the displacement distribution to make the test more sensitive, we defined a multimodality score to be equal to the dip statistic. Displacement distributions that differed statistically from normal, possessing a multimodality score exceeding a threshold, corresponded to oscillatory operating points. This procedure did not identify all of the operating points at which a bundle oscillated, however, for noise could obscure the dips between peaks in a distribution, resulting in a distribution that was asymmetric or broad.
To determine whether a distribution was excessively asymmetric we created two additional distributions. The right distribution was constructed by reflecting about the mean each displacement greater than the mean displacement; the left distribution was found in an analogous manner. This process yielded two symmetric distributions that corresponded to the mirroring of the left and right halves of the original distribution. The original distribution was considered asymmetric if the left distribution and right distribution were statistically distinct. We defined the asymmetry score as the Kolmogorov–Smirnov test statistic resulting from a comparison of the left and right distributions. A distribution was judged to be asymmetric if the score exceeded a threshold and was statistically significant.
Broad distributions were identified as those with negative excess kurtosis. We defined a thinness score as the excess kurtosis divided by its SE. This score has a normal distribution for large samples (47). A distribution was considered broad if the thinness score lay below a threshold and was statistically smaller than that of a normal distribution.
By searching iteratively for a set of thresholds corresponding to the three scores described above, we found a set of operating points that was continuous and devoid of holes: a simply connected region for which a hair bundle oscillated. Outside this region, the bundle was classified as quiescent. This classification scheme has the advantage that it is not based on the amplitude of a bundle’s noisy displacement, which is difficult to determine for many operating points. To emphasize the fact that the amplitude of a bundle’s noisy displacements was not used to classify operating points, quiescent operating points are illustrated with a color not found in the spectrum used to illustrate the amplitude of spontaneous oscillations.
The amplitude and frequency of spontaneous oscillations at each operating point corresponded to the tallest peak of the time trace’s Fourier transform. To reduce spectral leakage owing to the short duration of each time trace, the trace was multiplied by a Hamming window after subtraction of the mean displacement. The trace was then zero padded to improve the accuracy of determining the peak. Because the resulting Fourier transform contained spurious low-frequency and high-frequency peaks owing to the measurement system, we searched for the largest peak between a minimum of 0–2 Hz and a maximum of 100 Hz, within the range of best frequencies expected for the bullfrog's sacculus (32, 36). We excluded the power-supply frequency of 60 Hz. To account for the change in the height of this peak owing to windowing, we rescaled the value by a factor determined by applying the procedure described above to a sinusoidal time trace with a duration equal to that of the original trace.
To avoid including drift in the estimation of the root-mean-square (RMS) amplitude, we subtracted the mean from each time trace and found the local RMS magnitude for a moving window 1.5 times as large as the window used to remove the drift in the analysis of the displacement distribution. The drift was then removed from each of these time windows by subtracting a linear fit. The RMS magnitude of the entire time trace was defined to be the mean of the local RMS magnitudes.
Gentamicin Controls.
We evaluated the sensitivity of hair bundles to applied forces when oscillations were arrested. Transduction channels were blocked with 500 µM gentamicin sulfate applied in the endolymph of the upper chamber, a treatment whose reversibility allowed bundles to be reassessed after washout (17).
Sensitivity.
To evaluate a hair bundle’s response to periodic stimuli, we calculated the bundle’s phase-locked response , in which is the bundle’s Fourier transform at the frequency of driving, ωs. Sensitivity was then defined as the modulus of the bundle’s response function
| [12] |
in which is the Fourier component of the stimulus force at the driving frequency.
Phase Difference with Respect to Stimulation.
For those instances in which a sinusoidal stimulus was provided, the phase difference between the sinusoidal component of motion commanded at the fiber’s base ΔC(t) and that of the hair bundle X(t) was determined by the relation
| [13] |
in which (ωs) and (ωs) are the Fourier transforms of the motions at the frequency of driving, ωs, and indicates the real and the imaginary part of a variable. A negative phase difference corresponds to a phase lead of the hair bundle with respect to the fiber and a positive difference corresponds to a phase lag. This convention accords with previously published phase differences between a stimulus and the hair bundle’s response (10).
Quality Factor.
The response of a hair bundle often displayed resonance at some characteristic frequency fC. To estimate the bundle’s sharpness of tuning, we used an operational definition of the quality factor
| [14] |
Here Δf corresponds to the bandwidth at amplitude AC /√2, in which AC is the amplitude of the bundle’s response at the characteristic frequency. Larger values of Q correspond to sharper resonance. In most cases this operational definition underestimated the quality of resonance.
Vector Strength.
To assess the degree of entrainment between the stimulus fiber and the hair bundle, we measured the vector strength between the two signals. To do so, we first calculated the Hilbert transform of each signal,
| [15] |
in which is the inverse Fourier transform, sgn is the signum function, and is the Fourier transform of the bundle’s motion. From the analytic signal XA(t) = X(t) + iXH(t) we then calculated the instantaneous phase
| [16] |
in which ΔC,H(t) is the Hilbert transform of the sinusoidal component of motion commanded at the fiber’s base, ΔC(t). The mean vector length or vector strength for a signal of length N is then given by
| [17] |
in which 0 ≤ VS ≤ 1. The vector strength equals 1 if two signals are identical and completely entrained and approaches 0 as two signals become wholly dissimilar in instantaneous phase. This parameter thus corresponds to the degree of entrainment between two signals.
Hair-Bundle Modeling.
Simulations of a model of hair-bundle dynamics (16) were performed with Mathematica 9.0.0.0 and C. To mimic the stochastic effects observed experimentally, noise terms were added to the model to yield the equations
| [18] |
| [19] |
in which x is the bundle’s displacement, f is the force owing to adaptation, a is a negative stiffness owing to gating of the transduction channel, τ is the timescale of adaptation, b is a compliance coupling bundle displacement to adaptation, K is the sum of the bundle’s load stiffness and pivot-spring stiffness, Fc is the sum of the constant force intrinsic to the hair bundle and that owing to the load, and F is any time-dependent force applied to the bundle. All simulation results used the same values of a, b, and τ as our previous publication (16). The additional white noise terms ηx and ηf were δ-correlated random variables drawn from Gaussian distributions; the SDs of these distributions are denoted σx and σf. Eqs. 18 and 19 were integrated numerically by the Euler–Maruyama method. Because the model was designed to capture qualitative effects associated with active hair-bundle motility, the values of the variables and parameters have no quantitative meaning. To facilitate comparisons with the experimental results, however, we rescaled the displacements, frequencies, sensitivities, stiffnesses, and forces in figures.
The model qualitatively predicts the shape of the state diagram and the variation in oscillation amplitude and frequency within the region of spontaneous activity (16). We created artificial state diagrams by simulating a stochastic version of the model for a set of load stiffnesses and constant forces to produce time traces similar to those recorded experimentally. To determine the parameter values for which the virtual bundles oscillated, we applied the same procedures used to analyze the experimental results. The procedure correctly identified the oscillatory regions when the noise was small (Fig. S4 A and B). When the noise was large, however, the model bundles switched between stable states for operating points in the low-stiffness region of the diagram. The bundles additionally exhibited noise-induced oscillations for points in an excitable region that was classified as quiescent when the noise was small (Fig. S4 C and D). These behaviors suggest that the oscillatory regions found from experimental data included behaviors other than true limit-cycle oscillations at low stiffness values. Taken together, the simulations accorded well with the experimental state diagrams and highlighted additional behaviors induced by biological noise (Fig. 2 and Fig. S2).
Statistics.
Paired Student’s t tests were used to determine the significance of amplitude responses, quality factors, and vector strengths; significance was defined as P < 0.05. Binned phase differences were evaluated with Rayleigh’s test for nonuniformity of circular data.
A single number was used to describe the correlation between any two quantities for a given state diagram by finding Spearman’s rank-correlation coefficient for all values of the two quantities in the oscillatory region of the diagram. Owing to the grid structure of the sampled state diagram, there were many duplicate values for the stiffness and constant force that in conjunction with correlations between multiple quantities in a state diagram limited the magnitude of any particular correlation coefficient. These ties were taken into account by a permutation test to determine the statistical significance of the correlation given the sampling structure and the data. The P value for each coefficient was thus a better indication of the true significance of the correlation than the value of the coefficient itself.
Supplementary Material
Acknowledgments
We thank Dr. P. Martin and the members of our research group for comments on the manuscript. J.D.S. is supported by Grants F30DC013468 and T32GM07739 from the National Institutes of Health. D.Ó M. was a research associate and A.J.H. is an investigator of Howard Hughes Medical Institute.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1501453112/-/DCSupplemental.
References
- 1.Martin P. 2010. Active hair-bundle motility of the hair cells of vestibular and auditory organs. Active Processes and Otoacoustic Emissions, Springer Handbook of Auditory Research, eds Manley GA, Fay RR, Popper AN (Springer Science and Business Media, New York), pp 93–143.
- 2.Simmons DD, Meenderink SWF, Vassilakis PN. 2006 Anatomy, physiology, and function of auditory end-organs in the frog inner ear. Hearing and Sound Communication in Amphibians, Springer Handbook of Auditory Research, eds Narins PM, Feng AS, Fay RR, Popper AN (Springer Science and Business Media, New York), pp 184–220. [Google Scholar]
- 3.Hudspeth AJ. Making an effort to listen: Mechanical amplification in the ear. Neuron. 2008;59(4):530–545. doi: 10.1016/j.neuron.2008.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Martin P, Hudspeth AJ. Active hair-bundle movements can amplify a hair cell’s response to oscillatory mechanical stimuli. Proc Natl Acad Sci USA. 1999;96(25):14306–14311. doi: 10.1073/pnas.96.25.14306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hudspeth AJ. Integrating the active process of hair cells with cochlear function. Nat Rev Neurosci. 2014;15(9):600–614. doi: 10.1038/nrn3786. [DOI] [PubMed] [Google Scholar]
- 6.Green DM, Dai H. Is human hearing limited by Brownian motion? J Acoust Soc Am. 1991;89(4B):1889. [Google Scholar]
- 7.Spiegel MF, Watson CS. Performance on frequency-discrimination tasks by musicians and nonmusicians. J Acoust Soc Am. 1984;76(6):1690–1695. [Google Scholar]
- 8.Crawford AC, Fettiplace R. The mechanical properties of ciliary bundles of turtle cochlear hair cells. J Physiol. 1985;364:359–379. doi: 10.1113/jphysiol.1985.sp015750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Knudsen VO. The sensibility of the ear to small differences of intensity and frequency. Phys Rev. 1923;21:84–102. [Google Scholar]
- 10.Manley GA. Evidence for an active process and a cochlear amplifier in nonmammals. J Neurophysiol. 2001;86(2):541–549. doi: 10.1152/jn.2001.86.2.541. [DOI] [PubMed] [Google Scholar]
- 11.Martin P, Hudspeth AJ. Compressive nonlinearity in the hair bundle’s active response to mechanical stimulation. Proc Natl Acad Sci USA. 2001;98(25):14386–14391. doi: 10.1073/pnas.251530498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Eatock RA, Fay RR. Vertebrate Hair Cells. Springer, New York; 2006. [Google Scholar]
- 13.Howard J, Ashmore JF. Stiffness of sensory hair bundles in the sacculus of the frog. Hear Res. 1986;23(1):93–104. doi: 10.1016/0378-5955(86)90178-4. [DOI] [PubMed] [Google Scholar]
- 14.Manley GA, Popper AN, Fay RR. Evolution of the Vertebrate Auditory System. Vol 22 Springer, New York; 2004. [Google Scholar]
- 15.McHenry MJ, van Netten SM. The flexural stiffness of superficial neuromasts in the zebrafish (Danio rerio) lateral line. J Exp Biol. 2007;210(Pt 23):4244–4253. doi: 10.1242/jeb.009290. [DOI] [PubMed] [Google Scholar]
- 16.Ó Maoiléidigh D, Nicola EM, Hudspeth AJ. The diverse effects of mechanical loading on active hair bundles. Proc Natl Acad Sci USA. 2012;109(6):1943–1948. doi: 10.1073/pnas.1120298109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Martin P, Bozovic D, Choe Y, Hudspeth AJ. Spontaneous oscillation by hair bundles of the bullfrog’s sacculus. J Neurosci. 2003;23(11):4533–4548. doi: 10.1523/JNEUROSCI.23-11-04533.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Roongthumskul Y, Fredrickson-Hemsing L, Kao A, Bozovic D. Multiple-timescale dynamics underlying spontaneous oscillations of saccular hair bundles. Biophys J. 2011;101(3):603–610. doi: 10.1016/j.bpj.2011.06.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Barral J, Martin P. The physical basis of active mechanosensitivity by the hair-cell bundle. Curr Opin Otolaryngol Head Neck Surg. 2011;19(5):369–375. doi: 10.1097/MOO.0b013e32834a8c33. [DOI] [PubMed] [Google Scholar]
- 20.Barral J, Martin P. Phantom tones and suppressive masking by active nonlinear oscillation of the hair-cell bundle. Proc Natl Acad Sci USA. 2012;109(21):E1344–E1351. doi: 10.1073/pnas.1202426109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Eguíluz VM, Ospeck M, Choe Y, Hudspeth AJ, Magnasco MO. Essential nonlinearities in hearing. Phys Rev Lett. 2000;84(22):5232–5235. doi: 10.1103/PhysRevLett.84.5232. [DOI] [PubMed] [Google Scholar]
- 22.Hudspeth AJ, Jülicher F, Martin P. A critique of the critical cochlea: Hopf—a bifurcation—is better than none. J Neurophysiol. 2010;104(3):1219–1229. doi: 10.1152/jn.00437.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Manley GA, Fay RR, Popper AN. Active Processes and Otoacoustic Emissions in Hearing. Springer, New York; 2007. [Google Scholar]
- 24.Nadrowski B, Martin P, Jülicher F. Active hair-bundle motility harnesses noise to operate near an optimum of mechanosensitivity. Proc Natl Acad Sci USA. 2004;101(33):12195–12200. doi: 10.1073/pnas.0403020101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Camalet S, Duke T, Jülicher F, Prost J. Auditory sensitivity provided by self-tuned critical oscillations of hair cells. Proc Natl Acad Sci USA. 2000;97(7):3183–3188. doi: 10.1073/pnas.97.7.3183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lindner B, Dierkes K, Julicher F. 2009. Local exponents of nonlinear compression in periodically driven noisy oscillators. Phys Rev Lett 103(25):25061-1-4.
- 27.Strimbu CE, Fredrickson-Hemsing L, Bozovic D. Coupling and elastic loading affect the active response by the inner ear hair cell bundles. PLoS ONE. 2012;7(3):e33862. doi: 10.1371/journal.pone.0033862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Fredrickson-Hemsing L, Strimbu CE, Roongthumskul Y, Bozovic D. Dynamics of freely oscillating and coupled hair cell bundles under mechanical deflection. Biophys J. 2012;102(8):1785–1792. doi: 10.1016/j.bpj.2012.03.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kennedy HJ, Crawford AC, Fettiplace R. Force generation by mammalian hair bundles supports a role in cochlear amplification. Nature. 2005;433(7028):880–883. doi: 10.1038/nature03367. [DOI] [PubMed] [Google Scholar]
- 30.Fernández C, Goldberg JM. Physiology of peripheral neurons innervating otolith organs of the squirrel monkey. I. Response to static tilts and to long-duration centrifugal force. J Neurophysiol. 1976;39(5):970–984. doi: 10.1152/jn.1976.39.5.970. [DOI] [PubMed] [Google Scholar]
- 31.Tinevez JY, Jülicher F, Martin P. Unifying the various incarnations of active hair-bundle motility by the vertebrate hair cell. Biophys J. 2007;93(11):4053–4067. doi: 10.1529/biophysj.107.108498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Strimbu CE, Kao A, Tokuda J, Ramunno-Johnson D, Bozovic D. Dynamic state and evoked motility in coupled hair bundles of the bullfrog sacculus. Hear Res. 2010;265(1-2):38–45. doi: 10.1016/j.heares.2010.03.001. [DOI] [PubMed] [Google Scholar]
- 33.Choe Y, Magnasco MO, Hudspeth AJ. A model for amplification of hair-bundle motion by cyclical binding of Ca2+ to mechanoelectrical-transduction channels. Proc Natl Acad Sci USA. 1998;95(26):15321–15326. doi: 10.1073/pnas.95.26.15321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Strogatz SH. Nonlinear Dynamics and Chaos. Westview Press, Cambridge, MA; 1994. [Google Scholar]
- 35.Shlomovitz R, et al. Low frequency entrainment of oscillatory bursts in hair cells. Biophys J. 2013;104(8):1661–1669. doi: 10.1016/j.bpj.2013.02.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Koyama H, Lewis ER, Leverenz EL, Baird RA. Acute seismic sensitivity in the bullfrog ear. Brain Res. 1982;250(1):168–172. doi: 10.1016/0006-8993(82)90964-7. [DOI] [PubMed] [Google Scholar]
- 37.Yu XL, Lewis ER, Feld D. Seismic and auditory tuning curves from bullfrog saccular and amphibian papillar axons. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1991;169(2):241–248. doi: 10.1007/BF00215871. [DOI] [PubMed] [Google Scholar]
- 38.Benser ME, Issa NP, Hudspeth AJ. Hair-bundle stiffness dominates the elastic reactance to otolithic-membrane shear. Hear Res. 1993;68(2):243–252. doi: 10.1016/0378-5955(93)90128-n. [DOI] [PubMed] [Google Scholar]
- 39.Robles L, Ruggero MA. Mechanics of the mammalian cochlea. Physiol Rev. 2001;81(3):1305–1352. doi: 10.1152/physrev.2001.81.3.1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Howard J. 2001. Mechanics of Motor Proteins and the Cytoskeleton (Sinauer Associates, Sunderland, MA)
- 41.Jaramillo F, Hudspeth AJ. Displacement-clamp measurement of the forces exerted by gating springs in the hair bundle. Proc Natl Acad Sci USA. 1993;90(4):1330–1334. doi: 10.1073/pnas.90.4.1330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Martin P, Mehta AD, Hudspeth AJ. Negative hair-bundle stiffness betrays a mechanism for mechanical amplification by the hair cell. Proc Natl Acad Sci USA. 2000;97(22):12026–12031. doi: 10.1073/pnas.210389497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Le Goff L, Bozovic D, Hudspeth AJ. Adaptive shift in the domain of negative stiffness during spontaneous oscillation by hair bundles from the internal ear. Proc Natl Acad Sci USA. 2005;102(47):16996–17001. doi: 10.1073/pnas.0508731102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Barral J, Dierkes K, Lindner B, Jülicher F, Martin P. Coupling a sensory hair-cell bundle to cyber clones enhances nonlinear amplification. Proc Natl Acad Sci USA. 2010;107(18):8079–8084. doi: 10.1073/pnas.0913657107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bormuth V, Barral J, Joanny J-F, Jülicher F, Martin P. Transduction channels’ gating can control friction on vibrating hair-cell bundles in the ear. Proc Natl Acad Sci USA. 2014;111(20):7185–7190. doi: 10.1073/pnas.1402556111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hartigan JA, Hartigan PM. The dip test of unimodality. Ann Stat. 1985;13(1):70–84. [Google Scholar]
- 47.Cramer D. Basic Statistics for Social Research. Routledge, London; 1997. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.