EF-hand protein Ca²⁺ buffers regulate Ca²⁺ influx and exocytosis in sensory hair cells

Significance

Ca²⁺ ions serve as a key cellular signal and are tightly controlled. One mechanism to limit free Ca²⁺ ions is buffering by Ca²⁺-binding proteins, which are strongly expressed in sensory hair cells of the ear. Here we studied how genetic disruption of the Ca²⁺-binding proteins parvalbumin-α, calbindin-D28k, and calretinin affects exocytosis and sound encoding at the synapses of mouse inner hair cells (IHCs) and spiral ganglion neurons (SGNs). Mutant IHCs showed increased exocytosis, but the sound-evoked spiking activity in SGNs was unaltered. Together with mathematical modeling, this finding indicates that a large fraction of exocytosis in mutant IHCs occurred outside synapses. We conclude that Ca²⁺-binding proteins shape presynaptic Ca²⁺ signals to restrict exocytosis to active zones, thus enabling metabolically efficient sound encoding.

Abstract

EF-hand Ca²⁺-binding proteins are thought to shape the spatiotemporal properties of cellular Ca²⁺ signaling and are prominently expressed in sensory hair cells in the ear. Here, we combined genetic disruption of parvalbumin-α, calbindin-D28k, and calretinin in mice with patch-clamp recording, in vivo physiology, and mathematical modeling to study their role in Ca²⁺ signaling, exocytosis, and sound encoding at the synapses of inner hair cells (IHCs). IHCs lacking all three proteins showed excessive exocytosis during prolonged depolarizations, despite enhanced Ca²⁺-dependent inactivation of their Ca²⁺ current. Exocytosis of readily releasable vesicles remained unchanged, in accordance with the estimated tight spatial coupling of Ca²⁺ channels and release sites (effective “coupling distance” of 17 nm). Substitution experiments with synthetic Ca²⁺ chelators indicated the presence of endogenous Ca²⁺ buffers equivalent to 1 mM synthetic Ca²⁺-binding sites, approximately half of them with kinetics as fast as 1,2-Bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid (BAPTA). Synaptic sound encoding was largely unaltered, suggesting that excess exocytosis occurs extrasynaptically. We conclude that EF-hand Ca²⁺ buffers regulate presynaptic IHC function for metabolically efficient sound coding.

Intracellular Ca²⁺ signaling regulates a multitude of cellular processes. In sensory hair cells, Ca²⁺ is crucial for electrical frequency tuning, afferent synaptic transmission, and efferent modulation (reviewed in ref. 1). To separate these signaling pathways and maintain high temporal fidelity of neurotransmission, Ca²⁺ signals must be temporally limited and spatially confined to the site of action. Cells typically achieve this by localizing Ca²⁺ entry and by rapidly removing free Ca²⁺ ions via binding to cytosolic “buffers” and finally Ca²⁺ extrusion (2–4). Of the various EF-hand Ca²⁺-binding proteins, some seem to function primarily as Ca²⁺-dependent signaling proteins (e.g., calmodulin and Ca²⁺-binding proteins 1–8, CaBP1–8), whereas others [parvalbumin-α (PVα), calbindin-D28k (CB), and calretinin (CR)] are thought to mainly serve as mobile Ca²⁺ buffers.

Hair cells of various species strongly express the Ca²⁺-binding proteins PV, CB, and, in some cases, CR. This possibly reflects the need for buffers with different biophysical properties to functionally isolate different Ca²⁺ signaling mechanisms, which are spatially not well separated in these compact epithelial cells. Ca²⁺-binding proteins are particularly abundant in frog and chicken hair cells, which contain millimolar concentrations of parvalbumin-3 (5) as well as of CR (6, 7). An immune-EM study in rats indicated hundreds of micromolar of proteinaceous Ca²⁺-binding sites in inner hair cells (IHCs) (8). A patch-clamp study in gerbil IHCs reported endogenous buffers equivalent to approximately 0.4 mM 1,2-Bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid (BAPTA) (9). Genetic deletion of the EF-hand Ca²⁺-binding proteins PVα, CB, and CR in mice has facilitated the analysis of their function (10–13; reviewed in ref. 14), but the combined deletion of these proteins remains to be studied. IHCs provide an experimentally well-accessible presynaptic preparation that uses all three. Here, we studied IHC function and hearing in mice lacking the three buffers [triple buffer KO (TKO); Pv^−/−Cb^−/−Cr^−/−]. By using perforated and ruptured-patch recordings, we analyzed voltage-gated Ca²⁺ currents and exocytosis of Pv^−/−Cb^−/−Cr^−/− IHCs, in which we also substituted the deleted endogenous buffers with the synthetic Ca²⁺ chelators EGTA or BAPTA. Auditory systems function was probed by measuring otoacoustic emissions and auditory brainstem responses (ABRs) as well as by recordings from single spiral ganglion neurons (SGNs). We performed mathematical modeling to estimate concentrations of the endogenous mobile Ca²⁺ buffers and to better understand how these proteins control exocytosis at IHC synapses. We conclude that the endogenous buffer capacity of IHCs is well approximated by 1 mM synthetic Ca²⁺-binding sites with different kinetics. A tight spatial coupling between Ca²⁺ channels and sensors of exocytosis (Ca²⁺ channel-exocytosis coupling) precludes interference of PVα, CB, and CR with fusion of the readily releasable pool of vesicles (RRP). Instead, we suggest that these buffers jointly regulate IHC presynaptic function by restricting neurotransmitter release to active zones (AZs).

Results

IHCs of Hearing Mice Express PVα, CB, and CR.

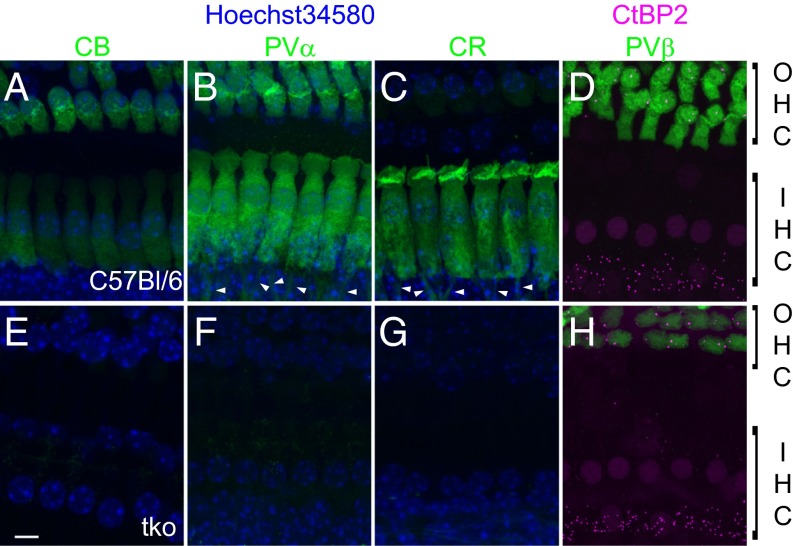
Hair cells in various species show specific expression patterns of the EF-hand Ca²⁺-binding proteins PVα, parvalbumin-β (PVβ) (oncomodulin), CB, and CR (5, 7, 8, 15), hereafter termed “mobile Ca²⁺ buffers” so as not to ignore the presence of other Ca²⁺ buffers such as ATP. We performed immunohistochemistry on apical organs of Corti of hearing C57BL/6 mice [postnatal day (P) 14–26] to characterize the expression of mobile Ca²⁺ buffers in mouse cochlear hair cells (Fig. 1). In agreement with results obtained in rats (8), we found mature mouse IHCs to express PVα, CB, and CR (Fig. 1 A–C), but not PVβ, which was strongly expressed in outer hair cells (OHCs) (Fig. 1D). Parallel immunostaining of organs of Corti from age-matched Pv^−/−Cb^−/−Cr^−/− mice confirmed the absence of these three mobile Ca²⁺ buffers from all tissues (Fig. 1 E–G) but the persistent expression of PVβ in OHCs (Fig. 1H).

Fig. 1.

IHCs of hearing mice express the EF-hand Ca²⁺-binding proteins PVα, CB, and CR. (A–H) Maximum projections of confocal stacks from whole-mount explants of the apical coils of P14–P26 organs of Corti of WT (Top) and Pv^−/−Cb^−/−Cr^−/− (TKO; Bottom) mice immunolabeled for calbindin-D28k (CB; A and E), parvalbumin-α (PVα; B and F), calretinin (CR; C and G), and parvalbumin-β (PVβ; D and H, all in green). An antibody against CtBP2 was used as a marker of presynaptic ribbons and cell nuclei (magenta, D and H). In all other panels, cell nuclei were stained with Hoechst 34580 (blue). IHC bodies of WT but not TKO organs of Corti are homogeneously stained for three Ca²⁺ buffers, CB, PVα, and CR. OHCs additionally contain PVβ, not present in IHCs and not targeted for deletion in the TKO mice. PVα and CR show immunoreactivity also in the afferent fibers (arrowheads). (Scale bar: 5 µm.)

Disruption of PVα, CB, and CR Increases the Amplitude and Inactivation of Ca²⁺ Current and Enhances Exocytosis in IHCs.

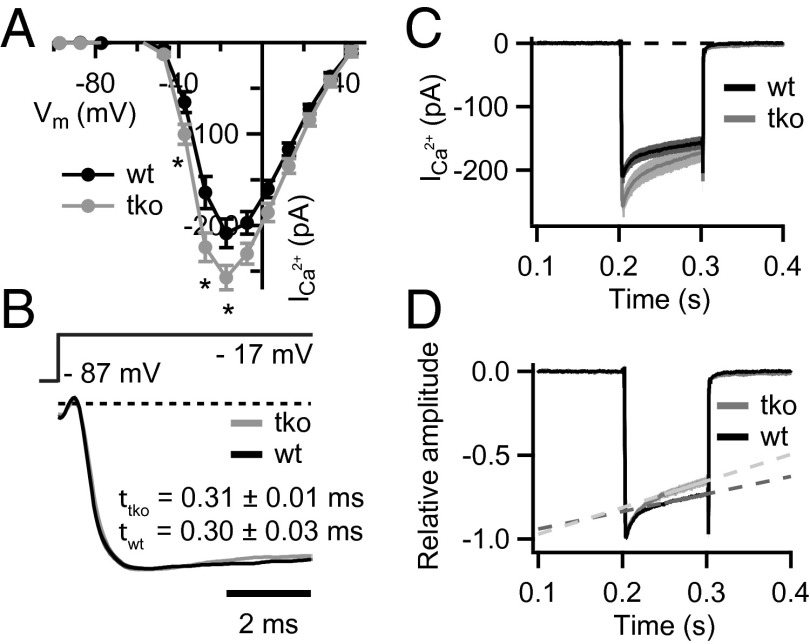
Next, we studied the presynaptic function of Pv^−/−Cb^−/−Cr^−/− IHCs by patch-clamp recordings of Ca²⁺ currents and exocytosis. We first examined the amplitude, voltage dependence, activation, and inactivation of the IHC Ca²⁺ current that is largely mediated by Ca_V1.3 channels (16–18). We used perforated-patch recordings to not interfere with the endogenous Ca²⁺ buffering. We found a 20% increase of the initial Ca²⁺ current, whereas its voltage-dependence was unchanged (Fig. 2A). Ca²⁺-current kinetics were analyzed at the potential eliciting the peak Ca²⁺ current (on average at −17 mV). The activation time constants were comparable between Pv^−/−Cb^−/−Cr^−/− and WT (Pv^+/+Cb^+/+Cr^+/+) IHCs (Fig. 2B). However, we observed a significant increase of Ca²⁺-current inactivation (nonnormalized currents; Fig. 2C). Inactivation was first assessed by analyzing the ratio of the current amplitude at the end of a 100-ms-long depolarization and the initial current amplitude. This ratio was smaller in Pv^−/−Cb^−/−Cr^−/− than in Pv^+/+Cb^+/+Cr^+/+ IHCs (mean ± SEM, 0.71 ± 0.02 vs. 0.79 ± 0.01; P = 0.01, Wilcoxon rank-sum test). As a second measure of the Ca²⁺-current inactivation, we fitted a linear function to the last 50 ms of the normalized Ca²⁺ currents. Its steeper slope for Pv^−/−Cb^−/−Cr^−/− IHCs corroborated the notion of a more pronounced inactivation (Fig. 2D).

Fig. 2.

Disruption of PVα, CB, and CR enhances Ca²⁺-current amplitude and inactivation. (A) Current–voltage relationship of the voltage-gated Ca²⁺ current in TKO (gray, n = 20) and WT (black, n = 23) IHCs from 2–3-wk-old mice. Note the slightly larger Ca²⁺ currents in the TKO IHCs (*P = 0.01–0.03, Student t test). (B) Normalized average Ca²⁺ currents in response to 10–100-ms depolarizations to the peak Ca²⁺-current potential on an expanded time scale demonstrate that the kinetics of the activation were not different among TKO and WT IHCs (P = 0.13, Wilcoxon rank-sum test). Data were fitted with I(t) = I₀ + I_max × (1 − e^−t/τ)^p, whereby the power (p) was fixed to 2 in most cases. (C and D) Absolute (C) and normalized (D) Ca²⁺ currents in response to 100-ms depolarizations to the peak Ca²⁺ current potential. A stronger Ca²⁺-current inactivation was observed in the TKO IHCs. Slopes of the linear fits (1/s) are 1.0 ± 0.1 and 1.6 ± 0.2 for the Ca²⁺ currents in WT (n = 16) and TKO (n = 14) IHCs, respectively (P = 0.02, Student t test).

To address potential mechanisms underlying the increased Ca²⁺-current amplitude, we evaluated the number and morphological appearance of the ribbon synapses in IHCs after hearing onset (P15–P18). The presynaptic ribbon protein Ribeye/CtBP2 and the postsynaptic glutamate receptor GluA 2/3 were visualized by confocal microscopy of immunolabeled organs of Corti (19). We found comparable numbers of ribbons (12.5 ± 0.9 and 13.9 ± 0.5; SI Appendix, Fig. S1), glutamate receptor clusters (12.5 ± 0.8 and 13.4 ± 1.1), as well as ribbon synapses (12.0 ± 0.9 and 12.6 ± 0.9 in six WT and five TKO organs of Corti, respectively). This argues against a potential up-regulation of synapse number as a cause for the increased Ca²⁺ current. It also rules out an excitotoxic degradation of synapses that one might have expected from potentially enhanced glutamate release in the absence of the three Ca²⁺ buffers.

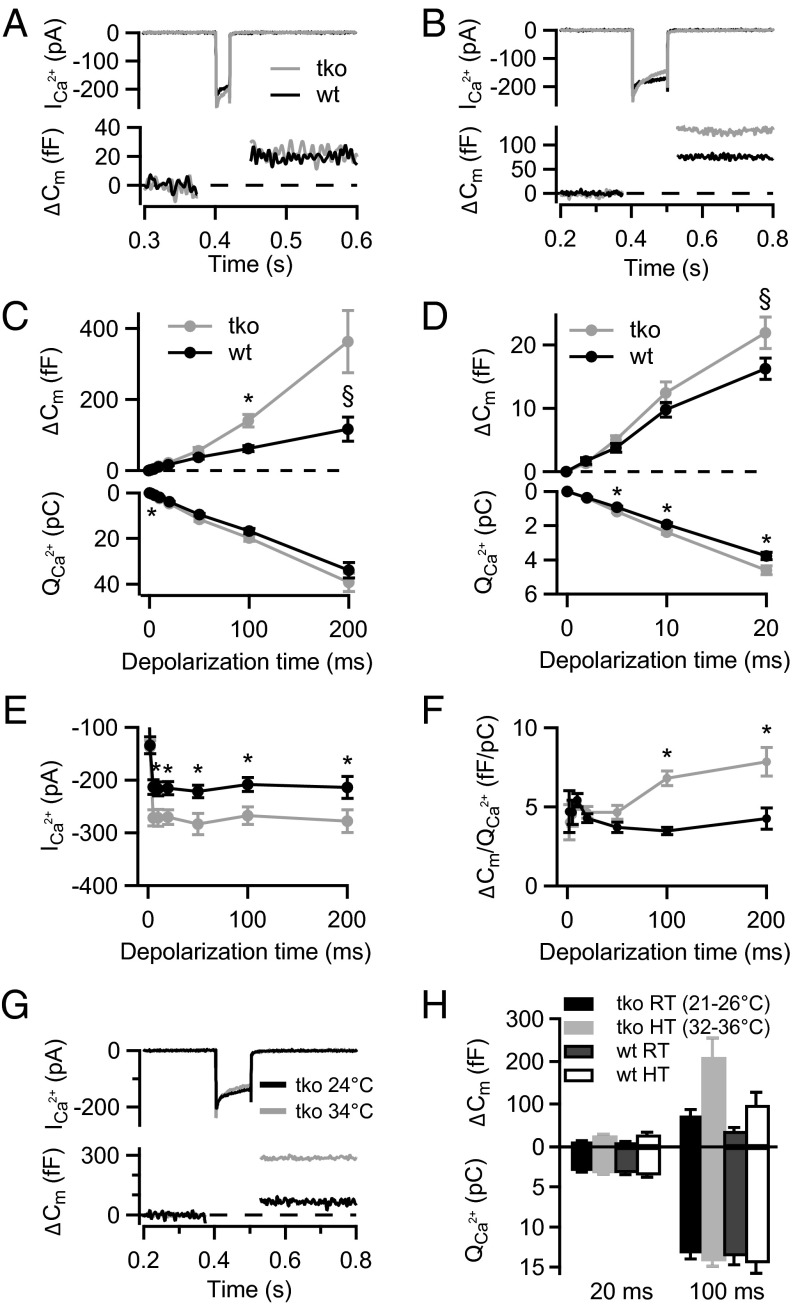
We then studied depolarization-induced exocytosis by using membrane capacitance (C_m) measurements, first in perforated-patch experiments and second in ruptured-patch recordings from Pv^−/−Cb^−/−Cr^−/− IHCs with varying concentrations of BAPTA or EGTA in the pipette solution. To probe for potential effects of Ca²⁺-buffer deficiency on exocytosis, cells were depolarized for different durations and C_m was measured before and after depolarization (Fig. 3). Interestingly, exocytosis upon short stimuli was not significantly altered (Fig. 3 C and D), a finding that can, according to our mathematical model, best be explained by tight Ca²⁺ channel–exocytosis coupling (as detailed later). However, we found more exocytosis in the Pv^−/−Cb^−/−Cr^−/− IHCs for longer stimuli (P < 0.05 for ΔC_m,100ms; Fig. 3C; figure legends provide P values of other ΔC_m measurements) despite comparable Ca²⁺-charge transfer. The ΔC_m amplitude was more variable for 200-ms depolarizations, but the higher efficiency of Ca²⁺ influx to drive sustained exocytosis in Pv^−/−Cb^−/−Cr^−/− IHCs can readily be appreciated from the ratio of exocytic increments over Ca²⁺-current integrals (Fig. 3F). Despite increased initial Ca²⁺ current, the Ca²⁺ charge transfer for long depolarizations was not significantly larger in Pv^−/−Cb^−/−Cr^−/− IHCs as a result of stronger Ca²⁺-current inactivation (Fig. 3C, Lower). Sustained exocytosis tended to be enhanced for Pv^−/−Cb^−/−Cr^−/− IHCs also in near physiological conditions (>32 °C, 2 mM extracellular [Ca²⁺]), indicating that this likely also occurs in vivo (Fig. 3 G and H). We conclude that the mobile Ca²⁺ buffers PVα, CB, and CR contribute to the regulation of presynaptic Ca²⁺ influx and exocytosis.

Fig. 3.

Enhanced sustained exocytosis in the absence of PVα, CB, and CR. (A and B) Representative Ca²⁺ currents (Top) and C_m (ΔC_m) responses (Bottom) of TKO (gray) and WT (black) IHCs to (A) 20-ms and (B) 100-ms depolarization to peak Ca²⁺-current potential, recorded in the perforated-patch configuration. (C) Exocytosis (ΔC_m; Top) and the corresponding Ca²⁺-current integrals (Q_Ca; Bottom) as a function of duration of depolarizations to peak Ca²⁺-current potential. The C_m increase in response to 100-ms depolarization (ΔC_m,100ms) was significantly higher in TKO (gray, n = 24) compared with WT IHCs [black, n = 23; *P = 0.0003, Wilcoxon rank-sum test; ^§P = 0.06, Wilcoxon rank-sum test (C) and Student t test (D)]. Note larger Q_Ca in TKO IHCs at short but not long depolarization (*P = 0.009 for 5 ms and P = 0.02 for 10- and 20-ms depolarization, Student t test). All responses are given as grand averages (calculated from the means of the individual cells) ± SEM. (D) ΔC_m (Top) and Q_Ca (Bottom) in response to short depolarizations evoking the exocytosis of the RRP displayed on an expanded time scale. (E) Ca²⁺-current amplitudes (I_Ca) were significantly increased in the TKO IHCs (*P < 0.0004, Student t test). (F) The Ca²⁺ efficiency of exocytosis was higher in the TKO IHCs for long depolarizations (*P = 1.5 × 10⁻¹⁰ for 100 ms and P = 0.007 for 200 ms depolarization, Wilcoxon rank-sum test). The extracellular [Ca²⁺] was 5 mM. (G) Representative Ca²⁺ currents (Top) and ΔC_m (Bottom) of a TKO IHCs recorded at room (black) or close to physiological temperature (gray) with 2 mM extracellular [Ca²⁺]. (H) Average ΔC_m and Q_Ca in response to 20- and 100-ms depolarizations recorded at room temperature (RT; black and dark gray) and high temperature (HT; close to physiological temperature, light gray and white) in WT (n = 4) and TKO (n = 5) IHCs. Note a two- to threefold increase in ΔC_m responses upon increase in temperature in the IHCs of both genotypes.

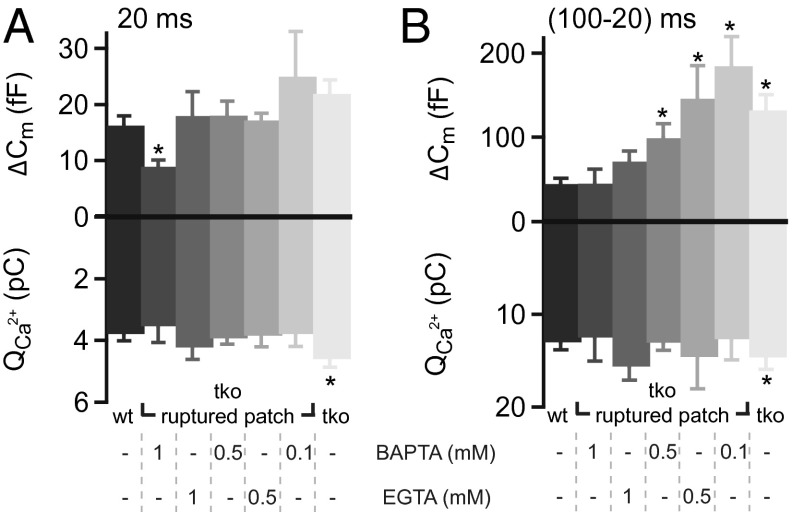
To approximate the concentration and binding kinetics of the mobile Ca²⁺ buffers of IHCs, we studied the effects of substituting endogenous Ca²⁺ buffers by BAPTA (“fast binding”: association rate constant k_on = 4 × 10⁸ M^−1⋅s⁻¹; see ref. 20) or EGTA (“slow binding”: k_on = 4.5 × 10⁶ or 10⁷ M^−1⋅s⁻¹; see refs. 20, 21) on RRP exocytosis (probed by 20-ms depolarizations) (22) and sustained exocytosis (approximated by the difference between the responses to 100- and 20-ms depolarizations). Synthetic buffers were loaded into Pv^−/−Cb^−/−Cr^−/− IHCs to restore the exocytic responses of Pv^+/+Cb^+/+Cr^+/+ IHCs in their native buffering conditions (Fig. 4). We found that 1 mM EGTA or BAPTA reduced sustained exocytosis in Pv^−/−Cb^−/−Cr^−/− IHCs to levels comparable to Pv^+/+Cb^+/+Cr^+/+ IHCs recorded in perforated-patch recordings (Fig. 4B). BAPTA (1 mM) best matched to the exocytic responses of Pv^+/+Cb^+/+Cr^+/+ IHC for prolonged depolarizations, but significantly diminished RRP exocytosis (Fig. 4A). Lower concentrations of fast or slow Ca²⁺ buffer, on the contrary, left RRP exocytosis unchanged, but could not reinstate the sustained exocytic response as seen in Pv^+/+Cb^+/+Cr^+/+ IHCs. From these experiments, we conclude that the endogenous concentration of mobile buffers in IHCs is equivalent to ∼1 mM synthetic Ca²⁺-binding sites, half of them with kinetics as fast as BAPTA. Of note, none of the tested concentrations of EGTA or BAPTA was able to accurately restore the exocytic responses as observed in Pv^+/+Cb^+/+Cr^+/+ IHCs.

Fig. 4.

Functional estimation of the concentration and kinetics of endogenous Ca²⁺-binding sites in IHCs. (A) ΔC_m and Q_Ca in response to depolarization for 20 ms (probing the RRP) in WT and TKO IHCs using perforated-patch (black and light gray) and in KO IHCs using ruptured-patch configuration with different concentrations of the exogenously added synthetic Ca²⁺ chelators BAPTA and EGTA (shades of gray). (B) Difference in the ΔC_m and Q_Ca in response to 100 and 20 ms (probing the sustained exocytosis). When testing the sustained component of exocytosis 0.5 mM of either buffer was insufficient in Ca²⁺ buffering. On the contrary, 1 mM BAPTA (but not EGTA) significantly reduced the amount of RRP exocytosis (A). Asterisks denote significant difference vs. WT controls (P < 0.01, Student t test or Wilcoxon rank-sum test). From left to right, n = 18, n = 6, n = 5, n = 12, n = 10, n = 7, and n = 12 IHCs were analyzed.

The Absence of PVα, CB, and CR Has Little Impact on Hearing.

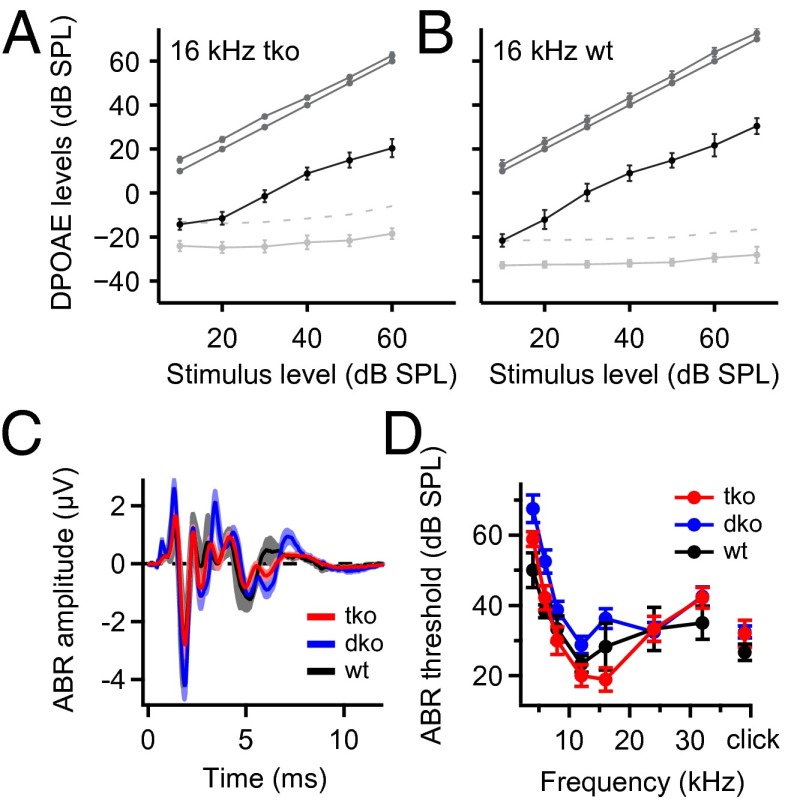
We first tested cochlear amplification by measuring distortion product otoacoustic emissions (DPOAEs), which were found to be intact in Pv^−/−Cb^−/−Cr^−/− mice (Fig. 5 A and B). We then investigated the synchronized neuronal signaling along the auditory pathway by measuring ABRs (Fig. 5 C and D). Over the time course of the project, we encountered variable ABR phenotypes of Pv^−/−Cb^−/−Cr^−/− mice. In the majority of animals, there was no noticeable increase in the ABR thresholds for tone bursts at different frequencies or clicks in comparison with age-matched Pv^+/+Cb^+/+Cr^+/+ mice (Fig. 5D). We additionally tested hearing in mice deficient only in PVα and CB (Pv^−/−Cb^−/−). They did not show a significant hearing deficit as assessed by ABR (Fig. 5 C and D), which is consistent with the majority of our Pv^−/−Cb^−/−Cr^−/− data.

Fig. 5.

Cochlear function is preserved in mice lacking the three most prominent EF-hand Ca²⁺ buffers. (A and B) Input/output functions of otoacoustic emissions (i.e., DPOAEs; black lines) of the TKO (A) and WT (B) mice at 16 kHz f₂ tone. Solid light gray lines indicate the noise floor; dotted light gray lines indicate 2 SDs above the noise floor. The dark gray lines represent both primary tones. All data represent grand averages over several animals. No significant difference was observed between the WT and TKO mice. (C) Average ABR in response to 80 dB clicks in WT (black), Pv^−/−Cb^−/− (DKO; blue), and TKO (red) mice. (D) Analysis of ABR thresholds revealed no significant difference among the three genotypes. All data are given as mean ± SEM.

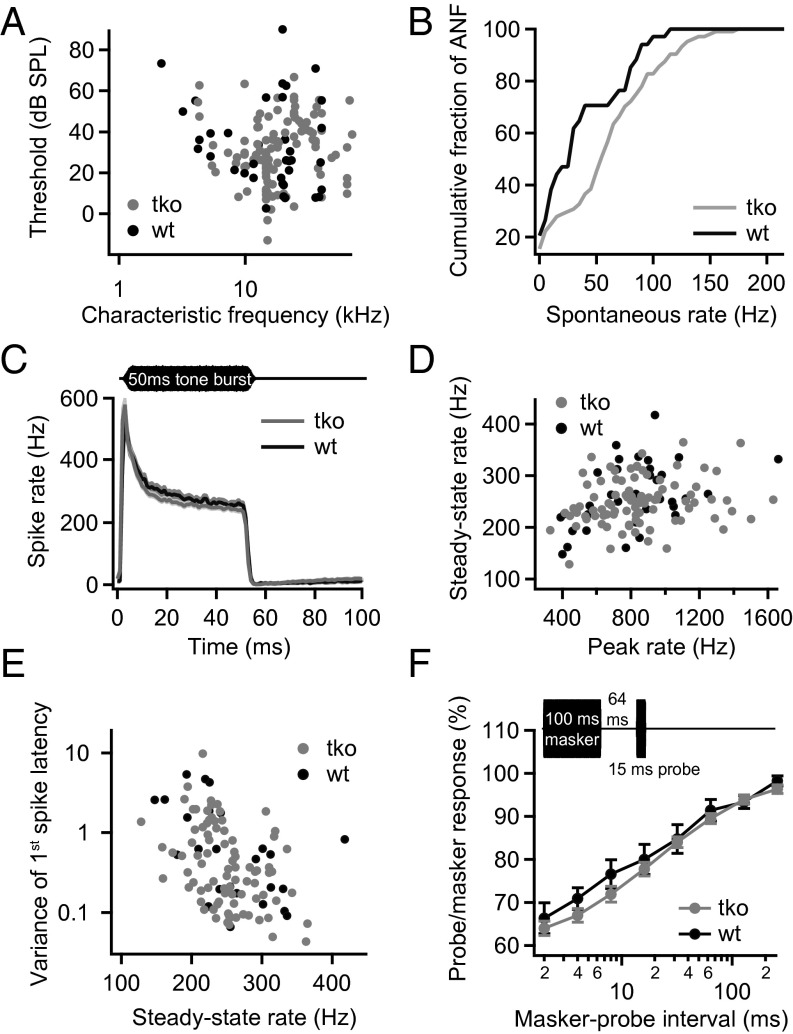
Next, we studied sound encoding at the single SGN level. Consistent with their near normal population responses (Fig. 5), the single fiber thresholds were comparable between Pv^−/−Cb^−/−Cr^−/− and Pv^+/+Cb^+/+Cr^+/+ SGNs (Fig. 6A). The rate of spontaneous SGN firing was increased in Pv^−/−Cb^−/−Cr^−/− mice (P = 0.04, Kolmogorov–Smirnov test; Fig. 6B), which likely reflects enhanced transmitter release from buffer-deficient IHCs in the absence of sound.

Fig. 6.

Disruption of PVα, CB, and CR has little impact on sound encoding by single SGNs. (A) Thresholds measured at the CF of each auditory nerve fiber. The thresholds of the TKO fibers (gray, n = 111) were comparable to WT controls (black, n = 37). (B) Spontaneous rate distributions in TKO mice (gray, n = 104) and control groups (black, n = 34). Higher spontaneous rates were observed in SGNs of the TKO animals. (C) Mean peristimulus time histograms (±SEM) plotting the instantaneous spiking rate in 1-ms time bins over the time course of stimulation with tone bursts at the CF of each SGN, 30 dB above threshold. The rates and the time course of adaptation were similar in TKO (gray, n = 87) and WT SGNs (black, n = 35). (D) The analysis of the peak rates (rate in largest 1-ms bin) vs. the steady-state spike rates (averaged over 10 ms from 35 ms after stimulus onset) shows comparable rates between TKO SGNs (gray) and WT controls (black). (E) The variance of the first spike latency was similar between fibers from TKO mice and WT controls. (F) Recovery from adaptation probed by a forward-masking paradigm (Inset): maximal masking and the time course of recovery were similar for TKO (gray, n = 35) and WT controls (black, n = 8). Stimuli were applied at CF, 30 dB above threshold.

We then stimulated each SGN with 50-ms tone bursts at 30 dB above threshold at the characteristic frequency (CF) to study sound-driven spike rates at saturating sound pressure levels (Fig. 6C). Like in previously published data (23–25), all SGNs showed a high onset firing rate followed by adaptation to reach a lower, but still sizable, steady-state rate. We found no significant differences in the peak rates in SGNs of Pv^−/−Cb^−/−Cr^−/− mice (Fig. 6D). Steady-state spike rates were comparable (SI Appendix, Fig. S2B) or even slightly lower in Pv^−/−Cb^−/−Cr^−/− mice (Fig. 6 C and D), in apparent contrast to the enhanced sustained exocytosis in IHCs (Fig. 3), an unexpected observation that we investigated in more detail by mathematical modeling (as detailed later). Pv^−/−Cb^−/−Cr^−/− SGNs also showed very good temporal precision of sound-onset coding (Fig. 6E). Forward masking experiments (26, 27) revealed a normal extent of depletion of the RRP and unaltered replenishment kinetics (Fig. 6F). In summary, the single SGN data agree with the notion of a largely unimpaired peripheral auditory function, including a normal temporal precision of sound encoding for transient and sustained stimuli (SI Appendix, Fig. S3).

No Obvious Up-Regulation of Perisynaptic Mitochondria or Plasma Membrane Ca²⁺ Pumps in IHCs Lacking PVα and CB.

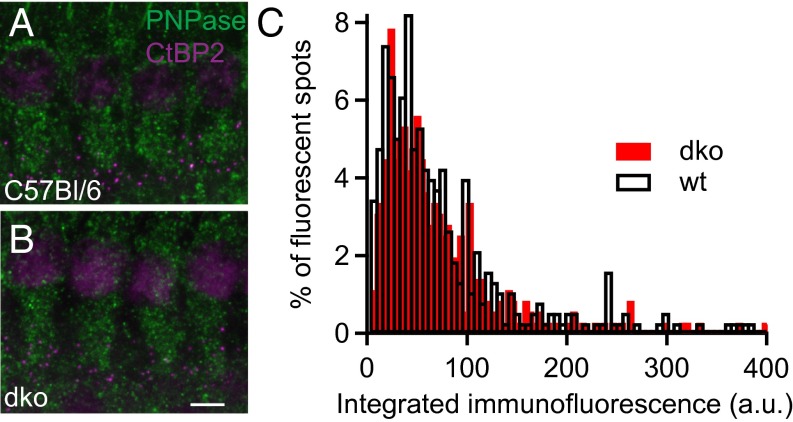
The weak effects of Ca²⁺-buffer deficiency on synaptic sound coding prompted us to test for a potential compensation by enhanced perisynaptic mitochondrial Ca²⁺ uptake (11, 28). To test whether mitochondria are present in increased number or are perhaps enlarged around the synapses in the Ca²⁺-buffer KOs (28), we performed semiquantitative immunohistochemistry in isolated organs of Corti of Pv^−/−Cb^−/− and C57BL/6 mice. Apical coils of the organs of Corti were stained for the mitochondria by using the marker PNPase (29) and ribbons (CtBP2; Fig. 7 A and B). Samples of both genotypes were processed identically and in parallel during immunohistochemistry and confocal imaging (Fig. 7C). Cumulative PNPase immunofluorescence was analyzed in a total of 1,440 C57BL/6 and 1,260 Pv^−/−Cb^−/− synapses from four different experiments on cochleae of eight C57BL/6 and Pv^−/−Cb^−/− mice. In none of the experiments did we observe a significantly increased presynaptic PNPase immunofluorescence in IHCs of Pv^−/−Cb^−/− mice, indicating a normal mitochondrial abundance despite the absence of PVα and CB. Similarly, we did not detect an up-regulation of the plasma membrane Ca²⁺-pumps (PMCAs; SI Appendix, Fig. S4).

Fig. 7.

Immunofluorescence analysis of perisynaptic abundance of mitochondria. (A and B) The whole mount of the C57BL/6 (WT) and DKO organs of Corti double stained for the mitochondrial marker PNPase (green) and the presynaptic marker CtBP2 (magenta) reveals similar abundance of mitochondria in IHCs of both genotypes. (Scale bar: 5 µm.) (C) Perisynaptic PNPase immunofluorescence intensity (integrated within a 0.5-µm radius around the center of mass of CtBP2 fluorescence in single confocal sections) in WT and DKO IHCs. A total of 377 synapses from four C57BL/6 (WT) organs and 357 synapses from four DKO organs were analyzed, and the distributions were statistically indistinguishable (P = 0.94, Wilcoxon rank-sum test).

Computational Analysis of IHC Exocytosis and SGN Spiking Indicates Enhanced Extrasynaptic Release in Pv^−/−Cb^−/−Cr^−/− IHCs.

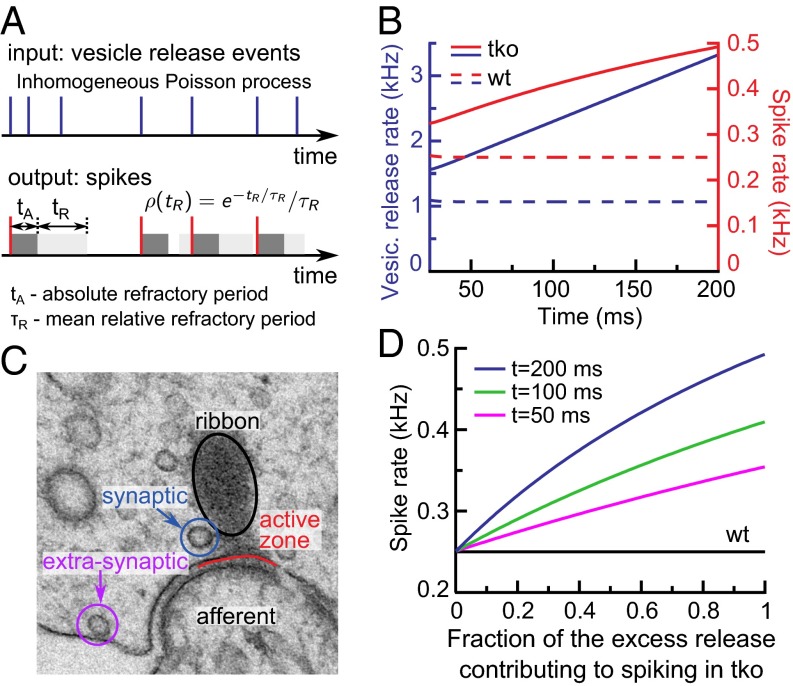
SGN activity is governed by transmitter release at the IHC ribbon synapse. To understand how increased IHC exocytosis of the Pv^−/−Cb^−/−Cr^−/− animals influences SGN spiking rate, we used mathematical modeling (24) (Fig. 8A and Materials and Methods). Specifically, we addressed the question whether the excess sustained exocytosis reflects an acceleration of synaptic vesicle replenishment by Ca²⁺ (30, 31) or extrasynaptic release caused by the wider spread of the synaptic Ca²⁺ signal. The model converts release events in IHCs into SGN spiking by taking into account neuronal refractoriness (32, 33). Refractory periods in WT and TKO SGNs were similar (1.11 ± 0.04 ms and 1.02 ± 0.03 ms, respectively; SI Appendix, Fig. S5C). By using these parameters and assuming that all sustained IHC exocytosis occurs synaptically, i.e., drives spiking in the postsynaptic SGNs, the spike rates predicted for Pv^−/−Cb^−/−Cr^−/− SGNs substantially exceeded the experimentally observed ones (Fig. 8B). The discrepancy persisted even when assuming unrealistically long refractory periods (SI Appendix, Fig. S5D). This indicates that a large fraction of the increased sustained exocytosis in the Pv^−/−Cb^−/−Cr^−/− IHCs occurs at extrasynaptic (i.e., ectopic) locations, and is ineffective in driving SGNs. Indeed, membrane-proximal vesicles outside the AZ are observed in hair cells (34, 35) (Fig. 8C). We then estimated what fraction of the excess sustained exocytosis in Pv^−/−Cb^−/−Cr^−/− IHCs could be synaptic (Fig. 8D). Only when this fraction was set at less than 10% did the difference between the computed and experimentally observed spike rates fall within the uncertainty range of the experimental data. Therefore, we conclude that only a minor part of the excess sustained exocytosis, if any, reflects enhanced vesicle replenishment caused by stronger Ca²⁺ signaling in the absence of mobile Ca²⁺ buffers.

Fig. 8.

Mathematical modeling of spike rates in WT and TKO SGNs. (A) Schematic representation of the model for release event to spike conversion (Materials and Methods). (B) Time dependence of vesicle release rate (blue) and spike rate (red) during sustained exocytosis (t > 25 ms) in WT (dashed lines) and TKO (solid lines). (C) An example of a transmission EM micrograph of an IHC ribbon synapse illustrating the concept of the synaptic vs. ectopic/extrasynaptic vesicle release. Image courtesy of C. Wichmann, University of Göttingen, Göttingen, Germany. (D) Modeled spike rate dependence on a putative fraction of the excess release contributing to the spike generation in SGNs in TKO compared with WT at average overall refractory period t_A + τ_R = 1.1 ms.

Tight Coupling Between Presynaptic Ca²⁺ Channels and Ca²⁺ Sensors of Exocytosis Limits the Interference of Mobile Ca²⁺ Buffers with IHC Synaptic Exocytosis.

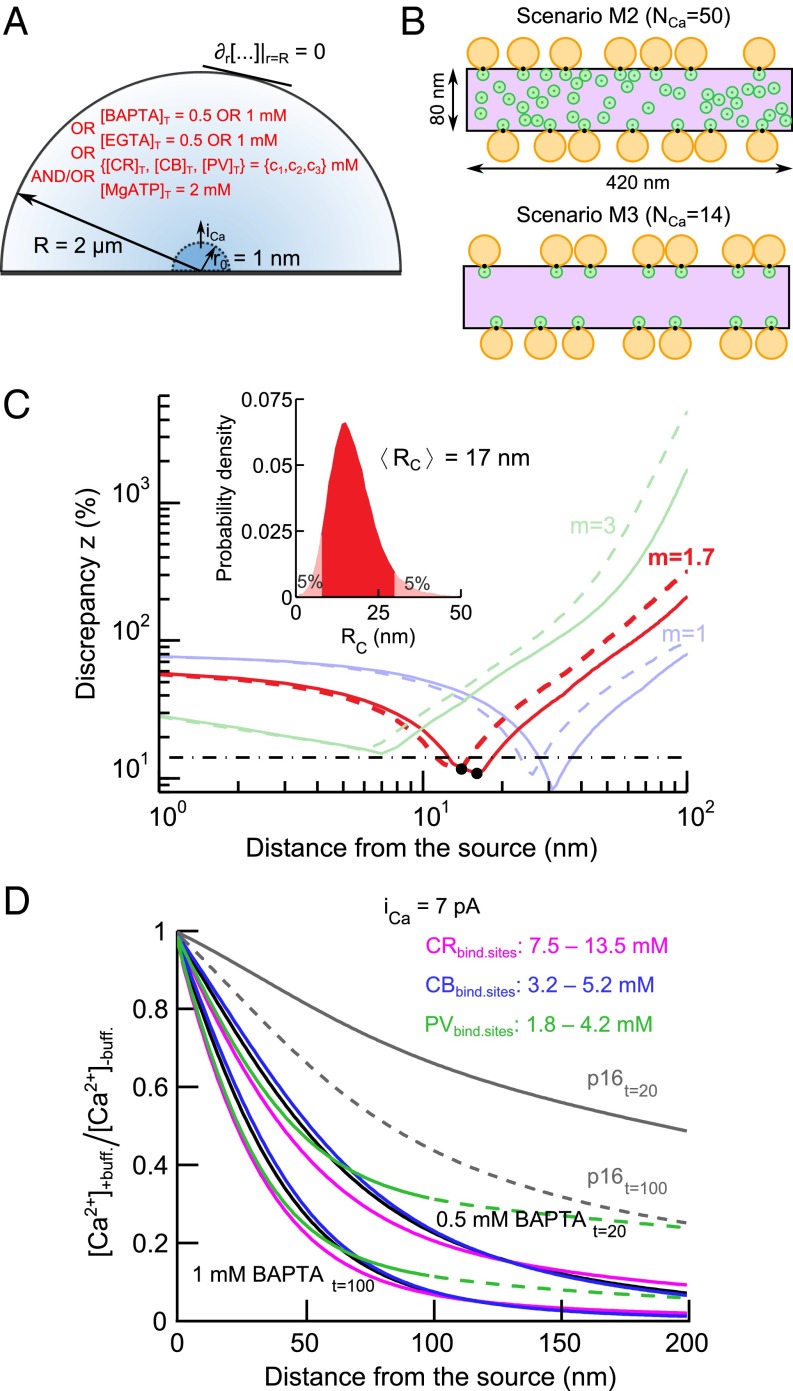
Our experimental observations suggest that endogenous EF-hand Ca²⁺-binding proteins possess only modest ability to influence synaptic transmitter release in IHCs. This might reflect a very small distance between the Ca²⁺ source (i.e., Ca²⁺ channels) and vesicles undergoing fusion at the AZ (“coupling distance”). To determine this coupling distance in IHCs, we constructed a model that predicts the relative amount of exocytosis triggered when changing the distance between the Ca²⁺ source and the Ca²⁺ sensor of release (Fig. 9A and Materials and Methods). We used this model to determine the effective coupling distance R_c (weighted average distance for all channels contributing to the [Ca²⁺] at the Ca²⁺ sensor; Materials and Methods and SI Appendix, section 8) that best matched exocytosis as observed experimentally under various Ca²⁺-buffering conditions at room temperature. The model was based on the spatiotemporal profile of intracellular [Ca²⁺] resulting from Ca²⁺ influx through a single 1-nm radius hemispherical source. The integrated exocytosis was assumed to follow [Ca²⁺] according to a power law relation: ΔC_m ∼ ([Ca²⁺])^m·q. The exponent q accounts for the supralinear dependence of [Ca²⁺] on Q_Ca: [Ca²⁺] ∼ Q_Ca^1/q that may result from partial buffer depletion at high Ca²⁺ influx (SI Appendix, section 7.4). The apparent Ca²⁺ cooperativity of exocytosis m was derived from prior experiments (36) and the value of 1.7 was obtained (SI Appendix, Fig. S6). We note that our previous studies aimed at determining the maximal apparent Ca²⁺ cooperativity of the RRP exocytosis, which is close to the intrinsic Ca²⁺ cooperativity, thus yielding an m in the range of 3–4 in 2-wk-old animals (36, 37). The model relationship of the present study needs to use an effective m value matched to the experimental conditions [i.e., in the presence of partial pool depletion/sensor saturation observed at high Q_Ca (36)].

Fig. 9.

Estimation of endogenous buffer concentrations and effective coupling distance between presynaptic Ca²⁺ channels and Ca²⁺ sensors of exocytosis. (A) Schematic representation of the hemispherical source model. (B) AZ scenarios M2 and M3 from Wong et al. (36) corresponding to the nanodomain-coupling regime. Orange discs represent RRP vesicles, green discs represent Ca²⁺ channels, black spots represent Ca²⁺ sensors of exocytosis, and violet area represents the presynaptic density. (C) Dependence of the discrepancy measure z on the effective coupling distance R_c. Different colors stand for different values of the apparent Ca²⁺ cooperativity of exocytosis, m. Dashed lines correspond to i_Ca of 0.3 pA; solid lines correspond to i_Ca of 7 pA. Black points denote the local minima of the discrepancy measure z for m of 1.7. Black dash-dotted line corresponds to the average of experimental SEM[ΔC_m]/mean[ΔC_m] at different Ca²⁺ buffering conditions. (Inset) Bootstrap distribution of R_c estimate for m of 1.7 and i_Ca of 7 pA, generated as described in Materials and Methods. (D) Spatial profiles of [Ca²⁺] reduction, [Ca²⁺]_+buff./[Ca²⁺]_−buff., caused by particular intracellular buffers during Ca²⁺ influx (i_Ca = 7 pA). Black lines show ratios of the Ca²⁺ profiles in the presence and absence of 0.5 mM and 1 mM BAPTA, gray lines in the presence and absence of endogenous buffers with concentrations as reported previously (8) in P16 rat IHCs (solid and dashed lines correspond to [Ca²⁺] spatial profiles at t = 20 ms and t = 100 ms, respectively). Colored lines are the best fits of [Ca²⁺]_+buff./[Ca²⁺]_−buff. with CR (magenta), CB (blue), and PVα (green) corresponding to 0.5 mM and 1 mM BAPTA.

Fig. 9C displays the discrepancy between modeled and experimentally observed exocytosis for assumed coupling distances between 1 and 100 nm and for three different values of m. When m is equal to 1.7, the minimum discrepancy is ∼11%, which is smaller than the experimental error [∼14% for the average SEM(ΔC_m)/mean(ΔC_m) under different Ca²⁺ buffering conditions; Fig. 9C, dash-dotted line]. For small Ca²⁺ influx, i_Ca, buffer depletion was negligible and the discrepancy between the model and the measurements insensitive to the absolute value of i_Ca. For instance, a Ca²⁺ influx of 0.3 pA (approximating the single channel current at −17 mV) (38) drove negligible buffer depletion and led to estimates of the effective coupling distance of 15 nm, for m of 1.7 (Fig. 9C, dashed red line). As buffer depletion effects might be more prominent for larger Ca²⁺ influx, we also determined R_c assuming conditions of strong Ca²⁺ influx. To this end, we calculated the extent of buffer depletion near the AZ by using a hemispherical source equivalent to the entire presynaptic density in a mature synapse (surface area ∼420 × 80 nm²) (36) and the maximal depolarization-evoked Ca²⁺ current per synapse in Pv^+/+Cb^+/+Cr^+/+ IHCs (15 pA). Near a 1-nm hemispherical source, a similar level of buffer depletion was obtained for an i_Ca of 7 pA (SI Appendix, section 7.3). Even for this extreme scenario, partial buffer depletion resulted in only a slight rightward shift of the discrepancy curves (Fig. 9C) with an R_c of 17 nm for an m of 1.7. We used bootstrapping to estimate the confidence range of the R_c estimate for i_Ca of 7 pA, which is affected by the estimation errors of m and ΔC_m. The 5–95 percentile range spanned from 8 to 30 nm (Fig. 9C, Inset).

In our previous work, we introduced some possible IHC presynaptic AZ arrangements (36). In spatially resolved simulations with two of these AZ topographies that correspond to the “nanodomain-coupling” regimen (Fig. 9B), R_c ranged between 15 and 27 nm (SI Appendix, section 8.4). They might thus be a good representation of the true IHC AZs. At the average R_c of 17 nm, the influence of the Ca²⁺ buffers on [Ca²⁺] at the Ca²⁺ sensor is small (0.5 mM BAPTA; Fig. 9D, black line). Together, these results indicate that endogenous Ca²⁺ buffers do not appreciably interfere with exocytosis at the AZ as a result of tight coupling between Ca²⁺ channels and Ca²⁺ sensors of exocytosis in IHCs of 2–3-wk-old mice. However, they effectively reduce extrasynaptic release at sites located more distant from the Ca²⁺ source.

Predicted Concentrations of Endogenous Buffers in Mature Mouse IHCs.

Finally, we used the model to establish lower and upper bounds on the concentrations of endogenous Ca²⁺ buffers in IHCs. Exocytosis of a given readily releasable vesicle is governed by [Ca²⁺] at the Ca²⁺ sensor. According to ΔC_m recordings (Fig. 4), [Ca²⁺] at the Ca²⁺ sensor of exocytosis in Pv^+/+Cb^+/+Cr^+/+ should be matched in Pv^−/−Cb^−/−Cr^−/− IHCs when they are loaded with 0.5 mM BAPTA. On the contrary, 1 mM BAPTA was required for adjusting sustained exocytosis of Pv^−/−Cb^−/−Cr^−/− IHCs to WT levels, likely by limiting [Ca²⁺] further away from the Ca²⁺ channel. The spatial [Ca²⁺] profiles in the presence of these two BAPTA concentrations thus define the range of plausible [Ca²⁺] levels in the presence of endogenous buffers.

Fig. 9D shows the predicted ratios of the spatial [Ca²⁺] profiles with 0.5 and 1 mM BAPTA and the best approximation of these [Ca²⁺] profiles in the presence of the endogenous Ca²⁺ buffers CB, CR, and PVα. The spatial [Ca²⁺] profiles with 0.5 and 1 mM BAPTA were fitted 20 and 100 ms after stimulus onset, respectively. Solving the model with concentrations of endogenous mobile Ca²⁺ buffers (0.5 mM Ca²⁺-binding sites in total) as estimated in rat IHCs by using quantitative immunogold EM (8) showed that these concentrations would be considerably less efficient than 0.5 mM BAPTA. According to our model, the concentration of Ca²⁺-binding sites equivalent to 0.5–1 mM BAPTA is between 3.2 and 5.2 mM for CB, between 7.5 and 13.5 mM for CR, and between 1.8 and 4.2 mM for PVα when each buffer is considered separately (Fig. 9D). We note that, to convert these concentrations of Ca²⁺-binding sites into equivalent protein concentrations, the values have to be divided by 4, 5, and 2 for CB, CR, and PV, respectively; thus, 0.5 mM BAPTA would correspond to 0.8, 1.5, and 0.9 mM of the three buffers. These values are consistent with previous estimates of EF-hand buffer concentrations in neurons (39–41) and hair cells (7). PVα alone could not fully reproduce the spatial [Ca²⁺] profiles predicted for 0.5 or 1 mM BAPTA over distances longer than 100 nm. However, it is likely that, at low concentrations, it acts together with higher amounts of CB and CR to shape the [Ca²⁺] signal at the IHC synapses.

As shown in Fig. 9D, the upper bounds on endogenous buffer Ca²⁺-binding site concentrations were estimated by probing [Ca²⁺] at a t = 100 ms after stimulus application. Negligible at first, the effect of accumulated Ca²⁺ on [Ca²⁺] during stimulation grows with time (SI Appendix, Fig. S7 A and B). This might affect the estimated upper bounds on endogenous Ca²⁺-binding site concentrations. We thus reestimated the upper bounds on the Ca²⁺-binding site concentrations by using spatial profiles of [Ca²⁺] calculated for times between 20 ms and 100 ms after stimulus application. As shown in SI Appendix, Fig. S10 (solid lines), the upper bound estimates were not considerably different at intermediate times for CB and PV (by ∼20% higher at t = 20 ms than at t = 100 ms). For CR, the difference in the estimated Ca²⁺-binding site concentrations was significant, being 50% higher at t = 20 ms than at t = 100 ms. In summary, our results suggest that the concentrations of endogenous buffers in IHCs are (approximately one order) higher than those obtained from immunogold counts (8) or the k_on rates of the buffers in situ (i.e., inside cells) are considerably higher than currently assumed (SI Appendix, section 7.1).

Discussion

In the present study we addressed the role of Ca²⁺ buffering EF-hand Ca²⁺-binding proteins in the presynaptic function of IHCs. By using KO mice lacking PVα, CB, and CR, we indicate that mobile Ca²⁺ buffers shape IHC synaptic Ca²⁺ current by decreasing its amplitude and attenuating inactivation. Independent of their regulation of Ca²⁺ channels, they constrain transmitter release to AZs, ensuring efficient presynaptic function. By using exocytosis as readout together with mathematical modeling, we provide quantitative functional estimates for the concentration of the endogenous Ca²⁺ buffers in IHCs. Furthermore, we estimated the effective coupling distance between the Ca²⁺ channels and sensors for exocytosis in IHCs to be very short (mean value of R_c = 17 nm). Surprisingly, sound encoding and hearing were largely intact upon disruption of the three Ca²⁺ buffers. This can be explained by “Ca²⁺ nanodomain control” of exocytosis, minimizing the impact of buffers on stimulus–secretion coupling at AZs.

Ca²⁺ Buffering in Mammalian IHCs.

Previous work on hair cells had provided estimates of the concentration of mobile Ca²⁺-binding sites (5–9, 42–44), demonstrated the significance of mobile and immobile Ca²⁺ buffers for shaping the spatiotemporal properties of synaptic Ca²⁺ microdomains (2, 44–46), and investigated the sensitivity of exocytosis to Ca²⁺ buffering (9, 22, 37, 47–49). The Pv^−/−Cb^−/−Cr^−/− mice now enabled us to refine the estimates of the concentration of mobile Ca²⁺-binding sites in hair cells and to study the role of the three endogenous Ca²⁺ buffers in hair cell presynaptic function and afferent auditory signaling.

We found that the length constants of Ca²⁺ buffering, defined by Ca²⁺-binding kinetics, diffusion coefficients, and concentrations of the three Ca²⁺ buffers, are large relative to the effective Ca²⁺ channel–Ca²⁺ sensor coupling distance. Consequently, exocytosis of the RRP, triggered by short depolarization pulses (<20 ms), was not noticeably affected by the three Ca²⁺ buffers. During longer depolarizations (≥20 ms), they reduced exocytosis in IHCs primarily by limiting Ca²⁺ spread from the AZ to ectopic release sites (Fig. 3C). In the substitution experiments, 1 mM BAPTA or EGTA reduced sustained exocytosis in Pv^−/−Cb^−/−Cr^−/− IHCs to levels observed in Pv^+/+Cb^+/+Cr^+/+ mice, whereas lower concentrations (≤0.5 mM) were insufficient. This is in good agreement with previous results in mice, in which imaging of synaptic Ca²⁺ microdomains yielded values equivalent to 0.5–2 mM Ca²⁺-binding sites of synthetic Ca²⁺ buffers (44). It also largely agrees with functional estimates on hair cells from other species (5–7, 9, 42). However, when estimating the concentrations of endogenous Ca²⁺-binding sites, a significant difference in the diffusion coefficients and the Ca²⁺ (un)binding rates of synthetic and endogenous buffers has to be taken into account. Relying on published Ca²⁺-binding rates, our model suggested that the concentration of Ca²⁺-binding sites is approximately one order of magnitude higher than reported in rat hair cells by using quantitative immunogold labeling (∼0.54 mM endogenous Ca²⁺-binding sites) (8). Alternatively, faster Ca²⁺-binding rates of the endogenous buffers (an order of magnitude higher than published) could account for the observations, or it could be a combination of both effects.

Modulation of Ca²⁺ Influx by Ca²⁺ Buffering EF-Hand Ca²⁺-Binding Proteins.

A somewhat unexpected finding was the enhanced initial Ca²⁺ influx in Pv^−/−Cb^−/−Cr^−/− IHCs. We did not observe more synapses in Pv^−/−Cb^−/−Cr^−/− IHCs, which could have been an obvious cause for a greater number of Ca²⁺ channels. Instead, potential mechanisms for the increased Ca²⁺ influx include more Ca²⁺ channels per synapse and an enhanced open probability. In addition, we found that Ca²⁺-current inactivation was enhanced in Pv^−/−Cb^−/−Cr^−/− IHCs. Reduced Ca²⁺ buffering could increase Ca²⁺-calmodulin–dependent inactivation (CDI). However, the enhanced inactivation was not reversed upon addition of synthetic Ca²⁺ chelators, which generally show little potency to antagonize CDI in mature IHCs (50, 51). Alternatively, EF-hand Ca²⁺-binding proteins might directly interact with the channel, which is established for calmodulin and CaBPs (52–55). Indeed, CR suppresses CDI in Ca_V2.1 channels (but not Ca_V1.2 channels) in HEK 293-T cells (56).

Ca²⁺ Nanodomain Control of Fusion at the IHC Ribbon Synapse.

Our previous work suggested that vesicle fusion at IHC ribbon synapses is induced by Ca²⁺ provided by one or few proximal Ca²⁺ channels (36, 37), nicknamed Ca²⁺ nanodomain control. In accordance, it has been demonstrated that not even 10 mM BAPTA completely blocks exocytosis in auditory hair cells (57). The present study took advantage of the disruption of endogenous Ca²⁺ buffers and substitution with synthetic Ca²⁺ buffers to further test this hypothesis. Based on experiments and modeling, we estimated the effective coupling distance R_c between Ca²⁺ channels and vesicular Ca²⁺ sensors at IHC AZs to be ∼17 nm with a 5–95 percentile range of 8–30 nm. Our previously proposed AZ scenarios of nanodomain control (36) (Fig. 9B) give R_c values that fit well into the proposed range and might thus represent a good approximation of the true IHC AZ arrangement. Such tight coupling increases efficacy and speed of synaptic transmission.

Mobile IHC Ca²⁺ Buffering and Hearing.

At first sight, finding a near-normal function of the cochlea in the Pv^−/−Cb^−/−Cr^−/− mice is surprising. In SGNs, only spontaneous spiking rates were increased, which might be related to the increased Ca²⁺ influx. In fact, a regulation of spontaneous firing rates by modulating Ca²⁺ channel open probability has been shown (58). A minor increase (e.g., 17%) in the number or open probability of Ca²⁺ channels could explain the significantly enhanced spontaneous rate in SGNs of Pv^−/−Cb^−/−Cr^−/− mice, but may not lead to an obvious enhancement of the evoked firing rates when driven by strong supratheshold stimulation (Fig. 6; see also ref. 59).

Sound encoding during continued stimulation was not significantly altered despite increased sustained IHC exocytosis. Mathematical modeling indicated that this discrepancy reflects extrasynaptic exocytosis of vesicles that contributes less efficiently to sound coding, if at all. Alternative explanations such as refractoriness (Fig. 8B and SI Appendix, Fig. S5D) and increased AMPA desensitization (49) seem unlikely. A supralinear rise of exocytosis during prolonged stimulation was reported for turtle hair cells and interpreted as Ca²⁺-dependent vesicle replenishment (60), but the relation to sound encoding remained to be elucidated, and a contribution of extrasynaptic exocytosis could not be ruled out.

Release away from the ribbon-type AZ has previously been observed in retinal bipolar cells (61, 62), where it is physiologically relevant for communication of bipolar cells to AII amacrine cells (62). The results of our study suggest that such extrasynaptic exocytosis of IHCs has little influence on the postsynaptic SGN spiking. Together with previous studies demonstrating a good correlation between the presynaptic release rate and postsynaptic spiking in WT and bassoon mutant animals (24), it further suggests little or no ectopic release in the presence of endogenous Ca²⁺ buffers. We conclude that the properties of the endogenous buffer Ca²⁺ binding and their diffusion kinetics allow for a metabolically efficient control of the Ca²⁺-dependent sound encoding.

Materials and Methods

Animals.

The TKO line Pv^−/−Cb^−/−Cr^−/− was generated by breeding the two double KO (DKO) lines, Pv^−/−Cb^−/− (63) (genetic background: C57BL/6 × 129/OlaHsd × 129/SvJ) and Pv^−/−Cr^−/− (64) (genetic background: C57BL/6 × 129/OlaHsd). The initial double-heterozygous litters (Pv^−/−Cb^+/−Cr^+/−) were used to generate the TKO line. The genotype was determined by PCR for the mutated loci in the three genes, Pvalb, Calb1, and Calb2, as reported before (65–67). The line was then maintained as an inbred line with a mixed C57BL/6 × 129/(OlaHsd × SvJ) background. We studied the auditory phenotype of DKO (Pv^−/−Cb^−/−) and TKO (Pv^−/−Cb^−/−Cr^−/−) mice. Control experiments were performed on WT animals (Pv^+/+Cb^+/+Cr^+/+) with the most similar background to TKO mice (mixed background of C57BL/6 and 129/OlaHsd). These animals originated from a previous heterozygote (Pv^+/−Cr^+/−) breeding. All experiments were done in compliance with the national animal care guidelines and were approved by the board for animal welfare of the University Medical Center Goettingen, the animal welfare office of the state of Lower Saxony, and the institutional animal care and use committee of the Massachusetts Eye and Ear Infirmary.

Immunohistochemistry and Confocal Microscopy.

Immunohistochemistry was performed as described previously (19). To analyze the abundance of mitochondria, we fixed organs of Corti in methanol at −20 °C for 20 min and double-stained hair cells for PNPase (mitochondria marker) (29) and CtBP2 (19) (to identify ribbons). In all other cases, organs were fixed with 4% (wt/vol) formaldehyde for 10–60 min on ice. The following antibodies were used: mouse IgG1 anti-CtBP2 (1:200; BD Biosciences), rabbit anti-GluR2/3 (1:200; Chemicon), mouse anti–calbindin-D28k, mouse anti-calretinin, mouse anti–parvalbumin-α, rabbit anti-oncomodulin (anti–parvalbumin-β; all 1:500; Swant), rabbit anti-PNPase (1:500; Proteintech), rabbit VGlut3 (1:500; Abcam), mouse 5F10 (pan-PMCA marker, 1:200; Abcam) and secondary Alexa Fluor 488- and Alexa Fluor 568-labeled antibodies (1:200; Molecular Probes). In some instances, nuclei were stained with Hoechst 34580 (1:1,000; Molecular Probes). Confocal images were acquired by using a laser-scanning confocal microscope (TCS SP2; Leica Microsystems) with 488-nm (Ar) and 561-nm (He-Ne) lasers and a 63× oil immersion objective. z-axis stacks of 2D images were taken with a step size of 0.5 μm. Z-projections were done in ImageJ (National Institutes of Health). The ribeye/CtBP2 and GluR2/3 immunofluorescence spots were counted in the z-stacks and divided by the number of IHCs. Juxtaposed spots of pre- and postsynaptic immunofluorescence were taken to identify intact IHC ribbon synapses. To assess the perisynaptic abundance of mitochondria, we measured the cumulative PNPase immunofluorescence intensity within a circle with a radius of 0.5 µm around the center of mass of the ribbon (CtBP2 immunofluorescence) in confocal sections of IHCs by using a custom-written MATLAB routine.

Patch-Clamp Recordings.

KO (Pv^−/−Cb^−/−Cr^−/−) and WT mice (Pv^+/+Cb^+/+Cr^+/+) with postnatal ages of 14–23 d were killed by decapitation. The apical cochlear turns were dissected in Hepes Hanks solution containing (in mM): 5.36 KCl, 141.7 NaCl, 1 MgCl₂, 0.5 MgSO₄, 10 Hepes, 11.1 d-glucose, and 3.42 l-glutamine, pH 7.2. IHCs were patch-clamped in the perforated-patch configuration as previously described (17). For estimation of endogenous buffer equivalents, Pv^−/−Cb^−/−Cr^−/− IHCs were patch-clamped in the ruptured-patch configuration. The pipette solution contained (in mM): 130 Cs-gluconate, 10 TEA-Cl, 10 4-AP (4-aminopyridine; Merck), 1 MgCl₂, 10 Hepes, 300 μg/mL amphotericin B (for perforated patch-clamp experiments; Calbiochem), 2 MgATP, and 0.3 NaGTP (both for ruptured-patch experiments), pH 7.2, with osmolarity of approximately 290 mOsm. In ruptured-patch experiments, pipette solution additionally contained different concentrations of exogenous buffers: 0.1, 0.5, or 1 mM BAPTA or 0.5 or 1 mM EGTA. The extracellular solution contained (in mM): 106 NaCl (113 mM in Fig. 3 G and H), 35 TEA-Cl, 2.8 KCl, 5 CaCl₂ (2 mM in Fig. 3 G and H), 1 MgCl₂, 10 Hepes, 1 CsCl, 11.1 d-glucose, pH 7.2, with osmolarity of approximately 300 mOsm. All chemicals were obtained from Sigma-Aldrich unless stated otherwise.

We used an EPC-9 amplifier (HEKA Electronics) controlled by Pulse software (HEKA Electronics). C_m increments (ΔC_m) were measured as previously described (22), averaging 400 ms before and after (skipping the first 40 ms) depolarization. To measure ΔC_m, IHCs were stimulated by depolarizations of different durations to peak Ca²⁺ current potential at intervals of 30–60 s. For Ca²⁺ current inactivation experiments, IHCs were depolarized for 100 ms. All voltages were corrected for liquid junction potential (−17 mV). In ruptured-patch experiments, measurements were initiated an average of 2.5 min after patch rupture to allow for the diffusion of exogenous buffer into the cytosol. The waiting time depended on the series resistance R_s, which relates to the kinetics of diffusional exchange as previously described (68). Unless stated otherwise, all recordings were performed at room temperature.

ABRs, Otoacoustic Emissions, and Recordings from Single SGNs.

Recordings of ABRs and DPOAEs (69) as well as extracellular recordings from SGNs (23, 24) were performed as described previously. Briefly, 12–16-wk-old mice were anesthetized by i.p. injection of xylazine (2.5 mg/kg) and ketamine (125 mg/kg, ABR and DPOAE) or xylazine (5 mg/kg) and urethane (1.32 mg/kg, for single SGN recordings). The occipital bone and cerebellum were partly removed, and SGNs near the auditory nerve’s entry zone into the cochlear nucleus were approached by a glass microelectrode filled with 2 M KCl and 4% (wt/vol) methylene blue during noise burst stimulation. Sound-responsive neurons were first characterized by obtaining their spontaneous rate, tuning curves, and responses to 50-ms tone bursts presented at the CF of the SGN, 30 dB above threshold. SGNs were distinguished from primary cochlear nucleus units based on their primary-like response characteristics and irregular firing pattern, as well as by the electrode position, which was confirmed after the end of the experiment. Spike detection was performed online based on a manually set amplitude criterion.

Data Analysis.

Data analysis was performed in Igor Pro (Wavemetrics) and MATLAB (Mathworks) software, confocal images were assembled for display by using ImageJ and Photoshop (Adobe Systems), and final figures were composed in Illustrator (Adobe Systems). To calculate activation time constants of Ca²⁺ currents, data were fitted with the following function: I(t) = I₀ + I_max × (1 − e^−t/τ)^p. In most cases, data could be well fitted with the parameter power (p) fixed to 2, or else p was set as a free parameter. Mean ΔC_m and Ca²⁺ current estimates present grand averages calculated from the mean estimates of individual IHCs. All results are expressed as mean ± SEM. Data were tested for randomness, normality (Jarque–Bera test), and equality of variances (F-test) and compared for statistical significance by using a Student t test (in case of normal distribution and equal variance of both samples) or Wilcoxon rank-sum test.

Mathematical Modeling.

Mathematical modeling was done by using MATLAB R2012b (Mathworks).

Conversion of neurotransmitter release to spikes.

The release rate was inferred from exocytic ΔC_m estimates of IHCs (at room temperature). In the model, the SGN generates a spike in response to each release event unless it is in the refractory state, which lasts for a period of t_A + t_R (t_A is the absolute refractory period, t_R the relative refractory period; Fig. 9A). Although t_A was fixed for a particular SGN, t_R was a random number drawn from a monoexponential distribution with a mean value τ_R. The stationary spike rate (R_sp^∞) is related to the release rate (R_r^∞) and the refractory period in the following way (32): R_sp^∞ = R_r^∞/[1 + R_r^∞·(t_A + τ_R)]. Given that changes in the sustained release rate (between 50 and 200 ms; Fig. 9B) are slow in comparison with the duration of the refractory period, we applied the adiabatic approximation: R_sp(t) ∼ R_r(t)/[1 + R_r(t)·(t_A + τ_R)]. To estimate the release rate R_r(t), the experimental ΔC_m(t) values were first converted to the number of released synaptic vesicles, N(t): N(t) = sc·ΔC_m(t)/(C_sv·N_syn). Here, a C_sv of 44.5 aF was taken as average ΔC_m upon fusion of single synaptic vesicle (70), the N_syn of 12 is the number of synapses per IHC as obtained from immunohistochemistry (Fig. 2). sc ≤ 1 is a scaling coefficient to account for differences between in vitro (patch-clamp) and in vivo (single unit recordings) conditions [such as the amplitude of stimulus-evoked IHC depolarization, temperature, ion homeostasis (e.g., [Ca²⁺]_e), and/or the case that a single release event may correspond to release of a few synaptic vesicles] (70, 71). Next, N(t) was fitted by A·t + B·(1 − e^-t/τ)ⁿ for the Pv^+/+Cb^+/+Cr^+/+ IHCs and A·t + B·(1 − e^−t/τ)ⁿ + t·(a·t + b) for the Pv^−/−Cb^−/−Cr^−/− IHCs (SI Appendix, Fig. S2A). Finally, the release rate R_r(t) was obtained by calculating the time derivative of N(t).

Refractory periods.

We collected experimental cumulative interspike intervals corresponding to the sustained part of PSTH (30–50-ms interval; Fig. 6C). The parameter t_A was estimated as the interspike interval smaller than 99.5% of the remaining interspike intervals in the sample from the SGN under consideration. To estimate τ_R, the cumulative interspike interval distribution excluding the 0.5% smallest interspike intervals was fitted for each SGN with the expression (which applies for the model formulated earlier):

$$P^M\left(t\right)=\{\begin{array}{c}1-\frac{{\left({\tau }_s-{\tau }_R-t_A\right)}^{-1}\cdot e^{-\frac{\left(t-t_A\right)}{{\tau }_R}}-{\tau }_R^{-1}\cdot e^{-\frac{\left(t-t_A\right)}{{\tau }_s-{\tau }_R-t_A}}}{{\left({\tau }_s-{\tau }_R-t_A\right)}^{-1}-{\tau }_R^{-1}},ift>t_A\\ 0,ift\le t_A\end{array}$$ [1]

where τ_s is experimental estimate of the mean interspike interval. The fitting was done by minimizing the relative discrepancy between the model and the experimental cumulative distributions ∑_i|P^M_i − P^E_i|/P^E_i in the range of P^E values between 0 and 0.9 (SI Appendix, Fig. S5 A and B).

Concentrations of the endogenous Ca²⁺ buffers and effective coupling distance between presynaptic Ca²⁺ channels and Ca²⁺ sensors of exocytosis.

Buffer concentrations and the effective Ca²⁺ channel–exocytosis coupling distance (i.e., R_c) were estimated by using a hemispherical Ca²⁺ source model (Fig. 9A). A hemispherical Ca²⁺ source with 1-nm radius was embedded in a hemispherical volume with 2-µm radius, which corresponds to the mean distance between neighboring synapses in IHCs (72). The simulation volume was filled with 2 mM MgATP and the chosen concentrations of BAPTA, EGTA, or endogenous buffers. Initially, the system was in a steady state with uniform distribution of Ca²⁺, Mg²⁺, and buffers. The boundary of the simulation volume was assumed to be reflective for all considered particle species. This effectively mimics the effect of Ca²⁺ coming from the neighboring synapses and also fixes the amount of buffers available per synapse. On the contrary, pure reflection of Ca²⁺ from the boundary ignores Ca²⁺ removal by the pumps and through exchange with the remaining volume of the IHC, which is considerably larger (2.2 pL) (73) than the volume of 12 hemispheres of 2 µm each (∼0.02 pL). It is shown in SI Appendix, section 7.6, however, that these effects do not considerably influence our results. Ca²⁺ concentration at time t and distance r from the source, [Ca²⁺](t,r), is governed by a system of reaction–diffusion equations as described in SI Appendix, section 7.1.

We assumed that the amount of release in a 20-ms time window was proportional to ([Ca²⁺](r))^m·q(r). [Ca²⁺](r) was estimated 20 ms after the onset of stimulus. During this time window, [Ca²⁺](r) in simulations was essentially stationary (apart from the initial equilibration of the profile, which, however, is very fast; SI Appendix, section 7.2).

To find R_c based on the experimental data, we minimized the mean relative deviation of the ratios of modeled and experimentally observed release during the first 20 ms in different Ca²⁺ buffering conditions:

$$z\left(r\right)={\displaystyle \sum _{j=1}^4{w}_j\cdot \frac{\left|a_j-b_j\left(r\right)\right|}{\min \left(a_j,b_j\left(r\right)\right)}}$$ [2]

Here, a_j = ΔC_m,0/ΔC_m,j is the ratio of ΔC_m values estimated in TKO IHCs (at room temperature) with 1 mM BAPTA (ΔC_m,0) and 1 mM EGTA (j = 1), 0.5 mM BAPTA (j = 2), 0.5 mM EGTA (j = 3), or no exogenous buffer (j = 4). b_j = ([Ca²⁺]₀(r)/([Ca²⁺]_j(r))^m·q(r), [Ca²⁺]₀(r)—the model’s estimate of [Ca²⁺] at distance r from the source in TKO IHCs loaded with 1 mM BAPTA, [Ca²⁺]_j(r)—the model’s estimates of [Ca²⁺] at distance r from the source in the other four buffering conditions as mentioned earlier. w_j is relative weight of the jth term in the sum, which depends on the ratio of the mean and SEM values of experimental ΔC_m estimates: w_j = [ΔC_m,j/SEM(ΔC_m,j)]/∑⁴_i=1[ΔC_m,i/SEM(ΔC_m,i)]. Note that ΔC_m estimated in different buffering conditions, corresponds to slightly different Q_Ca values which reflect different influx of Ca²⁺. To take this into account, we rescaled the actual i_Ca values for estimating each [Ca²⁺]. This was done so that the average Q_Ca = 3.78 pC measured for 20 ms depolarization in Pv^+/+Cb^+/+Cr^+/+ IHCs corresponded to the nominal i_Ca values. Bootstrapping was used to estimate the confidence interval of R_c (given as a 5–95 percentile range; Fig. 9C) because of uncertainty in experimental estimates of m and ΔC_m for different buffering conditions. A total of 10⁵ artificial data sets were generated by drawing numbers from normal distributions with their mean and SD values set to experimentally estimated mean and SEM values.

As shown in SI Appendix, section 8, the R_c of a particular AZ is not simply the average distance between Ca²⁺ sensors of exocytosis and Ca²⁺ channels. Rather, it is a nonlinear average of those distances weighted by the contributions of the corresponding channels to the [Ca²⁺] driving exocytosis at the AZ. This aspect is relevant for the functional interpretation of R_c. Qualitatively, the more a particular Ca²⁺ channel contributes to [Ca²⁺] at a particular release site and the more that release site contributes to the overall neurotransmitter release at the AZ, the more the distance between the channel and the corresponding Ca²⁺ sensor of exocytosis weighs in determining the R_c.

The fitting procedure for endogenous buffer concentration estimation was based on minimization of a relative discrepancy measure of the form ∑_i|c₁(r_i) − c₂(r_i)|/[c₁(r_i) + c₂(r_i)] for $\text{r}\in \left[0\text{;}200\right]\mathrm{nm}$.