Abstract
We present RIPMMARC (Rotation Invariant Patch-based Multi-Modality Analysis aRChitecture), a flexible and widely applicable method for extracting information unique to a given modality from a multi-modal data set. We use RIPMMARC to improve interpretation of arterial spin labeling (ASL) perfusion images by removing the component of perfusion that is predicted by the underlying anatomy. Using patch-based, rotation invariant descriptors derived from the anatomical image, we learn a predictive relationship between local neuroanatomical structure and the corresponding perfusion image. This relation allows us to produce an image of perfusion that would be predicted given only the underlying anatomy and a residual image that represents perfusion information that cannot be predicted by anatomical features. Our learned structural features are significantly better at predicting brain perfusion than tissue probability maps, which are the input to standard partial volume correction techniques. Studies in test-retest data show that both the anatomically predicted and residual perfusion signal are highly replicable for a given subject. In a pediatric population, both the raw perfusion and structurally predicted images are tightly linked to age throughout adolescence throughout the brain. Interestingly, the residual perfusion also shows a strong correlation with age in select regions including the hippocampi (corr= 0.38, p-value < 10−6), precuneus (corr= −0.44, p < 10−5), and combined default mode network regions (corr= −0.45, p < 10−8) that is independent of global anatomy-perfusion trends. This finding suggests that there is a regionally heterogeneous pattern of functional specialization that is distinct from that of cortical structural development.
1. Introduction
A fundamental challenge in the interpretation of functional images of the brain is the extent to which the observed function is driven by underlying structure, since the goal of most functional imaging is to provide insight into physiological and patho-physiological processes that may not be manifested in structural changes. In particular, a body of prior work establishes that perfusion and structural signal is shared across modalities. Franklin et al. recently showed that acute baclofen-induced perfusion decreases induce changes in T1-derived gray matter (GM) density [1]. A prior study showed increases in observed GM density following acute administration of levodopa [2]. Chronically, decreased perfusion may result in decreased cortical thickness [3]. This connection between brain perfusion and structure may confound efforts to correlate disease processes with either perfusion or structure [4, 5, 6, 7, 8, 9]. In brief, structural modalities are not purely structural and may inform and even directly predict functional signal.
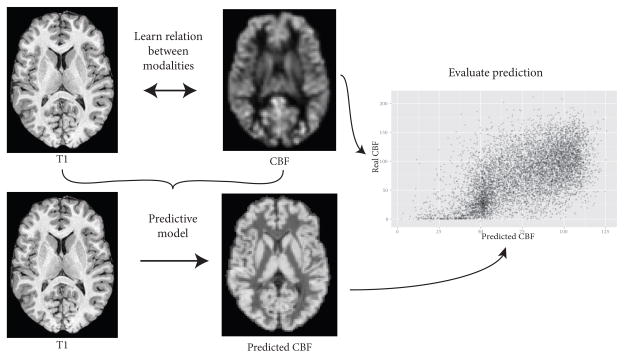
To improve interpretability of effects that are correlated across modalities, it is common to apply a correction to emphasize the information unique to a given modality. For example, many perfusion image processing protocols correct the perfusion image for partial volume effects due to variations in gray matter/white matter ratios [10], since gray matter and white matter have markedly different perfusion values [11]. In addition to partial volume and other technical challenges, though, perfusion in a given voxel may be at least partially determined by the underlying brain anatomy. Therefore, we seek to reframe this relation between brain anatomy and perfusion more broadly: Given a perfusion image and a structural anatomical image, how much information is unique to the perfusion image, and how much of the perfusion image can be reconstructed given the structural image? A schematic of this approach is shown in Figure 1.
Figure 1.
Schematic of predicting perfusion from structural MRI.
As a motivating example problem, we consider perfusion measurements of typically developing adolescents. Perfusion studies of typically developing children have shown changes over development [12, 13, 14, 15, 16, 17, 18]. In parallel, many studies have focused on structural brain changes over development, including such metrics as cortical thickness [19] and white matter structure [20]. Some of the changes in perfusion are likely due to development of the underlying anatomical substrate, including such developments as cortical thickness, gyrification indices [21, 22], and possibly other, more subtle anatomical changes. On the other hand, it is possible that some of the changes in perfusion are due only to changes in the perfusion of specific cortical areas that are not explained by structural changes. We seek to improve the interpretability of perfusion imaging by separating the component of cortical perfusion that can be explained by structural features from the component of cortical perfusion that is due to biological processes not driven by the underlying anatomy. This separation will help evaluate what unique information is gained by using perfusion imaging as compared to anatomical imaging modalities, thus enabling more principled and informative integration of perfusion imaging into multimodal neuroimaging population studies. The residual perfusion signal represents localized processes that are not explained by the global anatomy-perfusion relationship, signifying development of functional specialization.
Several image processing strategies incorporate knowledge of one modality to improve the interpretability of a second modality, especially where the two modalities offer complementary sources of information. One of the most commonly encountered variants of this problem occurs in positron emission tomograpy (PET) image processing. PET images have low spatial resolution, leading to significant partial volume effects (PVE) [23]. A widespread method for correcting these partial volume effects is to divide the PET image by gray and white matter probability images (e.g., [10]). By assuming that PET activity within white matter is known, it is then possible to reconstruct the amount of signal that would have resulted from a purely gray matter voxel. Similar strategies have been pursued for arterial spin labeling (ASL) perfusion [24] partial volume correction. Many ASL partial volume correction methods assume that white matter has perfusion that is 40% of a comparable unit of gray matter [25], based on quantitative in vivo measures of ASL perfusion [11], even though this ratio is almost certainly dependent on image resolution. More sophisticated models include partial volume correction based on locally determined gray matter activation [26, 27], a kinetic equation for multiple inversion time ASL [28], and specially designed pulse sequences [29]. In addition, some studies have incorporated the presence of brain lesions for partial volume correction of ASL images [30].
Fundamentally, partial volume correction (PVC) aims to reconstruct the ideal image that the scanner would have seen had technical impediments, such as scanner resolution and point spread function, not interfered. Although this correction is an important consideration when interpreting perfusion images, it does not attempt to account for true effects of underlying brain structure. Besides technical difficulties with obtaining accurate perfusion measurements, there may be genuine interactions between the underlying anatomy and the observed perfusion that go beyond white and gray matter probabilities. In this work, we address a different problem from PVC: How much brain perfusion can be related to the underlying structure, and how much cannot be predicted from the underlying structure?
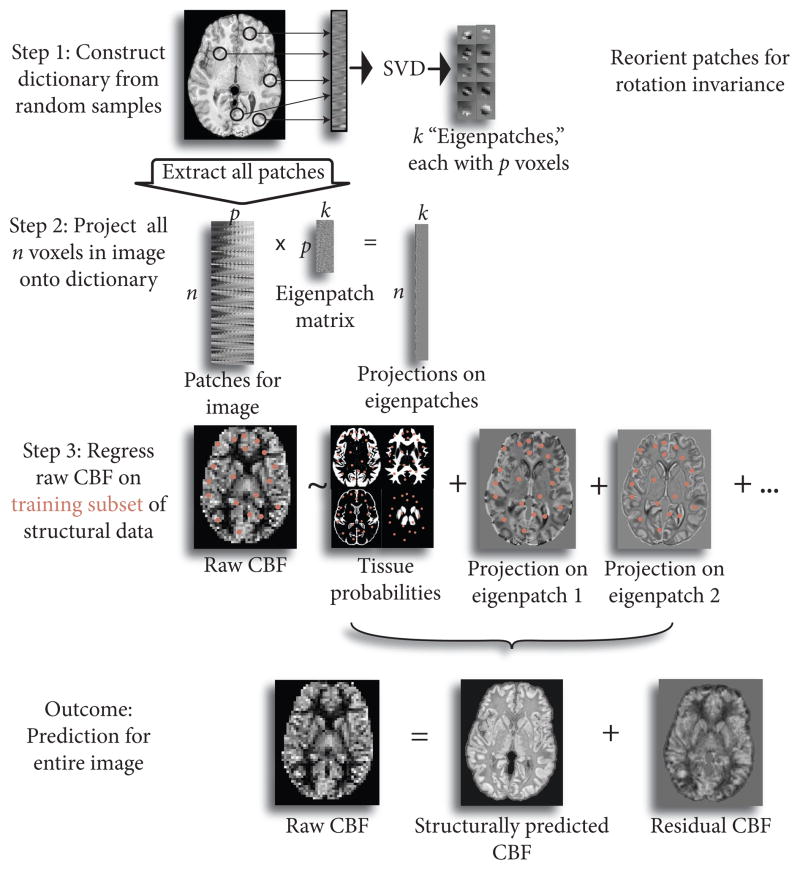
Moreover, generating a feature vector for each voxel that contains all the necessary information to reconstruct perfusion from anatomy is not straightforward. Gray matter and white matter probabilities are nearly always used when predicting perfusion from anatomical imaging, even though they provide only a limited model of the structure-perfusion relationship. Cortical thickness may also be correlated to perfusion. Here, we present RIPMMARC (Rotation Invariant Patch-based Multi-Modality Analysis aRChitecture), an alternative data-driven strategy of deriving structure-perfusion relationships implicitly. RIPMMARC provides a way to encode more detailed local structural information about a given voxel in an image than a scalar intensity value, and this information can be used to predict the perfusion at that point. From concurrently acquired structural and perfusion images, we learn a dictionary of anatomical patch features that can be used to predict perfusion, with the atoms, or elements, in the dictionary corresponding to paradigmatic textural and anatomical features. Mean-centering each input patch ensures that the dictionary contains gradient information invariant to raw intensity value, with intensity represented in corresponding tissue probability values. In contrast to traditional dictionary learning approaches, we construct rotation-invariant dictionaries to enable more complete sharing between similar anatomical structures across the brain. This rotation invariance allows, for example, sharing of information between right and left sides of the brain, which would not be possible when using traditional dictionary learning techniques. Rotation invariance is particularly important in 3D images, as the number of possible orientations increases with the number of dimensions. Projecting patches focused at every voxel in the image onto the rotation invariant dictionary produces a locally varying feature weight image for each atom in the dictionary. We combine the structural feature weights with the probabilitistic segmentation images in a linear model to predict perfusion from the structurally derived measures. This linear model then produces a “structurally predicted” perfusion image, corresponding to the predicted perfusion given the structural features, and a residual perfusion image, corresponding to the perfusion that cannot be explained by structural information. A graphical abstract of our method is shown in Figure 2.
Figure 2.
Graphical abstract of proposed method. Patches are sampled from image in modality 1 (here, T1) and SVD is used to learn optimal features (“eigenpatches”) to describe patches. Patches corresponding to each point in the image are then projected onto the “eigenpatches” to create a representation of the input image in feature space. We then use linear regression to predict the second image (here, perfusion image) from the feature-based description of the first image. This enables us to decompose the perfusion image into a component that is predicted from the structural image and the unique contribution of the perfusion image.
RIPMMARC is inspired by feature learning methods [31, 32, 33]; rotation-invariant feature transforms [34, 35, 36, 37] and dictionary learning methods [38, 39]; and modality synthesis algorithms [40, 41, 42, 43]. To the best of our knowledge, this work is the first to use rotation invariance for image synthesis. In addition, our work uses a much more expressive and accurate model for predicting CBF from structural information than prior work.
In sum, we make the following contributions: 1) We propose a novel rotation-invariant dictionary learning method for modality synthesis; 2) We show that these learned dictionaries are significantly better at predicting perfusion than segmentation probability or cortical thickness maps; 3) We demonstrate that this method produces consistent perfusion maps across session scans within a single subject; 4) We show that this method decomposes the raw CBF signal into structurally predicted and residual CBF signals, and all three signals are linked to age in a pediatric population; and 5) The residual perfusion values display a weaker correlation with age in the occipital cortex and precentral motor cortex and a stronger correlation with age in precuneus and hippocampus, suggesting regionally heterogeneous trajectories of functional specialization that are distinct from trajectories of cortical structural development.
2. Methods
2.1. Representations of Structure
Given an image I, we denote the segmentation probability for white matter (WM) and gray matter (GM) at a voxel x ∈ I as pGM,WM(x). We additionally denote the observed cerebral blood flow (CBF) value as cobs(x), and the corrected CBF value as ccorr(x). Standard ASL partial volume correction [25] takes the form
| (1) |
This specific formulation derives from a more general assumption of a linear relationship between the voxelwise white matter and gray matter densities. Denoting the true GM and WM CBF levels at voxel x as cGM,WM(x), we have
| (2) |
where assuming that cWM(x) = 0.4·cGM(x), as in the earliest work on PVC correction, leads to Equation 1. Alternatively, it is possible to learn the relation between GM and WM activity from the CBF image directly, either by sampling over lobes [25] or a local kernel centered on the voxel of interest [26]. Both approaches directly analyze the gray matter and white matter probability images as they relate to perfusion.
As explained in the introduction, we take a decidedly different approach to incorporating anatomy into CBF analysis. Instead of attempting to infer the unobservable true GM and WM perfusion in a voxelwise manner, we use all available anatomical information to create a “best guess” at what the observed perfusion would be given the anatomy at voxel x. Formulated as a prediction problem, we have
| (3) |
where we have replaced cGM,WM(x) with βGM,WM to emphasize that they are learned values that are constant across the image. The “residual(x)” term accounts for the observed perfusion that cannot be accounted for by the other predictors. In addition to the tissue membership probability values, we incorporate a structural feature vector that describes the anatomy surrounding the voxel of interest. Denoting the value of the n’th feature of voxel x as sn(x), n ∈ {1,…,k}, we obtain
| (4) |
where βn is the weight for the n’th feature. As before, the βn weights are learned over the entire image. Concatenating the anatomically derived predictors for voxel x on the right hand side of Equation 4 as Xx = [pGM(x), pWM(x),s1(x),…sk(x)] and the weights as β = [βGM, βWM, β1,…, βk]T allows us to reformulate Equation 4 as a standard linear regression:
| (5) |
where the ε term corresponds to the residual(x) term in Equation 4. Unlike in standard linear regression, the ε term here is not i.i.d. Gaussian noise; it corresponds to the component of perfusion imaging that cannot be predicted from anatomical information. Although the presence of structured residuals may motivate the use of nonlinear prediction techniques, we have found that linear regression works well for this problem and does not suffer from overfitting, even when training on a small proportion of the data. Further concatenating the observed CBF value across the image as Cobs = [cobs(1),…,cobs(m)], where there are m voxels in the image, and X = [X1; …;Xm], where [·;·] indicates row-wise concatenation, we obtain
| (6) |
The Xβ term corresponds to the component of perfusion that can be predicted from anatomical features, and the ε term corresponds to the component of perfusion that cannot be predicted from anatomical features. A greater correlation between Cobs and Xβ indicates a more accurate reconstruction of observed perfusion from anatomical features.
2.2. Dictionary Construction
We consider an image I with N scalar-valued voxels at locations xn ∈ I, n = 1,…,N. We seek a function s : I(xn) ↦ ℝk that produces a vector descriptor of the structure around each voxel. Denoting the neighborhood of voxel xn as
, where r is the radius of the neighborhood, we generate for each voxel xn in the image the vectorized patch P(xn) = vectorize ({I(xj) | xj ∈
 (xn) }) ∈ ℝp, where each neighborhood consists of p voxels and the “vectorize” operation returns the vector representation of elements in a set. In addition, we denote the mean-centered patch as Pc(xn) = P(xn) − mean(P(xn)). Mean-centering each patch serves to minimize the effect of intensity inhomogeneity and concurrently emphasize the gradient and texture information. We denote the sets of voxels in cortical gray matter and white matter as xGM,WM respectively. Because our studies focus on cortical perfusion, we only work with cortical voxels.
(xn) }) ∈ ℝp, where each neighborhood consists of p voxels and the “vectorize” operation returns the vector representation of elements in a set. In addition, we denote the mean-centered patch as Pc(xn) = P(xn) − mean(P(xn)). Mean-centering each patch serves to minimize the effect of intensity inhomogeneity and concurrently emphasize the gradient and texture information. We denote the sets of voxels in cortical gray matter and white matter as xGM,WM respectively. Because our studies focus on cortical perfusion, we only work with cortical voxels.
To generate the s feature descriptor function, we begin by constructing a rotation-invariant dictionary. Creating a rotation-invariant dictionary requires three steps: Determining a reference direction to reorient all patches to; reorienting all patches to that direction; and constructing a dictionary from the reoriented patches. To find the reference direction, we concatenate row-wise the vectorized patches Pc(xn) of 1000 voxels sampled randomly from around the cortex into a matrix S ∈ ℝ1000×p. The number of sample voxels to take is limited only by computational power, but we did not observe any improvement in performance when sampling more than 1000 voxels. Next, we perform an SVD of S to obtain its eigenvectors and consider the first eigenvector of S the canonical reference frame.
We used a closed-form solution to align the image patches to the reference frame. The problem of aligning the orientation of two vectors is known as Wahba’s problem [44], and the analytical solution is known as the Kabsch algorithm [45]. Aligning two images corresponds to aligning the orientations of the first eigenvector (or two eigenvectors for a 3D image) of the covariance matrix of the gradient of the image. We denote the gradient operator g :
 (xn) ↦ ℝD, where D is the number of dimensions in the image. The covariance matrix C (
(xn) ↦ ℝD, where D is the number of dimensions in the image. The covariance matrix C (
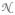 (xn)) of the gradient of the neighborhood
(xn)) of the gradient of the neighborhood
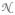 (xn) is then given by
(xn) is then given by
| (7) |
To align the patches of two voxels xi and xj, we denote the k’th eigenvector of C(
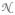 (xi)) as wk and the k’th eigenvector of C(
(xi)) as wk and the k’th eigenvector of C(
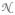 (xj)) as vk and calculate the rotation matrix Q that best aligns them:
(xj)) as vk and calculate the rotation matrix Q that best aligns them:
| (8) |
Denoting , we compute the singular value decomposition (SVD) of B: B = UΣVT. Then the analytical solution to Equation 8 is given by Q = UMVT, where . We then rotate the voxel coordinates xi by Q and use a linear interpolator to regenerate the neighborhood image after the rotation. A more computationally expensive alternative is to use the Radon transform to estimate orientation [46]. Using the Kabsch-based approach, we reorient all patches in S to the principal eigenvector of S. Then, we perform a second SVD of the reoriented patches. These eigenvectors make up the rotation-invariant dictionary. We retain enough eigenvectors to account for 95% variance explained. Pseudocode for this algorithm can be found in Algorithm 1.
Once we have the rotation-invariant dictionary, we construct the feature vector for a given voxel xn ∈ xGM by constructing the vectorized patch Pc(xn), reorienting the patch to the reference frame, and then multiplying the reoriented patch by each atom in the rotation-invariant dictionary. This procedure generates a k-vector for each voxel, with the i’th entry corresponding to the response of the i’th eigenvector to the voxel neighborhood. Pseudocode for this algorithm can be found in Algorithm 2.
2.3. Feature Learning
Once we have the rotation-invariant dictionary, we project the reoriented patches corresponding to each voxel in the image onto each rotation-invariant eigenpatch. This gives us an n ×k feature matrix, where n is the number of voxels in the image and k is the number of eigenpatches. The columns of this feature matrix correspond to the response of each eigenpatch to the patch centered on each voxel. In addition to the structural feature matrix, we use the GM and WM probabilities for each voxel in the image. The GM and WM probabilities are usually the two strongest predictors of blood flow in a given voxel, and we have found that they significantly increase the accuracy of CBF prediction. Thus, although modern PVC approaches [26] move beyond this simplistic relationship between tissue type and perfusion, even this primitive method of incorporating tissue probabilities into the prediction results in a feature that is highly predictive of perfusion, as it is a reasonable first-order approximation to the true relationship between tissue type and perfusion. The GM and WM probabilities also model each voxel’s intensity value.
Once we have the final structural predictor matrix, we run a linear model relating CBF to our predictor matrix:
| (9) |
To avoid overfitting, we train the model on 5% of the cortical voxels, sampled randomly, and then predict on the remaining 95% of the cortex. The use of a linear model and the fact that there are several orders of magnitude more training samples than predictors further minimize the risk of overfitting, and we did not observe a tendency to overfit in our data. We typically found a drop in variance explained of roughly 2% when going from training to testing data (Figure 13b). We note that in the current study, we learned the relationship between brain structure and perfusion on a per-subject basis. A graphical outline of the method is in Figure 2, and a more formal description of the algorithm is in Algorithm 2. An open-source ITK-based implementation can be found at https://github.com/bkandel/PatchAnalysis.
Algorithm 1.
Algorithm for generating reference frame and rotation-invariant dictionary.
Input: patch neighborhood operator
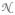 (xn), number of patches to sample m, input image I, target variance explained v. (xn), number of patches to sample m, input image I, target variance explained v. |
▷
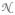 (xn) defines the points in the neighborhood of voxel xn. (xn) defines the points in the neighborhood of voxel xn. |
p ← number of voxels in
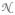 (xn). (xn). | |
| Initialize S ← [ ] | ▷ m × P sample patch matrix. |
| for i = 0,…,m −1 do | |
| xi ← random voxel in I. | |
t ← vector representation of {xj : xj ∈
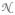 (xi)} (xi)} | |
| t ← t − mean(t). | ▷ Mean-center patch. |
| S ← [S t]. | ▷ Concatenate patches. |
| end for | |
| Compute eigenvector matrix V of S. | |
| Retain k1 eigenvectors to account for v variance explained. | ▷ V ∈ ℝp×k1. |
| for i = 0,…,m −1 do | |
| Reorient Si to V1. | ▷ Align each vectorized patch to reference frame. |
| end for | |
| Compute eigenvector matrix W of S. | ▷ Construct rotation-invariant dictionary. |
| Retain k2 eigenvectors to account for v variance explained. | ▷ Now, W ∈ ℝp×k2. |
| Output: W. | |
2.4. Parameter Settings
RIPMMARC has four free parameters: How many voxels to sample when constructing the dictionary; the ratio of testing to training data for the linear model; how many eigenvectors to retain; and the size of the patches. We have found that algorithm performance is insensitive to reasonable settings of the first three parameters, and the final parameter should be chosen in a principled way (Figure 13). The number of voxels to sample when constructing the dictionary is limited by computational power, but we have not observed improvements in prediction accuracy or dictionary stability when using more than 1000 voxels (Figure 13c). Similarly, the prediction accuracy does not improve when trained on more than 5% of the cortex (Figure 13b). Choosing how many eigenvectors to retain is an issue that does not have a clear resolution, but we have found that retaining enough eigenvectors to account for 95% variance explained is a good rule of thumb and works well in our experience. Beyond 95% variance explained, no improvement is seen (Figure 13a). The only parameter that has a significant effect on algorithm performance is the patch size. However, the patch size can be chosen to emphasize the spatial scale of features of interest. Because we are interested in features such as position along a sulcus, we chose a radius of 1.4 cm, but it is likely that this parameter will need to change for different applications.
Algorithm 2.
Algorithm for generating rotation-invariant patch-based description of image.
Input: patch neighborhood operator
 (xn), input image I, rotation-invariant dictionary W from Algorithm 1. (xn), input image I, rotation-invariant dictionary W from Algorithm 1. | |
| N ← number of voxels in I. | |
p ← number of voxels in
 (xn). (xn). | |
| Initialize P ← [ ] | ▷ N × p patch matrix for every pixel in image. |
| for i = 0,...,N −1 do | |
t ← vector representation of {xj : xj ∈
 (xi)}. (xi)}. | |
| t ← t − mean(t). | |
| Reorient t to W1. | |
| P ← [P t]. | ▷ Concatenate patches. |
| end for | |
| F → PW | ▷ Project patches of input image onto eigenvectors. |
| Output: F. | ▷ Matrix with response of each image voxel to each eigenpatch. |
2.5. Clinical Data
2.5.1. Test-Retest Data
The cohort consists of 12 healthy young adult participants (mean age 25.5±4.5 years, 7 female, 5 male). For each subject, data was acquired at two time points in the same day. For each time point, high resolution T1-weighted anatomic images were obtained using 3D MPRAGE imaging sequence and the following acquisition parameters: TR = 1620 ms, TI = 950 ms, TE = 3 ms, flip angle = 15°, 160 contiguous slices of 1.0 mm thickness, FOV = 192 × 256 mm2, matrix = 192×256, 1 NEX with a scan time of 6 min. The resulting voxel size was 1 mm. Additionally, pseudo-continuous ASL (pCASL) images were aquired with 80 alternating tag/control images all with 14 contiguous slices of 7.5mm thickness, FOV = 220 × 220mm2, matrix = 64 × 64; TR = 4000ms, tagging duration 1500ms, and postlabeling delay of 1 second. A complete description of this dataset can be found in [47].
2.5.2. Pediatric Data
Our pediatric data consists of 88 subjects, with mean age 11.72, range 7.07–17.46 years (Figure 3). Magnetization-Prepared Rapid Acquisition Gradient Echo (MPRAGE) images were acquired using a 3D inversion recovery sequence with TR/TE/TI = 2170/4.33/1100 ms. The resolution was 1×1×1mm2 with a matrix size of 256×256×192. Flip angle = 7° and total scan time was 8:08 minutes. Pseudo continuous arterial spin labeled (pCASL) images were acquired using TR/TE = 4000/22 ms, with resolution of 3.125×3.125×6mm3 over a 64×64×24 matrix. The M0 image was estimated by averaging the control (non-tagged) images. 40 label/control pairs were acquired. Generalized autocalibrating partially parallel acquisition (GRAPPA) was done using an acceleration factor of 2. Labeling duration was 1.5s and the post-labeling delay was 1.2s. Total imaging time was 5:30 minutes.
Figure 3.
Histogram of ages of pediatric population.
2.5.3. Image Preprocessing
The set of T1 images from the first session was used from each subject to construct a template using ANTs [48]. Additionally, a three-tissue segmentation of the template [49] allowed the labels to be partially masked so only cortex and deep gray structures were labeled. For each time point, the T1 image was registered to the template image using SyN [50]. The subject’s T1 image was also registered to the estimated M0 image as a reference for the pCASL using the antsIntrasubjectIntermodality.shscript in ANTs. These transforms were composed to map the cortical labels into ASL native space for each time point. All anatomical data was downsampled to 2mm isotropic resolution for analysis. For pCASL images, the M0 image served as a reference for motion-correction of all time-point volumes. Nuisance parameters, including motion and physiological confounds, were included as regressors, along with the tag-control binary label, in a robust regression scheme for CBF calculation [51]. Cerebral blood flow in physiological units was calculated from the difference between control and tagged images as
| (10) |
where f is the perfusion in physiological units (mL/100g/min); λ is the blood-tissue water partition coefficient (0.9 g/mL); ΔM is the mean difference between control and tagged images; α is the tagging efficiency (0.85); M0 is the equilibrium brain tissue magnetization, approximated by the mean of the control (non-tagged) images; T1b is the blood T1 value, modified for each subject based on gender and age, as below; w is the postlabeling delay (1 second); and τ is labeling duration (1.5 seconds). Full details are available in the open-source script at https://raw.github.com/stnava/ANTs/master/Scripts/antsASLProcessing.sh. For the pediatric data, the blood T1 value was adjusted for age and gender as T1 = (2115.6 −21.5 *age −73.3 *sex)ms, where female sex was set to 0 and male was set to 1, as suggested in [52]. One subject was eliminated because of extreme non-physiological CBF values, and two subjects were eliminated because of poor image quality with little differentiation between gray matter and white matter. Prior to dictionary construction, the pCASL and T1 images were resampled to 2mm isotropic resolution. To obtain region of interest (ROI) values for each subject, we warped the MNI template to the population-specific template generated with ANTs. This warp was concatenated with the template-to-subject warp to propagate the AAL label set to the subject space.
3. Results
Before analyzing real neuroimaging data, we first present two synthetic data analyses to provide a greater understanding of the motivation and mechanics of our method. We demonstrate the operation of the perfusion-anatomy decomposition on simple synthetic images to highlight the effect of orientation invariance when predicting perfusion. We then perform a simulated population experiment showing how observed changes in perfusion can in fact be due either to the underlying anatomy or changes in perfusion that are not explained by anatomical features. Following the synthetic experiments, we show that our anatomical features are much better than tissue probability maps or cortical thickness at predicting perfusion, and that both the anatomically predicted and residual functional images are highly reproducible within subjects. Finally, we demonstrate that the anatomically predicted and residual CBF signals in a pediatric population are tightly correlated with age in a region-specific manner, and that in certain instances have opposing trends.
3.1. Synthetic Image Decomposition
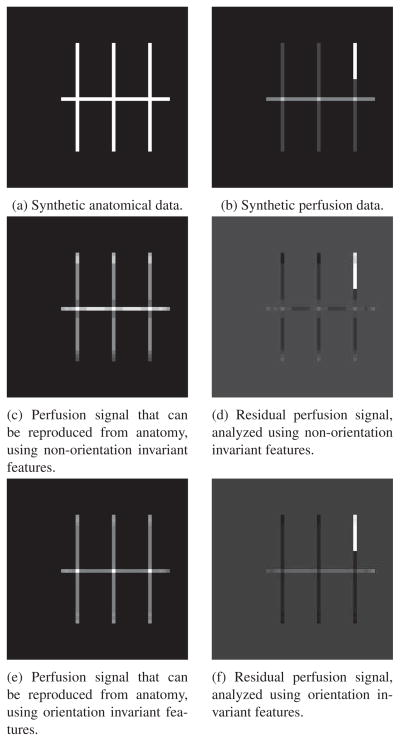
We generated synthetic data to demonstrate how the proposed method decomposes simulated functional images into its purely functional component and to the component that can be inferred from structure. Figure 4 shows the “anatomical” and “perfusion” components of the data. Some aspects of the perfusion data, such as the increased activity at the intersections of the lines, can be inferred from the structure of the image (when trained on an appropriate reference functional image). Other aspects of the functional data, such as the increased activity on the upper right-hand line, cannot be inferred from the structural data: Given a patch-based descriptor of a given voxel in the structural image, it is impossible to tell whether the corresponding perfusion voxel has a high or low value. In addition, certain functional values can only be inferred from the orientation of the structure. For example, the horizontal central line has a higher functional value than the vertical lines. Given only an orientation-invariant feature description of the central line, it is impossible to tell what the functional value is. Figure 4 shows the result of the decomposition. As expected, both decompositions do not predict the increased activity in the upper right-hand line from the structural data, but do reconstruct the increased activity at the intersections of the lines. Only the non-rotation invariant decomposition reconstructs the increased activity on the horizontal line. On the other hand, constructing orientation-invariant features enables sharing more data across regions, leading to a lower-variance reconstruction (Figure 4e). We consider the structure of neuroimaging data to be “rotation-invariant” in the sense that a gyrus pointing superiorly is equivalent to a gyrus pointing inferiorly. This rotation invariance enables information to be shared across hemispheres of the brain and reduces the chances of overfitting to a specific region.
Figure 4.
Synthetic perfusion and anatomical data. Some aspects of the perfusion data, such as the higher activity at the intersection of the lines, can be deduced from the underlying anatomy (the intersection of the lines), but other aspects of the perfusion data, such as the increased activity on the upper right line, cannot be deduced from the anatomy. 4c,4d: Decomposition of synthetic data using non-rotational invariant features. The constructed features include orientation, so the higher values in the horizontal line are correctly reconstructed. 4e,4f: Reconstructed perfusion and residual perfusion decomposition of Figure 4b. Because orientation invariant features were used, the higher perfusion of the horizontal line is not predicted, but the intersection of the lines does indicate a greater predicted functional signal. Orientation invariance enables greater information sharing across regions, leading to lower variance in the reconstruction as compared to the reconstruction using non-rotationally invariant features (4c).
3.2. Simulated Population Study
To demonstrate the need for a structure-function decomposition that differentiates between changes in perfusion that are due to structural abnormalities and those that are unrelated to the underlying structural substrate, we constructed a simulated data set that includes structural and functional effects. Throughout the brain, we simulated an ASL perfusion image based on the gray and white matter probability maps, with added noise. Using the notation from Section 2.1, at voxel x ∈ I:
| (11) |
To the images in the experimental group, we added additional anatomical and perfusion blobs in the following manner (Figure 5). In one blob (the “anatomical” blob), we increased the probability of gray matter. This caused a corresponding increase in the perfusion images. In the second blob, we increased the perfusion without a corresponding increase in GM probability, creating a perfusion increase that does not have a corresponding structural abnormality. Denoting CBF that is not predicted from the underlying anatomy as cr(x),
Figure 5.
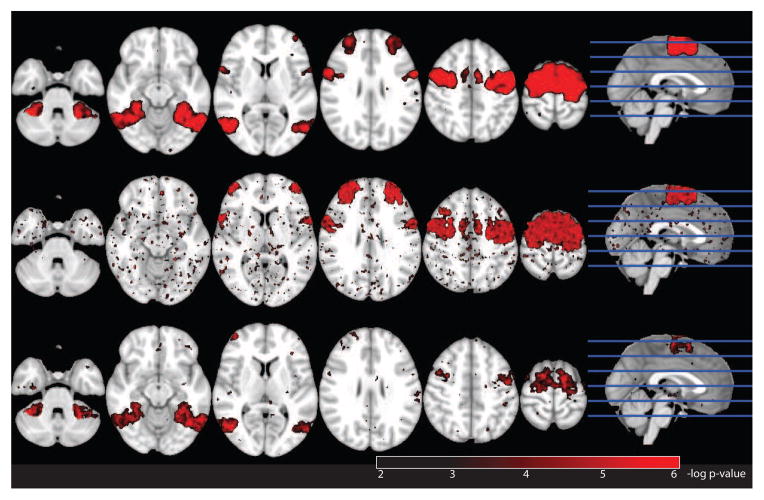
Negative log p-value map (FDR corrected) for raw perfusion (top), structurally predicted perfusion (middle), and residual perfusion (bottom). The structural, combined structural and functional, and functional areas all appear on the perfusion map. The structural and combined functional and structural blob appear on the structural p-value map, and the combined structural and functional blob and the purely functional blob appear on the functional p-value map.
| (12) |
In the third blob, we increased the GM probability and also added additional perfusion above that predicted by the increased GM probability. This blob represents an area that has both a structural abnormality (increased GM probability) and a perfusion abnormality (increased perfusion above that predicted by GM content). To recover an anatomy-perfusion decomposition of the images, we regressed out the anatomical information (GM and WM probability maps) from the perfusion images following the method in Section 2.3. This regression gave us two images: The perfusion predicted from structure, and the residual functional activation that is not explained by structure, in addition to the original perfusion images.
We ran a voxelwise t-test comparing control vs. experimental groups on the three types of images. The results are shown in Figure 5. The voxelwise p-statistic maps on the raw perfusion images shows all three blobs, because all three blobs indeed had increased perfusion in the experimental group (Figure 5, top). p-statistic maps on the residual functional images show both the residual perfusion blob and the combined anatomical and perfusion blob (Figure 5, middle). This image, however, ignores the potentially biologically important role of decreased perfusion caused by abnormal anatomy. The p-statistic map on the perfusion images as predicted by anatomy shows this missing information (Figure 5, bottom).
3.3. Sample subject
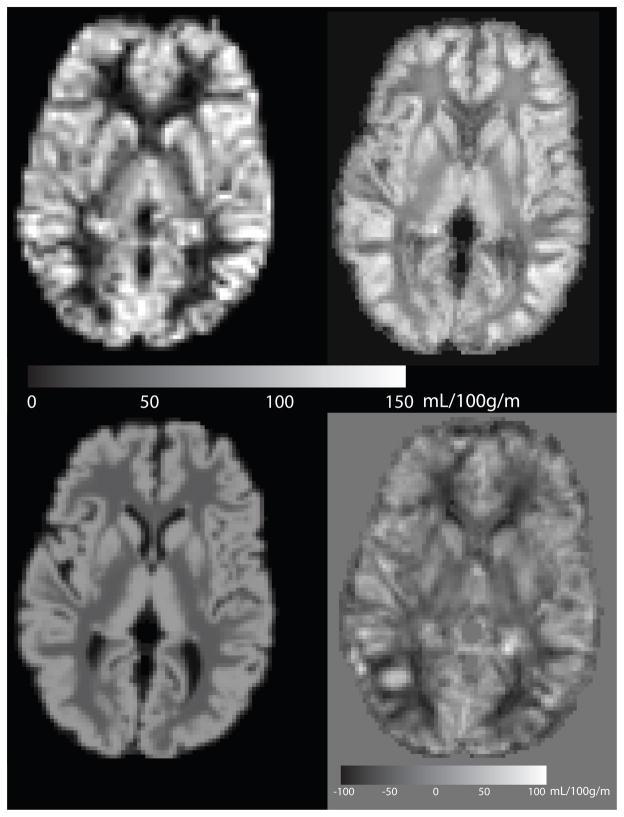
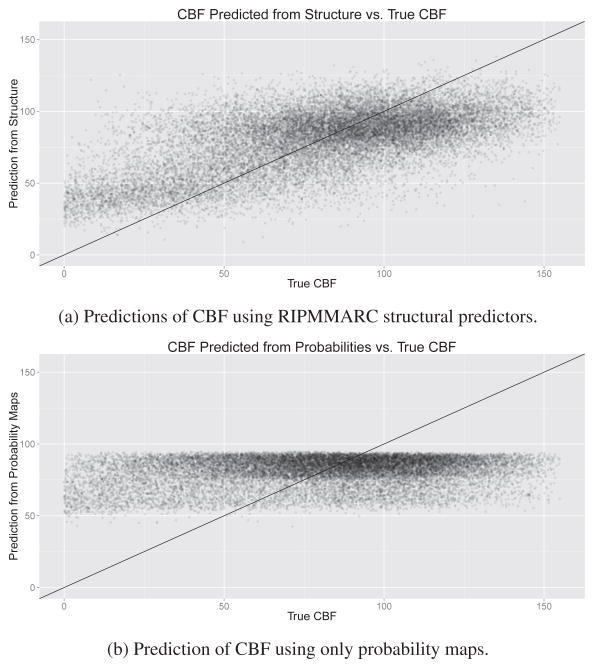
The raw perfusion image, the perfusion that can be predicted from structure, and the residual perfusion images for a sample subject are shown in Figure 6. For reference, the perfusion that can be predicted from probability maps is also shown. Our structural predictors are better at predicting CBF than the the probability maps, and in particular predicts higher perfusion in sulcal pits. A quantitative depiction of the correlation between predicted and actual CBF is given in Figure 7.
Figure 6.
Comparison of mean CBF image (top left), reconstruction from anatomy using RIPMMARC (top right), reconstruction from GM and WM probability images (bottom left), and residual perfusion image (bottom right). Mean CBF image is shown at ASL resolution (3.4mmx3.4mmx7.5mm); other images are shown at 2mm isotropic resolution.
Figure 7.
Predictions of CBF within cortical GM using our structural predictors and probability maps. Our structural predictors account for much more variance than probability maps, which exhibit a strong ceiling effect. This figure indicates that even within the cortex, where additional tissue probability information does not predict CBF, the proposed structural predictors can find a meaningful relation between structure and CBF.
3.4. Variance explained
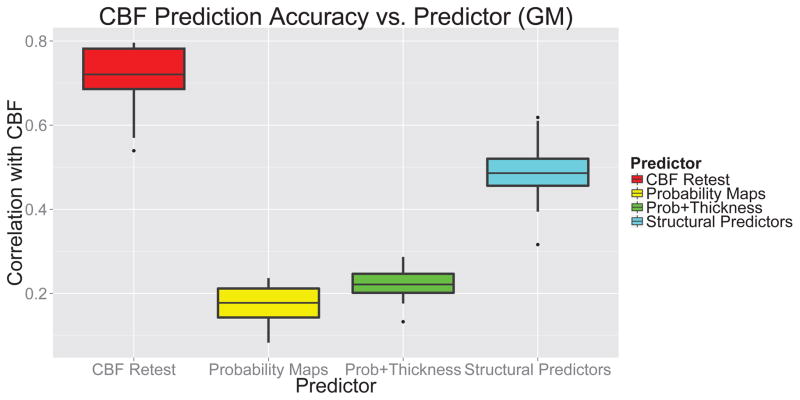
The structural features we compute are significantly better at predicting perfusion data than gray and white matter probability masks and than cortical thickness maps. Figure 8 compares predicted vs. actual perfusion values using the proposed method, segmentation probability maps, and cortical thickness for the test-retest cohort. The correlation is computed voxel-wise across the gray matter, and each sample corresponds to one subject. The higher correlation of our structural predictors with CBF as compared to the controls indicates that our predictors are more effective at explaining observed perfusion than the control predictors.
Figure 8.
Correlation of CBF with: retest CBF; probability images; probability images and thickness; and our structural predictors. Our structural predictors are much better at predicting CBF than probability images, and account for roughly half the reproducible ASL signal. This result indicates that our structural predictors are more appropriate for structural correction of perfusion than using only tissue probability images and cortical thickness.
3.5. Reproducibility
A key measure of the reliability of a clinical measurement is its test-retest reproducibility within a given subject. We evaluated the test-retest reproducibility of our anatomically-predicted and residual perfusion images and compared them to the reproducibility of the raw CBF signal and reproducibility of perfusion as predicted by tissue probability maps and cortical thickness (Figure 9). We evaluated reproducibility by voxel-wise correlation between the images at two time points for a given subject. The most reproducible measure was the CBF predicted by the probability maps, as this value is dependent only the CBF value averaged across an entire tissue compartment and is therefore highly reproducible. The voxel-wise reproducibility of CBF measurement was found to be 0.71±0.09, and this value serves as the upper bound on the reproducibility of predictions from spatially varying anatomical predictors. Predictions from probability maps and thickness on the one hand and our structural predictors have similar reproducibility to the raw CBF images. The residual CBF image was less reproducible as compared to raw CBF reproducibility (p-value=6.69 × 10−6), but still displayed relatively high reproducibility across subjects (0.52±0.07). Although the high reproducibility of the structurally predicted CBF was expected, the high reproducibility of the residual CBF indicates that it is not simply random noise and varies in a consistent way across subjects.
Figure 9.
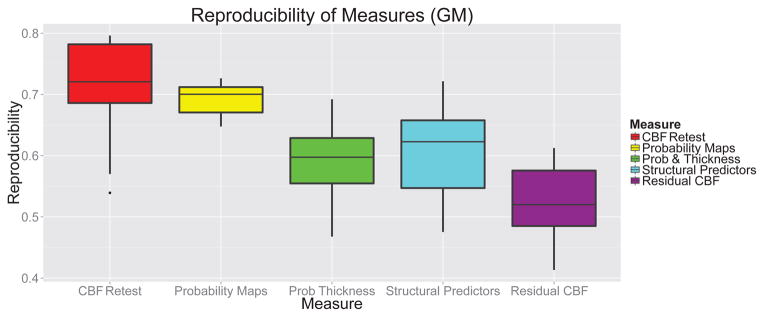
Reproducibility of mean CBF and derived CBF measures. Reproducibility is reported as the voxelwise correlation of the measure at two scans taken one hour apart. Although the reproducibility of the probability-derived CBF prediction is quite high, the low amount of variance explained by tissue probability values as opposed to RIPMMARC-derived predictors indicates that the reproducibility is most likely driven by whole-brain consistency in CBF values.
3.6. Pediatric Population Study
To return to the motivating problem of this work, we examined whether observed perfusion changes throughout adolescent development are predicted by a global model relating brain structure to perfusion. We examined trends from a variety of areas representing distinct functional domains and developmental characteristics. The hippocampus and precuneus represent higher-order memory and cognitive functions [53], and the occipital cortex and precentral gyrus represent sensorimotor regions that are presumed to mature relatively early in development [54, 55]. The default mode network (DMN), a collection of regions that are most active when subjects are not specifically engaged in any externally directed task [56], continues to undergo maturation during adolescence [57, 58]. We therefore also examined the CBF trends for the most consistent and conservative definition of the DMN, consisting of left and right precuneus, medial orbitofrontal cortex, and angular gyrus [56].
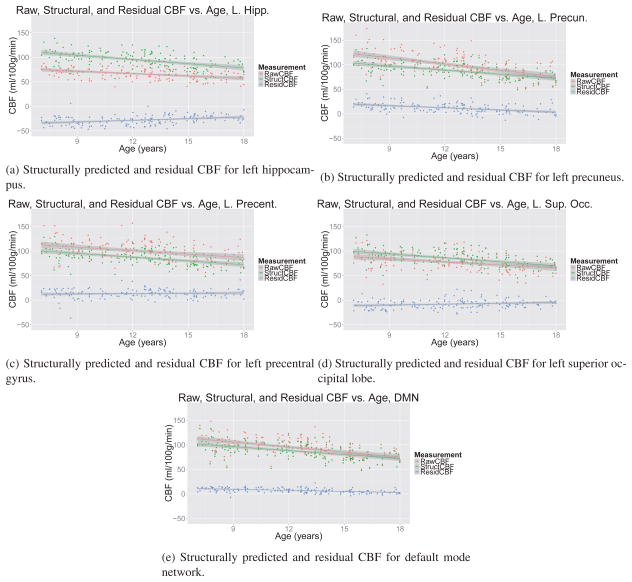
CBF trends are plotted in Figure 10, with quantitative results in Table 1. We found that although both the raw perfusion values and structurally predicted perfusion changed throughout adolescence in all regions examined, the functional specialization of different regions, as measured by the residual CBF values, followed a regionally varying trajectory. Hippocampal and precuneal residual CBF values showed a strong correlation with age, whereas the residual CBF values were not as strongly associated with age in the superior occipital cortex and the precentral gyrus. These trends were bilateral (see plots for the right hemisphere in Supplementary Material, section 7). With the exception of the hippocampus, the structurally predicted CBF had lower variance than the raw CBF, and in all areas the residual CBF had lower variance than the raw CBF. For simplicity and to minimize overfitting, we used linear regression and did not include an interaction between age and gender, but it is possible that this analysis masks nonlinear effects.
Figure 10.
Raw, anatomically predicted, and residual CBF as a function of age. The raw CBF signal contains a mixture of the structurally predicted and residual CBF signals. The residual CBF shows a spatially heterogeneous longitudinal trajectory of functional specialization, with earlier-developing regions, such as the superior occipital lobe and precentral gyrus, showing less change over adolescence than the later-developing precuneus and hippocampus. This relative stability is not apparent in the raw or structurally predicted CBF signal.
Table 1.
Statistics from linear models plotted in Figure 10. Although the raw and structurally predicted CBF values showed strong trends with age, the trends for the residual CBF was more variable. Residual CBF was strongly associated with age in the hippocampus and precuneus, but less so in superior occipital cortex and the precentral gyrus. This may suggest that there is a lesser degree of functional specialization in the precentral gyrus and occipital cortex than in hippocampus and precuneus throughout adolescence. Slope is given in units of CBF (ml/100g/min) per year.
| Raw CBF
|
Structural CBF
|
Residual CBF
|
||||
|---|---|---|---|---|---|---|
| Slope | p-value | Slope | p-value | Slope | p-value | |
| Left Hippocampus | −1.62±0.32 | 1.12 × 10−6 | −2.87±0.42 | 1.41 × 10−10 | 1.25±0.24 | 9.09 × 10−7 |
| Right Hippocampus | −1.28±0.34 | 2.3 × 10−4 | −2.89±0.42 | 10−10 | 1.61±0.24 | 3.99 × 10−10 |
| Left Precuneus | −4.28±0.55 | 7.27 × 10−13 | −2.8±0.41 | 1.08 × 10−10 | −1.48±0.24 | 4.41 × 10−9 |
| Right Precuneus | −4.09±0.54 | 2.04 × 10−12 | −2.84±0.4 | 5.69 × 10−11 | −1.25±0.26 | 3.7 × 10−6 |
| Left Precentral | −2.37±0.56 | 4.37 × 10−5 | −2.56±0.4 | 1.56 × 10−9 | 0.2±0.25 | 0.42 |
| Right Precentral | −2.2±0.55 | 10−4 | −2.55±0.4 | 2.05 × 10−9 | 0.35±0.25 | 0.16 |
| Left Occipital | −2.1±0.47 | 1.73 × 10−5 | −2.68±0.4 | 2.53 × 10−10 | 0.58±0.24 | 0.02 |
| Right Occipital | −2.64±0.47 | 9.79 × 10−8 | −2.65±0.4 | 6.76 × 10−10 | 0.01±0.23 | 0.96 |
| DMN | −3.42±0.47 | 1.12 × 10−11 | −2.69±0.41 | 6.09 × 10−10 | −0.73±0.11 | 2.21 × 10−9 |
4. Discussion
We have presented here a method to separate the anatomically predicted from the residual components of perfusion images as measured by ASL MRI. Our method to generate structural predictors gives much better prediction accuracy for predicting CBF than either probability maps or cortical thickness. The test-rest reproducibility of both the structurally predicted and residual CBF is close to that of the raw CBF, implying that both the structurally predicted and residual CBF maps contain stable signals. In addition, we found that although the anatomically predicted and raw CBF were closely related to age, the residual CBF showed a regionally heterogeneous pattern, suggesting that different brain regions undergo different amounts of functional specialization during development.
4.1. Interpretation of Structurally Predicted and Residual CBF
RIPMMARC takes CBF and structural images as input, and produces as output a structurally predicted CBF image and a residual CBF image. At first glance, the interpretation of these two outputs may be somewhat obscure, but we believe that when properly understood, each image has an intuitively clear interpretation that can be directly incorporated into clinical characterization of a subject. By way of analogy, we imagine an experiment tracking subject performance on a test of verbal ability in a group of children. A researcher may regress out “nuisance variables,” such as subject age and familial income, before examining the results. At the group level, the effect of these nuisance variables may in fact be of interest, but looking at an individual’s score without accounting for these nuisance variables would be misleading. In our method, we consider the “group effects” to be structural effects shared across the brain, whereas the “subject-level” measurements are the perfusion values at a given voxel. The group effects of underlying brain structure, similarly to age and familial income in our imagined verbal ability study, may be of independent interest, and we may be interested in looking at regional variations in perfusion as predicted by structural measures. When looking at a given voxel, though, we may also be interested in the amount of perfusion that is not predicted by the underlying neural architecture, just as one may look at a verbal ability result for a given subject when corrected for age and family income. For both the structurally predicted and residual CBF measurements, the units are in the same units of blood flow as the original mean CBF image. Negative values for the residual CBF image correspond to areas with less-than-expected perfusion as compared to structurally homologous regions elsewhere in the brain. Finding regions of the brain that consistently have lower CBF than other structurally similar regions may help clarify which specific anatomical or microstructural characteristics drive regional perfusion variations.
Biological Interpretation of CBF Measurements
The reproducibility of the residual CBF, as well as its correlation with age, indicate that it is not only the result of measurement noise, but these results do not provide a true validation that the residual CBF results from a discrete biological process. Although this study establishes an empirical link between local cortical structure and ASL-measured perfusion, it does not conclusively demonstrate a specific biological mechanism for this link. One plausible biological mechanism for a link between cortical structure and perfusion is astrocyte-mediated vasodilation. Astrocyte morphology and distribution is known to vary across the cortex [59], and recent work has demonstrated that astrocytes are capable of modulating arteriole vasoconstriction [60]. A careful evaluation of possible correlations between cortical structure and cytoarchitectonic and vascular modulation of perfusion is necessary to establish a clear causal link between cortical structure and perfusion.
4.2. Results from Population Study
We examined how structurally predicted and residual CBF vary across age in a pediatric population. We found that although the raw and structurally predicted CBF decreased across all regions throughout adolescence, the trends for residual CBF exhibited a spatially heterogeneous pattern. In the precuneus, the residual CBF decreased with age, whereas in the hippocampus, the residual CBF increased with age. In both regions, the residual CBF showed a strong bilateral correlation with age. In contrast, the residual CBF in the precentral gyrus and superior occipital cortex showed a much weaker correlation with age. These findings suggest that the functional specialization in some areas follows the cortical structural development, but in other areas displays a distinct trajectory. For example, the precentral gyrus and the occipital lobe are known to reach their mature cortical thickness relatively early in development [54], and we found that the residual CBF of these areas did not show a strong correlation with age. On the other hand, the hippocampus has also been found to reach structural maturity relatively early in adolescence [54], but we found a strong correlation between residual CBF and age here. The precuneus, in contrast, displays significant structural changes throughout adolescence [61], and the precuneal residual CBF was also found to correlate strongly with age. As a whole, these findings indicate that functional specialization may follow a trajectory that is distinct from that of cortical structural development.
In all regions examined, the trend throughout adolescence was for the residual CBF to move towards zero, implying that in older adolescents, a global model relating brain structure to perfusion is more accurate than in younger adolescents.
4.3. Comparison to Partial Volume Correction Techniques
Although the method proposed here falls into the general category of atrophy and structure correction techniques, it has a fundamentally different purpose from standard partial volume correction (PVC) techniques [62, 10, 63]. Our method directly addresses the question of the relationship between brain structure and perfusion, which is not the purpose of PVC techniques. PVC aims to recover what the scanner would have seen had technical impediments, such as partial volume effects, not interfered with the imaging. This correction is crucial to appropriately interpreting observed perfusion values, but does not aim to discover what proportion of perfusion can be accounted for by underlying brain structure. In contrast, we aim to recover both the effect of anatomy on the perfusion image and the perfusion that is independent of anatomy. The separation of structural from non-structural perfusion effects is distinct from PVC-based approaches, which incorporate the structural information directly into the output image. We did not explicitly investigate the relationship between the eigenpatch-derived predictions and partial volume effects. It is possible that the eigenpatch predictions are affected by partial volume artifacts. However, the gradient information included in the eigenpatch descriptors should also indicate how close a given voxel is to the edge of the cortex, thus implicitly accounting for partial volume effects.
4.4. Consideration of Resolution
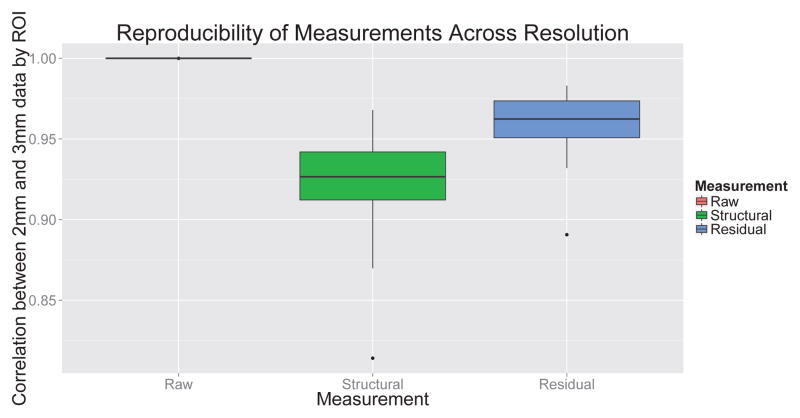
The different resolutions of arterial spin labeling MRI as compared to T1 MRI present significant challenges when attempting to analyze the relationship between the two modalities. Because the T1 image is at a much higher resolution than the ASL image, it is difficult to disentangle the effects of scanner characteristics on observed perfusion from true perfusion results. As opposed to PET imaging, quantitative analysis of ASL scanners using physical or computational phantoms is not widespread, although some initial efforts have been reported [64]. The lack of quantitative tools for analyzing scanner properties complicates the effort to work across resolutions. To examine the effect of anatomical variation on observed perfusion, we resampled both the ASL images and the T1 images to 2mm isotropic resolution. This resolution was observed to minimize interpolation artifacts from the ASL native space while still providing adequate anatomic detail. In addition, we explicitly examined the dependence of the results on resolution. We found that choosing the resolution to be 2mm or 3mm had a minimal effect on either structurally predicted or residual CBF (Figure 11).
Figure 11.
Assessment of effect of resolution on CBF measurements. Raw CBF measurements are not affected at all by resolution. Both structural and residual CBF are minimally affected by processing resolution: The ROI-wise correlation between structural and residual CBF at 2mm and 3mm resolution are greater than 0.92.
4.5. Limitations
Although this work demonstrates that the proposed method has promise, it does leave some unanswered questions that require further study. First, although the results in the pediatric population imply that the signal present in the residual CBF has biological significance, more study is necessary to validate this finding in a variety of populations to further elucidate its utility in broader applications. Second, we have not rigorously examined here how the dictionaries and coefficients vary across patients. Using only the predicted value from the dictionary learning approach without examining how the predictions are made may in fact throw away useful data, as the relationship between structure and perfusion itself may contain biologically significant information. To compare the structure-CBF relationship across subjects, though, it would be necessary to learn a consistent dictionary and apply it to all subjects. Carefully examining the variability of learned dictionaries across subjects and across different populations is necessary to establish appropriate techniques for constructing population-wide dictionaries. Third, the residual CBF retains significant amounts of the noise present in the raw CBF images, such as transit effect artifacts from large blood vessels as evident in Figure 6. The residual CBF image will in general be noisier than the structural CBF image, as the residual image will contain both biologically significant signal and noise, whereas the structurally predicted CBF image will not be affected by ASL noise. For ASL sequences that are noisier than pCASL, such as PASL-derived sequences, the additional noise may interfere with detection of the residual CBF signal. Finally, this method assumes a good registration between the ASL and T1 images. We have found that using an affine registration coupled with a small deformable registration is provides a reliable and accurate way to align cortical perfusion images. In applications with dynamic structural images, such as cardiac or muscular imaging, finding a good correspondence between structural and perfusion images may be more difficult.
4.6. Future Work
4.6.1. Variations of the Technique
In this work, we learned the relationship between brain structure and perfusion on a per-subject basis. The motivation for this is that although there may be global variations in the function that relates brain structure and perfusion, the function is a global signal over the entire brain, whereas the use of imaging is intended to highlight regionally varying measures of perfusion. This correction for global signal changes is similar in spirit to the use of relative CBF [65], where correcting for global perfusion has been found to increase the ability to find regional differences in blood flow. For application to patient populations, though, it may be more appropriate to learn the structure-perfusion relationship in an age-matched control cohort and apply the structure correction to the patient population. Alternatively, it may be ideal to learn eigen-patches from an independent population and project all subjects in the test population to that basis.
A related question that this study raises is how the structure-perfusion relationship changes across the brain. It may be more appropriate to learn the structure-perfusion relationship across individual lobes, rather than over the entire brain. RIPMARC can be easily modified to perform such an analysis by sampling the patches and training only over lobes, as opposed to over the whole brain.
The infrastructure for constructing a patch-based representation of imaging data has many other applications. It may be possible, for example, to use the patch descriptors to drive registration of images in cases where scalar intensity values are not sufficiently discriminatory. The patch-based descriptors would allow for a more expansive description of anatomy, similar to landmark-based registration techniques [66], while still enabling a dense representation of the images, as is common in voxel-based registration techniques [50].
4.6.2. Additional Applications
Although this study is limited to the connection between brain structure and perfusion, the method is fundamentally agnostic to imaging modality and can be applied across a wide range of imaging techniques. An obvious application of this work is atrophy correction for neurodegenerative populations [6]. Although several studies have shown that brain perfusion, as measured by ASL imaging, changes in Alzheimer’s Disease [67], the extent to which this decrease could be determined by atrophic and other structural changes has not been addressed using methods similar to the proposed work. Some studies have shown hippocampal hyperperfusion in early Alzheimer’s Disease, notwithstanding hippocampal atrophy [68]. These contrasting trends of increased perfusion and atrophy highlight the need for rigorous structural correction of perfusion imaging.
RIPMMARC may also be useful for missing image imputation. Standard methods for data imputation rely on methods borrowed from matrix imputation [69, 70]. Using an imputation method that incorporates image characteristics into the imputation may result in a more accurate imputation method. Traumatic brain injury represents a disease state where RIPMMARC may be particularly useful. In many cases, pre-injury perfusion scans of subjects are not available, confounding disease effects with natural inter-subject variation. By imputing perfusion based on structurally similar areas of the brain, RIPMMARC can provide a subject- and region-specific estimate of expected brain perfusion for the damaged region. Finally, RIPMMARC provides a scalable approach to novelty detection in multi-modal imaging studies.
5. Conclusion
The method presented here shows promise in decomposing CBF images into anatomically predicted and residual perfusion components. The algorithm proposed explains significantly more of the variance in CBF images than the segmentation probability maps commonly used for performing partial volume correction, and therefore may be more suitable for structural correction of perfusion images than tissue segmentation images. In addition, the method can be used to improve the interpretability of perfusion images by indicating how much of the observed changes in perfusion are caused by global structural trends and how much by localized processes. This separation of global from local effects can provide greater sensitivity for correlating spatially localized neuronal processes with perfusion images.
Supplementary Material
Highlights.
We propose a method to learn the connection between cortical structure and perfusion.
Our learned structural features predict perfusion better than gray matter content.
Both the predicted and residual perfusion values are highly reproducible.
In a pediatric population, both predicted and residual perfusion are linked to age.
Acknowledgments
DJW was supported by NIH awards R01-MH080892, R01-NS081077, and R01-EB014922; JAD was supported by awards P41 EB015893 and R01 MH080729; and JCG and BMK were supported by T32-EB009384 and HHSN276201000492P.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Franklin TR, Wang Z, Shin J, Jagannathan K, Suh JJ, Detre JA, OBrien CP, Childress AR. A VBM study demonstrating apparent effects of a single dose of medication on t1-weighted MRIs. Brain Structure and Function. 2013;218(1):97–104. doi: 10.1007/s00429-012-0385-6. URL http://link.springer.com/article/10.1007/s00429-012-0385-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Salgado-Pineda P, Delaveau P, Falcon C, Blin O. Brain t1 intensity changes after levodopa administration in healthy subjects: a voxel-based morphometry study. British Journal of Clinical Pharmacology. 2006;62(5):546551. doi: 10.1111/j.1365-2125.2006.02695.x. URL http://onlinelibrary.wiley.com/doi/10.1111/j.1365-2125.2006.02695.x/abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fierstra J, Poublanc J, Han JS, Silver F, Tymianski M, Crawley AP, Fisher JA, Mikulis DJ. Steal physiology is spatially associated with cortical thinning. Journal of Neurology, Neurosurgery & Psychiatry. 2010;81(3):290–293. doi: 10.1136/jnnp.2009.188078. URL http://jnnp.bmj.com/content/81/3/290. [DOI] [PubMed] [Google Scholar]
- 4.Villain N, Desgranges B, Viader F, de la Sayette V, Mzenge F, Landeau B, Baron J-C, Eustache F, Chtelat G. Relationships between hippocampal atrophy, white matter disruption, and gray matter hypometabolism in alzheimer’s disease. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2008;28(24):6174–6181. doi: 10.1523/JNEUROSCI.1392-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chtelat G, Desgranges B, Landeau B, Mzenge F, Poline JB, Sayette Vdl, Viader F, Eustache F, Baron J-C. Direct voxel-based comparison between grey matter hypometabolism and atrophy in alzheimer’s disease. Brain. 2008;131(1):60–71. doi: 10.1093/brain/awm288. URL http://brain.oxfordjournals.org/content/131/1/60. [DOI] [PubMed] [Google Scholar]
- 6.Chen JJ, Rosas HD, Salat DH. Age-associated reductions in cerebral blood flow are independent from regional atrophy. NeuroImage. 2011;55(2):468–478. doi: 10.1016/j.neuroimage.2010.12.032. URL http://www.sciencedirect.com/science/article/pii/S1053811910016162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tosun D, Rosen H, Miller BL, Weiner MW, Schuff N. MRI patterns of atrophy and hypoperfusion associations across brain regions in frontotemporal dementia. NeuroImage. 2012;59(3):2098–2109. doi: 10.1016/j.neuroimage.2011.10.031. URL http://www.sciencedirect.com/science/article/pii/S1053811911011943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tosun D, Mojabi P, Weiner MW, Schuff N. Joint analysis of structural and perfusion MRI for cognitive assessment and classification of alzheimer’s disease and normal aging. NeuroImage. 2010;52(1):186–197. doi: 10.1016/j.neuroimage.2010.04.033. URL http://www.sciencedirect.com/science/article/pii/S1053811910004453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jrnum H, Eskildsen SF, Steffensen EG, Lundbye-Christensen S, Simonsen CW, Thomsen IS, Frnd E-T, Thberge J, Larsson E-M. Longitudinal MRI study of cortical thickness, perfusion, and metabolite levels in major depressive disorder. Acta Psychiatrica Scandinavica. 2011;124(6):435446. doi: 10.1111/j.1600-0447.2011.01766.x. URL http://onlinelibrary.wiley.com/doi/10.1111/j.1600-0447.2011.01766.x/abstract. [DOI] [PubMed] [Google Scholar]
- 10.Muller-Gartner HW, Links JM, Prince JL, Bryan RN, McVeigh E, Leal JP, Davatzikos C, Frost JJ. Measurement of radiotracer concentration in brain gray matter using positron emission tomography: MRI-based correction for partial volume effects. Journal of Cerebral Blood Flow & Metabolism. 1992;12(4):571–583. doi: 10.1038/jcbfm.1992.81. URL http://www.nature.com/jcbfm/journal/v12/n4/abs/jcbfm199281a.html. [DOI] [PubMed] [Google Scholar]
- 11.Roberts DA, Detre JA, Bolinger L, Insko EK, Leigh JS., Jr Quantitative magnetic resonance imaging of human brain perfusion at 1.5 t using steady-state inversion of arterial water. Proceedings of the National Academy of Sciences of the United States of America. 1994;91(1):33–37. doi: 10.1073/pnas.91.1.33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chiron C, Raynaud C, Mazire B, Zilbovicius M, Laflamme L, Masure M-C, Dulac O, Bourguignon M, Syrota A. Changes in regional cerebral blood flow during brain maturation in children and adolescents. Journal of Nuclear Medicine. 1992;33(5):696–703. URL http://jnm.snmjournals.org/content/33/5/696. [PubMed] [Google Scholar]
- 13.Wintermark M, Lepori D, Cotting J, Roulet E, Melle Gv, Meuli R, Maeder P, Regli L, Verdun FR, Deonna T, Schnyder P, Gudinchet F. Brain perfusion in children: Evolution with age assessed by quantitative perfusion computed tomography. Pediatrics. 2004;113(6):1642–1652. doi: 10.1542/peds.113.6.1642. URL http://pediatrics.aappublications.org/content/113/6/1642. [DOI] [PubMed] [Google Scholar]
- 14.Biagi L, Abbruzzese A, Bianchi MC, Alsop DC, Del Guerra A, Tosetti M. Age dependence of cerebral perfusion assessed by magnetic resonance continuous arterial spin labeling. Journal of Magnetic Resonance Imaging. 2007;25(4):696702. doi: 10.1002/jmri.20839. URL http://onlinelibrary.wiley.com/doi/10.1002/jmri.20839/abstract. [DOI] [PubMed] [Google Scholar]
- 15.Jain V, Duda J, Avants B, Giannetta M, Xie SX, Roberts T, Detre JA, Hurt H, Wehrli FW, Wang DJJ. Longitudinal reproducibility and accuracy of pseudo-continuous arterial spin-labeled perfusion MR imaging in typically developing children. Radiology. 2012;263(2):527–536. doi: 10.1148/radiol.12111509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Satterthwaite TD, Wolf DH, Erus G, Ruparel K, Elliott MA, Gennatas ED, Hopson R, Jackson C, Prabhakaran K, Bilker WB, Calkins ME, Loughead J, Smith A, Roalf DR, Hakonarson H, Verma R, Davatzikos C, Gur RC, Gur RE. Functional maturation of the executive system during adolescence. The Journal of Neuroscience. 2013;33(41):16249–16261. doi: 10.1523/JNEUROSCI.2345-13.2013. URL http://www.jneurosci.org/content/33/41/16249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wang J, Licht DJ, Jahng G-H, Liu C-S, Rubin JT, Haselgrove J, Zimmerman RA, Detre JA. Pediatric perfusion imaging using pulsed arterial spin labeling. Journal of Magnetic Resonance Imaging. 2003;18(4):404413. doi: 10.1002/jmri.10372. URL http://onlinelibrary.wiley.com/doi/10.1002/jmri.10372/abstract. [DOI] [PubMed] [Google Scholar]
- 18.Wang J, Licht DJ. Pediatric perfusion MR imaging using arterial spin labeling. Neuroimaging Clinics of North America. 2006;16(1):149–167. doi: 10.1016/j.nic.2005.10.002. URL http://www.sciencedirect.com/science/article/pii/S1052514905001103. [DOI] [PubMed] [Google Scholar]
- 19.Shaw P, Kabani NJ, Lerch JP, Eckstrand K, Lenroot R, Gogtay N, Greenstein D, Clasen L, Evans A, Rapoport JL, Giedd JN, Wise SP. Neurodevelopmental trajectories of the human cerebral cortex. The Journal of Neuroscience. 2008;28(14):3586–3594. doi: 10.1523/JNEUROSCI.5309-07.2008. URL http://www.jneurosci.org/content/28/14/3586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tamnes C, stby Y, Fjell A, Westlye L, Due-Tnnessen P, Walhovd K. Brain maturation in adolescence and young adulthood: Regional age-related changes in cortical thickness and white matter volume and microstructure. Cerebral Cortex. 2010;20(3):534–548. doi: 10.1093/cercor/bhp118. [DOI] [PubMed] [Google Scholar]
- 21.Blanton RE, Levitt JG, Thompson PM, Narr KL, Capetillo-Cunliffe L, Nobel A, Singerman JD, McCracken JT, Toga AW. Mapping cortical asymmetry and complexity patterns in normal children. Psychiatry Research: Neuroimaging. 2001;107(1):29–43. doi: 10.1016/S0925-4927(01)00091-9. URL http://www.sciencedirect.com/science/article/pii/S0925492701000919. [DOI] [PubMed] [Google Scholar]
- 22.Su S, White T, Schmidt M, Kao C-Y, Sapiro G. Geometric computation of human gyrification indexes from magnetic resonance images. Human Brain Mapping. 2013;34(5):12301244. doi: 10.1002/hbm.21510. URL http://onlinelibrary.wiley.com/doi/10.1002/hbm.21510/abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hoffman EJ, Huang SC, Phelps ME. Quantitation in positron emission computed tomography: 1. effect of object size. Journal of computer assisted tomography. 1979;3(3):299–308. doi: 10.1097/00004728-197906000-00001. [DOI] [PubMed] [Google Scholar]
- 24.Williams DS, Detre JA, Leigh JS, Koretsky AP. Magnetic resonance imaging of perfusion using spin inversion of arterial water. Proceedings of the National Academy of Sciences of the United States of America. 1992;89(1):212–216. doi: 10.1073/pnas.89.1.212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Johnson NA, Jahng G-H, Weiner MW, Miller BL, Chui HC, Jagust WJ, Gorno-Tempini ML, Schuff N. Pattern of cerebral hypoperfusion in alzheimer disease and mild cognitive impairment measured with arterial spin-labeling MR imaging: initial experience. Radiology. 2005;234(3):851–859. doi: 10.1148/radiol.2343040197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Asllani I, Borogovac A, Brown TR. Regression algorithm correcting for partial volume effects in arterial spin labeling MRI. Magnetic Resonance in Medicine. 2008;60(6):13621371. doi: 10.1002/mrm.21670. URL http://onlinelibrary.wiley.com/doi/10.1002/mrm.21670/abstract. [DOI] [PubMed] [Google Scholar]
- 27.Asllani I, Habeck C, Borogovac A, Brown TR, Brickman AM, Stern Y. Separating function from structure in perfusion imaging of the aging brain. Human brain mapping. 2009;30(9):2927–2935. doi: 10.1002/hbm.20719. URL http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2733928/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chappell MA, Groves AR, MacIntosh BJ, Donahue MJ, Jezzard P, Woolrich MW. Partial volume correction of multiple inversion time arterial spin labeling MRI data. Magnetic Resonance in Medicine. 2011;65(4):11731183. doi: 10.1002/mrm.22641. URL http://onlinelibrary.wiley.com/doi/10.1002/mrm.22641/abstract. [DOI] [PubMed] [Google Scholar]
- 29.Petr J, Schramm G, Hofheinz F, Langner J, van den Hoff J. Partial volume correction in arterial spin labeling using a look-locker sequence. Magnetic Resonance in Medicine. 2012 doi: 10.1002/mrm.24601. URL http://onlinelibrary.wiley.com/doi/10.1002/mrm.24601/abstract. [DOI] [PubMed]
- 30.Schuff N, Matsumoto S, Kmiecik J, Studholme C, Du A, Ezekiel F, Miller BL, Kramer JH, Jagust WJ, Chui HC, Weiner MW. Cerebral blood flow in ischemic vascular dementia and alzheimer’s disease, measured by arterial spin-labeling magnetic resonance imaging. Alzheimer’s & Dementia. 2009;5(6):454–462. doi: 10.1016/j.jalz.2009.04.1233. URL http://www.sciencedirect.com/science/article/pii/S1552526009001010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ranzato M, Huang FJ, Boureau Y-L, LeCun Y. Unsupervised learning of invariant feature hierarchies with applications to object recognition. IEEE Conference on Computer Vision and Pattern Recognition, 2007. CVPR ’07; 2007. pp. 1–8. [DOI] [Google Scholar]
- 32.Aharon M, Elad M, Bruckstein A. K-SVD: An algorithm for designing over-complete dictionaries for sparse representation. IEEE Transactions on Signal Processing. 2006;54(11):4311–4322. doi: 10.1109/TSP.2006.881199. [DOI] [Google Scholar]
- 33.Mairal J, Bach F, Ponce J, Sapiro G, Zisserman A. Discriminative learned dictionaries for local image analysis. IEEE Conference on Computer Vision and Pattern Recognition, 2008. CVPR 2008; 2008. pp. 1–8. [DOI] [Google Scholar]
- 34.Lowe D. Object recognition from local scale-invariant features. The Proceedings of the Seventh IEEE International Conference on Computer Vision; 1999; 1999. pp. 1150–1157. [DOI] [Google Scholar]
- 35.Ke Y, Sukthankar R. PCA-SIFT: a more distinctive representation for local image descriptors. Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2004. CVPR 2004; 2004. pp. II–506–II–513. [DOI] [Google Scholar]
- 36.Bay H, Tuytelaars T, Gool LV. SURF: Speeded up robust features. In: Leonardis A, Bischof H, Pinz A, editors. Computer Vision ECCV 2006, no. 3951 in Lecture Notes in Computer Science. Springer; Berlin Heidelberg: 2006. pp. 404–417. URL http://link.springer.com/chapter/10.1007/11744023_32. [Google Scholar]
- 37.Toews M, Wells WM., III Efficient and robust model-to-image alignment using 3d scale-invariant features. Medical Image Analysis. 2013;17(3):271–282. doi: 10.1016/j.media.2012.11.002. URL http://www.sciencedirect.com/science/article/pii/S1361841512001533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Chen Y-C, Sastry C, Patel V, Phillips P, Chellappa R. Rotation invariant simultaneous clustering and dictionary learning. 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); 2012. pp. 1053–1056. [DOI] [Google Scholar]
- 39.Barthelemy Q, Larue A, Mayoue A, Mercier D, Mars J. Shift and 2d rotation invariant sparse coding for multivariate signals. IEEE Transactions on Signal Processing. 2012;60(4):1597–1611. doi: 10.1109/TSP.2012.2183129. [DOI] [Google Scholar]
- 40.Hertzmann A, Jacobs CE, Oliver N, Curless B, Salesin DH. Image analogies. Proceedings of the 28th annual conference on Computer graphics and interactive techniques; 2001. pp. 327–340. URL http://dl.acm.org/citation.cfm?id=383295. [Google Scholar]
- 41.Wang G, Wong T-T, Heng P-A. Deringing cartoons by image analogies. ACM Transactions on Graphics (TOG) 2006;25(4):1360–1379. URL http://dl.acm.org/citation.cfm?id=1183292. [Google Scholar]
- 42.Rueda A, Malpica N, Romero E. Single-image super-resolution of brain MR images using overcomplete dictionaries. Medical Image Analysis. 2013;17(1):113–132. doi: 10.1016/j.media.2012.09.003. URL http://www.sciencedirect.com/science/article/pii/S1361841512001326. [DOI] [PubMed] [Google Scholar]
- 43.Rousseau F. A non-local approach for image super-resolution using intermodality priors. Medical Image Analysis. 2010;14(4):594–605. doi: 10.1016/j.media.2010.04.005. URL http://www.sciencedirect.com/science/article/pii/S1361841510000411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wahba G. A least squares estimate of satellite attitude. SIAM Review. 1965;7(3):409–409. doi: 10.1137/1007077. URL http://epubs.siam.org/doi/abs/10.1137/1007077. [DOI] [Google Scholar]
- 45.Kabsch W. A solution for the best rotation to relate two sets of vectors. Acta Crystallographica Section A. 1976;32(5):922–923. doi: 10.1107/S0567739476001873. URL http://scripts.iucr.org/cgi-bin/paper?S0567739476001873. [DOI] [Google Scholar]
- 46.Jafari-Khouzani K, Soltanian-Zadeh H. Radon transform orientation estimation for rotation invariant texture analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2005;27(6):1004–1008. doi: 10.1109/TPAMI.2005.126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chen Y, Wang DJ, Detre JA. Testretest reliability of arterial spin labeling with common labeling strategies. Journal of Magnetic Resonance Imaging. 2011;33(4):940949. doi: 10.1002/jmri.22345. URL http://onlinelibrary.wiley.com/doi/10.1002/jmri.22345/abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Avants BB, Tustison NJ, Song G, Cook PA, Klein A, Gee JC. A reproducible evaluation of ANTs similarity metric performance in brain image registration. NeuroImage. 2011;54(3):2033–2044. doi: 10.1016/j.neuroimage.2010.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Avants B, Tustison N, Wu J, Cook P, Gee J. An open source multivariate framework for n-tissue segmentation with evaluation on public data. Neuroinformatics. 2011;9(4):381–400. doi: 10.1007/s12021-011-9109-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Avants B, Epstein C, Grossman M, Gee J. Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Medical Image Analysis. 2008;12(1):26–41. doi: 10.1016/j.media.2007.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Avants BB, Lakshmikanth SK, Duda JT, Detre JA, Grossman M. Robust cerebral blood flow reconstruction from perfusion imaging with an open-source, multi-platform toolkit. Proceedings of Perfusion MRI: Standardization, Beyond CBF and Everyday Clinical Applications, International Society for Magnetic Resonance in Medicine Scientific Workshop; Amsterdam. 2012. p. 21. [Google Scholar]
- 52.Wu W-C, Jain V, Li C, Giannetta M, Hurt H, Wehrli FW, Wang DJJ. In vivo venous blood t1 measurement using inversion recovery true-FISP in children and adults. Magnetic Resonance in Medicine. 2010;64(4):11401147. doi: 10.1002/mrm.22484. URL http://onlinelibrary.wiley.com/doi/10.1002/mrm.22484/abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Cavanna AE, Trimble MR. The precuneus: a review of its functional anatomy and behavioural correlates. Brain. 2006;129(3):564–583. doi: 10.1093/brain/awl004. URL http://brain.oxfordjournals.org/content/129/3/564. [DOI] [PubMed] [Google Scholar]
- 54.Gogtay N, Giedd JN, Lusk L, Hayashi KM, Greenstein D, Vaituzis AC, Nugent TF, Herman DH, Clasen LS, Toga AW, Rapoport JL, Thompson PM. Dynamic mapping of human cortical development during childhood through early adulthood. Proceedings of the National Academy of Sciences of the United States of America. 2004;101(21):8174–8179. doi: 10.1073/pnas.0402680101. URL http://www.pnas.org/content/101/21/8174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Rueckriegel SM, Blankenburg F, Burghardt R, Ehrlich S, Henze G, Mergl R, Herniz Driever P. Influence of age and movement complexity on kinematic hand movement parameters in childhood and adolescence. International Journal of Developmental Neuroscience. 2008;26(7):655–663. doi: 10.1016/j.ijdevneu.2008.07.015. URL http://www.sciencedirect.com/science/article/pii/S0736574808001238. [DOI] [PubMed] [Google Scholar]
- 56.Buckner RL, Andrews-Hanna JR, Schacter DL. The brain’s default network. Annals of the New York Academy of Sciences. 2008;1124(1):138. doi: 10.1196/annals.1440.011. URL http://onlinelibrary.wiley.com/doi/10.1196/annals.1440.011/abstract. [DOI] [PubMed] [Google Scholar]
- 57.Uddin LQ, Supekar KS, Ryali S, Menon V. Dynamic reconfiguration of structural and functional connectivity across core neurocognitive brain networks with development. The Journal of Neuroscience. 2011;31(50):18578–18589. doi: 10.1523/JNEUROSCI.4465-11.2011. URL http://www.jneurosci.org/content/31/50/18578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Supekar K, Uddin LQ, Prater K, Amin H, Greicius MD, Menon V. Development of functional and structural connectivity within the default mode network in young children. NeuroImage. 2010;52(1):290–301. doi: 10.1016/j.neuroimage.2010.04.009. URL http://www.sciencedirect.com/science/article/pii/S1053811910004039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Mittelbronn M, Dietz K, Schluesener HJ, Meyermann R. Local distribution of microglia in the normal adult human central nervous system differs by up to one order of magnitude. Acta Neuropathologica. 2001;101(3):249–255. doi: 10.1007/s004010000284. URL http://link.springer.com/article/10.1007/s004010000284. [DOI] [PubMed] [Google Scholar]
- 60.Howarth C. The contribution of astrocytes to the regulation of cerebral blood flow. Brain Imaging Methods. 2014;8:103. doi: 10.3389/fnins.2014.00103. URL http://journal.frontiersin.org/Journal/10.3389/fnins.2014.00103/full. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Tamnes CK, Walhovd KB, Dale AM, stby Y, Grydeland H, Richardson G, Westlye LT, Roddey JC, Hagler DJ, Due-Tnnessen P, Holland D, Fjell AM. Brain development and aging: Overlapping and unique patterns of change. NeuroImage. 2013;68:63–74. doi: 10.1016/j.neuroimage.2012.11.039. URL http://linkinghub.elsevier.com/retrieve/pii/S1053811912011512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Meltzer CC, Leal JP, Mayberg HS, Wagner HN, Jr, Frost JJ. Correction of PET data for partial volume effects in human cerebral cortex by MR imaging. Journal of computer assisted tomography. 1990;14(4):561–570. doi: 10.1097/00004728-199007000-00011. [DOI] [PubMed] [Google Scholar]
- 63.Thomas BA, Erlandsson K, Modat M, Thurfjell L, Vandenberghe R, Ourselin S, Hutton BF. The importance of appropriate partial volume correction for PET quantification in alzheimers disease. European Journal of Nuclear Medicine and Molecular Imaging. 2011;38(6):1104–1119. doi: 10.1007/s00259-011-1745-9. URL http://link.springer.com/article/10.1007/s00259-011-1745-9. [DOI] [PubMed] [Google Scholar]
- 64.Noguchi T, Yoshiura T, Hiwatashi A, Togao O, Yamashita K, Kobayashi K, Mihara F, Honda H. Quantitative perfusion imaging with pulsed arterial spin labeling: A phantom study. Magnetic Resonance in Medical Sciences. 2007;6(2):91–97. doi: 10.2463/mrms.6.91. [DOI] [PubMed] [Google Scholar]
- 65.Aslan S, Lu H. On the sensitivity of ASL MRI in detecting regional differences in cerebral blood flow. Magnetic Resonance Imaging. 2010;28(7):928–935. doi: 10.1016/j.mri.2010.03.037. URL http://www.sciencedirect.com/science/article/pii/S0730725X10001001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Thompson P, Toga A. A surface-based technique for warping three-dimensional images of the brain. IEEE Transactions on Medical Imaging. 1996;15(4):402–417. doi: 10.1109/42.511745. [DOI] [PubMed] [Google Scholar]
- 67.Wolk DA, Detre JA. Arterial spin labeling MRI: an emerging biomarker for alzheimer’s disease and other neurodegenerative conditions. Current Opinion in Neurology. 2012;25(4):421–428. doi: 10.1097/WCO.0b013e328354ff0a. URL http://journals.lww.com/co-neurology/pages/articleviewer.aspx?year=2012&issue=08000&article=00008&type=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Alsop DC, Casement M, de Bazelaire C, Fong T, Press DZ. Hippocampal hyperperfusion in alzheimer’s disease. NeuroImage. 2008;42(4):1267–1274. doi: 10.1016/j.neuroimage.2008.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Xiang S, Yuan L, Fan W, Wang Y, Thompson PM, Ye J for the Alzheimer’s Disease Neuroimaging Initiative. Bi-level multi-source learning for heterogeneous block-wise missing data. NeuroImage. doi: 10.1016/j.neuroimage.2013.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Thung KH, Wee CY, Yap PT, Shen D. Alzheimer’s Disease Neuroimaging Initiative, Neurodegenerative disease diagnosis using incomplete multi-modality data via matrix shrinkage and completion. NeuroImage. 2014;91:386–400. doi: 10.1016/j.neuroimage.2014.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.