Probabilistic algorithms for MEG/EEG source reconstruction using temporal basis functions learned from data

Abstract

We present two related probabilistic methods for neural source reconstruction from MEG/EEG data that reduce effects of interference, noise and correlated sources. Both methods localize source activity using a linear mixture of temporal basis functions (TBFs) learned from the data. In contrast to existing methods that use predetermined TBFs, we compute TBFs from data using a graphical factor analysis based model (Nagarajan et al., 2007a), which separates evoked or event related source activity from ongoing spontaneous background brain activity. Both algorithms compute an optimal weighting of these TBFs at each voxel to provide a spatiotemporal map of activity across the brain and a source image map from the likelihood of a dipole source at each voxel. We explicitly model, with two different robust parameterizations, the contribution from signals outside a voxel of interest. The two models differ in a trade-off of computational speed versus accuracy of learning the unknown interference contributions. Performance in simulations and real data, both with large noise and interference and/or correlated sources, demonstrate significant improvement over existing source localization methods.

Introduction

Magnetoencephalography (MEG) and electroencephalography (EEG) are popular methods for providing the spatiotemporal characteristics of human neural activity to both researchers and clinicians. Both techniques record the effects of neural activity at the scalp with millisecond precision. The increasing availability of whole-head MEG/EEG sensor arrays allows for higher-resolution spatiotemporal reconstruction of neural activity, thus increasing the demand for improved methods for source reconstruction.

Many sources of noise interfere with true signals in the MEG/EEG data, affecting all existing inverse method algorithms. Thermal or electrical noise are present at the MEG or EEG sensors themselves. Background room interference such as from powerlines and electronic equipment can be problematic. Biological noise such as heartbeat, eyeblink or other muscle artifact can also be present. Ongoing brain activity itself, including the drowsy-state alpha (~10Hz) rhythm can drown out evoked brain sources. Finally, many localization algorithms have difficulty in separating neural sources of interest that have temporally overlapping activity.

The magnitude of the stimulus-evoked neural sources are on the order of noise on a single trial, and so typically 50–200 averaged trials are needed in order to clearly distinguish the sources above noise. This limits the type of cognitive questions that can be answered, and is prohibitive for examining processes such as learning that can occur over just a few trials. Obtaining sufficient trials for successfully averaging out noise is time-consuming and therefore difficult for a subject or patient to hold still or pay attention through the duration of the experiment.

Algorithms proposed in this paper use a probabilistic graphical model framework: a general tool for learning unknown, underlying variables from observed sensor data. The graphical model depicts probabilistic dependencies between nodes, which include the observed data, computed lead field, unobserved evoked and interference factors, and sensor noise. Many inference algorithms exist to estimate the unknown quantities given the data and model. We have recently shown that this approach is effective for interference suppression, source separation and source localization of MEG data (Nagarajan et al., 2007a; Zumer et al., 2007).

The source reconstruction framework proposed in this paper is referred to as Neurodynamic Stimulus Evoked Factor Analysis Localization (NSEFALoc), which first uses a separate graphical model called Stimulus Evoked Factor Analysis (SEFA) to estimate temporal basis functions and then finds the best linear mixture (spatial weighting) of these basis functions at each source voxel. NSEFALoc1 models the activity outside a particular voxel by a full-rank covariance matrix and estimates unknown quantities by maximizing the likelihood. NSEFALoc2 parameterizes activity outside the voxel of interest as a linear mixture of a set of unknown Gaussian factors plus Gaussian sensor noise and estimates all unknown quantities using a Variational Bayesian Expectation-Maximization (VB-EM) algorithm (Attias, 1999; Ghahramani and Beal, 2001). Both techniques create an image of brain activity by scanning the brain, inferring the models from sensor data, and using them to compute the maximized likelihood of the data with the best set of parameters at each voxel, creating a spatial map to indicate the most likely locations of sources.

It is clear that improved performance for noisy data with correlated sources is a desirable trait for a new source reconstruction method, especially since some methods such as minimum adaptive variance beamforming (MVAB) is known to have reduced performance when at least two sources are highly correlated (Sekihara et al., 2002a). The simulations and real data tested here illustrate these issues and demonstrate improved performance of NSEFALoc over existing methods. In simulations, several parameters such as location of sources, rotating or fixed dipoles, SNR, and type of background noise were varied. The effect of number of sensors and timepoints (total data available) was also tested. Finally, robustness to choice of number of basis functions or factors by the user is shown. Furthermore, performance of all methods is compared using some real-data examples from an auditory evoked MEG dataset and a low-SNR somatosensory MEG dataset.

An initial report of this method was presented in Zumer et al. (2006). This current paper expands on the mathematical details and provides a more thorough analysis of performance in both simulations and real data, in comparison to established methods of MVAB (Sekihara et al., 2002b) and sLORETA (Pascual-Marqui, 2002).

Theory

In both NSEFALoc models, we assume the source activity is a linear combination of J × N temporal basis functions Φ computed from the data, spatially weighted at each voxel r by a Q × J dipole mixing matrix G^r. We compute the maximum likelihood at each voxel; the spatial peaks of this likelihood map correspond to the most likely source locations.

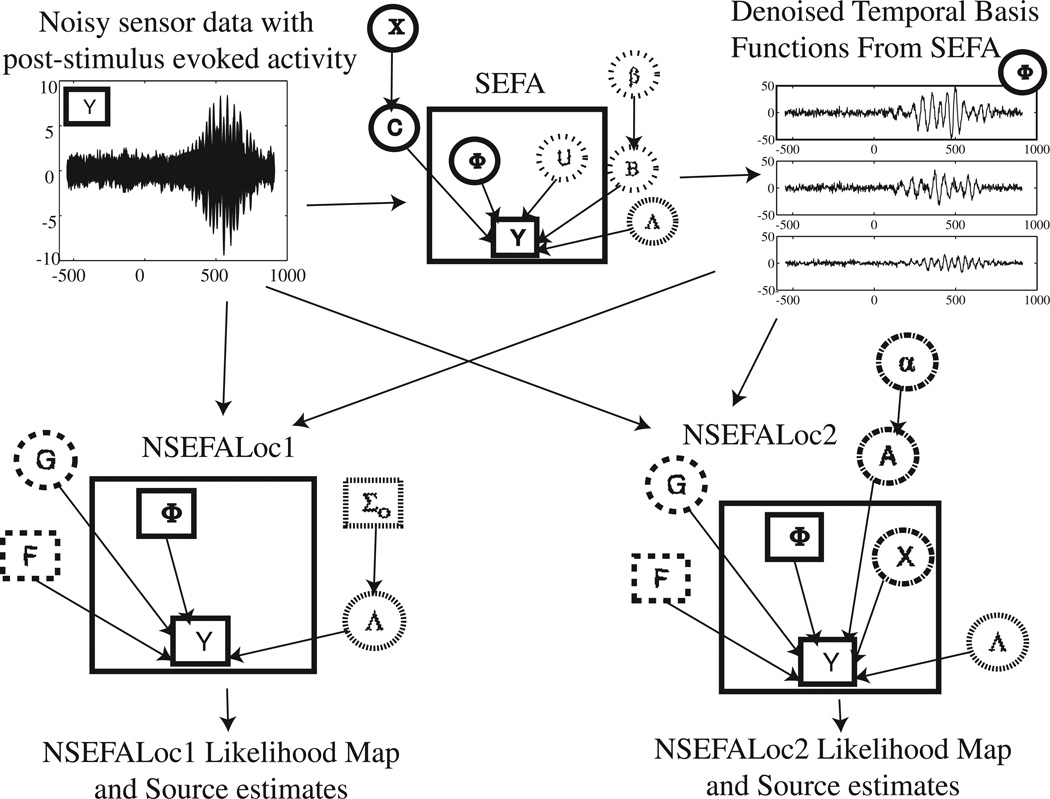
Figure 1 depicts the graphical models for the processing steps of both NSEFALoc models. SEFA (top middle) is a separate model that is first run as a preliminary step on the data Y prior to either NSEFALoc algorithm in order to learn the denoised evoked factors Φ (top right) to be used at temporal basis functions. In SEFA, evoked brain activity, biological noise, other room interference and sensor noise all contribute to the measured sensor data (top left). The second step is to run either or both NSEFALoc models, shown in the second row of Fig. 1. Both NSEFALoc models use the averaged sensor data and the temporal basis functions Φ as known/fixed quantities. Finally, both models output a likelihood map indicating the location of sources as well as the source time course estimates.

Fig. 1.

Graphical models for NSEFALoc1 and NSEFALoc2. Noisy sensor data is first processed by SEFA to determine the denoised temporal basis functions Φ, of which a linear mixture can produce any localized evoked source. These TBFs are then input as fixed bases to both NSEFALoc1 and NSEFALoc2, which estimate the spatial weighting G of these TBFs for each voxel. The likelihood map can be displayed, and the source estimate at its spatial peaks can be plotted. In each graphical model, quantities inside the large square are variables dependent on time while quantities outside are parameters/hyperparameters independent of time. Directed arrows between nodes indicate a probabilistic dependence. Square nodes are known (observed or computed) while circles nodes are unknown. The relative amounts of dashs/dots for each circle or square indicate groupings of nodes.

The mathematical notation used throughout this paper is as follows. Matrices are in bold upper case, vectors are in bold lower case (e.g. the nth column of the matrix Φ is ϕ_n, or a vector such as the hyperparameter α), and scalars are in non-bold lower case (e.g. the element from the kth row and lth column of matrix A is a_kl). Non-bold upper case Roman letters are used to denote the dimension of matrices or vectors, such as K number of MEG sensors.

Computing Temporal Basis Functions from data using SEFA

We assume that the neural activity at all possible source locations can be described as a linear combination of temporal basis functions, which we estimate using SEFA (Nagarajan et al., 2007a). SEFA uses the computational framework of Variational Bayesian Factor analysis (VBFA), but includes the additional concept of how MEG/EEG data are collected in order to further separate out noise components. In the stimulus evoked paradigm, some baseline control data is collected for several hundred milliseconds during the pre-stimulus period, then a stimulus occurs, evoking a neural response in the post-stimulus period.

The key idea of SEFA is that background activity, such as ongoing brain activity unrelated to the stimulus, other biological noise such as eyeblinks and heartbeat, other room noise, and sensor noise, will be present in both pre-stimulus and post-stimulus periods. However, only the evoked brain sources of interest will be present in post-stimulus period alone and not in the pre-stimulus period. Note this assumption is valid for the evoked response paradigm, but not the event-related synchronization/desynchronization analysis.

The data Y is partitioned into pre- and post-stimulus sections as:

$${\mathit{y}}_n=\mathit{B}{\mathit{u}}_n+{\mathit{\upsilon }}_{n}n=-N_{\mathit{\text{pre}}},\dots ,-1$$ (1)

$${\mathit{y}}_n=\mathit{C}{\mathit{\varphi }}_n+\mathit{B}{\mathit{u}}_n+{\mathit{\upsilon }}_{n}n=0,\dots ,N_{\mathit{\text{post}}}-1$$

Time ranges from −N_pre : 0 : N_post − 1 where N_pre (N_post) indicates the number of time samples in the pre- (post-)stimulus period. The K × M matrix B and the M × 1 vector u_n represent the background mixing matrix and background factors, respectively. The K × L matrix C and L × 1 vector ϕ_n are the evoked mixing matrix and evoked factors (temporal basis functions), respectively. The sensor noise term υ_n is described by diagonal precision matrix Λ_S, where the subscript S indicates the Λ learned from SEFA. The quantities Φ, U and V are the matrices for all time points for ϕ_n, u_n and υ_n.

The details of the model are described in Appendix A. The update rules are listed explicitly here again, since those listed in Nagarajan et al. (2007a) describe the one-stage model. Here, SEFA is computed by using a two-stage procedure, where B,U and Λ_S are first learned from just the pre-stimulus data alone. Then, B and Λ_S are held fixed and C, Φ and U are computed using just the post-stimulus data. Note that U needs to be recomputed for the post-stimulus period, since the projection from the data to the noisy source space is defined by B which is fixed, but the actual realization of noise strength in the post-stimulus changes from time point to time point.

We define

$${\mathit{\kappa }}_n=\left(\begin{array}{c}\hfill {\mathit{\varphi }}_n\hfill \\ \hfill {\mathit{u}}_n\hfill \end{array}\right);\mathbf{\Omega }=\left(\mathit{C}\overline{\mathit{B}}\right);\overline{\mathbf{\Omega }}=\left(\overline{\mathit{C}}\overline{\mathit{B}}\right);$$ (2)

The main update equation for ϕ_n from the post-stimulus data is:

$$q({\mathit{\kappa }}_n|{\mathit{y}}_n)=𝒩({\mathit{\kappa }}_n|{\overline{\mathit{\kappa }}}_n,\mathbf{\Gamma });$$

$${\overline{\mathit{\kappa }}}_n={\mathbf{\Gamma }}^{-1}{\overline{\mathbf{\Omega }}}^T{\mathbf{\Lambda }}_{\mathit{S}}{\mathit{y}}_n;$$

$$\mathbf{\Gamma }=\overline{{\mathbf{\Omega }}^T{\mathbf{\Lambda }}_{\mathit{S}}\mathbf{\Omega }}+\mathit{I}={\overline{\mathbf{\Omega }}}^T{\mathbf{\Lambda }}_{\mathit{S}}\overline{\mathbf{\Omega }}+K{\mathbf{\Psi }}^{-1}+\mathit{I}$$ (3)

$$=\left(\begin{array}{c}\hfill {\overline{\mathit{C}}}^T\hfill \\ \hfill {\overline{\mathit{B}}}^T\hfill \end{array}\right){\mathbf{\Lambda }}_{\mathit{S}}\left(\overline{\mathit{C}}\overline{\mathit{B}}\right)+K\left(\begin{array}{cc}{\mathbf{\Psi }}_{\mathit{C}}^{-1}\hfill & 0\hfill \\ 0\hfill & 0\hfill \end{array}\right)+\mathit{I}$$ (4)

NSEFALoc1

The NSEFALoc1 model and its solution are related to that proposed by Dogandzic and Nehorai (2000) and Baryshnikov et al. (2004). NSEFALoc1 differs from their work by precomputing the basis functions ϕ_n from the data using the estimated ϕ̄_n from SEFA. These SEFA estimates are preferred since interference and noise sources have been removed, and the spectral content and statistical properties have not been restricted. NSEFALoc1 also differs from the above methods by placing a Wishart prior distribution on the full-rank precision matrix, which assists learning many unknown quantities from potentially few data points. The NSEFALoc1 generative model for the K × 1 sensor data y_n is:

$${\mathit{y}}_n={\mathit{F}}^r{\mathit{G}}^r{\mathit{\varphi }}_n+{\mathit{w}}_n^r$$ (5)

Both NSEFALoc models are based on a physical description of neural activity, in which brain sources are modeled by current dipoles. For a given volume conductor forward model, the K × Q forward lead field matrix F^r represents the physical relationship between a dipole at voxel r and its influence on sensor k = 1 : K (Sarvas, 1987). In the most general case, including for EEG data, Q = 3 for all three possible directions of coordinate bases of a source dipole. In the case of the single-shell sphere as commonly used in MEG, the radial component of source dipoles contribute nothing to MEG sensors, thus Q = 2. If there is knowledge of subject-specific cortical anatomy, the source may be constrained to be perpendicular to the gray matter surface, thus Q = 1. Throughout the rest of this paper, the single-shell model with Q = 2 is used for both simulations and real data from MEG, although these methods could be easily extended to a multisphere model for MEG with Q = 3 or to EEG data with an appropriate forward model taking tissue conductivities into account.

The noise ${\mathit{w}}_n^r$ is modeled by zero-mean Gaussian distribution with a K × K precision matrix Λ₁ which is full-rank (not diagonal like in SEFA above), and the subscript 1 indicates the Λ learned in the NSEFALoc1 model. Both the parameters G and Λ₁ are unknown. For a large number of sensors K, the precision matrix becomes quite large and difficult to infer accurately from the data. It may also become ill-conditioned. Hence, a prior probability using a Wishart distribution is used for Λ₁:

$$p({\mathbf{\Lambda }}_{\mathbf{1}}=𝒲({\mathbf{\Lambda }}_{\mathbf{1}}|\nu ,{\mathbf{\Sigma }}_0)\propto {|{\mathbf{\Lambda }}_{\mathbf{1}}|}^{\nu /2}{e}^{-\frac{1}{2}Tr({\mathbf{\Sigma }}_0{\mathbf{\Lambda }}_{\mathbf{1}})}$$ (6)

where Σ₀ and ν are hyperparameters. A Wishart distribution is related to a multivariate Γ distribution.

The estimates Λ̂₁ and Ĝ are the value of each that maximizes the likelihood ℒ specific to each scanned voxel, given in Eq. (B-1). Their derivation is described in Appendix B and the final results are given here. Initially solving for ${\hat{\mathbf{\Lambda }}}_1^{-1}$ gives:

$${\hat{\mathbf{\Lambda }}}_1^{-1}=\frac{1}{N+\nu }({\mathit{R}}_{\mathit{Y}\mathit{Y}}-\mathit{F}\mathit{G}{\mathit{R}}_{\mathbf{\Phi }\mathit{Y}}+{\mathbf{\Sigma }}_0)$$ (7)

Solving for G^r gives:

$${\mathit{G}}^r={({\mathit{F}}^T{\mathit{S}}^{-1}\mathit{F})}^{-1}{\mathit{F}}^T{\mathit{S}}^{-1}{\mathit{R}}_{\mathit{Y}\mathbf{\Phi }}{\mathit{R}}_{\mathbf{\Phi }\mathbf{\Phi }}^{-1}$$

$$\mathit{S}=\frac{1}{N+\nu }({\mathit{R}}_{\mathit{Y}\mathit{Y}}-{\mathit{R}}_{\mathit{Y}\mathbf{\Phi }}{\mathit{R}}_{\mathbf{\Phi }\mathbf{\Phi }}^{-1}{\mathit{R}}_{\mathbf{\Phi }\mathit{Y}}+{\mathbf{\Sigma }}_0)$$ (8)

Since the expression for G is now known, this value can be plugged into Eq. 7 to find Λ₁. The maximized likelihood is then:

$${ℒ}^r=\frac{N+\nu }{2}\text{log}|{\mathbf{\Lambda }}_{\mathbf{1}}^r|+\mathit{\text{const}}.$$ (9)

whose spatial peaks correspond to the most likely source locations.

The data and factor covariance matrices referred to above are:

$${\mathit{R}}_{\mathit{Y}\mathit{Y}}=\sum _{n=1}^N{\mathit{y}}_n{\mathit{y}}_n^T,{\mathit{R}}_{\mathit{Y}\mathbf{\Phi }}=\sum _{n=1}^N{\mathit{y}}_n{\mathit{\varphi }}_n^T,{\mathit{R}}_{\mathbf{\Phi }\mathbf{\Phi }}=\sum _{n=1}^N{\mathit{\varphi }}_n{\mathit{\varphi }}_n^T$$ (10)

The source estimate from both NSEFALoc1 and NSEFALoc2 is given by G^rΦ. For NSEFALoc1, using Eqs. (8), (10), and (3), the source estimate per voxel r is

$${ŝ}_n^r={({\mathit{F}}^{rT}{\mathit{S}}^{-1}{\mathit{F}}^r)}^{-1}{\mathit{F}}^{rT}{\mathit{S}}^{-1}{\mathit{R}}_{\mathit{Y}\mathbf{\Phi }}{\mathit{R}}_{\mathbf{\Phi }\mathbf{\Phi }}^{-1}{\mathbf{\Gamma }}_{\mathbf{\Phi }}^{-1}{\overline{\mathbf{\Omega }}}^T{\mathbf{\Lambda }}_{\mathit{S}}{\mathit{y}}_n$$ (11)

where ${\mathbf{\Gamma }}_{\mathrm{\Phi }}^{-1}$ indicates the first set of rows only corresponding only to Φ, but all columns, and Λ_S is from Eq. (A-8).

NSEFALoc2

NSEFALoc2 also uses the TBFs Φ̄ estimated from SEFA described above. In contrast to NSEFALoc1, the contributions to post-stimulus sensor measurements not arising from a dipole source at the voxel r are now more explicitly modeled in NSEFALoc2. The J × 1 unknown interference factors ${\mathit{x}}_n^{\backslash r}$ correspond to activity in all voxels excluding r and A^\r is a K × J unknown mixing matrix, where \r means corresponding to activity not at r. The sensor noise has unknown diagonal precision Λ₂, where the subscript 2 indicates the Λ learned in the NSEFALoc2 model. The corresponding generative model for the sensor data Y is:

$${\mathit{y}}_n={\mathit{F}}^r{\mathit{G}}^r{\mathit{\varphi }}_n+{\mathit{A}}^{\backslash r}{\mathit{x}}_n^{\backslash r}+{\mathit{\upsilon }}_n^r$$ (12)

The following conditional probabilities complete specification of the model:

$$p({\mathit{y}}_n|{\mathit{x}}_n,\mathit{A},{\mathbf{\Lambda }}_{\mathbf{2}})=𝒩({\mathit{y}}_n|\mathit{F}\mathit{G}{\mathit{\varphi }}_n+\mathit{A}{\mathit{x}}_n,{\mathbf{\Lambda }}_{\mathbf{2}})$$ (13)

$$p({\mathit{x}}_n)=𝒩({\mathit{x}}_n|0,\mathit{I}),p({\mathit{\upsilon }}_n)=𝒩({\mathit{\upsilon }}_n|0,{\mathbf{\Lambda }}_{\mathbf{2}})p(\mathit{A})=\prod _{kj}p(a_{kj});p(a_{kj})=𝒩(a_{kj}|0,{({\lambda }_2)}_k{\alpha }_j)$$ (14)

Notice that in place of the (K² +K)/2 elements of the full-rank precision matrix Λ₁ in NSEFALoc1, now just the KJ + K elements of A and diagonal Λ₂ need to be inferred from the data. Since typically J << K (J <~ 10 and at UCSF K = 275), NSEFALoc2 has significantly less parameters and can thus be inferred more accurately.

We again use an VB-EM algorithm to infer the unknown quantities from the data and the derivation is given in Appendix C. The VBE-step updates for the variables are:

$$p({\mathit{x}}_n|{\mathit{y}}_n)=𝒩({\mathit{x}}_n|{\overline{\mathit{x}}}_n,\mathbf{\Gamma })$$

$${\overline{\mathit{x}}}_n={\mathbf{\Gamma }}^{-1}{\mathit{Ā}}^T{\mathbf{\Lambda }}_{\mathbf{2}}({\mathit{y}}_n-\mathit{F}\mathit{Ḡ}{\mathit{\varphi }}_n)$$

$$\mathbf{\Gamma }={\mathit{A}}^T{\mathbf{\Lambda }}_{\mathbf{2}}\mathit{A}+K\mathbf{\Psi }+\mathit{I}$$ (15)

In the VBM-step, the full posterior over A is found by finding the q(A|Y) that best approximates p(A|Y) and the MAP estimates of the parameters G and Λ₂ and hyperparameter α are found. The posterior distribution of A is thus:

$$q(\mathit{A}|\mathit{Y})=\prod _{k}q({\mathit{a}}_k|\mathit{Y});q({\mathit{a}}_k|\mathit{Y})=𝒩({\mathit{a}}_k|{\mathit{ā}}_k,{({\lambda }_2)}_k\mathbf{\Psi })$$

$$\mathit{Ā}=({\mathit{R}}_{\mathit{Y}\mathit{X}}-\mathit{F}\mathit{G}{\mathit{R}}_{\mathbf{\Phi }\mathit{X}}){\mathbf{\Psi }}^{-1}$$

$$\mathbf{\Psi }={\mathit{R}}_{\mathit{X}\mathit{X}}+\mathit{\alpha }$$ (16)

The MAP estimate of G is

$$\mathit{Ḡ}={({\mathit{F}}^T{\mathbf{\Lambda }}_{\mathbf{2}}\mathit{F})}^{-1}{\mathit{F}}^T{\mathbf{\Lambda }}_{\mathbf{2}}({\mathit{R}}_{\mathit{Y}\mathbf{\Phi }}-{\mathit{R}}_{\mathit{Y}\mathit{X}}{\mathbf{\Psi }}^{-1}{\mathit{R}}_{\mathit{X}\mathbf{\Phi }})$$

$${({\mathit{R}}_{\mathbf{\Phi }\mathbf{\Phi }}-{\mathit{R}}_{\mathbf{\Phi }\mathit{X}}{\mathbf{\Psi }}^{-1}{\mathit{R}}_{\mathit{X}\mathbf{\Phi }})}^{-1}$$ (17)

Solving for Λ₂ and α in NSEFALoc2 is very similar to solving for Λ_S and χ in SEFA, by letting ${\mathit{y}}_n^{\prime }={\mathit{y}}_n-\mathit{F}\mathit{G}{\mathit{\varphi }}_n$. Then, take the derivative of ℱ w.r.t. Λ₂ (or α) to obtain a similar solution:

$${\mathbf{\Lambda }}_{\mathbf{2}}=N{[\text{diag}({\mathit{R}}_{\mathit{Y}\prime \mathit{Y}\prime }-\mathit{Ā}{\mathit{R}}_{\mathit{X}\mathit{Y}\prime })]}^{-1}$$

$${\mathit{\alpha }}^{-1}=\text{diag}(\frac{1}{K}{\mathit{Ā}}^T{\mathbf{\Lambda }}_{\mathbf{2}}\mathit{Ā}+{\mathbf{\Psi }}_{\mathit{A}})$$ (18)

The expressions R_YX, R_Y′X, R_ΦX and R_XX represent the posterior covariance between the two subscripts, similar to matrices previously defined. The maximized likelihood function for NSEFALoc2 is the following, where the dependency on voxel location is made explicit:

$${ℒ}^r=\frac{N}{2}\text{log}\frac{|{\mathbf{\Lambda }}_{\mathbf{2}}^r/2\pi |}{|{\mathbf{\Gamma }}^r|}+\frac{K}{2}\text{log}|{\mathit{\alpha }}^r{\mathbf{\Psi }}^r|-\frac{1}{2}\sum _{n=1}^N({({\mathit{y}}_n-{\mathit{F}}^r{\overline{\mathit{G}}}^r{\mathit{\varphi }}_n)}^T{\mathbf{\Lambda }}_{\mathbf{2}}^r({\mathit{y}}_n-{\mathit{F}}^r{\overline{\mathit{G}}}^r{\mathit{\varphi }}_n-{\overline{\mathit{x}}}_n^T{\mathbf{\Gamma }}^r{\overline{\mathit{x}}}_n)$$ (19)

The source estimate for NSEFALoc2, using Eqs. (17) and (A-9) is:

$${ŝ}_n^r={({\mathit{F}}^T{\mathbf{\Lambda }}_{\mathbf{2}}\mathbf{F})}^{-1}{\mathit{F}}^T{\mathbf{\Lambda }}_{\mathbf{2}}({\mathit{R}}_{\mathit{Y}\mathbf{\Phi }}-{\mathit{R}}_{\mathit{Y}\mathit{X}}{\mathbf{\Psi }}^{-1}{\mathit{R}}_{\mathit{X}\mathbf{\Phi }})$$

$${({\mathit{R}}_{\mathbf{\Phi }\mathbf{\Phi }}-{\mathit{R}}_{\mathbf{\Phi }\mathit{X}}{\mathbf{\Psi }}^{-1}{\mathit{R}}_{\mathit{X}\mathbf{\Phi }})}^{-1}{\mathbf{\Gamma }}_{\mathrm{\Phi }}^{-1}{\overline{\mathbf{\Omega }}}^T{\mathbf{\Lambda }}_{\mathit{S}}{\mathit{y}}_n$$ (20)

Methods: Simulations, Performance Metrics, and Real Data

Simulation setup

The construction of simulated datasets and performance metrics were similar or identical to those described in Zumer et al. (2007). Simulations were created using a variety of realistic source configurations reconstructed on a 5mm voxel grid. A single-shell spherical volume conductor model for MEG data was used to calculate the forward lead field (Sarvas, 1987). While EEG models and data were not tested here, use of an appropriate forward model for EEG would make NSEFALoc amenable to EEG data as well.

Simulations and real data were analyzed using NUTMEG (Neurodynamic Utility Toolbox for MEG) (Dalal et al., 2004), a toolbox developed using MATLAB (MathWorks, Natick, MA, USA), obtainable from http://bil.ucsf.edu. NUTMEG is useful for coregistration of fiducial points to a structural MRI, selection of volume-of-interest, computation of forward field, filtering and other denoising preprocessing methods, as well as a variety of source reconstruction methods, including MVAB (Sekihara et al., 2002b), sLORETA (Pascual-Marqui, 2002), SAKETINI (Zumer et al., 2007), time-frequency methods (Dalal et al., 2007), and now NSEFALoc.

Gaussian-damped sinusoidal time courses at specific locations inside a voxel grid based on realistic head geometry. Sources were set to be active only during a post-stimulus period, which always composed 62.5% of the total data available, while the remaining 37.5% was pre-stimulus data. Typically 700 total datapoints were used, unless specified otherwise.

In some simulations, only Gaussian sensor noise was added to the projected simulated sources, termed the sensor noise only case. While this type of simulation is common in simulation testing, this clearly does not reflect true data which has interference sources somewhere in source space contributing to covariance across sensors.

In another set of simulations, termed simulated interference cases, background activity in source space was drawn from the Gaussian distributions assumed by the model to simulate ongoing brain activity. These background sources were placed in 30 random locations throughout the brain voxel grid, active in both pre- and post-stimulus periods. Their activity was projected onto the sensors and added to both Gaussian sensor noise and source activity. These simulated background brain sources add noise to the sensors in a spatially-correlated manner.

In order to test simulation performance using data with more realistic (and unknown) statistical distributions, a final set of simulations was created termed real brain noise. Real MEG sensor data was collected from a CTF MEG System with 275 axial gradiometers while a human subject was alert but not performing tasks or receiving stimuli. This background data thus includes real sensor noise plus real ongoing brain activity that could interfere with evoked sources and adds spatial correlation to the sensor data. Since throughout this work averaged data is used, this real data was binned into 100 trials of 700 data points each and averaged. The output Signal to Noise Ratio (SNR) and the corresponding output Signal to Noise-plus-Interference Ratio (SNIR) were varied. Output SNIR is calculated from the ratio of the sensor data resulting from sources only to the sensor data from noise plus interference, as shown in the first equation of the Results section of Nagarajan et al. (2007b).

Localization accuracy of a single source

A single source was placed randomly within the voxel grid space, projected to the sensors, and all three types of noise (sensor noise only, simulated interference, and real brain noise) were added to the simulated sensor data, at four different levels of SNIR. Twenty different realizations of random location were tested for each SNIR. The localization error (in Euclidean distance) between the maximum peak in the NSEFALoc1 and NSEFALoc2 likelihood maps, as well as the MVAB and sLORETA power maps (sum of squares of post-stimulus time points), and the true simulated source location was measured.

Constructing simulations with three sources

Multiple active sources are more realistic than a single active source. Moreover, any additional active source acts as interference towards the ability to localize the first source. Several simulation parameters were varied across different simulations. (i) Two different source configurations were used: one with three sources near the surface as depicted in Fig. 3 and the other configuration with three deeper sources. (ii) The orientation of the source was fixed in half the simulations and allowed to rotate over time in the other half. (iii) The correlation of two of the three sources with each other was set to be ρ = 0, ρ= 0.95, or ρ = 1; the third source was always uncorrelated with the other two sources. (iv) Each combination of parameters were tested for 10 different randomly generated source time courses and source orientations. (v) In addition to the true source contribution to the sensor data, the three cases of sensor noise only, simulated Gaussian interference or real brain noise were tested. (vi) SNIR was set at 5dB, 0dB, or −5dB, with corresponding SNR for each case of 10dB, 5dB, and 0dB. Thus, a total of 1080 simulations was run using all combinations of simulation parameters.

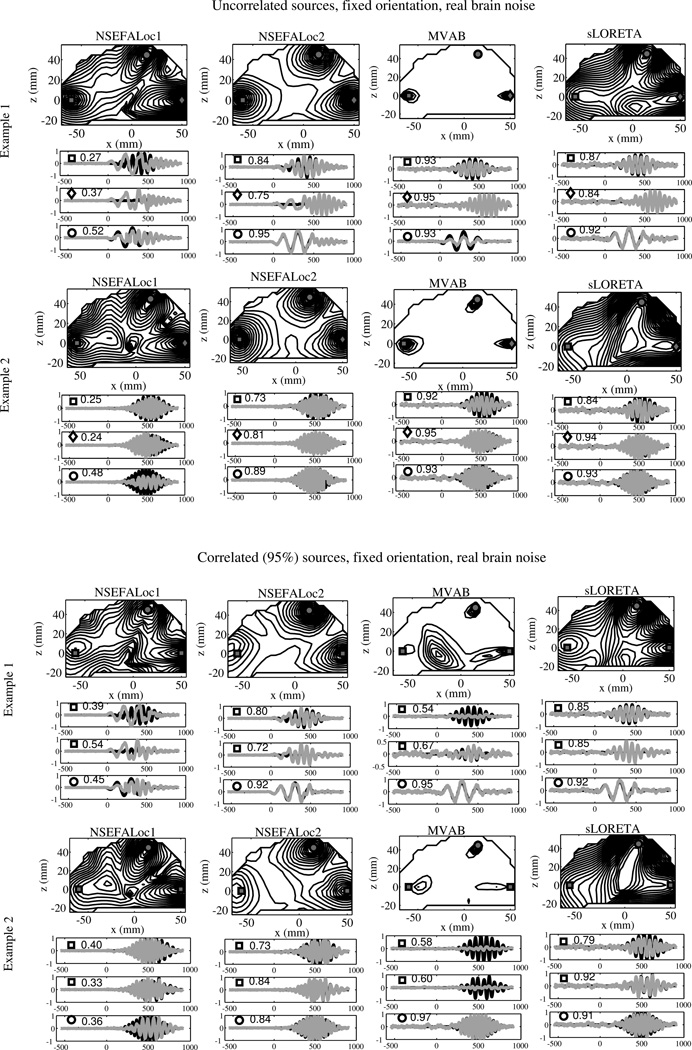
Fig. 3.

Performance of all methods in several example simulations. The top two examples all three true source locations, marked by square, diamond, and circle, are uncorrelated with each other. On the bottom half, the true sources labeled with squares indicate location of true sources highly correlated with each other, while the circle source is uncorrelated with the other two. While the source locations are the same for all examples, the time series are different for each. Intensity of map corresponds to normalized log-likelihood map for NSEFALoc1 and NSEFALoc2, and a normalized power map for MVAB and sLORETA. Below the localization map for each example, black lines indicate simulated time series for each of the three source locations; gray lines indicate estimates of the source time series at those three locations. The labels of squares, circles or diamonds are included in each time series plot to indicate correspondence with the location on the map. The correlation of the true time course and the estimated time course is shown next to the symbol within each time series plot.

Model order selection and hyperparameters

The experimenter is faced with choosing the number of temporal basis functions for NSEFALoc methods (i.e. number of factors in SEFA) and the number of non-localized evoked factors X in NSEFALoc2; the effect of this choice on performance should be tested. The hyperparameters are expected to zero-out extra dimensions to a large extent, but this also should be tested. Finally, the choice of SEFA for computing TBFs from the data should be compared to other options.

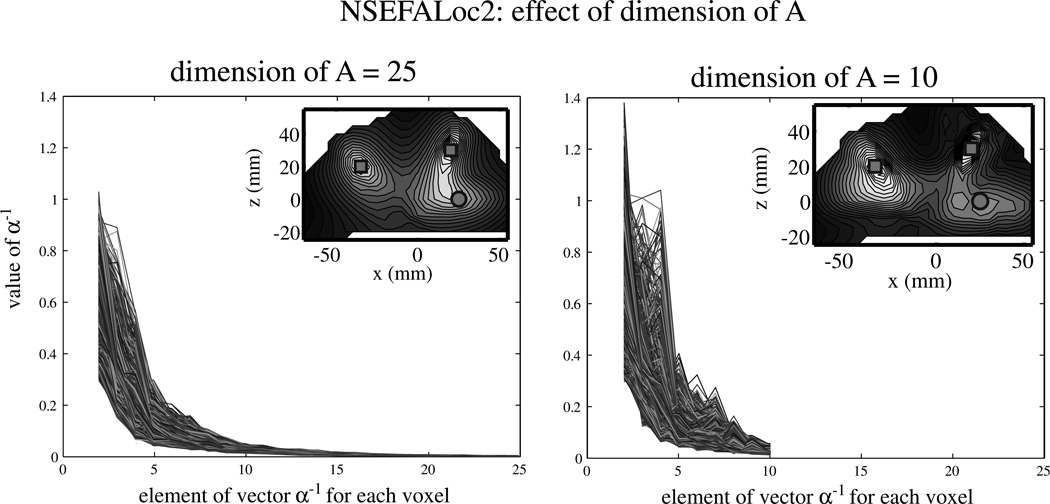
The choice of dimension for X (non-localized evoked factors) in NSEFALoc2 was run with either 25 or 10 dimensions for A. The inverse hyperparameter α⁻¹ over the mixing matrix A was normalized to the first hyperparameter for each of 1760 voxels examined.

The localization result for both dimension choices were examined. The number of TBFs used in both NSEFALoc methods was next tested and averaged over many simulations. In all simulations, three sources are present with fixed dipole orientation. In half, two of the three sources are perfectly correlated, while the other half of simulations have uncorrelated sources; thus either two or three TBFs are needed, respectively. Performance is characterized as described in the next subsection and is compared to MVAB and sLORETA.

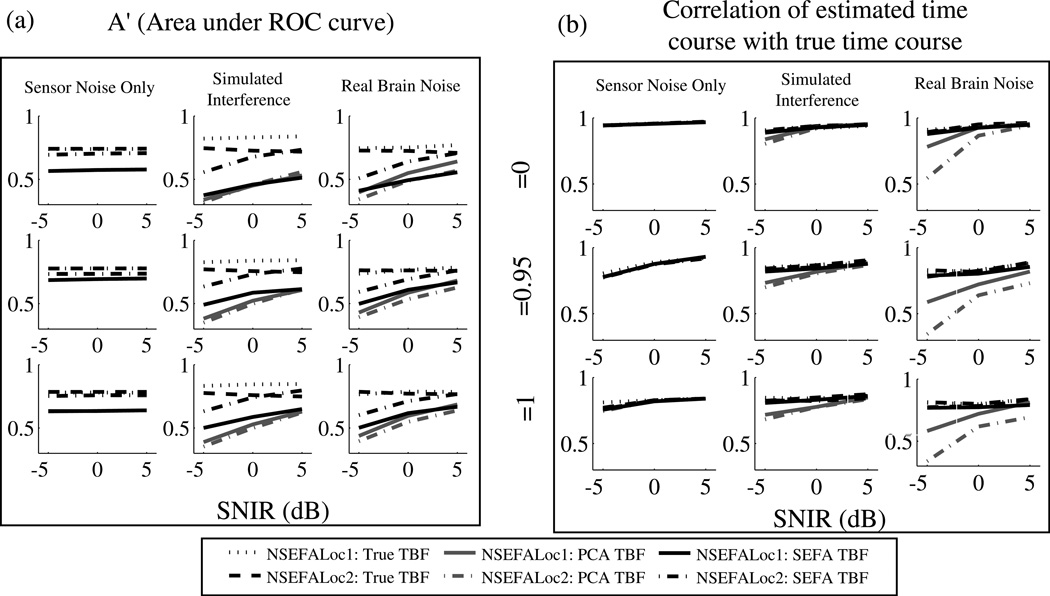
From Nagarajan et al. (2007a), SEFA seems to be a very good way to obtain temporal basis functions of the denoised evoked activity from real data when the true time course is not known. However, their use as in input to the NSEFALoc class of models is tested here. The simulations were the same as in Fig. 5 with three sources placed and three levels of correlation between two of the three sources, and either rotating or fixed dipole orientation. The use of SEFA to obtain TBFs was compared with using PCA and the true time courses. The number of temporal basis functions was held the same across the three different types of TBFs for each simulation (fewer were used when sources were known to be correlated).

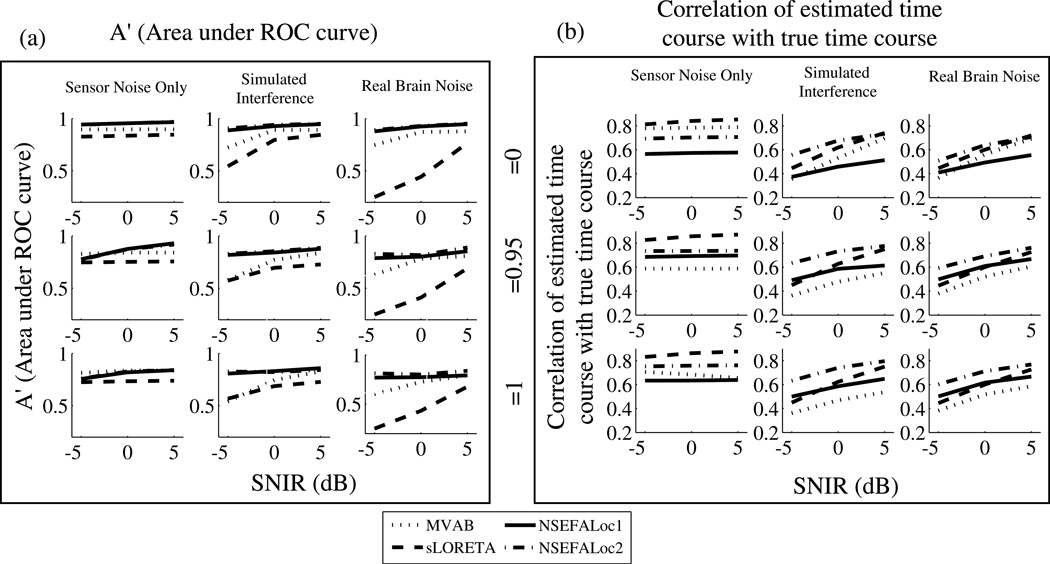
Fig. 5.

Performance of NSEFALoc1 and NSEFALoc2 relative to MVAB and sLORETA for variety of simulated datasets. Each datapoint is an average of 40 simulations, consisting of two different source locations and either a fixed or rotating source orientation. Standard errors were less than 0.05 for all points (not shown). (a) A measure of area under ROC curve A′ is plotted in 9 subplots as a function of SNIR for sensor noise only, simulated and real brain interference (across columns), and for each of three source correlation values (across rows). See text for discussion of the A′ metric. (b) The correlation of the estimated with the true time course is plotted for each method.

Performance evaluation

Performance was measured in two ways: localization ability and estimation of time course. To assess localization ability, it is important to take into account source strength, source localization error, and presence of false positives. Thus the ROC (receiver-operator characteristic) method was modified for brain imaging results as suggested by Darvas et al. (2004), which is a measure of hit rate versus false positive rate. The free-response ROC (FROC) curve in particular allows for multiple hits per image (Bunch et al., 1978).

A local peak is defined here as a voxel that is greater in value than its 26 three-dimensional neighbors. A hit is defined as a local peak that is within a specified distance of the true location and above a certain threshold. A miss is defined as a true source location that has no hit within the specified distance. A false positive is a local peak above a certain threshold but further than the specified distance from a true source location. A true negative is any voxel that is none of the above.

FROC curves are generated by varying the threshold and allowable distance error, thus varying the tradeoff of sensitivity and specificity. The following distances were used as allowable localization error of a local peak to a true location in order to be counted as a hit: $5*\sqrt{3}\mathrm{m}\mathrm{m},10*\sqrt{3}\mathrm{m}\mathrm{m}$, or $15*\sqrt{3}\mathrm{m}\mathrm{m}$. The threshold was varied to be 30%, 50%, 70% or 90% of the maximum value in the whole image. Thus, a hit rate (HR) and false positive rate (FR) was recorded for each of 12 combinations of threshold/error for each of the 1080 simulations.

Since these HR versus FR points do not increase monotonically, as they would if threshold were the only criteria varied, we chose to use the measure of A′ (similar to use in Zumer et al. (2007)). A′ is a way to approximate the area under the FROC curve for one HR/FR point (Snodgrass and Corwin, 1988). The larger the area under the FROC, the better the method is performing, since this means a higher HR relative to FR for specified thresholds/localization errors. For each simulation, the twelve computed A′ values were averaged to give one A′ value per simulation. The NSEFALoc1 and NSEFALoc2 likelihood maps were used as the spatial maps to test localization; the power maps were used for MVAB and sLORETA.

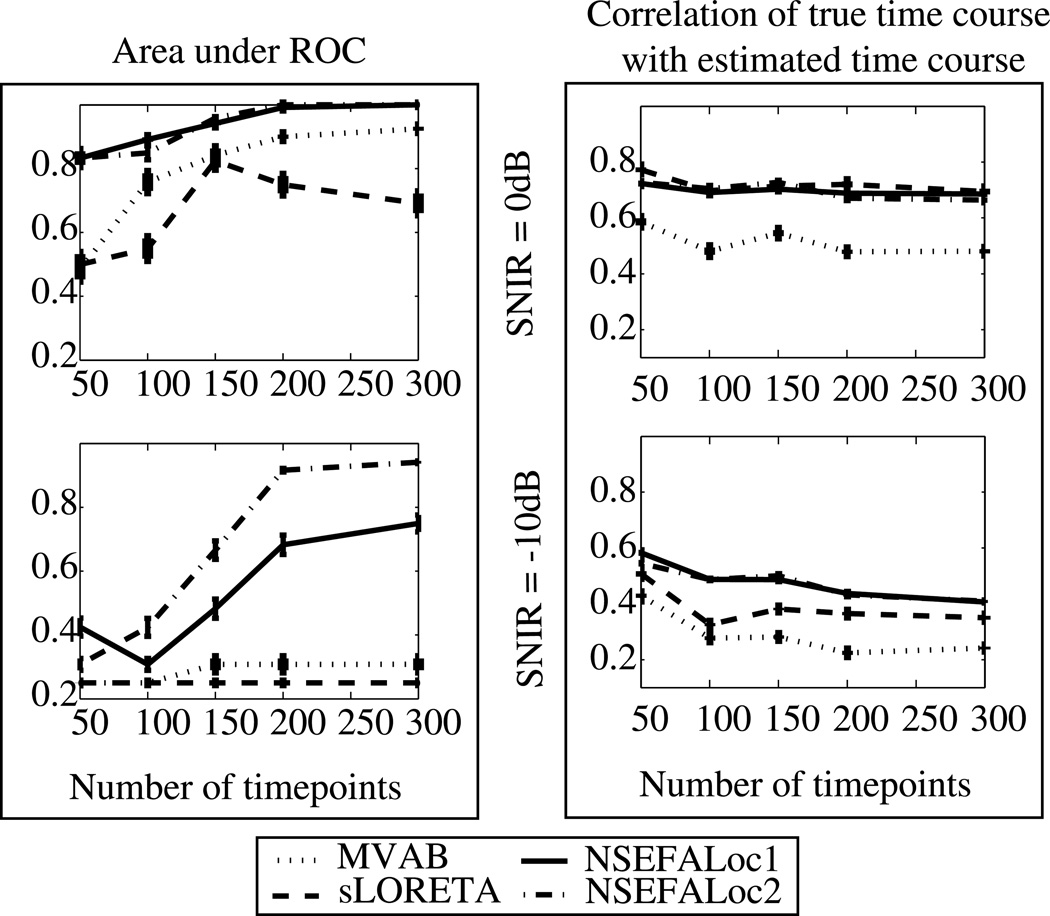
Simulation: effects of number of sensors and time points

Previous studies have shown advantage of sensor arrays with larger number of channels (Hamalainen et al., 1993). Likewise, increased amount of data points across time usually lead to improved estimation of unknown quantities. Therefore, the next set of simulations sought to determine how few sensors and how few time points were needed to preserve performance.

To test the effect of the number of sensors, simulations were created similarly to those discussed above with three uncorrelated sources. Two values of SNIR were created using real brain noise: 0dB and −10dB. Ten different realizations of source time course and orientation were tested for each case. All simulations discussed previously were created using the full 275 channel array from the CTF system. Here, only a random subset of sensors were selected, using 150, 74, or 37 sensors. The numbers 74 and 37 were specifically chosen to correspond to the BTi commercial MEG system previously installed in the UCSF lab until 2004.

To test the effect of the number of data points, the full set of 275 channels were used, but the available amount of data points was reduced. All previous simulations have used 700 total data points, where 62.5% were in the post-stimulus period. The ratio of data points in the post-stimulus period was kept the same, but the total number was reduced to 300, 200, 150, 100, or 50 time points.

Real MEG Data

Several real datasets were analyzed with the proposed method and compared to existing methods. For all data, the 275-channel CTF MEG System in a magnetically shielded room was used to collect data. All healthy subjects gave written, informed consent to participate in each study, according to UCSF institutional review board approval.

Auditory datasets were obtained by presenting 120 repetitions of a 1kHz tone binaurally to healthy subjects, at an intertrial interval of 1.4s. The trials were averaged locked to stimulus onset. This auditory stimulus is known to invoke bilateral auditory cortex to be active simultaneously, known to cause problems for the MVAB’s ability to localize the auditory sources.

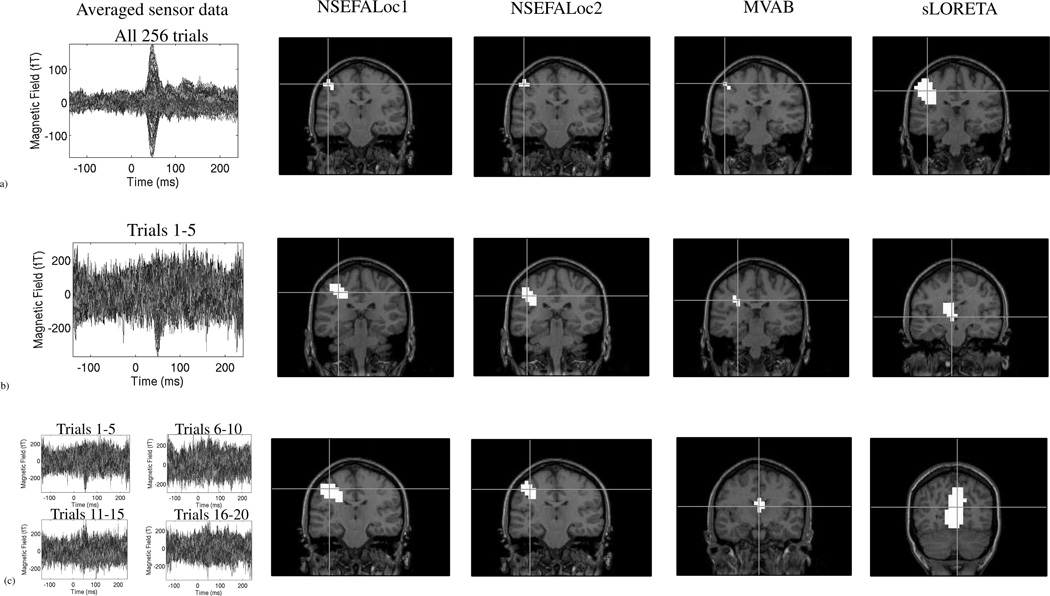
We next examine a somatosensory dataset in which the localization of primary somatosensory cortex is relatively easy for all methods when many trials are available to average. A small diaphragm was placed on the subject’s right index finger and was driven by compressed air. The stimulus was given 256 times every 500ms. However, if we limit the available data to only a small subset of trials, the lower SNR can become limiting for all source reconstruction methods. We first applied NSEFALoc1, NSEFALoc2, MVAB and sLORETA to the average of all 256 trials to assess performance for the standard (high) SNR case. We then applied all three methods to the average of only the first 5 trials. To further test if the performance was consistent across other sets of just 5-trial averages, we applied the three methods to the 5-trial average of trials 6–10, 11–15, and 16–20. We then averaged the results of these four different results. Any location found consistently will show up in the average.

Results

Single source localization

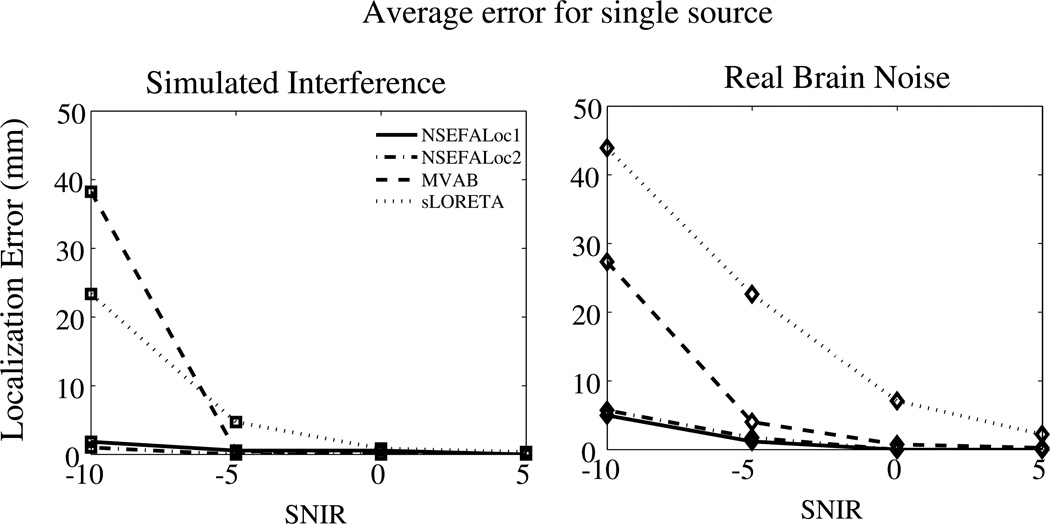
The mean localization errors for a simulated single source are shown in Fig. 2. Even at the lowest SNIR of −5dB, NSEFALoc1 and NSEFALoc2 localized the source to within 5mm error, which, for real data, is on the order of the error due to coregistration of MEG data with the subject’s MRI. For all values of SNIR, NSEFALoc1 and NSEFALoc2 resulted in reduced error compared to MVAB and sLORETA. Errors for the sensor noise only case were not shown since they were zero or essentially zero for all methods for all values of SNIR.

Fig. 2.

Average localization error over 20 realizations of a randomly placed single dipole source. Background activity was either Simulated Interference or Real Data. The standard error was typically 1mm, not larger than 4mm; errorbars were omitted from the plot.

Examples of multiple sources, including correlated sources

Next, performance of the proposed models was tested for three simultaneously active sources. Fig. 3 shows performance in two examples each with either three uncorrelated sources (top half) or with 2 of 3 sources correlated (bottom half). All sources were fixed in orientation across time, with real brain noise added with SNIR of 5dB. The only difference betwen the two examples in each half are the random realization of the source time course. Two examples are shown to illustrate how a change just in temporal dynamics can affect localization results. For each example, the log likelihood (or power) map is above a grouping of plots showing the estimated time courses (gray) of the three sources overlaid onto the true time courses (black). Note in the MVAB power maps, the three sources are labeled with a square, diamond and circle and the time courses plots are labeled accordingly. The bottom half of plots show two square sources and a circle source, indicating the two square sources are highly correlated.

The uncorrelated-source examples in Fig. 3 (top half) show that all methods localize all three sources either perfectly or near perfectly. The spatial peaks for MVAB are so focal they are hidden by the square, diamond and circle symbols. The sLORETA power map shows some difficulty in finding the lower left source perfectly, but does show a peak nearby. The NSEFALoc1 likelihood map finds all three sources perfectly, though in Example 2, there is a possible false positive around (x = −25, z = 5). The NSEFALoc2 likelihood map also finds all three sources perfectly, but also with a possible false positive around (x = −30, z = 35). Both NSEFALoc1 and NSEFALoc2 display log-likelihood maps, which lead to their increased spatial spread relative to the MVAB power map, but of course does not affect location of peaks.

The top half of Fig. 3 also shows all methods’ ability to estimate the source time course. These examples show that sLORETA estimates the shape and amplitude very well for all sources. NSEFALoc2 also estimates the times courses well, although there is some cross talk in Example 1, diamond source. NSEFALoc1 shows more severe crosstalk errors. MVAB estimates the time courses reasonably well, although a slight mis-estimation of amplitude is seen.

The performance of all methods was further tested when two of the three sources are highly correlated in time. The lower half of Fig. 3 shows the results from two simulation examples where two square sources are highly correlated in time (ρ = .95). The same real brain noise was added at SNIR=5dB and all other aspects of this simulation were the same as the uncorrelated case above, except that the right square source time course was adjusted to correlate strongly with the left square source time course. In all cases, the estimated time course plotted is the one extracted from the true location, regardless of the localization map peak locations.

These examples illustrate the failure of MVAB for correlated sources. The MVAB power map in Example 1 finds the uncorrelated Q-source, but largely mislocalizes the P-source and only weakly finds the P′-source. The reduction in power is seen in the P time course plot. The MVAB power map for Example 2 localizes all three sources within a reasonable error; however the amplitude of the peak location the two correlated sources (P and P′) is much reduced and might not be detected depending on the threshold, which is also indicated by the large reduction in time series amplitude. On the other hand, sLORETA is not in theory supposed to be sensitive to correlated sources; sLORETA finds all three sources in Example 1 (though one is weak and a center-of-the-head false positive is of larger amplitude) but, in Example 2, fails to show distinct peaks for the two correlated source locations P and P′. Despite these localization issues, the time course estimation of sLORETA in both shape and amplitude were very accurate.

Overall, NSEFALoc2 localizes the sources and estimates source time courses better than MVAB and sLORETA in these examples of correlated sources in the bottom half of Fig. 3, while NSEFALoc1 performance is in-between. NSEFALoc1 localizes the sources well in Example 1, but fails to find the P-source in Example 2, with a distant false positive instead. The time course estimates by NSEFALoc1 suffer from quite a bit of crosstalk. Finally, the NSEFALoc2 likelihood maps localize all three sources clearly with only a slight localization error in the P-source. Furthermore, the NSEFALoc2 time course estimation is quite good in both shape and amplitude, with much less crosstalk errors than NSEFALoc1 even thought the same set of temporal basis functions were used.

Model order and basis function selection results

The ability of SEFA to learn the correct dimension of evoked activity through the hyperparameters is demonstrated in Figures 11 and 12 of Nagarajan et al. (2007b), and so is not examined further here.

Fig. 4 shows examples of NSEFALoc2 performance while the dimension (number) of non-localized evoked factors X is varied. The main plots are of α⁻¹ (which controls number of evoked factors not at the voxel of interest) normalized to the first hyperparameter (which is omitted from the plot). Each line within all plots is the value for each of 1760 voxels analyzed. NSEFALoc2 was run with either 25 (upper left plot) or 10 (upper right plot) dimensions for A. From using 25 dimensions, it seems that the inverse hyperparameters get close to zero after about 10 and that the extra dimensions are not contributing much. By using only 10, the values stay roughly the same but do change somewhat. Furthermore, the localization results (inset in each plot) are roughly the same yet some differences exist. The left inset (25 dimension result) shows all three sources with strong likelihood, but the lower source is blurred with the source above it. The right inset (10 dimension result) shows all three sources as distinct peaks although the lower source is weaker, and also has a possible false positive near it.

Fig. 4.

Plots of α⁻¹ hyperparameter for NSEFALoc2. Each line within all plots is the value for each of 1760 voxels analyzed. The first hyperparameter is normalized to one but is not shown. Inset in each plot is the localization result with the given number of dimension chosen, and symbols indicate correct location. All three sources were rotating orientation and uncorrelated with each other, thus six independent time courses contributing to the sensor data. The left plot shows results when dimension of A was set to 10, while the right plot shows dimension of A set to 25.

Fig. 6 compares NSEFALoc1 and NSEFALoc2 with three types of temporal basis functions: the true source time sources, those obtained from SEFA (as the models were intended) or from PCA. The performance metrics of A′ and time course estimation were used to compare choice of TBFs. In real brain noise and simulated interference, using PCA to obtain TBFs resulted in the worst performance for both metrics of A′ and time course estimation. In comparing SEFA with the true time courses, A′ is not affected, but time course estimation is worse when using SEFA compared to true; however, NSEFALoc2 with SEFA TBFs performs reasonably close to the true TBFs (while NSEFALoc1 is considerably worse).

Fig. 6.

Performance of NSEFALoc1 and NSEFALoc2 as a function of three types of temporal basis function used: the true source time sources, those obtained from SEFA (as the models were intended) or from PCA. (a) A′ metric for localization ability. (b) Time course estimation accuracy (similar to Fig. 5).

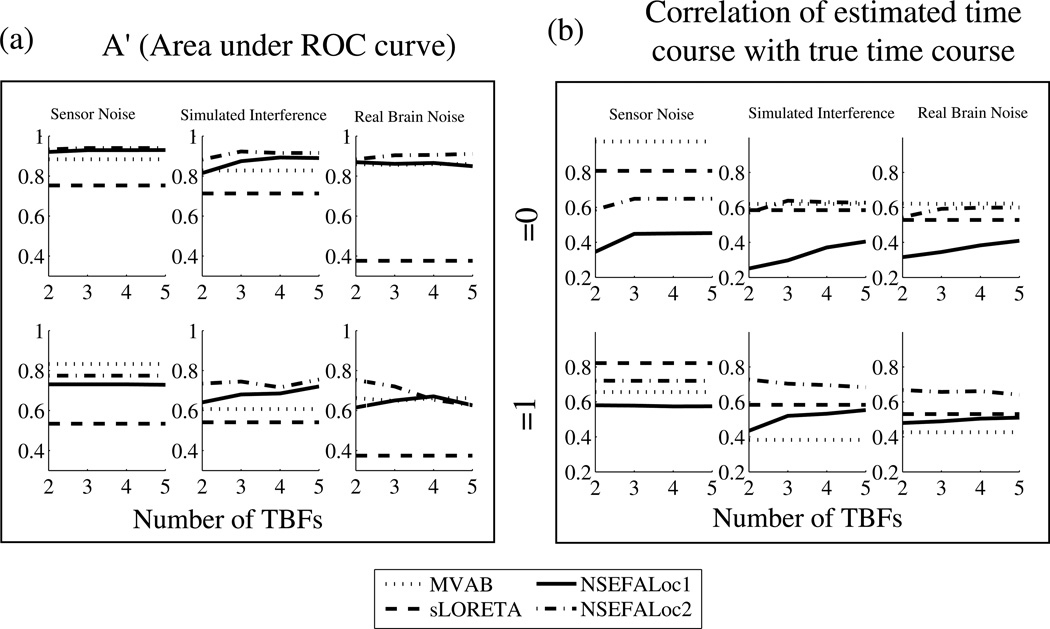
Finally, Fig. 7 shows performance (through the A′ metric and time course estimation) of all the methods as the number of dimensions was varied, averaged over many simulations. For MVAB, the x-axis represents the number of eigenvalues, for NSEFALoc1 and NSEFALoc2 it is the number of temporal basis functions, and it is meaningless for sLORETA whose performance does not depend on such a parameter.

Fig. 7.

Performance as a function of number of temporal basis functions for simulations with 3 fixed-orientation dipole sources. Source correlations of 0 and 1 were tested. Each data point is averaged over three values of SNIR (5, 0,−5dB). (a) A′ and (b) correlation of estimated and true time course.

Overall, the lines for all methods are relatively flat, indicating not too large of a dependence on number of dimension reduction. The time course estimation in sensor-noise only shows the clear improvement in using at least three dimensions. The correlated-source-case (bottom row) in interference or real brain noise show the clear advantage of NSEFALoc2 over MVAB for time course estimation. Interestingly, the A′ metric gets worse for NSEFALoc2 in correlated sources in real brain noise as the number of TBFs increase; this is probably due to incorrectly trying to fit the extra components to the wrong location confused by the correlated sources.

Performance evaluation results

The performance of the proposed methods is now shown according to the metrics of A′ (area under ROC curve) and time course estimation. Fig. 5(a) plots A′ for each method, for each value of source correlation and SNIR, and for all types of interference. NSEFALoc1 and NSEFALoc2 both show A′ higher than MVAB and sLORETA. For the perfectly correlated source cases, NSEFALoc2 localizes sources best for all noise types.

The other main test of performance was ability to estimate the source time course. The estimated time courses for all methods were obtained from the true source locations, regardless of whether their respective localization maps found that source as a hit. The correlation of the true time course with the estimated time course was computed for each simulation and the averages are plotted in Fig. 5(b). In the sensor noise only case, sLORETA (dashed) estimates the time course better than other methods regardless of source correlation, as previously understood for this method. However, when other source-space interference or real brain noise is added, this advantage of sLORETA is lost. Instead, similar to the A′ results, NSEFALoc2 estimates the source time course the best when sources are perfectly correlated in simulated interference and real brain noise cases.

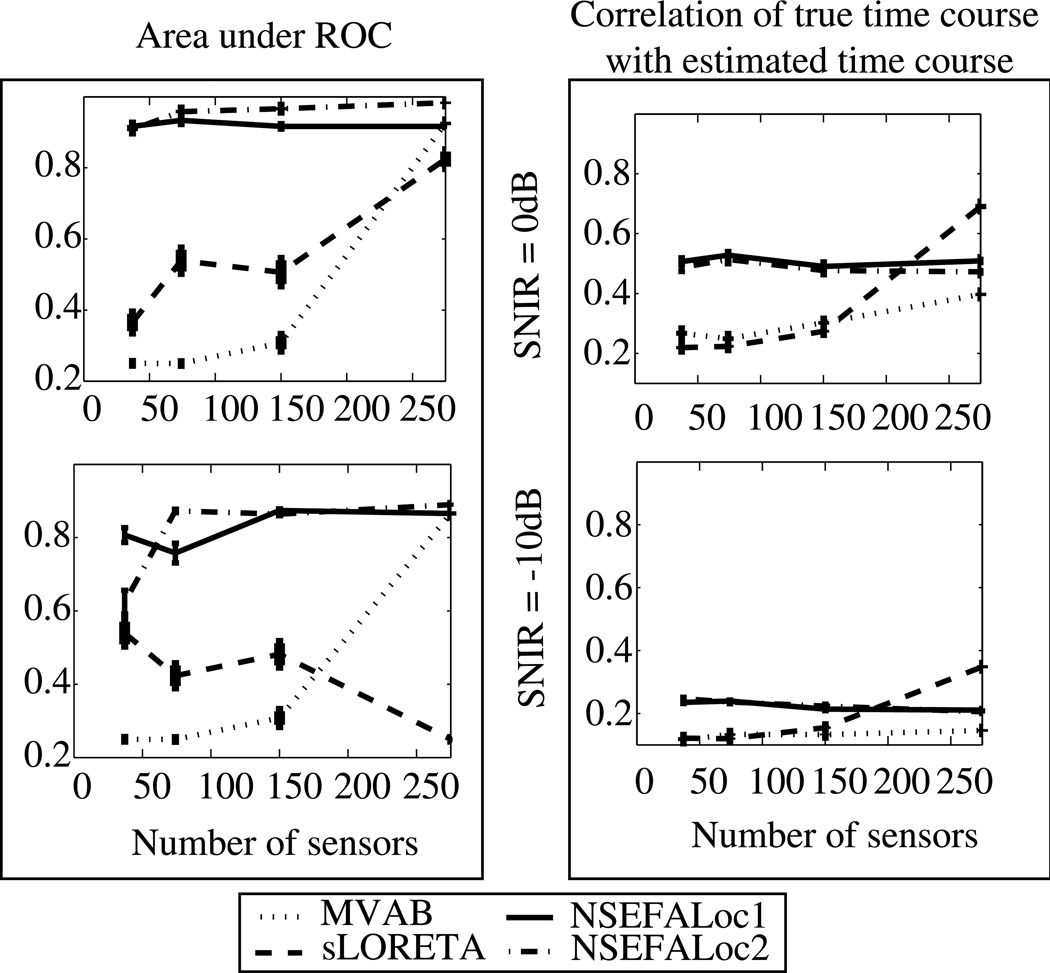
Results as number of sensors and time points is varied

Fig. 8 shows simulation performance resulting from reduced number of sensors. Fig. 8(a) shows the A′ metric as described above; Fig. 8(b) shows estimation accuracy of the source time courses. The top row in both (a) and (b) is for SNIR=0dB and the bottom row is for SNIR=−10dB. NSEFALoc1 and NSEFALoc2 did not show any major degradation in performance for either A′ or time course estimation in the moderate SNIR value of 0dB. For the very noisy case of SNIR=−10dB, A′ begins to decline more with only 37 sensors; time course estimation for the noisy SNIR=−10dB is poor for all number of sensors. In contrast to the probabilistic methods, both MVAB and sLORETA show decline in performance for both measures in the reduction from 275 to 150 sensors, but then plateaus for fewer sensors. In all cases of 150 sensors or fewer, both NSEFALoc methods outperform MVAB and sLORETA for both metrics.

Fig. 8.

(a) A′ and (b) time course estimation as a function of the number of MEG sensors for simulated data with 3 uncorrelated sources. The top row shows SNIR = 0dB and bottom row shows SNIR = −10dB using real brain noise. Error bars represent standard error.

Fig. 9 shows the performance results of all methods with decreased number of time points available. Fig. 9(a) shows the A′ localization accuracy metric; Fig. 9(b) shows the time course estimation. The top row in both (a) and (b) is for SNIR=0dB and the bottom row is for SNIR=−10dB. The A′ results show that both probabilistic methods outperform MVAB and sLORETA for all numbers of total data points; A′ performance begins to decline for 150 or fewer data points. sLORETA is a non-data-dependent method thus the inverse weight is not affected by number of time points available. The MVAB is dependent on the data to provide an estimate of the data covariance matrix. Since the simulations in both top and bottom rows are with relatively high noise (SNIR = 0dB and −10dB, respectively), the data covariance estimate might not change much with decreased data, since it is already noisy (note the time course correlation does not reach above 0.5 for any number of data points tested at SNIR=−10dB).

Fig. 9.

(a) A′ and (b) time course estimation as a function of the number of total data points for simulated data with 3 uncorrelated sources. The top row of each shows SNIR = 0dB and bottom row shows SNIR = −10dB using real brain noise. Error bars represent standard error.

On the other hand, the time course estimation results show that NSEFALoc1, NSEFALoc2 and sLORETA do not show a decline in performance with fewer data points and that all three methods generally perform equally well and better than MVAB. This is most likely due to NSEFALoc methods not requiring many data points in the first step of using SEFA to find temporal basis functions; once the temporal bases have been found, less data is then needed for localization of these bases.

Somatosensory results

The left panel of Fig. 10(a) shows typical somatosensory evoked MEG data with the largest peak at 50ms, expected to be coming from primary somatosensory cortex in the posterior wall of the central sulcus. The next four panels of Fig. 10(a) show localization performance of NSEFALoc1, NSEFALoc2, MVAB and sLORETA. All four methods accurately localize activity to the contralateral primary somatosensory cortex. However, performance changes when only 5 trials are used in the average. The left panel of Fig. 10(b) shows the sensor data averaged over trials 1–5 of the same somatosensory dataset. The next four panels of Fig. 10(b) show errors in localization in all methods. NSEFALoc1 and NSEFALoc2 show less error than MVAB and sLORETA, relative to the peak location found using all 256 trials. We note that other averages of 5 trials showed varied performance, but that, when averaging four different sets of 5-trial averages together, both NSEFALoc1 and NSEFALoc2 showed localization closest to primary somatosensory cortex, as shown in Fig. 10(c), whereas MVAB and sLORETA mislocalize this source.

Fig. 10.

Performance of methods using real somatosensory data as a function of the number of trials. Left column shows sensor data averaged over varied number of trials, while remaining columns show localization performance of NSEFALoc1, NSEFALoc2, MVAB and sLORETA. Row (a) shows performance of the three methods applied to the average of all 256 trials. Row (b) shows the localization performance to the average of only the first 5 trials. In order to show performance over other subsets of 5-trial averages, the spatial maps in row (c) are spatial averages of the localization of 4 different 5-trial averages. See Methods for details. Crosshairs in localization maps show peak location within “active” voxels at the slice of peak location, where the threshold for “active” was defined at 90% of the maximum for all maps.

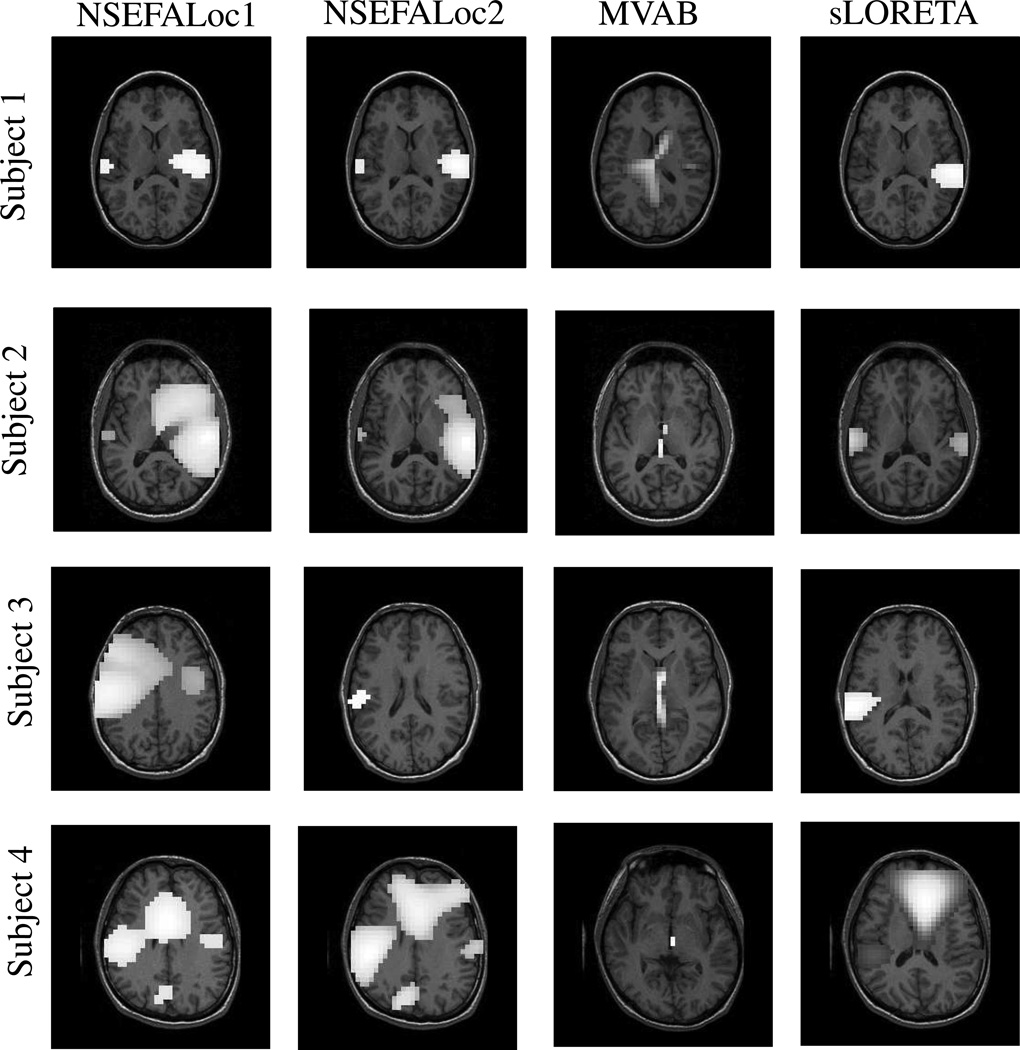
Auditory results

Fig. 11 shows localization results from all methods in four different subjects’ AEF datasets. NSEFALoc1 finds activation in bilateral auditory cortex in 4/4 subjects, though extra peaks appear in 3 subjects, and in Subject 3 the activation is too superior. NSEFALoc2 finds activation in bilateral auditory cortex in 3/4 subjects, with extra peaks in only one subject, and an additional subject in which only left auditory cortex is found. The strongest peak in the MVAB power maps in all 4 subjects is (falsely) in the center of the head, while a weaker activation on just the right side is seen in one subject. Finally, sLORETA finds bilateral auditory cortex in 2/4 subjects with extra peaks in one of the two, and only one side of auditory cortex is found in two other subjects. The sensor data for Subject 3 shows strong activation on the left side while very weak activation on the right, thus difficult to find for any method. While it is possible that the extra peaks seen in any of the methods are true sources co-activated with primary auditory cortex, the sensor data do not give a strong indication of extra sources, so most likely these extra peaks are false positives. In general, NSEFALoc1 and NSEFALoc2 found more correct source locations relative to less extraneous peaks than MVAB and sLORETA.

Fig. 11.

Performance of methods on real auditory evoked MEG datasets from two healthy human subjects. NSEFALoc1 and NSEFALoc2 results are likelihood maps and MVAB and sLORETA are power maps. The thresholds were set to portray each method optimally (i.e. including as many true sources as possible while not including other areas).

Discussion

Two methods are introduced which localize stimulus-evoked MEG/EEG sources and estimate their temporal activity in a probabilistic framework. Both model the sources as a linear combination of denoised temporal basis functions derived from the data using a variational Bayesian factor analysis method. The methods have reduced localization error relative to MVAB and sLORETA and are not as hampered by correlated sources. Additionally, the number or location of sources do not need to be specified, as in a standard dipole fitting method. Thus, these methods have clear advantages over current standard methods.

We showed results for MEG data only, although the equations can be easily applied to EEG data with an appropriate lead field. Sources can be constrained in location and orientation using the subject’s cortex defined by a structural MRI. Furthermore, NSEFALoc could be modified to work with a extended lead field based on spatial patch bases (Limpiti et al., 2006).

We have shown that the NSEFALoc models are not as sensitive to temporally correlated sources as the standard formulation of MVAB. However, it is possible to reduce the MVAB’s dependence on correlated sources through a modified weight matrix computed subject to additional constraints, if a rough idea of the location of sources is known (Dalal et al., 2006).

As the number of MEG and EEG channels has increased in recent years, the ability to accurately localize sources throughout the brain has increased (Vrba et al., 2004). However, performing calculations of high-dimensional data, such as inverting a data covariance matrix, becomes more difficult and can lead to errors. Meanwhile, the dimensionality of the underlying neural activity remains the same. Thus, many variations of PCA and ICA have been used on MEG/EEG data for removal of noise/artefactual components as well as for data dimension reduction (Jung et al., 2000; Ikeda and Toyama, 2000). Factor analysis also aims to reduce the dimensionality of the data to a linear mixture of factors that best account for the data while accounting for noise at the sensor level. An extended version, stimulus evoked factor analysis, has been used here to partition the factors thar are event-related activity from the factors are background interference. All methods which perform dimension reduction need a criterion for choosing the reduction number. Using PCA, a plot of eigenvalues can often give a reasonable intuition for the dimension of “signal” in the data. ICA has no ordering of components. In the method proposed here, there are two variables affecting model dimension: number of TBFs obtained from SEFA and the non-localized evoked factors (X) in NSEFALoc2. While a user must initially select a dimension for these terms, we showed that the use of hyperparameters in the model provides robustness to this selection by reducing the influence of unnecessary components.

For simple models with latent variables, the posterior distribution of a desired unknown variable can often be computed directly. However, for more interesting and realistic models, the posterior is often computationally intractable. In these cases, some approximation must be made. Since both SEFA and NSEFALoc2 models were computationally intractable as initially developed, we used a variational approximation for the joint posterior in both models. The main alternative to variational methods is sampling methods, such as Markov Chain Monte Carlo methods (Jun et al., 2005; Gelman and Rubin, 1996), which extensively estimate points in the distribution. MCMC is dependent on the sampled points and can be quite computationally costly. Nummenmaa et al. (2007a) do show advantages of MCMC over variational methods when the posterior distribution is not unimodal. However, the same researchers also show improvements of variational Bayesian methods over minimum norm methods in real data (Nummenmaa et al., 2007b).

Variational methods instead choose to factorize the joint distribution over factors and parameters assuming conditional independence of the factors and parameters, also termed the mean field approximation. Variational Bayesian methods compute the posterior distribution that maximizes the free energy ℱ, an approximation to the data likelihood ℒ. This approximation is an equality when the approximate posterior q equals the true posterior p.

Several other uses of variational Bayesian methods for the MEG/EEG inverse problem have been demonstrated. In general, they vary in how spatial priors, source covariance and noise covariance are treated, as well if they are a dipole or distributed model. Sato et al. (2004) show how variational Bayesian inversion methods can be used to improve MEG estimates with inclusion of fMRI data. Kiebel et al. (2008) use a variational Bayesian model for dipole models; one benefit is to contrast competing models of number and type of dipoles to overcome the usual problem of dipole models in choosing number of dipoles. Phillips et al. (2005) demonstrate a distributed source model that uses multiple source priors and learns their optimal weighting through hyperparameters. Friston et al. (2008) extend this further by establishing a multiple prior formulation where any number of source prior covariances can be included, but are projected to sensor space and their corresponding hyperparameters prune which prior terms are relevant in sensor space, thus avoiding large source-space matrices. Daunizeau and Friston (2007) use a variational inversion scheme to solve a multi-scale model for MEG/EEG where the quantity and functional connectivity between mesostate sources are learned. Trujillo-Barreto et al. (2008) have recently proposed a model that is similar to NSEFALoc in that it includes a set of temporal basis functions to model the source activity and accounts for the sensor noise and source noise separately in a probabilistic graphical model; unknown quantities are also learned through a VB-EM algorithm. Their method differs in several ways from NSEFALoc. They demonstrate their method using wavelet representation for TBFs; alternatively, SEFA could be used to estimate the TBFs in their model. They estimate source activity at all voxels at once rather than scanning each voxel at at time.

NSEFALoc1 and NSEFALoc2 present a tradeoff of computation time and source estimation accuracy. Throughout the results presented here, NSEFALoc2 tended to outperform NSEFALoc1. NSEFALoc1 estimates a full-rank noise covariance guided by a Wishart prior distribution in a single closed-form solution per voxel. NSEFALoc2, on the other hand, learns more precisely the unknown interference sources distant from the current voxel being scanned by learning an unknown mixing matrix with dimension smaller than the number of sensors. Thus, more robust estimates of noise covariances can be made with fewer parameters to estimate, though convergence usually requires about 20 EM iterations. These EM iterations require longer computation time: NSEFALoc1 computes estimates across a whole brain volume of about 11,000 voxels in roughly 5mins. while NSEFALoc2 takes 110 mins. for the same reconstruction, roughtly 0.6s per voxel on a standard Linux personal computer with 2.0GHz processor.

All methods which do not have a closed-form solution require initialization of the values to be iteratively updated. We have found that choice of initialization can change the final results somewhat but not largely, and so we did not extensively examine these effects. After finding one method of initialization that worked well in a few test simulations, that set was used for all results shown. Since the closed-form solution to NSEFALoc1 is easily obtained for each scanned voxel, aspects of this result were used to initialize quantities for NSEFALoc2, thus explaining some similarity in performance.

The NSEFALOC algorithms presented in this paper have some similarity to another algorithm SAKETINI recently proposed by us (Zumer et al., 2007). Both SAKETINI and NSEFALoc solve for hidden evoked factors, use unknown mixing matrices to model interference sources, and take advantage of stimulus timing. However, SAKETINI does not use fixed temporal basis functions, but instead learns hidden factors at each time point. Since the source time course estimates from both NSEFALoc and SAKETINI are effectively a weight matrix multiplying the sensor data, the temporal smoothness of the source estimates are comparable to the sensor data, possibly more smooth due to noise removal. However, since the source estimates from NSEFALoc are based on fixed temporal basis functions, additional smoothness could be imposed to these basis functions prior to source estimation; SAKETINI is not as amenable to these modifcations. The analysis of NSEFALoc is similar to the simulations and real data that SAKETINI was tested on in Zumer et al. (2007). A detailed comparison of performance between NSEFALoc and SAKETINI is forthcoming and is beyond the scope of this paper.

In this work, no specific spatial prior information was used, although it certainly can be incorporated. NSEFALoc only estimates one dipole at a time, by scanning through the voxel grid, thus estimation of number of dipoles is not explicitly performed. The likelihood map can be interpreted as a factorized map of the posterior probability of a source at each voxel. Thresholding of the likelihood map can be viewed as a posterior probability map thresholding procedure. This posterior probablity map lends itself for statistical analyses across subjects and conditions, a topic that could be explored in future work.

Appendix A: Full set of update rules for SEFA estimates

Here, SEFA is computed by using a two-stage procedure to avoid issues of identifiability between B and C, especially in cases of limited pre-stimulus data. In the limit of no pre-stimulus data, B and C could be concatenated as the same variable, as interference could not be distinguised from evoked activity. However, even with sufficient pre-stimulus data, if B and C are learned simultaneously, an evoked component present only in the post-stimulus data could inadvertantly be learned as a column of B due to identifiablity in this model.

To describe the full model in the Bayesian framework, prior probability distributions are given to these quantities:

$$p(\mathbf{\Phi })=\prod _{n}p({\mathit{\varphi }}_n);p({\mathit{\varphi }}_n)=𝒩({\mathit{\varphi }}_n|0,\mathit{I}),$$ (A-1)

$$p(\mathit{U})=\prod _{n}p({\mathit{u}}_n);p({\mathit{u}}_n)=𝒩({\mathit{u}}_n|0,\mathit{I}),$$ (A-2)

$$p(\mathit{V})=\prod _{n}p({\mathit{\upsilon }}_n);p({\mathit{\upsilon }}_n)=𝒩({\mathit{\upsilon }}_n|0,{\mathbf{\Lambda }}_{\mathit{S}}),p({\mathbf{\Lambda }}_{\mathit{S}})=\text{const}.$$ (A-3)

and hyperparameters χ and β are used for the mixing matrices to help learn their dimension:

$$p(\mathit{C})=\prod _{kl}p(c_{kl});p(c_{kl})=𝒩(c_{kl}|0,{({\lambda }_S)}_k{\chi }_l)$$ (A-4)

$$p(\mathit{B})=\prod _{km}p(b_{km});p(b_{km})=𝒩(b_{km}|0,{({\lambda }_S)}_k{\beta }_m)$$ (A-5)

Computation of the current model above is intractable due to the joint probability of the the parameters and factors. The variational approximation is used, which restricts the joint posterior to a product of factor distributions, but allows the solution to be computed analytically. The VB-EM algorithm iteratively maximizes the free energy ℱ with respect to (w.r.t.) each factorized distribution to, at least, a local maximum of ℱ, alternating w.r.t. the posteriors q(U|Y) and q(B|Y). Therefore, the following variational approximations are made to make the model computationally tractable:

$$p(\mathit{U},\mathit{B}|\mathit{Y})\approx q(\mathit{U},\mathit{B}|\mathit{Y})=q(\mathit{U}|\mathit{Y})q(\mathit{B}|\mathit{Y})$$

$$p(\mathbf{\Phi },\mathit{U},\mathit{C}|\mathit{Y})\approx q(\mathbf{\Phi },\mathit{U},\mathit{C}|\mathit{Y})=q(\mathbf{\Phi },\mathit{U}|\mathit{Y})q(\mathit{C}|\mathit{Y})$$ (A-6)

The update rules for the two-stage procedure are given. The following posterior estimates are obtained for the factors in the first-stage VBE-step:

$$q(\mathit{U}|\mathit{Y})=\prod _{n}q({\mathit{u}}_n|{\mathit{y}}_n);q({\mathit{u}}_n|{\mathit{y}}_n)=𝒩({\mathit{u}}_n|{\mathit{ū}}_n,\mathbf{\Gamma })$$

$${\mathit{ū}}_n={\mathbf{\Gamma }}^{-1}{\overline{\mathit{B}}}^T{\mathbf{\Lambda }}_{\mathit{S}}{\mathit{y}}_n;\mathbf{\Gamma }={\overline{\mathit{B}}}^T{\mathbf{\Lambda }}_{\mathit{S}}\overline{\mathit{B}}+K{\mathbf{\Psi }}_{\mathit{B}}^{-1}+\mathit{I}$$ (A-7)

In the first-stage VBM-step, the full posterior distribution of the background mixing matrix B is computed, including its precision matrix Ψ_B, and the MAP estimates of the noise precision Λ_S and the hyperparameter β.

$$q(\mathit{B}|\mathit{Y})=\prod _{k}q({\mathit{b}}_k|\mathit{Y});q({\mathit{b}}_k|\mathit{Y})=𝒩({\mathit{b}}_k|{\overline{\mathit{b}}}_k,{({\lambda }_S)}_k{\mathbf{\Psi }}_{\mathit{B}})$$

$$\overline{\mathit{B}}={\mathit{R}}_{\mathit{Y}\mathit{U}}{\mathbf{\Psi }}_{\mathit{B}};{\mathbf{\Psi }}_{\mathit{B}}={({\mathit{R}}_{\mathit{U}\mathit{U}}+\mathit{\beta })}^{-1}$$

$${\mathit{\beta }}^{-1}=\text{diag}(\frac{1}{K}{\overline{\mathit{B}}}^T{\mathbf{\Lambda }}_{\mathit{S}}\overline{\mathit{B}}+{\mathbf{\Psi }}_{\mathit{B}})$$

$${\mathbf{\Lambda }}_{\mathit{S}}^{-1}=\frac{1}{N}\text{diag}({\mathit{R}}_{\mathit{Y}\mathit{Y}}-\overline{\mathit{B}}{\mathit{R}}_{\mathit{Y}\mathit{U}}^T)$$ (A-8)

Now that B and Λ_S have been learned from the data, the statistics of these noise sources are assumed not to change.

The second-stage VBE-step results as:

$$q({\mathit{\kappa }}_n|{\mathit{y}}_n)=𝒩({\mathit{\kappa }}_n|{\overline{\mathit{\kappa }}}_n,\mathbf{\Gamma });$$

$${\overline{\mathit{\kappa }}}_n={\mathbf{\Gamma }}^{-1}{\overline{\mathbf{\Omega }}}^T{\mathbf{\Lambda }}_{\mathit{S}}{\mathit{y}}_n;$$

$$\mathbf{\Gamma }=\overline{{\mathbf{\Omega }}^T{\mathbf{\Lambda }}_{\mathit{S}}\mathbf{\Omega }}+\mathit{I}={\overline{\mathbf{\Omega }}}^T{\mathbf{\Lambda }}_{\mathit{S}}\overline{\mathbf{\Omega }}+K{\mathbf{\Psi }}^{-1}+\mathit{I}$$ (A-9)

$$=\left(\begin{array}{c}\hfill {\overline{\mathit{C}}}^T\hfill \\ \hfill {\overline{\mathit{B}}}^T\hfill \end{array}\right){\mathbf{\Lambda }}_{\mathit{S}}\left(\overline{\mathit{C}}\overline{\mathit{B}}\right)+K\left(\begin{array}{cc}{\mathbf{\Psi }}_{\mathit{C}}^{-1}\hfill & 0\hfill \\ 0\hfill & 0\hfill \end{array}\right)+\mathit{I}$$ (A-10)

In the second-stage VBM-step, the posterior distribution of the interference mixing matrix C is updated, including its precision Ψ_C, as well as the MAP value of the hyperparameter χ. Thus, the posterior distribution for C is:

$$q(\mathit{C}|\mathit{Y})=\prod _{k}q({\mathit{c}}_k|\mathit{Y});q({\mathit{c}}_k|\mathit{Y})=𝒩({\mathit{c}}_k|{\overline{\mathit{c}}}_k,{({\lambda }_S)}_k{\mathbf{\Psi }}_{\mathit{C}})$$

$$\overline{\mathit{C}}=({\mathit{R}}_{\mathit{Y}\mathbf{\Phi }}-\overline{\mathit{B}}{\mathit{R}}_{\mathit{U}\mathbf{\Phi }}){\mathbf{\Psi }}_{\mathit{C}}^{-1};{\mathbf{\Psi }}_{\mathit{C}}=({\mathit{R}}_{\mathbf{\Phi }\mathbf{\Phi }}+\mathit{\chi })$$

$${\mathit{\chi }}^{-1}=\text{diag}(\frac{1}{K}{\overline{\mathit{C}}}^T{\mathbf{\Lambda }}_{\mathit{S}}\overline{\mathit{C}}+{\mathbf{\Psi }}_{\mathit{C}})$$ (A-11)

The matrices, such as R_UΦ, represent the posterior covariance between the two subscripts

$${\mathit{R}}_{\mathbf{\Phi }\mathit{U}}=\sum _{n=1}^N{\overline{\mathit{\varphi }}}_n{\mathit{ū}}_n^T+N{\mathbf{\Sigma }}_{\mathbf{\Phi }\mathit{U}}{\mathit{R}}_{\mathbf{\Phi }\mathbf{\Phi }}=\sum _{n=1}^N{\overline{\mathit{\varphi }}}_n{\overline{\mathit{\varphi }}}_n^T+N{\mathbf{\Sigma }}_{\mathbf{\Phi }\mathbf{\Phi }}$$ (A-12)

where Σ = Γ⁻¹ is specified as:

$$\mathbf{\Sigma }=\left(\begin{array}{cc}{\mathbf{\Sigma }}_{\mathbf{\Phi }\mathbf{\Phi }}\hfill & {\mathbf{\Sigma }}_{\mathbf{\Phi }\mathit{U}}\hfill \\ {\mathbf{\Sigma }}_{\mathit{U}\mathbf{\Phi }}\hfill & {\mathbf{\Sigma }}_{\mathit{U}\mathit{U}}\hfill \end{array}\right)$$ (A-13)

Appendix B: Derivation of NSEFALoc1 estimates

For each scanned voxel, we consider the likelihood function over all the known data and hidden parameters:

$${ℒ}^r=\text{log}p(\mathit{Y},{\mathit{G}}^r,{\mathbf{\Lambda }}_{\mathbf{1}}^r)\propto \text{log}p(\mathit{Y}|{\mathbf{\Lambda }}_{\mathbf{1}}^r,{\mathit{G}}^r)+\text{log}p({\mathbf{\Lambda }}_{\mathbf{1}}^r)$$ (B-1)

$$\text{log}p(\mathit{Y}|{\mathbf{\Lambda }}_{\mathbf{1}}^r,{\mathit{G}}^r)=\sum _{n=1}^N\text{log}p({\mathit{y}}_n|{\mathbf{\Lambda }}_{\mathbf{1}}^r,{\mathit{G}}^r)$$

$$p({\mathit{y}}_n|{\mathbf{\Lambda }}_{\mathbf{1}}^r,{\mathit{G}}^r)=𝒩({\mathit{y}}_n|\mathit{F}{\mathit{G}}^r{\mathit{\varphi }}_n,{\mathbf{\Lambda }}_{\mathbf{1}}^r)$$

$$p({\mathbf{\Lambda }}_{\mathbf{1}}^r)=𝒲({\mathbf{\Lambda }}_{\mathbf{1}}^r|\nu ,{\mathbf{\Sigma }}_0)\propto {|{\mathbf{\Lambda }}_{\mathbf{1}}^r|}^{\nu /2}{e}^{-\frac{1}{2}Tr({\mathbf{\Sigma }}_0{\mathbf{\Lambda }}_{\mathbf{1}}^r)}$$ (B-2)

where Σ₀ and ν are hyperparameters. The graphical model in Fig. 1 indicates that G^r and ${\mathbf{\Lambda }}_{\mathbf{1}}^r$ are independent, and we give a flat prior on G^r.

We choose ν = K + 2 for the distribution to be normalizable. Whereas Σ₀ could be inferred by directly measuring the sample covariance, instead VBFA is used on the pre-stimulus data (like in the first stage of SEFA, but applied to the post-stimulus data). From VBFA on the post-stimulus data, Λ₀ is the diagonal sensor precision and B₀ is the interference mixing matrix, so ${\mathbf{\Sigma }}_0={({\mathit{B}}_0{\mathit{B}}_0^T+{\mathbf{\Lambda }}_0^{-1})}^{-1}$.

To solve for Λ₁, (assuming G is known), take the derivative of the likelihood:

$$\frac{\partial ℒ}{\partial {\mathbf{\Lambda }}_{\mathbf{1}}}=\frac{\partial }{\partial {\mathbf{\Lambda }}_{\mathbf{1}}}(-\frac{1}{2}\sum _{n=1}^N{({\mathit{y}}_n-\mathit{F}\mathit{G}{\mathit{\varphi }}_n)}^T{\mathbf{\Lambda }}_{\mathbf{1}}({\mathit{y}}_n-\mathit{F}\mathit{G}{\mathit{\varphi }}_n)+\frac{N}{2}\text{log}|{\mathbf{\Lambda }}_{\mathbf{1}}|+\frac{\nu }{2}\text{log}|{\mathbf{\Lambda }}_{\mathbf{1}}|-\frac{1}{2}Tr({\mathbf{\Sigma }}_0{\mathbf{\Lambda }}_{\mathbf{1}}))=0$$ (B-3)

Solving for ${\hat{\mathbf{\Lambda }}}_1^{-1}$, and further simplifying to:

$${\hat{\mathbf{\Lambda }}}_1^{-1}=\frac{1}{N+\nu }({\mathit{R}}_{\mathit{Y}\mathit{Y}}-\mathit{F}\mathit{G}{\mathit{R}}_{\mathbf{\Phi }\mathit{Y}}+{\mathbf{\Sigma }}_0)$$ (B-4)

Now ${\mathbf{\Lambda }}_{\mathbf{1}}^{-1}$ is a function of G (since G was assumed known when taking the derivative above); an expression for ${\mathbf{\Lambda }}_{\mathbf{1}}^{-1}$ not dependent on G is needed. To solve for G (assuming ${\mathbf{\Lambda }}_{\mathbf{1}}^{-1}$ is known), take the derivative of ℒ:

$$\frac{\partial ℒ}{\partial \mathit{G}}=\frac{\partial }{\partial \mathit{G}}(\frac{N}{2}\text{log}|{\mathbf{\Lambda }}_{\mathbf{1}}|-\frac{1}{2}\sum _{n=1}^N{(\mathit{Y}-\mathit{F}\mathit{G}{\mathit{\varphi }}_n)}^T{\mathbf{\Lambda }}_{\mathbf{1}}(\mathit{Y}-\mathit{F}\mathit{G}{\mathit{\varphi }}_n))=0$$ (B-5)

Using both Eq. B-4, and defining S as

$$\mathit{S}=\frac{1}{N+\nu }({\mathit{R}}_{\mathit{Y}\mathit{Y}}-{\mathit{R}}_{\mathit{Y}\mathbf{\Phi }}{\mathit{R}}_{\mathbf{\Phi }\mathbf{\Phi }}^{-1}{\mathit{R}}_{\mathbf{\Phi }\mathit{Y}}+{\mathbf{\Sigma }}_0),$$ (B-6)

then Ĝ can be written as:

$${\mathit{G}}^r={({\mathit{F}}^T{\mathit{S}}^{-1}\mathit{F})}^{-1}{\mathit{F}}^T{\mathit{S}}^{-1}{\mathit{R}}_{\mathit{Y}\mathbf{\Phi }}{\mathit{R}}_{\mathbf{\Phi }\mathbf{\Phi }}^{-1}$$ (B-7)

Since the expression for G is now known, this value can be plugged into Eq. B-4 to find Λ₁ independent of G.

Appendix C: Derivation of NSEFALoc2 estimates

In the VBE-step of NSEFALoc2, p(x_n|y_n) is found by finding the q(x_n|y_n) that maximizes the free energy ℱ and therefore best approximates p(x_n|y_n), where Θ = {G, Λ₂, α}. The variational approximation, similar to the SEFA model in Eq. A-6, that the parameters and variables are conditionally independent given the data, is used.

$$ℱ(q,\mathbf{\Theta })=\int d\mathit{X}d\mathit{A}q(\mathit{X}|\mathit{Y},\mathbf{\Theta })q(\mathit{A}|\mathit{Y},\mathbf{\Theta })[\text{log}p(\mathit{Y}|\mathit{X},\mathit{A},\mathbf{\Theta })+\text{log}p(\mathit{X})+\text{log}p(\mathit{A}|{\mathbf{\Lambda }}_{\mathbf{2}},\mathit{\alpha })-\text{log}q(\mathit{X}|\mathit{Y},\mathbf{\Theta }-\text{log}q(\mathit{A}|\mathit{Y},\mathbf{\Theta })]$$ (C-1)

Maximizing for q(X|Y) yields

$$\text{log}q(\mathit{X}|\mathit{Y})=E_{q(\mathit{A}|\mathit{Y})}(\text{log}p(\mathit{Y},\mathit{X},\mathit{A}|\mathbf{\Theta }))$$ (C-2)

It can be shown that q(X|Y) is also a Gaussian distribution. The mean of a Gaussian is the value that makes the derivative zero and the variance of the Gaussian is the slope of gradient, yielding:

$$p({\mathit{x}}_n|{\mathit{y}}_n)=𝒩({\mathit{x}}_n|{\overline{\mathit{x}}}_n,\mathbf{\Gamma })$$

$${\overline{\mathit{x}}}_n={\mathbf{\Gamma }}^{-1}{\mathit{Ā}}^T{\mathbf{\Lambda }}_{\mathbf{2}}({\mathit{y}}_n-\mathit{F}\mathit{Ḡ}{\mathit{\varphi }}_n)$$

$$\mathbf{\Gamma }={\mathit{A}}^T{\mathbf{\Lambda }}_{\mathbf{2}}\mathit{A}+K\mathbf{\Psi }+\mathit{I}$$ (C-3)

To find the MAP estimate of G, the derivative of the free energy is taken:

$$\frac{\partial ℱ}{\partial \mathit{G}}=\frac{\partial }{\partial \mathit{G}}{E}_{q(\mathit{X}|\mathit{Y})}{E}_{q(\mathit{A}|\mathit{y})}[\text{log}p(\mathit{Y}|\mathit{X},\mathit{A},\mathit{G})]=0$$

$$\frac{\partial }{\partial \mathit{G}}{E}_{q(\mathit{X}|\mathit{Y})}{E}_{q(\mathit{A}|\mathit{Y})}[-\frac{1}{2}\sum _{n=1}^N{({\mathit{y}}_n-\mathit{F}\mathit{G}{\mathit{\varphi }}_n-\mathit{A}{\mathit{x}}_n)}^T{\mathbf{\Lambda }}_{\mathbf{2}}({\mathit{y}}_n-\mathit{F}\mathit{G}{\mathit{\varphi }}_n-\mathit{A}{\mathit{x}}_n)]=0$$ (C-4)

Plugging in the value for Ā, we obtain:

$$\mathit{Ḡ}={({\mathit{F}}^T{\mathbf{\Lambda }}_{\mathbf{2}}\mathit{F})}^{-1}{\mathit{F}}^T{\mathbf{\Lambda }}_{\mathbf{2}}({\mathit{R}}_{\mathit{Y}\mathbf{\Phi }}-{\mathit{R}}_{\mathit{Y}\mathit{X}}{\mathbf{\Psi }}^{-1}{\mathit{R}}_{\mathit{X}\mathbf{\Phi }})$$

$${({\mathit{R}}_{\mathbf{\Phi }\mathbf{\Phi }}-{\mathit{R}}_{\mathbf{\Phi }\mathit{X}}{\mathbf{\Psi }}^{-1}{\mathit{R}}_{\mathit{X}\mathbf{\Phi }})}^{-1}$$ (C-5)

The rest of the updates are given in the main Theory section for NSEFALoc2.