Contribution of HIV-1 genomes that do not integrate to the basic reproductive ratio of the virus

Abstract

Recent experimental data indicate that HIV-1 DNA that fails to integrate (from now on called uDNA) can by itself successfully produce infectious offspring virions in resting T cells that become activated after infection. This scenario is likely important at the initial stages of the infection. We use mathematical models to calculate the relative contribution of unintegrated and integrated viral DNA to the basic reproductive ratio of the virus, R₀, and the models are parameterized with preliminary data. This is done in the context of both free virus spread and transmission of the virus through virological synapses. For free virus transmission, we find that under preliminary parameter estimates, uDNA might contribute about 20% to the total R₀. This requires that a single copy of uDNA can successfully replicate. If the presence of more than one uDNA copy is required for replication, uDNA does not contribute to R₀. For synaptic transmission, uDNA can contribute to R₀ regardless of the number of uDNA copies required for replication. The larger the number of viruses that are successfully transmitted per synapse, however, the lower the contribution of uDNA to R₀ because this increases the chances that at least one virus integrates. Using available parameter values, uDNA can maximally contribute 20% to R₀ in this case. We argue that the contribution of uDNA to virus reproduction might also be important for continued low level replication of HIV-1 in the presence of integrase inhibitor therapy. Assuming a 20% contribution of uDNA to the overall R₀, our calculations suggest that R₀=1.6 in the absence of virus integration. While these are rough estimates based on preliminary data that are currently available, this analysis provides a framework for future experimental work which should directly measure key parameters.

Introduction

Human immunodeficiency virus-1 (HIV-1) infects cells of the immune system, mainly CD4+ T cells and antigen presenting cells. The virus has an RNA genome, which upon infection is copied into DNA through reverse transcription. The DNA genome of the virus can subsequently integrate into the host genome, and this forms the template for transcription, eventually leading to the formation of new virus particles that are released from the infected cell. This cycle of infection and replication allows the virus to spread from cell to cell, leading to the exponential growth of the HIV-1 population during the acute phase of the infection. After initiation of immune responses and also depletion of many target cells during the acute phase (Zhang et al., 2004), the virus population settles around a steady state level during the chronic phase of infection, termed the set point viral load. The set point viral load is highly correlated with the speed at which infection progresses from the asymptomatic phase to AIDS (Lifson et al., 1997; Mellors et al., 1996).

Extensive clinical and experimental data document these dynamics both in vivo and during in vitro experiments. Mathematical models have been very useful to help interpret those data, to measure crucial parameters, and to generate testable hypotheses (Nowak and May, 2000; Perelson, 2002; Perelson and Ribeiro, 2013; Wodarz, 2006). One of the most fundamental measures is the basic reproductive ratio of the virus, defined as the average number of newly infected cells generated by a single infected cell (Anderson and May, 1991; Heffernan et al., 2005; Nowak and May, 2000). It has been estimated for HIV-1 in a variety of settings (Little et al., 1999; Nowak et al., 1997; Ribeiro et al., 2010), and has important implications for understanding disease progression as well as the response to anti-viral drug therapies (Bonhoeffer and Nowak, 1997; Bonhoeffer et al., 1997).

During the replication cycle of the virus, the step of integration is prone to failure, leading to the generation of unintegrated viral DNA genomes (uDNA). While some of the unintegrated DNA found in cells is simply pre-integration DNA that will eventually integrate, most viral DNA fails to integrate and remains extrachromosomal. Throughout the rest of this paper, we will use the term uDNA to refer to the latter, i.e. to viral DNA that fails to integrate. Pre-integration DNA is excluded from the current analysis and discussion, because it will eventually integrate. uDNA is present in both linear form, which is subject to exonuclease digestion at poorly defined rates, and circularized forms containing one and two long terminal repeats (1-LTR and 2-LTR circles). Circularized uDNA is highly stable and lost only through cell death or dilution during cell division. Gene expression has been detected from all forms of uDNA, linear and circular (Cara et al., 1996; Sloan and Wainberg, 2011; Trinite et al., 2013; Wu and Marsh, 2001).

According to the literature, uDNA is considered a replicative dead end and does not lead to the production of infectious offspring virus (e.g. (Butler et al., 2001)). Recent finding from two of us, however, indicate that the situation could be more complex (Gelderblom et al., 2008; Trinite et al., 2013). Thus, if a cell is coinfected with integrated and unintegrated virus, viral uDNA has been shown to successfully produce infectious offspring virus, indicating cooperative interactions (Gelderblom et al., 2008). Even more striking, our recent study has shown that cells that only contain viral uDNA (that fails to integrate) can successfully produce infectious offspring virus (Trinite et al., 2013). This has been shown using an integration-defective mutant, as well as with wild-type virus in cells treated with an integrase inhibitor (Trinite et al., 2013). Virus production in uDNA-infected cells occurs at a rate that is small compared to integrated genomes (Trinite et al., 2013); however, cells infected only with uDNA also live significantly longer than productively infected cells that contain iDNA, thus increasing the total amount of virus produced by those cells during their life-span (manuscript in preparation). Successful uDNA replication, however, does not seem to occur under all conditions. It is observed specifically in resting cells that are infected and subsequently become activated (Trinite et al., 2013), which could be especially relevant to the initial stages of the infection, a time when many resting CD4⁺ T cells are infected (Haase, 2011; Hladik and McElrath, 2008; Kinter et al., 2003; Li et al., 2005; Nishimura and Martin, 2011; Reilly et al., 2007; Zhang et al., 1999; Zhang et al., 2004) and the latent reservoir is established (Chun et al., 1998; Hatziioannou et al., 2014). Thus, uDNA could have importance for the ability of the virus to establish a persistent infection, reflected in the value of its basic reproductive ratio. Replication from uDNA might also play a role when virus load is reduced to very low levels during anti-viral therapies, and following treatment interruption, when latent viruses re-emerge.

This paper presents for the first time a mathematical model that allows successful virus replication both from cells containing integrated virus and from cells that only contain virus that fails to integrate. The aim of this study is to quantify the contribution of viral uDNA to the basic reproductive ratio of the virus, and thus to the ability of the virus to establish a persistent infection. We start with a standard virus dynamics model and include the possibility of uDNA replication. This model assumes that the virus spreads through the target cell population via the release of free virus particles. In this model, iDNA and uDNA replication contribute additively to the basic reproductive ratio of the virus, and their relative contributions are determined by the parameters describing the rate of virus production and cell death. This requires that a cell with a single copy of viral uDNA can produce offspring virus. While data indicate that this can indeed occur, it cannot currently be discounted that multiple uDNA copies are required to successfully produce offspring virus. In this case, uDNA replication does not contribute to the basic reproductive ratio of the virus, because multiple infection is a very unlikely event in the context of free virus transmission at relatively low virus loads. In addition to this model we also consider the assumption that the virus can spread directly from cell to cell, through the formation of virological synapses (Hubner et al., 2009). In this model, uDNA can contribute to the basic reproductive ratio of the virus even if multiple uDNA copies are required for successful replication. The reason is that synaptic transmission is well documented to deliver multiple infectious viruses, resulting in a high multiplicity of infection of cells (MOI) (Del Portillo et al., 2011). The exact contribution of uDNA to the basic reproductive ratio of the virus depends on the number of viruses that get transferred through the synapse. The larger this number, the higher the likelihood that a virus will integrate into the host genome, and thus the lower the contribution of uDNA to the basic reproductive ratio. In the context of available and preliminary parameters, the model suggests that uDNA replication might contribute 20% to the overall R₀ for free virus transmission, and maximally 20% for synaptic transmission, depending on the number of viruses that get successfully transmitted per synapse. While this is a relatively small fraction, we estimate that the basic reproductive ratio of HIV-1 in the absence of integrated virus can be still greater than one in the context of these parameter values, potentially allowing the occurrence of persistent, low-level viral replication during treatment with integrase inhibitors. These insights are discussed in the context of data that examine virus dynamics during raltegravir intensification of HAART.

The basic mathematical model of virus dynamics with free virus transmission

To set the scene, we briefly summarize a basic model of virus dynamics that has been analyzed extensively in the literature. It assumes transmission of free virus released from cells. For a review, see (Nowak and May, 2000; Perelson, 2002; Perelson and Ribeiro, 2013; Wodarz, 2006). It considers the populations of susceptible, uninfected cells, x, infected cells, y, and free virus, v. It is given by the following set of ordinary differential equations, which are written in “dot form” (equivalent to dx/dt, etc).

$$\begin{array}{l}\stackrel{.}{x}=\lambda -dx-\beta xv\\ \stackrel{.}{y}=\beta xv-ay\\ \stackrel{.}{v}=ky-uv\end{array}$$ (1)

Uninfected cells are generated with a rate λ, die with a rate d, and become infected by virus with a rate β. Infected cells die with a rate a, and produce free virus particles with a rate k. Free virus decays with a rate u. This model is characterized by two equilibria. If the virus fails to establish a persistent infection, the system converges to the following equilibrium: x⁽⁰⁾= λ/d; y⁽⁰⁾=0; v⁽⁰⁾=0. If the virus population successfully establishes a persistent infection, the system converges to the following equilibrium. $x^{(1)}=\frac{au}{\beta k};y^{(1)}=\frac{\lambda \beta k-\mathit{dau}}{a\beta k};v^{(1)}=\frac{\lambda \beta k-\mathit{dau}}{au\beta }$. Which outcome is observed depends on the basic reproductive ratio of the virus, R₀=λβk/dau. A persistent infection is established if R₀>1. For further details of this model, see (Nowak and May, 2000) and references therein.

Free virus transmission and uDNA Replication

Here, we consider an extension of the basic model that includes multiple infection of cells and takes into account the replication of both integrated and unintegrated viral genomes. Thus, we denote infected cells with i unintegrated and j integrated viruses by y_ij. Consistent with this notation, the variable y₀₀ represents the population of uninfected target cells. The model is thus given by the following set of ordinary differential equations (also see schematic in Figure 1a).

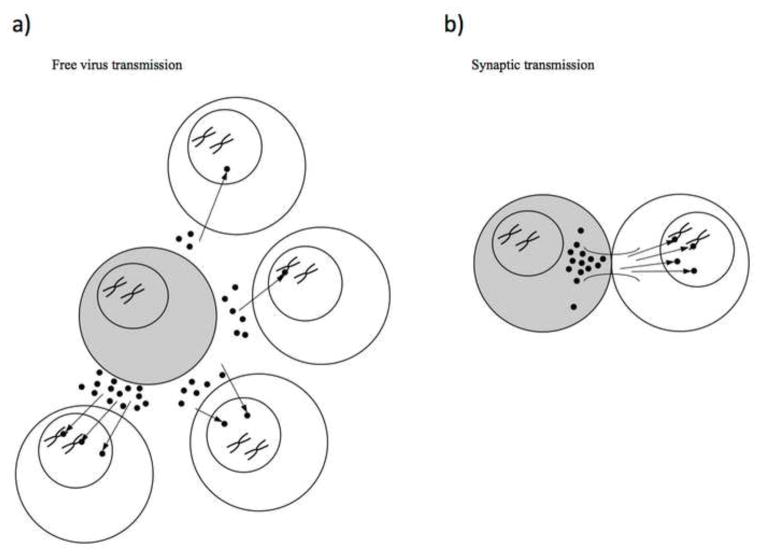
Figure 1.

Schematic of free virus and synaptic transmission modes. (a) In free virus transmission, viruses are released by an infected cell (grey) and can enter the target cell population. Different virus fates are shown with different target cells. Clockwise from the top: a single virus infects the target cell but remains unintegrated, a single virus infects a target cell and is integrated into the genome, multiple viruses infect a target cell but all remain unintegrated, and multiple viruses infect a target cell and some become integrated. (b) Synaptic transmission potentially involves a high number of viruses transferring into a target cell at once. These viruses can be integrated into the genome or remain unintegrated. In contrast to free virus transmission, the multiplicity of infection can be much higher. A single infected cell can potentially transmit via both modes of transmission.

$$\begin{array}{l}{\stackrel{.}{y}}_{0,0}=\lambda -{dy}_{0,0}-\beta y_{0,0}v\\ {\stackrel{.}{y}}_{i,j}=(1-p)\beta {vy}_{i-1,j}+p\beta {vy}_{i,j-1}-a_{i,j}{y}_{i,j}-\beta {vy}_{i,j}\\ \stackrel{.}{v}=\sum _{i=0}^N\sum _{j=0}^M{k}_{ij}{y}_{ij}-uv\end{array}$$ (2)

As in the previous model (1), infection occurs with a rate β. Upon infection, integration of the viral genome occurs with a probability p, while uDNA capable of replication is generated with a probability 1−p. As explained above, we consider only viral DNA that will not integrate (Trinite et al., 2013), rather than DNA that retains a functional pre-integration complex and might subsequently integrate. That is, pre-integration uDNA is not considered. The rest of the model is the same as the basic model discussed above. Kinetic parameters, such as the rate of virus production of infected cells and the rate of infected cell death can depend on the number of integrated and unintegrated viruses. Data indicate that cells infected with uDNA only replicate the virus with a slower rate but also die with a slower rate than cells infected with iDNA (manuscript in preparation). However, beyond this, there is no experimental evidence that the number of iDNA and uDNA copies in cells influences these parameters. Thus, we make the simplifying assumption that k_ij and a_ij can each have only two values. Cells with only unintegrated viruses produce virus at rate k_u and die at rate a_u. Cells with any amount of integrated viruses produce virus at a rate k_i and also die at a rate of a_i (whether uDNA is present or not). Note that in this model, the term iDNA refers to cells that are productively infected with integrated viral DNA. Latently infected cells are not taken into account here.

A couple of notes regarding the model structure: (i) The model includes a full multiple infection cascade, i.e. taking into account cells infected with i unintegrated and j integrated genomes. It could be argued that a simpler version of the model is sufficient, since only two types of infected cells are important to our analysis: those containing only uDNA and those containing iDNA. We have, however, chosen to explore the full model in order to avoid potential complications that can arise from simplified models (explored in Phan et al, submitted). (ii) uDNAs that fail to integrate can have different life-spans in the cells, depending on their exact form. The intracellular dynamics of uDNA (or iDNA) is not modeled here. We assume that the genomes considered in our models persist for the life-span of the infected cell.

As in the basic model of virus dynamics, this system is also characterized by two equilibria. In the absence of infection, the system converges to the trivial equilibrium, given by is y₀₀= λ/d, y_ij=0, and v=0. If the virus establishes a persistent infection, the system converges to the internal equilibrium where all populations are greater than zero (not written down due to complexity of expressions).

Using standard methods (see Supplementary Material), we can calculate the threshold for a successful infection from Model (2), defined by the stability of the virus-free steady state. This gives rise to the basic reproductive ratio of the virus in model (2), which is given by

$$R_0=p\frac{\lambda \beta k_i}{a_{i}ud}+(1-p)\frac{\lambda \beta k_u}{a_{u}ud}$$

This is similar to the expression for R₀ in the basic model (1), but has contributions from virus replication originating from iDNA (p) and uDNA (1−p). If we assume that integrated and unintegrated viruses contribute equally to virus replication and cell death, we can sum the terms and arrive at same expression for R₀ as in the basic model of virus dynamics, model (1). The same would be true if the burst size, defined as the average number of viruses produced per infected cell, was the same for both unintegrated and integrated viruses.

The analysis so far has assumed that a single copy of uDNA alone can lead to successful virus replication. Let us now assume a more complex situation in which more than one uDNA copy needs to be present in a cell for virus replication to be possible in the absence of iDNA. While there is currently no evidence that this is a requirement, this scenario also cannot currently be discounted. In this case, the basic reproductive ratio of the virus becomes:

$$R_0=p\frac{\lambda \beta k_i}{a_{i}ud}$$

In other words, unintegrated viruses do not contribute to establishing infection anymore. Intuitively, this can be explained as follows. At the beginning of infection, the number of uninfected cells is high while the number of viruses is relatively low. Thus, the chance that a cell is multiply infected is negligible. Since our current assumption requires multiple unintegrated viruses in a cell to start viral production, the cells infected with a single unintegrated virus are not yet productive at the very early stages of infection.

Synaptic virus transmission and uDNA Replication

Here, the model is modified to describe synaptic transmission of the virus. The model is given by the following set of ordinary differential equations (also see schematic, Figure 1b), which are based on previous work (Komarova and Wodarz, 2013; Komarova et al., 2012b; Komarova et al., 2013a; Komarova et al., 2013b).

$$\begin{array}{l}{\stackrel{.}{y}}_{0,0}=\lambda -{dy}_{0,0}-\beta y_{0,0}v-y_{0,0}\sum _{k=0}^N\sum _{l=0}^M{y}_{kl}\sum _{r=0}^N\sum _{s=0}^M{\gamma }_{rs}^{kl}\\ {\stackrel{.}{y}}_{i,j}=(1-p)\beta {vy}_{i-1,j}+p\beta {vy}_{i,j-1}-a_{i,j}{y}_{i,j}-\beta {vy}_{i,j}+\sum _{k=0}^N\sum _{l=0}^M{y}_{kl}(\sum _{r=0}^i\sum _{s=0}^j{y}_{rs}^{kl}{y}_{i-r,j-s}-y_{ij}\sum _{r=0}^{N-i}\sum _{s=0}^{M-j}{\gamma }_{rs}^{kl})\\ \stackrel{.}{v}=\sum _{i=0}^N\sum _{j=0}^M{k}_{ij}{y}_{ij}-uv\end{array}$$ (3)

for i≤N, j≤M, i+j≤N

Compared to model (2), it has one additional parameter: γ_rs^kl, which describes the probability that a cell with k unintegrated and l integrated viral genomes transmits r unintegrated and s integrated viruses (more precisely transmit genomes, r of which will be unintegrated and s will be integrated in the target cell). The γ term is an analog of the infectivity used in free virus transmission and is composed of 3 parts. Incorporated in this constant is the probability that a synapse is formed when two cells interact, the probability that r+s total viruses are successfully transmitted and the probability that r viral genomes are unintegrated while s viral genomes become integrated provirus in the target cell.

The equation describing the dynamics of uninfected cells, x, is identical to model (2) except with an added term for cell-to-cell transmission from other cells. The extra term describes cells with k and l unintegrated and integrated viral genomes transferring r viruses that will be unintegrated genomes and s that will be integrated genomes in the target cell. The equation for infected cells is also identical to that used in model (2) with the addition of terms that describe cell-to- cell interactions. The first term for cell-to-cell interactions describes other cells gaining viruses to form cells of type y_ij. The second term for cell-to-cell interactions describes cells of type y_ij gaining viruses by cell-to-cell transmission.

In the above equations, we place a limit on the number of viruses allowed per cell to be N. We also further limit the number of integrated viruses to be M. Thus, we only model y_ij for indexes such that i+j ≤ M. For simplicity, we did not explicitly write the equations for the endpoints, i.e. y_iM, y_Nj, y_NM. These species cannot be further infected in these equations.

Note that consistent with the other models, the synaptic transmission model is also given by ordinary differential equations, which imply perfect mixing of cells. In tissues, source cells are likely to form synapses with target cells in their vicinity, which could add a spatial component to the dynamics. Imaging data in lymph nodes, however, indicate that a lot of cell movement and mixing occurs in tissue (Germain et al., 2012). Thus, while synapses might be formed between neighboring cells, ongoing mixing means that a cell has a high chance to interact with many other cells in the system. A large migration rate in spatial models has been shown to lead to mass-action properties (Komarova et al., 2012a; Thalhauser et al., 2010), and hence the ODE modeling approach is justified here.

In order to arrive at an analytic result for R₀ for the system with cell to cell transmission, we use some simplifying assumptions. We first explore the system with synaptic transmission only by simplifying and separating the infectivity term, γ_rs^kl, to its constituent parts.

We assume that the rates of cell-to-cell transmission are determined by the presence of iDNA in the source cell. If a cell contains one or more integrated viral genomes, the kinetics of virus production and cell death are dictated by the integrated virus, and the potential presence of uDNA in the same cell is not assumed to make a difference. On the other hand, in the absence of iDNA, virus production by infected cells and the death rate of infected cells are determined by the parameters of the uDNA infection. It is assumed that the rate of virus production depends only on the type, but not the number, of viruses in the infected cell. Under this assumption, the parameter γ_rs^kl can be simplified to ${\widehat{\gamma }}_{r,s}^u$ and ${\widehat{\gamma }}_{r,s}^i$, for any k and l. Here, ${\widehat{\gamma }}_{r,s}^u$ is the reduced transmission rate from cells with only unintegrated viral genomes, which we set as $\eta {\widehat{\gamma }}_{r,s}^i$, η < 1. With these assumptions, we can find the new threshold for establishing an infection to be:

$$\begin{array}{l}{R}_0=\frac{{\beta }_{si}\lambda }{a_{i}d}+\frac{{\beta }_{su}\lambda }{a_{u}d}\\ {\beta }_{su}=\sum _{r=c}^N{\widehat{\gamma }}_{r,0}^u,{\beta }_{si}=\sum _{r=0}^N\sum _{s=1}^M{\widehat{\gamma }}_{r,s}^i\end{array}$$

Details are given in the Supplementary Material. This expression is similar to the one for free virus transmission in model (2), consisting of two components, one stemming from uDNA replication, the other from iDNA replication. Note that, in contrast to model (2), unintegrated viral genomes are now a factor in this expression, even when we require multiple unintegrated viral genomes to begin infection. Here, c is the threshold number of unintegrated viral genomes required to start cell-to-cell transmission. The term β_su is the sum of the ${\widehat{\gamma }}_{r,s}^u$ for synapses where at least the threshold number of viral genomes become unintegrated and none become integrated. The term β_si is the sum of the ${\widehat{\gamma }}_{r,s}^i$ for synapses where at least one transferred virus becomes an integrated provirus.

The parameters ${\widehat{\gamma }}_{r,s}^i$ and ${\widehat{\gamma }}_{r,s}^u$ (equal to $\eta {\widehat{\gamma }}_{r,s}^i$) in the above expression is a composite of different events, including the probability that r+s viruses are transmitted, and what proportion of these viruses become integrated. To relate ${\widehat{\gamma }}_{r,s}^i$ to more tangible parameters, we express ${\widehat{\gamma }}_{r,s}^i$ as a function of the probability of integration and distribution of viruses transferred per synapse. There is little known about the factors that determine what proportion of viruses become integrated but if we assume that each virus integrates independently at probability p then ${\widehat{\gamma }}_{r,s}^i$ and ${\widehat{\gamma }}_{r,s}^u$ can be replaced with more explicit formulas, and the threshold for successful infection is now:

$$R_0=\frac{\lambda }{a_{i}d}\sum _{r=0}^N\sum _{s=1}^M{\widehat{\gamma }}^h(1-{(1-p)}^{r+s})+\frac{\eta \lambda }{a_{u}d}\sum _{r=c}^N{\widehat{\gamma }}^h{(1-p)}^r$$

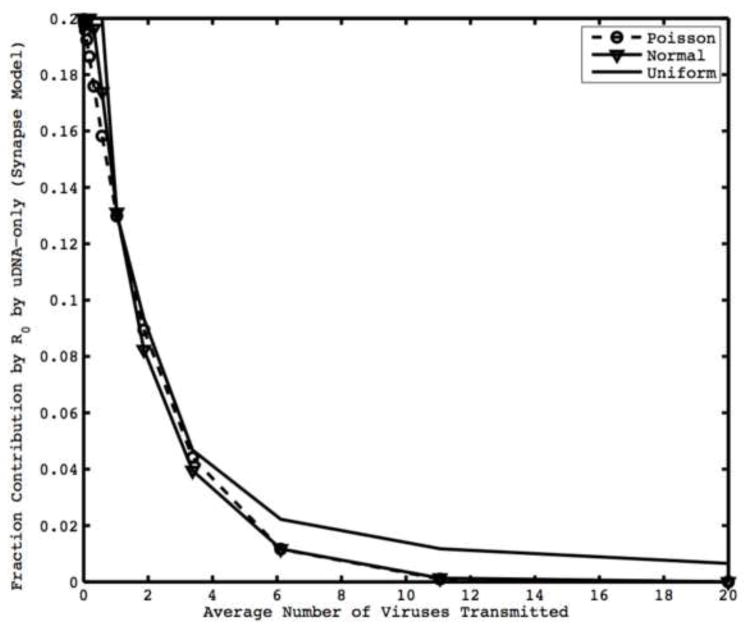
Here, γ̂_h is the probability that h viruses are successfully transferred by iDNA infected cells, where h=r+s, and η is the reduction in the rate of synapse formation of cells infected with a threshold number of unintegrated viral genomes. We can see from this expression that, if viruses integrate independently, as the average number of viruses transferred per cell increases, the relative contribution by unintegrated viral genomes decreases (Figure 2). Intuitively, if a cell transfers a larger number of viruses per synapse, the chance that at least one virus becomes integrated approaches certainty. Note that there need not be complete independence of integration between viruses for this trend to hold. This result remains robust in the context of different distributions for the probability of transferring h viruses, γ̂_h (Figure 2). Little is known about the distribution of the number of viruses transferred per synapse so we explore different commonly occurring distributions (Normal, Uniform, or Poisson). For example, if the number of successfully transmitted viruses follows a Poisson (h̄) distribution and each virus independently integrates, γ̂_h can be expanded and the R₀ for synaptic transmission is given by:

$$R_0=\frac{\lambda }{a_{i}d}\sum _{r=0}^N\sum _{s=1}^M\frac{{\overline{h}}^{r+s}{\mathrm{e}}^{-\overline{h}}}{(r+s)!}(1-{(1-p)}^{r+s})+\frac{\eta \lambda }{a_{u}d}\sum _{r=c}^N\frac{{\overline{h}}^r{\mathrm{e}}^{-\overline{h}}}{r!}{(1-p)}^r$$

Figure 2.

Fraction contribution to R₀ by cells with uDNA-only for synaptic transmission. Lines are different distributions of the number of viruses transferred per synapse. The contribution to R₀ by uDNA depends on average number of viruses transmitted but remains relatively constant with respect to the distribution of viruses transmitted. We assume that viruses integrate independently. Parameters are λ =10000, d=0.01, η=0.25, p=0.5, c=1, a_i=0.7, a_u=0.7.

According to this expression, the relative contribution of uDNA to the basic reproductive ratio of the virus not only depends on the number of viruses that are transmitted per synapse, but also on other parameters such as the number of uDNA copies required for successful replication, c, and the probability of intergration, p. These dependencies are shown in Figure 3.

Figure 3.

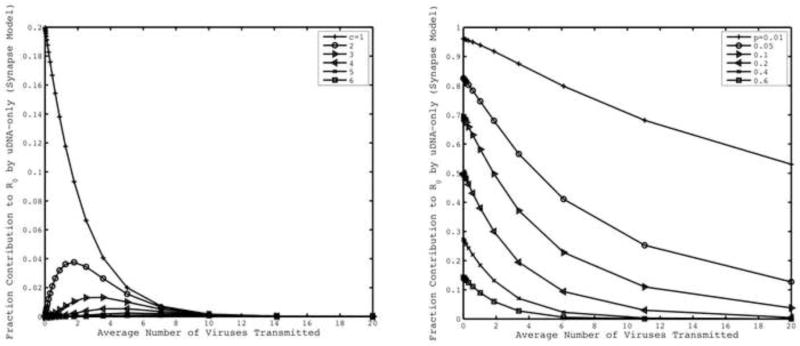
(left) Contribution of uDNA towards R₀ for synaptic transmission with varying threshold number of uDNA copies required for productive infection, c. (right) Contribution of uDNA towards R₀ for synaptic transmission with varying integration probabilities, p. We assume that viruses integrate independently and number of viruses transmitted follows a Poisson distribution. Default parameters are λ =10000, d=0.01, η=0.25, p=0.5, c=1, a_i=0.7, a_u=0.7.

Using measured parameters to estimate the relative contribution of uDNA to R₀

With the formulations derived so far, we can attempt to quantify the relative contribution of HIV-1 uDNA to the basic reproductive ratio of the virus, using parameter values as far as they are available. It is important to note that the parameter values used here are based on preliminary data that still need to be investigated in more detail, but they can be used to obtain first insights. One of the most important parameters is the virus output from cells that only contain uDNA compared to that observed in productively infected cells that contain iDNA. Following activation of infected resting T cells, it was found that during a time-span of two days, the amount of virus released from uDNA-infected cells was between 14.8% and 21.5% of that observed with iDNA-infected cells (Trinite et al., 2013). These numbers, however, do not tell the whole story because virus output was not measured during the entire life-span of the cells (which would give the “burst size” of infected cells), but only during a two hour window. Typically, slower virus replication correlates with a longer life-span of infected cells (Blankson et al., 2002; Gilchrist et al., 2004). Hence, when considering the total number viruses released during the life-span of the infected cells, it is likely that the relative contribution from uDNA-infected cells compared to iDNA-infected cells is larger than the percentages quoted above. To be conservative, we will assume that the burst size of cells only containing uDNA is 25% compared to that observed with productively infected cells that contain iDNA (this is also consistent with our current data, in preparation). Another important parameter is the probability that when a cell becomes infected and replicates, virus integration will take place. This was estimated in a separate study, where the extent of fluorescence following single-round infection with reporter viruses indicated whether cells were expressing from uDNA or from iDNA (in preparation). We found that among the viruses that will infect a cell and produce offspring virus, about 50% of the genomes are unintegrated (i.e. p=0.5). This is obviously a first estimate and we note that this figure could be revised in future research. At this stage, we do not have any solid evidence against the assumption that a single copy of uDNA can result in successful virus reproduction, so we will assume c=1.

Using these parameters, for free virus transmission, the contribution of uDNA replication to R₀ is 100*(1−p)r/(p+(1−p)r)%, where r is the ratio (k_u/a_u)/(k_i/a_i). With estimated parameter values, this contribution is found to be 20%.

For synaptic transmission, the parameterized model suggests that uDNA can contribute maximally 20% to the overall value of R₀. As mentioned above, the exact contribution depends on the average number of viruses that are successfully transmitted per synapse, a number that is currently not known. While tens to hundreds of viruses are passed through synapses, it is possible that the majority of these viruses fail to productively infect the cell. For example, the majority of viruses could end up as unintegrated virus that remains in a form in which it is a replicative dead end. These transmissions are not accounted for in our model.

Combining free virus and synaptic transmission

Finally, we can combine the results from free virus and synaptic-only transmission to arrive at the following value for R₀ for a system with both synaptic and cell-free transmission:

$$\begin{array}{l}{R}_0=p\frac{\lambda \beta k_i}{a_{i}ud}+\frac{{\beta }_{si}\lambda }{a_{i}d}+\frac{{\beta }_{su}\lambda }{a_{u}d}\\ {\beta }_{su}=\sum _{r=c}^N{\widehat{\gamma }}_{r,0}^u,{\beta }_{si}=\sum _{r=0}^N\sum _{s=1}^M{\widehat{\gamma }}_{r,s}^i\end{array}$$

Note that this expression is simply the sum of the R₀ from the cell-free and synaptic transmission models. Although we can estimate the contribution of unintegrated viral genomes to R₀ for both cell-free and synaptic transmission independently, little is known about the relative importance of synaptic and cell-free transmission at the start of infection.

Discussion

Our experimental data have shown that cells infected with HIV-1 genomes that never integrate can nevertheless successfully replicate the virus under specific conditions (Gelderblom et al., 2008; Trinite et al., 2013). Particularly, this phenomenon is observed if resting cells are infected that are subsequently activated (Trinite et al., 2013). We envision this scenario might be particularly important to the initial establishment of the infection, when the virus is seeking to establish a foothold and existence is precarious. At or near sites of virus entry, infection of resting T cells is likely to be a dominant way for the virus to spread (Haase, 2005; Li et al., 2005; Miller et al., 2005; Reilly et al., 2007; Zhang et al., 1999). Therefore, the question arises to what extent uDNA replication contributes to the basic reproductive ratio of the virus and thus to the ability of the virus to successfully grow from low numbers. Based on mathematical models that were partly parameterized with preliminary data, we made a first attempt to answer this question. According to this analysis, the answer depends on the transmission pathway by which the virus spreads through the target cell population. For free virus transmission, uDNA replication was found to contribute about 20% to R₀, while with synaptic transmission, the percentage depends on the number of viruses that successfully infect a cell through the synaptic pathway, with the maximum possible contribution being around 20%. These numbers obviously depend on the parameter estimates which, as mentioned before, are still preliminary in nature and require further investigation.

This result can be interpreted in a variety of ways. Let us assume that uDNA replication contributes 20% to R₀. According to the latest estimates, the basic reproductive ratio of HIV-1 was found to be around R₀=8 (Ribeiro et al., 2010). In this case the predicted R₀ resulting from the replication of only iDNA would be R₀⁽ⁱ⁾=6.4, and the predicted R₀ resulting from uDNA replication would be R₀^(u)=1.6. On the one hand, uDNA contributes relatively little to R₀. If no uDNA replication occurred at all, the virus would still reliably establish a persistent infection. On the other hand, if all virus replication stemming from integrated DNA was inhibited, the basic reproductive ratio of the virus would still be greater than one, promoting virus persistence, even though the replication kinetics are significantly slower. This has important implications for the use of integrase inhibitors (such as raltegravir) in a prophylactic setting that aims to prevent the infection from becoming established. According to the numbers derived here, integrase inhibitors might be at a disadvantage compared with drugs that intervene at other stages of the virus replication cycle (entry, reverse transcription, maturation), although integrase inhibitors are not typically administered alone. Our calculations also have implications for the viral response to integrase inhibitors during chronic infection. When virus loads are high during chronic infection, the contribution of uDNA to viral replication is probably negligible because most susceptible cells are activated T cells. When virus load has been reduced to very low levels by drug therapy, however, resting T cells might be important targets for the virus. It is possible that at low virus loads, uDNA replication provides an important mechanism by which the virus can persist at low levels in the face of continuous integrase inhibitor therapy. This is an interesting notion in the light of studies that analyzed virus dynamics during raltegravir intensification of HAART therapy (Buzón et al., 2010; Llibre et al., 2012). It is thought that during traditional HAART therapy (not utilizing integrase inhibitors), a certain amount of low level virus replication continues to occur in a subset of patients, contributing to viral persistence during treatment. When raltegravir is added to the treatment regimen, accumulation of episomal HIV-1 DNA is observed in some patients, indicating recently infected cells^{27, 28}. At the same time, however, ultrasensitive virus load measurements in the same patient remained stable despite the addition of raltegravir (Llibre et al., 2012). This could indicate that at those low levels, uDNA replication counters the effect of raltegravir treatment, contributing to the stable maintenance of virus load. It is important to note, however, that the dynamics of residual virus replication are complex, influencing not only virus growth but also CD8 T cell activity (Llibre et al., 2012), which can also affect the observed amount of virus load during treatment. The dynamics of residual virus replication and the effect of raltegravir intensification have also been recently studied mathematically in a different context (Luo et al., 2013).

It has to be pointed out that the basic reproductive ratio of HIV-1 has been measured during the exponential growth phase of the virus population that occurs in the primary phase of the infection. It is unclear, whether this represents the correct replication kinetics in the very early stages of the infection. It is possible that during the observed exponential growth phase, virus replication is faster than during the very early stages of the infection, because mainly activated T cells are the targets of infection. If the basic reproductive ratio in the crucial early phase of the infection is lower, then the R₀ resulting from uDNA replication might be less than one. On the other hand, it has been reported that mathematical models assuming a time delay between infection and virus production give rise to higher estimates for R₀ (Nowak et al., 1997). For SIV infection, the maximal R₀ calculated assuming a time delay of 24 hours was reported to be 68 (Nowak et al., 1997). In this case, uDNA replication alone could surely maintain a persistent infection. More detailed kinetic data, especially about the earliest stages of the infection, are needed to make more definite statements.

As is clear from this discussion, parameter estimates and the interpretation of our calculations remain uncertain due to lack of sufficient data at this stage. This analysis, however, serves as a guide for further experimental work to directly measure crucial parameters that will allow more precise calculations.

Finally, we would like to comment on an aspect of our work that was repeatedly discussed throughout the paper: the multiple infection of cells. In our model, we allowed cells to be simultaneously infected with i unintegrated and j integrated viruses. While multiple infection is not a central focus of our study, it enters in the context of certain assumptions. First, if a cell contains both uDNA and iDNA in the model, viral replication occurs at a rate driven by the iDNA (Gelderblom et al., 2008). Second, we also considered the possibility that multiple uDNA genomes per cell are required to initiate successful viral replication. There is ample evidence from in vitro studies that multiple HIV-1 particles can infect the same cell (Chen et al., 2005; Dang et al., 2004; Del Portillo et al., 2011; Levy et al., 2004). This is further accentuated by work demonstrating that synaptic transmission leads to the simultaneous transfer of tens to hundreds of viruses from the source cell to the target cell (Chen et al., 2007; Del Portillo et al., 2011; Hubner et al., 2009; Jolly et al., 2004; Rudnicka et al., 2009; Sattentau, 2008). The relevance of these processes in vivo are a little less clear. Multiple infection was shown to occur during virus growth in animal models (Levy et al., 2004). In a clinical setting, cells from the spleen of infected patients were shown to contain on average 3–4 proviruses (Jung et al., 2002). Other studies, however, argued that most cells in the blood and tissue are singly infected (Josefsson et al., 2013; Josefsson et al., 2011). The reason for this discrepancy is not known, although it could lie in different T cell subsets examined or from more rapid death of cells containing multiple genomes. However, the occurrence of viral recombination, and the likely contribution of this process to viral evolution in vivo indicates that multiple infection is also an important driving force in vivo (Jung et al., 2002; Levy et al., 2004; Neher and Leitner, 2010).

Supplementary Material

supplement. Text S1.

Mathematical details of the models discussed in the paper.

We use models to estimate the effect of unintegrated viral DNA on the R₀ of HIV. For free virus transmission, uDNA might contribute 20% to the total R₀. Under some assumptions, calculations suggest that R₀=1.6 without integration. If more than one uDNA copy is needed, uDNA does not contribute to cell-free R₀. For synaptic transmission, uDNA can contribute to R₀ at any copy number.