Decorrelation of retinal response to natural scenes by fixational eye movements

Significance

Our observation provides the first direct experimental confirmation, to our knowledge, of the prediction that fixational eye movements act to reduce the correlations in retinal response. Reduction of correlation was suggested as a design principle in the visual system a long time ago. It was argued that efficient representation of sensory information requires reducing the amount of redundancy in the neural response. Although these works are considered to be cornerstones of our understanding of visual processing, they still do not consider the actual input to the retina. Our result contributes to these classic works by showing that the amount of correlation in the retinal output can be reduced by the patterns of eye movements prior to any neural processing.

Abstract

Under natural viewing conditions the input to the retina is a complex spatiotemporal signal that depends on both the scene and the way the observer moves. It is commonly assumed that the retina processes this input signal efficiently by taking into account the statistics of the natural world. It has recently been argued that incessant microscopic eye movements contribute to this process by decorrelating the input to the retina. Here we tested this theory by measuring the responses of the salamander retina to stimuli replicating the natural input signals experienced by the retina in the presence and absence of fixational eye movements. Contrary to the predictions of classic theories of efficient encoding that do not take behavior into account, we show that the response characteristics of retinal ganglion cells are not sufficient in themselves to disrupt the broad correlations of natural scenes. Specifically, retinal ganglion cells exhibited strong and extensive spatial correlations in the absence of fixational eye movements. However, the levels of correlation in the neural responses dropped in the presence of fixational eye movements, resulting in effective decorrelation of the channels streaming information to the brain. These observations confirm the predictions that microscopic eye movements act to reduce correlations in retinal responses and contribute to visual information processing.

Much effort has been devoted to understanding how the neural code of the retina and downstream neurons can represent visual information efficiently given the statistical structure of the natural world (1–6). Although these theories have contributed tremendously to current understanding of early visual processing, they do not consider the observer’s motor activity but rather rely on the simplifying assumption that the input to the retina is a stationary image. However, even during fixation on a single point, small movements of the eye, head, and other parts of the body continually modulate visual input signals. Experiments have shown that elimination of retinal image motion leads to fading of vision (7, 8). Therefore, eye movements are essential for the normal functioning of the visual system.

It has been proposed that, rather than simply preventing adaptation in neural responses, fixational eye movements are a critical stage of information processing, in which predictable spatial correlations are discarded to enable encoding of luminance discontinuities by synchronous neural activity (9, 10). Thus, fixational eye movements counterbalance the spectral density of natural scenes and yield temporal modulations with equalized power over a broad range of spatial frequencies. Because spectral equalization is equivalent to decorrelation in space, this theory predicts that fixational eye movements should attenuate correlations in the responses of the retinal ganglion cells. Modeling results have provided support to this hypothesis (9, 10).

Results

To test the theoretical prediction that microscopic eye movements act as an information processing stage we conducted measurements on an isolated salamander retina (Methods) exposed to natural images with and without eye movements. We estimated pairwise correlations in the responses of ganglion cells when images of natural scenes were presented statically (the “stabilized fixation” condition) or moved in a way that simulated fixational eye movements (the “fixational instability” condition). Ganglion cell responses were measured using a planar array with 252 microelectrodes (Methods). A total of 142 ganglion cells from four isolated retinas of four different salamanders were used for analysis. Figs. 1–4 present our analysis for one dataset composed of 37 cells. The stimulus movie incorporated 10 natural images (11). Each image was projected on the photoreceptor layer and then moved across the screen to simulate fixational eye movements (Methods).

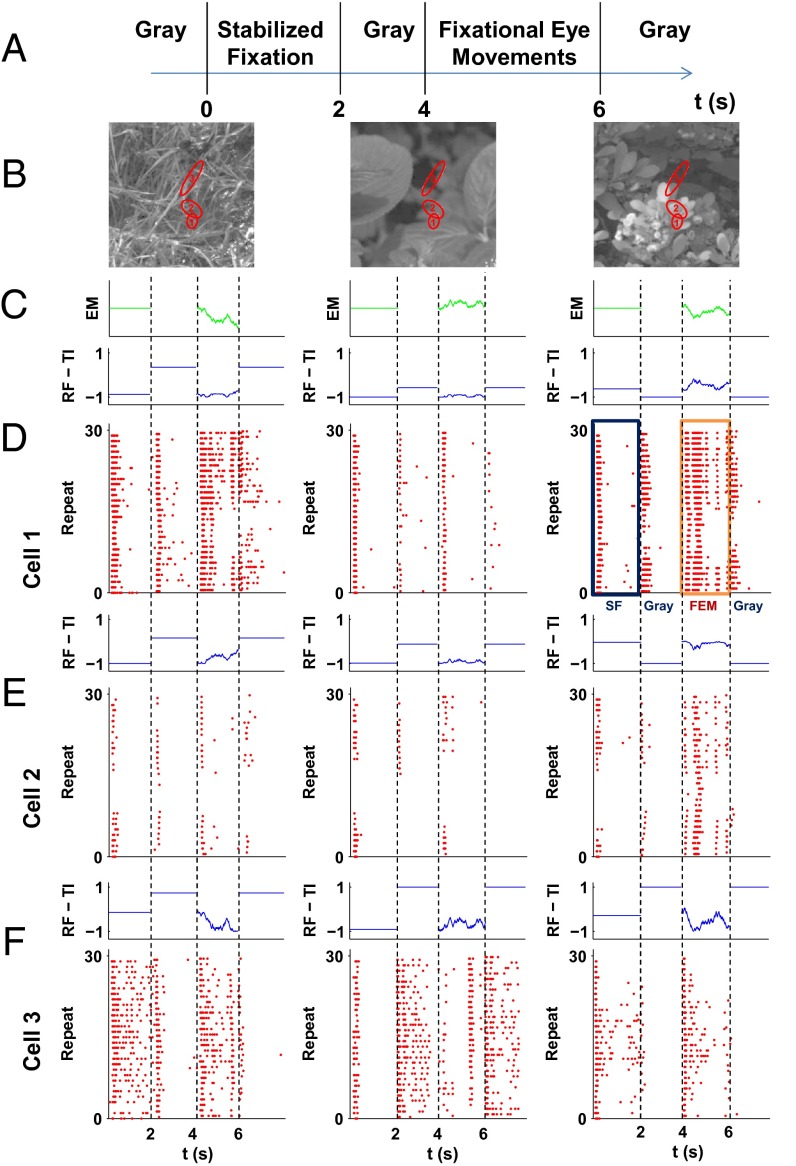
Fig. 1.

Several examples of retinal ganglion cell responses to fixational eye movements superimposed on natural images. (A) An example of the stimulus. At time (t) = 0 s, the image is flashed on the screen and remains static for 2 s. At t = 2 s, the image is replaced with a uniform gray screen for a random interval period of 1.5–2 s, then the fixational eye movements start for 2 s. At an average of t = 6 s, the image is replaced with a uniform gray screen again, with a random interval period of 1.5–2 s. (B) Examples of natural scenes that were used in the experiments. Red ellipses represent the 1-σ radius of receptive fields of selected cells. (C) The trace of fixational instability used for each image. (D–F) Top panels show the change in total illumination in each of the cells’ receptive fields due to the movement. Bottom panels are raster plots of the activity of the cells shown in B in response to the stimulus sequence. All cells responded to the onset of a new image. This onset response extinguished shortly after the image onset. The fixational eye movements evoked a different pattern of responses: They were not synchronized across cells and lasted for the entire segment.

Fig. 4.

Theoretical analysis shows that retinal nonlinearity sets the correlation structure. (A) We calculated the dependence of the correlations on distance in the retinal output as a function of fixational instability vs. the stabilized fixation. Both curves were obtained by numerical integration (Supporting Information, sections 1–6). Fixational instability resulted in a steeper curve, which reduced the correlations to values within two characteristic receptive field sizes, whereas the correlations in the stabilized fixation conditions extended to much larger distances. (B) We simulated the activity of identical cells uniformly distributed across the visual field with a slightly random shift under the assumption of a linear–nonlinear response function. The linear–nonlinear model fit the data well. This is an indication that nonlinearity may determine the correlation level in the retinal output.

Fig. 1A shows the schematic structure of the stimulus sequence. Images were displayed statically for 2 s (stabilized fixation period), which was later used to assess the retinal response to the correlational structure of the natural scene itself. The static image was followed by 1.5–2 s of a full-field flash of gray image. Then the same static image moved according to a simulated fixational eye movement trace for two more seconds. Finally, another full-field flash of gray image was presented. The 2-s interval was selected to replicate the frequency with which the salamander saccades or blinks under natural conditions (12). Salamander fixational eye movements were simulated by random walks, as proposed by Ölveczky et al. (13). This approximation replicates the observation that the mean square displacement of the line of sight grows linearly with time in the salamander (14), as it does in humans (10) (Methods). Fig. 1B presents examples of the natural scenes with representative receptive fields from the experiment superimposed. Fig. 1C shows examples of the eye movement traces used in the experiments.

Three examples of responses of retinal ganglion cells to the stimulus movie are presented in Fig. 1 D–F, together with the total mean intensity within the receptive field of an individual cell. Although individual cells differed considerably in their selectivity, most ganglion cells responded with a burst in activity to the appearance of a new image. The latency of this burst was 40–50 ms. Responses then quickly decayed to the level of spontaneous activity within about 500 ms. This response pattern is expected, because ganglion cells are highly sensitive to time-varying input signals and do not respond well to stationary stimuli. Thus, the onset of the image triggered broadly synchronized responses across the entire retina.

A markedly different pattern of retinal activity emerged during fixational eye movements. Cells responded with sporadic firing events over the course of stimulus presentation, yielding lower levels of mean responses and a much sparser pattern of activity in the retina (Fig. 1 D–F). Although rare, spiking events were highly reliable across trials. Because they depend on image identity, they could not be attributed to noise; rather, they were clearly driven by the fixational modulations of luminance experienced by each cell. As a result, responses were overall less synchronized and no longer limited to the brief interval following the onset of the stimulus, as in the case of the static image presentation.

To examine the impact of eye movements on correlated activity, we analyzed cell responses during the two periods of stabilized fixation and fixational eye movement (rectangles in Fig. 1D, Right) separately. We first calculated the peristimulus time histogram (PSTH) for each segment (with a time bin of 10 ms) and then estimated, for each pair of available cells, the correlation between their mean instantaneous firing rates.

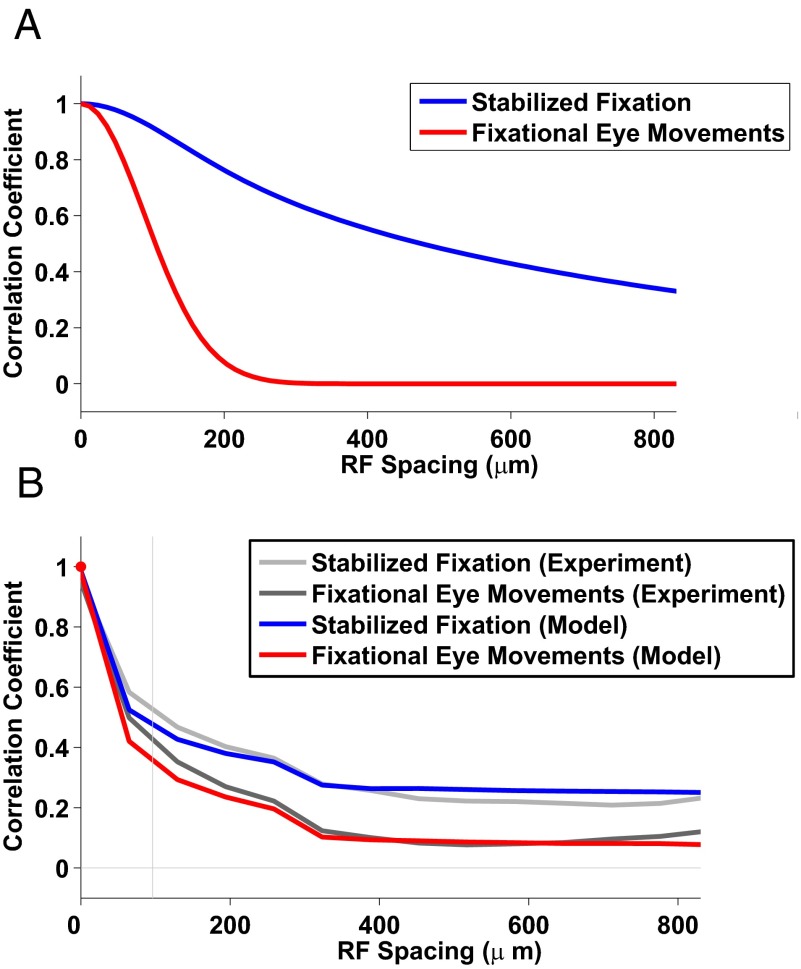
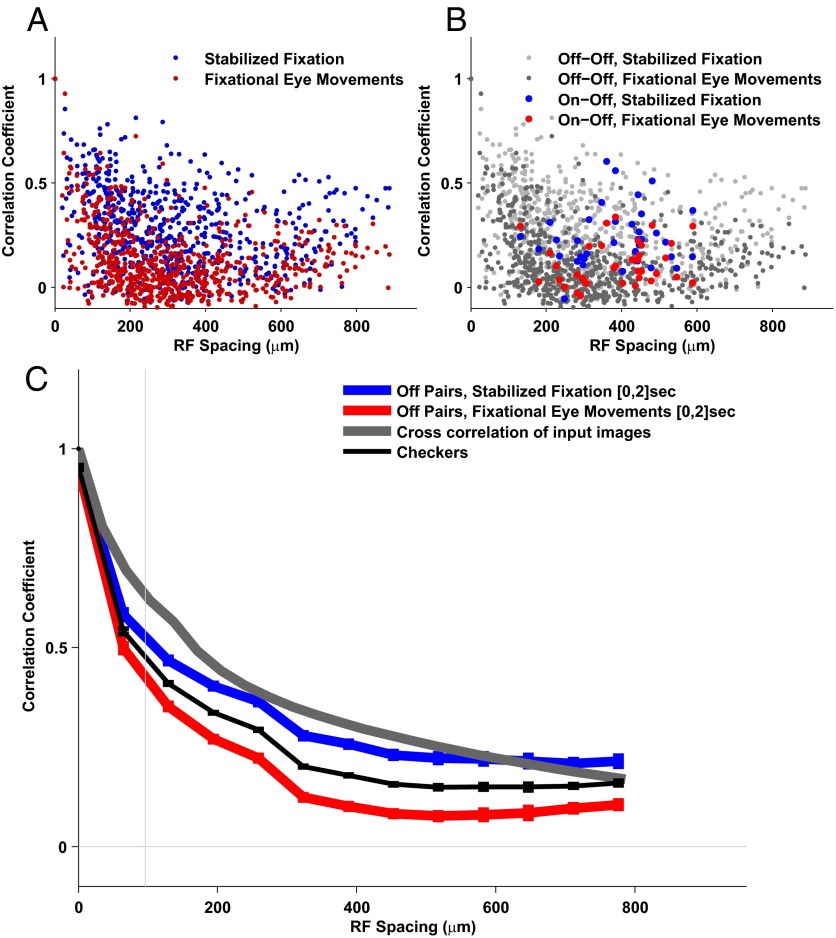
We found that the pairwise correlations were lower in response to fixational eye movements than during the static presentation of the same set of natural images. In the stabilized fixation condition significant correlations occurred even between neurons with distant receptive fields (Fig. 2A). In contrast, the spatial distribution of the correlations was narrower in the presence of eye movements, so that only cells with nearby receptive fields exhibited highly correlated responses (Fig. 2A). As shown in Fig. 2B, this effect was visible for pairs of neurons with similar (“Off–Off”) and opposite polarity (“On–Off”) (data from On–On pairs are not shown because too few cells of this type were present in the recordings).

Fig. 2.

Fixational eye movements strongly influence the spatial structure of correlations in retinal ganglion cell activity. (A) Pairwise correlation as a function of the receptive field distance. The correlation functions in response to the fixational eye movement stimulus were generally lower than the response to stabilized fixation. The correlation was significant even for distant pairs of cells for fixational eye movements. (B) Same as A; On–Off pairs and Off–Off pairs are shown separately. (C) Mean values of correlation for pairs of cells with similar receptive field spacing. The correlation for stabilized fixation decreased slowly with increasing distance and remained significant for distant cells. In the presence of fixational eye movements, the level of correlations dropped, as proposed by the theory. Only pairs of the same type (Off–Off) were used. The vertical line represents the mean receptive field size.

Fig. 2C summarizes the average structure of correlated activity as a function of the distance between receptive fields. Each data point represents the correlation values of all pairs within 50-µm overlapping windows up to 1,000 µm, approximately 10 times the mean radius of the recorded receptive fields.

Spatial correlations were highly influenced by fixational eye movements. Static presentations of natural images yielded highly correlated responses even for pairs of cells with distant receptive fields. This effect was presumably caused by the broad spatial correlations inherent in natural scenes, which expose neurons to similar input signals even when their receptive fields are relatively far apart. In contrast, levels of correlations were significantly attenuated when the same images were observed in the presence of fixational eye movements (Fig. 2B). These results suggest that spatiotemporal reformatting of visual input signals caused by fixational eye movements critically affected the correlated activity in the retinal output.

It should be emphasized that our results contribute to the predictions of classic theories of efficient encoding theories (3–6) that do not take eye movements into account. According to these theories, spatial filtering by retinal ganglion cells should be sufficient to disrupt the broad correlations of natural scenes. Our data show that retinal ganglion cells exhibited spatial correlations in the absence of fixational eye movement and eye movements can reduce the correlation in the retinal output.

To evaluate the structure of correlated activity with respect to reference benchmarks, we stimulated the retina with a random black and white checkerboard (measuring 120 μm on the side) in the absence of eye movements. This stimulus can be considered an approximation of spatial white noise that can elicit cell responses: It exhibits strong short-range correlations owing to the size of the single checkers but no long-range correlations (Fig. 2C).

We also calculated the normalized average cross-correlation and also the correlations of the input images (Fig. S8). The correlation (where the mean was not subtracted) describes the correlation that would be relevant if stabilized fixation would follow a gray level different from the spatial mean of the image intensity and illustrates the long-range correlations owing to the mean in the stimulus. The lower cross-correlation curve, for which the spatial mean of the image intensity was subtracted (Methods), is relevant for the case where the gray level is adjusted to this mean (that is, similar to the experimental setup). In the second case the correlation drops to zero at large distances. This would be also the case for the retina response if it were linear. Nonlinearity (the response is always positive whereas the input may be negative) keeps nonzero long-range correlations. These issues are discussed in Supporting Information, section 4. The difference between the correlation pattern in the stabilized fixation and the cross-correlation of natural images is due to the receptive field structure (4).

We found similar behavior when comparing the correlation pattern due to fixational instability in the full 2-s interval and partial fixational, second half of the interval, eye movement periods (Fig. S8). This is an indication that onset response during fixational eye movement is not significant in setting the correlation profile.

However, when we used the second half of the interval in the stable fixation case the retina fired spontaneously and the activity was not derived by the stimulus. As expected, the correlation pattern was changed. This result also indicates that indeed the fixational eye movements reduce correlation due to natural scenes but do not reduce it below the correlations that are observed during spontaneous activity, which could be solely attributed to the shared circuitry between retinal ganglion cells.

To summarize, we found experimentally that fixational eye movements effectively narrow the spatial extent of correlated activity between retinal ganglion cells. Pairs of neurons with distant receptive fields no longer exhibited correlated responses when natural images were viewed in the presence of normal fixational instability. This reduction in correlation did not come at the expense of a reduction in the precision of the neural code: In line with previous reports (15), neurons tended to fire very precisely during normal viewing of moving natural stimuli (Fig. 1).

To what extent does the decorrelation we found depend on the detailed structure of the fixational eye movements we used in the experiment? This is a key question because fixational instability can be achieved by many different mechanisms, such as various types of eye movements (e.g., drift or tremor) and movements of other parts of the body. Therefore, the structure of fixational instability can vary across time and across individuals. Theoretical considerations suggest that the effect should be highly robust with respect to the precise pattern of eye movements. To show this, we calculated the expected functional dependence of the correlations in the two cases: regular and enlarged fixational eye movement patterns (Methods). This was done by calculating the theoretical power spectrum of the response in the two cases. As a first step, we calculated the spatiotemporal frequencies of a typical ganglion cell and multiplied it by the spatiotemporal frequencies of the two patterns with our inputs. This yielded the spatiotemporal profile of the response in the two conditions: one-dimensional eye movement that was simulated by a random walk approximation with a regular diffusion constant (1X condition, Fig. 3A) and enlarged random walk with a diffusion constant 16 times larger than the standard diffusion constant (16X condition, Fig. 3B). Fig. 3C presents the power spectrum of the retinal responses in the presence of the two patterns of eye movements.

Fig. 3.

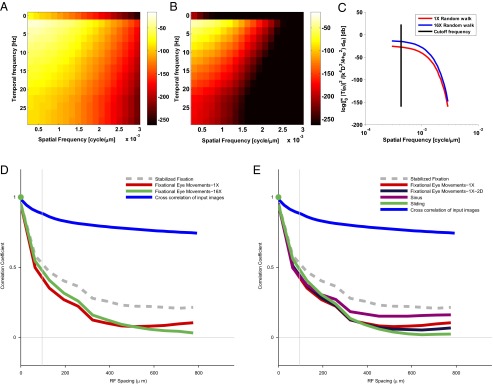
The spatial correlation pattern with different motion parameters. (A) The spatiotemporal response of the retinal output for the 1X eye movement condition. (B) The spatiotemporal response of the retinal output for the 16X eye movement condition. (C) The logarithmic plot of the output power spectrum of the spatial frequencies, where we summed over temporal frequencies to obtain the dependence on the spatial frequencies alone. (D) Mean correlation in response to enlarged (16X) eye movements, compared with the motion pattern in Fig. 2. The drop of the correlation was not strongly associated with the amplitude of the motion. (E) Correlations in response to various types of motion: 2D eye movements, sinusoidal motion, and sliding motion. The differences in the pattern of correlation between different types of motion are small compared with the stabilized fixation response.

Fig. 3C shows that below the cutoff frequency the responses in the two conditions were roughly constant. Thus, independent of the characteristics of eye movements, the expected spatial correlation was expected to be similar, because cells were exposed to similar whitened input within their range of sensitivity. In line with this prediction, similar patterns of correlation were observed for several types of small-amplitude movements, including the enlarged random walk (Fig. 3D, 16X and 1X conditions, respectively), the 2D random walk movement and sinusoidal movements, and a smooth monotonic sliding of the image in a single direction (Fig. 3E). These results may indicate that the decorrelation by fixational eye movements is robust over a broad range of motion characteristics.

Next we attempted to determine the critical mechanisms that produced the decorrelation observed in the experiment. For this purpose we first analyzed theoretically, under simplified assumptions, the expected effect of fixational eye movements on the pattern of correlations in the retinal output (see Supporting Information, section 4 for details). The theoretical estimates of correlated activity based on a linear model indicated that the spatial extent of the correlations should decrease faster with receptive field (RF) separation than the levels measured in the retina (Fig. 4A and Supporting Information, sections 1–3). That is, pairs of neurons with an RF at a distance of about 100 µm to were expected to exhibit practically uncorrelated responses in the fixational eye movement condition. However, higher levels of the correlations were obtained in the experiments. Specifically, the theoretical results dropped off quickly to zero, whereas the experimental curves dropped slowly over an extended range (Fig. 2C).

To better understand the disparity between the experimental and theoretical results we introduced a static nonlinearity (a form of rectification) into the model. This nonlinearity was included because center-surround antagonism alone cannot account for the persistent correlations found experimentally in both cases. Specifically, the center-surround antagonism should have reduced the long-distance correlations for stabilized fixation but left the long-distance correlations for fixational eye movements at zero level. We generated a theoretical prediction of the retinal output by simulating the cellular response for a population of model cells in response to the same stimulus the retina was exposed to in the experiments (Methods). Cells were uniformly distributed across the visual field with a random shift from a grid. The linear–nonlinear model had three parameters corresponding to the size of the center, the size of the surround, and their relative amplitude. Model parameters were fitted based on the experimental data obtained in the stabilized fixation condition and tested on the data from the fixational eye movement condition. This served as a control that the basic neuronal nonlinearity was captured by the model. Similar results were also obtained with several types of nonlinearity, thus showing that the form of the nonlinear function does not affect the result (Supporting Information, section 6).

We found that the model result fitted the experimental results well (Fig. 4B). This includes both the correlation patterns in the stabilized fixation and the fixational instability case. The correlation structure in the computational model for the stabilized fixation was higher than the correlation for the fixational eye movement, suggesting that nonlinear mechanisms contribute to attenuating correlations over long distances.

Discussion

Our results indicate that the incessant small eye movements that occur during visual fixation are a critical component of the code coding visual information by the retina. In keeping with previous findings (16) and contrary to the predictions of classic theories (4–6), the responses of retinal ganglion cells here were strongly influenced by the broad correlations of natural images in the absence of fixational eye movements. In contrast, fixational eye movements reduced the level of the correlations in the responses of distant retinal ganglion cells to natural scenes, an effect that was very robust with respect to the specific characteristics of retinal image motion.

Barlow’s proposal that a critical function of the early visual system is to reduce redundancy (16) led to the notion that the RF structure of the retinal ganglion cell is designed to counteract the correlated structure of natural images (5). However, some level of redundancy is beneficial when dealing with noise, and ganglion responses show high levels of redundancy when stimulated with natural movies (16). Our results along with those reported in Puchalla et al. (16) suggest that there is a delicate tradeoff between efficiency and reliability in the representation of visual information by the retina. In addition, a recent study (17) claimed that decorrelation does not primarily take place in the receptive field structure, but also by nonlinear processing in the retina. Finally, the receptive field size of salamander retinal ganglion cells extend to 2–3° of visual angle. This is much wider than the receptive fields of other animals used for visual processing studies. This implies that our results may hold for a wide range of receptive field sizes.

We showed that correlations in the retinal output can be reduced not only by the structure of center-surround antagonistic receptive field structure and nonlinear retina response but also by patterns of eye movements. For this effect to occur we need to assume very little about the exact patterns of fixational instability as long as they are small compared with receptive field average size. In addition, with the appropriate fixational instability the correlation is reduced considerably such that the overall effect of the fixational instability is strong.

The fixational eye movement decorrelation theory makes the specific prediction that fixational eye movements progressively decorrelate neural responses during the course of natural postsaccadic fixation (18). Specifically, the theory predicts that after an initial postsaccadic transient with broad spatial correlations the extent of correlation drops down to a level similar to that given by spontaneous activity. It is important to observe that a similarity in the structure of correlated activity with white noise does not imply that fixational eye movement responses do not convey useful information. Fig. 1 shows that cell responses are highly structured and reproducible during fixational eye movemnt; they are simply sparser, to a level comparable to that of spontaneous activity.

Finally, it should be noted that according to (13), most Off cells recorded from salamander retina are fast Off cells that are also object motion-sensitive cells. However, it should be noted that even if most cells belong to this population we still find great differences in their responses with and without fixational eye movements. However, this raises the importance of cross-species validation of our findings in the salamander in the future.

Methods

Electrophysiology.

Multielectrode array recordings (19, 20) were performed on adult Spanish ribbed newts (Pleurodeles waltl). All experiments were carried out according to the regulations of Ben-Gurion University of the Negev and the laws of the State of Israel. The experiment began by first adapting the salamanders to bright light for 30 min. Retinas were isolated from the eye and peeled from the sclera together with the pigment epithelium to ensure long and stable recordings. Retinas were placed with the ganglion cell layer facing a multielectrode array with 252 electrodes (Ayanda Biosystems) and superfused with oxygenated (95% O₂/5% CO₂) Ringer medium containing 110 mM NaCl, 22 mM NaHCO₃, 2.5 mM KCl, 1 mM CaCl₂, 1.6 mM MgCl₂, and 18 mM glucose, at room temperature. The electrode diameter was 10 µm and electrode spacing ranged from 40 to 80 µm. Recordings of up to 10 h were achieved consistently. Extracellularly recorded signals were amplified (MultiChannel Systems), digitized at 10 kHz on four personal computers, and stored for off-line spike sorting and analysis. Spike sorting was done by extracting the amplitude and width from each potential waveform, followed by manual clustering using an in-house program written in MATLAB.

Stimulation.

The stimuli were projected onto the salamander retina from a liquid-crystal display video monitor (VX2268wm; ViewSonic) at a frame rate of 60 Hz using standard optics. The stimulus movies were presented in grayscale. Ten natural images were selected from the Van Hateren Natural Image Database (11) and cropped to 200 × 200 pixels, which covered a square of 2,000 µm on the side on the retinal plane. The average power spectral density of the 10 natural images showed the expected 1/f^α with α ∼2.

The sequence of stimuli was as follows: An image was flashed and remained static for 2 s then was replaced by a uniform gray screen for a random period between 1.5 and 2 s, and then the previously flashed static image was presented with movement for 2 s, then replaced again by a plain gray screen for a random period between 1.5 and 2 s. The rationale behind this selection of stimuli was to maintain identical conditions. The gray level was adjusted to match the mean light intensity of the whole set of natural images. Several types of movement were used: (i) Fixational eye movements were simulated according to the approximation developed by Ölveczky et al. (13), based on the measured eye movement of the salamander (12). Specifically, we simulated the salamander eye movements as a random walk with a step size of 1 pixel (12 µm) every 1/60 s. (ii) Enlarged fixational eye movement with a step size of 48 µm. (iii) Random walks in two dimensions, parameters as in the basic experiment. (iv) Sinusoidal motion with an amplitude of 200 µm and a frequency of 5 Hz. This preserved the same mean square displacement as in the regular fixational eye movements. (v) Sliding motion in a single direction, by moving the image by 1 pixel (12 µm) every 1/60 s. The uniform gray segments, which were used between natural images, were projected for a random duration, distributed uniformly between 1.5–2 s, to prevent the locking of the response to a constant rate in the stimulus.

In addition, the theoretical analysis (9) predicted the retinal spatial correlation pattern in response to artificial stimuli with minimal spatial correlations. In the experiment, uncorrelated images were produced as random black and white checkerboards, where each checker had a side of 10 pixels (120 µm on the retinal plane). The stimulus power spectrum of the checkerboard was flat up to a cut- off frequency. These “white noise” images were projected in the same manner as the natural images, stabilized fixation for 2 s, followed by a gray image and then fixational eye movement for 2 s, and finally the gray image again.

Determination of the Receptive Fields.

The location of the receptive field of each cell was found by stimulating the retina with a random checkerboard for 45 min and calculating the spike-triggered average (STA) of the stimulus. The dot product of each location with the best STA was fitted with a 2D Gaussian to find the receptive field center and size. The average size was found to be ∼80 µm.

Data Analysis.

We calculated the average firing rate (PSTH) over 49 repetitions of each stimulus movie and split the results into two sets of responses: the stabilized fixation response and the fixational eye movement response. Then, we calculated the pairwise correlation (correlation coefficient) between two cells’ PSTH using Eqs. S4, S5, S15, and S16 in Supporting Information. The time windows used for correlation calculation contain the full 2-s stabilized fixation segment and the full 2-s fixational eye movement as described in Fig. 1A. For each pair of cells the spacing was calculated as the distance between the centers of the receptive fields. Mean correlation values were calculated using overlapping 100-µm windows and normalized by the average correlation in the first time bin near zero. This maximal distance was selected because at longer distances there were fewer pairs owing to the size of the multielectrode array.

Calculating Correlations of Natural Scenes.

We calculated the correlations and cross-correlations of natural scenes (21) (Fig. 2C). The difference between those terms is the subtraction of the DC component. Particularly, the correlation for a single image was calculated by using the following formula:

$$corr\left(u,v\right)=\frac{{\mathrm{\sum }}_{\mathit{x},\mathit{y}}\left[f\left(x,y\right)\right]\left[f\left(x-u,y-v\right)\right]}{{\left\{{\mathrm{\sum }}_{\mathit{x},\mathit{y}}{\left[f\left(x,y\right)\right]}^2{\left[f\left(x,y\right)\right]}^2\right\}}^{0.5}}.$$

For the cross-correlations we used this formula:

$$CC\left(u,v\right)=\frac{{\mathrm{\sum }}_{x,y}\left[f\left(x,y\right)-{\overline{f}}_{u,v}\right]\left[f\left(x-u,y-v\right)-{\overline{f}}_{u,v}\right]}{{\left\{{\mathrm{\sum }}_{x,y}{\left[f\left(x,y\right)-{\overline{f}}_{u,v}\right]}^2{\left[f\left(x,y\right)-{\overline{f}}_{u,v}\right]}^2\right\}}^{0.5}}.$$

Then, we averaged across our image dataset and used a sliding window to get the correlation as a function of distance. It is important to note that cross-correlations are used for removing the constant component from the power spectrum. Because the stimulus consists of gray field followed by natural image, the cross-correlation reflects the input better than just raw natural images.

Fitting the Theoretical Model to the Experimental Data.

To better understand the basic mechanisms that can explain the correlations as a function of distance for the stabilized fixation and fixational eye movements, we analyzed a linear and a static linear–nonlinear model. We modeled the receptive field of each neuron with two normalized Gaussians corresponding to the center and surround. The surround term has an amplitude parameter that controls the height of the Gaussian:

$$RF=\frac{1}{{\sigma }_{Center}}exp\left\{-\frac{{\left(x-x_{Center)}\right)}^2}{2{\sigma }_{Center}^2}\right\}-\frac{A}{{\sigma }_{Surround}}exp\left\{-\frac{{\left(x-x_{Surround)}\right)}^2}{2{\sigma }_{Surround}^2}\right\}.$$

Cells were uniformly distributed across the visual field with a random shift from a grid. For each neuron we calculated the generator function by convolving the input with the neuron’s receptive field. The estimated firing rate for the linear model was the raw generator signal, and for the nonlinearity model this result was transformed into a static nonlinearity with a threshold at zero. The final output of the nonlinear model was obtained by the rectifying function

$$\tilde{O}\left(x,t\right)=\{\begin{array}{rr}\hfill O\left(x,t\right),& \hfill O\left(x,t\right)<0\\ \hfill 0,& \hfill \mathrm{otherwise}\end{array}.$$

These models have three parameters overall that correspond to the size of the center, the size of the surround, and their relative amplitude. To obtain the parameter estimates we used a convex-simplex optimization process.

Predicting the Correlation Pattern in Eye Movements with Larger Amplitudes.

Following Kuang et al. (10) the spatiotemporal power spectrum of the retinal ganglion cell output is given by

$${\left|O\left(K,\omega \right)\right|}^2=S\left(K,\omega \right)\cdot {\left|RF\left(K,\omega \right)\right|}^2,$$

where $S(K,\omega )$ is the input power spectrum of a natural image during Brownian motion and is given by

$$S\left(K,\omega \right)=\frac{D}{\frac{K^4{D}^2}{4}+{\omega }^2}.$$

The receptive field $RF\left(K,\omega \right)$ is the filtered spatiotemporal response, which is described by $RF\left(K,\omega \right)=T\left(\omega \right)X\left(K\right)$, under the assumption that the response is separable. Fig. 3 A and B present the output for the two inputs. Fig. 3C is the logarithmic plot of the output power spectrum of the spatial frequencies, summed over temporal frequencies as follows:

$${\left|O\left(K\right)\right|}^2={\left|X\left(K\right)\right|}^2{\displaystyle \underset{\mathrm{0}}{\overset{\infty }{\int }}\frac{{\left|T\left(\omega \right)\right|}^{2}D}{\frac{K^4{D}^2}{4}+{\omega }^2}d\omega }.$$

The black line denotes the cutoff frequency of the ganglion cell. It is obvious that the two stimuli do not depend on the spatial frequencies for $K<K_{cutoff}$, which implies that the effect of the reduction of pairwise correlations for different eye movements should be similar, as can be seen in Fig. 3 D and E.