Spec-seq: determining protein–DNA-binding specificity by sequencing

Abstract

The specificity of protein–DNA interactions can be determined directly by sequencing the bound and unbound fractions in a standard binding reaction. The procedure is easy and inexpensive, and the accuracy can be high for thousands of sequences assayed in parallel. From the measurements, simple models of specificity, such as position weight matrices, can be assessed for their accuracy and more complex models developed if useful. Those may provide more accurate predictions of in vivo binding sites and can help us to understand the details of recognition. As an example, we demonstrate new information gained about the binding of lac repressor. One can apply the same method to combinations of factors that bind simultaneously to a single DNA and determine both the specificity of the individual factors and the cooperativity between them.

The binding of transcription factors (TFs) to DNA plays a fundamental role in the regulation of gene expression. TFs find and occupy their regulatory sequences, against a large excess of competing alternative DNA sequences, using sequence-specific interactions, direct contacts with both the bases in the major and minor grooves of the DNA, and also indirectly through sequence-dependent variations in DNA structure. It is the differences in binding affinity to different sequences, the specificity of the TF, that is critical for the proper functioning of the regulatory networks. The absolute affinity of a protein for a DNA sequence, usually defined as the association constant (or its reciprocal, the dissociation constant), is of lesser importance than the specificity because the concentration of DNA in a bacterial cell, or a eukaryotic nucleus, is so high that the TF will be bound almost entirely to DNA somewhere, and the critical issue is how it occupies the functional regulatory sites. There are many experimental methods for determining the affinity of a protein to a specific DNA sequence [1]; and traditionally, specificity was determined by comparing a preferred binding site either to bulk non-specific DNA or to a few variants of the preferred binding site to assess how those variants affect affinity. In recent years, there have been several new methods, such as protein binding microarrays (PBMs [2]) and related methods [3, 4], high-throughput SELEX (HT-SELEX or SELEX-seq [5–7]) and bacterial one-hybrid selections (B1H [8, 9]), that can assess specificity much more comprehensively, comparing millions of sites in parallel (reviewed in [10]). The data quality can be variable, sometimes being highly reproducible and sometimes not. In addition, those methods do not measure affinity directly, or even relative affinity, but rather something related to it, and computational analysis, based on some assumptions, is required to determine models of specificity, and the results can be highly dependent on the analysis method used [11–13]. Another approach is ‘mechanical induced trapping of molecular interactions’ (MITOMI), which can determine absolute affinities for thousands of binding sites in parallel through the use of a microfluidic device and multiple assays on each sequence at multiple concentrations [14]. But, it still requires non-linear curve fitting to obtain the binding affinities.

In this article, we describe Spec-seq, which has several advantages over previous methods. It cannot do millions of sequences in parallel, like PBM, SELEX-seq or B1H, and so is not as useful for general motif discovery. But for determining specificity, changes in binding energy for thousands of variants of a preferred sequence, it is fast and easy and highly accurate because it measures exactly what we need for specificity, the distribution between the bound and unbound fractions for the entire set of sequences in one experiment. In the following sections, we describe Spec-seq in general and then results from using it on the lac repressor where several novel and interesting findings emerged [15]. Finally, we describe how Spec-seq can be used to study combinatorial binding by two TFs and all of the parameters that can be obtained in a single experiment. Note that the following sections contain many equations but none of them more complex than taking ratios. Equations 1, 2 and 4 are definitions of affinity, relative affinity and cooperativity, respectively, and the remaining are ratios of measured quantities. Together these simple experimental measurements are sufficient to determine all of the parameters we need to characterize the specificity of TF binding to DNA, including combinatorial binding.

Spec-seq METHOD FOR DETERMINING BINDING SPECIFICITY

For a bimolecular interaaction between a protein $X$, and a particular DNA site with sequence ${\mathit{x}}_{\mathit{i}}$, the interaction is diagrammed as follows:

$$X+{\mathit{x}}_{\mathit{i}}\leftrightarrow X·{\mathit{x}}_{\mathit{i}}$$

where $X·{\mathit{x}}_{\mathit{i}}$ refers to the complex. The equilibrium binding constant (or association constant) of protein $X$ to the sequence ${\mathit{x}}_{\mathit{i}}$ is defined as follows:

$${\mathit{K}}_X\left({\mathit{x}}_{\mathit{i}}\right)=\frac{\left[X·{\mathit{x}}_{\mathit{i}}\right]}{\left[X\right]\left[{\mathit{x}}_{\mathit{i}}\right]}$$ (1)

where the brackets, ‘[…]’, refer to concentrations. Specificity refers to the differences in binding affinities for different DNA sequences, but there are several distinct ways in which the term is used [1]. For our purposes, it refers to quantitative measures of binding constant ratios for all, or a large subset, of possible binding sites.

$${\mathit{K}}_X\left({\mathit{x}}_1\right):{\mathit{K}}_X\left({\mathit{x}}_2\right):\dots :{\mathit{K}}_X\left({\mathit{x}}_{\mathit{n}}\right)=\frac{\left[X·{\mathit{x}}_1\right]}{\left[{\mathit{x}}_1\right]}:\frac{\left[X·{\mathit{x}}_2\right]}{\left[{\mathit{x}}_2\right]}:\dots :\frac{\left[X·{\mathit{x}}_{\mathit{n}}\right]}{\left[{\mathit{x}}_{\mathit{n}}\right]}$$ (2)

Importantly, determining relative binding affinities does not require measuring the free protein concentration, $\left[X\right]$, which is often the most difficult part of determining absolute binding constants. Figure 1A shows an example of several different DNA sequences competing for the binding to a specific protein. Some of each sequence will be bound and some unbound. If the reaction mixture is run on an electromobility shift assay (EMSA) gel, we can separate the bound and unbound fractions of the DNA (Figure 1B: the ${\mathit{B}}_X$ and ${\mathit{B}}_{-}$ bands of the gel, respectively) and then sequence each fraction. The ratios of each sequence in the bound and the unbound fraction are proportional to their binding constants, so their ratios give us the relative binding affinities we desire [15]:

$${\mathit{K}}_X\left({\mathit{x}}_1\right):{\mathit{K}}_X\left({\mathit{x}}_2\right):\dots :{\mathit{K}}_X\left({\mathit{x}}_{\mathit{n}}\right)=\frac{\mathit{N}\left({\mathit{x}}_1\text{|}{\mathit{B}}_X\right)}{\mathit{N}\left({\mathit{x}}_1\text{|}{\mathit{B}}_{-}\right)}:\frac{\mathit{N}\left({\mathit{x}}_2\text{|}{\mathit{B}}_X\right)}{\mathit{N}\left({\mathit{x}}_2\text{|}{\mathit{B}}_{-}\right)}:\dots :\frac{\mathit{N}({\mathit{x}}_{\mathit{n}}|{\mathit{B}}_X)}{\mathit{N}({\mathit{x}}_{\mathit{n}}|{\mathit{B}}_{-})}$$ (3)

where $\mathit{N}\left({\mathit{x}}_{\mathit{i}}\text{|}{\mathit{B}}_{\propto }\right)$ is the count of sequence ${\mathit{x}}_{\mathit{i}}$ in the band of the gel ${\mathit{B}}_{\propto }$ ($\alpha \in \left\{X,-\right\}$ bound or unbound, respectively). We have long used the approach of separating bound and unbound fractions to determine relative binding affinities [16–22], but its throughput and its accuracy was limited by the technologies available at the time. Current high-throughput sequencing technology allows us to assess relative affinities for thousands of sites in parallel. Furthermore, we are not limited to determining models for binding, such as position–weight matrices (PWMs) that assume independent contributions from the positions in the binding sites [23–26]. Such models are clearly approximations, sometimes reasonably good and sometimes not [11–13, 20, 27–30]. The accuracy is quite high because we measure exactly what is required for determining specificity; complex mathematical analysis is not needed, only calculating ratios are needed. Spec-seq is similar to SELEX-seq but obtaining accurate models from that requires complex mathematical analysis and non-linear regression because the unbound fraction is not sequenced [6]. As long as we have sufficient counts for every sequence in both fractions, the accuracy of the ratios is high. We could assay larger numbers of sequences but if the counts get too low the ratios will only be approximately correct, diminishing accuracy. In some situations that may be sufficient, in which case Spec-seq could be used on many more sequences in parallel.

Figure 1:

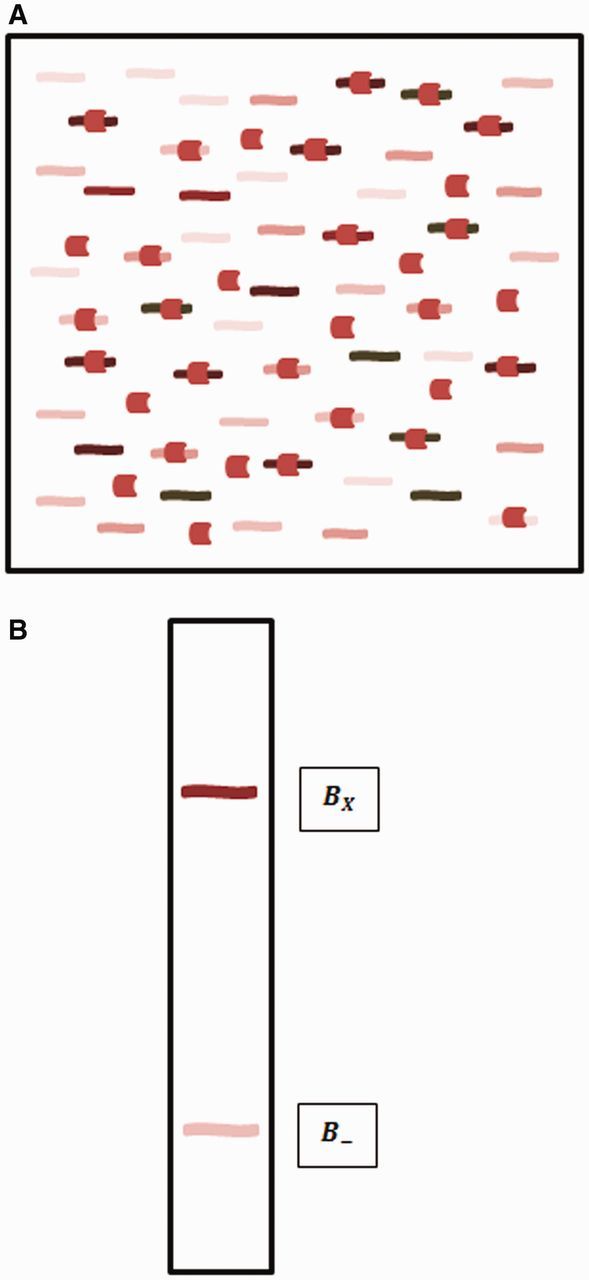
Binding reaction and separation of bound and unbound fractions. (A). A reaction tube with a DNA-binding protein (crescent shapes) and a mixture of different DNA sequences (curvy lines). Different sequences have different affinities for the protein, which are indicated by different shades of lines. Some of each sequence is bound to the protein and some is unbound, but higher affinity sequences are bound in higher proportion. (B). An EMSA gel, in which the bound and unbound fractions are separated into distinct bands (${\mathit{B}}_X$ and ${\mathit{B}}_{-}$, respectively).

APPLICATION TO THE lac REPRESSOR: MULTIPLE MODES OF BINDING DEPENDING ON OPERATOR LENGTH

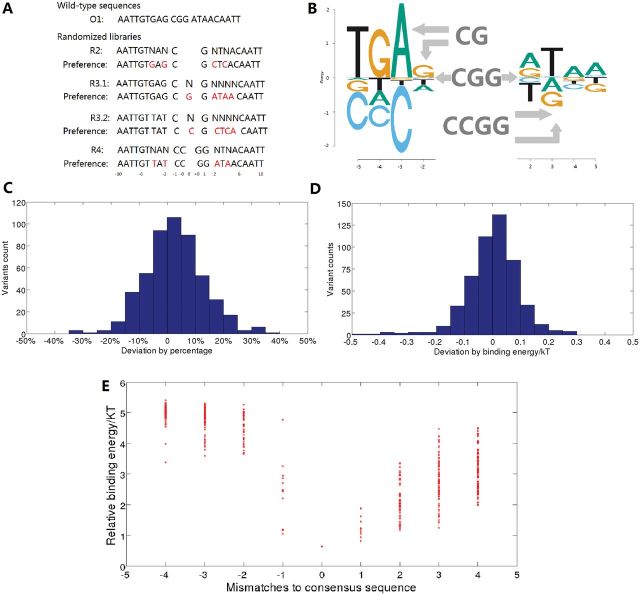
The lac repressor was the first discovered regulatory protein [31] and has been studied extensively in the subsequent years (see reviews in [32, 33]). One of the interesting findings about the lac operator sequence is that, although the protein binds as a dimer, the binding site is asymmetric with a central G and two differences between the left and right half-sites (Figure 2A). It had previously been observed that a symmetric variant, in which the central G is deleted and the right half-site is mutated to be equivalent to the left half-site, bound the lac repressor with slightly higher affinity that the wild-type operator [34]. We designed four different libraries that contained 2560 variant binding sites that included both variations in the distance between the half-sites and variations in each half-site (Figure 2A) and obtained relative binding affinities for each site using Spec-seq [15]. Figure 2B shows a brief summary of the results using an energy logo [25, 35]. For sites with the central G (libraries R3.1 and R3.2), the wild-type asymmetric operator has the highest affinity of all sequences tested. Furthermore, replacement of the central G with any other base greatly reduces affinity. For sites with the central G deleted (library R2), the symmetric site with two copies of the left half-site is preferred. But for sites with an insertion of an additional base in the center (library R4), the symmetric site with two copies of the right half-site is preferred. For each of the different libraries the preferred sequences have similar binding affinities, within about 0.5 kT of each other, even though they are quite distinct binding sites with different lengths and different preferred sequences. Those results demonstrate that the helix-turn-helix (HTH) domain of the lac repressor can prefer different sequences, or bind in different modes, and that the binding mode is determined by the distance of the half site-from the central CG of the operator [15, 32]. In the wild-type operator, the distance is different for the left and right half-sites and therefore the repressor prefers the asymmetric site, with the two HTH domains binding in alternative modes. In addition to those three preferred sites in each library, we also determined the relative affinities for all sites both within and between the four libraries because all of the sequences were competing for binding to the same pool of repressor protein. Figure 2C and D show that these determinations of relative affinity, and relative binding free energy (or $\Delta \Delta G$), are highly reproducible. In repeat experiments, the relative affinities are nearly always within 10% of each other, which corresponds to $\Delta \Delta G$ values within about 0.1 kT [15]. Figure 2E shows the entire range of binding energies as a function of the number of variations from the preferred binding site for each of the half-sites [15]. This allows us to assess the additivity approximation rigorously. Applying multiple regression to the various libraries, we can usually find PWMs that fit the entire data with R² > 0.7, and most predictions are within 0.5 kT of the measured binding energy, but we also find significant deviations from additivity when $\Delta \Delta G$ of multiple variants are compared with single variants [15]. A surprising result is that for library R2, all of the multiple mutants have higher binding energy than expected from the single variants, quite different from what is observed for several bHLH proteins where multiple mutants nearly always have lower energy than expected from additivity [14]. This has implications for the details of the interaction, including the relative contributions of enthalpy and entropy to binding [15].

Figure 2:

Lac repressor studies using Spec-seq. (A). The wild-type operator, O1, and four randomized libraries. In library R2, the central G (position 0) is deleted and the asymmetric bases from O1 (−4, −2, +2, +4) are randomized. In library R3.1 and R3.2, the central position (0) is randomized as are positions 2 to 5 (in R3.1) and −5 to −2 (in R3.2, note reversed orientation). In R4, an extra C is inserted (we now have two 0 positions, labeled −0 and +0) and positions −4, −2, +2, and +4 are randomized. Also shown are the highest affinity binding sites obtained for each library. (B). Energy logo from the R3 libraries, with the preferred sequence matching the O1 sequence. For sites with a CG spacer (R2 library), two copies of the left half-site are preferred. For sites with the CCGG spacer (R4 library), two copies of the right half-site are preferred. (C). From replicate experiments, performed with different protein concentrations, the fractional differences between the two measurements of relative affinity. The majority are within 10% of each other. (D). Data as shown in part C., but taking the logarithm to show the differences in binding energy for replicate measurements. The majority are within 0.1 kT of each other. (E). Plot of all of the energies from libraries R3.1 (right side) and R3.2 (left side) compared with the number of mismatches from the preferred binding site. This shows that the left half-site plateaus are at higher energy than the right half-site, and that variations to the left half-site are generally more detrimental to binding. Furthermore, many of the left-half site variants with two or more mutations have higher energy than predicted from the sum of single variants.

Spec-seq TO STUDY COMBINATORIAL BINDING

TFs often bind in combinations to control gene expression, especially in eukaryotes. When multiple TFs bind to a small region of DNA they may do so independently, but often there is some interaction between them. Interactions between multiple ligands binding to a common substrate are referred to as cooperativity, first observed in the binding of oxygen to hemoglobin, and there is extensive literature describing the analysis of such interactions [36]. The first observed cooperativity among TFs was found for binding of the lambda repressor to the lambda operator region [37] where cooperativity is critical for proper functioning of the lambda genetic switch [38, 39]. Since then, cooperativity has been observed among many different TFs and is probably common at all regulatory regions in eukaryotic genomes. A few examples include cooperativity among P53 proteins that is essential for their roles in tumor suppression and apoptosis [40, 41], the interactions among Sox and Oct proteins that determines the specific combinations that bind to specific regulatory regions and is required for their diverse developmental roles [42] and interactions between Hox proteins at developmentally important regulatory regions [43].

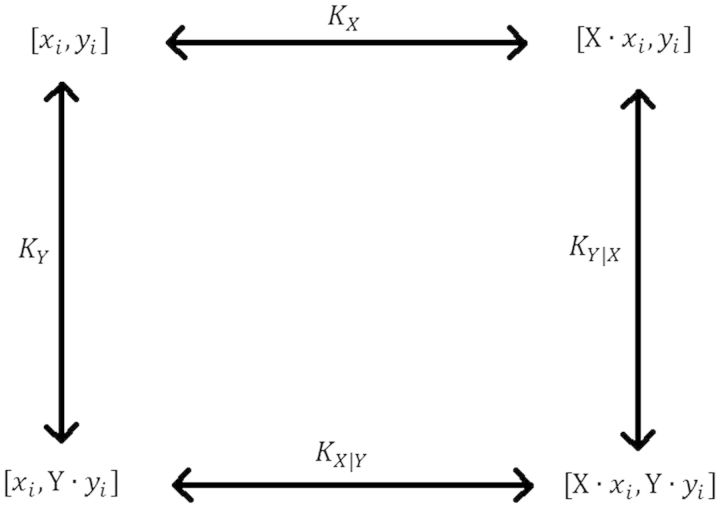
Spec-seq can be applied to combinatorial interactions for two (or more) TFs where the thousands of different sites can include both binding site variants as well as the variations in the spacing between them. Figure 3 describes the overall reaction of two proteins, X and Y, binding to a sequence S_i, which is a combination of two sites, ${\mathit{x}}_{\mathit{i}}$ and ${\mathit{y}}_{\mathit{i}}$ with some spacer, ${\mathit{z}}_{\mathit{i}}$, between them (${\mathit{z}}_{\mathit{i}}$ could be nothing if the sites are adjacent, but we can vary it to measure any effect on cooperativity). As above, we define the equilibrium constant of protein X to sequence ${\mathit{x}}_{\mathit{i}}$ as ${\mathit{K}}_X\left({\mathit{x}}_{\mathit{i}}\right)$, and we also have the equilibrium constant of protein Y to ${\mathit{y}}_{\mathit{i}}$ as ${\mathit{K}}_Y\left({\mathit{y}}_{\mathit{i}}\right)$. (Here we assume that ${\mathit{y}}_{\mathit{i}}$ and ${\mathit{z}}_{\mathit{i}}$ do not affect binding of X to ${\mathit{x}}_{\mathit{i}}$, but we can take that into account if necessary). We also have the binding constant of protein X to sequence ${\mathit{x}}_{\mathit{i}}$ when protein Y is already bound, ${\mathit{K}}_{X|Y}\left({\mathit{x}}_{\mathit{i}}\right)$, and similarly, the binding constant of protein Y to ${\mathit{y}}_{\mathit{i}}$ when X is already bound, ${\mathit{K}}_{Y|X}\left({\mathit{y}}_{\mathit{i}}\right)$. One interesting question is whether the specificity of one protein is altered in the presence of the other protein, a phenomenon that has been observed for certain Hox proteins and has been labeled as ‘latent specificity’ [43].

Figure 3:

Reaction diagram for binding of two proteins, X and Y, to a sequence with binding sites for each, x_i and y_i, respectively. Binding constants shown are for protein X binding alone K_X, for Y binding alone K_Y, and for each binding when the other is already bound, K_X|Y and K_Y|X.

The interaction between the X and Y is referred to as cooperativity, for which we use the symbol $\mathit{\omega }$ [42]. For a particular sequence S_i, ${\mathit{\omega }}_{\mathit{i}}$ is determined by comparing the binding constants for the proteins binding individually with the constants for both proteins binding:

$${\mathit{\omega }}_{\mathit{i}}=\frac{{\mathit{K}}_{X|Y}\left({\mathit{S}}_{\mathit{i}}\right)}{{\mathit{K}}_X\left({\mathit{S}}_{\mathit{i}}\right)}=\frac{{\mathit{K}}_{Y|X}\left({\mathit{S}}_{\mathit{i}}\right)}{{\mathit{K}}_Y\left({\mathit{S}}_{\mathit{i}}\right)}=\mathit{}\frac{{\mathit{K}}_{X,Y}\left({\mathit{S}}_{\mathit{i}}\right)}{{\mathit{K}}_X\left({\mathit{S}}_{\mathit{i}}\right){\mathit{K}}_Y\left({\mathit{S}}_{\mathit{i}}\right)}$$ (4)

${\mathit{\omega }}_{\mathit{i}}$ can be any nonnegative number; if ${\mathit{\omega }}_{\mathit{i}}=1$, then binding is independent (often referred to as having ‘no cooperativity’); if ${\mathit{\omega }}_{\mathit{i}}<1$ there is ‘anti-cooperativity’, with 0 for the case that binding of the two proteins is mutually exclusive (for example, if the binding sites overlap so that only one can bind at a time); if ${\mathit{\omega }}_{\mathit{i}}>1$ then binding of the second protein is facilitated by binding of the first, which indicates ‘positive cooperativity’, although this case is usually just referred to exhibiting cooperative binding. As indicated by the subscript, cooperativity may depend on the sequence, especially on the spacer part, ${\mathit{z}}_{\mathit{i}}$, just as the individual and joint binding constants may depend on the sequence.

Figure 4 describes an ideal experiment where the mixture of different sequences are bound to the proteins and then separated on an EMSA gel where four distinct bands are seen, one for each state of the DNA sequence: unbound (${\mathit{B}}_{-,-}$); bound individually by one of the proteins (${\mathit{B}}_{X,-}$ and ${\mathit{B}}_{-,Y}$); and bound by both proteins (${\mathit{B}}_{X,Y}$). An example where all four bands are observed is the combinatorial binding of Oct4 with different Sox TFs [42]. By cutting out and sequencing each of those bands, we can determine all of the relative parameters, how they vary with sequence, and also the absolute and relative cooperativity, for thousands of sequences simultaneously from a single experiment, as described with the following equations.

Figure 4:

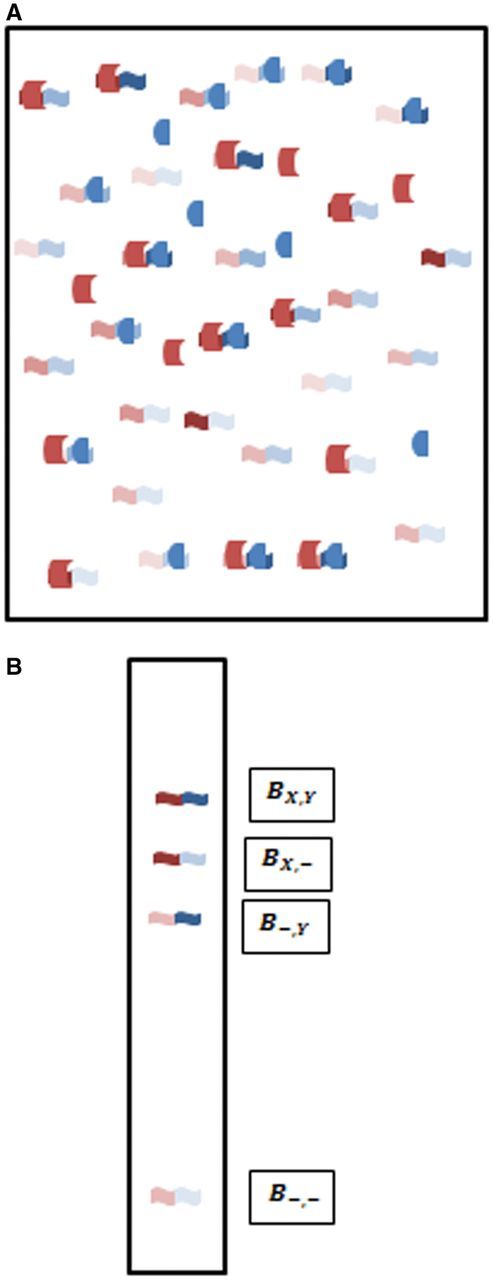
Binding reaction and separation of bound and unbound fractions for combinatorial system. (A). Mixtures of two proteins (crescent and bullet shapes) and DNA sequences that contain binding sites for each protein. Different shades indicate different affinities for the two proteins. Not shown is possibility to include various distances between the two binding sites. (B). EMSA gel showing four bands for unbound DNA (${\mathit{B}}_{-,-}$), bound by either X or Y alone (${\mathit{B}}_{X,-}$ or ${\mathit{B}}_{-,Y}$) or bound by both (${\mathit{B}}_{X,Y}$).

Just as above in equation (3), the relative affinities for individual proteins to all of the possible binding sites can be determined from the ratios in two bands, unbound and bound by X alone:

$$\begin{array}{l}{\mathit{K}}_X\left({\mathit{x}}_1\right):{\mathit{K}}_X\left({\mathit{x}}_2\right):\dots :{\mathit{K}}_X\left({\mathit{x}}_{\mathit{n}}\right)\\ =\frac{\mathit{N}\left({\mathit{x}}_1\text{|}{\mathit{B}}_{X,-}\right)}{\mathit{N}\left({\mathit{x}}_1\text{|}{\mathit{B}}_{-,-}\right)}:\frac{\mathit{N}\left({\mathit{x}}_2\text{|}{\mathit{B}}_{X,-}\right)}{\mathit{N}\left({\mathit{x}}_2\text{|}{\mathit{B}}_{-,-}\right)}:\dots :\frac{\mathit{N}({\mathit{x}}_{\mathit{n}}|{\mathit{B}}_{X,-})}{\mathit{N}({\mathit{x}}_{\mathit{n}}|{\mathit{B}}_{-,-})}\end{array}$$ (5)

and for protein Y, the unbound band and the band of protein Y alone:

$$\begin{array}{l}{\mathit{K}}_Y\left({\mathit{y}}_1\right):{\mathit{K}}_Y\left({\mathit{y}}_2\right):\dots :{\mathit{K}}_Y\left({\mathit{y}}_{\mathit{n}}\right)\\ =\frac{\mathit{N}\left({\mathit{y}}_1\text{|}{\mathit{B}}_{Y,-}\right)}{\mathit{N}\left({\mathit{y}}_1\text{|}{\mathit{B}}_{-,-}\right)}:\frac{\mathit{N}\left({\mathit{y}}_2\text{|}{\mathit{B}}_{Y,-}\right)}{\mathit{N}\left({\mathit{y}}_2\text{|}{\mathit{B}}_{-,-}\right)}:\dots :\frac{\mathit{N}({\mathit{y}}_{\mathit{n}}|{\mathit{B}}_{Y,-})}{\mathit{N}({\mathit{y}}_{\mathit{n}}|{\mathit{B}}_{-,-})}\end{array}$$ (6)

We can also determine the relative affinities for the same proteins to all possible sites when the other protein is already bound by comparing the band of both proteins with that of the individual proteins:

$$\begin{array}{l}{\mathit{K}}_{X|Y}\left({\mathit{x}}_1\right):{\mathit{K}}_{X|Y}\left({\mathit{x}}_2\right):\dots :{\mathit{K}}_{X|Y}\left({\mathit{x}}_{\mathit{n}}\right)\\ =\frac{\mathit{N}\left({\mathit{x}}_1\text{|}{\mathit{B}}_{X,Y}\right)}{\mathit{N}\left({\mathit{x}}_1\text{|}{\mathit{B}}_{-,Y}\right)}:\frac{\mathit{N}\left({\mathit{x}}_2\text{|}{\mathit{B}}_{X,Y}\right)}{\mathit{N}\left({\mathit{x}}_2\text{|}{\mathit{B}}_{-,Y}\right)}:\dots :\frac{\mathit{N}({\mathit{x}}_{\mathit{n}}|{\mathit{B}}_{X,Y})}{\mathit{N}({\mathit{x}}_{\mathit{n}}|{\mathit{B}}_{-,Y})}\end{array}$$ (7)

and

$$\begin{array}{l}{\mathit{K}}_{Y|X}\left({\mathit{y}}_1\right):{\mathit{K}}_{Y|X}\left({\mathit{y}}_2\right):\dots :{\mathit{K}}_{Y|X}\left({\mathit{y}}_{\mathit{n}}\right)\\ =\frac{\mathit{N}\left({\mathit{y}}_1\text{|}{\mathit{B}}_{X,Y}\right)}{\mathit{N}\left({\mathit{y}}_1\text{|}{\mathit{B}}_{X,-}\right)}:\frac{\mathit{N}\left({\mathit{y}}_2\text{|}{\mathit{B}}_{X,Y}\right)}{\mathit{N}\left({\mathit{y}}_2\text{|}{\mathit{B}}_{X,-}\right)}:\dots :\frac{\mathit{N}({\mathit{y}}_{\mathit{n}}|{\mathit{B}}_{X,Y})}{\mathit{N}({\mathit{y}}_{\mathit{n}}|{\mathit{B}}_{X,-})}\end{array}$$ (8)

Comparisons between the relative affinities with and without the other protein bound, for instance, between the ratios in equations 5 and 7, and between 6 and 8, will determine whether the specificity changes, for one (or both) protein, when the other protein is also bound, referred to as ‘latent specificity’ [43].

The absolute cooperativity for each sequence can be determined if we also measure the total DNA in each band (from the band fluorescent intensities), $\mathit{I}({\mathit{B}}_{-,-})$, $\mathit{I}({\mathit{B}}_{X,-})$, $\mathit{I}({\mathit{B}}_{-,Y})$ and $\mathit{I}({\mathit{B}}_{X,Y})$:

$$\mathit{\theta }=\frac{\mathit{I}({\mathit{B}}_{X,Y})\mathit{I}({\mathit{B}}_{-,-})}{\mathit{I}({\mathit{B}}_{X,-})\mathit{I}({\mathit{B}}_{-,Y})}$$ (9)

$\mathit{\theta }$ is the average cooperativity of all the sequences, and if there is only one sequence it is just $\mathit{\omega }$ for that sequence [42]. Having determined that average we can then determine the absolute cooperativities for each individual sequence:

$${\mathit{\omega }}_{\mathit{i}}=\mathit{\theta }\frac{\mathit{P}({\mathit{S}}_{\mathit{i}}|{\mathit{B}}_{X,Y})\mathit{P}({\mathit{S}}_{\mathit{i}}|{\mathit{B}}_{-,-})}{\mathit{P}({\mathit{S}}_{\mathit{i}}|{\mathit{B}}_{X,-})\mathit{P}({\mathit{S}}_{\mathit{i}}|{\mathit{B}}_{-,Y})}$$ (10)

where $\mathit{P}({\mathit{S}}_{\mathit{i}}|{\mathit{B}}_{\alpha ,\beta })$ is the probability of sequence ${\mathit{S}}_{\mathit{i}}$ within the set of sequences from the band ${\mathit{B}}_{\alpha ,\beta }$. The relative cooperativity, how it changes in different sequences, is just the ratios of the absolute cooperativities over all sequences, which eliminates the factor $\mathit{\theta }$ (if we want to know only relative coperativities, the measurements used in equation (9) are not needed). We expect that cooperativity may change due to variations in the spacing and/or sequence between the binding sites for X and Y, the component we refer to above as ${\mathit{z}}_{\mathit{i}}$, but it could also change for other reasons.

We get all of the parameters that we need to characterize the individual and combinational binding events for the entire set of sequences from a single experiment, with the exception of absolute binding constants. If we also desire that, it need only be obtained for a single sequence and the rest can be inferred from the relative values. While the total number of variants that can be tested simultaneously is only in the thousands, much less than the universe of all possible combinatorial sites, that will often be enough for a comprehensive view of the binding potential across a genome. For example, we might synthesize DNA that contains the top 50 sites for protein X and also for protein Y, for 2500 different combinations, and even add in a few different spacings, and still be able to accurately determine the relative binding affinities to all of those sequences from a typical short-read sequencing run of ∼ 100 million reads. Doing a few experiments in parallel containing different sets of sequences, which could all be run on additional lanes of the same gel, could expand that repertoire considerably.

CONCLUSIONS

Spec-seq is a fast, easy and reliable method for determining the specificity of a DNA-binding protein. It can measure relative binding affinities for thousands of sites in parallel. It can also be applied to combinations of factors binding to the same DNA where both specificity and cooperativity can be determined simultaneously. Analysis of the data requires nothing more complex than taking ratios, although regression may be applied to infer models, such as PWMs, if desired [15]. The same method could be applied to RNA-binding proteins with the complication that binding affinity may depend on both sequence and structure of the RNA.

Key points.

• Spec-seq provides high accuracy measurements of relative binding affinity to thousands of binding sites in parallel.

• Analysis of the data requires taking only ratios of measured quantities; no non-linear curve fitting is needed.

• Models of specificity, such as PWMs, can be rigorously tested and more complex models developed if useful.

• Binding of two (or more) factors can be studied using the same approach, allowing for the determination of cooperativity between factors as well as specificity for the individual factors.

• Lac repressors shows alternative modes of binding that depend on the length of the binding site.

FUNDING

This work has been supported by grants from the National Institutes of Health [HG000249 and HG005970].

Biographies

Gary Stormo is a Joseph Erlanger Professor in Genetics at Washington University School of Medicine. He was an undergraduate at Caltech and a graduate student, post-doc and faculty member at the University of Colorado. He is a Fellow of the International Society for Computational Biology.

Zheng Zuo is a graduate student in Biomedical Engineering at Washington University in St. Louis. He graduated from Peking University in 2008 with a Bachelor’s degree in Physics.

Yiming Kenny Chang is a graduate student in the Molecular Genetics and Genomics program at Washington University in St Louis. He received his undergraduate degree in Genetics from Rutgers University and his Master’s degree in Biotechnology from University of Pennsylvania.