Abstract
The paper re-evaluates Verhulst and Monod models. It has been claimed that standard logistic equation cannot describe the decline phase of mammalian cells in batch and fed-batch cultures and in some cases it fails to fit somatic growth data. In the present work Verhulst, population-based mechanistic growth model was revisited to describe successfully viable cell density (VCD) in exponential and decline phases of batch and fed-batch cultures of three different CHO cell lines. Verhulst model constants, K, carrying capacity (VCD/ml or μg/ml) and r, intrinsic growth factor (h−1) have physical meaning and they are of biological significance. These two parameters together define the course of growth and productivity and therefore, they are valuable in optimisation of culture media, developing feeding strategies and selection of cell lines for productivity. The Verhulst growth model approach was extended to develop productivity models for batch and fed-batch cultures. All Verhulst models were validated against blind data (R2 > 0.95). Critical examination of theoretical approaches concluded that Monod parameters have no physical meaning. Monod-hybrid (pseudo-mechanistic) batch models were validated against specific growth rates of respective bolus and continuous fed-batch cultures (R2 ≈ 0.90). The reduced form of Monod-hybrid model CL/(KL + CL) describes specific growth rate during metabolic shift (R2 ≈ 0.95). Verhulst substrate-based growth models compared favourably with Monod-hybrid models. Thus, experimental evidence implies that the constants in the Monod-hybrid model may not have physical meaning but they behave similarly to the biological constants in Michaelis–Menten enzyme kinetics, the basis of the Monod growth model.
Keywords: CHO, Verhulst, Monod, Model constants, Metabolic shift
Introduction
In the present study, two types of unstructured, unsegregated models were examined with the view to develop biologically significant mechanistic models which can be used for monitoring and optimisation.
The first type, a mathematical one, is based on the Verhulst and Gompertz functions (Verhulst 1847; Gompertz 1825), which are extensions of the Malthusian (Malthus 1798) population model. The logistic function (Verhulst 1838; Robertson 1908) is one of most classic growth models. The major advantages of this logistic function are mathematical simplicity and biological interpretability (Wan et al. 2000). Therefore, Verhulst logistic model has played a central role in many aspects of theoretical and applied physiology (Krebs 1996). However, Verhulst model is asymptotic, describing only exponential phase of growth (Jolicoeur and Pontier 1989; Goudar et al. 2005). Furthermore, in some cases the logistic model fails to fit somatic (body cells) growth data satisfactorily (Ricklefs 1968; Cui and Lawson 1982; Jolicoeur and Pontier 1992; Wan et al. 1998). Therefore, to fit growth data set many attempts have been made to construct a generalised form of ordinary 3-parameter logistic equation (Richards 1959; Cui and Lawson 1982; Jolicoeur and Pontier 1989, 1992; Wan et al. 1998). Notably amongst them is a four-parameter generalised logistic model (Jolicoeur and Pontier 1989) to describe exponential and decline phases of population of Paramecium caudatum; Wan et al. (2000) developed a new four-parameter generalised model to describe somatic growth in 12 mammalian species; Goudar et al. (2005), who used the four-parameter model to describe growth, also developed the logistic model for the productivity of CHO cells. Four-parameter generalised models are descriptive (empirical) and not explicative (theoretical) (Jolicoeur and Pontier 1989). The model constants (parameters) are fitted by least-squares, requiring a large experimental data set (Jolicoeur and Pontier 1989; Goudar et al. 2005). Thus, a four-parameter generalised model is empirical and their constants have no physical or biological significance.
In the present study, the Verhulst function is revisited with a completely new perspective. The Verhulst-modelling approach was chosen because it is simplistic, yet effective and mechanistic in nature (Wan et al. 2000). Two separate Verhulst population-based (V-PB) logistic models were developed, one to describe exponential phase and the other for decline phase of CHO populations in batch and fed-batch cultures. Finally, for monitoring purposes, the two Verhulst (V-PB) models were replaced by a single model in the form of Heaviside function to describe the complete cycle of the exponential and decline phases of population. The method of modelling V-PB for the growth was adapted to develop the Verhulst model for productivity (V-Pr) for batch and fed-batch cultures. The Verhulst substrate-based (V-SB) models, wherein the growth rate is proportional to the product of the initial cell density and substrate concentration, for batch and fed-batch cultures were developed specifically to compare with the respective Monod models, which are also substrate-based.
The model constants Ks, carrying capacity (growth or productivity/ml) and rs, intrinsic factors (h−1) for batch and fed-batch are computed mathematically from the Verhulst equations using growth or productivity data. Verhulst model constants, K and r, together define the trajectory or course of bioprocess. All Verhulst models—V-PB, V-SB and V-Pr for the batch and fed-batch cultures were validated against a new set of data.
The second type, borne of commercial necessity, is the Monod model (1949). The saturation constants (Ks) in the Monod-type equation cannot be determined experimentally and therefore, they are either chosen arbitrarily or from literature to give the “best fit” for the growth curve (Roels 1983; Liu 2007; Nielson et al. 2003). The Monod equation is not a theoretical model because the constants within it have no physical meaning (Kovarova-Kovatr and Egli 1998; Alexander 1999; Ferenci 1999; Liu 2007) and they show a wide variation (Roels 1983; Bailey and Ollis 1986; Grady et al. 1999). Thus, the Monod model is purely an empirical one based on fitting experimental data by choosing model constants arbitrarily (Grady et al. 1999). However, Flickinger and Drew (1999) disagreed, pointing out that many microbiologists consider Monod equation as having deep inherent meaning rather than just an empirical formula. In order to resolve the controversy, Liu (2007) reviewed various representative mathematical approaches (i.e., kinetic, thermodynamic and substrate transport) for deriving the Monod equation in the expectation of finding physical meaning of the model constants within. However, he concluded that because of different assumptions are in each of the approaches, no physical meaning of the Monod constants (Ks) can be arrived at and that the Monod equation would only have numerical meaning for microbial growth but might not have biological basis other than a regression-based mathematical formula.
Bearing this in mind, the present study attempts to provide experimental evidence to validate biological significance of the model constants in the Monod equation. Therefore, the constants in the Monod models were determined from the batch experiment by using regression methods rather than selecting them arbitrarily from the literature to fit the data. The resulting Monod-hybrid (pseudo-mechanistic) batch models were applied subsequently to the corresponding bolus and continuous fed-batch cultures for validation.
The efficacies of all models were determined in terms of “goodness of fit” (R2). The Verhulst and Monod models were compared for their efficacies (“R2”) and the model constants within them were evaluated for the physical meaning and biological significance.
Materials and methods
Cell lines and cultures
The data on batch and fed batch cultures of three CHO cell lines were used in the present study; two cell lines were cultured in our laboratory (CHOK1 SV producing MAb and CHO320 producing IFN-γ) and the data for the third cell line (CHO IFN-γ) was from the published work (Chee et al. 2005).
CHOK1SV cells were cultured in 50 ml flasks (referred to as D1); CHO320 cells were cultured in 3 and 15 l stirred tank bioreactors (referred to as D2 and D3, respectively); CHO IFN-γ cells were reported to have been cultured in a 3 l bioreactor (referred to as D4). The batches are referred to as B, the bolus (periodic feeding) fed-batches as BFB and the continuous (continuous feeding) fed-batches as CFB (Table 1).
Table 1.
Bioreactor runs in the present study
| Bioreactor | Type of culture/cell line | Feeding regime | Process designation |
|---|---|---|---|
| 50 mL | Batch CHOK1 SV (MAb) | None | B-Dl |
| 50 mL | Fed-batch CHOK1 SV (MAb) | Bolus | FB-D1 |
| 3 L | Batch CHO 320 (IFN-γ) | None | B-D2 |
| 3 L | Fed-batch CHO 320 (IFN-γ) | Bolus | BFB-D2 |
| 3 L | Fed-batch CHO 320 (IFN-γ) | Continuous | CFB-02 |
| 15 L | Batch CHO 320 (IFN-γ) | None | B-D3 |
| 15 L | Fed-batch CHO 320 (IFN-γ) | Bolus | BFB-D3 |
| 15 L | Fed-batch CHO 320 (IFN-γ) | Continuous | CFB-D3 |
| 3 L | Batch CHO IFN-γ (Chee et al. 2005) | None | B-D4 |
| 3 L | Fed-batch CHO IFN-γ (Chee et al. 2005) | Continuous | CFB-D4 |
B batch, FB fed-batch, BFB bolus fed-batch, CFB continuous fed-batch, D1 data 1 (50 ml) for cell line CHOK1 SV (MAb), D2 data 2 (3 l) for cell line CHO 320 (IFN-γ), D3 data 3 (15 l) for cell line CHO 320 (IFN-γ), D4 data 4 (3 l) for CHO IFN-γ, MAb monoclonal antibody
Small scale experimental data were obtained using CHOK1SV cell line expressing monoclonal antibody (MAb) B72.3-IgG4 (kindly supplied by Lonza Biologics, Slough, UK). Cells were maintained in a chemically defined CD-CHO medium (Bioscience, Dublin, Ireland) supplemented with 25 μM methylamine sulphoxamine (MSX) (Sigma Aldrich, Dublin, Ireland) and cultivated in 50 ml medium in 250 ml Erlenmeyer Flasks in an orbital shaker incubator stirred at a speed of 140 rpm and temperature maintained at 37 °C. Cultures were seeded at 3 × 105 cells/ml from a stock of cells in the exponential phase (viability >95 %). Cells were grown in triplicate in batch and fed-batch cultures. The fed-batch cultures were fed with 5 ml of commercial feed (CHO-CD-Efficient-Feed; Bioscience) at 24 h intervals. Samples of 2.5 ml were withdrawn at 24 h intervals and analysed for cell number and viability by staining with propodium iodide and using Cell Lab Quanta SC flow cytometer (Beckman Coulter Inc., Galway, Ireland) and the productivity of MAb was measured by ELISA according to Bi et al. (2004).
The second cell line used in this work was CHO 320, a DHFR deficient mutant of CHOK1, which produces human interferon-γ (IFN-γ). Cells were maintained in Ex-CELL CD CHO serum-free medium (Sigma-Aldrich) supplemented with 4 mM glutamine and 20 mM glucose. Experiments were conducted in both 3 l bench-top and 15 l pilot scale bioreactors (Applikon Biotechnology Ltd., Schiedam, Netherlands). Pluronic F68 (0.1 % v/v), 1 μM methotrexate (MTX) and antifoam C (5 ppm) were also added in the bioreactors. The feed consisted of glucose (653 mM), glutamine (58.8 mM) and soy hydrolysate powder (58.8 g/l) (Irvine Scientific, Santa Ana, CA, USA) dissolved in glucose-free Ex-cell serum-free medium (Bioscience). The pH, dissolved oxygen, temperature and agitation were controlled at constant values of 7.2, 50 % of air saturation, 37 °C and 120 rpm respectively. Samples were taken daily and the cell density and viability were determined by haemocytometer count and the trypan blue dye exclusion method. Glucose, glutamine, glutamate and ammonia were measured offline with the Nova Bioprofile 400 (Nova Biomedical, Runcorn, Cheshire, UK). Lactate was determined by enzymatic assay (Megazyme, Bray, Ireland). Two fed-batch feeding regimes were modelled in this study: manually fed with bolus additions at 24 h intervals and continuously fed.
Finally, data published by Chee et al. (2005) on CHO IFN-γ cell line were used to verify and validate the methodology used for developing the Verhulst and the Monod models. The cells were cultured in 5L bioreactor (B. Braun, Melsungen, Germany) with working volume of 4 l culture medium (HyQ CHO MPS medium from Hyclone, Logan, UT, USA). Fed batch operation was performed using a modified online dynamic feeding strategy as described by Lee et al. (2003). Details of fed batch and set-point control operations can be found in the published work of Chee et al. (2005).
Goodness of “fit” (R2)
A measure of “fit” of a model to the experimental data is defined as the coefficient of determination:
| 1 |
| 2 |
where R2 = goodness of fit, yi = observations, = average of observations, ŷ = estimated value of the observation and ε = error term, yi − ŷ, i = 1, 2, 3, …n.
Modelling of bioprocesses
Verhulst population-based (V-PB) logistic models for growth
The Malthus exponential model (Malthus 1798) predicted unlimited growth in population based on infinite resources.
| 3 |
where N(0) and N(t) are cell numbers at time 0 and t, and r is constant of proportionality.
Verhulst modified the Malthusian model to take into account finite resources for growth. The Verhulst model can be derived by truncating Taylor series after second term (Dym 2004):
| 4 |
wherein r1, r2, r3, …etc. ≻ 0. r1 Corresponds to uninhibited or net growth rate, and if the series is truncated after 2nd term, then r2 signifies that growth rate stops when N(t) = Nmax, i.e., dN/dt = 0 and elimination of r2 yields:
| 5 |
Let r1 = r = initial or intrinsic growth rate, and at t = 0, N(t) = N(0) = N0 and Nmax = K saturation level or carrying capacity. Thus Eq. (3) becomes:
| 6 |
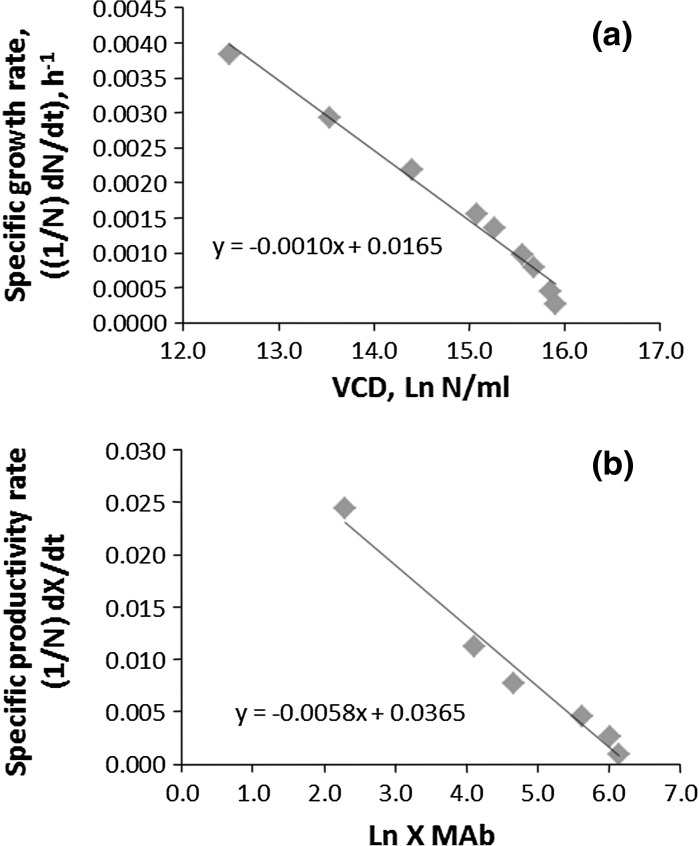
In Eq. (4), r (h−1) becomes the relative growth rate when the effects of limiting factors are negligible (Brown and Rothery 1993), i.e., (1/N) dN/dt, the rate constant for potential exponential growth of the population. When the population size equals K (cell density/unit volume), also known as the equilibrium or saturation level, then from Eq. (6) the growth rate becomes zero and the population remains at that level. The multiplicative factor 1 − (N/K) accounts for a saturation level characteristic (K) of the environment that will give a stable population level. The Verhulst model constants, K, the carrying capacity (or overall saturation constant), and r, intrinsic growth rate, are determined by plotting the experimental data, ln N(t) versus (1/N) dN/dt; the intersect at the y-axis gives the value of r (h−1) (specific growth rate, μ) and the one at x-axis represents the value of K (ln viable cell density (VCD)/unit volume) (Fig. 1a).
Fig. 1.
Determination of Verhulst constants: a D1, data 1 (50 ml) for cell line CHOK1 SV, KV-PB, carrying capacity (16.50 Ln VCD/ml), rV-PB, intrinsic growth factor (0.0165 h−1); b D1, data 1 (50 ml) for cell line CHOK1 SV, KV-MAb, carrying capacity (6.29 Ln MAb/ml), rV-PB, intrinsic productivity factor (0.0365 h−1)
Solving Eq. (6) by separating variables yields:
| 7 |
Equation (7) is called the Verhulst logistic equation, describing exponential growth rate with defined limitations. Equation (7) is asymptotic to the carrying capacity, i.e., as t → ∞, N(t) ≈ K with specific growth rate (1/N) dN/dt decreasing linearly as the population increases, with slope −r/K, reaching zero at N ≈ K.
However, Eq. (7) describes the exponential growth phase only, and hence another equation is required to describe the decline phase. Experimental data, used in the present work (vide infra), indicated that the cell growth and decline phases are symmetric at the point of maximum growth, Nmax at time, tmax and therefore, the rate of decline in the vicinity of the peak of the cell density can be approximated to the rate of growth. Thus, the decline phase can be described by replacing the intrinsic growth rate constant in Eq. (7) from +r to −r, and N0 = Nmax i.e.
| 8 |
Equations (7) and (8) can be expressed with a single equation using the Heaviside step function:
| 9 |
where H = heaviside,
| 10 |
Here, the constant, α, is based on the best ‘fit’ for the data. For the present data: α = 0.001 for batch culture and α = 0.00075 for fed-batch culture.
Verhulst substrate-based (V-SB) logistic model for growth
In the Verhulst (PB) model, the limited resources along with the growth were implicit in the K, carrying capacity. In order to determine explicitly the effects of the nutrients, particularly limiting substrate, Verhulst logistic equation was developed further to quantify the relationship between growth and the substrate (Edelstein-Keshet 2005). Thus, the reproductive rate k is simply proportional to the concentration C of the substrate,
| 11 |
where k, is constant of proportionality with dimensions, t−1.
| 12 |
where α is units of nutrient consumed to produce one unit of population increment (i.e., yield Y = 1/α). Integrating Eq. (12) gives:
| 13 |
At t = 0, N(t) = 0 and hence C0 = C(0) + αN(0) is a constant. If the initial population is very small then C0 is equal to the initial amount of nutrient, C. Thus, substituting for C in the Eq. (14) yields:
| 14 |
The substrate based logistic Eq. (14) appears in population dynamics in the following form (Edelstein-Keshet 2005):
| 15 |
where N0 = N(0) = initial population, r′ = (kC0) = intrinsic growth parameter, rate of consumption and B = (C0/α) = carrying capacity, cell density.
The solution of the Eq. (15) is:
| 16 |
Thus, according to the Eq. (15) the carrying capacity and intrinsic growth parameter are influenced by substrate concentration and the rate at which it is converted into biomass (Y). The values of B, carrying capacity and r′, intrinsic growth factor are determined by substituting in the Eq. (15) values for dN/dt, the cell populations, N(0), N(t) and initial concentration of substrate C0. Thus, it is possible to determine the course or trend of the growth after 24 h and since, glucose is the growth substrate in all bioprocesses, the model can be used for optimising its initial concentration.
Verhulst logistic model for productivity of MAb (V-Pr)
The Verhulst population balanced concept was extended to productivity of MAb (V-Pr) by CHO-K1SV in the batch and fed-batch cultures. Thus, the cell growth Eq. (7) becomes:
| 17 |
where X1 = Ln MAb at 24 h and X(t) after t-h, and, as before, KX = productivity potential and rx = productivity rate. The parameters, KX and rx, are determined in the same way as in the growth models, i.e., the logarithm of MAb titre, Ln X, to the specific rate of production, (1/X) dX/dt. The x-abscissa intercept of the resulting line is KX, productivity potential and rx, specific productivity rate is the y-ordinate intercept (Fig. 1b).
The parameters, carrying capacity and intrinsic growth factor, in the mathematical models for V-PB and V-SB for the growth and V-Pr for the productivity are of physical meaning (i.e., dimensional) and also biological significance and hence the models are classed as mechanistic (Prajneshu 1998; Wan et al. 2000). Thus, the K and B (cell density) are the carrying capacity (a function of medium composition and mode of bioprocess i.e., batch or fed-batch) and r and rx (h−1), are intrinsic rate factors (reflecting the physiological state of the cells and mode of bioprocess). Thus, Ks and rs are physical entities of biological and physical significance; if they were not of biological significance, then they would have been classed as empirical, just like ‘black-box’ cases (Roels 1983; Prajneshu 1998). Thus, all Verhulst-type models described here are mechanistic.
Monod-type logistic models for growth
During the last half-century, the concepts in microbial growth kinetics have been dominated by the relatively simple semi-empirical model proposed by Monod (1949). The Monod model introduces the concept of growth controlling or limiting substrate. Thus, there is a causal relationship between the exhaustion of the limiting substrate and hence the Monod model can be considered deterministic.
Monod found that the logistic equation does not describe accurately bacterial growth. Therefore, Monod developed a new model, fashioned after Michaelis–Menten enzyme kinetics that fits the data:
| 18 |
where μ and μmax are specific growth rates, Cs is the concentration of the limiting substrate (kmol m−3) and the constant Ks, normally referred to as saturation constant, is equal to the substrate concentration at which the specific growth is half of μmax (h−1).
The Monod-type of logistic Eq. (18) is unstructured, unsegregated and deterministic, requiring no knowledge of underlying mechanism of biological phenomena. They are very useful for model-based application for monitoring and control of bioprocesses (Kontoravdi et al. 2010).
Monod made the link between growth and substrate utilisation:
| 19 |
where
| 20 |
where is the yield coefficient, a measure of the conversion efficiency of a growth substrate into cell density (N).
Thus, Eq. (18) describes an unstructured, unsegregated and deterministic model, with the rather erroneous assumption that cells grow with constant composition and yield, i.e., growth is independent of biomass composition (Thingstad 1987).
The Verhulst’s logistic equation is based on the concept of a saturation level for a stable population in a given growth environment and resources. In Monod models (Monod 1949) this concept is narrowed to a specific growth resource, termed a “growth-limiting substrate”, as in the substrate-enzyme-product reactions. In classical macroscopic models, the cells are considered nothing but catalysts for the conversion of substrate into products (Provost, and Bastin 2004). Therefore, the Monod’s empirical expression, which is a mathematical homologue (Roels 1983) of the Michaelis–Menten equation for enzyme reactions, relating the specific growth rate to substrate concentration, works very well in practice.
When glucose is the limiting substrate (as in most fermentation processes), the value of Ks, the saturation constant, is in the micro-molecular range (milligrams per litre). Therefore, its value is difficult to determine experimentally (Nielson et al. 2003). Hence, the Ks are selected from the literature (Nielson et al. 2003) and adjusted to fit the experimental data. However, a large variation has been observed in the published values of saturation constants because they (constants) do not reflect the effects of media and growth conditions between the bioprocesses (Kovarova-Kovatr and Egli 1998; Alexander 1999; Ferenci 1999; Grady et al. 1999).
Therefore, it was decided to develop Monod-hybrid model in search of physical meaning of saturation constants Ks. It has been argued that substrate uptake is often involved in substrate metabolism (a series of enzymatic reactions within the cell). In developing a Monod-hybrid model it is assumed that à priori knowledge is known, i.e., Ks represents all the reactions lumped together to fit the average substrate influence on the cellular reactions. Thus, Ks represents the overall saturation constant for the whole growth process, i.e., all of the cellular reactions are pooled into a single reaction, which converts substrate into biomass (Nielson et al. 2003). This is why the Monod model works so well in fitting the experimental growth kinetic data. Given the relative success of the Monod approach, several other unstructured kinetic models have been developed and proposed (Nielson et al. 2003).
Sometimes the metabolic end products, e.g., lactic acid, alcohol, ammonia, etc. inhibit cell growth, in the same way as enzyme inhibitors in enzyme reactions. Therefore, the Michaelis–Menten equation for non-competitive inhibition in enzyme is also applicable for the cell growth. Thus, an inclusion of inhibitory term in Eq. (18) yields the analogue of Michaelis–Menten equation:
| 21 |
where Cp denotes concentration of inhibitor produced by the cells and KI, is the saturation constant for inhibition.
Portner and Schafer (1996) found that irrespective of the cultivation mode, i.e., batch or fed-batch, the growth of the cell lines follows the same kinetics and, therefore, it is possible that data gained from batch experiments can be extended to continuous fed-batch cultures (Kontoravdi et al. 2010; Hu 2004). Therefore, in the present work, a numerical approach was developed to estimate the Monod model constants, using transformed batch Data-2, -3 and -4, and then the batch models, thus arrived at, were applied to their respective bolus and continuous fed-batch cultures.
In the present study, CHO 320 (IFN-γ) and CHO IFN-γ cell lines were grown in the medium containing the substrates, glucose and glutamine; the end-metabolites (inhibitors) of which are lactate and ammonia respectively. Therefore, the Monod logistic Eq. (21) becomes
| 22 |
where μ, is growth rate, μmax is maximum growth rate, CG, CGT, CL and CA are the concentration of glucose, glutamine, lactate and ammonia respectively, and KG, KGT, KL and KA are the corresponding Monod model constants and i = 1, 2, 3 … n. In Eq. (20), except for the Monod model constants, all other variables are determined experimentally. Glucose was the limiting substrate in the D2 and D3, and glutamine in the D4.
The values of Monod constants in the Eq. (22) were determined by using the experimental Batch Data D2, D3 and D4. Cell growth is inherently nonlinear. The function (lsqcurve) in MATLAB was used for determining the model constants. The function (MATLAB-lsqcurve), given the initial guesses, finds coefficients of x to best suit the nonlinear function fun (x, xdata) to the ydata (in the least-squares sense). The accuracy of the constants increases with an increasing number of observations. The Monod constants, thus determined, were used to develop Monod batch models, which were then applied to the corresponding fed-batch data (bolus and continuous) to calculate μt at different times (22). The cell number then can be computed by using the following expression:
| 23 |
where N is Ln VCD at t ant t + 1, ∆t is time interval between t and t + 1 and μt is the specific growth rate at time t.
Results and discussion
Abbreviations for the bioreactors are given in Table 1. The Verhulst models: V-PB and V-SB were developed for prediction of cell density (VCD/ml) in all batch and fed-batch cultures of data: D1, D2 and D4, and V-Pr for prediction of productivity (MAb μg/l) in batch and fed-batch cultures of D1. The Monod-type logistic models were developed for prediction of growth only in the batch and fed-batch cultures of the data: D2, D3 and D4. The results of model constants for the Verhulst and the Monod models are included in Table 2 and the efficacies of Verhulst and Monod models are given in Table 3.
Table 2.
Estimation of constants (parameters) for Verhulst and Monod models
| Parameter | D1 | D2 | D3 | D4 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| B | FB | B | BFB | CFB | B | BFB | CFB | B | CFB | |
| KV-PB | 16.53 | 16.89 | 14.846 | 15.538 | 15.703 | NM | NM | NM | 15.567 | 16.769 |
| rV-PB | 0.0165 | 0.0142 | 0.0183 | 0.0185 | 0.016 | NM | NM | NM | 0.015 | 0.011 |
| KV-SB | NM | NM | 14.956 | 16.20 | 16.250 | NM | NM | NM | 16.113 | 17.007 |
| rV-SB | NM | NM | 0.0186 | 0.0154 | 0.014 | NM | NM | NM | 0.0130 | 0.010 |
| KV-MAb | 6.29 | 6.80 | NM | NM | NM | NM | NM | NM | NM | NM |
| rV-MAb | 0.0365 | 0.0313 | NM | NM | NM | NM | NM | NM | NM | NM |
| KG | NM | NM | 3.70E−05 | 3.70E−05 | 3.70E−05 | 1.046 | 1.046 | 1.046 | 1.00E−07 | 1.00E−07 |
| KGt | NM | NM | 3.40E−09 | 3.40E−09 | 3.40E−09 | 0.159 | 0.159 | 0.159 | 0.07 | 0.07 |
| KL | NM | NM | 21.49 | 21.49 | 21.49 | 38.43 | 38.43 | 38.43 | 118 | 118.0 |
| KA | NM | NM | 5.14E+2 | 5.14E+2 | 5.14E+2 | 1.27E+3 | 1.27E+3 | 1.27E+3 | 15.7 | 15.7 |
Verhulst parameter values for cell line CHOK1 SV (MAb) (D1), CHO 320 (IFN-γ) (D2), CHO IFN-γ (D4): KV-PB, rV-PB, KV-SB, rV-SB, KV-MAb and rV-MAb; Monod parameter values for the cell lines CHO 320 (IFN-γ) (D2), CHO 320 (IFN-γ) (D3) and CHO IFN-γ (D4)
NM not measured
Table 3.
Validation of Verhulst and Monod growth and productivity models
| Model | D1 | D2 | D3 | D4 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| B | FB | B | BFB | CFB | B | BFB | CFB | B | CFB | |
| V-PB | 0.99 | 0.98 | 0.97 | 0.99 | 0.97 | NM | NM | NM | 0.98 | 0.91 |
| V-SB | NM | NM | 0.97 | 0.98 | 0.98 | NM | NM | NM | 0.95 | 0.91 |
| V-MAb | 0.99 | 0.99 | NM | NM | NM | NM | NM | NM | NM | NM |
| Monod | NM | NM | 0.97 | 0.90 | 0.89 | 0.95 | 0.89 | 0.85 | 0.95 | 0.91 |
V-PB Verhulst population balance, V-SB Verhulst substrate balance, V-MAb Verhulst Monoclonal antibody, NM not measured; all other abbreviations as described in Table 1
Verhulst models
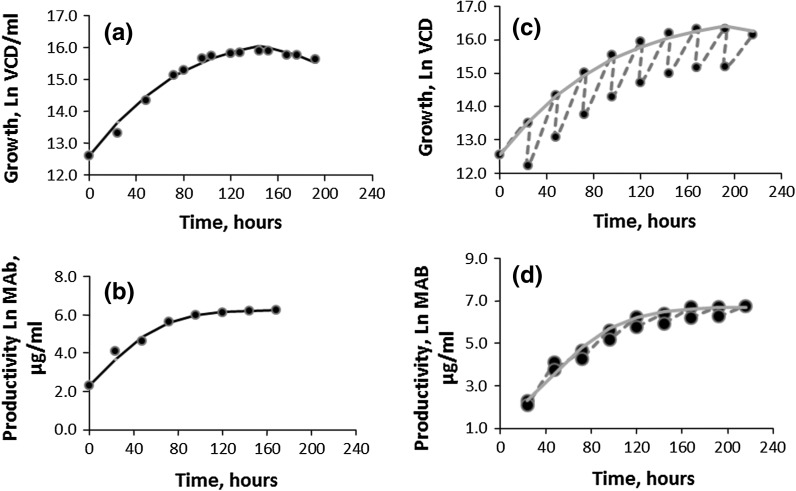
The Verhulst models were validated by comparing the predicted values with the respective new experimental data. The results are presented in Table 3 and Fig. 3a–d. Figure 2a, b represents the new batch and fed-batch data (growth and productivity, respectively) for validation of the Verhulst models. Thus, Fig. 2 describes the experimental growth data of the new batch and fed-batch (50 ml bioreactor) and Fig. 2b describes the productivity data of the new batch and fed-batch cultures (50 ml bioreactor). Figure 3 describes the validation of the Verhulst models for the growth and productivity: (a) B-batch growth data; (b) B-batch productivity data; (c) BFB-fed-batch growth data; (d) BFB-fed-batch productivity data.
Fig. 3.
Validation of the Verhulst models Figure a B-batch growth data; b B-batch productivity data; c BFB-fed-batch growth data; d BFB-fed-batch productivity data. filled circle observed, solid line model, dotted line joining VCD and MAb densities before and after addition of the nutrients
Fig. 2.
Verhulst models for growth and productivity of the cell line CHOK1 SV (MAb) (D1): a Experimental data for growth: B-batch (filled circle) and BFB-fed-batch (open circle); b experimental data for productivity: B-batch (filled circle) and BFB-fed-batch (open circle)
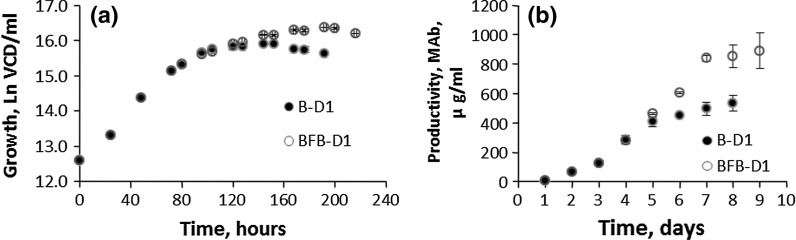
The Verhulst Population-Based (V-PB) models for the growth and productivity of B-D1 and BFB-D1 were found to be in almost complete agreement (R2 > 0.985) with the observed values of VCD and MAb titre. Thus, the results of the Verhulst models for growth and productivity confirmed that the model constants K (Nmax, VCD/ml) and r (intrinsic growth rate, h−1) are physical dimensional entities. Besides, the differences in intrinsic factor r, as in the batch and fed-batch, influence inversely the carrying capacity, K, i.e., the lower the r, the higher the K (Table 2; Fig. 1a, b). In the case of the fed-batch culture (BFB-D1), a lower intrinsic growth factor is not only indicative of higher cell numbers but more importantly a longer exponential phase (B-D1: 144 h, BFD1: 176 h), as shown in Fig. 2a, b. Thus, the Verhulst model constants, K and r, having physical dimension are of biological significance because together they define trajectory of the bioprocess.
The results in the Fig. 2a, b show that the observed values of the growth and productivity for the batch culture (VCD: 8.4 x 106 cells/ml and MAb: 532 μg/ml) and fed-batch culture (VCD: 12.3 x 106 cells/ml and MAb: 875 μg/ml) are in the same proportion as their respective carrying capacities (Ks): KVCD: 15.1 x 106 cells/ml versus 1.6 x 106 cells/ml and KMAb: 546 versus 841 μg/ml. Thus, the carrying capacity is a good indicator of the potential for growth and productivity. It is important to note that whilst CHO cells reached the carrying capacity of the productivity KV-MAb (overall saturation constant), they fell well short (≈45 %) of the carrying capacity for the growth KV-PB because the Verhulst models do not make separate allowances for the part of the substrate, which is used for cellular functions other than growth as well as inhibitory effects of lactate.
The carrying capacity of growth and productivity in the Verhulst models indicated that though the batch and fed-batch cultures (B-D1 and FB-D1, see Table 1) did not reach their full growth potential but they did achieve their full potential for MAb production. This suggests that the antibody production is non-growth associated and the higher productivity in the fed-batch culture can be attributed to the longer exponential phase and longevity as compared to batch culture (Agrawal et al. 1989; Llyod et al. 1999).
It is evident from the comparison of growth and productivity of the B-D1 and BFB-D1 that the carrying capacity K (or Nmax, and Xmax) depends on the composition of the culture medium for a given cell line, e.g., batch and fed-batch. The growth and productivity in the fed-batch culture is higher than that in the batch culture since the growth resources are replenished periodically (Fig. 2a, b respectively). Thus, the Ks reflect the potential of a given culture medium for the growth or productivity. On the other hand, intrinsic factors, rs depend mainly on the physiological state of the cells though it is also influenced by the growth medium. Contrary to Goudar et al. (2005), Hu and Peshwa (1991) are of the view that the kinetics rate of state variables cannot determine the physiological state of the culture because of the intrinsic complexity of animal cells.
As discussed before, the reason for the lower value of growth factor r for the fed-batch culture is the periodic additions of soy hydrolysate, which may cause metabolic shift from proliferation to protein synthesis (Korke et al. 2004; Kumar et al. 2007). This is evident from the data for 50 ml bioreactor which showed an increase in MAb production (B-D1 546 μg/ml, BFB-D1: 841 μg/ml) and a reduction in lactate production (B-D1: 24 mM/l, BFB-D1: 17 mM/l), a sign of slowing down of growth. The model simulation indicated that a high level of lactate can contribute to the reduction of glycolytic process (hence growth), as well as, acting as a driving force for its conversion to pyruvate (Mullkutla et al. 2012). It is evident from the growth results for B-D1 and BFB-D1 (Fig. 2a, b) that the intrinsic growth factor r (0.0177 and 0.0142 h−1 for B-D1 and BFB-D1, respectively) influences the carrying capacity K for growth, but, most importantly, the length of the exponential phase (B-D1: 144 h, BFD1: 176 h). It has been shown that the expression of proteins like MAb reaches its peak in the exponential phase (Leelavatcharamas et al. 1996; Mochida et al. 2000), particularly when the feed contains soy peptides since it alleviates the metabolic stress. Therefore, the longer the exponential phase lasts, the greater the MAb productivity. Thus, the Verhulst model constants, K and r, which are of biological significance, can be employed in a large scale production as reliable indicators of growth and productivity, and useful for optimisation of the cell cultures. The comparison of the Verhust models for the growth and productivity indicates that a single exponential model can describe the productivity in the batch and fed-batch cultures. The productivity profiles of the batch and fed-batch plateaued when the productivity potential (KX) is reached (Fig. 2b). Thus, it appears that the mechanism of the productivity may be different than the growth one.
The V-PB and V-Pr models were also found to be very effective (R2 ≈ 1) in predicting the growth (VCD) and productivity (MAb titre) in the B-D1 and BFB-D1 cultures of CHOK1SV cell line (Fig. 3a–d). Most importantly Fig. 3c, d, representing growth and productivity, respectively, of the fed-batch culture, show that the predictive power of V-PB and V-Pr remains unchanged despite the changes in the composition and volume of the culture medium, resulting from the daily (24 hourly) feedings of soy hydrolyse (dotted line joining the growth and productivity densities before and after addition of nutrients). Therefore, Verhulst models could be useful in optimising media composition for growth and productivity. It is also worth noting that unlike Monod-type models, the Verhulst models and their descendants, like “a four-parameter generalized logistic” models are not affected by the death rate of the cells (Goudar et al. 2005).
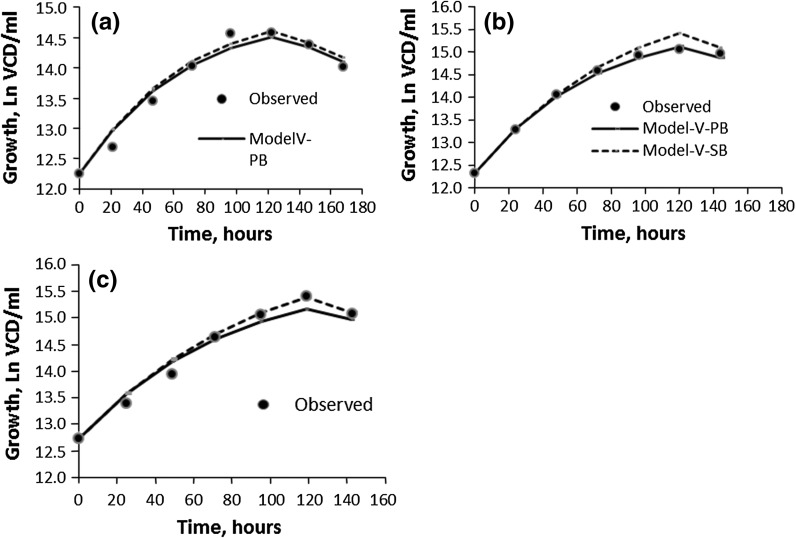
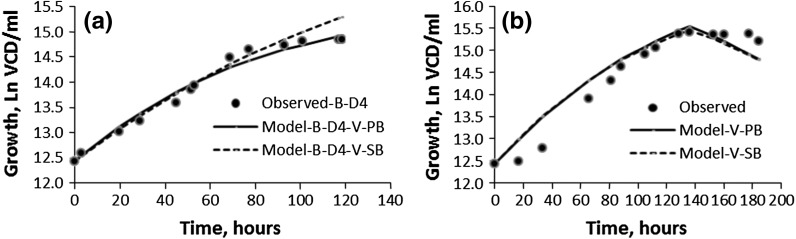
The efficacies of the two Verhulst models, i.e., V-PB and V-SB, for D2 (cell line: CHO 320 (IFN-γ); bioreactor capacity: 3 l) and D4 (cell line: CHO IFN-γ; bioreactor capacity: 3 l; Chee et al. 2005) were compared by plotting the predicted model values against the observed ones (Figs. 4a–c, 5a, b) respectively. The results indicated that, except for CFB-D4 (R2 = 0.91), both V-PB and V-SB models were very good predictors of VCDs (R2 ≥ 0.95) in all three modes of operations, i.e., Batch (B-D2 and B-D4), bolus Fed-batch (BFB-D2) and Continuous culture (CFB-D2 and D4). However, there is a slight, but noticeably discrepancy between the values predicted by V-PB and V-SB (Figs. 4a–c, 5a). The differences between them are reflected in their respective Ks and rs i.e., the lower the rs, the higher the Ks (Table 2).
Fig. 4.
Validation of Verhulst growth models (population balance and substrate balance for the cell line CHO 320 (IFN-γ) (D2): a B; b BFB; c CFB. (filled circle observed, solid line model-V-PB, dotted line model-V-SB)
Fig. 5.
Validation of Verhulst growth models (population balance and substrate balance) for the cell line CHO IFN-γ (D4): a B; b CFB (filled circle observed, solid line model-V-PB, dotted line model-V-SB)
The Verhulst growth models (V-PB and V-SB) did not perform so well with the fed-batch case CFB-D4 (R2 = 0.91) compared to the batch B-D4 case (R2 = 0.98 and 0.95, respectively). The culture medium for CFB-D4 with glutamine as a limiting substrate (0.3 mM) is specifically designed for maintenance and promotion of cell functions such as substrate for protein synthesis, an oxidative fuel protein synthesis, inter-organ nitrogen transfer etc. (Newholme et al. 2003). Thus, it appears that in the glutamine limited CFB-D4 culture medium there is a definite metabolic shift from proliferation to protein synthesis (Korke et al. 2004; Kumar et al. 2007), which may account for the “goodness of fit” (R2 = 0.91) not being as good as in the V-PB and V-SB models for B-D4. In contrast, BFB-D2 and CFB-D2 cultures (R2 ≥ 0.95) are grown in glucose limiting media where cells are not subjected to metabolic shift. This point is further discussed under the Monod model for CFBS.
Evaluation of Monod-hybrid models
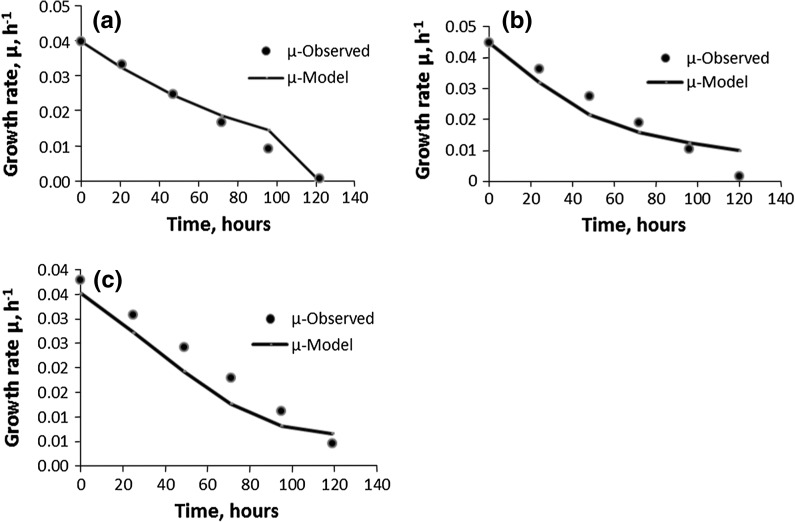
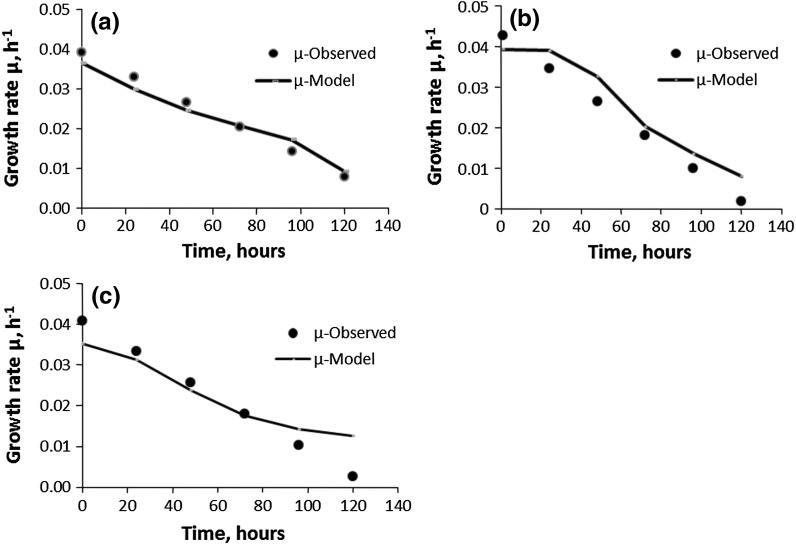
The Monod model constants, KG, KGt, KL and KA (Table 2), in the Eq. (20) were determined by regression method using the transformed experimental batch data: B-D2, B-D3 and B-D4 (Table 2). The Monod batch models, thus arrived at, are applied to the respective bolus and continuous fed-batch cultures for validation. The efficacies of the Monod batch models are described in Figs. 6, 7 and 8, and the results of “goodness of fit” are given in Table 3. The Monod batch models gave very good correlation (R2 ≈ 0.95) with the B-D2 (Fig. 6a), B-D3 (Fig. 7a) and B-D4 (Fig. 8a). However, effectiveness of the extension of the Monod batch models to the corresponding bolus and continuous fed-batch cultures has been somewhat mixed (cf. Table 3).
Fig. 6.
Validation of Monod growth models for the cell line CHO 320 (IFN-γ) (D2): a B; b BFB; c CFB (filled circle observed, solid line model)
Fig. 7.
Validation of Monod growth models for the cell line CHO 320 (IFN-γ) (D3): (a) B; (b) BFB; (c) CFB (filled circle observed, solid line model)
Fig. 8.
Validation of Monod growth models for the cell line CHO IFN-γ: (D4): (a) B; (b) CFB (filled circle observed, solid line model, dotted line model-L)
Except for CFBS-D4, these Monod models, when compared with the Verhulst fed-batch models (R2 ≥ 0.97, cf. Table 3), did not correlate as well with the experimental data for the BFB-D2 and BFB-D3 (Fig. 6b; R2 = 090 and Fig. 7b: R2 = 0.89, respectively) and, CFB-D2 and CFB-D3 (Fig. 6c: R2 = 0.89 and Fig. 7c: R2 = 0.85, respectively) fed-batch cultures with the glucose as limiting substrate. Since the correlation values for the bolus and continuous fed-batch cultures are of the same order for 3 l bench scale and 15 l pilot scale bioreactors imply that the regression methodology used for determining the Monod constants is valid. Therefore, there must be some other possible explanations for the discrepancies between the R2 values of the Monod and the Verhulst models for the D2 and D3 fed-batch cultures as discussed below.
The most probable reason could be that the inhibitory effects of the lactate which is nearly threefold higher in BFB-D2 and BFB-D3, and CFB-D2 and CFB-D3 compared to their respective batch cultures. Glucose is a limiting substrate in the bolus and continuous fed-batches of D2 and D3. High levels of glucose can result in high levels of lactate through glycolysis. Lactate accumulation can reduce the pH throughout the culture and low pH can be detrimental to cell viability and productivity (Hassell et al. 1991). High lactate concentration leads to the dramatic osmolality increase that accompanies the addition of base needed to maintain pH (Li et al.2010). Thus, high lactate concentration has destabilising effects on the cells growth and viability (Li et al.2010). Thus, this very high concentration of lactate might have a distorting effect when the Monod batch models are extended to the fed-batch cultures of D2 and D3. Despite this, all of the Monod batch models, B-D2 and B-D3 for BFB and CFB of D2 and D3 were found to be good indicators of growth, thus, validating the regression methods used in the determination of the Monod model constants (parameters).
In D4, the limiting substrate is glutamine. The correlation between the B-D4 model and experimental data for the CFB-D4 was found to be of the same order for the Monod and the Verhulst models (R2 ≈ 0.91). Therefore, the Monod B-D4 growth model for CFB-D4 can be considered to be as good as the Verhulst model for it. Thus, the carrying capacity K, for growth in the Verhulst model, which is an “overall saturation constant”, appears to be equivalent to the “combined saturation constants”, KG, KGt, KL and KA, in the Monod growth model. This is compelling evidence in support of Monod’s concept of fashioning logistic growth model for yeast after Michaelis–Menten enzyme kinetics (Monod 1949).
As discussed before with the Verhulst models, the CFB-D4 culture with glutamine as the limiting substrate is prone to the metabolic shift from growth to protein production as evident from the increase in the production of IFN-γ by CHO IFN-γ cell line from 3 mg/l in the batch culture to 27 mg/l in the fed-batch culture. Moreover, and more importantly, it was noticed with CFB-D4 (see Table 1) that as the lactate concentration starts dropping (from 28 to 21 mM/l) from 152 h onward (i.e., the start of decline phase), the Monod model for the growth rate (μ) (Fig. 8b), starts deviating from the observed growth profile. However, the reduced form of the Monod model, i.e., [CL/(KL + CL)], for this region (152–249 h) found to be effective in bringing the estimated values of the growth rate (μ) in line with the observed ones (Fig. 8b-Model-L). The effectiveness of the reduced form of the model (152–249 h) suggests that the role of the lactate changes from being an inhibitor to the growth supporting substrate (Nielson et al. 2003) in the decline phase, i.e., effectively describing the decline phase. Thus, the reduced form of the Monod model is a mathematical description of “metabolic flux”. This is a significant finding because the reduced form of Monod-hybrid model is identical to the Michaelis–Menten enzyme kinetic equation. The present work implies that the Verhulst and the Monod models are not able to cope with exceptional phenomena such as metabolic shift in continuous fed-batch cultures and this fact must be taken into account in simulation work for optimisation of a bioprocess.
Since both Verhulst and Monod models show the same “goodness of fit” deficiencies, it is within reason to use an empirical factor (such as 1.09 in the present case) to bring in line the predicted values of growth rate (μs) with the observed ones.
Thus, the model constants derived from the batch data are also valid for fed-batch cultures, confirming the supposition that the growth of the cell lines follows the same kinetics irrespective of mode of the cultivation, batch or fed-batch (Portner and Schafer 1996); the combined effect of Monod model constants is the same as the Verhulst model constants; the reduced form of Monod-hybrid model describing the decline phase of the fed-batch culture is the same as the Michaelis–Menten equation. All of these findings taken together imply explicitly that the constants in Monod-hybrid model are of biological significance. Thus, the constants in the Monod model may not have physical meaning, but they certainly behave as if they are of biological significance.
In summary, the Verhulst model effectively described the batch and fed-batch growth kinetics of all three cell lines (R2 > 0.95). Verhulst logistic models for growth and productivity are mechanistic, i.e., the model constants (K and r) have physical meaning and they are of biological significance influencing directly growth and productivity, i.e., a slightest difference in the intrinsic growth factor r, as in the batch and fed-batch cultures, is magnified in their carrying capacity, K. Thus, intrinsic growth factor truly reflects the physiological state of the cell culture not the rates of other state variables (Hu and Peshwa 1991). The study also shows that the Verhulst models (V-PB, V-Pr) are quite robust, unaffected by changes in volume and composition and hence could be very useful for the laboratory scale (~50 ml) optimisation of culture media for growth and productivity or developing a feeding strategy for fed-batch or for screening the cell lines for specific productivity (μg/cell-day). Further, Verhulst models, V-PB and V-SB, are unperturbed by the mode of bio-reactor i.e., batch, bolus or continuous or limiting-substrate (glucose or glutamine) or volume capacity (50 ml, 3 l or 15 l). Since the Verhulst model constants, K and r, have physical meaning and are of biological significance, they can be employed in large-scale production as reliable indicators of growth and productivity and are useful for optimisation of cell cultures. The V-SB model is particularly useful for determining the values of carrying capacity, B, and the intrinsic growth factor, r, at the end of the first cell cycle, i.e., 24 h, because taken together they set the trajectory for the cell growth. Since glucose is the growth substrate in all bioprocesses, the model can be used for optimising its initial concentration.
The experimental evidence (3 and 15 l CHO cultures) suggests strongly that the Monod-hybrid model is pseudo-mechanistic, i.e., model constants within them may or may not have physical meaning, but their influence on the growth is biologically significant. Thus, the constants in the Monod models, determined by regression methods (MATLAB) using the relevant batch data, were found to be effective in predicting growth in the bolus and continuous fed-batch cultures (D2, D3 and D4); however, sufficiently large observations are required to improve their accuracy. Nevertheless, the positive results in the application of the Monod batch models indicate that batch processes can be used for standardisation and optimisation of the fed-batch cultures. The comparison of the two types of logistic models suggests that the carrying capacity for growth in the Verhulst model is an “overall saturation constant” equivalent to the “combined saturations constants”, KG, KGt, KL and KA, in the Monod model. Further, the effectiveness of the reduced form of Monod-hybrid model to describe decline phase (cf. Fig. 8b) clearly justifies Monod’s concept of fashioning the logistic growth model for yeast after Michaelis–Menten enzyme kinetics. The results (Figs. 5, 8) clearly support the modelling methods used in the present work. Finally, the present work provides a mathematical description of “metabolic shift”, which could have a distorting effect on the model simulation for optimisation. Yet, this problem of modelling of growth during metabolic shift in fed-batch cultures remains hitherto unaddressed.
List of symbols
- K
Carrying capacity for VCD
- KV-PB
Carrying capacity, Verhust-population based for VCD
- KV-SB
Carrying capacity, Verhust-substrate eased for VCD
- KV-MAb
Carrying capacity, Verhust for MAb
- r
Intrinsic growth factor
- rX
Intrinsic productivity factor
- rV-PB
Intrinsic growth factor, Verhulst population based for VCD
- rV-SB
Intrinsic growth factor, Verhulst substrate based for VCD
- rV-MAb
Intrinsic growth factor, Verhulst for MAb
- KG
Glucose Monod constant
- KGt
Glutamine Monod constant
- KL
Lactate Monod constant
- KA
Ammonia Monod constant
References
- Agrawal P, Koshy G, Ramseier M. An algorithm for operating a fed-batch fermenter at optimum specific growth rate. Biotechnol Bioeng. 1989;33:115–125. doi: 10.1002/bit.260330115. [DOI] [PubMed] [Google Scholar]
- Alexander M. Biodegradation and biomediation. 2. London: Academic Press; 1999. [Google Scholar]
- Bailey JE, Ollis DF. Biochemical engineering fundamentals. Singapore: McGraw-Hill; 1986. [Google Scholar]
- Bi J-X, Shuttleworth J, Al-Rubeai M. Uncoupling of cell growth and proliferation results in enhancement of productivity in p21CIP1-arrested CHO cells. London: Wiley; 2004. [DOI] [PubMed] [Google Scholar]
- Brown D, Rothery P (1993) Models in biology, mathematics, statistics and computing. Wiley, Chichester, UK
- Chee Fung Wong D, Tin Kam Wong K, Tang Goh L, Kiat Heng C, Gek Si (2005) Impact of dynamic online Fed-Batch strategies on metabolism, productivity and N-glycosylation quality in CHO cell cultures. Biotechnol Bioeng 89:164–177 [DOI] [PubMed]
- Cui Q, Lawson GJ. Study on models of single populations: an expansion of the logistic and exponential equations. J Theor Biol. 1982;98:645–659. doi: 10.1016/0022-5193(82)90143-6. [DOI] [Google Scholar]
- Dym C (2004) Principles of mathematical modelling. Elsevier Academic Press, London
- Edelstein-Keshet L (2005) Chapter 4: An introduction to continuous models. In: Mathematical models in biology. SIAM, Philadelphia, USA
- Ferenci T. Growth of bacterial cultures’ 50 years on: towards an uncertainty principle instead of constants in bacterial growth kinetics. Res Microbial. 1999;150:431–438. doi: 10.1016/S0923-2508(99)00114-X. [DOI] [PubMed] [Google Scholar]
- Flickinger MC, Drew W. Encyclopaedia of bioprocess technology: fermentation, biocatalysis and bioseparation. New York: Wiley; 1999. [Google Scholar]
- Gompertz B. On the nature of the function expressiveness of the law of human mortality and new mode of determining the value of life contingencies. Philos Trans R Soc Lon. 1825;115:513–585. doi: 10.1098/rstl.1825.0026. [DOI] [Google Scholar]
- Goudar C, Klaus J, Kontantinov K, Piret J. Logistic equations effectively model mammalian cell batch and fed-batch kinetics by logically constraining the Fit. Biotechnol Prog. 2005;21:1109–1118. doi: 10.1021/bp050018j. [DOI] [PubMed] [Google Scholar]
- Grady CPL, Daigge GT, Lim HC. Biological wastewater treatment. New York: Marcel Dekker; 1999. [Google Scholar]
- Hassell T, Gleave S, Butler M. Growth inhibition in animal cell culture: the effect of lactate and ammomnia. Appl Biochem Biotechnol. 1991;30:29–41. doi: 10.1007/BF02922022. [DOI] [PubMed] [Google Scholar]
- Hu W-S (2004) Stoichiometry and kinetics of cell growth and productivity formation. In: Cellular Bioprocess Technology. University of Minnesota
- Hu W-S, Peshwa MV. Selection of microcarrier diameter. Biotechnol Bioeng. 1991;30:548–557. doi: 10.1002/bit.260300412. [DOI] [PubMed] [Google Scholar]
- Jolicoeur P, Pontier J. Asymptotic growth and decline: a four-parameter generalization of the logistic curve. J Theor Biol. 1989;141:563–571. doi: 10.1016/S0022-5193(89)80237-1. [DOI] [Google Scholar]
- Jolicoeur P, Pontier J. Asymptotic models for the longitudinal growth of human stature. Am J Hum Biol. 1992;4:461–468. doi: 10.1002/ajhb.1310040405. [DOI] [PubMed] [Google Scholar]
- Kontoravdi C, Pistikopoulos EN, Manatalaris A. A. Systematic development of predictive mathematical model for animal cell cultures. Comput Chem Eng. 2010;34:1192–1198. doi: 10.1016/j.compchemeng.2010.03.012. [DOI] [Google Scholar]
- Korke R, Gatti Mde L, Lau AL, Lim JW, Seow TK, Chung MC, Hu WS. Large scale gene expression profiling of metabolic shift of mammalian cells in culture. J Biotechnol. 2004;107:1–17. doi: 10.1016/j.jbiotec.2003.09.007. [DOI] [PubMed] [Google Scholar]
- Kovárová-Kovar K, Egli T. Growth kinetics of suspended microbial cells: from single-substrate-controlled growth to mixed-substrate kinetics. Microbiol Mol Biol Rev. 1998;62:646–666. doi: 10.1128/mmbr.62.3.646-666.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krebs CJ. Ecology. 4. New York: Harper and Row; 1996. pp. 198–229. [Google Scholar]
- Kumar N, Gammell P, Clynes M. Proliferation control strategies to improve productivity and survival during CHO based production culture. Cytotechnology. 2007;53:33–46. doi: 10.1007/s10616-007-9047-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee Y, Yean Y, Yap GS, Hu W-S, Wong Cathy TK. Low-glutamine fed-batch cultures of 293-HEK serum-free suspension cells for adenovirus production. Biotechnol Prog. 2003;19:501–509. doi: 10.1021/bp025638o. [DOI] [PubMed] [Google Scholar]
- Leelavatcharamas V, Emery AN, Al-Rubeai M (1996) Monitoring the proliferative capacity of cultured animal cells by cell cycle analysis. In: Al-Rubeai M, Emery AN (eds) Flow cytometry applications in cell culture. Marcel Dekker Inc. p. 1–15
- Li F, Vijayasankaran N, Shen AY, Kiss R, Amanullah A. Cell selection processes for monoclonal antibody production. MAbs. 2010;2:466–477. doi: 10.4161/mabs.2.5.12720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y. Overview of some theoretical approaches to derivation of the Monod equation. Appl Microbial Biotechnol. 2007;73:1241–1250. doi: 10.1007/s00253-006-0717-7. [DOI] [PubMed] [Google Scholar]
- Lloyd DR, Leelavatcharamus V, Emery AN, Al-Rubeai M (1999) The role of the cell cycle in determining gene expression and productivity in CHO cells. Cytotechnology 30:49–57 [DOI] [PMC free article] [PubMed]
- Malthus T (1798) An essay on the principle of population. Printed for J. Johnson, in St. Paul’s Church-Yard London, UK
- Mochida H, Wang PC, Nayve F, Jr, Sato R, Harigae M, Nomura N, Matsumura M. Effects oh high cell density on growth-associated monoclonal antibody production by hybridoma T0405 cells immobilized in macroporous cellulose carriers. Biotechnol Bioprocess Eng. 2000;5:110–117. doi: 10.1007/BF02931881. [DOI] [Google Scholar]
- Monod J. The growth of bacterial cultures. Ann Rev Microbiol. 1949;3:371–394. doi: 10.1146/annurev.mi.03.100149.002103. [DOI] [Google Scholar]
- Mullkutla BC, Gramer M, Hu WS. On metabolic shift to lactate consumption in fed-batch culture of mammalian cells. Metab Eng. 2012;14:138–149. doi: 10.1016/j.ymben.2011.12.006. [DOI] [PubMed] [Google Scholar]
- Newholme P, Lima MMR, Procopio J, Pithon-Curi TC, Bazotte RB, Curi R. Glutamine and glutamate as vital metabolites. Braz J Med Biol Res. 2003;36:153–163. doi: 10.1590/S0100-879X2003000200002. [DOI] [PubMed] [Google Scholar]
- Nielson J, Villadsen J, Liden G (2003) Modeling of growth kinetics. In: Bioreaction engineering principles, 2nd edn. Kluwer Academic/Plenum Publishers, New York
- Portner R, Schafer T. Modelling hybridoma cell growth and metabolism—a comparison of selected models and data. J Biotechnol. 1996;49:119–135. doi: 10.1016/0168-1656(96)01535-0. [DOI] [PubMed] [Google Scholar]
- Prajneshu G. (1998) A nonlinear statistical model for aphid population growth. Ind Soc Agril Statist 51:73–80
- Provost A, Bastin G. Dynamic metabolic modelling under the balanced growth condition. J Process Control. 2004;14:717–728. doi: 10.1016/j.jprocont.2003.12.004. [DOI] [Google Scholar]
- Richards F. A flexible growth functions for empirical use. J. Exper Bot. 1959;10:290–300. doi: 10.1093/jxb/10.2.290. [DOI] [Google Scholar]
- Ricklefs RE. Patterns of growth in birds. J Exp Bot. 1968;110:419–451. [Google Scholar]
- Robertson TB (1908) On the normal rate of growth of an individual and its biochemical significance. Arch Entwickl Org 25:581–914
- Roels JA (1983) Energetics and kinetics in biotechnology. Elsevier, New York
- Thingstad TF. Utilization of N, P and organic C by heterophobic bacteria 1. Online of a chemostat theory with a consistent concept of ‘maintenance’ metabolism. Mar Ecol Prog Ser. 1987;35:99–109. doi: 10.3354/meps035099. [DOI] [Google Scholar]
- Verhulst PF (1838) Notice sur la loi que la population suit dans son accroissment. Correspodance Mathematique et Physique 10:113–121
- Verhulst PF (1847) Deuxième memoire sur la loi ďaccrossement de la population. Mem Acad r Sci Lett Belg 20:1–32
- Wan XR, Zhong WQ, Wang MJ. New flexible growth equation and its application to the growth of small mammals. Growth Dev Aging. 1998;62:27–36. [PubMed] [Google Scholar]
- Wan X, Wang M, Wang G, Zhong WQ. A new four-parameter, generalized logistic equation and its applications to mammalian somatic growth. Acta Theriol. 2000;45:145–153. doi: 10.4098/AT.arch.00-16. [DOI] [Google Scholar]