Significance
An efficient way to form a new declarative memory is to repeat a short-term training many times with a rest between the training sessions, because the learned memory is consolidated after training. This suggests that the brain still keeps actively working even after training, but the synaptic dynamics during posttraining periods has been studied rarely. The posttraining memory consolidation is also observed in cerebellar motor learning. To investigate the mechanism, we formulated a simple theoretical model of the cerebellum with a minimal number of elements and learning-related changes in synaptic efficacy at multiple locations. Computer simulations with this model closely reproduced learning behavior for oculomotor reflexes in wild-type mice and explained peculiar learning behavior in genetically manipulated mice.
Keywords: cerebellum, plasticity, memory consolidation, posttraining period, Marr–Albus–Ito theory
Abstract
Long-term depression (LTD) at parallel fiber–Purkinje cell (PF–PC) synapses is thought to underlie memory formation in cerebellar motor learning. Recent experimental results, however, suggest that multiple plasticity mechanisms in the cerebellar cortex and cerebellar/vestibular nuclei participate in memory formation. To examine this possibility, we formulated a simple model of the cerebellum with a minimal number of components based on its known anatomy and physiology, implementing both LTD and long-term potentiation (LTP) at PF–PC synapses and mossy fiber–vestibular nuclear neuron (MF–VN) synapses. With this model, we conducted a simulation study of the gain adaptation of optokinetic response (OKR) eye movement. Our model reproduced several important aspects of previously reported experimental results in wild-type and cerebellum-related gene-manipulated mice. First, each 1-h training led to the formation of short-term memory of learned OKR gain at PF–PC synapses, which diminished throughout the day. Second, daily repetition of the training gradually formed long-term memory that was maintained for days at MF–VN synapses. We reproduced such memory formation under various learning conditions. Third, long-term memory formation occurred after training but not during training, indicating that the memory consolidation occurred during posttraining periods. Fourth, spaced training outperformed massed training in long-term memory formation. Finally, we reproduced OKR gain changes consistent with the changes in the vestibuloocular reflex (VOR) previously reported in some gene-manipulated mice.
Long-term depression (LTD) at parallel fiber–Purkinje cell (PF–PC) synapses in the cerebellar cortex has been thought to be the major mechanism of motor learning (1). This Marr–Albus–Ito hypothesis (2, 3), however, has been challenged since Miles and Lisberger’s proposal (4) that long-term potentiation (LTP) at mossy fiber–vestibular nuclear neuron (MF–VN) synapses, not LTD at PF–PC synapses, underlies vestibuloocular reflex (VOR) gain adaptation (4–7). In a recent study on optokinetic response (OKR) gain adaptation, we found evidence that might resolve the controversy: LTD at PF–PC synapses (PF-LTD) and LTP at MF–VN synapses (MF-LTP) play different roles in OKR adaptation (8–10). Namely, PF-LTD accounts for short-term memory in PCs during 1-h training, whereas MF-LTP forms long-term memory in VN after the 1-h training that accumulates during repeated trials of 1-h training. It thus appears as if short-term memory formed in PCs during 1-h training is transferred to VN after training to consolidate as long-term memory (8–10).
To investigate the mechanisms of this memory transfer and posttraining consolidation, we conducted a computer simulation study using a simple theoretical model of the cerebellovestibular system including both LTD and LTP at PF–PC synapses and MF–VN synapses. Although several theoretical models have addressed the question of how multiple plasticity mechanisms work together in cerebellar motor learning (11–14), none has explicitly taken the memory consolidation process during posttraining periods into consideration. Our model reproduced previously reported oculomotor behavioral data obtained from wild-type mice (8–10). Notably, the simulated nuclear long-term memory formed mostly after training and relatively little during training, consistent with the hypothesis of posttraining memory consolidation. We also conducted computer simulation of OKR gain adaptation in three strains of gene-manipulated mice in which either PF-LTD or PF-LTP was impaired specifically, or inhibition of PCs was blocked, and reproduced gain changes consistent with those in VOR gain adaptation in those mice (15–17).
Results
Simple Model of Long-Term OKR Gain Adaptation.
We formulated a simple model of the cerebellum with a minimal number of components (Fig. 1 A and B). Details of the formulation are found in Materials and Methods. Briefly, OKR gain in the model at time t is given by the following:
| [1] |
where gOKR is a constant that determines the initial gain value. v(t) and w(t) are the synaptic weights of MF–VN synapses and PF–PC synapses, respectively, and wMLI is the synaptic weight of PF–molecular-layer interneuron (MLI) synapses, which was assumed to be constant 1.0. v(t) was set at 1.0 initially and then updated by the following:
| [2] |
where τv is the time constant of v(t). w(t) was set at 1.0 initially, and then updated by the following:
| [3] |
where τlearn and τrecov are time constants of w(t) during training and after training, respectively. We used separate equations for w(t) because, in slice experiments, PF-LTD is induced quickly within 5 min from the onset of the induction protocol and reaches a steady state 30 min after the induction, but it can last for more than 24 h (18, 19). w0 is the baseline synaptic weight, which is achieved by the balance between PF-LTP and PF-LTD induced by the association of the spontaneous activity of PFs with that of the climbing fiber (CF). cOKR represents the temporal correlation in activity between PFs and the CF during training, which induces PF-LTD. Thus, we considered three types of plasticity contributing to the dynamics of PF–PC synapses: spontaneous PF-LTP, spontaneous PF-LTD, and training-induced PF-LTD. Throughout the present study, we use the following parameter set: gOKR = 0.3, τv = 5.5 h, τlearn = 20 min, τrecov = 2.5 h, w0 = 1.0, and cOKR = 0.3. All of these values were obtained by fitting the OKR gain in the simulation as in Fig. 1C to that in figure 1A of ref. 8.
Fig. 1.
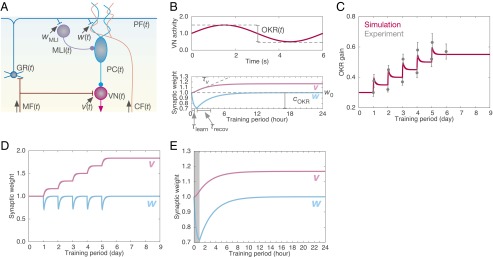
Model overview. (A) Diagram of the cerebellar network. Elements (MF, GR, MLI, PC, VN, and CF), and synaptic weights (w, wMLI, v) are defined in the text. All of the variables except wMLI are a function of time. (B) Parameter definitions. (Top) OKR(t), the depth of modulation of the VN activity in response to sinusoidal MF signals with unit amplitude. (Bottom) w0, the baseline value of w; cOKR, the decrement of w during training; τlearn and τrecov, time constants of w during and after training, respectively; τv defines the slope of the increment of v. (C) Dynamics of the present model in long-term training for 5 d. OKR gain change in the simulation (red) and experimental data (gray) from ref. 8 are compared. Vertical bars indicate the SEM (n = 12). (D) Synaptic weight of PF–PC synapses (w, light blue) and MF–VN synapses (v, pink) throughout the 5-d training. (E) The values of w and v on the first day. The shaded region indicates the 1-h training period.
Cerebellar Learning by Multiple Plasticity Mechanisms at Multiple Sites.
The dynamics of the present model is shown in Fig. 1C (OKR gain) and Fig. 1 D and E (weights of PF–PC and MF–VN synapses). Initially, OKR gain was 0.3. Each day, a 1-h training increased the gain quickly by about 0.12. After the training, the gain gradually decreased and reached a steady state within 23 h. This result suggests that short-term memory forms by 1-h training and thereafter disappears in 1 d. On the other hand, the OKR gain after every training did not return to the level immediately before the onset of the training. As a result, by repetition of the training for 5 d, the OKR gain showed a graded increase up to 0.55, suggesting that long-term memory forms throughout the 5 d. The simulation results fit well with the previous observation (figure 1A in ref. 8), precisely within SEMs, except for the gain before training on the second and third days. Fig. 1D shows that, underlying OKR gain change in Fig. 1C, there were combined changes of PF–PC and MF–VN synaptic weights as in Eq. 1. PF–PC synaptic weight repeated a decrease and complete recovery five times, whereas MF–VN synaptic weight increased gradually day by day, mainly after every training session. We plotted the weight change on the first day separately in Fig. 1E. During the training, MF–VN synaptic weight increased only by 0.03. After that, the weight still increased by 0.17 at the end of the day, indicating that the weight changed mainly after training. These results indicate that PF–PC synapses store short-term memory that is formed through 1-h training and decays within 1 d, whereas MF–VN synapses store long-term memory that is acquired by repeated training and maintained for days. We note that MF–VN synaptic weight did not diverge to infinity nor decay to zero spontaneously during posttraining periods. Such persistence of the increased MF–VN synaptic weight implies the formation of long-term memory.
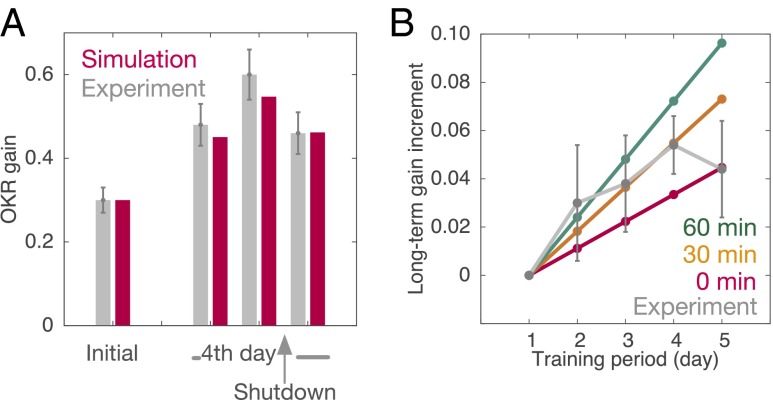
Previous experiments have shown that, if the activity of the cerebellar cortex is shut down by bilateral local injection of lidocaine immediately after training on the last day of a 4-d training, the OKR gain decreases to the level before the training on the same day (8). This shutdown was simulated by setting the activity of PCs to 0 after the last training (see details in SI Text). This manipulation caused OKR gain to decrease to its pretraining level. MF–VN synaptic weight failed to increase after training, whereas PF–PC synaptic weight remained intact, indicating disruption of long-term memory formation. Fig. 2A compares the simulated OKR gain before and after the shutdown in the simulation result and experimental data (8). The model reproduces the experimentally observed OKR gain. We note that the shutdown decreases the modulation of VN activity in response to sinusoidal MF signals, which is proportional to OKR gain, whereas it increases the baseline activity of VN.
Fig. 2.
Disruption of long-term OKR gain learning. (A) Shutting down the cerebellar cortex immediately after training of the fourth day. Simulated OKR gain (red) with experimental data (gray) from ref. 8 are compared. Vertical bars indicate SEM (n = 6). (B) Posttraining muscimol infusion to the cerebellar cortex after 0, 30, or 60 min of training (red, orange, and green, respectively). Long-term gain increment in simulation (color) and in experimental data (gray) from ref. 9 are plotted for comparison. Vertical bars indicate SEM (n = 6).
Infusion of the GABAA receptor agonist, muscimol, to the cerebellar cortex immediately after training disrupts memory transfer (9). Muscimol infusion suppresses firing of PCs by the activation of GABAA receptors on PCs, and thereby VN is released from PC inhibition. We conducted computer simulation of OKR adaptation under muscimol infusion into the cerebellar cortex during posttraining periods. Specifically, we set the PC activity at 0, as in the shutdown simulation, with a delay of 0, 30, or 60 min after each training. Fig. 2B plots the OKR gain before the daily training against the training period (day) in the simulation results and experimental data (9). The simulated OKR gain increased linearly day by day and the slope became steeper with the delay. Average increases of long-term OKR gain obtained by the experiment fall almost in the domain indicated between the lines of 0 and 60 min (9). Because it takes some time for the infused muscimol to activate entire GABAA receptors on PCs after every training session (9), the experimental results support the plausibility of our model.
Massed Versus Spaced Training Effects.
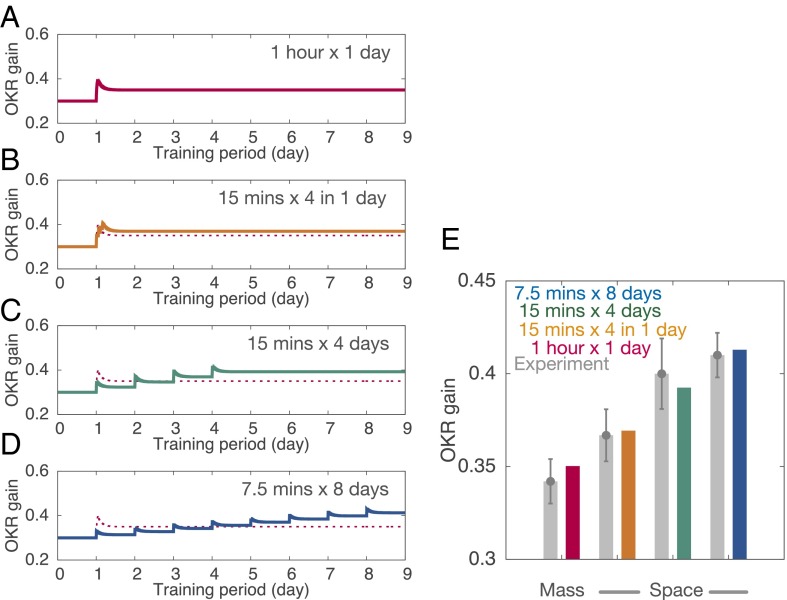
An experiment has shown that a single 1-h training session led to less long-term OKR gain increase when measured 24 h after training, compared with a series of shorter sessions spaced by sufficient rest, such as 15-min training followed by 1 h of rest and repeated four times, or a single 15-min training each day and repeated for 4 d, or a single 7.5-min training each day and repeated for 8 d (10). These results indicate that spaced training outperforms massed training for long-term memory formation; this phenomenon is known as the spacing effect in general (20). We reproduced the spacing effect using the present model.
Fig. 3 shows the OKR gain obtained from simulations in the following paradigms: (A) a single massed training for 1 h, (B) four 15-min trainings spaced by 1-h rest periods, (C) a single 15-min training each day and repeated for 4 d, and (D) a single 7.5-min training each day and repeated for 8 d. Among these four paradigms, the massed training showed the largest instantaneous OKR gain immediately after the training (Fig. 3A). The spaced training sessions showed a mild increase in instantaneous OKR gain after each training, but the gain showed a graded increase across training sessions (Fig. 3 B–D). After the last training session, the gain in spaced training paradigms exceeded that in the massed training (Fig. 3E). These results show that spaced training with appropriate intervals facilitates long-term memory formation, consistent with experimental results (10).
Fig. 3.
Spacing effect for OKR gain adaptation. (A) Massed training, 1-h training in a day. (B) Spaced training, 15-min training spaced by 1 h, four times in a day. (C) Spaced training, 15-min training each day for 4 d. (D) Spaced training, 7.5-min training each day for 8 d. In all cases, total training time was 1 h. Conventions are as in Fig. 1C. In B–D, OKR gain in A is plotted by a thin dashed line for comparison. (E) Comparison of simulated OKR gain (color) with experimental data (gray) from ref. 10. Colors for simulation data represent training paradigms as in A–D. Error bars in the experimental data indicate SEM (n = 11, 9, 7, and 5 for A–D, respectively).
Motor Learning in Genetically Manipulated Animals.
Two recent studies have revealed that genetically manipulated PF-LTP–deficient mice exhibited severe motor deficits and failure of VOR gain adaptation (15), whereas PF-LTD–deficient mice showed seemingly normal VOR gain adaptation (16). It has therefore been proposed that PF-LTP, rather than PF-LTD, plays an essential role in cerebellar motor learning. The same group also reported that selective depletion of GABAA receptors on PCs disrupted long-term memory consolidation while short-term learning remained intact in mice showing mild ataxia (17). Our model for OKR gain adaptation would be applicable to VOR gain adaptation by assuming that MFs mediate vestibular signals instead of optokinetic signals in OKR gain adaptation, because other elements are common to the two gain adaptations. To simulate OKR adaptation in those gene-manipulated mice, we modified simulation settings in some cases for compensation that may occur in genetically manipulated mice (see details in SI Text).
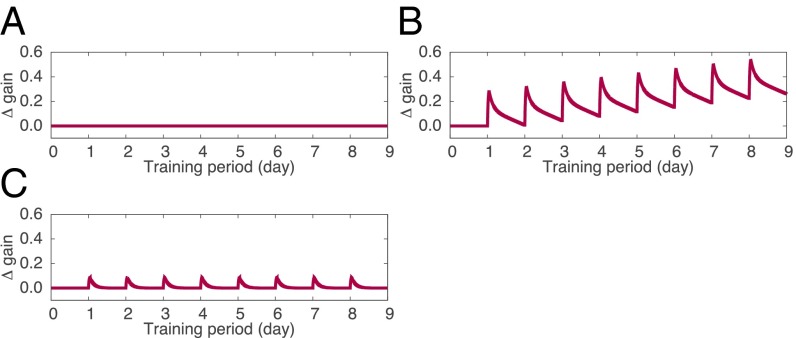
We first considered the case of PF-LTP–deficient mice. In our model, the baseline weight of PF–PC synapses, w0, is determined by the balance of spontaneous PF-LTP and PF-LTD. According to the model as it is, impairment of PF-LTP results in a negative value for the baseline weight so that the value of w(t) is clamped to 0 at the resting state. Thus, the PF–PC synaptic weight vanishes, and consequently PF-LTD no longer occurs. As a result, PF-LTP–deficient simulation showed no change in OKR gain throughout the 8-d training (Fig. 4A), similar to the VOR gain observed experimentally (16). If we consider that the motor performance of mice is a consequence of postnatal long-term learning, motor performance deficits in PF-LTP–deficient animals would result from the failure of long-term learning that started at birth (16).
Fig. 4.
Simulation of long-term OKR gain adaptation in gene-manipulated animals. (A) PF-LTP–deficient simulation. (B) PF-LTD–deficient simulation. (C) Selective depletion of GABAA receptors on PCs. In all panels, we plotted the gain change (Δgain), not the gain value itself, because we do not have experimental data of actual OKR gain values and rather we intended to show whether learning, either short-term or long-term, occurs in each case.
Second, we considered the case of PF-LTD–deficient mice. Due to the lack of spontaneous PF-LTD, the baseline weight w0 becomes larger than that in the normal condition. This may cause overactivation of PCs and consequently complete inactivation of VN; hence, the MF–VN synaptic weight does not increase due to the present learning rule; rather it decays to 0 at rest. In a conventional PF-LTD induction protocol, conjunctive activation of PFs at 1 Hz with the CF at 1 Hz is held for 5 min (21); this stimulation corresponds to spontaneous PF-LTD, because both PFs and the CF elicit spikes tonically without temporal modulation. We assumed that, in PF-LTD–deficient animals, only spontaneous PF-LTD is impaired while training-induced PF-LTD remains intact (i.e., MF–VN synaptic weight can change). A computer simulation of an 8-d training demonstrated that OKR gain in PF-LTD–deficient mice successfully increased day by day, indicating long-term memory formation, although the gain in this condition decayed gradually during rest (Fig. 4B). This atypical learning capability could still lead to seemingly normal OKR adaptation in PF-LTD–deficient mice (15).
Finally, we considered the effect of selective depletion of GABAA receptors on PCs. This manipulation tends to shift the membrane potential of VN toward a hyperpolarized state by strengthened inhibition from PCs, which may result in a negative baseline of OKR gain. We assumed that the gain is compensated for genetically, and therefore we added a constant to the OKR gain for compensation. Simulation conducted in this setting showed that the OKR gain increased after each training but did not accumulate by the repetition of training (Fig. 4C). This suggests that blocking inhibitory inputs to PCs impairs long-term memory consolidation, leaving short-term gain adaptation intact, consistent with the VOR results (17).
Discussion
In this study, we presented a simple theoretical model of the cerebellum that incorporates LTP and LTD at PF–PC synapses and a bidirectional Hebbian rule at MF–VN synapses. The MF–VN synapses update the synaptic weight according to the correlation between the presynaptic MF activity and the postsynaptic VN activity.
Our model successfully reproduces experimental results for long-term OKR adaptation in the following sequential ways. (i) Short-term memory is formed in PCs with PF-LTD by a single session of training. (ii) After the training, the activity of VN is higher than that before training, because the inhibition exerted by PCs is weakened by PF-LTD. (iii) This enhanced VN activity causes LTP at MF–VN synapses by the Hebbian mechanism. (iv) Meanwhile, PF–PC synapses recover from PF-LTD gradually by spontaneous PF-LTP, and this causes a slow decrease in VN activity. (v) The recovery from PF-LTD erases the learned short-term memory, whereas (vi) the slow decrease of VN activity acts to stop the learning at MF–VN synapses. Thus, long-term memory is eventually formed and consolidated. These serial processes explain how short-term memory is transferred from the cerebellar cortex to the nuclei and consolidated there as long-term memory after training.
In contrast to previous models (11–14), our model takes into account the synaptic dynamics during posttraining periods explicitly and reproduces the posttraining memory transfer. Moreover, the explicit use of posttraining periods allows our model to naturally reproduce the spacing effect, whereby the total duration of posttraining periods is more important than that of training periods for long-term memory formation. An inconsistency of the present model would be that the long-term OKR gain in the model increases linearly over time (Fig. 1C), whereas that in the experiment increases in an S-shape. This comes from the linearity of the model. We could incorporate an additional term or nonlinearity to match the simulation result more closely with experiments, but we chose to keep the model as simple as possible.
Electrophysiological studies consistently indicate that plastic changes at MF–VN or MF–cerebellar nuclear neuron (CN) synapses follow a Hebbian rule, which induces synaptic modification by the cooperation of presynaptic MF activity and the postsynaptic nuclear neuron activity (22–27). Specifically, LTP at MF–VN or MF–CN synapses is induced by a combination of tetanic stimulation of MFs with the rebound depolarization of VN neurons induced by the release from prolonged hyperpolarization (23, 25, 27). To model this type of LTP at MF–VN synapses, our Hebbian rule has an additional parameter called a sliding threshold (28). MF–VN synapses undergo LTP only when the postsynaptic VN activity exceeds the threshold, and is paired with the presynaptic MF activity. To exceed the threshold, VN must be released from prolonged hyperpolarization or inhibition exerted by PCs, in accord with experimental results (23, 25, 27). These experimental results would justify the threshold mechanism. The threshold value also changes according to the history of postsynaptic VN activity. Higher threshold values make MF–VN synapses more difficult to undergo LTP. This sliding mechanism is important for robust memory consolidation. In contrast, previous theoretical models (11–14) use a non-Hebbian rule, by which MF–VN synaptic weight decreases when the presynaptic MF and the PC innervating the same VN are coactive or coinactive, and it increases when only one of the two is active. Our model is therefore more biologically plausible with regard to the assumed learning rule.
We extracted the essence of the posttraining memory consolidation from the known anatomy and physiology of the cerebellum and described it using only three equations. Our model reproduces OKR gain data in wild-type mice (8). We also applied our model to OKR gain adaptation in gene-manipulated mice that exhibited peculiar changes in VOR gain (15–17). A computational model for VOR gain adaptation has been proposed (12), in which nuclear learning occurs simultaneously with cortical learning. In that model, nuclear memory forms fully during training and accumulates by repetition of training; posttraining periods were not considered explicitly, suggesting that the total duration of the training but not that of the posttraining periods determines the amount of nuclear memory formed. Therefore, that model would not show the spacing effect. Moreover, in that model, cortical and nuclear learning start simultaneously, but nuclear memory is formed fully even when cortical learning is imperfect. On the other hand, in our model, nuclear memory would be formed only partially during cortical learning when cortical learning is imperfect, because nuclear learning occurs mostly after cortical learning. In this way, considering posttraining periods explicitly or not would provide different results.
Generalization of our model to other types of cerebellar motor learning may not be so straightforward. In Pavlovian eyeblink conditioning, a conditioned response seems to be consolidated in the cerebellar cortex (29–32). Even in OKR adaptation, a trace of long-term memory remains in the cerebellar cortex as the decrease in the number of PF–PC synapses (33, 34), which might represent eye movement trajectory or information on OKR phase (35–37). Moreover, consolidation of motor memory in general should be investigated in depth from reflex to voluntary movement, particularly in primates including humans. A behavioral study of long-term VOR gain learning in monkeys (38) has shown similar memory consolidation to that seen in cats (7) and mice (8), suggesting that memory consolidation mechanisms are preserved from rodents to primates in reflexes such as VOR and OKR. On the other hand, cerebral sensorimotor cortices are thought to be involved in the learning of voluntary movement (39). To discuss memory consolidation in human voluntary movement control, we need to locate the sites of motor memory in the cerebral cortex and cerebellum, and discriminate their functional roles. However, we have very little knowledge on these issues at present. Rather, the present study provides a necessary conceptual piece to tackle the memory mechanism of voluntary movement control in the future. Another theoretical study (40) described voluntary motor learning by a set of dynamical equations with two time constants, which is similar to our model. This study described the behavioral changes purposefully, thereby missing the biological interpretations of synaptic plasticity that are considered in our model.
Accumulating evidence suggests the involvement of different forms of plasticity at multiple sites within the cerebellum (21, 41–44). Plasticity at MF–VN or MF–CN synapses has been shown to mediate certain functions other than storing long-term OKR gain information. These are (i) robust VOR at very high frequencies (12), (ii) savings where relearning a memory that was previously learned and extinguished occurs faster than learning a new memory (45), (iii) adaptive and dynamic gain control for a closed-loop arm manipulation (46), and (iv) context-dependent switching in voluntary arm movement while wearing prism goggles (47). Nevertheless, we propose that PF-LTD plays the primary role in the induction of learning. Moreover, our model provides a likely interpretation about the experimental results of long-term VOR adaptation in mice deficient in PF-LTD (15) and PF-LTP (16) by assuming that spontaneous PF-LTD is affected but training-induced PF-LTD is intact in PF-LTD–deficient mice (15). To date, there is no evidence that the PF-LTD examined in in vitro electrophysiological studies is equivalent to the PF-LTD that occurs in awake animals during motor learning (21). Therefore, PF-LTD, specifically training-induced PF-LTD, is still central to cerebellar learning. This view is logical because PF-LTD is driven by teaching or error signals conveyed by CFs. MLIs also receive CF inputs and exhibit bidirectional plasticity (48). They could influence the spontaneous activity of PCs after training, thereby affecting long-term memory formation indirectly. CF collaterals might provide teaching signals to the VN. Such connections, however, do not exist in rats (49), suggesting that PCs, but not CF collaterals, control plasticity at MF–VN synapses.
In summary, the present model, taking posttraining memory consolidation into account explicitly, provides a theoretical basis toward elucidating multiple plasticity mechanisms in cerebellar learning and memory beyond the Marr–Albus–Ito theory.
Materials and Methods
We derived a system of differential equations based on the known anatomy and physiology of the cerebellum. Fig. 1A illustrates the cerebellar neural circuit that the present model is based on (50).
Let MF(t), GR(t), PC(t), MLI(t), VN(t), and CF(t) be the activities of MFs, granule cells (GRs), PCs, MLIs including stellate and basket cells, excitatory VNs that receive direct cerebellar inhibition, and a CF at time t, respectively. We considered population activity for each cell type, rather than single-neuron activity.
We assumed that GRs simply transmit MF signals to PCs and MLIs via PFs, the axons of GRs:
| [4] |
We also assumed that MLIs simply transmit GR activity to PCs:
| [5] |
where wMLI is a constant representing the synaptic weight of PFs to the interneurons. PCs receive excitatory inputs from PFs and inhibitory inputs from MLIs:
| [6] |
where w(t) is the synaptic weight of PFs to PCs at time t, and PC0 is the spontaneous activity of PCs. VNs receive inputs from MFs and PCs:
| [7] |
where v(t) is the synaptic weight of MFs to the VN at time t, and VN0 is the spontaneous activity of VN.
w(t) and v(t) can change by learning. w(t) is updated by the following rule:
| [8] |
where τw is a time constant that is much longer than the time constant of stimulus patterns conveyed by MF, and represents the temporal average of f(t) over the time span much shorter than τw. The first term on the right-hand side represents spontaneous decay of the synapses. The second term represents LTP triggered by sole activation of GRs (51, 52). The third term represents LTD, which is triggered by conjunctive activation of GRs via PFs and the CF innervating the target PC (1). The term cOKR in Eq. 1 is derived from the term in Eq. 8 and defined as , which represents the temporal correlation between modulation of MFs and that of the CF to drive cortical learning (for derivation, see SI Text). v(t) is updated by the following rule:
| [9] |
where τv is a time constant. The first term on the right-hand side represents LTD triggered by activation of MFs alone (24). The second term represents bidirectional plasticity induced by conjunctive activation of MFs and VN, that is, a form of Hebbian learning. The parameter θ(t) is a sliding threshold that switches between LTP and LTD depending on the postsynaptic activity (28). Specifically, θ(t) is a running average of VN(t) defined by the following:
| [10] |
This formulation is consistent with the results of electrophysiological studies of LTP induction by MF stimulation paired with postsynaptic current injection (23, 25, 27) as mentioned in Discussion.
We omitted other types of neurons and their connections (Discussion). Derivation of OKR gain and related learning rules, and conditions of computer simulation, are described in SI Text.
Supplementary Material
Acknowledgments
T.Y. and W.L. thank Prof. Robert Hecht-Nielsen at University of California, San Diego, and Prof. Nobito Yamamoto at the University of Electro-Communications, for allowing T.Y. and W.L. to collaborate. This study was supported by Japan Society for the Promotion of Science Grants-in-Aid for Scientific Research 20700301 and 26430009, and The University of Electro-Communications Tenure Track Program (6F15). We thank the Japan Society for the Promotion of Science (SP13031) and the National Science Foundation (OISE-1308822) for funding and enabling this collaboration.
Footnotes
The authors declare no conflict of interest.
*This Direct Submission article had a prearranged editor.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1413798112/-/DCSupplemental.
References
- 1.Ito M. Long-term depression. Annu Rev Neurosci. 1989;12:85–102. doi: 10.1146/annurev.ne.12.030189.000505. [DOI] [PubMed] [Google Scholar]
- 2.Marr D. A theory of cerebellar cortex. J Physiol. 1969;202(2):437–470. doi: 10.1113/jphysiol.1969.sp008820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Albus J. A theory of cerebellar function. Math Biosci. 1971;10(1-2):25–61. [Google Scholar]
- 4.Miles FA, Lisberger SG. Plasticity in the vestibulo-ocular reflex: A new hypothesis. Annu Rev Neurosci. 1981;4:273–299. doi: 10.1146/annurev.ne.04.030181.001421. [DOI] [PubMed] [Google Scholar]
- 5.Dufossé M, Ito M, Jastreboff PJ, Miyashita Y. A neuronal correlate in rabbit’s cerebellum to adaptive modification of the vestibulo-ocular reflex. Brain Res. 1978;150(3):611–616. doi: 10.1016/0006-8993(78)90825-9. [DOI] [PubMed] [Google Scholar]
- 6.Ito M. Cerebellar control of the vestibulo-ocular reflex—around the flocculus hypothesis. Annu Rev Neurosci. 1982;5:275–296. doi: 10.1146/annurev.ne.05.030182.001423. [DOI] [PubMed] [Google Scholar]
- 7.Kassardjian CD, et al. The site of a motor memory shifts with consolidation. J Neurosci. 2005;25(35):7979–7985. doi: 10.1523/JNEUROSCI.2215-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Shutoh F, Ohki M, Kitazawa H, Itohara S, Nagao S. Memory trace of motor learning shifts transsynaptically from cerebellar cortex to nuclei for consolidation. Neuroscience. 2006;139(2):767–777. doi: 10.1016/j.neuroscience.2005.12.035. [DOI] [PubMed] [Google Scholar]
- 9.Okamoto T, Shirao T, Shutoh F, Suzuki T, Nagao S. Post-training cerebellar cortical activity plays an important role for consolidation of memory of cerebellum-dependent motor learning. Neurosci Lett. 2011;504(1):53–56. doi: 10.1016/j.neulet.2011.08.056. [DOI] [PubMed] [Google Scholar]
- 10.Okamoto T, Endo S, Shirao T, Nagao S. Role of cerebellar cortical protein synthesis in transfer of memory trace of cerebellum-dependent motor learning. J Neurosci. 2011;31(24):8958–8966. doi: 10.1523/JNEUROSCI.1151-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Medina JF, Mauk MD. Simulations of cerebellar motor learning: Computational analysis of plasticity at the mossy fiber to deep nucleus synapse. J Neurosci. 1999;19(16):7140–7151. doi: 10.1523/JNEUROSCI.19-16-07140.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Porrill J, Dean P. Cerebellar motor learning: When is cortical plasticity not enough? PLoS Comput Biol. 2007;3(10):1935–1950. doi: 10.1371/journal.pcbi.0030197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Masuda N, Amari S. A computational study of synaptic mechanisms of partial memory transfer in cerebellar vestibulo-ocular-reflex learning. J Comput Neurosci. 2008;24(2):137–156. doi: 10.1007/s10827-007-0045-7. [DOI] [PubMed] [Google Scholar]
- 14.Clopath C, Badura A, De Zeeuw CI, Brunel N. A cerebellar learning model of vestibulo-ocular reflex adaptation in wild-type and mutant mice. J Neurosci. 2014;34(21):7203–7215. doi: 10.1523/JNEUROSCI.2791-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Schonewille M, et al. Reevaluating the role of LTD in cerebellar motor learning. Neuron. 2011;70(1):43–50. doi: 10.1016/j.neuron.2011.02.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Schonewille M, et al. Purkinje cell-specific knockout of the protein phosphatase PP2B impairs potentiation and cerebellar motor learning. Neuron. 2010;67(4):618–628. doi: 10.1016/j.neuron.2010.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wulff P, et al. Synaptic inhibition of Purkinje cells mediates consolidation of vestibulo-cerebellar motor learning. Nat Neurosci. 2009;12(8):1042–1049. doi: 10.1038/nn.2348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Murashima M, Hirano T. Entire course and distinct phases of day-lasting depression of miniature EPSC amplitudes in cultured Purkinje neurons. J Neurosci. 1999;19(17):7326–7333. doi: 10.1523/JNEUROSCI.19-17-07326.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Le TD, et al. Lipid signaling in cytosolic phospholipase A2α-cyclooxygenase-2 cascade mediates cerebellar long-term depression and motor learning. Proc Natl Acad Sci USA. 2010;107(7):3198–3203. doi: 10.1073/pnas.0915020107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ebbinghaus H. 1885. Über das Gedächtnis; reprinted (1913) Memory: A Contribution to Experimental Psychology (Teachers College, Columbia University, New York)
- 21.Ito M, Yamaguchi K, Nagao S, Yamazaki T. Long-term depression as a model of cerebellar plasticity. Prog Brain Res. 2014;210:1–30. doi: 10.1016/B978-0-444-63356-9.00001-7. [DOI] [PubMed] [Google Scholar]
- 22.Caria MA, Melis F, Solinas A, Tavera C, Mameli O. Frequency-dependent LTP/LTD in guinea pig Deiters’ nucleus. Neuroreport. 2001;12(11):2353–2358. doi: 10.1097/00001756-200108080-00014. [DOI] [PubMed] [Google Scholar]
- 23.Pugh JR, Raman IM. Potentiation of mossy fiber EPSCs in the cerebellar nuclei by NMDA receptor activation followed by postinhibitory rebound current. Neuron. 2006;51(1):113–123. doi: 10.1016/j.neuron.2006.05.021. [DOI] [PubMed] [Google Scholar]
- 24.Zhang W, Linden DJ. Long-term depression at the mossy fiber-deep cerebellar nucleus synapse. J Neurosci. 2006;26(26):6935–6944. doi: 10.1523/JNEUROSCI.0784-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.McElvain LE, Bagnall MW, Sakatos A, du Lac S. Bidirectional plasticity gated by hyperpolarization controls the gain of postsynaptic firing responses at central vestibular nerve synapses. Neuron. 2010;68(4):763–775. doi: 10.1016/j.neuron.2010.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Menzies JRW, Porrill J, Dutia M, Dean P. Synaptic plasticity in medial vestibular nucleus neurons: Comparison with computational requirements of VOR adaptation. PLoS One. 2010;5(10):e13182. doi: 10.1371/journal.pone.0013182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Person AL, Raman IM. Deactivation of L-type Ca current by inhibition controls LTP at excitatory synapses in the cerebellar nuclei. Neuron. 2010;66(4):550–559. doi: 10.1016/j.neuron.2010.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dayan P, Abbott LF. Theoretical Neuroscience. MIT; Cambridge, MA: 2001. [Google Scholar]
- 29.Cooke SF, Attwell PJE, Yeo CH. Temporal properties of cerebellar-dependent memory consolidation. J Neurosci. 2004;24(12):2934–2941. doi: 10.1523/JNEUROSCI.5505-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Attwell PJ, Cooke SF, Yeo CH. Cerebellar function in consolidation of a motor memory. Neuron. 2002;34(6):1011–1020. doi: 10.1016/s0896-6273(02)00719-5. [DOI] [PubMed] [Google Scholar]
- 31.Kellett DO, Fukunaga I, Chen-Kubota E, Dean P, Yeo CH. Memory consolidation in the cerebellar cortex. PLoS One. 2010;5(7):e11737. doi: 10.1371/journal.pone.0011737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Longley M, Yeo CH. Distribution of neural plasticity in cerebellum-dependent motor learning. Prog Brain Res. 2014;210:79–101. doi: 10.1016/B978-0-444-63356-9.00004-2. [DOI] [PubMed] [Google Scholar]
- 33.Aziz W, et al. Distinct kinetics of synaptic structural plasticity, memory formation, and memory decay in massed and spaced learning. Proc Natl Acad Sci USA. 2014;111(1):E194–E202. doi: 10.1073/pnas.1303317110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wang W, et al. Distinct cerebellar engrams in short-term and long-term motor learning. Proc Natl Acad Sci USA. 2014;111(1):E188–E193. doi: 10.1073/pnas.1315541111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hirata Y, Lockard JM, Highstein SM. Capacity of vertical VOR adaptation in squirrel monkey. J Neurophysiol. 2002;88(6):3194–3207. doi: 10.1152/jn.00698.2001. [DOI] [PubMed] [Google Scholar]
- 36.Yamazaki T, Nagao S. A computational mechanism for unified gain and timing control in the cerebellum. PLoS One. 2012;7(3):e33319. doi: 10.1371/journal.pone.0033319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Yamazaki T, Igarashi J. Realtime cerebellum: A large-scale spiking network model of the cerebellum that runs in realtime using a graphics processing unit. Neural Netw. 2013;47(11):103–111. doi: 10.1016/j.neunet.2013.01.019. [DOI] [PubMed] [Google Scholar]
- 38.Anzai M, Kitazawa H, Nagao S. Effects of reversible pharmacological shutdown of cerebellar flocculus on the memory of long-term horizontal vestibulo-ocular reflex adaptation in monkeys. Neurosci Res. 2010;68(3):191–198. doi: 10.1016/j.neures.2010.07.2038. [DOI] [PubMed] [Google Scholar]
- 39.Krakauer JW, Shadmehr R. Consolidation of motor memory. Trends Neurosci. 2006;29(1):58–64. doi: 10.1016/j.tins.2005.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Smith MA, Ghazizadeh A, Shadmehr R. Interacting adaptive processes with different timescales underlie short-term motor learning. PLoS Biol. 2006;4(6):e179. doi: 10.1371/journal.pbio.0040179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Hansel C, Linden DJ, D’Angelo E. Beyond parallel fiber LTD: The diversity of synaptic and non-synaptic plasticity in the cerebellum. Nat Neurosci. 2001;4(5):467–475. doi: 10.1038/87419. [DOI] [PubMed] [Google Scholar]
- 42.Boyden ES, Katoh A, Raymond JL. Cerebellum-dependent learning: The role of multiple plasticity mechanisms. Annu Rev Neurosci. 2004;27:581–609. doi: 10.1146/annurev.neuro.27.070203.144238. [DOI] [PubMed] [Google Scholar]
- 43.Gao Z, van Beugen BJ, De Zeeuw CI. Distributed synergistic plasticity and cerebellar learning. Nat Rev Neurosci. 2012;13(9):619–635. doi: 10.1038/nrn3312. [DOI] [PubMed] [Google Scholar]
- 44.D’Angelo E. The organization of plasticity in the cerebellar cortex: From synapses to control. Prog Brain Res. 2014;210:31–58. doi: 10.1016/B978-0-444-63356-9.00002-9. [DOI] [PubMed] [Google Scholar]
- 45.Medina JF, Garcia KS, Mauk MD. A mechanism for savings in the cerebellum. J Neurosci. 2001;21(11):4081–4089. doi: 10.1523/JNEUROSCI.21-11-04081.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Garrido JA, Luque NR, D’Angelo E, Ros E. Distributed cerebellar plasticity implements adaptive gain control in a manipulation task: A closed-loop robotic simulation. Front Neural Circuits. 2013;7(159):1–20. doi: 10.3389/fncir.2013.00159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Nagao S, Honda T, Yamazaki T. Transfer of memory trace of cerebellum-dependent motor learning in human prism adaptation: A model study. Neural Netw. 2013;47:72–80. doi: 10.1016/j.neunet.2013.01.017. [DOI] [PubMed] [Google Scholar]
- 48.Jörntell H, Ekerot CF. Reciprocal bidirectional plasticity of parallel fiber receptive fields in cerebellar Purkinje cells and their afferent interneurons. Neuron. 2002;34(5):797–806. doi: 10.1016/s0896-6273(02)00713-4. [DOI] [PubMed] [Google Scholar]
- 49.Sugihara I, Ebata S, Shinoda Y. Functional compartmentalization in the flocculus and the ventral dentate and dorsal group y nuclei: An analysis of single olivocerebellar axonal morphology. J Comp Neurol. 2004;470(2):113–133. doi: 10.1002/cne.10952. [DOI] [PubMed] [Google Scholar]
- 50.Ito M. The Cerebellum and Neural Control. Raven; New York: 1984. [Google Scholar]
- 51.Sakurai M. Synaptic modification of parallel fibre-Purkinje cell transmission in in vitro guinea-pig cerebellar slices. J Physiol. 1987;394:463–480. doi: 10.1113/jphysiol.1987.sp016881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Lev-Ram V, Mehta SB, Kleinfeld D, Tsien RY. Reversing cerebellar long-term depression. Proc Natl Acad Sci USA. 2003;100(26):15989–15993. doi: 10.1073/pnas.2636935100. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.