Nanomechanics and intermolecular forces of amyloid revealed by four-dimensional electron microscopy

Significance

The biomechanics of amyloid underlies its function in living organisms. We use four-dimensional electron microscopy to systematically dissect the nanoscale origins of amyloid elasticity by measuring the bond stiffnesses of the intermolecular forces stabilizing each of its three characteristic packing interfaces. We find amyloid to have a pronounced mechanical anisotropy with longitudinal, hydrogen bonding 20 times stiffer than transverse, amphiphilic, and electrostatic interactions. Such strongly anisotropic elastic properties are likely to give rise to length-dependent mechanical behavior with short fibrils possessing significantly different material properties than longer fibrils. This is of great importance in understanding fibril–membrane interactions and fragmentation mechanisms, both of which are thought to play a crucial role in the spread of amyloid diseases.

Abstract

The amyloid state of polypeptides is a stable, highly organized structural form consisting of laterally associated β-sheet protofilaments that may be adopted as an alternative to the functional, native state. Identifying the balance of forces stabilizing amyloid is fundamental to understanding the wide accessibility of this state to peptides and proteins with unrelated primary sequences, various chain lengths, and widely differing native structures. Here, we use four-dimensional electron microscopy to demonstrate that the forces acting to stabilize amyloid at the atomic level are highly anisotropic, that an optimized interbackbone hydrogen-bonding network within β-sheets confers 20 times more rigidity on the structure than sequence-specific sidechain interactions between sheets, and that electrostatic attraction of protofilaments is only slightly stronger than these weak amphiphilic interactions. The potential biological relevance of the deposition of such a highly anisotropic biomaterial in vivo is discussed.

The intricate interplay of intermolecular forces stabilizing amyloid at the atomic level has yet to be fully elucidated (1). Amyloid fibrils are narrow (70–200 Å), elongated (1–3 μm), twisted (pitch $\sim$ 1,000 ± 500 Å) aggregates containing a universal “cross-β” core structure (2) composed of arrays of β-sheets running parallel to the long axis of the fibrils (3). Their hierarchical structure is stabilized by three main protein–protein interfaces: (i) stacking of hydrogen-bonded β-strands within a single β-sheet (intrasheet), (ii) cross-β-sheet packing into a multisheet protofilament (intersheet), and (iii) lateral association of protofilaments (interprotofilament) (4). Each of these packing interfaces gives rise to characteristic diffraction pattern reflections corresponding to the intrasheet (4.8 Å), intersheet (8–12 Å, depending on sidechain volume), and interprotofilament (determined by chain length) spacings (5).

By applying a laser-induced, temperature (T-) jump to amyloid, we can infinitesimally expand the material, thereby probing the intermolecular forces acting across each of the packing interfaces (6). Static, global heating, particularly of amyloid-like microcrystals (7), disrupts molecular structure, precluding such delicate perturbations. To capture the rapid expansion and recovery of an amyloid specimen, a precisely timed, pulsed (probe) electron beam, following the laser (pump) pulse, is used to generate a series of time-resolved diffraction patterns. By accurately measuring the movement $\left(\mathrm{\Delta }x\right)$ of the reflection (initially occurring at an equilibrium separation, $x_e$) upon initiation of the ultrafast temperature jump, we determine the relative expansion, or strain, $\mathit{ϵ}=\mathrm{\Delta }x/x_e$. Atomistic simulations predict that the stretching elasticity of amyloid is linear for strains up to only $\mathit{ϵ}\sim 0.1$%, i.e., ${10}^{-3}$ (8). The exquisite sensitivity and high spatiotemporal resolution of four-dimensional (4D) electron microscopy (9, 10) enables us to measure such minute deformations and directly probe, at the atomic level, the stiffness of the intermolecular forces stabilizing amyloid.

Results and Discussion

Intrasheet.

Previously, we have shown that 4D electron diffraction of a network of amyloid fibrils can yield information on the atomic expansion dynamics of the fibrils’ constituent β-sheets (6). Here, we report our investigation of the picometer-scale stretching of the intrasheet interface as a function of amino acid sequence with a view to better understanding, at the atomic level, the contribution of interbackbone hydrogen bonding and sidechain interactions to its rigidity.

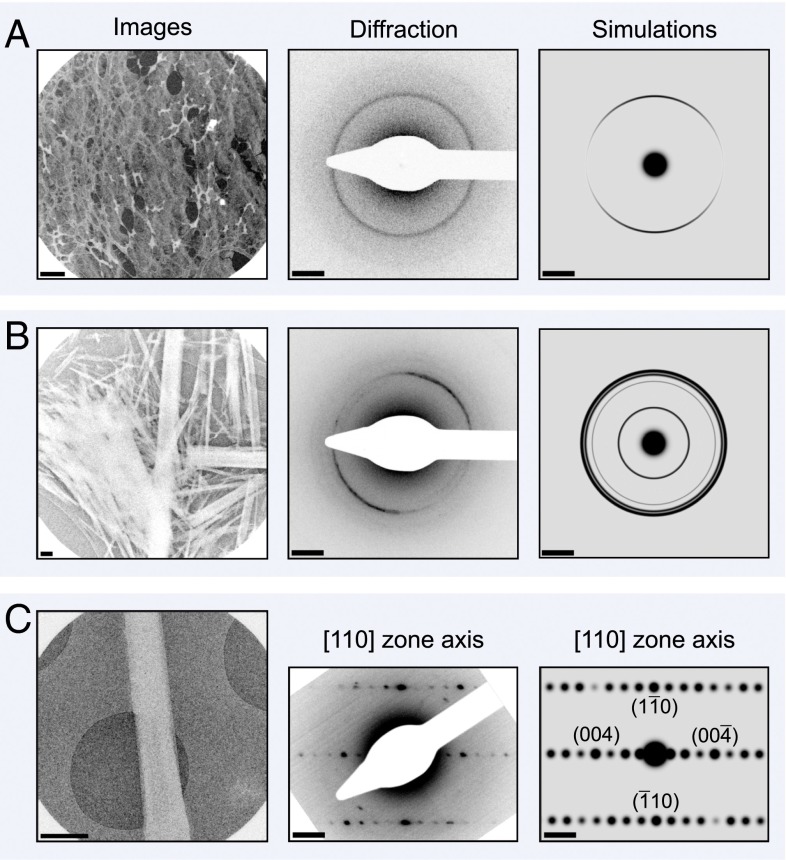
To reach our objective, we investigated the atomic expansion dynamics of fibril networks (Fig. 1A, Left) formed by five different peptides and proteins with diverse native structures, various chain lengths, and disparate amino acid sequences: insulin (11), peptide fragment 105-115 of transthyretin, TTR(105-115) (4), residues 1-40 of amyloid β-peptide, Aβ(1-40) (12), residues 1-42 of amyloid β-peptide, Aβ(1-42) (13), and lysozyme (14). Under identical experimental conditions, electron diffraction experiments were performed on each of the fibril networks and the relative expansion of the fibrils, as indicated by the change in radius of the $x_e$ = 4.8 $\text{Å}$ fiber diffraction ring (Fig. 1A, Middle and Right) upon excitation by the pump pulse (fluence $\sim$4 mJ/cm²), allowed us to determine the stiffness of the intermolecular forces holding the intrasheet interface together.

Fig. 1.

Images, selected area diffraction patterns, and simulated diffraction patterns of (A) a network of amyloid fibrils, (B) an ensemble of amyloid-like microcrystals, and (C) a single microcrystal taken using our 4D electron microscope. Protein density is shown in white on (A and B) lacey carbon substrate and (C) holey silicon nitride substrate, respectively. (A) Image and diffraction patterns of a network of amyloid fibrils. Note the strong 4.8-Å reflection––a hallmark of amyloid structure corresponding to the interstrand separation within β-sheets. (B) Image and diffraction patterns of an ensemble of amyloid-like microcrystals. The 4.8-Å (1 1 0) Bragg peaks give rise to the most intense Debye–Scherrer ring. Other reflections can be used to gain a more complete picture of lattice dynamics. (C) Image and diffraction patterns of a single amyloid microcrystal. Note the intense, paired ($\overline{1}$ 1 0) and (1 $\overline{1}$ 0) spots at 4.8 Å, and the (0 0 4) and (0 0 $\overline{4}$) spots at 5.4 Å. The scale bar in the real-space images corresponds to a distance of 1 μm and in the diffraction images it is equal to 1 nm⁻¹.

As in our previous study (6), we bind a small amyloidophilic dye molecule, Congo red, to the outer surface of the fibrils to efficiently transfer energy to the peptide or protein molecules, although it is important to note that the dye does not perturb the cross-β structure because it is bound to the outer surface of the fibrils (15). The dye used to transfer energy to the fibrils is common to all so that a valid comparison of dynamics can be made between the five datasets.

We initiate a slight expansion of the constituent β-sheets by inducing a small temperature jump, $\mathrm{\Delta }T$, in the fibrils (ranging from 4.0 to 6.1 K, Fig. S1), using a pump fluence $\sim$4 mJ/cm², and capture the increase in β-strand separation by diffracting the fibrils using a timed probe electron pulse with delay times ranging from −100 to 500 ns in 50-ns increments. With all of the fibril networks, the expansion is rapid (Fig. S2). We note that the rise of the expansion is within the T-jump resolution. This rise simply reflects the time for heat transfer from the dye to the protein and it is typically on a subnanosecond timescale (16). Here, it is of no relevance.

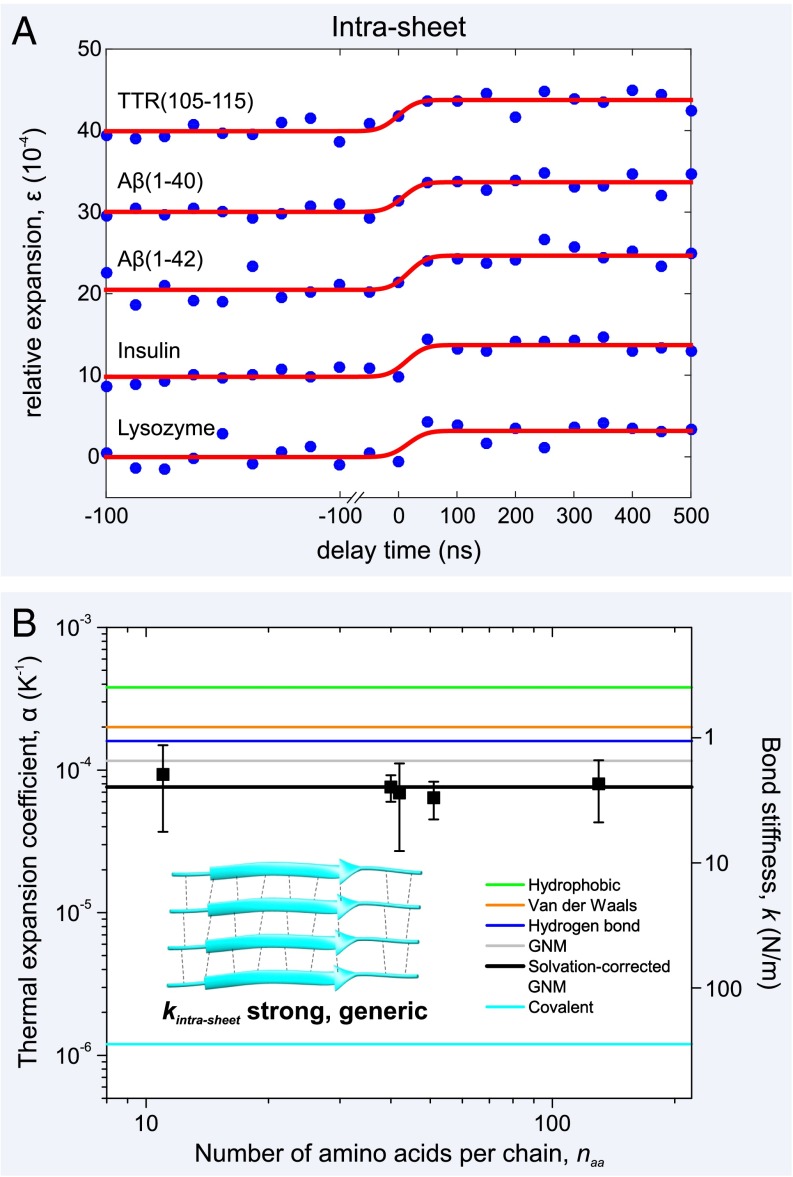
The relative expansion, ε, of the insulin, TTR(105-115), Aβ(1-42), Aβ(1-40), and lysozyme fibrils is $3.9\pm 0.4\times$ 10⁻⁴, $3.8\pm 0.5\times$ 10⁻⁴, $4.2\pm 0.6\times$ 10⁻⁴, $3.6\pm 0.4\times$ 10⁻⁴, and $3.2\pm 0.6\times$ 10⁻⁴, respectively (Fig. 2A). Because we have determined the T-jump for each system by monitoring the temporal change of the diffraction intensity (SI Methods), we can calculate the individual thermal expansion coefficients, α, for each of the fibril networks (Fig. 2B) and find that they are approximately constant, spanning a small range of 0.6–0.9$\times$ 10⁻⁴ K⁻¹.

Fig. 2.

Atomic expansion dynamics of amyloid fibrils as a function of amino acid sequence and chain length. (A) Plots of the relative expansion of the amyloid fibrils formed by five peptides and proteins as a function of time (curves have been shifted for clarity). Upon initiation of the T-jump, there is a rapid (Fig. S2) expansion of between 3.2–4.2 $\times$ 10⁻⁴ by all of the amyloid fibril networks, irrespective of sequence or chain length, $n_{aa}$. (B) By determining the T-jump for each of the fibril networks (Fig. S1), the thermal expansion coefficients, α, can be plotted, along with experimental error bars. This physical quantity is inversely proportional to the square of the bond stiffness, k (right axis), and a simple GNM, together with values of α from the literature (19–21), can be used to explain the experimental results (see main text). A schematic of the fibril’s constituent β-sheets is shown (Inset) with individual β-strands, connected by interbackbone hydrogen bonds (black dashed lines), shown as cyan ribbons. The representative β-sheet image was created using Protein Data Bank (PDB) ID code 2M5N.

Intermolecular bond stiffness, k, is directly related to the thermal expansion coefficient, α, via the empirical “Barker’s rule” (17), $Y=15/{\alpha }^2=k{x}_e/A$, where Y is Young’s modulus and A is the cross-sectional area through which the bond acts. The interstrand bonding within the fibrils’ constituent β-sheets, $k_{\mathit{int}rasheet}$, can be coarse-grained as a simple network of springs acting in parallel to stabilize the intrasheet interface (Fig. 2B, Inset). We use this Gaussian network model (GNM) (18) approach to decompose the various contributions to the bonding using

$$k_{\mathit{int}rasheet}=k_{H\text{-}bond}+k_{vdW}+k_{hydrophobic}=\frac{15A}{x_e}\left[\frac{1}{{\alpha }_{H\text{-}bond}^2}+\frac{1}{{\alpha }_{vdW}^2}+\frac{1}{{\alpha }_{hydrophobic}^2}\right],$$ [1]

where the subscripts “H-bond,” “vdW,” and “hydrophobic” denote hydrogen bonding, van der Waals packing interactions, and hydrophobic attraction, respectively.

By using values from the literature, we plot the positions of ${\alpha }_{H\text{-}bond}$ (19), ${\alpha }_{vdW}$ (20), and ${\alpha }_{hydrophobic}$ (21) (Fig. 2B), so that a comparison with the experimental data may be made. By Eq. 1, we predict an intrasheet thermal expansion coefficient, ${\alpha }_{GNM}$, of 1.2$\times$ 10⁻⁴ K⁻¹. However, we have previously found that partial dehydration of amyloid fibrils in the vacuum of the microscope decreases thermal expansion by $\sim$35% owing to a slight stiffening of the hydrogen-bonding network (6). Taking this into account, the solvation-corrected ${\alpha }_{GNM}$ is reduced to 0.8$\times$ 10⁻⁴ K⁻¹, in excellent agreement with our experimental values, $0.8\pm 0.1\times$ 10⁻⁴ K⁻¹.

We now use Eq. 1 to determine Young’s modulus and the intrasheet force constant, $k_{\mathit{int}rasheet}$. The fibril networks have Young's moduli, Y, ranging from 1.7 to 3.7 GPa, in good agreement with previous studies (18, 22). Note, however, that here we are measuring the stiffness of an amyloid fibril network, not just a single fibril. This is an important distinction because fibril thickness varies throughout the network, due to polymorphism (4, 23), and may affect material properties (24). Eq. 1 gives $k=\left(15A/x_e\right)\left(1/{\alpha }^2\right)$, where $A=(3.5$ Å$\times 10$ Å) originates from an interresidue spacing of 3.5 $\text{Å}$ and an intersheet spacing of 10 $\text{Å}$, resulting in an intrasheet bonding stiffness, $k_{\mathit{int}rasheet}$, of 2.0 $\pm$ 0.5 N/m.

It is clear from the experimental results that α, Y, and $k_{\mathit{int}rasheet}$ are approximately constant and display only a weak dependence on amino acid sequence, or chain length, $n_{aa}$ (Fig. 2). This suggests that the exceptional rigidity of the intrasheet interface is defined largely by sequence-independent, intermolecular hydrogen bonding with sidechain–sidechain interactions (van der Waals, hydrophobic) playing only a minor role in stabilizing the fibrils’ constituent β-sheets (25, 18). Indeed, the intrasheet bonding stiffness, $k_{\mathit{int}rasheet}=2.0\pm 0.5$ N/m, is identical to the bond stiffness of other cooperatively hydrogen-bonded materials ($k_{H\text{-}bond}=2-3$ N/m), such as ice (26, 27). It is important to note that although the intrasheet bond stiffness, $k_{\mathit{int}rasheet}$, in mature fibrils arises mainly from generic interbackbone hydrogen bonding, the relative propensity to form such filamentous aggregates will vary with sequence (28).

Intersheet.

Electron diffraction patterns of fibril networks (Fig. 1A, Middle and Right) do not reveal either the “sidechain” spacing of 8–12 $\text{Å}$ in the intersheet direction, or the interprotofilament spacing along the peptide chain length. To determine the magnitude of the forces stabilizing these crucial packing interfaces, we performed 4D electron diffraction on (i) an ensemble of photoresponsive amyloid-dye cocrystals and then (ii) on a single, submicrometer crystal.

The 3D amyloid microcrystals have a cross-β structure (Fig. 3B) with $\sim$10% orange-G dye molecules bound to the outer surface of the paired β-sheets (7). Each orange-G molecule acts as an absorbing center to efficiently transfer energy to the peptide molecules (29), although it is important to note that the dye does not perturb the structure of the cross-β motif (Figs. 3B and 4B). When these crystals are randomly oriented (Fig. 1B, Left), Debye–Scherrer rings are formed (Fig. 1B, Middle and Right). It is the relative change in radius of these reflections upon excitation by the T-jump that allows us to resolve structural dynamics of the peptide molecules within the 3D amyloid microcrystals (Fig. 3A).

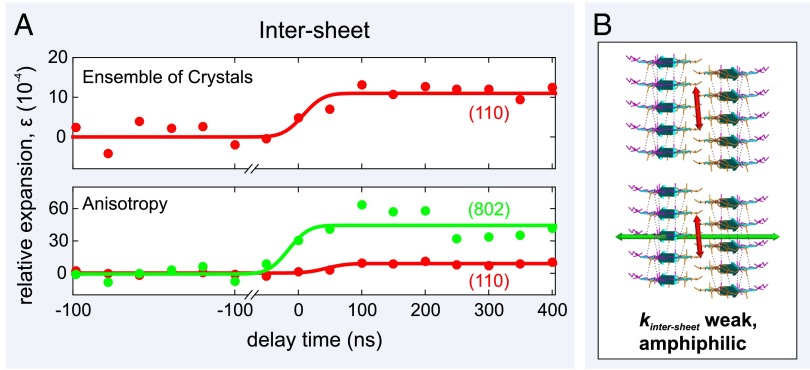
Fig. 3.

Atomic expansion dynamics of an ensemble of amyloid-like microcrystals measured using 4D electron microscopy. (A) Plots of the relative expansion of the amyloid-like microcrystals as a function of time. (B) Schematics of the expansion of the amyloid microcrystals' paired β-sheet structure. Individual β-strands, connected by interbackbone hydrogen bonds (black dashed lines), are shown as cyan ribbons. The interstrand separation is 4.8 Å, whereas the intersheet separation is 10.4 Å. The ensemble of 3D microcrystals displays an expansion of the β-sheets (along the [1 1 0] direction) of 9.2 $\pm$ 0.8$\times {10}^{-4}$ (red arrow), whereas the dynamics along the [8 0 2] direction shows that there is a much larger expansion of 46 $\pm$ 11$\times {10}^{-4}$ (green arrow) in the sheet–sheet direction.

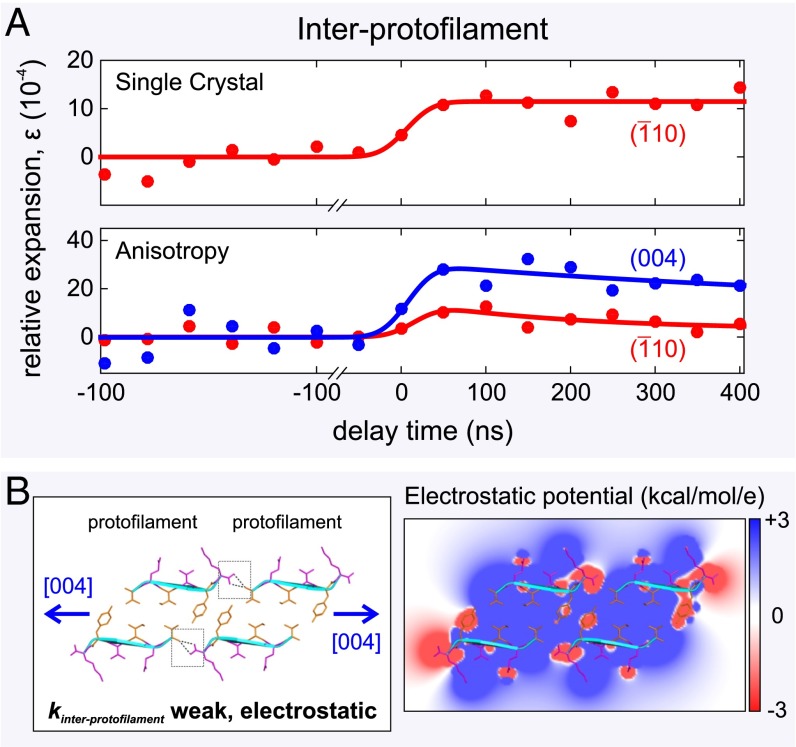
Fig. 4.

Atomic expansion dynamics of a single amyloid-like microcrystal measured using 4D electron microscopy. (A) The single 3D microcrystal displays an expansion of the β-sheets of 11 $\pm$ 4.0$\times {10}^{-4}$, whereas the dynamics along the [0 0 4] direction shows that there is a much larger expansion of 28 $\pm$ 8.0$\times {10}^{-4}$ in the interprotofilament direction. (B, Left) Schematic of the expansion of the protofilament–protofilament interface with the stabilizing bifurcated hydrogen bonds (dashed black lines) highlighted by two gray boxes. Individual β-strands are shown as cyan ribbons. (B, Right) A cross-section of the electrostatic potential surface of the protofilament–protofilament complex is shown ranging from +3 kcal⋅mol⁻¹ per electron (blue) to −3 kcal⋅mol⁻¹ per electron (red), with white representing uncharged regions of the constituent peptides. For clarity, an overlaid ribbon and stick representation makes individual sidechains more identifiable. The cross-β structure was created using PDB ID code 3OVL.

We collected a series of diffraction frames (Fig. 1B, Middle) from an ensemble of crystals on lacey carbon grids (Fig. 1B, Left), using delay times ranging from −100 to 400 ns in 50-ns increments (Fig. 3A) and a pump fluence $\sim$6 mJ/cm². The greater number of reflections visible in the Debye–Scherrer pattern (Fig. 1B, Middle and Right, and Fig. S3), compared with the fibril diffraction pattern (Fig. 1A, Middle and Right), allows us to obtain a fuller picture of the structural dynamics. We can measure not only T-jump expansion in the backbone–backbone, intrasheet direction but also in the sidechain–sidechain, intersheet direction in an approach identical to that recently used to explore the atomic expansion dynamics of anisotropic multiwalled carbon nanotubes (30). In addition to the (1 1 0) intrasheet reflection at 4.8 $\text{Å}$, we resolve the (8 0 2) reflection at 5.2 $\text{Å}$ and the (10 0 2)/(8 0 3) reflection at 4.4 $\text{Å}$ (Fig. S3), both of which are in the intersheet direction. Interestingly, upon initiation of the laser-induced T-jump ($\sim$8 K), the movement of the intersheet (8 0 2) and (10 0 2)/(8 0 3) reflections is rapid ($<$ 50 ns) and over 4 times larger than that of the intrasheet (1 1 0) reflection. For the same set of diffraction patterns, a relative expansion of 9.2 $\pm$ 0.8$\times {10}^{-4}$ is detected along the [1 1 0] direction (Fig. 3A, Bottom), whereas along the intersheet [8 0 2] and [10 0 2]/[8 0 3] directions the relative expansions are 46 $\pm$ 11$\times {10}^{-4}$ and 43 $\pm$ 12$\times {10}^{-4}$, respectively (Fig. 3A, Bottom).

The [1 1 0] lattice vector is not entirely parallel to the intrasheet direction [0 1 0], and neither are [8 0 2] and [10 0 2]/[8 0 3] parallel to the intersheet direction [1 0 0]. We therefore calculate the component of the displacement vector acting along each of these directions by multiplying by the cosine of the angle between the lattice vectors for this monoclinic unit cell, e.g., the angle between [1 1 0] and [0 1 0] is $5.15°$. Thus, we obtain a relative expansion along the [0 1 0] direction of 9.2 $\pm$ 0.8$\times {10}^{-4}$, and relative expansions of 40.6 $\pm$ 9.7$\times {10}^{-4}$ or 39.4 $\pm$ 11$\times {10}^{-4}$ along the [1 0 0] direction depending on whether we consider the [8 0 0] or [10 0 0] component, respectively. On average, the ratio of the strains acting along the [1 0 0] and [0 1 0] directions is 4.3 $\pm$ 0.8.

The anisotropy of intermolecular forces stabilizing the amyloid cross-β structure is now apparent (Fig. 3B). Invoking the equipartition theorem and assuming that the elastic potential energy introduced to the crystal lattice by the laser, U, is distributed in all directions equally, the laser-induced strain in the intrasheet direction [0 1 0], ${\mathit{ϵ}}_{\mathit{int}rasheet}$, is over 4 times less than that in the intersheet direction [1 0 0], ${\mathit{ϵ}}_{\mathit{int}ersheet}$.

Given that $U=\left(1/2\right)Y{\mathit{ϵ}}^2$, we can therefore write

$$Y_{\mathit{int}rasheet}{\mathit{ϵ}}_{\mathit{int}rasheet}^2=Y_{\mathit{int}ersheet}{\mathit{ϵ}}_{\mathit{int}ersheet}^2,$$ [2]

where $Y_{\mathit{int}rasheet}$ and $Y_{\mathit{int}ersheet}$ are Young’s moduli in the intrasheet and intersheet directions, respectively. Then, the ratio $Y_{\mathit{int}rasheet}$:$Y_{\mathit{int}ersheet}$ is equal to 18.8 $\pm$ 7.3, meaning that the rigidity in the backbone–backbone, intrasheet direction is, on average, almost 20 times greater than that in the sidechain–sidechain, intersheet direction.

Previously, we determined Young’s modulus of these amyloid microcrystals to be 1.2 GPa (29). This corresponds approximately to Young’s modulus along the long axis of the crystal needle, $Y_{\mathit{int}rasheet}$. Given that $Y_{\mathit{int}ersheet}$ is $\sim$5% of the value of $Y_{\mathit{int}rasheet}$, $Y_{\mathit{int}ersheet}=0.06$ GPa. This significantly lower modulus suggests much weaker intermolecular forces acting between paired β-sheets than within individual β-sheets. Interestingly, referring to Fig. 2B, using Barker’s rule and the experimentally determined value of ${\alpha }_{hydrophobic}=3.8\times$ 10⁻⁴ K⁻¹ (21), we calculate Young’s modulus for materials stabilized by amphiphilic intermolecular interactions, $Y_{hydrophobic}$, to be 0.1 GPa. This agrees very well with the value of $Y_{\mathit{int}ersheet}$, indicating that the intersheet interface is mediated by interactions between hydrophobic and hydrophilic sidechains. This is confirmed when we use a coarse-grained model for the stiffness of the sheet–sheet interface (18), $Y_{\mathit{int}ersheet}=k_{\mathit{int}ersheet}/h$, where $k_{\mathit{int}ersheet}$ is the intersheet bond stiffness and h is an intersheet spacing of 10.4 $\text{Å}$, to calculate $k_{\mathit{int}ersheet}$ = 0.07 N/m. The spring constant $k_{hydrophobic}$ has an expected range of between 0.04 and 0.1 N/m, varying from hydrophilic to hydrophobic (8, 31, 32). Not surprisingly, given that the sequence of the amyloid-crystal-forming peptide (VQIVYK) is only weakly hydrophobic (average sequence hydrophobicity, +0.24), our measured $k_{\mathit{int}ersheet}$ = 0.07 N/m falls at the midpoint of these values.

Interprotofilament.

Finally, we investigated the nature of the bonding stabilizing the laterally associated protofilaments (Fig. 4B, Left). The interprotofilament interface can be probed by examining movements of the (0 0 l) reflections, but these are the weakest reflections and not visible in the Debye–Scherrer diffraction pattern (Fig. 1B, Middle and Right). Therefore, we examined the diffraction from a single amyloid microcrystal on holey silicon nitride substrate (Fig. 1C, Left) so that individual Bragg reflections could be resolved. The specimen was tilted with respect to the (probe) electron beam so that the crystal could be viewed down the [1 1 0] zone axis, making the (0 0 l) and ($\overline{1}$ 1 0) spots clearly visible in the diffraction pattern (Fig. 1C, Middle and Right). It is the relative change in the decreased separation of the paired ($\overline{1}$ 1 0) and (1 $\overline{1}$ 0) spots at 4.8 $\text{Å}$, and the (0 0 4) and (0 0 $\overline{4}$) spots at 5.4 $\text{Å}$ (Fig. 1C, Right), upon initiation of the laser-induced T-jump ($\sim$10 K) that allows us to resolve structural dynamics in these directions.

As expected, the relative expansions along the intrasheet [0 1 0] direction of a single crystal, $11\pm 4.0\times {10}^{-4}$ (Fig. 4A, Top), and a network of amyloid microcrystals, $11\pm 1.0\times {10}^{-4}$ (Fig. 3A, Top), are identical, indicating that “single-particle” and ensemble dynamics are indistinguishable. However, the movement of the weak (0 0 4) reflections can now be discerned and we measured the relative expansion in the interprotofilament [0 0 1] direction of 28 $\pm$ 8.0$\times {10}^{-4}$ (Fig. 4A, Bottom). The ratio of the strains acting along the interprotofilament direction, ${\mathit{ϵ}}_{\mathit{int}erprotofilament}$, and the intrasheet direction, ${\mathit{ϵ}}_{\mathit{int}rasheet}$, is 2.5 $\pm$ 1.2. This ratio indicates that the expansion between laterally associated protofilaments (Fig. 4B, Left) is less than intersheet expansion under identical experimental conditions, suggesting that marginally stronger intermolecular forces act between protofilaments than between paired β-sheets. By applying Eq. 2 to the interprotofilament case, we determine Young’s modulus in the protofilament–protofilament direction, $Y_{\mathit{int}erprotofilament}$, to be 0.16$\times Y_{\mathit{int}rasheet}$ or 0.19 GPa. $Y_{\mathit{int}erprotofilament}$ is approximately 3 times greater than the intersheet Young modulus, $Y_{\mathit{int}ersheet}$ (0.06 GPa), and when converted into a bond stiffness acting between the protofilaments $k_{\mathit{int}erprotofilament}=\left(A/x_e\right)Y_{\mathit{int}erprotofilament}$, where $A=(4.8$ Å$\times 10.4$ Å) arises from an intrasheet spacing of 4.8 $\text{Å}$ and an intersheet spacing of 10.4 $\text{Å}$ and $x_e$ = 6.4 $\text{Å}$ is the equilibrium separation of peptide chains (Cα–Cα) in the interprotofilament direction, gives a value of 0.14 N/m. Therefore, $k_{\mathit{int}erprotofilament}$ is twice as rigid as $k_{\mathit{int}ersheet}$ (0.07 N/m) and slightly greater than the upper bound of a spring constant arising from amphiphilic interactions, $k_{hydrophobic}$ (0.1 N/m).

Examination of the protofilament–protofilament packing interface (Fig. 4B, Left) reveals that adjacent protofilaments are interconnected in a head-to-tail manner, stabilized by dipole–dipole interactions between the N and C termini of peptide chains in neighboring protofilaments (Fig. 4B, Right) and by two bifurcated hydrogen bonds (here one H-bond donor is bound to two H-bond acceptors, C=O$\dots$H$\dots$O=C) between the terminal C=O and N–H groups (4) (Fig. 4B, Left). A coarse-grained estimate of the spring constant, $k_{electrostatic}$, arising from lateral electrostatic attraction between protofilaments (SI Methods), is 0.02–0.05 N/m. Because the measured $k_{\mathit{int}erprotofilament}$ is 0.14 N/m, the interprotofilament bonding stiffness must be further increased by $\sim$0.1 N/m (additive because springs are acting in parallel) owing to the presence of the bifurcated hydrogen bond. These interprotofilament hydrogen bonds are likely to be significantly weaker than the intrasheet hydrogen bonds, $k_{\mathit{int}rasheet}$ (2.0 $\pm$ 0.5 N/m), because (i) bifurcated hydrogen bonds are $\sim$ 50% weaker than canonical hydrogen bonds (33) and (ii) density functional theory calculations have shown that the anhydrous, low dielectric constant environment within two-sheet protofilaments, and the cooperative stacking of innumerable backbone, hydrogen-bond-forming amide groups, strengthens canonical hydrogen bonds by between a factor of 3 and 6 (34). The combination of these effects ($6/0.5$ is a reduction of a factor of 12) can explain the weakness of solvated, bifurcated interprotofilament hydrogen bonds relative to the rigid intrasheet hydrogen bonds. Thus, it is the combination of electrostatic attraction and bifurcated hydrogen bonding which stabilizes the laterally associated protofilaments formed by short peptides.

Biological Relevance.

Here we have shown, at the atomic level, that the intermolecular forces acting to stabilize the three main protein–protein interfaces in the hierarchical structure of amyloid (4) are highly anisotropic, with $k_{\mathit{int}rasheet}\gg k_{\mathit{int}erprotofilament}\mathrm{\gtrsim }{k}_{\mathit{int}ersheet}$. We have identified the molecular origins of each of these intermolecular bond stiffnesses with $k_{\mathit{int}rasheet}$ governed mainly by rigid, sequence-independent interbackbone hydrogen bonding, $k_{\mathit{int}erprotofilament}$, due to a combination of weak, bifurcated hydrogen bonds and dipole–dipole electrostatic attraction and $k_{\mathit{int}ersheet}$ arising from specific, sidechain–sidechain amphiphilic interactions.

Because interatomic bond stiffness largely determines mechanical stiffness (26), the exceptional rigidity of amyloid (18, 22, 29) derives overwhelmingly from a longitudinal, interbackbone hydrogen-bonding network with lateral, intersidechain, and electrostatic interactions almost 20 times less important. Such a large degree of anisotropy leads to length-dependent mechanical properties of amyloid (Fig. 5). If we consider that $k_{\mathit{int}erprotofilament}\sim k_{\mathit{int}ersheet}$ (transversely isotropic), then amyloid has bond stiffnesses $k_{long}=2.0$ N/m and $k_{lat}=0.1$ N/m, with a degree of anisotropy, $k_{lat}/k_{long}=0.05$, almost identical to microtubules (35) $\left(k_{lat}/k_{long}=0.1/4.0=0.025\right)$.

Fig. 5.

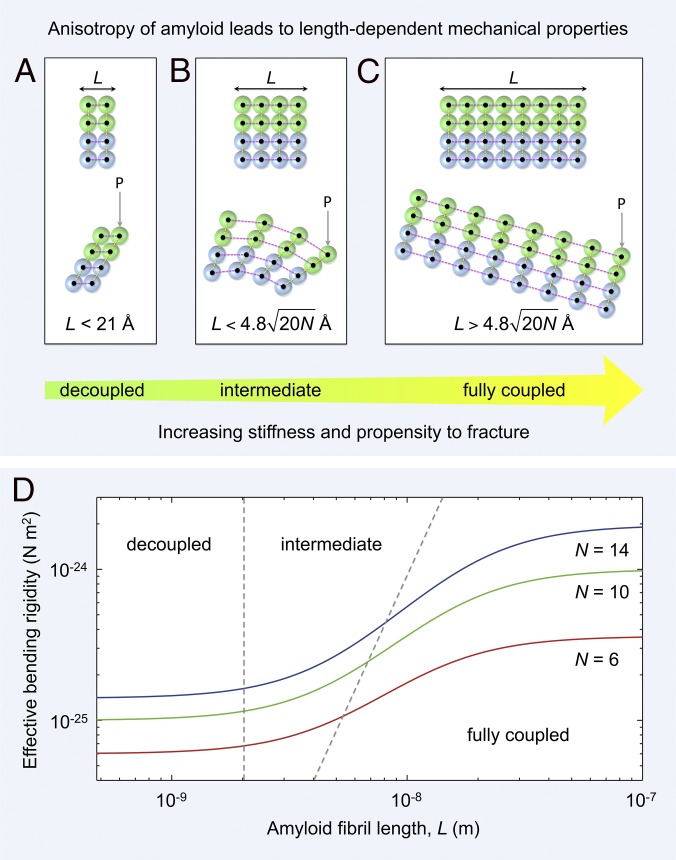
Mechanical anisotropy of amyloid leads to length-dependent material properties. (A–C) An amyloid fibril is a network of rigid β-strands (colored spheres) interconnected via elastic (strong) longitudinal (magenta dashed lines) and (weak) lateral bonds (yellow dashed lines). Amyloid fibrils of different lengths, L, along the hydrogen-bonding axis are shown schematically as two laterally connected protofilaments (green and blue spheres represent the first and second protofilament, respectively). (A) A short fibril (Upper) bends under a load P through shearing of lateral intersheet and interprotofilament bonds [Lower, decoupled regime (36)]. (B) Fibrils of intermediate length (Upper) bend through a combination of extension or compression of longitudinal bonds and shearing of lateral intersheet and interprotofilament bonds [Lower, intermediate regime (36)]. (C) For long fibrils (Upper), longitudinal bonds stretch or compress during bending, with shear contributions becoming negligible [Lower, fully coupled regime (36)]. (D) The predicted shear-weakening effect (36) on the effective bending rigidity of fibrils is plotted as a function of fibril length (SI Methods). Data are plotted for doublet (red line), triplet (green line), and quadruplet (blue line) fibril polymorphs formed by TTR(105-115) (4). The boundaries between decoupled, intermediate, and fully coupled bending are shown as gray dashed lines.

Bending of an individual amyloid fibril (Fig. 5 A–C) involves extension or compression of longitudinal bonds and shearing of lateral intersheet and interprotofilament bonds. By analogy with cytoskeletal bundle mechanics (36), a protofilament coupling parameter, γ, can be defined which is a measure of the competition between intersheet/interprotofilament shearing and fibril stretching:

$$\gamma =\frac{k_{lat}}{k_{long}}\left(\frac{L^2}{{\delta }^2}\right),$$ [3]

where L is the fibril length and δ is the axial spacing of intersheet/interprotofilament bonds ($\delta =4.8$ Å). Thus, the competition between bending and shear deformations is governed by (i) the degree of anisotropy, (ii) the spacing of the intersheet/interprotofilament “cross-links,” and (iii) the fibril length (36). When $\gamma \ll 1$, “decoupled” bending (36) occurs through shearing of adjacent β-sheets or protofilaments (Fig. 5A). In the “intermediate” regime $1\ll \gamma \ll N$ (36), fibril bending occurs through a combination of fibril stretching and sheet–sheet or protofilament–protofilament shearing (Fig. 5B). Finally, in the limit $\gamma \gg N$, where N is the total number of intersheet and interprotofilament interfaces per 4.8 Å layer of fibril, “fully coupled” bending (36) is achieved through extension or compression of longitudinal bonds (Fig. 5C).

The consequence of these dissimilar deformation mechanisms is that at low fibril aspect ratio, shear contributions to bending become increasingly significant (36, 37). The length scales of each of these regimes can be calculated using Eq. 3. We predict that decoupled bending occurs when the fibril length is less than 21 Å, that a combination of bending and shearing occurs in the range 21 Å $<L<4.8\sqrt{20N}$ Å, and that fully coupled bending (as described by Euler–Bernoulli beam theory) occurs at lengths greater than $L>4.8\sqrt{20N}$ Å.

The nanomechanical effect of shear-dominated bending below the critical length scale, $L^{\mathrm{\ast }}\sim$ 4.8$\sqrt{20N}$ Å (at $\gamma \sim N$), is to increase the flexibility of the fibril (Fig. 5D) because bending under a tensile load, P, can be accommodated through shearing of compliant intersheet and interprotofilament bonds (Fig. 5 A and B). Such “shear weakening” reduces the effective bending rigidity of the fibrils typically by up to an order of magnitude (Fig. 5D). Indeed, we predict that fibrils only attain a constant bending rigidity at lengths greater than $\sim$1,000 Å (Fig. 5D), which is comparable to one helical pitch repeat of a twisted amyloid fibril (4, 37). Below this length scale, and in particular below $L^{\mathrm{\ast }}\sim$ 100 Å, there is a significant reduction in bending stiffness due to shear contributions from intersheet and interprotofilament sliding (Fig. 5 A, B, and D).

The biological implication of this model is that extremely short fibrils are flexible and ductile whereas longer fibrils are stiff and brittle (38) [if we assume, as experiment suggests (39), that fibril fracture occurs through the breakage of longitudinal hydrogen bonds]. Higher rupture forces would be required to fragment low aspect ratio fibrils, because they can deform through shear, whereas longer, high aspect ratio fibrils would become increasingly fracture-prone due to the $L^{-2}$ scaling of critical buckling force for an Euler–Bernoulli beam (36). The proposed length dependence of amyloid fibrils’ stiffness and fracture mechanics may have ramifications in vivo. Fibril fragmentation creates more growing fibril ends, thus favoring the proliferation of new fibrils (40). Our results suggest that breakage of longer, brittle fibrils may result in the accumulation of shorter, less fracture-prone, and potentially more cytotoxic (41), low aspect ratio fibrils. In addition, whereas longer, mechanically stiff fibrils are able to disrupt (42) or perforate cell membranes (43), short fibrils, although shear weakened, are still sufficiently stiff ($Y\sim$ several hundred MPa) and pervasive to insert themselves into a lipid bilayer and stiffen the highly flexible ($Y\sim$ 1 MPa) cell membrane (44).

Conclusions

Finally, the preponderance of sequence-independent intermolecular hydrogen bonding over amphiphilic sidechain interactions in stabilizing the amyloid state is an inversion of the situation for globular proteins where the collapse-inducing hydrophobic force leads to a spherical tertiary structure with nonpolar residues buried in the core and largely polar residues on the surface of the protein. By contrast, the 20-fold dominance of unidirectional intermolecular hydrogen bonding, achievable by all polypeptide backbones, over sequence-specific, sidechain interactions in defining the high rigidity of the amyloid cross-β structure explains not only the quasi-1D morphology of amyloid fibrils, but also the accessibility of the amyloid state to peptides and proteins, irrespective of sequence.

Materials and Methods

VQIVYK orange-G cocrystals and amyloid fibrils were prepared as described previously (7, 18). VQIVYK orange-G cocrystals or amyloid fibrils were applied to lacey carbon (Electron Microscopy Sciences) or silicon nitride 50-nm microporous (Transmission Electron Microscopy windows) grids. Four-dimensional electron diffraction patterns were acquired in stroboscopic mode (Fig. 1) using timed photoelectron packets (120 kV, LaB₆ source) and a green pump pulse (λ = 532 nm, repetition rate 1 kHz). Diffraction patterns were acquired at a CCD camera length of 1.0 m and 1.5 m. All analysis and rendering of figures was performed in MATLAB, Chimera (45), or PyMOL (46). Full methods are available in SI Methods.