Kernel methods for large-scale genomic data analysis

Abstract

Machine learning, particularly kernel methods, has been demonstrated as a promising new tool to tackle the challenges imposed by today’s explosive data growth in genomics. They provide a practical and principled approach to learning how a large number of genetic variants are associated with complex phenotypes, to help reveal the complexity in the relationship between the genetic markers and the outcome of interest. In this review, we highlight the potential key role it will have in modern genomic data processing, especially with regard to integration with classical methods for gene prioritizing, prediction and data fusion.

INTRODUCTION

Kernel methods are based on mathematical functions that smooth data in various ways. Generally, there are two major uses for kernel methods. One is kernel density estimation, a nonparametric method to estimate the probability density function of a random variable. This differs from our discussion on kernel methods that focuses on kernel machines and regression concepts, a nonparametric approach to estimate the relation between an outcome ‘trait’ variable (e.g. phenotype such as disease status or a quantitative health measure) and high-dimension genomic data. Some advantages of kernel methods, relative to traditional regression models, are allowance for high-dimension genomic data, nonlinear relations between outcomes and genomic data, flexible ways to include structured information and computational sophistication. In the following sections, we discuss ways to construct kernels for genomic data; how kernel machine methods can be viewed in a more popular regression framework; how kernel methods can be used to test associations between high-dimensional genomic data and a trait; how kernel methods can be used to construct predictive models; and how structured information, such as genome annotations, can be built into kernel methods.

KERNELS FOR GENOMIC DATA

A basic ingredient for kernel machine learning is a kernel function. A kernel function converts information for a pair of subjects into a quantitative measure representing their similarity with respect to genetic information, with the requirement that the function must create a symmetric positive semi-definite (psd) matrix when applied to any subsets of subjects. The psd requirement ensures a statistical foundation for using the kernel in penalized regression models. From a statistical perspective, the kernel matrix can be viewed as a covariance matrix, a point we later show how this aids in the construction of kernels.

For genome-wide association studies (GWAS), a popular kernel is a weighted linear kernel. Single nucleotide polymorphism (SNP) genotypes can be coded as G having values 0, 1 or 2 according to the number of copies of the minor allele. For q SNPs, a weighted linear kernel for subjects i and j, can be expressed as $K_{ij}={\displaystyle {\sum }_{k=1}^q{w}_k{G}_{ik}{G}_{jk}}$, where $w_k$ weights each SNP, such as by the standard error of the estimated minor allele frequency (MAF), $w_i=1/\sqrt{p_i(1-p_i)}$, or other types of functions based on MAF [1], or based on functional information. Because a common allele could be carried by many subjects by chance alone, giving greater weight to sharing of rarer SNP genotypes can increase the strength of relation between the kernel matrix and a trait [2]. Higher-order polynomials could also be used for kernel functions, to capture nonlinear associations of a trait with genotypes. For example, a quadratic kernel that captures the additive effects of alleles, the quadratic effects of alleles and first-order SNP–SNP interactions can be represented as $K_i={(1+{\displaystyle {\sum }_{k=1}^p{w}_k{G}_{ik}{G}_{jk}})}^2$. The ‘1’ in this kernel is analogous to the intercept in regression models. Higher-order polynomials could be used to capture higher-order interactions. An exponential type of kernel could be used, such as a Gaussian kernel $K_i=\exp [-{{\displaystyle {\sum }_{k=1}^q(G_{ik}-G_{jk})}}^2/\delta ]$, corresponding to radial basis functions. Another popular kernel for genomic data, determined by ‘alike-instate’, is based on whether genotypes match, $K_{ij}={\displaystyle {\sum }_{k=1}^p{w}_k(2-|G_{ik}-G_{jk}|)}$ [1].

Other types of kernels are possible, such as kernels based on the probability density of attributes, called Fisher kernels [3–5] or marginalized kernels [6]. See Schaid [7] for more details and examples. A useful kernel for a wide range of genomic attributes that accounts for missing data is the general coefficient of similarity proposed by Gower [8]. Gower’s general measure of similarity is a weighted average over observed attributes, $S_{ij}={\displaystyle \sum _{k=1}^q{s}_{ijk}w(x_{ik},x_{jk})}/{\displaystyle \sum _{k=1}^q{\delta }_{ijk}w(x_{ik},x_{jk})}$, where $s_{ijk}$ is the similarity score for subjects i and j for attribute k, ${\delta }_{ijk}=1$ for an informative or noninformative comparison (a noninformative comparison is when data for an attribute are missing for either subject), and the weight $w(x_{ik},w_{jk})$ can depend not only on the attribute k, but also on the observed attributes for subject i and j, for example, giving greater weight for matches on rare levels than on common levels. Advantages of this general coefficient are that it allows for different types of attributes (dichotomous, categorical and quantitative), it allows use of weights when summing over attributes and it is psd if there are no missing data.

KERNEL MACHINE AND ASSOCIATION TEST: FROM A REGRESSION PERSPECTIVE

The balance of making high-dimensional kernels and then using them to model the association of traits with genomic information lies in the ways that statistical models are constrained, such as by penalized nonparametric regression models, support vector machines or a Bayesian perspective. For a review of the ties among these popular statistical approaches see Schaid [9]. Fortunately, there is a solid mathematical statistical theory that supports the wide utility of kernel methods and penalized regression, called ‘Reproducing Kernel Hilbert Space’, RKHS [10, 11].

To provide an intuitive explanation of penalized nonparametric regression with least squares kernel machines, consider the usual ordinary least squares regression setup, $Y=X{\beta }_1+G{\beta }_2+e$, where Y is a vector of traits for n subjects, X is an $n\times p$ parametric design matrix to account for covariates (e.g. age, gender), ${\beta }_1$ is a p dimensional vector, Gis an $n\times q$ matrix for q SNP genotypes, ${\beta }_2$ is a q dimensional vector for the association of genotypes with the trait and eis a vector of residual errors. For high dimensional data ($q>n$), this model cannot be fit without further constraints. One approach is to retain the parametric covariate matrix X, but replace the parametric genetic part, $G{\beta }_2$, with a nonparametric function, $f(G)$, and assume constraints on f. This is where the kernel matrix and the theory of RKHS help. The kernel matrix K is used to constrain the fit of the model by defining a function space that contains possible values of the function f. It can be shown that $f=K\alpha$, where α is a vector of parameters to estimate. The nonparametric function can be fit by minimizing, with respect to α, the penalized function $loss(\alpha )=(Y-X{\beta }_1-K\alpha )\text{'}(Y-X{\beta }_1-K\alpha )$ $+\lambda {\alpha }^{\prime }K\alpha$, which is a sum of squared residuals with the penalty $\lambda {\alpha }^{\prime }K\alpha$. The tuning parameter, λ, balances the model goodness-of-fit with complexity. When $\lambda =0$, the model interpolates the genetic data. In contrast, as $\lambda \to \infty$, the genetic data drop out, resulting in the usual least squares regression on only the covariates X.

Determining an optimal tuning parameter, λ, requires cross-validation for complex models. However, for quantitative traits and least squares kernel machines, the penalized model can be conveniently fit with standard software for mixed models as follows. By assuming f has a multivariate normal distribution, $f\sim N(mean=0,\mathrm{var}={\sigma }_K^{2}K)$, and $e\sim N(0,{\sigma }_e^{2}I)$, the resulting maximum likelihood estimators (alternatively restricted maximum likelihood estimators) ${\widehat{\sigma }}_K^2$ and ${\widehat{\sigma }}_e^2$ map to the tuning parameter as $\lambda ={\sigma }_e^2/{\sigma }_K^2$. Hence, when the genomic information explains little of the trait variation, ${\sigma }_K^2<<{\sigma }_e^2$, resulting in large values of λ, so the genomic information essentially drops out of the model. In contrast, when genomic information explains much of the trait variation, ${\sigma }_K^2>>{\sigma }_e^2$, resulting in small values of λ, the kernel function plays a large role in smoothing the fit of the data. For further details see [12–14].

The link of least squares learning machines with linear mixed models provides a Bayesian view of the nonparametric function of genetic data, by treating f as a random vector with mean 0 and covariance matrix ${\sigma }_K^{2}K$, which is closely aligned with using identity-by-descent to model genetic variance components [15]. This view has served well to devise statistical methods to test the association of traits with high-dimensional genomic data. Noting that the structured variance matrix for the nonparametric function of the SNP genotype data has the form ${\sigma }_K^{2}K$, the association of a trait with the genomic information can be based on testing whether ${\sigma }_K^2=0$. Based on generalized linear mixed models, score statistics can be easily computed. For a regression model with fixed effects as adjusting covariates in a matrix X, the residuals from fitting this model, $(Y-X\widehat{\beta })$, are used to test their association with a genomic kernel by a quadratic form statistic, $Q=(Y-X\widehat{\beta })\text{'}K(Y-X\widehat{\beta })$. For quantitative traits, this Q is often divided by $2{\widehat{\sigma }}_e^2$ [12, 13], but not for binary traits in a method called SKAT (SNP-set/sequence kernel association test) [1].

The distribution of the quadratic form kernel statistic, Q, is not standard; it is a mixture of independent chi-squares with mixing weights that depend on the eigenvalues of the kernel matrix (and the projection matrix from a regression model of adjusting covariates). Several approaches have been used to compute P-values. One is based on using the first two moments of the null distribution of Q to approximate a scaled chi-square distribution [13, 16], an exact method is based on Davies method of inverting the characteristic function of the chi-square mixture [17], and another is based on a saddle-point method by Kounen [18]. Our unpublished simulations suggest that Davies and Kounen methods provide similar results, but the scaled chi-square method can be inaccurate for small P-values.

An advantage of viewing the kernel matrix as a prior structured covariance matrix is that it can be used to construct statistics that can be optimized over a range of scenarios. For example, ignoring adjusting covariates, Lee et al. [19] emphasizes that viewing the regression $Y=G{\beta }_2+e$ with ${\beta }_2\sim N(0,{\sigma }_K^{2}K)$ provides a robust score statistic when the direction of genetic effects (signs of β) are unspecified and possibly in opposite directions. Yet, when the direction of effects are all in the same direction (same sign), it would be more powerful to create a ‘burden’ scored for each subject by creating a weighted sum of the SNP genotypes for each subject, and use that sum in a regression equation. This burden test can be constructed as a kernel that imposes high correlation among the βs. With this concept, they were able to construct an optimal statistic that ranges from a global SKAT test to the burden test, based on a kernel matrix that includes a correlation coefficient for the βs.

The benefits of using kernel methods to construct tests for association of a trait with genomic data have been realized for rare genetic variants [17], with extensions to gene–gene interactions [20, 21] and family-based studies that must account for pedigree relationships [18, 22, 23]. Because kernel methods for association testing focus on relatively small genomic regions, expanding kernel approaches to testing large genomic regions, as well as complex genomic structured data based on gene pathways, remains a significant challenge. Kernels that include too much irrelevant [1] genomic information will likely dilute the association signal. As discussed in subsequent sections, kernels for prediction might provide robust predictions, yet without identifying the underlying regions most strongly associated. Hence, there is a trade-off between predictions based on broad genomic kernel methods, versus attempting to identify the causal regions that ‘drive’ the association.

BUILDING EFFICIENT PREDICTIVE MODELS FROM LARGE-SCALE GENOMIC DATA

One important goal in genomic data analysis is to predict phenotypes—such as disease risk or continuous traits—for different individuals based on known genomic information. The problem can be formalized as supervised machine learning. A common practice is to build the prediction model based on top-ranked markers from GWAS and a few known susceptibility loci from previous studies. This cherry-picking strategy shows poor performance in most cases. It attributes to the fact that top genetic variants usually explain a small proportion of phenotypic variation, and genetic studies are inclined to suffer from low replicability. Alternatively, one can train a prediction model based on all genome-wide markers as well as all other available information (features) such as epigenetic markers. Kernel machine (KM) methods provide an efficient solution for this strategy by facilitating feature selection/weighting and prediction in a unified framework.

For the disease risk prediction, the binary classifier such as the support vector machine may be readily used. This well-developed method basically seeks to find the optimal hyperplane that separates the data into two classes with the maximum margin, where nonlinear classification is attained by using the kernel trick. The SVM (support vector machine) methods offer two appealing advantages in prediction using high-dimensional genomic data. First, it is able to deal with all markers simultaneously without applying initial marker selection or pruning. Second, it takes into account potential complex relationship among markers, although it was observed that modeling interaction may not substantially improve prediction [24]. However, SVM is inherently a black box approach that provides only a classification rule, and it is hard to extract further information from the results. Its application in genomic prediction has been limited despite some promising results [25]. The kernel logistic regression (KLR) [26] is an alternative classifier with more desirable features. As a kernelized version of logistic regression, KLR not only offers a natural estimate of probability but also integrates nicely with other probabilistic approaches. In addition, it is easy to extend to multiclass prediction. In fact, the hinge loss function used in the SVM has a similar shape with the KLR’s loss, which is more smoothed, and the two methods are expected to yield similar prediction performance. The differences observed in their applications are more likely to come from parameter tuning and kernels rather than any inherent differences in the methods. However, the original KLR does not scale well with large data sets. There are few fast and sparse-driven versions of KLR available, and not yet seen in genomic prediction. The KLR is also closely related to another method called logistic kernel machine [27]. Despite the similar model setup, the latter was mainly geared toward facilitating gene testing and discovery.

Many strategies can be adopted to improve the whole-genome risk prediction. The first is by exploiting the block structure that underlies the genomic data. A natural way to incorporate this feature is to train the predictive model based on multiple kernel learning (MKL) [28, 29], which will be further discussed in the following section. Alternatively, a two-step procedure can be carried out by training the KLR at the gene region or pathway level, followed by building an ensemble predictive model based on the individual gene estimates [30]. This is another example of the flexibility of KLR compared with other determinist classifiers. To further improve the prediction accuracy, sparsity can be enforced at each stage. Given all the estimates from the gene level, L1-Regularization (penalized on absolute values of coefficients) is easy to incorporate (using packages such as glmnet) at the second step. The implementation of sparse KLR in the first step is, however, more involved and it is not yet available in standard software. A computationally more feasible alternative is to use kernelized feature extraction techniques, e.g. through the ‘kpca’ function in the ‘kernlab’ package. The nonlinear relationships are then embedded into lower dimension of the feature space, represented by the dominating eigenvectors of the kernel matrix. Based on the reduced space, a further regularized logistic regression at the gene level can be trained more efficiently—in its primal form. The relationship between the two-step and MKL method is closely comparable with that between the adaptive Lasso and group Lasso problem. Besides giving a risk score, both strategies help gain insights into the contribution to the response from specific genes. Driven partially by the missing heritability problem, predicting complex quantitative traits (or genetic values) with the aid of genetic markers is attracting attention in human genetics as well [31]. KM-based methods have been recently proposed as promising new tools as alternative to traditional best linear unbiased prediction methods that originate for animal and plant breeding [10, 32, 33]. These new developments, focused on regularization tuning and general kernel choice, can also be further improved by taking the genomic block structure into consideration.

It should be noted that, however, using KM-based methods and finer modeling does not necessarily drastically improve the prediction. The performance in real data analysis is always limited by factors such as the sample size and information content embedded in the collected data, as well as the true pattern underlying the biological mechanism. On the other hand, without thwarting the performance, the kernel approximation can be applied to significantly reduce the computational cost. Such approximation can be achieved by lower-dimension basis extraction as discussed above, or reversely by reconstructing the kernel based on the low-rank spectrum. Most kernel-based methods, such as the original KLR [26], have a computational complexity of order O(n³). This is prohibitive when we have large-scale training samples. The low-rank spectral reconstruction of a kernel can be performed by the Nyström method, which can speed up many regression-oriented algorithms when used together with the matrix inversion lemma [34, 35]. The approximation quality of these methods is protected by a reasonable and key assumption that the genomic data, like most of other large data, live in a lower dimension space and the spectra of the kernel matrices often decay quickly.

A schematic diagram of kernel machine methods for large-scale genomic data described in this article is shown in Figure 1. Kernel methods enable us to perform powerful association testing at gene-region/pathway level and efficient prediction of phenotype at genome-wide level. The cluster structure of genome is naturally modeled in the framework, which can further incorporate transcriptome and phenome structures as implemented in the structured mapping (we discuss below). Kernel functions and the kernel trick are used to map genomic data into an implicit high-dimensional space, in which a linear model can be adequate. From this perspective, the genomic data space can be conceptualized as three distinct layers of space: the original input data space (X), the transformed feature space (H) created by the kernel functions and the reduced kernel space (through kernel approximation). The methods we discuss in this article, such as the least-square KM, SVM/KLR, feature vector machine (FVM) and sparse additive models (SpAM)/MKL, allow efficient exploration of data pattern for model fitting in the feature space H. These methods are the kernel counterpart of the liner mixed model, logistic regression, lasso and group lasso, respectively. Methods that work in the reduced kernel space allow building efficient predictive models and play important roles in the large-scale data fusion.

Figure 1:

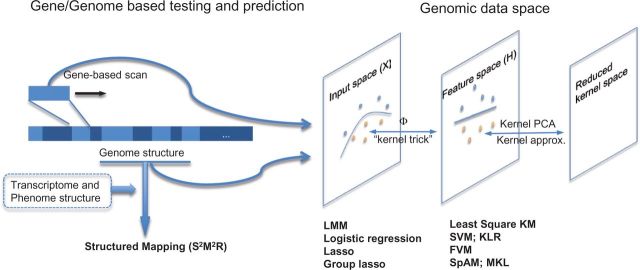
A schematic diagram of kernel methods and machine learning techniques in genomic data analysis.

MKL AND GENOMIC DATA FUSION

Instead of selecting a fixed single kernel, MKL uses multiple candidate kernels to map the data into the other space and achieves better performance by finding an optimal weight for each base kernel. As the paradigm is originally proposed as an extension to the single kernel SVM, MKL has commonly been framed as a supervised classifier. In essence, MKL seeks to construct a composite kernel as a liner combination of different kernels, and model complexity can be controlled by applying various regularizations on the combination coefficients (kernel coefficients). It can be used to learn which data source or feature cluster is more informative for the classification/prediction. This step can be optimized together with the base kernel parameters simultaneously in a quadratically constrained linear programing [28]. A common approach is to impose L1-norm constraint on the kernel coefficients. Hence, solving the feature selection problem under such setting will be equivalent to group lasso. Therefore, MKL is a hybrid method that effectively integrates feature selection and kernel selection, which is done by shrinking some regression coefficients and kernel coefficients to zero. It is thus a promising tool for the learning with structured genomic data as discussed above and for the integration of data from different sources—with each kernel being a feature cluster and a data type, respectively.

When choosing and designing appropriate algorithms in solving MKL, it is important to consider factors that control kernel sparsity, feature selection in base kernels and the involved computational complexity. In the genomic data applications, the number of data types (such as gene expression, DNA methylation and CNV (copy-number variation) data) is often limited. However, in each data type a large number of base kernels can be constructed based on feature sets that are grouped by biological functions (such as pathway information and interaction networks) or by statistical scoring. Therefore, it is desirable to control the number of active kernels by choosing regularization schemes that encourage the sparsity of kernel coefficients. This is particularly important in building predictive models because a large proportion of irrelevant kernels will substantially reduce the prediction performance. To further improve the prediction performance, a feature screening step can be performed per kernel before applying MKL. Seoane et al. [36] recently proposed a feature selection MKL scheme and showed that the predictive accuracy can be improved by using kernels, which exclusively use those genes that are known members of particular pathways. Overall, the applications of MKL in genomic data are currently limited but will increase alongside the publicly available large-scale and Omics data sets such as the TCGA (The Cancer Genome Atlas) initiative (cancergenome.nih.gov) [37].

A closely related concept called kernel-based data fusion [38] or kernel fusion has attracted increased attention in the recent years. Both data fusion and the MKL are facilitated by the nice closure property in kernel algebra: the sum or weighted sum of kernels is another valid kernel. In conjunction with the kernel trick, kernel matrices generated from heterogeneous data can thus be transformed into a global kernel with unified feature space. Kernel fusion methods also allow an easy integration of data with different types and structures in function prediction. These methods, together and other machine learning approaches, provide novel tools for gene function prediction and annotation, which can be further embedded in gene prioritizing [39, 40]. The concept of data fusion is, however, rather broad defined to include all the analyses that integrate data from different ‘views’. In this article, we have focused our discussion primarily on association test and prediction learning tasks. See Yu et al. [41] for a detailed introduction of kernel-based data fusion and its application in Bioinformatics, including both supervised and unsupervised methods.

STRUCTURED ASSOCIATION MAPPING

The main statistical paradigm for structured association mapping is a new statistical formalism for GWAS known as the sparse structured multivariate and multitask regression (S²M²R) [42] or the structured input/output regression. This emerging paradigm departs significantly from the traditional test-statistics-based [43] or PCA-based [44] methods, which do not strongly leverage various structural information present in the genome, phenome and transcriptome to improve the accuracy of identifying candidate causal variations in the DNA at a full-genome scale. S²M²R complements such inadequacy by exploiting a wide spectrum of omic structures available with the data as exemplified below using a principled mathematical formalism that enjoys strong statistical guarantees and efficient computational algorithms, rather than using ad hoc heuristics of unknown asymptotic properties.

An important source of genome structural information is genome annotations that include known transcription factor binding sites, exon regions, transposable element locations and conservation scores. These data can be considered as prior knowledge about SNPs that can be used to guide the search for disease susceptibility loci. For example, SNPs in highly conserved regions are more likely to be true association SNPs, as conserved regions are often functionally important. Taking advantage of genome annotation, adaptive multitask lasso (AMTL), which is an instance of S²M²R, finds genome-transcriptome or genome–phenome associations [45]. AMTL defines different penalties to SNPs according to genome annotation (SNPs with small penalties are more likely to be selected), and simultaneously incorporates L1/L2 penalty to perform multitask learning on correlated traits.

Related clinical traits or gene expressions as revealed in a phenotypic network or a gene-expression clustering tend to be influenced by a common and small subset of SNPs. Biologically, this might be the case when a mutation in a genetic regulator affects expression levels of multiple genes in a common pathway. Such structural information present in the transcriptome or phenome introduces constraints on the gene expression matrix or phenotype matrix (instead of on the genotype matrix as seen in the genome structure case) of the S²M²R problem, as leveraged by the GFlasso [46] and the Tree-lasso[47] algorithms in analyzing GWAS underlying correlated Asthma traits and clustered expression traits in yeast, respectively. Such structure bearing networks or clustering can be obtained using well-known machine learning techniques based on correlation or partial correlation or from known gene–gene or protein–protein interactions that are experimentally validated.

FEATURE-WISE KERNELIZED LASSO AND SPARE ADDITIVE MODELS

Functional influences can be generated by multiple SNPs in a complex nonadditive fashion, and such nonadditive effects can be difficult, if possible, to be detected through linear regression-based approaches. Recent advancements in kernel-aided nonparametric regression hold the key to capture such complex effects. A recent paper [48] showed that there exists a deep connection between regularized regression-based and margin-based (SVM) predictive modeling learning, in which a lasso regression formulation can be recast into an SVM formulation. Therefore, kernel tricks can be easily introduced. With particular choices of kernel functions, nonredundant genetic variations with strong statistical dependence on phenotypes can be found in terms of kernel-based independence measures such as the Hilbert–Schmidt independence criterion.

Specifically, suppose we are given a response vector $y\in {\mathbb{R}}^n$ and a covariate matrix

$$X={\left[x^{\left(\text{1}\right)}\text{,}\mathrm{...}\text{,}{x}^{\left(n\right)}\right]}^T\text{=}\left[x_1,\mathrm{...},x_p\right]\in {\mathbb{R}}^{n\times p},$$

where $x^{\left(i\right)}\in {\mathbb{R}}^n$ is i-th sample vector (i-th row of X) and $x_j\in {\mathbb{R}}^n$ is the vector of j-th feature for all samples (j-th column of X). The lasso optimization problem is as follows:

$$\underset{\beta \in {\mathbb{R}}^p}{\min }\frac{1}{2}||y-X\mathit{\beta }||+\text{λ}{||\mathit{\beta }||}_1,$$

where $\mathit{\beta }\in {\mathbb{R}}^p$ is the regression coefficient vector and λ is the regularization parameter. Owing to the sparse property of $l_1$ norm, the regression coefficients for some features become exactly zeros, hence achieving variable selection in linear models. It has been shown [48] that the above formulation of lasso problem is equivalent to

$$\begin{array}{cc}{\displaystyle \underset{\beta \in {\mathbb{R}}^p}{\min }}& \frac{1}{2}{\mathit{\beta }}^T{X}^{T}X\mathit{\beta }\\ \text{s.t.}& \left|x_j^T\left(y-X\mathit{\beta }\right)\right|\le \frac{\text{λ}}{2},j=1,\dots ,p\end{array}$$

By recognizing that the above problem only depends on the inner product between feature vectors $x_j$ (columns of X), one can use the ‘kernel trick’ on the feature space (rather than the sample space in standard applications of kernel methods) to allow for nonlinear correlation of features. More specifically, the feature vectors $x_j$ and the response vector y are transformed by a nonlinear function $\psi :{\mathbb{R}}^n\to {\mathbb{R}}^d$ and the problem (6) becomes

$$\begin{array}{cc}{\displaystyle \underset{\beta \in {\mathbb{R}}^p}{\min }}& \frac{1}{2}{\mathit{\beta }}^{T}K\mathit{\beta }\\ \text{s.t.}& \left|K\left({\text{x}}_j,\text{y}\right)\text{-}{\displaystyle \sum _{k=1}^p{\mathit{\beta }}_k\text{K}\left({\text{x}}_j,{\text{x}}_k\right)}\right|\le \frac{\text{λ}}{2},j=1,\dots ,p\end{array}$$

where $K\left(u,v\right)=\psi {\left(u\right)}^T\psi \left(v\right)$ and $K_{jk}=K\left(x_j,x_k\right)$. The above quadratic problem formulation, called the FVM, can be used to identify dominating variables that are nonlinearly correlated with the response. However, the nonlinear dependency relationships of the response and those selected variables are largely not characterized explicitly.

Even with the methods for detecting nonadditive or interactive effects of SNPs, it is still inadequate to deal with the scenario where there exists nonlinear effect of individual SNP on the phenotype of interest, for example, a longitudinal effect on the phenotype that can be obvious in time series of certain clinical traits or gene expression traits. To estimate the potential nonlinear dependency of the response variables on the explanatory variables, a more direct approach is to use additive models [49]

$$\text{E}[Y|X_1,\dots ,X_p]={\displaystyle \sum _{j=1}^p{f}_j\left(X_j\right)},$$

where $f_1,\dots ,f_p$ are one-dimensional smooth component functions (one for each variable) that can capture the nonlinear relationships of the response and features. To perform (nonlinear) variable selection in additive models, the so-called SpAM [29] was proposed to impose a sparsity constraint on the index set of nonzero component functions via regularization in function spaces:

$$\underset{f_1,\dots ,f_p}{\min }\frac{1}{2}\text{E}\left[{\left(Y-{\displaystyle \sum _{j=1}^p{f}_j\left(X_j\right)}\right)}^2\right]+\text{λ}{\displaystyle \sum _{j=1}^p\sqrt{E\left[f_j^2\left(X_j\right)\right]}},$$

where the expectation is over joint distribution of $\left(X_1,\dots ,X_p,Y\right)$. The second term is the regularization functional penalty that behaves like an $l_1$ ball across different components to encourage functional sparsity. An iterative procedure based on a cyclic coordinate descent algorithm was developed to solve the above optimization problem. The advantage of the SpAM approach is that it is symbolically almost identical to the lasso formulation. Therefore, it is feasible to incorporate structural information as discussed in the previous section to further improve its statistical power, as demonstrated in Group SpAM [50].

The widely used MKL [29] methods, as discussed earlier, is typically for learning a kernel Gram matrix in a predictive model, and therefore cannot be directly used for feature selection problems (i.e. the kernel-induced transformation is over all genome variations, and the selection is made over the choice of kernel transformations, not over variables in the genomic inputs). Under certain choice of the kernel function such as an element-wise additive basis, it can be shown that MKL is equivalent to SpAM [51]. Alternatively, it is also possible to apply the kernel for feature transformation as in FVM, instead of for data transformation, so that transformed features (i.e. genome variations) can be put under selection.

DISCUSSION

We conclude by briefly discussing the main advantages and the necessity for future research in applying kernel machine methods for large-scale genomic data analysis. First, KM methods are readily integrated with other probabilistic approaches, and most of them can be formulated and easily understood by viewing them from a regression perspective. Although conceived as a data-driven technology, KM also incorporate knowledge-driven factors, such as the choice of kernels and weights, and the structure of genomic information portrayed by publically available annotation. Second, they are computationally friendly. The kernel trick allows an efficient search in the higher dimensional space, while the related estimation problems are often cast as convex optimization problems that can be solved by many established algorithms and packages. As discussed above, the block structure of the genomic data should be taken into account to achieve both computational efficiency and statistical efficiency. Lastly, and most emphatically, all the KM and machine learning methods should not work as a black box, but rather an open and extensible framework that adapts nicely to many tasks in processing modern genomic data. It is most meaningful to build an integrative analysis pipeline that performs gene discovery and prediction, as well as data fusion across different platforms and sources. One main limitation of kernel methods is the high computational cost involved in the learning, which is at least quadratic (and often higher) in the numbers of training samples. With the volume of genomic data growing more rapidly than ever, additional research on topics such as the kernel approximation (e.g. the Random Fourier and Nyström approximation [34, 52, 53]) for genetic designs need to be conducted to further improve the scalability to sample size and dimensionality. Another drawback stems from the fact that it is difficult to predefine an optimal kernel function (functions) for a specific application given the complex data structure and data types (e.g. data generated from different platforms) in genomics. Therefore, methods that facilitate MKL and ensemble learning [54] should also be considered in the future to enable the scalability to data sources and heterogeneity. How best to use prior knowledge to structure the genomic information for increased power will become increasingly important as biological annotation improves in quality and quantity.

Key Points.

• Kernel machine learning methods provides promising tools for large-scale and high-dimensional genomic data processing.

• KM methods can also be viewed from a regression perspective and can be integrated with classical methods for gene prioritizing, prediction and data fusion.

• Need to further improve the scalability to sample size, dimensionality and data heterogeneity.

FUNDING

This research was supported by the US Public Health Service, National Institutes of Health (NIH), contract grant GM065450 (DJS), NIH 1R01GM093156 and 1R01GM087694 (EPX).

Biographies

Xuefeng Wang is an Assistant Professor at Stony Brook University and a member of the CEWIT Bioinformatics and Biostatistics Laboratories at SBU.

Eric P. Xing is an Associate Professor in the School of Computer Science at Carnegie Mellon University. His laboratory has research interests in the development of machine learning and statistical methodology.

Daniel J. Schaid is a Professor in the Division of Biomedical Statistics and Informatics at Mayo Clinic. His research interests lie in study design, data analysis and computational methods for human genetic studies.