Pattern Selection by Dynamical Biochemical Signals

Abstract

The development of multicellular organisms involves cells to decide their fate upon the action of biochemical signals. This decision is often spatiotemporally coordinated such that a spatial pattern arises. The dynamics that drive pattern formation usually involve genetic nonlinear interactions and positive feedback loops. These complex dynamics may enable multiple stable patterns for the same conditions. Under these circumstances, pattern formation in a developing tissue involves a selection process: why is a certain pattern formed and not another stable one? Herein we computationally address this issue in the context of the Notch signaling pathway. We characterize a dynamical mechanism for developmental selection of a specific pattern through spatiotemporal changes of the control parameters of the dynamics, in contrast to commonly studied situations in which initial conditions and noise determine which pattern is selected among multiple stable ones. This mechanism can be understood as a path along the parameter space driven by a sequence of biochemical signals. We characterize the selection process for three different scenarios of this dynamical mechanism that can take place during development: the signal either 1) acts in all the cells at the same time, 2) acts only within a cluster of cells, or 3) propagates along the tissue. We found that key elements for pattern selection are the destabilization of the initial pattern, the subsequent exploration of other patterns determined by the spatiotemporal symmetry of the parameter changes, and the speeds of the path compared to the timescales of the pattern formation process itself. Each scenario enables the selection of different types of patterns and creates these elements in distinct ways, resulting in different features. Our approach extends the concept of selection involved in cellular decision-making, usually applied to cell-autonomous decisions, to systems that collectively make decisions through cell-to-cell interactions.

Introduction

Pattern formation processes occur in many contexts such as in Biology, Chemistry, and Physics (1–5). Spatially extended systems such as developing epithelia, chemical reactions, solids, and liquid crystals show stable states that are spatially organized, hereafter named “patterns”. The simplest spatial organization is the homogeneous or uniform state. More complex patterns are periodic spatiotemporal structures. In the case of developing embryos, patterns of gene expression arise in tissues (6). Examples include the patterns of stripes formed in the zebrafish skin (7) and during vertebrate segmentation (8), and periodic fine-grained patterns (also known as salt-and-pepper patterns) appearing during neurogenesis (9) and sensory cell differentiation (10), among others. The spatial organization of periodic patterns arises from spatial coupling. In embryonic tissues, the spatial coupling is mediated by diffusing molecules and/or can be direct from cell to cell through molecules anchored at the cell membrane. Because spatiotemporal pattern formation involves many interacting components, it is a complex process and, in addition, it is often counterintuitive. Therefore, mathematical modeling has been crucial for advancement in our understanding of pattern formation dynamics and for proposing new mechanisms of pattern formation. This is the case of the work by Turing (4) in the context of Developmental Biology (11).

Transitions between different patterns occur frequently during embryonic development. Specifically, the same set of genes can be initially expressed in a pattern and subsequently change their expression to form another pattern. These transitions are induced by biochemical signals. An example of this phenomenon occurs during inner ear development. In this developmental process, a fine-grained pattern that makes hair cell differentiation arises from an initial homogeneous pattern that raised through propagation over another homogeneous state (the prosensory patch) (10,12,13). Both the initial homogeneous and the subsequent fine-grained patterns involve the expression of ligand Jagged1 and of Notch receptor Notch1, and the transition from one to the other is driven by the activation of the expression of the proneural gene Atoh1 (13,14).

Transitions from one type of pattern to another one have usually been described as a dynamical process in which the initial pattern becomes unstable when control parameters change and the system evolves to the unique stable pattern that corresponds to the new parameter values (1,4,5,15–17). The initial and final patterns are each determined by the system conditions (i.e., the parameter values and boundary conditions). Nevertheless, quite often the situation can be different and much more interesting. Specifically, for the new set of control parameter values, several different patterns can be stable—what we will refer hereinafter as “multistability”. In this multistable scenario, one may ask which of the stable patterns is going to arise and how this pattern selection is induced.

There is experimental evidence pointing out at multistability and selection of patterns in developing embryos, specifically for patterning processes driven by Notch signaling. Notch is a transmembrane receptor protein that mediates cell-to-cell interactions upon binding to a Notch ligand at the membrane of an adjacent cell (18). In the Drosophila’s eye, photoreceptor neuron precursors adopt distinct cell fates (R1/R6 or R7) in a cell-to-cell coordinated manner upon the spatially sequential activation of the protein ligand. Changes in only the spatiotemporal sequence of this signal (i.e., ligand activation) alters the pattern that is formed (19), suggesting that under the same final conditions, different patterns can exist (i.e., those of the wild-type conditions and those driven by the manipulated temporal sequence of the biochemical signal). Another example also arises from ommatidial photoreceptor patterning in the fly. It has been shown that different patterns of R8 photoreceptors (salt-and-pepper and stripes patterns) can arise in genetically identical tissues through Notch signaling pathway (20). In addition to this experimental evidence, computational studies of pattern formation by Notch signaling have shown that different patterns can be stable solutions for the same set of parameter values (20–22). Examples of these patterns are the homogeneous one (H), periodic salt-and-pepper patterns (P), and periodic stripe patterns (S).

It is known that initial conditions can determine the selection of a pattern (20,23–25). However, little is known on how selection of different patterns occurs from the same initial pattern and conditions, upon the action of a signal. Herein, we address this question and focus on pattern formation mechanisms based on the Notch signaling pathway to exemplify it. To this end, we built upon the knowledge gained from studies on the selection of states through biochemical or environmental signals in multistable dynamics of noninteracting cells. For single, noninteracting cells, mathematical modeling results have shown that bifurcations driven by the signal (which can be modeled as time-dependent changes of the parameter values) enable the selection of a specific state (26–29). The dynamical evolution of the signal has also been shown to be relevant for selection (30–33). Hence, the use of nonautonomous dynamics (i.e., with time-dependent parameters) becomes necessary for modeling selection-signal-induced processes (33). In addition, in many different biological contexts, selection of a cell state in individual cells has been shown to be a probabilistic process with a stochastic outcome that has a well-defined probability. This stochastic choice has been termed “cellular decision-making” (34). Moreover, the intrinsic stochasticity of the dynamics cannot be frequently neglected because it can modify the stability and therefore, the chance of each state choice when there are multiple stable states (35,36). Cellular decision-making has also started being applied to cell-to-cell interactions (37).

Herein, we perform a computational study to provide key elements for pattern selection upon the action of a signal. To this end, we make use of time-varying parameters (i.e., nonautonomous) in stochastic dynamical systems with spatial interactions. This is in contrast with contemporary studies on pattern formation and selection, studies that usually deal with parameters that are constant both in time and space. We considered three alternative situations, which all have been shown to take place in developing tissues: 1) the inductive signal arises in all the tissue at the same time, 2) it acts only on a small domain of the tissue, and 3) it spatiotemporally propagates like a wavefront. The first situation is the natural extension of selection of states in individual noninteracting cells to the case of selection of spatial patterns, which involve spatial interactions. The second and third situations are specific only to spatially extended and coupled systems.

Materials and Methods

Model

The model establishes a minimal description of the dynamics of the activities of the Notch pathway (s_i) and of the ligand (l_i) in each cell i, as first described in Collier et al. (38). It phenomenologically includes the process of Notch signal activation, according to which a fragment of the Notch receptor translocates into the nucleus of a cell and transcriptionally represses several genes upon binding to a ligand at the membrane of an adjacent cell (18). Specifically, the gene encoding the protein ligand is repressed. Thus, a ligand-expressing cell drives lateral inhibition to its neighbors, i.e., it inhibits the expression of the ligand in its adjacent cells. When all cells interact with each other through lateral inhibition, spontaneous symmetry breaking (driving the periodic patterning, arising from small variability between cells) can occur (25,38–40). We also took into account that the protein ligand can impede Notch signaling by binding to the Notch receptor within the same cell, an action known as “cis-inhibition” (19,41–47).

We extended the dimensionless model proposed in Formosa-Jordan and Ibañes (22) for cis-inhibition to phenomenologically include stochastic dynamics arising from intrinsic noise, such that the stochastic differential equation for each species in the Itô interpretation (48,49) is as follows:

$$\{\begin{array}{c}\frac{d{s}_i}{dt}=P_s\left(\langle l_i\rangle ,l_i,t\right)-s_i+\sqrt{P_s\left(\langle l_i\rangle ,l_i,t\right)+s_i}{\xi }_i\left(t\right),\\ \frac{d{l}_i}{dt}=v\left(P_l\left(s_i\right)-l_i+\sqrt{P_l\left(s_i\right)+l_i}{\chi }_i\left(t\right)\right).\end{array}$$ (1)

The deterministic part is formed by the production terms, P_s(〈l_i〉,l_i,t) and P_l(s_i), minus the degradation terms. The value v accounts for the ratio between the timescale of the dynamics of the ligand and the signal activities and is set to v = 1. The stochastic multiplicative terms are proportional to the square-root of the corresponding production plus the degradation terms. Here,

$$\langle l_i\rangle \equiv \sum _{j\in nn\left(i\right)}{l}_j/z$$

is the average ligand activity of the z nearest-neighbor (nn(i)) cells of cell i. The values ξ_i and χ_i are independent Gaussian random numbers of zero mean and are uncorrelated in space and time,

$$\langle {\xi }_i\left(t\right){\xi }_j\left(t^{\prime }\right)\rangle =\frac{1}{V}{\delta }_{ij}\delta \left(t-t^{\prime }\right)$$

and

$$\langle {\chi }_i\left(t\right){\chi }_j\left(t^{\prime }\right)\rangle =\frac{1}{V}{\delta }_{ij}\delta \left(t-t^{\prime }\right),$$

with V being a characteristic volume. We used a white noise according to the standard procedures from Master to Langevin equations (48,49).

The productions of Notch and ligand activities are

$$\begin{array}{c}{P}_s\left(\langle l_i\rangle ,l_i,t\right)=\frac{r_t^i\left(t\right)\langle l_i\rangle }{1+r_t^i\left(t\right)\langle l_i\rangle +r_c^i\left(t\right)l_i},\\ P_l\left(s_i\right)=\frac{1}{1+b{s}_i^n},\end{array}$$ (2)

where n is an exponent representing the degree of nonlinearity of ligand inhibition by the signal and b indicates the strength of such ligand inhibition. Here, $r_t^i\left(t\right)\equiv r_{trans}^i\left(t\right)$ and $r_c^i\left(t\right)\equiv r_{cis}^i\left(t\right)$ are the strengths of trans- and cis-interactions of cell i, respectively. Trans-interactions correspond to those between ligands and receptors in adjacent cells while cis-interactions arise from the binding of the ligands and receptors in the same cell. In addition, the strengths rⁱ_t(t) and rⁱ_c(t) are proportional to the rate of maximal ligand production, which is not explicitly seen in the equations due to the nondimensionalization of variables being used. Herein we considered that rⁱ_t(t) and rⁱ_c(t) can change over time and be different between cells, as described in Path Definition and Characterization, below.

Note that the dynamical model is an example of a regulatory circuit with mutual inhibition and self-activation (i.e., a toggle switch between adjacent cells, see Fig. S1 in the Supporting Material). The value rⁱ_t favors mutual inhibition while rⁱ_c promotes self-activation. In the absence of cis-inhibition and fluctuations, Eqs. 1 and 2 recover the model proposed by Collier et al. (38).

The dynamics of Eqs. 1 and 2 were numerically integrated on a two-dimensional array of 12 × 12 regular hexagonal cells with toroidal periodic boundary conditions, unless otherwise stated. The algorithm presented in Carrillo et al. (50) extended to time-dependent parameter values was used for integration with time step dt = 0.1 (robustness of the results was checked for dt = 0.01, Fig. S2). Equations 1 and 2 can drive negative values because of the stochastic fluctuations. To avoid them, a noncrossing boundary to negative values was used, such that negative values are converted to zero (Fig. S2). To confirm the correctness of our results, we checked that the states reached by cells correspond to distributions of values centered on the exact deterministic solutions of the Eqs. 1 and 2 (Fig. S2), which can be theoretically computed as described in Formosa-Jordan and Ibañes (22). Snapshots of the tissue state, as depicted in all figures, correspond to a linear grayscale of ligand activity values with white for l = 0 and black for l = 1.

Multistability and relative stability of patterns

Herein we defined different patterns by their spatial symmetries and not by the exact values of the variables s and l. The model above in the absence of fluctuations (deterministic dynamics) and for homogeneous and constant parameter values (rⁱ_t(t) = r_t and rⁱ_c(t) = r_c for ∀i,t) in perfect hexagonal lattices with toroidal periodic boundary conditions has been analyzed in Formosa-Jordan and Ibañes (22). It has been shown to exhibit different stationary stable patterns for the same set of parameter values. Some of these patterns are homogeneous (H), periodic salt-and-pepper (P), and stripe (S) patterns (Fig. S3). Stability of the H-, P-, and S-patterns for the stochastic dynamics of the model and its comparison with the deterministic dynamics was verified at specific sets of parameter values. The domains where the H-, P-, or S-patterns are deterministically stable were depicted in the r_t–r_c space using the data in Formosa-Jordan and Ibañes (22). Other pattern solutions can be stable too in these domains (22). Linear stability analysis indicates that the fastest growing mode that destabilizes the H solution corresponds to the periodicity of the P-pattern (22). Therefore, the P-pattern is expected to arise spontaneously from the H-pattern through small random variability between the values of the signal and/or ligand for this model dynamics. Accordingly, formation and thereby selection of the S- or other patterns is expected to require mechanisms that impose properly the specific spatial symmetries of these patterns, in contrast with selection of the P- or H-patterns. We only focused on the selection of the S-pattern, besides selection of the P- and H-patterns. In addition, we evaluated whether a stable pattern can spontaneously invade and propagate over another stable one. To this end, we set as initial condition for one-half of the tissue a pattern solution that is stable, and for the other-half, another stable pattern solution. We numerically integrated the stochastic dynamics until a stationary situation was reached (until a final time, t = 500). For the parameter values being evaluated, the P-pattern was able to invade the H solution and not vice versa. Accordingly, we termed the P-pattern to be spatially more stable than the H-pattern.

Path definition and characterization

Changes of rⁱ_t and rⁱ_c over time from value r_a0 to value r_af and from cell to cell were phenomenologically modeled by time-dependent continuous hyperbolic tangent functions as

$$r_a^i\left(t\right)\equiv r_a^{\left(j,k\right)}\left(t\right)=\frac{1}{2}\left(\left(r_{af}-r_{a0}\right)\text{tanh}\left(\frac{t-t_a-t_{\text{prop}}k}{\alpha }\right)+r_{a0}+r_{af}\right){\delta }_{j,k\in D},$$ (3)

where a stands for t ($trans$) or c ($cis$) and two indexes, j, k, were used to label the cell i (denoting the row, j, and the column, k). Parameter α sets the timescale of the parameter change, t_a is the time at which the parameter has reached the value (r_a0 + r_af)/2, and t_prop sets the spatiotemporal scale of propagation of the parameter change across the tissue. For t_prop = 0 (Scenarios 1 and 2), all cells within the spatial domain D change simultaneously the value of the parameter, and D stands either for all the tissue (Scenario 1) or for a small fraction of it (Scenario 2). For t_prop > 0 (Scenario 3), the change of parameter value occurs as a propagating planar front across the tissue (i.e., simultaneously in all cells of row j and propagating along rows). To ensure that initially the parameter is at value r_a(t = 0) ≈ r_a0, we set t_a = −α tanh(−0.995). For sequential changes of parameters rⁱ_t and rⁱ_c or vice versa, we defined t_d ≡ |t_c − t_t| as the delay between these changes. To ensure that changes of rⁱ_t followed changes of rⁱ_c (or vice versa) and did not overlap, we set t_d >> α.

We also considered transient changes of rⁱ_t and rⁱ_c from r_a0 to r_af and back to r_a0. These were modeled through Eq. 3 for each change, from r_a0 to r_af and backward, with t_a = t_a1 for the first change from r_a0 to r_af and t_a = t_a1 + t_up + ϕ for the change from r_af to r_a0, where ϕ measured the time period during which the parameter is at value r_af. The same value of α was used for both changes.

We defined the following timescales to characterize the path across the r_t−r_c parameter space: t_up = t_a + α arctanh(2P−1) for P = 0.9933 measured the time spent from the departure from a vertex point to the arrival at the subsequent vertex point of the path in the parameter space; and τ measured the time spent on an intermediate (not the initial nor the final) vertex. When the path is constituted by a single intermediate vertex point, τ is computed as τ = t_d – t_up. When there are several intermediate vertex points, we used a subindex with the name of the vertex to denote the time spent at each vertex point. Herein we exemplify the case of three vertex points and denote each of them by a number reflecting the order in which they are visited: τ₁ = t_d – t_up, τ₂ = ϕ₁ = t_d, and τ₃ = t_d – t_up + ϕ₂ – ϕ₁. For paths involving t_prop > 0 (Scenario 3), we defined N_rows = τ/t_prop as the number of cell rows with the parameter values of an intermediate vertex point.

Criterion for pattern selection

We evaluated whether a path drives the selection of the H-, P-, or S-patterns. Due to the stochasticity of the dynamics, we measured the normalized frequencies R_H, R_p, and R_S of cases that selected the H-, P-, and S-patterns for a given path. To measure R_H,P,S, we discriminated systematically which pattern was selected for each stochastic temporal evolution (i.e., numerical integration of the dynamics) of the path. To this end, we defined the three-component order parameters (for x = s,l), which take distinct values for each pattern as

$${\eta }_x^{\theta }=\frac{1}{N}\sum _{i=1}^N\left|x_i-{\langle x_i\rangle }_{\theta }\right|,$$ (4)

where N is the total number of cells in the tissue and brackets stand for averages over the two nearest-neighboring cells along each spatial direction with θ = 0, −, and +, which denote the directions that form an angle 0°, −60°, and +60°, respectively, with the horizontal. The characteristic values of these order parameters for each pattern for deterministic dynamics and perfect periodicity are ${\eta }_x^{\theta }=0$ $\forall \theta$ for the H-pattern; ${\eta }_x^{\theta }={\overline{\eta }}_x>0$ $\forall \theta$ with

$${\overline{\eta }}_x=\frac{{\eta }_x^0+{\eta }_x^{-}+{\eta }_x^{+}}{3}$$

for the P-pattern; and for the perfectly aligned S-pattern, the order parameter has only one null component, which corresponds to the component in the direction parallel to the stripes.

For each stochastic temporal evolution of the dynamics, we computed numerically the order parameters η^θ_x at the final time t_max = 10,000. We decided whether the system exhibited at t_max the H-, P-, or S-pattern according to the following criteria: 1) The system exhibited the H-pattern if ${\overline{\eta }}_x<0.2$ for x = s,l. The values of the order parameters extracted for the steady H-pattern of the stochastic dynamics were not null, but they were very small, because of the stochasticity. The threshold value 0.2 was chosen by taking into account this stochasticity and the specific values of the order parameters for the P- and S-patterns at the relevant parameter values. 2) The system exhibited the P-pattern if $\left|{\overline{\eta }}_x-{\overline{\eta }}_x^{th}\right|<0.2$ and ${\overline{\eta }}_x>0.2$ for x = s,l, with ${\overline{\eta }}_x^{th}$ being the theoretical expected value of ${\overline{\eta }}_x$ for the perfect P-pattern of deterministic dynamics (Tables S1 and S2 in the Supporting Material), which can be evaluated theoretically without numerical integration of the dynamics (22,51). The 20% difference between ${\overline{\eta }}_x$ and ${\overline{\eta }}_x^{th}$ was chosen to take into account that the final pattern may not be perfectly periodic. 3) The system exhibited the S-pattern if ${\overline{\eta }}_x>0.2$ and σ_x > 0.8 being ${\sigma }_x=1-{\eta }_x^{\text{min}}/{\eta }_x^{\text{max}}$, where ${\eta }_x^{\text{min}}$ and ${\eta }_x^{\text{max}}$ are the minimum and the maximum components of $\left({\eta }_x^0,{\eta }_x^{-},{\eta }_x^{+}\right)$, respectively. Parameter σ_x described the degree of stripes formation.

Results and Discussion

The scenarios and their dynamical paths

Our interest is to evaluate how one certain pattern and not another one is selected when there are multiple patterns that are stable. We focused on three different patterns, defined only by their symmetries: the homogeneous pattern (H), the fine-grained lateral inhibition pattern (P), and the stripe pattern (S) (Fig. S3). We considered selections of these patterns induced by biochemical signals and emerging from the same initial pattern and conditions (Fig. S3).

We modeled the action of biochemical signals as spatiotemporal changes of the trans rⁱ_t and cis rⁱ_c interaction strengths (Materials and Methods). We chose these interactions to be modulated over time and space (among cells) because there are context-dependent proteins that can modulate them, like the glycosyltransferase Fringe (43,52,53) or the ubiquitin ligase Neuralized (54). Moreover, changes in the activation of the ligand, which are known to drive transitions from one pattern to another one (e.g., in vertebrate inner ear development and in the differentiation of photoreceptors in the Drosophila’s eye), impinge also on these parameters. The spatiotemporal sequence of the changes in the values of rⁱ_t and rⁱ_c defines what herein we named “dynamical paths”. The temporal changes of the parameters of a cell can be depicted as a trajectory across the r_t–r_c parameter space. For simplicity, we devised trajectories that, for each cell, involved changing either rⁱ_t or rⁱ_c, or one after the other. Accordingly, these trajectories were constituted by vertical and/or horizontal lines along the r_t–r_c parameter space (e.g., as in Fig. 1, A and B).

Figure 1.

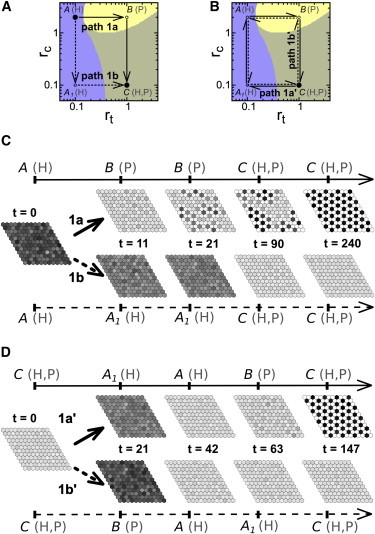
Pattern selection achieved through a specific global path. (A and B) Paths (arrows) across the parameter space of trans r_t and cis r_c interaction strengths. (Solid circles) Initial and final points of the paths; (open circles) intermediate vertex points. The temporal evolution of the paths is shown in Fig. S4. It is indicated within parentheses at relevant points of the path (denoted by letters A, B, A₁, and C) whether the homogeneous (H) and/or the salt-and-pepper (P) patterns are stable. The paths cross different domains (colors) each defined by which of these patterns are stable: H (blue), P (yellow), or H and P (gray). These domains have been plotted using data for deterministic dynamics with periodic boundary conditions in Formosa-Jordan and Ibañes (22). Stability of these patterns for stochastic dynamics is found in Fig. S5. (A) Paths 1a (continuous line) and 1b (dashed line) start at point A and end at point C. (B) Paths 1a′ and 1b′ start and finish at the same point C. Path 1a′ (continuous line) is clockwise whereas path 1b′ (dashed line) is counterclockwise. (C and D) Snapshots of the tissue state over time (t) when the same signal acts in all cells of the tissue at the same time (Scenario 1) and changes the values of the parameters (C) permanently according to paths 1a or 1b, or (D) transiently according to paths 1a′ and 1b′. The system initially (t = 0) exhibits the H-pattern. The parameter space points, and whether the H- or P-patterns are stable for these parameter values, are indicated at each depicted time. Additional parameter values are τ = 10, t_up = 11, t_prop = 0, b = 1000, n = 2, V = 1000, and those detailed in Table S1 and Materials and Methods. To see this figure in color, go online.

We considered three scenarios: 1) the signals act on all the tissue at the same time, 2) they act on a group of cells, and 3) they act sequentially over all cells of the tissue. In the three scenarios, all cells had equivalent dynamics (i.e., all cells had the same parameter values) before the signals act (initial time) and at the final time. To study selection processes, parameter values at the final time were such that multiple patterns were stable (Materials and Methods). In Scenario 1 we analyzed whether and how the selection of a pattern depends on the path, and it extends cell-autonomous decision-making to spatially interacting systems. Therefore, we focused only on the selection of those patterns that do not require any spatial cue to be formed. These correspond to patterns that either do not involve a periodicity (H) or are periodic but have the spatial symmetries that grow the fastest from linear instabilities (P) (Materials and Methods). In Scenario 2, we propose an intrinsically spatially based mechanism for the selection of patterns that can spontaneously invade another pattern (Materials and Methods). Finally, in Scenario 3 we propose another spatially based mechanism that enables the selection of a pattern with a more singular symmetry like the stripe pattern (S) (Materials and Methods). We analyzed several paths driven by signals and numbered them according to the scenario (1, 2, or 3) to which they belong.

Scenario 1: patterns are selected by specific global paths

In this first scenario, we evaluated how selection between the H- and P-patterns can occur when a biochemical signal acts in all tissue at the same time. To test the relevance of the path for the selection process, we constructed two different paths that connect in different manners the initial and the final conditions. In the initial condition, only the H-pattern is stable (point A in the r_t–r_c parameter space of Fig. 1 A). In the final condition, both the H- and the P-patterns are stable (point C in Fig. 1 A). Thus, the two paths could be visualized as two different trajectories across the r_t–r_c parameter space that connects the initial and final points. For simplicity, these two paths were constructed as sequential changes in rⁱ_t = r_t and rⁱ_c = r_c parameters, and the two paths differ in the order of these changes (Fig. 1 A). According to which parameter changes first (r_t or r_c), the path transiently explores a domain where the P-pattern is stable and the H-pattern is not (path 1a) or it only traverses domains where the H-pattern is stable (path 1b) (Fig. 1 A).

Fig. 1 C shows some frames of the tissue state along time for each path. At the end of the paths, selection of a different pattern becomes evident: through path 1a the P-pattern is selected, while path 1b selects the H-pattern. The results show that selection of a new pattern that is distinct from the initial one (P from H) occurs through a path that drives the transient destabilization of the initial pattern. We confirmed this result with other paths and for other initial patterns as well (Fig. S6). This is consistent with cell decision-making through bifurcations in cell-autonomous systems.

We then envisaged two paths that drive the destabilization of all the initially stable patterns. These paths start and end at the same point of the parameter space, where both the H- and P-patterns are stable (Fig. 1 B). In addition, the two paths trace exactly the same cyclic trajectory over the parameter space, but evolve in opposite sequential order (clockwise and counterclockwise): path 1a′ and path 1b′ (Fig. 1 B). Our results show that selection of a pattern that is distinct from the initial one becomes possible for the two paths (Figs. 1 C and S7), because both paths transiently destabilize the initial pattern. In addition, the results show that each path selects a different pattern independently of the initial one (Figs. 1 C and S7). The pattern that is selected corresponds to the one that is stable at the last intermediate point of the path: the P-pattern is selected through path 1a′, while the H-pattern is selected through path 1b′ (Figs. 1 C and S7). These results show that identical trajectories across the phase diagram but evolved in opposite sequential order can drive distinct pattern selections, which are independent of the initial pattern.

We next evaluated whether these selection processes are robust and reasoned that the timescales of the path could be relevant. To this end, we looked at the selection process as a function of the time τ_X spent at the intermediate X parameter space point (X being the point A₁, B, or A, depending on the path, as shown in Fig. 1, A and B) (Materials and Methods). When the initial state is never destabilized, this time is irrelevant, as expected (Figs. 2, A and B, and S6). In contrast, a minimal time at the parameter space region driving the selection is required for robust selection of a new pattern to happen (Figs. 2, A and B, S6 and S7). To ensure that the final distinct domain visited during the path is the one that sets the selection, we analyzed path 1a′ (Fig. 1 B) for different time intervals τ_B spent at the final intermediate point B with unchanged time intervals spent at the previous vertex points (τ_A = τ_A1 = 0, Fig. 2 B). The similarity of this selection curve with the one with all τ variables (τ_B = τ_A1 = τ_A) indicates that the last intermediate distinct domain is the relevant one to decide which pattern is selected.

Figure 2.

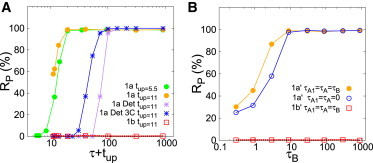
Pattern selection through a specific global path is robust and requires a minimal yet short time. Frequency of selection of the P-pattern (R_p in percentage) versus a characteristic time of the signal. The same signal acts in all cells of the tissue at the same time (Scenario 1) and changes the values of their parameters (A) permanently or (B) transiently, according to the paths in Fig. 1, A and B, respectively. (A) Results for path 1a for stochastic dynamics (circles), and in the absence of fluctuations (stars) (Det); and results for path 1b (squares). (Blue stars) Low-dimensional system of three cells interacting in pairs (3C). (B) (Circles) Path 1a′ (solid for τ_A1 = τ_A =τ_B; and open, τ_A1 = τ_A = 0). (Squares) Path 1b′. ϕ = 191 for these three curves. Other parameter values as in Fig. 1, with t_up = 11 and 12 $\times$ 12 cells unless otherwise specified. The deterministic curves (Det in the legend) use a $10\%$ uniform random variability in the initial condition. In all cases, each point corresponds to 1000 repetitions of the selection process. To see this figure in color, go online.

The frequency of selection follows a sharp thresholdlike response curve as a function of the time during which destabilization occurs (Figs. 2, A and B, S6, and S7). For instance, in the case of path 1a (Fig. 1 A), the characteristic time spent at the region where the H-pattern is not stable is approximately t_up + τ, as shown by analyzing different τ and t_up values (Fig. 2 A). The value t_up is the time spent since the departure from the A or B parameter space point until the arrival to the subsequent one along the path, whereas τ is the time spent at the intermediate vertex point B (Materials and Methods). For small t_up + τ values, selection of the P-pattern is not robust but probabilistic. Our results show that stochasticity in the dynamics enables robust selections at times shorter than in the absence of fluctuations (Fig. 2 A). In contrast, the high-dimensionality of many interacting cells increases the threshold characteristic time for robust pattern selection (Fig. 2 A). To have a sense of whether the time required for robust selection in all these cases is long or short, we compared it with the corresponding characteristic timescale T of the formation of the full P-pattern from an unstable homogeneous pattern (Fig. S8; Table S2). This time T is shortened by fluctuations and in low-dimensional systems (Table S2). In all cases being shown, T is longer than the time t_up + τ required for robust selection (Fig. 2 A; Table S2).

Taken together, the results show that the dynamical path defined by the biochemical signal or signals, and not only the initial and final conditions, is a critical element for pattern selection. Selection of a new pattern involves the transient destabilization of the initial state and the subsequent exploration of a new pattern that will finally end in the desired selection. This is accomplished through a proper path that has to evolve dynamically slow enough to first enable destabilization and afterwards emergence of a new state. The pattern selected corresponds to the latest different pattern explored during the path. If the path evolves too quickly, selection might not be robust and become probabilistic. However, our results show that robust selection can involve short timescales compared to those required for full pattern formation. Accordingly, this robust selection can become visible at late times (i.e., at the end of the path) and not when the selection is actually taking place or when the signal is acting (Fig. 1 D).

Scenario 2: pattern selection by local paths

We wondered whether selection of the P-pattern in all the tissue could occur from biochemical signals that act locally only in a small subset of cells. We reasoned that such selection can occur if the P-pattern is spatially more stable than the H-pattern and thus can spontaneously propagate over the H solution (Materials and Methods). This spontaneous propagation occurs for the parameter values of point C of the parameter space of Fig. 1 A where both the H- and P-patterns are stable (Fig. S4). We then envisaged a path that acts only and transiently in a cluster of cells (path 2a in Fig. 3 A). Hence, all cells have the same equivalent dynamics (i.e., those characterized by the parameter values of point C) at initial and final times. The path drives the cells within the cluster to evolve from the parameter space point C to a point where the H-pattern is unstable (B) and backward (Fig. 3 A). When this path acts, the P-pattern is selected (Fig. 3 C). The P-pattern forms within the cluster and propagates all through the tissue. Therefore, selection of a more spatially stable pattern can be driven by transient signals acting locally within the tissue. The transient local signal drives the selection of the new pattern within the cluster. Then, because the new pattern is spatially more stable, it spontaneously (without the action of any signal) invades the remaining tissue. Note that path 2a is such that if the signal acted in all cells and not only within a cluster, the P-pattern would be selected as well, as expected from Scenario 1 (Fig. S6).

Figure 3.

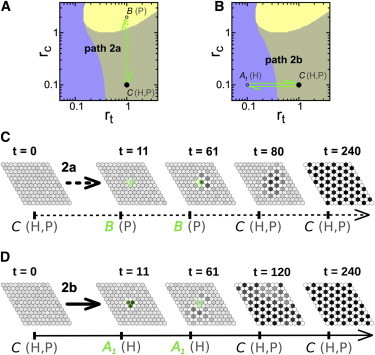
Pattern selection achieved through a spatially localized signal. (A and B) Paths (arrows) 2a (A) and 2b (B) in the parameter space of Fig. 1, A and B. These paths involve transient temporal changes of a single parameter value (Fig. S9) acting in a cluster of cells. (Solid circles) Initial and final points of the paths; (open circles) intermediate vertex points. (C and D) Snapshots of the tissue state over time (t) when the system initially (t = 0) exhibits the H-pattern and the signal acts only in three cells (green cell borders), which change their control parameter values transiently according to paths 2a (C) and 2b (D). The remaining cells of the tissue have constant parameter values corresponding to those of parameter space point C. Parameter values are τ = 50 and t_up = 11 and those in Fig. 1. To see this figure in color, go online.

In Scenario 1, we found that selection of a new pattern involved the transient destabilization of the initial pattern. Specifically if the path described the trajectory from point C to A₁, where only the H-pattern is stable, and backward (Fig. 3 B), the P-pattern was not selected from the H one (Fig. S6). We devised this same change to occur only within a subset of clustered cells (path 2b in Fig. 3 B). Our results show that in this case the P-pattern can be selected in the whole tissue (Fig. 3 D). Snapshots of the dynamical evolution of the state of cells reveals that the P-pattern starts to emerge at the boundary outside the clustered cells, i.e., where the signal is not acting (Fig. 3 D). This initial nucleation of the pattern then spreads to all the tissue. Thus, this signal drives selection of the P-pattern only if it acts on a subset of cells and not in all the tissue. In this case, the destabilization of the H-pattern arises from the spatial inhomogeneities the signal drives on the tissue through the large differences between the average values of the ligand and signal activities of the H-pattern at points A₁ and C (Table S1). Thus, the P-pattern can only arise at the boundary where the signal acts.

We explored the robustness of these selection processes as a function of the time τ spent at the intermediate point (B for path 2a and A₁ for path 2b) and of the number of cells on which the signal acts. In all cases, the selection process shows a thresholdlike response requiring a minimal time to be robust (Fig. 4, A and B). For path 2a (Fig. 3 A), this minimal time is larger than when the signal acts in all the tissue (Fig. 4 A). The minimal time decreases as the number of cells responding to the signal is larger (Fig. 4 A). For path 2b (Fig. 3 B), the selection process required much longer timescales (Fig. 4 B). This is to be expected because the pattern does not form from a linear, small, instability, but from a nonlinear one. In addition, the minimal time increases with the size of the cluster of cells (Fig. 4 B). It is also worthwhile to stress that the selection becomes less robust, becoming less sharp. The distinct behavior that paths 2a and 2b show for the time required for robust selection as a function of the size of the cluster of cells indicate that we may expect nonmonotonic functionalities on the size of the cluster for more complex paths. This is indeed the case, as shown in Fig. S10.

Figure 4.

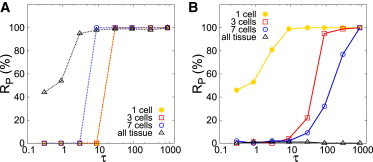
The robustness of the selection process depends on the amount of cells that sense the signal. (A) Frequency of selection of the P-pattern (R_p in percentage) for 100 repetitions versus (B) the time τ spent at the intermediate parameter space vertex point of the path. The signal drives the change of the control parameters only in the number of cells detailed in the legend, located at the center of the tissue, according to (A) path 2a and (B) path 2b of Fig. 3, A and B, respectively. All parameter values as in Fig. 3. To see this figure in color, go online.

Together, these results show that selection of a pattern that is more stable than another stable one and can spatially invade it, can be triggered by a signal acting locally in a cluster of cells and propagate across the tissue spontaneously, without requiring the signal anymore. The signal can destabilize the initial pattern either dynamically inside the cluster of cells or in a spatial manner by setting borders. Therefore, the instability can arise either within the region where the signal acts or outside this domain, at its border.

Scenario 3: spatiotemporal paths can select the stripe pattern

It is quite common to have patterns that, although they are stable, cannot arise spontaneously from an H-pattern unless specific spatial symmetries are broken. In our model, the stripe S-pattern is such a case (Materials and Methods). To ensure stochastic stability of this pattern, we focused on the phase diagram for n = 4 (Fig. 5 A). We evaluated whether selection of the S-pattern can arise when the system is initially at the H-pattern. According to the phase diagram (Fig. 5 A), transient destabilization of the initial H-pattern can occur, but it does not drive a univocal selection. Although H now becomes unstable, both the S- and P-patterns are stable and able to be selected (e.g., at point B).

Figure 5.

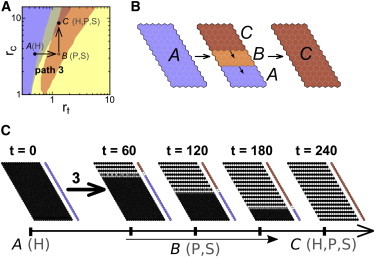
Stripes selection achieved through a propagating signal. (A) Path (arrows) across the parameter space of trans r_t and cis r_c interaction strengths. (Solid circles) Initial and final points of the path; (open circles) intermediate vertex points. The temporal evolution of the path is shown in Fig. S12. It is indicated within parentheses at relevant points of the path (denoted by letters A, B, and C) whether the homogeneous (H), the salt-and-pepper (P), and/or stripes (S) patterns are stable. The path crosses different domains (colors), each defined by which of these patterns are stable: H (blue), P (yellow), H and P (gray), S and P (orange), or H, P, and S (red). These domains have been plotted using data for deterministic dynamics with periodic boundary conditions in Formosa-Jordan and Ibañes (22). Stability of these patterns for stochastic dynamics and fixed boundary conditions at bottom and top rows is found in Fig. S11. (B) Representation of path 3 across the tissue (denoted by the black border) at the initial (left), an intermediate (middle), and the final (right) times. Small arrows within the tissue denote the spatial direction of change of the parameter values from top to bottom rows. Colors and letters, as in (A), denote the parameter values of cells. (C) Snapshots of the tissue state over time (t) when the system starts (t = 0) with the homogeneous H-pattern and parameters change over time according to path 3 (i.e., propagating from top to bottom cell rows). The column of colored cells at the right of each panel shows the point of the parameter space at which each cell row is located (blue for point A, white for B, and red for C). Parameter values are t_prop = 7, N_rows = 2, b = 1000, n = 4, and V = 10,000; and r_c and r_t values can be found in Table S3. A lattice of N = 18 × 31 cells with fixed boundary conditions at bottom and top rows (s = 0 and l = 0 for neighbors on top of the first row and below the last row) and periodic conditions between left and right sides were used. To see this figure in color, go online.

To drive the selection from the H-pattern to the S-pattern, we envisaged that signals could act in domains of the tissue, which could break the spatial symmetry appropriately. Evaluation of the relative stability of the S-pattern for stochastic dynamics indicated that the S-pattern cannot propagate over the H-pattern (Fig. S11), discarding a mechanism like Scenario 2. Therefore, if the S-pattern was to arise in a small spatial domain of the tissue, it would not propagate spontaneously over the whole tissue. This prompted us to consider spatiotemporal signals and paths that sweep rows of cells along time (Fig. 5 B, Materials and Methods). These kinds of spatiotemporal paths could be driven, for instance, by diffusing morphogens.

We designed that changes of parameter values within a cell over time trace the trajectory shown in Fig. 5 A, which traverses a region where the H-pattern becomes unstable. These changes evolved progressively from row to row (path 3) (Fig. 5 B). Fig. 5 C shows that the S-pattern can be selected through this path.

We evaluated how the selection of the S-pattern depends on the time t_prop the path takes to evolve from row to row and on how many rows (N_rows) are at point B of the path where the H-pattern is unstable (Fig. 5, A and B). For short t_prop (i.e., fast propagation of the signal over the tissue), the S-pattern is not selected but the P-pattern is (Figs. 6 and S13). Specifically, t_prop = 0 corresponds to the signal acting in all cells at the same time, and not propagating (Scenario 1). Therefore, nonpropagating signals cannot select the S-pattern as expected (Fig. S14). For higher values of t_prop (i.e., slower propagation of the signal), the S-pattern is robustly selected, with the stripes arising sequentially as the signal propagates, and finally all the tissue exhibits the S-pattern (Figs. 6 and S13). If the signal propagates too slowly (large t_prop), the stripes become destabilized and the P-pattern is selected again (Figs. 6 and S13). These two limits give an optimal selection of the S-pattern within a range of t_prop. Increasing the value of N_rows enlarged the maximal t_prop for optimal selection of the S-pattern, albeit up to a maximal range (Figs. 6 and S13). The range of t_prop values for which the selection of the S-pattern occurs is of the same order as the time for the formation of stripes in a few rows surrounded by the H-pattern (data not shown). We also found that short t_prop values, below the optimal range, drove stripes to be formed consistently only partially within the tissue (Fig. S13). In contrast, for t_prop values above the optimal range, in some stochastic circumstances all the tissue could form the S-pattern, while only partially in other cases (Fig. S13). We checked that the selection of stripes can also occur through spatiotemporal paths that start and end up at the same multistable point of the phase diagram, exhibiting features similar to those described above (Fig. S15).

Figure 6.

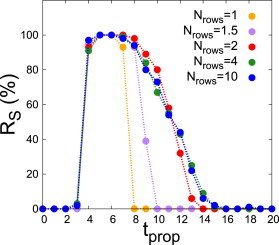
Robust selection of stripes occurs for an optimal signal propagation time along the tissue. Frequency of selection of the S-pattern (R_s in percentage) for path 3 (Fig. 5, A and B) versus t_prop (propagating time) for 100 repetitions. Results for different number of cell rows being simultaneously at point B of the path (N_rows, see legend) are shown. All other parameter values as in Fig. 5. To see this figure in color, go online.

These results show that selection of the S-pattern, which cannot arise through random variability from the H-pattern, requires a spatiotemporal path that favors its spatial symmetry. Yet, and in contrast with the other selection processes being analyzed, there is an optimal timescale for the signals to select the S-pattern.

Conclusions

Previous works have addressed the question of how different cellular patterns can be established in a tissue, e.g., how a system can select between spots and stripes (15–17,20,23). These works focused on the univocal correspondence between the parameter values and initial conditions with the selected pattern. Our work sheds light on new mechanisms for the selection among multiple stable patterns based on time-dependent parameter variation, which we called “dynamical paths”. Our results show that the selection of a specific pattern does not simply depend on the initial and final values of the control parameters. The main factor in our approach is the specific path followed by parameter changes and the spatiotemporal characteristics of these changes such that the path drives the selection. Herein, changes of the parameter values are understood as the result of biochemical signals. We expect these mechanisms to help us to understand some of the pattern formation processes occurring in the context of development.

We have presented different dynamical paths that select patterns that are all stable for the same value of the parameters. To this end, we have made use of a model of tissue differentiation based on cell-to-cell communication through the Notch signaling pathway. We have shown that patterns that can spontaneously break the spatial symmetry can be robustly selected through paths that only involve temporal, and not spatial, dynamics. The timescales of the path (i.e., of the parameter changes) can be shorter than the time required for the full pattern to emerge. Therefore, the selection can become evident after the path has finished, i.e., at the final set of parameter values. In this sense, the tissue has a memory of the conditions (the path) to which it has been subjected. Even for fast paths, the selection can be robust. Indeed, the selection exhibits a thresholdlike behavior as a function of the characteristic timescale of the path.

We have shown that when several patterns are stable and one is able to spatially invade another one, the invading pattern can be selected through signals acting in a small subset or cluster of cells. Such selection spontaneously propagates through all the tissue, without requiring the further action of the signal. Moreover, our results have shown that selection can arise among cells that are not within the cluster of cells where the biochemical signal acts. In this case, the initial pattern becomes destabilized by the spatial inhomogeneities the signal drives at the boundary of its acting domain. In all these cases, selection also exhibits a sharp threshold response with time. The robustness of the selection process depends on the size of the cluster of cells as well, and this dependence can be antagonistic for different paths.

Finally, our results show patterns that cannot arise spontaneously because of their symmetries; they require spatiotemporal signals that set appropriate symmetries. This is the case of the S-pattern. A propagating front can drive its selection, yet robust selection only occurs for a range of optimal propagation times.

Summarizing, the most relevant aspects involved in the selection of a pattern among multiple stable ones through dynamical paths are: 1) The destabilization of the initial pattern either by dynamical (Scenario 1) or spatial (Scenario 2) mechanisms. 2) The different stable patterns that the path visits during its evolution, the last explored pattern being the most relevant one for the final selection when all are explored for long enough times; therefore, the order that signals acting sequentially have, is relevant. 3) The interplay between two relevant timescales, which is the characteristic time of the parameter changes that sets the time spent in the exploration of a pattern and the characteristic time to form the pattern. 4) Selection that can be triggered at localized clustered regions and spontaneously extends to all the tissue, when the selected pattern can propagate over the initial one. 5) Time-specific symmetries of the spatiotemporal parameter that exhibit changes for more singular pattern selections.

It has been shown that dynamic filopodia in Drosophila enables the creation of sparser salt-and-pepper patterns mediated by Notch signaling (55,56). This is an example of a stochastic spatial and time-dependent trans-interactions strength (r_t) extended to longer-range interactions. A more recent study suggests that growing cell projections in certain cells in zebrafish embryos would drive stripes formation through Notch signaling (7), what could probably be understood as a pattern selection phenomenon through a dynamical path. Hence, an extension of our framework to more complicated dynamical paths in the parameter space might be helpful for studying these and other phenomena that exhibit more complicated spatiotemporal patterning.

Notch signaling is just an example of a pathway that is orchestrated and modulated by different agents along time and space. Therefore, the patterning selection mechanism characterized here could also be applied to other signaling pathways acting during development. In addition, in this work we explored what happens if trans- and cis-interaction strengths in Notch pathway are modulated in time, but other parameters could also be explored, like the signaling intensity elicited by a ligand when interacting with the receptor. Indeed, recently it has been shown that there is spatiomechanical regulation for signal activation, what could probably drive time-dependent signaling efficiency for the Notch receptor (57).