Nucleation of Polymorphic Amyloid Fibrils

Abstract

One and the same protein can self-assemble into amyloid fibrils with different morphologies. The phenomenon of fibril polymorphism is relevant biologically because different fibril polymorphs can have different toxicity, but there is no tool for predicting which polymorph forms and under what conditions. Here, we consider the nucleation of polymorphic amyloid fibrils occurring by direct polymerization of monomeric proteins into fibrils. We treat this process within the framework of our newly developed nonstandard nucleation theory, which allows prediction of the concentration dependence of the nucleation rate for different fibril polymorphs. The results highlight that the concentration dependence of the nucleation rate is closely linked with the protein solubility and a threshold monomer concentration below which fibril formation becomes biologically irrelevant. The relation between the nucleation rate, the fibril solubility, the threshold concentration, and the binding energies of the fibril building blocks within fibrils might prove a valuable tool for designing new experiments to control the formation of particular fibril polymorphs.

Introduction

The structure and mechanism of formation of amyloid fibrils are being widely researched, not only because they are involved in many human diseases (1), but because of their variety of applications as novel biomaterials in nanoscience (2). Although amyloid fibrils share a common cross-β structure formed by intertwined layers of β-sheets extending in a direction parallel to the fibril axis (3), the conformation and the stacking of the β-strands in β-sheets can differ in fibrils of the same protein, a phenomenon known as fibril polymorphism (4–6). For example, stacking polymorphism of fibrils has been observed in microcrystals of short hexapeptides, where β-strands within β-sheets can arrange in a parallel or antiparallel way, and the orientation and stacking of β-sheets can differ (7). The stacking of β-sheets in fibrils can also lead to differences in fibril thickness, which in turn can lead to differences in the twisting behavior and helical pitch of these fibrils, as has been shown for fragments of bovine serum albumin (8) and the TTR peptide (9). A well known example of conformational polymorphism can be seen in fibrils of the amyloid β (Aβ) peptide associated with Alzheimer’s disease, which have several distinct morphologies, including those where the β-strands in the fibril adopt an extended or hairpin conformation (10,11). The Aβ fibrils also exhibit packing polymorphism, where the molecules are in the same conformation but pack in the fibril with different stacking or symmetry (11–13). Numerous examples of polymorphism can be found in fibrils of proteins including α-synuclein (14), yeast and mammalian prion proteins (15,16), and insulin (17) (more complete lists can be found in the literature (4–6,18)). The biological relevance of amyloid fibril polymorphism comes from the observation that the toxicity of polymorphs can differ (see, e.g., Tycko and colleagues (11,19).). A prominent example is strain polymorphism and species barriers in prions. In this phenomenon, the prion protein can propagate multiple strains (fibril structures), each of which results in a different pathology. Propagation is sequence-dependent, which prevents prion transmission between related species (see, e.g., Jones and Surewicz (15), Collinge and Clark (20), and Diaz-Avalos et al. (21). The conditions under which fibril polymorphism can be observed are manifold. Fibril morphology depends on intrinsic factors such as the protein amino acid sequence, and it has been observed that a single point mutation can switch the fibril morphology from predominately parallel to predominately antiparallel (22). It also depends on solution conditions (pH value (23) and salts (24)) and other external factors (temperature (25), whether it is quiescent or agitated (11), and seeds (26)), but even under the same conditions, there are variations in fibril morphology (27).

How polymorphic amyloid fibrils form, and under what conditions, is the subject of intense research (4–6). It is generally accepted that amyloid fibrils form by a nucleation and growth mechanism (see, e.g., Knowles et al. (28), Lomakin et al. (29), and Kashchiev et al. (30)). The nucleation of amyloid fibrils refers to the process of random generation of nanofibrils that have the ability to grow irreversibly. Unless the nanofibril size exceeds the size of the nucleus, the nanofibril is more likely to dissolve than to grow. Depending on the solution conditions, amyloid fibrils nucleate in one step (directly from the solution) or in two steps (where step one is the appearance of nonfibrillar oligomers in the solution and step two is the oligomer conversion into fibrils) (31). In analogy to crystal nucleation where the structure of the nucleus determines the structure of the bulk solid, the structure of the fibril nucleus might determine the structure of the fibril formed in the solution. This implies that every fibril polymorph requires a distinct nucleation event and certain nucleation events may occur more frequently than others. Amyloid fibril growth refers to the process of addition of monomers to either the fibril ends or fibril surfaces, leading to lengthening and thickening, respectively, of the fibril. During growth, fibrils can be affected by other processes, such as fragmentation (11,28), coalescence, Ostwald ripening, and secondary nucleation events such as the nucleation of fibrils on the surface of existing ones (32). Although a common feature of fibril polymorphism is that they are self-propagating, such growth effects can also lead to the formation of fibril polymorphs or determine which polymorph dominates. For example, fibril coalescence and Ostwald ripening can lead to fibrils with different thickness and thus different twisting behavior and helical pitch, as in the case of bovine serum albumin (8) and the TTR peptide (9) mentioned above. It has also been shown that the fragmentation rate is the reason that Aβ40 fibrils with twofold symmetry form in agitated solutions and Aβ40 fibrils with three-fold symmetry form in the absence of shear (11).

To better understand why and how polymorphic amyloid fibrils form, and under what conditions, it is necessary to develop a theoretical model of their formation. Models based on protein physicochemical properties have been developed to predict aggregation propensities, but they are unable to differentiate between polymorphic fibril structures (33–36). In a similar way, models on the molecular level based on rate equations have been used to analyze protein fibrillation experiments (28,37,38), but they are also unable to differentiate between polymorphic fibril structures, because they work with a fixed fibril shape. Fibril polymorphism has been investigated in various molecular dynamics (MD) simulation studies that use a full atomistic description of proteins (39–43), but at present these studies are restricted to calculations of the thermodynamic stability of fibrils composed of short peptide fragments. Using a simplified protein model, it has been possible to perform MD simulations showing that one protein can self-assemble into different fibril morphologies, and that their formation can be kinetically (rather than thermodynamically) controlled (44).

Here, we approach the problem by considering the nucleation of amyloid fibrils into polymorphic structures when the process occurs in one step by direct polymerization of monomers into fibrils. Two-step nucleation of polymorphic fibrils, and fibril polymorphism that occurs during fibril growth, or is determined by fibril growth, are not considered. Recently, our simulations showed that amyloid fibril nucleation occurring by direct polymerization of monomers is a peculiar kind of nucleation that does not comply with standard nucleation theory (45,46), because the concept of the existence of a critical nucleus breaks down (the nucleus size does not have a unique value) and there exist jumps in the nucleation rate of many orders of magnitude at certain concentrations (47,48). This called for the development of a new description of amyloid fibril nucleation that is able to describe this nonstandard nucleation of amyloid fibrils (30,49). The objective of this article is to apply this new nucleation model to the phenomenon of amyloid fibril polymorphism and to predict how the fibril solubility, the threshold concentration below which fibril formation becomes biologically irrelevant, and the nucleation rate are affected by changes in the conformation and stacking of the fibril building blocks (the β-strands) or their arrangement within the fibril. Our considerations of fibril polymorphism pertain to changes in 1) the β-strand length associated with the onset of polyglutamine disorders (50); 2) the conformation of the β-strand from extended to hairpin reported for Aβ₄₀ (10); 3) the parallel and antiparallel stacking of β-strands in β-sheets, as observed in short peptides and natural proteins (7,22); and 4) the asymmetry in hydrophobicity between the two β-sheet surfaces, which can lead to different stacking of β-sheets in fibrils (7). The emphasis of this work is to reveal general rules that underlie the nucleation of one and the same protein into different fibril polymorphs and to provide conceptual insight into factors that can tip the nucleation process in favor of one or another fibril polymorph. For this reason, we apply our theoretical framework to a model peptide rather than to a specific protein.

Materials and Methods

Model

In our model (30,49,51), each β-strand (a segment of a protein chain composed of typically up to 10 amino acids) is represented by a right rectangular prism (Fig. 1). Due to their strong hydrogen bonds, the β-strands can arrange themselves laterally into β-sheets. The sheets consist of different numbers m of β-strands ($m=\mathrm{1,2,3},\dots$) and are parallel to the fibril lengthening axis. Along its thickening axis, the fibril is built up of iβ-sheets ($i=\mathrm{1,2,3},\dots$) held together by, for example, relatively weak hydrophobicity-mediated bonds between the β-strands. Because the orientation of side chains within a β-strand alternates, the hydrophobicity of the two β-sheet surfaces is generally different. In our model (49), we assume that for a 1β-sheet, i.e., a single β-sheet, the strongly hydrophobic (SH) surface is always on top, as indicated by the red surface/line in Fig. 1, whereas the weakly hydrophobic (WH) surface is at the bottom (Fig. 1, blue surface/line). In addition, a β-strand can only bind to a WH β-sheet surface with its WH side (blue binds to blue) and to an SH β-sheet surface with its SH side (red binds to red). Thus, the hydrophobicity of the surface of a nanofibril alternates as the number of β-sheets increases (red, blue, red, blue, etc.). Since the fibril width is fixed and equal to the β-strand length, the fibril can be considered as a two-dimensional (2D) aggregate in the m,i plane, with building blocks (the β-strands) arranged in a 2D lattice with simple rectangular symmetry.

Figure 1.

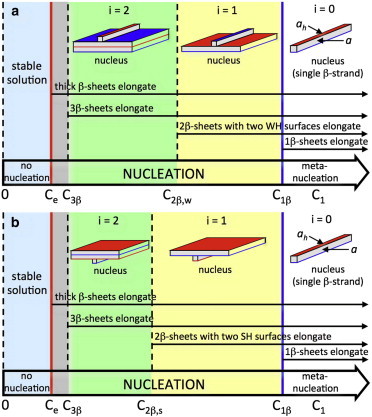
Phase diagram for fibrils composed of β-strands with one WH (blue) and one SH (red) side. The fibril solubility, $C_{\text{e}}$, indicates the concentration ranges in which the protein solution is in stable ($0\le C_1\le C_{\text{e}}$) or metastable ($C_1>C_{\text{e}}$) thermodynamic equilibrium at a given temperature. (a) In the metanucleation range ($i=0$), the nucleus is a single β-strand. In the first ($i=1$) nucleation range, a 2β-sheet with two WH surfaces can elongate and the nucleus is a 1β-sheet with one β-strand attached with its SH side to the SH 1β-sheet surface. In a similar way, in the second nucleation range ($i=2$), a 3β-sheet with one SH and one WH surface can elongate, and the nucleus is a 2β-sheet with one β-strand attached with its WH side to the weak 2β-sheet surface. (b) As in (a), but in the first ($i=1$) and second ($i=2$) nucleation ranges, the fibril nuclei are 1β- and 2β-sheets (with two SH surfaces) with one β-strand attached to the WH and SH sides, respectively. To see this figure in color, go online.

Essential parameters in our theory to describe the ontogenesis of the smallest nanosized amyloid fibrils are the dimensionless specific surface energies $\psi =a\sigma /kT=E/2kT$ and ${\psi }_{\text{w}}=a_{\text{h}}{\sigma }_{\text{w}}/kT=E_{\text{w}}/2kT,$ ${\psi }_{\text{s}}=a_{\text{h}}{\sigma }_{\text{s}}/kT=E_{\text{s}}/2kT$ of the fibril faces perpendicular to the lengthening m axis and the thickening i axis, respectively. σ represents the dimensional specific surface energy of the fibril surfaces, a the areas of the β-strand faces (Fig. 1), k the Boltzmann constant, and T the absolute temperature. The second equality in these equations results from using the approximate relations $\sigma =E/2a,{\sigma }_{\text{s}}=E_{\text{s}}/2a_{\text{h}}$, and ${\sigma }_{\text{w}}\mathrm{=}{E}_{\text{w}}/2a_{\text{h}}$ between σ and the binding energy, E, between nearest-neighbor β-strands (52).

To model conformational polymorphism of β-strands within fibrils, it is necessary to introduce the binding energies $\epsilon$ and ${\epsilon }_s$, ${\epsilon }_{\mathit{w}}$ between nearest-neighbor amino acids due to hydrogen bonding, and to strong and weak hydrophobic bonding, respectively. Although our model can be applied to heteropolypeptides, in this work, for simplicity, we consider only homopolypeptides for which the binding energies between amino acids in neighboring β-strands are the same. Then, E can be written as $\mathit{E}=\mathit{n}\epsilon$, $E_{\text{s}}=n_{\text{s}}{\epsilon }_{\text{s}}$, and $E_{\text{w}}=n_{\text{w}}{\epsilon }_{\text{w}}$, where n is the number of amino acids between two nearest-neighbor β-strands in a β-sheet that form hydrogen bonds, and n_s, n_w are the number of amino acids that form strong and weak hydrophobic bonds, respectively, between nearest-neighbor β-strands in successive β-sheets. The dimensionless specific surface energies ψ_s and ψ_w can then be written as

$${\psi }_{\text{s}}=n_{\text{s}}{\alpha }_{\text{s}}$$ (1)

$${\psi }_{\text{w}}=n_{\text{w}}{\alpha }_{\text{w}},$$ (2)

where ${\alpha }_{\text{s}}={\epsilon }_{\text{s}}/2kT$ and ${\alpha }_{\text{w}}={\epsilon }_{\text{w}}/2kT$ are the dimensionless specific surface energies per amino acid due to strong and weak hydrophobic bonds, respectively.

It is important to note that the dimensionless specific surface energy, $\psi$, can contain contributions from both nearest-neighbor hydrogen bonding and hydrophobicity-mediated bonds and is given by

$$\psi =n\alpha +c_{\text{s}}{n}_{\text{s}}{\alpha }_{\text{s}}+c_{\text{w}}{n}_{\text{w}}{\alpha }_{\text{w}},$$ (3)

where $\alpha =\epsilon /2kT$ represents the dimensionless specific surface energies per amino acid due to hydrogen bonds, and c_s, c_w are parameters determining the contributions of the strong- and weak-hydrophobicity-mediated bonds, respectively, to $\psi$. For our illustrations, we set $c_{\text{s}}=c_{\text{w}}=0.5$, which means that the contribution of the strength of the hydrophobicity-mediated bonds to $\psi$ is taken to be the average of the weak and strong hydrophobic surfaces.

To calculate ψ_s, ψ_w and $\psi$ for hetero polypeptides, the binding energies between amino acid pairs need to be known so that the dimensionless specific surface energies can be calculated by summation over amino acid pairs in neighboring β-strands (53).

Phase diagram

Understanding the thermodynamic phase diagram is a prerequisite for applying nucleation theory to the formation of new phases. Experiments with different fibril polymorphs of Aβ40 show that their solubility differs (13,54). Both theoretical considerations (30,49,51) and a computer-simulated peptide solubility diagram (55,56) reveal that for the irreversible elongation of differently thick amyloid fibrils, thermodynamics requires different ranges of the concentration C₁ of monomeric β-strands (peptides or protein segments) in the solution. Fig. 1 illustrates schematically these ranges at a fixed absolute temperature, T, at which the β-strands are in practically fully extended conformation. These ranges are limited by the equilibrium concentration (or solubility), C_e, of the bulk fibrillar phase and the equilibrium concentrations (or solubilities) $C_{1\beta }$, $C_{2\beta ,\text{w}}$, $C_{2\beta ,\text{s}}$, $C_{3\beta }$, etc., of the fibrils constituted of one β-sheet, two equally long β-sheets with two WH or two SH surfaces, three equally long β-sheets, etc., respectively. The solubilities are merely the C₁ values at which the respective iβ-sheets, i.e., fibrils built up of i β-sheets, neither lengthen nor dissolve. The iβ-sheets with an odd number i of layers have always one WH and one SH surface, and their solubility, $C_{i\beta }$, is related to C_e by the expression (49)

$$C_{i\beta }=C_{\text{e}}\exp \left[({\psi }_{\text{w}}+{\psi }_{\text{s}})/i\right]\left(i=\mathrm{1,3,5},\dots \right).$$ (4)

The existence of two solubility values for iβ-sheets with an even number i of layers is due to the fact that they can have either two WH or two SH surfaces, and their solubilities $C_{i\beta ,\text{w}}$ and $C_{i\beta ,\text{s}}$ are related to C_e by the expressions (49)

$$C_{i\beta ,\text{w}}=C_{\text{e}}\exp \left(2{\psi }_{\text{w}}/i\right)$$ (5)

$$C_{i\beta ,\text{s}}=C_{\text{e}}\exp \left(2{\psi }_{\text{s}}/i\right),$$ (6)

with ($i=\mathrm{2,4,6},\dots$). In this work, we mostly consider the symmetric case where the hydrophobicity of both β-strand surfaces is the same, i.e., ${\psi }_{\text{w}}={\psi }_{\text{s}}\equiv {\psi }_{\text{h}}$, and the three equations above simplify to one (51):

$$C_{i\beta }=C_{i\beta ,\text{w}}=C_{i\beta ,\text{s}}=C_{\text{e}}\exp \left(2{\psi }_{\text{h}}/i\right)\left(i=\mathrm{1,2,3},\dots \right).$$ (7)

As indicated in Fig. 1, the $C_1>C_{1\beta }$ range (range $i=0$ in the figure) corresponds to metanucleation, a process of fibril formation without energy barrier, because then each protein monomer (i.e., single β-strand) in the solution acts as a fibril nucleus since attachment of another monomer to it allows irreversible elongation. When $C_1>C_{2\beta ,\text{w}}$, 2β-sheets with two weak hydrophobic surfaces can lengthen irreversibly. It is important to note that in the $C_{2\beta ,\text{w}}<C_1<C_{1\beta }$ range (Fig. 1, i = 1), the 1β-sheets tend to dissolve and their appearance is due to fluctuations. In this range, the fibril nucleus is a 1β-sheet plus one β-strand attached with its SH side to the SH 1β-sheet side, so that a fibril prenucleus is any of the randomly formed, differently long 1β-sheets in the solution. When $C_1>C_{2\beta ,\text{s}}$, the 2β-sheets with two strong hydrophobic surfaces also can lengthen irreversibly, and in the $C_{2\beta ,\text{s}}<C_1<C_{1\beta }$ range (Fig. 1, $i=1$) the corresponding fibril nucleus is a 1β-sheet plus one β-strand attached with its WH side to the WH 1β-sheet side (see Fig. 1). The situation is analogous to that of the 3β-sheets when $C_1>C_{3\beta }$, because then these sheets can elongate irreversibly, and in the $C_{3\beta }<C_1<C_{2\beta \text{w}}$ or $C_{3\beta }<C_1<C_{2\beta \text{s}}$ ranges (Fig. 1, range $i=2$), the fibril nucleus is a 2β-sheet with one β-strand attached sidewise.

The general rules are, therefore, that in the ith supersaturation range, defined by (49)

$$C_{\text{e}}\exp \left[2{\psi }_{\text{w}}/\left(i+1\right)\right]<C_1<C_{\text{e}}\exp \left[\left({\psi }_{\text{w}}+{\psi }_{\text{s}}\right)/i\right]$$ (8)

$$C_{\text{e}}\exp \left[2{\psi }_{\text{s}}/\left(i+1\right)\right]<C_1<C_{\text{e}}\exp \left[\left({\psi }_{\text{w}}+{\psi }_{\text{s}}\right)/i\right]$$ (9)

($i=\mathrm{1,3,5},\dots$), the fibril nuclei are composed of an odd number i of β-sheets plus one β-strand attached to the SH or WH side, respectively (Fig. 1). In these ranges, all different-length iβ-sheets are fibril prenuclei, and these sheets plus one iβ-strand attached to the WH or SH surface are the fibril nuclei for the (i + 1)β-sheet-thick fibrils with either two WH or SH sides that can lengthen irreversibly. In a similar way, in the ith supersaturation range, defined by

$$C_{\text{e}}\exp \left[({\psi }_{\text{w}}+{\psi }_{\text{s}})/(i+1)\right]<C_1<C_{\text{e}}\exp (2{\psi }_{\text{w}}/i)$$ (10)

$$C_{\text{e}}\exp \left[({\psi }_{\text{w}}+{\psi }_{\text{s}})/(i+1)\right]<C_1<C_{\text{e}}\exp (2{\psi }_{\text{s}}/i)$$ (11)

($i=\mathrm{2,4,6},\dots$), the fibril nuclei are composed of an even number i of β-sheets plus one β-strand attached to the SH or WH side, respectively (Fig. 1). For the symmetric case (${\psi }_{\text{s}}={\psi }_{\text{w}}\equiv {\psi }_{\text{h}}$), the four equations above simplify to one general rule that in the ranges (51)

$$C_{\text{e}}\exp \left[2{\psi }_{\text{h}}/(i+1)\right]<C_1<C_{\text{e}}\exp (2{\psi }_{\text{h}}/i)$$ (12)

($i=\mathrm{0,1,2,3},\dots$), all differently long iβ-sheets are fibril prenuclei, and these sheets plus one β-strand attached to one of their two sides are the nuclei of the ($i+1$)β-sheet-thick fibrils that can lengthen irreversibly.

Nucleation rate

Which fibrils form in a protein solution, and how fast they do so, is determined by the nucleation rate, J (m⁻³ s⁻¹). Experiments on protein aggregation are often performed at fixed temperature, T, and based on the phase diagram discussed above, we can write down expressions for J in the nucleation and metanucleation ranges. The concentration dependence of the nucleation rate in the metanucleation range (Fig. 1, i = 0), in which each monomer in the solution acts as fibril nucleus, is given by (49)

$$J=A_1{C}_1^2\left(1-A_2{C}_1^{-1}\right)$$ (13)

($C_1>C_{1\beta }$), where $A_1=2k_{\text{e}}/C_{\text{e}}$, $A_2=C_{\text{e}}\exp \left({\psi }_{\text{w}}+{\psi }_{\text{s}}\right)$, k_e is the attachment frequency of monomers to one of the two hydrogen-bond sides of a given monomer at equilibrium, C_e is the fibril solubility, and the threshold concentration, $C_{1\beta }$, given by

$$C_{1\beta }=C_{\text{e}}\exp ({\psi }_{\text{s}}+{\psi }_{\text{w}}),$$ (14)

is obtained from Eq. 4 with $i=1$. For the symmetric case (${\psi }_{\text{s}}={\psi }_{\text{w}}\equiv {\psi }_{\text{h}}$), the constants simplify to (30) $A_1=2k_{\text{e}}/C_{\text{e}}$, $A_2=C_{\text{e}}\exp \left(2{\psi }_{\text{h}}\right)$, and $C_{1\beta }=C_{\text{e}}\exp \left(2{\psi }_{\text{h}}\right)$.

The formula for J in the ith nucleation range when the fibril nuclei are composed of an odd number ($i=\mathrm{1,3,5},\dots$) of β-sheets plus one β-strand (corresponding to supersaturation ranges ($i=\mathrm{1,3,5},\dots$) is given by (49)

$$J=A_1{C}_1^{i+2}\frac{1-A_2{C}_1^{-1}}{{\left(1-A_3{C}_1^i\right)}^2},$$ (15)

with $A_1=(2k_{\text{e}}/C_{\text{e}}^{i+1})\exp (-2\psi i-{\psi }_{\text{w}}+{\psi }_{\text{s}})$ and $A_2=C_{\text{e}}\exp \left[2{\psi }_{\text{w}}/(i+1)\right]$ (for $C_{\text{e}}\exp \left[2{\psi }_{\text{w}}/(i+1)\right]<C_1<C_{\text{e}}\exp \left[({\psi }_{\text{w}}+{\psi }_{\text{s}})/i\right]$) or $A_1=(2k_{\text{e}}/C_{\text{e}}^{i+1})\exp (-2\psi i-{\psi }_{\text{s}}+{\psi }_{\text{w}})$ and $A_2=C_{\text{e}}\exp \left[2{\psi }_{\text{s}}/(i+1)\right]$ (for $C_{\text{e}}\exp \left[2{\psi }_{\text{s}}/(i+1)\right]<C_1<C_{\text{e}}\exp \left[({\psi }_{\text{w}}+{\psi }_{\text{s}})/i\right]$ when the β-strand is on the SH or WH side, respectively, of the nucleus. The constant A₃ is given by $A_3=C_{\text{e}}^{-i}\exp \left[-({\psi }_{\text{w}}+{\psi }_{\text{s}})\right]$ in both cases.

When the fibril nuclei are composed of an even number $i=\mathrm{2,4,6},\dots$ of β-sheets plus one β-strand (supersaturation ranges $i=\mathrm{2,4,6},\dots$), the fibril nucleation rate is again given by Eq. 15, but with $A_1=(4k_{\text{e}}/C_{\text{e}}^{i+1})\exp (-2\psi i)$ and $A_2=C_{\text{e}}\exp \left[({\psi }_{\text{w}}+{\psi }_{\text{s}})/(i+1)\right]$. As to the constant A₃, it is given by $A_3=C_{\text{e}}^{-i}\exp (-2{\psi }_{\text{w}})$ (for $C_{\text{e}}\exp \left[({\psi }_{\text{w}}+{\psi }_{\text{s}})/(i+1)\right]<C_1<C_{\text{e}}\exp (2{\psi }_{\text{w}}/i)$) when the β-strand is on one of the prenucleus two WH sides, or by $A_3=C_{\text{e}}^{-i}\exp (-2{\psi }_{\text{s}})$ (for $C_{\text{e}}\exp \left[({\psi }_{\text{w}}+{\psi }_{\text{s}})/(i+1)\right]<C_1<C_{\text{e}}\exp (2{\psi }_{\text{s}}/i)$) when the β-strand is on one of the nucleus two SH sides. For the symmetric case, the fibril nucleation rate is again given by Eq. 15, but with $A_1=(4k_{\text{e}}/C_{\text{e}}^{i+1})\exp (-2\psi i)$, $A_2=C_{\text{e}}\exp \left[2{\psi }_{\text{h}}/(i+1)\right]$, and $A_3=C_{\text{e}}^{-i}\exp (-2{\psi }_{\text{h}})$ in the supersaturation ranges specified by Eq. 12.

Fibril solubility

Different fibril polymorphs will have different solubilities (13,54). As the effect of changing molecular interactions between β-strands on $C_{\text{e}}$ is not always known experimentally, we estimate it theoretically by making use of the van’t Hoff equation and the Haas-Drenth lattice model (57) for protein crystals. The integrated van’t Hoff equation is given by $C_{\text{e}}=C_{\text{r}}\exp (-\lambda )$, where $C_{\text{r}}$ is a practically temperature-independent reference concentration and $\lambda =L/kT$ is the dimensionless latent heat of peptide aggregation into β-sheets. Here, L is the latent heat of peptide aggregation into such aggregates. In the Haas-Drenth lattice model (57) for protein crystals, λ is half the dimensionless binding energy of peptides in the aggregates, which is equivalent to the dimensionless broken bond energy $\lambda =2\psi +{\psi }_{\text{s}}+{\psi }_{\text{w}}$ at the periphery of a fibril in the m,i plane. The fibril solubility is then given by

$$C_{\text{e}}=C_{\text{r}}\exp \left(-2\psi -{\psi }_{\text{s}}-{\psi }_{\text{w}}\right)$$ (16)

and simplifies to $C_{\text{e}}=C_{\text{r}}\exp \left[-2(\psi +{\psi }_{\text{h}})\right]$ in the symmetric case.

Results

The recipe to apply our newly developed nonstandard nucleation theory to predict the $J\left(C_1\right)$ dependence for different fibril polymorphs is as follows. 1) Dimensionless specific surface energies ψ_s, ψ_w and $\psi$ for different fibril polymorphs are calculated from Eqs. 1–3. This requires knowledge of the conformation of the β-strands in the fibril, as they define the number, n, of bonds between amino acids, and the associated binding energies between them. 2) Fibril solubility, $C_{\text{e}}$, for different fibril polymorphs is calculated from Eq 16. This requires the knowledge of $C_{\text{e}}$ for one fibril polymorph, which serves as a reference structure. 3) The $J\left(C_1\right)$ dependence is calculated from Eqs. 13–15, which requires knowledge of the elongation rate, $k_{\text{e}}$. We apply this recipe to the fibril polymorphs illustrated in Fig. 2. As mentioned in the Introduction, the emphasis of this work is to provide conceptual insight into factors that can tip the nucleation process in favor of one or another fibril polymorph. For this reason, we apply our theoretical framework to a model peptide rather than to a specific protein.

Figure 2.

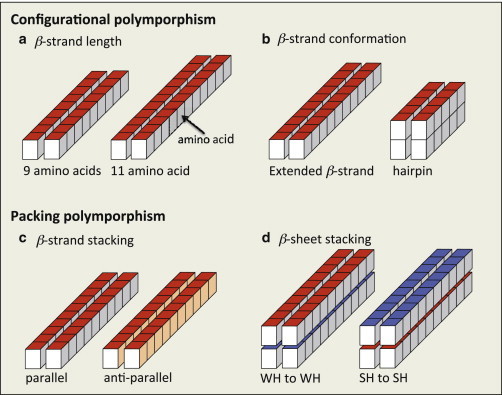
Illustration of fibril polymorphs considered in this work. (a and b) Conformational polymorphism where the fibril polymorphs are composed of extended β-strands of different lengths (9 or 11 amino acids) (a) and β-strands in an extended or hairpin conformation (b). (c and d) Stacking polymorphism where the fibril polymorphs are composed of extended β-strands that stack either parallel or antiparallel in β-sheets (c), and β-sheets that stack by binding either with their two WH or with their two SH surfaces (d). Red and blue surfaces indicate the SH and WH β-strand sides, respectively. Light gray and light orange surfaces indicate the strong- and weak-hydrogen-bonding β-strand sides, respectively. To see this figure in color, go online.

Conformational polymorphism

Perhaps the simplest example of conformational polymorphism is where the numbers of amino acids in the β-strands within a fibril differ. The β-strand length is relevant because it has been associated with polyglutamine disorders (50). Polyglutamine disorders are a class of nine neurodegenerative disorders, including Huntington’s disease, that are associated with the aggregation of polyglutamine repeats. The hallmark feature of these diseases is that the onset of the disease correlates with the length of the polyglutamine repeats. The aggregation and pathologies are typically observed above a threshold of 35–40 repeats, and the longer the repeat, the sooner the symptoms appear (50,58). To illustrate the effect of the β-strand length on $J\left(C_1\right)$ dependence, we consider β-strands composed of 9, 10, and 11 amino acids (Fig. 2 a) that assemble in their fully extended conformation in a nanosized amyloid fibril. Step 1 of the recipe is to determine the dimensionless specific surface energies. As the structure of the β-strands in the fibril is fully extended, the number, n, of amino acids that form hydrogen bonds between two nearest-neighbor β-strands in a β-sheet and the numbers n_w, n_s of amino acids that form hydrophobic bonds between two nearest-neighbor β-strands are the same and given by $n=n_{\text{s}}=n_{\text{w}}=9$, 10, and 11 for β-strands of length 9, 10, and 11, respectively. Assuming that the dimensionless specific surface energy per amino acid due to hydrogen-bonding is $\alpha =1$ (corresponding to $\epsilon =2$ kT, a value in the range of hydrogen bonding energies measured experimentally (59)), that the ones due to strong and weak hydrophobic bonds are ${\alpha }_{\text{s}}={\alpha }_{\text{w}}=0.1$ (corresponding to ${\epsilon }_{\text{s}}={\epsilon }_{\text{w}}=0.2$ kT, a value typically used in protein simulations (60)), and that the parameter $c_{\text{s}}=c_{\text{w}}=0.5$, the values for the dimensionless specific surface energies are obtained from Eqs. 1–3 and given by $\psi =9.9$, ${\psi }_{\text{s}}={\psi }_{\text{w}}={\psi }_{\text{h}}=0.9$ for β-strands of length 9, $\psi =11$, ${\psi }_{\text{s}}={\psi }_{\text{w}}={\psi }_{\text{h}}=1$ for β-strands of length 10, and $\psi =12.1$, ${\psi }_{\text{s}}={\psi }_{\text{w}}={\psi }_{\text{h}}=1.1$ for β-strands of length 11. These ψ values are in the range of values estimated for short fibrils (31,56). Step 2 of the recipe is to calculate the fibril solubility, $C_{\text{e}}$, for different fibril polymorphs. Assuming that the fibril solubility for fibrils composed of β-strands with 10 amino acids is $C_{\text{e}}=6.0\times {10}^{21}$ m⁻³ (= 10 μM) (see, e.g., Aggeli et al. (61)), we calculate from Eq. 16 that $C_{\text{r}}=1.6\times {10}^{32}$ m⁻³. It is important to note that as the binding energies of β-strands of different lengths within the fibrils are different, their fibril solubilities are different as well (see Materials and Methods). Assuming that $C_{\text{r}}=1.6\times {10}^{32}$ m⁻³ is independent of the length, and substituting $C_{\text{r}}$ and the $\psi$ and ${\psi }_{\text{h}}$ values above in Eq. 16, the solubilities for fibrils composed of 9- and 11-amino-acid peptides are $C_{\text{e}}=6.62\times {10}^{22}$ m⁻³ (= 110 μM) and $C_{\text{e}}=5.41\times {10}^{21}$ m⁻³ (= 0.9 μM), respectively. Fig. 3 a illustrates the obtained (exponential) decrease of $C_{\text{e}}$ with increasing length (Eq. 16). Step 3 of the recipe is to calculate the $J\left(C_1\right)$ dependence for the different fibril polymorphs. Using a typical value for the fibril elongation rate, $k_{\text{e}}={10}^{-4}$ s⁻¹ (see, e.g., Knowles et al. (28)), and assuming that it is independent of the length, allows us to calculate the $J\left(C_1\right)$ dependence from Eqs. 13–15 with the A values for the symmetric case (because ${\psi }_{\text{s}}={\psi }_{\text{w}}\equiv {\psi }_{\text{h}}$). As can be seen in Fig. 4 a, the characteristic feature of the $J\left(C_1\right)$ dependence is the sharp rise at the transition concentrations, $C_{i\beta }$, over a very narrow concentration range; the rise is 7 orders of magnitude at the nucleation/metanucleation border $C_{1\beta }$ and even more at $C_{2\beta }$. As mentioned in the Introduction, such a sharp rise in the nucleation rate is a peculiar kind of nucleation and does not comply with standard nucleation theory (30). The importance of $C_{1\beta }$ comes from the fact that it appears as a threshold concentration below which fibril formation becomes biologically irrelevant, because only one fibril can be nucleated within a day in volumes of ∼1 μm³ or smaller, comparable to that of a cell. Fig. 4 a also shows that the main effect of increasing the β-strand length on $J\left(C_1\right)$ dependence is to shift $C_{1\beta }$ to lower concentrations and to promote protein fibrillation, because metanucleation commences at lower $C_1$ values. Using the C_e values calculated above in Eq. 14, the threshold concentrations for fibrils with 9, 10, and 11 amino acids are $C_{1\beta }=4.0\times {10}^{23}$ m⁻³ (665.5 μM), $C_{1\beta }=4.4\times {10}^{22}$ m⁻³ (73.8 μM), and $C_{1\beta }=4.9\times {10}^{21}$ m⁻³ (8.1 μM), respectively (Fig. 3 a). The dependence of $C_{1\beta }$ on $C_{\text{e}}$ (Eq. 14), however, highlights that $C_{\text{e}}$ is the determining factor in amyloid fibril nucleation and is the main reason why fibrils composed of longer β-strands nucleate faster. Even though we have considered here only a short model peptide, the prediction that the nucleation rate increases with increasing β-strand length is compatible with the experimental observation that the onset of the disease correlates with the length of the polyglutamine repeats (50).

Figure 3.

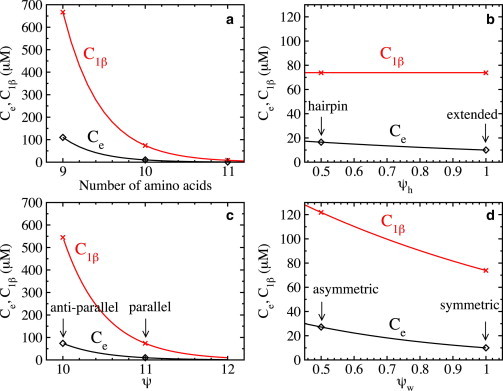
Solubility, C_e (diamonds), and threshold concentration, $C_{1\beta }$ (crosses), of fibrils of different compositions, as follows. (a) Extended β-strands of length 9, 10, and 11 amino acids. The corresponding values for the dimensionless surface energies are ${\psi }_{\text{h}}=0.9$, 1, and 1.1 and $\psi =9.9$, 11, and 12.1 for strand lengths of 9, 10, and 11, respectively. (b) Extended β-strands and β-strands in a hairpin conformation. The corresponding surface energies are $\psi =11$ (for both) and ${\psi }_{\text{h}}=1$ (extended) or 0.5 (hairpin). (c) Extended β-strands in a parallel and an antiparallel arrangement. The corresponding surface energies are ${\psi }_{\text{h}}=1$ (for both) and $\psi =10$ (antiparallel) or 11 (parallel). (d) Extended β-strands with asymmetric hydrophobic surfaces between β-sheets. The corresponding values for the dimensionless surface energies are ${\psi }_{\text{s}}=1$ (for all) and $\psi =11$, 10.75 and ${\psi }_{\text{w}}=1$, 0.5 for the symmetric and the asymmetric hydrophobic surfaces, respectively. For all compositions shown, the solid red and black lines are obtained from Eqs. 14 and 16, respectively. To see this figure in color, go online.

Figure 4.

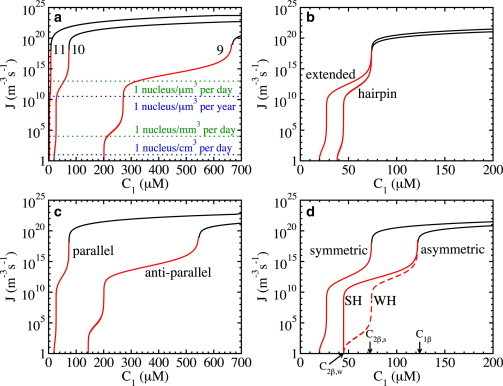
Concentration dependence of the nucleation rate, J, for fibrils of different composition. (a) Extended β-strands of length 9, 10, and 11 amino acids (as indicated). (b) Extended β-strands and β-strands in a hairpin conformation (as indicated). (c) Extended β-strands in parallel and antiparallel arrangements (as indicated). (d) Extended β-strands with symmetric and asymmetric hydrophobic surfaces between β-sheets, as indicated. In the asymmetric case, the labels WH and SH indicate the nucleation rate where the fibril nucleus is a 1β-sheet plus one β-strand attached to the SH and WH sides of the sheet, respectively. The corresponding values for the dimensionless surface energies are as in Fig. 3. In all cases, the black and red lines indicate the rate in the metanucleation and nucleation ranges, respectively. To see this figure in color, go online.

Another example of conformational polymorphism in amyloid fibrils has been reported for the amyloid-β peptide where the Aβ₄₀ peptide is in the extended and the hairpin conformation (10,12). To investigate how such a change in the conformation affects $J\left(C_1\right)$ dependence, we consider fibrils composed of β-strands with 10 amino acids in an extended conformation (as above) and a hairpin conformation (Fig. 2 b). The main difference for fibrils composed of β-strands in a hairpin conformation is that only half of the amino acids of the β-strand contribute to the hydrophobicity-mediated bonds between successive β-sheets, and therefore, $n_{\text{s}}=n_{\text{w}}=n/2=5$. All other parameters are the same (i.e., $\alpha =1$, ${\alpha }_{\text{w}}={\alpha }_{\text{s}}=0.1$, and $c_{\text{w}}=c_{\text{s}}=0.5$). As in the previous example, the values for the dimensionless surface energies for fibrils composed of β-strands in a hairpin conformation are obtained from Eqs. 1–3 and are given by $\psi =11$, ${\psi }_{\text{s}}={\psi }_{\text{w}}={\psi }_{\text{h}}=0.5$ (step 1 of the recipe). The value $\psi =11$ is the same for both fibril polymorphs, as the number of hydrogen and hydrophobic bonds in the direction of the fibril lengthening axis is the same. Again using $C_{\text{r}}=1.6\times {10}^{32}$ m⁻³ with $\psi =11$, ${\psi }_{\text{h}}=0.5$ in Eq. 16 shows that the conformational change shifts $C_{\text{e}}=1.63\times {10}^{22}$ m⁻³ (27.1 μM) to slightly higher concentrations (see Fig. 3 b) (step 2 of the recipe). As in the previous example, we calculate $J\left(C_1\right)$ dependence from Eqs. 13–15 with $k_{\text{e}}={10}^{-4}$ s⁻¹ and the A values for the symmetric case (step 3 of the recipe). Fig. 3 b shows that the main effect of this conformational change is a small decrease of $J\left(C_1\right)$, mainly because the threshold concentration $C_{1\beta }=4.4\times {10}^{22}$ m⁻³ (73.8 μM) is unchanged. This can be shown by substitution of Eq. 16 into Eq. 14, which eliminates ${\psi }_{\text{s}},{\psi }_{\text{w}}$ in the exponents of $C_{1\beta }$, so that it only depends on $\psi$. Thus, the shift of $C_{\text{e}}$ to slightly higher concentrations compensates the corresponding shift of $C_{1\beta }$ to lower ones. The prediction that the nucleation rates of fibrils composed of peptides in an extended β-strand and hairpin conformation differ only slightly might explain why both fibril structures have been observed experimentally (10,12).

Packing polymorphism

We first consider packing polymorphism where β-strands within β-sheets are in a parallel or antiparallel arrangement (Fig. 2 c), as has been observed in fibrils of short peptides and natural proteins (7,22). As before, the fibril building block is the extended β-strands composed of 10 amino acids. To distinguish between parallel and antiparallel stacking, we assume that the hydrogen-bonding energy between β-strands in a β-sheet is weaker when stacked in an antiparallel arrangement than when stacked parallel. Thus, for antiparallel stacking, we set the specific surface energy per amino acid due to hydrogen bonding to $\alpha =0.9$, which is smaller compared to $\alpha =1$ for parallel arrangement. All other values for the model parameter are unchanged (i.e., $c_{\text{w}}=c_{\text{s}}=0.5$ and $n_{\text{s}}=n_{\text{w}}=n=10$). The corresponding value for the dimensionless surface energy due to hydrogen bonding for antiparallel stacking is $\psi =10$ (calculated as before), whereas the values for the surface energy due to hydrophobicity-mediated bonds are ${\psi }_{\text{s}}={\psi }_{\text{w}}={\psi }_{\text{h}}=1$, as before (step 1 of the recipe). The fibril solubility $C_{\text{e}}=4.4\times {10}^{22}$ m⁻³ (74 μM) is obtained from Eq. 16 with $C_{\text{r}}=1.6\times {10}^{32}$ m⁻³ (step 2 of the recipe), which shows that a change in the arrangement of the β-strand in a β-sheet from parallel to antiparallel shifts $C_{\text{e}}$ to much higher concentrations (Fig. 3 c). Assuming again that $k_{\text{e}}={10}^{-4}$ s⁻¹ is independent of the stacking, the $J\left(C_1\right)$ dependence is calculated from Eqs. 13–15 with the A values for the symmetric case (step 3 of the recipe), illustrating that a change in the arrangement of the β-strands in a β-sheet from parallel to antiparallel shifts $C_{1\beta }$ to higher concentration and that it hampers protein fibrillation, because metanucleation commences at higher $C_1$ values (Fig. 4 c). Using the C_e value calculated above (Eq 14), the threshold concentration is $C_{1\beta }=3.3\times {10}^{23}$ m⁻³ (545 μM) (see Fig. 3 c). It is worth noting that a mixture of parallel and antiparallel fibrils in the protein solution can only be observed at concentrations in the metanucleation range of both fibrils, i.e., when $C_1>C_{1\beta }=545$ μM, and provided that the magnitude of the metanucleation rates are comparable and sufficiently high (see Fig. 4 c). It should be noted that as it is not known a priori whether antiparallel stacking decreases the specific surface energy per amino acid due to hydrogen bonding, we could also have assumed that this stacking increases it, in which case antiparallel fibrils would nucleate faster. The general rule is, however, that increasing the specific surface energy per amino acid due to hydrogen bonding promotes protein fibrillation, and the strong effect on the $J\left(C_1\right)$ dependence might explain that a single point mutation can switch the fibril morphology from predominately parallel to predominately antiparallel (22).

Another example of packing polymorphism is when β-sheets stack differently, as observed in short peptides (7). Along its thickening axis, the fibril is built up of β-sheets which are held together by, e.g., relatively weak hydrophobicity-mediated bonds between the β-strands. Because the orientation of side chains within a β-strand alternates, the hydrophobicity of the two β-sheet surfaces is generally different. This asymmetry leads to fibrils that can have either two strong and two weak, or one strong and one weak, hydrophobic surfaces (Fig. 2 d), but which ones form? As in our previous work (49), to model the effect of asymmetry, we decrease the weak specific surface tension per amino acid due to hydrophobic bonding between β-strands in consecutive β-sheets to ${\alpha }_{\text{w}}=0.05$, with ${\alpha }_{\text{s}}=0.1$ kept constant. The values of all other parameters are the same as for the extended β-strand with symmetric hydrophobic surfaces (i.e., $c_{\text{s}}=c_{\text{w}}=0.5$, $n_{\text{s}}=n_{\text{w}}=n=10$). The corresponding values for the dimensionless surface energies are obtained from Eqs. 1–3 and are given by ${\psi }_{\text{s}}=1$, ${\psi }_{\text{w}}=0.5$, $\psi =10.75$ (step 1 of the recipe), and the corresponding asymmetry ratio is ${\psi }_{\text{w}}/{\psi }_{\text{s}}=0.5$. The fibril solubility is again obtained from Eq. 16 and is given by $C_{\text{e}}=7.3\times {10}^{22}$ m⁻³ (27 μM) (step 2 of the recipe). Thus, increasing the asymmetry (by decreasing the asymmetry ratio) shifts $C_{\text{e}}$ to higher concentrations (Fig. 3 d). We calculate the $J\left(C_1\right)$ dependence from Eqs. 13 and 15 with $k_{\text{e}}={10}^{-4}$ s⁻¹ and the A values for the asymmetric case (step 3 of the recipe). However, a characteristic feature in this case is that in a given concentration range there exist different fibril nuclei (see Fig. 1). In Fig. 4 d, we show that in the first nucleation range (Fig. 1, i = 1), the nucleation rate for fibrils where the fibril nucleus is a single β-sheet plus one β-strand attached to the SH side can be substantially higher than that where the β-strand is attached to the WH side. This implies that in the concentration range $C_{2\beta ,\text{w}}<C_1<C_{2\beta ,\text{s}}$ there is a morphological selection, as only fibrils with two WH surfaces can grow, whereas those with two SH surfaces cannot (see Fig. 1). The values for $C_{2\beta ,\text{w}}=2.7\times {10}^{22}$ m⁻³ (45 mM) and $C_{2\beta ,\text{s}}=4.4\times {10}^{22}$ m⁻³ (74 mM) are obtained from Eqs. 5 and 6. In Fig. 4 d, we also show the corresponding $J\left(C_1\right)$ dependence for the symmetric case, where it can be seen that the main effect of increasing the asymmetry (decreasing ${\psi }_{\text{w}}$ at constant ${\psi }_{\text{s}}$) is to shift $C_{1\beta }$ to a higher concentration and to hamper protein fibrillation, because metanucleation commences at higher $C_1$ values. Using the C_e values calculated in Eq. 14, the threshold concentration for fibrils with asymmetry ratios of 0.5 is $C_{1\beta }=7.3\times {10}^{22}$ m⁻³ (121 mM). A solution mixture containing fibrils with two strong and two weak hydrophobic surfaces, and one strong and one weak hydrophobic surface, can only be observed at concentrations in the metanucleation regime of all fibrils, i.e., when $C_1>C_{1\beta }=121$ mM, provided the magnitudes of the metanucleation rates are comparable and sufficiently high (see Fig. 4 d). Note that although the effect of asymmetry is due to changes in the hydrophobicity (as in the case of the conformational change from an extended β-strand to a hairpin), the shift of $C_{\text{e}}$ to higher concentrations does not compensate the corresponding shift of $C_{1\beta }$ to lower ones. This is so because a change in ${\alpha }_{\text{w}}$ also changes $\psi$ (see Eq. 3), which is not the case when the conformation changes from an extended β-strand to a hairpin. The effect of asymmetry on $J\left(C_1\right)$ dependence provides new insight into how a change in the side-chain-side-chain interactions between the β-strands can lead to a change in the stacking of β-sheets within fibrils (7).

Discussion

Fibrils solubility and polymorphism

The results obtained from this study highlight the important role of the threshold concentration, $C_{1\beta }$, and the fibril solubility $C_{\text{e}}$ in amyloid fibril nucleation, and they illustrate that $C_{\text{e}}$ is the determining factor, because $C_{1\beta }$ depends on $C_{\text{e}}$ (Eq. 14). Describing the phenomenon of fibril polymorphism on the basis of fibril solubility, $C_{\text{e}}$, and the threshold concentration, $C_{1\beta }$, provides an alternate view of this important problem and opens new ways to control the formation of particular fibril polymorphs experimentally by changing $C_{1\beta }$ and $C_{\text{e}}$. Therefore, we express both quantities in terms of the binding energies between neighboring β-strands in the fibril. An approximate relation between $C_{\text{e}}$ and the binding energies can be obtained by subtituting Eqs. 1–3 into Eq. 16. This gives

$$C_{\text{e}}=C_{\text{r}}\exp \left[-(n\epsilon +c_{\text{s}}{n}_{\text{s}}{\epsilon }_{\text{s}}+c_{\text{w}}{n}_{\text{w}}{\epsilon }_{\text{w}}+n_{\text{s}}{\epsilon }_{\text{s}}/2+n_{\text{w}}{\epsilon }_{\text{w}}/2)/kT\right],$$ (17)

where $\epsilon$, ${\epsilon }_{\text{s}}$, and ${\epsilon }_{\text{w}}$ are the binding energies between nearest-neighbor amino acids due to hydrogen bonding and to strong and weak hydrophobic bonds, respectively. The n values are the corresponding numbers of these bonds, and c_s and c_w are parameters determining the contributions of hydrophobicity-mediated bonds. In a similar way, the dependence of $C_{1\beta }$ on the binding energies is obtained by substitution of Eqs. 1, 2, and 17 into Eq. 1:

$$C_{1\beta }=C_{\text{r}}\exp \left[-(n\epsilon +c_{\text{s}}{n}_{\text{s}}{\epsilon }_{\text{s}}+c_{\text{w}}{n}_{\text{w}}{\epsilon }_{\text{w}})\text{/}kT\right].$$ (18)

These two relatively simple equations allow us to understand and rationalize the results obtained for the concentration dependence of the nucleation rate for different fibril polymorphs in terms of changes in the binding energies. First, we consider the conformational polymorphism due to an increase of the β-strand length within fibrils. Figs. 3 a and 4 a illustrate that increasing the β-strand length decreases $C_{\text{e}}$ and promotes protein fibrillation, because $C_{1\beta }$ is shifted to much lower $C_1$ values. The reason for this is that increasing the β-strand length increases n, n_s, and n_w, which decreases both $C_{\text{e}}$ and $C_{1\beta }$ (Eqs. 17 and 18). As ε is 10 times larger than ε_s and ε_w, however, this decrease is dominated by the increase in the binding energy due to hydrogen bonds. Second, we consider the packing polymorphism due to parallel or antiparallel stacking of β-strands in a β-sheet. Figs. 3 c and 4 c illustrate that a change in the stacking of the β-strands in a β-sheet from parallel to antiparallel increases both $C_{\text{e}}$ and $C_{1\beta }$ and thereby hampers protein fibrillation. This decrease is solely due to the decrease in the hydrogen-bonding energy, as a change in the stacking arrangement only lowers ε, whereas ε_s and ε_w are unchanged (see Eqs. 17 and 18). Third, we consider the conformational polymorphism due to a change in the conformation of the β-strand from extended to hairpin. Figs. 3 b and 4 b illustrate that this conformational change only increases $C_{\text{e}}$, whereas $C_{1\beta }$ is unchanged, and consequently, protein fibrillation is only slightly hampered. As this conformational change only decreases the numbers n_s and n_w of hydrophobic contacts between β-strands in consecutive β-sheets (and not n), this effect is entirely due to a change in the hydrophobic binding energy (see Eqs. 17 and 18). Fourth, we consider the packing polymorphism due to the asymmetry between the weak and strong hydrophobic β-strand surfaces, which can lead to different packing of β-sheets within fibrils. Figs. 3 d and 4 d show that increasing the asymmetry increases both $C_{\text{e}}$ and $C_{1\beta }$, thereby hampering protein fibrillation. This effect is also entirely due to a decrease in the hydrophobic binding energy between β-strands, since with increasing asymmetry only ε_w is lowered, whereas ε and ε_s are unchanged (see Eqs. 17 and 18). The morphological selection between fibrils with two WH and SH β-sheet surfaces occurs thanks to the inequality $C_{2\beta ,\text{w}}<C_{2\beta ,\text{s}}$, and by substitution of Eqs. 1, 2, and 17 into Eqs. 5 and 6, it can be shown that this inequality is due to the fact that ε_w < ε_s.

General rule

Consideration of these four examples reveals a general rule underlying fibril polymorphism, namely, that changes in the conformation of the fibril building blocks or their packing that increase their binding energy within fibrils (due to both hydrogen and hydrophobic bonds) lower the fibril solubility, $C_{\text{e}}$, and hence the threshold concentration, $C_{1\beta }$, which in turn promotes protein fibrillation. In other words, the nucleation rate of the fibril polymorphs composed of fibril building blocks with higher binding energy is higher. Although this rule seems intuitive, we show here that it naturally emerges by treating the nucleation of amyloid fibrils into polymorphic structures within our newly developed nonstandard nucleation. The power of the theoretical framework presented here is that it provides a tool for both qualitative and quantitative prediction of which polymorph forms based on the fundamental interactions between the fibril building blocks.

Limitations

Finally, we emphasize that the results obtained above apply to one-step fibril nucleation, i.e., when the monomeric β-strands polymerize directly into fibrils, and that the analysis treats homogeneous nucleation of amyloid fibrils occurring when nucleation-active foreign particles or substrates are absent from the solution. Two-step nucleation of polymorphic fibrils and fibril polymorphism that occurs during fibril growth or is determined by fibril growth are not considered. It is important to note that application of the general expressions for the fibril nucleation rate, J, as an explicit function of the concentration to different fibril polymorphs requires that the reference concentration, C_r, and the attachment frequency, k_e, of monomers to one of the two fibril ends at equilibrium are constant. Furthermore, the relation between the fibril solubility and the binding energies is approximate and pertains to sufficiently low temperatures. It should also be mentioned that the entropy loss when a β-strand is attached to the fibril is taken into account in our newly developed nonstandard nucleation model (30,49). This is so because in contrast to classical nucleation theory, in the derivation of the analytical expression for the nucleation rate, the length distribution of fibril nuclei in the solution is considered (see Kashchiev et al. (30)). The remarkably good description of simulation data for the nucleation rate by our so-derived expression (see Fig. 5 of Kashchiev et al. (30)) indicates that entropy effects are indeed well accounted for. Entropy effects due to vibrations of the β-strand within fibrils are not explicitly considered, but ideas of how to do that can be found in Ferrone (62), and they could be the basis of an important extension of our model. The entropic effects, however, are automatically accounted for when experimental data for C_e and ψ, ψ_h are used.

Conclusions

We conclude that the nucleation of polymorphic amyloid fibrils can be treated within our newly developed nonstandard nucleation theory. This treatment allows the prediction of $J\left(C_1\right)$ dependence for different fibril polymorphs, which highlights the important role of the threshold monomer concentration, $C_{1\beta }$, and the protein solubility, $C_{\text{e}}$. Experimental studies of amyloids often focus on their structure, assembly mechanism, and interactions with the biological environment. Not so many experiments focus on determining the fibril solubility and how it changes with fibril structure and amino acid sequence. Describing the phenomenon of fibril polymorphism on the basis of fibril solubility, $C_{\text{e}}$, and threshold concentration, $C_{1\beta }$, opens up new ways to design experimental strategies to stimulate or prevent the formation of particular fibril polymorphs, and for this, our approximate relations between $C_{\text{e}}$, $C_{1\beta }$, and the binding energies between neighboring β-strands in the fibril (Eqs. 17 and 18) might prove a valuable tool.