The effects of reputational and social knowledge on cooperation

Significance

Cooperation is essential for societies to prosper. Recent experiments show that cooperation emerges in dynamic networks in which subjects can select their connections. However, these studies fixed the amount of reputation information available and did not display the network to subjects. Here, we systematically vary the knowledge available to subjects about reputation and the network to investigate experimentally their roles in determining cooperation in dynamic networks. Common knowledge about everyone’s reputation is the main driver of cooperation leading to dense and clustered networks. The addition of common knowledge about the network affects the distribution of cooperative activity: cooperators form a separate community and achieve a higher payoff from within-community interactions than members of the less cooperative community.

Abstract

The emergence and sustenance of cooperative behavior is fundamental for a society to thrive. Recent experimental studies have shown that cooperation increases in dynamic networks in which subjects can choose their partners. However, these studies did not vary reputational knowledge, or what subjects know about other’s past actions, which has long been recognized as an important factor in supporting cooperation. They also did not give subjects access to global social knowledge, or information on who is connected to whom in the group. As a result, it remained unknown how reputational and social knowledge foster cooperative behavior in dynamic networks both independently and by complementing each other. In an experimental setting, we show that global reputational knowledge is crucial to sustaining a high level of cooperation and welfare. Cooperation is associated with the emergence of dense and clustered networks with highly cooperative hubs. Global social knowledge has no effect on the aggregate level of cooperation. A community analysis shows that the addition of global social knowledge to global reputational knowledge affects the distribution of cooperative activity: cooperators form a separate community that achieves a higher cooperation level than the community of defectors. Members of the community of cooperators achieve a higher payoff from interactions within the community than members of the less cooperative community.

Cooperation among a group of individuals can create a surplus that benefits everyone, but it is often undermined by self-interested incentives to free ride on others’ contributions (1). What drives the emergence of cooperative behavior and how it is possible to sustain it over time are fundamental questions that have been of long-standing interest to social scientists (2). The most common abstract representation of the trade-off individuals face between cooperating and free-riding is the prisoner’s dilemma game, which has been widely studied both theoretically and experimentally (3, 4).

Recent simulation-based (5, 6) and experimental (7–10) studies investigating individuals playing the prisoner’s dilemma game in a group have shown that the ability to form and break connections, and thereby select with whom to play the game, has a significant effect on the level of cooperation. The possibility of forming new connections with cooperative individuals encourages defectors to switch to cooperative behavior even if many of their neighbors are defecting (11). The process of network formation relies on two dimensions of information available to individuals, which we dub reputational and social knowledge. Reputational knowledge is what individuals know about the previous actions of others in the group. Social knowledge is what individuals know about the structure of the social network within the group, which determines who plays the game with whom.

In the context of repeated interactions between two players, reputational knowledge has long been recognized as an important factor in determining cooperation both in theoretical (2, 12, 13) and experimental (2, 14–17) settings. In the two-player case, it is indifferent whether information about the other player’s previous actions comes from a player’s past interaction or from an external reputational mechanism because the two channels coincide. However, this is not the case in a group of individuals in whom the social network determines interactions. If the information about others’ previous actions comes from the social network and indirect communication is infeasible, reputational knowledge will only be available about an individual’s connections, whereas if a reputational mechanism external to the network is present, then an individual will have reputational knowledge about everyone independent of the network. Previous experimental studies have focused on the specific cases in which reputational knowledge is available for either every other individual (7, 9, 10) or only the neighbors (8), and therefore they cannot disentangle whether an external reputational mechanism is necessary for cooperation or whether reputational knowledge available through the social network itself may suffice.

Social knowledge matters in the link formation process because it aids individuals in identifying opportunities in the network (18, 19). For instance, in the context of cooperation, it may help identify loci of cooperative activity in the group, which in turn may have an effect on the aggregate level of cooperation. Surprisingly, the role that differences in the level of social knowledge have in the network formation process, and the influence they have on individual behavior in games on networks, have received little attention in both the theoretical (20) and the experimental (21) literatures. Previous experimental studies about cooperation on networks provide subjects only with information on the identity of their neighbors, and therefore do not investigate the role of social knowledge in determining the network structure and the level of cooperation.

Reputational and social knowledge are not just independent channels but also interact to determine the social network that emerges, and consequently the level of cooperation. Individuals use information about previous actions to decide to whom to connect (9), and therefore the extent of reputational knowledge available may matter in determining the density of the network. As already mentioned, individuals use information about the network to decide to whom to link; for example, they may decide to link to the connections of their neighbors, thereby increasing the level of clustering of the network. The presence of both reputational and social knowledge may combine to further enhance these effects. Previous studies do not vary the level of reputational and/or social knowledge available to subjects, and therefore, in addition to not being able to identify their independent influence, they cannot explore the combined effects of reputational and social knowledge in determining the network structure and, ultimately, the level of cooperation.

Using web-based experiments, we aim to identify the role of reputational and social knowledge in the emergence of cooperation and the structural features of the network associated with cooperative activity. The general set-up is a group of subjects playing several rounds of a prisoner’s dilemma game on a network, with each round consisting of a network formation stage followed by the game played on the resulting network. The treatment variables are reputational and social knowledge. In our baseline treatment, subjects only know who their neighbors are and what the neighbors’ previous actions were. Two further treatments build on the baseline by adding reputational and social knowledge about everyone respectively, allowing a separate investigation of the two channels. A final treatment has reputational and social knowledge about everyone, allowing an exploration of their combined effect on cooperation and the network structure.

Experimental Setup

We recruited 364 US-based subjects using the online labor market Amazon Mechanical Turk (AMT), which provides a more diverse subject pool compared with the typical student samples used in laboratory studies (22, 23). Each subject is assigned to a group of 13 and participates in the experiment only once. Unlike some other studies that use subjects from AMT (9, 24, 25), we emulate the workflow and procedures of lab-based experiments by requiring subjects to read the instructions and complete the experiment in a single uninterrupted session, and by preventing multiple participation even by subjects who have only seen the instructions (see SI Appendix for details), which is analogous to the procedures of two recent contributions (7, 10).

An experimental session consists of 13–16 rounds of a multiplayer prisoner’s dilemma game on an endogenous network. The first round starts with the empty network with no link between subjects. After round 13, there is a 50% probability that the game terminates in each of the following rounds. Each round consists of three stages. The first two stages determine the network on which subjects play the game. In stage 1, subjects can propose costless links to any of the other subjects and can unilaterally remove any of their existing links. There is no limit to the number of links each subject can remove or propose. If two subjects both propose a link to each other, or if a subject removes a link, then the link is added or removed, respectively. If a subject has proposed a link to another subject who has not done the same, then in stage 2 the recipient of the proposal can accept or reject the proposal. At the end of stage 2, the network is updated with all of the linking decisions.

In stage 3, subjects play a prisoner’s dilemma game by choosing a cooperate (C) or defect (D) action that applies to all their neighbors. The game is completely symmetric in payoffs: (C,C) gives 3 points to each subject, (D,D) gives −3 points, (C,D) gives 5 points to the defector and −5 points to the cooperator, and both subjects get 0 points if they are not linked. The symmetry of the payoff structure leads to intuitive welfare implications: a society of social isolates has welfare 0, and changes to welfare are exclusively driven by the (C,C) and (D,D) links. In the data, the welfare level is driven by the number of (C,C) links, so our analysis focuses on the level of cooperation, which we define as the links where both subjects choose a cooperative action as a proportion of the 78 potential links in the network.

At the end of a round, subjects receive the following information: a reminder of the action they chose, the actions chosen by each neighbor (or everyone, depending on the treatment), and the number of points they receive from the game with each of the other subjects. The current network is carried over to the next round. At the end of the experiment, for each subject, we select 12 pairings between the subject and one of the other subjects (two random pairings in each of six randomly selected rounds) and convert the sum of points won in those pairings into dollars for payment.

The choice of payoffs and the payment method in our experimental design provides the correct incentive structure to allow the formation of meaningful and realistic network structures, and consequently the isolation of which network features are generated by global reputational and global social knowledge, respectively. The symmetry of payoffs in the gains/losses domains means that both the absence of a connection and connections between a defector and a cooperator lead to no change in social surplus. The only way to produce social surplus is a connection between two cooperators, and, conversely, the only way to reduce social surplus by an equal amount is a connection between two defectors. This is in contrast to other studies that have nonnegative (10) or small negative (8, 9) payoffs, which lead to the emergence of overconnected networks because the losses from being connected to a defector are nonexistent or negligible. Moreover, the random selection of pairs for payment, independent of whether a connection exists or not, ensures that there are uniform incentives throughout the experiment in forming connections, so the payment system does not introduce biases in the emerging network structure. For instance, if we had excluded unconnected pairs from the random selection for payment, then subjects would have incentives to form just one (or very few) link(s) with a cooperator to ensure a specific pairing is picked. This choice is in contrast to previous studies that pay the cumulative number of points subjects have earned (8–10), which may lead to satisficing in the latest rounds, and therefore lower incentives to change the network.

We conduct four treatments to examine the relative importance of reputational and social knowledge. In the baseline (B) treatment, subjects only have access to local reputational knowledge: a list of their current neighbors with the last five actions chosen by each one of them and a list of the nonneighbors without any information on their past actions. They also have access to local social knowledge only, so they have no information on the structure of the network beyond their neighbors. In the reputation (R) treatment, they have access to global reputational knowledge, so they see a list of the last five actions for every other subject, but they are still limited to local social knowledge. In the network (N) treatment, they have access to global social knowledge, so they see a network figure that shows the connections among all of the subjects in the group, but they only have access to local reputational knowledge. Finally, in the reputation and network (RN) treatment, they have access to global reputational and social knowledge by seeing the whole network and the last five actions for all other subjects. The network figure is interactive, allowing subjects to hover over a node to highlight its neighbors and to drag nodes around to rearrange the network visualization.

Results

We begin by investigating how the cooperation level, payoffs, and structure of the network vary at the aggregate level across treatments. In the statistical analysis, we aggregate the data at the session level (n = 7 for each treatment) and apply the nonparametric Kruskal-Wallis test to compare across multiple groups to detect treatment effects, followed by the Dunn’s test with Benjamini-Hochberg adjustment for multiple comparisons to explore differences between any two treatments. The choice of a nonparametric test and the application of a correction for multiple comparisons with a small (n = 7) sample per treatment after aggregation is very conservative, and therefore any statistically significant finding denotes a sizable treatment effect. The aggregate analysis focuses on rounds 6–13, when information about the previous five actions is available. In this section, KW-D refers to the combination of these tests, and we report adjusted P values for the Dunn’s test (the Kruskal-Wallis is always significant; see SI Appendix for all of the details and P values, including a separate analysis of the interaction effect between the treatment variables).

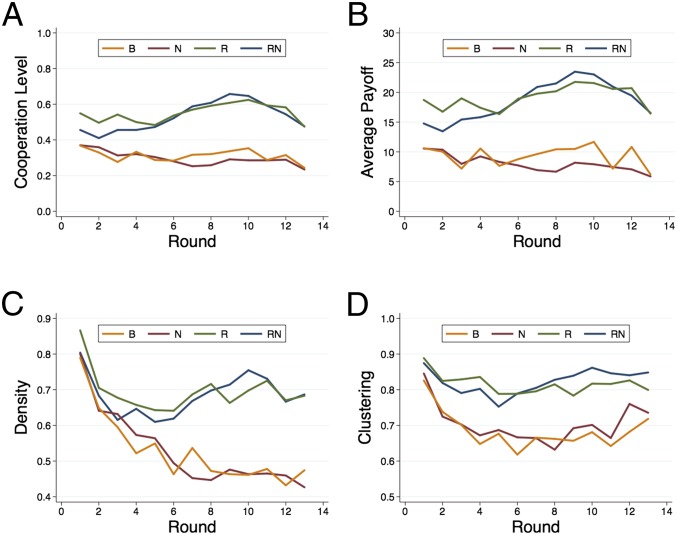
Fig. 1A shows the evolution of the level of cooperation: the availability of global reputational knowledge is the main determinant of the emergence and sustenance of a high level of cooperation. Subjects in the RN treatment achieve an average cooperation level that is larger than in the B (KW-D, P = 0.036) and N (KW-D, P = 0.060) settings. Likewise, the cooperation level in the R treatment is higher than the B (KW-D, P = 0.032) and N (KW-D, P = 0.036) settings. There is no significant difference in cooperation level between the RN and R treatments, and between the N and B ones. The evolution of the payoffs subjects receive follows closely the evolution of the level of cooperation. Fig. 1B shows that a consequence of the observed differences in cooperation is that subjects in the global reputation R and RN treatments achieve average payoffs that are approximately twice as large as those of subjects in the B and N settings (KW-D: RN vs. B, P = 0.041; RN vs. N, P = 0.032; R vs. B, P = 0.031; R vs. N, P = 0.063).

Fig. 1.

(A) Cooperation level, (B) average payoff, (C) density, and (D) clustering over 13 rounds of play for treatments B (yellow), N (red), R (green), and RN (blue). See SI Appendix, Aggregate level for a full statistical analysis and results.

The differences in cooperation and payoffs across treatments are mainly driven by the dynamics, rather than the initial play in the first round, as there is no significant difference at the 5% level in first-round cooperation or payoffs between any of the treatments. However, treatments R and RN begin with qualitatively higher cooperation levels, and the effect is significant at the 10% level for R compared with treatments B and N (KW-D, R vs. B, P = 0.084; R vs. N, P = 0.050). As a result, subjects earn a marginally higher average payoff in the first round in R and RN compared with B and N, and the effect is significant at the 10% level for R (KW-D, R vs. B, P = 0.058; R vs. N, P = 0.088). A potential explanation is that subjects are more cooperative in the first round because they are aware that their actions will be common knowledge to the group, and this effect is slightly more pronounced in the R treatment because the lack of global network information makes the presence of reputational information more salient. This is consistent with previous findings that contributions in a public good game are higher if subjects are aware that their decisions will affect their reputation in a subsequent indirect reciprocity game (26).

High cooperativeness is associated with the emergence of specific structural properties of the network. Fig. 1C shows the evolution of the density of the network, which is the ratio of the connections in the realized network to the number of connections in the complete network, where all subjects are connected with each other. All treatments start with the same, very high level of density. However, after a few rounds there is a clear differentiation between treatments R and RN with global reputation, where the network remains dense, and treatments B and N with local reputation, where the network becomes sparser (KW-D: RN vs. B, P = 0.017; RN vs. N, P = 0.028; R vs. B, P = 0.012; R vs. N, P = 0.014). Fig. 1D shows the evolution of the clustering level of the network, which captures the extent to which a subject’s connections are connected to each other. Similar to the evolution of density, the networks that form in the first round display the same high level of clustering, and the presence of global reputational knowledge leads to the emergence of highly clustered networks (KW-D: RN vs. B, P = 0.017; RN vs. N, P = 0.022; R vs. B, P = 0.030; R vs. N, P = 0.048).

We can gain additional insight on the relation between cooperation and network structure by conducting an individual-level analysis to investigate how the association between the position of an individual in the network and the individual’s cooperativeness depends on the availability of reputational and social knowledge. For each treatment, we conduct a logit panel estimation with SEs clustered at the session level, where the dependent variable is the action taken by subjects. We focus on several covariates that capture an individual’s position in the network structure, and we include a large number of controls (see SI Appendix for details).

In the baseline treatment B, no network metric is a significant correlate of cooperativeness, suggesting that the formation of a social structure associated with cooperativeness is not possible when subjects only know the identity and the previous actions of their neighbors. However, network metrics become significant once we add global reputational and global social knowledge independently in the R and N treatments, respectively, and these differ depending on the treatment, which suggests that each type of knowledge plays a different role in the network formation process.

The availability of global reputational knowledge is necessary for the emergence of cooperative hubs: in the R and RN treatments, the number of connections (Degree) of an individual is a highly significant (R: coefficient = 13.38; RN: coefficient = 36.80; P < 0.001 for both) positive correlate of cooperative behavior, whereas the correlation is insignificant in the B and N treatments, in which only local reputation about the neighbors is available. In other words, cooperators thrive and amass more connections when reputational knowledge about others is available, increasing in this way the density of the overall network. When global reputational knowledge is available, the other significant negative correlate of cooperativeness is Betweenness (27): individuals who connect otherwise separate parts of the network tend to be defectors in both the R (coefficient = −10.85; P < 0.001) and RN (coefficient = −19.61; P < 0.01) treatments, but the correlation is again insignificant in the N and B treatments.

The addition of global social knowledge to the baseline leads to a significant positive correlation (coefficient = 1.21; P < 0.05) between the level of clustering and cooperativeness in the N treatment. This is because the probability that a subject proposes a link to another subject in the N treatment is increasing in the number of neighbors they have in common (coefficient = 0.18; P < 0.001), but this relation is insignificant in any of the other treatments (see SI Appendix for details). Interestingly, in the R treatment, where global reputational knowledge is available but global social knowledge is absent, clustering is negatively associated with cooperativeness (coefficient = −2.08; P < 0.05). In the RN treatment, the two effects cancel out, and clustering is not correlated with cooperativeness.

In summary, our analysis so far shows that the availability of global reputational knowledge increases the level of cooperation, payoffs, and the density and clustering level of the network, whereas global social knowledge does not have an effect on these aggregate metrics. However, mouse movement tracking data reveal that subjects make active use of the network information. The information about the network is displayed using an interactive figure that allows subjects to highlight the neighbors of a node by mouse hovering and to rearrange the network layout by dragging nodes around. On average, subjects hover over 4.3 (SD = 1.5) and 4.9 (SD = 1.3) nodes in each round of the RN and N treatments, respectively. Moreover, subjects drag a node to rearrange the network 10.5% of the times they hover over it in the N treatment and 11.8% of the times in the RN treatment (see SI Appendix for details). For what purpose are subjects using the interactive figure, and does it have any effect on outcomes?

As we have seen, in the N treatment, subjects use the network information in the network formation process: the probability that a subject proposes a link to another subject is increasing in the number of neighbors they have in common. The aggregate data analysis may hide the more subtle role played by global social knowledge in the network formation process, so we further explore its role by conducting an analysis of the communities that emerge in the evolution of the network. We use the well-known Louvain (28) algorithm to detect communities within the network (see SI Appendix for details).

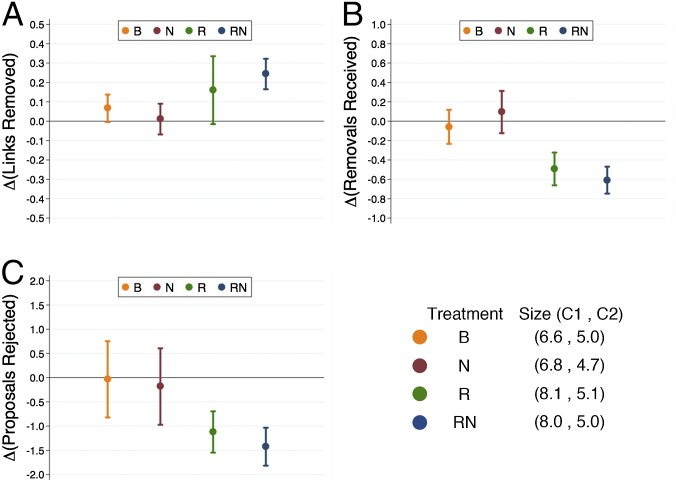
We rank the communities according to their size and focus on the largest (C1) and second largest (C2) ones after they have reached a stable composition. The most frequent outcome of the algorithm is the decomposition of the network into two communities, and C1 and C2 together make up, on average, 85% of the group for all treatments. C1 has an average size of 8.0 and 8.1 subjects in treatments R and RN, respectively, and an average size of 6.6 and 6.8 subjects in B and N, respectively. The size of C2 is about five subjects, on average. There is no significant difference in the size of C1 or C2 across treatments. In the statistical analysis, we aggregate the data at the session level and explore within-treatment differences between C1 and C2 by using the nonparametric Mann–Whitney test (M-W hereafter). A stability analysis reveals that the composition of the communities becomes more stable after round 5, which further corroborates the choice to conduct the analyses by aggregating the data from round 6 onward (see SI Appendix for details).

An analysis of the dynamics of link formation within treatment at the community level reveals that the presence of both global reputational and global social knowledge creates a differentiation in the behavior of subjects in C1 compared with that of subjects in C2. Fig. 2A shows that in the RN treatment subjects in C1 remove more connections on average than subjects in C2: the difference between the average number of connections removed by a member of C1 and by a member of C2 is significant in RN (M-W, P = 0.018), but it is insignificant in any of the other treatments. The mirror image of this metric is the number of links that are removed by others, and the results are consistent: RN is again the only treatment in which there is a significant difference between C1 and C2 (M-W, P = 0.002), and as we would expect, it is members of the C2 community that have more links removed than members of the C1 community (Fig. 2B).

Fig. 2.

Difference between members of the largest and the second-largest communities in average (A) links removed, (B) removals received, and (C) proposals rejected per round for treatments B, N, R, and RN. Analyses are based on aggregated data at the session level after round 5. Error bars indicate ±1 SEM. Here we only present the P values for significant comparisons (M-W, P < 0.05). Between C1 and C2 within each treatment: (A) links removed: RN, P = 0.018; (B) removals received: RN, P = 0.002; and (C) proposals rejected: RN, P = 0.018. See SI Appendix, Community level for a full statistical analysis and results.

The removal of connections by members of C1 is only effective if the subjects who are outside (or have been expelled) are unable to (re)join the C1 community. Fig. 2C shows that this is indeed the case: the difference between the average number of link proposals rejected by a member of C1 and those rejected by a member of C2 is significant in RN (M-W, P = 0.018), but it is insignificant in any of the other treatments. This shows that there are differences in the network formation process between members of C1 and C2 that are only present when both global reputational and global social knowledge are available, but do these differences have an effect on outcomes?

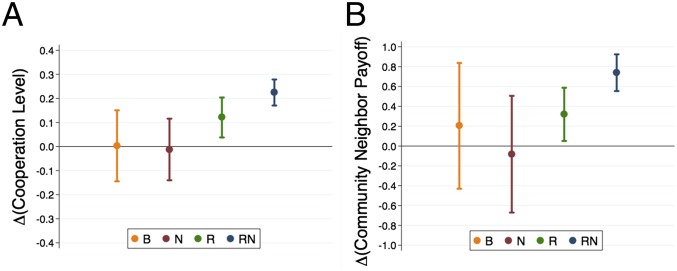
The addition of global social knowledge to global reputational knowledge has an effect on the distribution of cooperative activity in the group. Fig. 3A shows the difference in the cooperation level between communities C1 and C2 for each treatment. In the RN treatment, community C1 has a 37% higher level of cooperation than community C2 (M-W, P = 0.025), whereas in all other treatments there is no significant difference between the level of cooperative activity in C1 and C2. In other words, the availability of both global reputational and social knowledge allows cooperators to form their own community by actively removing links from defectors and refusing to link with them again, and therefore relegating them to the C2 community. When either global reputational or global social knowledge is unavailable, this process does not occur and cooperators are evenly distributed between the two communities.

Fig. 3.

Differences between members of the largest and the second-largest communities in (A) cooperation level and (B) average payoff per interaction with a community member for treatments B, N, R, and RN. Analyses are based on aggregated data at the session level after round 5. Error bars indicate ±1 SEM. Here we only present the P values for significant comparisons (M-W, P < 0.05). Between C1 and C2 within each treatment: (A) cooperation level: RN, P = 0.025; and (B) community neighbor payoff: RN, P = 0.018. See SI Appendix, Community level for a full statistical analysis and results.

The regression analysis at the individual level confirms that the presence of both global reputational and global social knowledge leads to an uneven distribution of cooperative activity in the group. In all of the regressions, we include a Community dummy that is equal to 1 if the individual belongs to C1 and equal to 0 if the individual does not belong to C1. In the RN treatment, there is a positive and significant association between the Community dummy and the level of cooperation (coefficient = 2.02; P = 0.01), whereas there is no significant association for any other treatment. In other words, cooperators congregate in the same community when both global reputational and social knowledge are available, while they are spread out across different communities otherwise.

When both global reputational and global social knowledge are present, members of C1 generate, on average, more surplus from each interaction with another member of their own community compared with members of C2. Fig. 3B shows the difference between the average payoff generated by an interaction with a neighbor within community C1 and by an interaction with a neighbor within community C2 for each treatment, which we can interpret as a measure of how much surplus a community generates. In the RN treatment, each interaction in the C1 community generates, on average, 0.74 additional payoff points than an interaction in the C2 community (M-W, P = 0.018), whereas the difference is insignificant for any of the other treatments. This effect is sizable: a member of C1 in RN has, on average, 6.4 links with other members of C1, so if the subject were instead a member of C2, and had the same number of links with C2 members, then the potential loss in payoff would be 4.7 points per round, or approximately 23% of the average payoff per round in RN.

Discussion

The point of departure of this study was recent experimental literature showing that the possibility for subjects to choose their partners by forming and breaking connections leads to the emergence of cooperation in the prisoner’s dilemma game. In these studies, reputational knowledge was kept fixed, so subjects knew either only the previous actions of their neighbors (8) or the previous actions of everyone in the group (7, 9, 10). Moreover, subjects only had access to local social knowledge, and thus had no information about the structure of the network with the exception of their neighbors. Our contributions are to show that the extent of reputational knowledge and the extent of social knowledge play crucial and different roles for the emergence and distribution of cooperation, as well as the network features associated with cooperative activity.

Our first contribution is to show that the presence of global reputational knowledge is crucial for the emergence and sustenance of a high level of cooperation. This highlights that the main driver of the results in previous experiments (7, 9, 10) was the implicit assumption of the availability of global reputational knowledge. The treatments in which subjects have access to the previous five actions of everyone in the group achieve a significantly higher level of cooperation than the treatments in which they only have access to the neighbors’ previous five actions. These findings are in agreement with a recent, similar experiment (29) that shows that reputation fosters cooperation by varying the number of past actions available to subjects. The results show the crucial role of global reputational knowledge in determining the emergence of cooperative hubs: individuals who have a high number of connections because they are highly cooperative.

Our second contribution is to show that the availability of global social knowledge on its own affects the process of network formation but has no effect on the overall level of cooperation, payoff, and aggregate network metrics. Specifically, we show that the availability of global social knowledge is associated with a subject’s tendency to propose connections to other subjects who are already connected to her neighbors, which leads to a positive correlation between the individual’s clustering coefficient and her cooperativeness. Previous theoretical work (18, 19) has highlighted the importance of social knowledge in the process of network formation, and our study shows the first evidence to our knowledge of its influence in the network formation process. Moreover, the role of social knowledge in games on networks has so far been almost completely unexplored experimentally, with the exception of a recent experiment showing that social knowledge matters in public good games on networks (21). The systematic experimental study of the role of social knowledge in network formation and in game play across different types of games is a promising area of future studies.

Our third contribution is to show that the availability of both global reputational and global social knowledge has an effect on the distribution of cooperative activity in the group. The presence of both types of knowledge allows cooperators to remove links from defectors and reject their link proposals in future rounds. In this way, cooperators are able to form a community that is more cooperative than the community of defectors, and it generates a larger social surplus from within community interactions. An open question for future research is the scalability and robustness of these findings to the overall size of the group. It is reasonable to imagine that the complexity of processing information about the network grows exponentially with the size of the network, making it more challenging to use it in the process of network formation. However, at the same time, the benefits from belonging to the cooperative community grow with the size of the community, making the establishment of a large cooperative community more attractive in a larger group.

The finding that global reputational information is crucial for the emergence of a high level of cooperation is consistent with previous “theoretical and empirical studies of indirect reciprocity [that] stress the importance of monitoring not only partners in continuing interactions but also all individuals within the social network” (30) and with the finding that cooperation is higher in connected networks within which everyone is monitored (31). As predicted by theory (32, 33), experimental studies on indirect reciprocity with well-mixed populations show that reputation is important for cooperation (14, 34) and that the level of cooperation increases with the richness of the reputation information (35), as well as the punishment/reward technology (36) available. In this study, we find that, in the context of dynamic networks, cooperation almost doubles if reputation is available about everyone, rather than just one’s connections.

The experimental result that the presence of global reputational knowledge is essential for the emergence of a high level of cooperation contributes to a growing and fruitful two-way dialogue between the theoretical and experimental literatures that study cooperation in networked contexts. For instance, a recent experimental contribution has shown that the structural features of a fixed network have an effect on the level of cooperation if the benefits from cooperation are large enough (37): this is in agreement with theoretical studies (38–42) and reconciles the fact that the theoretical predictions had not received support from previous experimental studies on fixed networks (24, 43–46). In an analogous fashion, our experimental results deviate from several theoretical studies showing that global reputational knowledge is not necessary for the emergence of a high level of cooperation (5, 47–52). Our experimental results suggest that some element of human psychology not included in the theoretical models may be the driver of the important role of global reputational knowledge in the experiment. Investigating the behavioral mechanism driving this discrepancy is a fruitful area of future research.

Mechanisms that collect information about reputation have existed for a long time (53, 54), but the development of social networking tools (e.g., Facebook, LinkedIn) that augment individuals’ social knowledge is a recent phenomenon. We still have a limited theoretical and empirical understanding of the effects of having access to this additional social knowledge (19). The results of our study suggest that an effect of these tools is to facilitate the formation of communities whose members share behavioral commonalities. In the context of cooperation, we find that access to global social knowledge in addition to global reputational knowledge allows the emergence of a community of cooperators. Exploring whether this type of effect of social knowledge extends to other domains is an important direction for future inquiries.

Materials and Methods

We recruited US-based subjects on AMT, using a simple qualification task and a sociodemographic survey to obtain their AMT ID information. We invited a randomly drawn subset of these subjects to a total of nine metasessions that took place at 11:00 AM EST between December 12 and 21, 2013. Each metasession comprised between two and five simultaneous experimental sessions, with the exact number depending on turnout. In each metasession, subjects signed in using a URL to our UbiquityLab web platform and participated in a session by completing the following steps: Waiting Room; Instructions and Interface Tour; Quiz; Game; Final Questionnaire; and Payment Confirmation. We paid subjects using AMT within 30 minutes after the end of each metasession. In total, 390 subjects took part in 30 experimental sessions: we used 28 sessions (seven sessions per treatment, 364 subjects in total) because two sessions experienced dropped out subjects after the game started and were excluded from our main analysis. The average earnings per subject were $5.13, including a $2 fixed fee for participation (55). Subjects remained completely anonymous throughout the qualification task and the experiment. Repeated and multiple participation were prevented by logging subjects’ AMT IDs and their IP addresses. See the SI Appendix for further details about the experiment. This research was approved by the Cambridge Experimental and Behavioral Economics Group on the use of human subjects, and informed consent was obtained from subjects before participation.