Recombination in diverse maize is stable, predictable, and associated with genetic load

Significance

Meiotic recombination is known to vary over 1,000-fold in many eukaryotic organisms, including maize. This regional genomic variation has enormous consequences for plant breeders, who rely on meiotic cross-overs to fine-map quantitative traits and introgress favorable alleles. Deleterious mutations are also predicted to accumulate preferentially within low-recombination regions, particularly within historically outcrossing species, such as maize. Here, we show that meiotic recombination is predictable across diverse crosses based on several genomic features of the reference genome. We demonstrate that the extant patterns of recombination are historically stable and tied to variation in the number of deleterious mutations. The ability of plant breeders to exploit recombination to purge segregating deleterious alleles will determine the efficacy of future crop improvement.

Abstract

Among the fundamental evolutionary forces, recombination arguably has the largest impact on the practical work of plant breeders. Varying over 1,000-fold across the maize genome, the local meiotic recombination rate limits the resolving power of quantitative trait mapping and the precision of favorable allele introgression. The consequences of low recombination also theoretically extend to the species-wide scale by decreasing the power of selection relative to genetic drift, and thereby hindering the purging of deleterious mutations. In this study, we used genotyping-by-sequencing (GBS) to identify 136,000 recombination breakpoints at high resolution within US and Chinese maize nested association mapping populations. We find that the pattern of cross-overs is highly predictable on the broad scale, following the distribution of gene density and CpG methylation. Several large inversions also suppress recombination in distinct regions of several families. We also identify recombination hotspots ranging in size from 1 kb to 30 kb. We find these hotspots to be historically stable and, compared with similar regions with low recombination, to have strongly differentiated patterns of DNA methylation and GC content. We also provide evidence for the historical action of GC-biased gene conversion in recombination hotspots. Finally, using genomic evolutionary rate profiling (GERP) to identify putative deleterious polymorphisms, we find evidence for reduced genetic load in hotspot regions, a phenomenon that may have considerable practical importance for breeding programs worldwide.

Although the selective pressures contributing to its origin and persistence continue to be debated, recombination is widely recognized for its roles in promoting the diversity necessary to respond to continually shifting environments, in addition to preventing the build-up of genetic load by decoupling linked deleterious and beneficial variants (1–3). In practice, increased local recombination enhances breeders’ abilities to map quantitative traits and introduce favorable alleles into breeding lines.

Recombination’s importance has spurred interest in the causes and predictability of the local recombination frequency, which is usually characterized by hotspots with cross-over rates of up to several hundred-fold the genomic background (4–6). The predictability across diverse sources of germplasm is particularly salient in maize, a species with many large structural variants in which the average genetic distance between two inbred lines exceeds that between humans and chimpanzees (7). Moreover, elevated residual heterozygosity within low-recombining regions of maize recombinant inbred lines (RILs) suggests that heterosis in maize results from complementation of alternative deleterious alleles within these regions by dominant beneficial alleles segregating in repulsion (8–10). These low-recombination regions include the large [∼100 megabases (Mb)] pericentromeres harbored by all chromosomes, which collectively contain ∼20% of the gene space (9). Despite high theoretical interest for over 50 y and the practical utility of deleterious variant discovery, the genome-wide relationship between recombination rate and genetic load is poorly studied in plant genomes with the size, repeat composition, and genetic diversity typical of maize.

On a molecular level, chromatin structure heavily influences the cross-over rate in plants. Not only are heterochromatic regions generally depleted of cross-overs (11), but KO of cytosine-DNA-methyl-transferase (MET1) in Arabidopsis thaliana leads to both genome-wide CpG hypomethylation and a relative increase in the proportion of cross-overs within the euchromatic chromosomal arms (12–14). Nucleotide content may also be associated with the local frequency of recombination, potentially due to the effect of GC-biased gene conversion (bGC) during resolution of heteroduplexes that form at cross-over junctions (15).

In this study we use genotyping-by-sequencing (GBS) data (16) to identify the locations of 136,000 cross-over events in the US and Chinese (CN) maize nested association mapping (NAM) populations, two sets of RILs derived from crosses of inbred maize founder lines to distinct common parents. We show that despite the tremendous diversity among NAM founders within and between these two families, recombination is remarkably consistent and associated with a number of genomic features on a fine scale, including probable deleterious variation.

Results

Broad-Scale Patterns of Cross-Overs.

Using GBS data for 4,714 RILs in US-NAM and 1,382 RILs in CN-NAM, we defined nearly 136,000 intervals containing cross-overs: 103,459 in US-NAM and 32,536 in CN-NAM. Although we excluded heterozygous cross-overs for further analyses (SI Appendix, Supplemental Results), we find that the densities of homozygous cross-overs, heterozygous cross-overs, and cross-overs detected using an earlier GoldenGate assay (9) are nearly identical genome-wide (SI Appendix, Fig. S1). Because only about 29% of the potential sites were genotyped in US-NAM and 28% in CN-NAM, the interval sizes between known sites that were flanking cross-overs varied considerably. The size distribution of cross-over intervals in B73 reference genome coordinates has a long tail (mean = 305 kb, median = 127 kb) (SI Appendix, Fig. S2). However, 10% of cross-over intervals are less than 10 kb. This long tail of interval sizes is expected, given the long stretches of retrotransposons between genes. Despite local differences, the distribution of cross-overs is remarkably consistent between families and across the NAM populations. Because the common parents used for the US-NAM and CN-NAM populations are unrelated (SI Appendix, Fig. S3), the similarity between populations is not an artifact of using only one common parent for all families.

Cross-over counts per RIL per chromosome and per family are consistent between populations (SI Appendix, Figs. S4 and S5). Per-chromosome counts for both populations are consistent with the physical size of each chromosome. The counts for the CN-NAM population are consistently higher than the counts for the US-NAM population because the CN-NAM population was self-pollinated for two more generations, which would have converted three-quarters of the heterozygous cross-overs to homozygous cross-overs.

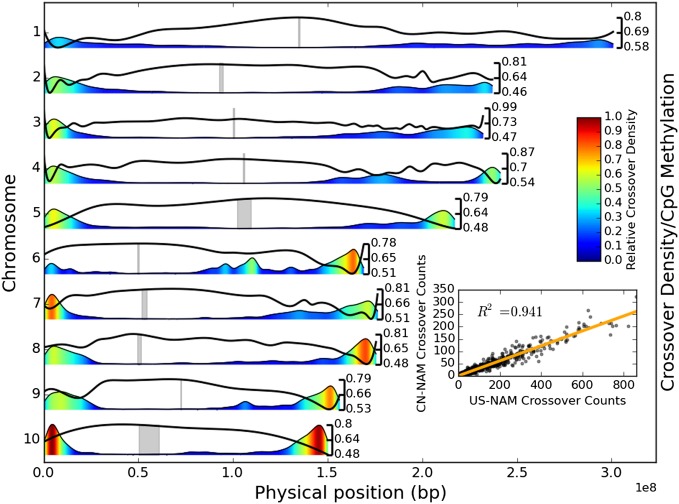
Histograms of cross-over counts in 2-Mb windows for each of the NAM populations (Fig. 1) show similar patterns. First, cross-overs are strongly suppressed in a large pericentromeric region on every chromosome, encompassing ∼100 Mb around each centromere. Second, cross-over density is high in the last 30 Mb of each chromosome but often declines in the last 1 Mb, encompassing the telomeres. Third, there appears to be at least one major dip in the cross-over density on the long arm of each chromosome, with the most extreme dips on chromosomes 4 and 6.

Fig. 1.

Genome-wide cross-over density in US-NAM and its association with CpG methylation and CN-NAM. Kernel density estimates of cross-over density are shown by both height and color, relative to the maximum density across all chromosomes, and black lines give the relative frequency of methylated CpGs, with scales given on the right side. The locations of centromeres are shown in gray. (Inset) Relationship between 1-Mb cross-over counts of US-NAM and CN-NAM populations is given.

A more detailed comparison of cross-over distributions can be made by dividing each chromosome into windows and comparing cross-over counts. Counts for US-NAM and CN-NAM (Fig. 1) are strongly correlated (r² = 0.941). To test count equality in individual windows, each chromosome was divided into segments of 200 cross-overs to ensure that every comparison had similar statistical power. A χ² test of equal counts in the two populations was then conducted on every window. Of 697 windows tested, the null hypothesis is rejected for 16 (2.3%) windows using a Bonferroni-adjusted alpha of 0.05 and 50 windows (7.2%) using a false discovery rate (FDR) of 0.05 (SI Appendix, Fig. S6). A test of differences between families within the US-NAM population using windows that each contained a total of 250 cross-overs gave similar results, rejecting 23 (5.4%) windows using a Bonferroni-adjusted alpha of 0.05 and 71 windows (16.6%) using an FDR of 0.05 (SI Appendix, Fig. S7).

The high consistency of cross-over frequencies between populations and across families suggests that recombination is largely predictable. Indeed, at the megabase scale, a linear model with terms for GBS marker density, distance from the telomere, DNA methylation, GC content, and repeat content explains ∼85% of the variance in cross-over density (Table 1). A majority of this variance can be explained by GBS marker density and the distance from the telomere alone, because the GBS marker density is negatively associated with both CpG methylation and repeat content due to the methylation sensitivity of the ApeKI restriction enzyme (SI Appendix, Fig. S8). However, methylation and repeat content explain high proportions of the unconfounded variance (Table 1), and removal of GBS from the model only decreases the explained variance by 1% (SI Appendix, Table S1). In particular, the CpG methylation has a strong negative relationship with the cross-over density and corresponds to several long arm cross-over density dips (Fig. 1). Although CHG methylation is highly correlated with CpG methylation, it does not correspond as well to these dips (SI Appendix, Fig. S9). The relationship of cross-over density to CHH methylation is less straightforward, but the linear model suggests that increased CHH methylation is associated with increased recombination at high CpG methylation levels and with decreased recombination at low CpG methylation (Table 1 and SI Appendix, Figs. S10 and S11).

Table 1.

Coefficients for terms in a linear model of homozygous cross-over density in 1-Mb windows

Term	Estimate	SE	SS	F	P
GBS	0.3156	0.023	24.4	192.2	<2 × 10−16
Telomere	−0.0922	0.010	10.9	85.7	<2 × 10−16
CpG	−0.2197	0.027	8.2	64.9	<2 × 10−16
CHH	0.1513	0.018	9.3	73.4	<2 × 10−16
CpG:CHH	0.1153	0.007	31.6	249.4	<2 × 10−16
GC	0.0450	0.010	2.8	21.9	3.03 × 10−6
Repeat	−0.1822	0.018	12.8	101.1	<2 × 10−16

Cross-validation R² = 0.8377. Note that all explanatory variables have been centered and scaled to have an SD of 1. SS, sum-of-squares (type III).

Reduced Recombination and Structural Variation.

In a few families, we observed megabase-scale regions outside the pericentomere, with no cross-overs. In particular, 217.9–245.5 Mb on chromosome 1 in B73 × CML333, 167.2–176.5 Mb on chromosome 3 in B73 × Mo18W, and 177.8–194.1 Mb on chromosome 5 in B73 × CML322 and B73 × CML52 completely lack cross-overs (SI Appendix, Fig. S12). Because all regions in the affected populations contain many polymorphic loci, there is no indication of major deletions relative to B73 at any of these locations. Intriguingly, the maize/sorghum synteny map (www.symapdb.org) contains an inversion relative to the syntenic region in sorghum from 221.9 Mb to 244.8 Mb, which almost exactly matches the region on chromosome 1 with no cross-overs (SI Appendix, Fig. S13). The same sorghum region is also syntenic to maize chromosome 5, but with no inversion present on chromosome 5. An inversion in CML333 relative to B73 would explain the absence of cross-overs in the 28-Mb region on chromosome 1, with CML333 containing the ancestral configuration. Although neither of the other two regions can be explained by features on the maize/sorghum synteny map, inversions are also the likely cause for those recombinationally inert segments.

Fine-Scale Correlates of Recombination.

To explore the genomic covariates of recombination on a fine scale, we used two independent methods to define narrow regions of high recombination. First, we defined regions containing a concentration of narrow (<10 kb) cross-over intervals using smoothing splines. We hereafter define these regions as recombination hotspots (n = 410, mean size = 10.5 kb, median size = 9.76 kb). Based on simulations from a null distribution of cross-over intervals under the observed broad-scale recombination pattern, we estimate a hotspot FDR of 0.5% (SI Appendix, Fig. S14). These hotspots contain 30.6% of all narrow intervals in US-NAM. However, because our ability to define narrow intervals depends on the local GBS marker density, we also defined a set of regions, hereafter termed controls, containing equivalent GBS densities but no narrow intervals (SI Appendix, Figs. S15 and S16). We also developed a Bayesian method to infer the probability of a cross-over occurring between any two adjacent GBS markers. This probabilistic technique allowed us to compare the estimated probability of an interval cross-over with the probability expected under the assumption of a uniform distribution. We refer to this measure as cross-over enrichment. We estimate that hotspots have cross-over rates ranging from threefold to over 100-fold the rate expected if cross-overs were uniformly distributed (mean = 20.2-fold, median = 16.6-fold). Controls have significantly lower cross-over enrichment [95% range = (0.53-fold, 13.73-fold), mean = 1.64-fold, median = 1.33-fold] but are not highly depleted of cross-overs (SI Appendix, Fig. S17). Furthermore, cross-over enrichment in hotspots is positively correlated between US-NAM and CN-NAM (Pearson r = 0.433, P = 6.12 × 10⁻²⁴) (SI Appendix, Fig. S18), indicating the preservation of local recombination patterns across diverse germplasm.

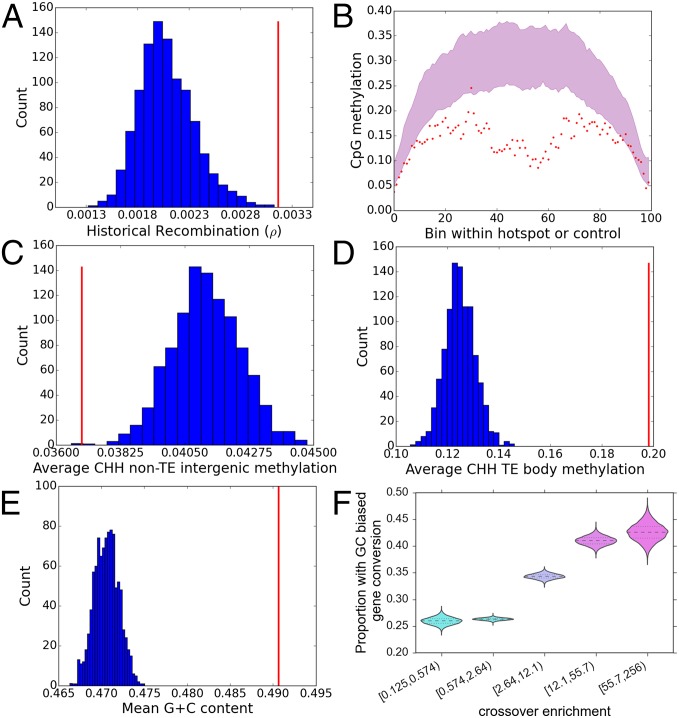
The remarkable consistency of both broad-scale and local-scale recombination patterns across the US-NAM and CN-NAM populations led us to investigate whether historical patterns of recombination are preserved at the local level. We compared the mean historical effective recombination rate (ρ = 4Nec) in the hotspots with permuted sets of controls to test whether the values of ρ estimated by Hufford et al. (17) are significantly higher in the hotspots. We find that the hotspots have ∼35% higher historical recombination when ρ is estimated from improved lines (P = 0.001, permutation test) and 28% higher historical recombination when ρ is estimated from maize landraces (P = 0.024, permutation test). Estimates of ρ in teosintes also follow the trend of higher historical recombination in hotspots, with a suggestive, albeit nonsignificant, difference from the controls (P = 0.1, permutation test) (Fig. 2A and SI Appendix, Figs. S19 and S20).

Fig. 2.

Fine-scale correlates of recombination in US-NAM. (A) Mean historical recombination rate within improved maize lines over 1,000 permutations of controls (blue histogram) compared with the mean historical recombination rate within hotspots (red line). (B) Ninety-five percent confidence interval for mean CpG methylation over 100 bins in 1,000 permutations of controls (red-shaded region) compared with the mean values in hotspots (red dots). Mean CHH methylation in hotspots compared with controls in non-TE intergenic regions (C) and TE bodies (D). (E) Mean G + C contents in 1,000 permutations of controls (blue histogram) compared with mean G + C contents within hotspots (red line). (F) Posterior densities for the proportion of intervals with evidence of bGC at varying levels of enrichment for cross-overs.

Several experimental results from A. thaliana demonstrate that induction of DNA hypomethylation within euchromatic regions can increase the local rate of recombination (12–14). Accordingly, we tested whether hotspots are significantly depleted of methylated cytosines in all three plant contexts (CpG, CHG, and CHH) using bisulfite sequencing data from B73 (18). Compared with the controls, the central regions of hotspots display approximately one-half the rate of CpG and CHG methylation but show no significant difference in the rate of CHH methylation (Fig. 2B and SI Appendix, Figs. S21 and S22). Due to the methylation sensitivity of the ApeKI enzyme used to generate GBS markers, both hotspots and controls have reduced methylation in their boundary regions. Nonetheless, we find that the hypomethylation of hotspot centers compared with controls is maintained even when we limit the controls to those controls with a mean GBS depth at or above the mean GBS depth in the hotspots (SI Appendix, Figs. S23–S25), demonstrating that the effect is not an artifact of higher cross-over resolution in hypomethylated regions. Moreover, when controlling for GBS marker density, the estimated cross-over enrichment is negatively associated with both CpG and CHG methylation within hotspots (SI Appendix, Tables S2 and S3). Intriguingly, the pattern of enrichment depends on sequence context for CHH and CHG methylation. Hotspot CpGs are hypomethylated in gene bodies, transposable elements (TEs), and non-TE intergenic regions relative to controls. By contrast, CHH methylation is significantly reduced in hotspot gene bodies and non-TE intergenic regions but enriched by twofold within hotspot TEs (Fig. 2 C and D and SI Appendix, Fig. S26). CHG hotspot methylation is similarly reduced in genic bodies and non-TE intergenic regions but not significantly different from controls within TE bodies. Finally, although we find significantly enriched sequence motifs within recombination hotspots, cytosine methylation is still a much stronger predictor of recombination frequency at the 30-kb scale (SI Appendix, Fig. S27 and Table S4).

Interestingly, the number of cytosines is also enhanced within the hotspots relative to the controls. Mean GC content within the hotspots exceeds mean GC content of the controls by ∼2% (P < 0.001, permutation test) (Fig. 2E). Assuming an average control GC content of 47% and an average length of 1 kb involved in crossing over, this 2% figure implies a GC excess of 20% (67% vs. 47%) within a median 10-kb hotspot region. We also find a significant positive association between GC content and cross-over enrichment after controlling for GBS marker density, with an effect size indicating an estimated 1.1% enrichment in GC content for every twofold increase in cross-over enrichment (SI Appendix, Table S5). These results parallel findings of positive associations between recombination and GC content within metazoan genomes, which are attributed to the effects of GC-bGC (19). As such, we tested whether hotspots have a higher frequency of bGC using the phylogenetic-hidden Markov model (phyloHMM) approach implemented in the phastBias program (20). We find that the mean maximum posterior probability of bGC in hotspots is approximately twice the probability of bGC expected in the controls (SI Appendix, Fig. S28). Additionally, across the genome, nearly twice as many of the most recombinogenic regions have evidence of bGC compared with the least recombinogenic regions (Fig. 2F).

Reduced Genetic Load in Recombination Hotspots.

One well-described theoretical advantage of meiotic recombination is the existence of a mechanism for breaking linkages between advantageous and deleterious alleles (21). Therefore, in the presence of selective sweeps, we expect higher numbers of deleterious alleles (the genetic load) to segregate in genomic regions with lower recombination. Although we cannot yet empirically assess the relative fitness of most segregating variants, we can infer the historical action of purifying selection on a given site using comparative genomic approaches. Here, we use genomic evolutionary rate profiling (GERP) to quantify the extent of purifying selection on each site in the Zea mays genome. GERP rates estimate purifying selection in terms of rejected substitutions relative to a putatively neutral reference rate (22). Therefore, scores above 0 may be interpreted to reflect the historical action of purifying selection, and mutations at such sites are more likely, on average, to be deleterious. In support of this supposition, we find that, on average, higher GERP rates at polymorphic sites are associated with lower minor allele frequencies, and that the rates at third codon positions are lower than the rates at the first and second codon positions (SI Appendix, Figs. S29 and S30).

We inferred differences in the genetic load of regions by comparing the proportions of polymorphic sites with GERP scores greater than 0, which we term “deleterious polymorphisms.” A greater proportion of these sites are assumed to reflect a greater burden of deleterious alleles. To limit ourselves to the most reliable GERP estimates, we also limited our analysis to sites where all seven species were aligned. Comparing hotspots with controls, we find that hotspots have a significantly lower proportion of deleterious polymorphisms (Fig. 3A). The deleterious polymorphisms within the hotspots are also significantly lower than the average proportion of deleterious polymorphisms genome-wide, and this difference is enhanced as the threshold for defining a deleterious polymorphism is increased, ranging from an ∼7% difference between proportions at a threshold of no rejected substitutions to a 15% difference at a threshold of two rejected substitutions (SI Appendix, Fig. S31). We find that the reduced number of deleterious polymorphisms in hotspots is not explained by their higher GC content, because hotspots are significantly depleted of deleterious polymorphisms even when limiting control regions to those regions with GC content greater than or equal to GC content of the hotspots (SI Appendix, Figs. S32 and S33). Furthermore, this trend of reduced deleterious polymorphisms within areas of high recombination is supported by our genome-wide estimates of cross-over enrichment, which shows a decrease in the proportion of deleterious polymorphisms from ∼53% in the lowest recombination regions to 45% in the highest (Fig. 3B).

Fig. 3.

Proportion of deleterious polymorphisms with differing recombination. (A) Proportion of deleterious polymorphisms in hotspots compared with the range in 1,000 permutations of controls. (B) Posterior density for the proportion of deleterious polymorphisms in intervals across the genome with varying levels of enrichment for cross-overs.

Discussion

In this study of both broad-scale and fine-scale patterns of recombination, we demonstrate that recombination is consistent and predictable across diverse maize lines. In all cases, we find that ∼25% of the genome has less than a 1 in 1,000 probability of a cross-over per megabase per RIL. These low-recombination regions, containing 12% of the annotated gene space, potentially impose a substantial linkage drag burden. Our results show that deleterious mutations are enriched in low-recombination regions genome-wide. This lack of recombination in highly burdened regions will make the use of conventional breeding techniques to eliminate deleterious alleles highly challenging.

Earlier studies of kernel phenotypes have noted high recombination variability between lines (23–26). In particular, several earlier studies demonstrate that heavily methylated TEs can suppress recombination within and around the repetitive region in heterozygotes (23, 27, 28). We do not dispute these findings, given that the number of individuals per family in US-NAM and CN-NAM (n ≤ 200) is too small to have sufficient power for the detection of familial differences on the order of a few tens of kilobases. Indeed, both our small-scale and large-scale results favor a model whereby hypermethylated TEs can suppress recombination. Moreover, we do observe less consistency in small-scale recombination patterns between US-NAM and CN-NAM than at the broad scale. This reduced correlation is in line with higher between-line variability on the narrow scale, although it may partially be due to the smaller sample size of the CN-NAM population. Thus, our results suggest that narrow-scale between-family differences average out at the megabase scale, meaning that distinct sets of line crosses are likely to have similar power for quantitative trait locus (QTL) detection during initial linkage mapping. However, fine-mapping of QTL may still be complicated by unique structural variation among different families.

The inclusion of DNA methylation as a significant predictor of recombination has strong experimental support, primarily within A. thaliana. KO mutations to two enzymes necessary for the maintenance of CpG methylation, the methyltransferase MET1 and the chromatin remodeler decrease in DNA methylation (DDM1), cause genome-wide hypomethylation and a euchromatin-specific increase in the recombination rate (12, 13, 29). However, our use of a methylation-sensitive restriction enzyme, ApeKI, to generate the GBS markers, if not explicitly taken into account, could lead to a spurious association between cross-over density and methylation. We address these potential confounding effects in two distinct ways. First, we defined controls for each hotspot that were selected to have nearly equal GBS marker density. Second, we explicitly estimated the probability of a cross-over occurring between any two adjacent GBS markers while imposing a uniform prior. The use of such a prior prevents overestimation of the recombination rate in marker-dense regions, whereas our fully Bayesian approach allows the influence of the prior to be tempered by the amount of data available.

Our results demonstrate that DNA methylation is associated with recombination in all plant contexts. CHH methylation, which is known to mark transposons proximal to active genes in maize (30), is highly enriched within hotspot TEs even though it is slightly depleted in hotspots, outside of the TEs. The confinement of a significant drop in CpG and CHG methylation to the center of the hotspots, outside of the TEs, suggests that enhanced recombination is also related to a cis-decrease in symmetrical DNA methylation. Given the highly distinctive patterns of hotspot DNA methylation between symmetrical and nonsymmetrical DNA contexts, we believe the study of recombination following experimental loss of small RNA-dependent DNA methylation, which is required for de novo methylation of CHH motifs, is likely to be a fruitful area of research.

Strong fine-scale positive associations between recombination and GC content are well described in metazoans (19), but this phenomenon has received less attention in plants (15, 31). GC-bGC can have a significant impact on nucleotide content, because it mimics Darwinian selection by favoring the transmittance of G + C over A + T alleles when in the heterozygous state at recombination junctions. Here, we quantitatively show that higher recombination rates are associated with an increased probability of bGC. This result contrasts with a recent study of A. thaliana, which found that recombination appears to target AT-rich regions preferentially (32). However, the high selfing rate of A. thaliana is likely to reduce the impact of bGC significantly when it does occur. In humans, bGC is associated with a higher incidence of disease-related alleles and a faster rate of substitution (20, 33). Although our analysis of genetic load suggests the former effect is mitigated by the increased rate of recombination, detailed analysis of deleterious alleles within the bGC tracts may be a promising avenue of further research, because the action of bGC can theoretically maintain deleterious alleles at high frequency even within large populations (34).

The domestication of Z. mays from its wild progenitor, teosinte, involved only a modest bottleneck in genetic diversity (35), and the deliberate cultivation of maize inbreds only began within the past century. Therefore, maize is thought to harbor significant numbers of rare deleterious alleles. In this study, we quantitatively demonstrate that much of this deleterious variation is likely to reside within low-recombination regions. The enrichment of deleterious alleles in low-recombination regions is expected because reduced recombination permits deleterious alleles to hitchhike to high frequency during selective sweeps (21). However, our finding contrasts with a recent study of putatively deleterious nonsynonymous polymorphisms in maize, which were not significantly enriched in regions of low recombination (36). We believe our methods are better able to assess whether an increase in the frequency of deleterious alleles accompanies reduced recombination due to our use of a measure that does not rely on genome annotation. Including all potentially deleterious polymorphisms not only provides us with greater statistical power to detect a significant trend but also gives us a better sample of the slightly deleterious alleles that are most likely to be affected by reduced recombination (21).

An abundance of easily assayed kernel phenotypes has long made maize a convenient subject for targeted studies of meiotic recombination, and these assays have supported the localization of cross-over events to low-copy regions of the genome (37, 38). Our study of meiotic recombination across two diverse sets of germplasm strongly supports a generalized, historically stable confinement of most cross-over events to low-copy regions of the genome and, in particular, underscores the importance of DNA methylation in delineating recombinogenic regions at both a broad scale and a fine scale. We show that extant patterns of regional cross-over variation influence the rate of nucleotide substitution through bGC, underlining the need to consider forces other than selection and drift in recombination hotspots. Importantly, our findings provide direct evidence for substantial genetic load segregating within the low-recombination regions of the genome, which we hope will inspire novel approaches to accelerate crop improvement.

Materials and Methods

Germplasm.

We analyzed cross-overs occurring in germplasm from two populations of RILs. The US-NAM maize population consists of 5,000 F₆ RILs generated from crosses of 25 diverse inbred founders: B97, CML52, CML69, CML103, CML228, CML247, CML277, CML322, CML333, Hp301, Il14H, Ki3, Ki11, Ky21, M37W, M162W, Mo18W, MS71, NC350, NC358, Oh43, Oh7B, P39, Tx303, and Tzi8, with common parent B73, followed by five generations of selfing (39). The CN-NAM maize population consists of 11 RIL populations derived from crosses of the common parent Huangzaosi with the inbred lines Zheng58, Ye478, Qi319, Weifeng322, Lv28, Pa405, Duo229, K12, Mo17, Huobai, and Huangyesi3 (40). Each line was selfed to the F₇ generation to produce 1,971 total RILs. Only nine of the 11 families were used to analyze cross-overs, because two of the founder lines were derived from the common parent. The resulting extensive identical by descent (IBD) regions would have masked many of the cross-overs and required significant modification of the imputation pipeline.

Identification of Cross-Over Intervals.

Cross-over intervals were identified using GBS data. The methods used to sequence DNA samples (16) and to call polymorphic sites (41) have been previously described. Briefly, DNA samples were created by bulking tissue: four plants per RIL for US-NAM and 10 plants per RIL for CN-NAM. Reduced representation libraries were created by digestion of each sample with the ApeKI restriction enzyme, followed by sequencing of generated short reads. The resulting reads were trimmed to 64 bp and then aligned to the B73 reference genome. Polymorphisms were called in reads aligning to the same position. The analysis described here was performed using ZeaGBS Build 2.6, which contained over 952,844 polymorphic sites called on about 33,000 DNA samples.

After extracting data for the NAM populations from the larger dataset, each biparental family was analyzed separately to find intervals. That process involved first identifying the parental haplotypes for each family. Then, for each RIL at every nonmissing site, each allele was recoded with the identity of the parent from which that allele came. The Viterbi algorithm (42) was then used to call heterozygous loci and correct genotyping errors. The haplotype-calling algorithm is described in greater detail elsewhere (43).

Linear Model for Cross-Over Density.

We calculated the number of cross-overs occurring in 1-Mb nonoverlapping windows across the genome. If a given interval fell over more than one window, we added the proportion of the interval present in each of the respective windows to their counts. Using a forward selection strategy with the “lm” function in R, and raising the dependent variable to the power of 0.25 to obtain homoscedastic, normal residuals, we obtained the following model:

$$\mathrm{Crossover}\hspace{0.17em}\mathrm{densit}{\mathrm{y}}^{0.25}\sim \mathrm{GBS}\hspace{0.17em}\mathrm{density}+\mathrm{Distance}\hspace{0.17em}\mathrm{from}\hspace{0.17em}\mathrm{telomere}$$

$$+\mathrm{CpG}\hspace{0.17em}\mathrm{methylation}+\mathrm{CHH}\hspace{0.17em}\mathrm{methylation}+\mathrm{GC}\hspace{0.17em}\mathrm{Content}$$

$$+\mathrm{Repeat}\hspace{0.17em}\mathrm{Content}+\mathrm{CpG}\hspace{0.17em}\mathrm{methylation}:\mathrm{CHH}\hspace{0.17em}\mathrm{methylation}$$

This model used all of the predictor variables we initially considered on the basis of prior biological knowledge. To assess their predictive power while guarding against overfitting, we performed 10-fold cross-validation. At each iteration, we trained the model using the 1-Mb windows from nine of the 10 maize chromosomes, reserving the 10th chromosome for prediction only. The reported R² values are based on the correlation of these predictions with the observed values.

Fine-Scale Identification of Recombination Hotspots and Control Regions.

Fine-scale recombination hotspots were identified for each chromosome by fitting a cubic smoothing spline to the cumulative distribution of intervals with a length of 10 kb or less using the “UnivariateSpline” function in SciPy (44), where the independent variable was taken to be the midpoint of the intervals. We then identified peaks in the first derivative as midpoints of the hotspots, setting a threshold of 0.00025 by manual inspection. This threshold yielded a total of 555 putative hotspots. The end points of these hotspots were found by taking the most extreme end points of the intervals less than 10 kb that were located within 5 kb of the peak.

Our ability to identify recombination hotspots depends, in part, on the GBS marker density. Therefore, to allow for inference regarding local factors associated with recombination rather than GBS marker density, we identified sets of control regions for each hotspot with approximately equal GBS marker density but lower levels of recombination. Specifically, for each hotspot, we identified genomic regions that contained the same number of GBS markers within a physical size that differed by less than 10% from the hotspot but lacked cross-overs that were completely contained within these regions. To ensure that the mean GBS marker density of the hotspots and the controls was approximately even during bootstrap testing, we further limited the hotspots to those hotspots that had at least 500 control regions, reducing the number of hotspots to a total of 410.

Bayesian Inference of Genome-Wide Cross-Over Probabilities.

In addition to identifying regions with many narrow cross-over intervals, we estimated the probability of a cross-over occurring within any subinterval between adjacent GBS markers on a given chromosome. We carried out inference using a Gibbs sampling algorithm on the following model:

$$\alpha \sim U\left(0,M\right)$$

$$\theta \sim Dir\left(\alpha H\right)$$

$$z_i\sim Mult(c{\theta }_{\left\{j:j\in x_i\right\}},1)$$

Each z_i represents the latent variable referring to the specific subinterval in which the cross-over found somewhere within the observed interval, x_i, actually occurred. The probability of a cross-over occurring in a given subinterval is then provided by θ_i, which parameterizes a multinomial distribution. The prior for the θ_i is a Dirichlet distribution with a uniform distribution on its single hyperparameter, α. The hyperparameter α is given a uniform prior between 0 and M, which we set to be 50,000, because this value was well above the range of highest posterior density in all chromosomes. To allow the influence of α to be driven by the data, we sampled α during each iteration of Gibbs sampling using sampling importance resampling (45). This hyperparameter is then multiplied by a vector, H, to parameterize the Dirichlet, where H is given by the proportion of the chromosome occupied by each subinterval.

Permutation Testing for Genomic Feature Associations.

We compared DNA methylation, historical recombination, GC content, and GERP scores between identified hotspots and control regions. B73 CpG, CHG, and CHH methylation was taken from a whole-genome bisulfite sequencing study (18). All coordinates were based on the Z. mays B73 AGPv2 genome. For the analysis of DNA methylation, we divided each hotspot or control into 100 bins of equal size (e.g., a region with a size of 10 kb would be split into 100 bins with a size of 100). Methylation means for each sequence context (CpG, CHG, and CHH) were then calculated across each bin for hotspots and for controls. Values of historical recombination (4Nec) in maize improved lines, landraces, and teosintes were taken from an earlier study using HapMap2 data (17). We also limited 4Nec estimates to those estimates based on at least 30 markers. Genes and TEs were taken from the Z. mays v.2 5b filtered gene set and 5a Maize Transposable Element Consortium (MTEC) repeat set, respectively.

For each comparison, we ran 1,000 bootstrap iterations of the control region. Each iteration proceeded chromosome by chromosome, where, for each chromosome, a selection of nonoverlapping control regions equaling the number of hotspots for that chromosome was chosen.