Endocytic proteins drive vesicle growth via instability in high membrane tension environment

Significance

Biological cells are engaged in an incessant uptake of macromolecules for nutrition and inter- and intracellular communication; this entails significant local bending of the plasma membrane and formation of cargo-carrying vesicles executed by a designated set of membrane-deforming proteins. The energetic cost incurred in forming vesicles is directly related to the stressed state of the membrane and, hence, that of the cell. In this study, we reveal a protein-induced “snap-through instability” that offsets tension and drives vesicle growth during clathrin-mediated endocytosis, the main pathway for the transport of macromolecules into cells. Because these proteins (actin and BAR proteins) are involved in other interfacial rearrangements in cells, the predicted instability could be at play in cells at-large.

Abstract

Clathrin-mediated endocytosis (CME) is a key pathway for transporting cargo into cells via membrane vesicles; it plays an integral role in nutrient import, signal transduction, neurotransmission, and cellular entry of pathogens and drug-carrying nanoparticles. Because CME entails substantial local remodeling of the plasma membrane, the presence of membrane tension offers resistance to bending and hence, vesicle formation. Experiments show that in such high-tension conditions, actin dynamics is required to carry out CME successfully. In this study, we build on these pioneering experimental studies to provide fundamental mechanistic insights into the roles of two key endocytic proteins—namely, actin and BAR proteins—in driving vesicle formation in high membrane tension environment. Our study reveals an actin force-induced “snap-through instability” that triggers a rapid shape transition from a shallow invagination to a highly invaginated tubular structure. We show that the association of BAR proteins stabilizes vesicles and induces a milder instability. In addition, we present a rather counterintuitive role of BAR depolymerization in regulating the shape evolution of vesicles. We show that the dissociation of BAR proteins, supported by actin–BAR synergy, leads to considerable elongation and squeezing of vesicles. Going beyond the membrane geometry, we put forth a stress-based perspective for the onset of vesicle scission and predict the shapes and composition of detached vesicles. We present the snap-through transition and the high in-plane stress as possible explanations for the intriguing direct transformation of broad and shallow invaginations into detached vesicles in BAR mutant yeast cells.

Clathrin-mediated endocytosis (CME) is one of the key metabolic pathways for transporting macromolecules into eukaryotic cells (1–7); it is characterized by a chain of remodeling events that transforms an almost flat patch of plasma membrane into a cargo-carrying closed vesicle. The journey from a patch to a shallow invagination, then to a mature vesicle, and finally to a detached vesicle is executed by an elaborate set of proteins that act in a well-orchestrated fashion. Because this shape evolution entails significant local bending of the membrane, it is highly sensitive to the resting tension in the membrane. A higher tension in a membrane makes a membrane taut and harder to bend, thus increasing the energetic cost required to form new vesicles. As a consequence, in cells experiencing high membrane tension, such as yeast cells and mammalian cells with polarized domains or those subjected to increased tension, actin dynamics has been found to be necessary to provide additional driving force to successfully complete CME (8–14). Although this fact has been established by seminal experimental studies, how actin forces actually drive vesicle formation and facilitate vesicle scission is not well understood. In addition, the role of another key membrane remodeling protein—the BAR protein—in overcoming tension has not yet been explored. In this paper, we pursue a detailed theoretical and computational analysis to unravel some previously unidentified mechanisms by which these key endocytic proteins (actin and BAR proteins) offset membrane tension, drive vesicle growth, and assist vesicle scission.

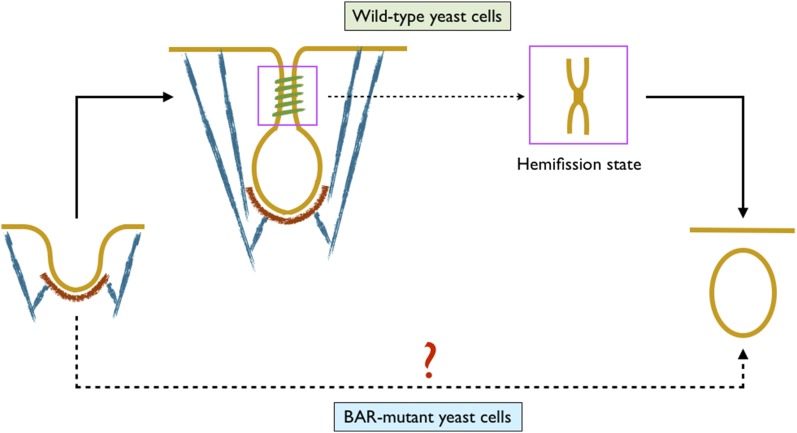
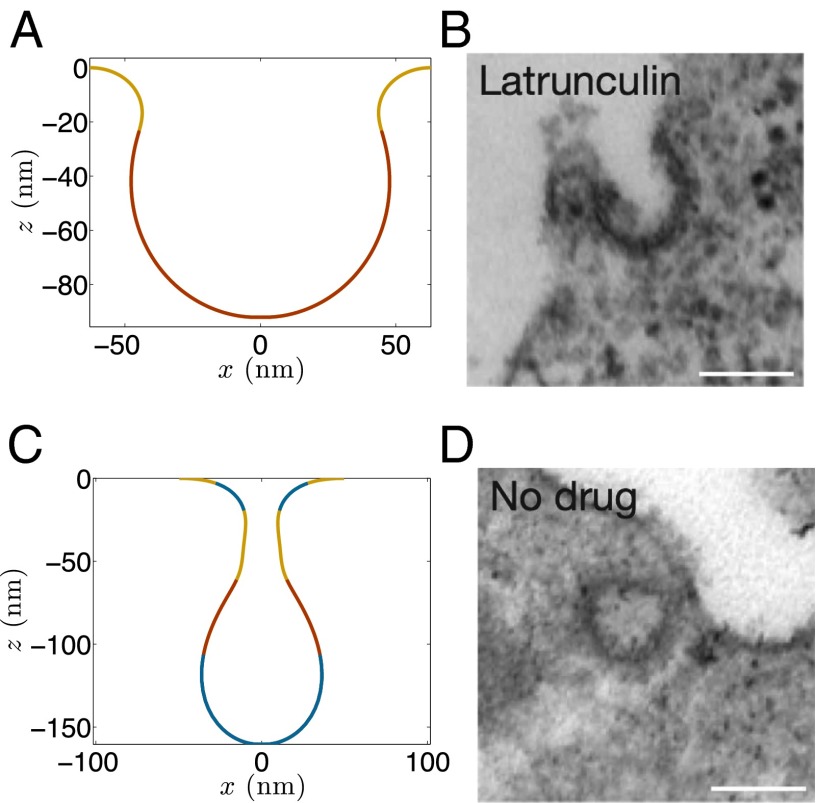
We begin by posing a conundrum. In yeast cells, clathrin, actin, and BAR proteins contribute to vesicle formation in different capacities. Though the inhibition of actin polymerization completely arrests endocytosis (9, 11, 12, 14), the absence of clathrin and BAR proteins only leads to ∼50% and 25% reduction in the internalization events, respectively (14–18). Although a high scission rate is maintained in BAR mutant cells, there is a fundamental difference between the shape evolution process in these and the wild-type cells. In the wild-type cells, a shallow invagination turns into an elongated vesicle with a constricted neck before scission, which is successfully imaged in experimental studies (Fig. 1) (14, 18, 19). In contrast, such an intermediate shape is not observed in BAR mutant cells. After a shallow and broad invagination, experimental images directly show detached vesicles in the cytoplasm (Fig. 1) (18). This is rather intriguing because the existing model of membrane scission requires lipids to come in close proximity and pass through a hemifission state before scission to avoid any leak during the topological transition (20–23). How then does a shallow invagination directly transform into a detached vesicle? We will show in later sections that this conundrum is at the core of the shape-evolution mechanism in the presence of resting tension in the plasma membrane and is critical for understanding the roles of actin and BAR proteins in CME.

Fig. 1.

The conundrum: In wild-type yeast cells, actin and BAR proteins turn a shallow invagination into a mature vesicle with a narrow tubular domain before scission (lipid membrane is shown in yellow, clathrin coat in red, actin filaments in blue, and BAR coat in green). In BAR mutant yeast cells, the intermediate vesicle with a constricted neck is not observed. A detached vesicle is directly seen after an initial broad invagination. Because a nonleaky scission requires lipids to come in close proximity and transition through a hemifission state, how broad and shallow invaginations undergo scission remains intriguing. This puzzle is at the core of this study. The figure is not drawn to scale.

Several theoretical and computational studies have advanced our physical understanding of CME in both mammalian and yeast cells (24–27). Liu et al. (24) studied vesicle formation and scission in yeast cells under the action of curvature-generating proteins and actin filaments. The study highlighted a critical role of lipid phase boundary-induced line tension in budding and scission. In a follow-up work, temporal and spatial coordination of endocytic proteins was studied in an integrated model to simulate endocytosis in mammalian and yeast cells (25). The study showed a dynamic two-way coupling between the membrane geometry and the various biochemical reactions. Agrawal and Steigmann (26) used a unified theory of heterogeneous membrane to show that clathrin coat could drive vesicle formation without assistance from line tension in the absence of a resting plasma membrane tension. Agrawal et al. (27) studied the roles of epsin and clathrin in the nucleation of membrane vesicles. Although these studies have provided fundamental mechanistic insights into CME, the physical underpinnings of the remodeling mechanism in the presence of tension and the specific roles played by key proteins in countering tension remain unaddressed.

In this study, we simulate membrane–protein interactions at the continuum scale to explore the consequences of finite tension. We first model the effect of actin forces in driving the growth of a shallow clathrin-coated vesicle. We find that until a critical force is reached, the vesicle undergoes smooth transition. Once the critical force is crossed, it experiences a snap-through transition that drastically elongates and squeezes the vesicle; this leads to a significant in-plane stress in the tubular region of the vesicle that far exceeds the rupture tension. We then model the effect of BAR proteins. We find that the attachment of BAR proteins also drives vesicle formation by instability, but it is much gentler compared with the actin case. To our surprise, we find that after the instability has occurred, the dissociation of BAR proteins leads to a larger elongation and growth of the vesicle. We predict vesicle shapes at different stages of CME that closely match those observed experimentally in yeast cells. To test the in-plane stress as a criterion for membrane scission, we simulate the geometries of detached vesicles. We find that the vesicles in the actin-driven case (in the absence of BAR proteins) are smaller than the vesicles in the BAR-driven case. In the latter case, the BAR proteins end up in the vesicle along with the clathrin coat as observed in ref. 18. Finally, we show that the membrane tension is the key parameter that regulates vesicle morphology.

The Model

The central feature of our model is that it incorporates protein-induced heterogeneities in the membrane in a seamless manner. As shown in refs. 26 and 28, this generalization has a crucial consequence: it breaks down the well-known requirement that the surface tension has to be uniform in the entire membrane, as is the case for a homogenous membrane. This feature is pertinent because tension and its impact on membrane remodeling are at the center of this study. The fact that nonuniform tension can exist in the plasma membrane of cells is supported by experimental studies. The tension-based variation in the roles of actin dynamics on the apical and basolateral surfaces of polarized MDHK cells (13) unambiguously shows that the tensions in the two parts of the same plasma membrane are different. It is, therefore, extremely crucial to capture the local variations in surface tension by allowing for heterogeneities in the membrane to model all of the nuances of the membrane–protein interactions and their effect on membrane geometry. A brief overview of the key physical concepts that govern membrane–protein energetics is discussed next (details provided in SI Appendix).

Lipid Membrane.

The lipid bilayer is modeled as a two-dimensional surface embedded in three-dimensional space. Because a relative misalignment of the lipids costs energy, a bilayer offers flexural stiffness. For an isotropic fluid bilayer, the areal strain energy density depends on the local mean curvature (H) and the Gaussian curvature (K) of the surface (1, 29–32). For our model, we use the well-known Helfrich–Canham energy density, $W=k_B{H}^2+k_{G}K$, where $k_B$ and $k_G$ are the bending moduli. The values of these parameters and those discussed later are presented in SI Appendix, Table S2. Because a lipid bilayer sustains a very small areal dilation (less than 2–3%), we assume that any arbitrary patch on the bilayer surface maintains its area (1, 33); this results in a Lagrange multiplier field $\mathit{\lambda }$, which is well known as the surface tension in the membrane.

Clathrin Coat.

Trilegged proteins, called triskelions, assemble to form a clathrin scaffold that imparts a spherical geometry to the underlying bilayer (Fig. 2A). The preferred mean curvature of the sphere, called the spontaneous curvature, is isotropic in nature. In other words, the curvature induced by clathrin is identical in all of the directions in the tangent plane at any point on the coated membrane surface. In addition to curvature generation, clathrin scaffold along with other initial coat proteins stiffens the membrane, resulting in an increase in the bending moduli of the coated domain (34). These effects manifest themselves in the form of a modified strain energy density $W={\widehat{k}}_B{\left(H-C\right)}^2+{\widehat{k}}_{G}K$, where C is the spontaneous curvature and $\left\{{\widehat{k}}_B,{\widehat{k}}_G\right\}$ are the modified bending moduli.

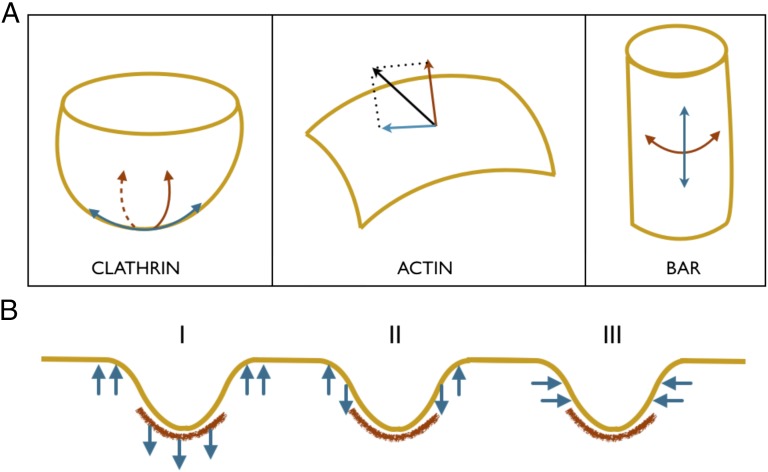
Fig. 2.

(A) Remodeling mechanisms of the three key endocytic proteins. (Left) Clathrin coat imposes spherical geometry on to a bilayer. The induced curvature is isotropic in nature. (Center) Actin filaments apply pulling/pushing forces on to a bilayer. This force gives rise to an in-plane component and a normal component. (Right) BAR imposes cylindrical geometry on to a bilayer. In contrast to the clathrin coat, the BAR coat induces anisotropic curvature. In addition, the two protein coats increase the effective bending stiffness of the underlying bilayer. (B) Forces applied by actin network/bundles. The precise arrangement of the actin filaments at the endocytic site is not yet well established. As a result, the distribution of actin forces on an invagination is also not well understood. We therefore model three different potential loading scenarios, inspired from the existing viewpoints in the literature, to simulate vesicle growth.

Actin Forces.

Polymerizing actin filaments apply a force $\mathbf{f}$ on membrane invaginations. At a point on the bilayer with a unit surface normal $\mathbf{n}$, projection of $\mathbf{f}$ yields a normal component $\left(\mathbf{f}\cdot \mathbf{n}\right)\mathbf{n}$ and an in-plane component $\mathbf{f}-\left(\mathbf{f}\cdot \mathbf{n}\right)\mathbf{n}$ (red and blue arrows in Fig. 2A). Because the precise architecture of the actin network in the vicinity of the invagination and the resulting forces are not yet well established, we model a few different forcing scenarios shown in Fig. 2B. In the first case, we assume that the actin filaments form a branched network and are connected to a portion of the clathrin coat. Hip1R in mammalian cells and sla2p in yeast cells have been known to establish this clathrin–actin link (35–37). We assume that the actin filaments apply a vertical distributed load on the invagination; this is inspired from the model proposed by Idrissi et al. (19) based on their ultrastructural analysis of endocytic profiles obtained using immunoelectron microscopy (12). A similar model was proposed as a likely driving mechanism when the initial coat is unable to drive vesicle growth (38). In the second case, we assume that the actin filaments form bundles that apply vertical forces on an annulus at the interface of the clathrin domain and the uncoated membrane. This model is aligned with the dendritic actin network with collar-like arrangement observed via high-resolution platinum replica electron microscopy and electron tomography (39), and is also in agreement with the parallel bundled network scenario proposed by Drubin and coworkers (14) and used in the computational study by Liu et al. (25) on yeast cells. In the third case, we assume that the actin bundles apply inward-acting horizontal forces near the base of the invagination. This loading condition has been discussed by Collins et al. (39) and Kirchhausen and coworkers (13) in the context of mammalian cells. For all of the loading conditions, we assume that the downward-acting forces are balanced by equal upward-acting forces that impose global force equilibrium, and this should be true in the real scenario as the actin network or bundle has to take support from some structure to apply forces on to the vesicle. A natural consequence of this condition is that it allows the parent bilayer to maintain planar geometry outside the remodeling domain as observed in experimental images.

BAR Coat.

BAR dimers are crescent-shaped proteins that bend the underlying bilayer by forming a cylindrical scaffold. Unlike the clathrin coat, the BAR coat imposes different preferred curvatures in the longitudinal and the circumferential directions (Fig. 2A); as a consequence, interaction of a bilayer with BAR proteins breaks the isotropy present in a typical bilayer. Such a bilayer possesses local orthotropic symmetry, and its strain energy depends on an additional physical parameter D, referred to as the curvature deviator (40–43). In addition, similar to the clathrin coat, the BAR coat also stiffens the membrane (44). To incorporate these effects, we prescribe a more generalized bending energy that has a quadratic dependence on D and a corresponding spontaneous curvature $D_0$. The resultant strain energy takes the form: $W={\widehat{K}}_1{(H-C)}^2+{\widehat{K}}_2{(D-D_0)}^2+{\widehat{K}}_{3}K,$ where $\left\{{\widehat{K}}_1,{\widehat{K}}_2,{\widehat{K}}_3\right\}$ are the modified bending moduli.

We combine these contributions from the membrane and the endocytic proteins to construct the total free energy of the membrane patch. Minimization of the free energy yields the Euler–Lagrange equations that govern the morphology of the membrane patch. Because of heterogeneity, we obtain two force–balance equations in the tangential and the normal directions. The equation in the normal direction, called the shape equation, drives changes in the curvatures (hence the geometry), whereas the one in the tangential direction drives changes in membrane tension. We solve these governing equations for an axisymmetric geometry in conjunction with a few geometric relations and the appropriate boundary conditions to compute the shape transitions of the vesicle and the internal stresses. Further details of the model and the equations are presented in SI Appendix.

Results

Actin Forces Drive Membrane Invagination via Instability.

We first present the actin-driven growth of a vesicle for loading case I (Fig. 2B) in the absence of BAR proteins. We assume that an initial invagination has been created by a clathrin domain of 3,200 nm². This estimate of coat size is based on the study of Kukulski et al. (18) in which clathrin was found to form a hemispherical coat on vesicles with an average size of 6,400 nm². We assume that the resting tension in the membrane is 0.5 mN/m. This estimate is computed from the Young–Laplace relation based on an estimated turgor pressure of 1 kPa in yeast cells (45), which have an average cell diameter of 1 μm (46). The vesicle shapes are computed in response to an increase in the intensity of the actin forces. Such an increase in the force intensity (force per unit area) is expected to arise from an increasing filament density, which is observed experimentally in the vicinity of the vesicle (36). Similar to Liu et al. (25), we neglect the pressure across the membrane because the force intensity due to actin is an order of magnitude higher than the osmotic pressure.

Fig. 3 presents our first key finding (Movie S1). The upper row shows the vesicle morphology at three discrete stages of actin loading. As expected, the invagination grows as the actin force intensity is increased. The first shape is the initial invagination driven by the clathrin coat in the absence of actin forces (Fig. 3A). As the actin forces are increased, the invagination grows deeper reaching the geometry shown in Fig. 3B, in a continuous manner. However, a further slight increase in the actin force leads to an unexpected shape change characterized by a drastic increase in vesicle length and a concurrent reduction in the tubule width (Fig. 3C). To gain insight into this discontinuous shape transition, we plot the force–deflection response of the vesicle (Fig. 3D). The force–deflection curve exhibits a classic snap-through instability and comprises of three phases. In the first phase, the invagination grows monotonically as the force intensity is increased. This branch tracks shape evolution from the geometry in Fig. 3A to Fig. 3B. After reaching a peak force of ∼190 pN, the system jumps to a point on the third linear branch with a much larger invagination length and positive slope; this represents the discontinuous transition from the shape in Fig. 3B to that in Fig. 3C, whereas the intermediate shapes are skipped during the loading phase. The second branch with a negative slope is unstable and never realized by the system.

Fig. 3.

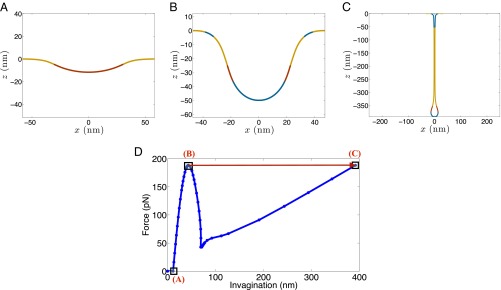
Actin-driven vesicle growth exhibits classic snap-through instability. (A–C) Vesicle geometries at different stages. (A) Vesicle shape at vanishing actin force; (B) vesicle shape just before instability; and (C) vesicle shape just after the snap-through instability (Movie S1). (D) Overall force–deflection response. The jump undergone by the vesicle at the critical actin force is highlighted with a red arrow. The intermediate states on the force–deflection curve are not realized. The snap-through transition results in a significant elongation and constriction of the vesicle. The simulations have been performed at a resting tension of 0.5 mN/m.

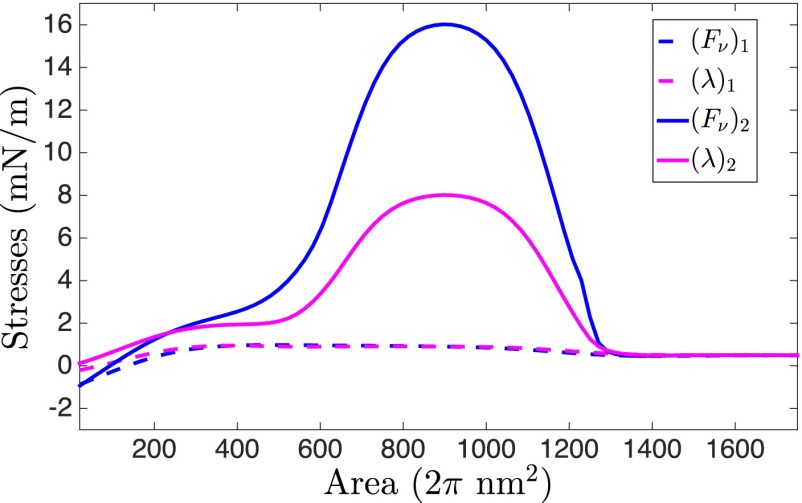
How do the computed geometries compare with the experimentally observed shapes? The simulated shape just before instability is very similar to the shallow 50-nm invaginations observed in BAR (Rvs 161/167) mutant yeast cells by Briggs and coworkers (18). In addition, the computed and experimentally measured angles between the membranes (defined in SI Appendix, Fig. S5) during the shape evolution show a very good agreement (SI Appendix, Fig. S6). In contrast, a highly elongated vesicle after the instability predicted by our model has not been experimentally observed in these BAR mutant cells. Instead, as noted previously, the experiments report a detached vesicle directly after a shallow invagination, which leads to a natural question: Why is the computed postinstability shape not seen in experiments? To investigate this issue, we compute the surface tension and the tangential stress in the vesicle as it undergoes shape evolution. It should be noted that unlike soap films, the net tangential stress in a bilayer comprises of two components: the surface tension and the bending-induced stress. The stresses for the shapes just before and after instability are presented in Fig. 4. $F_{\nu }$ is the net in-plane stress, and $\mathit{\lambda }$ is the surface tension. The maximum tangential stress in the vesicle just before the snap-through transition reaches a value of 1 mN/m. After the transition, the in-plane stress increases to 17 mN/m. To get a sense of how high this stress is, we compute an average estimate of the lysis tension of a bilayer. Because a typical bilayer can withstand a maximum of ∼3% areal strain and has an average stretch modulus of 250 mN/m (1, 33), it can endure a rupture stress of ∼7.5 mN/m. The peak stress in the postinstability vesicle far exceeds this critical value and as a result, before the elongated vesicle is realized, the bilayer is likely to undergo rupture. Because the tubular domain is narrow ($\approx$ 5 nm in diameter), the lipids in the inner monolayer are adjacent to each other, which can allow a nonleaky scission to proceed via the hemifission state. Thus, a snap-through instability followed by a high stress-induced scission provides a mechanism by which shallow invaginations can end up directly as detached vesicles, furnishing a quantitatively tested answer to the mystery observed in BAR mutant yeast cells.

Fig. 4.

Stresses within the vesicle just prior to ${\left(\right)}_1$ and after ${\left(\right)}_2$ instability. Net in-plane stress $\left(F_{\nu }\right)$ is shown in blue, and the surface tension $\left(\mathit{\lambda }\right)$ in magenta. The net in-plane stress comprises of the surface tension and the bending-induced stress. The peak in-plane stress in the vesicle before instability is 1 mN/m, whereas after instability, it increases significantly to 17 mN/m in the narrow tubule region, which far exceeds the rupture stress of 7.5 mN/m that a bilayer can typically sustain. As a consequence, the postinstability shape is not stable and the vesicle would directly undergo scission during the snap-through transition.

BAR Proteins Act as Facilitators.

We now simulate the effect of BAR-coat proteins on shape evolution. To this end, we incorporate the effect of BAR proteins starting from an intermediate stage corresponding to a net vertical actin force that is lower than the critical force needed to induce snap-through transition. Here, we present the results for a net actin force of 160 pN (84% of the critical force value). To isolate the effect of BAR scaffold on vesicle growth, we hold the actin force and the clathrin domain fixed during the shape evolution. We follow the BAR dimer assembly trend observed in yeast cells characterized by two main phases: the polymerization phase, where dimers self-assemble on actin-driven partial invaginations at a uniform rate, and the depolymerization phase, where they begin to dissociate at a uniform rate (25, 47). This observed change in BAR concentration could be a consequence of an increase in either the areal density of the dimers or in the area over which polymerization has occurred, or both. For our simulations, we allow both the areal density and area of BAR-coated domain to increase and decrease simultaneously in the two phases (Fig. 5A). We further assume that the BAR coat-induced curvatures and stiffnesses are linearly proportional to the dimer concentration. This assumption is based on the rationale that an increased proximity between the dimers would lead to a stronger lattice with enhanced remodeling capabilities. Such a behavior has indeed been experimentally observed for amphiphysins that bind onto vesicles at dilute concentrations (48).

Fig. 5.

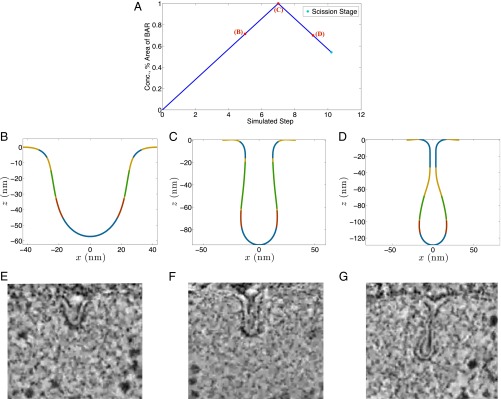
BAR-driven shape evolution of a vesicle. (A) Areal density and surface area of the BAR proteins (blue curve). Areal density and surface area increase in the initial polymerization phase and decrease in the depolymerization phase. The spontaneous curvatures and the stiffness of the BAR scaffold have been assumed to be proportional to the areal density. (B and C) Vesicle shapes during the polymerization phase (membrane is shown in yellow, clathrin domain in red, actin domain in blue, and BAR domain in green). (D) Vesicle shape during the depolymerization phase (Movie S2). The presence of BAR scaffold provides structural stability making the actin-driven transition more controlled. Intriguingly, the depolymerization of BAR proteins shows a counterintuitive response. Instead of undoing the expected squeezing effect, BAR removal results in a further elongation and constriction of the vesicle. (E–G) Observed vesicle shapes in wild-type yeast cells. E–G republished with permission from Elsevier; www.sciencedirect.com/science/journal/00928674.

Fig. 5 B–G shows our second key finding (Movie S2). In the BAR-driven case, the shape transition occurs in a more gradual and controlled fashion, in contrast to the rapid and discontinuous transition in the actin-driven case; this is a consequence of the stabilizing effect of the BAR scaffold because it increases the flexural rigidity of the coated domain, thereby reducing its compliance to bending. The BAR proteins transform the shallow invagination to a more U-shaped invagination, as shown in Fig. 5B. An increase in the BAR density and area leads to vesicle elongation and a narrowing of the neck domain (Fig. 5C). Once past this point, a decrease in the density and the area of the BAR coat has a counterintuitive impact on the vesicle morphology. Instead of decreasing the invagination, the removal of the BAR coat leads to a further elongation and narrowing of the vesicle (Fig. 5D). This irreversibility suggests that the vesicle again undergoes instability during the shape transition, this time triggered by the BAR scaffold. Thus, for a prescribed concentration (hence spontaneous curvatures and stiffness), and area of BAR proteins, there exist two vesicle geometries corresponding to the two branches (polymerization and depolymerization). The two solution branches meet at a unique set of BAR-coat values. For the simulated case, this turning point corresponds to a preferred radius of curvature of 15 nm in the circumferential direction, bending moduli of $200\hspace{0.17em}{k}_{\text{B}}T$, and an area of attachment of 3,700 nm². We compare the computed vesicle geometries with those observed by Briggs and coworkers (18) for wild-type yeast cells (Fig. 5 E–G). The shapes show a remarkable agreement at three different stages of vesicle formation. In addition, we also see an excellent agreement in the angles between the membranes and the tip radius computed from our simulations and those measured by Briggs and coworkers (18) (SI Appendix, Figs. S7 and S8).

What makes the postinstability geometries in Fig. 5 experimentally tractable for visualization? To explain this question, we again compute the stresses in the vesicle as it undergoes BAR-driven invagination. Unlike the highly invaginated vesicle in the actin case, the in-plane stress for the shapes in Fig. 5 B–D are well below the rupture limit, making them stable structures that could potentially be imaged in experiments. If we continue to decrease the BAR density and the BAR domain size, we see enhanced elongation and narrowing of the tubule leading to higher internal stresses. Eventually, a shape is obtained for which the in-plane stress reaches the critical rupture stress (SI Appendix, Fig. S9). All of the intermediate shapes are therefore conducive to imaging and might be the reason for a variation in vesicle shapes observed in wild-type yeast cells (18).

Detached Vesicle Shapes Support Stress-Based Scission Criterion.

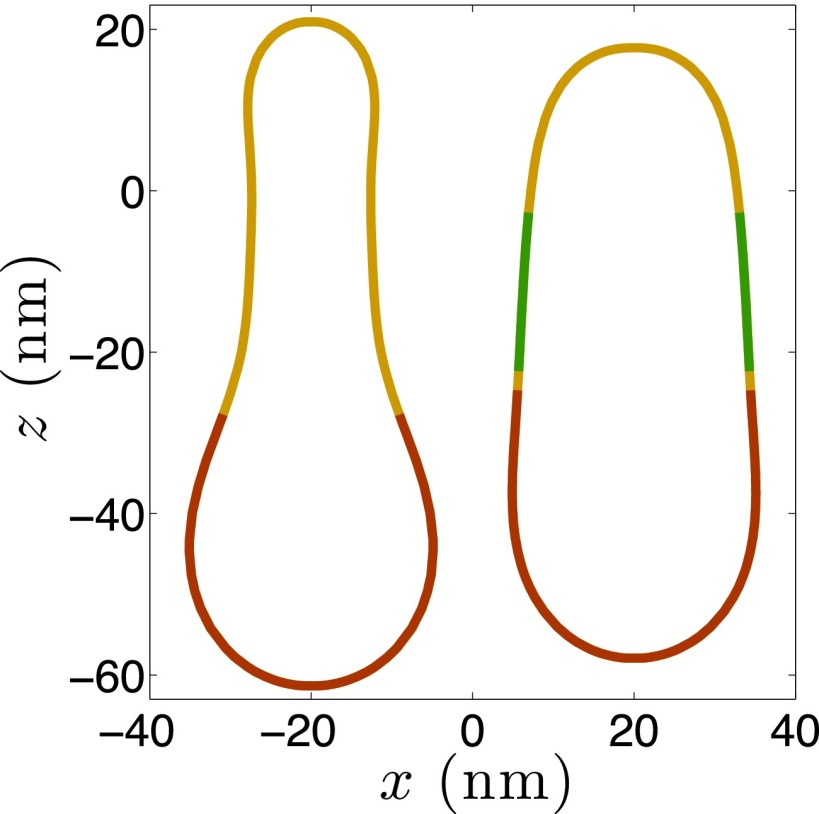
To further test the role of membrane stresses in CME, we simulate the geometry of detached vesicles for actin-driven and BAR-driven cases. Although scission is an intricate process in itself involving participation of special scission proteins or lipids, like dynamin in mammalian cells or PIP2 in yeast cells, we identify the probable sites for scission based on the in-plane stress profile. We hypothesize that the external work needed from scission proteins/lipids for executing membrane scission would be minimal at these sites. We therefore detach the vesicle at the site of maximum in-plane stress and simulate the geometry of the closed vesicle. In addition, we constrain the area and volume of the detached membrane domain before and after scission. The geometries of the vesicles for the actin-driven and BAR-driven cases are shown in Fig. 6. Both vesicles exhibit a prolate geometry, unlike the nearly spherical vesicles observed in mammalian cells at low resting tension values. The vesicle in the actin-driven case possesses a more teardrop geometry. Interestingly, the vesicles observed by Briggs and coworkers (18) in yeast cells also fall into two categories: tear-dropped vesicles and prolate vesicles; their study also revealed a size variation in the wild-type and BAR mutant cells. For the wild-type cells, the vesicles had an average surface area of 6,400 nm² and in the BAR mutant cells, the average size reduced to 5,000 nm². These values are in excellent agreement with the computed vesicle sizes of 5,500 and 6,480 nm² for the actin- and BAR-driven cases, respectively, based on the in-plane stress criterion. In addition, as the peak stress is reached at the interface of the BAR coat and the uncoated membrane tubule, our model predicts that the BAR-coated domain, along with the clathrin-coated domain, becomes part of the detached vesicles. This prediction is aligned with the findings of Kukulski et al. (18) who found the detached vesicles to be coated with both clathrin and BAR proteins. This match between the simulations and experimental data further strengthens the peak stress-based criterion for scission.

Fig. 6.

Shapes of detached vesicles obtained for the actin-driven (Left) and BAR-driven (Right) shape evolutions. The scission was assumed to occur at the site where the in-plane stress in the vesicle reaches the rupture stress. Both the vesicles exhibit a nonspherical shape, with the actin-driven vesicle having a more tear-dropped geometry. In addition, the size of the actin-driven vesicle is smaller compared with that of the BAR-driven vesicle. These findings are consistent with the observations of Kukulski et al. (18) in BAR mutant and wild-type yeast cells.

Discussion

Actin–BAR Synergy Imparts Robustness to the Endocytic Machinery.

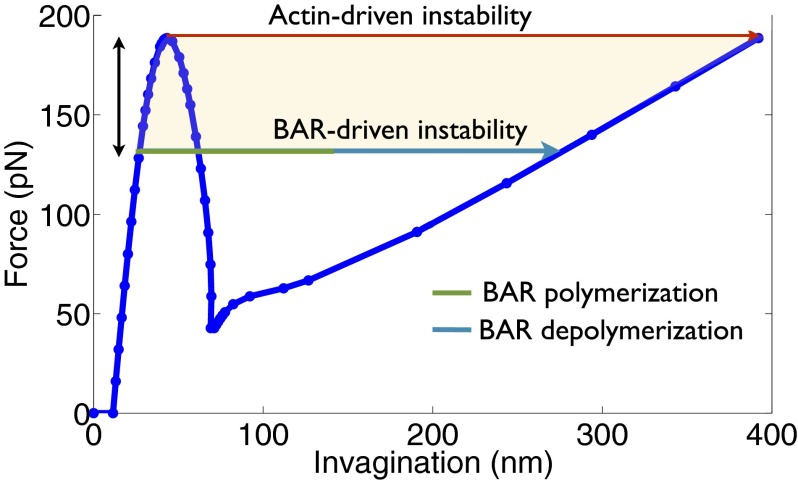
Our study on actin-driven vesicle growth predicts a net vertical force of ∼190 pN for inducing instability at a resting tension of 0.5 mN/m (Figs. 3 and 7). In terms of force per actin filament, it amounts to an average force of ∼2.4 pN, which is distributed over an area of 1,600 nm² in the clathrin-coated domain. This value is comparable to the compressive load required to buckle actin filaments obtained experimentally by Kovar and Pollard (49) and Footer et al. (50). However, if the BAR proteins begin to polymerize before the critical actin force is reached, the instability could be induced sooner. In fact, BAR proteins establish an alternative transition pathway that connects the equilibrium solutions on the first and the third branches of the actin-driven force–deflection curve (Fig. 7). The BAR association phase (in cyan in Fig. 7) induces the instability and drives the initial membrane invagination. Once the instability has been triggered by the BAR proteins and the BAR proteins begin to dissociate, the vesicle has a natural tendency to go to the equilibrium solution on the third branch of the force–deflection curve corresponding to the initial actin force at which the BAR proteins began to polymerize. Thus, once the BAR polymerization has tipped the system over, BAR disassembly reduces the stabilization effect of the scaffold and the vesicle growth becomes more actin driven. It is for this reason that the disassembly of BAR proteins leads to larger elongation and tubulation of a vesicle.

Fig. 7.

Synergistic roles of actin and BAR proteins in executing CME. In the absence of BAR proteins, a tension-dependent critical actin force is needed to induce instability and drive vesicle growth. In the presence of BAR scaffold, a lower actin force suffices. A reduced dependence on actin force is accompanied with a stronger squeezing effect of the BAR scaffold. However, a certain amount of actin force would always be needed to form an initial invagination that would allow polymerization of BAR proteins and enable them to drive invagination. This interplay results in a broad range in which the two proteins can work cooperatively to counter membrane tension and drive invagination. The shaded region shows such a domain that ensures that the final vesicle obtained after complete BAR dissociation experiences close to rupture stress.

The above discussion highlights a remarkable synergy between the actin and BAR proteins in driving vesicle growth. If we look at the above findings from a slightly different perspective, we can link the timing of the BAR activity to the functionality of the BAR proteins. Liu et al. (25), for example, observed short phases of BAR polymerization and depolymerization after an initial phase of actin dynamics. Such a timing of the arrival of BAR proteins and their brief stay can now be seen to be more function oriented than coincidental. The BAR proteins arrive after the actin forces have set the stage and brought the system close to instability. The BAR proteins serve to tip the system over and depart, allowing instability driven transition to proceed. Thus, a short but well-timed activity of BAR proteins is enough to drive vesicle growth and facilitate CME.

If we take this argument a step further, we can predict a domain over which actin and BAR proteins can synergistically drive vesicle growth (shaded area in Fig. 7). The upper limit of this domain is defined by the pure actin-driven path. To define a lower limit, we require the vesicle after BAR dissociation to experience rupture stress for a successful completion of CME. For this pathway, the green domain represents BAR polymerization-dependent invagination and the cyan domain represents BAR depolymerization-driven invagination. The actin force required for this path is ∼30% lower than the critical actin force needed to induce instability in the absence of BAR proteins (double-sided vertical arrow in Fig. 7). For any force above this threshold value and lower than the peak force (shaded region in Fig. 7), actin and BAR can synergistically drive vesicle formation and set the stage for scission; this showcases an inherent robustness of the endocytic machinery where the two proteins can work together to complete CME. If, in addition to in-plane stresses, other scission effects, such as the line tension induced by PIP2, are at play, the actin force requirement would decrease further, thereby expanding the domain of actin–BAR cooperativity. However, a certain actin force would always be needed to create an initial invagination onto which BAR dimers can polymerize, making actin forces indispensable for CME in tense plasma membranes.

Instability and Morphological Evolution.

The snap-through transition in Fig. 3D, is primarily driven by the actin forces. Application of actin forces on a planar membrane in the absence of clathrin domain leads to a similar force–deflection curve with a marginal reduction in the critical force (SI Appendix, Fig. S10). These curves bear similarity to that computed for a tether pulled out of a vesicle by a point force (51). As the pulling force is increased, the tether elongates linearly till it reaches a critical point, beyond which it undergoes a first-order shape transition and continues to elongate at a constant force. The main difference between the force–deflection curves obtained in this study and the one by Derényi et al. (51) lies in the third branch. Though our curves show positive slope indicating structural stiffening, the one obtained by Derényi et al. (51) remains horizontal. This difference mainly stems from the fact that we apply counter forces from the actin network onto the planar membrane adjacent to the vesicle site. If we suppress this force in the absence of clathrin domain and apply only pulling forces on the bud of the vesicle, we recover a force–deflection curve with a horizontal third branch (SI Appendix, Fig. S11). We would also like to note that the force–deflection curves obtained by us and Derényi et al. (51) do not exhibit any activation barrier associated with the initiation of the invagination, as predicted in the case of a tether pulled out of a spherical vesicle by Smith et al. (52). A possible reason for this difference could be the initial flat geometry considered by us and Derényi et al. (51) as opposed to a spherical shape considered by Smith et al. (52). In addition to membrane tethers, instability-induced morphological changes have also been predicted for closed vesicles. For example, Smith et al. (53) predicted an unbinding pathway via metastable shapes characterized by discontinuous transition for adhered vesicles. Agrawal and Steigmann (54) showed that a closed vesicle with a preferred spontaneous curvature undergoes a snap-through transition when subjected to point loads.

Tension Differentiates CME in Yeast and Mammalian Cells.

Although membrane tension has been postulated to be an important factor leading to differences in yeast and mammalian cells, it has not yet been quantitatively examined. Mammalian cells have, on average, a lower resting tension in the plasma membrane because of a lower turgor pressure (55). The tension estimates vary from 0.003 mN/m in chick neurons (56) to 0.02 mN/m in molluscan neurons (57). For the case of vanishing tension, clathrin-driven vesicle formation has been shown to reproduce the experimental findings (26). For higher tension (0.5 mN/m), we have shown a good match between the simulations and the shape evolution in yeast cells (14, 18). We now present the results for an intermediate value of 0.08 mN/m and compare them with the experimental findings of (13) in mammalian cells subjected to increased tension generated by either osmotic swelling or stretching. In addition to lowering the resting tension value, we increase the clathrin coat size to 20,800 nm², which is in between the value used for yeast cells and that for a closed spherical coat (32,000 nm² for a spherical vesicle of radius 50 nm), which would ideally form in a low-tension environment in mammalian cells.

The computed shapes with the above parameters are shown in Fig. 8. The shape in Fig. 8A corresponds to a clathrin-induced invagination in the absence of actin forces, and it matches well with the stalled vesicles (Fig. 8B) observed by Boulant et al. (13). The shape in Fig. 8C is obtained after the occurrence of the snap-through transition, which bears resemblance to the mature vesicles observed by Boulant et al. (13) (Fig. 8D). The good agreement between the computed vesicle shapes at different tension values and those observed in yeast and mammalian cells provides quantitative evidence that tension indeed is a key factor that differentiates CME in the two cell types. The vesicle in Fig. 8C has a maximum in-plane stress of 0.46 mN/m, almost an order of magnitude less than the rupture tension, thereby, making it stable. We note that vesicles with elongated tubular domains have also been observed in dynamin-mutant mammalian cells (58). Because actin burst in mammalian cells (under low resting tension) occurs just before scission, our work suggests that actin forces lead to elongation of the vesicles but are unable to dissociate vesicles from the plasma membrane due to inadequate scission stress.

Fig. 8.

Vesicle shapes obtained at lower resting tension and larger clathrin coat domain. (A) Vesicle shape obtained in the absence of actin force. (B) A partially stalled vesicle observed in MDCK cells subjected to increased tension (13). (C) Vesicle shape with actin force. (D) A mature vesicles observed in MDCK cells with enhanced tension (13). (A and B) and (C and D) show close resemblance. B and D republished with permission from Macmillan Publishers Ltd: Nature Cell Biology, ref. 13, Copyright 2011.

Tension Governs Vesicle Morphology.

If we generalize the actin-driven shape evolution studies to a wider range of tension values, we find that the vesicle geometry and the initiation and extent of discontinuous shape transition are a function of the resting tension in the membrane. Fig. 9A shows the critical force needed to induce instability as a function of the resting tension in the planar bilayer. These results have been obtained for a fixed clathrin coat size of 3,200 nm². The critical force increases monotonically with an increase in the resting tension. This trend is aligned with the recent studies by Basu et al. (59) and Aghamohammadzadeh and Ayscough (55) that found actin requirement to be proportional to the turgor pressure and, hence, resting tension in yeast cells. In addition, we compute the invagination length at the critical point before $\left(Z_1\right)$ and after transition $\left(Z_2\right)$. An increase in tension reduces the initial invagination depth at which the snap-through transition occurs in a linear fashion (Fig. 9B). In contrast, the jump in the invagination length $\left(Z_2-Z_1\right)$ increases almost linearly as the tension is ramped up. Elongation of vesicles is also accompanied with a narrowing of the width of the tubular domain. Thus, beyond a critical resting tension, invaginated vesicles after instability would experience significant in-plane stresses, making them experimentally intractable until stabilized by BAR-coat proteins. For a clathrin area of 3,200 nm², we predict this critical value to be ∼0.2 mN/m. These predictions can be tested in experiments by systematically varying tension in the plasma membrane, either by osmotic swelling or stretching, and imaging the vesicles.

Fig. 9.

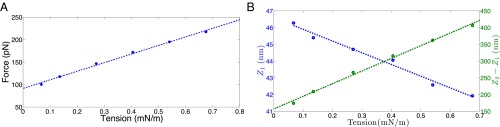
Effect of resting tension. (A) The critical actin force required to induce instability increases monotonically with the resting tension present in the bilayer. (B) The invagination length before instability $\left(Z_1\right)$ decreases with the resting tension (blue curve). In contrast, the jump in the invagination length $\left(Z_2-Z_1\right)$ increases with the resting tension (green curve); as a consequence, shallower invaginations will transform into more elongated vesicles at higher resting tension, which in turn would increase the in-plane stress in the postinstability vesicle, making it susceptible to rupture.

Actin Induced In-Plane Stress Should Be a Key Determinant of Scission.

Our study provides strong evidence that in-plane stress should play an integral role in governing membrane scission. Our explanation of the discontinuous transition observed in BAR mutant yeast cells and the vesicle shapes and sizes generated by our model support this prediction. Although other mechanisms have been implicated in scission, membrane stress could facilitate the topological transition and determine the site for membrane scission. For example, Liu et al. (24) proposed the role of line tension in vesicle formation and scission in yeast cells. The arrival of synaptojanin in the later stages hydrolyzes PIP2 in the clathrin-coated domain, giving rise to a line tension at the interface of the clathrin and BAR-coated domains. However, it is important to note that even in the absence of BAR proteins, scission events occur in ∼75–80% of the endocytic events (18), which alludes to a role of additional mechanisms in executing scission. We propose actin-induced in-plane stress to be a potential candidate. In wild-type mammalian cells, because actin burst occurs in the latter part of endocytosis, actin-induced stress could assist dynamin in scission. In addition, actin-induced in-plane stress in the neck domain could facilitate dynamin polymerization (60). This idea is supported by the recent work of Campelo and Kozlov (61), which predicts that high stress facilitates insertion of shallow proteins within the bilayer. Thus, in-plane stress could act as a facilitator for dynamin-induced scission.

Limitations.

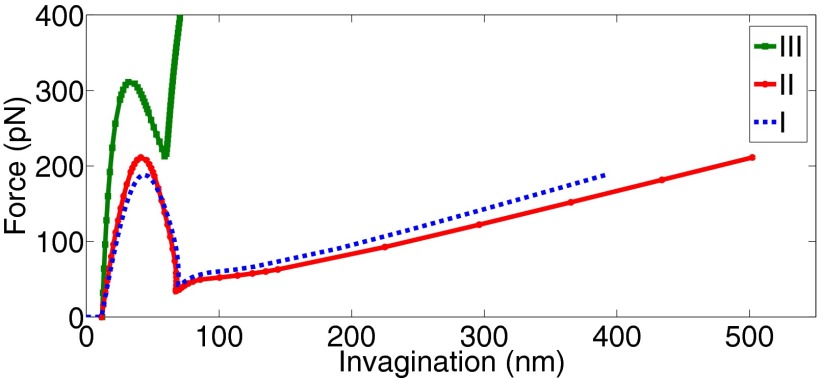
The major limitation of our mathematical framework is that it is not equipped to model topological changes and, hence, cannot be used to simulate vesicle scission. It is for this reason that our model predicts highly elongated vesicles after snap-through transition that would otherwise undergo scission. The other limitation of our study is that the actin-loading scenarios modeled are based on the proposals made in the literature and might not be very accurate. However, the findings made above are true for both the distributed network and bundle-type actin loadings (cases I and II in Fig. 2B). Barring some minor quantitative differences, the overall nature of the force–deflection response of the vesicle remains unchanged for the first two cases (Fig. 10), which suggests that our predictions should hold for a wide variation in the actin-loading mechanisms. Only the horizontal loading (case III in Fig. 2B) requires a much higher actin force (almost twice), induces negative in-plane stress in the tubule region and leads to short spherical vesicles typically not seen in yeast cells (Fig. 10). These major differences indicate that a purely horizontal force driven vesicle formation is not likely to exist in the high tension regime. The shape evolutions for cases II and III are presented in SI Appendix, Figs. S12 and S13.

Fig. 10.

Force–deflection curves for the different actin loading cases presented in Fig. 2B. All three cases show snap-through transition. Cases I and II show similar response with vesicles undergoing a significant elongation after instability. In contrast, case III predicts much smaller invaginations and requires much larger force to induce instability.

Concluding Remarks.

In this study, we investigated the individual roles of actin forces and BAR scaffold in executing CME in high membrane tension environment. We presented a snap-through instability-driven remodeling mechanism that governs vesicle shape evolution and provided quantitative insights into the actin-BAR synergy that imparts robustness to the endocytic machinery. Because actin dynamics plays an integral role in other endocytic pathways, such as phagocytosis, macropinocytosis, and caveolae-mediated endocytosis (62), it is probable that instability could also be at play in these processes. In addition, because other cellular processes, such as cellular division and locomotion, are associated with large-scale remodeling of cellular interfaces, it would not be surprising if protein-induced instabilities, regulated by interface tension, contribute to these phenomena as well.