Stochasticity and Stereotypy in the Ciona Notochord

Abstract

Fate mapping with single cell resolution has typically been confined to embryos with completely stereotyped development. The lineages giving rise to the 40 cells of the Ciona notochord are invariant, but the intercalation of those cells into a single-file column is not. Here we use genetic labeling methods to fate map the Ciona notochord with both high resolution and large sample sizes. We find that the ordering of notochord cells into a single column is not random, but instead shows a distinctive signature characteristic of mediolaterally-biased intercalation. We find that patterns of cell intercalation in the notochord are somewhat stochastic but far more stereotyped than previously believed. Cell behaviors vary by lineage, with the secondary notochord lineage being much more constrained than the primary lineage. Within the primary lineage, patterns of intercalation reflect the geometry of the intercalating tissue. We identify the latest point at which notochord morphogenesis is largely stereotyped, which is shortly before the onset of mediolateral intercalation and immediately after the final cell divisions in the primary lineage. These divisions are consistently oriented along the AP axis. Our results indicate that the interplay between stereotyped and stochastic cell behaviors in morphogenesis can only be assessed by fate mapping experiments that have both cellular resolution and large sample sizes.

Introduction

A fundamental question in developmental biology is the degree to which embryogenesis is stereotyped versus stochastic. Fate mapping experiments in diverse organisms reveal many stereotyped aspects of embryonic development. In the nematode C. elegans, the cell divisions and morphogenetic movements of embryogenesis are essentially invariant, and the embryo is small and simple enough that these lineages and movements have been completely described (Sulston et al., 1983). In vertebrates and many other species, however, embryonic development generates predictable patterns but is not invariant from embryo to embryo. This is indicated by the non-deterministic nature of many fate maps (Clarke and Tickle, 1999; England and Adams, 2007), the partially stochastic nature of many developmental processes (Eldar and Elowitz, 2010; Raj and van Oudenaarden, 2008) and the remarkable regulative and plastic properties of some of these embryos (Davidson, 1990; Martinez Arias et al., 2013).

Fate mapping with single cell resolution is not straightforward in vertebrate embryos and other embryos with large cell numbers, so it is possible that their cell lineages and movements may be more stereotyped than currently believed, or that hidden patterns may emerge from finer scale analysis. Embryos with completely stereotyped development can be represented with simple and absolute fate maps. In the more common situation that particular blastomeres may have multiple potential outcomes, either in terms of the cell types they differentiate into or their eventual location within the embryo, then fate maps should ideally be thought of in a probabilistic framework. Single cell labeling by microinjection is a traditional method for fate mapping with single cell resolution, but is technically demanding and difficult to scale up to large sample sizes. It also does not necessarily provide information on lineage relationships within labeled clones. New imaging technologies such as SPIM (Huisken et al., 2004; Keller et al., 2008) raise the possibility of fate mapping entire embryos by in toto timelapse imaging (Hockendorf et al., 2012; Khairy and Keller, 2010; Megason and Fraser, 2003). Many embryos would need to be imaged, however, to get statistical power on the embryo to embryo variability. Genetic labeling methods offer interesting possibilities for fate mapping with large numbers of replicates (Legue and Joyner, 2010; Livet et al., 2007; Loulier et al., 2014; Salipante and Horwitz, 2007; Yochem and Herman, 2003).

Ascidians are close chordate relatives of the vertebrates and have a conserved chordate embryonic body plan with a particularly small, simple embryo (Munro et al., 2006; Passamaneck and Di Gregorio, 2005). The early lineages in ascidian embryos are invariant and have been described with single cell resolution up to the onset of gastrulation (Nishida, 1987; Nishida and Satoh, 1983; Nishida and Satoh, 1985). While many aspects of ascidian morphogenesis are known to be invariant, there are several processes that are at least partly stochastic. Foremost among these is the intercalation of the 40 notochord cells into a single-file column. This intercalation process involves mediolaterally-biased intercalation and boundary capture phenomena similar to those observed in vertebrate embryos (Jiang et al., 2005; Munro and Odell, 2002a; Munro and Odell, 2002b; Veeman et al., 2008). A variety of labeling strategies have shown that the notochord cells from the left and right sides of the embryo intercalate with one another in a stochastic fashion where they do not alternate perfectly (Nishida, 1987; Nishida and Satoh, 1983; Nishida and Satoh, 1985).

The anterior 32 'primary' notochord cells are derived from blastomeres A7.3 and A7.7, whereas the posterior 8 'secondary' notochord cells are derived from B8.6. Fate mapping experiments in the ascidian Halocynthia have suggested that the A7.3 and A7.7 blastomeres that give rise to the anterior 32 notochord cells both contribute randomly to the primary notochord (Nishida, 1987). These observations implied that ascidian notochord intercalation is highly stochastic.

In a recent study of how the notochord develops its characteristic tapered shape, we found that certain cell divisions in the notochord primordium are asymmetric such that anterior daughters are smaller than posterior daughters in the anterior of the primordium, whereas posterior daughters are smaller in the posterior of the primordium (Veeman and Smith, 2013). This provided an essential component to our quantitative model of how the notochord becomes tapered, but it implied that there must be a relatively tight mapping between cell position in the early notochord primordium and the intercalated notochord. This challenged the widespread view that ascidian notochord intercalation is highly stochastic.

To reconcile these observations, we developed a fine fate map of the Ciona notochord. We took advantage of the ability to easily introduce transgenes into the fertilized egg by electroporation (Corbo et al., 1997). This transient transgenesis gives rise to mosaic expression. By varying the amount of DNA used, one can control the degree of mosaicism. It is not clear if the introduced DNA is being propagated as an extrachromosomal array, free plasmid or some other fashion, but there is good evidence that the mosaic expression is clonal in nature (Corbo et al., 1997; Zeller et al., 2006). Here we deliberately used low doses of a tissue-specific GFP reporter plasmid to label small clones of cells in the notochord. The advantage of this method is that very large numbers of clones can be generated as compared to traditional fate mapping by single blastomere microinjection. The blastomere that was labeled to give rise to any particular clone is not known, but the large numbers possible allow distinct classes of clone to be identified and retrospectively associated with particular blastomeres.

Methods

Embryo culture and electroporation

Adult Ciona intestinalis were obtained from Marine Research and Educational Products (San Diego, CA) and housed in a recirculating aquarium. Fertilized eggs were dechorionated by standard methods and electroporated with a Bio-Rad Gene Pulser Xcell using Time Constant mode with settings of 50V, time constant 17 ms and a 4mm electrode gap. The electroporation solution was made by adding 300 µl of dechorionated eggs in artificial seawater to a mixture of 480 µl 0.77M mannitol and 20 µl of DNA. Typical experiments used only 5–10 µg of a plasmid driving GFP expression under the control of the notochord–specific Brachyury promoter/enhancer (Bra>GFP). Electroporated eggs were moved to dishes of artifical seawater containing 0.01% BSA and cultured at 21°C until the desired stage. Embryos were staged according to Hotta’s staging series (Hotta et al., 2007).

Cell lineage nomenclature

We use the standard Conklin system for naming blastomeres (Conklin, 1905), following Meinertzhagen’s convention for later blastomeres whereby the more anterior blastomere receives the higher (even) number (Cole and Meinertzhagen, 2004). The primary notochord is derived from the left and right side equivalents of blastomeres A7.3 and A7.7. In this nomenclature system the first letter encodes the parental blastomere at the 8-cell stage (A vs. P and animal vs. vegetal), the first number indicates the cell cycle generation and the third number indicates the blastomere number. A7.3 for example divides to give A8.6 and A8.5. A8.6 divides to give rise to A9.12 and A9.11… The postmitotic primary notochord consists of A10.17–A10.24 and A10.49–A10.56. Right side blastomeres are indicated with an asterisk.

Staining and imaging

Embryos were fixed overnight in 2% paraformaldehyde in artificial seawater then washed several times with PBS+0.2% Triton X-100 (PBSTr). Blocking and labeling steps used PBSTr with 5% heat inactivated goat serum. Embryos were labeled using a polyclonal antibody against GFP and Alexa-labeled secondary antibodies (Invitrogen). We also used Bodipy-FL-phallacidin (Invitrogen) to label cell cortices. Stained embryos were adhered to poly-L-lysine coated coverslips, dehydrated through a brief isopropanol series, cleared and mounted in Murrays Clear (BABB), and imaged on a Zeiss 700 laser scanning confocal microscope, typically using a 40× 1.3NA objective.

Analysis

Confocal stacks were opened using FIJI/ImageJ (Schindelin et al., 2012; Schneider et al., 2012) and carefully examined to ensure that the embryos showed no obvious defects in development. Each notochord cell from front to back was scored as being either GFP expressing or not expressing. We only considered embryos with 16, 8 or 4 labeled cells in the anterior 32 primary notochord cells, and/or 4 labelled cells in the posterior 8 secondary notochord cells. We only rarely observed evidence of any mixing between the primary and secondary lineages. These embryos usually had defects in morphogenesis and were not considered further. We frequently found that labeled populations of cells could be further resolved based on the intensity of expression, e.g. embryos with 8 labeled cells often had 4 strongly expressing cells and 4 weakly expressing cells. This likely reflects asymmetric segregation of the electroporated plasmid. In that case, we would have scored it as both an 8-cell event and two 4-cell events. We also identified embryos with 16 labeled cells with 8 expressing strongly and 8 weakly. Embryos with more complex combinations of labeled cells were also common but not included in our analyses. All statistical analyses and simulations were performed in Matlab (Mathworks).

Results and Discussion

Ciona transgenesis by electroporation is known to give rise to mosaic expression in a clonal fashion (Corbo et al., 1997; Zeller et al., 2006). In the course of other experiments, we noted that it was relatively common to find embryos electroporated with notochord-specific expression constructs that had exactly 16, 8 or 4 expressing cells in the primary notochord. More complex expression patterns predominated when high doses of plasmid were electroporated, likely reflecting the superposition of multiple clonal events. When electroporating low doses of plasmid, however, then embryos with 16, 8 or 4 expressing cells were more frequent. It occurred to us that this could be used as the basis of a fate mapping strategy, as embryos with 16, 8 or 4 expressing cells most likely represented notochord precursors being effectively labeled before the 4^th last, 3^rd last or 2^nd last cell divisions respectively. For convenience we refer to these as 16-cell, 8-cell and 4-cell clones, though we will discuss later the evidence for whether these always represent single clonal events.

We imaged large numbers of embryos electroporated with Bra>GFP that expressed the reporter in exactly 16, 8 or 4 primary notochord cells (Fig. 1), and compared the resulting distributions of labeled anterior-posterior positions to the null hypothesis that intercalation is completely random. We simulated data for the null hypothesis by using simple computer scripts to randomly select 16, 8 or 4 positions in 32 place strings. For both the experimentally observed and randomly simulated data, we recorded and visualized the specific patterns of labeled and unlabeled cells as binary strings.

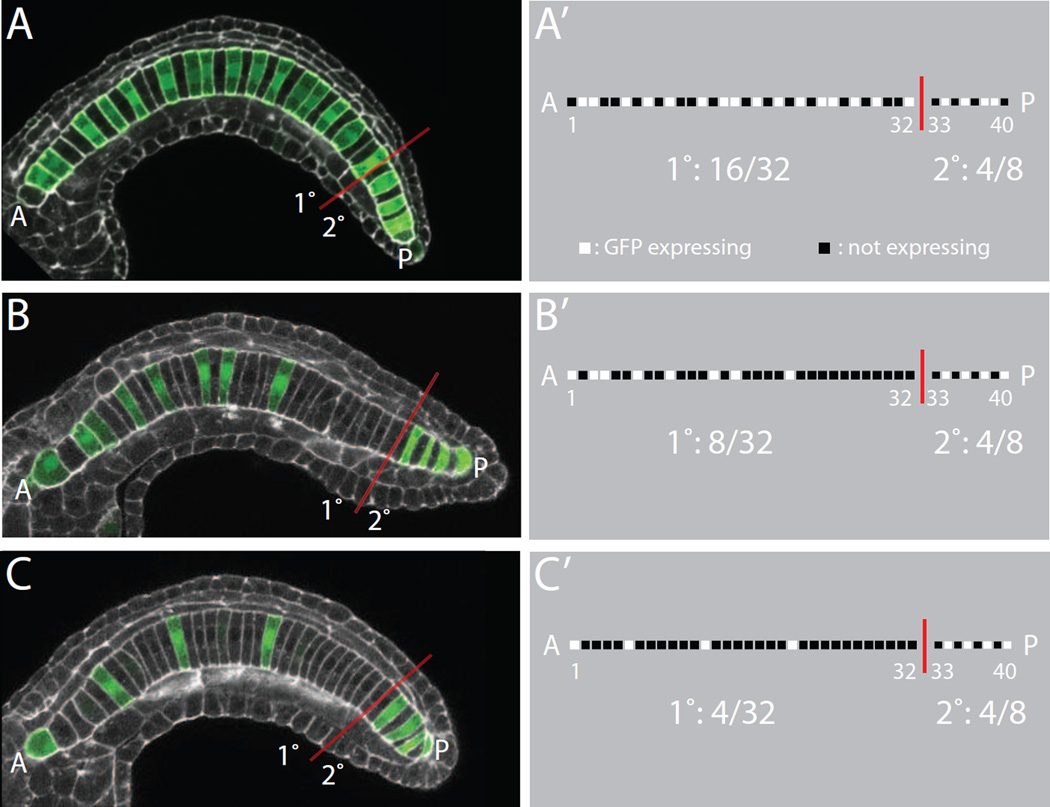
Figure 1. Quantifying mosaic transgene expression patterns.

A,B,C) Confocal images of different mosaic expression patterns of an electroporated Bra>GFP expression plasmid in Ciona embryos (green). Phallacidin staining of the actin cytoskeleton is shown in white. The anterior tip of the intercalated notochord is to the left and indicated with an ‘A’. The posterior tip of the intercalated is to the right and indicated with a ‘P’. The boundary between the primary and secondary notochord lineages between cell 32 and 33 is indicated with a red line. A’,B’,C’) Schematic representation of the expression patterns seen in A, B and C. Each notochord cell is scored as being expressing or not expressing. This is represented as a binary string for each embryo. All three embryos have 4 of the 8 secondary notochord cells expressing GFP. The embryo in A,A’ shows transgene expression in 16 of the 32 primary notochord cells, whereas the embryo in B,B’ has only 8 expressing primary notochord cells and the embryo in C,C’ has only 4 expressing primary notochord cells.

16-cell clones

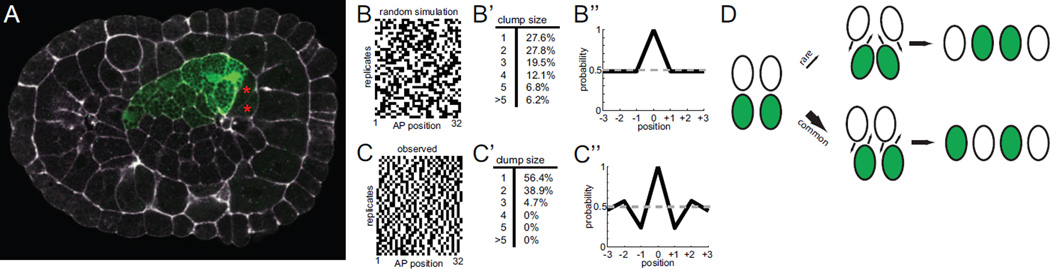
Embryos with 16 labeled cells in the primary notochord typically reflect the entire left half or right half of the primary notochord primordium being genetically labeled (Fig. 2A). We imaged 39 examples of this class of embryo, and also ran simulations of what would be expected if intercalation were completely random. The simulated data is shown in Fig. 2B as binary strings with cell position from anterior to posterior indicated along the X axis and different simulated embryos along the Y axis. The experimental data is shown in Fig. 2C. Visual comparison shows that the observed and simulated data are very different. The experimentally observed distributions of labeled cell positions appear more dispersed than would be predicted if the ordering of notochord cells into a single-file column was truly random. To confirm this, we quantified the size distributions of groups of labeled cells. In the randomly simulated data it is common to see labeled cells as singletons or in clumps of 1–5 cells (Fig. 2B’). In the experimental data, however, we found most labeled cells existed as singletons or in clumps of 2 (Fig 2C’). Clumps of 3 were rare and we observed no clumps of 4 or more. We also quantified these patterns of dispersal by correlating the GFP expression status of particular cells with that of their neighbors at varying distances. In the randomly simulated data, if one particular cell is expressing GFP then all of the other cells have an equal 15/31 (~0.48) probability of also expressing GFP (Fig. 2B’’). In the experimental data, however, we found that the two cells immediately flanking a labeled cell were much less likely to also be labeled, whereas the next closest cells were more likely to be labeled (Fig 2C’’). This pattern of repeated anticorrelation and correlation decays over several cell diameters.

Figure 2. Analysis of primary 16-cell clones.

A) 16-cell primary clone at the onset of mediolateral intercalation showing that the entire right side of the primary notochord primordium is labeled. Not all 16 cells are visible in this focal plane. The right secondary notochord cells have not yet undergone their final division and are marked with red asterisks. Bra>GFP is shown in green and phallacidin staining in white. B) Simulated 16-cell mosaic expression patterns under the hypothesis that notochord intercalation is completely random. C) Mosaic expression patterns for 39 different embryos that showed expression in 16/32 primary notochord cells. The 39 replicates are shown from top to bottom. The AP axis of the notochord is shown from left to right. B’,C’) Quantification of the clumping of labeled cells into groups of different sizes. In the experimental data, most of the labeled cells are singletons (a single labeled cell flanked by two non-labeled cells) or in clumps of only two labeled cells. B’’,C’’) Correlation analysis. A sliding window approach was used to correlate the GFP positive/negative status of each cell with that of its anterior and posterior neighbors. The X axis indicates the probability that cells at varying distances will have the same GFP expression status as the cell at the middle of the window. D) Cartoon diagram indicating two major classes of cell intercalation event. Two cells from one side of the embryo can intercalate between two cells from the other side of the embryo (top). Alternatively, a single cell from one side of the embryo can intercalate between two cells from the other side of the embryo (bottom). The clump size analysis and correlation analysis suggest that the latter possibility is most common.

These results indicate that while intercalation is not a completely stereotyped process, it is also not a completely random process. It instead shows a characteristic signature expected of a tissue that is converging and extending by the process of mediolateral intercalation. In particular, it shows that labeled cells are consistently dispersed by unlabeled cells intercalating between them (and vice-versa). The correlation analysis indicates that intercalation is quite predictable over short spatial scales, with one labeled cell typically intercalating between two unlabeled cells or vice-versa (Fig. 2D). A less frequent event would be for two labeled cells to intercalate between two unlabeled cells or vice versa, which explains the decay in the autocorrelation function at increasing spatial scales. The scale over which this autocorrelation persists/decays is biologically meaningful, and indicates the distance over which the intercalatory behaviors of individual cells influence the behaviors of their neighbors.

8-cell clones

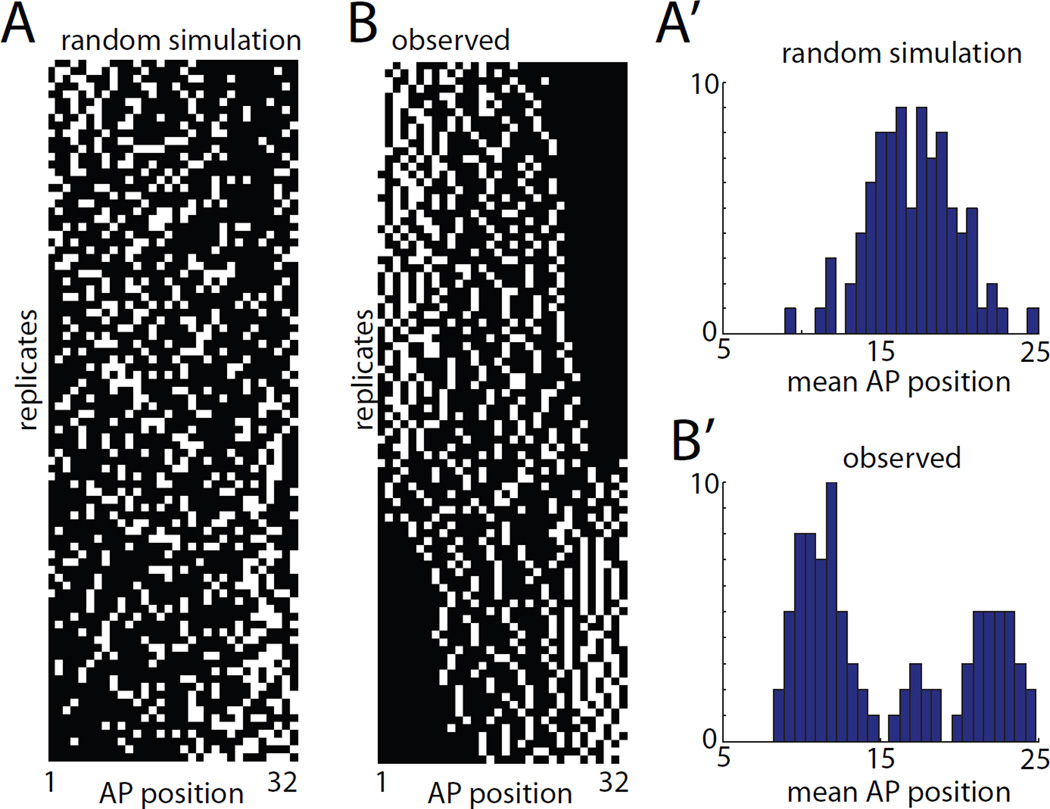
Nishida labeled blastomeres A7.3 and A7.7 in Halocynthia and found that the resulting 8-cell clones were broadly and seemingly randomly distributed among the anterior 32 notochord cells (Nishida, 1987). Our genetic labeling strategy made it feasible to analyze a much larger number of embryos with labeled 8-cell clones than in these previous studies using single-blastomere microinjection of tracer substances. If A7.3 and A7.7 are fully equivalent in the AP positions to which they contribute then we would expect a broad unimodal distribution of mean AP position. This can be seen for simulated data in Fig. 3A,A’. Instead, we observed a distinctly trimodal population in the ninety 8-cell clones we imaged, with two major peaks and an intermediate minor peak (Fig. 3B,B’). The simplest explanation for this result is that the descendants of A7.3 and A7.7 are differentially distributed along the AP axis and that the small intermediate group consists not of true 8-cell clones but instead of double 4-cell clones from these two sublineages.

Figure 3. Analysis of primary 8-cell clones.

A) 8-cell mosaic expression patterns simulated under the hypothesis that notochord intercalation is completely random. B) Experimentally observed mosaic expression patterns in 90 embryos expressing GFP in 8/32 primary notochord cells. Different replicates are ordered from top to bottom by mean AP position. The AP axis of the notochord is shown from left to right. A’,B’) Histograms of mean AP position for the 8 labeled cells from the randomly simulated (A’) and experimentally observed (B’) data. The randomly simulated data is unimodal, whereas the experimentally observed data shows two large peaks and a smaller central peak.

4-cell clones

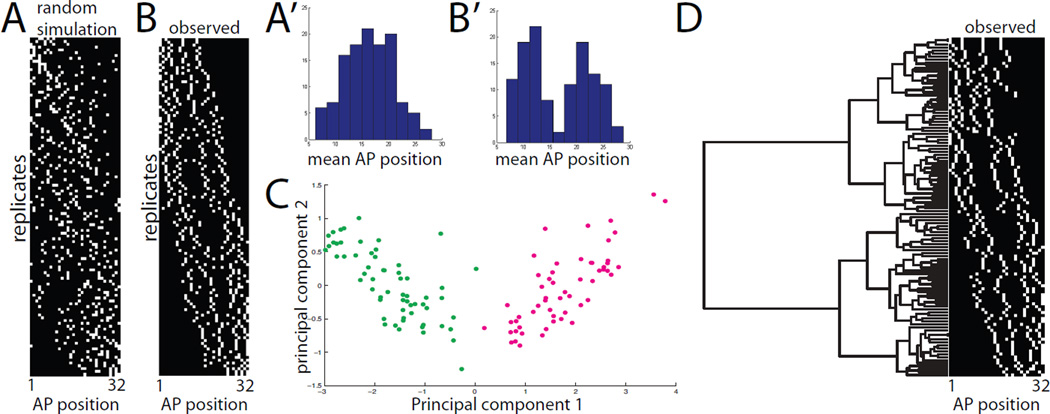
We imaged 120 4-cell clones and compared our experimental results to data simulated under the assumption that intercalation is completely random (Fig. 4A,B). We found that the resulting distribution of mean AP positions was distinctly bimodal and that the minor intermediate peak seen in the 8-cell clones was absent (Fig. 4B’). This supports the conclusion that the smaller intermediate peak did not represent single clonal events. We seldom observed embryos with only two expressing notochord cells, so we are confident that the 4-cell clones almost always represent single clonal events.

Figure 4. Analysis of primary 4-cell clones.

A) 4-cell mosaic expression patterns simulated under the hypothesis that notochord intercalation is completely random. B) Experimentally observed mosaic expression patterns in 120 embryos expressing GFP in 4/32 primary notochord cells. Different replicates are ordered from top to bottom based on mean AP position. The AP axis of the notochord is shown from left to right. A’,B’) Histograms of mean AP position for the 4 labeled cells from the randomly simulated (A’) and experimentally observed (B’) data. The randomly simulated data is unimodal, whereas the experimentally observed data is bimodal. C) Principal components analysis of the 120 experimentally observed 4-cell clones. The AP indices of the first, second, third and fourth cells in each 4-cell clone were used as 4 dimensions for PCA. The first two principal components were found to account for 98% of the sample variance. Two very distinct populations are obvious in the plot of PC1 versus PC2, but neither is obviously resolved into two subpopulations. D) Clustering analysis of experimentally observed primary 4-cell clones. The AP indices of the first, second, third and fourth cells in each clone were used as 4 dimensions for hierarchical UPGMA clustering using standardized Euclidean distances. Two deep branches are seen at the base of the tree corresponding to the two distinct classes of clone. Subsequent branching might represent differences based on cell lineage but might also represent different developmental possibilities.

While the distribution of these 4-cell clones again supported the idea that A7.3 and A7.7 contribute differentially along the notochord’s AP axis, the distribution was not obviously tetramodal, suggesting that A8.6 and A8.5, and also A8.14 and A8.13, might be largely equivalent. We used Principal Components Analysis (Hotelling, 1933; Pearson, 1901) to determine whether further subpopulations might be revealed in a more sophisticated multidimensional analysis. In principal component space we again saw only two clearly distinct populations (Fig. 4C). This suggests that the AP distribution of A8.6 and A8.5 descendants overlap extensively, as do A8.14 and A8.13. It does not exclude the possibility, however, that there may be slight differences in their AP distributions, as suggested by the elongation and distinct orientations of these populations in the principal component space. We also performed a UPGMA hierarchical clustering analysis (Sokal and Michener, 1958) that again revealed two particularly distinct clusters (Fig. 4D).

Early clonal analysis

Our overall strategy of fate mapping by mosaic electroporation can also be used before the notochord has intercalated into a single file column (Fig. 5A–F). At the onset of gastrulation the primary notochord lineage consists of an arc of 8 cells (Fig. 5E). It divides once during gastrulation to give rise to a double arc of 16 cells. Late gastrulation and early neurulation overlap somewhat in Ciona, and the primary notochord cells divide a final time during this time period to form a primordium in the approximate shape of a disk (Fig. 5F). We again electroporated low doses of Bra>GFP but fixed embryos at this early unintercalated disk stage and then imaged embryos with 4 expressing cells in the primary lineage.

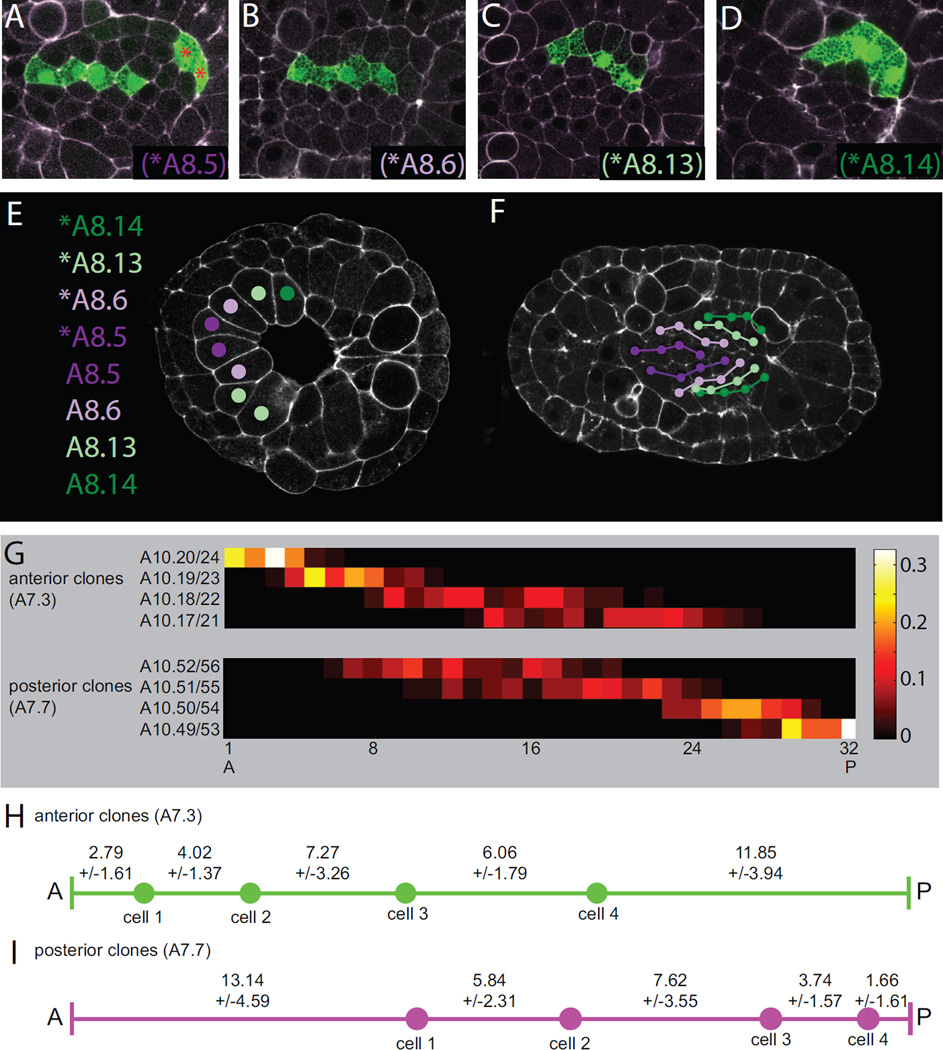
Figure 5. Early clonal analysis and cell AP distributions as a function of lineage.

A,B,C,D) 4 distinct classes of 4-cell primary clone were evident when examined after the final cell division in the primary notochord lineage but shortly before the onset of intercalation. These early 4-cell clones formed distinct columns along the AP axis. Based on their mediolateral positions, these could be identified as being derived from A) *A8.5, B) *A8.6, C) *A8.13 or D) *A8.14. E) The primary notochord lineage is derived from an arc of 8 cells at the onset of gastrulation consisting of the left and right blastomere pairs for A8.5, A8.6, A8.13 and A8.14. F) Cell lineage relationships for all 32 primary notochord cells at the onset of intercalation as based on the early fate mapping shown in A–D. G) Heat maps showing the AP distributions of the first, second, third and fourth cells in both the anterior and posterior subpopulations of primary 4-cell clones. The anterior population is inferred to be derived from A8.5 and A8.6, and the identities of the first, second, third and fourth members of each clone are indicated within two cell equivalence groups. The posterior population is inferred to be derived from A8.13 and A8.14, and two cell equivalence groups are labeled accordingly. The color map indicates the probabilities for each equivalence group that they will contribute to each position along the AP axis. H,I) Schematic representations of the mean spacing between the front of the notochord and the first labeled cell, between the first and second labeled cells, between the second and third labeled cells, between the third and fourth labeled cells, and between the fourth labeled cell and the posterior end of the primary notochord. H) shows the anterior subpopulation of primary 4-cell clones. I) shows the posterior subpopulation of 4-cell clones.

We found that these early 4-cell clones consistently formed contiguous strings stretched out along the AP axis (Fig. 5A–D). This indicates that these divisions are all oriented AP, or at least consistently resolve to give a clearly anterior and clearly posterior daughter. We were able to identify distinct mediolateral positions for these strings that clearly correspond to A8.5 (Fig. 5A), A8.6 (Fig. 5B), A8.13 (Fig. 5C) and A8.14 (Fig. 5D). Development to this point is sufficiently stereotyped that we were able to map the clonal relationships from many labeled embryos onto a single representative embryo (Fig. 5F).

We found that the descendants of A7.3, which are more medial in the arc of notochord cells at early gastrula stage, are consistently more anterior than the descendants of A7.7, which were originally more lateral (purple vs. green in Fig. 5F). This reflects the more lateral cells being displaced to the posterior by the closure of the blastopore. We conclude that A7.3 gives rise to the ‘anterior’ class of clones whereas A7.7 gives rise to the ‘posterior’ clones.

Fine-scale mapping

If the primary notochord cells divided mediolaterally then their order in the intercalated notochord would be somewhat arbitrary, because it would be random whether a given cell intercalates in front of or behind its sibling neighbor. As the primary notochord divisions are all oriented AP, however, sibling cells will instead be separated by intercalation events but their AP order will be preserved. This allows relatively precise identities to be assigned to individual cells in 4-cell clones, limited only by the equivalent behaviors of A8.6 and A8.5, and A8.14 and A8.13. For example, the anteriormost cell in an ‘anterior’ 4-cell clone must be either A10.20 or A10.24. This allows the AP distributions of individual notochord cells to be mapped within two cell equivalence groups (Fig. 5G). For the anterior class of clone (A7.3 derived), the anteriormost cell is almost always found in the first 4 cells of the notochord. The other three cells in the clone occupy progressively more posterior and broadly distributed positions along the AP axis. For the posterior class of clone (A7.7 derived) it is the most posterior cell that is tightly distributed at the posterior end of the primary notochord, and its more anterior siblings/cousins occupy progressively more anterior and broadly distributed positions. These distributions fit with what is known about the temporal progression of cell intercalation, which proceeds from the ends to the middle of the notochord (Veeman and Smith, 2013).

Because the 4-cell clones are initially contiguous along the AP axis, the spacing between these labeled cells in the intercalated notochord indicates how many other cells have intercalated between them. Similarly, the spacing between the front of the notochord and the first cell in an anterior 4 cell clone indicates how many cells intercalated in front of that cell. The position of the posterior-most cell in a posterior 4-cell clone reflects the number of primary cells that intercalated behind it. We find that cells at the front and back of the primary notochord consistently have a smaller number of cells intercalate in front or back of them than cells in the middle of the primary notochord (Fig. 5H,I). This likely reflects these cells having fewer medial and lateral neighbors and consequently being quicker to complete intercalation than cells in the middle of the notochord primordium.

Secondary notochord intercalation is highly stereotyped

We also imaged a large number of embryos with mosaic expression in the eight cells of the secondary notochord lineage. We never saw any embryos with 2 or 6 labeled cells in the secondary notochord, but embryos with 4 labeled cells were common. These are conceptually similar to the 16-cell primary clones in that they reflect the entire left or right half of the lineage being labeled. Unlike the primary lineage, where there are 6.01×10⁸ ways that 16 labeled cells can be distributed in a string of 32 cells, there are only 70 ways that 4 labeled cells can be distributed in a string of 8. If intercalation is a random process, those possible arrangements would all be equally likely. We imaged 152 4-cell secondary clones and found that many of these possible arrangements were never observed whereas others were greatly overrepresented (Fig. 6A).

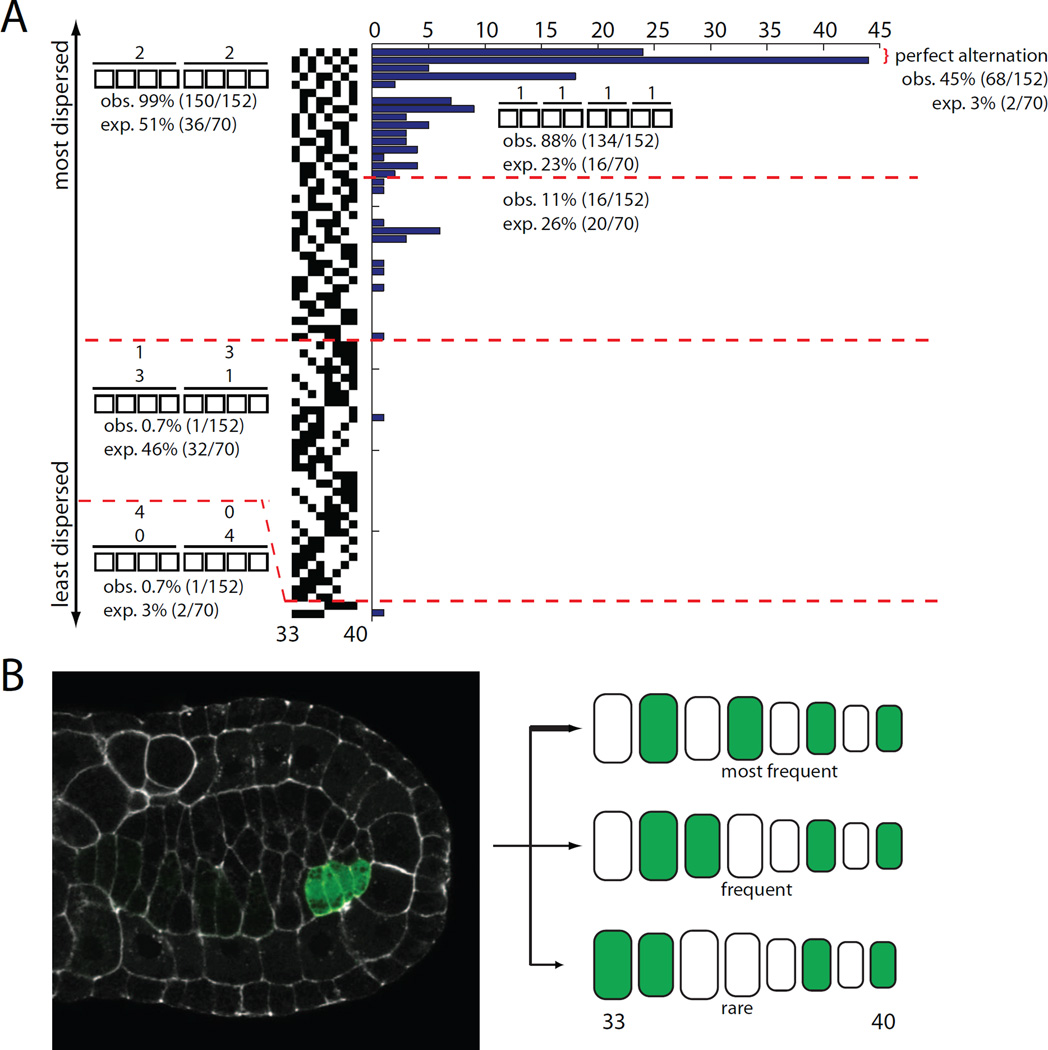
Figure 6. Analysis of secondary lineage 4-cell clones.

A) There are seventy different possible arrangements of 4 labeled cells in 8. They are presented here ordered from most dispersed (perfect alternation between labeled and unlabeled cells) at the top to least dispersed (4 labeled cells next to 4 unlabeled cells) at the bottom. If intercalation is completely random, then all 70 of these arrangements should be equally likely. The histogram indicates how often these different arrangements of labeled cells were actually observed among the 152 secondary 4-cell clones we imaged. B) 4-cell secondary clone on the left side of the embryo. The secondary lineage is slower to undergo the final division than the primary lineage, so there has already been some intercalation in the primary lineage. The cartoon diagram indicates the relative frequency of different patterns of intercalation detected.

In particular, we found that 98.7% of secondary 4-cell clones had two labeled cells in the anterior half of the secondary notochord (cells 33–36) and two in the posterior half (cells 37–40). 88.2% had one labeled cell in positions 33–34, another in positions 35–36, another in positions 37–38 and another in positions 39–40. Furthermore, 44.8% of the secondary 4-cell clones alternated perfectly between labeled and unlabeled cells, which is far more than the 2.9% that would be predicted if intercalation were random.

The secondary notochord is derived from the left and right B8.6 blastomeres, which each divide twice to give rise to a total of 8 cells. The simplest explanation for the observed patterns of intercalation is that intercalation in this lineage must be quite stereotyped, with the anterior descendants at each division consistently remaining anterior of both their posterior siblings and the contralateral equivalents of those posterior siblings (Fig. 6B). Even the intercalation of left side and right side cell pairs is not completely random, as there is a strong preference for cells to cleanly alternate.

Conclusions

Fate maps are a unifying concept in developmental biology that provide a necessary framework for studying the mechanisms of patterning and morphogenesis. There are good fate maps available covering aspects of development in many model organisms, but these fate maps frequently lack single cell resolution. Fate maps with single cell resolution describe cell lineages and thus address a much broader range of questions than coarser fate maps. Fate maps with single cell resolution have been elucidated for C. elegans (Sulston et al., 1983) and the early stages of some other organisms with essentially invariant development, but are only beginning to be developed for organisms with non-invariant development. One of the main arguments for building these maps is that they may reveal functionally important patterns of cell behavior that are not apparent on a coarser scale.

In the present study, we have shown that fate maps of Ciona notochord intercalation analyzed with single cell resolution do indeed reveal unexpected patterns of cell behavior. Cells from the left and right sides of the embryo do not intercalate in a perfectly stereotyped alternating pattern, but their behavior is far from random. Intercalation is found to be highly dispersive, and patterns of intercalation are shown to be quite predictable over short spatial scales with distinct patterns of correlation and anticorrelation at varying distances. Descendants of A7.3 and A7.7 are not randomly distributed in the primary notochord but instead contribute preferentially to the anterior and posterior respectively. There is extensive overlap between these fates however, unlike the secondary notochord lineage which contributes exclusively to the posteriormost eight cells. For both the A7.3 and A7.7 sublineages, the most anterior and posterior cells in the early intercalating primordium are constrained to a narrower range of AP positions than the more central cells. Intercalation in the secondary lineage is particularly constrained to a narrow set of preferred patterns. Many of these details can potentially be explained by the geometry of the early notochord primordium and the mechanics of intercalation.

This quantitative analysis of intercalation patterns raises several interesting questions about the molecular mechanisms of intercalation. The correlation analysis on 16-cell clones indicates that intercalation is not an independent event for each cell. Instead, there is a gradually decaying zone of influence within which the intercalatory behaviors of one cell influence the behaviors of its neighbors (and vice-versa). The nature of this cell-cell influence is not clear. Is it purely mechanical, with the movements of one cell physical displacing its neighbors, or does it involve cell-cell signaling mechanisms? It is intriguing to speculate that there might be mutants or other perturbations in which the notochord is able to intercalate into a single-file column but where the statistical mapping between cell positions before and after intercalation is altered.

Another insight from this study is that there are stark differences in intercalatory behavior between the primary and secondary notochord lineages. In the primary lineage, there is a rough mapping between AP position at the start and end of intercalation, especially for the most anterior and posterior cells, but all cells show considerable variation within a range of typical AP positions. In the secondary notochord lineage, the patterns of intercalation are far more stereotyped. Does this reflect differences in cell division patterns and tissue architecture between primary and secondary notochord cells, or are the molecular mechanisms of intercalation fundamentally different between these two lineages? Primary and secondary notochord cells show differences in gene expression (Reeves et al., 2014; Tanaka et al., 1996) and have different phenotypes in response to mutation of the planar cell polarity gene prickle (Jiang et al., 2005), but this is the first demonstration of fundamentally different behaviors. The penultimate cell division in the secondary lineage has been shown to be highly asymmetric (Veeman and Smith, 2013), and we speculate that the stereotyped nature of intercalation in the secondary notochord may act to ensure a stereotyped progression of cell volumes to help control the taper of the posterior notochord tip.

The observation of distinct cell behaviors between the primary and secondary notochord lineages is also relevant to the previous observation that these lineages do not seem to mix (Nishida, 1987). We only rarely saw evidence for mixing between primary and secondary notochord cells, and this was usually in the context of embryos with minor defects in intercalation. The functional basis for this compartmentalization remains unclear. The secondary cells on average complete intercalation slightly earlier than their close primary neighbors (Veeman and Smith, 2013) but not to the extent that would be expected to prevent cell mixing. The secondary lineage is somewhat slower to undergo the final cell division, but both primary and secondary notochord cells engage in active cell intercalation during a largely overlapping time window. A potential architectural difference is that the secondary cells are the only notochord cells posterior to the closed blastopore (not shown), though it is not clear how that might act to maintain a boundary. Alternatively, distinct mechanisms of intercalation in the primary and secondary lineages might inherently prevent cell mixing.

Our strategy of fate mapping by mosaic expression of an electroporated transgene has the strength of allowing large numbers of labeled clones to be analyzed. Distinct clusters in the data reflect two potential causes. One possibility is that they result from the labeling of distinct blastomeres and thus reflect cell lineage. An alternate possibility is that they may reflect discrete developmental trajectories that may not directly correlate with lineage. For the ‘anterior’ and ‘posterior’ classes of 8 and 4-cell clone, there is strong evidence that these reflect cell lineage, because our early fate mapping experiments clearly showed that the descendants of A7.3 are more anterior than the descendants of A7.7 in a way that closely matched the AP distributions of the two classes in the intercalated notochord.

There are 4 blastomere pairs that could be labeled, however, to give rise to 4-cell clones in the primary notochord, indicating that there could be as many as 4 lineage-based clusters within that data set. Only two clusters are immediately apparent, and although various methods can be used to partition these clusters further (K-means clustering [not shown], Gaussian mixture modeling [not shown], PCA [Fig. 4C], UPGMA clustering [Fig. 4D]) there is no strong support to infer that these partitions reflect cell lineages. One possibility is that the descendants of A8.6 vs A8.5 and A8.14 vs A8.13 are entirely equivalent in terms of their AP positions in the intercalated notochord. Another possibility is that there are modest differences between these blastomeres that would be evident with a larger sample size. It is unlikely that there are dramatic differences between these sibling blastomere pairs, because that would have been evident with our current sample size.

An interesting possibility is that trends and patterns in lineage tracing experiments may not always reflect cell lineages but may instead reflect different discrete or continuous developmental trajectories. We note that the AP positions of the cells in 4-cell clones are quite correlated with one another, suggesting that these groupings might initially move together during the early stages of intercalation. The extent to which early intercalation events influence or constrain subsequent cell behaviors remains to be determined.

With the exception of completely invariant species, development in most organisms has both stereotyped aspects and stochastic aspects. It is easy to conceive of there being a continuum of possibilities from completely stereotyped to heavily stochastic, but in the absence of fate mapping with single cell resolution, it is not known where most developing tissues lie along this spectrum. Here we used genetic fate mapping methods to show that Ciona notochord intercalation is not completely stereotyped but is far more predictable than previously believed. The advantage of genetic labeling is that large numbers of labeled clones can be generated, allowing for the robust assessment of embryo to embryo variability.

An alternate strategy for fate mapping with single cell resolution is to directly image the divisions and behaviors of the relevant cells by in toto timelapse imaging. Ciona is too opaque for in toto live imaging of early notochord morphogenesis, but this could potentially be done in related ascidians with more transparent embryos such as Phallusia mammilatta or Ascidiella aspersa (McDougall et al., 2014; Robin et al., 2011). It is important to note, however, that these direct imaging approaches are technically challenging and very difficult to scale up to the high-throughput analysis of many embryos. These methods will be very valuable for looking at cell-cell interactions during development and studying the developmental histories of individual cells, but the small number of embryos that will be feasible to analyze in this way will make it difficult to get good statistics on embryo-embryo variability. In this respect, the endpoint analysis of genetically-labeled cell clones is more amenable, as shown here, to the high throughput needed to determine the balance between stochasticity and stereotypy in developing tissues. The Ciona notochord is particularly powerful in this respect because of the ability to unambiguously define cell position within the 40 cells of the intercalated notochord and the ability to identify cells by lineage in 4-cell clones within narrow equivalence groups.

We developed a new Ciona fate mapping method based on mosaic transgene expression.

This was used to extensively quantify the patterns of notochord cell intercalation.

Intercalation is not invariant but is far more stereotyped than previously believed.

Navigation of individual notochord cells is strongly influenced by neighbors.

Distinct cell behaviors are seen between the 1° and 2° notochord lineages.