Abstract
The broad class of tasks in genetics and epigenetics can be reduced to the study of various features that are distributed over the genome (genome tracks). The rapid and efficient processing of the huge amount of data stored in the genome-scale databases cannot be achieved without the software packages based on the analytical criteria. However, strong inhomogeneity of genome tracks hampers the development of relevant statistics. We developed the criteria for the assessment of genome track inhomogeneity and correlations between two genome tracks. We also developed a software package, Genome Track Analyzer, based on this theory. The theory and software were tested on simulated data and were applied to the study of correlations between CpG islands and transcription start sites in the Homo sapiens genome, between profiles of protein-binding sites in chromosomes of Drosophila melanogaster, and between DNA double-strand breaks and histone marks in the H. sapiens genome. Significant correlations between transcription start sites on the forward and the reverse strands were observed in genomes of D. melanogaster, Caenorhabditis elegans, Mus musculus, H. sapiens, and Danio rerio. The observed correlations may be related to the regulation of gene expression in eukaryotes. Genome Track Analyzer is freely available at http://ancorr.eimb.ru/.
Keywords: epigenetics, genome tracks, gene expression, transcription start sites, bioinformatic tool
1. Introduction
Data mining of extensive genome-scale databases, such as the Human Epigenome Atlas,1 ENCODE,2 Eukaryotic Promoter Database,3 DBTSS,4 database on CpG islands,5 FANTOM5,6 and many others, cannot be performed without efficient bioinformatic tools. Typically, the researcher is interested in finding correlations between various characteristics distributed over the genome (commonly termed genome tracks). The trends in the close or remote positioning between genomic features may indicate their coordinated action in chromatin packing, recombination, replication, or transcription.7 The features on the genome can be presented as points [e.g. transcription start sites (TSS), DNA double-strand breaks (DSBs), contacts between chromosomes], stretches (transposons, exons and introns, CpG islands), or profiles defined throughout the sites (expression profiles, protein-binding profiles). The stretches can be described in terms of their lengths and positions of some characteristic points (starts/centres/ends). The effects related to these two parameters (overlapping and positioning of stretches) should be studied separately. A part of correlational analysis related to the mutual positioning of starts/centres/ends of stretches can also be reduced to the study of point distributions. The processing of profiles is rather complicated. The processing of data from several experiments and data on the background noise results in identifying the maxima in profiles or the significant regions distributed over the genome. Such maxima and regions can further be treated as points and stretches. Therefore, the general assessment of correlations between features of two types always includes an estimation of the closeness between two point sets.
Despite the seemingly simple formulation, such analysis remains a challenge.8–10 The distribution of distances between consecutive genome track elements proved to be significantly different from that in the reference random model, with the variations in lengths between consecutive genomic elements being much stronger than the approximately homogeneous distribution of randomly positioned elements (see Results). In this sense, the distribution of genome track elements may be called inhomogeneous. The strong inhomogeneity in the distribution of genomic features over the genome, which is inherent to most genetic data, hampers statistical analysis. The application of simple and standardized methods, such as correlation functions, needs the coarse graining of data over 10–100 kb bins11 and smears the resolution of correlations. The proper approach should be based on the relevant statistical criteria. The developed analytical criteria and respective packages ought to be robust against the spatial inhomogeneity of feature distribution.
Among the available packages, the Genomic HyperBrowser12,13 is based on Monte Carlo (MC) simulations for the assessment of the statistical significance of correlations between genome tracks of two types, whereas GenometriCorr14 uses the combination of statistically grounded analytical criteria with a permutation test. The application of simulations generally needs at least two rounds of simulations with an enhanced number of realizations to prove the statistical convergence of a method and is rather time consuming. The simulations are difficult to implement for the study of large genome-scale data sets. In contrast to packages based on the simulations, packages based on the analytical criteria (i.e. on the mathematical expressions derived in advance) do not need a large number of trial realizations for assessment of statistical significance and, therefore, save a lot of computational time.
Primarily, we were interested in the applications of available packages to the particular correlations between DSBs and epigenetic features. We began by testing available packages. In a random independent set of points, the position of each point does not depend on the positions of other random points or on the positions of points of any other (random or not) set. Thus, if at least one of two sets is random and independent, correlations between the two sets should be absent. Testing of both packages, Genomic HyperBrowser and GenometriCorr, for the absence of correlations between a random independent set and a strongly inhomogeneous, non-random genomic set revealed that the packages may indicate artificial correlations in this case. Moreover, as both packages do not suggest a measure for assessment of intrinsic inhomogeneity, the attribution between a random set and a non-random inhomogeneous set is not known a priori. If the true attribution was permuted, the correct assessment of correlations actually failed in both packages. The failure is perhaps related to problems in statistical assessment. Note that our remarks are concerned only with the particular options in the Genomic HyperBrowser and GenometriCorr corresponding to the study of correlations between two point sets. Therefore, we were prompted to develop an original statistical algorithm and package, the Genome Track Analyzer, based on this algorithm. Our package is freely available at http://ancorr.eimb.ru/. The usage of the analytical criteria permits the rapid processing of large-scale data. We tried to formulate our resulting analytical criteria in terms of Gaussian z-statistics that is familiar to most researchers.
The testing of available packages and the study of particular examples proved that the assessment of genome track inhomogeneity and the robustness of the algorithm against inhomogeneity are crucial for the correct analysis of correlations between genome tracks. In this article, we present the quantitative measure for inhomogeneity of genome tracks, robust statistical criteria, and an algorithm for the analysis of correlations between two genome tracks, and we compare the different packages. Furthermore, we demonstrate the application of our package to the study of particular correlations between different genetic and epigenetic features related to the regulation of gene expression in eukaryotes. Among our particular applications, the correlations between CpG islands and TSS are well studied and serve in our work mainly as an additional test, whereas the correlations between TSS on the forward and reverse strands in eukaryotic genomes, as well as the correlations between DSBs and H3K4me3 marks in the Homo sapiens genome, can be considered as original. The correlations between protein-binding profiles for Drosophila melanogaster were likely not studied using the similar statistical methods. They reflect the mutual dependence between features that was established experimentally. The correlations between particular genomic tracks obtained with the Genomic HyperBrowser and GenometriCorr were compared with that obtained using our package.
2. Materials and methods
In this section, we describe the basic theory and the main algorithm. The genome tracks proved to be often inhomogeneous and strongly different from quasi-homogeneous random distributions. We present the quantitative criteria for assessment of genome track inhomogeneity. The algorithm developed in this article is robust against inhomogeneity effects. It is implied that, after preprocessing (Preprocessing of input genetic data), the genetic data will correspond to the set of points that divides the genome (or a genome region) under study into a set of fragments.
2.1. Reference model
The reference model used in this work for the assessment of correlation significance is based on the random division of an interval. Let the interval of length M be divided by N – 1 points into N fragments:
| (1) |
Here, Li is the length of fragment. The respective mean length is given by:
| (2) |
We will use henceforth the normalized lengths:
| (3) |
The probability that the normalized lengths of fragments () exceed some a priori chosen values () is defined by De Finetti distribution:15
| (4) |
where if and if . The analytical derivation of De Finetti distribution and some relevant results can be found in previous publications.16,17 We present below the auxiliary statistical criteria needed for the main algorithm.
The corresponding one-fragment probability is defined as:
| (5) |
and, at the limit of large N, can be approximated by the exponential distribution . The mean minimum length from k fragments and its dispersion are:
| (6) |
The characteristic maximum and minimum values in the complete set of normalized lengths corresponding to random division of an interval can be estimated as:17
| (7) |
If the input data are filtered out with respect to outliers, the potential outliers should be compared with extreme values in the reference model.
2.2. Assessment of genome track inhomogeneity
When studying correlations between genome tracks, it is useful to begin with the preliminary assessment of input data. In our package, the (in)homogeneity of length distribution related to the genome tracks is assessed by two methods. In the first method, the distribution of normalized fragment lengths is compared with one-fragment distribution (5) by the Kolmogorov–Smirnov criterion. In the second method, the homogeneity of length distribution can be assessed with an entropy-like function:17
| (8) |
As can be proved, the function (8) at the restriction (1) attains its minimum equal to zero for l1 = l2 = … = lN = 1. This distribution corresponds to the most homogeneous one. The higher the value of the entropy (8), the stronger the variations in fragment lengths or the higher the inhomogeneity of input data. The mean value and dispersion of structural entropy for the random division of an interval are:
| (9) |
where C = 0.577215… is the Euler constant. The (in)homogeneity of the input data can be estimated in terms of the z-ratio:
| (10) |
The z-ratio (10) obeys approximately Gaussian statistics for the random deviations.
2.3. Ordering of genomic features
Many genetic features are ordered with respect to each other, e.g. 5′-ends of CpG islands often precede the TSS. Such ordering may be related to the coordinated regulation mechanisms. The level of ordering for the pairs of points can be assessed by the criterion:
| (11) |
where P is the total number of pairs and P+ is the number of pairs in which the points of one type precede the points of the other type. At the limit of large P, the deviations (11) also obey Gaussian statistics.
2.4. Preprocessing of input genetic data
2.4.1. Points
If the input genetic data correspond to the particular sites, e.g. sites of DSBs, TSS, etc., they are commonly used without additional preprocessing. If needed, preliminary clustering of points can be performed.
2.4.2. Stretches
The stretches, such as CpG islands, transposons, etc., are replaced by points in the starts/centres/ends of the stretches. The overlapping of stretches is permissible. The mean distance between consecutive reference points should be much longer than the characteristic length of stretches.
2.4.3. Profiles
The profiles characterizing DNA–protein binding are assumed to be defined throughout the sites. The formats of profiles may depend on the database or vary even within a particular database. Commonly, the peaks in profiles should be determined from several experimental sets and from the set with background data. In this case, using the data from several experiments as well as the data on the background noise, the maxima in profiles or the significant regions can be identified over the genome by one of numerous available packages.18–20 Then, such maxima and regions can be processed as points and stretches. We integrated into our server the popular peak-caller MACS2,21 which is convenient for processing ChIP-Seq data. If needed, the researcher can use any other available caller for profile preprocessing. Some profiles are presented in databases in aggregated form comprising several data sets. After identifying peaks with an available caller or when using aggregated profiles, further clustering preprocessing of profiles can be performed. In our package, such clustering preprocessing first filters out the insignificant values lower than a given threshold (in terms of the mean + n SD). Then, the significant values exceeding a given threshold are clustered by the following rule: the consecutive points nearer than a given distance belong to the same cluster. The values of the threshold and the clustering distance are defined by the user. The site corresponding to a cluster is determined by the centre-of-mass rule:
| (12) |
where Hi is the height of profile at the site mi. As the correlations may depend on the clustering distance (Correlations between protein-binding profiles), we recommend using a variable clustering distance that covers a range of characteristic lengths for the problem concerned. The format of input data for points is txt and for stretches is BED/BED6, whereas the profiles can be loaded in SGR, WIG, bigWIG, or bedGraph.
2.5. Algorithm
The analysis shows that most genetic data are strongly inhomogeneous, i.e. the variations in lengths corresponding to genome tracks are stronger than that corresponding to the random division of the genome in the same number of fragments (Assessment of genome track inhomogeneity). Therefore, the criteria and algorithm for assessment of mutual correlations between two genome tracks should be robust against inhomogeneity of corresponding length distributions. The algorithm presented below satisfies this requirement.
It is assumed that the genome strand under study is restricted by terminal points corresponding to one or two genome tracks. Such a definition excludes the possible edge effects. Within such a strand, let the number of points related to the first set be NA (the related points will be denoted for brevity by A), whereas the corresponding number of points for the second set is NB (the related points will be denoted by B). Then, the fractions of points are determined as
| (13) |
The division of points on the same strand into two sets generates a string of points that may formally be presented as a sequence composed of A and B. The neighbouring points of two types can be encountered only within the following sequences: ABA, BAB, AABB, BBAA, and their combinations. Our algorithm relies on the following rules:
The subsequences (A)k or (B)k (k ≥ 3) are discarded, because they cannot be associated with the neighbouring points of the other type. The subsequences AABB or BBAA are also discarded.
This leaves us only two fundamental types of subsequences: ABA and BAB. All other possible sequences under consideration are their combinations. Our algorithm processes the entire sequence of points, splitting it into fundamental subsequences ABA and BAB from left to right. In the process of splitting, consequent fundamental subsequences can have only one common border letter, and they cannot overlap by two or more letters. For example, ABABA is split into ABA and ABA.
In the subsequence BAB, the pair of the nearest neighbours is determined relative to the A point and corresponds to the minimum of two lengths in the combinations BA and AB, whereas in the subsequence ABA the pair of the nearest neighbours is determined relative to the B point and corresponds to the minimum of two lengths in the combinations AB and BA.
Consider, for example, the combination ABA. Let the distance for AB be L1 and the distance for BA be L2. The mean local distance for this combination is:
| (14) |
whereas the respective normalized length between the nearest neighbours (NN) is determined as:
| (15) |
A similar normalization was used also by Favorov et al.14
The correlations between two sets of points are assumed to be absent if at least one of the sets A and B is random and independent. Consider the situation when one of the sets is random (R), whereas the other is a non-random inhomogeneous (I) set. This implies the correspondence A, B ↔ R, I or ABA, BAB ↔ RIR, IRI. It is very important that the statistics turns out to be different for the combinations IRI and RIR. The moments for the normalized lengths in the combinations IRI are defined by Equation (6) for k = N = 2:
| (16) |
The significance of divergence between and the mean normalized length obtained in a particular realization may be assessed by the z-ratio:
| (17) |
which obeys the standard Gaussian statistics N(0, 1) at the limit of large number of combinations KIRI. Let the neighbouring points for a combination RIR be P1 and P2, i.e. RIR can be considered as a part of combination Р1RIRР2. The random points (R) in the combination RIR are homogeneously distributed within intervals Р1I and IР2. The corresponding moments for the normalized lengths (15) in the combinations RIR are calculated as
| (18) |
where θ(x) is the Heaviside step function, θ(x) = 1 if x > 0 and θ(x) = 0 if x < 0. The angular brackets denote the averaging over an ensemble of realizations. The bulky but straightforward computations provide the explicit expressions:
| (19) |
where
| (20) |
If the averaging over the ensemble of realizations is replaced by the mean in a particular realization, (here the dots correspond to the expressions in the right-hand side of Equation (19), and KRIR is the total number of combinations RIR), the variable
| (21) |
obeys Gaussian statistics N(0, cς) with dispersion . Here, the wave over the reference random values corresponds to the replacement in Equation (19) and is the mean normalized length for the combinations RIR. The variable corresponding to the standard Gaussian statistics N(0, 1) can be obtained by the normalization:
| (22) |
The normalization parameter cς depends weakly on the ratio between the numbers of points belonging to random and inhomogeneous sets, NR/NI. The simulations yield the dependence, NR/NI = 0.25; 0.5; 1; 2; 4 and cς = 0.833; 0.837; 0.855; 0.862; 0.881. We used the linear interpolation for cς within this range of ratios NR/NI, while beyond this range the values of cς were taken to be equal to the boundary quantities.
The united Gaussian criterion of proximity between two sets of points is formulated in terms of:
| (23) |
where
| (24) |
| (25) |
and the other nomenclature is as defined in Equations (16)–(22). The correspondence A, B ↔ R, I or ABA, BAB ↔ RIR, IRI is defined by the criterion (10). The set with the higher |zS| is associated with an inhomogeneous set, whereas the set with the lower |zS| is associated with a random set. The criterion (23) remains valid when the inhomogeneous non-random set tends towards a random set. The positive values of zcorr reflect a trend towards shorter distances between point sets relative to the reference model (or correlations), whereas the negative values of zcorr reflect a trend towards longer distances between point sets (or anticorrelations). The ordering between the pairs of the nearest neighbours contributing to sum (24) can be additionally assessed by zP-criterion (11).
The mean fraction of the nearest neighbours between two random sets of points is
| (26) |
In particular, if fA = fB = 0.5, the mean fraction is FNN = 1/6. This fraction is assessed relative to the complete set of points N = NA + NB, i.e. the mean number of pairs of the nearest neighbors is determined as N·FNN. The significant bias against frequency (26) is interesting for assessment of trends in natural selection and large-scale genome organization.
3. Results
3.1. Tests and comparison of different packages
The distribution of genome tracks over the genome is often strongly inhomogeneous. As a typical example, we chose the exons on the forward and reverse strands of 23 human chromosomes (the Y-chromosome was discarded due to insufficient data). Both the Kolmogorov–Smirnov and entropy criteria revealed strong inhomogeneity of this set (Supplementary data S1). The positions of points in any random set are independent of that of exons and should be uncorrelated with them. This test was used to verify the predictions in different packages. For a particular MC realization, the P-value characterizing the significance of correlations between exons and a random set was calculated for each chromosome separately. The correlations were assumed to be significant if P < 0.05. Then, we calculated the observed fraction of events with predicted P < 0.05 per 100 MC realizations (false discovery rate, FDR). As neither Genomic HyperBrowser12,13 nor GeometriCorr14 suggests the criteria for the comparison of the inhomogeneity of two sets, we performed the blind computations in which the attribution of two sets was unknown.
Statistical analysis of correlations between genome tracks with Genomic HyperBrowser was performed to test the hypothesis: point–point located nearby? The correlations in this package were assessed via MC simulations, in which one of the sets was preserved, whereas the other was replaced by MC samples. The maximal number of MC samples was 1,000. To create single-line commands suitable for batch processing, we used Perl scripts written by ourselves. GenometriCorr used the combination of the Kolmogorov–Smirnov test for the normalized lengths together with a permutation test for distances between the points of two sets. In GenometriCorr, the user should manually set the extreme 5′- and 3′-ends of the data range to define the limits of the chromosome region under study for correct correlations. This option is called ‘mapping’ and is turned off by default. For setting mapping, we used an R script written by ourselves. The number of permutations for the assessment of absolute distance P-value was 1,000. For our package, we used the united Gaussian criterion (23) with attribution of sets by the entropy z criterion (10). The results are compared in Table 1.
Table 1.
FDR for the tests on the absence of correlations between exons in human chromosomes and random sets
| Number of points in random sets relative to that of exons | Fraction of events with P < 0.05 per 100 MC realizations |
|||||
|---|---|---|---|---|---|---|
| Exons on forward strand |
Exons on reverse strand |
|||||
| 2-Fold less | Equal, ±10% | 2-Fold more | 2-Fold less | Equal, ±10% | 2-Fold more | |
| Genomic HyperBrowser12,13 | ||||||
| P-value, exon positions preserved, random set MC randomized | 0.253 | 0.253 | 0.247 | 0.249 | 0.250 | 0.248 |
| Adjusted P-value, exon positions preserved, random set MC randomized | 0.227 | 0.228 | 0.227 | 0.227 | 0.231 | 0.228 |
| P-value, random set preserved, exon positions MC randomized | 0.538 | 0.597 | 0.670 | 0.588 | 0.635 | 0.773 |
| Adjusted P-value, random set preserved, exon positions MC randomized | 0.523 | 0.582 | 0.656 | 0.573 | 0.628 | 0.768 |
| GenometriCorr14 | ||||||
| Relative distance KS P-value, exons—reference; random—query | 0.047 | 0.049 | 0.051 | 0.051 | 0.048 | 0.050 |
| Absolute distance P-value, exons—reference; random—query | 0.109 | 0.106 | 0.100 | 0.110 | 0.107 | 0.109 |
| Relative distance KS P-value, random—reference; exons—query | 0.537 | 0.437 | 0.428 | 0.579 | 0.450 | 0.215 |
| Absolute distance P-value, random—reference; exons—query | 0.705 | 0.697 | 0.662 | 0.725 | 0.693 | 0.599 |
| Genome Track Analyzer | ||||||
| United z-criterion, Equation (23) | 0.056 | 0.052 | 0.051 | 0.044 | 0.046 | 0.048 |
All tests were performed with predicted P-values <0.05. The expected mean value and standard deviation for FDR per 100 MC realizations should be 0.05 ± 0.005.
FDR, false discovery rate; MC, Monte Carlo; KS, Kolmogorov–Smirnov test.
The results in Table 1 reveal strong dependence of the FDR on the attribution of sets. If exon positions are preserved, while the random set is MC randomized, the Genomic HyperBrowser provides the FDR about five times higher than the expected rate. GenometriCorr provides the correct rate for the relative distance KS P-value and the correspondence exons—reference, random—query, whereas the usage of the absolute distance P-value provides the FDR ∼2-fold higher than the expected rate at the same correspondence. The permutation in set attribution (i.e. the random set is preserved, while exon positions are MC randomized for the Genomic HyperBrowser and random—reference, exons—query for GenometriCorr) leads to the complete failure of the correlation prediction in both packages. This proves that the preliminary assessment of randomness/inhomogeneity is crucial for the correct statistical predictions.
The computation time needed for one random realization in Genomic HyperBrowser was 1 h 35 min, in GenometriCorr 52 min, and in Genome Track Analyzer 9 s. This time included the duration of loading and processing of input data, direct computations, and processing of output data. In particular, for our package, the time needed for the loading and processing of input data was 8 s, and the processing of output data needed 1 s, whereas the direct computations took only 0.01 s.
3.2. Correlations between CpG islands and TSS
The software package was applied to the analysis of particular genetic problems. The first one concerned the correlations between CpG islands and transcription start sites.5,22–24 The positions and overlapping of CpG islands with TSS affect gene expression in eukaryotes. The data on CpG islands on human chromosomes were taken from URL http://rafalab.jhsph.edu/CGI/,5 whereas the data on TSS were taken from the Eukaryotic Promoter Database (http://epd.vital-it.ch/ H. Sapiens hg19 version EPDnew 003).3 Our method supported the strong correlations between CpG islands and TSS with clear preceding ordering between 5′-ends of CpG islands and TSS. The study also showed overlap between CpG island and the nearest TSS (Supplementary data S2).
3.3. Correlations between TSS on the forward and reverse strands
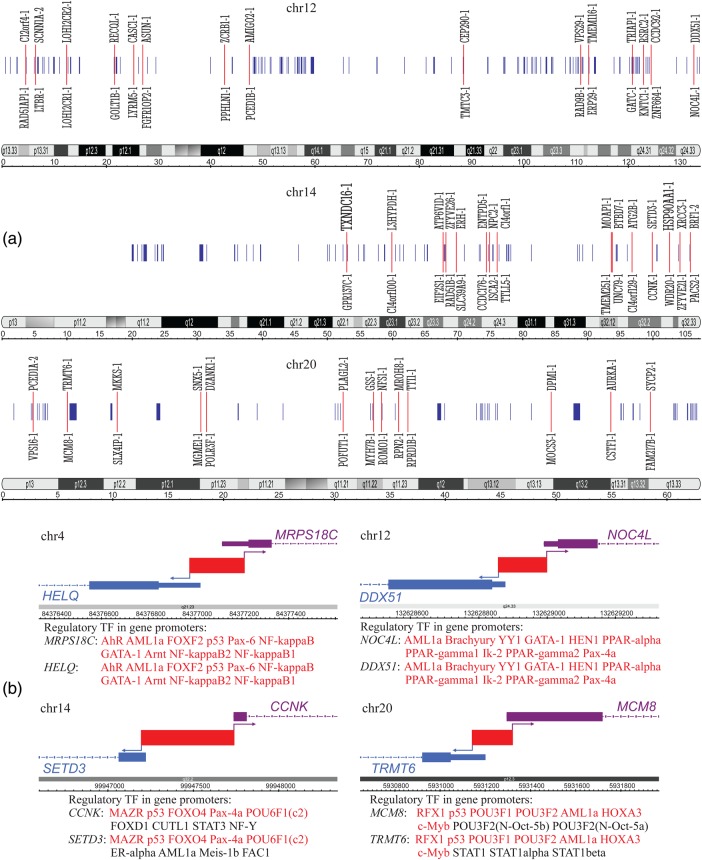
Additionally, we found significant correlations between TSS on the forward and reverse strands of D. melanogaster, Caenorhabditis elegans, Mus musculus, H. sapiens, and Danio rerio (zebrafish) genomes. The positions of TSS on the reverse strand were projected to the forward strand. The detailed results are presented for D. melanogaster and H. sapiens. In Table 2, we included only the chromosomes in which the number of nearest neighbours exceeded 50 to ensure the applicability of Gaussian statistics. These data show clear positional and ordering correlations for the significant fraction of the TSS on two strands. Implying that expression regulation factors are upstream of TSS, the bias in projected TSS on the reverse strand preceding neighbouring TSS on the forward strand indicates that some regulatory elements such as CpG islands, enhancers, silencers, etc., may be common. Such a mode of regulation expression has, in fact, been experimentally established.25–27 The statistical significance of these correlations versus the counterpart random model proves the positive selection of such a mode of expression regulation during evolution. The fraction of the nearest neighbours for TSS turned out to be less than the theoretical prediction for the random sets with the same fractions of points [Equation (26)] for the H. sapiens genome and rather close to the theoretical prediction for the D. melanogaster genome (Table 2). The histograms for the relative and absolute lengths between neighbouring TSS, scattering plot, and the list of the top nearest TSS on the reverse and forward strands are summarized in Supplementary data S3. The histograms for both H. sapiens and D. melanogaster genomes show the length distributions peaked at the small distances between neighboring TSS in accordance with significant positional correlations. The histograms for the absolute lengths revealed a sharp drop at the distances exceeding the characteristic nucleosome length of ∼200 bp. Though the absolute and relative lengths between neighbouring TSS were significantly correlated (Spearman correlation coefficients exceeded 0.7, P < 0.001), only the criteria formulated in terms of relative lengths proved to be robust against the inhomogeneity of genome tracks. The distribution of the nearest neighbouring TSS on the forward and reverse strands across particular chromosomes of the H. sapiens genome is shown in Fig. 1a, which was drawn with the Integrated Genome Browser.28 The distributions of the TSS pairs across all chromosomes of the H. sapiens genome listed in Table 2 can be found in Supplementary data S4.
Table 2.
Correlations between transcription start sites on the forward and reverse strands
| Chromosome | z | P | zP | P | TSS forward | TSS reverse | NN |
|---|---|---|---|---|---|---|---|
| A. Homo sapiens genome | |||||||
| chr1 | 2.59 | 0.010 | 5.93 | <0.001 | 1,226 | 1,156 | 230 |
| chr2 | 3.77 | <0.001 | 4.28 | <0.001 | 817 | 728 | 177 |
| chr3 | 3.01 | 0.003 | 4.60 | <0.001 | 643 | 663 | 133 |
| chr4 | 0.28 | 0.779 | 2.07 | 0.038 | 446 | 471 | 103 |
| chr5 | 4.39 | <0.001 | 4.42 | <0.001 | 570 | 497 | 113 |
| chr6 | 4.34 | <0.001 | 5.22 | <0.001 | 609 | 617 | 132 |
| chr7 | 0.65 | 0.516 | 2.97 | 0.003 | 562 | 509 | 109 |
| chr8 | 2.76 | 0.006 | 4.48 | <0.001 | 397 | 423 | 72 |
| chr9 | 2.97 | 0.003 | 3.39 | <0.001 | 443 | 507 | 95 |
| chr10 | 1.97 | 0.049 | 4.27 | <0.001 | 471 | 475 | 106 |
| chr11 | 3.52 | <0.001 | 5.02 | <0.001 | 696 | 656 | 129 |
| chr12 | 4.21 | <0.001 | 5.36 | <0.001 | 623 | 656 | 147 |
| chr14 | 4.28 | <0.001 | 4.64 | <0.001 | 382 | 363 | 90 |
| chr15 | 1.94 | 0.052 | 5.74 | <0.001 | 338 | 359 | 82 |
| chr16 | 3.73 | <0.001 | 6.30 | <0.001 | 571 | 422 | 113 |
| chr17 | 5.08 | <0.001 | 6.37 | <0.001 | 633 | 725 | 150 |
| chr19 | 4.28 | <0.001 | 7.65 | <0.001 | 823 | 772 | 178 |
| chr20 | 2.57 | 0.010 | 4.06 | <0.001 | 320 | 291 | 70 |
| chr22 | 1.77 | 0.077 | 4.16 | <0.001 | 268 | 269 | 63 |
| chrX | 2.24 | 0.025 | 1.43 | 0.153 | 477 | 453 | 96 |
| B. Drosophila melanogaster genome | |||||||
| chr2L | 11.98 | <0.001 | 15.68 | <0.001 | 1,393 | 1,379 | 454 |
| chr2R | 13.72 | <0.001 | 14.73 | <0.001 | 1,578 | 1,529 | 481 |
| chr3L | 12.57 | <0.001 | 15.59 | <0.001 | 1,528 | 1,570 | 473 |
| chr3R | 14.19 | <0.001 | 16.61 | <0.001 | 1,762 | 1,852 | 583 |
| chrX | 12.42 | <0.001 | 14.08 | <0.001 | 1,176 | 1,198 | 387 |
The positions of TSS on the reverse strand were projected to the forward strand. z and zP are calculated by Equations (23) and (11) and characterize the positional and ordering correlations between TSS, respectively. The 1% significance thresholds for |z| and |zP| in the case of random correlations correspond to 2.58, while 5% significance thresholds correspond to 1.96. The positive values of zP indicate that projected TSS on the reverse strand precede TSS on the forward strand. The corresponding P-values were calculated using Gaussian statistics. The data were filtered by the number of pairs of the nearest neighbours (NN) exceeding 50 to ensure the applicability of Gaussian statistics.
Figure 1.
(a) The distributions of the nearest neighbouring transcription start sites (NN TSS) on the forward and reverse strands across particular chromosomes of the Homo sapiens genome. The cytobands across corresponding chromosomes and relevant length scales are shown below the TSS. The length scale is in megabases. The blue vertical lines correspond to the pairs of NN TSS. The 15 closest pairs on each chromosome are marked by the red lines, and the names of the corresponding NN TSS are indicated. Names shown above the red lines correspond to the TSS on the forward strand, whereas names shown below the red line correspond to the TSS on the reverse strand (names are given according to EPD notation). (b) Particular examples of NN TSS pairs in the H. sapiens genome. The transcriptions factors (TF) participating in the regulation of expression of a particular gene are listed after the name of the gene. The TF that match genes on both strands are marked in red. The data on binding sites for TF associated with genes were taken from http://www.genecards.org.
The analysis of some nearest TSS duplets revealed that they correspond to rather short intergenic regions between pairs of closely located genes that reside on different strands. They may have mutual enhancers or bidirectional promoters, and thus should correspond to genes with coordinated expression. The particular examples are shown in Fig. 1b. Currently, we are analysing these gene pairs to determine the role of this type of genome organization for coordinated regulation of genes in the human genome.
3.4. Correlations between protein-binding profiles
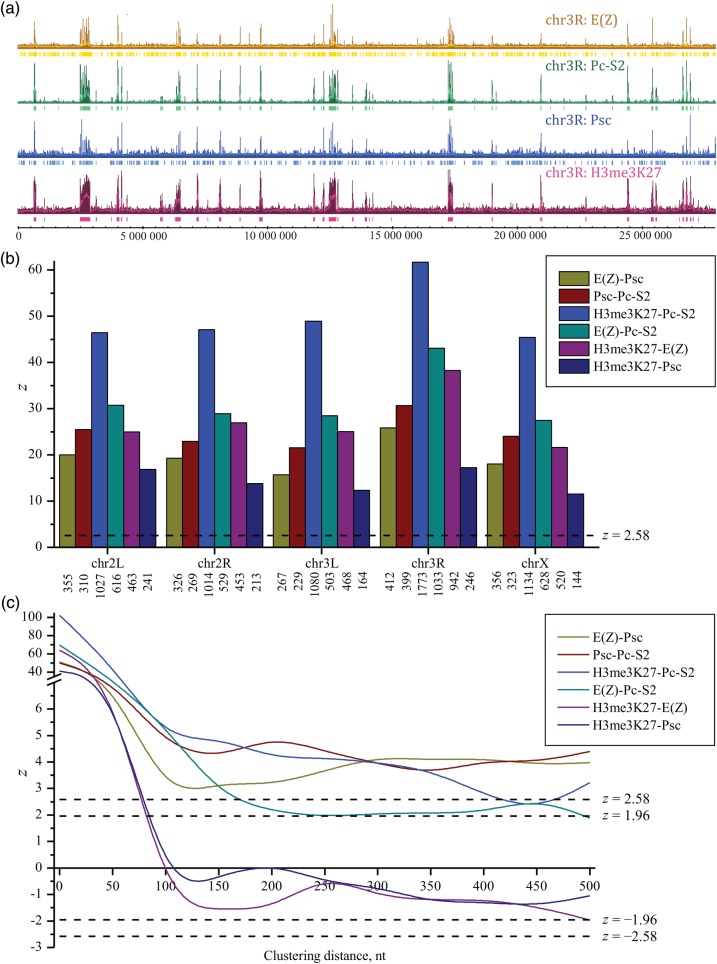
The second problem concerned the relationships between profiles characterizing DNA binding with proteins E(Z), Pc-S2, and Psc, and H3me3K27 marks in the chromosomes of D. melanogaster. E(Z), Pc-S2, and Psc belong to the polycomb group (PcG) of proteins, which are important for maintaining the transcriptional repression of homeotic genes.29–32 The corresponding processed and aggregated profiles were obtained by Schwartz et al.29 and were taken from EMBL ArrayExpress accession E-MEXP-535.33 The profiles were preliminarily filtered by the cut-off threshold mean + 2 SD and clustered with a distance in the range 50–500 nt with steps of 50 nt (Preprocessing of input genetic data). The data before and after preprocessing with a clustering distance of 50 nt are shown in Fig. 2a. The corresponding z-ratios [Equation (23)] indicate strong correlations between binding profiles for the PcG proteins and for H3me3K27 marks (Fig. 2b). The correlations strongly depend on the clustering distance (Fig. 2c and Supplementary data S5). As the characteristic binding region for the PcG proteins is ∼50 nt,34 the clustering distance of 50 nt may be considered as optimal in this example. The cut-off threshold affects the number of nearest neighbours, but it retains the mode of correlations at a given clustering distance. These observations are in accordance with the data on the coordinate action of the E(Z), Pc-S2, and Psc proteins, and the H3me3K27 marks in the silencing mechanisms for D. melanogaster.29,30
Figure 2.
(a) The binding profiles for proteins E(Z), Pc-S2, and Psc, and for H3me3K27 histone marks over chromosome 3R of Drosophila melanogaster. For the study of correlations, these profiles were preliminary filtered by the cut-off threshold mean + 2 SD and clustered with distance of 50 nt [Preprocessing of input genetic data and Equation (12)]. The input data after preprocessing are shown below initial profiles. (b) z-ratios [Equation (23)] characterizing pairwise positional correlations between profiles for proteins E(Z), Pc-S2, and Psc, and for the H3me3K27 mark in the different chromosomes of D. melanogaster. The input data were preprocessed as described above. The numbers below the chromosome nomenclature correspond to that of the nearest neighbours. The horizontal broken lines for z-ratios correspond to 5% (|z| = 1.96) and 1% (|z| = 2.58) significance thresholds for random correlations. (c) Ratios characterizing positional correlations between profiles for proteins E(Z), Pc-S2, and Psc, and for H3me3K27 histone marks in the chromosome 2R of D. melanogaster at the different clustering lengths. The profiles were preliminary filtered by the cut-off threshold mean + 2 SD. The positive values of zcorr reflect a trend towards shorter distances between profiles relative to the reference model (or correlations), whereas the negative values of zcorr reflect a trend towards longer distances between profiles (or anticorrelations).
3.5. Correlations between DSBs and histone marks
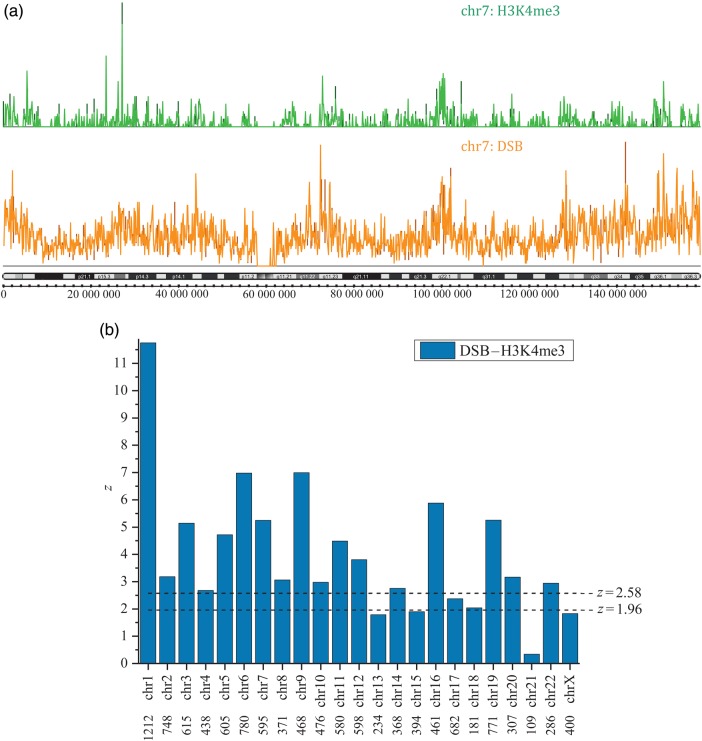
Finally, we studied the relationships between DSBs and histone mark H3K4me3 in human chromosomes. DSBs induced by physical, chemical, or genetic agents provide important information about the large-scale organization of chromatin and may potentially be related to genomic stability, including translocations, deletions, or amplifications.35–37 H3K4me3 is a well-known, promoter-specific histone modification that is associated with transcription and active genes. Recently, it was demonstrated that this epigenetic mark selectively directs global TFIID recruitment to active genes, some of which are p53 targets.38 The data on nucleotide-resolved DSBs were submitted to GEO with accession number GSE53811. DSBs were preliminarily preprocessed: DSBs mapped below 5% and above 95% of coverage were cut-off; the remaining DSBs were clustered within a distance of 1 kb (Preprocessing of input genetic data). Such a clustering distance provides the distribution of lengths between consecutive DSBs, which is similar to that observed in gel electrophoresis.35,36 The profiles for histone marks were taken from ENCODE accession wgEncodeEH000953 in the pre-aligned format BAM and were then processed with MACS2.21 The MACS2 peak-caller was used with the option ‘callpeak’ for identifying significant regions (treated like stretches in our package). Then, the correlations of corresponding midpoints of stretches with DSBs were studied with our package. The summary of correlations is shown in Fig. 3 and reveals clear positional correlations between these features. Such correlations support the hypothesis regarding the relationships between DSBs and coordinated gene expression.35,36
Figure 3.
(a) The distributions of DNA double-strand breaks (DSBs) and H3K4me3 histone marks over human chromosome 7. The distributions of DSBs and histone marks were coarse-grained over bins of 100 kb, i.e. the heights in these distributions correspond to the number of points in the bins of 100 kb. Both sets were preprocessed as described in the main text. The distribution of cytobands across chromosome 7 is shown above the length scale. (b) z-ratios [Equation (23)] characterizing pairwise positional correlations between distributions of DSBs and H3K4me3 in the human chromosomes. The correlations for the Y-chromosome are not shown due to poor statistics. The numbers below the chromosome nomenclature correspond to that of the nearest neighbours. The horizontal broken lines for z-ratios correspond to 5% (z = 1.96) and 1% (z = 2.58) significance thresholds for random correlations.
The correlations between particular genomic tracks in the following sections, Correlations between CpG islands and TSS, Correlations between TSS on the forward and reverse strands, Correlations between protein-binding profiles, and Correlations between DSBs and histone marks, obtained with Genomic HyperBrowser, GenometriCorr, and Genome Track Analyzer are mutually compared in Supplementary data S6. The comparison showed that the detected correlations appeared to be significant in all three packages (with minor divergence depending on the package and method). The significance of correlations in all packages indicates that they are real, non-artificial correlations. Generally, the coincidence of the correlation significance obtained with the different packages may depend on the particular chosen example (see Tests and comparison of different packages).
4. Discussion
Our study proves that the proper treatment of inhomogeneity inherent to genome tracks is essential for the correct assessment of correlations between genome tracks. We tried a series of algorithms, including our variants and those suggested by others,12–14 and found that none of the algorithms that used absolute length scales satisfied the test for the absence of correlations between a random independent set and a strongly inhomogeneous non-random set (Tests and comparison of different packages and Table 1). The choice of the relative lengths with local normalization turned out to be crucial for the absence of correlations between a strongly inhomogeneous set and a random one. The significant inhomogeneity inherent to genome tracks and strong variations in characteristic lengths may be related to the large-scale chromatin organization (see Ref. 17 for discussion and further references).
All z-criteria (10), (11), and (23) used in our package are based on the central limit theorem. The variations in the vicinity |z| ≤ 2.7 proved to be approximately Gaussian for the random sets. The application of Gaussian criteria implies that the number of pairs of nearest neighbours, K, should be sufficiently large. The convergence can be assessed by the parameter . We determined that 50–100 representatives or more are sufficient for Gaussian approximation in the corresponding z-criteria. For the small sets, the statistical scattering becomes large and the deviations from Gaussian statistics may be significant. As the tails of distributions for z-ratios are non-Gaussian, we used the coarse-grained scale for the presentation of significance for output z-values: |z| < 1.8, insignificant; 1.8< |z| <1.96, fuzzy; 1.96< |z| <2.58, significant; and |z| > 2.58, highly significant. In the visual presentation of the software, all grades are marked by different colours.
Our analytical criteria proved to be robust against the inhomogeneous distribution of lengths corresponding to genome tracks, which is typical of genetic problems. The analytical criteria significantly shorten the time of computational analysis and permit the study of larger data sets in comparison with MC simulations (Tests and comparison of different packages). Note that the analysis of large output data arrays needs the application of extreme value statistics for the assessment of their statistical significance. For example, in the case of random correlations, ∼5% of output z-values can exceed the threshold |z| >1.96. Generally, the distribution of the large output array of z-values can be compared with Gaussian distribution by the Kolmogorov–Smirnov criterion.
A similar approach can be applied to the study of distributions of nucleotide content or DNA physico-chemical characteristics over the genome. In the latter case, these parameters should, initially, be coarse-grained over a window of length W. The distribution of parameters over consecutive non-overlapping windows can further be treated in line with profile preprocessing (Preprocessing of input genetic data). If needed, the continuous criteria used in our package can be replaced by their corresponding discrete counterparts.17 In the next step, we will include the more detailed analysis of correlations between stretches that are characterized by both the positions of the stretch centres and the overlap of stretches. To conclude, the Genome Track Analyzer provides an efficient tool for the study of correlations between genome features with useful applications to many genetic problems. The study of correlations between genome tracks may shed light on the intricate regulation networks in the different organisms.
Supplementary data
Supplementary data are available at www.dnaresearch.oxfordjournals.org.
Funding
This work was supported by the Russian Fund of Basic Research (grant number 14-04-01638) and a grant from the Molecular and Cellular Biology Program of the Russian Academy of Sciences.
Supplementary Material
Acknowledgements
The authors are grateful to A. Favorov for helpful communications and are also grateful to D. Fedoseeva and N. Kochanova for discussion on bidirectional transcription.
References
- 1.Bernstein B.E., Stamatoyannopoulos J.A., Costello J.F., et al. The NIH Roadmap Epigenomics Mapping Consortium. Nat. Biotechnol. 2010;28:1045–8. doi: 10.1038/nbt1010-1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Tragante V., Moore J.H., Asselbergs F.W. The ENCODE project and perspectives on pathways. Genet. Epidemiol. 2014;38:275–80. doi: 10.1002/gepi.21802. [DOI] [PubMed] [Google Scholar]
- 3.Dreos R., Ambrosini G., Cavin Perier R., Bucher P. EPD and EPDnew, high-quality promoter resources in the next-generation sequencing era. Nucleic Acids Res. 2013;41:D157–64. doi: 10.1093/nar/gks1233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yamashita R., Sugano S., Suzuki Y., Nakai K. DBTSS: Database of Transcriptional Start Sites progress report in 2012. Nucleic Acids Res. 2012;40:D150–4. doi: 10.1093/nar/gkr1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wu H., Caffo B., Jaffee H.A., Irizarry R.A., Feinberg A.P. Redefining CpG islands using hidden Markov models. Biostatistics. 2010;11:499–514. doi: 10.1093/biostatistics/kxq005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.FANTOM Consortium, R.P., CLST. A promoter-level mammalian expression atlas. Nature. 2014;507:462–70. doi: 10.1038/nature13182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bush W.S., Moore J.H. Chapter 11: genome-wide association studies. PLoS Comput. Biol. 2012;8:e1002822. doi: 10.1371/journal.pcbi.1002822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Daley D.J., Vere-Jones D. An introduction to the theory of point processes. New York: Springer; 2003. [Google Scholar]
- 9.Jacobsen M. Point process theory and applications: marked point and piecewise deterministic processes. Boston, MA: Birkhäuser; 2006. [Google Scholar]
- 10.Bickel P.J., Brown J.B., Huang H., Li Q. An overview of recent developments in genomics and associated statistical methods. Philos. Trans. A Math. Phys. Eng. Sci. 2009;367:4313–37. doi: 10.1098/rsta.2009.0164. [DOI] [PubMed] [Google Scholar]
- 11.Zhang Z.D., Paccanaro A., Fu Y., et al. Statistical analysis of the genomic distribution and correlation of regulatory elements in the ENCODE regions. Genome Res. 2007;17:787–97. doi: 10.1101/gr.5573107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sandve G.K., Gundersen S., Rydbeck H., et al. The Genomic HyperBrowser: inferential genomics at the sequence level. Genome Biol. 2010;11:R121. doi: 10.1186/gb-2010-11-12-r121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sandve G.K., Gundersen S., Johansen M., et al. The Genomic HyperBrowser: an analysis web server for genome-scale data. Nucleic Acids Res. 2013;41:W133–41. doi: 10.1093/nar/gkt342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Favorov A., Mularoni L., Cope L.M., et al. Exploring massive, genome scale datasets with the GenometriCorr package. PLoS Comput. Biol. 2012;8:e1002529. doi: 10.1371/journal.pcbi.1002529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Feller W. An introduction to probability theory and its applications. New York: Wiley; 1967. [Google Scholar]
- 16.Chechetkin V.R. Spectral sum rules and search for periodicities in DNA sequences. Phys. Lett. A. 2011;375:1729–32. [Google Scholar]
- 17.Chechetkin V.R. Statistics of genome architecture. Phys. Lett. A. 2013;377:3312–6. [Google Scholar]
- 18.Pepke S., Wold B., Mortazavi A. Computation for ChIP-seq and RNA-seq studies. Nat. Meth. 2009;6:S22–32. doi: 10.1038/nmeth.1371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wilbanks E.G., Facciotti M.T. Evaluation of algorithm performance in ChIP-seq peak detection. PLoS ONE. 2010;5:e11471. doi: 10.1371/journal.pone.0011471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hower V., Evans S.N., Pachter L. Shape-based peak identification for ChIP-Seq. BMC Bioinformatics. 2011;12:15. doi: 10.1186/1471-2105-12-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhang Y., Liu T., Meyer C.A., et al. Model-based analysis of ChIP-Seq (MACS) Genome Biol. 2008;9:R137. doi: 10.1186/gb-2008-9-9-r137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Illingworth R.S., Bird A.P. CpG islands – ‘a rough guide. FEBS Lett. 2009;583:1713–20. doi: 10.1016/j.febslet.2009.04.012. [DOI] [PubMed] [Google Scholar]
- 23.Bell C.G., Wilson G.A., Butcher L.M., Roos C., Walter L., Beck S. Human-specific CpG ‘beacons’ identify loci associated with human-specific traits and disease. Epigenetics. 2012;7:1188–99. doi: 10.4161/epi.22127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Krinner S., Heitzer A.P., Diermeier S.D., Obermeier I., Langst G., Wagner R. CpG domains downstream of TSSs promote high levels of gene expression. Nucleic Acids Res. 2014;42:3551–64. doi: 10.1093/nar/gkt1358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tchurikov N.A., Kretova O.V., Moiseeva E.D., Sosin D.V. Evidence for RNA synthesis in the intergenic region between enhancer and promoter and its inhibition by insulators in Drosophila melanogaster. Nucleic Acids Res. 2009;37:111–22. doi: 10.1093/nar/gkn926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kim T.K., Hemberg M., Gray J.M., et al. Widespread transcription at neuronal activity-regulated enhancers. Nature. 2010;465:182–7. doi: 10.1038/nature09033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Richard P., Manley J.L. How bidirectional becomes unidirectional. Nat. Struct. Mol. Biol. 2013;20:1022–4. doi: 10.1038/nsmb.2657. [DOI] [PubMed] [Google Scholar]
- 28.Nicol J.W., Helt G.A., Blanchard S.G., Jr, Raja A., Loraine A.E. The Integrated Genome Browser: free software for distribution and exploration of genome-scale datasets. Bioinformatics. 2009;25:2730–1. doi: 10.1093/bioinformatics/btp472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Cao R., Zhang Y. The functions of E(Z)/EZH2-mediated methylation of lysine 27 in histone H3. Curr. Opin. Genet. Dev. 2004;14:155–64. doi: 10.1016/j.gde.2004.02.001. [DOI] [PubMed] [Google Scholar]
- 30.Schwartz Y.B., Kahn T.G., Nix D.A., et al. Genome-wide analysis of polycomb targets in Drosophila melanogaster. Nat. Genet. 2006;38:700–5. doi: 10.1038/ng1817. [DOI] [PubMed] [Google Scholar]
- 31.Kwong C., Adryan B., Bell I., et al. Stability and dynamics of polycomb target sites in Drosophila development. PLoS Genet. 2008;4:e1000178. doi: 10.1371/journal.pgen.1000178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Brown J.L., Kassis J.A. Architectural and functional diversity of polycomb group response elements in Drosophila. Genetics. 2013;195:407–19. doi: 10.1534/genetics.113.153247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Rustici G., Kolesnikov N., Brandizi M., et al. ArrayExpress update – trends in database growth and links to data analysis tools. Nucleic Acids Res. 2013;41:D987–90. doi: 10.1093/nar/gks1174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Schuettengruber B., Oded Elkayam N., Sexton T., et al. Cooperativity, specificity, and evolutionary stability of polycomb targeting in Drosophila. Cell Rep. 2014;9:219–33. doi: 10.1016/j.celrep.2014.08.072. [DOI] [PubMed] [Google Scholar]
- 35.Tchurikov N.A., Kretova O.V., Sosin D.V., Zykov I.A., Zhimulev I.F., Kravatsky Y.V. Genome-wide profiling of forum domains in Drosophila melanogaster. Nucleic Acids Res. 2011;39:3667–85. doi: 10.1093/nar/gkq1353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tchurikov N.A., Kretova O.V., Fedoseeva D.M., et al. DNA double-strand breaks coupled with PARP1 and HNRNPA2B1 binding sites flank coordinately expressed domains in human chromosomes. PLoS Genet. 2013;9:e1003429. doi: 10.1371/journal.pgen.1003429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Crosetto N., Mitra A., Silva M.J., et al. Nucleotide-resolution DNA double-strand break mapping by next-generation sequencing. Nat. Meth. 2013;10:361–5. doi: 10.1038/nmeth.2408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lauberth S.M., Nakayama T., Wu X., et al. H3K4me3 interactions with TAF3 regulate preinitiation complex assembly and selective gene activation. Cell. 2013;152:1021–36. doi: 10.1016/j.cell.2013.01.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.