Protein unfolding rates correlate as strongly as folding rates with native structure

Abstract

Although the folding rates of proteins have been studied extensively, both experimentally and theoretically, and many native state topological parameters have been proposed to correlate with or predict these rates, unfolding rates have received much less attention. Moreover, unfolding rates have generally been thought either to not relate to native topology in the same manner as folding rates, perhaps depending on different topological parameters, or to be more difficult to predict. Using a dataset of 108 proteins including two-state and multistate folders, we find that both unfolding and folding rates correlate strongly, and comparably well, with well-established measures of native topology, the absolute contact order and the long range order, with correlation coefficient values of 0.75 or higher. In addition, compared to folding rates, the absolute values of unfolding rates vary more strongly with native topology, have a larger range of values, and correlate better with thermodynamic stability. Similar trends are observed for subsets of different protein structural classes. Taken together, these results suggest that choosing a scaffold for protein engineering may require a compromise between a simple topology that will fold sufficiently quickly but also unfold quickly, and a complex topology that will unfold slowly and hence have kinetic stability, but fold slowly. These observations, together with the established role of kinetic stability in determining resistance to thermal and chemical denaturation as well as proteases, have important implications for understanding fundamental aspects of protein unfolding and folding and for protein engineering and design.

Introduction

Extensive experimental^1,2 and theoretical^3–5 research has been conducted to understand protein folding rates. In seminal studies, Plaxco et al. found that a simple measure of the topology of the native state, the relative contact order (RCO), correlated well with folding rates for a small set of monomeric proteins that showed two-state behavior.⁶ Later, they revised their conclusions to show that absolute contact order (ACO), which in addition to topology includes effects of protein length, correlated better for a larger dataset including multistate folders.⁷ It has long been noted that folding rates depend on protein length, but the quantitative, physical basis for this dependence remains under investigation^8–13 and additional studies have demonstrated that consideration of both topology and length leads to improved correlations compared to topology alone.^14,15 Here, we use structural complexity as a broad term to encompass the complexity imparted by both the topology and the length of the protein, and rate, when referring to the unfolding and folding rate constants (k_u and k_f, respectively).

The correlation of ACO with folding rates suggests that while the transition state for folding lacks much of the well-defined structure of the native state, it nevertheless has a broadly similar structure and complexity, as has been suggested from theory and simulation^5,15–17 and demonstrated experimentally.¹⁸ Many alternative measures of native state structural complexity have also been found to correlate with folding rates.^19–24 In particular, two measures have emerged as being consistently well correlated: the ACO and the long range order (LRO). LRO was found not only to correlate well overall¹⁹ but also to correlate well across different structural classes of proteins.¹⁴ Recently, the correlation of folding rates with ACO was explicitly derived from theory.²⁵

In contrast, relatively little work on the relationship between unfolding rates and native structure has been reported, with the existing studies suggesting that while native structure should correlate with unfolding,²⁶ the measures of structural complexity that work well for predicting folding do not perform well for unfolding.^27–29 In particular, work by Jung et al. concluded that while structural complexity does correlate with both unfolding and folding rates, the predictive parameters are different.^27,28 Harihar and Selvaraj compared LRO with unfolding rates, finding a moderate correlation overall, but greatly differing correlations for the alpha, beta, and mixed structural classes.²⁹ In these studies, relatively small datasets of ∼ 25 two-state folding proteins were used. In particular, the approach in two later studies was to use the small consensus dataset compiled by Maxwell et al.³⁰ in order to avoid noise in the data resulting from experimental differences.^27,29 However, noise resulting from sequence-specific effects can also be considerable, as noted in studies of homologous proteins.^31–33 Thus, the use of a small dataset for examining a relationship with such considerable noise may be a fraught endeavor. For instance, the original very strong correlation of folding rate with RCO⁶ was later found to be considerably weaker when larger datasets including multistate folders were used.^7,14

Here, in order to clearly identify general relationships between folding/unfolding rates and structural complexity, we have used a relatively large set of kinetic data for monomeric proteins obtained using similar experimental approaches. Proteins with disulfide bonds or large prosthetic groups are excluded because they are known to cause anomalous kinetics. The dataset is largely similar to that of Garbuzynskiy et al., who recently elucidated relationships between protein length, stability, and folding rates.³⁴ Using our dataset of 108 two-state and multistate folders (see Methods, Supporting Information Table SII), we tested various measures of structural complexity, discovering that two commonly used parameters, ACO and LRO, not only correlate strongly with folding rates but also correlate strongly, and equally well, with unfolding rates. Furthermore, the results are very similar for different structural classes of proteins. Importantly, these results address the previously reported apparent differences between the structural determinants of unfolding and folding rates which may have been a consequence of the comparatively smaller datasets that obscured the true relationships. The finding that the same measures of structural complexity are equally predictive of unfolding and folding rates has important implications for fundamental understanding of the process of protein unfolding. It also suggests that for the protein engineer, a key choice needs to be made when selecting a scaffold for design to achieve the desired balance between the typically desirable properties of fast folding and slow unfolding.

Results and Discussion

To identify general trends with increased confidence, we used a previously established large dataset^30,34 augmented with additional proteins (see Methods). We analyzed this dataset using a range of measures of structural complexity found previously to be correlated with folding rates (Supporting Information Table SI). Two well-established parameters, ACO and LRO (see Methods), exhibited superior correlations, which are described in detail later. We note that the trends for unfolding rates for the full dataset shown in Figure 1 also hold in general (with some variations in statistical significance) for various subsets of the data (Table I).

Figure 1.

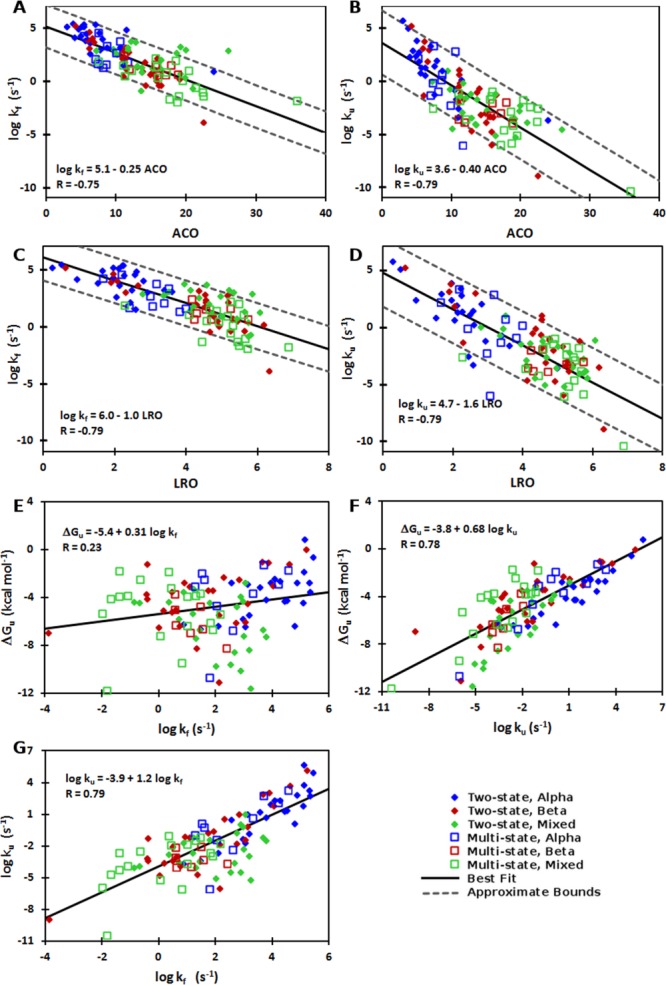
Correlations between structural complexity, folding and unfolding rates, and thermodynamic stability. Correlations are shown between (A) folding rates and ACO, (B) unfolding rates and ACO, (C) folding rates and LRO, (D) unfolding rates and LRO, (E) folding rates and thermodynamic stability, (F) unfolding rates and thermodynamic stability, and (G) unfolding and folding rates. The lines of best fit (solid black) and corresponding equations and correlation values are given for the whole dataset, values for subsets of data are given in Table I for two-state (filled diamonds), multistate (open squares), alpha (blue), beta (red), and mixed (green) proteins. Dotted lines for panels A–D denote ±10-fold and ±100-fold variation in k_f and k_u, respectively.

Table I.

Correlations and Linear Fits of Unfolding and Folding Rate Constants, Measures of Native Structure, and Thermodynamic Stability

Parameter x	Parameter y	Dataset (size)	Linear fit: y = b + m* x		Pearson correlation
			m	b	R	Pa
ACO	log kf	Full (108)	−0.25	5.1	−0.75	1.4 × 10−20
		Two-state (73)	−0.25	5.4	−0.73	3.6 × 10−13
		Multistate (35)	−0.20	4.0	−0.75	2.7 × 10−7
		Alpha (33)	−0.22	5.3	−0.62	1.1 × 10−4
		Beta (34)	−0.35	6.1	−0.86	4.9 × 10−11
		Mixed (41)	−0.16	3.7	−0.52	5.1 × 10−4
		Maxwell (28)	−0.14	4.1	−0.48	9.5 × 10−3
ACO	log ku	Full (108)	−0.40	3.6	−0.79	3.0 × 10−24
		Two-state (73)	−0.46	4.4	−0.82	3.9 × 10−19
		Multistate (35)	−0.30	1.9	−0.70	2.8 × 10−6
		Alpha (33)	−0.48	4.5	−0.70	6.4 × 10−6
		Beta (34)	−0.55	5.4	−0.82	3.5 × 10−9
		Mixed (41)	−0.25	1.0	−0.67	2.0 × 10−6
		Maxwell (28)	−0.30	2.1	−0.71	2.7 × 10−5
LRO	log kf	Full (108)	−1.0	6.0	−0.79	2.9 × 10−24
		Two-state (73)	−0.94	6.0	−0.80	2.0 × 10−17
		Multistate (35)	−1.0	5.6	−0.75	2.7 × 10−7
		Alpha (33)	−0.96	5.9	−0.69	1.0 × 10−5
		Beta (34)	−1.1	6.3	−0.82	4.3 × 10−9
		Mixed (41)	−0.95	5.8	−0.54	2.6 × 10−4
		Maxwell (28)	−0.93	6.2	−0.68	7.6 × 10−5
LRO	log ku	Full (108)	−1.6	4.7	−0.79	6.9 × 10−24
		Two-state (73)	−1.6	4.9	−0.82	3.4 × 10−19
		Multistate (35)	−1.4	3.7	−0.64	3.5 × 10−5
		Alpha (33)	−1.8	5.2	−0.68	1.3 × 10−5
		Beta (34)	−1.7	5.9	−0.79	3.6 × 10−8
		Mixed (41)	−1.2	3.0	−0.56	1.4 × 10−4
		Maxwell (28)	−1.5	4.7	−0.74	5.6 × 10−6
log kf	ΔGF-U	Full (108)	0.31	−5.4	0.23	1.8 × 10−2
		Two-state (73)	0.37	−5.6	0.27	2.3 × 10−2
		Multistate (35)	0.23	−5.1	0.15	4.0 × 10−1 NS
		Alpha (33)	0.78	−6.6	0.47	5.2 × 10−3
		Beta (34)	0.49	−5.3	0.36	3.8 × 10−2
		Mixed (41)	−0.52	−5.1	−0.33	3.6 × 01−2
		Maxwell (28)	−0.49	−4.4	−0.26	1.9 × 10−1 NS
log ku	ΔGF-U	Full (108)	0.68	−3.8	0.78	2.4 × 10−23
		Two-state (73)	0.69	−4.0	0.80	2.2 × 10−17
		Multistate (35)	0.76	−3.0	0.79	1.4 × 10−8
		Alpha (33)	0.77	−4.4	0.89	7.0 × 10−12
		Beta (34)	0.69	−3.3	0.83	1.7 × 10−9
		Mixed (41)	0.82	−3.2	0.66	3.0 × 10−6
		Maxwell (28)	0.98	−3.8	0.77	1.9 × 10−6
log kf	log ku	Full (108)	1.2	−3.9	0.79	6.4 × 10−24
		Two-state (73)	1.3	−4.1	0.79	7.4 × 10−17
		Multistate (35)	1.2	−3.8	0.72	1.1 × 10−6
		Alpha (33)	1.6	−4.8	0.83	2.6 × 10−9
		Beta (34)	1.4	−3.9	0.82	2.6 × 10−9
		Mixed (41)	0.62	−3.7	0.50	9.8 × 10−4
		Maxwell (28)	0.64	−3.3	0.42	2.5 × 10−2

Individual correlations and linear fits are shown for subsets of the data as in Figure 1. Additionally, values for the commonly used dataset of Maxwell et al. are shown for comparison.

^aTwo-tailed probability value.

^NS Correlation is not significant at the 0.05 level (5.0 × 10⁻²).

ΔG_F-U = G_F − G_U = −RT ln (k_f/k_u), where R is the gas constant and T is the absolute temperature in Kelvin, gives the Gibbs free energy of the folded state relative to the unfolded state.

Unfolding rates correlate with ACO, LRO, folding rates, and stability

Strikingly, the logarithm of both k_u and k_f have equally negative correlation coefficients with ACO and LRO [Fig. 1(A–D), Table I], which suggests these measures of structural complexity are similarly predictive of both rates (small variations in correlation are expected owing to differing experimental conditions and the necessary extrapolation of the rates from kinetic data). Thus, both unfolding and folding rates decrease with increasing structural complexity. These results contrast with those of previous studies using smaller datasets of 22 and 25 proteins which concluded that one parameter was not equally well suited for predicting both unfolding and folding.^27,28 Further, we find that the correlation for unfolding holds well across different structural classes (Table I), whereas another analysis²⁹ suggested all-beta proteins have a much weaker correlation with LRO that is opposite in sign to that for all-alpha and mixed structural classes. These apparent discrepancies are likely caused by the small dataset sizes used in the earlier study where the alpha and beta classes had 5 and 7, compared here with 33 and 34 proteins, respectively.

We also note that unfolding rates are strongly correlated with folding rates [Fig. 1(E) and Table I], and that ACO and LRO are strongly correlated with rates at the transition midpoints (i.e., under conditions of equal thermostability; Supporting Information Fig. S1, Table SI). Thus, ACO and LRO may report on the structural complexity and relative energy of the transition state.³⁵ There is also a weaker correlation between protein length and the unfolding and folding rates (Supporting Information Table SI). Together these trends indicate that protein topological complexity and size affect both folding and unfolding rates.

Lastly, there is a strong correlation between unfolding rate and thermodynamic stability [Fig. 1(F), Table I]. In contrast, the correlation of folding rate with thermodynamic stability is weak [Fig. 1(G), Table I], as has been found previously.^6,36 The larger contribution of unfolding rate to thermodynamic stability has been noted before,^{27,28,32,33,37} and is also apparent in the differences between the upper and lower limits of the dataset, where the upper limit on fast folding and unfolding is similar, while the lower bound for unfolding is substantially slower than that for folding (Supporting Information Table SII). These results suggest that variations in thermodynamic stability, which are determined by the ratios of folding to unfolding rates, are dominated by unfolding rather than folding rates (Table I). Why is this so? Folding may have a biologically imposed lower limit in vivo, such that it is sufficiently fast to avoid degradation or aggregation,³⁸ and an upper limit imposed by physical constraints even for the most topologically simple folds.³⁴ Conversely, while there may be a similar physical limit for fast unfolding, the biological limit for slow unfolding, which may be related to the need for eventual protein turnover,³⁹ may be more malleable due to the greatly differing roles and lifetimes of natural proteins.

Experimental and theoretical support for correlation between unfolding rates and native structure

Multiple lines of evidence suggest that unfolding rates should correlate with native structural complexity. First, while the relationships between unfolding rates and structure observed here may appear to be at odds with prior studies,^27–29 this is likely spurious due to trends being obscured previously when analyzing smaller datasets with substantial noise. Specifically, for a given value of a structural parameter (ACO or LRO), the variation in the observed unfolding rates is ± ∼10-fold larger than that for the folding rates [Fig. 1(A–D)]. Thus, compared to folding rates, to detect significant correlations between unfolding rates and structural parameters, the absolute range of unfolding rates needs to be larger. The smaller datasets used in previous unfolding analyses,^27–29 which were based on the more curated set of Maxwell et al.,³⁰ had a range of ∼ eight orders of magnitude for the unfolding rates (6 × 10⁻⁶ – 1 × 10² s⁻¹). The larger dataset used here spans ∼16 orders of magnitude (4 × 10⁻¹¹ – 5×10⁵ s⁻¹), and as such the correlation between unfolding rate and structural complexity can be observed more clearly. Second, as the rates at the transition midpoint (where k_u is equal to k_f, and ΔG is 0) report on the transition state energy, the correlation of these rates with measures of structural complexity suggests that both the folding and unfolding rates (under conditions of different ΔG) should also be correlated with those same measures of structural complexity. Third, a recently developed method based on physical principles and protein structural class and size was able to predict both unfolding and folding rates for a set of 52 two-state folding proteins.⁴⁰ Finally, an analysis of 53 two-state and 19 multistate folders using a complex fractal parameter found comparable correlations with unfolding and folding rates, although the strength of the correlation was weaker than reported here.²⁴ The above considerations provide support for our observation of the significant correlations of structural complexity with both folding and unfolding rates.

Implications for design

The correlations reported herein indicate that the same measures of structural complexity predict both folding and unfolding rates equally well, and consequently, it may be difficult to modulate one aspect of the structure to alter (e.g., gain) folding speed, while leaving unfolding speed unaffected. Thus, it may seem a daunting task to achieve the desirable outcome of both fast folding and slow unfolding simultaneously. However, while the correlations of structural complexity and folding/unfolding rates have high statistical significance (Table I), there is nevertheless considerable variation around the lines of best fit, which we roughly estimate to be in the range of ± two orders of magnitude for folding and ± three orders of magnitude for unfolding rates [Fig. 1(A–D)]. Although some of this variation may be caused by more complex topological features such as nested structures,^25,35,41 it has been noted previously^14,42 and well documented experimentally, for example, by comparison of homologous proteins,^{31–33,36,42} that while the native structure may place upper and lower boundaries on folding and unfolding rates, sequence-specific effects can be substantial. This is also illustrated by the effects, sometimes quite large, of point mutations on kinetics.^43,44 In addition, single mutations tend to have a larger absolute effect on unfolding rather than folding rates based on our analysis of a dataset collected by Naganathan and Muñoz⁴⁵ where the change in unfolding rate is ∼15-fold greater on average than for folding rates (Supporting Information Table SIII). Together, the above points suggest that while the scaffold may define broad ranges for folding/unfolding rates, sequence-specific engineering can provide substantial scope to modulate these rates in order to achieve to some extent, fast folding and slow unfolding.

Fortunately, much work has been done on the sequence-specific determinants of folding and unfolding rates, and some lessons may be learned from this. First, the nature of functional sites in proteins may modulate topological complexity and alter kinetics. This was studied for two beta-trefoil proteins: the functional myristoyl binding site of Hisactophilin is a cavity within the protein core which reduces structural complexity and so may speed folding and unfolding, whereas the binding site of Interleukin-1 beta is formed by two long loops which increase structural complexity and may slow the kinetics.⁴⁶ Second, both residual structure in the denatured state^47,48 and nonnative interactions in the transition state^49–51 can increase the folding rate independent of the overall topology. Third, unfolding rates can be slowed by introducing hydrophobic residues on the surface of the native structure, which may increase local rigidity and the barrier to local hydration,⁵² or by surface electrostatic interactions, which may act as clips.⁵³ Lastly, it may be possible through computational simulation to identify particular weak points in the structure which, if strengthened, could increase unfolding cooperativity and therefore increase the height of the unfolding barrier.⁵⁴ Thus, multiple approaches may be used to modulate sequence-specific interactions in order to alter folding/unfolding rates.

Conclusions

We have shown, using a large dataset with highly significant correlations, that the measures of structural complexity that have emerged as strong predictors of folding rates, ACO and LRO, are equally predictive of unfolding rates, contrary to what has been reported previously when using smaller datasets.^27–29 In addition, the correlations are fairly robust to kinetic mechanism, whether two-state or multistate, and structural class, whether alpha, beta, or mixed. From a fundamental protein folding point of view, this suggests that the structural complexity reported on by ACO and LRO is a key determinant of both folding and unfolding processes.

These results have important implications for protein engineering and design. Specifically, a topologically simple scaffold may fold quickly, and so attain in vivo activity^34,38; but, it will also unfold quickly, reducing kinetic stability and resistance to thermal or chemical denaturation and degradation by proteases.^55,56 Conversely, a topologically complex scaffold may possess the high kinetic stability that would be ideal for harsh industrial conditions or crowded and proteolytic biological environments,⁵⁶ but it may have difficulty folding fast enough to be biologically viable.^8,34 These conflicting kinetic constraints may limit the prospects when both fast folding and kinetic stability are required, or when improving a particular scaffold that is desirable for other reasons (such as function). However, these difficulties can be overcome as in existing proteins where the large variation in folding/unfolding rates and significant effects of point mutations⁴⁴ (Supporting Information Table SIII) demonstrate that appropriately designed sequences can ease constraints placed on the folding and unfolding rates by the structural complexity of the protein scaffold.

Methods

Our dataset is largely that of Garbuzynskiy et al.³⁴ (which includes the smaller dataset of Maxwell et al.³⁰). We added data from the Kinetic DataBase⁵⁷ and other published kinetic data including our own^32,58–60 as well as data on our engineered ThreeFoil protein⁶¹ (for which the kinetic experiments will be published separately). In adding data, we followed the general criterion used by Garbuzynskiy et al.,³⁴ using only monomeric, single domain proteins, which lack disulfide bonds and prosthetic groups. In addition, the experimental temperature was in the range, or could be reliably extrapolated, to ∼25°C, and the folding and unfolding rates were measured at, or could be extrapolated to, 0 M denaturant. The specific details of the sources for each member of the 108 protein dataset are given in Supporting Information Table SII.

ACO, the average sequence separation between contacting heavy atoms, was calculated as described by Ivankov et al.⁷

where N_c is the total number of contacts between heavy atoms, and |i − j| is the sequence separation in residues for a given contacting pair of atoms. Contacts are considered between heavy atoms less than 6 Å apart.

The formula for calculating LRO is that of Gromiha and Selvaraj¹⁹

where L is the protein length, R_c is the total number of contacting residues and n_i,j is 1 when |i − j| ≥ 12 and 0 otherwise. We have modified the definition of a contact between residues to be the same as in ACO rather than the original criterion of a Cα separation less than 8 Å. This modified form yields slightly improved correlations for both folding and unfolding; using 6 Å may correct for underestimation of long range contacts between large residues in cores.

Glossary

ACO

absolute contact order

LRO

long range order

RCO

relative contact order.

Supporting Information

Additional Supporting Information may be found in the online version of this article.

Supplementary Information