Atomic accuracy models from 4.5 Å cryo-electron microscopy data with density-guided iterative local refinement

Abstract

Direct electron detectors have made it possible to generate electron density maps at near atomic resolution using cryo-electron microscopy single particle reconstructions. Critical current questions include how best to build models into these maps, how high quality a map is required to generate an accurate model, and how to cross-validate models in a system independent way. We describe a modeling approach that integrates Monte Carlo optimization with local density guided moves, Rosetta all-atom refinement, and real space B-factor fitting, yielding accurate models from experimental maps for three different systems with resolutions 4.5 Å or higher. We characterize model accuracy as a function of data quality, and present a model validation statistic that correlates with model accuracy over the three test systems.

Introduction

Recent developments in direct electron detectors as well as improved image data analysis have led to vast improvement in the resolution achievable by single-particle electron cryo-microscopy (cryoEM)^1,2. Tools for automatic structure determination, model rebuilding, all-atom refinement, and model validation are needed for single-particle reconstructions with near atomic resolution. Currently available X-ray crystallographic tools^3-5 perform relatively poorly with density maps worse than 3 Å resolution, failing to converge on an accurate atomic model⁵. Methods have been developed specifically for building and refining structures into cryoEM density maps, including tools to fit crystal structures into density^6-8, to fit secondary structure elements and assign sequence followed by all-atom refinement^9,10, and to rebuild missing regions of protein backbone guided by experimental density data^11,12. However, these methods rely on the existence of a high-quality starting model or known secondary structure assignment.

In this paper, we present a unified approach to model building, refinement, and model validation using near atomic resolution cryoEM reconstructions. Starting from homologous structures, using density maps over a wide range of resolutions, we show that when the resolution is better than 4.5 Å the approach is able to converge on an accurate all-atom model largely independent of starting model accuracy. The approach can automatically correct sequence registration errors, and has a substantially better radius of convergence than the widely used MDFF method.

Results

We sought to develop a cryoEM model refinement protocol that follows experimental density as much as possible while maintaining the physico-chemical accuracy of the model. As described in the Methods, we integrated approaches from crystallographic refinement, ab initio structure prediction, and segment rebuilding and refinement in comparative modeling to enable progression from a poor starting model – where the overall topology is correct but with large local backbone deviations – to an atomically accurate model in one seamless protocol.

We adapted to density-guided model building a sampling strategy previously developed for comparative modeling¹³. In this strategy, backbone fragments collected from the Protein Data Bank (PDB)¹⁴ are inserted via superposition onto the current model, and Cartesian space minimization against a low-resolution energy function “stitches closed” the broken peptide bonds. To sample more effectively guided by a cryoEM map, before stitching, we first optimize each fragment to fit the density in the region. A Monte Carlo trajectory is carried out with trial moves consisting of replacement of a region that fits the density poorly with a backbone fragment from the PDB pre-minimized to fit the density. In the pre-minimization step, coordinate constraints at the fragment endpoints maintain proper peptide bond geometry, and Ramachandran and rotameric constraints maintain reasonable backbone and sidechain geometry. Because these fragments are minimized in isolation, testing of a large set of fragments at each position is computationally feasible, quickly identifying backbone conformations consistent with both local sequence and the experimental data. All steps of modeling take into account the native symmetry of the complex, with all subunits present in multi-subunit complexes.

Since cryoEM maps are frequently better in resolution in some regions than others, atomic B factors are fit against cryoEM density data to maximize the real-space correlation between model and map. The protocol alternates between B factor refinement and model rebuilding until the correlation between the map and the model converges. Finally, because the fit of a model to experimental data alone provides little information on model quality (as the model was refined against that same experimental data), we developed a cross validation metric utilizing independently collected data that provides a map-quality independent assessment of model accuracy.

Model Building and Refinement

To evaluate the new refinement protocol and compare it to alternate approaches, we use three recently collected experimental datasets: 20S proteasome at 3.3 Å resolution, the periplasmic domains of the needle complex, PrgH/K, at 4.6 Å resolution, and a peptide fiber assembly at 4.3 Å resolution. To test the dependence of the method on the number of images used in the reconstruction and map resolution, we generated reconstructions for 20S at 4.1, 4.4, 5.0, and 6.0 Å resolutions, and reconstructions of PrgH/K at 5.4 and 7.1 Å, using subsets of the particle images to realistically evaluate the challenges arising from limited data. At the highest resolution, much sidechain density is visible; at 4.0-4.5 Å resolution, limited sidechain density is observed, but individual strands and the pitch of helices is visible; at 5 Å and worse, individual beta strands and the pitch of helices are indistinguishable.

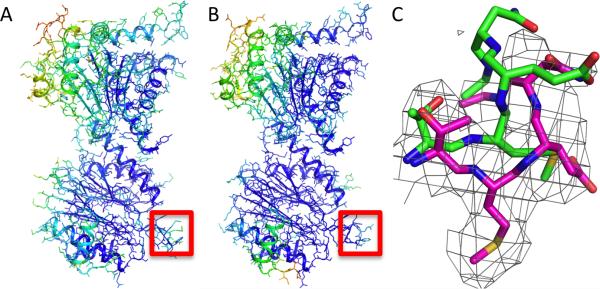
We focus first on the 20S proteasome as the very large amount of collected data and the wide range of structural variation in homologues allow systematic investigation of the dependence of the method on the resolution of the map and the accuracy of the starting model. We refined the 20S crystal structure (PDB code: 1PMA) into the highest-resolution reconstruction to generate a reference model for comparison; to allow evaluation of the refined model versus the crystal structure, we first split the particle images into two sets and generate two independent reconstructions. We set atomic B factors to uniform, and refine coordinates and B factors iteratively into the reconstruction. As illustrated (Fig. 1a,b), after refinement, the B factors fit to the reconstruction show very good agreement with those of the crystal structure (R²=0.74). Refinement of the crystal structure leads to subtle changes in the backbone in several loops (Fig. 1) that increase agreement with the independent reconstruction, suggesting the refined model more accurately represents the structure on the EM grid than does the crystal structure.

Figure 1.

Refinement of 20S proteasome crystal structure into high-resolution cryoEM density. Atomic B-factors obtained from cryoEM model refinement correlate with the deposited X-ray B factors. (A,B) The crystal structure (PDB code: 1PMA) and the cryoEM model refined against the 3.3 Å map. The model is colored by the B-factor in the crystal structure (A), and by the Rosetta real-space B-factor fit to the cryoEM map (B). (C) An example of loop region that reconfigures in the cryoEM model: green, crystal structure; magenta, Rosetta refined model. The independent map density (not used in refinement) is shown.

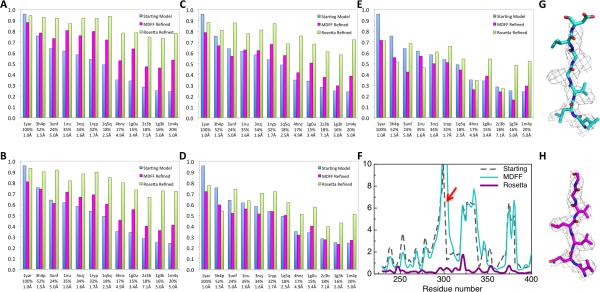
To explore the role of starting-model accuracy on model refinement, we constructed comparative models from 11 homologues ranging from 12% to 40% sequence identity and another crystal structure with 100% sequence identity (PDB code: 1YAR). Errors in these starting structures are diverse, and cover challenges commonly seen in structure refinement, including rigid body movement of helices and strands, missing residues from the template, changes in loop conformation, and misaligned residues. Using the fraction of Cα within 1 Å of the reference structure as a measure of model accuracy, the input models ranged from 15% to 96% accurate (Fig. 2a-e, blue bars), with root mean squared deviations (RMSD) from 1.0 to 7.1 Å to the reference model.

Figure 2.

Dependence of model accuracy on starting model quality and map resolution. For a series of comparative models of 20S, Rosetta and MDFF refinement was initiated from comparative models based on templates indicated on the x-axis. The fraction of Cα atoms within 1 Å of the reference model is indicated on the y-axis for (blue) the starting comparative models, (magenta) the MDFF refined models, and (green) the Rosetta refined models. The templates are arranged from the best starting model to the worst based on the fraction of Cα atoms within 1 Å of the reference model. Sequence identity of the template and RMSD to the reference model is labeled under the PDB ID. Models were refined against 20S maps reconstructed using (A) 120,000 (B) 5,000 (C) 3,000 (D) 1,200 and (E) 1,000 particles, yielding 3.3, 4.1, 4.4, 5.0 and 6.0 Å resolution, respectively. (F) Deviations to the reference model (y-axis) from (black) the starting model based on 1g3k, (cyan) the MDFF refined model and (magenta) the Rosetta refined model for each residue (x-axis). Structure and electron density of the regions highlighted with red arrow is shown for (G) MDFF models and (H) Rosetta models.

To simultaneously evaluate the dependence of refined model accuracy on starting model quality and map resolution, and the accuracy of model validation metrics, we generated independent training and testing maps at 3.3, 4.1, 4.4, 5.0, and 6.0 Å resolutions, and refined each of the starting models into each of the training maps (Fig. 2). In all cases, models were built excluding all peptide fragments from structures with higher sequence identity then that of the worst starting model (12%). For comparison to a widely used current method, we built full length comparative models from each starting model using Modeller¹⁵, and refined them using the MDFF molecular dynamics flexible fitting protocol¹⁶. The refined models were evaluated by determining the fraction of residues with Cα atoms within 1 Å of those in the refined crystal structure.

The new protocol shows less dependence on starting model accuracy at higher resolutions (Fig. 2a-e, Supplemental Fig. 1). While the accuracy of the starting models (blue bars) falls off dramatically with decreasing sequence identity, the accuracy of the refined Rosetta models (green) for the 3.3, 4.1 and 4.4 Å maps is quite good, even with distant starting models. For the majority of input templates, resulting models are over 75% accurate, with errors primarily in surface loops. However, at 5 and 6Å resolution, the performance of the method decreases, occasionally making the starting model worse. The extensive backbone sampling carried out during refinement is a double-edged sword: it allows dramatic improvement of starting models at high resolution, but can degrade starting models when the experimental data provides insufficient restraints. The dramatic decrease in performance going from 4.4 to 5.0 (and 6.0) Å may reflect the blurring of beta strands in beta sheets or the difficulty placing Cβ atoms in helices. Since resolution alone does not provide a perfect picture of map quality, this approach should not be used on maps lacking features such as resolution of individual strands or the pitch of helices.

The widely used MDFF method was much less sensitive to the resolution of the density map, but more sensitive to the accuracy of the starting model, likely due to stronger tethering to the starting model; this reduces model degradation at low resolution, but at high resolution makes it difficult to improve distant starting models. To increase the range of motion in MDFF, we tried reducing the restraints to the starting model and incrementally increasing the density weight. With lower restraint weight and higher density weight, the models moved further to better fit the density, but overall model geometry is compromised as indicated by increased MolProbity^17,18 scores. In contrast, models can move substantially in Rosetta to fit the density while maintaining good MolProbity scores. For example, starting from 1g0u at 3.3 Å, the MolProbity score of the MDFF model increases from 2.4 to 3.0; the Rosetta-refined model scores 1.7. Deviations of the starting, MDFF-refined and Rosetta-refined models to the reference model for each residue are illustrated (Fig. 2f). When starting from distant models, Rosetta generates superior quality models (Fig. 2a-e) on all but the 5.0 and 6.0 Å map.

The Rosetta refinement protocol is able to correct the majority of errors from the input structure for 3.3-4.4 Å maps because the rebuilding procedure can quickly overcome local barriers. Density data is used to select and then optimize individual fragments, making backbone conformational sampling focused and efficient. As highlighted (Fig. 2F), in many cases, models can be incorrectly fit into the density with errors in sequence registration and misplaced secondary structure elements. On these datasets, residues as far as 10 Å away from the native placement in the starting model are remodeled correctly using the new protocol. With map resolutions better than 4.5 Å, both backbone and core sidechains are placed correctly. On the other hand, with lower-resolution maps, density information is not enough to guide correct placement of fragments, and many incorrect sampled models fit the density equally well.

Model validation

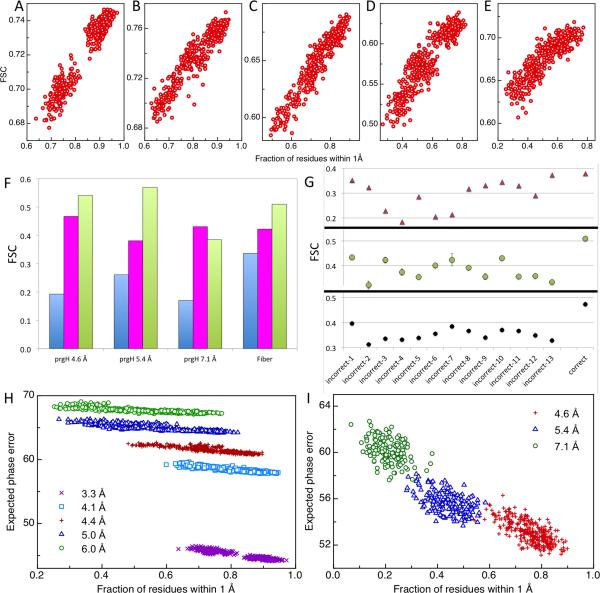
The fit of a refined model to an independent test map provides an unbiased measurement of model quality. We found previously that the medium resolution Fourier shell correlation (FSC) was more predictive than real space correlation¹⁹. While the entire model-map FSC curve is informative, when generating many models, it is valuable to have a single number that reflects model quality, thus, we integrate the FSC over the medium resolution range. As shown in Figure 3, this integrated FSC on an independent map (or free FSC) correlates with model accuracy quite well, particularly at high resolution. Furthermore, the real space correlation between models and the independent testing map over segments of the chain correlates with the local accuracies of models. In high-resolution maps, as the local correlation decreases, the fraction of incorrectly modeled residues increases (Supplementary Fig. 2). This allows the identification of local errors that are not eliminated by the automated protocol.

Figure 3.

Model evaluation using independent maps. For each Rosetta-refined model of 20S at (A) 3.3 Å, (B) 4.1 Å, (C) 4.4 Å, (D) 5.0 Å, and (E) 6.0 Å resolution, the integrated FSC between model and testing map is plotted (y-axis) against the fraction of residues within 1 Å of the reference model (x-axis). More accurate models have higher independent map integrated FSC. (F) Evaluation of (blue) input models, (magenta) MDFF-, and (green) Rosetta-refined models for prgH and fiber based on the independent map integrated FSC. (G) Fiber models based on models (green); the MDFF models also identify the correct threading but with much weaker signal different sequence threading possibilities were refined in (magenta) MDFF and (green) Rosetta. The correct threading is distinguished by the highest integrated FSC in the Rosetta refined (magenta). The integrated FSC between Rosetta models refined in this study and a higher resolution density map available more recently (black) validates the threading identified using Rosetta and the lower resolution map (green). (H,I) Expected phase error (y-axis) correlates with the accuracies of refined models (x-axis). Refinement was carried out with reconstructed maps of 20S proteasome (H) at (magenta) 3.3Å, (cyan) 4.1 Å, (red) 4.4 Å, (blue) 5.0 Å and (green) 6.0 Å, and with maps of prgH (I) at (red) 4.6 Å, (blue) 5.4 Å and (green) 7.1 Å. The expected phase error tracks absolute model quality better than the integrated FSC (Supplemental Fig. 3).

Testing on other systems

For the PrgH/K ring and the peptide fiber, there is no crystal structure of the complex in the same multimeric configuration to use as a gold standard, so we rely on the FSC against an independent reconstruction to evaluate model accuracy.

The first system, PrgH/K, is a C24 symmetric ring, with data to 4.6 Å resolution. We also utilize lower-resolution reconstructions made with subsets of the entire dataset that have estimated resolutions of 5.4 and 7.1 Å. The starting model is a hybrid derived from two sources: one subunit comes from a crystal structure in a different multimeric conformation, while the second subunit comes from a homologous structure. At each resolution, we fit Rosetta and MDFF models against a training map reconstructed from half of the images, and measure the FSC against a testing map. Similar to 20S, there are substantially better fits to the independent data with the Rosetta models versus the MDFF models at 4.6 and 5.4 Å resolution, but the MDFF-generated model at 7.1 Å has better FSC than the Rosetta-generated model (Fig 3).

In the fiber case, the map is of a repeating helical fiber structure. The challenge is not identifying the backbone conformation but rather determining the orientation and sequence registration of the helix in the two density maps. The 4.3 Å map has a single copy of the helix in the asymmetric unit. Even at this resolution, the nearly-palindromic nature of the sequence made sequence registration difficult. Instead of fragment-based assembly, we enumerated the 14 possible sequence registrations and refined each model. There is a clear signal for one particular sequence registration (Fig. 3), with an independent-map agreement improvement of over 0.02 compared to the next-best registration. With MDFF, the overall independent-map agreement is worse for this registration, and there is little signal for this registration relative to other possible registrations. A more recent higher-resolution reconstruction (Fig. 3f) has strong signal for this registration, further suggesting that it is correct.

Estimated Phase Error

Even at high resolution, integrated model-map FSC, while very effective at evaluating the relative accuracy of multiple models to a single map, does not provide a measure of absolute accuracy of models in different maps (Fig. 3a-e and Supplemental Fig. 3). FSC also has a number of weaknesses that make it somewhat undesirable as an evaluation metric: (i) different resolution ranges are summed over for different maps so the values are not comparable; and (ii) the FSC correlation does not take into account the signal-to-noise in each shell, which may vary even in maps at the same resolution. An absolute measure assessing the accuracy of a model in a map is thus desirable.

We sought to develop a likelihood-based measure for evaluating the agreement between model and map, that gives reasonable accuracy measures independent of map. As described in the Methods, we developed a measure of expected phase error (EPE) in reciprocal space. While not perfect, the EPE is more comparable between different resolution maps (Fig. 3g,h) than is the integrated FSC. Obtaining an absolute scale measure of model quality that is less sensitive to noise remains an important area of research.

Discussion

Starting from experimental density maps with 4.5 Å resolution or better, for three different systems, we have shown it is possible to consistently generate models with near atomic level accuracy. Since there is not a standard definition of map resolution, we also provide a more qualitative description of the map quality necessary for our method to be usefully applied: inspection of the maps in our test set (Supplemental Fig. 4) suggests that the pitch of helices, individual strands and some large aromatic sidechains should be at least in part visible.

By using ideas from crystallographic refinement, such as independent model validation and atomic B factor fitting, we have improved model generation from cryoEM maps. A next step is to use modeling to reduce map error, as is done in crystallography through map rephasing and density modification. Although single particle reconstructions contain equally accurate amplitude and phase information, we may still use modeling to reduce errors in the image reconstruction process. For example, using intermediate models rather than heuristic scaling factors (as in ref²⁰) to rescale map intensities as a function of resolution should more accurately recapitulate high-resolution details. Models may also be used to reduce errors in determining particle orientation or particle conformation in heterogeneous systems. Such methodological advances could substantially improve the determination of atomic models from cryoEM reconstructions.

Online Methods

An overview of the model-building process is illustrated (Supplemental Fig. 5). Initial models are derived from either a crystal structure of an alternate state (PrgH), a crystal structure of a homologue (20S), a manually built comparative model based on a low-resolution structure (PrgK) or an idealized helix (fiber). When starting with an alignment to a known structure, rather than a full-length model, RosettaCM¹ – guided by the experimental data² – was used to rebuild gaps in the alignment. For the proteasome, 200 comparative models were generated from each starting point; for the fiber, 10 models were generated. Rosetta forcefield used for optimization, including fit-to-density, was used to select the best model.

Map generation

For all datasets, “gold standard” independent reconstructions³ were made using maximum likelihood reconstruction⁴. The reported resolutions in the manuscript correspond to the FSC=0.143 value of the two half maps. One of these reconstructions was used only for rebuilding and refinement (the “training” map), while the other was used only for validation (the “testing” map). Subsets of the complete particle set were selected, split into two halves; each half-set was used to create lower-resolution training and testing maps. In all cases, B factor correction⁵ was applied to the map before refinement, to amplify data in high-resolution shells.

MDFF

Models were initially built with Modeller^6,7 in the cases where no crystal structure was available. For each starting homologue, five Modeller models were built, with unaligned terminal residues removed. Each of these starting points was used as inputs for MDFF. MDFF modeling was carried out using the protocol described by Schulten and co-workers⁸. Energy minimization was used to optimize bond geometries and remove clashes in the input model; a molecular dynamics simulation was carried out for 100 pico-seconds, followed by a final energy minimization. The MDFF electron density term was used in all three steps with a weight of 1, 0.3 and 10 respectively.

Density-guided model building

Multiple independent Monte Carlo trajectories are carried out, each consisting of several hundred of the density refined fragment moves described below; trajectories begin with 17 residue fragments and then shift to 9 residue fragments. At each step of the trajectory, a random position in the protein is chosen, with frequency weighted by local density agreement: residues with a local correlation less than 0.6 are sampled frequently (4x base), those with correlation 0.6-0.8 sampled occasionally (base), and those with correlation above 0.8 sampled rarely (0.04x base). A set of 25 fragments of 17 or 9 residues in length is selected based on the sequence identity to the target structure. Each fragment is then superimposed on the current model so that the two N- and C-terminal residues overlap with the corresponding residues in the current model. Then, for each fragment, we: (a) rigid-body minimize the fragment into density, (b) optimize sidechain rotamers to best fit the density, and (c) minimize all torsions against a forcefield assessing agreement with density, agreement of the terminal residues of the fragment with the corresponding positions in the current model, and backbone and sidechain torsional probabilities. Because this optimization is done with small fragments, ignoring interactions with the remainder of the protein, it is very quick, allowing the 25 fragments to be optimized and evaluated in about 1 CPU second. At each position, the fragment with best fit to the density that has an RMS of less than 0.5A over the terminal residues is selected. Backbone atomic positions from the selected fragment then replace the corresponding backbone in the current model, and the entire structure is minimized in Cartesian space (as in ref⁹) to regularize backbone geometry at the stitching site. The minimization is done using a smooth version of the Rosetta centroid level energy function¹ which primarily consists of sterics and backbone hydrogen bonding supplemented with density agreement.

Real-space B-factor refinement

To better model the density maps and generate more accurate models, we refined atomic B factors against the maps optimizing the real-space correlation between model and map. Given that atom i has a B factor B_i, we calculate the density of the model as:

$${\rho }_c=\sum _{atomsi}{\left(\frac{\pi }{f_i+B_i∕4}\right)}^{\frac{3}{2}}\exp \left(-\frac{{\pi }^2}{f_i+B_i∕4}{\Vert x-x_i\Vert }^2\right)$$

Here, f is a scattering factor fit to each element. Our implementation makes use of a single-Gaussian scattering for each atom type, but it is straightforward to extend this to a standard 5-Gaussian scattering model¹⁰.

B factor refinement is carried out using quasi-Newton optimization, with the gradient of the B factor of atom i (located at coordinates x_i) given in real space by:

$$\frac{\partial RSCC}{\partial B_i}=\frac{1}{{\sigma }_c^2}\left({\sigma }_c\cdot \frac{\partial \sum {\rho }_c{\rho }_o}{\partial B_i}-\sum {\rho }_c{\rho }_o\cdot \frac{\partial \sum {\rho }_c^2}{\partial B_i}\right)$$

Here, ρ_c and ρ_o are the calculated and observed density, σ_c is the standard deviation of the calculated density, the observed density has been standardized to mean 0 and standard deviation 1 over a mask around the protein, and sums are over the density map. Then:

$$\begin{array}{cc}\hfill & \frac{\partial \sum {\rho }_c{\rho }_o}{\partial B_i}=\sum _x{\rho }_o\left(x\right)\left(2\cdot {(x-x_i)}^2-\frac{3f_i+3B_i∕4}{{\pi }^2}\right)\hfill \\ \hfill & \frac{\partial \sum {\rho }_c^2}{\partial B_i}=\sum _{x}2\cdot {\rho }_c\left(x\right)\left(2\cdot {(x-x_i)}^2-\frac{3f_i+3B_i∕4}{{\pi }^2}\right)\hfill \end{array}$$

To prevent overfitting of B values, we also use restraints so that nearby atoms have similar B values, using the same formulation as phenix.refine¹¹:

$$E=\sum _{\begin{array}{c}\hfill atomsi,j\hfill \\ \hfill \Vert x_i-x_j\Vert <5\mathrm{Å}\hfill \end{array}}\frac{1}{\Vert x_i-x_j}\cdot \frac{{(B_i-B_j)}^2}{(B_i+B_j)}$$

Since atomic coordinate errors can lead to artificially high B values in refinement, which leads to reduced forces acting on these (incorrect) atom positions in subsequent rounds of coordinate refinement, we perform several rounds of refinement with uniform B values before our first cycle of B factor refinement.

Atomic refinement

Atomic refinement is based on the Rosetta relax protocol where cycles of discrete sidechain optimization are alternated with cycles of quasi-Newton optimization. In all cases, the relevant symmetry was included in the Rosetta refinement to model the full biological unit. An additional term assesses agreement to density. For speed considerations, we use approximate model-map correlation as our metric: an atom's density is convoluted over the entire map, with spline interpolation used to quickly compute the ∑ρ_cρ_o term in the correlation, with ρ_c the computed map and ρ_o the experimental map. With proper normalization of ρ_c and ρ_o, this approximation only differs from a real-space correlation by the term ∑ρ_c²; assuming this is constant is equivalent to assuming a constant atom density, which is not unreasonable.

B-factor optimization is carried out using a similar approximation for computational efficiency. Our fast density formulation pre-computes a three-dimensional grid where f(x)=∑_zρ_c(z+x); that is, the overlap between calculated and observed density when a single atom is placed at x; this was extended to a four-dimensional grid where f(x,B)=∑_zρ_c(z+x). Grid spacing was uniform in 1/B², which allows for 8-12 grid points in the B dimension to accurately approximate this space.

Using this approximation, B factors can be very quickly fit by refining atoms along the B dimension of the 4D surface. However, when refining along the B dimension, the assumption of a relatively constant ∑ρ_c² is violated. To remedy this, we compute the exact correlation at a number of fixed values of B_mean (corresponding to each discrete sample in the B dimension). These values are used as a scaling factor for the spline coefficients of each B slice. This allows us to use 4D interpolation to both fit B values, and refine atomic coordinates taking into account atomic B factors. All of our refinement steps are followed by exact B-factor refinement at the end, which tends to further improve real-space correlation by about 0.01-0.02.

Finally, previous work has shown that relaxing bond ideality is important for both structure prediction as well as refinement against crystallographic data¹¹. Thus, the final two cycles of refinement are carried out in Cartesian space, allowing for bond angle and bond length deviations to improve energetics and fit to the experimental data slightly.

Validation metrics

Following previous work⁹, models were validated against an independent reconstruction using the integrated FSC of the model and independent reconstruction in high-resolution shells. Additionally, an alternate likelihood-based model validation metric was explored. To motivate this, we formulate the probability of the data given the model. Assuming each structure factor is independent:

$$P(E_{obs}\mid E_{model})=\sum _{\begin{array}{c}\hfill resolution\hfill \\ \hfill range\hfill \end{array}}P(e_{obs}\mid e_{model})=\sum _{\begin{array}{c}\hfill resolution\hfill \\ \hfill range\hfill \end{array}}{\int }_{\begin{array}{c}\hfill complex\hfill \\ \hfill plane\hfill \end{array}}P(e_{obs}\mid e_{true})\cdot P(e_{true}\mid e_{model})\cdot d{e}_{ture}$$

Here, E_model and E_obs are the model and map structure factors (with lowercase e referring to individual structure factors), normalized in resolution bins so that ∑|E(r_i)|²=1. The term e_true represents the (unknown) ground truth structure factors. In the integral, the first term accounts for errors in the reconstruction, and the second accounts for errors in the model. While fully exploring this formulation remains an important topic of future research, parameterization of each of these terms is not straightforward and is out of the scope of this manuscript.

Instead, in this manuscript, we explore a more computationally tractable formulation of model error, the expected phase error. By computing errors in phase space, we no longer need to worry about integration over different resolution ranges, since the expected phase error goes to 90 degrees in the limit of completely random data. We can integrate over all resolutions – independent of estimated map resolution – and have a reasonable measure of model quality comparable between different maps. Our measure assumes phase errors are normally distributed in phase space with deviation σ_k:

$$P\left(\measuredangle {\alpha }_{hkl}^{train}{\alpha }_{hkl}^{test}\right)\sim \mathcal{N}(x;0,{\sigma }_k)$$

These deviations are estimated from the independent reconstructions, and are computed separately for each resolution bin by calculating deviations in model phase error between different bins.

Under this assumption, given the phase error δ = α_model-α_map between model and test map, we can compute:

$$EPE=arg\left({\int }_{-\infty }^{+\infty }{e}^{i\mid x\mid }\cdot \mathcal{N}(x;\delta ,{\sigma }_k)dx\right)=arg\left(\frac{1}{2}{e}^{-\frac{{\sigma }_k^2}{2}i\delta }\cdot \left(erf\left(\frac{\delta -i{\sigma }_k^2}{{\sigma }_k\sqrt{2}}\right)+e^{2i\delta }\cdot erf\left(\frac{\delta -i{\sigma }_k^2}{{\sigma }_k\sqrt{2}}\right)\right)\right)$$

In bins where the two maps agree (e.g. in low-resolution bins), the error is simply the difference between model phase and the independent map phase. As the agreement reduces in higher-resolution bins, the error is smoothed out; at the extreme – at resolutions that contain no information – the error is uniformly 90 degrees given the model-map agreement.