Stability analysis of memristor-based fractional-order neural networks with different memductance functions

Abstract

In this paper, the problem of the existence, uniqueness and uniform stability of memristor-based fractional-order neural networks (MFNNs) with two different types of memductance functions is extensively investigated. Moreover, we formulate the complex-valued memristor-based fractional-order neural networks (CVMFNNs) with two different types of memductance functions and analyze the existence, uniqueness and uniform stability of such networks. By using Banach contraction principle and analysis technique, some sufficient conditions are obtained to ensure the existence, uniqueness and uniform stability of the considered MFNNs and CVMFNNs with two different types of memductance functions. The analysis results establish from the theory of fractional-order differential equations with discontinuous right-hand sides. Finally, four numerical examples are presented to show the effectiveness of our theoretical results.

Introduction

We know that fractional calculus is an old branch of mathematics, which mainly deals with derivatives and integrals of arbitrary non-integer order. It was firstly introduced 300 years ago. Due to lack of application background and its complexity, it did not attract much attention for a long time. Recently, it had been applied to model many real-world phenomena in various fields of physics, engineering and economics, such as dielectric polarization, electromagnetic waves, viscoelastic system, heat conduction, biology, finance etc (Podlubny 1999; Kilbas et al. 2006; Ahmeda and Elgazzar 2007; Hilfer 2000). The fractional-order model gives more accurate results than the corresponding integer-order model. The reasons depend on two main advantages of fractional-order models in comparison with its integer-order counterparts, one is the fractional order parameter that enriches the system performance by increasing one degree of freedom and other one is that fractional derivatives provide an excellent instrument for the description of memory and hereditary properties of various processes. That is, fractional-order model has an infinite memory. Based on the wide range of applications, fractional calculus had increased the interest and attracted the attention of many researchers. Some good results have been proposed in the literature see Laskin (2000), Deng and Li (2005), Delavari et al. (2012), Peng et al. (2008) and Wu et al. (2009) references therein.

In the past few decades, stability analysis of neural networks have received considerable attention and many researches have found being applied in various fields such as communication systems, image processing, signal processing, pattern recognition, optimization problems and other engineering areas see Seow et al. (2010), Guo and Li (2012), Bouzerdoum and Pattison (1993) and Kosko (1988) references therein. In Wu et al. (2012), the authors have been studied the robust asymptotic stability analysis for uncertain BAM neural networks with both interval time-varying delays and stochastic disturbances. Some new synchronization condition were obtained for discontinuous neural networks with time-varying mixed delays by using state feedback and impulsive control in Yang et al. (2014). In recent years, fractional calculus, based on its significant features (more degrees of freedom and infinite memory) has been used to modeling the artificial neural networks, the fractional-order formulation of neural network models is also justified by research results about biological neurons. The study of fractional-order neural networks model have more complexity due to the solution methods of fractional calculus. Some of the researchers have analyzed the fractional-order neural networks and proposed few interesting results see Yu et al. (2012), Kaslik and Sivasundaram (2012), Chen et al. (2013), Boroomand and Menhaj (2009), Zou et al. (2014) and references therein.

On the other hand, due to the potential applications of neural networks are yields new aspects of theories required for novel or more effective functions and mechanisms, that is, the applications are involved in the complex-valued signals (Hirose 2012; Nitta 2004; Tanaka and Aihara 2009). This indicates that the dynamic analysis of complex-valued neural networks is very important. The complex-valued neural networks is an extension of real-valued neural networks with complex-valued state, output, connection weight, and activation function. The use of complex-valued inputs/outputs, weights and activation functions make it possible to increase the functionality of the neural networks, their performance and to reduce the training time. In real-valued neural networks, their activation function is usually chosen to be bounded and analytic. However, in the complex domain, according to the Liovilles theorem (Mathews and Howell 1997), every bounded entire function must be constant. Thus, if the activation function is entire and bounded in the complex domain, then it is constant. This is not suitable. Therefore, choosing appropriate activation function is the main challenge in complex-valued neural networks. However, compared with real-valued recurrent neural networks, research for complex-valued ones has achieved slow and little progress as there are more complicated properties. Nowadays, some of the authors have focused their attention on the study of those complicated properties of complex-valued neural networks and proposed some interesting results see Hu and Wang (2012), Duan and Song (2010), Rao and Murthy (2009), Zhou and Song (2013), Huang et al. (2014), Chen and Song (2013), Xu et al. (2013) and references therein.

Memristor is one of the newly modeled two terminal nonlinear circuit device in the electronic circuit theory. It was theoretically first developed by Chua (1971), and the memristor element has been designed and fabricated by a team from the Hewlett-Packard Company (Tour and He 2008; Strukov et al. 2008). After the invention of practical model of memristor element, the memristor become a very interesting topic because of its potential applications in nonvolatile memory storage, new type of computers will have no booting time, brain like computers etc. This new circuit shares many properties of resistors and shares the same unit of measurement (i.e. ohm). The memristor element have attracted much attention based on the following two main properties. The first one is its memory characteristic and the second one is its nanometer dimensions. The memory characteristic was determined by its physical structure and external input. When the voltage applied on memristor is turned off, the memristor remembers its past values until it is turned on for the next time. It is well known that memristor element reveal features just like as the neurons in the human brain have. Based on these features, the memristor element has been used to build a new model of neural networks. We know that the neural networks can be constructed by nonlinear circuit and have been studied extensively. In this circuit, the self feedback connection weights and connection weights are implemented by resistors. Suppose that we use memristors instead of resistors, then the neural networks model is said to be memristor-based neural networks. The memristor-based neural network is a state-dependent switching system due to the fact that the parameter values of connection weights are changed according to their state. Very recently, the analysis of dynamic behaviors of memristor-based neural networks have been studied by many researchers and some excellent results have been proposed in the literature see Zhang et al. (2013), Yang et al. (2014), Wu and Zeng (2012, 2013, 2014), Wu et al. (2011, 2013a, b), Cai and Huang (2014), Guo et al. (2013), Qi et al. (2014), Wen et al. (2013), Chen et al. (2014) and references therein. The memristor-based neural networks is a differential equation with discontinuous right-hand sides because that it is a state-dependent switching system. It shows that the solutions of this differential equation are not yet been calculated in classical sense. Filippov (1988) proposed a solution method, that is to transform a differential equations with discontinuous right-hand sides into a differential inclusion by using the theories of differential inclusion. Most of the researchers investigated the memristor-based neural networks and proposed some related results by using the framework of Filippov solution see Zhang et al. (2013), Yang et al. (2014), Wu and Zeng (2012, 2013, 2014), Wu et al. (2011, 2013a, b), Cai and Huang (2014) Guo et al. (2013), Qi et al. (2014), Wen et al. (2013), Chen et al. (2014) and references therein. In Yang et al. (2014), the authors extensively studied the problem of exponential synchronization of memristive Cohen–Grossberg neural networks with mixed delays. Several sufficient conditions have been derived for the globally exponentially stability of memristive neural networks with time-varying impulses in Qi et al. (2014). In Wu and Zeng (2014), the authors investigated the passivity problem for memristor-based neural networks with two different types of memductance functions and some sufficient conditions for the passivity of addressed memristor-based neural networks were proposed.

Motivated by the above discussion, the analysis of fractional-order neural networks and memristor-based neural networks have become an ongoing research area. Based on the applications and features of both fractional-order neural networks and memristor-based neural networks, it is necessary to analysis the dynamic behaviors of memristor-based fractional-order neural networks (MFNNs). In Chen et al. (2014), the authors introduced the memristor-based neural networks and proposed some sufficient conditions to ensure the global Mittag–Leffler stability and synchronization are established by using Lyapunov method. The problem of the existence, uniqueness and uniform stability analysis of MFNNs with two different types of memductance functions has not been investigated in the existing literature. In this paper, we consider both real-valued and complex-valued memristor-based fractional-order neural networks (CVMFNNs) with time delay and two different types of memductance functions. Some sufficient conditions that guarantee the existence, uniqueness and uniform stability for both addressed networks are derived by using Banach contraction principle and the framework of Fillipov solution.

The rest of this paper is organized as follows. In “Preliminaries” section, the model of real-valued and CVMFNNs with time delays and two different types of memductance functions is described. Some of the necessary definitions, lemmas and assumptions are also provided in this section. Some sufficient conditions for the existence and uniqueness of solution and uniform stability for the both proposed networks are derived by using the Banach contraction principle and the framework of Fillipov solution in “Main results” section. In “Numerical examples” section, four numerical examples are given to demonstrate the effectiveness of our theoretical results. Finally the conclusion of this paper is given in “Conclusion” section.

Notation

${\mathcal{R}}^n$ and ${\mathcal{C}}^n$ denotes the n-dimensional Euclidean space and n-dimensional complex space respectively. Throughout this paper, the solutions of all the systems considered in the following are intended in Filippov’s sense. co$\{\widehat{\mathrm{\Pi }},\check{\mathrm{\Pi }}\}$ denotes closure of the convex hull of ${\mathcal{R}}^n$ generated by real numbers $\widehat{\mathrm{\Pi }}$ and $\check{\mathrm{\Pi }}$. Similarly, co$\{\widehat{\mathrm{\Phi }},\check{\mathrm{\Phi }}\}$ denotes closure of the convex hull of ${\mathcal{C}}^n$ generated by complex numbers $\widehat{\mathrm{\Phi }}$ and $\check{\mathrm{\Phi }}$. $z(t)=x(t)+iy(t)$ denote the complex-valued function, where $x(t),y(t)\in {\mathcal{R}}^n$. $\text{Denote}{m}_{pq}=max\{sup|{\widehat{m}}_{pq}|,sup|{\check{m}}_{pq}|\},n_{pq}=max\{sup|{\widehat{n}}_{pq}|,sup|{\check{n}}_{pq}|\},{\mathit{\beta }}_{pq}=max\{sup|{\widehat{\mathit{\beta }}}_{pq}|,sup|{\check{\mathit{\beta }}}_{pq}|\},{\mathit{\gamma }}_{pq}=max\{sup|{\widehat{\mathit{\gamma }}}_{pq}|,sup|{\check{\mathit{\gamma }}}_{pq}|\},{\mathit{\beta }}_{pq}^R=max\{sup|{\widehat{\mathit{\beta }}}_{pq}^R|,sup|{\check{\mathit{\beta }}}_{pq}^R|\},{\mathit{\gamma }}_{pq}^R=max\{sup|{\widehat{\mathit{\gamma }}}_{pq}^R|,sup|{\check{\mathit{\gamma }}}_{pq}^R|\},{\mathit{\beta }}_{pq}^I=max\{sup|{\widehat{\mathit{\beta }}}_{pq}^I|,sup|{\check{\mathit{\beta }}}_{pq}^I|\}\text{and}{\mathit{\gamma }}_{pq}^I=max\{sup|{\widehat{\mathit{\gamma }}}_{pq}^I|,sup|{\check{\mathit{\gamma }}}_{pq}^I|\}.$

Preliminaries

In this section, we give some basic definitions, lemmas and assumptions which can be used later to derive our main results of this paper.

Definition 1

The fractional integral of order $\mathit{\alpha }$ for a function f is defined as

$$\begin{array}{c}\hfill I^{\mathit{\alpha }}f(t)=\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{t_0}^t{(t-\mathit{\tau })}^{\mathit{\alpha }-1}f(\mathit{\tau })d\mathit{\tau },\end{array}$$ 1

where $t\ge t_0$ and $\mathit{\alpha }>0,\mathrm{\Gamma }(·)$ is the gamma function defined as $\mathrm{\Gamma }(\mathit{\alpha })={\int }_0^{\infty }{t}^{\mathit{\alpha }-1}{e}^{-t}dt$.

Definition 2

The Caputo fractional derivative of order $\mathit{\alpha }$ for a function $f\in C^{n+1}([t_0,\infty ),\mathcal{R})$ (the set of all $n+1$ order continuous differentiable functions on $[t_0,\infty )$) is defined by

$$\begin{array}{c}\hfill {}_{t_0}^C{D}_t^{\mathit{\alpha }}f(t)=\frac{1}{\mathrm{\Gamma }(n-\mathit{\alpha })}{\int }_{t_0}^t\frac{f^{(n)}(\mathit{\tau })}{{(t-\mathit{\tau })}^{\mathit{\alpha }-n+1}}d\mathit{\tau },\end{array}$$ 2

where $t>t_0$ and n is a positive integer such that $n-1<\mathit{\alpha }<n\in Z^{+}$.

Lemma 1

If the Caputo fractional derivative$D_{t_0}^{\mathit{\alpha }}f(t)$$(n-1\le \mathit{\alpha }<n)$is integrable, then:

$$\begin{array}{c}\hfill I_{t_0}^{\mathit{\alpha }}{D}_{t_0}^{\mathit{\alpha }}f(t)=f(t)-\sum _{p=0}^n\frac{f^{(p)}(t_0)}{p!}{(t-t_0)}^p.\end{array}$$ 3

Especially, for$0<\mathit{\alpha }<1$, one can obtain:

$$\begin{array}{c}\hfill I_{t_0}^{\mathit{\alpha }}{D}_{t_0}^{\mathit{\alpha }}f(t)=f(t)-f(t_0).\end{array}$$ 4

Consider the real-valued memristor-based fractional-order neural networks (RVMFNNs) described by the following differential equation:

$$\begin{array}{c}\hfill D^{\mathit{\alpha }}{\mathit{\omega }}_p(t)=-e_p{\mathit{\omega }}_p(t)+\sum _{q=1}^n{\widehat{m}}_{pq}({\mathit{\omega }}_q(t)){\widehat{f}}_q({\mathit{\omega }}_q(t))+\sum _{q=1}^n{\widehat{n}}_{pq}({\mathit{\omega }}_q(t)){\widehat{g}}_q\left({\mathit{\omega }}_q(t-\mathit{\tau }(t))\right)+I_p,\end{array}$$ 5

where $t\ge 0,p=1,\dots ,n$, n corresponds to the number of units in a neural network, $\mathit{\omega }(t)={({\mathit{\omega }}_1(t),\dots ,{\mathit{\omega }}_n(t))}^T,{\mathit{\omega }}_p(t)$ denotes the state variable associated with the pth neuron, $e_p>0$ is a constant, $I_p$ denote external input vector, ${\widehat{f}}_q({\mathit{\omega }}_q(t))$ and ${\widehat{g}}_q({\mathit{\omega }}_q(t-\mathit{\tau }(t)))$ are the nonlinear activation functions of the qth unit at time t and $t-\mathit{\tau },{\widehat{m}}_{pq}({\mathit{\omega }}_q(t))$ and ${\widehat{n}}_{pq}({\mathit{\omega }}_q(t))$ are connection memristive weights without and with time delays, which are defined as

$$\begin{array}{c}\hfill {\widehat{m}}_{pq}({\mathit{\omega }}_q(t))=\frac{W_{pq}}{{\mathrm{C}}_p}\times \text{sgn}{}_{pq},{\widehat{n}}_{pq}({\mathit{\omega }}_q(t))=\frac{{\tilde{M}}_{pq}}{{\mathrm{C}}_p}\times \text{sgn}{}_{pq},\text{sgn}{}_{pq}=\left\{\begin{array}{cc}1,\hfill & p\ne q,\hfill \\ -1,\hfill & p=q,\hfill \end{array}\right.\end{array}$$ 6

in which $W_{pq}$ and ${\tilde{M}}_{pq}$ are represents the memductances of memristors $R_{pq}$ and $F_{pq}$. $R_{pq}$ represents the memristor between the activation function ${\widehat{f}}_p({\mathit{\omega }}_p(t))$ and ${\mathit{\omega }}_p(t)$ and $F_{pq}$ represents the memristor between the activation function ${\widehat{g}}_p({\mathit{\omega }}_p(t-\mathit{\tau }(t)))$ and ${\mathit{\omega }}_p(t)$.

Combining with the physical structure of a memristor device, then one see that

$$\begin{array}{c}\hfill W_{pq}=\frac{d{q}_{pq}}{d{\mathit{\sigma }}_{pq}},\text{and}{\tilde{M}}_{pq}=\frac{d{\tilde{q}}_{pq}}{d{\tilde{\mathit{\sigma }}}_{pq}},\end{array}$$ 7

where $q_{pq}$ and ${\tilde{q}}_{pq}$ are the charges corresponding to the memristors $R_{pq}$ and $F_{pq},{\mathit{\sigma }}_{pq}$ and ${\tilde{\mathit{\sigma }}}_{pq}$ are denotes magnetic flux corresponding to memristor $R_{pq}$ and $F_{pq}$ respectively.

The initial conditions associated with (5) are of the form

$${\mathit{\omega }}_p(t)={\mathit{\phi }}_p(t),t\in [-\mathit{\tau },0],p=1,\dots ,n,$$ 8

where ${\mathit{\phi }}_p(t)\in C([-\mathit{\tau },0],\mathcal{R}),$ and norm of an element in $C([-\mathit{\tau },0],{\mathcal{R}}^n)$ is $\Vert \mathit{\phi }\Vert ={\sum }_{p=1}^n{sup}_{t\in [-\mathit{\tau },0]}\{e^{-t}|{\mathit{\phi }}_p(t)|\}$.

Consider the CVMFNNs described by the following differential equation:

$$\begin{array}{c}\hfill D^{\mathit{\alpha }}{z}_p(t)=-{\mathit{ϵ}}_p{z}_p(t)+\sum _{q=1}^n{\widehat{\mathit{\beta }}}_{pq}(z_q(t))f_q(z_q(t))+\sum _{q=1}^n{\widehat{\mathit{\gamma }}}_{pq}(z_q(t))g_q\left(z_q(t-\mathit{\tau }(t))\right)+H_p,\end{array}$$ 9

where $t\ge 0,p=1,\dots ,n$, n corresponds to the number of units in a neural network, $z(t)={(z_1(t)\dots ,z_n(t))}^T,z_p(t)$ denotes the complex-valued state variable associated with the pth neuron, ${\mathit{ϵ}}_p>0$ is a constant, $H_p$ denote external input vector, $f_q(z_q(t))$ and $g_q(z_q(t-\mathit{\tau }(t)))$ are the nonlinear complex-valued activation functions of the q th unit at time t and $t-\mathit{\tau },{\widehat{\mathit{\beta }}}_{pq}(z_q(t))$ and ${\widehat{\mathit{\gamma }}}_{pq}(z_q(t))$ are complex-valued connection memristive weights without and with time delays, which are defined as

$$\begin{array}{c}\hfill {\widehat{\mathit{\beta }}}_{pq}(z_q(t))=\frac{{\mathbb{W}}_{pq}}{{\mathbf{C}}_p}\times \text{sgn}{}_{pq},{\widehat{\mathit{\gamma }}}_{pq}(z_q(t))=\frac{{\mathbb{M}}_{pq}}{{\mathbf{C}}_p}\times {\text{sgn}}_{pq},{\text{sgn}}_{pq}=\left\{\begin{array}{cc}1,\hfill & p\ne q,\hfill \\ -1,\hfill & p=q,\hfill \end{array}\right.\end{array}$$ 10

in which ${\mathbb{W}}_{pq}$ and ${\mathbb{M}}_{pq}$ are represents the memductances of memristors ${\mathbb{R}}_{pq}$ and ${\mathbb{F}}_{pq}$. ${\mathbb{R}}_{pq}$ represents the memristor between the activation function $f_p(z_p(t))$ and $z_p(t)$ and ${\mathbb{F}}_{pq}$ represents the memristor between the activation function $g_p(z_p(t-\mathit{\tau }(t)))$ and $z_p(t)$.

Combining with the physical structure of a memristor device, then one see that

$$\begin{array}{c}\hfill {\mathbb{W}}_{pq}=\frac{d{\mathbf{q}}_{pq}}{d{\mathit{\varsigma }}_{pq}},\text{and}{\mathbb{M}}_{pq}=\frac{d{\tilde{\mathbf{q}}}_{pq}}{d{\tilde{\mathit{\varsigma }}}_{pq}},\end{array}$$ 11

where ${\mathbf{q}}_{pq}$ and ${\tilde{\mathbf{q}}}_{pq}$ are the charges corresponding to the memristors ${\mathbb{R}}_{pq}$ and ${\mathbb{F}}_{pq},{\mathit{\varsigma }}_{pq}$ and ${\tilde{\mathit{\varsigma }}}_{pq}$ are denotes magnetic flux corresponding to memristor ${\mathbb{R}}_{pq}$ and ${\mathbb{F}}_{pq}$ respectively.

The initial conditions associated with (9) are of the form

$$\begin{array}{c}\hfill z_p(t)={\mathit{\psi }}_p(t)+i{\mathit{\chi }}_p(t),t\in [-\mathit{\tau },0],p=1,\dots ,n,\end{array}$$ 12

where ${\mathit{\psi }}_p(t),{\mathit{\chi }}_p(t)\in C([-\mathit{\tau },0],\mathcal{R}),$ and norm of an element in $C([-\mathit{\tau },0],{\mathcal{R}}^n)$ is $\Vert \mathit{\psi }\Vert ={\sum }_{p=1}^n{sup}_{t\in [-\mathit{\tau },0]}\{e^{-t}|{\mathit{\psi }}_p(t)|\}$ and $\Vert \mathit{\chi }\Vert ={\sum }_{p=1}^n{sup}_{t\in [-\mathit{\tau },0]}\{e^{-t}|{\mathit{\chi }}_p(t)|\}$.

Many studies show that pinched hysteresis loops are the fingerprint of memristive devices. Under different pinched hysteresis loops, the evolutionary tendency or process of memristive systems evolves into different forms. It is generally known that the pinched hysteresis loop is due to the nonlinearity of memductance function. As two typical memductance functions, in this paper, we discuss the following four cases.

Case 1

The memductance function $W_{pq}$ and ${\tilde{M}}_{pq}$ are given by

$$\begin{array}{c}\hfill W_{pq}=\left\{\begin{array}{cc}{a}_{pq},\hfill & |{\mathit{\sigma }}_{pq}|<l_{pq},\hfill \\ b_{pq},\hfill & |{\mathit{\sigma }}_{pq}|>l_{pq},\hfill \end{array}\right.{\tilde{M}}_{pq}=\left\{\begin{array}{cc}{a}_{pq}^{\prime },\hfill & |{\tilde{\mathit{\sigma }}}_{pq}|<l_{pq},\hfill \\ b_{pq}^{\prime },\hfill & |{\tilde{\mathit{\sigma }}}_{pq}|>l_{pq},\hfill \end{array}\right.\end{array}$$ 13

where $a_{pq},b_{pq},a_{pq}^{\prime },b_{pq}^{\prime }$ and $l_{pq}>0$ are constants, $p,q=1,2,\dots ,n$.

Case 2

The memductance function $W_{pq}$ and ${\tilde{M}}_{pq}$ are given by

$$\begin{array}{c}\hfill W_{pq}=c_{pq}+3d_{pq}{\mathit{\sigma }}_{pq}^2,{\tilde{M}}_{pq}=c_{pq}^{\prime }+3d_{pq}^{\prime }{\tilde{\mathit{\sigma }}}_{pq}^2,\end{array}$$ 14

where $c_{pq},d_{pq},c_{pq}^{\prime }$ and $d_{pq}^{\prime }$ are constants, $p,q=1,2,\dots ,n$.

Case 3

The complex-valued memductance function ${\mathbb{W}}_{pq}$ and ${\mathbb{M}}_{pq}$ are given by

$$\begin{array}{cc}\hfill {\mathbb{W}}_{pq}& =\left\{\begin{array}{cc}{\mathit{\theta }}_{pq},\hfill & |{\mathit{\varsigma }}_{pq}|<l_{pq},\hfill \\ {\mathit{\vartheta }}_{pq},\hfill & |{\mathit{\varsigma }}_{pq}|>l_{pq},\hfill \end{array}\right.{\mathbb{M}}_{pq}=\left\{\begin{array}{cc}{\mathit{\theta }}_{pq}^{\prime },\hfill & |{\tilde{\mathit{\varsigma }}}_{pq}|<l_{pq},\hfill \\ {\mathit{\vartheta }}_{pq}^{\prime },\hfill & |{\tilde{\mathit{\varsigma }}}_{pq}|>l_{pq},\hfill \end{array}\right.{\mathbb{W}}_{pq}^R=\left\{\begin{array}{cc}{\mathit{\theta }}_{pq}^R,\hfill & |{\mathit{\varsigma }}_{pq}^R|<l_{pq},\hfill \\ {\mathit{\vartheta }}_{pq}^R,\hfill & |{\mathit{\varsigma }}_{pq}^R|>l_{pq},\hfill \end{array}\right.\hfill \\ \hfill {\mathbb{M}}_{pq}^R& =\left\{\begin{array}{cc}{{\mathit{\theta }}^{\prime }}_{pq}^R,\hfill & |{\tilde{\mathit{\varsigma }}}_{pq}^R|<l_{pq},\hfill \\ {{\mathit{\vartheta }}^{\prime }}_{pq}^R,\hfill & |{\tilde{\mathit{\varsigma }}}_{pq}^R|>l_{pq},\hfill \end{array}\right.{\mathbb{W}}_{pq}^I=\left\{\begin{array}{cc}{\mathit{\theta }}_{pq}^I,\hfill & |{\mathit{\varsigma }}_{pq}^I|<l_{pq},\hfill \\ {\mathit{\vartheta }}_{pq}^I,\hfill & |{\mathit{\varsigma }}_{pq}^I|>l_{pq},\hfill \end{array}\right.{\mathbb{M}}_{pq}^I=\left\{\begin{array}{cc}{{\mathit{\theta }}^{\prime }}_{pq}^I,\hfill & |{\tilde{\mathit{\varsigma }}}_{pq}^I|<l_{pq},\hfill \\ {{\mathit{\vartheta }}^{\prime }}_{pq}^I,\hfill & |{\tilde{\mathit{\varsigma }}}_{pq}^I|>l_{pq},\hfill \end{array}\right.\hfill \end{array}$$ 15

where ${\mathit{\theta }}_{pq},{\mathit{\vartheta }}_{pq},{\mathit{\theta }}_{pq}^{\prime },{\mathit{\vartheta }}_{pq}^{\prime },{\mathit{\theta }}_{pq}^R,{\mathit{\vartheta }}_{pq}^R,{\mathit{\theta }}_{pq}^{\prime R},{\mathit{\vartheta }}_{pq}^{\prime R},{\mathit{\theta }}_{pq}^I,{\mathit{\vartheta }}_{pq}^I,{\mathit{\theta }}_{pq}^{\prime I},{\mathit{\vartheta }}_{pq}^{\prime I}$ and $l_{pq}>0$ are constants, $p,q=1,2,\dots ,n$.

Case 4

The complex-valued memductance function ${\mathbb{W}}_{pq}$ and ${\mathbb{M}}_{pq}$ are given by

$$\begin{array}{cc}\hfill {\mathbb{W}}_{pq}& ={\mathit{\rho }}_{pq}+3{\mathit{\varrho }}_{pq}{(\mathit{\varsigma })}_{pq}^2,{\mathbb{M}}_{pq}={\mathit{\rho }}_{pq}^{\prime }+3{\mathit{\varrho }}_{pq}^{\prime }{(\tilde{\mathit{\varsigma }})}_{pq}^2,{\mathbb{W}}_{pq}^R={\mathit{\rho }}_{pq}^R+3{\mathit{\varrho }}_{pq}^R{({\mathit{\varsigma }}^R)}_{pq}^2,\hfill \\ \hfill {\mathbb{M}}_{pq}^R& ={\mathit{\rho }}_{pq}^{\prime R}+3{\mathit{\varrho }}_{pq}^{\prime R}{({\tilde{\mathit{\varsigma }}}^R)}_{pq}^2,{\mathbb{W}}_{pq}^I={\mathit{\rho }}_{pq}^I+3{\mathit{\varrho }}_{pq}^I{({\mathit{\varsigma }}^I)}_{pq}^2,{\mathbb{M}}_{pq}^I={\mathit{\rho }}_{pq}^{\prime I}+3{\mathit{\varrho }}_{pq}^{\prime I}{({\tilde{\mathit{\varsigma }}}^I)}_{pq}^2,\hfill \end{array}$$ 16

where ${\mathit{\rho }}_{pq},{\mathit{\varrho }}_{pq},{\mathit{\rho }}_{pq}^{\prime },{\mathit{\varrho }}_{pq}^{\prime },{\mathit{\rho }}_{pq}^R,{\mathit{\varrho }}_{pq}^R,{\mathit{\rho }}_{pq}^{\prime R},{\mathit{\varrho }}_{pq}^{\prime R},{\mathit{\rho }}_{pq}^I,{\mathit{\varrho }}_{pq}^I,{\mathit{\rho }}_{pq}^{\prime I}$ and ${\mathit{\varrho }}_{pq}^{\prime I}$ are constants, $p,q=1,2,\dots ,n$.

According to the features of memristors given in cases 1–4, then the following four cases can be happen.

Case1′

In the case 1, then

$$\begin{array}{c}\hfill {\widehat{m}}_{pq}({\mathit{\omega }}_q(t))=\left\{\begin{array}{cc}{\widehat{m}}_{pq},\hfill & |{\mathit{\omega }}_q(t)|>T_q,\hfill \\ {\check{m}}_{pq},\hfill & |{\mathit{\omega }}_q(t)|<T_q,\hfill \end{array}\right.{\widehat{n}}_{pq}({\mathit{\omega }}_q(t))=\left\{\begin{array}{cc}{\widehat{n}}_{pq},\hfill & |{\mathit{\omega }}_q(t)|>T_q,\hfill \\ {\check{n}}_{pq},\hfill & |{\mathit{\omega }}_q(t)|<T_q,\hfill \end{array}\right.\end{array}$$ 17

where the switching jumps $T_q>0$, connection weights ${\widehat{m}}_{pq},{\check{m}}_{pq},{\widehat{n}}_{pq},$ and ${\check{n}}_{pq}$ are constants, $p,q=1,2,\dots ,n$.

Case 2′

In the case 2, ${\widehat{m}}_{pq}({\mathit{\omega }}_q(t))$ and ${\widehat{n}}_{pq}({\mathit{\omega }}_q(t))$ are continuous functions, then

$$\begin{array}{c}\hfill {\underline{\mathrm{\Lambda }}}_{pq}\le {\widehat{m}}_{pq}({\mathit{\omega }}_q(t))\le {\overline{\mathrm{\Lambda }}}_{pq}\text{and}{\underline{\mathrm{{\rm Y}}}}_{pq}\le {\widehat{n}}_{pq}({\mathit{\omega }}_q(t))\le {\overline{\mathrm{{\rm Y}}}}_{pq},\end{array}$$ 18

where ${\underline{\mathrm{\Lambda }}}_{pq},{\overline{\mathrm{\Lambda }}}_{pq},{\underline{\mathrm{{\rm Y}}}}_{pq}$ and ${\overline{\mathrm{{\rm Y}}}}_{pq}$ are constants, $p,q=1,2,\dots ,n$.

Case 3′

In the case 3, then

$$\begin{array}{cc}\hfill {\widehat{\mathit{\beta }}}_{pq}(z_q(t))& =\left\{\begin{array}{cc}{\widehat{\mathit{\beta }}}_{pq},\hfill & |z_q(t)|>T_q,\hfill \\ {\check{\mathit{\beta }}}_{pq},\hfill & |z_q(t)|<T_q,\hfill \end{array}\right.{\widehat{\mathit{\gamma }}}_{pq}(z_q(t))=\left\{\begin{array}{cc}{\widehat{\mathit{\gamma }}}_{pq},\hfill & |z_q(t)|>T_q,\hfill \\ {\check{\mathit{\gamma }}}_{pq},\hfill & |z_q(t)|<T_q,\hfill \end{array}\right.\hfill \\ \hfill {\widehat{\mathit{\beta }}}_{pq}^R(u_q(t))& =\left\{\begin{array}{cc}{\widehat{\mathit{\beta }}}_{pq}^R,\hfill & |u_q(t)|>T_q,\hfill \\ {\check{\mathit{\beta }}}_{pq}^R,\hfill & |u_q(t)|<T_q,\hfill \end{array}\right.{\widehat{\mathit{\gamma }}}_{pq}^R(u_q(t))=\left\{\begin{array}{cc}{\widehat{\mathit{\gamma }}}_{pq}^R,\hfill & |u_q(t)|>T_q,\hfill \\ {\check{\mathit{\gamma }}}_{pq}^R,\hfill & |u_q(t)|<T_q,\hfill \end{array}\right.\hfill \\ \hfill {\widehat{\mathit{\beta }}}_{pq}^I(v_q(t))& =\left\{\begin{array}{cc}{\widehat{\mathit{\beta }}}_{pq}^I,\hfill & |v_q(t)|>T_q,\hfill \\ {\check{\mathit{\beta }}}_{pq}^I,\hfill & |v_q(t)|<T_q,\hfill \end{array}\right.{\widehat{\mathit{\gamma }}}_{pq}^I(v_q(t))=\left\{\begin{array}{cc}{\widehat{\mathit{\gamma }}}_{pq}^I,\hfill & |v_q(t)|>T_q,\hfill \\ {\check{\mathit{\gamma }}}_{pq}^I,\hfill & |v_q(t)|<T_q,\hfill \end{array}\right.\hfill \end{array}$$ 19

where the switching jumps $T_q>0$, connections weights ${\widehat{\mathit{\beta }}}_{pq},{\check{\mathit{\beta }}}_{pq},{\widehat{\mathit{\gamma }}}_{pq},{\check{\mathit{\gamma }}}_{pq},{\widehat{\mathit{\beta }}}_{pq}^R,{\check{\mathit{\beta }}}_{pq}^R,{\widehat{\mathit{\gamma }}}_{pq}^R,{\check{\mathit{\gamma }}}_{pq}^R,{\widehat{\mathit{\beta }}}_{pq}^I,{\check{\mathit{\beta }}}_{pq}^I,{\widehat{\mathit{\gamma }}}_{pq}^I$ and ${\check{\mathit{\gamma }}}_{pq}^I$ are constants, $p,q=1,2,\dots ,n$.

Case 4′

In the case 4, ${\widehat{\mathit{\beta }}}_{pq}(z_q(t))$ and ${\widehat{\mathit{\gamma }}}_{pq}(z_q(t))$ are complex-valued continuous functions, then

$$\begin{array}{cc}\hfill {\underline{\mathrm{\Delta }}}_{pq}& \le {\widehat{\mathit{\beta }}}_{pq}(z_q(t))\le {\overline{\mathrm{\Delta }}}_{pq}\text{and}{\underline{\mathrm{\Theta }}}_{pq}\le {\widehat{\mathit{\gamma }}}_{pq}(z_q(t))\le {\overline{\mathrm{\Theta }}}_{pq},\hfill \\ \hfill {\underline{\mathrm{\Delta }}}_{pq}^R& \le {\widehat{\mathit{\beta }}}_{pq}^R(u_q(t))\le {\overline{\mathrm{\Delta }}}_{pq}^R\text{and}{\underline{\mathrm{\Theta }}}_{pq}^R\le {\widehat{\mathit{\gamma }}}_{pq}^R(u_q(t))\le {\overline{\mathrm{\Theta }}}_{pq}^R,\hfill \\ \hfill {\underline{\mathrm{\Delta }}}_{pq}^I& \le {\widehat{\mathit{\beta }}}_{pq}^I(v_q(t))\le {\overline{\mathrm{\Delta }}}_{pq}^I\text{and}{\underline{\mathrm{\Theta }}}_{pq}^I\le {\widehat{\mathit{\gamma }}}_{pq}^I(v_q(t))\le {\overline{\mathrm{\Theta }}}_{pq}^I,\hfill \end{array}$$ 20

where ${\underline{\mathrm{\Delta }}}_{pq},{\overline{\mathrm{\Delta }}}_{pq},{\underline{\mathrm{\Theta }}}_{pq},{\overline{\mathrm{\Theta }}}_{pq},{\underline{\mathrm{\Delta }}}_{pq}^R,{\overline{\mathrm{\Delta }}}_{pq}^R,{\underline{\mathrm{\Theta }}}_{pq}^R,{\overline{\mathrm{\Theta }}}_{pq}^R,{\underline{\mathrm{\Delta }}}_{pq}^I,{\overline{\mathrm{\Delta }}}_{pq}^I,{\underline{\mathrm{\Theta }}}_{pq}^I$, and ${\overline{\mathrm{\Theta }}}_{pq}^I$ are constants, $p,q=1,2,\dots ,n$.

Remark 1

The memristor-based neural networks is one of the special kind of differential equations with discontinuous right-hand sides because that it is a state-dependent switching system. Thus, the connection weights are changed depending on their state variable. It shows that the solutions of this differential equation are not yet been calculated in the straightforward manner. Therefore, Filippov (1988) proposed a solution method, that to transform differential equations with discontinuous right-hand sides into a differential inclusion by using the theories of differential inclusion. Many of the authors studied the memristor-based neural networks and proposed some good results in the framework of Filippov solution see Zhang et al. (2013), Yang et al. (2014), Wu and Zeng (2012, 2013, 2014), Wu et al. (2011, 2013a, b), Cai and Huang (2014), Guo et al. (2013), Qi et al. (2014), Wen et al. (2013), Chen et al. (2014) and references therein. If the connection weights are not changed according to the state variable then the memristor-based neural networks become a class of conventional neural networks system.

Definition 3

A set-valued map $\mathcal{F}$ with nonempty values is said to be upper-semicontinuous at $x_0\in \mathcal{E}\subset {\mathcal{R}}^n$ if, for any open set $\mathcal{P}$ containing $\mathcal{F}(x_0)$, there exists a neighborhood $\mathcal{Q}$ of $x_0$ such that $\mathcal{F}(\mathcal{Q})\subset \mathcal{P},\mathcal{F}(x)$ is said to have a closed (convex, compact) image if for each $x\in \mathcal{E},\mathcal{F}(x)$ is closed (convex, compact).

Definition 4

For the system $\frac{dx}{dt}=g(x),x\in {\mathcal{R}}^n$, with discontinuous right-hand sides, a set-valued map is defined as

$$\begin{array}{c}\hfill \mathrm{\Phi }(x)=\bigcap _{\mathit{\delta }>0}\bigcap _{\mathit{\mu }(\mathcal{P})=0}\overline{co}\left[g(\mathcal{B}(x,\mathit{\delta }))╲\mathcal{P}\right],\end{array}$$

where $\overline{co}[\mathcal{E}]$ is the closure of the convex hull of set $\mathcal{E},\mathcal{B}(x,\mathit{\delta })=\{y:\Vert y-x\Vert \le \mathit{\delta }\},$ and $\mathit{\mu }(\mathcal{P})$ is a Lebesgue measure of set $\mathcal{P}$. A solution in Filippov’s sense of the Cauchy problem for this system with initial condition $x(0)=x_0$ is an absolutely continuous function $x(t),t\in [0,T]$, which satisfies $x(0)=x_0$ and the differential inclusion:

$$\begin{array}{c}\hfill \frac{dx}{dt}\in \mathrm{\Phi }(x),\text{for}\text{a.e.}t\in [0,T].\end{array}$$

Definition 5

The solution of systems (5) and (9) is said to be stable if for any $\mathit{\epsilon }>0$ there exists $\mathit{\delta }(t_0,\mathit{\epsilon })>0$ such that $t\ge t_0\ge 0,\Vert \mathit{\chi }(t)-\mathit{\psi }(t)\Vert <\mathit{\delta }$ implies $\Vert z_1(t,t_0,\mathit{\chi })-z(t,t_0,\mathit{\psi })\Vert <\mathit{\epsilon }$ for any two solutions $z_1(t,t_0,\mathit{\chi })$ and $z(t,t_0,\mathit{\psi })$. It is uniformly stable if the above $\mathit{\delta }$ is independent of $t_0$.

Assumption 1

${\widehat{f}}_q(·),{\widehat{g}}_q(·)$ satisfy the Lipschitz conditions, i.e., for any $x,y\in \mathcal{R},$ there exist positive constants $L_q,G_q$ such that

$$\begin{array}{c}\hfill \Vert {\widehat{f}}_q(x)-{\widehat{f}}_q(y)\Vert \le L_q\Vert x-y\Vert ,\Vert {\widehat{g}}_q(x)-{\widehat{g}}_q(y)\Vert \le G_q\Vert x-y\Vert .\end{array}$$ 21

Assumption 2

$e_p,m_{pq},n_{pq},L_q$ and $G_q$ satisfy the following conditions:

$$\begin{array}{c}\hfill \Vert m^{\ast }\Vert +\Vert n^{\ast }\Vert <\overline{e},\end{array}$$

$$\begin{array}{cc}& \text{where}\overline{e}=min(1-e_{max},e_{min}),e_{max}=\underset{\forall q}{max}\{e_q\},e_{min}=\underset{\forall q}{min}\{e_q\},\hfill \\ \hfill & \Vert m^{\ast }\Vert =\sum _{p=1}^n|m_p^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\{|m_{pq}|L_q\},\Vert n^{\ast }\Vert =\sum _{p=1}^n|n_p^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|n_{pq}|G_q\right\}.\hfill \end{array}$$

Assumption 3

${\mathit{ϵ}}_p,{\mathit{\beta }}_{pq},{\mathit{\gamma }}_{pq},{\mathit{\lambda }}_q$ and ${\mathit{\mu }}_q$ satisfy the following conditions:

$$\begin{array}{c}\hfill \sum _{q=1}^n\Vert {\mathit{\zeta }}_q^{\ast }\Vert +\sum _{q=1}^n\Vert {\mathit{\eta }}_q^{\ast }\Vert +\sum _{q=1}^n\Vert {\mathit{\xi }}_q^{\ast }\Vert +\sum _{q=1}^n\Vert {\mathit{\pi }}_q^{\ast }\Vert <\overline{\mathit{ϵ}},\end{array}$$

$$\begin{array}{cc}& \text{where}\overline{\mathit{ϵ}}=min(|1-{\mathit{ϵ}}_{max}|,{\mathit{ϵ}}_{min}),{\mathit{ϵ}}_{max}=\underset{\forall p}{max}\left\{{\mathit{ϵ}}_p\right\},{\mathit{ϵ}}_{min}=\underset{\forall p}{min}\left\{{\mathit{ϵ}}_p\right\},\hfill \\ \hfill & \Vert {\mathit{\zeta }}^{\ast }\Vert =\sum _{p=1}^n|{\mathit{\zeta }}_p^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|{\mathit{\beta }}_{pq}|{\mathit{\lambda }}_q\right\},\Vert {\mathit{\eta }}^{\ast }\Vert =\sum _{p=1}^n|{\mathit{\eta }}_p^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|{\mathit{\gamma }}_{pq}|{\mathit{\mu }}_q\right\},\hfill \\ \hfill & \Vert {\mathit{\zeta }}_1^{\ast }\Vert =\sum _{p=1}^n|{\mathit{\zeta }}_{1p}^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|{\mathit{\beta }}_{pq}^R|{\mathit{\lambda }}_q^{RR}\right\},\Vert {\mathit{\zeta }}_2^{\ast }\Vert =\sum _{p=1}^n|{\mathit{\zeta }}_{2p}^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|{\mathit{\beta }}_{pq}^R|{\mathit{\lambda }}_q^{RI}\right\},\hfill \\ \hfill & \Vert {\mathit{\zeta }}_3^{\ast }\Vert =\sum _{p=1}^n|{\mathit{\zeta }}_{3p}^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|{\mathit{\beta }}_{pq}^I|{\mathit{\lambda }}_q^{IR}\right\},\Vert {\mathit{\zeta }}_4^{\ast }\Vert =\sum _{p=1}^n|{\mathit{\zeta }}_{4p}^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|{\mathit{\beta }}_{pq}^I|{\mathit{\lambda }}_q^{II}\right\},\hfill \\ \hfill & \Vert {\mathit{\eta }}_1^{\ast }\Vert =\sum _{p=1}^n|{\mathit{\eta }}_{1p}^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|{\mathit{\gamma }}_{pq}^R|{\mathit{\mu }}_q^{RR}\right\},\Vert {\mathit{\eta }}_2^{\ast }\Vert =\sum _{p=1}^n|{\mathit{\eta }}_{2p}^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|{\mathit{\gamma }}_{pq}^R|{\mathit{\mu }}_q^{RI}\right\},\hfill \\ \hfill & \Vert {\mathit{\eta }}_3^{\ast }\Vert =\sum _{p=1}^n|{\mathit{\eta }}_{3p}^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|{\mathit{\gamma }}_{pq}^I|{\mathit{\mu }}_q^{IR}\right\},\Vert {\mathit{\eta }}_4^{\ast }\Vert =\sum _{p=1}^n|{\mathit{\eta }}_{4p}^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|{\mathit{\gamma }}_{pq}^I|{\mathit{\mu }}_q^{II}\right\},\hfill \\ \hfill & \Vert {\mathit{\xi }}_1^{\ast }\Vert =\sum _{p=1}^n|{\mathit{\xi }}_{1p}^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|{\mathit{\beta }}_{pq}^I|{\mathit{\lambda }}_q^{RR}\right\},\Vert {\mathit{\xi }}_2^{\ast }\Vert =\sum _{p=1}^n|{\mathit{\xi }}_{2p}^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|{\mathit{\beta }}_{pq}^I|{\mathit{\lambda }}_q^{RI}\right\},\hfill \\ \hfill & \Vert {\mathit{\xi }}_3^{\ast }\Vert =\sum _{p=1}^n|{\mathit{\xi }}_{3p}^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|{\mathit{\beta }}_{pq}^R|{\mathit{\lambda }}_q^{IR}\right\},\Vert {\mathit{\xi }}_4^{\ast }\Vert =\sum _{p=1}^n|{\mathit{\xi }}_{4p}^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|{\mathit{\beta }}_{pq}^R|{\mathit{\lambda }}_q^{II}\right\},\hfill \\ \hfill & \Vert {\mathit{\pi }}_1^{\ast }\Vert =\sum _{p=1}^n|{\mathit{\pi }}_{1p}^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|{\mathit{\gamma }}_{pq}^I|{\mathit{\mu }}_q^{RR}\right\},\Vert {\mathit{\pi }}_2^{\ast }\Vert =\sum _{p=1}^n|{\mathit{\pi }}_{2p}^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|{\mathit{\gamma }}_{pq}^I|{\mathit{\mu }}_q^{RI}\right\},\hfill \\ \hfill & \Vert {\mathit{\pi }}_3^{\ast }\Vert =\sum _{p=1}^n|{\mathit{\pi }}_{3p}^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|{\mathit{\gamma }}_{pq}^R|{\mathit{\mu }}_q^{IR}\right\},\Vert {\mathit{\pi }}_4^{\ast }\Vert =\sum _{p=1}^n|{\mathit{\pi }}_{4p}^{\ast }|=\sum _{p=1}^n\underset{\forall q}{max}\left\{|{\mathit{\gamma }}_{pq}^R|{\mathit{\mu }}_q^{II}\right\}.\hfill \end{array}$$

Assumption 4

Let $z=u+iv$, where $i$ denotes the imaginary unit, that is, $i=\sqrt{-1}$. $f_q(z)$ and $g_q(z(t-\mathit{\tau }))$ can be expressed by separating into its real and imaginary part as

$$\begin{array}{cc}\hfill f_q(z)=& f_q^R(u,v)+i{f}_q^I(u,v)\text{and}\hfill \\ \hfill g_q(z(t-\mathit{\tau }))=& g_q^R(u(t-\mathit{\tau }),v(t-\mathit{\tau }))+i{g}_q^I(u(t-\mathit{\tau }),v(t-\mathit{\tau })),\hfill \end{array}$$

where $f_q^R(·,·):{\mathcal{R}}^2⟶\mathcal{R}$ and $f_q^I(·,·):{\mathcal{R}}^2⟶\mathcal{R}$ and $g_q^R(·,·):{\mathcal{R}}^2⟶\mathcal{R}$ and $g_q^I(·,·):{\mathcal{R}}^2⟶\mathcal{R}$. For notational simplicity, $u(t-\mathit{\tau })$ and $v(t-\mathit{\tau })$ are denoted by $u_{\mathit{\tau }}$ and $v_{\mathit{\tau }}$ respectively.

1. The partial derivatives of $f_q(·,·)$ with respect to $u,v$: $\mathit{\partial }{f}_q^R/\mathit{\partial }u,\mathit{\partial }{f}_q^R/\mathit{\partial }v,\mathit{\partial }{f}_q^I/\mathit{\partial }u$ and $\mathit{\partial }{f}_q^I/\mathit{\partial }v$ exist and are continuous. Similarly, the partial derivatives of $g_q(·,·)$ with respect to $u,v$: $\mathit{\partial }{g}_q^R/\mathit{\partial }u,\mathit{\partial }{g}_q^R/\mathit{\partial }v,\mathit{\partial }{g}_q^I/\mathit{\partial }u$ and $\mathit{\partial }{g}_q^I/\mathit{\partial }v$ exist and are continuous.

2. The partial derivatives $\mathit{\partial }{f}_q^R/\mathit{\partial }u,\mathit{\partial }{f}_q^R/\mathit{\partial }v,\mathit{\partial }{f}_q^I/\mathit{\partial }u$ and $\mathit{\partial }{f}_q^I/\mathit{\partial }v$ are bounded, that is, there exist positive constant numbers ${\mathit{\lambda }}_q^{RR},{\mathit{\lambda }}_q^{RI},{\mathit{\lambda }}_q^{IR},{\mathit{\lambda }}_q^{II}$ such that

   $$\begin{array}{c}\hfill |\mathit{\partial }{f}_q^R/\mathit{\partial }u|\le {\mathit{\lambda }}_q^{RR},|\mathit{\partial }{f}_q^R/\mathit{\partial }v|\le {\mathit{\lambda }}_q^{RI},|\mathit{\partial }{f}_q^I/\mathit{\partial }u|\le {\mathit{\lambda }}_q^{IR},|\mathit{\partial }{f}_q^I/\mathit{\partial }v|\le {\mathit{\lambda }}_q^{II}.\end{array}$$
3. Also, the partial derivatives $\mathit{\partial }{g}_q^R/\mathit{\partial }u,\mathit{\partial }{g}_q^R/\mathit{\partial }v,\mathit{\partial }{g}_q^I/\mathit{\partial }u$ and $\mathit{\partial }{g}_q^I/\mathit{\partial }v$ are bounded, that is, there exist positive constant numbers ${\mathit{\mu }}_q^{RR},{\mathit{\mu }}_q^{RI},{\mathit{\mu }}_q^{IR},{\mathit{\mu }}_q^{II}$ such that

   $$\begin{array}{c}\hfill |\mathit{\partial }{g}_q^R/\mathit{\partial }u|\le {\mathit{\mu }}_q^{RR},|\mathit{\partial }{g}_q^R/\mathit{\partial }v|\le {\mathit{\mu }}_q^{RI},|\mathit{\partial }{g}_q^I/\mathit{\partial }u|\le {\mathit{\mu }}_q^{IR},|\mathit{\partial }{g}_q^I/\mathit{\partial }v|\le {\mathit{\mu }}_q^{II}.\end{array}$$

   Then, according to the mean value theorem for multivariable functions, we have that for any $u,u^{\prime },v,v^{\prime }\in {\mathcal{R}}^n$

   $$\begin{array}{cc}\hfill |f_q^R(u^{\prime },v^{\prime })-f_q^R(u,v)|& \le {\mathit{\lambda }}_q^{RR}|u^{\prime }-u|+{\mathit{\lambda }}_q^{RI}|v^{\prime }-v|,\hfill \\ \hfill |f_q^I(u^{\prime },v^{\prime })-f_q^I(u,v)|& \le {\mathit{\lambda }}_q^{IR}|u^{\prime }-u|+{\mathit{\lambda }}_q^{II}|v^{\prime }-v|,\hfill \\ \hfill |g_q^R(u_{\mathit{\tau }}^{\prime },v_{\mathit{\tau }}^{\prime })-g_q^R(u_{\mathit{\tau }},v_{\mathit{\tau }})|& \le {\mathit{\mu }}_q^{RR}|u_{\mathit{\tau }}^{\prime }-u_{\mathit{\tau }}|+{\mathit{\mu }}_q^{RI}|v_{\mathit{\tau }}^{\prime }-v_{\mathit{\tau }}|,\hfill \\ \hfill |g_q^I(u_{\mathit{\tau }}^{\prime },v_{\mathit{\tau }}^{\prime })-g_q^I(u_{\mathit{\tau }},v_{\mathit{\tau }})|& \le {\mathit{\mu }}_q^{IR}|u_{\mathit{\tau }}^{\prime }-u_{\mathit{\tau }}|+{\mathit{\mu }}_q^{II}|v_{\mathit{\tau }}^{\prime }-v_{\mathit{\tau }}|.\hfill \end{array}$$ 22

Assumption 5

$f_q(·),g_q(·)$ satisfy the Lipschitz conditions in the complex domain, i.e., for any $u,v\in \mathcal{C},$ there exist positive constants ${\mathit{\lambda }}_q,{\mathit{\mu }}_q$ such that

$$\begin{array}{c}\hfill \Vert f_q(u)-f_q(v)\Vert \le {\mathit{\lambda }}_q\Vert u-v\Vert ,\Vert g_q(u)-g_q(v)\Vert \le {\mathit{\mu }}_q\Vert u-v\Vert .\end{array}$$ 23

Main results

In this section, some sufficient conditions for the existence, uniqueness and uniform stability of considered both RVMFNNs and CVMFNNs are derived.

Real-valued memristor-based fractional-order neural networks

We first consider RVMFNNs with time delays and two different types of memductance functions. By using Filippov’s solution, differential inclusion and Banach contraction principle, some sufficient conditions are obtained to ensure the existence, uniqueness and uniform stability of considered RVMFNNs.

Theorem 1

Under the case$1^{\prime }$, if Assumption 1–2 are satisfied, then the system (5) is satisfying the initial condition (8) is uniformly stable.

Proof

By theories of differential inclusions and set-valued maps, from (5), if follows that

$$\begin{array}{c}\hfill D^{\mathit{\alpha }}{\mathit{\omega }}_p(t)\in -e_p{\mathit{\omega }}_p(t)+\sum _{q=1}^{n}co\{{\widehat{m}}_{pq},{\check{m}}_{pq}\}{\widehat{f}}_q({\mathit{\omega }}_q)+\sum _{q=1}^{n}co\{{\widehat{n}}_{pq},{\check{n}}_{pq}\}{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }})+I_p,\end{array}$$ 24

or equivalently, for $p,q=1,2,\dots ,n,$ there exists a measurable functions ${\tilde{m}}_{pq}(t)\in co\{{\widehat{m}}_{pq},{\check{m}}_{pq}\}$ and ${\tilde{n}}_{pq}(t)\in co\{{\widehat{n}}_{pq},{\check{n}}_{pq}\}$ such that

$$\begin{array}{c}\hfill D^{\mathit{\alpha }}{\mathit{\omega }}_p(t)=-e_p{\mathit{\omega }}_p(t)+\sum _{q=1}^n{\tilde{m}}_{pq}(t){\widehat{f}}_q({\mathit{\omega }}_q)+\sum _{q=1}^n{\tilde{n}}_{pq}{(t)}_{pq}{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }})+I_p,\end{array}$$ 25

for $p,q=1,2,\dots ,n,|{\tilde{m}}_{pq}(t)|\le max\{|{\widehat{m}}_{pq}|,|{\check{m}}_{pq}|\}\le m_{pq}$ and $|{\tilde{n}}_{pq}(t)|\le max\{|{\widehat{n}}_{pq}|,|{\check{n}}_{pq}|\}\le n_{pq}$.

Consider ${\mathit{\omega }}^{\prime }$ and $\mathit{\omega }$ with ${\mathit{\omega }}^{\prime }\ne \mathit{\omega }$. ${\mathit{\omega }}^{\prime }(t)=({\mathit{\omega }}_1^{\prime }(t),\dots ,{\mathit{\omega }}_n^{\prime }(t))$ and $\mathit{\omega }(t)=({\mathit{\omega }}_1(t),\dots ,{\mathit{\omega }}_n(t))$ are any two solutions of the system (5) with initial conditions ${\mathit{\omega }}_p^{\prime }(s)={\mathit{\phi }}_p^{\prime }(s),$ where ${\mathit{\phi }}_p^{\prime }(s)\in C([-\mathit{\tau },0],{\mathcal{R}}^n),{\mathit{\phi }}_p^{\prime }(0)=0,{\mathit{\omega }}_p(s)={\mathit{\phi }}_p(s)$, where ${\mathit{\phi }}_p(s)\in C([-\mathit{\tau },0],{\mathcal{R}}^n),{\mathit{\phi }}_p(0)=0,p\in n$. We have

$$\begin{array}{cc}\hfill D^{\mathit{\alpha }}({\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t))& \le -e_p({\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t))+\sum _{q=1}^n{m}_{pq}[{\widehat{f}}_q({\mathit{\omega }}_q^{\prime })-{\widehat{f}}_q({\mathit{\omega }}_q)]\hfill \\ \hfill & +\sum _{q=1}^n{n}_{pq}[{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }}^{\prime })-{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }})].\hfill \end{array}$$

Now multiply $D^{-\mathit{\alpha }}$ on both sides, we can write

$$\begin{array}{cc}\hfill {\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)& \le D^{-\mathit{\alpha }}[-e_p({\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t))+\sum _{q=1}^n{m}_{pq}[{\widehat{f}}_q({\mathit{\omega }}_q^{\prime })-{\widehat{f}}_q({\mathit{\omega }}_q)]\hfill \\ \hfill & +\sum _{q=1}^n{n}_{pq}[{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }}^{\prime })-{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }})]],\hfill \end{array}$$ 26

From (26), we have

$$\begin{array}{cc}\hfill {\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)& \le \frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}[-e_p({\mathit{\omega }}_p^{\prime }(s)-{\mathit{\omega }}_p(s))+\sum _{q=1}^n{m}_{pq}\left[{\widehat{f}}_q({\mathit{\omega }}_q^{\prime })-{\widehat{f}}_q({\mathit{\omega }}_q)\right]\hfill \\ \hfill & +\sum _{q=1}^n{n}_{pq}\left[{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }}^{\prime })-{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }})\right]]\mathrm{d}s.\hfill \end{array}$$

By taking absolute value and multiply $e^{-t}$ on both sides, we get

$$\begin{array}{cc}\hfill e^{-t}|{\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)|& \le \frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{e}^{-t}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}[e_p|{\mathit{\omega }}_p^{\prime }(s)-{\mathit{\omega }}_p(s)|\hfill \\ \hfill & +\sum _{q=1}^n|m_{pq}||{\widehat{f}}_q({\mathit{\omega }}_q^{\prime })-{\widehat{f}}_q({\mathit{\omega }}_q)|+\sum _{q=1}^n|n_{pq}||{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }}^{\prime })-{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }})|]\mathrm{d}s\hfill \\ \hfill & \le e_p\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|{\mathit{\omega }}_p^{\prime }(s)-{\mathit{\omega }}_p(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|m_{pq}|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}[L_q|{\mathit{\omega }}_q^{\prime }(s)-{\mathit{\omega }}_q(s)|]\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|n_{pq}|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}[G_q|{\mathit{\omega }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\omega }}_{q\mathit{\tau }}(s)|]\mathrm{d}s\hfill \\ \hfill & \le e_p\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|{\mathit{\omega }}_p^{\prime }(s)-{\mathit{\omega }}_p(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|m_{pq}|L_q\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|{\mathit{\omega }}_q^{\prime }(s)-{\mathit{\omega }}_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|n_{pq}|G_q\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|{\mathit{\omega }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\omega }}_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & \le e_p\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u+\sum _{q=1}^n|m_{pq}|L_q\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|{\mathit{\omega }}_q^{\prime }(s)-{\mathit{\omega }}_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|n_{pq}|G_q\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{\mathit{\tau }}{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|{\mathit{\phi }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\phi }}_{q\mathit{\tau }}(s)|\mathrm{d}s+\sum _{q=1}^n|n_{pq}|G_q\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{\mathit{\tau }}^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|{\mathit{\omega }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\omega }}_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill e^{-t}|{\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)|& \le e_p\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +m_p^{\ast }\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_q^{\prime }(t)-{\mathit{\omega }}_q(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +n_p^{\ast }\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{-\mathit{\tau }}^0{(t-\mathit{\gamma }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\gamma })}{e}^{-\mathit{\gamma }}|{\mathit{\phi }}_q^{\prime }(\mathit{\gamma })-{\mathit{\phi }}_q(\mathit{\gamma })|\mathrm{d}\mathit{\gamma }\hfill \\ \hfill & +n_p^{\ast }\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{(t-\mathit{\gamma }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\gamma })}{e}^{-\mathit{\gamma }}\times |{\mathit{\omega }}_q^{\prime }(\mathit{\gamma })-{\mathit{\omega }}_q(\mathit{\gamma })|\mathrm{d}\mathit{\gamma }\hfill \\ \hfill & \le e_p\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +m_p^{\ast }\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_q^{\prime }(t)-{\mathit{\omega }}_q(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +n_p^{\ast }\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\phi }}_q^{\prime }(t)-{\mathit{\phi }}_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{t-\mathit{\tau }}^t{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & +n_p^{\ast }\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_q^{\prime }(t)-{\mathit{\omega }}_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & \le e_p\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)|\}+m_p^{\ast }\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_q^{\prime }(t)-{\mathit{\omega }}_q(t)|\}\hfill \\ \hfill & +n_p^{\ast }\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\phi }}_q^{\prime }(t)-{\mathit{\phi }}_q(t)|\}{e}^{-\mathit{\tau }}+n_p^{\ast }\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_q^{\prime }(t)-{\mathit{\omega }}_q(t)|\}{e}^{-\mathit{\tau }}\hfill \\ \hfill & \le e_p\underset{t}{sup}\left\{e^{-t}|{\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)|\right\}+m_p^{\ast }\Vert {\mathit{\omega }}^{\prime }(t)-\mathit{\omega }(t)\Vert +n_p^{\ast }\Vert {\mathit{\phi }}^{\prime }(t)-\mathit{\phi }(t)\Vert +n_p^{\ast }\Vert {\mathit{\omega }}^{\prime }(t)-{\mathit{\omega }}_{(}t)\Vert .\hfill \end{array}$$ 27

From (27), we can obtain

$$\begin{array}{cc}\hfill \Vert {\mathit{\omega }}^{\prime }(t)-\mathit{\omega }(t)\Vert & =\sum _{j=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)|\}\hfill \\ \hfill & \le \left[e_{max}+\Vert m^{\ast }\Vert +\Vert n^{\ast }\Vert \right]\Vert {\mathit{\omega }}^{\prime }(t)-\mathit{\omega }(t)\Vert +\left[\Vert n^{\ast }\Vert \right]\Vert {\mathit{\phi }}^{\prime }(t)-\mathit{\phi }(t)\Vert .\hfill \end{array}$$ 28

The above Eq. (28) can be rewritten as

$$\begin{array}{c}\hfill \Vert {\mathit{\omega }}^{\prime }(t)-\mathit{\omega }(t)\Vert \le \frac{\Vert n^{\ast }\Vert }{1-\left(e_{max}+\Vert m^{\ast }\Vert +\Vert n^{\ast }\Vert \right)}\Vert {\mathit{\phi }}^{\prime }(t)-\mathit{\phi }(t)\Vert .\end{array}$$ 29

From (29), we can say that for $\forall \mathit{\epsilon }>0,$ then there exist a $\mathit{\delta }=\frac{1-\left(e_{max}+\Vert m^{\ast }\Vert +\Vert n^{\ast }\Vert \right)}{\Vert n^{\ast }\Vert }\mathit{\epsilon }>0$ such that $\Vert {\mathit{\omega }}^{\prime }(t)-\mathit{\omega }(t)\Vert <\mathit{\epsilon }$ when $\Vert {\mathit{\phi }}^{\prime }(t)-\mathit{\phi }(t)\Vert <\mathit{\delta }$. Thus, the solution $\mathit{\omega }(t)$ is uniformly stable.

Theorem 2

Under the case$2^{\prime }$, if Assumption 1–2 are satisfied, then the system (5) is satisfying the initial condition (8) is uniformly stable.

Proof

By (5), if follows that

$$\begin{array}{c}\hfill D^{\mathit{\alpha }}{\mathit{\omega }}_p(t)\le -e_p{\mathit{\omega }}_p(t)+\sum _{q=1}^n{\tilde{\mathrm{\Lambda }}}_{pq}{\widehat{f}}_q({\mathit{\omega }}_q)+\sum _{q=1}^n{\widetilde{\mathrm{{\rm Y}}}}_{pq}{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }})+I_p,\end{array}$$ 30

Transform (30) into the compact form as follows:

$$\begin{array}{c}\hfill D^{\mathit{\alpha }}\mathit{\omega }(t)\le -E\mathit{\omega }(t)+\tilde{\mathrm{\Lambda }}\widehat{f}(\mathit{\omega }(t))+\widetilde{\mathrm{{\rm Y}}}\widehat{g}\left(\mathit{\omega }(t-\mathit{\tau }(t))\right)+I,\end{array}$$ 31

where $\mathit{\omega }(t)={({\mathit{\omega }}_1(t),\dots ,{\mathit{\omega }}_n(t))}^T,I={(I_1,\dots ,I_n)}^T,\widehat{f}(\mathit{\omega }(t))={({\widehat{f}}_1({\mathit{\omega }}_1(t)),\dots ,{\widehat{f}}_n({\mathit{\omega }}_n(t)))}^T$$\widehat{g}(\mathit{\omega }(t-\mathit{\tau }(t)))={({\widehat{g}}_1({\mathit{\omega }}_1(t-\mathit{\tau }(t))),\dots ,{\widehat{g}}_n({\mathit{\omega }}_n(t-\mathit{\tau }(t))))}^T,$${\tilde{\mathrm{\Lambda }}}_{pq}=max\{|{\underline{\mathrm{\Lambda }}}_{pq}|,|{\overline{\mathrm{\Lambda }}}_{pq}|\},\tilde{\mathrm{\Lambda }}={({\tilde{\mathrm{\Lambda }}}_{pq})}_{n\times n},{\widetilde{\mathrm{{\rm Y}}}}_{pq}=max\{|{\underline{\mathrm{{\rm Y}}}}_{pq}|,|{\overline{\mathrm{{\rm Y}}}}_{pq}|\},\widetilde{\mathrm{{\rm Y}}}={({\widetilde{\mathrm{{\rm Y}}}}_{pq})}_{n\times n}$.

Consider ${\mathit{\omega }}^{\prime }$ and $\mathit{\omega }$ with ${\mathit{\omega }}^{\prime }\ne \mathit{\omega }$. ${\mathit{\omega }}^{\prime }(t)=({\mathit{\omega }}_1^{\prime }(t),\dots ,{\mathit{\omega }}_n^{\prime }(t))$ and $\mathit{\omega }(t)=({\mathit{\omega }}_1(t),\dots ,{\mathit{\omega }}_n(t))$ are any two solutions of the system (31) with initial conditions ${\mathit{\omega }}_p^{\prime }(s)={\mathit{\phi }}_p^{\prime }(s),$ where ${\mathit{\phi }}_p^{\prime }(s)\in C([-\mathit{\tau },0],{\mathcal{R}}^n),{\mathit{\phi }}_p^{\prime }(0)=0,{\mathit{\omega }}_p(s)={\mathit{\phi }}_p(s)$, where ${\mathit{\phi }}_p(s)\in C([-\mathit{\tau },0],{\mathcal{R}}^n),{\mathit{\phi }}_p(0)=0,p\in n$. We have

$$\begin{array}{cc}\hfill D^{\mathit{\alpha }}({\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t))\le & -e_p({\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t))+\sum _{q=1}^n{\tilde{\mathrm{\Lambda }}}_{pq}\left[{\widehat{f}}_q({\mathit{\omega }}_q^{\prime })-{\widehat{f}}_q({\mathit{\omega }}_q)\right]\hfill \\ \hfill & +\sum _{q=1}^n{\widetilde{\mathrm{{\rm Y}}}}_{pq}\left[{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }}^{\prime })-{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }})\right].\hfill \end{array}$$

Now multiply by $D^{-\mathit{\alpha }}$ on both sides, we can write

$$\begin{array}{cc}\hfill {\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)\le & D^{-\mathit{\alpha }}[-e_p({\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t))+\sum _{q=1}^n{\tilde{\mathrm{\Lambda }}}_{pq}\left[{\widehat{f}}_q({\mathit{\omega }}_q^{\prime })-{\widehat{f}}_q({\mathit{\omega }}_q)\right]\hfill \\ \hfill & +\sum _{q=1}^n{\widetilde{\mathrm{{\rm Y}}}}_{pq}\left[{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }}^{\prime })-{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }})\right]],\hfill \end{array}$$ 32

From (32), we have

$$\begin{array}{cc}\hfill {\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)& \le \frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}[-e_p({\mathit{\omega }}_p^{\prime }(s)-{\mathit{\omega }}_p(s))\hfill \\ \hfill & +\sum _{q=1}^n{\tilde{\mathrm{\Lambda }}}_{pq}[{\widehat{f}}_q({\mathit{\omega }}_q^{\prime })-{\widehat{f}}_q({\mathit{\omega }}_q)]+\sum _{q=1}^n{\widetilde{\mathrm{{\rm Y}}}}_{pq}[{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }}^{\prime })-{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }})]]\mathrm{d}s.\hfill \end{array}$$

By taking absolute value and multiply by $e^{-t}$ on both sides of the above, we get

$$\begin{array}{cc}\hfill e^{-t}|{\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)|& \le \frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{e}^{-t}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}[e_p|{\mathit{\omega }}_p^{\prime }(s)-{\mathit{\omega }}_p(s)|+\sum _{q=1}^n|{\tilde{\mathrm{\Lambda }}}_{pq}||{\widehat{f}}_q({\mathit{\omega }}_q^{\prime })-{\widehat{f}}_q({\mathit{\omega }}_q)|\hfill \\ \hfill & +\sum _{q=1}^n|{\widetilde{\mathrm{{\rm Y}}}}_{pq}||{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }}^{\prime })-{\widehat{g}}_q({\mathit{\omega }}_{q\mathit{\tau }})|]\mathrm{d}s\hfill \\ \hfill & \le e_p\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|{\mathit{\omega }}_p^{\prime }(s)-{\mathit{\omega }}_p(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Lambda }}}_{pq}|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}[L_q|{\mathit{\omega }}_q^{\prime }(s)-{\mathit{\omega }}_q(s)|]\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\widetilde{\mathrm{{\rm Y}}}}_{pq}|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}[G_q|{\mathit{\omega }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\omega }}_{q\mathit{\tau }}(s)|]\mathrm{d}s\hfill \\ \hfill & \le e_p\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|{\mathit{\omega }}_p^{\prime }(s)-{\mathit{\omega }}_p(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Lambda }}}_{pq}|L_q\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|{\mathit{\omega }}_q^{\prime }(s)-{\mathit{\omega }}_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\widetilde{\mathrm{{\rm Y}}}}_{pq}|G_q\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|{\mathit{\omega }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\omega }}_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & \le e_p\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u+\sum _{q=1}^n|{\tilde{\mathrm{\Lambda }}}_{pq}|L_q\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|{\mathit{\omega }}_q^{\prime }(s)-{\mathit{\omega }}_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\widetilde{\mathrm{{\rm Y}}}}_{pq}|G_q\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{\mathit{\tau }}{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|{\mathit{\phi }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\phi }}_{q\mathit{\tau }}(s)|\mathrm{d}s+\sum _{q=1}^n|{\widetilde{\mathrm{{\rm Y}}}}_{pq}|G_q\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{\mathit{\tau }}^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|{\mathit{\omega }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\omega }}_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill e^{-t}|{\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)|& \le e_p\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +m_p^{\ast }\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_q^{\prime }(t)-{\mathit{\omega }}_q(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +n_p^{\ast }\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{-\mathit{\tau }}^0{(t-\mathit{\nu }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\nu })}{e}^{-\mathit{\nu }}|{\mathit{\phi }}_q^{\prime }(\mathit{\nu })-{\mathit{\phi }}_q(\mathit{\nu })|\mathrm{d}\mathit{\nu }\hfill \\ \hfill & +n_p^{\ast }\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{(t-\mathit{\nu }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\nu })}{e}^{-\mathit{\nu }}|{\mathit{\omega }}_q^{\prime }(\mathit{\nu })-{\mathit{\omega }}_q(\mathit{\nu })|\mathrm{d}\mathit{\nu }\hfill \\ \hfill & \le e_p\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +m_p^{\ast }\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_q^{\prime }(t)-{\mathit{\omega }}_q(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +n_p^{\ast }\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\phi }}_q^{\prime }(t)-{\mathit{\phi }}_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{t-\mathit{\tau }}^t{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & +n_p^{\ast }\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_q^{\prime }(t)-{\mathit{\omega }}_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & \le e_p\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)|\}+m_p^{\ast }\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_q^{\prime }(t)-{\mathit{\omega }}_q(t)|\}\hfill \\ \hfill & +n_p^{\ast }\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\phi }}_q^{\prime }(t)-{\mathit{\phi }}_q(t)|\}{e}^{-\mathit{\tau }}+n_p^{\ast }\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_q^{\prime }(t)-{\mathit{\omega }}_q(t)|\}{e}^{-\mathit{\tau }}\hfill \\ \hfill & \le e_p\underset{t}{sup}\{e^{-t}|{\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)|\}+m_p^{\ast }\Vert {\mathit{\omega }}^{\prime }(t)-\mathit{\omega }(t)\Vert +n_p^{\ast }\Vert {\mathit{\phi }}^{\prime }(t)-\mathit{\phi }(t)\Vert +n_p^{\ast }\Vert {\mathit{\omega }}^{\prime }(t)-\mathit{\omega }(t)\Vert .\hfill \end{array}$$ 33

From (33) we can obtain

$$\begin{array}{cc}\hfill \Vert {\mathit{\omega }}^{\prime }(t)-\mathit{\omega }(t)\Vert & =\sum _{j=1}^n\underset{t}{sup}\left\{e^{-t}|{\mathit{\omega }}_p^{\prime }(t)-{\mathit{\omega }}_p(t)|\right\}\hfill \\ \hfill & \le \left[e_{max}+\Vert m^{\ast }\Vert +\Vert n^{\ast }\Vert \right]\Vert {\mathit{\omega }}^{\prime }(t)-\mathit{\omega }(t)\Vert +\Vert n^{\ast }\Vert \Vert {\mathit{\phi }}^{\prime }(t)-\mathit{\phi }(t)\Vert .\hfill \end{array}$$ 34

The above Eq. (34) can be rewritten as

$$\begin{array}{c}\hfill \Vert {\mathit{\omega }}^{\prime }(t)-\mathit{\omega }(t)\Vert \le \frac{\Vert n^{\ast }\Vert }{1-\left(e_{max}+\Vert m^{\ast }\Vert +\Vert n^{\ast }\Vert \right)}\Vert {\mathit{\phi }}^{\prime }(t)-\mathit{\phi }(t)\Vert .\end{array}$$ 35

From (35), we can say that for $\forall \mathit{\epsilon }>0,$ then there exist a $\mathit{\delta }=\frac{1-\left(e_{max}+\Vert m^{\ast }\Vert +\Vert n^{\ast }\Vert \right)}{\Vert n^{\ast }\Vert }\mathit{\epsilon }>0$ such that $\Vert {\mathit{\omega }}^{\prime }(t)-\mathit{\omega }(t)\Vert <\mathit{\epsilon }$ when $\Vert {\mathit{\phi }}^{\prime }(t)-\mathit{\phi }(t)\Vert <\mathit{\delta }$. Thus, the solution $\mathit{\omega }(t)$ is uniformly stable.

Theorem 3

If Assumptions 1 and 2 hold, there exist a unique equilibrium point in system (5), which is uniformly stable.

Proof

Let $e_p{\mathit{\omega }}_p^{\ast }={\mathfrak{u}}_p^{\ast }$ and constructing a mapping $T:{\mathcal{R}}^n\to {\mathcal{R}}^n,$ defined by

$$\begin{array}{c}\hfill T_p{\mathfrak{u}}_p\le \sum _{q=1}^n{m}_{pq}{\widehat{f}}_q\left(\frac{{\mathfrak{u}}_p}{e_p}\right)+\sum _{q=1}^n{n}_{pq}{\widehat{g}}_q\left(\frac{{\mathfrak{u}}_p}{e_p}\right)+I_p,\end{array}$$ 36

where $p=1,2,\dots ,n,T(\mathfrak{u})={(T_1(\mathfrak{u}),T_2(\mathfrak{u}),\dots ,T_n(\mathfrak{u}))}^T$.

Now, we will show that $T$ is a contraction mapping on ${\mathcal{R}}^n$ endowed with the Euclidean space norm. In fact, for any two different points $\mathfrak{u}={({\mathfrak{u}}_1,{\mathfrak{u}}_2,\dots ,{\mathfrak{u}}_n)}^T,\mathfrak{v}={({\mathfrak{v}}_1,{\mathfrak{v}}_2,\dots ,{\mathfrak{v}}_n)}^T,$ we have

$$\begin{array}{cc}\hfill \Vert T(\mathfrak{u})-T(\mathfrak{v})\Vert & =\sum _{p=1}^n|T(\mathfrak{u})-T(\mathfrak{v})|\hfill \\ \hfill & \le \sum _{p=1}^n|\sum _{q=1}^n{m}_{pq}\left[{\widehat{f}}_q\left(\frac{{\mathfrak{u}}_q}{e_q}\right)-{\widehat{f}}_q\left(\frac{{\mathfrak{v}}_q}{e_q}\right)\right]+\sum _{q=1}^n{n}_{pq}\left[{\widehat{g}}_q\left(\frac{{\mathfrak{u}}_q}{e_q}\right)-{\widehat{g}}_q\left(\frac{{\mathfrak{v}}_q}{e_q}\right)\right]|\hfill \\ \hfill & \le \sum _{p=1}^n\left(\sum _{q=1}^n\frac{(m_{pq}{L}_q+n_{pq}{G}_q)}{e_q}|{\mathfrak{u}}_q-{\mathfrak{v}}_q|\right)\hfill \\ \hfill & \le \sum _{p=1}^n\frac{(m_p^{\ast }+n_p^{\ast })}{e_{min}}\left(\sum _{q=1}^n|{\mathfrak{u}}_q-{\mathfrak{v}}_q|\right)\hfill \\ \hfill & \le \frac{(\Vert m^{\ast }\Vert +\Vert n^{\ast }\Vert )}{\overline{e}}\Vert \mathfrak{u}-\mathfrak{v}\Vert .\hfill \end{array}$$ 37

Based on Assumption 1,

$$\begin{array}{c}\hfill \Vert T(\mathfrak{u})-T(\mathfrak{v})\Vert <\Vert \mathfrak{u}-\mathfrak{v}\Vert ,\end{array}$$ 38

which implies that $T$ is a contraction mapping on ${\mathcal{R}}^n$. Hence, there exists a unique fixed point ${\mathfrak{u}}^{\ast }$ such that $T({\mathfrak{u}}^{\ast })={\mathfrak{u}}^{\ast },$ i.e.

$$\begin{array}{c}\hfill {\mathfrak{u}}_p^{\ast }=\sum _{q=1}^n{m}_{pq}{\widehat{f}}_q\left(\frac{{\mathfrak{u}}_p}{e_p}\right)+\sum _{q=1}^n{n}_{pq}{\widehat{g}}_q\left(\frac{{\mathfrak{u}}_p}{e_p}\right)+I_p,\end{array}$$ 39

That is

$$\begin{array}{c}\hfill -e_p{\mathit{\omega }}_p^{\ast }+\sum _{q=1}^n{m}_{pq}{\widehat{f}}_q({\mathit{\omega }}_q^{\ast })+\sum _{q=1}^n{n}_{pq}{\widehat{g}}_q({\mathit{\omega }}_q^{\ast })+I_p=0,\end{array}$$ 40

for $p=1,2,\dots ,n,$ which implies that ${\mathit{\omega }}^{\ast }$ is an equilibrium point of system (5). Moreover, it follows from Theorem 1 and Theorem 2 that ${\mathit{\omega }}^{\ast }$ is uniformly stable.

Remark 2

If $\mathit{\alpha }=1$, then system (5) can be written as

$$\begin{array}{c}\hfill {\dot{\mathit{\omega }}}_p(t)=-e_p{\mathit{\omega }}_p(t)+\sum _{q=1}^n{\widehat{m}}_{pq}({\mathit{\omega }}_q(t)){\widehat{f}}_q({\mathit{\omega }}_q(t))+\sum _{q=1}^n{\widehat{n}}_{pq}({\mathit{\omega }}_q(t)){\widehat{g}}_q({\mathit{\omega }}_q(t-\mathit{\tau }(t)))+I_p,\end{array}$$ 41

where $t\ge 0,p=1,\dots ,n$. Then, the sufficient conditions for the existence, uniqueness and uniform stability of RVMFNNs in Theorems 1–3 reduced to the integer order real-valued memristor-based neural networks (41).

Remark 3

Some sufficient conditions for the existence, uniqueness and uniform stability of RVMFNNs are derived in Theorems 1 and 2 based on Filippov’s solution, differential inclusion theory and Banach contraction principle. Next we are going obtain some sufficient conditions for the existence, uniqueness and uniform stability of CVMFNNs in the following Theorems based on Filippov’s solution, differential inclusion theory and Banach contraction principle.

Complex-valued memristor-based fractional-order neural networks:

In this section, we describe CVMFNNs with time delays and two different types of memductance functions. First, we separate the CVMFNNs into its equivalent two RVMFNNs then by using Filippov’s solution, differential inclusion and Banach contraction principle, some sufficient conditions are obtained to show the existence, uniqueness and uniform stability of considered CVMFNNs.

Theorem 4

Under the case$3^{\prime }$, if Assumptions 3–4 are satisfied, then the system (9) is satisfying the initial condition (12) is uniformly stable.

Proof

Complex-valued memristor-based fractional-order neural networks system (9) can be expressed by separating real and imaginary parts, we get

$$\begin{array}{cc}\hfill D^{\mathit{\alpha }}{u}_p(t)& =-{\mathit{ϵ}}_p{u}_p(t)+\sum _{q=1}^n{\widehat{\mathit{\beta }}}_{pq}^R(u_q(t))f^R(u,v)-\sum _{q=1}^n{\widehat{\mathit{\beta }}}_{pq}^I(v_q(t))f^I(u,v)+\sum _{q=1}^n{\widehat{\mathit{\gamma }}}_{pq}^R(u_q(t))\hfill \\ \hfill & \times g^R(u(t-\mathit{\tau }),v(t-\mathit{\tau }))-\sum _{q=1}^n{\widehat{\mathit{\gamma }}}_{pq}^I(v_q(t))\times g^I(u(t-\mathit{\tau }),v(t-\mathit{\tau }))+H^R,\hfill \end{array}$$ 42

$$\begin{array}{cc}\hfill D^{\mathit{\alpha }}{v}_p(t)& =-{\mathit{ϵ}}_p{v}_p(t)+\sum _{q=1}^n{\widehat{\mathit{\beta }}}_{pq}^I(v_q(t))f^R(u,v)+\sum _{q=1}^n{\widehat{\mathit{\beta }}}_{pq}^R(u_q(t))f^I(u,v)+\sum _{q=1}^n{\widehat{\mathit{\gamma }}}_{pq}^I(v_q(t))\hfill \\ \hfill & \times g^R(u(t-\mathit{\tau }),v(t-\mathit{\tau }))+\sum _{q=1}^n{\widehat{\mathit{\gamma }}}_{pq}^R(v_q(t))g^I(u(t-\mathit{\tau }),v(t-\mathit{\tau }))+H^I.\hfill \end{array}$$ 43

By theories of differential inclusions and set-valued maps, from (42) and (43), it follows that

$$\begin{array}{cc}\hfill D^{\mathit{\alpha }}{u}_p(t)& \in -{\mathit{ϵ}}_p{u}_p(t)+\sum _{q=1}^{n}co\left\{{\widehat{\mathit{\beta }}}_{pq}^R,{\check{\mathit{\beta }}}_{pq}^R\right\}{f}^R(u,v)-\sum _{q=1}^{n}co\left\{{\widehat{\mathit{\beta }}}_{pq}^I,{\check{\mathit{\beta }}}_{pq}^I\right\}{f}^I(u,v)+\sum _{q=1}^{n}co\left\{{\widehat{\mathit{\gamma }}}_{pq}^R,{\check{\mathit{\gamma }}}_{pq}^R\right\}\hfill \\ \hfill & \times g^R(u(t-\mathit{\tau }),v(t-\mathit{\tau }))-\sum _{q=1}^{n}co\left\{{\widehat{\mathit{\gamma }}}_{pq}^I,{\check{\mathit{\gamma }}}_{pq}^I\right\}{g}^I(u(t-\mathit{\tau }),v(t-\mathit{\tau }))+H^R,\hfill \end{array}$$ 44

$$\begin{array}{cc}\hfill D^{\mathit{\alpha }}{v}_p(t)& \in -{\mathit{ϵ}}_p{v}_p(t)+\sum _{q=1}^{n}co\left\{{\widehat{\mathit{\beta }}}_{pq}^I,{\check{\mathit{\beta }}}_{pq}^I\right\}{f}^R(u,v)+\sum _{q=1}^{n}co\left\{{\widehat{\mathit{\beta }}}_{pq}^R,{\check{\mathit{\beta }}}_{pq}^R\right\}{f}^I(u,v)+\sum _{q=1}^{n}co\left\{{\widehat{\mathit{\gamma }}}_{pq}^I,{\check{\mathit{\gamma }}}_{pq}^I\right\}\hfill \\ \hfill & \times g^R(u(t-\mathit{\tau }),v(t-\mathit{\tau }))+\sum _{q=1}^{n}co\left\{{\widehat{\mathit{\gamma }}}_{pq}^R,{\check{\mathit{\gamma }}}_{pq}^R\right\}{g}^I(u(t-\mathit{\tau }),v(t-\mathit{\tau }))+H^I.\hfill \end{array}$$ 45

or equivalently, for $p,q=1,2,\dots ,n$ there exists a measurable functions ${\tilde{\mathit{\beta }}}_{pq}^R(t)\in co\{{\widehat{\mathit{\beta }}}_{pq}^R,{\check{\mathit{\beta }}}_{pq}^R\},{\tilde{\mathit{\beta }}}_{pq}^I(t)\in co\{{\widehat{\mathit{\beta }}}_{pq}^I,{\check{\mathit{\beta }}}_{pq}^I\},{\tilde{\mathit{\gamma }}}_{pq}^R(t)\in co\{{\widehat{\mathit{\gamma }}}_{pq}^R,{\check{\mathit{\gamma }}}_{pq}^R\},$ and ${\tilde{\mathit{\gamma }}}_{pq}^I(t)\in co\{{\widehat{\mathit{\gamma }}}_{pq}^I,{\check{\mathit{\gamma }}}_{pq}^I\}$ such that

$$\begin{array}{cc}\hfill D^{\mathit{\alpha }}{u}_p(t)& =-{\mathit{ϵ}}_p{u}_p(t)+\sum _{q=1}^n{\tilde{\mathit{\beta }}}_{pq}^R(t)f^R(u,v)-\sum _{q=1}^n{\tilde{\mathit{\beta }}}_{pq}^I(t)f^I(u,v)\hfill \\ \hfill & +\sum _{q=1}^n{\tilde{\mathit{\gamma }}}_{pq}^R(t)g^R(u(t-\mathit{\tau }),v(t-\mathit{\tau }))-\sum _{q=1}^n{\tilde{\mathit{\gamma }}}_{pq}^I(t)g^I(u(t-\mathit{\tau }),v(t-\mathit{\tau }))+H^R,\hfill \end{array}$$ 46

$$\begin{array}{cc}\hfill D^{\mathit{\alpha }}{v}_p(t)& =-{\mathit{ϵ}}_p{v}_p(t)+\sum _{q=1}^n{\tilde{\mathit{\beta }}}_{pq}^I(t)f^R(u,v)+\sum _{q=1}^n{\tilde{\mathit{\beta }}}_{pq}^R(t)f^I(u,v)\hfill \\ \hfill & +\sum _{q=1}^n{\tilde{\mathit{\gamma }}}_{pq}^I(t)g^R(u(t-\mathit{\tau }),v(t-\mathit{\tau }))+\sum _{q=1}^n{\tilde{\mathit{\gamma }}}_{pq}^R(t)g^I(u(t-\mathit{\tau }),v(t-\mathit{\tau }))+H^I.\hfill \end{array}$$ 47

Clearly, for $p,q=1,2,\dots ,n,|{\tilde{\mathit{\beta }}}_{pq}^R(t)|\le max\{|{\widehat{\mathit{\beta }}}_{pq}^R|,|{\check{\mathit{\beta }}}_{pq}^R|\}\le {\mathit{\beta }}_{pq}^R,|{\tilde{\mathit{\beta }}}_{pq}^I(t)|\le max\{|{\widehat{\mathit{\beta }}}_{pq}^I|,|{\check{\mathit{\beta }}}_{pq}^I|\}\le {\mathit{\beta }}_{pq}^I,|{\tilde{\mathit{\gamma }}}_{pq}^R(t)|\le max\{|{\widehat{\mathit{\gamma }}}_{pq}^R|,|{\check{\mathit{\gamma }}}_{pq}^R|\}\le {\mathit{\gamma }}_{pq}^R$ and $|{\tilde{\mathit{\gamma }}}_{pq}^I(t)|\le max\{|{\widehat{\mathit{\gamma }}}_{pq}^I|,|{\check{\mathit{\gamma }}}_{pq}^I|\}\le {\mathit{\gamma }}_{pq}^I$.

Consider $z^{\prime }=u^{\prime }+i{v}^{\prime }$ and $z=u+iv$ with $u^{\prime }\ne u$ and $v^{\prime }\ne v$. $z^{\prime }(t)=(z_1^{\prime }(t),\dots ,z_n^{\prime }(t))$ and $z(t)=(z_1(t),\dots ,z_n(t))$ are any two solutions of the system (9) with initial conditions $z_p^{\prime }(s)={\mathit{\psi }}_p^{\prime }(s)+i{\mathit{\chi }}_p^{\prime }(s),$ where ${\mathit{\psi }}_p^{\prime }(s),{\mathit{\chi }}_p^{\prime }(s)\in C([-\mathit{\tau },0],{\mathcal{R}}^n),{\mathit{\psi }}_p^{\prime }(0)=0,{\mathit{\chi }}_p^{\prime }(0)=0,z_p(s)={\mathit{\psi }}_p(s)+i{\mathit{\chi }}_p(s)$, where ${\mathit{\psi }}_p(s),{\mathit{\chi }}_p(s)\in C([-\mathit{\tau },0],{\mathcal{R}}^n),{\mathit{\psi }}_p(0)=0,{\mathit{\chi }}_p(0)=0,p\in n$. We have

$$\begin{array}{cc}\hfill D^{\mathit{\alpha }}(u_p^{\prime }(t)-u_p(t))& \le -{\mathit{ϵ}}_p(u_p^{\prime }(t)-u_p(t))+\sum _{q=1}^n{\mathit{\beta }}_{pq}^R\left[f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)\right]\hfill \\ \hfill & -\sum _{q=1}^n{\mathit{\beta }}_{pq}^I\left[f_q^I(u_q^{\prime },v_q^{\prime })-f_q^I(u_q,v_q)\right]+\sum _{q=1}^n{\mathit{\gamma }}_{pq}^R\left[g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})\right]\hfill \\ \hfill & -\sum _{q=1}^n{\mathit{\gamma }}_{pq}^I\left[g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})\right],\hfill \\ \hfill D^{\mathit{\alpha }}(v_p^{\prime }(t)-v_p(t))& \le -{\mathit{ϵ}}_p(v_p^{\prime }(t)-v_p(t))+\sum _{q=1}^n{\mathit{\beta }}_{pq}^I\left[f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)\right]\hfill \\ \hfill & +\sum _{q=1}^n{\mathit{\beta }}_{pq}^R\left[f_q^I(u_q^{\prime },v_q^{\prime })-f_q^I(u_q,v_q)\right]+\sum _{q=1}^n{\mathit{\gamma }}_{pq}^I\left[g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})\right]\hfill \\ \hfill & +\sum _{q=1}^n{\mathit{\gamma }}_{pq}^R\left[g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})\right].\hfill \end{array}$$

Now multiply by $D^{-\mathit{\alpha }}$ on both sides, we can write

$$\begin{array}{cc}\hfill u_p^{\prime }(t)-u_p(t)& \le D^{-\mathit{\alpha }}[-{\mathit{ϵ}}_p(u_p^{\prime }(t)-u_p(t))+\sum _{q=1}^n{\mathit{\beta }}_{pq}^R\left[f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)\right]\hfill \\ \hfill & -\sum _{q=1}^n{\mathit{\beta }}_{pq}^I\left[f_q^I(u_q^{\prime },v_q^{\prime })-f_q^I(u_q,v_q)\right]+\sum _{q=1}^n{\mathit{\gamma }}_{pq}^R\left[g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})\right]\hfill \\ \hfill & -\sum _{q=1}^n{\mathit{\gamma }}_{pq}^I\left[g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})\right]],\hfill \end{array}$$ 48

$$\begin{array}{cc}\hfill v_p^{\prime }(t)-v_p(t)& \le D^{-\mathit{\alpha }}[-{\mathit{ϵ}}_p(v_p^{\prime }(t)-v_p(t))+\sum _{q=1}^n{\mathit{\beta }}_{pq}^I\left[f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)\right]\hfill \\ \hfill & +\sum _{q=1}^n{\mathit{\beta }}_{pq}^R\left[f_q^I(u_q^{\prime },v_q^{\prime })-f_q^I(u_q,v_q)\right]+\sum _{q=1}^n{\mathit{\gamma }}_{pq}^I\left[g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})\right]\hfill \\ \hfill & +\sum _{q=1}^n{\mathit{\gamma }}_{pq}^R\left[g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})\right]].\hfill \end{array}$$ 49

From (48), we have

$$\begin{array}{cc}\hfill u_p^{\prime }(t)-u_p(t)& \le D^{-\mathit{\alpha }}[-{\mathit{ϵ}}_p(u_p^{\prime }(t)-u_p(t))+\sum _{q=1}^n{\mathit{\beta }}_{pq}^R\left[f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)\right.]-\sum _{q=1}^n{\mathit{\beta }}_{pq}^I[f_q^I(u_q^{\prime },v_q^{\prime })\hfill \\ \hfill & \left.-f_q^I(u_q,v_q)\right]+\sum _{q=1}^n{\mathit{\gamma }}_{pq}^R\left[g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})\right]-\sum _{q=1}^n{\mathit{\gamma }}_{pq}^I\left[g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })\right.\hfill \\ \hfill & -g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]]\hfill \\ \hfill & \le \frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}[-{\mathit{ϵ}}_p(u_p^{\prime }(s)-u_p(s))+\sum _{q=1}^n{\mathit{\beta }}_{pq}^R\left[f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)\right]\hfill \\ \hfill & -\sum _{q=1}^n{\mathit{\beta }}_{pq}^I\left[f_q^I(u_q^{\prime },v_q^{\prime })-f_q^I(u_q,v_q)\right]+\sum _{q=1}^n{\mathit{\gamma }}_{pq}^R\left[g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})\right]\hfill \\ \hfill & -\sum _{q=1}^n{\mathit{\gamma }}_{pq}^I\left[g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})\right]]\mathrm{d}s.\hfill \end{array}$$

By taking absolute value and multiply by $e^{-t}$ on both sides of the above, we get

$$\begin{array}{cc}\hfill e^{-t}|u_p^{\prime }(t)-u_p(t)|& \le \frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{e}^{-t}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}[{\mathit{ϵ}}_p|u_p^{\prime }(s)-u_p(s)|+\sum _{q=1}^n|{\mathit{\beta }}_{pq}^R||f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)|\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\beta }}_{pq}^I||f_q^I(u_q^{\prime },v_q^{\prime })-f_q^I(u_q,v_q)|+\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^R||g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})|\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^I||g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})|]\mathrm{d}s\hfill \\ \hfill & \le {\mathit{ϵ}}_p\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_p^{\prime }(s)-u_p(s)|\mathrm{d}s+\sum _{q=1}^n|{\mathit{\beta }}_{pq}^R|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}\hfill \\ \hfill & \times e^{-(t-s)}{e}^{-s}[{\mathit{\lambda }}_q^{RR}|u_q^{\prime }(s)-u_q(s)|+{\mathit{\lambda }}_q^{RI}|v_q^{\prime }(s)-v_q(s)|]\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\beta }}_{pq}^I|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}[{\mathit{\lambda }}_q^{IR}|u_q^{\prime }(s)-u_q(s)|\hfill \\ \hfill & +{\mathit{\lambda }}_q^{II}|v_q^{\prime }(s)-v_q(s)|]\mathrm{d}s+\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^R|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times [{\mathit{\mu }}_q^{RR}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|+{\mathit{\mu }}_q^{RI}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|]\mathrm{d}s+\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^I|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}\hfill \\ \hfill & e^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}[{\mathit{\mu }}_q^{IR}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|+{\mathit{\mu }}_q^{II}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|]\mathrm{d}s\hfill \\ \hfill & \le {\mathit{ϵ}}_p\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_p^{\prime }(s)-u_p(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\beta }}_{pq}^R|{\mathit{\lambda }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_q^{\prime }(s)-u_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\beta }}_{pq}^R|{\mathit{\lambda }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|v_q^{\prime }(s)-v_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\beta }}_{pq}^I|{\mathit{\lambda }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_q^{\prime }(s)-u_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\beta }}_{pq}^I|{\mathit{\lambda }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|v_q^{\prime }(s)-v_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^R|{\mathit{\mu }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^R|{\mathit{\mu }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^I|{\mathit{\mu }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^I|{\mathit{\mu }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & \le {\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|u_p^{\prime }(t)-u_p(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u+\sum _{q=1}^n|{\mathit{\beta }}_{pq}^R|{\mathit{\lambda }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}\hfill \\ \hfill & \times {\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_q^{\prime }(s)-u_q(s)|\mathrm{d}s+\sum _{q=1}^n|{\mathit{\beta }}_{pq}^R|{\mathit{\lambda }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}\hfill \\ \hfill & \times {\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|v_q^{\prime }(s)-v_q(s)|\mathrm{d}s+\sum _{q=1}^n|{\mathit{\beta }}_{pq}^I|{\mathit{\lambda }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}\hfill \\ \hfill & e^{-(t-s)}{e}^{-s}|u_q^{\prime }(s)-u_q(s)|\mathrm{d}s+\sum _{q=1}^n|{\mathit{\beta }}_{pq}^I|{\mathit{\lambda }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}\hfill \\ \hfill & \times |v_q^{\prime }(s)-v_q(s)|\mathrm{d}s+\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^R|{\mathit{\mu }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{\mathit{\tau }}{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times |{\mathit{\psi }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\psi }}_{q\mathit{\tau }}(s)|\mathrm{d}s+\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^R|{\mathit{\mu }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{\mathit{\tau }}^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times |u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|\mathrm{d}s+\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^R|{\mathit{\mu }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{\mathit{\tau }}{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times |{\mathit{\chi }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\chi }}_{q\mathit{\tau }}(s)|\mathrm{d}s+\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^R|{\mathit{\mu }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{\mathit{\tau }}^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times |v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\mathrm{d}s+\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^I|{\mathit{\mu }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{\mathit{\tau }}{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times |{\mathit{\psi }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\psi }}_{q\mathit{\tau }}(s)|\mathrm{d}s+\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^I|{\mathit{\mu }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{\mathit{\tau }}^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times |u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|\mathrm{d}s+\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^I|{\mathit{\mu }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{\mathit{\tau }}{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times |{\mathit{\chi }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\chi }}_{q\mathit{\tau }}(s)|\mathrm{d}s+\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^I|{\mathit{\mu }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{\mathit{\tau }}^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill e^{-t}|u_p^{\prime }(t)-u_p(t)|& \le {\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|u_p^{\prime }(t)-u_p(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u+\left[{\mathit{\zeta }}_{1p}^{\ast }+{\mathit{\zeta }}_{3p}^{\ast }\right]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)\hfill \\ \hfill & -u_q(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u+[{\mathit{\zeta }}_{2p}^{\ast }+{\mathit{\zeta }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}\hfill \\ \hfill & \times \frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u+[{\mathit{\eta }}_{1p}^{\ast }+{\mathit{\eta }}_{3p}^{\ast }]\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{-\mathit{\tau }}^0{(t-\mathit{\nu }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\nu })}{e}^{-\mathit{\nu }}\hfill \\ \hfill & \times |{\mathit{\psi }}_q^{\prime }(\mathit{\nu })-{\mathit{\psi }}_q(\mathit{\nu })|\mathrm{d}\mathit{\nu }+[{\mathit{\eta }}_{1p}^{\ast }+{\mathit{\eta }}_{3p}^{\ast }]\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{(t-\mathit{\nu }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\nu })}{e}^{-\mathit{\nu }}\hfill \\ \hfill & \times |u_q^{\prime }(\mathit{\nu })-u_q(\mathit{\nu })|\mathrm{d}\mathit{\nu }+[{\mathit{\eta }}_{2p}^{\ast }+{\mathit{\eta }}_{4p}^{\ast }]\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{-\mathit{\tau }}^0{(t-\mathit{\nu }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\nu })}{e}^{-\mathit{\nu }}\hfill \\ \hfill & \times |{\mathit{\chi }}_q^{\prime }(\mathit{\nu })-{\mathit{\chi }}_q(\mathit{\nu })|\mathrm{d}\mathit{\nu }+[{\mathit{\eta }}_{2p}^{\ast }+{\mathit{\eta }}_{4p}^{\ast }]\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{(t-\mathit{\nu }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\nu })}{e}^{-\mathit{\nu }}\hfill \\ \hfill & \times |v_q^{\prime }(\mathit{\nu })-v_q(\mathit{\nu })|\mathrm{d}\mathit{\nu }\hfill \\ \hfill & \le {\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|u_p^{\prime }(t)-u_p(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +[{\mathit{\zeta }}_{1p}^{\ast }+{\mathit{\zeta }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)-u_q(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +[{\mathit{\zeta }}_{2p}^{\ast }+{\mathit{\zeta }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +[{\mathit{\eta }}_{1p}^{\ast }+{\mathit{\eta }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\psi }}_q^{\prime }(t)-{\mathit{\psi }}_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{t-\mathit{\tau }}^t{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & +[{\mathit{\eta }}_{1p}^{\ast }+{\mathit{\eta }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)-u_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & +[{\mathit{\eta }}_{2p}^{\ast }+{\mathit{\eta }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\chi }}_q^{\prime }(t)-{\mathit{\chi }}_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{t-\mathit{\tau }}^t{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & +[{\mathit{\eta }}_{2p}^{\ast }+{\mathit{\eta }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & \le {\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|u_p^{\prime }(t)-u_p(t)|\}+[{\mathit{\zeta }}_{1p}^{\ast }+{\mathit{\zeta }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)-u_q(t)|\}\hfill \\ \hfill & +[{\mathit{\zeta }}_{2p}^{\ast }+{\mathit{\zeta }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}+[{\mathit{\eta }}_{1p}^{\ast }+{\mathit{\eta }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}\hfill \\ \hfill & |{\mathit{\psi }}_q^{\prime }(t)-{\mathit{\psi }}_q(t)|\}{e}^{-\mathit{\tau }}+[{\mathit{\eta }}_{1p}^{\ast }+{\mathit{\eta }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)-u_q(t)|\}{e}^{-\mathit{\tau }}\hfill \\ \hfill & +[{\mathit{\eta }}_{2p}^{\ast }+{\mathit{\eta }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\chi }}_q^{\prime }(t)-{\mathit{\chi }}_q(t)|\}{e}^{-\mathit{\tau }}\hfill \\ \hfill & +[{\mathit{\eta }}_{2p}^{\ast }+{\mathit{\eta }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}{e}^{-\mathit{\tau }}\hfill \\ \hfill & \le {\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|u_p^{\prime }(t)-u_p(t)|\}+[{\mathit{\zeta }}_{1p}^{\ast }+{\mathit{\zeta }}_{3p}^{\ast }]\Vert u^{\prime }(t)-u(t)\Vert \hfill \\ \hfill & +[{\mathit{\zeta }}_{2p}^{\ast }+{\mathit{\zeta }}_{4p}^{\ast }]\Vert v^{\prime }(t)-v(t)\Vert +[{\mathit{\eta }}_{1p}^{\ast }+{\mathit{\eta }}_{3p}^{\ast }]\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert \hfill \\ \hfill & +[{\mathit{\eta }}_{1p}^{\ast }+{\mathit{\eta }}_{3p}^{\ast }]\Vert u^{\prime }(t)-u_{(}t)\Vert +[{\mathit{\eta }}_{2p}^{\ast }+{\mathit{\eta }}_{4p}^{\ast }]\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert \hfill \\ \hfill & +[{\mathit{\eta }}_{2p}^{\ast }+{\mathit{\eta }}_{4p}^{\ast }]\Vert v^{\prime }(t)-v(t)\Vert .\hfill \end{array}$$ 50

From (50) we can obtain

$$\begin{array}{cc}\hfill \Vert u^{\prime }(t)-u(t)\Vert & =\sum _{j=1}^n\underset{t}{sup}\{e^{-t}|u_p^{\prime }(t)-u_p(t)|\}\hfill \\ \hfill & \le \left[{\mathit{ϵ}}_{max}+\Vert {\mathit{\zeta }}_1^{\ast }\Vert +\Vert {\mathit{\zeta }}_3^{\ast }\Vert +\Vert {\mathit{\eta }}_1^{\ast }\Vert +\Vert {\mathit{\eta }}_3^{\ast }\Vert \right]\Vert u^{\prime }(t)-u(t)\Vert \hfill \\ \hfill & +\left[\Vert {\mathit{\zeta }}_2^{\ast }\Vert +\Vert {\mathit{\zeta }}_4^{\ast }\Vert +\Vert {\mathit{\eta }}_2^{\ast }\Vert +\Vert {\mathit{\eta }}_4^{\ast }\Vert \right]\Vert v^{\prime }(t)-v(t)\Vert \hfill \\ \hfill & +\left[\Vert {\mathit{\eta }}_1^{\ast }\Vert +\Vert {\mathit{\eta }}_3^{\ast }\Vert \right]\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\left[\Vert {\mathit{\eta }}_2^{\ast }\Vert +\Vert {\mathit{\eta }}_4^{\ast }\Vert \right]\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert .\hfill \end{array}$$ 51

The above Eq. (51) can be rewritten as

$$\begin{array}{cc}\hfill \Vert u^{\prime }(t)-u(t)\Vert & \le \frac{1}{\left(1-\left({\mathit{ϵ}}_{max}+\Vert {\mathit{\zeta }}_1^{\ast }\Vert +\Vert {\mathit{\zeta }}_3^{\ast }\Vert +\Vert {\mathit{\eta }}_1^{\ast }\Vert +\Vert {\mathit{\eta }}_3^{\ast }\Vert \right)\right)}\hfill \\ \hfill & \times \left\{\left[\Vert {\mathit{\zeta }}_2^{\ast }\Vert +\Vert {\mathit{\zeta }}_4^{\ast }\Vert +\Vert {\mathit{\eta }}_2^{\ast }\Vert +\Vert {\mathit{\eta }}_4^{\ast }\Vert \right]\Vert v^{\prime }(t)-v(t)\Vert \right.\hfill \\ \hfill & \left.+\left[\Vert {\mathit{\eta }}_1^{\ast }\Vert +\Vert {\mathit{\eta }}_3^{\ast }\Vert \right]\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\left[\Vert {\mathit{\eta }}_2^{\ast }\Vert +\Vert {\mathit{\eta }}_4^{\ast }\Vert \right]\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert \right\}.\hfill \end{array}$$ 52

Similarly, we consider the Eq. (49), one can easily obtain as follows

$$\begin{array}{cc}\hfill v_p^{\prime }(t)-v_p(t)& =D^{-\mathit{\alpha }}[-{\mathit{ϵ}}_p(v_p^{\prime }(t)-v_p(t))+\sum _{q=1}^n{\mathit{\beta }}_{pq}^I[f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)]\hfill \\ \hfill & +\sum _{q=1}^n{\mathit{\beta }}_{pq}^R[f_q^I(u_q^{\prime },v_q^{\prime })-f_q^I(u_q,v_q)]+\sum _{q=1}^n{\mathit{\gamma }}_{pq}^I[g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]\hfill \\ \hfill & +\sum _{q=1}^n{\mathit{\gamma }}_{pq}^R[g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]],\hfill \\ \hfill v_p^{\prime }(t)-v_p(t)=& \frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}[-{\mathit{ϵ}}_p(v_p^{\prime }(s)-v_p(s))+\sum _{q=1}^n{\mathit{\beta }}_{pq}^I[f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)]\hfill \\ \hfill & +\sum _{q=1}^n{\mathit{\beta }}_{pq}^R[f_q^I(u_q^{\prime },v_q^{\prime })-f_q^I(u_q,v_q)]+\sum _{q=1}^n{\mathit{\gamma }}_{pq}^I[g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]\hfill \\ \hfill & +\sum _{q=1}^n{\mathit{\gamma }}_{pq}^R[g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]]\mathrm{d}s.\hfill \end{array}$$

By taking absolute value and multiply by $e^{-t}$ on both sides, we have

$$\begin{array}{cc}\hfill e^{-t}|v_p^{\prime }(t)-v_p(t)|& \le \frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{e}^{-t}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}\left\{{\mathit{ϵ}}_p|v_p^{\prime }(s)-v_p(s)|+\sum _{q=1}^n|{\mathit{\beta }}_{pq}^I||f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)|\right.\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\beta }}_{pq}^R||f_q^I(u_q^{\prime },v_q^{\prime })-f_q^I(u_q,v_q)|+\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^I||g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})|\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^R||g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})|\left.\right\}\mathrm{d}s\hfill \\ \hfill & ={\mathit{ϵ}}_p\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|v_p^{\prime }(s)-v_p(s)|\mathrm{d}s+\sum _{q=1}^n|{\mathit{\beta }}_{pq}^I|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}\hfill \\ \hfill & \times {\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}\left[\right.{\mathit{\lambda }}_q^{RR}|u_q^{\prime }(s)-u_q(s)|+{\mathit{\lambda }}_q^{RI}|v_q^{\prime }(s)-v_q(s)|\left.\right]\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\beta }}_{pq}^R|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}\left[\right.{\mathit{\lambda }}_q^{IR}|u_q^{\prime }(s)-u_q(s)|\hfill \\ \hfill & +{\mathit{\lambda }}_q^{II}|v_q^{\prime }(s)-v_q(s)|\left.\right]\mathrm{d}s+\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^I|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times \left[{\mathit{\mu }}_q^{IR}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|+{\mathit{\mu }}_q^{II}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\right]\mathrm{d}s\hfill \\ \hfill & ={\mathit{ϵ}}_p\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_p^{\prime }(s)-u_p(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\beta }}_{pq}^I|{\mathit{\lambda }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_q^{\prime }(s)-u_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\beta }}_{pq}^I|{\mathit{\lambda }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|v_q^{\prime }(s)-v_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\beta }}_{pq}^R|{\mathit{\lambda }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_q^{\prime }(s)-u_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\beta }}_{pq}^R|{\mathit{\lambda }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|v_q^{\prime }(s)-v_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^I|{\mathit{\mu }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^I|{\mathit{\mu }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^R|{\mathit{\mu }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^R|{\mathit{\mu }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & ={\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|v_p^{\prime }(t)-v_p(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\beta }}_{pq}^I|{\mathit{\lambda }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_q^{\prime }(s)-u_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\beta }}_{pq}^I|{\mathit{\lambda }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|v_q^{\prime }(s)-v_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\beta }}_{pq}^R|{\mathit{\lambda }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_q^{\prime }(s)-u_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\beta }}_{pq}^R|{\mathit{\lambda }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|v_q^{\prime }(s)-v_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^I|{\mathit{\mu }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{\mathit{\tau }}{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|{\mathit{\psi }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\psi }}_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^I|{\mathit{\mu }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{\mathit{\tau }}^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^I|{\mathit{\mu }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{\mathit{\tau }}{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|{\mathit{\chi }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\chi }}_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^I|{\mathit{\mu }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{\mathit{\tau }}^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^R|{\mathit{\mu }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{\mathit{\tau }}{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|{\mathit{\psi }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\psi }}_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^R|{\mathit{\mu }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{\mathit{\tau }}^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^R|{\mathit{\mu }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{\mathit{\tau }}{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|{\mathit{\chi }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\chi }}_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\mathit{\gamma }}_{pq}^R|{\mathit{\mu }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{\mathit{\tau }}^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill e^{-t}|y_p^{\prime }(t)-v_p(t)|& \le {\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|v_p^{\prime }(t)-v_p(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u+[{\mathit{\xi }}_{1j}^{\ast }+{\mathit{\xi }}_{3j}^{\ast }]\hfill \\ \hfill & \times \sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)-u_q(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u+[{\mathit{\xi }}_{2j}^{\ast }+{\mathit{\xi }}_{4j}^{\ast }]\hfill \\ \hfill & \times \sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +[{\mathit{\pi }}_{1j}^{\ast }+{\mathit{\pi }}_{3j}^{\ast }]\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{-\mathit{\tau }}^0{(t-\mathit{\nu }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\nu })}{e}^{-\mathit{\nu }}|{\mathit{\psi }}_q^{\prime }(\mathit{\nu })-{\mathit{\psi }}_q(\mathit{\nu })|\mathrm{d}\mathit{\nu }\hfill \\ \hfill & +[{\mathit{\pi }}_{1j}^{\ast }+{\mathit{\pi }}_{3j}^{\ast }]\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{(t-\mathit{\nu }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\nu })}{e}^{-\mathit{\nu }}|u_q^{\prime }(\mathit{\nu })-u_q(\mathit{\nu })|\mathrm{d}\mathit{\nu }\hfill \\ \hfill & +[{\mathit{\pi }}_{2j}^{\ast }+{\mathit{\pi }}_{4j}^{\ast }]\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{-\mathit{\tau }}^0{(t-\mathit{\nu }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\nu })}{e}^{-\mathit{\nu }}|{\mathit{\chi }}_q^{\prime }(\mathit{\nu })-{\mathit{\chi }}_q(\mathit{\nu })|\mathrm{d}\mathit{\nu }\hfill \\ \hfill & +[{\mathit{\pi }}_{2j}^{\ast }+{\mathit{\pi }}_{4j}^{\ast }]\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{(t-\mathit{\nu }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\nu })}{e}^{-\mathit{\nu }}|v_q^{\prime }(\mathit{\nu })-v_q(\mathit{\nu })|\mathrm{d}\mathit{\nu }\hfill \\ \hfill & ={\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|v_p^{\prime }(t)-v_p(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +[{\mathit{\xi }}_{1j}^{\ast }+{\mathit{\xi }}_{3j}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)-u_q(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +[{\mathit{\xi }}_{2j}^{\ast }+{\mathit{\xi }}_{4j}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +[{\mathit{\pi }}_{1j}^{\ast }+{\mathit{\pi }}_{3j}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\psi }}_q^{\prime }(t)-{\mathit{\psi }}_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{t-\mathit{\tau }}^t{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & +[{\mathit{\pi }}_{1j}^{\ast }+{\mathit{\pi }}_{3j}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)-u_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & +[{\mathit{\pi }}_{2j}^{\ast }+{\mathit{\pi }}_{4j}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\chi }}_q^{\prime }(t)-{\mathit{\chi }}_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{t-\mathit{\tau }}^t{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & +[{\mathit{\pi }}_{2j}^{\ast }+{\mathit{\pi }}_{4j}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & ={\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|y_p^{\prime }(t)-v_p(t)|\}+[{\mathit{\xi }}_{1j}^{\ast }+{\mathit{\xi }}_{3j}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)-u_q(t)|\}\hfill \\ \hfill & +[{\mathit{\xi }}_{2j}^{\ast }+{\mathit{\xi }}_{4j}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}\hfill \\ \hfill & +[{\mathit{\pi }}_{1j}^{\ast }+{\mathit{\pi }}_{3j}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\psi }}_q^{\prime }(t)-{\mathit{\psi }}_q(t)|\}{e}^{-\mathit{\tau }}\hfill \\ \hfill & +[{\mathit{\pi }}_{1j}^{\ast }+{\mathit{\pi }}_{3j}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)-u_q(t)|\}{e}^{-\mathit{\tau }}\hfill \\ \hfill & +[{\mathit{\pi }}_{2j}^{\ast }+{\mathit{\pi }}_{4j}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\chi }}_q^{\prime }(t)-{\mathit{\chi }}_q(t)|\}{e}^{-\mathit{\tau }}\hfill \\ \hfill & +[{\mathit{\pi }}_{2j}^{\ast }+{\mathit{\pi }}_{4j}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}{e}^{-\mathit{\tau }}\hfill \\ \hfill & \le {\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|v_p^{\prime }(t)-v_p(t)|\}+[{\mathit{\xi }}_{1j}^{\ast }+{\mathit{\xi }}_{3j}^{\ast }]\Vert u^{\prime }(t)-u(t)\Vert \hfill \\ \hfill & +[{\mathit{\xi }}_{2j}^{\ast }+{\mathit{\xi }}_{4j}^{\ast }]\Vert v^{\prime }(t)-v(t)\Vert +[{\mathit{\pi }}_{1j}^{\ast }+{\mathit{\pi }}_{3j}^{\ast }]\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert \hfill \\ \hfill & +[{\mathit{\pi }}_{1j}^{\ast }+{\mathit{\pi }}_{3j}^{\ast }]\Vert u^{\prime }(t)-u_{(}t)\Vert +[{\mathit{\pi }}_{2j}^{\ast }+{\mathit{\pi }}_{4j}^{\ast }]\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert \hfill \\ \hfill & +[{\mathit{\pi }}_{2j}^{\ast }+{\mathit{\pi }}_{4j}^{\ast }]\Vert v^{\prime }(t)-v(t)\Vert .\hfill \end{array}$$ 53

From (53) we can obtain

$$\begin{array}{cc}\hfill \Vert v^{\prime }(t)-v(t)\Vert & =\sum _{j=1}^n\underset{t}{sup}\{e^{-t}|v_p^{\prime }(t)-v_p(t)|\}\hfill \\ \hfill & \le \left[{\mathit{ϵ}}_{max}+\Vert {\mathit{\xi }}_2^{\ast }\Vert +\Vert {\mathit{\xi }}_4^{\ast }\Vert +\Vert {\mathit{\pi }}_2^{\ast }\Vert +\Vert {\mathit{\pi }}_4^{\ast }\Vert \right]\Vert v^{\prime }(t)-v(t)\Vert \hfill \\ \hfill & +\left[\Vert {\mathit{\xi }}_1^{\ast }\Vert +\Vert {\mathit{\xi }}_3^{\ast }\Vert +\Vert {\mathit{\pi }}_1^{\ast }\Vert +\Vert {\mathit{\pi }}_3^{\ast }\Vert \right]\Vert u^{\prime }(t)-u(t)\Vert \hfill \\ \hfill & +\left[\Vert {\mathit{\pi }}_1^{\ast }\Vert +\Vert {\mathit{\pi }}_3^{\ast }\Vert \right]\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\left[\Vert {\mathit{\pi }}_2^{\ast }\Vert +\Vert {\mathit{\pi }}_4^{\ast }\Vert \right]\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert .\hfill \end{array}$$ 54

The above Eq. (54) can be rewritten as

$$\begin{array}{cc}\hfill \Vert v^{\prime }(t)-v(t)\Vert & \le \frac{1}{\left(1-\left[{\mathit{ϵ}}_{max}+\Vert {\mathit{\xi }}_2^{\ast }\Vert +\Vert {\mathit{\xi }}_4^{\ast }\Vert +\Vert {\mathit{\pi }}_2^{\ast }\Vert +\Vert {\mathit{\pi }}_4^{\ast }\Vert \right]\right)}\hfill \\ \hfill & \times \left\{\left[\Vert {\mathit{\xi }}_1^{\ast }\Vert +\Vert {\mathit{\xi }}_3^{\ast }\Vert +\Vert {\mathit{\pi }}_1^{\ast }\Vert +\Vert {\mathit{\pi }}_3^{\ast }\Vert \right]\Vert u^{\prime }(t)-u(t)\Vert \right.\hfill \\ \hfill & \left.+\left[\Vert {\mathit{\pi }}_1^{\ast }\Vert +\Vert {\mathit{\pi }}_3^{\ast }\Vert \right]\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\left[\Vert {\mathit{\pi }}_2^{\ast }\Vert +\Vert {\mathit{\pi }}_4^{\ast }\Vert \right]\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert \right\}.\hfill \end{array}$$ 55

From the Eqs. (52) and (55), we can write in the following form,

$$\begin{array}{c}\hfill \Vert u^{\prime }(t)-u(t)\Vert \le \frac{1}{{\mathcal{M}}_1}\left\{{\mathcal{M}}_2\Vert v^{\prime }(t)-v(t)\Vert +{\mathcal{M}}_3\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +{\mathcal{M}}_4\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert \right\},\end{array}$$ 56

$$\begin{array}{c}\hfill \Vert v^{\prime }(t)-v(t)\Vert \le \frac{1}{{\mathcal{N}}_1}\left\{{\mathcal{N}}_2\Vert u^{\prime }(t)-u(t)\Vert +{\mathcal{N}}_3\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +{\mathcal{N}}_4\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert \right\},\end{array}$$ 57

where

$$\begin{array}{cc}\hfill {\mathcal{M}}_1& =\left(1-\left({\mathit{ϵ}}_{max}+\left[\Vert {\mathit{\zeta }}_1^{\ast }\Vert +\Vert {\mathit{\zeta }}_3^{\ast }\Vert +\Vert {\mathit{\eta }}_1^{\ast }\Vert +\Vert {\mathit{\eta }}_3^{\ast }\Vert \right]\right)\right),\hfill \\ \hfill {\mathcal{M}}_2& =\left(\Vert {\mathit{\zeta }}_2^{\ast }\Vert +\Vert {\mathit{\zeta }}_4^{\ast }\Vert +\Vert {\mathit{\eta }}_2^{\ast }\Vert +\Vert {\mathit{\eta }}_4^{\ast }\Vert \right),\hfill \\ \hfill {\mathcal{M}}_3& =\left(\Vert {\mathit{\eta }}_1^{\ast }\Vert +\Vert {\mathit{\eta }}_3^{\ast }\Vert \right),{\mathcal{M}}_4=\left(\Vert {\mathit{\eta }}_2^{\ast }\Vert +\Vert {\mathit{\eta }}_4^{\ast }\Vert \right),\hfill \\ \hfill {\mathcal{N}}_1& =\left(1-\left[{\mathit{ϵ}}_{max}+\Vert {\mathit{\xi }}_2^{\ast }\Vert +\Vert {\mathit{\xi }}_4^{\ast }\Vert +\Vert {\mathit{\pi }}_2^{\ast }\Vert +\Vert {\mathit{\pi }}_4^{\ast }\Vert \right]\right),\hfill \\ \hfill {\mathcal{N}}_2& =\left(\Vert {\mathit{\xi }}_1^{\ast }\Vert +\Vert {\mathit{\xi }}_3^{\ast }\Vert +\Vert {\mathit{\pi }}_1^{\ast }\Vert +\Vert {\mathit{\pi }}_3^{\ast }\Vert \right),{\mathcal{N}}_3=\left(\Vert {\mathit{\pi }}_1^{\ast }\Vert +\Vert {\mathit{\pi }}_3^{\ast }\Vert \right),\hfill \\ \hfill {\mathcal{N}}_4& =\left(\Vert {\mathit{\pi }}_2^{\ast }\Vert +\Vert {\mathit{\pi }}_4^{\ast }\Vert \right).\hfill \end{array}$$

The Eqs. (56) and (57) can be rewritten in the following form

$$\begin{array}{c}\hfill \Vert u^{\prime }(t)-u(t)\Vert \le \frac{{\mathcal{M}}_2}{{\mathcal{M}}_1}\Vert v^{\prime }(t)-v(t)\Vert +\frac{{\mathcal{M}}_3}{{\mathcal{M}}_1}\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\frac{{\mathcal{M}}_4}{{\mathcal{M}}_1}\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert ,\end{array}$$ 58

$$\begin{array}{c}\hfill \Vert v^{\prime }(t)-v(t)\Vert \le \frac{{\mathcal{N}}_2}{{\mathcal{N}}_1}\Vert u^{\prime }(t)-u(t)\Vert +\frac{{\mathcal{N}}_3}{{\mathcal{N}}_1}\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\frac{{\mathcal{N}}_4}{{\mathcal{N}}_1}\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert .\end{array}$$ 59

Substituting (59) into (56), we have

$$\begin{array}{cc}\hfill \Vert u^{\prime }(t)-u(t)\Vert & \le \frac{{\mathcal{M}}_2}{{\mathcal{M}}_1}\left\{\frac{{\mathcal{N}}_2}{{\mathcal{N}}_1}\Vert u^{\prime }(t)-u(t)\Vert +\frac{{\mathcal{N}}_3}{{\mathcal{N}}_1}\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\frac{{\mathcal{N}}_4}{{\mathcal{N}}_1}\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert \right\}\hfill \\ \hfill & +\frac{{\mathcal{M}}_3}{{\mathcal{M}}_1}\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\frac{{\mathcal{M}}_4}{{\mathcal{M}}_1}\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert ,\hfill \\ \hfill & =\frac{{\mathcal{M}}_2{\mathcal{N}}_2}{{\mathcal{M}}_1{\mathcal{N}}_1}\Vert u^{\prime }(t)-u(t)\Vert +\left(\frac{{\mathcal{M}}_2{\mathcal{N}}_3}{{\mathcal{M}}_1{\mathcal{N}}_1}+\frac{{\mathcal{M}}_3}{{\mathcal{M}}_1}\right)\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert \hfill \\ \hfill & +\left(\frac{{\mathcal{M}}_2{\mathcal{N}}_4}{{\mathcal{M}}_1{\mathcal{N}}_1}+\frac{{\mathcal{M}}_4}{{\mathcal{M}}_1}\right)\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert ,\hfill \\ \hfill \Vert u^{\prime }(t)-u(t)\Vert & \le \left(\frac{\frac{{\mathcal{M}}_2{\mathcal{N}}_3}{{\mathcal{M}}_1{\mathcal{N}}_1}+\frac{{\mathcal{M}}_3}{{\mathcal{M}}_1}}{1-\frac{{\mathcal{M}}_2{\mathcal{N}}_2}{{\mathcal{M}}_1{\mathcal{N}}_1}}\right)\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\left(\frac{\frac{{\mathcal{M}}_2{\mathcal{N}}_4}{{\mathcal{M}}_1{\mathcal{N}}_1}+\frac{{\mathcal{M}}_4}{{\mathcal{M}}_1}}{1-\frac{{\mathcal{M}}_2{\mathcal{N}}_2}{{\mathcal{M}}_1{\mathcal{N}}_1}}\right)\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert .\hfill \end{array}$$

Similarly, substituting (58) into (57), we have

$$\begin{array}{cc}\hfill \Vert v^{\prime }(t)-v(t)\Vert & \le \frac{{\mathcal{N}}_2}{{\mathcal{N}}_1}\left\{\frac{{\mathcal{M}}_2}{{\mathcal{M}}_1}\Vert v^{\prime }(t)-v(t)\Vert +\frac{{\mathcal{M}}_3}{{\mathcal{M}}_1}\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\frac{{\mathcal{M}}_4}{{\mathcal{M}}_1}\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert \right\}\hfill \\ \hfill & +\frac{{\mathcal{N}}_3}{{\mathcal{N}}_1}\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\frac{{\mathcal{N}}_4}{{\mathcal{N}}_1}\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert ,\hfill \\ \hfill & =\frac{{\mathcal{N}}_2{\mathcal{M}}_2}{{\mathcal{N}}_1{\mathcal{M}}_1}\Vert v^{\prime }(t)-v(t)\Vert +\left(\frac{{\mathcal{N}}_2{\mathcal{M}}_3}{{\mathcal{N}}_1{\mathcal{M}}_1}+\frac{{\mathcal{N}}_3}{{\mathcal{N}}_1}\right)\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert \hfill \\ \hfill & +\left(\frac{{\mathcal{N}}_2{\mathcal{M}}_4}{{\mathcal{N}}_1{\mathcal{M}}_1}+\frac{{\mathcal{N}}_4}{{\mathcal{N}}_1}\right)\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert ,\hfill \\ \hfill \Vert v^{\prime }(t)-v(t)\Vert & \le \left(\frac{\frac{{\mathcal{N}}_2{\mathcal{M}}_3}{{\mathcal{N}}_1{\mathcal{M}}_1}+\frac{{\mathcal{N}}_3}{{\mathcal{N}}_1}}{1-\frac{{\mathcal{N}}_2{\mathcal{M}}_2}{{\mathcal{N}}_1{\mathcal{M}}_1}}\right)\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\left(\frac{\frac{{\mathcal{N}}_2{\mathcal{M}}_4}{{\mathcal{N}}_1{\mathcal{M}}_1}+\frac{{\mathcal{N}}_4}{{\mathcal{N}}_1}}{1-\frac{{\mathcal{N}}_2{\mathcal{M}}_2}{{\mathcal{N}}_1{\mathcal{M}}_1}}\right)\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert .\hfill \end{array}$$

If we take,

$$\begin{array}{cc}\hfill \Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert & \le \frac{{\mathit{\epsilon }}_1}{2\left(\frac{\frac{{\mathcal{M}}_2{\mathcal{N}}_3}{{\mathcal{M}}_1{\mathcal{N}}_1}+\frac{{\mathcal{M}}_3}{{\mathcal{M}}_1}}{1-\frac{{\mathcal{M}}_2{\mathcal{N}}_2}{{\mathcal{M}}_1{\mathcal{N}}_1}}\right)}=\frac{{\mathit{\epsilon }}_1}{2{\mathit{\delta }}_1},\hfill \\ \hfill \Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert & \le \frac{{\mathit{\epsilon }}_1}{2\left(\frac{\frac{{\mathcal{M}}_2{\mathcal{N}}_4}{{\mathcal{M}}_1{\mathcal{N}}_1}+\frac{{\mathcal{M}}_4}{{\mathcal{M}}_1}}{1-\frac{{\mathcal{M}}_2{\mathcal{N}}_2}{{\mathcal{M}}_1{\mathcal{N}}_1}}\right)}=\frac{{\mathit{\epsilon }}_1}{2{\mathit{\delta }}_2},\hfill \end{array}$$

where ${\mathit{\delta }}_1=\left(\frac{\frac{{\mathcal{M}}_2{\mathcal{N}}_3}{{\mathcal{M}}_1{\mathcal{N}}_1}+\frac{{\mathcal{M}}_3}{{\mathcal{M}}_1}}{1-\frac{{\mathcal{M}}_2{\mathcal{N}}_2}{{\mathcal{M}}_1{\mathcal{N}}_1}}\right)$ and ${\mathit{\delta }}_2=\left(\frac{\frac{{\mathcal{M}}_2{\mathcal{N}}_4}{{\mathcal{M}}_1{\mathcal{N}}_1}+\frac{{\mathcal{M}}_4}{{\mathcal{M}}_1}}{1-\frac{{\mathcal{M}}_2{\mathcal{N}}_2}{{\mathcal{M}}_1{\mathcal{N}}_1}}\right)$.

Then Eq. (56) becomes,

$$\begin{array}{cc}\hfill \Vert u^{\prime }(t)-u(t)\Vert & \le {\mathit{\epsilon }}_1.\hfill \end{array}$$ 60

Similarly if we take,

$$\begin{array}{cc}\hfill \Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert & \le \frac{{\mathit{\epsilon }}_2}{2\left(\frac{\frac{{\mathcal{N}}_2{\mathcal{M}}_3}{{\mathcal{N}}_1{\mathcal{M}}_1}+\frac{{\mathcal{N}}_3}{{\mathcal{N}}_1}}{1-\frac{{\mathcal{N}}_2{\mathcal{M}}_2}{{\mathcal{N}}_1{\mathcal{M}}_1}}\right)}=\frac{{\mathit{\epsilon }}_2}{2{\mathit{\delta }}_3},\hfill \\ \hfill \Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert & \le \frac{{\mathit{\epsilon }}_2}{2\left(\frac{\frac{{\mathcal{N}}_2{\mathcal{M}}_4}{{\mathcal{N}}_1{\mathcal{M}}_1}+\frac{{\mathcal{N}}_4}{{\mathcal{N}}_1}}{1-\frac{{\mathcal{N}}_2{\mathcal{M}}_2}{{\mathcal{N}}_1{\mathcal{M}}_1}}\right)}=\frac{{\mathit{\epsilon }}_2}{2{\mathit{\delta }}_4},\hfill \end{array}$$

where ${\mathit{\delta }}_3=\left(\frac{\frac{{\mathcal{N}}_2{\mathcal{M}}_3}{{\mathcal{N}}_1{\mathcal{M}}_1}+\frac{{\mathcal{N}}_3}{{\mathcal{N}}_1}}{1-\frac{{\mathcal{N}}_2{\mathcal{M}}_2}{{\mathcal{N}}_1{\mathcal{M}}_1}}\right)$ and ${\mathit{\delta }}_4=\left(\frac{\frac{{\mathcal{N}}_2{\mathcal{M}}_4}{{\mathcal{N}}_1{\mathcal{M}}_1}+\frac{{\mathcal{N}}_4}{{\mathcal{N}}_1}}{1-\frac{{\mathcal{N}}_2{\mathcal{M}}_2}{{\mathcal{N}}_1{\mathcal{M}}_1}}\right)$.

Then Eq. (57) becomes,

$$\begin{array}{cc}\hfill \Vert v^{\prime }(t)-v(t)\Vert & \le {\mathit{\epsilon }}_2.\hfill \end{array}$$ 61

From Eqs. (60) and (61), we can say that for $\forall \mathit{\epsilon }=max\{{\mathit{\epsilon }}_1,{\mathit{\epsilon }}_2\}>0,$ then there exist a $\mathit{\delta }=\mathit{\epsilon }/max\{{\mathit{\delta }}_5,{\mathit{\delta }}_6\}>0,{\mathit{\delta }}_5=max\{{\mathit{\delta }}_1,{\mathit{\delta }}_3\},{\mathit{\delta }}_6=max\{{\mathit{\delta }}_2,{\mathit{\delta }}_4\}$ such that $\Vert z^{\prime }(t)-z(t)\Vert <\mathit{\epsilon }$ when $\Vert {\mathit{\chi }}^{\ast }(t)-{\mathit{\psi }}^{\ast }(t)\Vert <\mathit{\delta }$. Thus, the solution $z(t)$ is uniformly stable.

Theorem 5

Under the case$4^{\prime }$, if Assumption 3–4 are satisfied, then the system (9) is satisfying the initial condition (12) is uniformly stable.

Proof

Complex-valued memristor-based fractional-order neural networks system (9) can be expressed by separating real and imaginary parts, we get

$$\begin{array}{cc}\hfill D^{\mathit{\alpha }}{u}_p(t)& =-{\mathit{ϵ}}_p{u}_p(t)+\sum _{q=1}^n{\mathit{\beta }}_{pq}^R(u_q(t))f^R(u,v)-\sum _{q=1}^n{\mathit{\beta }}_{pq}^I(v_q(t))f^I(u,v)+\sum _{q=1}^n{\mathit{\gamma }}_{pq}^R(u_p(t))\hfill \\ \hfill & \times g^R(u(t-\mathit{\tau }),v(t-\mathit{\tau }))-\sum _{q=1}^n{\mathit{\gamma }}_{pq}^I(v_q(t))g^I(u(t-\mathit{\tau }),v(t-\mathit{\tau }))+H^R,\hfill \end{array}$$ 62

$$\begin{array}{cc}\hfill D^{\mathit{\alpha }}{v}_p(t)& =-{\mathit{ϵ}}_p{v}_p(t)+\sum _{q=1}^n{\mathit{\beta }}_{pq}^I(v_q(t))f^R(u,v)+\sum _{q=1}^n{\mathit{\beta }}_{pq}^R(u_q(t))f^I(u,v)+\sum _{q=1}^n{\mathit{\gamma }}_{pq}^I(v_q(t))\hfill \\ \hfill & \times g^R(u(t-\mathit{\tau }),v(t-\mathit{\tau }))+\sum _{q=1}^n{\mathit{\gamma }}_{pq}^R(v_q(t))g^I(u(t-\mathit{\tau }),v(t-\mathit{\tau }))+H^I.\hfill \end{array}$$ 63

$$\begin{array}{cc}\hfill D^{\mathit{\alpha }}{u}_p(t)& \le -{\mathit{ϵ}}_p{u}_p(t)+\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^R{f}^R(u,v)-\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^I{f}^I(u,v)\hfill \\ \hfill & +\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^R{g}^R(u(t-\mathit{\tau }),v(t-\mathit{\tau }))-\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^I{g}^I(u(t-\mathit{\tau }),v(t-\mathit{\tau }))+H^R,\hfill \end{array}$$ 64

$$\begin{array}{cc}\hfill D^{\mathit{\alpha }}{v}_p(t)& \le -{\mathit{ϵ}}_p{v}_p(t)+\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^I{f}^R(u,v)+\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^R{f}^I(u,v)\hfill \\ \hfill & +\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^I{g}^R(u(t-\mathit{\tau }),v(t-\mathit{\tau }))+\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^R{g}^I(u(t-\mathit{\tau }),v(t-\mathit{\tau }))+H^I.\hfill \end{array}$$ 65

Clearly, for $p,q=1,2,\dots ,n$

$$\begin{array}{c}\hfill {\tilde{\mathrm{\Delta }}}_{pq}^R=max\left[|{\underline{\mathrm{\Delta }}}_{pq}^R|,|{\overline{\mathrm{\Delta }}}_{pq}^R|\right],{\tilde{\mathrm{\Delta }}}_{pq}^I=max\left[|{\underline{\mathrm{\Delta }}}_{pq}^I|,|{\overline{\mathrm{\Delta }}}_{pq}^I|\right],{\tilde{\mathrm{\Theta }}}_{pq}^R=max\left[|{\underline{\mathrm{\Theta }}}_{pq}^R|,|{\overline{\mathrm{\Theta }}}_{pq}^R|\right],\text{and}{\tilde{\mathrm{\Theta }}}_{pq}^I=max\left[|{\underline{\mathrm{\Theta }}}_{pq}^I|,|{\overline{\mathrm{\Theta }}}_{pq}^I|\right].\end{array}$$

Consider $z^{\prime }=u^{\prime }+i{v}^{\prime }$ and $z=u+iv$ with $u^{\prime }\ne u$ and $v^{\prime }\ne v$. $z^{\prime }(t)=(z_1^{\prime }(t),\dots ,z_n^{\prime }(t))$ and $z(t)=(z_1(t),\dots ,z_n(t))$ are any two solutions of the system (9) with initial conditions $z_p^{\prime }(s)={\mathit{\psi }}_p^{\prime }(s)+i{\mathit{\chi }}_p^{\prime }(s),$ where ${\mathit{\psi }}_p^{\prime }(s),{\mathit{\chi }}_p^{\prime }(s)\in C([-\mathit{\tau },0],{\mathcal{R}}^n),{\mathit{\psi }}_p^{\prime }(0)=0,{\mathit{\chi }}_p^{\prime }(0)=0,z_p(s)={\mathit{\psi }}_p(s)+i{\mathit{\chi }}_p(s)$, where ${\mathit{\psi }}_p(s),{\mathit{\chi }}_p(s)\in C([-\mathit{\tau },0],{\mathcal{R}}^n),{\mathit{\psi }}_p(0)=0,{\mathit{\chi }}_p(0)=0,p\in n$. We have

$$\begin{array}{cc}\hfill D^{\mathit{\alpha }}(u_p^{\prime }(t)-u_p(t))& \le -{\mathit{ϵ}}_p(u_p^{\prime }(t)-u_p(t))+\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^R[f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)]\hfill \\ \hfill & -\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^I[f_q^I(u_q^{\prime },v_q^{\prime })-f_q^I(u_q,v_q)]+\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^R[g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]\hfill \\ \hfill & -\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^I[g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})],\hfill \\ \hfill D^{\mathit{\alpha }}(v_p^{\prime }(t)-v_p(t))\le & -{\mathit{ϵ}}_p(v_p^{\prime }(t)-v_p(t))+\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^I[f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)]\hfill \\ \hfill & +\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^R[f_q^I(u_q^{\prime },v_q^{\prime })-f_q^I(u_q,v_q)]+\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^I[g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]\hfill \\ \hfill & +\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^R[g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})].\hfill \end{array}$$

Now multiply by $D^{-\mathit{\alpha }}$ on both sides, we can write

$$\begin{array}{cc}\hfill u_p^{\prime }(t)-u_p(t)& \le D^{-\mathit{\alpha }}[-{\mathit{ϵ}}_p(u^{\prime }(t)-u_p(t))+\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^R[f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)]\hfill \\ \hfill & -\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^I[f_q^I(u_q^{\prime },v_q^{\prime })-f_q^I(u_q,v_q)]+\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^R[g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]\hfill \\ \hfill & -\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^I[g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]],\hfill \end{array}$$ 66

$$\begin{array}{cc}\hfill v_p^{\prime }(t)-v_p(t)& \le D^{-\mathit{\alpha }}[-{\mathit{ϵ}}_p(v_p^{\prime }(t)-v_p(t))+\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^I[f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)]\hfill \\ \hfill & +\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^R[f_q^I(u_q^{\prime },v_q^{\prime })-f_q^I(u_q,v_q)]+\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^I[g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]\hfill \\ \hfill & +\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^R[g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]].\hfill \end{array}$$ 67

From the Eq. (66), we have

$$\begin{array}{cc}\hfill u_p^{\prime }(t)-u_p(t)& \le D^{-\mathit{\alpha }}[-{\mathit{ϵ}}_p(u_p^{\prime }(t)-u_p(t))+\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^R[f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)]-\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^I[f_q^I(u_q^{\prime },v_q^{\prime })\hfill \\ \hfill & -f_q^I(u_q,v_q)]+\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^R[g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]-\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^I[g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })\hfill \\ \hfill & -g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]]\hfill \\ \hfill \le & \frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}[-{\mathit{ϵ}}_p(u_p^{\prime }(s)-u_p(s))+\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^R[f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)]\hfill \\ \hfill & -\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^I[f_q^I(u_q^{\prime },v_q^{\prime })-f_q^I(u_q,v_q)]+\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^R[g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]\hfill \\ \hfill & -\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^I[g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]]\mathrm{d}s.\hfill \end{array}$$

By taking absolute value and multiply by $e^{-t}$ on both sides, we get

$$\begin{array}{cc}\hfill e^{-t}|u_p^{\prime }(t)-u_p(t)|& \le \frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{e}^{-t}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}[{\mathit{ϵ}}_p|u_p^{\prime }(s)-u_p(s)|+\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^R||f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)|\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^I||f_q^I(u_q^{\prime },v_q^{\prime })-f_q^I(u_q,v_q)|+\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^R||g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})|\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^I||g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})|]\mathrm{d}s\hfill \\ \hfill & \le {\mathit{ϵ}}_p\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_p^{\prime }(s)-u_p(s)|\mathrm{d}s+\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^R|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}\hfill \\ \hfill & \times e^{-(t-s)}{e}^{-s}[{\mathit{\lambda }}_q^{RR}|u_q^{\prime }(s)-u_q(s)|+{\mathit{\lambda }}_q^{RI}|v_q^{\prime }(s)-v_q(s)|]\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^I|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}[{\mathit{\lambda }}_q^{IR}|u_q^{\prime }(s)-u_q(s)|\hfill \\ \hfill & +{\mathit{\lambda }}_q^{II}|v_q^{\prime }(s)-v_q(s)|]\mathrm{d}s+\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^R|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times [{\mathit{\mu }}_q^{RR}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|+{\mathit{\mu }}_q^{RI}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|]\mathrm{d}s+\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^I|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}\hfill \\ \hfill & e^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}[{\mathit{\mu }}_q^{IR}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|+{\mathit{\mu }}_q^{II}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|]\mathrm{d}s\hfill \\ \hfill & \le {\mathit{ϵ}}_p\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_p^{\prime }(s)-u_p(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^R|{\mathit{\lambda }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_q^{\prime }(s)-u_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^R|{\mathit{\lambda }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|v_q^{\prime }(s)-v_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^I|{\mathit{\lambda }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_q^{\prime }(s)-u_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^I|{\mathit{\lambda }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|v_q^{\prime }(s)-v_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^R|{\mathit{\mu }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^R|{\mathit{\mu }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^I|{\mathit{\mu }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^I|{\mathit{\mu }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & \le {\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|u_p^{\prime }(t)-u_p(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u+\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^R|{\mathit{\lambda }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}\hfill \\ \hfill & \times {\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_q^{\prime }(s)-u_q(s)|\mathrm{d}s+\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^R|{\mathit{\lambda }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}\hfill \\ \hfill & \times {\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|v_q^{\prime }(s)-v_q(s)|\mathrm{d}s+\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^I|{\mathit{\lambda }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}\hfill \\ \hfill & e^{-(t-s)}{e}^{-s}|u_q^{\prime }(s)-u_q(s)|\mathrm{d}s+\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^I|{\mathit{\lambda }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}\hfill \\ \hfill & \times |v_q^{\prime }(s)-v_q(s)|\mathrm{d}s+\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^R|{\mathit{\mu }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{\mathit{\tau }}{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times |{\mathit{\psi }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\psi }}_{q\mathit{\tau }}(s)|\mathrm{d}s+\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^R|{\mathit{\mu }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{\mathit{\tau }}^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times |u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|\mathrm{d}s+\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^R|{\mathit{\mu }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{\mathit{\tau }}{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times |{\mathit{\chi }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\chi }}_{q\mathit{\tau }}(s)|\mathrm{d}s+\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^R|{\mathit{\mu }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{\mathit{\tau }}^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times |v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\mathrm{d}s+\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^I|{\mathit{\mu }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{\mathit{\tau }}{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times |{\mathit{\psi }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\psi }}_{q\mathit{\tau }}(s)|\mathrm{d}s+\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^I|{\mathit{\mu }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{\mathit{\tau }}^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times |u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|\mathrm{d}s+\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^I|{\mathit{\mu }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{\mathit{\tau }}{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times |{\mathit{\chi }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\chi }}_{q\mathit{\tau }}(s)|\mathrm{d}s+\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^I|{\mathit{\mu }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{\mathit{\tau }}^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times |v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill e^{-t}|u_p^{\prime }(t)-u_p(t)|& \le {\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|u_p^{\prime }(t)-u_p(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u+[{\mathit{\zeta }}_{1p}^{\ast }+{\mathit{\zeta }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)\hfill \\ \hfill & -u_q(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u+[{\mathit{\zeta }}_{2p}^{\ast }+{\mathit{\zeta }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}\hfill \\ \hfill & \times \frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u+[{\mathit{\eta }}_{1p}^{\ast }+{\mathit{\eta }}_{3p}^{\ast }]\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{-\mathit{\tau }}^0{(t-\mathit{\nu }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\nu })}{e}^{-\mathit{\nu }}\hfill \\ \hfill & \times |{\mathit{\psi }}_q^{\prime }(\mathit{\nu })-{\mathit{\psi }}_q(\mathit{\nu })|\mathrm{d}\mathit{\nu }+[{\mathit{\eta }}_{1p}^{\ast }+{\mathit{\eta }}_{3p}^{\ast }]\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{(t-\mathit{\nu }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\nu })}{e}^{-\mathit{\nu }}\hfill \\ \hfill & \times |u_q^{\prime }(\mathit{\nu })-u_q(\mathit{\nu })|\mathrm{d}\mathit{\nu }+[{\mathit{\eta }}_{2p}^{\ast }+{\mathit{\eta }}_{4p}^{\ast }]\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{-\mathit{\tau }}^0{(t-\mathit{\nu }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\nu })}{e}^{-\mathit{\nu }}\hfill \\ \hfill & \times |{\mathit{\chi }}_q^{\prime }(\mathit{\nu })-{\mathit{\chi }}_q(\mathit{\nu })|\mathrm{d}\mathit{\nu }+[{\mathit{\eta }}_{2p}^{\ast }+{\mathit{\eta }}_{4p}^{\ast }]\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{(t-\mathit{\nu }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\nu })}{e}^{-\mathit{\nu }}\hfill \\ \hfill & \times |v_q^{\prime }(\mathit{\nu })-v_q(\mathit{\nu })|\mathrm{d}\mathit{\nu }\hfill \\ \hfill & \le {\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|u_p^{\prime }(t)-u_p(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +[{\mathit{\zeta }}_{1p}^{\ast }+{\mathit{\zeta }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)-u_q(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +[{\mathit{\zeta }}_{2p}^{\ast }+{\mathit{\zeta }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +[{\mathit{\eta }}_{1p}^{\ast }+{\mathit{\eta }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\psi }}_q^{\prime }(t)-{\mathit{\psi }}_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{t-\mathit{\tau }}^t{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & +[{\mathit{\eta }}_{1p}^{\ast }+{\mathit{\eta }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)-u_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & +[{\mathit{\eta }}_{2p}^{\ast }+{\mathit{\eta }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\chi }}_q^{\prime }(t)-{\mathit{\chi }}_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{t-\mathit{\tau }}^t{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & +[{\mathit{\eta }}_{2p}^{\ast }+{\mathit{\eta }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & \le {\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|u_p^{\prime }(t)-u_p(t)|\}+[{\mathit{\zeta }}_{1p}^{\ast }+{\mathit{\zeta }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)-u_q(t)|\}\hfill \\ \hfill & +[{\mathit{\zeta }}_{2p}^{\ast }+{\mathit{\zeta }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}+[{\mathit{\eta }}_{1p}^{\ast }+{\mathit{\eta }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}\hfill \\ \hfill & |{\mathit{\psi }}_q^{\prime }(t)-{\mathit{\psi }}_q(t)|\}{e}^{-\mathit{\tau }}+[{\mathit{\eta }}_{1p}^{\ast }+{\mathit{\eta }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)-u_q(t)|\}{e}^{-\mathit{\tau }}\hfill \\ \hfill & +[{\mathit{\eta }}_{2p}^{\ast }+{\mathit{\eta }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\chi }}_q^{\prime }(t)-{\mathit{\chi }}_q(t)|\}{e}^{-\mathit{\tau }}\hfill \\ \hfill & +[{\mathit{\eta }}_{2p}^{\ast }+{\mathit{\eta }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}{e}^{-\mathit{\tau }}\hfill \\ \hfill & \le {\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|u_p^{\prime }(t)-u_p(t)|\}+[{\mathit{\zeta }}_{1p}^{\ast }+{\mathit{\zeta }}_{3p}^{\ast }]\Vert u^{\prime }(t)-u(t)\Vert \hfill \\ \hfill & +[{\mathit{\zeta }}_{2p}^{\ast }+{\mathit{\zeta }}_{4p}^{\ast }]\Vert v^{\prime }(t)-v(t)\Vert +[{\mathit{\eta }}_{1p}^{\ast }+{\mathit{\eta }}_{3p}^{\ast }]\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert \hfill \\ \hfill & +[{\mathit{\eta }}_{1p}^{\ast }+{\mathit{\eta }}_{3p}^{\ast }]\Vert u^{\prime }(t)-u_{(}t)\Vert +[{\mathit{\eta }}_{2p}^{\ast }+{\mathit{\eta }}_{4p}^{\ast }]\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert \hfill \\ \hfill & +[{\mathit{\eta }}_{2p}^{\ast }+{\mathit{\eta }}_{4p}^{\ast }]\Vert v^{\prime }(t)-v(t)\Vert .\hfill \end{array}$$ 68

From (68) we can obtain

$$\begin{array}{cc}\hfill \Vert u^{\prime }(t)-u(t)\Vert & =\sum _{j=1}^n\underset{t}{sup}\{e^{-t}|u_p^{\prime }(t)-u_p(t)|\}\hfill \\ \hfill & \le \left[{\mathit{ϵ}}_{max}+\Vert {\mathit{\zeta }}_1^{\ast }\Vert +\Vert {\mathit{\zeta }}_3^{\ast }\Vert +\Vert {\mathit{\eta }}_1^{\ast }\Vert +\Vert {\mathit{\eta }}_3^{\ast }\Vert \right]\Vert u^{\prime }(t)-u(t)\Vert \hfill \\ \hfill & +\left[\Vert {\mathit{\zeta }}_2^{\ast }\Vert +\Vert {\mathit{\zeta }}_4^{\ast }\Vert +\Vert {\mathit{\eta }}_2^{\ast }\Vert +\Vert {\mathit{\eta }}_4^{\ast }\Vert \right]\Vert v^{\prime }(t)-v(t)\Vert \hfill \\ \hfill & +\left[\Vert {\mathit{\eta }}_1^{\ast }\Vert +\Vert {\mathit{\eta }}_3^{\ast }\Vert \right]\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\left[\Vert {\mathit{\eta }}_2^{\ast }\Vert +\Vert {\mathit{\eta }}_4^{\ast }\Vert \right]\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert .\hfill \end{array}$$ 69

The above Eq. (69) can be rewritten as

$$\begin{array}{cc}\hfill \Vert u^{\prime }(t)-u(t)\Vert & \le \frac{1}{\left(1-\left({\mathit{ϵ}}_{max}+\Vert {\mathit{\zeta }}_1^{\ast }\Vert +\Vert {\mathit{\zeta }}_3^{\ast }\Vert +\Vert {\mathit{\eta }}_1^{\ast }\Vert +\Vert {\mathit{\eta }}_3^{\ast }\Vert \right)\right)}\hfill \\ \hfill & \times \left\{\right.\left[\Vert {\mathit{\zeta }}_2^{\ast }\Vert +\Vert {\mathit{\zeta }}_4^{\ast }\Vert +\Vert {\mathit{\eta }}_2^{\ast }\Vert +\Vert {\mathit{\eta }}_4^{\ast }\Vert \right]\Vert v^{\prime }(t)-v(t)\Vert \hfill \\ \hfill & +\left[\Vert {\mathit{\eta }}_1^{\ast }\Vert +\Vert {\mathit{\eta }}_3^{\ast }\Vert \right]\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\left[\Vert {\mathit{\eta }}_2^{\ast }\Vert +\Vert {\mathit{\eta }}_4^{\ast }\Vert \right]\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert \left.\right\}.\hfill \end{array}$$ 70

Similarly, we consider the Eq. (67), one can easily obtain as follows

$$\begin{array}{cc}\hfill v_p^{\prime }(t)-v_p(t)& \le D^{-\mathit{\alpha }}[-{\mathit{ϵ}}_p(v_p^{\prime }(t)-v_p(t))+\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^I[f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)]\hfill \\ \hfill & +\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^R[f_q^I(u_q^{\prime },v_q^{\prime })-f_q^I(u_q,v_q)]+\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^I[g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]\hfill \\ \hfill & +\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^R[g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]],\hfill \\ \hfill v_p^{\prime }(t)-v_p(t)\le & \frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}[-{\mathit{ϵ}}_p(v_p^{\prime }(s)-v_p(s))+\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^I[f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)]\hfill \\ \hfill & +\sum _{q=1}^n{\tilde{\mathrm{\Delta }}}_{pq}^R[f_q^I(u_q^{\prime },v_q^{\prime })-f_q^I(u_q,v_q)]+\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^I[g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]\hfill \\ \hfill & +\sum _{q=1}^n{\tilde{\mathrm{\Theta }}}_{pq}^R[g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})]]\mathrm{d}s.\hfill \end{array}$$

By absolute value and multiply by $e^{-t}$ on both sides, we have

$$\begin{array}{cc}\hfill e^{-t}|v_p^{\prime }(t)-v_p(t)|& \le \frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{e}^{-t}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}\left\{{\mathit{ϵ}}_p|v_p^{\prime }(s)-v_p(s)|+\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^I||f_q^R(u_q^{\prime },v_q^{\prime })-f_q^R(u_q,v_q)|\right.\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^R||f_q^I(u_q^{\prime },v_q^{\prime })-f_q^I(u_q,v_q)|+\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^I||g_q^R(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^R(u_{q\mathit{\tau }},v_{q\mathit{\tau }})|\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^R||g_q^I(u_{q\mathit{\tau }}^{\prime },v_{q\mathit{\tau }}^{\prime })-g_q^I(u_{q\mathit{\tau }},v_{q\mathit{\tau }})|\left.\right\}\mathrm{d}s\hfill \\ \hfill & ={\mathit{ϵ}}_p\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|v_p^{\prime }(s)-v_p(s)|\mathrm{d}s+\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^I|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}\hfill \\ \hfill & \times {\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}\left[\right.{\mathit{\lambda }}_q^{RR}|u_q^{\prime }(s)-u_q(s)|+{\mathit{\lambda }}_q^{RI}|v_q^{\prime }(s)-v_q(s)|\left.\right]\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^R|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}\left[\right.{\mathit{\lambda }}_q^{IR}|u_q^{\prime }(s)-u_q(s)|\hfill \\ \hfill & +{\mathit{\lambda }}_q^{II}|v_q^{\prime }(s)-v_q(s)|\left.\right]\mathrm{d}s+\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^I|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\left[{\mathit{\mu }}_q^{RR}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|+{\mathit{\mu }}_q^{RI}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\right]\mathrm{d}s+\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^R|\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}\hfill \\ \hfill & \times \left[{\mathit{\mu }}_q^{IR}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|+{\mathit{\mu }}_q^{II}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\right]\mathrm{d}s\hfill \\ \hfill & ={\mathit{ϵ}}_p\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|v_p^{\prime }(s)-v_p(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^I|{\mathit{\lambda }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_q^{\prime }(s)-u_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^I|{\mathit{\lambda }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|v_q^{\prime }(s)-v_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^R|{\mathit{\lambda }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_q^{\prime }(s)-u_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^R|{\mathit{\lambda }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|v_q^{\prime }(s)-v_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^I|{\mathit{\mu }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^I|{\mathit{\mu }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^R|{\mathit{\mu }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^R|{\mathit{\mu }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & ={\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|v_p^{\prime }(t)-v_p(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^I|{\mathit{\lambda }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_q^{\prime }(s)-u_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^I|{\mathit{\lambda }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|v_q^{\prime }(s)-v_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^R|{\mathit{\lambda }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|u_q^{\prime }(s)-u_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Delta }}}_{pq}^R|{\mathit{\lambda }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s)}{e}^{-s}|v_q^{\prime }(s)-v_q(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^I|{\mathit{\mu }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{\mathit{\tau }}{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|{\mathit{\psi }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\psi }}_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^I|{\mathit{\mu }}_q^{RR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{\mathit{\tau }}^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^I|{\mathit{\mu }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{\mathit{\tau }}{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|{\mathit{\chi }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\chi }}_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^I|{\mathit{\mu }}_q^{RI}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{\mathit{\tau }}^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^R|{\mathit{\mu }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{\mathit{\tau }}{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|{\mathit{\psi }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\psi }}_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^R|{\mathit{\mu }}_q^{IR}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{\mathit{\tau }}^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|u_{q\mathit{\tau }}^{\prime }(s)-u_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^R|{\mathit{\mu }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{\mathit{\tau }}{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|{\mathit{\chi }}_{q\mathit{\tau }}^{\prime }(s)-{\mathit{\chi }}_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill & +\sum _{q=1}^n|{\tilde{\mathrm{\Theta }}}_{pq}^R|{\mathit{\mu }}_q^{II}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{\mathit{\tau }}^t{(t-s)}^{\mathit{\alpha }-1}{e}^{-(t-s+\mathit{\tau })}{e}^{-(s-\mathit{\tau })}|v_{q\mathit{\tau }}^{\prime }(s)-v_{q\mathit{\tau }}(s)|\mathrm{d}s\hfill \\ \hfill e^{-t}|v_p^{\prime }(t)-v_p(t)|& \le {\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|v_p^{\prime }(t)-v_p(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u+[{\mathit{\xi }}_{1p}^{\ast }+{\mathit{\xi }}_{3p}^{\ast }]\hfill \\ \hfill & \times \sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)-u_q(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u+[{\mathit{\xi }}_{2p}^{\ast }+{\mathit{\xi }}_{4p}^{\ast }]\hfill \\ \hfill & \times \sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +[{\mathit{\pi }}_{1p}^{\ast }+{\mathit{\pi }}_{3p}^{\ast }]\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{-\mathit{\tau }}^0{(t-\mathit{\nu }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\nu })}{e}^{-\mathit{\nu }}|{\mathit{\psi }}_q^{\prime }(\mathit{\nu })-{\mathit{\psi }}_q(\mathit{\nu })|\mathrm{d}\mathit{\nu }\hfill \\ \hfill & +[{\mathit{\pi }}_{1p}^{\ast }+{\mathit{\pi }}_{3p}^{\ast }]\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{(t-\mathit{\nu }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\nu })}{e}^{-\mathit{\nu }}|u_q^{\prime }(\mathit{\nu })-u_q(\mathit{\nu })|\mathrm{d}\mathit{\nu }\hfill \\ \hfill & +[{\mathit{\pi }}_{2p}^{\ast }+{\mathit{\pi }}_{4p}^{\ast }]\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{-\mathit{\tau }}^0{(t-\mathit{\nu }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\nu })}{e}^{-\mathit{\nu }}|{\mathit{\chi }}_q^{\prime }(\mathit{\nu })-{\mathit{\chi }}_q(\mathit{\nu })|\mathrm{d}\mathit{\nu }\hfill \\ \hfill & +[{\mathit{\pi }}_{2p}^{\ast }+{\mathit{\pi }}_{4p}^{\ast }]\sum _{q=1}^n\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{(t-\mathit{\nu }-\mathit{\tau })}^{\mathit{\alpha }-1}{e}^{-(t-\mathit{\nu })}{e}^{-\mathit{\nu }}|v_q^{\prime }(\mathit{\nu })-v_q(\mathit{\nu })|\mathrm{d}\mathit{\nu }\hfill \\ \hfill & ={\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|v_p^{\prime }(t)-v_p(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +[{\mathit{\xi }}_{1p}^{\ast }+{\mathit{\xi }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)-u_q(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +[{\mathit{\xi }}_{2p}^{\ast }+{\mathit{\xi }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^t{u}^{\mathit{\alpha }-1}{e}^{-u}\mathrm{d}u\hfill \\ \hfill & +[{\mathit{\pi }}_{1p}^{\ast }+{\mathit{\pi }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\psi }}_q^{\prime }(t)-{\mathit{\psi }}_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{t-\mathit{\tau }}^t{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & +[{\mathit{\pi }}_{1p}^{\ast }+{\mathit{\pi }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)-u_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & +[{\mathit{\pi }}_{2p}^{\ast }+{\mathit{\pi }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\chi }}_q^{\prime }(t)-{\mathit{\chi }}_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_{t-\mathit{\tau }}^t{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & +[{\mathit{\pi }}_{2p}^{\ast }+{\mathit{\pi }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}{e}^{-\mathit{\tau }}\frac{1}{\mathrm{\Gamma }(\mathit{\alpha })}{\int }_0^{t-\mathit{\tau }}{\mathit{\theta }}^{\mathit{\alpha }-1}{e}^{-\mathit{\theta }}\mathrm{d}\mathit{\theta }\hfill \\ \hfill & ={\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|v_p^{\prime }(t)-v_p(t)|\}+[{\mathit{\xi }}_{1p}^{\ast }+{\mathit{\xi }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)-u_q(t)|\}\hfill \\ \hfill & +[{\mathit{\xi }}_{2p}^{\ast }+{\mathit{\xi }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}\hfill \\ \hfill & +[{\mathit{\pi }}_{1p}^{\ast }+{\mathit{\pi }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\psi }}_q^{\prime }(t)-{\mathit{\psi }}_q(t)|\}{e}^{-\mathit{\tau }}\hfill \\ \hfill & +[{\mathit{\pi }}_{1p}^{\ast }+{\mathit{\pi }}_{3p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|u_q^{\prime }(t)-u_q(t)|\}{e}^{-\mathit{\tau }}\hfill \\ \hfill & +[{\mathit{\pi }}_{2p}^{\ast }+{\mathit{\pi }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|{\mathit{\chi }}_q^{\prime }(t)-{\mathit{\chi }}_q(t)|\}{e}^{-\mathit{\tau }}\hfill \\ \hfill & +[{\mathit{\pi }}_{2p}^{\ast }+{\mathit{\pi }}_{4p}^{\ast }]\sum _{q=1}^n\underset{t}{sup}\{e^{-t}|v_q^{\prime }(t)-v_q(t)|\}{e}^{-\mathit{\tau }}\hfill \\ \hfill & \le {\mathit{ϵ}}_p\underset{t}{sup}\{e^{-t}|v_p^{\prime }(t)-v_p(t)|\}+[{\mathit{\xi }}_{1p}^{\ast }+{\mathit{\xi }}_{3p}^{\ast }]\Vert u^{\prime }(t)-u(t)\Vert \hfill \\ \hfill & +[{\mathit{\xi }}_{2p}^{\ast }+{\mathit{\xi }}_{4p}^{\ast }]\Vert v^{\prime }(t)-v(t)\Vert +[{\mathit{\pi }}_{1p}^{\ast }+{\mathit{\pi }}_{3p}^{\ast }]\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert \hfill \\ \hfill & +[{\mathit{\pi }}_{1p}^{\ast }+{\mathit{\pi }}_{3p}^{\ast }]\Vert u^{\prime }(t)-u_{(}t)\Vert +[{\mathit{\pi }}_{2p}^{\ast }+{\mathit{\pi }}_{4p}^{\ast }]\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert \hfill \\ \hfill & +[{\mathit{\pi }}_{2p}^{\ast }+{\mathit{\pi }}_{4p}^{\ast }]\Vert v^{\prime }(t)-v(t)\Vert .\hfill \end{array}$$ 71

From (71) we can obtain

$$\begin{array}{cc}\hfill \Vert v^{\prime }(t)-v(t)\Vert & =\sum _{j=1}^n\underset{t}{sup}\{e^{-t}|v_p^{\prime }(t)-v_p(t)|\}\hfill \\ \hfill & \le \left[{\mathit{ϵ}}_{max}+\Vert {\mathit{\xi }}_2^{\ast }\Vert +\Vert {\mathit{\xi }}_4^{\ast }\Vert +\Vert {\mathit{\pi }}_2^{\ast }\Vert +\Vert {\mathit{\pi }}_4^{\ast }\Vert \right]\Vert v^{\prime }(t)-v(t)\Vert \hfill \\ \hfill & +\left[\Vert {\mathit{\xi }}_1^{\ast }\Vert +\Vert {\mathit{\xi }}_3^{\ast }\Vert +\Vert {\mathit{\pi }}_1^{\ast }\Vert +\Vert {\mathit{\pi }}_3^{\ast }\Vert \right]\Vert u^{\prime }(t)-u(t)\Vert \hfill \\ \hfill & +\left[\Vert {\mathit{\pi }}_1^{\ast }\Vert +\Vert {\mathit{\pi }}_3^{\ast }\Vert \right]\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\left[\Vert {\mathit{\pi }}_2^{\ast }\Vert +\Vert {\mathit{\pi }}_4^{\ast }\Vert \right]\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert .\hfill \end{array}$$ 72

The above Eq. (72) can be rewritten as

$$\begin{array}{cc}\hfill \Vert v^{\prime }(t)-v(t)\Vert & \le \frac{1}{\left(1-\left[{\mathit{ϵ}}_{max}+\Vert {\mathit{\xi }}_2^{\ast }\Vert +\Vert {\mathit{\xi }}_4^{\ast }\Vert +\Vert {\mathit{\pi }}_2^{\ast }\Vert +\Vert {\mathit{\pi }}_4^{\ast }\Vert \right]\right)}\hfill \\ \hfill & \times \left\{\left[\Vert {\mathit{\xi }}_1^{\ast }\Vert +\Vert {\mathit{\xi }}_3^{\ast }\Vert +\Vert {\mathit{\pi }}_1^{\ast }\Vert +\Vert {\mathit{\pi }}_3^{\ast }\Vert \right]\Vert u^{\prime }(t)-u(t)\Vert \right.\hfill \\ \hfill & \left.+\left[\Vert {\mathit{\pi }}_1^{\ast }\Vert +\Vert {\mathit{\pi }}_3^{\ast }\Vert \right]\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\left[\Vert {\mathit{\pi }}_2^{\ast }\Vert +\Vert {\mathit{\pi }}_4^{\ast }\Vert \right]\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert \right\}.\hfill \end{array}$$ 73

From the Eqs. (70) and (73), we can write in the following form,

$$\begin{array}{cc}\hfill \Vert u^{\prime }(t)-u(t)\Vert & \le \frac{1}{{\mathcal{M}}_1}\left\{{\mathcal{M}}_2\Vert v^{\prime }(t)-v(t)\Vert +{\mathcal{M}}_3\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +{\mathcal{M}}_4\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert \right\},\hfill \end{array}$$ 74

$$\begin{array}{cc}\hfill \Vert v^{\prime }(t)-v(t)\Vert & \le \frac{1}{{\mathcal{N}}_1}\left\{{\mathcal{N}}_2\Vert u^{\prime }(t)-u(t)\Vert +{\mathcal{N}}_3\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +{\mathcal{N}}_4\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert \right\},\hfill \end{array}$$ 75

where

$$\begin{array}{cc}\hfill {\mathcal{M}}_1& =\left(1-\left({\mathit{ϵ}}_{max}+\left[\Vert {\mathit{\zeta }}_1^{\ast }\Vert +\Vert {\mathit{\zeta }}_3^{\ast }\Vert +\Vert {\mathit{\eta }}_1^{\ast }\Vert +\Vert {\mathit{\eta }}_3^{\ast }\Vert \right]\right)\right),\hfill \\ \hfill {\mathcal{M}}_2& =\left(\Vert {\mathit{\zeta }}_2^{\ast }\Vert +\Vert {\mathit{\zeta }}_4^{\ast }\Vert +\Vert {\mathit{\eta }}_2^{\ast }\Vert +\Vert {\mathit{\eta }}_4^{\ast }\Vert \right),\hfill \\ \hfill {\mathcal{M}}_3& =\left(\Vert {\mathit{\eta }}_1^{\ast }\Vert +\Vert {\mathit{\eta }}_3^{\ast }\Vert \right),{\mathcal{M}}_4=\left(\Vert {\mathit{\eta }}_2^{\ast }\Vert +\Vert {\mathit{\eta }}_4^{\ast }\Vert \right),\hfill \\ \hfill {\mathcal{N}}_1& =\left(1-\left[{\mathit{ϵ}}_{max}+\Vert {\mathit{\xi }}_2^{\ast }\Vert +\Vert {\mathit{\xi }}_4^{\ast }\Vert +\Vert {\mathit{\pi }}_2^{\ast }\Vert +\Vert {\mathit{\pi }}_4^{\ast }\Vert \right]\right),\hfill \\ \hfill {\mathcal{N}}_2& =\left(\Vert {\mathit{\xi }}_1^{\ast }\Vert +\Vert {\mathit{\xi }}_3^{\ast }\Vert +\Vert {\mathit{\pi }}_1^{\ast }\Vert +\Vert {\mathit{\pi }}_3^{\ast }\Vert \right),{\mathcal{N}}_3=\left(\Vert {\mathit{\pi }}_1^{\ast }\Vert +\Vert {\mathit{\pi }}_3^{\ast }\Vert \right),\hfill \\ \hfill {\mathcal{N}}_4& =\left(\Vert {\mathit{\pi }}_2^{\ast }\Vert +\Vert {\mathit{\pi }}_4^{\ast }\Vert \right).\hfill \end{array}$$

The Eqs. (74) and (75) can be rewritten in the following form

$$\begin{array}{c}\hfill \Vert u^{\prime }(t)-u(t)\Vert \le \frac{{\mathcal{M}}_2}{{\mathcal{M}}_1}\Vert v^{\prime }(t)-v(t)\Vert +\frac{{\mathcal{M}}_3}{{\mathcal{M}}_1}\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\frac{{\mathcal{M}}_4}{{\mathcal{M}}_1}\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert ,\end{array}$$ 76

$$\begin{array}{c}\hfill \Vert v^{\prime }(t)-v(t)\Vert \le \frac{{\mathcal{N}}_2}{{\mathcal{N}}_1}\Vert u^{\prime }(t)-u(t)\Vert +\frac{{\mathcal{N}}_3}{{\mathcal{N}}_1}\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\frac{{\mathcal{N}}_4}{{\mathcal{N}}_1}\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert .\end{array}$$ 77

Substituting (77) into (74), we have

$$\begin{array}{cc}\hfill \Vert u^{\prime }(t)-u(t)\Vert & \le \frac{{\mathcal{M}}_2}{{\mathcal{M}}_1}\left\{\frac{{\mathcal{N}}_2}{{\mathcal{N}}_1}\Vert u^{\prime }(t)-u(t)\Vert +\frac{{\mathcal{N}}_3}{{\mathcal{N}}_1}\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\frac{{\mathcal{N}}_4}{{\mathcal{N}}_1}\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert \right\}\hfill \\ \hfill & +\frac{{\mathcal{M}}_3}{{\mathcal{M}}_1}\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\frac{{\mathcal{M}}_4}{{\mathcal{M}}_1}\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert ,\hfill \\ \hfill & =\frac{{\mathcal{M}}_2{\mathcal{N}}_2}{{\mathcal{M}}_1{\mathcal{N}}_1}\Vert u^{\prime }(t)-u(t)\Vert +\left(\frac{{\mathcal{M}}_2{\mathcal{N}}_3}{{\mathcal{M}}_1{\mathcal{N}}_1}+\frac{{\mathcal{M}}_3}{{\mathcal{M}}_1}\right)\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert \hfill \\ \hfill & +\left(\frac{{\mathcal{M}}_2{\mathcal{N}}_4}{{\mathcal{M}}_1{\mathcal{N}}_1}+\frac{{\mathcal{M}}_4}{{\mathcal{M}}_1}\right)\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert ,\hfill \\ \hfill \Vert u^{\prime }(t)-u(t)\Vert & \le \left(\frac{\frac{{\mathcal{M}}_2{\mathcal{N}}_3}{{\mathcal{M}}_1{\mathcal{N}}_1}+\frac{{\mathcal{M}}_3}{{\mathcal{M}}_1}}{1-\frac{{\mathcal{M}}_2{\mathcal{N}}_2}{{\mathcal{M}}_1{\mathcal{N}}_1}}\right)\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\left(\frac{\frac{{\mathcal{M}}_2{\mathcal{N}}_4}{{\mathcal{M}}_1{\mathcal{N}}_1}+\frac{{\mathcal{M}}_4}{{\mathcal{M}}_1}}{1-\frac{{\mathcal{M}}_2{\mathcal{N}}_2}{{\mathcal{M}}_1{\mathcal{N}}_1}}\right)\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert .\hfill \end{array}$$

Similarly, substituting (76) into (75), we have

$$\begin{array}{cc}\hfill \Vert v^{\prime }(t)-v(t)\Vert & \le \frac{{\mathcal{N}}_2}{{\mathcal{N}}_1}\left\{\frac{{\mathcal{M}}_2}{{\mathcal{M}}_1}\Vert v^{\prime }(t)-v(t)\Vert +\frac{{\mathcal{M}}_3}{{\mathcal{M}}_1}\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\frac{{\mathcal{M}}_4}{{\mathcal{M}}_1}\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert \right\}\hfill \\ \hfill & +\frac{{\mathcal{N}}_3}{{\mathcal{N}}_1}\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\frac{{\mathcal{N}}_4}{{\mathcal{N}}_1}\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert ,\hfill \\ \hfill & =\frac{{\mathcal{N}}_2{\mathcal{M}}_2}{{\mathcal{N}}_1{\mathcal{M}}_1}\Vert v^{\prime }(t)-v(t)\Vert +\left(\frac{{\mathcal{N}}_2{\mathcal{M}}_3}{{\mathcal{N}}_1{\mathcal{M}}_1}+\frac{{\mathcal{N}}_3}{{\mathcal{N}}_1}\right)\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert \hfill \\ \hfill & +\left(\frac{{\mathcal{N}}_2{\mathcal{M}}_4}{{\mathcal{N}}_1{\mathcal{M}}_1}+\frac{{\mathcal{N}}_4}{{\mathcal{N}}_1}\right)\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert ,\hfill \\ \hfill \Vert v^{\prime }(t)-v(t)\Vert & \le \left(\frac{\frac{{\mathcal{N}}_2{\mathcal{M}}_3}{{\mathcal{N}}_1{\mathcal{M}}_1}+\frac{{\mathcal{N}}_3}{{\mathcal{N}}_1}}{1-\frac{{\mathcal{N}}_2{\mathcal{M}}_2}{{\mathcal{N}}_1{\mathcal{M}}_1}}\right)\Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert +\left(\frac{\frac{{\mathcal{N}}_2{\mathcal{M}}_4}{{\mathcal{N}}_1{\mathcal{M}}_1}+\frac{{\mathcal{N}}_4}{{\mathcal{N}}_1}}{1-\frac{{\mathcal{N}}_2{\mathcal{M}}_2}{{\mathcal{N}}_1{\mathcal{M}}_1}}\right)\Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert .\hfill \end{array}$$

If we take,

$$\begin{array}{cc}\hfill \Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert & \le \frac{{\mathit{\epsilon }}_1}{2\left(\frac{\frac{{\mathcal{M}}_2{\mathcal{N}}_3}{{\mathcal{M}}_1{\mathcal{N}}_1}+\frac{{\mathcal{M}}_3}{{\mathcal{M}}_1}}{1-\frac{{\mathcal{M}}_2{\mathcal{N}}_2}{{\mathcal{M}}_1{\mathcal{N}}_1}}\right)}=\frac{{\mathit{\epsilon }}_1}{2{\mathit{\delta }}_1},\hfill \\ \hfill \Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert & \le \frac{{\mathit{\epsilon }}_1}{2\left(\frac{\frac{{\mathcal{M}}_2{\mathcal{N}}_4}{{\mathcal{M}}_1{\mathcal{N}}_1}+\frac{{\mathcal{M}}_4}{{\mathcal{M}}_1}}{1-\frac{{\mathcal{M}}_2{\mathcal{N}}_2}{{\mathcal{M}}_1{\mathcal{N}}_1}}\right)}=\frac{{\mathit{\epsilon }}_1}{2{\mathit{\delta }}_2},\hfill \end{array}$$

where ${\mathit{\delta }}_1=\left(\frac{\frac{{\mathcal{M}}_2{\mathcal{N}}_3}{{\mathcal{M}}_1{\mathcal{N}}_1}+\frac{{\mathcal{M}}_3}{{\mathcal{M}}_1}}{1-\frac{{\mathcal{M}}_2{\mathcal{N}}_2}{{\mathcal{M}}_1{\mathcal{N}}_1}}\right)$ and ${\mathit{\delta }}_2=\left(\frac{\frac{{\mathcal{M}}_2{\mathcal{N}}_4}{{\mathcal{M}}_1{\mathcal{N}}_1}+\frac{{\mathcal{M}}_4}{{\mathcal{M}}_1}}{1-\frac{{\mathcal{M}}_2{\mathcal{N}}_2}{{\mathcal{M}}_1{\mathcal{N}}_1}}\right)$.

Then Eq. (74) becomes,

$$\begin{array}{cc}\hfill \Vert u^{\prime }(t)-u(t)\Vert & \le {\mathit{\epsilon }}_1.\hfill \end{array}$$ 78

Similarly if we take,

$$\begin{array}{cc}\hfill \Vert {\mathit{\psi }}^{\prime }(t)-\mathit{\psi }(t)\Vert & \le \frac{{\mathit{\epsilon }}_2}{2\left(\frac{\frac{{\mathcal{N}}_2{\mathcal{M}}_3}{{\mathcal{N}}_1{\mathcal{M}}_1}+\frac{{\mathcal{N}}_3}{{\mathcal{N}}_1}}{1-\frac{{\mathcal{N}}_2{\mathcal{M}}_2}{{\mathcal{N}}_1{\mathcal{M}}_1}}\right)}=\frac{{\mathit{\epsilon }}_2}{2{\mathit{\delta }}_3},\hfill \\ \hfill \Vert {\mathit{\chi }}^{\prime }(t)-\mathit{\chi }(t)\Vert & \le \frac{{\mathit{\epsilon }}_2}{2\left(\frac{\frac{{\mathcal{N}}_2{\mathcal{M}}_4}{{\mathcal{N}}_1{\mathcal{M}}_1}+\frac{{\mathcal{N}}_4}{{\mathcal{N}}_1}}{1-\frac{{\mathcal{N}}_2{\mathcal{M}}_2}{{\mathcal{N}}_1{\mathcal{M}}_1}}\right)}=\frac{{\mathit{\epsilon }}_2}{2{\mathit{\delta }}_4},\hfill \end{array}$$

where ${\mathit{\delta }}_3=\left(\frac{\frac{{\mathcal{N}}_2{\mathcal{M}}_3}{{\mathcal{N}}_1{\mathcal{M}}_1}+\frac{{\mathcal{N}}_3}{{\mathcal{N}}_1}}{1-\frac{{\mathcal{N}}_2{\mathcal{M}}_2}{{\mathcal{N}}_1{\mathcal{M}}_1}}\right)$ and ${\mathit{\delta }}_4=\left(\frac{\frac{{\mathcal{N}}_2{\mathcal{M}}_4}{{\mathcal{N}}_1{\mathcal{M}}_1}+\frac{{\mathcal{N}}_4}{{\mathcal{N}}_1}}{1-\frac{{\mathcal{N}}_2{\mathcal{M}}_2}{{\mathcal{N}}_1{\mathcal{M}}_1}}\right)$. Then Eq. (75) becomes,

$$\begin{array}{cc}\hfill \Vert v^{\prime }(t)-v(t)\Vert & \le {\mathit{\epsilon }}_2.\hfill \end{array}$$ 79

From Eqs. (78) and (79), we can say that for $\forall \mathit{\epsilon }=max\{{\mathit{\epsilon }}_1,{\mathit{\epsilon }}_2\}>0,$ then there exist a $\mathit{\delta }=\mathit{\epsilon }/max\{{\mathit{\delta }}_5,{\mathit{\delta }}_6\}>0,{\mathit{\delta }}_5=max\{{\mathit{\delta }}_1,{\mathit{\delta }}_3\},{\mathit{\delta }}_6=max\{{\mathit{\delta }}_2,{\mathit{\delta }}_4\}$ such that $\Vert z^{\prime }(t)-z(t)\Vert <\mathit{\epsilon }$ when $\Vert {\mathit{\chi }}^{\ast }(t)-{\mathit{\psi }}^{\ast }(t)\Vert <\mathit{\delta }$. Thus, the solution $z(t)$ is uniformly stable.

Theorem 6

If Assumptions 3–5 hold, there exist a unique equilibrium point in system (9), which is uniformly stable.

Proof

Let ${\mathit{ϵ}}_p{z}_p^{\ast }=u_p^{\ast }$ and constructing a mapping $T:{\mathcal{C}}^n\to {\mathcal{C}}^n,$ defined by

$$\begin{array}{c}\hfill T_p{u}_p\le \sum _{q=1}^n{\mathit{\beta }}_{pq}{f}_q\left(\frac{u_p}{{\mathit{ϵ}}_p}\right)+\sum _{q=1}^n{\mathit{\gamma }}_{pq}{g}_q\left(\frac{u_p}{{\mathit{ϵ}}_p}\right)+H_p,\end{array}$$ 80

where $p=1,2,\dots ,n,T(u)={(T_1(u),T_2(u),\dots ,T_n(u))}^T$.

Now, we will show that $T$ is a contraction mapping on ${\mathcal{C}}^n$ endowed with the complex space norm. In fact, for any two different points $u={(u_1,u_2,\dots ,c_n)}^T,v={(v_1,v_2,\dots ,v_n)}^T,$ we have

$$\begin{array}{cc}\hfill \Vert T(u)-T(v)\Vert & =\sum _{p=1}^n|T(u)-T(v)|\hfill \\ \hfill & \le \sum _{p=1}^n|\sum _{q=1}^n{\mathit{\beta }}_{pq}\left[f_q\left(\frac{u_q}{{\mathit{ϵ}}_q}\right)-f_q\left(\frac{v_q}{{\mathit{ϵ}}_q}\right)\right]+\sum _{q=1}^n{\mathit{\gamma }}_{pq}\left[g_q\left(\frac{u_q}{{\mathit{ϵ}}_q}\right)-g_q\left(\frac{v_q}{{\mathit{ϵ}}_q}\right)\right]|\hfill \\ \hfill & \le \sum _{p=1}^n\left(\sum _{q=1}^n\frac{({\mathit{\beta }}_{pq}{\mathit{\lambda }}_q+{\mathit{\gamma }}_{pq}{\mathit{\mu }}_q)}{{\mathit{ϵ}}_q}|u_q-v_q|\right)\hfill \\ \hfill & \le \sum _{p=1}^n\frac{({\mathit{\zeta }}_p^{\ast }+{\mathit{\eta }}_p^{\ast })}{{\mathit{ϵ}}_{min}}\left(\sum _{q=1}^n|u_q-v_q|\right)\hfill \\ \hfill & \le \frac{(\Vert {\mathit{\zeta }}^{\ast }\Vert +\Vert {\mathit{\eta }}^{\ast }\Vert )}{\overline{\mathit{ϵ}}}\Vert u-v\Vert .\hfill \end{array}$$ 81

Based on Assumption 5,

$$\begin{array}{c}\hfill \Vert T(u)-T(v)\Vert <\Vert u-v\Vert ,\end{array}$$ 82

which implies that $T$ is a contraction mapping on ${\mathcal{C}}^n$. Hence, there exists a unique fixed point $u^{\ast }$ such that $T(u^{\ast })=u^{\ast },$ i.e.

$$\begin{array}{c}\hfill u_p^{\ast }=\sum _{q=1}^n{\mathit{\beta }}_{pq}{f}_q(\frac{u_p}{{\mathit{ϵ}}_p})+\sum _{q=1}^n{\mathit{\gamma }}_{pq}{g}_q(\frac{u_p}{{\mathit{ϵ}}_p})+H_p,\end{array}$$ 83

That is

$$\begin{array}{c}\hfill -{\mathit{ϵ}}_p{z}_p^{\ast }+\sum _{q=1}^n{\mathit{\beta }}_{pq}{f}_q(z_q^{\ast })+\sum _{q=1}^n{\mathit{\gamma }}_{pq}{g}_q(z_q^{\ast })+H_p=0,\end{array}$$ 84

for $p=1,2,\dots ,n,$ which implies that $z^{\ast }$ is an equilibrium point of system (9). Moreover, it follows from Theorem 4 and Theorem 5 that $z^{\ast }$ is uniformly stable.

Remark 4

If $\mathit{\alpha }=1$, then system (9) can be written as

$$\begin{array}{c}\hfill {\dot{z}}_p(t)=-{\mathit{ϵ}}_p{z}_p(t)+\sum _{q=1}^n{\widehat{\mathit{\beta }}}_{pq}(z_q(t))f_q(z_q(t))+\sum _{q=1}^n{\widehat{\mathit{\gamma }}}_{pq}(z_q(t))g_q(z_q(t-\mathit{\tau }(t)))+H_p,\end{array}$$ 85

where $t\ge 0,p=1,\dots ,n$. Then, the sufficient conditions for the existence, uniqueness and uniform stability of CVMFNNs in Theorems 4–6 reduced to the integer order complex-valued memristor-based neural networks (85).

Remark 5

Many of the authors investigated the dynamic properties of memristor-based neural networks with time delays such as global stability, synchronization, anti-synchronization, passivity and dissipativity see Zhang et al. (2013), Yang et al. (2014), Wu and Zeng (2013, 2014), Chen et al. (2014), Wu and Zeng (2012), Wu et al. (2011, 2013a, b), Cai and Huang (2014), Guo et al. (2013), Qi et al. (2014), Wen et al. (2013) and references therein. In Wu and Zeng (2014), the authors investigated the passivity problem for memristor-based neural networks with two different types of memductance functions and some sufficient conditions were proposed for satisfying the passivity conditions of addressed memristor-based neural networks. In Chen et al. (2014), the authors introduced the memristor-based neural networks and proposed some sufficient conditions that guarantee the global Mittag–Leffler stability and synchronization by using Lyapunov method. The existence, uniqueness and uniform stability analysis of memristor-based fractional-order neural networks with two different types of memductance functions has not been investigated in the literature. In this paper, the authors consider both real-valued and CVMFNNs with time delay and two different types of memductance functions. This obtained results improve and extent to the results proposed in previous works.

Numerical examples

In this section, we give some numerical examples to show the effectiveness of our proposed theoretical results.

Example 1

Consider memristor-based fractional-order neural networks with time delays

$$\begin{array}{c}\hfill D^{\mathit{\alpha }}{\mathit{\omega }}_p(t)=-e_p{\mathit{\omega }}_p(t)+\sum _{q=1}^n{\widehat{m}}_{pq}({\mathit{\omega }}_q(t)){\widehat{f}}_q({\mathit{\omega }}_q(t))+\sum _{q=1}^n{\widehat{n}}_{pq}({\mathit{\omega }}_q(t)){\widehat{g}}_q({\mathit{\omega }}_q(t-\mathit{\tau }(t)))+I_p,\end{array}$$ 86

where $e_1=2,e_2=1,I_1=-1.7,I_2=1.2,\mathit{\tau }=0.6,$ the fractional order $\mathit{\alpha }$ is chosen as $\mathit{\alpha }=0.9$ and the activation functions described by ${\widehat{f}}_q({\mathit{\omega }}_q(t))={\widehat{g}}_q({\mathit{\omega }}_q(t))=tanh({\mathit{\omega }}_q(t)),$

$$\begin{array}{cc}\hfill {\widehat{m}}_{11}({\mathit{\omega }}_1(t))& =\left\{\begin{array}{cc}0.75,\hfill & |{\mathit{\omega }}_1(t)|>1,\hfill \\ 0.65,\hfill & |{\mathit{\omega }}_1(t)|<1,\hfill \end{array}\right.{\widehat{m}}_{12}({\mathit{\omega }}_2(t))=\left\{\begin{array}{cc}-0.4,\hfill & |{\mathit{\omega }}_2(t)|>1,\hfill \\ -0.5,\hfill & |{\mathit{\omega }}_2(t)|<1,\hfill \end{array}\right.\hfill \\ \hfill {\widehat{m}}_{21}({\mathit{\omega }}_1(t))& =\left\{\begin{array}{cc}-0.25,\hfill & |{\mathit{\omega }}_1(t)|>1,\hfill \\ -0.35,\hfill & |{\mathit{\omega }}_1(t)|<1,\hfill \end{array}\right.{\widehat{m}}_{22}({\mathit{\omega }}_2(t))=\left\{\begin{array}{cc}0.6,\hfill & |{\mathit{\omega }}_2(t)|>1,\hfill \\ 0.5,\hfill & |{\mathit{\omega }}_2(t)|<1,\hfill \end{array}\right.\hfill \\ \hfill {\widehat{n}}_{11}({\mathit{\omega }}_1(t))& =\left\{\begin{array}{cc}-0.15,\hfill & |{\mathit{\omega }}_1(t)|>1,\hfill \\ -0.25,\hfill & |{\mathit{\omega }}_1(t)|<1,\hfill \end{array}\right.{\widehat{n}}_{12}({\mathit{\omega }}_2(t))=\left\{\begin{array}{cc}0.1,\hfill & |{\mathit{\omega }}_2(t)|>1,\hfill \\ 0.05,\hfill & |{\mathit{\omega }}_2(t)|<1,\hfill \end{array}\right.\hfill \\ \hfill {\widehat{n}}_{21}({\mathit{\omega }}_1(t))& =\left\{\begin{array}{cc}-0.12,\hfill & |{\mathit{\omega }}_1(t)|>1,\hfill \\ -0.25,\hfill & |{\mathit{\omega }}_1(t)|<1,\hfill \end{array}\right.{\widehat{n}}_{22}({\mathit{\omega }}_2(t))=\left\{\begin{array}{cc}-0.7,\hfill & |{\mathit{\omega }}_2(t)|>1,\hfill \\ -0.8,\hfill & |{\mathit{\omega }}_2(t)|<1.\hfill \end{array}\right.\hfill \end{array}$$

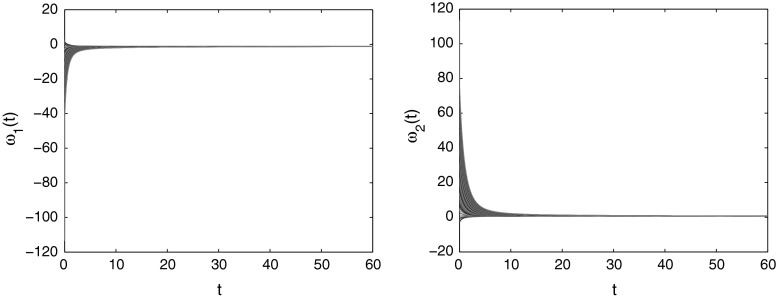
Clearly, $L_p=G_p=1$. The Assumption 2 is verified by using the above parameters. However, system (86) has a unique uniformly stable solution according to Theorems 1 and 3. Also, according to Theorem 3, system (86) has a unique equilibrium point ${\mathit{\omega }}^{\ast }={({\mathit{\omega }}_1^{\ast },{\mathit{\omega }}_2^{\ast })}^T$ and which is said to be uniformly stable. Figure 1 shows that the solution of system (86) is converges uniformly to the equilibrium point ${\mathit{\omega }}^{\ast }$.

Fig. 1.

Time responses and state trajectories of RVMFNNs (86) with $\mathit{\alpha }=0.9$

Example 2

Consider memristor-based fractional-order neural networks with time delays

$$\begin{array}{c}\hfill D^{\mathit{\alpha }}{\mathit{\omega }}_p(t)=-e_p{\mathit{\omega }}_p(t)+\sum _{q=1}^n{\widehat{m}}_{pq}({\mathit{\omega }}_q(t)){\widehat{f}}_q({\mathit{\omega }}_q(t))+\sum _{q=1}^n{\widehat{n}}_{pq}({\mathit{\omega }}_q(t)){\widehat{g}}_q({\mathit{\omega }}_q(t-\mathit{\tau }(t)))+I_p,\end{array}$$ 87

where $e_1=2,e_2=1,I_1=-1.7,I_2=1.2,\mathit{\tau }=0.6,$ the fractional order $\mathit{\alpha }$ is chosen as $\mathit{\alpha }=0.9$ and the activation functions described by ${\widehat{f}}_q({\mathit{\omega }}_q(t))={\widehat{g}}_q({\mathit{\omega }}_q(t))=tanh({\mathit{\omega }}_q(t)),$

$$\begin{array}{cc}\hfill {\widehat{m}}_{11}({\mathit{\omega }}_1(t))& =-0.6sin({\mathit{\omega }}_1(t)),{\widehat{m}}_{12}({\mathit{\omega }}_2(t))=0.8cos({\mathit{\omega }}_2(t)),{\widehat{m}}_{21}({\mathit{\omega }}_1(t))=0.8sin({\mathit{\omega }}_1(t)),\hfill \\ \hfill {\widehat{m}}_{22}({\mathit{\omega }}_2(t))& =-0.6cos({\mathit{\omega }}_2(t)),{\widehat{n}}_{11}({\mathit{\omega }}_1(t))=0.9sin({\mathit{\omega }}_1(t)),{\widehat{n}}_{12}({\mathit{\omega }}_2(t))=0.6cos({\mathit{\omega }}_2(t)),\hfill \\ \hfill {\widehat{n}}_{21}({\mathit{\omega }}_1(t))& =0.6sin({\mathit{\omega }}_1(t)),{\widehat{n}}_{22}({\mathit{\omega }}_2(t))=0.9cos({\mathit{\omega }}_2(t)).\hfill \end{array}$$

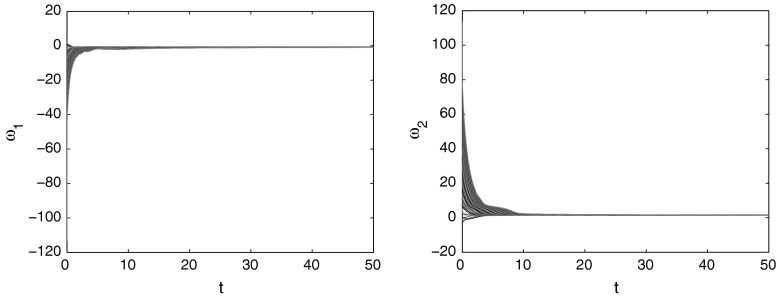
Obviously, $L_p=G_p=1$. By using the above parameters the Assumption 2 is verified easily. Therefore, system (87) has a unique uniformly stable solution according to Theorems 2 and 3. Also, according to Theorem 3, system (87) has a unique equilibrium point ${\mathit{\omega }}^{\ast }={({\mathit{\omega }}_1^{\ast },{\mathit{\omega }}_2^{\ast })}^T$ and which is said to be uniformly stable. Figure 2 shows that the solution of system (87) is converges uniformly to the equilibrium point ${\mathit{\omega }}^{\ast }$.

Fig. 2.

Time responses and state trajectories of MFNNs (87) with $\mathit{\alpha }=0.9$

Example 3

Consider a class of complex-valued memristor-based fractional-order neural networks with time delays

$$\begin{array}{c}\hfill D^{\mathit{\alpha }}{z}_p(t)=-{\mathit{ϵ}}_p{z}_p(t)+\sum _{q=1}^n{\widehat{\mathit{\beta }}}_{pq}(z_q(t))f_q(z_q(t))+\sum _{q=1}^n{\widehat{\mathit{\gamma }}}_{pq}(z_q(t))f_q(z_q(t-\mathit{\tau }(t)))+H_p,\end{array}$$ 88

where ${\mathit{ϵ}}_1=8,{\mathit{ϵ}}_2=6,H_1=-3+i,H_2=2+4i,\mathit{\tau }=0.6,$ the fractional order $\mathit{\alpha }$ is chosen as $\mathit{\alpha }=0.9$ and the activation functions described by $f_q(z_q(t))=\frac{1-e^{-u_q(t)}}{1+e^{-u_q(t)}}+i\frac{1}{1+e^{-v_q(t)}},g_q(z_q(t))=\frac{1-e^{-v_q(t)}}{1+e^{-v_q(t)}}+i\frac{1}{1+e^{-u_q(t)}},$

$$\begin{array}{cc}\hfill {\widehat{\mathit{\beta }}}_{11}^R(u_1(t))& =\left\{\begin{array}{cc}2,\hfill & |u_1(t)|>1,\hfill \\ 1,\hfill & |u_1(t)|<1,\hfill \end{array}\right.{\widehat{\mathit{\beta }}}_{12}^R(u_2(t))=\left\{\begin{array}{cc}3,\hfill & |u_2(t)|>1,\hfill \\ 2,\hfill & |u_2(t)|<1,\hfill \end{array}\right.\hfill \\ \hfill {\widehat{\mathit{\beta }}}_{21}^R(u_1(t))& =\left\{\begin{array}{cc}3,\hfill & |u_1(t)|>1,\hfill \\ 2,\hfill & |u_1(t)|<1,\hfill \end{array}\right.{\widehat{\mathit{\beta }}}_{22}^R(u_2(t))=\left\{\begin{array}{cc}-1,\hfill & |u_2(t)|>1,\hfill \\ -2,\hfill & |u_2(t)|<1,\hfill \end{array}\right.\hfill \\ \hfill {\widehat{\mathit{\beta }}}_{11}^I(v_1(t))& =\left\{\begin{array}{cc}4,\hfill & |v_1(t)|>1,\hfill \\ 3,\hfill & |v_1(t)|<1,\hfill \end{array}\right.{\widehat{\mathit{\beta }}}_{12}^I(v_2(t))=\left\{\begin{array}{cc}1,\hfill & |v_2(t)|>1,\hfill \\ 0.5,\hfill & |v_2(t)|<1,\hfill \end{array}\right.\hfill \\ \hfill {\widehat{\mathit{\beta }}}_{21}^I(v_1(t))& =\left\{\begin{array}{cc}-2,\hfill & |v_1(t)|>1,\hfill \\ -3,\hfill & |v_1(t)|<1,\hfill \end{array}\right.{\widehat{\mathit{\beta }}}_{22}^I(v_2(t))=\left\{\begin{array}{cc}2,\hfill & |v_2(t)|>1,\hfill \\ 1,\hfill & |v_2(t)|<1,\hfill \end{array}\right.\hfill \\ \hfill {\widehat{\mathit{\gamma }}}_{11}^R(u_1(t))& =\left\{\begin{array}{cc}-1,\hfill & |u_1(t)|>1,\hfill \\ -2,\hfill & |u_1(t)|<1,\hfill \end{array}\right.{\widehat{\mathit{\gamma }}}_{12}^R(u_2(t))=\left\{\begin{array}{cc}2,\hfill & |u_2(t)|>1,\hfill \\ 1,\hfill & |u_2(t)|<1,\hfill \end{array}\right.\hfill \\ \hfill {\widehat{\mathit{\gamma }}}_{21}^R(u_1(t))& =\left\{\begin{array}{cc}2,\hfill & |u_1(t)|>1,\hfill \\ 1,\hfill & |u_1(t)|<1,\hfill \end{array}\right.{\widehat{\mathit{\gamma }}}_{22}^R(u_2(t))=\left\{\begin{array}{cc}1,\hfill & |u_2(t)|>1,\hfill \\ 0.5,\hfill & |u_2(t)|<1,\hfill \end{array}\right.\hfill \\ \hfill {\widehat{\mathit{\gamma }}}_{11}^I(v_1(t))& =\left\{\begin{array}{cc}3,\hfill & |v_1(t)|>1,\hfill \\ 2,\hfill & |v_1(t)|<1,\hfill \end{array}\right.{\widehat{\mathit{\gamma }}}_{12}^I(v_2(t))=\left\{\begin{array}{cc}-3,\hfill & |v_2(t)|>1,\hfill \\ -4,\hfill & |v_2(t)|<1,\hfill \end{array}\right.\hfill \\ \hfill {\widehat{\mathit{\gamma }}}_{21}^I(v_1(t))& =\left\{\begin{array}{cc}-4,\hfill & |v_1(t)|>1,\hfill \\ -5,\hfill & |v_1(t)|<1,\hfill \end{array}\right.{\widehat{\mathit{\gamma }}}_{22}^I(v_2(t))=\left\{\begin{array}{cc}2,\hfill & |v_2(t)|>1,\hfill \\ 1,\hfill & |v_2(t)|<1,\hfill \end{array}\right.\hfill \end{array}$$

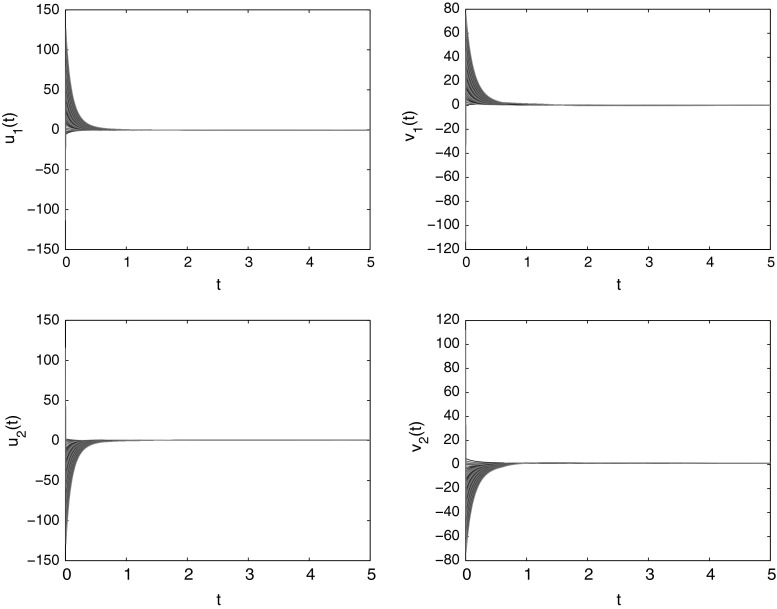
Obviously, ${\mathit{\lambda }}_p^{RR}={\mathit{\lambda }}_p^{II}=0.1,{\mathit{\lambda }}_p^{IR}={\mathit{\lambda }}_p^{RI}=0,{\mathit{\mu }}_p^{RR}={\mathit{\mu }}_p^{II}=0,{\mathit{\mu }}_p^{IR}={\mathit{\mu }}_p^{RI}=0.1$. By using the above parameters the Assumption 3 is verified easily. Therefore, system (88) has a unique uniformly stable solution according to Theorems 4 and 6. Also, according to Theorem 6, system (88) has a unique equilibrium point $u^{\ast }={(u_1^{\ast },u_2^{\ast })}^T,v^{\ast }={(v_1^{\ast },v_2^{\ast })}^T$ and which is said to be uniformly stable. Figure 3 shows that the solution of system (88) is converges uniformly to the equilibrium point $u^{\ast },v^{\ast }$.

Fig. 3.

Time responses and state trajectories of real and imaginary parts of CVMFNNs (88) with $\mathit{\alpha }=0.9$

Example 4

Consider a class of complex-valued memristor-based fractional-order neural networks with time delays

$$\begin{array}{c}\hfill D^{\mathit{\alpha }}{z}_p(t)=-{\mathit{ϵ}}_p{z}_p(t)+\sum _{q=1}^n{\widehat{\mathit{\beta }}}_{pq}(z_q(t))f_q(z_q(t))+\sum _{q=1}^n{\widehat{\mathit{\gamma }}}_{pq}(z_q(t))f_q(z_q(t-\mathit{\tau }(t)))+H_p,\end{array}$$ 89

where ${\mathit{ϵ}}_1=8,{\mathit{ϵ}}_2=6,H_1=-3+i,H_2=2+4i,\mathit{\tau }=0.6,$ the fractional order $\mathit{\alpha }$ is chosen as $\mathit{\alpha }=0.9$ and the activation functions described by $f_q(z_q(t))=\frac{1-e^{-u_q(t)}}{1+e^{-u_q(t)}}+i\frac{1}{1+e^{-v_q(t)}},g_q(z_q(t))=\frac{1-e^{-v_q(t)}}{1+e^{-v_q(t)}}+i\frac{1}{1+e^{-u_q(t)}},$

$$\begin{array}{cc}\hfill {\widehat{\mathit{\beta }}}_{11}^R(u_1(t))& =2,{\widehat{\mathit{\beta }}}_{12}^R(u_2(t))=3,{\widehat{\mathit{\beta }}}_{21}^R(u_1(t))=3,{\widehat{\mathit{\beta }}}_{22}^R(u_2(t))=-1,\hfill \\ \hfill {\widehat{\mathit{\beta }}}_{11}^I(v_1(t))& =4,{\widehat{\mathit{\beta }}}_{12}^I(v_2(t))=1,{\widehat{\mathit{\beta }}}_{21}^I(v_1(t))=-2,{\widehat{\mathit{\beta }}}_{22}^I(v_2(t))=2,\hfill \\ \hfill {\widehat{\mathit{\gamma }}}_{11}^R(u_1(t))& =-1,{\widehat{\mathit{\gamma }}}_{12}^R(u_2(t))=2,{\widehat{\mathit{\gamma }}}_{21}^R(u_1(t))=2,{\widehat{\mathit{\gamma }}}_{22}^R(u_2(t))=1,\hfill \\ \hfill {\widehat{\mathit{\gamma }}}_{11}^I(v_1(t))& =3,{\widehat{\mathit{\gamma }}}_{12}^I(v_2(t))=-3,{\widehat{\mathit{\gamma }}}_{21}^I(v_1(t))=-4,{\widehat{\mathit{\gamma }}}_{22}^I(v_2(t))=2.\hfill \end{array}$$

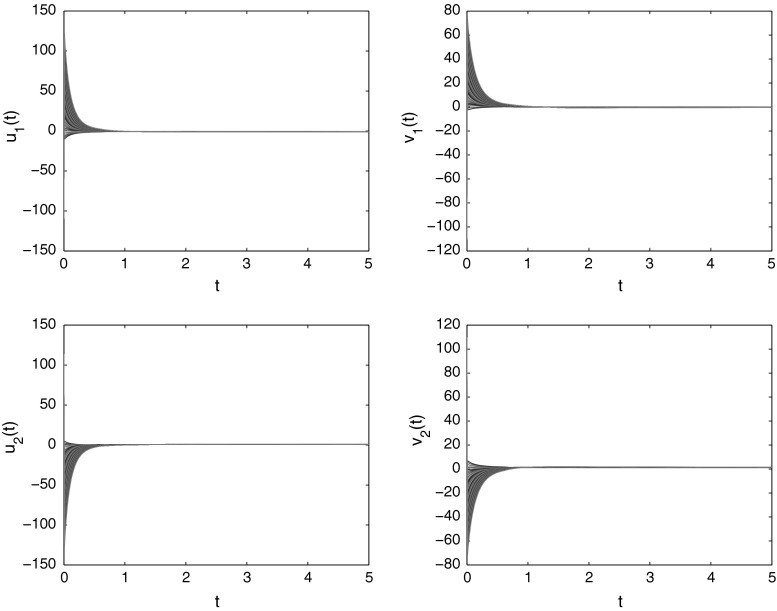
Clearly, we know that ${\mathit{\lambda }}_p^{RR}={\mathit{\lambda }}_p^{II}=0.1,{\mathit{\lambda }}_p^{IR}={\mathit{\lambda }}_p^{RI}=0,{\mathit{\mu }}_p^{RR}={\mathit{\mu }}_p^{II}=0,{\mathit{\mu }}_p^{IR}={\mathit{\mu }}_p^{RI}=0.1$. By using the above parameters the Assumption 3 is verified easily. Moreover, system (89) has a unique uniformly stable solution according to Theorems 5 and 6. Also, according to Theorem 6, system (89) has a unique equilibrium point $u^{\ast }={(u_1^{\ast },u_2^{\ast })}^T,v^{\ast }={(v_1^{\ast },v_2^{\ast })}^T$ and which is said to be uniformly stable. Figure 4 shows that the solution of system (89) is converges uniformly to the equilibrium point $u^{\ast },v^{\ast }$.

Fig. 4.

Time responses and state trajectories of real and imaginary parts of CVMFNNs (89) with $\mathit{\alpha }=0.9$

Conclusion

In this paper, the authors have been extensively investigated the problem of existence of uniform stability of a class of MFNNs with time delay and two different types of memductance functions as well as CVMFNNs with time delay and two different types of memductance functions. By using Banach contraction principle, differential inclusion and framework of Filippov solution, some new sufficient conditions that ensure that the existence and uniform stability of the addressed MFNNs and CVMFNNs with time delay and two different types of memductance functions have been derived. Numerical examples are also demonstrate the effectiveness of our theoretical results.