Quantile rank maps: a new tool for understanding individual brain development

Abstract

We propose a novel method for neurodevelopmental brain mapping that displays how an individual’s values for a quantity of interest compare with age-specific norms. By estimating smoothly age-varying distributions at a set of brain regions of interest, we derive age-dependent region-wise quantile ranks for a given individual, which can be presented in the form of a brain map. Such quantile rank maps could potentially be used for clinical screening. Bootstrap-based confidence intervals are proposed for the quantile rank estimates. We also propose a recalibrated Kolmogorov-Smirnov test for detecting group differences in the age-varying distribution. This test is shown to be more robust to model misspecification than a linear regression-based test. The proposed methods are applied to brain imaging data from the Nathan Kline Institute Rockland Sample and from the Autism Brain Imaging Data Exchange (ABIDE) sample.

Introduction

Neuroimaging studies have yielded valuable insights about developmental abnormalities associated with psychiatric disorders. For example, the influential study of Shaw et al. (2007) found that the attainment of peak cortical thickness is delayed in children with attention-deficit/hyperactivity disorder (ADHD), particularly in prefrontal regions implicated in control of cognitive processes. Findings of this sort are often framed in terms of developmental “trajectories,” defined as the mean of a quantity of interest as a function of age.

Recently, however, there has been increasing interest in methodology that can go beyond population means, and provide information about individuals. One general approach along these lines seeks to derive an imaging-based index of brain maturation that can serve to “predict” an individual’s age. By applying support vector algorithms to resting state functional MRI data, Dosenbach et al. (2010) achieved accurate classification of age group (child vs. adult) as well as accurate prediction of age values. Brown et al. (2012) used multimodal anatomical MRI data to derive an index of development that they found to be highly correlated with age. Franke et al. (2012) developed a BrainAGE measure based on relevance vector regression applied to structural MRI data, and found this measure to be significantly lower than chronological age in a group of preterm-born adolescents. In a similar vein (but without using brain imaging data), Gur et al. (2014) plotted estimated neurocognitive age against chronological age in individuals endorsing psychotic symptoms; such “neurocognitive growth charting” revealed a developmental lag in these individuals.

While studies such as these have produced notable successes, any attempt to distill whole-brain data into a scalar measure of maturity necessarily sacrifices a great deal of information about an individual brain’s particular features. Here we pursue an alternative approach based on estimating the age-specific distribution of any structural or functional quantity of interest in the brain. This can be viewed as a brain mapping counterpart to growth charts in the traditional sense: i.e., the graphs of age-specific percentiles for height and weight that are routinely used by pediatricians to chart children’s development. Having estimated such distributions for each of a set of brain regions, we can, for a given individual, produce a personalized brain map that shows how his/her measure of interest for each region compare with age-specific norms. Maps of this kind are what we call quantile rank maps.

In related previous work, Reiss and Huang (2012) studied the development of functional connectivity by means of nonparametric quantile regression (Koenker et al., 1994), which estimates a prespecified quantile (e.g., the 90th percentile) as a smooth function of age. Here, by contrast, we wish to map where a given individual’s brain measures lie relative to age-specific distributions. For that purpose, rather than prespecifying one or more quantiles of interest as in (nonparametric) quantile regression, we need to be able to input the individual’s measures at each region and output the age-specific quantile ranks for each. Thus we need a method that estimates the entire distribution, at a given age. An early method of this kind is the LMS method of Cole and Green (1992). Here, we pursue the generalized additive models for location, scale and shape approach (GAMLSS; Rigby and Stasinopoulos, 2005), a more recent computational framework that encompasses a wide class of models including LMS.

In pediatrics, height and weight growth charts are used to efficiently classify individual children’s trajectories of physical growth as typical or atypical. In a similar way, brain imaging-derived measurements can provide important information about brain development, maturation and aging. Structural MRI-derived measurements, such as cortical thickness or volume, can show how neuroanatomy changes over time; functional MRI-derived measurements, such as functional connectivity between regions of interest (ROIs), can indicate how brain networks evolve. Age-specific quantile ranks of these measurements are informative and intuitive, and may ultimately be applied in clinical practice for screening of neuropsychiatric disorders.

In the nearer term, maps of age-specific quantile ranks offer a new, and sometimes more sensitive, way to adjust for age in group comparisons of brain measures. We propose a novel recalibrated version of the Kolmogrov-Smirnov test for that purpose, and show that it can detect group differences that are missed by conventional tests.

Longitudinal data are considered the gold standard for modeling growth and other changes in the brain (e.g. Gogtay et al., 2004; Thompson et al., 2011), and indeed are indispensible for inferring individual trajectories, as opposed to age-varying population norms (cf. Reiss et al., 2015). Nevertheless, for modeling “trajectories” in the latter sense, cross-sectional data can be informative and, due to their greater availability, have been and will continue to be widely used. This paper focuses on the cross-sectional case, but in the Discussion we briefly consider extensions to longitudinal data.

Methods

Modeling an age-varying distribution

In what follows we use Y to denote the positive response of interest, conceived as a random variable; y will denote particular realized values of Y. Let (t_i, y_i), i = 1, …, n, be the age and response for subject i. Following the GAMLSS framework of Rigby and Stasinopoulos (2005), we assume that the distribution of Y depends on parameters

$$\mathit{\theta }(t)=[{\theta }_1(t),\dots ,{\theta }_p(t)]$$ (1)

such that for k = 1, …, p, θ_k(t) can be modeled (possibly after being transformed by a “link” function; see “Fitting the model” below) as a smooth function of age t. The first two parameters θ₁ and θ₂ are the location (e.g., mean or median) and scale parameters, while the remaining parameters are shape parameters (e.g., skewness or kurtosis). In practice, one or two shape parameters are often adequate.

GAMLSS is a framework for modeling a rich family of distributions, which may depend nonlinearly on covariates such as age. Whereas most statistical models focus on one aspect of the outcome distribution (usually its mean, or a specific quantile as in quantile regression), GAMLSS aims at modeling the entire distribution, which is advantageous for detecting an individual’s deviation from normal development.

Here we focus on a well-known special case of GAMLSS, the LMS model (Cole and Green, 1992), which assumes that given t, Y follows a Box-Cox-transformed normal distribution; that is, we posit functions [θ₁(t), θ₂(t), θ₃(t)] = [μ(t), σ(t), ν(t)] such that the transformed response

$$Z=\{\begin{array}{cc}\frac{{[Y/\mu (t)]}^{\nu (t)}-1}{\sigma (t)\nu (t)},\hfill & \text{for}\nu (t)\ne 0\hfill \\ \frac{1}{\sigma (t)}\text{log}\left[\frac{Y}{\mu (t)}\right],\hfill & \text{for}\nu (t)=0,\hfill \end{array}$$ (2)

is assumed to be standard normal. Here μ(t) is the median of Y for age t. For σ(t) = 1, the right side of (2) is the result of applying the transformation of Box and Cox (1964), a standard tool for attaining approximate normality, to Y/μ(t) with parameter ν(t). The scale parameter σ(t) can be interpreted as the approximate coefficient of variation of Y (Cole and Green, 1992). Below, z_i denotes the ith transformed response, i.e., (2) with Y = y_i.

The key idea captured by the LMS model, and one that is often supported by developmental data in neuroscience and beyond, is that just as the median response μ varies with age, so do the amount of variation, determined by σ, and the shape of the distribution, represented by ν.

Fitting the model

The median μ(t), log scale parameter log[σ(t)], and transformation parameter ν(t) are all assumed to be smooth functions of age t. (Taking the log of σ(t) ensures a positive estimate of σ(t); this is an example of what we referred to, just below equation (1), as transformation by a link function.) These three functions can then be estimated by penalized B-splines (Green and Silverman, 1994; Eilers and Marx, 1996). Let b(t) = [b₁(t), …, b_K(t)]^T denote a set of B-spline basis functions defined throughout the age range of interest. We assume that the three functions lie in the span of this basis, i.e.,

$$\mu (t)=\mathit{b}{(t)}^T{\mathit{\beta }}_{\mu },\text{log}[\sigma (t)]=\mathit{b}{(t)}^T{\mathit{\beta }}_{\sigma },\text{and}\nu (t)=\mathit{b}{(t)}^T{\mathit{\beta }}_{\nu },$$ (3)

where β_μ, β_σ, β_ν ∈ ℝ^K are vectors of spline coefficients. These coefficients are chosen to maximize the penalized log-likelihood

$$l_{[p]}=\sum _{i=1}^n{l}_i-{\lambda }_{\mu }\int {[\mu ″(t)]}^{2}dt-{\lambda }_{\sigma }\int {[\sigma ″(t)]}^{2}dt-{\lambda }_{\nu }\int {[\nu ″(t)]}^{2}dt,$$ (4)

where $l_i=-\frac{1}{2}\text{log}(2\pi )-\frac{1}{2}{z}_i^2$ is the normal log-likelihood that results from inserting (3) into (2), and the three subtracted terms are so-called roughness penalties applied to the fitted curves. Such penalization, the degree of which is controlled by the non-negative tuning parameters λ_μ, λ_σ, and λ_ν, avoids the overly wiggly estimates of the trajectories μ(t), σ(t) and ν(t) (overfitting) that would ensue if we simply maximized the log likelihood ${\sum }_{i=1}^n{l}_i$. Roughness penalties have been applied previously to neuroimaging data to estimate trajectories of brain change (e.g., Fjell et al., 2010; Alexander-Bloch et al., 2014; Satterthwaite et al., 2014).

Criterion (4) can be maximized with the gamlss package for R (R Core Team, 2014), which proceeds by a two-step approach (Appendix C of Rigby and Stasinopoulos, 2005; see also Rigby and Stasinopoulos, 2014, section 4):

1. The first and second derivatives of the penalized log-likelihood l_[p] (4) with respect to the spline coefficients $\mathit{\beta }={({\mathit{\beta }}_{\mu }^T,{\mathit{\beta }}_{\sigma }^T,{\mathit{\beta }}_{\nu }^T)}^T$ are computed. These are denoted by h = ∂l_[p]/∂β and H = ∂²l_[p]/∂β∂β^T.

2. The penalized log-likelihood is maximized by a Newton-Raphson algorithm in which, at the rth step, a new estimate β^(r+1) is obtained by solving H^(r)(β^(r+1) − β^(r)) = h^(r). This is iterated until convergence.

To choose the tuning parameters λ_μ, λ_σ, and λ_ν, which control the smoothness of the three functions, we used the local maximum likelihood approach implemented in gamlss (Rigby and Stasinopoulos, 2005, 2014).

Estimation of person-specific quantile ranks

Using “hats” to denote the parameter function estimates obtained as above, it follows from (2) that the estimated age-specific cumulative distribution function is

$${\hat{F}}_t(y)=\widehat{\text{Pr}}(Y\le y|t)=\{\begin{array}{cc}\mathrm{\Phi }\left[\frac{{\{y/\hat{\mu }(t)\}}^{\hat{\nu }(t)}-1}{\hat{\sigma }(t)\hat{\nu }(t)}\right],\hfill & \text{for}\hat{\nu }(t)\ne 0,\hfill \\ \mathrm{\Phi }[\frac{1}{\hat{\sigma }(t)}\text{log}\{y/\hat{\mu }(t)\}],\hfill & \text{for}\hat{\nu }(t)=0,\hfill \end{array}$$ (5)

where Φ is the standard normal cumulative distribution function. Equivalently, for any τ ∈ (0, 1), the τ quantile (the 100τ percentile) of the response for a given age t is

$${\hat{q}}_{\tau }(t)=\{\begin{array}{cc}\hat{\mu }(t){[1+\hat{\nu }(t)\hat{\sigma }(t)z_{\tau }]}^{\frac{1}{\hat{\nu }(t)}},\hfill & \text{for}\hat{\nu }(t)\ne 0,\hfill \\ \hat{\mu }(t)\text{exp}[\hat{\sigma }(t)z_{\tau }],\hfill & \text{for}\hat{\nu }(t)=0,\hfill \end{array}$$ (6)

where z_τ is the τ quantile of the standard normal distribution.

With these formulas in hand we can assign individual quantile ranks. Given an individual of age t with response y, his/her estimated age-specific quantile rank is given by (5) as τ̂ = F̂_t(y), or equivalently, the unique value τ̂ ∈ (0, 1) such that q_τ̂ (t) = y.

Confidence intervals (CIs) for an individual’s quantile rank can be derived by a bootstrap procedure. For b = 1, …,B, we

1. draw a bootstrap sample (a sample of n drawn with replacement from the n observations); and

2. fit the LMS model to this sample, resulting in an estimated cumulative distribution function ${\hat{F}}_{t;b}^{*}(·)$.

For a given subject with data (t, y), this procedure yields bootstrap quantile rank estimates

$${\hat{\tau }}_1^{*}={\hat{F}}_{t;1}^{*}(y),\dots ,{\hat{\tau }}_B^{*}={\hat{F}}_{t;B}^{*}(y).$$

If we denote the sorted bootstrap estimates by ${\hat{\tau }}_{(1)}^{*}\le \dots \le {\hat{\tau }}_{(B)}^{*}$, then a 100(1 − α)% CI is given by $[{\hat{\tau }}_{(\lfloor B\alpha /2\rfloor )}^{*},{\hat{\tau }}_{(\lceil B(1-\alpha /2)\rceil )}^{*}]$. The quantile rank estimate together with its 95% CI can serve to quantify the evidence that an individual’s response is an extreme value in the population.

Recalibrated Kolmogorov-Smirnov test for group differences

Now suppose we have two samples of images, one from a control group and one from a group with a disorder, and wish to construct a brain map showing regions for which the age-specific distributions differ between the groups. For instance, our Autism Brain Imaging Data Exchange (ABIDE) data set consists of subjects with autism spectrum disorder (ASD) and controls, and we are interested in mapping between-group differences in functional connectivity (see the “Autism Brain Imaging Data Exchange data” section below). Group differences can be assessed by a Wald test or other test of equal location, or by a covariate-adjusted group effect in a regression model as in Di Martino et al. (2014). However, we would like to pursue a testing approach that is sensitive to arbitrary differences in age-specific distributions. Moreover, from a clinical standpoint, we might wish for a test that does not treat the typical and atypical groups symmetrically, but rather asks how those with a disorder tend to deviate from typical development.

Our proposed testing approach is based on the Kolmogorov-Smirnov (K-S) test. We first apply the LMS model to the data from the typical controls to derive an estimated distribution for typical subjects, then obtain the quantile ranks for the atypical subjects with respect to this distribution. If the two groups do not differ on the given measure, then the estimated quantile ranks of atypical subjects should approximately follow a uniform distribution. If we ignore the error in this approximation, then testing the group difference is equivalent to testing the distribution deviation from the uniform distribution, which can be done via the K-S test statistic

$$D_n=\underset{\tau \in [0,1]}{\text{sup}}|F_n(\tau )-\tau |,$$ (7)

where F_n(·) is the empirical distribution of the estimated quantile ranks for the atypical group. Critical values of this distribution are computed numerically in standard software such as R (R Core Team, 2014).

However, in our simulation studies, we found that naïve application of the K-S test led to anti-conservative results—specifically, a type I error rate of about 0.13 at nominal level 0.05. Intuitively, this occurs because the use of estimated, rather than true, quantile ranks to form the empirical distribution F_n tends to inflate the supremum in (7).

For applications such as our brain mapping examples, in which a large number of tests are performed, a resampling device can be used to recalibrate the null distribution of the K-S statistic:¹

1. From among the various measures (e.g., the brain regions for which the two groups are compared), select those M (say, 100) which have the least significant K-S statistics. (The non-significance means these measures are very similarly distributed in the two groups, so they reflect how the procedure behaves when the null hypothesis is true—i.e., the null distribution that we aim to simulate.)

2. For m = 1, …,M, take P (say 100 again) random permutations of the group labels, and for each, redo the entire procedure of fitting the LMS model to the mth measure for the typical group and computing the K-S statistic for the atypical group.

3. The empirical distribution of the resulting MP K-S statistics serves as our recalibrated null distribution for the K-S test. Thus, for instance, if the observed K-S statistic exceeds the 95th percentile of this distribution, we reject the null hypothesis at the .05 level.

For the ABIDE data, of the 6216 edges (connections between ROI pairs) of interest, we selected the M = 100 edges for which the ordinary K-S test p-value was 0.944 or greater, and ran P = 100 permutations for each. Computing the 10000 K-S test statistics took approximately 3.5 hours using a Dell laptop Latitude E6230 with Intel Core i7-3540M processor and 8GB Memory.

Simulation study

We conducted a simulation study to examine the performance of the recalibrated K-S test and compare it with the linear model-based test. The simulated outcomes were designed to mimic the intrinsic functional connectivity (iFC) values in the ABIDE sample analyzed below, consisting of 391 typically developing controls and 344 individuals with ASD (see the “Autism Brain Imaging Data Exchange data” section and Supplementary Appendix A).

As described in Supplementary Appendix B, two parameters were varied in the simulations. First, simulated control and ASD groups were generated assuming either linear or nonlinear quantile curves, similar to those estimated for the edges shown in the top row of Figure 1. Second, the ASD group’s values were perturbed by random deviations generated from one of two distibutions:

1. a Cauchy distribution with location 0 and scale δ, where δ=0, 0.04, 0.06, 0.08, 0.1, 0.12, 0.15, 0.2; or

2. δ times a log-standard-normal distribution, where δ = 0, 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07.

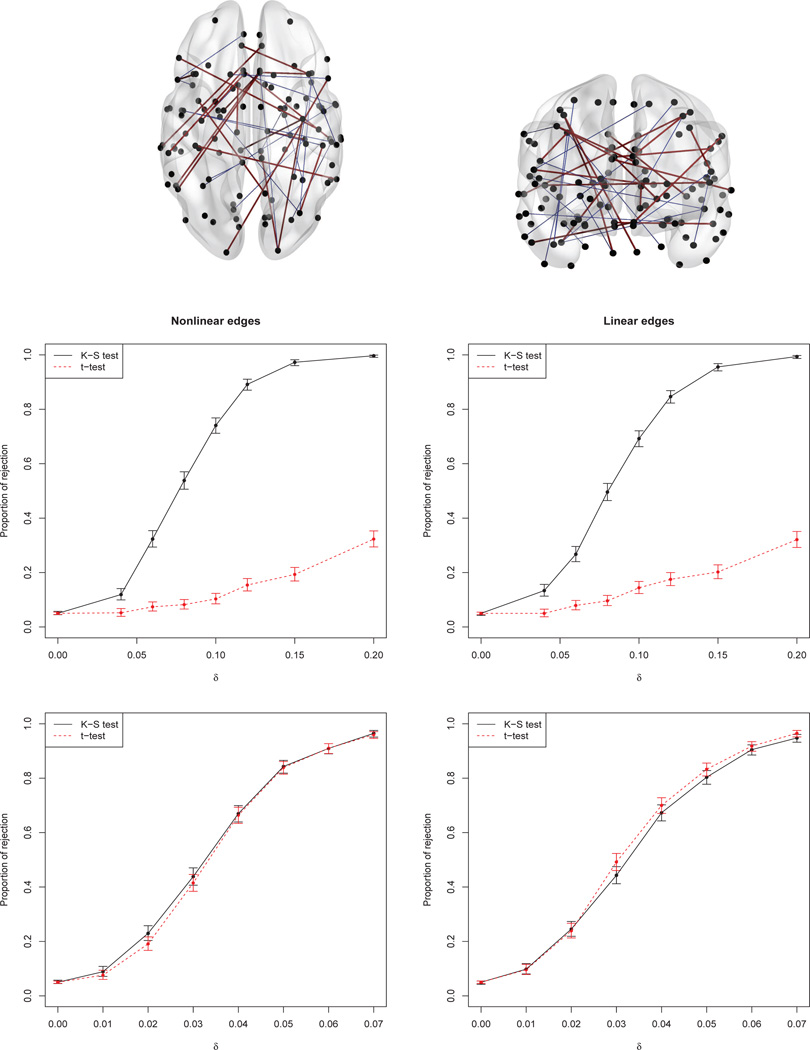
Figure 1.

Top: Twenty randomly selected “nonlinear edges” (blue lines) and twenty “linear edges” (purple lines) used for the simulations (see Appendix B). Second row: Proportion of rejections (type I error under δ = 0, power for δ > 0) together with the 95% CI, based on 1000 replicates, for Cauchy-distributed deviations. Last row: Same, for log-normal deviations.

These two distributions were chosen to mimic two plausible forms of departure from normality. The Cauchy distribution is symmetric about zero but with heavier tails than the normal distribution; thus scenario 1 entails a group difference that the Wald test would tend not to detect. (Examples of group differences that are more evident in the tails than in the mean will be seen below in our ABIDE data analyses.) The log-normal distributions in scenario 2 are skewed with positive means. Thus the atypical group’s mean is shifted to the right under the alternative hypothesis, so the Wald test is expected to work well. The type I error rate (probability of rejection when δ = 0) was estimated based on 5000 replicates, while power was estimated using 1000 replicates for each positive value of δ.

Simulation results are summarized in the middle and bottom panels of Figure 1, for the Cauchy and log-normal distributions respectively. Both tests maintain the nominal level of 0.05. Power curves for the Cauchy deviations show that the model-based Wald test cannot capture the between-group difference, as expected; the recalibrated K-S test is much more successful. With the log-normal deviations, the model-based Wald test can detect the group difference about as well as the recalibrated K-S test. Here the shape of the quantile curves also affects the results. When the quantile curves are nonlinear (lower left), the recalibrated K-S test may be slightly more powerful than the linear model-based Wald test; when they are linear (lower right), the linear model is adequate and the Wald test based on it appears slightly more powerful. In summary, compared with the Wald test, the recalibrated K-S test appears to be considerably more powerful when the deviations entail no location shift, and to have comparable power when there is such a shift.

Real-data results

Nathan Kline Institute Rockland pilot sample

The enhanced Nathan Kline Institute Rockland Sample (NKI-RS) is a large community-ascertained lifespan sample of individuals who provided neuroimaging, genetic, and other variables (Nooner et al., 2012). The study aims to identify abnormalities in developmental and aging processes associated with the risk of neuropsychiatric disorders. The pilot sample considered here includes both structural MRI and resting-state fMRI scans for 150 subjects, age 7–85, of whom 63 (42%) are female.

The raw images were preprocessed with FreeSurfer 5.1 (http://surfer.-nmr.mgh.harvard.edu) to obtain the ROI-level data (Destrieux et al., 2010; Yang et al., 2014). Tissue segmentation, co-registration of MRI and fMRI volumes, intensity normalization within and between scans, and bias field correction were applied. The 74 anatomical cortical ROIs listed in Destrieux et al. (2010) were delineated in each hemisphere: 21 frontal lobe ROIs, 8 insular, 8 limbic, 11 temporal, 11 parietal, and 15 occipital. One of the frontal ROIs in each hemisphere was a mixture of grey matter and cerebrospinal fluid (CSF) and was therefore excluded, leaving a total of 146 cortical ROIs in our analysis.

For each ROI, several representative statistics were computed, including mean cortical thickness and fractional amplitude of low-frequency fluctuations (fALFF; Zou et al., 2008). Cortical thickness is measured as the distance between the gray/white and pial surfaces throughout the cerebral cortex (Fischl and Dale, 2000). Thinning of the cortex has been found in neuropsychiatric disorders such as ADHD (Shaw et al., 2006; Proal et al., 2011) and Alzheimer’s disease (Dickerson et al., 2009). fALFF quantifies the amplitude of low frequency oscillations, a fundamental feature of the resting brain; it is defined as the power within the low-frequency range (0.01–0.1 Hz) divided by the total power in the detectable frequency range. Reduction in fALFF has been found in disorders such as ASD, schizophrenia and amnestic mild cognitive impairment (Hoptman et al., 2010; Han et al., 2011; Di Martino et al., 2014).

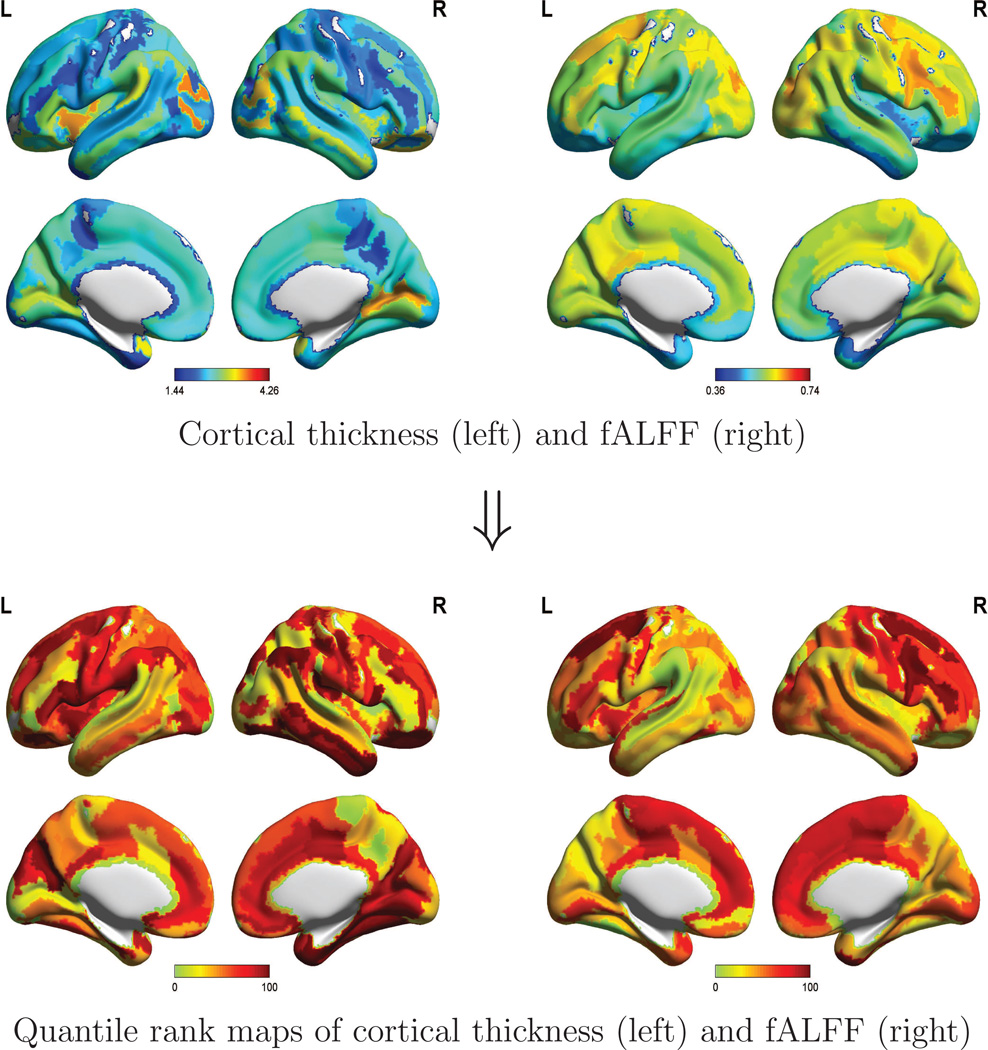
Cortical thickness and fALFF for a randomly selected subject (age 53), along with the corresponding quantile rank maps, are displayed in Figure 2, which was created using BrainNetViewer (http://www.nitrc.org/projects/bnv/) and the MNI152 standard brain. This individual’s quantile ranks, for cortical thickness and fALFF, are seen to vary dramatically among different ROIs, with similar patterns in the left and right hemispheres. Due to the disparities across regions, a relatively low raw value need not correspond a low quantile rank: for example, the subject shown here has low cortical thickness in the anterior cingulate compared to other ROIs, but a rather high quantile rank. In this sense, quantile rank maps can be more informative than the raw value maps.

Figure 2.

Maps of cortical thickness and fALFF for a randomly selected participant in the NKI Rockland pilot sample. Raw values of these measures are displayed above for 146 ROIs; inserting these values (y) into formula (5) yields the quantile ranks τ̂ = F̂_t(y) that are mapped below.

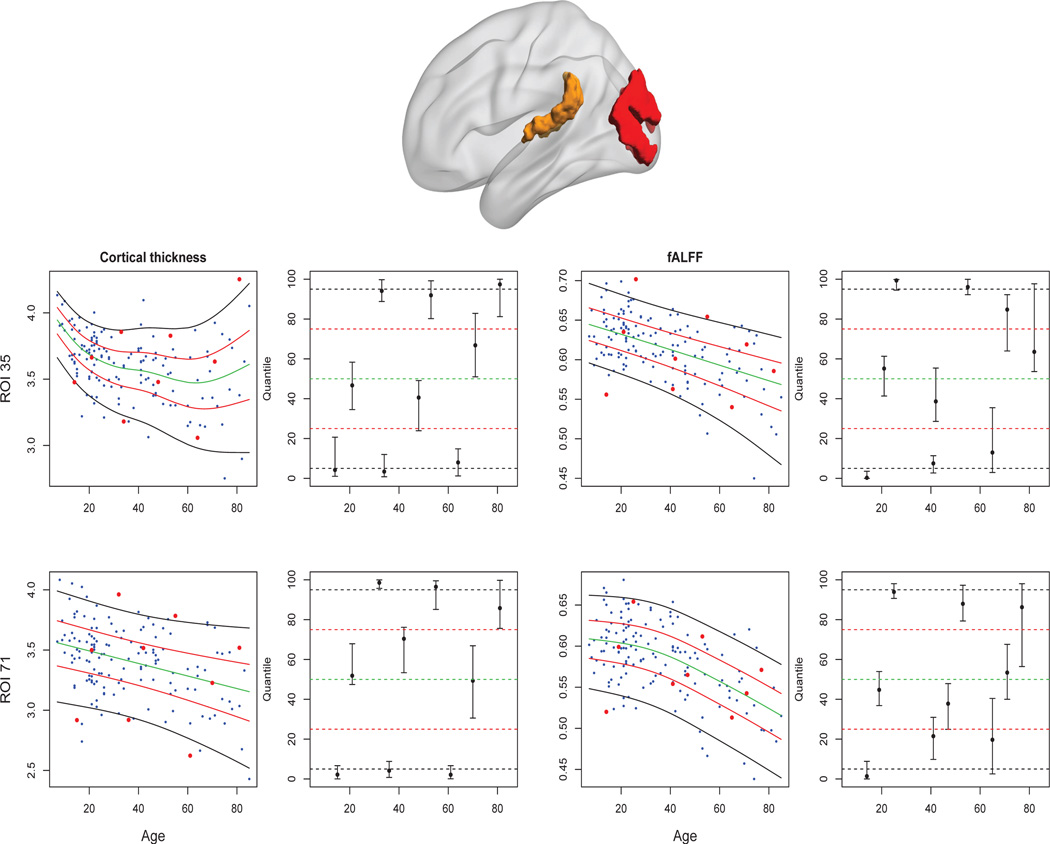
Figure 3 displays the quantile rank estimates for cortical thickness and fALFF, together with 95% CIs based on 500 bootstrap samples, for two ROIs in nine subjects. More specifically, we divided the age range into nine equal intervals, and chose the individuals with the minimal quantile rank in the 1st, 4th and 7th intervals; median quantile rank in the 2nd, 5th and 8th intervals; and maximal quantile ranks in the 3rd, 6th and 9th intervals. ROI 35 is the left middle occipital gyrus (in the visual area), and ROI 71 is the left polar plane of the superior temporal gyrus (in the auditory area; see the top panels of Figure 3). The left and right bottom panels of Figure 3 display results for cortical thickness and fALFF respectively. The CIs for the nine selected subjects (second and fourth columns of Figure 3) suggest that the extreme quantile ranks are generally estimated more precisely than those in the middle of the distribution. The CIs in the last three age intervals are relatively wide due to the low number of participants over 60. The estimated 5%, 25%, 50%, 75%, and 95% quantile curves for cortical thickness and fALFF in these two ROIs are shown in the first and third columns of Figure 3.

Figure 3.

Top: ROI 35 (left middle occipital gyrus of the visual area) is shown in red, and ROI 71 (left polar plane of the superior temporal gyrus of the auditory area) is shown in yellow. Bottom panels: cortical thickness (left columns); fALFF (right columns). The first and third columns display the raw data and estimated 5%, 25%, 50%, 75%, 95% quantile curves together with the data used to estimate the distributions. For the nine individuals represented by red dots, quantile rank estimates with 95% confidence intervals are shown in the second and fourth columns.

Autism Brain Imaging Data Exchange data

Autism spectrum disorders pose many challenges for psychiatry and neuroscience due to their lifelong nature, complexity and substantial heterogeneity. The ABIDE database (Di Martino et al., 2014) was aggregated to advance research on the neurophysiological mechanisms underlying ASD. Our analysis included 735 subjects from the ABIDE sample, with age range 6–40: 344 with ASD and 391 typically developing controls. For each subject’s data, the first four time points of the resting-status fMRI time series were removed to minimize possible T1 stabilization effects. Then the following preprocessing steps were applied: slice timing correction, motion realignment, intensity normalization, nuisance signal correction, temporal filtering, registration to the Montreal Neurological Institute template, and spatial filtering. Intrinsic functional connectivity (iFC) was computed as the Fisher-transformed pairwise correlations among the BOLD time series for the 112 ROIs defined by the Harvard-Oxford Atlas (Kennedy et al., 1998), a whole-brain structural parcellation comprising 48 cortical and 8 subcortical regions in each hemisphere.

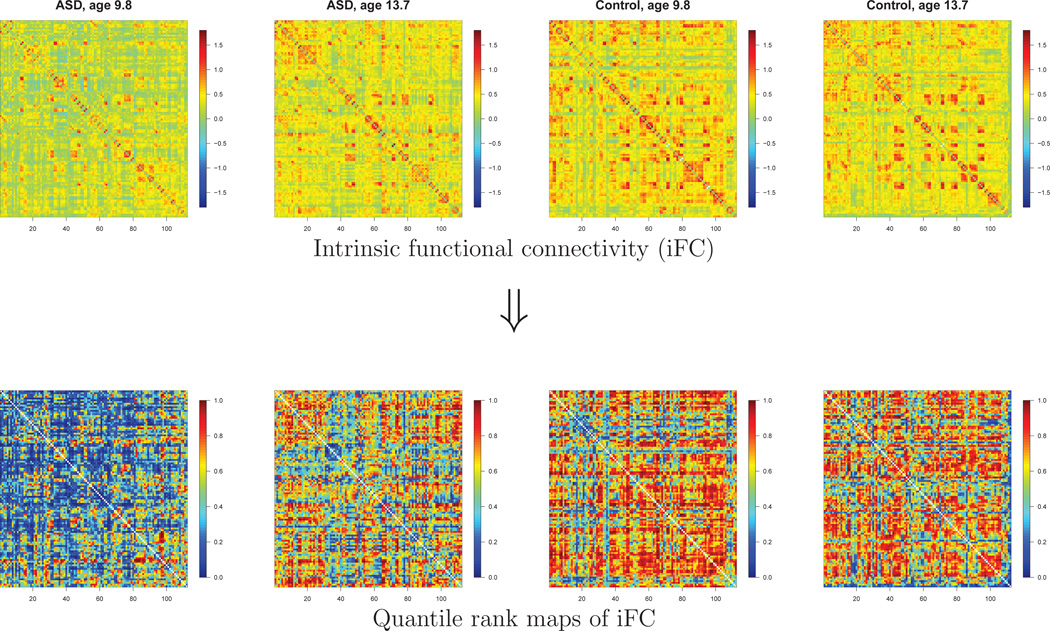
In the top left panels of Figure 4, we show the 112 × 112 iFC matrices for the 2 ASD subjects from the New York University site with the highest Autism Diagnostic Observation Schedule (ADOS) scores, a standard measure of autism severity (Lord et al., 2000). For comparison, the right panels of Figure 4 show the functional connectivity maps of age-matched controls (i.e., the control subjects from NYU who were closest in age to each of these 2 ASD subjects). Although the heterogeneities among the subjects are large, Figure 4 suggests that these ASD subjects have lower functional connectivity overall than the age-matched typical controls. In the bottom panels of Figure 4, we show the quantile rank “maps” (connectivity matrices) of the 4 subjects.

Figure 4.

Quantile rank maps (matrices) of the 2 ASD subjects with the highest ADOS scores (first two columns) and age-matched typical controls (last two columns) from the New York University site. Top panels: Fisher-transformed correlation maps. Bottom panels: Quantile rank maps.

To investigate functional connectivity anomalies in the ASD group, we applied our proposed testing approach:

1. After applying the exponential transformation to render the connectivity scores nonnegative, we fitted the LMS model (2) to the controls to obtain the age-specific distributions of the typical population at each of the 6216 edges.

2. We estimated the age-specific quantile ranks for all the ASD individuals at all edges.

3. We compared the distribution of the estimated quantile ranks of the ASD individuals to the Uniform(0, 1) distribution, which they are expected to follow if the two groups do not differ in functional connectivity.

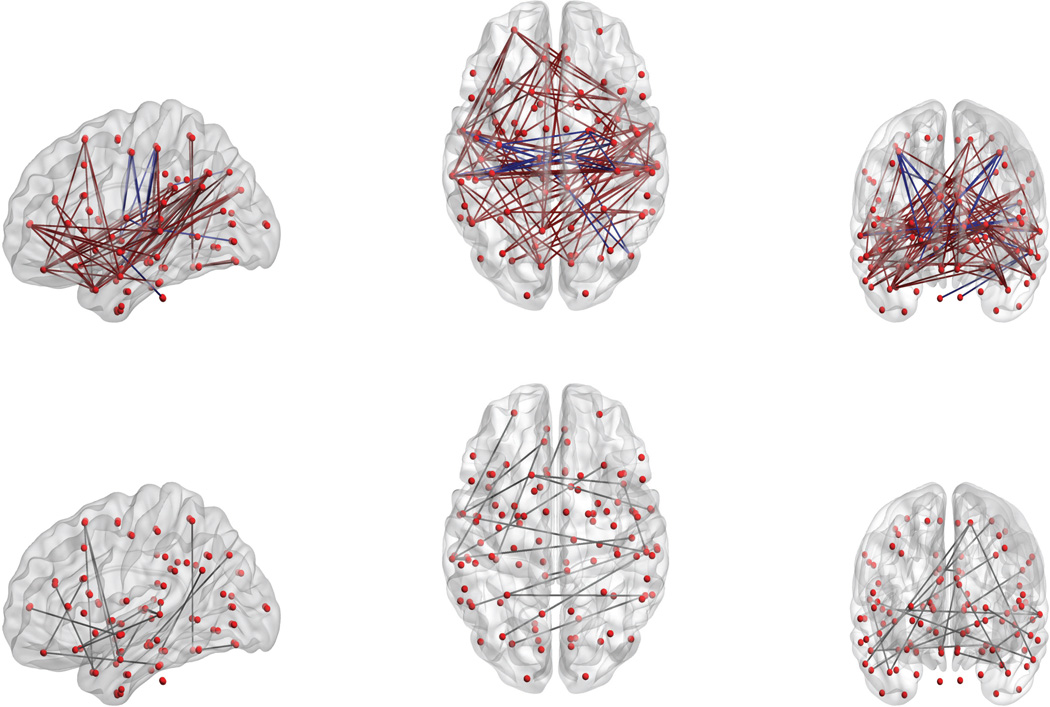
When the naïve K-S test was applied in step 3, 870 edges remained significant in the sense that the false discovery rate (FDR; Benjamini and Hochberg, 1995) was below .05. But with the proposed recalibrated K-S test, the number of significant edges (after FDR correction) dropped to 113. In Figure 5 these edges are displayed using the BrainNet Viewer MATLAB tool (Xia et al., 2013). Of these 113 edges, 33 are within the left hemisphere, 22 are within the right hemisphere, and 58 are interhemispheric. Based on the overall means for the two groups, we found hypoconnectivity in the ASD group (ASD<TC, light green and purple lines) for 88 edges, and hyperconnectivity (ASD>TC, blue lines) for 25 edges. Most of the latter edges involve the thalamus, in line with the subcortical-to-cortical hyperconnectivity found by Di Martino et al. (2014) in the ASD group. Fifty-four of the 112 ROIs are involved in the 113 edges. Under the scheme of Mesulam (1998), 6 of these ROIs are in the primary sensory-motor area, 23 in the unimodal association area, 10 in the heteromodal association area, 9 in the paralimbic area, 1 in the limbic area, and 5 in the subcortical area.

Figure 5.

Top panels: The 113 edges (pairs of ROIs) found to be significantly different between ASD subjects and age-matched typical controls. The ASD group evinced hypoconnectivity for 88 of these edges (ASD<TC, brown lines), and hyperconnectivity for 25 (ASD>TC, purple lines). Bottom panels: Of the 88 edges with hypoconnectivity in the ASD group, the 19 edges shown were detected by the K-S test only, but not by a t-test.

For comparison, we fitted linear models regressing iFC on age and diagnosis group, and tested the effect of diagnosis in these models. The lower panel of Figure 5 shows the 19 edges that were detected by our proposed approach, but not by the linear model-based test. Of the 19 edges, 7 are within the left hemisphere, 1 is within the right hemisphere, and 11 are interhemispheric. Many of these edges connect the temporal lobe to other regions. These results could perhaps shed light on the temporal-lobe abnormalities that have been linked to social cognition deficits in ASD (Zilbovicius et al., 2006).

As we would expect from the optimal power properties of the Wald test for normal linear models (Shao, 2003), this test also detects 109 edges not detected by the proposed test; in general most of these edges seem to have fairly linear growth patterns. Our recalibrated K-S test, then, is recommended to supplement, rather than to supplant, the more straightforward Wald test.

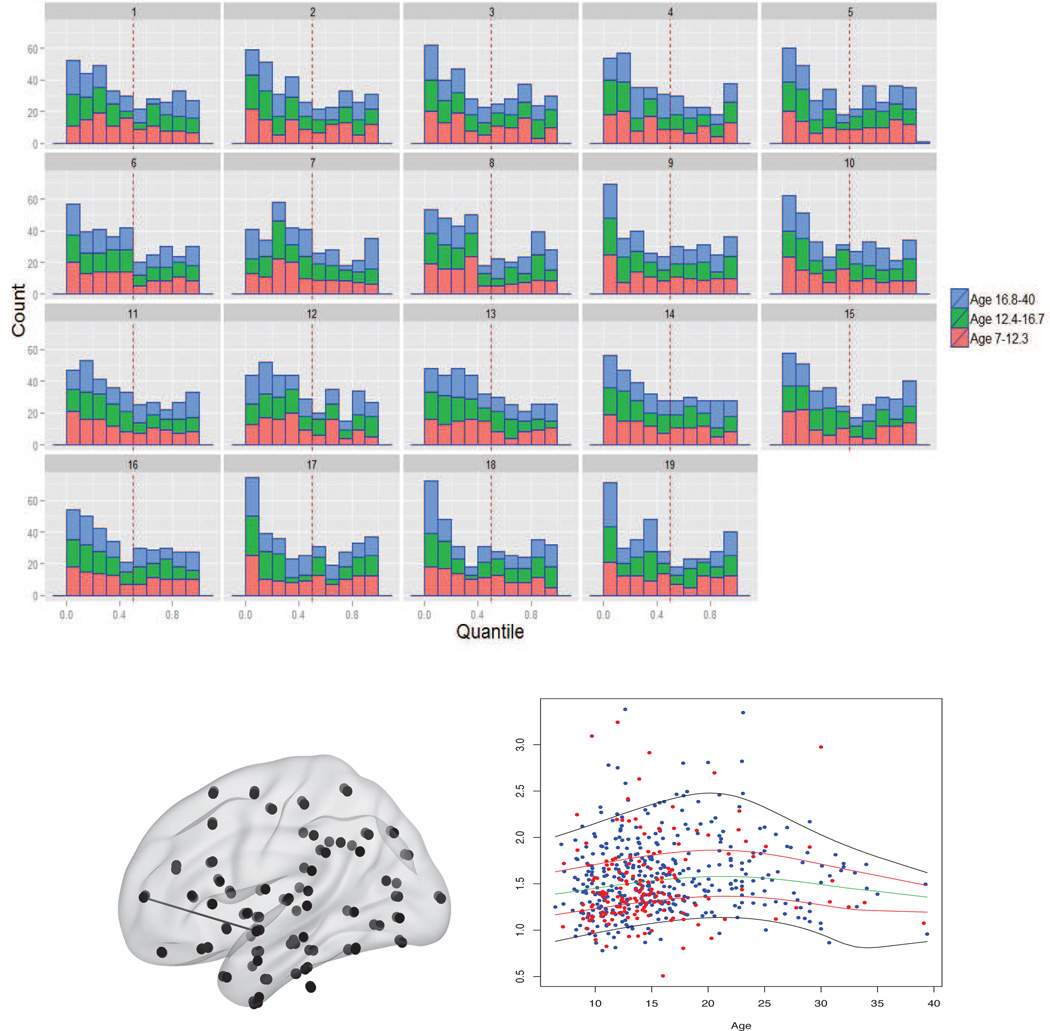
The top panel of Figure 6 shows histograms of the ASD subjects’ quantile ranks at these 19 edges. Each bar represents the number of ASD individuals who fall within a decile of the control distribution for their age. The ASD subjects are seen to have a preponderance of low quantile ranks at these edges. In the lower right panel of Figure 6 we display, for the first of these 19 edges, and quantile curves estimated for the control subjects. The group difference, which was missed by the linear model, is quite evident from the high proportion of red dots (representing ASD individuals) located near the lower quantile curves.

Figure 6.

Top panels: Histogram of the quantile ranks of the ASD subjects at the 19 edges declared significant by the recalibrated K-S test but not by Wald tests. Each bar displays counts within the lower (red), middle (green), and upper (blue) thirds of the age distribution. Bottom panels: (Left) Location of the first of the 19 edges: left frontal pole–left superior temporal gyrus, anterior division. (Right) Raw data for this edge (with control and ASD individuals represented by blue and red dots, respectively), and estimated 5%, 25%, 50%, 75%, 95% quantile curves for the control group.

Discussion

Age-specific quantiles of weight and height of children are widely used in pediatrics, and can provide very important information regarding children’s developmental performance. Brain imaging-derived measurements have the potential to play an analogous role with respect to brain maturation and aging. Specifically, structural MRI-derived measurements, such as cortical thickness and volume, can show how the brain anatomy changes over time; functional MRI-derived measurements, such as functional connectivity between ROIs, can indicate how brain networks evolve over time. The age-specific quantiles of those measurements for subjects are informative and intuitive, and in the future they may perhaps be applied clinically to screen for risk of neuropsychiatric disorders (see Insel, 2014).

We have introduced quantile rank maps for measures defined on ROIs (or connections of interest). Extension to voxel-level data is straightforward but computationally intensive. To reduce the computational burden, a two-step approach may be used. In the first step, we can apply restricted likelihood ratio test (RLRT) to partition voxels into two parts according to whether the mean functions significantly change over time (Reiss et al., 2014). In the second step, we can fit the LMS model to the significant voxels, then obtain the time-varying distributions. For nonsignificant voxels, it may suffice to estimate a simple (non-age-varying) distribution. This two-step approach will reduce the number of LMS fits, thereby saving considerable computing time.

We have developed a recalibrated K-S test to detect group differences based on quantiles. This test can capture group differences in distribution, even if the mean difference is negligible. It is more robust to the misspecification of the model than a regression-based test. In practice, if the distribution shows considerable nonlinear variation over time, the recalibrated K-S test for the group difference may be more powerful than the test based on a linear model. The recalibrated K-S test and the bootstrap-based CI are implemented in R code available from the authors.

There are a few limitations in the presented methods. First, we did not take advantage of information regarding spatial location of the brain regions. Efficient use of this spatial information may lead to more robust results and is worthy of further research. Second, we did not borrow information across different imaging modalities, such as structural and functional MRIs in the NKI Rockland sample. Appropriately integrating information across different modalities might provide extra value compared to modality-specific analyses, and is another interesting topic for future work. Third, both examples presented here employ cross-sectional data, which are less informative than longitudinal data for studying neurodevelopmental processes. For longitudinal neuroimaging data, incorporating subject-level random effects could yield more accurate estimation of the age-varying distributions, and hence of the quantile ranks. In contrast to the nonlinear (Gompertz) mixed-effects model applied by Sadeghi et al. (2013) to white matter maturation, a mixed-effects GAMLSS would not impose parametric assumptions and, by estimating the entire distribution for each age, it would provide an estimated quantile rank for each individual in the sample.

Highlights.

• We present a method for fitting smooth growth curves to a brain measure of interest.

• This allows for mapping an individual’s quantile rank at each of a set of regions.

• We propose a new test for group differences based on age-varying distributions.

• Our methods are illustrated with two magnetic resonance imaging data sets.