Controlling roll perturbations in fruit flies

Abstract

Owing to aerodynamic instabilities, stable flapping flight requires ever-present fast corrective actions. Here, we investigate how flies control perturbations along their body roll angle, which is unstable and their most sensitive degree of freedom. We glue a magnet to each fly and apply a short magnetic pulse that rolls it in mid-air. Fast video shows flies correct perturbations up to 100° within 30 ± 7 ms by applying a stroke-amplitude asymmetry that is well described by a linear proportional–integral controller. For more aggressive perturbations, we show evidence for nonlinear and hierarchical control mechanisms. Flies respond to roll perturbations within 5 ms, making this correction reflex one of the fastest in the animal kingdom.

1. Introduction

Locomoting organisms evolved mechanisms to control their motion and maintain stability against mechanical disturbances. The control challenge is prominent in small flying insects since their small moment of inertia renders them susceptible even to gentle air currents [1–4]. Moreover, they fly at Reynolds numbers Re = 10²–10⁴, in which flows are unsteady [5,6]. Most importantly, recent analytical and numerical analyses, as well as mechanical models, indicate that flapping flight is aerodynamically unstable, on a time scale of a few wing-beats [7–19]. It is, therefore, intriguing how insects overcome such control challenges and manage to fly with impressive stability, manoeuvrability and robustness, outmanoeuvring any man-made flying device.

Among the body Euler angles—yaw, pitch and roll—roll is most sensitive to perturbing torques since the moment of inertia of the insect's long axis is smallest [1,2]. Recent fluid dynamics simulations suggest roll is unstable due to an unsteady aerodynamic mechanism, where roll is positively coupled to sideways motion via asymmetry of the leading-edge vortex attached to each wing [14–18]. The coupling is driven by the wings' flapping and causes the roll angle to grow. Such results indicate that when left uncontrolled, flies can lose their body attitude due to roll perturbations within four wing-beats. In these fluid dynamics simulations, the wings were modelled as rigid plates. Controlling roll is also crucial for maintaining direction and altitude. Thus, any basic understanding of insect flight demands quantitative analysis of roll control.

Previous studies used tethered animals to measure changes in wing motion in response to imposed roll rotations [20–25] and visual roll stimuli [24–30]. In such experiments, however, the tethered insect does not control its motion and often exhibits wing kinematics and torques qualitatively different from those in free flight [31,32]. Tethered [33,34] as well as free-flight [35–38] assays have also been used to study how insects control their head motion for gaze stabilization in response to visual and mechanical stimuli. More recently, free-flight experiments used vortices [1–3] and impulsive gusts [4] to perturb insects, highlighting the sensitivity of the roll angle to perturbations. Understanding roll control, however, requires fast and accurate quantitative measurements of wing and body kinematics in response to controlled mid-air perturbation impulses—a methodology recently applied to study yaw control [39]. Crucially, these previous works typically consider only the linear response [30,39–45]. Whether nonlinear mechanisms come into play in natural free flight, where both large and coupled perturbations are common [1] remains unknown.

Here, we perturb a fruit fly (Drosophila melanogaster) by gluing a magnet to its back and applying an approximately 5 ms magnetic pulse that rolls it in mid-air (figure 1a). The perturbation amplitude ranges from roll deflections of 5° to multiple rotations along the roll angle as defined in figure 1b. We use high-speed video to film the fly's corrective manoeuvre and measure its wing and body kinematics [46]. We find that for roll perturbations up to 70° flies generate corrective torques by applying a stroke-amplitude asymmetry that is determined by the output of a linear proportional–integral (PI) controller for roll perturbations. The asymmetry starts only one wing-beat (approx. 5 ms) after the perturbation onset, making the roll correction reflex one of the fastest in the animal kingdom [47]. Surprisingly, however, we find that linear control is not sufficient to explain the response for multiple rotations nor the overarching control structure for simultaneously handling yaw, pitch and roll.

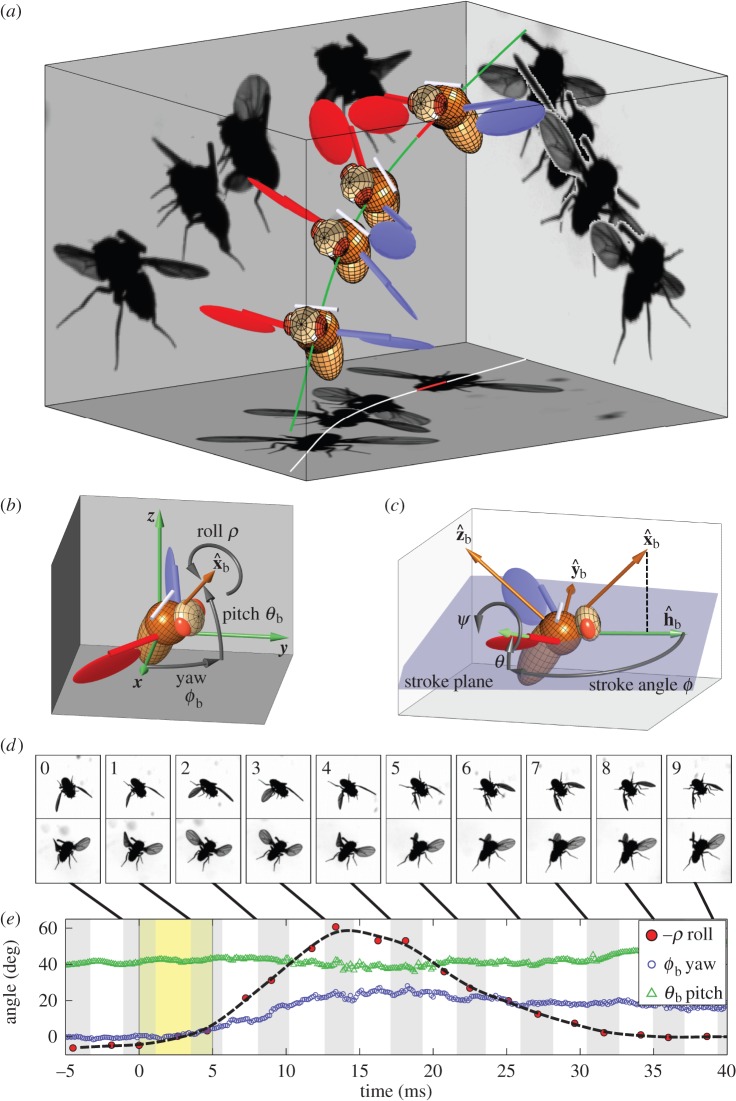
Figure 1.

Roll perturbation and correction. (a) Images from three orthogonal cameras of a roll correction manoeuvre. The three-dimensional-rendered fly represents the measured kinematics. The perturbation location (red line) is shown on the fly's centre-of-mass trajectory (green). In the second snapshot, the fly is rolled 60° to its left. (b) Definition of body Euler angles with respect to the laboratory frame. 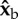is the long body axis. (c) Definition of the body frame 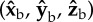and wing Euler angles, measured in the body frame with respect to the stroke plane (shaded blue). (d) Top and side views of 10 consecutive wing strokes of the manoeuvre, taken when the wings are at their forward-most position. The perturbation wing-beat is numbered 0. (e) Body Euler angles versus time. Perturbation was applied between 0 and 5 ms (yellow). White and grey stripes represent forward and back strokes, respectively. Yaw and pitch were sampled at 8000 Hz. Roll was measured manually at the middle of each half-stroke and smoothed by a spline (dashed line). Measurement errors are comparable to the symbol size.

2. Material and methods

2.1. Animal preparation

We use common fruit flies (Drosophila melanogaster) from an out-bred laboratory stock. After the flies are anaesthetized at a temperature of 0–4°C, we glue a carbon steel pin, 1.5–2 mm long, 0.15 mm in diameter and mass 0.2 mg (Gordon Brush, CA, USA), to the notum, the dorsal surface of the fly's thorax. The pin is glued horizontally, parallel to the line connecting the two wing hinges (figure 1). The pin did not interfere with the motion of the wings. The pin added approximately 20% to the fly's mass, less than the natural fluctuations in its body mass. In addition, the change in the body centre of mass position due to the pin was small, about 3.5% of the body length.

To demonstrate the effect of the pin on the fly's inertia tensor, we estimated the pin inertia and added it to the body-only inertia tensor, I_body, calculated in [48]:

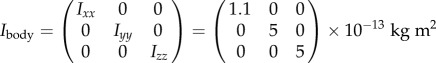2.1

and

2.2

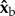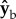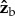The , and body axes are defined in figure 1c, such that 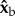is the roll axis. Note that the moment of inertia tensor is defined in the body frame of reference, such that I_xx is the moment of inertia along the 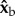axis, I_yy is the moment of inertia along the 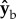axis and I_zz is the moment of inertia along the 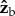axis. The inertia tensor of the untreated fly is diagonal since it is well approximated by an ellipsoid. The pin roughly triples the inertia along roll, which means that naturally, without the pin, the fly is three times more susceptible to roll perturbations than in our experiments and is also expected to be more manoeuvrable. Thus, for a given roll perturbation, the recovery times measured in our experiments set an upper bound to the recovery time of naturally occurring flies. The moments of inertia along 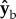and 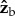increase by 20%, which is comparable to the increase in mass. The pin's contribution to the off-diagonal terms of the inertia tensor is negligible. Thus, while the pin does change the moment of inertia, it introduces no significant coupling between the rotation axes and roll remains the most sensitive degree of freedom.

2.2. Mid-air perturbations and videography

In each experiment, approximately 15 prepared flies were released in a transparent cubic chamber of side length 13 cm, equipped with two Helmholtz coils that are used to generate a vertical magnetic field (inner diameter 10 cm, outer diameter 12 cm, copper wire diameter 0.8 mm and 240 turns) [39,46]. Three synchronized fast cameras (Phantom v. 7.1, Vision Research) were focused on a cubic filming volume at the centre of the chamber. The side length of the filming volume was either 2.2 or 4.3 cm, such that it was far enough from the chamber boundaries to avoid their effect, for example, owing to take-off and landing manoeuvres. One camera was directed downwards and the other two were directed horizontally, such that cameras are all orthogonal to each other. The cameras operated at 8000 frames s^–1 and 512 × 512 pixel resolution. The cameras were back-lit by a red light-emitting diode (Diamond Dragon, Osram Opto Semiconductors) with characteristic wavelength of 625 ± 10 nm (peak ± spectrum width at 50% intensity). Fruit flies are marginally sensitive to light in this wavelength range [49].

Recording was initiated by an optical trigger consisting of two expanded laser beams (wavelength 633 nm) crossing in the middle of the filming volume and two corresponding photo-diode detectors. When a fly entered the filming volume, the reduction in the laser beam intensity was detected by a custom built circuit that triggered the cameras as well as a 5 ms (one wing-beat) vertical magnetic pulse generated by the two Helmholtz coils located on the floor and ceiling of the chamber. Such a short pulse is required to characterize the control mechanism on roll perturbations, since this degree of freedom is unstable on a time scale of a few wing-beats [14–18]. Controlling the voltage across the coils enables us to vary the magnetic field strength up to approximately 10^–2 T, which is about 1000 times stronger than the Earth's magnetic field.

Since fruit flies fly with their body axis pitched up at approximately 45° and since the moment of inertia along their body axis is smaller than along the other axes (equations (2.1) and (2.2)), the largest deflection is generated along the body roll axis, with smaller perturbations along pitch and yaw (figure 1a,b).

2.3. Motion tracking

We analysed 20 sequences that span a perturbation range between 5° and 100°, in which the flies perform a steady flight before and after the correction manoeuvre. Using a custom image analysis algorithm [46], we extracted a three-dimensional kinematic description of the fly (figure 1) consisting of its body position and orientation (figure 1b) as well as the Euler angles (figure 1c) for both wings. Our motion tracking algorithm includes the following steps.

2.3.1. Pre-processing

Following background subtraction, we define two binary thresholds for each image: one for the darker body (without the wings) and one for the entire fly. In both side-view images, we automatically track and remove the fly's legs. In the top-view image, we segment the wings based on their motion by correlating a given frame with frames taken a quarter wing stroke (eight frames) before and after it. The motion-based segmentation is better than an intensity-based method, since a wing's intensity changes with the view angle and might appear as dark as the body. The pre-processing step results in seven binary images: a body-only image for each of the three views, two side-view images with the body and wings but without the legs, and a top-view image for each wing. Removing the legs and segmenting the wings is necessary to avoid self-occlusions in the three-dimensional hull reconstruction, which might result in fictitious wing-like protrusions in the reconstructed three-dimensional hull.

2.3.2. Hull reconstruction

Hull reconstruction is performed by dividing the filming volume into voxels and back-tracing each voxel to its corresponding pixel in each camera. A voxel is added to the three-dimensional hull if and only if its corresponding pixels values are 1 in all three views. We use a pinhole camera model to reconstruct three hulls. The three body-only images are used to reconstruct the body hull. The three-dimensional hull of each wing is obtained from its top-view image along with the two side-view images of the entire fly (with the legs removed).

2.3.3. Hull analysis

The body hull is used to find the body centre of mass and body Euler angles. An initial guess of the vector describing the body long axis is obtained from principal component analysis [46]. To reduce errors due to wing–body occlusions that add fictitious voxels to the body hull, we refine the initial guess by finding the positions of the body's anterior and posterior ends. These positions are calculated as the mean positions of 10% of the body voxels farthest from the body centre on each side. The body axis vector connects the anterior and posterior ends. The initial guess for the body centre of mass position is then refined to be the midpoint of this line. The body axis vector is used to find the body yaw and pitch angles. The body roll angle was measured manually at the middle of every half stroke. In this measurement, we used the combined hull of body and wings to visually estimate the positions of the wing hinges and the body roll angle. Other methods based on the small angle between the fly's thorax and abdomen are prone to large errors [46]. The wing Euler angles were defined in the body frame of reference relative to the stroke plane (figure 1c). While in some insects, such as locusts, wing deformation is considerable and induces significant aerodynamic effects [50], in D. melanogaster wing flexibility is small and the aerodynamic forces are well described by a flat rigid wing [51]. Our measurements of D. melanogaster indicate that wing bending is negligible during most of the wing stroke and reaches no more than 5° during the wing's rapid (less than 0.3 ms) rotation between the down-stroke and up-stroke. Hence, in analysing the wing hull, we assume a flat rigid wing defined by its vein and chord vectors. We define the stroke plane using the body pitch angle of the fly before the perturbation, 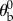, which is typically 45°. 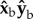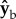The stroke plane is defined in the body frame of reference by rotating the plane by degrees about the axis. Thus, for example, if the fly body is pitched up by 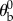and not rolled ρ = 0, the stroke plane coincides with the 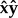plane in the laboratory frame of reference. We note that in previous work from our group the wing angles were defined in the laboratory frame [46]. In addition, here the stroke angle ϕ is defined as the angle between the projection of the wing-vein (leading edge) on the stroke plane and 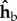, which is the projection of the long body axis (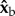) on the stroke plane (figure 1c). This definition better represents the wing actuation.

Finally, some of the movies were analysed manually. The results of these analyses showed very small differences when compared with results from the motion tracking algorithm.

2.4. Control experiments

We verified that flies without a magnet glued to their back were not affected by the magnetic field pulse. In addition, we verified that without an applied magnetic field, flies with a glued magnet flew similar to flies without a magnet. In particular, no statistical differences were observed in their heading, velocities and turning rates. Such results are not surprising since the change in mass is comparable to natural body weight fluctuations.

3. Results

3.1. Body and wing kinematics during roll correction manoeuvre

A representative example of a fly recovering from a 60° roll perturbation is shown in figure 1 and electronic supplementary material, movie S1. Body Euler angles, roll (ρ), yaw (ϕ_b) and pitch (θ_b), are plotted in figure 1e. The magnetic field was applied between t = 0 and 5 ms and induced a maximum roll velocity of 7000° s⁻¹ resulting in a deflection of 60° within t = 13.5 ms (figure 1d, frame 3). The fly recovered its initial roll angle within 35 ms, or eight wing-beats. Top views show a clear asymmetry in wing stroke angles during the manoeuvre, which starts a single wing-beat (5 ms) after the perturbation (figure 1d, frames 1–4). During the manoeuvre, the left wing stroke amplitude increases, whereas the right wing stroke amplitude decreases. After some delay, the fly also spreads its legs from their folded position (frames 4–8) as in a typical landing response [52–54]. In addition, smaller deflections of 25° left in yaw and 5° down in pitch were induced, as the applied torque is not completely aligned with a principal body axis (figure 1e).

The wing kinematics in terms of the wing Euler angles is shown in figure 2a–d. We quantify the asymmetry in wing kinematics by plotting the wing stroke angles during the manoeuvre (figure 2a). We find large differences (up to 70°) between their peak-to-peak amplitudes (figure 2d). The amplitude asymmetry began one wing-beat after the onset of the perturbation, and lasted for five wing-beats. The flapping frequency of both wings remained nearly constant during the manoeuvre. Hence, to maintain the amplitude asymmetry, the left wing moved faster than the right (figure 2b). To first order, this difference in velocity leads to asymmetry in the aerodynamic forces of the two wings and generates a correcting torque.

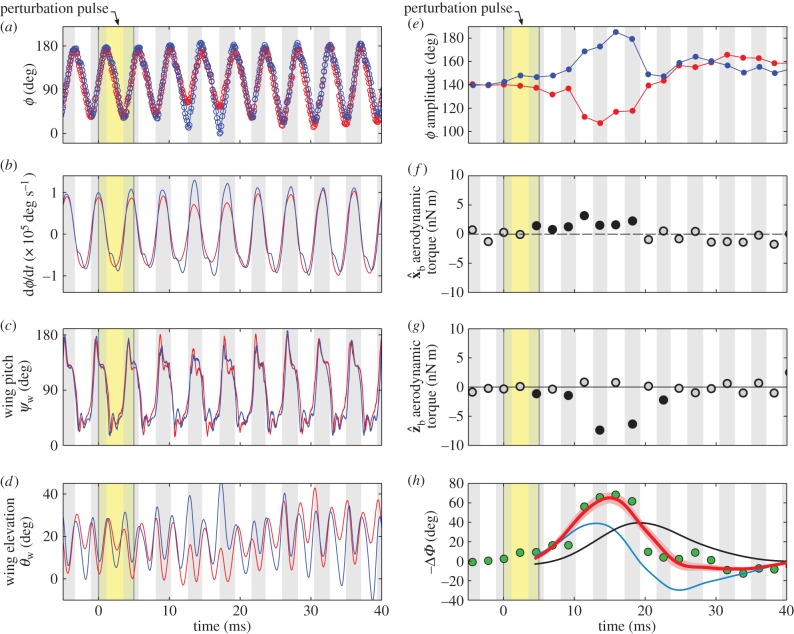
Figure 2.

Roll correction mechanism for the manoeuvre in figure 1. Time is measured in milliseconds and the yellow stripe indicates the time of the magnetic pulse. White and grey stripes indicate forward and back stroke, respectively. In (a–e), red indicates the right wing and blue indicates the left wing data. (a–d) The wing Euler angles as a function of time. The angles are defined in the body frame of reference in figure 1c. (a) The stroke angles ϕ_w and (b) their angular velocity 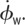. (c) The wing pitch angles ψ_w. (d) The wing elevation angles θ_w. (e) The peak-to-peak amplitude of the stroke angles ϕ for each half-stroke. (f,g) Mean aerodynamic torque in each half stroke, calculated from the measured kinematics using a quasi-steady-state aerodynamic force model. Solid symbols highlight the correcting wing strokes. (f) The torque component along the body axis 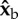. Positive torque induces a corrective right roll, (g) the torque component along 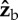. Negative values have corrective effect. (h) Wing stroke amplitude difference ΔΦ (green) and a PI controller fit (equation (3.1), red), with ΔT = 4.4 ± 0.25 ms, K_p = 6 ± 0.5 ms and K_i = 0.7 ± 0.05 (fitted values ± CI). The effect of the CI on the fitted curve is shown in shaded red. Contributions of the first and second terms of equation (3.1) are shown in blue and black, respectively. Measurement errors are comparable to the symbol size. (Online version in colour.)

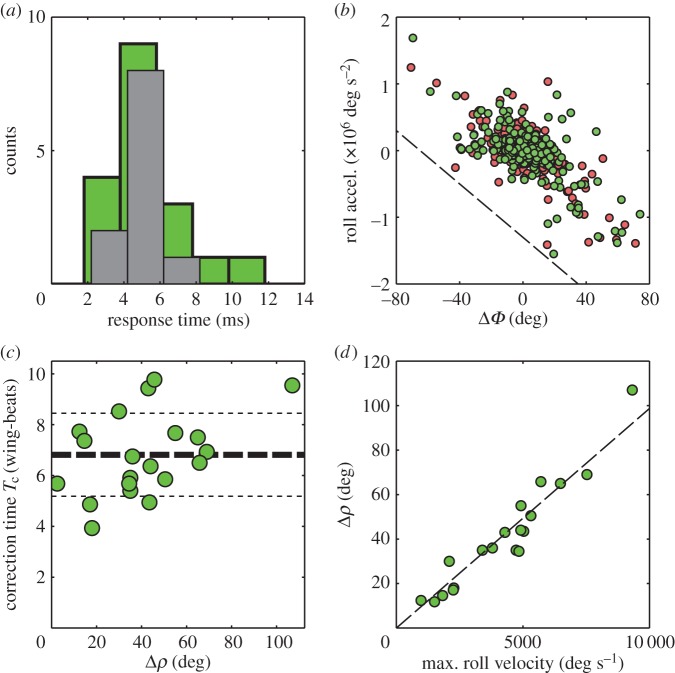
The salient correction feature—a wing stroke-amplitude asymmetry with a response time of approximately one wing-beat—was observed in all the recorded events (figure 6a). The response time was both measured directly from wing kinematics as well as obtained from control model-fitting, as shown below. Moreover, this feature was robust to variability in initial flight pose and velocity. For example, the same mechanism was observed for hovering flies (electronic supplementary material, movie S2), flies with non-zero roll angle at the perturbation onset (electronic supplementary material, movie S3), and even for flies subject to two consecutive perturbing pulses (electronic supplementary material, movie S4, figures S3 and S4). Previous experiments with tethered flies associated stroke-amplitude asymmetry with roll correction manoeuvre [21,22]. This mechanisms has also been used for roll control in an insect-scale flapping robot [55].

Figure 6.

(a) Response time histograms for multiple perturbation events: delay time of fitted PI controllers (n = 11, dark grey) and the time to reach ΔΦ = 10° measured from wing kinematics (n = 20, green). Histograms are shifted to improve visibility. (b) Mean roll acceleration versus ΔΦ for 299 forward strokes (red) and 304 back strokes (green). The correlation coefficient of these two quantities is –0.67 (p-value < 10^–12). The dashed line has a slope of −20 × 10³ s⁻². (c) Roll correction time T_c measured in wing-beats as a function of Δρ for 20 events. The mean correction time (thick dashed line) is 6.8 ± 1.6 wing-beats (mean ± s.d.). Thin dashed lines indicate 1σ margins. (d) Maximum roll displacement Δρ as a function of the maximum roll angular velocity for 20 events. The dashed line has a fitted slope of 9.9 ms with a 95% confidence interval of ±0.75 ms. (Online version in colour.)

3.2. Correcting torques

To calculate the aerodynamic torque generated by the insect, we used the full measured wing and body kinematics combined with a quasi-steady-state model for the aerodynamic force [51] produced by each wing. The calculated torques are similar for other quasi-steady-state force models [56,57] as well. The components of the aerodynamic torque vector along the 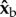(roll) and 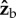body axes were averaged over half-strokes and plotted in figure 2f,g (see figure 1c for axes definition). The torque magnitude is roughly 5 nN m and is comparable to torques exerted by tethered fruit flies [24]. 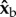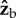Both the and torque components exhibit distinct peaks (solid circles) that appear simultaneously with the stroke-amplitude asymmetry.

The 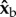component of the torque is easy to interpret since its only effect is to rotate the insect about the roll axis. The torque along the 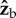axis acts to change all three Euler angles, because the insect flies with a finite body pitch angle of about 45°. Figure 3 and electronic supplementary material, movie S6, give a specific example for this geometric effect, by showing the changes in body yaw, pitch and roll angles as a result of a geometric rotation along the 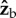axis. The initial body orientation we used was the typical flight pose of the fly: 45° pitch up and zero roll. Figure 3 shows that for small rotations along 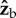, both the induced roll and yaw rotations are almost equal to the imposed 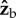rotation. This observation implies that the torque that the fly exerts along the 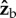axis has a comparable corrective effect on both yaw and roll. The full dynamics of the body rotations is described by the Euler equations of motion and is much more complicated and less intuitive than considering only rotations. The Euler equations have strong coupling between the components of the angular velocity, and become even more complicated when representing them in the Euler angles: yaw, pitch and roll. Nonetheless, the argument above gives a solid geometric intuition that a rotation along 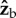has similar effects on yaw and roll.

Figure 3.

The effect of a rotation along the axis on the three Euler angles: roll (red), yaw (dashed black) and pitch (dashed blue). We assumed that the fly is initially posed at zero roll and pitched up by 45°, and rotated it along its axis (see figure 1c for axis definition). The purely geometric calculation shows that a rotation along 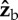results in rotations along all three Euler angles. Specifically, for small rotations the magnitudes of the roll and yaw displacements are comparable. (Online version in colour.)

The flies apply a torque along 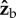during the backstrokes of the active part of the manoeuvre, and a torque along 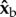during the forward strokes (figure 2f,g). The direction of the torque during a wing stroke cycle can be intuitively understood by a simple toy model (figure 4). We assume that the fly's body is pitched up by 45° and that during the middle of both the forward and back strokes the wings flaps with an angle of attack of 45°. The total aerodynamic force generated by a fly's wing, including both lift and drag, is typically perpendicular to the wing's surface, as has been characterized experimentally [51] and theoretically. At the middle of a forward stroke, the aerodynamic forces of both wings are parallel to 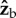and their torque arm is along 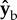, which is parallel to the wing span direction. Hence, the force imbalance resulting from the stroke-amplitude asymmetry induces a net roll torque along 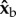. Similarly, at the middle of a back stroke, the imbalanced aerodynamic forces from both wings are directed along 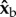and their torque arm is still along , which induces a net torque along the 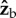direction. Interestingly, this toy model implies that the fly cannot exert an exclusive correcting roll torque during the back strokes but, as shown above, the 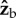torque has a corrective effect on both roll and yaw.

Figure 4.

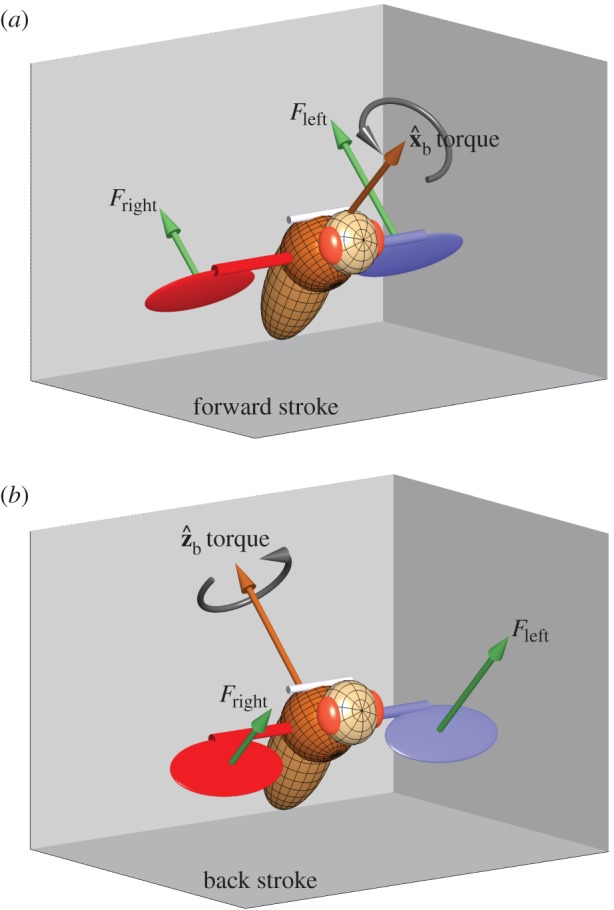
A toy model for torque production. Consider a fly with a body pitch angle of 45° and applying a stroke-amplitude asymmetry, such that its left wing (blue) exerts a larger aerodynamic force than its right wing (red) F_left > F_right. The aerodynamic forces (green arrows) are perpendicular to the surface of each wing. (a) During the middle of a forward stroke, the wings are assumed to flap with an angle of attach of 45°, hence the aerodynamic forces are perpendicular to the body 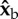(roll) axis. Since their torque arms are along the span vector, which is parallel to the 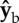body axis, the net aerodynamic torque is along 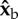. The torque is exerting a roll acceleration to the right. (b) During the middle of a back stroke, we also assume an angle of attack of 45°, which implies that the aerodynamic forces are perpendicular to the 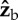body axis. The torque arms are still along 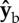, hence the net torque is along the 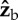axis. The net torque has a combined effect on the body Euler angles, including roll right, yaw right and pitch down as shown in figure 3.

3.3. Control model

3.3.1. Fitting parameters for a proportional–integral control model

The response of the fly to the perturbation in terms of the wing stroke-amplitude asymmetry can be described by the response of a linear, PI controller

3.1

Here, the output ΔΦ_model is the difference between the right and left wing stroke amplitudes, and the controller's input is the body roll velocity, 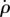, which flies measure using their rate-gyro sensor system associated with the haltere organs [21,58,59]. The controller is defined by three parameters: the proportional gain K_p, the integral gain K_i and a delay ΔT. Using the measured 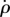, ρ and ΔΦ, we fit for these three controller parameters. The procedure for parameter fitting and estimating their confidence intervals (CI) is detailed in the electronic supplementary material.

The control block-diagram of the fly and its roll-perturbation controller is shown in figure 5. The input signal of the controller is the roll angular velocity measured by the haltere sensors (S) and delayed by ΔT. The controller output ΔΦ is an actuation signal converted by the wings (W) into the counter-torque exerted by the fly (figure 6b). The counter-torque is opposite to the external perturbation torque τ_ext, thereby forming a negative feedback loop, which is crucial for roll correction. The corrective nature of the aerodynamic torque exerted by the fly is shown in figures 2–4 and 6.

Figure 5.

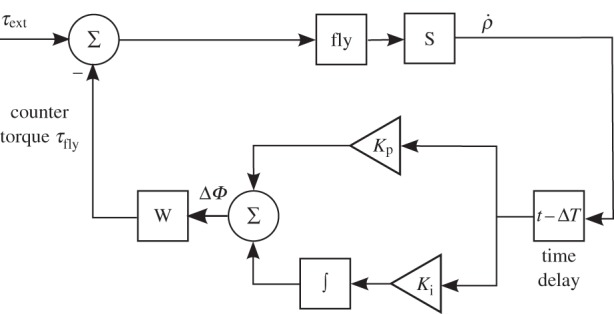
Control block-diagram. The fly's dynamics is described by the fly block and the haltere sensors (S) measure its roll velocity 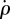. The 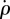signal is fed into a time-delay block that represents a neuromuscular response time. The delayed signal is then split into two branches: the proportional term with the K_P coefficient and the integral term with the K_i coefficient. The sum of both terms gives the actuation signal ΔΦ, also described in equation (3.1). The actuation signal is converted by the wings (W) into the counter-torque exerted by the fly. The counter-torque is opposite to the external perturbation torque τ_ext, thereby forming a negative feedback loop that eventually corrects for the external perturbation.

The same control model could have been called a PD model (proportional–derivative) with its input signal being the roll angle ρ rather than 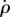. In a PD model, the proportional term would consist of the roll angle and the derivative term would consist of the roll velocity, resulting in an identical form to equation (3.1). We chose the PI terminology for this model to emphasize that the fly measures its angular velocity and integrates this signal to obtain roll displacement. Note that the PI controller model determines the roll displacement by integrating the roll velocity. Hence, the controller alone cannot determine the absolute roll angle and can elicit correction of roll displacements with respect to a pre-perturbation reference roll angle (see Discussion).

Fitting the PI model to the manoeuvre in figures 1 and 2, we find that this controller response (red curve, figure 2g) is sufficient to reproduce the time-dependence of ΔΦ (green circles). The fitted parameters are ΔT = 4.4 ± 0.25 ms, K_p = 6 ± 0.5 ms and K_i = 0.7 ± 0.05 (values ± CI), with R² = 0.9 for the fit. Notably, the response time is comparable to a single wing-beat, consistent with the direct measurement of the wing kinematics (figures 1, 2 and 6a). The fast rise time can be attributed to the term proportional to the roll velocity (figure 2g, blue curve). The fitted curve is insensitive to variations within the CI (figure 2g, shaded red). Similar results are shown in electronic supplementary material, figure S3, for a movie in which the fly was subject to a double-pulse perturbation.

In-depth analysis of 11 correction manoeuvres showed the ΔΦ response is consistent with the PI controller model (table 1, mean R² = 0.86). Fitting control parameters for each manoeuvre separately, we find K_p = 4.8 ± 2.4 ms and K_i = 0.6 ± 0.3 (mean ± s.d.). The mean response time ΔT = 4.6 ± 1 ms is comparable to a single wing-beat period (figure 6a). The confidence intervals for parameters in each event are smaller than the standard deviation, indicating that differences between fitted controllers can be attributed to natural variation between flies (table 2).

Table 1.

Fitting results for the PI control model, including confidence intervals (CI) for the fitted parameters.

movie	ΔT ± CI (ms)	Kp ± CI (ms)	Ki ± CI	R2
1	4.4 ± 0.25	6.0 ± 0.5	0.70 ± 0.05	0.90
2	4.6 ± 1.0	2.5 ± 0.7	0.35 ± 0.03	0.80
3	3.6 ± 0.3	3.5 ± 0.5	0.90 ± 0.05	0.91
4	4.4 ± 0.4	4.0 ± 1.0	0.70 ± 0.12	0.76
5	5.1 ± 0.3	5.0 ± 0.5	0.50 ± 0.05	0.96
6	5.3 ± 1.0	2.5 ± 0.5	0.10 ± 0.05	0.83
7	5.6±0.3	8.5 ± 0.6	0.25 ± 0.10	0.86
8	2.6 ± 1.0	2.0 ± 1.0	0.75 ± 0.07	0.87
9	4.3 ± 0.5	4.5 ± 1.0	0.95 ± 0.06	0.77
10	6.7 ± 0.6	9.5 ± 0.8	0.15 ± 0.10	0.91
11	4.1 ± 0.6	5.0 ± 0.6	0.85 ± 0.15	0.86

Table 2.

Mean variation of the PI controller parameters.

parameter	ΔT	Kp	Ki
mean ± s.d.	4.6 ± 1.0 ms	4.8 ± 2.4 ms	0.6 ± 0.3
mean CI value	0.57 ms	0.66 ms	0.08
s.d./CI ratio	1.75	3.64	3.75

3.3.2. Alternative proportional–integral–differential control models

Prior literature has shown that flies do not show a significant response to angular accelerations but do sense and respond to angular velocities via the haltere organs [21]. These observations suggest control models that do not use angular acceleration as an input (the differential term in PID, see §4.3 as well as in electronic supplementary material). In the framework presented here, this restricts our models to those containing only the terms proportional to the angular velocity (P) or its integral the angular displacement (I).

For completeness, we also fit the data with two simpler control models. We tested an integral-only (I) controller and a proportional-only (P) controller by fitting them to the measured ΔΦ as described above (table 3). The metrics used to assess the controller fit are R² and the root-mean-square error (r.m.s.e.) of the difference between the measured ΔΦ and the value predicted by the control model, averaged across the movies in our dataset (tables 3 and 4). As expected, because the PI model includes both P and I models, it fits the data better with a lower r.m.s.e. value and higher R² value. However, the subset models can be rejected based on more substantial reasons. The P-controller is unrealistic, since it does not contain the roll angle, which is the quantity the fly is evidently controlling. Specifically, a P-controller would bring the fly to zero angular velocity but at an arbitrary roll angle. The I-controller is also unrealistic, since its best fits yielded latency times that are too short for an animal, between 0 and 0.3 ms. Table 4 shows an example for the manoeuvre in figures 1 and 2, in which the fitted time delay ΔT = 0 is unfeasible. The I-controller requires such a short latency because the roll angle (I-term) peaks later than the roll velocity (figure 2g; electronic supplementary material, figure S4f), which forces the I-controller to respond almost immediately. In summary, the P-term is required to explain the observed latency, and the I-term is required since it represents the controlled quantity. Together, they combine to produce a PI controller, which seems to be a minimal model for the roll-perturbation controller.

Table 3.

Fitting results for three linear control models.

model	functional form	r.m.s.e.
PI		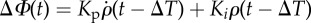6.7°
P		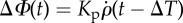16.4°
I	ΔΦ(t) =     Kiρ(t − ΔT)	10.5°

Table 4.

Fitting results for three linear control models for the movie in figures 1 and 2.

model	ΔT (ms)	r.m.s.e. (°)	R2
PI	4.4	8.7	0.90
P	6.9	20	0.47
I	0.0	14	0.74

3.3.3. Hallmarks of linear control

To further illustrate that wing asymmetry generates corrective roll dynamics, we determine the mean roll acceleration for approximately 600 half-strokes and plot it versus ΔΦ (figure 6b). The ΔΦ asymmetry is negatively correlated with the roll acceleration generated by the fly, such that ΔΦ generates a counter-torque that forms a negative feedback with a corrective effect for the roll perturbation. Thus, for example, negative ΔΦ is correlated with positive roll acceleration (figures 1 and 2; electronic supplementary material, figures S3 and S4). Thus, while the controller output is computed in terms of ΔΦ, figure 6b shows that ΔΦ is proportional to roll acceleration, which in turn enables the fly to control the roll angle.

The data also show two hallmarks of linear control. First, the correction time is insensitive to the maximum roll deflection, Δρ. Here, the correction time T_c is the time between onset of the perturbation and the moment when the roll angle reaches 10% of Δρ. Plotting T_c as a function of Δρ shows the correction time is 6.8 ± 1.6 wing-beats (mean ± s.d., n = 20) with little dependence on perturbation amplitude (figure 6c). Second, we find that Δρ increases linearly with maximum roll velocity (figure 6d). Collectively, these data suggest that, as with yaw [39], the response to roll perturbations is well described by a reduced order model of a linear PI controller with time delay.

3.4. Evidence for prioritized control

The perturbing torque was horizontal and not aligned with a principal body axis, since a fly's typical body pitch angle is 45°. The torque induced the largest angular deflection along the body roll axis and secondary deflections along the other body axes. In particular, we found that both the yaw angle and the direction of the body velocity were altered significantly. In yaw, we find that when the fly is rolled to its right there is a corresponding rightward yaw deflection and vice versa (figure 7a). Maximum yaw deflection was observed at the same time as the maximum roll deflection, about four wing-beats after the onset of the perturbation. Across our entire dataset, the maximum yaw deflections increase roughly as ≈(1/2)Δρ with significantly greater scatter at large Δρ.

Figure 7.

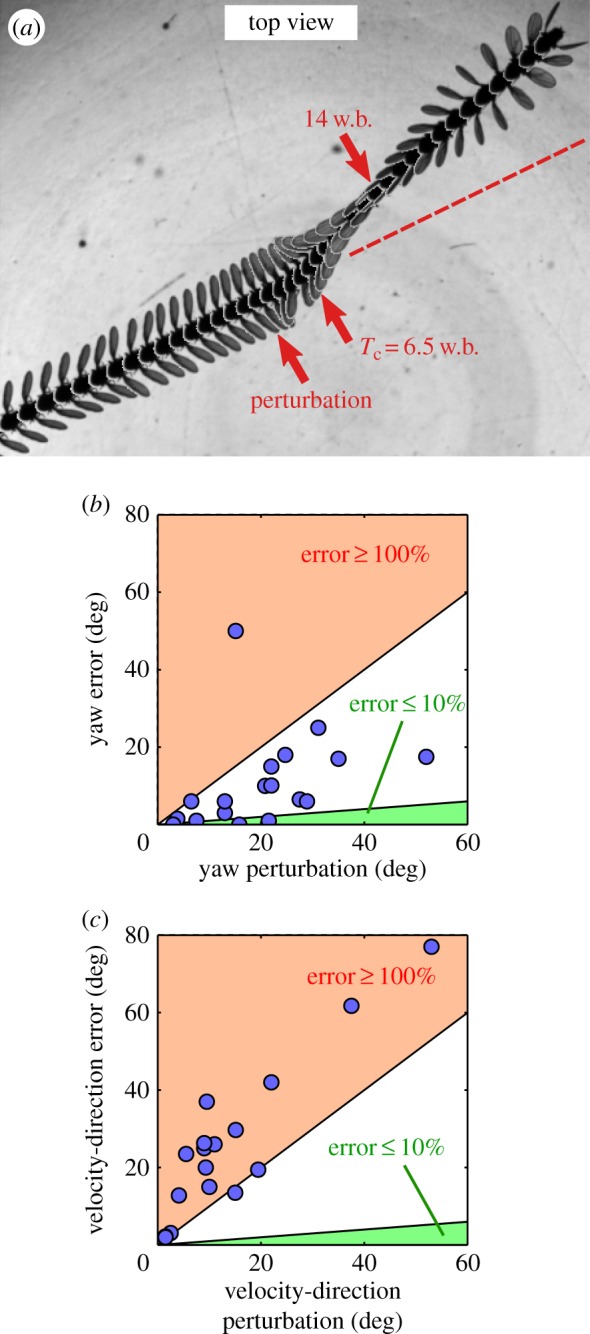
(a) Superimposed top-view images of a typical roll correction manoeuvre following a perturbation of Δρ = 45° leftward in roll, 30° leftward in yaw and 5° down in pitch. The perturbation time t = 0, correction time T_c, and t = 14 wing-beats are indicated by red arrows. The fly moved from left to right and the snapshots were taken every 4.5 ms. After roll has been corrected, the fly continued in a straight trajectory with uncorrected differences of 8° in yaw and 15° in the velocity heading. The 7° difference between the two angles is attributed to small side-slip motion before the perturbation, such that the fly's velocity was misaligned with its yaw angle. The dashed red line illustrates a hypothetical unperturbed trajectory. (b) Yaw difference (‘error’) between t = 0 and 11 wing-beats as a function of the maximum yaw perturbation. The 11 wing-beat time is after the roll manoeuvre has ended and also corresponds to the time in which approximately 10% yaw error is achieved after yaw-only perturbations. The green area represents ‘error’ less than or equal to 10%. The orange area above the unity slope represents an increase of the perturbation. (c) A similar plot for the direction of the body velocity. (Online version in colour.)

In contrast to previous experiments where perturbations were restricted to yaw and were corrected with small errors [39], here we observed that the secondary deflections along the yaw and body velocity orientations were often left partially uncorrected (figure 7b,c). A typical example of a fly perturbed during forward flight is shown in figure 7a by a superposition of top-view images. Following the external torque, the fly was deflected by 45° leftward along the roll axis, 30° leftward in yaw and 5° down in pitch. As indicated by the flight trajectory, while the fly fully corrected its roll angle with T_c = 6.5 wing-beats, deflections of 8° in yaw and 15° in the direction of the body velocity persisted until the end of the measurement. From previous experiments [39], we know that a yaw-only perturbation of 30° should have been corrected within 14 wing-beats to 2° accuracy. In the current experiment, however, larger residual deflections (‘error’) in yaw and the velocity heading persist long after 14 wing-beats (see label in figure 7a).

Figure 7b shows the yaw ‘errors’ as a function of the imposed yaw deflection for multiple perturbation events. The yaw ‘errors’ were measured at t = 11 wing-beats, a time by which the roll manoeuvre has already ended, and we did not observe any other distinct manoeuvres for yaw correction. The plot shows yaw ‘errors’ larger than 10% of the imposed yaw perturbation (above the green region in figure 7b). Remarkably, a similar plot for the ‘errors’ in the body velocity direction at 11 wing-beats shows that they are even larger than the imposed perturbation to the body velocity orientation (orange area in figure 7c). Thus, the velocity orientation was not even partially corrected. Instead, its deflection increased during the roll correction. The qualitatively different yaw response with and without the roll deflection hints that the fly prioritizes roll correction while compromising other angles.

3.5. Extreme perturbations

3.5.1. Experimental measurement

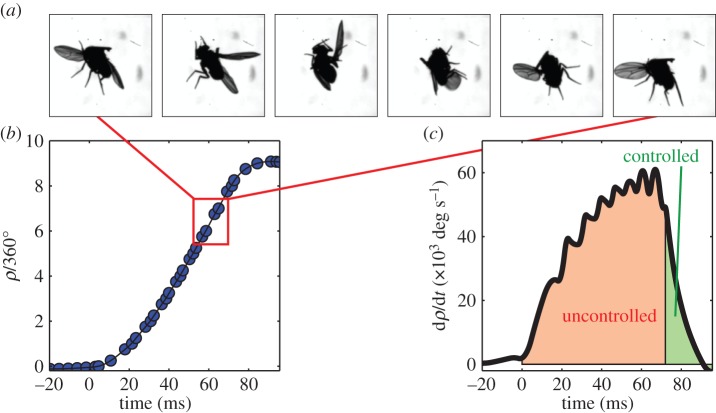
To test the linear control model for roll, we challenged the flies with extreme perturbations in which they were spun multiple times in mid-air by a series of magnetic pulses. The fly shown in figure 8a and electronic supplementary material, movie S5, was rotated eight times to its right. The accumulated roll angle exceeded 3000° (figure 8b) and the maximum roll velocity was over 60 000° s⁻¹ (figure 8c). During the perturbation, the fly was unable to oppose the magnetic torque. In fact, the right wing, which in a typical correction manoeuvre flaps with a larger stroke amplitude, hardly flapped at all and occasionally seemed disconnected from its flight power muscles. We captured three such events, all showing the same behaviour. Remarkably, once the magnetic pulses stopped, the flies regained control within three to four wing-beats. The response of flies to such extreme perturbation can shed light on the validity limits of the linear control model and provide hypotheses regarding nonlinear features of the flight controller.

Figure 8.

Extreme perturbation. (a) Snapshots, taken 1.25 ms apart, of a fly being rotated clockwise at approximately 60 000° s⁻¹ by a pulse train of magnetic torques. (b) Roll kinematics during the manoeuvre (blue circles), and its smoothing spline (black line). The perturbation was on between t = 0 and 72 ms. Measurement errors are smaller than the symbol size. (c) Roll velocity versus time (black line). The fly was unable to control its flight during the perturbation (orange shading, uncontrolled) and actively corrected roll once the perturbation stopped (green shading, controlled). The fly levelled itself to ρ = 20° within four wing-beats after the perturbation stopped, towards ρ = 0. (Online version in colour.)

The response to these extreme perturbations indicates that flies are able to come back to nearly zero roll angle independently of the number of imposed revolutions along roll. While a linear PI controller model well describes the response of flies to single-impulse perturbations, this model cannot account for the response to extreme perturbations. Under such perturbations, the integral term of the PI controller should have accumulated a signal corresponding to a 3000° deflection. This signal would both saturate the actuation response of ΔΦ and, more importantly, the resulting correction manoeuvre would require the fly to rotate 3000° in the opposite direction. Clearly, flies circumvent this scenario. While the strategy the flies use is not clear, we hypothesize that above some perturbation amplitude the roll controller switches from a linear PI to another control behaviour that should include two mechanisms. The first mechanism would limit or reset the value of the integral term. In control theory such an operation is termed integral ‘anti-windup’. The second mechanism would employ an additional sensory modality that measures the direction of gravity independent of the halters to correct for roll. It is plausible that in such manoeuvres the time scales are long enough that flies may be able to incorporate such an additional sensory modality.

3.5.2. Passive versus active damping

Our calculations show that roll deceleration is only explained by active flapping, rather than passive aerodynamic damping due to the wings. To estimate the role of passive aerodynamic damping in the recovery of fruit flies from extreme perturbation, we calculated an upper limit for the damping during the manoeuvre shown in figure 8. The upper limit was estimated by considering a fly rolling along its long axis (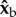) with its wings static with respect to the body and maximally stretched sideways with ϕ = 90° and ψ = 45° (figure 9, inset). This configuration, in which the normal to the wing surface is parallel to the wing's velocity induced by body rotation, achieves maximum drag that passively damps the rotation along roll. The aerodynamic drag force F_drag on each wing was calculated using a quasi-steady-state force model [51,60] of the form

3.2

Here, ρ_air is air density, S is the wing area, 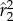is a dimensionless shape factor, C_D is the drag coefficients determined experimentally using a scaled-up model of a fruit fly wing [51] and U_tip is the velocity of the tip of the wing. The aerodynamic torque of the two wings is τ = 2LF_drag, where L is the torque arm with respect to the body centre-of-mass, corresponding to the body radius plus 2/3 of the wing span (centre-of-pressure position). We solve the equation of motion for roll: 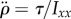, with the initial condition 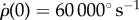corresponding to the end of the external perturbation in the experiment (figure 8), and ρ(0) = 0, which was arbitrarily chosen.

Figure 9.

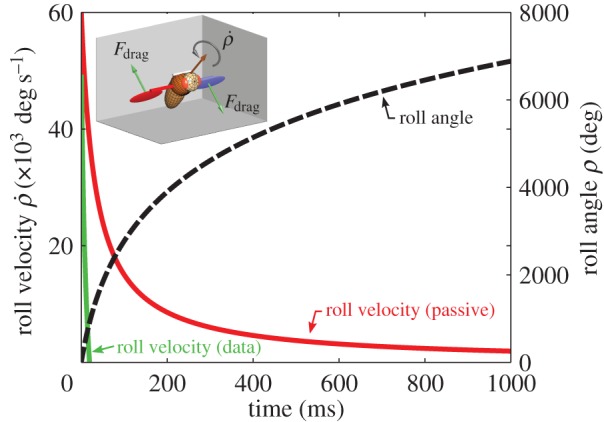
The contribution of passive roll damping to the recovery from a roll extreme perturbation. Plotting the calculated dynamics of the roll velocity (red) and roll angle (dashed black line) under passive aerodynamic damping. The measured data for the roll velocity are copied from figure 8c (green). The calculation assumed an upper limit for the damping torque. The initial condition consisted of a roll velocity of 60 000° s⁻¹ as in the experiment described in figure 4, and zero roll angle at t = 0. The slow approximately 1/t decay of the roll velocity indicates that passive damping alone cannot explain the fast recovery observed in the experiment. Inset shows the configuration of the rotating fly. The fly is rotating about its roll axis (orange) and each wing is pitched to ψ_w = 45° such that its angle of attack with respect to the ambient air is 90°. The green arrows indicate the aerodynamic drag forces on each wing.

The solution for and ρ(t) (figure 9) shows that their decay is much slower than in the observed recovery manoeuvre (figure 8). While in the experiment the fly managed to completely brake its roll velocity approximately 25 ms after the perturbation torques had ended, by this time the passively damped model slowed down only to approximately 30 000° s⁻¹, which is half its initial velocity. The scaling of the decay is obtained from its equation of motion that has the form 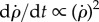. Its solution decays slowly as 1/t, such that even by t = 1000 ms the roll velocity is 2000° s⁻¹ and the roll angle has completed almost 20 rotations (figure 9). These calculations show that, while it may be useful in slowing down at short times, passive damping alone cannot account for the corrective torques and active torque generation must be considered. Since the maximum wing stroke angular velocity (figure 2b) is approximately twice as fast as the imposed roll velocity of 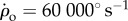, the corrective torque due to flapping is much larger than passive damping: the two wings experience rotation equivalent to 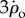and 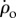, respectively, and since the aerodynamic force is quadratic in the wing's airflow, the maximum active braking torque could be estimated to be approximately 3² + 1² = 10 times larger than passive damping.

While the above calculation was done for the extreme, multiple rotation, perturbation, it is even more relevant for slower perturbations in the ‘linear regime’ (figures 1–4), since the damping force is quadratic in the wing velocity and, hence, even less significant.

4. Discussion

4.1. Response time of the roll correction reflex

The average response time of the roll reflex is 5 ms (a single wing-beat). The response time is defined as the time from the onset of the perturbation until a stroke-amplitude asymmetry of ΔΦ = 10° was detected (figure 6a, green). A similar response time was obtained from fitting the PI controller (figure 6a, grey and table 1). The onset of the perturbation was chosen as a reference time for the response. Importantly, here we measure a behavioural response time, from a stimulus to a mechanical action. This measurement is distinct from measurements of the neural response time, from a stimulus to the activation of a given neuron in the response pathway. The behavioural response typically requires the collective action of sensory neurons, inter-neurons and motor neurons to elicit a measurable mechanical behaviour.

The roll reflex is 3.5 times faster than the response of fruit flies to yaw perturbations [39] and 2.5 times faster than their response to pitch perturbations [13]. These differences highlight the relative importance of roll control. The roll response is also five times faster than visual startle response in flies (25 ms) [61] and the entire correction manoeuvre is completed before the flies can elicit a visual response.

The 5 ms response time places this reflex among the fastest behavioural reflexes in the animal kingdom. It is comparable to the head-roll compensation reflex in blowflies (5–7.5 ms) [25], the startle response in teleost fish (5–10 ms) [47,62], the mandible strike of trap-jaw ants (4–10 ms) [63] and the escape response of cockroaches (11–18 ms) [64,65]. Among these animals, the fruit fly is by far the most studied and experimentally accessible organism, which opens the way for studying the neurobiology of roll control as a model system for extremely fast reflexes.

4.2. The duration of the correction manoeuvre

Our data show that 90% of the roll perturbation is corrected within 30 ± 7 ms (6.8 ± 1.6 wing-beats). The correction time is comparable to the flies' visual response time of 25–30 ms [61], implying that flies do not use their compound eyes during roll correction. This observation is consistent with previous studies on the integration of haltere and visual signals in tethered flies, showing temporal filtering of rotational information: the visual system is used to measure slow rotations while the halteres are used to measure fast rotations [22,23].

4.3. Stroke-amplitude asymmetry

The wing stroke-amplitude asymmetry measured in our experiments reaches approximately 80°, as shown, for example in figures 1d and 2; electronic supplementary material, figures S3b, S4 and movies. This asymmetry is significantly larger than the maximum asymmetry of 10–15° measured in experiments with tethered flies that were rotated inside a gimbaled apparatus [21]. The difference in the maximum asymmetry can be attributed to the different magnitude of the roll perturbations in the tethered experiments and the free-flight experiments reported here, both in terms of the angular displacement and angular velocity. The maximum angular displacement obtained in tethered experiments was 30° [21–23], while the current free-flight experiments reach 100° (figure 6c,d). The maximum angular velocity in the tethered experiments was 800° s⁻¹ [21–23], compared with 9400° s⁻¹ in the free-flight experiments (figure 6d). The smaller velocity in the tethered preparations stems from the large inertia of the rotating gimbaled apparatus. In addition, the imposed rotations in the tethered experiments were oscillatory with a characteristic period of approximately 1 s, while the mid-air perturbations were torque impulses of only 5 ms. Since the fly's halteres sense angular velocity and the maximum angular velocity perturbations were more than 10 times faster in the free-flight experiments, it is plausible that the reason for the larger wing stroke asymmetry response was simply the stronger stimuli.

To check this conjecture, we used the PI controller model to predict the roll response of tethered fruit flies previously published by Dickinson [21]. In one of these tethered experiments, flies were mounted on a gimbaled apparatus oscillating along the roll axis with an amplitude 25°, a period of 0.6 s, and a maximum velocity of 250° s⁻¹. Importantly, the flies had no visual cues relating to the imposed rotation. As shown in the electronic supplementary material, figures S4 and S5, we find that the PI control model well describes the response data (R² = 0.8). Moreover, the PI control model shows that the response of the fly is independent of its roll acceleration, supporting a PI rather than a PID control model (electronic supplementary material, figure S6). We do find that the values of the controller parameters fitted for the tethered experiment are different from the controller parameters fitted to the free-flight experiment reported here (table 2). Possible reasons for this difference are natural variability among flies (as characterized by the free-flight data) as well as the different experimental methods: using tethered compared to free flying animals. Finally, since the tethered flies did not have any visual cue about the imposed rotation, the data strongly suggest that the fly's roll response is mediated by the haltere-based mechanical sensors, consistent with the PI control model.

4.4. The PI controller model

The PI controller model determines the roll displacement by integrating the roll velocity. This controller alone cannot determine the absolute roll angle. Hence, we hypothesize that to avoid accumulation of errors while integrating the haltere angular velocity readout, the fly may be adjusting the reference roll angle by combining information from another sensory modality, such as the compound eyes or ocelli. Owing to the known temporal filtering the fly applies to the rotational information it acquires—using the haltere readout in its response to fast rotations and the visual system in its response to slow rotations [22,23]—we conjecture that the PI controller model describes a reflexive response to the fast perturbations applied in our experiments, while adjusting the absolute roll angle at a slower time scale using the visual system. Our measurements of the fly's response to extreme perturbations, where the fly seems to know where ‘down’ is although its roll integrator most probably saturates, are consistent with this hypothesis, since these manoeuvres are long enough to allow an incorporation of information from slower sensors.

4.5. Comparing roll and yaw control

Although the control mechanisms for body roll and yaw [39] are mathematically equivalent, there are substantial differences between these two degrees of freedom and the fly's response to perturbations along these angles. First, roll is an unstable degree of freedom while yaw is stable. Moreover, in yaw, the perturbation velocity is passively damped to half its value after only two wing-beats [66]. Second, if a roll perturbation is not fully corrected the fly will start turning and losing altitude, whereas in yaw, if a perturbation is not fully corrected the fly can keep flying only in a different direction. Third, the one wing-beat response time of the fly to roll perturbation is 3.5 times faster than the yaw response time. Together, it is clear that controlling roll perturbations is more challenging than controlling yaw perturbations.

4.6. Hypothesized nonlinear control architecture under complex perturbations

An open problem arising from our study is understanding the structure of the overarching controller for all the body angles. When modelling the control system, treating roll separately from yaw is justified by the much faster time scales of the response and correction associated with roll. As previously measured in [39], the response time of fruit flies to yaw-only perturbations is 3.5 wing-beats (17.5 ms), whereas their response time to the perturbations in the current study is only one wing-beat (5 ms and sometimes even less). In the current experiments, by t = 17.5 ms, the flies have already been actively correcting roll for 2.5 wing-beats. Beyond t = 17.5 ms, we do not see any different correction manoeuvre that may indicate the onset of yaw correction. As mentioned above, the 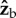torque pulses have some corrective effect on yaw; however, the onset time of these torques suggests they are a part of the roll manoeuvre. In addition, we observe sizeable residual deflection in yaw, long after the roll correction is finished and also long after any hypothetical yaw correction should have been performed. These results show that roll and yaw are, indeed, coupled: rather than fully correcting for both angles at the same time, it seems that flies prioritize roll correction over yaw. This may be another reason that explains why the decoupled roll-only controller well approximates the observed response. To map out the full controller, it will be necessary to measure the insect's response to sophisticated perturbations along multiple axes, whose direction, amplitude and timing are individually controlled. Such measurements will further reveal the strategies insects use to manage their actuation resources and achieve the grace and performance of their flight.

Funding statement

T.B. was supported by the Cross Disciplinary Postdoctoral Fellowship of the Human Frontier Science Program. In addition, the work was supported in part by an NSF-CBET award no. 0933332 and an ARO award no. 61651-EG.