Abstract
Mixed-effects beta regression (BR), boundary-inflated beta regression (ZOI), and coarsening model (CO) were investigated for analyzing bounded outcome scores with data at the boundaries in the context of Alzheimer’s disease. Monte Carlo simulations were conducted to simulate disability assessment for dementia (DAD) scores using these three models, and each set of simulated data were analyzed by the original simulation model. One thousand trials were simulated, and each trial contained 250 subjects. For each subject, DAD scores were simulated at baseline, 13, 26, 39, 52, 65, and 78 weeks. The simulation-reestimation exercise showed that all the three models could reasonably recover their true parameter values. The bias of the parameter estimates of the ZOI model was generally less than 1%, while the bias of the CO model was mainly within 5%. The bias of the BR model was slightly higher, i.e., less than or in the order of 20%. In the application to real-world DAD data from clinical studies, examination of prediction error and visual predictive check (VPC) plots suggested that both BR and ZOI models had similar predictive performance and described the longitudinal progression of DAD slightly better than the CO model. In conclusion, the investigated three modeling approaches may be sensible choices for bounded outcome scores with data on the edges. Prediction error and VPC plots can be used to identify the model with best predictive performance.
Electronic supplementary material
The online version of this article (doi:10.1208/s12248-014-9655-y) contains supplementary material, which is available to authorized users.
KEY WORDS: Alzheimer's disease, beta regression, boundary data, bounded outcome scores, disability assessment for dementia
INTRODUCTION
Bounded outcome scores can be often found in various measures for Alzheimer’s disease (AD), such as (1) the cognitive component of the AD assessment scale (ADAS-Cog) (1), (2) disability assessment for dementia (DAD) (2), (3) mini-mental state examination (MMSE) (3), and (4) functional assessment questionnaire (4). Other examples include visual analog scale (VAS) for measuring quality of life (5).
Bounded outcome measurements are viewed as percentage-like data after being scaled into [0,1] interval. One challenge with this type of data is that their distribution can vary from unimodal to J, L, or U shaped, and standard statistical approaches may not be valid in general (6–9). Another challenge for bounded outcome data is that some data may be present at the boundaries of the interval (i.e., 0 or/and 1), which further complicates the analysis of such data (10–12).
Several modeling approaches have been used to handle bounded outcome data in presence of boundary data (10,13–17). Beta regression (BR) has been advocated to model percentage-scaled dependent variable due to its flexibility in capturing various skewed unimodal and bimodal distributions, particularly when normalizing transformations do not work well (6). Although BR models are very useful for proportion data, the link functions that it uses (e.g., logit link) do not allow the observations to be on the boundaries. In this case, rescaling the boundary data away from boundaries before fitting the BR model was proposed to circumvent the boundary problem (7,13). More recently, zero- and one-inflated beta regression models (ZOI) have been proposed to circumvent the problem associated with boundary data (10,12). Coarsening (CO) models have been shown to be another viable option to model the bounded outcome data (14,18).
In this manuscript, we investigate the DAD scores, a daily functioning measure for AD. The DAD score is a continuous variable with a range from 0 to 100. As multiple modeling choices are available to allow for complete modeling of the boundary values and the entire continuous space, a question of interest could be which model is more suitable for a particular dataset of this AD endpoint. We conducted simulations using BR, ZOI, and the CO models to generate total DAD data with values existing at the edges. Then the performance of each model was evaluated by estimation using the original simulation model. The three models were compared and applied to the real-world placebo data from clinical studies for AD.
METHODS
Mixed-Effects Beta Regression
The mixed-effects BR model assumes that conditional on the random effects, the response variable follows a beta distribution as denoted by:
| 1 |
with a density function as follows:
| 2 |
where yij is the response variable (0 < yij < 1) for the ith subject (i = 1 … m) at the jth time (j = 1 … nj), μij is the conditional expectation (mean) of the response process (0 < μij < 1), which is linked to a function of random effects (ηi ~ N(0, Σ)) and fixed-effects (θ’s) as depicted below in Eq. 3, and τ is the precision parameter (τ > 0). Specifically, conditional on μij and τ, yij’s are independent.
Using a logit link function, a BR model can be formed as:
| 3 |
where g(θ, ηi ,xij) is some function of the regression covariates, the fixed effect (θ), and random effect (ηi).
The BR model assumes that yij is a variable between 0 and 1. To accommodate data at the boundaries (i.e., 0 or/and 1), the scaling method reported in Verkuilen and Smithson will be used to move the boundary data slightly away from the edges (7,13). The scores are linearly transformed from their original scale (y’ij) to the open-unit interval (0, 1) by first taking y*ij = (y’ij − a)/(b − a), where b is the highest possible score on the test and a is the smallest possible score, and then avoiding zeros and ones by taking yij = y*ij (1−δ) + δ/2, where δ is a small constant. In this analysis, δ was set to 1 × 10−8 to rescale the data for the BR model.
Mixed-Effects Zero- and One-Inflated Beta Regression
The ZOI model uses the beta law to define the continuous component of the distribution (Eq. 2), while the discrete component (i.e., boundary data) is characterized by a mixture distribution as follows:
| 4 |
where f(y * ij; μij, τ) is the density function for beta distribution (Eq. 2), π0 and π1 represent the probability of observations at zero and one, respectively. The sum of the probability of the zero and one is supposed to be less than 1.
Mixed-Effects Coarsening Model for Boundary Data
A coarsened grid approach has been proposed for bounded outcome scores with data on boundaries (14,18). This approach assumes that an underlying latent process (variable, U) within a bounded interval gives rise to observed scores with data at the boundaries via a coarsening mechanism.
Suppose that the normalized response score, y*ij, is a grouped version of a continuous latent process Uij, which takes values in (0, 1) and follows a logit-normal distribution:
| 5 |
Let 0 < a1 < … < am < 1 be a partition of unit interval (0,1). y*ij is defined to be k/m if ak ≤ Uij < ak + 1,k = 1, …, m−1; m is the range of scores on the original scale. At the boundaries, y*ij = 0 when 0 < Uij < 0.5/m and y*ij = 1 when (m − 0.5)/m < Uij < 1. Other normalization transformation (e.g., Czado transformation) can be also used with the CO approach (18).
Simulations
The simulation data were generated in a context of disease progression according to DAD scores in patients with AD. The simulations were inspired by the example given in the Application section of this manuscript. Each of the investigated models (i.e., BR, ZOI, and CO model) was used to simulate the data. A logit link function was assumed for the BR, the nonboundary part of the ZOI, and the CO model. Also, for all the three models, a linear progression model was assumed on the logit scale. Borrowing from the previous research (19–21), the placebo effect (fplb(tij)) was assumed to characterize the transient improvement of the disease in AD. The drug effect (fdrg(Ci)) was assumed to be disease modifying and to work on the slope (rate of progression) of the model. The following equation describes the abovementioned disease progression, placebo, and drug effects:
| 6 |
where θ0 is the intercept that characterizes baseline disease state, and θ1 characterizes the rate of disease progression. The random effects of intercept and slope (η0i and η1i, respectively) are assumed to follow a multivariate normal distribution with mean equal to the null vector and variance-covariance matrix:
| 7 |
The placebo effect (fplb(tij)) and the drug effect (fdrg(Ci)) can be described by an inverse Bateman function and an Emax model, respectively, as follows:
| 8 |
| 9 |
where γ is a factor defining the magnitude of the placebo effect, Kon is the rate constant for the onset rate of the placebo effect, Emax represents the maximum disease-modifying effect for the hypothetical drug, EC50 denotes the concentration at which 50% of the maximum effect on the logit scale is achieved, and Ci represents the drug exposure (e.g., summary pharmacokinetic measures such as trough concentration) for the ith subject, which follows a lognormal distribution with a geometric mean of 0.26 and a standard deviation of 1 on the log scale. The simulation parameters are specified as follows: θ0 = 2, θ1 = −0.01, γ = 0.5, Kon = 0.1, Emax = 0.6, EC50 = 0.2, a = 0, b = 100, ω00 = 1, and ω11 = 0.0144. For the BR model, the precision parameter, τ, was set to 3, while for the CO model, σ was set to 0.88. Extensive Monte Carlo simulation studies (N = 1,000) were conducted in R 2.14.0, and 250 subjects were simulated for each study. This sample size is relevant to a phase 2 clinical study for AD. DAD scores were simulated for each subject at baseline, 13, 26, 39, 52, 65, and 78 weeks. For the CO model, the simulated underlying latent continuous scores (Uij) were discretized using (k − 0.5)/100 ≤ Uij < (k + 0.5)/100, where k = 1, 2, …, 99. At the boundaries, y*ij = 0 when 0 < Uij < 0.005 and y*ij = 1 when 0.995 < Uij < 1. To keep consistency with the CO model, the boundary data for the BR model were generated using the same cutoff points at the boundaries, i.e., if the simulated score was less than 0.005, it was converted to 0, while if the simulated score was greater or equal to 0.995, it was converted 1.
For the ZOI model, a multinomial logistic model was assumed for the probability of the zero and one over time as follows:
| 10 |
| 11 |
where α0 and α1 are the intercepts for zero and one at time 0 on the logit scale, while β0 and β1 are the coefficients for change of DAD scores (i.e., disease status) over time on the logit scale (Eq. 6). This latent variable approach links the individual linear predictor with latent random effects of the nonboundary data to the probability of the 0 and 1, and allows the association of boundary data with the trend of disease status (i.e., nonboundary data). In addition, the multinomial logistic model ensured the sum of the probability of the zero and one to be less than 1. α0 and α1 were set to −6.54 and −10.1, respectively, while β0 and β1were set to −1.76 and 3.39, respectively. The boundary data at the upper bound of score interval was created at levels of approximately 1%, 5%, 10%, and 20% by assigning appropriate values for α1 of the ZOI model and θ0 for the BR and CO models.
The simulated data were analyzed by the three models using NONMEM®. The performance of the models was evaluated by re-estimating the model parameters for each simulated dataset and by comparing bias (%) and the relative root mean squared error (RRMSE; %) as follows:
| 12 |
| 13 |
where N is the total number of simulated datasets, ϕ is the true value of the parameters in Eqs. 6–11, and is the estimate for the nth simulated dataset.
Application of the Models to Progression of Alzheimer’s Disease
In this section, we demonstrate the application of a mixed-effects BR, CO, and ZOI models to describe the progression of DAD scores in patients with AD. The placebo data from phase 3 studies for an investigational drug in patients with mild to moderate AD were used. The data consists of 972 AD patients having DAD measurements available at baseline, 13, 26, 39, 52, 65, and 78 weeks. Approximately 0.3% and 11.5% of the DAD data are on the lower and upper boundaries, respectively.
In this analysis, the logit link function that is similar to Eq. 6 in the simulation was used for the BR, the nonboundary part of the ZOI, and the CO model. However, no placebo effect and drug effect were evaluated, i.e., fplb(tij) = 0 and fdrg(Ci) = 0. Before implementing the CO model, the DAD scores were discretized first using the CO model concept, i.e., the cut points were k − 0.5 (k = 1, 2, …, 99). Also, if the score was less than 0.5, it was converted to 0, while if the score was greater or equal to 99.5, it was converted 100.
For the ZOI model, the boundary data were modeled using Eqs. 10 and 11 (model 1). In addition, two alternative models were tested for the log odds of the 0 and 1 in the ZOI model. The first model (model 2) assumed an arbitrary slope on time for changes of probability of 0 or 1 over the time as follows:
| 14 |
| 15 |
where κ0 and κ1 are the slope for change of probability of 0 and 1 over time on the logit scale. The other model assumed that the log odds of the 0 and 1 were function of both time and disease progression (i.e., the nonboundary data, model 3):
| 16 |
| 17 |
The BR, CO, and selected ZOI models were compared using prediction error and visual predictive check (VPC). The prediction error (PE) was defined as: where yij is the value of the observation in the ith subject at jth time; and E(yij) is the expected value of the jth observation in the ith subject. For the BR model ; for the ZOI model, ; for the CO model, , where Φ is the cumulative density function of . The PE for the overall data was calculated for the three models. To assess the performance of the models at the boundaries and inner points of the (0, 1) interval, we also calculated the PE on the boundaries and inner points separately.
The percentile VPC was used to assess the model. The median and 5th and 95th percentiles of the observed data were computed, and then the median and 90% prediction intervals of these quantities were computed based on 1,000 simulations and compared with the observed percentiles. The uncertainties of the parameter estimates were not used in the simulations for the VPC. The NONMEM codes for the ZOI, CO, and BR models are presented in the Appendices 1, 2, and 3, respectively.
RESULTS
The majority of NONMEM runs (approximately 95% or above) were successfully converged. Results from successful model minimizations were used to calculate the bias and RRMSE of parameters. Tables I, II, and III show the bias and RRMSE for the model parameter estimates of the investigated models.
Table I.
Estimation Bias and Relative Root Mean Squared Error (RRMSE) for the Zero- and One-Inflated Beta Regression Model (ZOI)
| Bias (%) | RRMSE (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| 1% | 5% | 10% | 20% | 1% | 5% | 10% | 20% | |
| θ 0 | −0.3 | −0.3 | −0.2 | −0.3 | 1.5 | 1.5 | 1.5 | 1.4 |
| θ 1 | −0.3 | −0.2 | −0.1 | 0.1 | 3.4 | 3.5 | 3.2 | 3.6 |
| γ | −0.3 | −0.2 | 0 | −0.2 | 3.1 | 3.2 | 6.8 | 6.7 |
| K on | −0.1 | −0.2 | −0.2 | 0.1 | 5.6 | 5.7 | 2.3 | 1.9 |
| E max | 1 | 2.1 | −0.2 | 0.1 | 6.6 | 15.9 | 2.8 | 3.3 |
| EC50 | 3.5 | 1.8 | 1.9 | 1.1 | 21.6 | 16.1 | 5.4 | 7 |
| α 0 | 2.9 | 2.7 | 2.4 | 2.7 | 6.9 | 6.6 | 9.1 | 6.6 |
| α 1 | 1.4 | 0.9 | 0.1 | −0.4 | 7.2 | 4.3 | 26.4 | 21.5 |
| β 0 | 1.1 | 0.8 | 0.5 | 0.6 | 13.6 | 12.9 | 13.7 | 13.3 |
| β 1 | 2.7 | 1.3 | −0.1 | −0.6 | 8.6 | 5.3 | 3 | 2.5 |
| ω 00 | −0.9 | −0.7 | −0.6 | −1.2 | 4.3 | 4 | 3.6 | 3.8 |
| ω 11 | −1.4 | −1.3 | −1.3 | −2 | 5.3 | 5.2 | 4.7 | 5.3 |
θ 0 baseline disease state, θ 1 rate of disease progression, γ magnitude of the placebo effect, K on onset rate of the placebo effect, E max maximum disease-modifying effect, EC 50 concentration at which 50% of the maximum effect, α 0 intercept for zero, α 1 intercept for one, β 0 coefficient for change of disease status on zero, β 1 coefficient for change of disease status on one, ω 00 standard deviation of interindividual variability on baseline, ω 11 standard deviation of interindividual variability on rate of progression
Table II.
Estimation Bias and Relative Root Mean Squared Error (RRMSE) for the Beta Regression Model (BR)
| Bias (%) | RRMSE (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| 1% | 5% | 10% | 20% | 1% | 5% | 10% | 20% | |
| θ 0 | 2.9 | 4.5 | 4.8 | 4 | 7.1 | 5.2 | 5.2 | 4.3 |
| θ 1 | 5.1 | 2.1 | 3.8 | 3.3 | 9.9 | 8.9 | 8.2 | 8 |
| γ | 2.8 | 0 | −3.8 | −12.4 | 10.8 | 10.8 | 10.6 | 16.7 |
| K on | 7 | 8.9 | 17.7 | 21.2 | 24.2 | 47.1 | 30.2 | 48.9 |
| E max | 10.7 | 10.4 | 16.7 | 20.4 | 35.1 | 24.8 | 28.9 | 28.9 |
| EC50 | 11.2 | 9.3 | 24.5 | 3.7 | 96.5 | 56.8 | 81.4 | 53.1 |
| ω 00 | 7.8 | 12.9 | 12.6 | −3.3 | 8.5 | 13.3 | 13 | 4.5 |
| ω 11 | 1.2 | −7.8 | −20.7 | −23.8 | 8.9 | 10.3 | 22.1 | 40.3 |
θ 0 baseline disease state, θ 1 rate of disease progression, γ magnitude of the placebo effect, K on onset rate of the placebo effect, E max maximum disease-modifying effect, EC 50 concentration at which 50% of the maximum effect, ω 00 standard deviation of interindividual variability on baseline, ω 11 standard deviation of interindividual variability on rate of progression
Table III.
Estimation Bias and Relative Root Mean Squared Error (RRMSE) for the Coarsening Model (CO)
| Bias (%) | RRMSE (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| 1% | 5% | 10% | 20% | 1% | 5% | 10% | 20% | |
| θ 0 | −1.4 | −0.4 | −0.3 | −0.2 | 8.3 | 2.1 | 1.5 | 1.1 |
| θ 1 | −0.1 | 0.2 | −0.1 | 0.4 | 6.4 | 6.3 | 6.6 | 6.9 |
| γ | 0.9 | 1.4 | 0.7 | 0.8 | 9 | 9 | 9.6 | 9.4 |
| K on | 2.7 | 1.9 | 3 | 2.5 | 18.6 | 18.2 | 19.8 | 20.5 |
| E max | 2.3 | 1.7 | 2.2 | 2.6 | 15 | 14.7 | 15.8 | 14.4 |
| EC50 | 13.3 | 10.3 | 11.7 | 9.6 | 51.8 | 49.7 | 53 | 47.1 |
| ω 00 | −0.6 | −0.8 | −1.3 | −2.2 | 3.2 | 3.2 | 3.4 | 3.8 |
| ω 11 | −1 | −1.2 | −1.6 | −2.1 | 5 | 5.2 | 5.2 | 6 |
θ 0 baseline disease state, θ 1 rate of disease progression, γ magnitude of the placebo effect, K on onset rate of the placebo effect, E max maximum disease-modifying effect, EC 50 concentration at which 50% of the maximum effect, ω 00 standard deviation of interindividual variability on baseline, ω 11 standard deviation of interindividual variability on rate of progression
Overall, the bias of the model parameter estimates was less than or in the order of 20% for all the three models. The bias of the ZOI model was generally less than 1% with a few exceptions, while the bias of the parameter estimates of the CO model was also mainly within 5%. However, the CO model exhibited some difficulties in estimating EC50, for which the bias was approximately 10%. The bias from the BR model was slightly higher but was still within 10% for most parameters when the boundary data were less than 5%. The higher bias of the BR model was probably due to rescaling of the data. When amount of boundary data increased from 1% to 20%, there was little influence on the performance of CO and ZOI by the change in the percentage of boundary data. The amount of boundary data appeared to have some impact on the parameter estimates of the BR model, i.e., the bias of the BR model tended to increase with an increase in the percentage of the boundary data from 5% to 20%.
Relatively large variability was associated with the estimates of EC50. The RRMSE of EC50 for the BR and CO model was greater than 50%, while the RRMSE of EC50 was within 20–30% for the ZOI model. There was little influence of percentage of the boundary data on the RRMSE of the parameter estimates for all the three models. In general, the variability in the placebo-related parameter (e.g., Kon) and the drug-related parameters (i.e., Emax and EC50) was larger. This is probably caused by the estimation difficulties associated with the nonlinearity for the placebo response model and the drug effect model.
Modeling Results for DAD Progression in AD Subjects
The parameter estimates for the BR, CO, and ZOI model of the DAD data were listed in Table IV. The estimated baseline DAD score and DAD progression rate were similar based on the 3 different models. The estimated baseline ranged from 84 to 89, while the rate of progression ranged from −0.36 to −0.3 points/week. The negative slope (rate of progression) values suggest a loss of functional abilities in terms of DAD compared with baseline.
Table IV.
Parameter Estimates for the DAD Progression in Patients with Mild to Moderate Alzheimer’s Disease
| Logit scale | Original scale | |||||
|---|---|---|---|---|---|---|
| Estimate | 90% CI | Estimate | 90% CI | |||
| Beta regression | ||||||
| Baseline | 1.77 | 1.68 | 1.86 | 85.45 | 84.35 | 86.48 |
| Rate of progression (point/week) | −0.012 | −0.014 | −0.011 | −0.30 | −0.34 | −0.28 |
| SD of IIV on baseline | 1.26 | 1.200 | 1.320 | |||
| SD of IIV on rate of progression | 0.015 | 0.013 | 0.017 | |||
| Coarsening model | ||||||
| Baseline | 2.12 | 1.99 | 2.25 | 89.28 | 87.99 | 90.45 |
| Rate of progression (point/week) | −0.014 | −0.016 | −0.013 | −0.36 | −0.39 | −0.32 |
| SD of IIV on baseline | 1.77 | 1.660 | 1.880 | |||
| SD of IIV on rate of progression | 0.019 | 0.017 | 0.021 | |||
| Zero- and one-inflated beta regression | ||||||
| Baseline | 1.68 | 1.60 | 1.76 | 84.29 | 83.24 | 85.29 |
| Rate of progression (point/week) | −0.012 | −0.013 | −0.011 | −0.30 | −0.33 | −0.27 |
| Intercept for zero | −6.54 | −7.91 | −5.17 | |||
| Intercept for one | −10.10 | −11.19 | −9.01 | |||
| Evolution of DAD on zero | −1.76 | −2.45 | −1.07 | |||
| Evolution of DAD on one | 3.39 | 2.99 | 3.79 | |||
| SD of IIV on baseline | 1.15 | 1.09 | 1.21 | |||
| SD of IIV on rate of progression | 0.013 | 0.012 | 0.015 | |||
CI confidence interval, SD standard deviation, IIV interindividual variability
Table V compares the 3 ZOI models tested. Compared with the arbitrary time functions for the boundary data in the ZOI model (model 2, Eqs. 14 and 15), the disease status model (model 1) markedly improved the objective function value (i.e., OFV decreased from −4,392 to −6,308). The model incorporating both time and disease status (model 3) provided identical OFV as model 1, and the slopes on time were not statistically significant, suggesting that disease status over time explained all the variability over time, and the arbitrary time function was not needed.
Table V.
Comparison of Parameter Estimates for Three Different Zero and One-Inflated Beta Regression (ZOI) Models in Patients with Mild to Moderate Alzheimer’s Disease
| Model 1 (OFV = −6308) | Model 2 (OFV = −4392) | Model 3 (OFV = −6308) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | 90% CI | Estimate | 90% CI | Estimate | 90% CI | ||||
| Baseline | 1.68 | 1.60 | 1.76 | 1.57 | 1.50 | 1.64 | 1.68 | 1.60 | 1.76 |
| Rate of progression | −0.012 | −0.013 | −0.011 | −0.012 | −0.013 | −0.011 | −0.012 | −0.013 | −0.011 |
| Intercept for zero (α 0) | −6.54 | −7.91 | −5.17 | −7.01 | −8.20 | −5.82 | −6.46 | −8.14 | −4.78 |
| Intercept for one (α 1) | −10.10 | −11.19 | −9.01 | −1.81 | −1.98 | −1.64 | −10.10 | −11.23 | −8.97 |
| Evolution of DAD on zero (β 0) | −1.76 | −2.45 | −1.07 | −1.78 | −2.42 | −1.14 | |||
| Evolution of DAD on one (β 1) | 3.39 | 2.99 | 3.79 | 3.38 | 2.98 | 3.78 | |||
| Slope of time on zero (κ 0) | 0.027 | 0.006 | 0.048 | −0.002 | −0.017 | 0.013 | |||
| Slope of time on one (κ 1) | −0.006 | −0.010 | −0.003 | −0.001 | −0.008 | 0.005 | |||
| SD of IIV on intercept | 1.15 | 1.09 | 1.21 | 1.06 | 1.00 | 1.12 | 1.15 | 1.09 | 1.21 |
| SD of IIV on progression rate | 0.013 | 0.012 | 0.015 | 0.013 | 0.011 | 0.014 | 0.013 | 0.012 | 0.014 |
CI confidence interval, SD standard deviation, IIV interindividual variability, OFV objective function value
The percentile VPC plots (Fig. 1) suggests that both BR and ZOI models described the longitudinal progression of DAD reasonably well, as the predicted percentiles (the 5th, 50th, and 95th) closely matched the corresponding observed percentiles. The CO model overpredicted the median profile but underpredicted the 5th percentile.
Fig. 1.
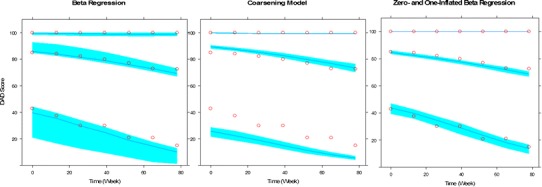
Visual predictive check for the models of disability assessment of dementia (DAD). In each panel, the upper, middle, and lower profiles indicated by the open circles represent the 95th, 50th, and 5th percentiles of the observed data. The upper, middle, and lower curves indicated by the lines are the median model-based prediction for the 95th, 50th, and 5th percentiles. The shaded areas are the 90% confidence intervals of the corresponding percentiles of the simulations based on the model
Table VI lists the prediction error between the BR, ZOI, and CO models. Compared with the BR and ZOI models, although the prediction error of the CO model appeared to be smaller at the boundaries, the CO model did not predict the nonboundary data as well as the other two models. Overall, the BR and ZOI models had almost identical prediction error, and seemed to predict the DAD data better than the CO model. This finding is consistent with the observation from the VPC.
Table VI.
Comparison of Prediction Error for the Beta Regression (BR), Coarsening Model (CO), and Zero- and One-Inflated Beta Regression (ZOI) Models in Patients with Mild to Moderate Alzheimer’s Disease
| ZOI | BR | CO | |
|---|---|---|---|
| Zero | 1.4 | 0.3 | 0.7 |
| One | 1.3 | 1.2 | 0.5 |
| Nonboundary | 23 | 24 | 27.5 |
| Overall | 25.7 | 25.5 | 28.7 |
DISCUSSION
Since bounded outcome scores are bounded within certain range, their conditional expectation function is nonlinear (22). In addition, the error distributions of bounded outcome data are heteroskedastic because their variance approaches zero as their conditional mean approaches either side of the edges (22). Therefore, regular regression models, such as normal linear or nonlinear regression models, are not suitable for such situations (12,22). In this manuscript, we compared the BR, ZOI, and CO models for such data. The simulations have shown that all the models have the ability to reasonably recover the underlying true values. In the application, we have shown that in the real-world modeling practice, VPC and prediction error can be used to identify the model that better describes a particular set of data.
Rescaling of the data is required for the BR model. It was recommended that sensitivity analysis is needed for different choices of the small constant (δ) used in the data rescaling (13). Based on the simulation scenarios where 1% and 10% boundary data was generated, we performed a sensitivity analysis to evaluate the estimation accuracy with δ = 0.01, 1 × 10−5, and 1 × 10−8. The results (Supplementary Table 1) suggest that in the current simulation scenarios, the magnitude of the bias for fixed effect parameters was less than or in the order of 20% regardless of choice of δ. Further simulations suggested that 20% bias of parameter estimates may only lead to approximately 5% or less change in the median prediction of the DAD scores over the time (data not shown). It seems that the random-effects parameters tended to be underestimated when δ was large. In addition, it is interesting to notice that when the amount of boundary data was 10%, the accuracy of some parameter estimates (i.e., θ0, Kon, and EC50) became worse with decrease in δ. Rescaling of the boundary data forces the BR model to accommodate the boundary data. A simple simulation (Appendix 4) suggests that although the smaller δ (e.g., 1 × 10−8) allowed the rescaled data to resemble the original data, the BR model estimated distribution appears to deviate markedly from the distribution of the 90% nonboundary data since it had to account for the rescaled data near the boundary during estimation (Supplementary Fig. 1). Conversely, a relatively larger δ (e.g., 0.01) better described the majority of the nonboundary data (Supplementary Fig. 2). θ0, Kon, and EC50 may be more sensitive to the deviation from the distribution of the nonboundary data than the other model parameters. Therefore, sensitivity analysis may be critical to evaluate the influence of choice of δ in real-world analysis.
It is worth mentioning that, while rescaling is required for the BR model to move the boundary data away from the edges, coarsening (i.e., grouping or rounding) of the data is needed for the CO model, where the cutoff point for coarsening process may be subjective (14). This is particularly true when the CO model is applied to the continuous bounded outcome data. Therefore, the underlying assumption for both BR and CO models is that boundary observations do not represent qualitatively different responses from the other data within the boundaries but instead are the result of finite precision of measurement. By contrast, the ZOI model separately models the boundary data and the data within the boundaries through a mixture model approach, and no data modifications are required for this approach. We developed a ZOI model by linking the probability of the 0 and 1 with the disease status (the nonboundary data). This extension allows the probability of boundary data consistent with the trend of the nonboundary data and interpretation of the covariate effects for the overall data, which is easier to understand (23).
Inverse Bateman Function (IBF) was often used to describe the placebo response that temporarily improves the disease symptom (19–21). The IBF contains two exponential expressions with an amplitude parameter that control the rate of appearance and loss of placebo response. The IBF placebo model was first attempted in the simulation study. However, it was found that the parameters of the IBF placebo model could not be accurately estimated even when the structural model was correctly specified, and the bias of these parameter estimates could be more than 10,000%. This was probably because the sampling times were not optimized for implementing the three-parameter IBF model. Therefore, we only used the two parameters characterizing amplitude (γ) and rate of placebo response development (Kon) in the simulation study.
The measurements of cognition and daily function are key outcome endpoints for clinical trials in AD (24). The DAD scale is a validated activities of daily living (ADL) measure that was designed for patients with AD and was used as one of the co-primary efficacy endpoints in phase 2/3 clinical studies (25,26).The higher total DAD score suggests better functioning. It was reported that average decline in DAD was approximately 15 points after a year, i.e., a declining rate of about 0.3 point/week (27). This result is consistent with the declining rate (0.3–0.36 points/week) estimated based on the placebo data from the phase 3 studies (Table V).
In summary, BR, ZOI, and CO models can reasonably handle the boundary data and may be sensible modeling choices for bounded outcome scores with data at the boundaries. The BR and ZOI models appeared to predict the longitudinal progression of DAD better than the CO model in the application to the data from the clinical studies, while the BR and ZOI models had almost identical predictive performance in this example.
Electronic supplementary material
(DOCX 20 kb)
(DOCX 21 kb)
(DOCX 17.4 kb)
ACKNOWLEDGMENTS
There is no conflict of interest. Steven Xu, Mahesh Samtani, and Partha Nandy are employees of Johnson & Johnson Pharmaceutical Research & Development. Min Yuan is an associate professor at University of Science and Technology of China and is partially supported by the National Science Foundation of China (NSFC), grant no. 11201452 and no. 11271346.
APPENDIX 1
Table VII.
A Sample NONMEM Code for the Mixed-Effects Boundary-Inflated Beta Regression Model Is Presented Below

APPENDIX 2
Table VIII.
A Sample NONMEM Code for the Mixed-Effects Coarsening Model Is Presented Below

APPENDIX 3
Table IX.
A Sample NONMEM Code (28) for the Beta Regression Model is Presented Below

APPENDIX 4
Nine hundred (900) random data were sampled from a beta distribution, beta(95, 5). Then, 100 of 1’s were added to the data as boundary data. BR was performed to re-estimate the parameters of the beta distribution based on the combined data after rescaling with a small δ. The density of the original data, rescaled data, and re-estimated distribution are shown in Supplementary Figs. 1 (δ = 1e−8) and 2 (δ = 1e−2).
REFERENCES
- 1.Rosen WG, Mohs RC, Davis KL. A new rating scale for Alzheimer's disease. Am J Psychiatry. 1984;141(11):1356–64. doi: 10.1176/ajp.141.11.1356. [DOI] [PubMed] [Google Scholar]
- 2.Gelinas I, et al. Development of a functional measure for persons with Alzheimer's disease: the disability assessment for dementia. Am J Occup Ther. 1999;53(5):471–81. doi: 10.5014/ajot.53.5.471. [DOI] [PubMed] [Google Scholar]
- 3.Folstein MF, Folstein SE, McHugh PR. “Mini-mental state”. A practical method for grading the cognitive state of patients for the clinician. J Psychiatr Res. 1975;12(3):189–98. doi: 10.1016/0022-3956(75)90026-6. [DOI] [PubMed] [Google Scholar]
- 4.Tekin S, et al. Activities of daily living in Alzheimer's disease: neuropsychiatric, cognitive, and medical illness influences. Am J Geriatr Psychiatry. 2001;9(1):81–6. doi: 10.1097/00019442-200102000-00013. [DOI] [PubMed] [Google Scholar]
- 5.Wewers ME, Lowe NK. A critical review of visual analogue scales in the measurement of clinical phenomena. Res Nurs Health. 1990;13(4):227–36. doi: 10.1002/nur.4770130405. [DOI] [PubMed] [Google Scholar]
- 6.Swearingen CJ, Melguizo Castro MS, Bursac Z. Modeling percentage outcomes: the %beta_regression macro. SAS®Global Forum Proceedings. 2011;335:1–12.
- 7.Smithson M, Verkuilen J. A better lemon squeezer? Maximum-likelihood regression with beta-distributed dependent variables. Psychol Methods. 2006;11(1):54–71. doi: 10.1037/1082-989X.11.1.54. [DOI] [PubMed] [Google Scholar]
- 8.Cribari-Neto F, Zeileis A. Beta Regression in R. J Stat Softw. 2010;34(2):1–24. [Google Scholar]
- 9.Ferrari SP, Cribari-Neto F. Beta regression for modelling rates and proportions. J Appl Stat. 2004;31(7):799–815. doi: 10.1080/0266476042000214501. [DOI] [Google Scholar]
- 10.Ospina R, Ferrari SP. Inflated beta distributions. Stat Pap. 2010;51:111–26. doi: 10.1007/s00362-008-0125-4. [DOI] [Google Scholar]
- 11.Ospina R, Ferrari SP. A general class of zero-or-one inflated beta regression models. Comput Stat Data Anal. 2011;56(6):1609–23. doi: 10.1016/j.csda.2011.10.005. [DOI] [Google Scholar]
- 12.Ospina R, Ferrari SP. A general class of zero-or-one inflated beta regression models. Comput Stat Data Anal. 2012;56(6):1609–23. doi: 10.1016/j.csda.2011.10.005. [DOI] [Google Scholar]
- 13.Verkuilen J, Smithson M. Mixed and mixture regression models for continuous bounded responses using the beta distribution. J Educ Behav Stat. 2012;37(1):82–113. doi: 10.3102/1076998610396895. [DOI] [Google Scholar]
- 14.Molas M, Lesaffre E. A comparison of three random effects approaches to analyze repeated bounded outcome scores with an application in a stroke revalidation study. Stat Med. 2008;27(30):6612–33. doi: 10.1002/sim.3432. [DOI] [PubMed] [Google Scholar]
- 15.Ito K, Hutmacher M, Corrigan B. Modeling of Functional Assessment Questionnaire (FAQ) as continuous bounded data from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database [Poster]. American Conference on Pharmacometrics. In American Conference on Pharmacometrics. San Diego; 2011.
- 16.Ito K, Hutmacher MM, Corrigan BW. Modeling of Functional Assessment Questionnaire (FAQ) as continuous bounded data from the ADNI database. J Pharmacokinet Pharmacodyn. 2012;39(6):601–18. doi: 10.1007/s10928-012-9271-3. [DOI] [PubMed] [Google Scholar]
- 17.Hutmacher MM, et al. Estimating transformations for repeated measures modeling of continuous bounded outcome data. Stat Med. 2012;30(9):935–49. doi: 10.1002/sim.4155. [DOI] [PubMed] [Google Scholar]
- 18.Hu C, et al. Bounded outcome score modeling: application to treating psoriasis with ustekinumab. J Pharmacokinet Pharmacodyn. 2011;38(4):497–517. doi: 10.1007/s10928-011-9205-5. [DOI] [PubMed] [Google Scholar]
- 19.Ito K, et al. Disease progression meta-analysis model in Alzheimer's disease. Alzheimers Dement. 2010;6(1):39–53. doi: 10.1016/j.jalz.2009.05.665. [DOI] [PubMed] [Google Scholar]
- 20.Holford NH, Peace KE. Results and validation of a population pharmacodynamic model for cognitive effects in Alzheimer patients treated with tacrine. Proc Natl Acad Sci U S A. 1992;89(23):11471–5. doi: 10.1073/pnas.89.23.11471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Holford NH, Peace KE. Methodologic aspects of a population pharmacodynamic model for cognitive effects in Alzheimer patients treated with tacrine. Proc Natl Acad Sci U S A. 1992;89(23):11466–70. doi: 10.1073/pnas.89.23.11466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kieschnick R, McCullough BD. Regression analysis of variates observed on (0, 1): percentages, proportions and fractions. Stat Model. 2003;3:193–213. doi: 10.1191/1471082X03st053oa. [DOI] [Google Scholar]
- 23.Albert JM, Wang W, Nelson S. Estimating overall exposure effects for zero-inflated regression models with application to dental caries. Stat Methods Med Res. 2011 [DOI] [PMC free article] [PubMed]
- 24.Feldman H, Sauter A, Donald A, Gelinas I, Gauthier S, Torfs KA, et al. The disability assessment for dementia scale: a 12-month study of functional ability in mild to moderate severity Alzheimer disease. Alzheimer Dis Assoc Disord. 2001;15(2):89–95. doi: 10.1097/00002093-200104000-00008. [DOI] [PubMed] [Google Scholar]
- 25.Salloway S, Sperling R, Fox NC, et al. Two phase 3 trials of bapineuzumab in mild-to-moderate Alzheimer's disease. N Engl J Med. 2014;370:322–33. doi: 10.1056/NEJMoa1304839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Salloway S, Sperling R, Gilman S, Fox NC, Blennow K, Raskind M, et al. A phase 2 multiple ascending dose trial of bapineuzumab in mild to moderate Alzheimer disease. Neurology. 2009;73(24):2061–70. doi: 10.1212/WNL.0b013e3181c67808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Suh GH, Ju YS, Yeon BK, Shah A. A longitudinal study of Alzheimer's disease: rates of cognitive and functional decline. Int J Geriatr Psychiatr. 2004;19(9):817–24. doi: 10.1002/gps.1168. [DOI] [PubMed] [Google Scholar]
- 28.Xu XS, Samtani MN, Dunne A, Nandy P, Vermeulen A, Ridder F. Mixed-effects beta regression for modeling continuous bounded outcome scores using NONMEM when data are not on the boundaries. J Pharmacokinet Pharmacodyn. 2013;1–8 [DOI] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX 20 kb)
(DOCX 21 kb)
(DOCX 17.4 kb)


