Predicting Pediatric Age-Matched Weight and Body Mass Index

Abstract

The empirical scaling from adult to pediatric using allometric size adjustments based on body weight continued to be the mainstream method for pediatric dose selection. Due to the flexibility of a polynomial function to conform to the data trend, an empirical function for simulating age-matched weight and body mass index by gender in the pediatric population is developed by using a polynomial function and a constant coefficient to describe the interindividual variability in weight. A polynomial of up to fifth order sufficiently described the pediatric data from the Center for Disease Control (CDC) and the World Health Organization (WHO). The coefficients of variation to describe the variability were within 17%. The percentages of the CDC simulated weights for pediatrics between 0 and 5 years that fell outside the WHO 90% and 95% confidence boundaries were well within the expected percentage values, indicating that the CDC dataset can be used to substitute for the WHO dataset for the purpose of pediatric drug development. To illustrate the utility of this empirical function, the CDC-based age-matched weights were simulated and were used in the prediction of the concentration–time profiles of tenofovir in children based on a population pharmacokinetic model whose parameters were allometrically scaled. We have shown that the resulting 95% prediction interval of tenofovir in newborn to 5 years of age was almost identical whether the weights were simulated based on WHO or CDC dataset. The approach is simple and is broadly applicable in adjusting for pediatric dosages using allometry.

Electronic supplementary material

The online version of this article (doi:10.1208/s12248-014-9657-9) contains supplementary material, which is available to authorized users.

INTRODUCTION

Allometric size adjustments provide a mechanistic, physiologically based approach that integrates physiological parameters like blood flows and weight of organs (1). The discussion of allometry here is primarily based on the mathematical power law expression $\left(Y=a\cdot {\left(\frac{\mathrm{weight}}{\mathrm{median}}\right)}^b\right)$, where Y is the parameter of interest, weight refers to body weight normalized by the median, a is the median weight-centered parameter value, and b is the allometric exponent). Size is the primary covariate and is frequently referenced to a 70-kg person using the allometric exponent of 0.75 for clearance and 1 for volume (2). The use of these coefficients is supported by fractal geometric concepts and observations from diverse areas in biology (3). This approach was shown to perform poorly for interspecies scaling, even after several types of correction (4). One of the main limitations in the extrapolation from one species to another is when significant differences in metabolic pathways and enzyme activities exist. For intraspecies scaling, however, it is expected to work much better given that organ sizes increase proportionately over age, and it is not highly confounded by differences in the body composition and organ functionalities (5–8). The extrapolation from the adult data to pediatric takes into account size differences but does not account for maturation processes in enzymatic activities or ontology, which are other sources of pharmacokinetic variabilities (9). For example, the hepatic metabolic capacity in neonate is different from that of a 5-year-old child. Some enzymes are present at birth (CYP3A7, UGT), whereas others develop over time (2E1, 2D6, 3A4, and 2C9) (10). Nonlinear allometric size adjustments using fixed allometric coefficients have been used repeatedly in pediatric dose extrapolation (5,11–13). Body weight is the primary variable used for dosing drug in children (10,14). When allometric size scaling is applied in population pharmacokinetic for extrapolation to pediatric population, the current practice is to simulate age-matched weights from individual table values which often assumed uniform distribution for specific weight range for an age interval. This “square box” approach could potentially allocate a larger weight of older children to a younger individual and vice versa (e.g., 15 kg for a 1-year-old). The resulting weights often do not reflect the true age–weight relationship in the pediatric population. Sumpter and Holford previously developed a Hill-type equation to describe the relationship between weight and postmenstrual age from neonates to adults (15). Their model was rather quite complex, and its application in pharmaceutical drug development was also limited. A continuous function across an age range would be more efficient and accurate, and a polynomial function is well suited for this purpose.

Two major sources of pediatric growth charts are the World Health Organization (WHO) and the Center for Disease Control (CDC) (16,17). The CDC growth chart was criticized for leaning on the heavier side such that infants would be more likely to be considered underweight and less likely as overweight (18,19). This is particularly relevant at a time of increasing awareness of the problems of obesity. The WHO published a new growth chart from children who were under 5 years of age from six countries including Brazil, Ghana, India, Norway, Oman, and the USA (specifically California) (16). The data were more representative of the growth pattern of pediatrics around the world. These two data sources were used to develop polynomial functions to characterize weight–age relationship in the pediatric population.

MATERIALS AND METHODS

Model Development

The age-matched weights and body mass index in pediatric male and female from newborn to 20 years reported by the CDC and from 0 to 5 years collected by the WHO (20) were used to develop polynomial functions to describe their relationship.

The polynomial function f(x) of up to the eighth order was evaluated:

$$f\left(x\right)=A{x}^8+B{x}^7+C{x}^6+D{x}^5+E{x}^4+F{x}^3+G{x}^2+\mathit{Hx}+I$$ 1

where A:I are coefficients of the polynomial function. The above function was fitted to the median body weight and body mass index (BMI) as a function of age and modeled separately for males and females, as well as for dataset from the CDC and WHO. The CDC dataset had the data from 0 to 2 years and from 2 to 20 years truncated. The model for the CDC age–weight relationship was developed based on the truncated dataset. The Akaike information criterion (AIC) and the combination of visual inspection of the graphical outputs were used to evaluate which polynomial order was most suitable to describe the median dataset.

Once the polynomial function for the median dataset was determined, the 5th and 95th percentiles of the body weight and BMI were used to determine the coefficient of variation (CV%) that characterizes the interindividual variability such that:

$$\begin{array}{l}5\mathrm{th}\mathrm{percentile}\\ =\left(A{x}^8+B{x}^7+C{x}^6+D{x}^5+E{x}^4+F{x}^3+G{x}^2+\mathit{Hx}+I\right)\\ \times exp\left(-1.644854\epsilon \right)\end{array}$$ 2

$$\begin{array}{l}95\mathrm{th}\mathrm{percentile}\\ =\left(A{x}^8+B{x}^7+C{x}^6+D{x}^5+E{x}^4+F{x}^3+G{x}^2+\mathit{Hx}+I\right)\\ \times exp\left(1.644854\epsilon \right)\end{array}$$ 3

where the critical value 1.644854 is the inverse of the standard normal cumulative distribution. The parameters A:I are fixed to the previously determined coefficients. The ε, which is the CV for the interindividual variability, is evaluated by the nonlinear least square algorithm (nls). The resulting model-generated results from Eq. 1 through 3 were compared to the median, 5th, and 95th percentiles of the CDC and WHO datasets using chi-squared test.

The final model was further evaluated by simulating 10,000 individuals in each group and sampling (with replacement) from the set of age values from the CDC and WHO datasets. The median, 2.5th, and 97.5th percentiles from the simulation were compared graphically to the reported percentiles from the two agencies. The percentages of the simulated body weight outside the specific age–weight boundaries (90% and 95% CI) of that reported by the two agencies were then determined programmatically.

To evaluate whether the pediatric data from the WHO and CDC for ages between 0 and 5 years are similar enough, the reported median, 3rd, 5th, 95th, and 97th percentiles were compared graphically and also by evaluating the percentage of simulated individual weight between the ages of 0 and 5 years using the polynomial model for one agency that fall outside the specific age–weight boundaries (90% and 95% CI) of the other agency and vice versa.

The adequacy of the model to describe the data was determined by comparing visually how well the predicted 95% prediction interval approximated the reported 95% CI of the data from the two agencies. Assuming that the model is adequate, the 95% prediction interval of the simulated datasets should be close to these bands. The final polynomial models for the CDC dataset were used to randomly simulate age-matched weight data from a total of about 3,000 children and adolescents to be used in the allometric scaling of select population pharmacokinetic model of tenofovir from the literature (21).

Population Pharmacokinetic Model of Tenofovir

The two-compartment model described for tenofovir (21) had the following pharmacokinetic parameters: apparent oral clearance (CL/F), apparent intercompartmental clearance (Q/F), apparent volume of distribution of the central compartment (V_c/F), apparent volume of distribution of the peripheral compartment (V_p/F), and absorption rate constant (k_a). The relative bioavailability term (F) was fixed to 1. Exponential interindividual variability terms were included in the pharmacokinetic parameters CL/F and V_c/F. Allometric scaling by weight centered on 70 kg was associated with CL/F, V_c/F, and V_p/F, using the power coefficient of 0.75 for the clearance and 1 for the volume parameters. The parameter values were 59.8 L/h for CL/F, 92.8 L/h for Q/F, 386 L for V_c/F, 666 L for V_p/F, and 0.43 h⁻¹ for k_a. The interindividual variability estimates, ω, were 0.48 for ω_CL/F and 1.39 for ω_Vc/F, and the covariance between CL/F and V_c/F was 0.73. The simulation (n = 1,000) was based on pediatric age between 5 and 18 years which was the age range of the 93 pediatric patients in the original study, assuming 50% males and 50% females. The dosage used in the simulation for pediatrics ages 5 to 18 years followed their recommendation wherein children without lopinavir and ritonavir combination should receive 150, 225, and 300 mg tenofovir if their weights are 20 to 30, 30 to 40, and over 40 kg, respectively. The age-matched weights for this population (5 to 18 years) were simulated using the polynomial functions developed for the CDC dataset.

We also simulated tenofovir profiles for pediatrics less than 5 years of age using the following dosage regimens assuming oral tablet formulation: 80, 100, 120, and 140 mg for <12 kg body weight, 12 kg ≤ weight < 14 kg, 14 kg ≤ weight <17 kg, and 17 kg ≤ weight < 20 kg, respectively. The polynomial functions for the CDC and WHO dataset for newborn to 5 years were used to simulate age-matched weights, separately with 1,000 virtual individuals for each group.

Simulation of Sumpter and Holford Model

The empirical model using Eq. 1 of Sumpter and Holford (15) was used to simulate 10,000 age-matched weights in pediatric population (gestational age between 0 and 18 years). The interindividual variability was characterized by an exponential model. A graphical approach similar to one previously described was utilized to evaluate the suitability of their model to describe the CDC dataset.

Software

The evaluation of polynomial function was performed using the general linear model ; the test of the appropriate order of polynomial was evaluated using the 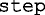function which gave the AIC values associated with the polynomial order. The determination of the CV for the exponential error model associated with the polynomial function was accomplished using the nonlinear least square function 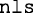. The model-predicted age-matched data and the percentiles from the two agencies were compared using the chi-squared test (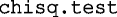). The fitting and evaluation algorithms and the 10,000 simulations to determine the 95% prediction intervals including the simulations based on equations from Sumpter and Holford (15) were done in R 3.1.0.

The 1,000 individual profiles of tenofovir were simulated using the population pharmacokinetic model of tenofovir from the literature (21). The simulation was accomplished using NONMEM (version VII.2) and NM-TRAN preprocessor (ICON Development Solutions, Ellicott City, MD). The subroutine was ADVAN4 TRANS4. The models were run using PerlspeaksNONMEM 3.5.5 running ActivePerl 5.12 (ActiveState, Vancouver, Canada) and G-fortran 95.

RESULTS

The polynomial functions to simulate the age-matched weight and BMI are listed in Table I, wherein the coefficients of the polynomial function, relative standard error, the CV%, AIC values, and percent of the simulated weights outside the 90% and 95% CI of the reported data for each group are displayed. The fourth and fifth order polynomial equations were sufficient to describe the age–weight relationship in pediatrics by evaluating graphically the simulated data between 0 and 20 years of age. The median and specific percentiles of age-matched weight data in male and female subjects between the ages of 0 and 20 years reported by the CDC are plotted in Fig. 1. Figure 2 shows the simulations for the WHO dataset for newborn to 5-year-old children. In the CDC dataset, we noticed that the polynomial function established for the expanded age group had a tendency to simulate larger weights in the 0- to 2-year age group. Alternatively, when we used a higher order polynomial equation, the new model fitted the lower age group well, but there were larger deviations in the upper age range. For this reason, we used the truncated datasets (0–2 and 2–20 years) and developed separate polynomial functions for each dataset. The exponential error model best characterized the interindividual variability since the distribution of body weight above the median was larger than that below the median. The additive error model which assumed identical distributions above and below the median was deemed unsuitable to describe the interindividual variability. The proportional error model was not attempted since it is equivalent to a first-order geometric series expansion of an exponential model structure. Given that the ε was related to the polynomial function by an exponential relationship, the standard deviations were, in fact, constant CV in the linear scale. In the CDC dataset, we noticed that the CVs were smaller in the younger age group with values approximately 11% to 12%, whereas the 5- to 20-year age groups were between 17 and 18%; thus, a separate CV was evaluated for the age–weight relationship for newborn to 5 years. The magnitude of the CV% values was consistent in the ≤5-year age group and the 0–2-year age group of the CDC dataset, as well as the 0–5-year age group of the WHO dataset. The simulated age–weight data are summarized by the 95% prediction interval, represented as gray lines in Figs. 1 and 2. The polynomial equations adequately described the age-matched weight data, given that the 95% prediction intervals as a function of age of the simulated data were within the 95% CI of the original CDC and WHO datasets (Figs. 1 and 2). In addition, the percent of the simulated dataset that fell outside the 90% and 95% confidence boundaries closely matched the expected values (Table I).

Table I.

Polynomial Coefficients, Relative Standard Error, Constant Coefficient, Akaike Information Criterion of the Polynomial Function of the Age-Matched Weight or BMI, and Percent of Simulated Individuals’ Weights or BMI Outside the 90 and 95% Confidence Bands of the CDC and WHO Datasets by Gender and Age Group

Gender	Polynomial coefficients						AIC	CV%	% outside
	x 5	x 4	x 3	x 2	x 1	x 0		ε a	(90% CI, 95% CI)
Body weight
Age range 2–20 years, CDC
Female	2.09 × 10−4 (2.3%)	−0.01153 (2.1%)	0.2161 (2.0%)	−1.571 (2.1%)	6.616 (1.6%)	4.265 (2.6%)	−597.54	ε age < 5 (12) ε age ≥ 5 (18)	9.9%, 6.2%
Male	0	−1.99 × 10−3 (1.7%)	0.07245 (1.9%)	−0.728 (2.5%)	4.720 (1.9%)	5.472 (2.3%)	−437.89	ε age < 5 (11) ε age ≥ 5 (17)	9.6%, 5.5%
Age range 0–2 years, CDC
Female	0	−0.1214 (1.6%)	1.208 (1.2%)	−4.571 (0.6%)	9.6 (0.2%)	3.41 (0.1%)	−377.3	(12)	9.7%, 6.0%
Male	0	−0.1774 (2.3%)	1.691 (1.5%)	−6.052 (0.8%)	11.314 (0.3%)	3.55 (0.2%)	−338.25	(11)	9.1%, 5.4%
Age range 0–5 years, WHO
Female	0.034 (9.7%)	−0.4883 (8.6%)	2.617 (7.2%)	−6.522 (5.7%)	9.885 (2.9%)	3.524 (2.0%)	−331.10	(12)	11%, 7%
Male	0.04 (10.7%)	−0.5691 (9.5%)	3.041 (8.0%)	−7.612 (6.2%)	11.127 (3.4%)	3.758 (2.4%)	−294.18	(11)	11%, 7%
Body mass index
Age range 2–20 years, CDC
Female	0	0	−0.0043 (2.0%)	0.1609 (0.2%)	−1.3263 (0.3%)	19.169 (0.4%)	−961.17	ε 2 ≤ age < 6 (8) ε 6 ≤ age < 8 (11) ε 8 ≤ age ≤ 20 (17)	9.5%, 4.6%
Male	0	0	−0.003 (1.9%)	0.1317 (1.4%)	−1.2002 (1.7%)	19.332 (0.3%)	−1,003.65	ε 2 ≤ age < 6 (6) ε 6 ≤ age < 8 (10) ε 8 ≤ age ≤ 20 (14)	9.1%, 5.0%

CV coefficient of variation, CDC Center for Disease Control, WHO World Health Organization, AIC Akaike information criterion, CI confidence interval

^aLog-normal distribution assumed

Fig. 1.

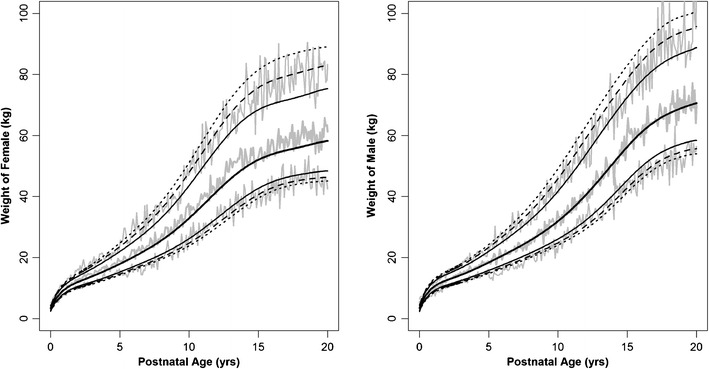
Age-matched weight in male and female infants, children, and adolescents between newborn and 20 years of age. The middle gray line represents the median and the outer gray lines are 95% prediction interval of the 10,000 simulated weights by the age. The CDC data are represented by black lines: median; , 80% confidence interval (CI); , 90% CI; , 95% CI of CDC growth charts. Source data from Center for Disease Control

Fig. 2.

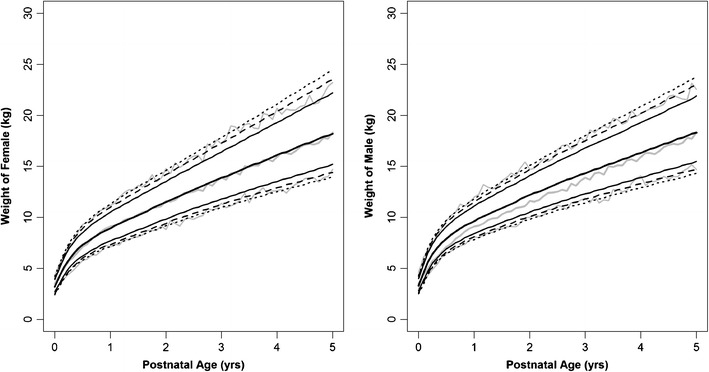
Age-matched weight in male and female pediatrics from newborn to 5 years. The middle gray line represents the median and the outer gray lines are 95% prediction interval of the 10,000 simulated weights by the age. The WHO data are represented by black lines: , median; , 80% confidence interval (CI); , 90% CI; , 95% CI of WHO growth charts. Source data from World Health Organization

To determine whether one could use the CDC dataset in lieu of the WHO dataset, we evaluated the percentage of the simulated pediatric weights for one agency that fell outside the confidence boundary of the other agency (Table II). The percentages of simulated pediatric (0–5 years) male weights using the polynomial function for the CDC male dataset that falls outside the WHO confidence boundaries (90% and 95% CI) were 9.1% and 5.6%, respectively; for female pediatric weights, these percentages were 8.4% and 4.9%, respectively. The major deviation was in pediatric male weights simulated from the polynomial function based on the WHO dataset when compared to the CDC confidence bounds with percentage values of 18.8% and 13.6%, respectively. The simulated WHO female pediatric weights were also within the expected percentages that fell outside the confidence limits at 9.2% and 5.5%, respectively.

Table II.

Comparison of CDC Simulated Dataset for 0 to 5 years of Age to WHO Confidence Boundaries and Vice Versa

Description	% outside (90% CI, 95% CI)
Percentage of CDC simulated pediatric male weights outside the WHO CI bounds	(9.1, 5.6)
Percentage of CDC simulated pediatric female weights outside the WHO CI bounds	(8.4, 4.9)
Percentage of WHO simulated pediatric male weights outside the CDC CI bounds	(18.8, 13.6)
Percentage of WHO simulated pediatric female weights outside the CDC CI bounds	(9.2, 5.5)

CDC Center for Disease Control, WHO World Health Organization, CI confidence interval

The simulations for the age-matched BMI in pediatrics between 2 and 20 years are shown in Fig. 3; the polynomial coefficients, distribution parameters, and precision are also listed in Table I. The 95% prediction intervals of the simulated BMI were contained within the 95% CI of the surveyed data from the CDC. Due to the asymmetric distribution of BMI above and below the median that could not be characterized by the exponential error model assuming constant CV, the median was shifted slightly upwards to accommodate for a symmetric log-linear distribution, such that the distances from the median to the 2.5th or the 97.5th percentiles are identical in the log scale. Thus, the gray line representing the median of the simulated BMI is slightly larger than the median of the CDC dataset. This approach significantly simplifies the simulation process.

Fig. 3.

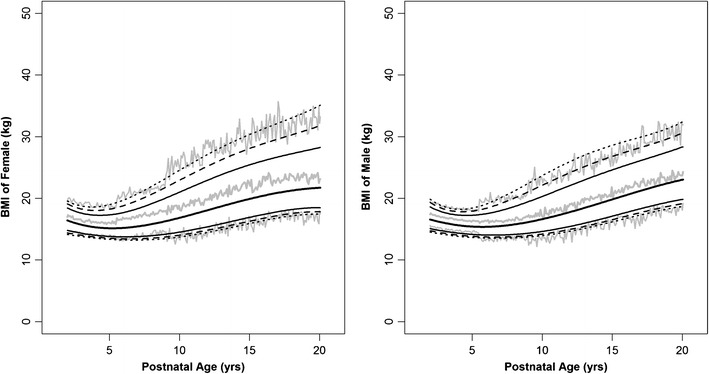
Age-matched body mass index in male and female children and adolescents between 2 and 20 years. The middle gray line represents the median and the outer gray lines are 95% prediction interval of the 10,000 simulated weights by the age. The CDC data are represented by black lines: , median; , 80% confidence interval (CI); , 90% CI; , 95% CI of CDC growth charts. Source data from Center for Disease Control

To evaluate the predictive utility of these polynomial functions, the population pharmacokinetic model of tenofovir in pediatrics from Bouazza et al. (21) was simulated. The dosage used in the simulation followed their recommendation wherein children without lopinavir and ritonavir combination should receive 150, 225, and 300 mg tenofovir if their weights are 20 to 30, 30 to 40, and over 40 kg, respectively. We further simulated tenofovir profiles for dosage regimens for newborn to 5 years of age using the weight based on the polynomial functions developed for both the CDC and WHO dataset: 80 mg for less than 12 kg body weight, 100 mg between 12 and 14 kg, 120 mg between 14 and 17 kg, and 140 mg between 17 and 20 kg. The pharmacokinetic was described by a two-compartment model with first-order absorption parameterized on CL/F, V_c/F, V_p/F, Q/F, and k_a with population values (interindividual variability) of 59.8 L/h (0.48), 386 L (1.39), 666 L, 92.8 L/h, and 0.43 h⁻¹, respectively. The 95% prediction interval and median of the simulated profiles for pediatric ages 5 to 19 years are represented by dashed line and for newborn to 5 years by the dotted line (for CDC-based weights) and shaded area (for WHO-based weights). The boundaries contained majority of the actual data, as shown in Fig. 4. This figure also showed that the tenofovir profiles overlapped closely whether the weights were simulated from either the CDC or the WHO datasets for pediatrics ages 0 to 5 years.

Fig. 4.

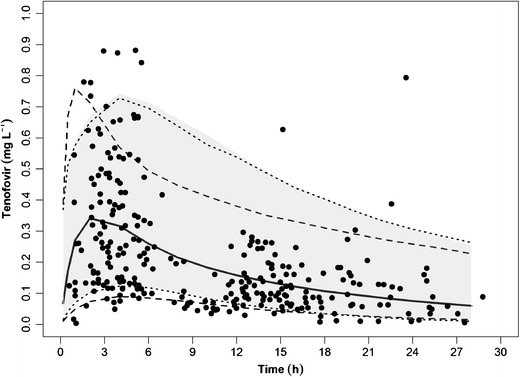
Simulation of tenofovir concentrations in 1,000 pediatric patients between the age of 5 and 19 years, showing 95% prediction intervals (dashed lines) and median (solid line) based on population pharmacokinetic model of tenofovir. The dotted lines and shaded areas are 95% prediction intervals for newborn to 5 years based on weights simulated from the CDC and WHO, respectively. Actual data from Bouazza et al. (21) are represented by filled circles

DISCUSSIONS

Sumpter and Holford previously used a Hill-type function to describe body weight and postmenstrual age relationship in premature neonates, infants, children, and adults (15). However, with this approach using the CDC and WHO datasets and adding 9 months to adjust from postnatal age to postmenstrual age, their equation did not quite capture the overall variability of the CDC dataset (Fig. 5). Additionally, their simulated weights had an upward tendency in the older adolescents, whereas the distributions in the younger pediatrics tended to be overly large. This prompted us to utilize a simpler approach using polynomials to establish an empirical formulation for the purpose of simulating age-matched weight and body mass index in pediatric population. The utility of an empirical function and distribution for prediction of weight by age has important applications in designing clinical trials for studying drug exposure and effect in children. We note that the body weight and BMI are a measure of size scaling. Other physiologically based assumptions will be required to account for maturity especially in the younger age groups. We have also shown that using the polynomial function to simulate age-matched weights in pediatric population, the population pharmacokinetic model of tenofovir in the literature predicted well the observed concentration–time course in the pediatric population.

Fig. 5.

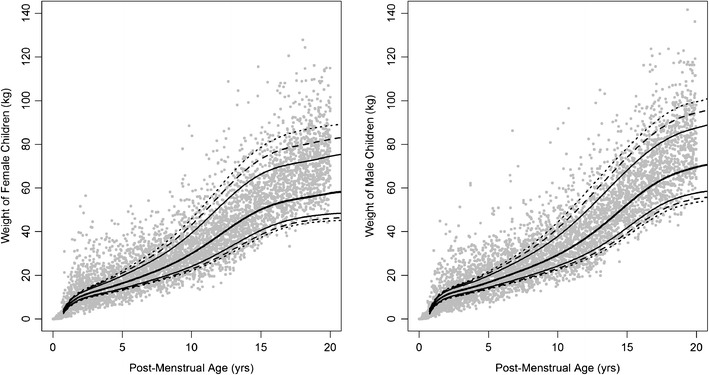
Age-matched weight in male and female pediatrics 0 to 18 years in age based on equations from Sumpter and Holford (15). Points represent simulated age-matched weight. The CDC data are represented by black lines: , median; , 80% confidence interval (CI); , 90% CI; , 95% CI of CDC growth charts. Source data from Center for Disease Control

The empirical relationships of 0 to 20 years of age with body weight and body mass index were established using polynomial equations, since polynomials are known for their versatility. The log-normal distribution best characterized the interindividual variability in body weight and BMI distribution. The two population references from the CDC and WHO have been used in many normalization of adult dose according to age and body weight for pediatric dosage prediction in the literature (22,23). The CDC dataset tended to have larger body weights between 0.5- and 2.5-year-old children than the WHO dataset (see Supplemental Figure). We have determined that the percentages of the simulated weights of one agency that were outside the 90% and 95% confidence limit of the other agency were within the expected values, except for the simulated WHO male pediatric weights against the CDC confidence bounds. The result suggests that the simulated CDC age-matched weights in pediatric population can be used in lieu of the WHO pediatric body weight. In addition, we have shown that the resulting 95% prediction intervals of tenofovir in newborn to 5 years of age were very close and almost identical whether the weights were simulated based on WHO or CDC dataset. The results are important in the sense that the CDC and WHO pediatric weights are interchangeable from modeling and simulation perspectives in support of pediatric drug development.