Free-Energy Landscape and Characteristic Forces for the Initiation of DNA Unzipping

Abstract

DNA unzipping, the separation of its double helix into single strands, is crucial in modulating a host of genetic processes. Although the large-scale separation of double-stranded DNA has been studied with a variety of theoretical and experimental techniques, the minute details of the very first steps of unzipping are still unclear. Here, we use atomistic molecular-dynamics simulations, coarse-grained simulations, and a statistical-mechanical model to study the initiation of DNA unzipping by an external force. Calculation of the potential of mean force profiles for the initial separation of the first few terminal basepairs in a DNA oligomer revealed that forces ranging between 130 and 230 pN are needed to disrupt the first basepair, and these values are an order of magnitude larger than those needed to disrupt basepairs in partially unzipped DNA. The force peak has an echo of ∼50 pN at the distance that unzips the second basepair. We show that the high peak needed to initiate unzipping derives from a free-energy basin that is distinct from the basins of subsequent basepairs because of entropic contributions, and we highlight the microscopic origin of the peak. To our knowledge, our results suggest a new window of exploration for single-molecule experiments.

Introduction

Many essential genetic processes, such as replication, transcription, recombination, and DNA repair, involve unzipping of double-stranded DNA (dsDNA) by proteins that disrupt the hydrogen (H)-bonds between complementary bases on opposite strands (1). A detailed understanding of the nature of DNA mechanical separation dynamics, and of the energetics and forces for the conformations that occur during unzipping, is also relevant for single-molecule DNA sequencing. High-resolution measurements of the forces may lead to novel ways to sequence DNA by enabling investigators to read the base identities from the distinct signatures that result from separating the different types of basepairs (2). Moreover, single-molecule studies in which DNA is being pulled via atomic force microscopy (AFM) (3) or by optical (4) or magnetic (5) tweezers, or is unzipped through nanometer-sized pores (6) are particularly useful for gauging the mechanical response to external stimuli. Such insights into DNA elasticity (7) and the resilience of its double strand to unzipping can provide useful information for designing nanomechanical devices constructed of DNA (8) and building molecularly engineered DNA scaffolds for molecular-size electronics or for crystalline-state biomolecules that otherwise would be impossible to crystallize (9).

Recent experiments performed by pulling dsDNA apart with a constant force (10–14) showed that dsDNA separates into single-stranded DNA (ssDNA) when the applied force exceeds a critical value F_c ∼ 12 pN. Moreover, for forces near F_c, the dynamics of the unzipping process is highly irregular. Rather than a smooth time evolution, the position of the unzipping fork progresses through a series of long pauses separated by rapid bursts of unzipping (11). However, because of their low spatial resolution, single-molecule techniques cannot yet reveal the first steps of opening a fully basepaired double helix from a blunt end, e.g., the opening of the terminal basepair. For AFM, for example, typical force constants of the cantilever are in the 10–20 pN/Å range, which, using equipartition arguments, yields fluctuations on the scale of several angstroms, and the best resolution that can be reached via AFM is currently estimated to be on the order of 10 basepairs (15–17). As a consequence, one cannot straightforwardly unzip only the first few basepairs of the sequence in current pulling experiments.

The opening of terminal basepairs in blunt-end duplexes is important for initiating DNA melting (18,19). It is also a biologically important step in the action of nucleic acid processing enzymes (20) and in nucleic acid end recognition by retroviral integrases (21). Moreover, the DNA replication process is a good example of instances in which dsDNA must be unzipped mechanically by polymerases (22). Concomitantly with the understanding that terminal basepair opening is biologically relevant, it is important to note the fact (as established experimentally and computationally) that the first basepair frays naturally and exists in a relatively fast equilibrium between paired and unpaired or frayed states. Although this equilibrium is fast compared with the timescale of the pulling apparatus that could be used in single-molecule experiments to probe the unzipping, it is slow relative to the capabilities of all-atom molecular-dynamics (MD) simulations. The fraying of first basepairs has been studied in NMR experiments (23,24), which provided estimates for the equilibrium and kinetic constants for the paired-frayed conformational transition. Thermodynamic data were consistent with the view that frayed states are unfavorable enthalpically due to loss of stacking stabilization, but are stable entropically. The experimental estimates for the populations of the frayed state were in the 10–30% range for cytosine-guanine (CG) pairs and up to 50% for adenine-thymine (AT) pairs, with ample variance depending on experimental conditions. A recent simulation study (19) additionally provided atomistic details of terminal basepair fraying. The kinetics of fraying has been also investigated, with experimental reports concluding that this process is faster than 1 ms (25), and a computational study of multiple free basepair spontaneous stacking/unstacking in aqueous solution at 310 K showing that transitions occurred on a timescale of 10 ns (26).

In the theoretical arena, the fundamentals of DNA denaturation have been studied since the 1960s, and several generations of models for DNA unzipping have been developed (27–31). Arguably the most popular ones are the Peyrard-Bishop (PB) model (32) and its extension, the Peyrard-Bishop-Dauxois (PBD) model (33), which includes an extra term in stacking to better reproduce experimental data. These models have been used extensively to describe DNA thermal denaturation (34) and the dynamics of pulling DNA by an external force (35). Other models have been developed to investigate quantitatively the difference between DNA unzipping by force and thermal or fluctuation-induced melting of dsDNA (28), and to study interactions between two single DNA strands (30).

Although these modeling approaches have revealed the fundamental statistical mechanical picture, they are not detailed enough to capture all of the intricacies of unzipping. An important advance was recently made via the semi-microscopic theory of DNA mechanical unzipping proposed by Cocco et al. (36,37). This theory accounts for H-bonds, stacking interactions, and elastic forces to investigate experimentally observable aspects of DNA unzipping by externally applied forces or torques. Quite interestingly, in this model, the calculation of the forces needed to keep the two extremities of the dsDNA molecule separated by a given distance leads to the prediction of the existence of an extremely large force barrier that opposes initial double-helix unzipping, namely, an ∼250 pN force peak occurring at ∼2 Å separation from the equilibrium basepair distance (37). This is remarkable because it is more than an order of magnitude larger than the unzipping forces for DNA in the bulk (i.e., forces averaged over scores of unzipped basepairs) previously measured in various experimental settings.

Because both analytically solvable models and experiments can only reveal a limited number of observables (e.g., force and extension), it is crucial to complement them with all-atom simulations. This allows one to better understand the dynamics and observe the microscopic effects that pulling forces have on all degrees of freedom and physical properties of the system (38). A previous atomistic MD study of DNA mechanical denaturation (39) focused on the sequence effects that occur during nonequilibrium DNA unzipping (with pulling speeds orders of magnitude larger than those in single-molecule tweezer experiments) and not on the equilibrium forces needed for the initiation step. The authors observed jumps and pauses in denaturation, which they attributed to the inhomogeneity of the DNA sequence they used (AT-rich regions melt earlier (i.e., at smaller forces) than GC-rich regions because AT basepairs contain two H-bonds, whereas GC basepairs contain three H-bonds).

The purpose of this study is to provide a better understanding of the onset of DNA denaturation and to explore the origin of any unusually high forces that occur at the very early stage of unzipping (i.e., the opening of the first one or two basepairs) via detailed molecular simulations and subsequent theoretical analysis. To this end, the rest of the article is organized as follows: First, we compute, along the base separation coordinate, the mean force and free-energy profiles of a dodecamer of helical B-DNA with the base sequence d(CGCAAATTTCGC)₂ using MD simulations, umbrella sampling, and the weighted histogram analysis method (WHAM) to obtain an atomically detailed potential of mean force (PMF) profile. Then, in addition to atomistic calculations, to explore the presence of force peaks in simulations with lower (mesoscopic) levels of details and to extend the range of DNA sequences studied, we also perform simulations using a coarse-grained DNA model with three sites per nucleotide (40). Lastly, we also show that we can derive this force peak analytically in the formalism of the PB model (32). Taken collectively, our simulation and analysis results reveal that the opening of the first DNA basepair needs significantly larger forces than the opening of the subsequent ones, not only to break the H-bonds that form that basepair but also to overcome an entropic barrier due to stacking interactions. Additionally, we reveal that a second-order contribution to the force peak stemming from nonnative H-bonds (i.e., between basepairs that were not originally H-bonded in the intact dsDNA) exists, and that concomitantly with the development of the force peak, a peak in the torque about the DNA axis develops upon initial unzipping.

Materials and Methods

All-atom MD simulations

We simulated in atomic detail the first steps in the mechanical denaturation of a dodecamer of helical B-DNA with the sequence d(CGCAAATTTCGC)₂. Fig. 1 schematically depicts the DNA sequence and the forces that are exerted to induce mechanical unzipping. It displays the four nucleotides (G, C, A, and T) and the H-bonds between the basepairs. The same labeling and coloring strategy used in Fig. 1 is followed for the other figures in this article. The external forces applied to initiate unzipping are also shown. In the atomistic simulations, they were applied on the two O3′ atoms of the first basepair, i.e., the O3′ atom of the C1 residue at the 5′ end (i.e., the first Cyt residue on one strand), and the O3′ atom of the G12 residue at the 3′ end of the other strand. (Numbering is such that bases are labeled 1–12 from the 5′ to the 3′ direction on both strands; see also Fig. 6.) To account for the natural fraying of terminal basepairs, we used two starting geometries in the simulation: a paired first basepair and a frayed one. For the frayed first basepair case, the initial equilibrium distance between O3′ atoms pulled apart is the same as that for the paired case, and the C1 residue at the 5′ end (on DNAs1-DNA strand1) and the G12 residue at 3′ end (on DNAs2- DNA strand2) were flipped out of the backbone by altering the corresponding dihedral angles. The structures thus prepared then underwent MD simulations using version 34 of the CHARMM software package (41) with the CHARMM27 nucleic acid parameters (42,43). The reaction coordinate was defined as the separation between the C and G O3′ atoms of residues 1 and 12, respectively, and we applied harmonic constraints to the separation distance ρ of these atoms. The functional form of the potential used was k_u(ρ − ρ₀)². Using umbrella sampling trajectories, we collected statistical data for free-energy calculations during the structural changes along the coordinate. The selected atoms were harmonically restrained so as to maintain a separation within ∼1 Å of the specified equilibrium distance ρ₀, ranging from 14.50 Å (the basepairing equilibrium value) to 30.00 Å (which corresponds to a 15.5 Å separation from basepairing equilibrium) with increments of 0.05 Å for the first 4.5 Å separation and 0.25 Å for the rest of the windows. The last configuration of the trajectory in each window was used as the initial condition for the next window. We calculated a total of 130 windows, each of which ran for 800 ps. We then postprocessed each 800 ps trajectory using WHAM (44,45). The more numerous umbrella sampling windows for the first 4.5 Å were generated for better resolution in the initial free-energy profile. We used the explicit solvent TIP3P potential for water (46). The DNA structure was overlaid with a water box that was previously equilibrated at 300 K, with dimensions 56 Å × 56 Å × 56 Å, and was initially aligned so that the DNA molecule’s primary axis would be parallel to the x axis. The water box contained 3362 TIP3P water molecules and 22 sodium ions, which were needed to make the solution electrically neutral. Periodic boundary conditions were used and electrostatic interactions were accounted for using the particle-mesh Ewald method (47), with a real-space cutoff at 12.0 Å for nonbonded interactions. The leapfrog Verlet algorithm was used with Nosé-Hoover dynamics (48,49) and with a coupling constant (thermal inertia parameter) of 50 internal (AKMA) units (50) to keep the temperature constant at 300 K throughout the simulations. The system underwent 100 steps of steepest-descent minimization followed by 1000 steps of the adaptive-basis Newton-Raphson minimization. It was then heated to 300 K over an equilibration period of 800 ps, with harmonic restraints applied to the O3′ atoms to prevent the helical axis from becoming unaligned with the z axis. These restraints were then gradually removed during the production runs. The SHAKE algorithm (51) was used to constrain all covalently bound hydrogen atoms.

Figure 1.

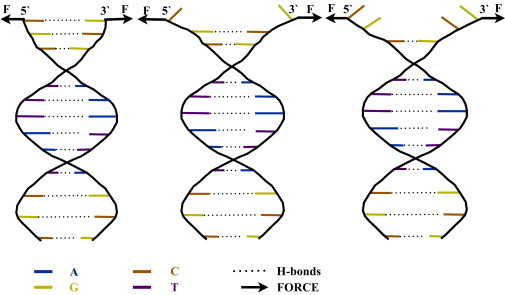
Schematic representation of the DNA sequence and the forces applied for unzipping. Bases G, C, A, and T are shown in yellow, orange, blue, and magenta, respectively, and the bonds forming the basepairs are shown with a dotted line. Forces were applied on two backbone atoms of the first basepair: 1) the O3′ atom of the C1 residue at the 5′ end of one strand and on the O3′ atom of the G12 residue at the 3′ end of the other strand in the all-atom simulations and 2) the pseudo-atoms describing the sugars of the same residues in the coarse-grained simulations. The terminal C1-G12 basepair is an example of what we refer to in the text as the first basepair that needs a higher force to be unzipped in comparison with the subsequent basepairs. To see this figure in color, go online.

Figure 6.

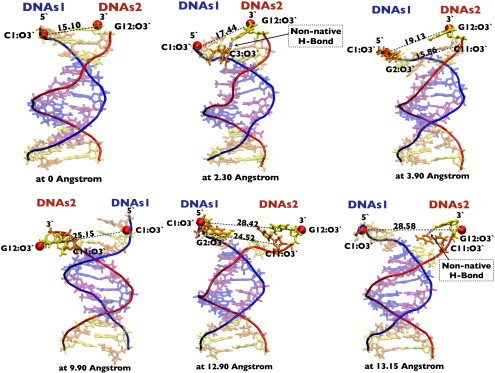
Snapshots of some of the intermediate structures that form while unzipping DNA, extracted from our atomistic simulations using VMD. Transient bonds that form during unzipping are shown with a dashed blue line. Nucleotides G, C, A, and T are shown in yellow, orange, blue, and magenta, respectively. The two DNA strand backbones are shown in blue and red. To see this figure in color, go online.

We postprocessed the biased umbrella sampling trajectories using WHAM (44), as implemented in Grossfield (45), to obtain the unbiased free-energy values as well as the thermodynamic quantities from an unbiased system. Error bars were calculated by Monte Carlo bootstrap error analysis, with repeated computations of the average of resampled data and calculation of the standard deviation of the average of the resampled data. The latter is an estimate for the statistical uncertainty of the average computed using the real data. Because for separation distances below 4.5 Å the energy is averaged over more windows than it is for higher separations, this leads to the smaller error bars in that region of interest. The force along the reaction coordinate was computed as the derivative of W(ρ) with respect to ρ, F(ρ) = −dW/dρ and is rigorously (52) the canonical-ensemble thermodynamical average of the force needed to keep the two strands separated by a distance ρ.

To determine the vectorial force components, we computed the mean force along the Cartesian x, y and z axes by taking the derivative of W(ρ) with respect to x_i, y_i, and z_i of the ith atoms involved:

$$\langle f_{x_i}\rangle \equiv -\langle \frac{dW}{d{x}_i}\rangle =-\frac{dW}{d\rho }\langle \frac{d\rho }{d{x}_i}\rangle =-\frac{dW}{d\rho }\frac{\left(\langle x_i\rangle -x_{ref}\right)}{\rho \cdot N},$$ (1)

with the corresponding permuted expressions for the y and z directions. We were also interested in computing any torque τ to which DNA is subjected upon an increase in the separation distance by finding the backbone vector forces (on atoms C1:O3′ and G12:O3′) in the x, y, and z directions, and performing the cross product with the radii vectors of the DNA helix (53). For example, the torque in the helical z direction is

$$\langle {\tau }_{z_i}\rangle =-\frac{dW}{d\rho }\cdot \frac{\left(x\hat{ı}+y\hat{j}\right)\times \left(\left(\langle x_i\rangle -x_{ref}\right)\hat{ı}+\left(\langle y_i\rangle -y_{ref}\right)\hat{j}\right)}{\rho \cdot N},$$ (2)

with similar expressions for the x and y directions.

Coarse-grained simulations

For coarse-grained simulations, we used the three-site-per-nucleotide DNA model developed by Knotts et al. (54) with the parametrization described in Florescu and Joyeux (40). In this model, each nucleotide is mapped onto three interaction sites (beads): one for the phosphate, one for the sugar ring, and one for the base. The equilibrium positions of the three beads are derived from the coordinates of the atoms they replace, as follows: for phosphates and sugars, the bead is placed in the center of mass of the atomic structure of the respective group, for adenine and guanine it is placed on the position of the N1 atom of the given base, and for cytosine and thymine it has the coordinates of the N3 atom of the given base. The interaction potential between these beads comprises six terms:

$$E_{pot}=V_{bond}+V_{angle}+V_{dihedral}+V_{stack}+V_{bp}+V_{qq},$$ (3)

where V_bond, V_angle, and V_dihedral are the bonded contributions (stretch, angle bending, and torsion, respectively), and base stacking (V_stack), basepairing (V_bp), and electrostatic interactions (V_qq) (the nonbonded terms) are described by

$$\begin{array}{l}{V}_{bond}=k_1\sum _i{\left(d_i-d_i^0\right)}^2+k_2\sum _i{\left(d_i-d_i^0\right)}^4\hfill \\ V_{angle}=\frac{k_{\theta }}{2}\sum _i{\left(\theta -{\theta }_i^0\right)}^2\hfill \\ V_{dihedral}=k_{\varphi }\sum _i\left[1-\text{cos}\left({\varphi }_i-{\varphi }_i^0\right)\right]\hfill \\ V_{stack}=\mathit{ϵ}\sum _{i<j}\left[{\left(\frac{r_{ij}^0}{r_{ij}}\right)}^{12}-2{\left(\frac{r_{ij}^0}{r_{ij}}\right)}^6+1\right]\hfill \\ V_{bp}={\mathit{ϵ}}_{AT}\sum _{ATbasepairs}\left[5{\left(\frac{r_{ij}^0}{r_{ij}}\right)}^{12}-6{\left(\frac{r_{ij}^0}{r_{ij}}\right)}^{10}+1\right]+{\mathit{ϵ}}_{GC}\sum _{GCbasepairs}\left[5{\left(\frac{r_{ij}^0}{r_{ij}}\right)}^{12}-6{\left(\frac{r_{ij}^0}{r_{ij}}\right)}^{10}+1\right]\hfill \\ V_{qq}=\frac{e^2}{4\pi {\mathit{ϵ}}_{H_{2}O}}\sum _{i<j}\frac{exp-\left(\frac{r_{ij}}{{\kappa }_D}\right)}{r_{ij}},\hfill \end{array}$$ (4)

where d_i denotes the distance between two beads connected by the bond i, θ_i is the angle between three consecutive sites on the same strand, and ϕ_i is the dihedral angle defined by four consecutive beads (also along the same strand). In the nonbonded terms, r_i,j is the distance between sites i and j. In all equations the values with the superscript index 0 are equilibrium values for the respective quantities. For their numerical values, we refer the reader to Knotts et al. (54). The force constants for the bonded terms are as follows: k₁ = 0.26 kcal⋅mol⁻¹Å⁻², k₂ = 26 kcal⋅mol⁻¹Å⁻⁴, k_θ = 104 kcal⋅mol⁻¹, and k_ϕ = 1.04 kcal⋅mol⁻¹. The stacking interactions act between the first and second nearest neighbors and $\mathit{ϵ}=0.26$ kcal⋅mol⁻¹. The basepairing term acts only between native pairs, with ${\mathit{ϵ}}_{AT}=3.90$ kcal⋅mol⁻¹ and ${\mathit{ϵ}}_{GC}=4.37$ kcal⋅mol⁻¹. Finally, electrostatic interactions are considered to occur only between phosphates, which carry one elementary charge each. In the expression of the Debye-Hückel potential, e is the electron charge, ${\mathit{ϵ}}_{H_{2}O}=78{\mathit{ϵ}}_0$ is the dielectric constant for water at room temperature expressed as a function of the dielectric permittivity of vacuum, and r_D = 13.603 Å is the Debye length for a 50 mM Na⁺ ion concentration. Compared with Knotts et al. (54), we use different values, ${\mathit{ϵ}}_{AT}$ and ${\mathit{ϵ}}_{GC}$, and exclude nonnative basepairing. This was done because the original set of parameters can sometimes cause the formation of two pairing bonds per base, which can induce melting temperatures that are too high. Consequently, we modified the pairing energy values to correctly describe thermal and mechanical denaturation. We simulated the mechanical unzipping of the dodecamer simulated in the atomistic model, d(CGCAAATTTCGC)₂, plus two other dodecamers, d(TGCAAATTTCGC)₂ and d(CTCAAATTTCGC)₂, in which we changed the first and second basepairs, respectively, from CG to AT. We propagated the dynamics by integrating Langevin’s equations:

$$m_j\frac{d^2{\mathbf{r}}_j}{d{t}^2}=-\nabla E_{pot}-m_j\gamma \frac{d{\mathbf{r}}_j}{dt}+\sqrt{2m_j\gamma k_{B}T}{\xi }_j\left(t\right)$$ (5)

where m_j is the mass of site j, r_j is its position vector, and the friction coefficient γ and Gaussian white noise ξ_j (t) obey fluctuation dissipation:

$$\langle {\xi }_i\left(t\right){\xi }_j\left(t\text{'}\right)\rangle ={\delta }_{i,j}\delta \left(t-t\text{'}\right)$$ (6)

The first term on the right-hand side of Eq. 5 denotes the forces that result from the potential, the second one describes the friction due to the solvent, and the third one is a thermal random noise. We integrated the equations of motion using a second-order algorithm with a time step of 10 fs and a friction coefficient γ of 5 ns⁻¹. A detailed discussion regarding the choice of γ and its influence on the simulation results can be found in Florescu and Joyeux (40). The temperature was set to 293 K. We modeled mechanical unzipping of the DNA sequence by pulling apart the sugar groups that are part of the first basepair at a constant rate. We then computed the average of the projection along the separation axis of the internal forces acting on the two beads. For each point, the force was averaged over 10⁷ time steps (0.1 μs), corresponding to an increase in separation distance of 0.1 Å. We previously used this approach and validated the model and its parameters with respect to DNA unzipping; we refer the reader to Florescu and Joyeux (40) for the details of this validation.

Results and Discussion

Using the computational techniques presented in Materials and Methods, we performed equilibrium studies of the forces required for the mechanical unzipping of short DNA sequences. We simulated pulling by the first basepair up to a separation distance of 14 Å from equilibrium using all-atom MD (CHARMM), and up to 50 Å using the coarse-grained model described above. The analysis of the simulation results presented here is mainly focused on what happens at small separation distances, that is, corresponding to the opening of the first two basepairs. To our knowledge, this is the first time that the onset of DNA mechanical denaturation has been studied in such detail. From the all-atom simulations, we computed a free-energy profile (the PMF), whose derivative with respect to the separation coordinate was used according to the definition of the PMF (52) to obtain the average force needed to keep the first basepair open at any given separation. Because terminal DNA basepairs are known to fray, we had to use two sets of initial conditions: one basepaired and one frayed (as described in the Introduction). Additionally, since the fraying/unfraying equilibrium is established on a timescale much shorter than that of the pulling apparatus used in single-molecule pulling (typically A/ms), during a typical pulling, one expects to experience time averaging between the two states, so pulling would give the weighted mean (e.g., 30–70% or 10–90%) of the fully paired and fully frayed profiles. The free-energy profile along the separation coordinate is shown in Fig. 2. Over a baseline of increasing free energy as a function of separation (whose constant slope averages to the value of the minimum bulk force needed to unzip DNA), we observed significant pits or free energy. They introduce higher slopes in the profile, and since the slopes are proportional to the magnitude of the mean force, they are responsible for the larger forces for the separation of the first and second basepairs (see Fig. 3). We also computed conformational entropies (55) at each separation distance using the quasi-harmonic analysis method (56), in which quasi-harmonic frequencies are calculated from diagonalizing the mass-weighted covariance matrix of nucleic acid atomic conformational fluctuations in each umbrella sampling window. The calculated conformational entropy profile around the first basepair unzipping is shown in the inset to Fig. 2. We observed a substantial conformational entropy contribution to the antlion pit in the free-energy profile along the first basepair unzipping distance, pointing to a large entropic contribution to the initial slope of the free energy and hence to the force peak.

Figure 2.

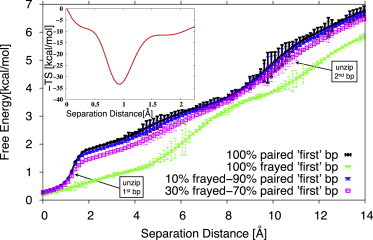
Free energy of DNA unzipping from all-atom simulations with various frayed − paired populations for the first basepair: fully paired (black), fully frayed (green), 10% − 90% frayed − paired (blue), and 30% − 70% frayed − paired (pink). Arrows point to the onset of first and second basepair unzipping. The significantly deeper, antlion-pit free-energy well for first basepair separation (between 0 and 2 Å) is a key feature that explains the steep increase in the force required for initial unzipping (see main text). Inset: the conformational entropy contribution to the free-energy profile along the separation distance for unzipping the first basepair. To see this figure in color, go online.

Figure 3.

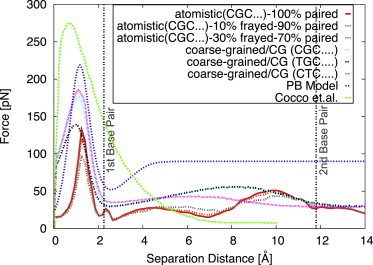
Mean force on the terminal basepairs need to maintain them at a given separation, as a function of that separation distance. Shown are atomistic simulations for the fully paired first basepair (red), first basepair 10% frayed and 90% (orange dashed line), and 30% frayed and 70% paired (light-brown dashed line), together with the results of Cocco et al. (37) (green dashed line), the PB model (dark-blue dotted line), and coarse-grained simulations (pink dotted line). We also show results (in light blue and black) for coarse-grained simulations of the same sequence with the first basepair and second basepairs changed from C-G to A-T. The vertical lines mark the distances beyond which the first and second basepairs are fully unzipped. To see this figure in color, go online.

From the coarse-grained simulations, we computed directly the corresponding force at each distance by equilibrium averaging of the force needed to keep the distance between the phosphates of the first basepairs at a given separation. In this section, we focus on the analysis of the force peak obtained via these simulations, but first we start with an analytical computation of the forces using the PB model (32,57). According to this model, the potential energy of a sequence of N + 1 basepairs whose first basepair (n = 0) is pulled by a force F perpendicular to the sequence is (57)

$$V=\sum _{n=0}^N\left[D\left(1-e^{-a{y}_n}\right)+\frac{K}{2}{\left(y_n-y_{n+1}\right)}^2\right]-F{y}_0$$ (7)

where y_n is the deviation from equilibrium of the distance between the bases of the n − th basepair. The first term describes the pairing interaction and the second one describes the stacking interaction. By differentiating Eq. 7 with respect to y_n, one obtains

$$\begin{array}{l}\frac{\partial V}{\partial y_0}=2aD{e}^{-a{y}_0}\left(1-e^{-a{y}_0}\right)+K\left(y_0-y_1\right)-F\hfill \\ \frac{\partial V}{\partial y_n}=2aD{e}^{-a{y}_n}\left(1-e^{-a{y}_n}\right)+K\left(2y_n-y_{n+1}-y_{n-1}\right)\hfill \\ \text{for}n>0\hfill \end{array}$$ (8)

Imposing that the conformation with minimum energy satisfies ∂V/∂y_n = 0 for all values of n in the second equality of Eq (8), and taking its continuum n limit, one gets

$$\frac{d^{2}u}{d{n}^2}-A{e}^{-u}\left(1-e^{-u}\right)=0$$ (9)

where u = ay and A = 2a²D/K. The two general solutions of this equation read

$$u=\text{ln}\left[\frac{A}{C_1^2}+\frac{1}{4C_1}{e}^{\pm C_1\left(n+C_2\right)}+\frac{A}{C_1}\left(\frac{A}{C_1^2}-1\right)e^{\mp C_1\left(n+C_2\right)}\right]$$ (10)

where C₁ and C₂ are two integration constants. The physical solution requires that u tends toward 0 when n tends toward + ∞, meaning that the far end of the sequence is still zipped, which is possible if (and only if) $C_1^2=A$. The physical solution can therefore be recast in the form

$$u\left(n_{thresh}|n\right)=\text{ln}\left[1+\frac{1}{4\sqrt{A}}{e}^{-\sqrt{A}\left(n-n_{thresh}\right)}\right]$$ (11)

where, due to the large value of A (see below), n_thresh represents approximately the rank of the basepair up to which the sequence is unzipped. The first line of Eq. 8 is then used together with the minimum condition ∂V/∂y_n = 0 to determine the force F (n_thresh) that is necessary to keep the sequence unzipped up to basepair n_thresh:

$$F\left(n_{thresh}\right)=2aD{e}^{-u\left(n_{thresh}|0\right)}\left(1-e^{-u\left(n_{thresh}|0\right)}\right)+\frac{K}{a}\left(u\left(n_{thresh}|0\right)-u\left(n_{thresh}|1\right)\right).$$ (12)

When we substitute in the above equation the typical values for the parameters of the PB model (D = 0.063eV, K = 0.025eV Å⁻², and a = 4.2 Å⁻¹ (57), so that A = 88.9056), we find that there is a high force barrier for opening the first basepair (see Fig. 3; as discussed below, we also observe this barrier in mesoscopic and atomistic simulations). The position and height of the barrier can, in principle, be obtained analytically as a function of D, K and by searching for the maximum of F in Eq. 12, but the final expressions are too long and tedious to be reproduced here. Numerically, the force threshold is 218.69 pN. We checked the validity of Eq. 12 by integrating numerically Hamilton’s equations of motion. This led to a force threshold within 1 pN of the value derived from Eq. 12.

The force-separation curves obtained through the three methods are displayed in Fig. 3. The results obtained using the PB model are plotted with a blue dotted line, the red line indicates those obtained from all-atom simulations for the fully paired first basepair, the orange dashed line indicates atomistic simulations for the 10% frayed and 90% paired first basepair, the light-brown dashed line indicates atomistic simulations for the 30% frayed and 70% paired first basepair, and the magenta dotted line indicates coarse-grained simulations. Moreover, the figure also displays results of coarse-grained simulations for two variations of the DNA sequence. In the first one, the first basepair has been changed from CG to AT (black dotted line), and in the second one the same substitution has been done for the second basepair (magenta dotted line). We note the presence of not only the initial high-force peak to separate the first basepair but also an echo, a second peak of a relatively smaller force (∼50 pN, but still larger than the bulk separation force). Finally, for comparison, we also show the result from a previous study by Cocco et al. (37) as a green dashed line. In that work, the authors developed a semi-microscopic model for the binding of the two nucleic acid strands, which also predicts the presence of a high energetic barrier for DNA mechanical unzipping and attributes its origin to the higher rigidity of the double helix as compared with the single DNA strand.

In the coarse-grained and all-atom simulations, two force peaks are also observed at small separations. The first one is very sharp and occurs at the beginning of unzipping. Its magnitude varies between 132 and 219 pN depending on the model used. This range is in agreement with the values predicted by other theoretical work (37,39). It is noteworthy that in the coarse-grained simulations displayed in Fig. 3, for the two dodecamers that have CG basepairing at position 2 the peaks are identical, whereas for the dodecamer that has AT basepairing at the second position the peak is lower and occurs at a slightly smaller interstrand displacement. Also within reason is the fact that when the first unzipped basepair is the same (CG) in two different dodecamers (i.e., in which the first basepair stacks on an AT versus a CG basepair) in the coarse-grained simulations, the force profiles are nearly identical for the first peak (see Fig. 3).

The observation of these two force peaks is explained by the free-energy plot in Fig. 2, which has two local minima (with steeper slopes, yielding the force peaks) at the same separation distances at which the force peaks are observed. The inset to Fig. 2 shows that the conformational entropy part of the total entropy contribution to the free energy well around the first basepair for the fully paired first basepair (black line in Fig. 2) has a strong contribution, which accounts in part for the high force peak. These small interstrand separations (certainly for the first peak and most likely also for the second one) are likely below the minimum resolution one can use to investigate them through typical AFM experiments (15–17). Such peaks remain to be observed experimentally in single-molecule experiments as increased force-distance resolutions become available. As an encouraging alternative, unzipping experiments have already recorded pausing events whose magnitude may well be associated with the overcoming of these energy barriers (11).

An interesting feature is the second force peak, located at the larger separation associated with the second basepair rupture. It is weaker (∼50 pN) and wider than the first peak and reminiscent of the unzipping echoes reported in Danilowicz et al. (11). For even larger separations (echo diminishing; see above), the force tends toward a constant value (the so-called critical force, in the large-scale unzipping studies), which is the force needed to keep the two DNA strands separated. It has been shown experimentally (13) that this force is constant for homogeneous sequences and fluctuates if the sequences are inhomogeneous. Our values for these large-scale separation forces are close to 20 pN, which is within the range of measured values (11,14). It is also notable that although both the semi-microscopic model of Cocco et al. (37) and the analytical PB treatments lead to the appearance of a first peak, neither approach features a second peak, which is indicative of the fact that they are, in effect, local models. The second peak is observed in both our atomistic and coarse-grained studies because they involve longer-range interactions encompassing more degrees of freedom, hinting at a more nuanced picture for the balance of forces at play at the end of DNA duplexes.

The fact that this high barrier for initiation of unzipping is observed in both types of studies provides information about its origin, but it is also a validation of the coarse-grained models. Moreover, by observing the gradual increase in the number of interactions included in these models, we can assess which are the main contributors to the observed force peaks. The PB model contains only two terms: stacking between consecutive bases on the same strand and pairing between complementary bases on opposite strands. Therefore, the high force needed to initiate DNA unzipping has to stem from the need to overcome these two types of interactions in a manner that depends on whether the terminal or bulk basepairs are broken. This hypothesis is also confirmed by the fact that when a basepair is changed from CG to AT, the magnitude of this force decreases accordingly (a GC basepair contains three H-bonds, whereas an AT has only two, making it easier to break). Also in common, both the coarse-grained and atomistic models showed that the basepairing opening pathway was toward the major groove (see Movie S1 in the Supporting Material), which is in accord with previous studies showing that this direction is more favorable (58–60).

To further check our hypothesis, we plotted separately some of the energy terms for both the all-atom and coarse-grained models as a function of the separation distance. They are displayed in Figs. 4 and 5 for the all-atom simulations and the coarse-grained model, respectively. The first panel depicts the basepairing energy. Our coarse-grained model does not account for nonnative pairing, so we only plot the energy of the first basepair in red and that of the second one in dotted green. It can be seen clearly that there is a sharp increase in energy at a separation distance corresponding to the first and second force peaks, respectively. Moreover, the slope corresponding to the separation of the second basepair is weaker, thus accounting for the smaller magnitude of the second peak. This is confirmed by the H-bonding energy terms in the all-atom model, which display similar tendencies (see also the distance dependence of H-bonding in Fig. S1). For the all-atom simulations, we also plot some of the nonnative pairing terms. As expected, these terms display only small variations, suggesting that their contribution to the force peak is minor. The other panels of Figs. 4 and 5 display the van der Waals and electrostatic terms separately (Fig. 4, b and c), and stacking (Fig. 5 b) and electrostatic (Fig. 5 c) interactions for the coarse-grained model, for several combinations of bases, either on the same strand or on different strands.

Figure 4.

Select terms of the all-atom Hamiltonian as a function of separation distance, averaged over all simulation windows. (a) Native H-bond energy between the first and second basepairs (solid red and dashed green lines, respectively), and some nonnative H-bond energies. (b) van der Waals term between the first basepair and different bases on the same DNA strand and/or complementary DNA strands. (c) Electrostatic interactions between the first basepair and different bases on the same DNA strand and/or complementary DNA strands. To see this figure in color, go online.

Figure 5.

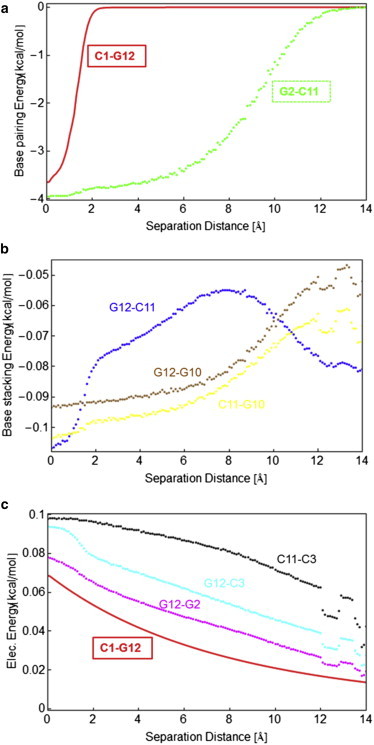
Select terms of the coarse-grained Hamiltonian as a function of separation distance, averaged over all simulation runs. (a) Pairing energies between the first and second basepairs (solid red line and green dots, respectively). (b) Base-stacking energies between the first and second bases, and first and third bases on one of the two DNA strands (the curves for the second strand are similar). (c) Electrostatic interactions between the first basepair and different bases on the complementary DNA strands. To see this figure in color, go online.

At this point, comparison between the two types of representations becomes more tedious because of the simplifications made in constructing the coarse-grained model. First, coarse-grained electrostatic interactions only act between phosphates and only have a repulsive part, as can be seen in Fig. 5 c. They essentially help prevent different DNA segments from overlapping, but they also increase the rigidity and the persistence length of the backbones. The stacking interactions could be compared with the sum of the van der Waals and electrostatic terms for the CHARMM force field. Both representations predict that the variation of these energy terms is rather small compared with that of the pairing/H-bonding terms. Nevertheless, there is a stacking barrier at the separation distances where the two peaks occur (Fig. 4 b), which shows that they do contribute to the high force needed to initiate unzipping. This is also seen from the intermediate atomic structures displayed in Fig. 6, which depicts six snapshots of some of the conformations that DNA takes during unzipping, as extracted from the umbrella sampling MD simulations and plotted using VMD. The first panel shows the equilibrated sequence and the red dots show the points where the separating force is applied. The second conformation corresponds to roughly the same separation distance where the force peak occurs. Note the intrastrand bond between the first two bases on the second strand (G12-C11). This is also confirmed by the plot of the energy (van der Waals term) in Fig. 4 b and the stacking energy in Fig. 5 b. This bond is broken at larger separations (the second configuration), where a transient across-strand bond between G12 and C3 (i.e., a nonnative H-bond) is formed and then again transiently reforms. Moreover, this also happens for several other nonnative H-bonds (as seen in the fourth and sixth panels of Fig. 6). In the fifth and sixth panels, the second basepair is already opening, but now intrastrands bonds between bases seem to have recovered, as also suggested by the van der Waals G2-C1 and G12-C11 energy terms plotted in Fig. 4 b. More generally, we observe that these nonnative interactions have either an H-bond or electrostatic character, rather than a van der Waals interaction. However, it is difficult to evaluate how much these changes in the interactions along one strand could ultimately contribute to a diminution of its rigidity. A similar trend is observed for the plots of the stacking energy in the coarse-grained simulations (see Fig. 5 b, where the energy terms are only shown for one DNA strand but are similar for the other one): the energy for the G12-C11 interaction increases at higher separations and then decreases again. It is fair to admit that our coarse-grained model is not detailed enough to capture the change in the nature of the forces determining the interactions. However, it can be observed from visual inspection of the atomic structures in Fig. 6 (see also Movie S1), as well as from coarse-grained calculations (data not shown), that some of the bases rotate when opening, as suggested by the simulations of Santosh and Maiti (39). That work also suggested the presence of a torsional barrier to unzipping, which is confirmed in our atomistic simulations (see Supporting Material).

Taken together, our results suggest that the occurrence of a force barrier when the first DNA basepair is opened has two main causes: the breaking of H-bonds between the first bases on each strand, and stacking interactions between these bases and their nearest neighbor along the same strand. When the sequence is completely zipped, there are few fluctuations in its conformation, and this is seen in the high forces needed to break the H-bonds. Once the bonds that form the first basepair are broken, the bases have access to more configurations (as evidenced by the higher entropy; see inset to Fig. 2), fluctuations increase (the chain is also more flexible) and the second basepairs are easier to open. This phenomenology can also be used to describe the microscopic origin of the cooperativity manifested by statistical models. It also agrees with previous simulations of DNA basepair opening, which suggested that a strictly local model of the opening of DNA basepairs would not hold (59,60). An additional factor to consider is the contribution to the force from the solvent, which was shown to be a major determinant for the dsDNA helical conformation (38). Moreover, the interpretation of the initial barrier as having an important contribution from stacking interactions within the same strand (in addition to the breaking of H-bonds) is in line with earlier calculations on the cost of unstacking (61,62), which showed a 2–4 kcal/mol barrier before the bases become independently solvated at ∼2A increased separation.

The presence of such a high force barrier involved in DNA mechanical unzipping has already been discussed in the literature, but the presence of a second peak has, to our knowledge, not been previously reported. This second peak is especially well observed in the atomistic simulations because of their high resolution. Moreover, we expect that if these simulations were run for a higher separation and a longer sequence, a third peak corresponding to the opening of the third basepair could be observed. Although we ran our coarse-grained simulations until the separation distance reached 50 Å, we did not observe other force peaks, because at higher separations, denaturation will proceed in a very fast and irregular manner, with significant noise. This is confirmed by the plot of the number of open basepairs as a function of separation, which shows a large increase at distances higher than 20 Å, similar to the phase transition that has been observed for larger sequences (34). However, we also ran a set of coarse-grained simulations on a homogeneous CG sequence of similar length, and in this case did not observe the occurrence of a third peak at a separation distance of ∼18 Å, which is smaller and wider than the second one (data not shown). Our findings are supported by an earlier atomistic simulation study of DNA mechanical denaturation using the AMBER force field (39). In that work, the authors applied an increasing force perpendicular to the helix axis and plotted the separation and the number of open basepairs as a function of the force, for various temperatures. For 300 K, which is closest to the temperature we use, they observed that the basepairs started to separate at a critical force of 237 pN, after which unzipping progressed through jumps and pauses. In passing, we note that this involves an out-of-equilibrium situation and the use of a different simulation protocol that does not use the umbrella sampling restraints in our simulations. Similar discrepancies between the experimental force and the rapidly pulling force in simulations were previously discussed in studies of the end-to-end stretching of DNA (63).

As discussed in the Introduction, experimental studies have established the fact that DNA ends fray in solution, that is, that the terminal basepair can open spontaneously due to thermal fluctuations. For a sequence with a GC terminal basepair, the fraying probability is around 10%. We accounted for this in our work by running an additional set of simulations in which the first basepair was initially open (frayed) and then computing a weighted averaged force profile between the two configurations (paired and frayed) with weights that correspond to the experimental probabilities of the open and close states. We also point out that the requirement in statistical mechanical models for a large force to initiate unzipping is not in conflict with the observations of DNA terminal basepair fraying. For example, using the Langer barrier-crossing theory, Cocco et al. (37) showed that there occurs a fluctuation-assisted crossing of the free-energy barrier for opening corresponding to this force.

It is instructive at this point to make a comparison between the resolutions and accuracies of the two types of simulations used in this work. On one hand, the fact that they both manage to capture the position of the two force peaks proves the robustness of the coarse-grained model as well as the entropic-well origin derived from the atomistic representation. The magnitude of the critical force is different in all descriptions used herein, and its value actually decreases when the resolution of the model is increased, suggesting that the coarse-grained models would tend to overestimate this force. One would expect the opposite trend, since in the simpler model a smaller number of configurations are available to the system, resulting in reduced entropy. On the other hand, in the all-atom case, one captures more intermediate states with energy very close to that of the fully unzipped basepair, making the transition less abrupt. Although both types of models manage to describe the main phenomena with similar accuracy, the all-atom simulations provide more details about the intermediate states that occur during unzipping and their dynamics. Some aspects, such as the various types of interactions that form between neighboring bases along the same strand, and non-Watson-Crick interstrand H-bonds, can only be captured by atomistic simulations. An ideal method would be a combination of the two: the coarse-grained models would allow simulations of larger durations, and the more interesting events could then be simulated in more detail using atomistic force fields.

Conclusions

We used molecular simulations at two resolution levels and an analytical (PB) model to perform a detailed study of the onset of DNA mechanical denaturation. Our results provide new (to our knowledge) information about the transient interactions that occur during this process. We observe a large force peak at ∼2 Å separation and a second, smaller peak at distances ranging between 8 and 12 Å. We predict that the force peaks on the profile will continue, albeit with lower values, for the opening of subsequent basepairs (a third small peak was seen in the coarse-grained simulations; data not shown), but will become indiscernible due to an increase in the signal/noise ratio.

To understand the origin of these force peaks, we computed free-energy profiles and further analyzed conformational entropy contributions, H-bonding interactions (for both native (i.e., canonical Watson-Crick pairing) and nonnative connections), and stacking interactions of the first few bases at the end of the DNA molecule where the unzipping force is applied. We observed secondary contributions to the force peaks from entropic effects associated with the other types of interactions within the DNA sequence. By analyzing the timescale, we identified the essential feature that leads to the presence of the initial large force peak(s). The first well is narrower than the second and subsequent ones because of less entropy (i.e., with fewer states in the reaction coordinate); hence it is steeper, leading to a larger slope. The force needed for unzipping is thus higher because of the lower entropy of the chains zipped up for the first basepair as opposed to the second one, and this effect diminishes in ripples, or echoes, as the separation between the strands increases. Eventually, when a significant portion of DNA is in the single-stranded form, the separation forces drop to the 12–20 pN limit observed in the experiments, as basepair separation becomes akin to melting, which is known to be driven by fluctuations and therefore strongly depends on the conformations available to the now floppier single-stranded force handles.

The observed higher forces for unzipping initiation relative to the forces needed in single-molecule pulling point to a difference in behavior in boundary versus bulk pairs. Although to date we are not aware of any direct experimental evidence to confirm or disprove the presence of the large forces needed for initiation, indirect confirmation may exist. For example, proton exchange has been used to probe basepair opening kinetics in 5′-d(CGCGAATTCGCG)-3′ and related dodecamers (64). The enthalpy changes for opening of the central basepairs are correlated to the opening entropy changes. This enthalpy-entropy compensation minimizes the variations in the opening free energies among these central basepairs. Deviations from the enthalpy-entropy compensation pattern are observed for basepairs located close to the ends of the duplex structure, suggesting a different mode of opening for these basepairs. It is possible that the difference in unzipping the first basepairs revealed in our work could be a manifestation of this difference in the opening modes observed in NMR data.

Longer simulations at the actual separation forces with a variety of atomistic DNA force fields or more sophisticated sampling schemes of the actual kinetics of the transition (65), together with new experimental techniques offering increased resolution (such as force-clamp spectroscopy (66) and nanopore unzipping technologies (2)), may provide more insight into the sequence-dependent thermodynamics and kinetics of Watson-Crick (67) and alternative (68) basepairing phenomena.

Author Contributions

A.M., A.M.F., and I.A. designed the research. A.M., A.M.F., E.B., and J.W. performed the research. A.M.F., M.J., and I.A. contributed analytical tools. A.M., A.M.F., and I.A. analyzed the data. A.M., A.M.F., E.B., and I.A. wrote the manuscript.