Abstract
The impact of flow disturbances on platelet adhesion is complex and incompletely understood. At the molecular scale, platelet glycoprotein Ibα (GPIbα) must associate with the von Willebrand factor A1 domain (VWF-A1) with a rapid on-rate under high hemodynamic forces, as occurs in arterial thrombosis, where various transport mechanisms are at work. Here, we theoretically modeled the coupled transport-reaction process of the two-dimensional (2D) receptor-ligand association kinetics in a biomembrane force probe to explicitly account for the effects of molecular length, confinement stiffness, medium viscosity, surface curvature, and separation distance. We experimentally verified the theoretical approach by visualizing association and dissociation of individual VWF-A1-GPIbα bonds in a real-time thermal fluctuation assay. The apparent on-rate, reciprocal of the average time intervals between sequential bonds, decreased with the increasing gap distance between A1- and GPIbα-bearing surfaces with an 80-nm threshold (beyond which bond formation became prohibitive) identified as the combined contour length of the receptor and ligand molecules. The biomembrane force probe spring constant and diffusivity of the protein-bearing beads also significantly influenced the apparent on-rate, in accordance with the proposed transport mechanisms. The global agreement between the experimental data and the model predictions supports the hypothesis that receptor-ligand association behaves distinctly in the transport- and reaction-limited scenarios. To our knowledge, our results represent the first detailed quantification of physical regulation of the 2D on-rate that allows platelets to sense and respond to local changes in their hemodynamic environment. In addition, they provide an approach for determining the intrinsic kinetic parameters that employs simultaneous experimental measurements and theoretical modeling of bond association in a single assay. The 2D intrinsic forward rate for VWF-A1-GPIbα association was determined from the measurements to be (3.5 ± 0.67) × 10−4μm2 s−1.
Introduction
Many biological processes involve biophysically and biochemically regulated reversible binding and unbinding between specific receptors and ligands on cell surfaces. An important example is the interaction of the platelet glycoprotein Ibα (GPIbα) with von Willebrand factor (VWF) that mediates platelet thrombus formation at all stages, including initiation (1–3), development (4,5), and even final occlusion (6,7). The recent demonstrations of rapid discoid platelet aggregation and accumulation (an activation-independent mechanism) at sites of localized flow disturbances and their implications for atherothrombosis—the leading cause of death globally at >25%) (8–11)—highlight the need to understand the biophysical regulation of nanoscale prothrombotic interaction via single-molecule force spectroscopies (12–15). Many lines of evidence support the key role of the GPIbα-VWF interaction in shear-dependent thrombus formation (1,5,16–19). A fast on-rate of GPIbα-VWF association is required for rapid platelet recruitment in high-shear conditions such as those seen in arterioles and stenotic arteries (1,8,20,21). Similar to the case for flow-enhanced leukocyte tethering mediated by selectin-ligand interactions (22,23), increasing flow augments platelet adhesion despite the shorter encounter durations, until an optimal flow level is achieved. In fact, a minimal flow rate is required for platelets to tether to and roll on VWF-bearing surfaces (1,16,24). However, our understanding of the biophysical regulation of this protein-protein association and its implications for flow-imposed platelet adhesion is limited.
During hemostasis or thrombosis, platelets are carried by blood flow toward the affected vessel wall where VWF is immobilized. At the cellular scale, both experimental and computational results demonstrate that the continuous collision between platelets and red blood cells (RBCs) drives the lateral diffusion of platelets and pushes them against the vessel wall (platelet margination) (25,26). They also undergo translational Brownian diffusion, as they are susceptible to thermal excitation from the environment. Both modes of physical transport move the platelets toward the thrombogenic surfaces, bringing the interacting receptors and ligands into close proximity. For VWF to dock with GPIbα, the two molecules also have to properly orient their binding pockets through rotational diffusion, a molecular-scale transport mechanism, in addition to platelet-level convection and diffusion. Thus, bond association should depend on the relative velocity and separation distance of the opposing protein-bearing surfaces, the Brownian motion of platelets, and the rotational diffusivity of the molecules (23,27).
Compared to the wide range of experiments on bond dissociation at the single-molecule level (28,29), there has been much less focus on experimental quantification of bond association kinetics, and its detailed regulation mechanisms remain to be explored. Adhesion frequency assay and thermal fluctuation assay with ultrasensitive force techniques capable of detecting single-bond interactions, such as use of a biomembrane force probe (BFP), have been employed to measure the two-dimensional (2D) kinetics of binding between various receptors and ligands residing on opposing surfaces (30). The thermal fluctuation assay is a powerful tool for measuring 2D kinetics by pinpointing bond association and dissociation events from a time sequence by monitoring the fluctuations of an ultrasensitive probe (31,32). However, the reciprocal waiting time from the previous bond dissociation to the next bond formation only gives an apparent parameter, as this measurement lumps the intrinsic association timescale with transport timescales from both the cellular and molecular levels. To extract the intrinsic kinetic on-rate from the reciprocal waiting-time measurements requires a theoretical framework to deconvolute these involved transport timescales.
In this work, we first developed a Fokker-Planck-type equation to describe the BFP experiment as the process of a ligand-coated bead diffusing toward and reacting with a receptor-bound surface. The theoretical model was validated by a series of experiments with constructs of GPIbα extracellular domain (glycocalicin (GC)) and VWF-A1 domain (A1). The BFP thermal fluctuation assay was improved to allow more precise kinetic measurements under simultaneous manipulation of several factors of the transport mechanisms that are hypothesized to regulate GC-A1 association: separation distance of protein-bearing surfaces, BFP spring constant, bead size, and medium viscosity. To our knowledge, these combined experimental and theoretical results provide the first quantification of an intrinsic GPIbα-VWF association rate, elucidate the transport mechanisms by which the 2D association kinetics of surface-bound receptors and ligands is regulated, and shed light on transport regulation of platelet tethering on thrombogenic surfaces.
Materials and Methods
Proteins and antibodies
Recombinant VWF-A1 domain (residues 1238–1471) and glycocalicin, described previously (12), were gifts from Drs. Miguel Cruz (Baylor College of Medicine, Houston, TX) and Jing-fei Dong (Puget Sound Blood Center, Seattle, WA), respectively. Mouse anti-human anti-A1 mAb (5D2) was a gift from Dr. Michael Berndt (Curtin University, Perth, Australia) and anti-GPIbα mAb (AK2) was purchased (Thermo Fisher Scientific, Waltham, MA).
Functionalization of glass beads
A1 and GC were precoupled covalently with maleimide-PEG3500-NHS (∼3500 mol wt; JenKem, TX). Modified proteins A1 and GC were mixed with streptavidin-maleimide (Sigma, St. Louis, MO) linked to silanized beads (radius 1.1∼2.1 μm) (Fig. 1 B, left and right, respectively), and washed, as previously described (31). After resuspension in phosphate-buffered saline (PBS) with 1% human serum albumin (HSA), A1 and GC were coated onto respective bead surfaces, and were ready for immediate use in BFP experiments. Molecular site densities of probe and target beads were determined by flow cytometry (33).
Figure 1.
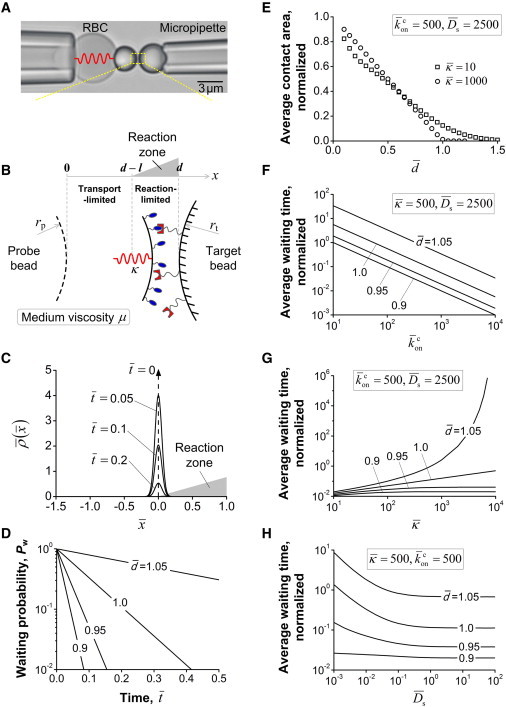
Model of receptor-ligand association in BFP measurement. (A) BFP photomicrograph. A micropipette-aspirated red blood cell (RBC), with a probe bead (left; radius rp) attached to its apex was aligned with an opposing target bead (right; radius: rt) aspirated by another micropipette. The gap distance between the two beads was tracked through image analysis software. (B) Schematic of bond association process in the assay. VWF-A1 and GC were covalently coupled to the probe bead (left) and the target bead (right), respectively. The gap distance between the bead apices is d initially, and the combined molecular length, l, sets a contact threshold for possible bond formation. When d > l, bond association has to involve probe-bead diffusion under the constraint of RBC linkage (spring constant κ) for a nonzero contact area. (C) Time evolution of the probabilistic location of an unbound BFP probe bead, (). The shape of the reaction zone reflects the linearly increasing profile of the reaction term as the probe bead approaches the surface of the target bead (d = l in this case). (D) Results of bond waiting probability, Pw, versus elapsed time, , for increasing gap distance, (). (E) Average contact area (normalized by ) versus . (F–H) Average waiting time normalized by the timescale l2/ versus the dimensionless parameters (F), (G), and (H), with a range of values. To see this figure in color, go online.
BFP setup
As an improvement of the previously described BFP system (31), we used a high-speed camera at 1500 frames/s (fps) to acquire both the probe-bead left edge position, xp (Fig. 1 A, left side), and the target-bead right edge position, xt (Fig. 1 A, right side). The gap distance between the opposing surfaces of the probe and the target can be regarded as d = |xt − xp − 2(rp + rt)|. The raw data of d versus time, t, consisted of four phases (Fig. 2 A). The target bead was driven by a computer-controlled piezoelectric translator (PZT) to approach the probe bead at a speed of 2 μm/s (Fig. 2 A, black). After a short contact of ∼0.1 s (green), the target was retracted (purple) and held from the probe by a controlled separation distance, d, and the PZT was stopped for a preset time span (usually 8∼15 s, but 100 s was used for some measurements when the BFP spring constant κ = 0.4 pN/nm, bead-bead separation was close to l, and/or Ficoll was added) to allow VWF-A1 on the probe to form a bond with GC on the target (Fig. 2 A, blue and red, respectively). Based on the rationale of the BFP force-clamp assay (34–36), the bond force in the gap-controlled thermal fluctuation assay can be directly estimated as f = κ⋅Δxp, where Δxp is the measured probe-bead deflection, considered as RBC deformation.
Figure 2.
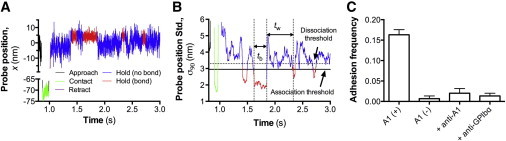
BFP thermal fluctuation assay. (A) In each test cycle, the target bead first approached the probe bead (black), stayed in contact for 0.1 s (green), retracted (purple), and was held in space (blue/red). (B) Plot of sliding standard deviation (Std.) of 90 consecutive points (σ90) of the probe position in (A) versus time t. Horizontal lines represent the threshold values to identify bond association (solid line) and dissociation (dashed line) events. Bond and no-bond states were distinguished in red and blue segments, respectively. (C) Adhesion frequencies between target beads coated with GC and probe beads coated with A1 (A1(+), first column), without A1 (A1(−), second column), with A1 + 50 μg/mL anti-A1 blocking mAb 5D2 (+anti-A1, third column), and with A1 plus 50 μg/mL anti-GPIbα blocking mAb AK2 (+anti-GPIbα, fourth column). Binding frequencies, represented as mean ± SE, were measured from three probe-target pairs per condition and each probe-target pair was tested repeatedly for 100 contact-retract cycles. To see this figure in color, go online.
BFP experiment preparation
According to a protocol approved by the Institutional Review Board of the Georgia Institute of Technology, human red blood cells were obtained from human peripheral blood of healthy donors by finger prick, washed, biotinylated, and stored for experiments as previously described (31). The BFP (Fig. 1 A, left) consisted of an RBC aspirated by micropipette to function as an ultrasensitive force transducer and a probe bead attached to the apex of the RBC via biotin-streptavidin interaction. It has been shown from mechanical equilibrium of the RBC membrane that membrane tension is proportional to aspiration pressure, Δp, and that the radius of the probe micropipette lumen, Rp, is dependent on the radius of the spherical portion of the aspirated RBC, R0, according to Rp × Δp/2(1 − Rp/R0) (37). For small-magnitude extension or compression, the RBC behaves like a Hookean spring, with the spring constant determined by the equation (30,38)
where Rc is the radius of the circular contact area between the RBC and the probe bead. Thus, we manipulated κ by tuning the pressure difference (Δp) between the outside and inside of the probe micropipette through a customized manometer in the range 0.1–0.69 pN/nm. A target bead was aspirated by another micropipette aligned on the opposite side (Fig. 1 A, right). Experiments were conducted at constant room temperature (25°C) in HEPES-Tyrode buffer (134 mM NaCl, 12 mM NaHCO3, 2.9 mM KCl, 0.34 mM sodium phosphate monobasic, 5 mM HEPES, and 5 mM glucose, 1% bovine serum albumin, pH 7.4). Note that an RBC has a biconcave discoid shape in isotonic medium; to cause RBCs to swell and form spheres after being aspirated (Fig. 1 A, left), biotinylated RBCs were modified with nystatin (Sigma).
Kinetic analysis for the thermal fluctuation assay
Similar to the previously described thermal fluctuation method (31), bond association and dissociation were detected from the abrupt reduction and resumption, respectively, of thermal fluctuations of the probe beads (Fig. 2 A). The ensemble standard deviation of the horizontal positions, denoted as σ, was employed to quantify the amplitude of thermal fluctuations. Thus, a decrease in σ indicates bond association and an increase in σ indicates bond dissociation, since bond formation equivalently adds more constraint to the motion of probe beads.
We approximated the ensemble standard deviation, σ, by a sliding standard deviation of 90 consecutive data points, σ90, from the x-t trajectory and plotted it against t (Fig. 2 B). We chose 90 points by balancing the competing needs for accurate representation of the σ value and temporal resolution. Two horizontal lines could therefore be drawn to serve as the thresholds to distinguish bound from unbound states (Fig. 2 B, solid and dashed lines, respectively) among the opposing beads. The abrupt changes in σ90 pinpoint the events of bond formation and dissociation. The period from the instant of dissociation of an existing bond to the instant of formation of the next bond is termed waiting time, tw, and the period from the instant of bond formation to the instant of the following bond dissociation is termed bond lifetime, tb (Fig. 2 B). The survival frequency of waiting time, Pw (versus in the model, where ρ(x,t) is governed by Eq. 6) can be extracted from experiments as the fraction of events with a waiting time ≥tw. Thus, the negative slope of the ln(Pw)-versus-tw plot (Fig. 3 A) or the reciprocal of the average waiting time, 〈tw〉 (Fig. 3 B), provides an estimate for cellular on-rate of = mrml〈Ac〉 (Eq. 7).
Figure 3.
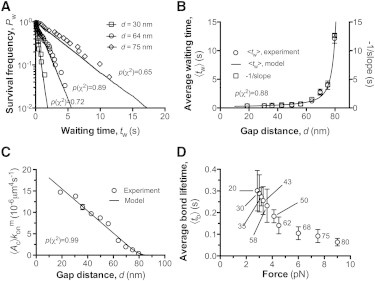
Dependence of 2D association kinetics on the gap distance. (A) The natural log of waiting frequency Pw, calculated as the fraction of measurements with a waiting time >tw, was plotted versus tw for the indicated values of gap distance and fitted by our model. (B) Plots of the average waiting time 〈tw〉 and the negative reciprocal of slope of the linear-fit in (A) versus gap distance d. (C) Apparent 2D on-rate , calculated from the negative slope of the linear-fit in (A), was plotted against the gap distance d. was calculated by dividing the cellular on-rate by the product of the protein densities on the probe (A1) and target (GC) beads, e.g., mrml = 1.95 × 105μm−4 determined by flow cytometry (cf. Materials and Methods). The p-values for model fit to experiment data were indicated accordingly from the χ2 goodness-of-fit tests. (D) Plots of average bond lifetimes 〈tb〉 versus bond force. Gap distances corresponding to forces are indicated. The error bars represent SEM. All the data of experiments (symbols) and models (curves) were obtained at a fixed value of BFP spring constant (κ = 0.25 pN/nm). Each data point was derived from 20∼40 measurements.
Numerical solution to the Fokker-Planck type governing equation
The solution to the partial differential equation in Eq. 6 with prescribed boundary and initial conditions was carried out by pdepe solver in MATLAB (39). The numerical procedure led to discrete values of the probability distribution ρ(x,t) at 1100 equally spaced values of space variable x at discrete times t. The time increment was taken to be <1/5000 of the average waiting time. Within an ensemble of nominally identical events, association is characterized by the fraction of events for which no bond forms after the elapsed time t in the observation, equivalent to the survival frequency of waiting time, Pw, in BFP measurement. The values of Pw(t) at time points t that were extracted by numerical integration of the probability distribution over those spatial intervals within −10d ≤ x ≤ d (see, e.g., Fig. 1, C and D), a range found to be sufficiently accurate to represent the interval (−∞, d]. Chi-squared goodness-of-fit tests were performed for model fit to the data (e.g., Fig. 3 A) using the chi2gof command in MATLAB, and the p-values, p(χ2), were used to determine how close the agreement is between the model and the data.
Results and Discussion
Model
The BFP is a micropipette-aspirated red blood cell (RBC) with a probe bead glued to its apex that functions as a force transducer with a spring constant κ (Fig. 1 A, left). It is aligned against a target bead aspirated by another pipette (Fig. 1 A, right). The probe bead is of a size comparable to that of a platelet (e.g., 2∼5 μm in diameter), small enough to exhibit nanometer-scale Brownian motion within the confinement of the BFP spring. The probe and target beads, coated with receptors and ligands, respectively, with separately measured densities, are precisely controlled and monitored in space and time. Physically, bond formation anchors the probe bead to the target bead, thereby reducing the thermal fluctuation of the probe bead, which allows for detection of bond formation (31,32). The 2D association kinetics is regulated biophysically, because before a receptor and a ligand can react biochemically, their binding sites have to come into close proximity and proper orientation by means of physical transport (Fig. 1 B). Thus, the experimentally measured 2D on-rate of bond association based only on a simple chemical reaction kinetic, e.g., the law of mass balance, reflects convoluted timescales of both transport and reaction.
To quantitatively understand the biophysical regulation of bond association, we first used mathematical modeling to include in the mass balance law the various transport mechanisms that give rise to these mixed timescales. For simplicity, we model the instantaneous motion of the probe bead under thermal forces as one-dimensional along the x axis (Fig. 1 B). Statistically, a large ensemble of thermally driven random motions of the probe bead are described by the probability density function, ρ(x,t), e.g., the probability of finding the apex of the probe bead in the region (x, x + Δx) without forming a bond at time t is ρ(x,t)Δx. In addition to the Brownian motion of the probe bead confined by the harmonic potential of the BFP spring, we allow bond formation in a range of axial positions around an initial separation distance, d, between the two reactive surfaces. Using the classical Smoluchowski equation to describing random motions, we introduce j(x,t) as the flux of probe-bead motion in the x direction at time t. This equation consists of a diffusive term to model the Brownian motion of the probe bead and a convective term by the confinement of the RBC (40):
| (1) |
where kB is the Boltzmann constant and T is absolute temperature, U(x) = κx2/2 is the harmonic potential of the BFP spring, and the diffusivity of the probe bead (radius rp) in the medium (viscosity μ) is
| (2) |
according to the Stokes-Einstein relation. The local loss in ρ(x,t) per unit time due to bond formation is modeled by a sink term on a 2D surface perpendicular to the x axis according to the mass action law
| (3) |
where is an apparent molecular on-rate (represented in μm2 s−1) that characterizes the rate for a receptor to associate a ligand per molecular density; mr and ml are the site densities of receptors (e.g., GC) and ligands (e.g., A1) on the target bead and probe bead, respectively. Ac is the contact area, calculated by a parabolic approximation to the spherical geometry of opposing beads:
| (4) |
where l is the total contour length of the receptor and ligand, and rp and rt are the radii of the probe and target beads, respectively.
Bond association is not expected when the opposing molecules cannot touch each other. Thus, the range of probe-bead positions in which the receptor-ligand reaction can possibly occur, termed the reaction zone, is defined through d and l as (d − l, d) (Fig. 1 B). The restriction that ρ is affected by bond formation only in the reaction zone is therefore treated by the sink term in Eq. 3 multiplied by [H(x − d + l) − H(x − d)], where H is the Heaviside step function. It can be seen readily that within the reaction zone (d − l ≤ x ≤ d), Ac(x) linearly increases from 0 to 2πrprtl/(rp + rt) as the instantaneous separation distance between the two beads (d − x) becomes smaller.
in Eq. 3 contains transport information from molecular-level diffusivity (Dm) and intrinsic rate constant for the forward reaction of molecular docking (kf). The overall resistance to apparent binding is considered as the sum of the two individual resistances of molecular-level diffusion and molecular docking in series. Explicitly, the reciprocal apparent molecular on-rate, , is the sum of the reciprocal molecular diffusivity and reciprocal intrinsic forward-rate (41) such that
| (5) |
Like the probe-bead diffusion coefficient, the molecular diffusion coefficient, Dm, which is also reversely proportional to the medium viscosity, μ, assumed the form kBT/(cμl), where c is a coefficient related to the shape of the molecules and l is the combined size of the molecules.
The law of mass conservation states that the local rate of change in ρ(x,t) must be equal to the negative local flux divergence of probe-bead transport minus the local loss due to bond association. Accounting for various terms given by Eqs. 1–5, the mass conservation law can be expressed by a partial differential equation for the probability density function, ρ(x,t):
| (6) |
The boundary conditions are j(d, t) = 0 and ρ(−∞, t) = 0, indicating that the motion of the probe bead is bounded by the fixed target bead at x = d in one direction but unlimited in the other direction. The condition that the apex of the probe bead is given at position x = 0 initially is expressed by ρ(x,0) = δ(x), where δ(x) is the Dirac Δ function.
Relation to the simple association kinetic equation
A simplified equation can be deduced from Eq. 6, which has been previously employed to describe the association kinetics between surface-bound receptors and ligands (31). Integrating Eq. 6 over −∞ < x < d and noting that the flux term vanishes at the boundary and that [H(x − d + l) − H(x − d)] = 1 within the reaction zone (d − l ≤ x ≤ d) and 0 elsewhere, Eq. 6 reduces to
| (7) |
where is the probability of finding the probe-bead apex outside the target surface at x = d, not forming a bond, by time t. It may be termed the waiting probability, related to the previously used adhesion probability by Pa(t) = 1 − Pw(t) (31). is given by Eq. 5, and 〈Ac〉 is a weighted (by the probability density, ρ) average of the contact area over the reaction zone and time:
| (8) |
where the angled brackets on the righthand side mean the average over time. Equation 7, with the initial condition that , represents the simplified model of the irreversible association kinetic equation previously used to analyze the thermal fluctuation experiment for measuring the apparent 2D on-rate of receptor-ligand association (31).
Thus, Eq. 6 can be thought of as a generalization of Eq. 7 by expanding the single location of reaction, the contact surface between the probe bead and target bead at a fixed axial point, x = d, to a distributed reaction zone, d − l ≤ x ≤ d, and allowing for transport of the probe bead within and beyond this zone as described by the flux term of Eq. 6. Equation 6 contains 10 parameters, d, l, κ, μ, kf, kBT, mr, ml, rp, and rt (Table 1), of which some are partly accounted for by 〈Ac〉, but others do not explicitly appear in Eq. 7. For example, the expression for Pw includes d implicitly; as such, the measured waiting time for bond association would depend on the separation distance. To use Eq. 7 to fit the BFP data, therefore, 〈Ac〉 has to be treated as a function of d (see Fig. 3 C). In a similar way, 〈Ac〉 has to be considered a function of κ, μ, and rp to account for the effects of these parameters on cellular and/or molecular transport if Eq. 7 is to be used for data analysis (see Figs. 4 B and 5 B). Hence, 〈Ac〉 is called the apparent 2D on-rate that lumps mixed timescales. By comparison, kf represents the intrinsic forward rate, as the parameters describing the biophysical regulation have been explicitly included in Eq. 6.
Table 1.
List of parameters in the BFP experiment
| Parameter | Definition | Value | Relative errora (confidence interval) |
|---|---|---|---|
| d | gap distance (nm) | 15∼80 | 1.76% |
| κ | BFP spring constant (pN/nm) | 0.15∼0.40 | 3.46% |
| μ | medium viscosity (cP or mPa⋅s) | 1.0∼2.6 | 1.66% |
| rp | radius of the probe bead (μm) | 1.1∼2.1 | 1.64% |
| rt | radius of the target bead (μm) | 1.75 | 1.64% |
| ml | VWF-A1 site density on the probe bead (μm−2) | 1597 | 3.80% |
| mr | GC site density on the target bead (μm−2) | 122 | 6.40% |
| kBT | Boltzmann constant multiplied by Kelvin temperature (pN⋅nm) | 4.1 | — |
| l | combined molecular length (nm) | 80 (μ = 1 cP) | 3.52% |
| 62 (μ = 2.6 cP) | |||
| apparent molecular on-rate (μm2 s−1) | 4.7 × 10−5 (μ = 1 cP) | 19.0% | |
| 2.5 × 10−5 (μ = 2.6 cP) | |||
| Dm | molecular diffusivity (μm2 s−1) | 5.4 × 10−5 (μ = 1 cP) | 19.0% |
| 2.7 × 10−5 (μ = 2.6 cP)b | |||
| kf | 2D intrinsic forward rate (μm2 s−1) | 3.5 × 10−4 | Confidence interval: ±0.67 × 10−4 confidence level: 72% |
Relative errors of the measurements for each parameter are represented by the standard deviation (σ) of N > 3 measurements divided by the mean value. Error propagation analysis was performed to give an uncertainty in predicting l, , Dm, and kf. In the range of mean ± 2σ that corresponds to a 95.4% confidence interval for each parameter, the combination of parameter variations can mostly shift the l, , Dm, and kf predictions by the percentages indicated. The confidence level for these predicted values is (95.4%)7 = 72%.
Adding Ficoll increased the medium viscosity by 2.6 times but shortened the effective molecular length by a factor of 62/80, so effectively, Dm was lowered approximately twofold.
Figure 4.
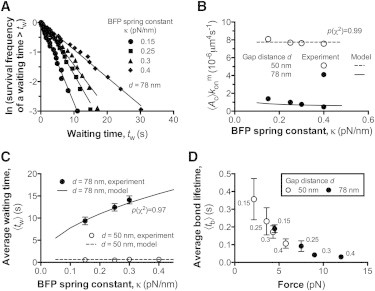
Dependence of 2D association kinetics on the BFP spring constant. (A) The bond waiting time distributions under indicated BFP spring constant κ and matched by our model. (B) Apparent 2D on-rates were plotted versus κ. The adjustment in κ was achieved by varying the aspiration pressure in the micropipette. (C) Plots of the average waiting time 〈tw〉 versus κ. (D) Plots of the average bond lifetimes 〈tb〉 versus force, κ corresponding to each force are indicated. The error bars represent SEM. All the data of experiments (symbols) and models (curves) were obtained at constant gap distances (d = 50, 78 nm).
Figure 5.
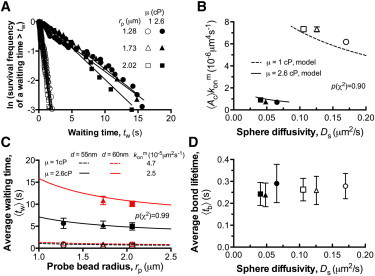
Dependence of 2D association kinetics on microsphere diffusivity. (A) The bond waiting time distributions under indicated microsphere radius (rp) and medium viscosity (μ), in agreement with our model. Different values of Ds are obtained by varying rp or μ. The values of medium viscosity were independently measured as 1.0 and 2.6 cP at room temperature (25°C) for 0 and 6% (w/v) Ficoll, respectively. (B) Apparent 2D on-rates were plotted versus Ds. Ds is defined by the Stokes-Einstein relationship. (C) Plots of the average waiting time 〈tw〉 versus rp for different μ and d. (D) Plots of the average bond lifetimes 〈tb〉 versus Ds. The error bars represent SEM. All the data of experiments (symbols) and models (curves) were obtained at a fixed κ = 0.15 pN/nm and d = 55 or 60 nm. The symbol keys in (B)–(D) are the same as (A). To see this figure in color, go online.
Model characterization
A numerical procedure (see Materials and Methods) was employed to solve ρ(x,t) using Eq. 6 with prescribed values of the 10 parameters appearing in the model. In the comparison between our model and experiments, all parameter values were direct measurements from separate experiments (as listed in Table 1), except for the combined molecular length, l, and the apparent molecular on-rate, , which were sought to globally match the measurements in Figs. 3, 4, and 5.
Before comparing the model predictions to experimental data, let us explore the generalized transport-reaction formalism (Eq. 6) in a broad range of involved parameters. All the parameters are grouped into four dimensionless numbers as , , , and :
| (9) |
where is the dimensionless separation distance, is the dimensionless BFP spring constant, given by a confinement energy scaled by the thermal energy, is equivalent to a cellular on-rate, and is the ratio of the probe-bead diffusivity to the apparent molecular on-rate. The dimensionless time and space variables are defined by and , respectively. The dimensionless probability density function is , so that the area under each curve of versus is the waiting probability .
Within an ensemble of nominally identical events, association decreases the fraction of events that do not form a bond after the elapsed time, , in the observation, as reflected by the reduction in the area under the -versus- curve with increasing time (Fig. 1 C). This is equivalent to the waiting-time survival frequency in BFP measurements; therefore, Pw is referred to as waiting probability in the model but as survival frequency in experiment. The values of at different time points were extracted by numerical integration, and they exhibit the asymptotic behavior → 0 as time becomes sufficiently large. The Pw-versus- curves appear as straight lines in the semilog plot, and the negative slope of each line can be approximated by (23), where (Fig. 1 D). This supports the approximation of Eq. 7, whose dimensionless form is with as solutions. The reciprocal of should approximate the average waiting time, , which can be directly calculated by
| (10) |
where is the probability density of bond association, e.g., the local negative slope of Pw-versus- curves. Since is a function of (Fig. 1 E), our model predicts that when the receptor-ligand separation distance, , increases, the average waiting time increases. It can be intuited, based on this observation, that for bond formation to possibly occur, receptors and ligands have to make physical contact, requiring that the separation distance between the reactant-bearing beads be smaller than the combined contour length of the molecular complex.
The dimensionless waiting time, , is inversely proportional to the dimensionless cellular on-rate, (Fig. 1 F), since the reciprocal, , approximates . The gap distance governs the relative contribution of transport and reaction terms to the overall binding process. The boundary between reaction- and transport-limited regions is at ∼ = 1. Following the approach by Lauffenburger and Linderman (41), the dominating resistance to receptor-ligand association is from the binding reaction for < 1 and from probe-bead transport for > 1. As becomes larger than unity, the change in becomes much more rapid depending on the dimensionless BFP spring constant, (Fig. 1 G),and the probe-bead diffusivity, (Fig. 1 H), as the resistance to bond formation transitions from the reaction-limited to the transport-limited region, and the transport resistance becomes stronger for either larger values of or smaller values of . Deviations in tethering stiffness (in ), molecule length (in and ), and medium viscosity (in ), together with surface gap distance (), can result in a broad range of kinetic association response that may relate to tight regulation mechanisms in the cellular on-rate of physiological phenomena.
BFP experiment for measuring biophysically regulated bond association
To test the model predictions from the preceding section, we functionalized a BFP to measure the binding kinetics between A1 and GC coated onto the probe bead (Fig. 1, A and B, left) and the target bead (Fig. 1, A and B, right), respectively. Bond association and dissociation events were detected from the reduction in and resumption of the thermal fluctuation amplitudes (31), which were measured by the sliding standard deviation of 90 data points from the time sequence in the setup. As exemplified in Fig. 2, A and B, the lower level of standard deviation indicates the bound state (Fig. 2 B, red) whereas the higher level indicates the unbound state (Fig. 2 B, blue). The experimental waiting time, tw, was measured as the period from the instant of dissociation of an existing bond to the instant of association of the next bond. The distance jump in probe-bead position (e.g., >3 nm) provides another indication of bond formation, since the probe bead was pulled by the molecular spring of the GC-A1 bond toward the target bead. The binding specificity was confirmed, as GC-bearing target beads adhered at significantly higher frequencies to probe beads coated with A1 than to those without A1 (Fig. 2 C), and adding anti-A1 or anti-GPIbα monoclonal antibodies abolished the adhesion (Fig. 2 C).
Dependence of 2D association kinetics on separation distance
The dependence of GC-A1 association kinetics on separation distance, d, was determined by measuring a set of waiting times, tw, at a constant gap distance between the opposing bead surfaces, which was then varied in the range 20–80 nm. At each fixed value of d, the ensemble of tw measurements were analyzed by their distribution, or survival frequency, Pw, defined as the fraction of measurements with a waiting time >tw and equivalent to the waiting probability in the model (31,34). Pw decayed with tw nearly exponentially, as data aligned well along a straight line in a semilog plot (Fig. 3 A), suggesting that the GC-A1 interaction follows the kinetics of irreversible single-bond association (31). Furthermore, the model-simulated time evolutions of Pw (Fig. 3 A, curves) matched well the measured distributions of association events (Fig. 3 A, symbols) for all d values investigated. In accordance with theory (Fig. 1 D), the reciprocal of the dimensional cellular on-rate from experiments ( = mrml〈Ac〉 ) (23), estimated from the negative slope of each linearized waiting-time distribution (31), compared well with the average waiting time of that distribution, as expected from an approximate exponential distribution (Fig. 3 B). It is important to note that both metrics increased with increasing gap distance, d, as predicted by our model. Moreover, the simulated apparent 2D on-rate, 〈Ac〉 , fits well with the data, which were obtained by dividing the experimental by the product of GC and A1 site densities measured independently (Fig. 3 C). The model fit to the data returns l = 80 nm and = 4.7 × 10−5 μm2 s−1 as best-fit parameters (see Table 1 for relative errors and confidence intervals), and the variation of 〈Ac〉 data with d was fully accounted for by the dependence of Ac on d (Eq. 8). As d increased from 20 to 80 nm, 〈Ac〉 dropped ∼36-fold, from 14.7 × 10−6 to 0.4 × 10−6 μm4 s−1 (Fig. 3 C). As expected, almost no bond formation event was observed for d values >80 nm, e.g., exceeding the combined contour length of GC (42) and VWF-A1 (43). These results validate our model and provide, to our knowledge, the first set of 〈Ac〉 -versus-d measurements for a receptor-ligand interaction of physiological importance.
Since force regulates receptor-ligand dissociation (44,45), the average bond lifetime, 〈tb〉 (related to the reciprocal off-rate koff of GC-A1 dissociation), also changed with gap distance d (Fig. 3 D). Upon bond formation over the given gap distance, the elongated molecular complex from its natural length should be subject to a tensile force. By tracking the probe-bead deflection, Δxp (considered as RBC deformation), similar to the BFP force-clamp assay (34–36), the bond force can also be measured as f = κ × Δxp. As d increased from 20 to 80 nm, f increased from ∼2 to 9 pN and 〈tb〉 decreased from 0.3 to 0.06 s (Fig. 3 D). The monotonic decreasing trend between d and 〈tb〉 agrees with our previously observed GPIbα-A1 slip bond at low forces (<16 pN) where increased force accelerates bond dissociation (36).
Dependence of 2D association kinetics on Brownian motion
Unlike platelets in the blood stream, whose Brownian motion is free, in the BFP, the probe bead is attached to the apex of a pressurized RBC, whose Brownian motion is confined by a harmonic potential well with a curvature defined by the BFP spring constant, κ. The dependence of VWF-GPIbα interaction kinetics on κ was explored theoretically (Fig. 1 G) and experimentally investigated by varying the BFP spring constants (Fig. 4).
As κ increased from 0.15 to 0.4 pN/nm, the waiting-time distributions of bond association were right-shifted (Fig. 4 A). 〈Ac〉 decreased slightly at d = 50 nm, from 8.09 × 10−6 to 7.56 × 10−6 μm4 s−1, but significantly at d = 78 nm, from 1.40 × 10−6 to 0.48 × 10−6 μm4 s−1 (Fig. 4 B). These data are intuitive given that the softer the BFP spring, the larger the range of the probe bead’s Brownian motion, the smaller the transport effect, and the lower the binding resistance. The increased sensitivity of 〈Ac〉 to κ with larger d is also predicted by the model: the average waiting time, 〈tw〉, becomes more sensitive to κ as the separation distance changes the receptor-ligand association from a reaction-limited (d/l < 1) to a transport-limited (d/l > 1) process (refer to the dimensionless plot in Fig. 1 G). Again, we simulated the bond association with our model at different values of κ. With the determined l and values (see the preceding section), we saw satisfactory agreement (p(χ2) > 0.9) between the simulated and experimental results for the 〈Ac〉 - and 〈tw〉-versus-κ relationships (Fig. 4, B and C).
In contrast to the positive dependence of 〈tw〉 on κ, the bond lifetime, 〈tb〉, showed negative dependence on κ (Fig. 4 D). As κ increased from 0.15 to 0.4 pN/nm, 〈tb〉 decreased from 0.35 to 0.11 s at d = 50 nm and from 0.19 to 0.03 s at d = 78 nm. Using the BFP spring law, f = κ × Δxp, varying κ effectively changes the force on a GC-A1 bond at a given d value. Plotting 〈tb〉 measured at different κ and d values against the bond force revealed the same slip-bond trend at low forces (Fig. 4 D) as observed previously Fig. 3 D.
Dependence of 2D association kinetics on diffusion
Our model describes two kinds of dependence of association kinetics on diffusion. The first is the diffusivity of the BFP bead (Ds in Eq. 2), where the probe bead is subjected to diffusion in chamber media under the confinement of the RBC spring, with the molecules coated onto it thus allowed to move randomly. The second kind is molecular diffusion (Dm in Eq. 5), where the receptors and ligands are subjected to rotational diffusion, which orients their binding sites for molecular docking.
To investigate the distinct effects of Ds and Dm on bond formation, we varied the probe-bead radius, rp, and added 6% (w/v) of Ficoll to the media to increase the medium viscosity by 2.6-fold (23). Average waiting times, 〈tw〉, for GC-A1 association were measured at constant values of d = 55 nm and κ = 0.15 pN/nm. Increasing μ from 1 to 2.6 cP by Ficoll significantly right-shifted the waiting-time distributions (Fig. 5 A) and reduced 〈Ac〉 by almost ninefold at all of the bead radii used (Fig. 5 B). However, varying only the probe-bead radius, rp, had a negligible effect on the waiting-time distributions, 〈Ac〉 and 〈tw〉 (Fig. 5, A–C), which can be explained by the cancellation of two competing effects when rp was increased, namely, the increase in contact area Ac and simultaneous decrease in Ds. This also suggests that the probe-bead diffusion was quite limited due to the increased medium viscosity. As expected, the diffusion-related parameters μ and rp had no influence on the average bond lifetimes (Fig. 5 D), in contrast to d and κ, which significantly affected 〈tb〉 through force.
Altering μ by 2.6-fold should lead to a reduced Dm that scales as μ-1. According to in Eq. 5, the corresponding change in should be <2.6-fold for a 2.6-fold variation in μ or Dm, noting that kf is the intrinsic on-rate constant of GC-A1 docking and is independent of μ and other transport factors. The experimentally observed reduction in 〈Ac〉 by approximately ninefold (Fig. 5 B) suggests that 〈Ac〉 was also influenced by Ficoll, and the only possible factor is the molecular length, l (refer to Eq. 4). A recent study showed that the macromolecular crowding effect in the presence of Ficoll reduced the overall size of an unfolded protein polymer chain (46). Since our proteins were covalently linked via polyethyleneglycol polymers, we hypothesized that adding Ficoll may shorten the molecular length. Therefore, the influence of Ficoll on bond association is twofold: 1) it affects the diffusion of GC-A1 at the molecular level; and 2) it changes the effective length of the molecules. Qualitatively, employing the best-fit values (4.7 × 10−5 and 2.5 × 10−5 μm2 s−1 for μ = 1 and 2.6 cP, respectively (Fig. 5 C)) in Eq. 5 allowed us to determine l = 62 nm with Ficoll and l = 80 nm without it. Dm was computed to be 5.4 × 10−5 and 2.7 × 10−5 μm2/s for the two conditions, respectively, and the intrinsic rate constant for the forward reaction (kf) was extracted as 3.5 × 10−4 μm2 s−1 (Table 1). These results suggest that molecular-scale diffusion, and not reaction, was the limiting factor for GC-A1 bond formation when the two molecules were in contact. This result was then confirmed by separate experiments at d = 60 nm, which resulted in the same l, , Dm, and kf values, providing a good match (p(χ2) > 0.9) with the measurements (Fig. 5 C).
Conclusions
It is increasingly recognized that receptor-ligand on-rates measured in the fluid phase using 3D technologies such as surface plasmon resonance do not provide a complete description for bond formation in 2D when the same molecules are anchored to opposing surfaces (47–51). Some aspects of the differential molecular diffusions and binding-induced entropy losses between 2D and 3D have been treated by mathematical modeling; however, the 2D surfaces in existing studies were assumed to be fixed and stationary (52). Using scaling-law analysis of flow-enhanced tethering of cells and selectin-bearing beads to a ligand-coated surface, we demonstrated in a previous study that the tethering rate is governed by the interplay of the molecular docking on-rate with three transport mechanisms: relative sliding between the two protein-carrying surfaces, Brownian motion of the cells/beads, and molecular diffusion (23). Using hyaluronan-induced repulsion, the Bongrand group showed that the frequency of bond formation decreased by more than one order of magnitude when the equilibrium distance between the two protein carrier surfaces increased from 40 to 180 nm (53). These studies have identified additional transport processes in 2D that are not apparent in 3D: receptors are carried by cells or beads, which travel in a flow field parallel and perpendicular to the ligand-coated surface, thereby impacting molecular contact. To fill the gap in theoretical treatment, we used a Fokker-Planck-type diffusion-reaction equation to model the confined Brownian motion of the ligand carrier bead over a separation distance to a receptor-bearing surface for 2D association. Of more importance, we used BFP experiments to examine bond association in a precisely controlled fashion without relative sliding of the protein carrier surfaces. We found by this combined theoretical and experimental approach that the GC-A1 bond formation was impacted by the receptor-ligand separation distance (Fig. 3), the extent of confinement of the protein carrier bead in Brownian motion (Fig. 4), and the cellular as well as molecular diffusion (Fig. 5). Our results extend the previous work, elucidate the biophysical regulation of 2D association kinetics, and provide insight into transport-regulated platelet adhesion to a thrombogenic surface.
In a recent study using the BFP force-clamp assay, we observed a triphasic force-dependent GPIbα-A1 dissociation kinetics: as force increases, it first shortens (slip), then prolongs (catch), and finally shortens (slip) the bond lifetimes (36). The bond lifetime measurements from the thermal fluctuation assay presented here agree with the previous results (Figs. 3 D and 4 D), showing that increasing separation distance, d, and BFP spring constant, κ, affected bond dissociation in the same way as pulling the bonds in the force-clamp assay. However, the bead diffusion coefficient was found to only affect the waiting time of bond formation, not the bond lifetime (Fig. 5). Thus, our results support the notion that the on-rate is regulated by transport and the off-rate is regulated by force.
The transport-reaction formalism (Eq. 6) describing 2D association kinetics in BFP is related to several special cases previously studied. The classical Smoluchowski equation describing Brownian motion in a harmonic potential can be recovered in the absence of the reaction term. Equation 6 can be reduced to Eq. 7, the commonly used association kinetic equation (31). As rp shrinks to the molecular scale and becomes much smaller than rt, the formalism should describe the association between opposing molecular pairs, as modeled in Erdmann and Schwarz (54) and Qian et al. (55), though the dynamic transport process is neglected therein. With the additional condition of κ = 0, Eq. 6 reduces to the scenario of 3D association-rate measurement (56). Equation 6 can be further extended to model additional modes of transport, such as relative sliding between protein carrier surfaces, as in the case of platelets flowing over thrombogenic surfaces. Of more importance, this kind of mathematical models allows us to extract the intrinsic on-rates from experimental data and should help to reconcile the discrepant interpretation between 2D and 3D association rates. The single-bond-level characterization of GPIbα-VWF association presented here provides a fundamental understanding of the physical regulation in platelet adhesion on thrombogenic surfaces and reveals generic features of transport-governed bond formation for other receptor-ligand interactions.
It is worth noting that in a physiological setting with blood flow, the RBC-dependent platelet margination is the first step of transport working at a cellular scale. At this micrometer scale, the Brownian motion of a platelet is small compared to the shear-induced diffusion due to its collisions with the RBC and its drift velocity in the near-wall region due to RBC tank-treading motion (26,57,58). According to our results, when separation distance is at a molecular scale <80 nm, the molecular gap distance, Brownian motion of the molecule-carrying cell, and molecular diffusion will take effect, forming as a second step of transport. The intrinsic on-rate at this point starts playing an important role in regulating platelet adhesion. Future studies could extend this combined single-molecule approach and analysis by 1) elucidating the biophysical regulation of more receptor-ligand interactions in platelet adhesion and dissecting their relative contributions to prothrombotic effects of disturbed flow; and 2) combining it with the abovementioned cellular transport modeling to simulate actual platelet adhesion under flow with multiple modes of transport, providing cellular-to-molecular-level insights on how cell adhesion is regulated by the physical environment.
Author Contributions
C.Z., L.J., and J.Q. designed the research, L.J. and J.Q. performed the research and analyzed the data, C.Z., L.J., and J.Q. wrote the article. The authors have no conflict of interest to declare.
Acknowledgments
We thank Miguel Cruz for providing VWF-A1, Jing-fei Dong for providing glycocalicin, and Michael Berndt for providing anti-A1 mAb (5D2). We thank Wei Chen for helpful discussions on BFP instrumentation.
This work was supported by National Institutes of Health grant HL093723. J.Q. acknowledges support from the National Natural Science Foundation of China (11321202).
Footnotes
Lining Ju and Jin Qian contributed equally to this work.
Lining Ju’s present address is Heart Research Institute and Charles Perkins Centre, The University of Sydney, Camperdown, NSW 2006, Australia.
References
- 1.Savage B., Saldívar E., Ruggeri Z.M. Initiation of platelet adhesion by arrest onto fibrinogen or translocation on von Willebrand factor. Cell. 1996;84:289–297. doi: 10.1016/s0092-8674(00)80983-6. [DOI] [PubMed] [Google Scholar]
- 2.Savage B., Almus-Jacobs F., Ruggeri Z.M. Specific synergy of multiple substrate-receptor interactions in platelet thrombus formation under flow. Cell. 1998;94:657–666. doi: 10.1016/s0092-8674(00)81607-4. [DOI] [PubMed] [Google Scholar]
- 3.Ruggeri Z.M., Dent J.A., Saldívar E. Contribution of distinct adhesive interactions to platelet aggregation in flowing blood. Blood. 1999;94:172–178. [PubMed] [Google Scholar]
- 4.Reininger A.J., Heijnen H.F.G., Ruggeri Z.M. Mechanism of platelet adhesion to von Willebrand factor and microparticle formation under high shear stress. Blood. 2006;107:3537–3545. doi: 10.1182/blood-2005-02-0618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Nesbitt W.S., Westein E., Jackson S.P. A shear gradient-dependent platelet aggregation mechanism drives thrombus formation. Nat. Med. 2009;15:665–673. doi: 10.1038/nm.1955. [DOI] [PubMed] [Google Scholar]
- 6.Ni H., Denis C.V., Wagner D.D. Persistence of platelet thrombus formation in arterioles of mice lacking both von Willebrand factor and fibrinogen. J. Clin. Invest. 2000;106:385–392. doi: 10.1172/JCI9896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Brill A., Fuchs T.A., Wagner D.D. von Willebrand factor-mediated platelet adhesion is critical for deep vein thrombosis in mouse models. Blood. 2011;117:1400–1407. doi: 10.1182/blood-2010-05-287623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jackson S.P., Nesbitt W.S., Westein E. Dynamics of platelet thrombus formation. J. Thromb. Haemost. 2009;7(Suppl 1):17–20. doi: 10.1111/j.1538-7836.2009.03401.x. [DOI] [PubMed] [Google Scholar]
- 9.Goyal A., Bhatt D.L., Wilson P.W., Reduction of Atherothrombosis for Continued Health (REACH) Registry Investigators Attained educational level and incident atherothrombotic events in low- and middle-income compared with high-income countries. Circulation. 2010;122:1167–1175. doi: 10.1161/CIRCULATIONAHA.109.919274. [DOI] [PubMed] [Google Scholar]
- 10.Jackson S.P. Arterial thrombosis—insidious, unpredictable and deadly. Nat. Med. 2011;17:1423–1436. doi: 10.1038/nm.2515. [DOI] [PubMed] [Google Scholar]
- 11.McFadyen J.D., Jackson S.P. Differentiating haemostasis from thrombosis for therapeutic benefit. Thromb. Haemost. 2013;110:859–867. doi: 10.1160/TH13-05-0379. [DOI] [PubMed] [Google Scholar]
- 12.Yago T., Lou J., Zhu C. Platelet glycoprotein Ibα forms catch bonds with human WT vWF but not with type 2B von Willebrand disease vWF. J. Clin. Invest. 2008;118:3195–3207. doi: 10.1172/JCI35754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhang X., Halvorsen K., Springer T.A. Mechanoenzymatic cleavage of the ultralarge vascular protein von Willebrand factor. Science. 2009;324:1330–1334. doi: 10.1126/science.1170905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Auton M., Sedlák E., Cruz M.A. Changes in thermodynamic stability of von Willebrand factor differentially affect the force-dependent binding to platelet GPIbα. Biophys. J. 2009;97:618–627. doi: 10.1016/j.bpj.2009.05.009. (alpha) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kim J., Zhang C.-Z., Springer T.A. A mechanically stabilized receptor-ligand flex-bond important in the vasculature. Nature. 2010;466:992–995. doi: 10.1038/nature09295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Doggett T.A., Girdhar G., Diacovo T.G. Alterations in the intrinsic properties of the GPIbα-VWF tether bond define the kinetics of the platelet-type von Willebrand disease mutation, Gly233Val. Blood. 2003;102:152–160. doi: 10.1182/blood-2003-01-0072. [DOI] [PubMed] [Google Scholar]
- 17.Siljander P.R.-M., Munnix I.C.A., Heemskerk J.W. Platelet receptor interplay regulates collagen-induced thrombus formation in flowing human blood. Blood. 2004;103:1333–1341. doi: 10.1182/blood-2003-03-0889. [DOI] [PubMed] [Google Scholar]
- 18.Stalker T.J., Traxler E.A., Brass L.F. Hierarchical organization in the hemostatic response and its relationship to the platelet-signaling network. Blood. 2013;121:1875–1885. doi: 10.1182/blood-2012-09-457739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Colace T.V., Diamond S.L. Direct observation of von Willebrand factor elongation and fiber formation on collagen during acute whole blood exposure to pathological flow. Arterioscler. Thromb. Vasc. Biol. 2013;33:105–113. doi: 10.1161/ATVBAHA.112.300522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ruggeri Z.M. Platelets in atherothrombosis. Nat. Med. 2002;8:1227–1234. doi: 10.1038/nm1102-1227. [DOI] [PubMed] [Google Scholar]
- 21.Kaplan Z.S., Jackson S.P. The role of platelets in atherothrombosis. Hematology (Am Soc Hematol Educ Program) 2011;2011:51–61. doi: 10.1182/asheducation-2011.1.51. [DOI] [PubMed] [Google Scholar]
- 22.Finger E.B., Puri K.D., Springer T.A. Adhesion through L-selectin requires a threshold hydrodynamic shear. Nature. 1996;379:266–269. doi: 10.1038/379266a0. [DOI] [PubMed] [Google Scholar]
- 23.Yago T., Zarnitsyna V.I., Zhu C. Transport governs flow-enhanced cell tethering through L-selectin at threshold shear. Biophys. J. 2007;92:330–342. doi: 10.1529/biophysj.106.090969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Doggett T.A., Girdhar G., Diacovo T.G. Selectin-like kinetics and biomechanics promote rapid platelet adhesion in flow: the GPIbα-vWF tether bond. Biophys. J. 2002;83:194–205. doi: 10.1016/S0006-3495(02)75161-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Turitto V.T., Weiss H.J. Red blood cells: their dual role in thrombus formation. Science. 1980;207:541–543. doi: 10.1126/science.7352265. [DOI] [PubMed] [Google Scholar]
- 26.Yeh C., Eckstein E.C. Transient lateral transport of platelet-sized particles in flowing blood suspensions. Biophys. J. 1994;66:1706–1716. doi: 10.1016/S0006-3495(94)80962-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zhu C., Yago T., McEver R.P. Mechanisms for flow-enhanced cell adhesion. Ann. Biomed. Eng. 2008;36:604–621. doi: 10.1007/s10439-008-9464-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Liang J., Fernández J.M. Mechanochemistry: one bond at a time. ACS Nano. 2009;3:1628–1645. doi: 10.1021/nn900294n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Claridge S.A., Schwartz J.J., Weiss P.S. Electrons, photons, and force: quantitative single-molecule measurements from physics to biology. ACS Nano. 2011;5:693–729. doi: 10.1021/nn103298x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chen W., Zarnitsyna V.I., Zhu C. Measuring receptor-ligand binding kinetics on cell surfaces: from adhesion frequency to thermal fluctuation methods. Cell Mol. Bioeng. 2008;1:276–288. doi: 10.1007/s12195-008-0024-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Chen W., Evans E.A., Zhu C. Monitoring receptor-ligand interactions between surfaces by thermal fluctuations. Biophys. J. 2008;94:694–701. doi: 10.1529/biophysj.107.117895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bartsch T.F., Fišinger S., Florin E.L. Detecting sequential bond formation using three-dimensional thermal fluctuation analysis. ChemPhysChem. 2009;10:1541–1547. doi: 10.1002/cphc.200900211. [DOI] [PubMed] [Google Scholar]
- 33.Yago T., Wu J., McEver R.P. Catch bonds govern adhesion through L-selectin at threshold shear. J. Cell Biol. 2004;166:913–923. doi: 10.1083/jcb.200403144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Chen W., Lou J., Zhu C. Forcing switch from short- to intermediate- and long-lived states of the αA domain generates LFA-1/ICAM-1 catch bonds. J. Biol. Chem. 2010;285:35967–35978. doi: 10.1074/jbc.M110.155770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chen W., Lou J., Zhu C. Observing force-regulated conformational changes and ligand dissociation from a single integrin on cells. J. Cell Biol. 2012;199:497–512. doi: 10.1083/jcb.201201091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ju L., Dong J.-F., Zhu C. The N-terminal flanking region of the A1 domain regulates the force-dependent binding of von Willebrand factor to platelet glycoprotein Ibα. J. Biol. Chem. 2013;288:32289–32301. doi: 10.1074/jbc.M113.504001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Evans E., Ritchie K., Merkel R. Sensitive force technique to probe molecular adhesion and structural linkages at biological interfaces. Biophys. J. 1995;68:2580–2587. doi: 10.1016/S0006-3495(95)80441-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Evans E., Heinrich V., Kinoshita K. Nano- to microscale dynamics of P-selectin detachment from leukocyte interfaces. I. Membrane separation from the cytoskeleton. Biophys. J. 2005;88:2288–2298. doi: 10.1529/biophysj.104.051698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Skeel R.D., Berzins M. A method for the spatial discretization of parabolic equations in one space variable. SIAM. J. Sci. Stat. Comput. 1990;11:1–32. [Google Scholar]
- 40.Freund L.B. Characterizing the resistance generated by a molecular bond as it is forcibly separated. Proc. Natl. Acad. Sci. USA. 2009;106:8818–8823. doi: 10.1073/pnas.0903003106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lauffenburger D.A., Linderman J.J. Oxford University Press; Oxford, United Kingdom: 1996. Receptors: Models for Binding, Trafficking, and Signaling. [Google Scholar]
- 42.Fox J.E., Aggerbeck L.P., Berndt M.C. Structure of the glycoprotein Ib.IX complex from platelet membranes. J. Biol. Chem. 1988;263:4882–4890. [PubMed] [Google Scholar]
- 43.Varughese K.I., Celikel R., Ruggeri Z.M. Structure and function of the von Willebrand factor A1 domain. Curr. Protein Pept. Sci. 2002;3:301–312. doi: 10.2174/1389203023380620. [DOI] [PubMed] [Google Scholar]
- 44.Carvalho F.A., Connell S., Santos N.C. Atomic force microscopy-based molecular recognition of a fibrinogen receptor on human erythrocytes. ACS Nano. 2010;4:4609–4620. doi: 10.1021/nn1009648. [DOI] [PubMed] [Google Scholar]
- 45.Schmidt S.W., Filippov P., Clausen-Schaumann H. Single-molecule force-clamp experiments reveal kinetics of mechanically activated silyl ester hydrolysis. ACS Nano. 2012;6:1314–1321. doi: 10.1021/nn204111w. [DOI] [PubMed] [Google Scholar]
- 46.Homouz D., Stagg L., Cheung M.S. Macromolecular crowding modulates folding mechanism of α/β protein apoflavodoxin. Biophys. J. 2009;96:671–680. doi: 10.1016/j.bpj.2008.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Dustin M.L., Bromley S.K., Zhu C. Identification of self through two-dimensional chemistry and synapses. Annu. Rev. Cell Dev. Biol. 2001;17:133–157. doi: 10.1146/annurev.cellbio.17.1.133. [DOI] [PubMed] [Google Scholar]
- 48.Huang J., Zarnitsyna V.I., Zhu C. The kinetics of two-dimensional TCR and pMHC interactions determine T-cell responsiveness. Nature. 2010;464:932–936. doi: 10.1038/nature08944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Huppa J.B., Axmann M., Davis M.M. TCR-peptide-MHC interactions in situ show accelerated kinetics and increased affinity. Nature. 2010;463:963–967. doi: 10.1038/nature08746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Zarnitsyna V., Zhu C. T cell triggering: insights from 2D kinetics analysis of molecular interactions. Phys. Biol. 2012;9:045005. doi: 10.1088/1478-3975/9/4/045005. [DOI] [PubMed] [Google Scholar]
- 51.Zhu C., Jiang N., Evavold B.D. Insights from in situ analysis of TCR-pMHC recognition: response of an interaction network. Immunol. Rev. 2013;251:49–64. doi: 10.1111/imr.12016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Wu Y., Vendome J., Honig B. Transforming binding affinities from three dimensions to two with application to cadherin clustering. Nature. 2011;475:510–513. doi: 10.1038/nature10183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Robert P., Limozin L., Bongrand P. Biomolecule association rates do not provide a complete description of bond formation. Biophys. J. 2009;96:4642–4650. doi: 10.1016/j.bpj.2009.03.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Erdmann T., Schwarz U.S. Bistability of cell-matrix adhesions resulting from nonlinear receptor-ligand dynamics. Biophys. J. 2006;91:L60–L62. doi: 10.1529/biophysj.106.090209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Qian J., Wang J., Gao H. Lifetime and strength of adhesive molecular bond clusters between elastic media. Langmuir. 2008;24:1262–1270. doi: 10.1021/la702401b. [DOI] [PubMed] [Google Scholar]
- 56.Wofsy C., Goldstein B. Effective rate models for receptors distributed in a layer above a surface: application to cells and Biacore. Biophys. J. 2002;82:1743–1755. doi: 10.1016/S0006-3495(02)75526-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Crowl L., Fogelson A.L. Analysis of mechanisms for platelet near-wall excess under arterial blood flow conditions. J. Fluid Mech. 2011;676:348–375. [Google Scholar]
- 58.Zhao H., Shaqfeh E.S.G., Narsimhan V. Shear-induced particle migration and margination in a cellular suspension. Phys. Fluids. 2012;24:011902. [Google Scholar]


