Split diversity in constrained conservation prioritization using integer linear programming

Abstract

1. Phylogenetic diversity (PD) is a measure of biodiversity based on the evolutionary history of species. Here, we discuss several optimization problems related to the use of PD, and the more general measure split diversity (SD), in conservation prioritization.

2. Depending on the conservation goal and the information available about species, one can construct optimization routines that incorporate various conservation constraints. We demonstrate how this information can be used to select sets of species for conservation action. Specifically, we discuss the use of species' geographic distributions, the choice of candidates under economic pressure, and the use of predator–prey interactions between the species in a community to define viability constraints.

3. Despite such optimization problems falling into the area of NP hard problems, it is possible to solve them in a reasonable amount of time using integer programming. We apply integer linear programming to a variety of models for conservation prioritization that incorporate the SD measure.

4. We exemplarily show the results for two data sets: the Cape region of South Africa and a Caribbean coral reef community. Finally, we provide user-friendly software at http://www.cibiv.at/software/pda.

Introduction

Many important challenges in biodiversity conservation involve the prioritization of species, habitats or ecosystems for the allocation of limited conservation funding. These problems require techniques that allow the selection of units that maximize a quantity of interest, such as species diversity, phylogenetic diversity or ecosystem function, subject to some number of constraints (e.g. Purvis, Gittleman & Brooks ²⁰⁰⁵). A basic approach is to focus on taxon richness (Gaston & Spicer ²⁰⁰⁴) in order to maximize the number of taxa conserved. However, the assumption that all taxa are equally valuable may make taxon richness too simplistic (May 1990).

One approach to incorporating variation among species is to use indices that take into account phylogenetic information (Vanewright, Humphries & Williams ¹⁹⁹¹; Crozier ¹⁹⁹²; Faith ¹⁹⁹²), the most popular being phylogenetic diversity (PD; Faith ¹⁹⁹²). PD is the amount of evolutionary history encompassed by a given number of taxa (e.g. species) and is often predictive of phenotypic diversity or the ecosystem function provided by a set of taxa (Isaac et al. ²⁰⁰⁷; Cadotte, Dinnage & Tilman ²⁰¹²; Srivastava et al. ²⁰¹²; Winter, Devictor & Schweiger ²⁰¹³). Given a phylogenetic tree for a set of taxa, the PD of a taxon subset is calculated as the sum of branch lengths of the minimal subtree spanned by those taxa. PD depends on the availability of a single, reliable phylogenetic tree estimate with branch lengths and cannot readily be calculated when one wishes to use information from multiple trees. The single tree may be a species tree reconstructed from many genes that may have different evolutionary rates (Graur & Li ²⁰⁰⁰) or even support different tree topologies (Nei 1987). One may instead wish to weigh evidence across these gene trees, or across a number of candidate trees from bootstrap samples (Felsenstein 1985) or from a Bayesian posterior distribution (Yang & Rannala ¹⁹⁹⁷). To resolve this issue, we have recently introduced the concept of split diversity (SD), which generalizes PD by combining information from multiple trees (Minh, Klaere & von Haeseler ²⁰⁰⁹).

Integer linear programming (ILP; Gomory ¹⁹⁵⁸) is a widely used technique to solve optimization problems in various scientific disciplines (e.g. Jünger et al. ²⁰¹⁰) with great potential for conservation decision-making. ILP solves problems by optimizing a linear objective function subject to linear constraints acting on integral variables (such as the inclusion or exclusion of species). Theoretically, solving ILP is nondeterministic polynomial-time hard (NP-hard), meaning that to guarantee an optimal solution it may be necessary to evaluate exponentially many subsets of species (e.g. Karp ¹⁹⁷²).

With the advances of state-of-the-art ILP software packages such as CPLEX (2012) and GUROBI (2012) (free of charge for academic use) many NP-hard problems can be solved within a reasonable time while ensuring optimal solutions (Jünger et al. ²⁰¹⁰; and references therein).

Integer linear programming was first applied to the minimum representation problem in biodiversity conservation (Cocks & Baird ¹⁹⁸⁹). Subsequently, ILP has been applied to more complex topics such as minimizing the total land mass protected while maximizing the biodiversity (taxon richness or PD) given limited resources (e.g. Underhill ¹⁹⁹⁴; Possingham, Ball & Andelman ²⁰⁰⁰; Rodrigues & Gaston ²⁰⁰²; Önal & Briers ²⁰⁰³; Haight & Snyder ²⁰⁰⁹). Moreover, ILP also works for the more general SD measure (Minh, Klaere & von Haeseler ²⁰¹⁰) and predator–prey relationships (Faller 2010). However, to the best of our knowledge, none of the previous work considered species' diet compositions in the ILP formulations.

Here, we further show the efficiency and flexibility of ILP to maximize SD for more generalized conservation questions, the spatial reserve selection and viable taxon selection. We exemplify our approach with two case studies: the Cape of South Africa and the Caribbean coral reef community. We also show that the inclusion of ecological constraints into the ILP formulations is straightforward. Using the GUROBI library, the ILP problems are solved within a few seconds. We provide an implementation in the PDA software package (Minh, Klaere & von Haeseler ²⁰⁰⁹).

Materials and methods

Spatial reserve selection under split diversity

The classical minimum representation problem (Cocks & Baird ¹⁹⁸⁹) and spatial reserve selection (Moilanen, Wilson & Possingham ²⁰⁰⁹) assume that one has sufficient resources to protect all taxa (Data S1). However, if the minimal cost required exceeds the allocated budget, one can alternatively minimize the costs such that at least p% of the diversity is still preserved. To measure biodiversity, we utilize the concept of split diversity (SD; Minh, Klaere & von Haeseler ²⁰⁰⁹), but we note that other diversity measures are also applicable.

Spatial reserve selection was formulated as integer quadratic programming (Possingham, Ball & Andelman ²⁰⁰⁰), where one optimizes a quadratic objective function given linear constraints. Further, this problem was discussed and reformulated as ILP (Önal & Briers ^{2002, 2003}). Here, we transform the quadratic objective function into linear function and extend the initial problem to account for SD.

Let X = {s₁, s₂, …, s_n} denote the set of n taxa of interest. Further, for area i ∈ {1, …, m} let R_i ⊂ X denote the taxa present in area i. The question is then

Problem 1 (Spatial reserve selection under SD constraints): Given the taxon set X, m areas, the costs per unit boundary and a diversity threshold p, find the cheapest area subset 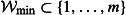such that the set of taxa preserved in W_min must constitute at least p% of the total SD of X.

We now formulate Problem 1 in ILP parlance. To this end, we construct the m × n presence/absence matrix 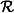, where r_ij = 1 if taxon s_j is present in area i, and r_ij = 0 otherwise. Moreover, we encode an arbitrary subset 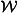of areas by the binary vector (x₁, x₂,…, x_m), where x_i = 1 if 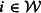, and x_i = 0 otherwise.

The spatial reserve selection includes the area conservation costs (e.g. acquisition and maintenance costs of the area) and boundary costs in terms of the cost of fencing the entire selected areas, where high boundary costs prevent highly fragmented areas. For area i ∈ {1, …, m}, we denote its cost by c_i. To quantify the boundary length, we define a symmetric m × m matrix with each entry b_ij being the shared boundary length between area i and j. If i and j are not adjacent we set b_ij = 0. Finally, b_ii equals the perimeter of i. β defines the conservation cost per unit boundary length.

For each pair of adjacent areas i and j (b_ij > 0), we introduce variable z_ij, where z_ij = 1 if x_i = x_j = 1 and z_ij = 0, otherwise (i.e., ).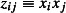

The linear function equivalent to quadratic objective function in Possingham, Ball & Andelman (2000) is given by

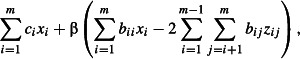where variables z_ij are constrained by z_ij ≤ x_i and 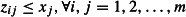, which ensures that z_ij = x_ix_j Note that the number of introduced variables z_ij is typically much smaller than 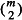as only pairs of spatially adjacent areas are relevant.

To introduce SD constraints, we follow the notations of Minh, Klaere and von Haeseler (2010) by denoting an input split system as (Σ, λ) where Σ is a set of splits (bipartitions of X) and λ the split-weight function. A split σ ∈ Σ is represented by an n-element binary vector (σ₁, σ₂,…, σ_n), where n is the number of taxa and σ_i takes a value of 0 or 1 depending on the bipartition that s_i belongs to. Note that the vector (1 − σ₁, 1 − σ₂,…, 1 − σ_n) represents the same split.

For an area subset 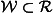, denote X|w the subset of taxa present in at least one area in W. To compute SD of X|w based on the split system (Σ, λ), we introduce a so-called split variable y_σ for every split σ, where y_σ = 1 if σ separates at least two taxa of X|w, and y_σ = 0 otherwise. It then follows that

Finally, problem 1 is formulated as:

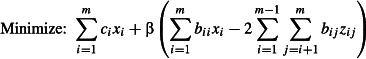eqn 1.1

eqn 1.2

eqn 1.3

eqn 1.4

eqn 1.5

The objective function (1.1) together with constraints (1.2) is equivalent to that of the spatial reserve selection. The so-called split constraints (1.3 and 1.4) determine the values of y_σ. The inequality (1.5) ensures the conservation target p% of SD.

Taxon selection under viability constraints

We now turn to another problem that arises when predator–prey interactions between species are incorporated into conservation decisions. If the candidate species for prioritization depend on each other, as in a food web representing the predator–prey relationships among community members, our prioritization can account for such information. For example, we may wish to select a set of taxa S with maximal diversity under the constraint that these taxa form a viable food web (Moulton, Semple & Steel ²⁰⁰⁷). Here, we focus on the bottom-up dependencies represented in food webs, so that a taxon is defined as viable in S if it is either a basal taxon in the food web (i.e. a species without prey such as a primary producer) or a predator that has at least one prey in S. S is called viable if all its taxa are viable. The problem is now formulated as:

Problem 2 (Viable taxon selection): Given a food web and a phylogenetic tree, choose a viable subset of at most k taxa, which maximizes PD.

Problem 2 has been solved using ILP (Faller 2010). In the following, we will further generalize the problem from PD to SD (Problem 3) and propose an extended definition of viability that includes diet composition (Problem 4).

Extension to SD

Problem 3 (Viable taxon selection under SD): Given a food web and a split system (Σ, λ), choose a viable subset of at most k taxa, which maximizes SD.

We transform Problem 3 into an ILP. To this end, we introduce for each taxon s_i ∈ X a taxon variable v_i. A subset S ⊂ X is represented by a vector (v₁,…, v_n), where v_i = 1 if s_i ∈ S and v_i = 0 if s_i ∉ S. For each split σ ∈ Σ, we introduce a split variable y_σ, where y_σ = 1 if σ separates at least two taxa in S, and y_σ = 0 otherwise.

Following the notation of Moulton, Semple & Steel (2007), we denote by D = (X, A) a directed acyclic graph representing the food web, where A denotes the set of arrows (directed edges) represented as a pair of taxa, s.t. (s_i, s_j) ∈ A if taxon s_i feeds on s_j. We denote by C_i the set of preys of s_i. If C_i = ∅, s_i is called a basal prey.

Problem 3 is then equivalent to:

eqn 3.1

eqn 3.2

eqn 3.3

eqn 3.4

eqn 3.5

The resulting solution (v₁, …, v_n) corresponds to a set S_max, which is ensured by constraint (3.2) to contain at most k taxa. Preservation of split σ_i is provided by the constraints (3.3 and 3.4) and viability of a subset is assured by constraint (3.5).

If we want some of the taxa to be included in S_max irrespective of constraints, we simply set the corresponding ν_j = 1.

Extension to account for diet composition

Problems 2 and 3 consider a predator as a viable member of a food web even if only one of its prey taxa is conserved. However, if the conserved prey taxon makes up only a small fraction of the predator's diet, the predator is unlikely to maintain sufficient food intake to be treated as a viable species. For that reason, we introduce a more realistic definition of viability that considers the diet composition of predators. To this end, we denote by D = (X, W) a weighted food web of the taxon set X, where W is the diet composition matrix. Here, we weight the arrow (s_j, s_i) of the food web by w_ij, the proportion of prey s_i in the diet of predator s_j, such that the diet composition for each predator sums up to 100%, (i.e. 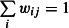for every predator s_j).

Using (X, W), we compute the total diet of a predator s_j over all of its prey taxa in a set S as:

This allows us to set a constraint that each predator must have a minimum proportion of its prey composition preserved for a set of taxa to be viable. We define a subset S of taxa as d%-viable if every predator s_j ∈ S has the score δ (s_j|S) ≥ d.

Problem 4 (d%-viable taxon selection under SD): Given a weighted food web D = (X, W) and a split system (Σ, λ), select a d%–viable subset of at most k taxa, which maximizes SD.

Problem 4 is again solved with ILP by simply modifying constraint (3.5) in Problem 3 to:

Software availability

We provide a user-friendly software package PDA (Minh, Klaere & von Haeseler ²⁰⁰⁹), freely available at http://www.cibiv.at/software/pda, to carry out conservation prioritization analysis based on PD and SD including various constraints. The user inputs a phylogenetic tree or a split network and additional information relevant for the conservation decision problem (i.e. areas data, costs for areas, costs for species, weighted or non-weighted dependency networks such as food webs). As a result, PDA outputs optimal taxon or area sets selected by ILP and detailed information about the sets. Additional details are explained in the user manual.

Results

Case study I: The cape of South Africa

We analyse a data set consisting of 735 flowering plant genera (Forest et al. ²⁰⁰⁷; Data S1) distributed over 201 quarter-degree squares (QDS; ca. 25 × 27 km²) of the Cape of South Africa, a biodiversity hotspot (Myers et al. ²⁰⁰⁰). The Cape region is a small area (ca. 90 000 km²) in the southernmost part of the African continent and is one of the most botanically species-rich areas of the world with more than 9000 species, of which almost 70% are endemic (Goldblatt & Manning ²⁰⁰²). This especially rich biodiversity has been extensively documented (Goldblatt & Manning ²⁰⁰²; Linder ^{2003, 2005}) and its importance as one of the major repositories of global biological diversity has been widely acknowledged (Linder 2001; Kuper et al. ²⁰⁰⁴; Mittermeier et al. ²⁰⁰⁵; Kreft & Jetz ²⁰⁰⁷). Among the 735 genera in this data set, 274 include at least one species classified as vulnerable, endangered or critically endangered (Raimondo et al. ²⁰⁰⁹); these will be referred here as threatened genera. Of the 274 threatened genera, 17 belong to the top-20 most-threatened genera of South Africa, based on the proportion of their species that are threatened (Raimondo et al. ²⁰⁰⁹).

QDS selection under split diversity

The minimum representation and spatial reserve selection (for the analysis, see Data S3) are solely based on the concept of genus richness. However, it was shown that genus richness and PD are decoupled in the Cape of South Africa and that PD is more appropriate than genus richness in certain conservation scenarios (Forest et al. ²⁰⁰⁷). Here, we take one step further by considering split diversity (Minh, Klaere & von Haeseler ²⁰⁰⁹) across the 100 bootstrap trees based on the rbcL sequence alignment (Data S2). Moreover, we extend the reserve selection to account for a diversity constraint that at least p% of SD must be preserved, which can be solved again with ILP (Problem 1; Materials and Methods). If p = 100%, the problem is identical to the spatial reserve selection. If p < 100%, we only protect a fraction of taxa, needing only a fraction of the areas. Such a scenario is typically applied when the available budget does not suffice to save 100% of diversity.

To conserve p = 95%, only seven QDS are necessary (depicted in blue and hatched; in Fig. 1), while for p = 100% 28 QDS were selected (Fig. S1). The selected QDS cover the Cape Peninsula (three QDS), part of the afrotemperate forests along the southern coast (three QDS) and one QDS in the Port Elizabeth area. Notably, the total cost in terms of area, which shall be incurred when 95% of the SD is conserved, is 2410 km², less than one-fifth of the area needed for a conservation goal of 100% (Fig. S1). This means saving the last 5% of diversity needs four times the budget required by the first 95%.

Fig 1.

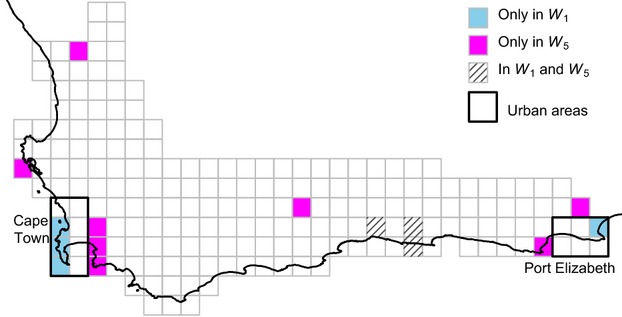
QDS selected to conserve 95% of split diversity under uniform conservation cost (W₁) and under prioritization of rural areas (W₅).

Impact of economic pressure

The reserve selections presented so far implicitly assume uniform conservation cost per km². This is unrealistic since it is more expensive to establish reserves in the vicinity of big cities (Cape Town and Port Elizabeth) than in rural areas. We therefore extend the model by increasing the conservation cost per km² of QDS in the urban areas relative to those of rural areas. The cost ratio between the urban and rural areas represents the economic pressure put on urban areas. Because the ILP solution can be rapidly computed, we could analyse several different scenarios. As QDS close to Cape Town and Port Elizabeth are defined here as more expensive, the conservation cost increases for fixed p (Fig. 2a).

Fig 2.

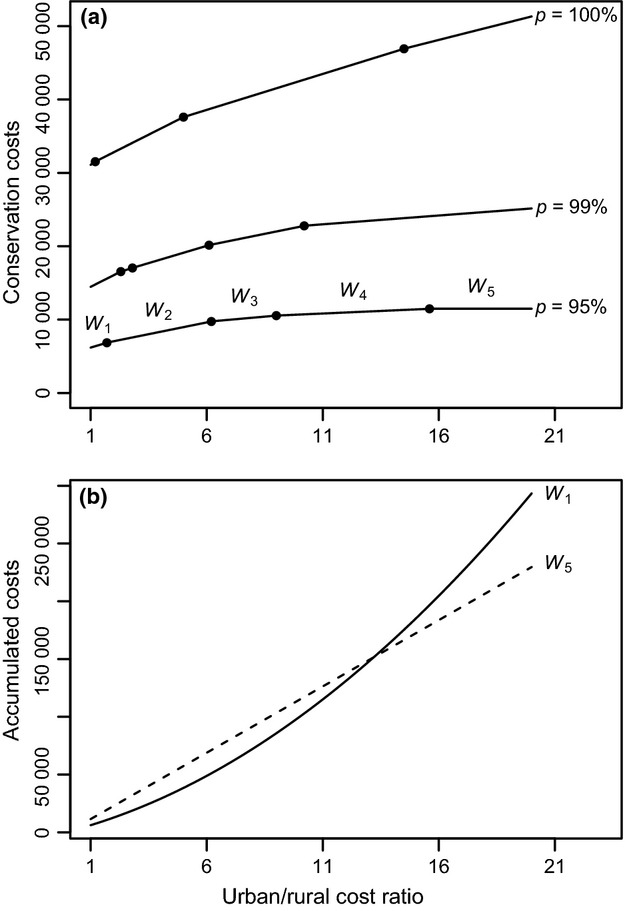
(a) Minimal costs to conserve p = 95%, 99% and 100% of split diversity with varying urban/rural cost ratios. The points on the curves indicate the change in the optimal sets of QDS found by ILP. For p = 95%, we identified five optimal sets denoted by W₁ to W₅. Also note that preserving the last 1% of diversity more than doubles the conservation cost. (b) Accumulated costs for optimal sets of QDS W₁ and W₅ as the cost ratios gradually increase over time.

Because we want to conserve a certain fraction of current diversity at minimal costs, sometimes the selected QDS-set will change. Each interval of the curves in Fig. 2a reflects a selected set of QDS. For example, for p = 95%, five different sets of optimal QDS are identified and denoted as W₁ to W₅ (Fig. 2a and Table 1). The selected QDS in W₁ to W₅ gradually move away from the cities (Table 1 and Fig. S3). For price ratios larger than 15·6, all selected QDS (W₅) are outside urban regions and a further increase of costs next to big cities does not affect the conservation decision, indicated by a slope of zero (Fig. 2a). Minimizing costs has different effects on the conservation success of threatened genera (Table 1). If we consider the most-threatened genera, then irrespective of the costs we will always lose Polhillia (Leguminosae). This genus occurs in 8 QDS (Fig. S4), which are never included in the selected QDS. Nevertheless, we always preserve 585 (ca. 80%) genera regardless of the cost ratios, 235 (ca. 86%) of which are threatened.

Table 1.

Features of the five optimal sets of QDS (W₁ to W₅) to preserve 95% of split diversity under different urban/rural cost ratios. The sets of QDS for W₂, W_3, W₄ can be found in Fig. S3

Urban/rural cost ratio range	1–1·7	1·8–6·2	6·3–9·0	9·1–15·6	>15·6
QDS-set	W1 (Fig. 1)	W2	W3	W4	W5 (Fig. 1)
#QDS	7	7	9	9	11
#Urban QDS	4	3	3	1	0
Area (km2)	2410	2150	3200	3805	4970
#Genera	648	656	660	657	662
#Threatened genera	244	249	254	253	250
Most-threatened genera that are not conserved	Polhillia Clivia Daubenya Marasmodes	Polhillia Clivia Daubenya	Polhillia	Polhillia Clivia Daubenya	Polhillia Clivia Daubenya

Figure 2a allows a second interpretation of the costs for biodiversity efforts that will lead to economically more sustainable conservation decisions. If we take the urban/rural cost ratio as the economic pressure put on the urban areas in the future, then we can read the graph as the extrapolation of running costs incurred in the future for a fixed value of p. For each set of QDS selected the costs to protect will increase linearly with increasing price ratio (this follows from the ILP formulation of the problem). The total costs that will accumulate over the years will therefore grow quadratically. The only exceptions are selected areas where the conservation costs are independent of the price ratio, like W₅ for p = 95%. However, the conservation costs at present are 11 482 virtual price units for W₅ compared with 6186 virtual price units for W₁. But in the long run, the accumulated costs will be lower for W₅ (Fig. 2b). Therefore, given the prediction about the economic pressure imposed on urban areas, it may be better to select W₅ right from the beginning, because the most inexpensive selection (W₁) will already accumulate more costs if the price ratio is larger than 13·2 (Fig. 2b).

Case study II: Caribbean coral reef community

The second case study demonstrates how predator–prey interactions can be incorporated in the analysis used for conservation prioritization. We examine a food web representing the predator–prey relationships of 242 taxa (mostly species) and 6 aggregated trophic groups from a Caribbean coral reef community (Table S1).

Of the 248 nodes in the food web, all but the four basal nodes depend on consumption of at least one other taxon, and all but one (tiger shark, Galeocerdo cuvier) is prey for at least one other taxon. The food web is characterized by a complex structure and extensive omnivory, with food chains of as many as 25 links. Thus, this ecological network features extensive and complex dependencies among species that must be accounted for if we are to select a viable subset of taxa.

For the 242 taxa, we obtained sequences for six distinct genes if available (Table S3), computed for each gene a multiple sequence alignment and reconstructed six maximum likelihood (ML) trees (Fig. S7), that served as input to infer a split system (Σ, λ) (Data S2 and Fig. S9). We also computed the ML tree T (Fig. S8) from the concatenated alignments. We used T and (Σ, λ) to compute PD and SD, respectively. The split system (Σ, λ) contains 558 non-trivial splits (i.e. splits that contain at least two taxa on either side), which is 2·3 times more splits than T. This indicates that the six gene trees are incongruent. This incongruence has a number of potential causes, including insufficient phylogenetic information, noise in the alignments or even non-treelike evolution (Doolittle 1999; Philippe et al. ²⁰¹¹).

We now discuss the optimal taxon sets obtained under different constraints. We require that the aggregate trophic groups are always included in the optimal sets, because they are at the base of the food web and because they represent taxonomically diverse collections of organisms rather than defined taxa.

Maximizing PD or SD without taking into account the food web leads to inviable sets, where Synodus foetens and Antennarius striatus do not find prey (Data S3 and Fig. S5). Therefore, in the following, we require that the optimal SD set is viable (i.e. each predator must have at least one prey in the set). The problem is then called Viable Taxon Selection under SD (Problem 3).

The resulting optimal set denoted S₁ (red and blue nodes; Fig. 3) containing 10% of the taxa has a relative SD of 57·67% compared with the total SD of all taxa (i.e. only 0·22% less than the taxon-set chosen solely on SD). This loss in relative diversity is due to the replacement of Antennarius striatus (the ‘non-viable’ species, Data S3) with Elacatinus evelynae. Therefore, S₁ ‘repairs’ the viability with negligible loss of diversity.

Fig 3.

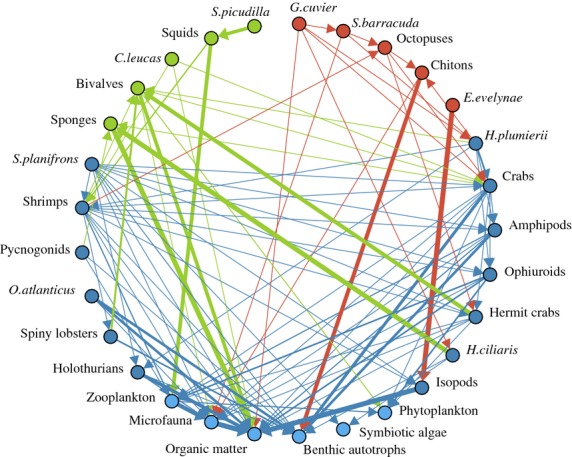
Food web restricted to only those taxa present in S₁ or S₂ (see main text). Red, green and blue nodes depict the taxa present exclusively in S₁, exclusively in S₂, and in both sets, respectively. Light blue nodes correspond to aggregated groups. Arrows connect from predators to their preys with thickness reflecting the prey proportion in the predator diet. Arrows pointing to or from green and red nodes are coloured green and red respectively. Arrows between blue nodes are coloured blue. Note that the arrows between green and red nodes are ignored.

We now look in more detail at the diet composition of the species in S₁. For each predator s_j ∈ S₁, we compute its proportion of diet conserved in 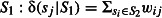, where 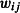is the proportion of prey s_i in the diet of s_j (Materials and Methods). For the taxa Galeocerdo cuvier, octopuses, Sphyraena barracuda and Holacanthus ciliaris (four red nodes; Fig. 3) only 11%, 7%, 6% and 2% of their diet is conserved, while for pycnogonids, hermit crabs, spiny lobsters and Haemulon plumierii the diet proportion conserved ranges between 20% and 50% (Table S4).

The above observations indicate that the simple viability constraint (conserving at least one prey per predator) might result in some predators having an insufficient availability and variety of prey. To address this, we applied the d%-viability constraint, which requires that every taxon in the optimal SD set must have at least d% of its diet composition conserved (Materials and Methods). Note that the d%-viability constraint reduces to the simple viability constraint if we set d = ∈ (i.e. a very small number). Despite this additional constraint, the problem of d%-viable taxon selection can still be solved by ILP (Problem 4, Materials and Methods).

As an illustration, for k = 24 and d = 30%, the optimal set S₂ (green and blue nodes; Fig. 3) has a relative SD of 56·36%, a reduction of 1·31% compared with S₁. Moreover, more stringent viability constraints with higher d still provide almost equally optimal subsets (Data S3 and Fig. S6).

S₂ has five species (green nodes; Fig. 3) not present in S₁. At the same time, five taxa (red nodes; Fig. 3) are not present in S₂, of which G. cuvier, octopuses and S. barracuda have less than 30% diet conserved by their preys in S₁. On the other hand, pycnogonids, H. ciliaris and hermit crabs, which have less than 30% diet conserved in S₁, now become 30%-viable in S₂. This is because the newly added taxon (bivalves; green node; Fig. 3) is a prey of hermit crabs, contributing 80% to their diet. Another new taxon (sponges) being a prey of pycnogonids and H. ciliaris contributes to their diets 15% and 97% respectively, making them 30%-viable.

Computational time and optimality

The computational time to solve all the problems with the PDA software was less than 8 s on a 2·66 GHz computer. 98% of the runs for different parameters of Problem 4 consumed less than 1 s with a maximum of 3 s. Simulations with varying complexities of split networks and food webs yielded average run times of 2 s, with a maximum of 8 s.

We also applied the software Marxan 2.1.1 (Ball, Possingham & Watts ²⁰⁰⁹; Data S3) to the minimum representation and spatial reserve selection (subproblems of Problem 1) for the first case study. Marxan found optimal solutions in only 7/50 runs and 3/50 runs, respectively. Marxan also required 20 min for 50 runs. Therefore, Marxan does not guarantee optimal solutions while requiring more computations than PDA.

Discussion

We have presented ILP solutions for various biodiversity optimization problems that incorporate SD and include economic and ecological constraints. The first advantage of ILP compared to other approaches is its flexibility: we can account for a variety of constraints while using the same basic formulations. While many other computational techniques have been introduced for some of the problems presented (Chernomor et al. ²⁰¹⁴; and references therein), here, we further show that ILP provides a general framework to address many more problems without much extra effort. Therefore, the PDA software provided here complements existing conservation prioritization tools such as Marxan or Zonation (Moilanen, Kujala & Leathwick ²⁰⁰⁹).

The second advantage of ILP is the computational efficiency and the guarantee of optimality. Thanks to the powerful GUROBI solver employed, the analyses were carried out within seconds (Data S3). This is contrary to the computing times reported by Pressey, Possingham & Margules (1996) but in accordance with others (Rodrigues & Gaston ²⁰⁰²; Önal ²⁰⁰⁴). The different time requirements might be explained by inefficient ILP solvers (LP_SOLVE and LINGO) whereas Rodrigues & Gaston (2002) used the well-known CPLEX library (see also Önal ²⁰⁰⁴).

We demonstrated the practical utility of ILP with two large-scale case studies: the flora of the Cape region of South Africa and the Caribbean reef food web. In the first case study, the inclusion of the increasing protection costs in urban areas acts as a paradigm of how future developments may influence present day decisions. Such a model suggests a long-term conservation goal that appears expensive for the time being but will be more sustainable in the future. Admittedly, one limitation of the Cape region example is the simple cost model, mainly due to the unavailability of land price data. However, more complex cost indices can be easily incorporated thanks to the flexibility of the ILP paradigm. Further limitations include the somewhat coarse nature of the data (i.e. genus-level phylogenetic trees and quarter-degree square distribution data). The latter may be inappropriate for the conservation purposes due to the large area covered by a QDS (ca 675 km²) and the heterogeneity of the landscape in the Cape of South Africa. This situation leads to a relatively high species turnover along environmental and geographical gradients (Cowling, Holmes & Rebelo ¹⁹⁹²).

The Caribbean food web example demonstrates the usage of viability constraints in conservation prioritization thanks to the availability of food web and diet composition data. Such food webs allow us to analyse an entire set of species as an interaction network rather than as isolated units. We find that in the case of the Caribbean food web, including viability constraints results in only small reductions in the amount of biodiversity that can be preserved. This is explained by the fact that the most evolutionarily distant taxa are concentrated on the low trophic levels of the food web. Therefore, by maximizing PD or SD for the Caribbean community, we already obtained almost viable sets. However, taxon selection based on viability also highlighted which representatives of each subclade contribute to viability of the set. In practice, incorporating viability constraints has the potential to prevent the use of limited resources on specialist taxa unless a sufficient resource base to support them is also preserved.

While the incorporation of predator–prey links and diet composition gets us closer to ecological realism, there are nonetheless many factors that are not accounted for in the examples described here. First, we are only considering predator–prey relationships, and not other interaction types such as mutualism, facilitation or interference competition (Kefi et al. ²⁰¹²). This framework should be applicable to other types of interaction networks, such as mutualism networks, that allow viability criteria to be specified. For example, a viable taxon may require the preservation of at least one mutualist partner sufficient to contribute a certain fraction of mutualist benefit. We also consider only the bottom-up dependencies within food webs, not top-down effects of predators on their prey (e.g. apparent competition, trophic cascades). The proper incorporation of the complexity of interactions that result from top-down effects may require a move from a static representation of a food web to a population-dynamic model that explicitly includes extinction due to population decline (Ebenman, Law & Borrvall ²⁰⁰⁴). However, this is beyond the scope of this paper.

One may also need to consider how and if it is appropriate to incorporate diet composition to ensure that each taxon has at least d% of its food base preserved. Most published food webs contain only a topological representation of predator–prey relationships, and large food webs such as the Caribbean data set that include weights representing energy flow or diet composition are rare. However, even in the absence of diet composition data, one has the option of assigning the links between a predator and each of its n prey a weight of 1/n, assuming that they are of equal importance. This allows the application of additional criteria; for example, that a viable predator must have access to at least 50% of its prey taxa. Where diet composition data are available, they provide a means of indirectly considering taxon abundances, as more abundant taxa will generally make up a greater proportion of their predators’ diets. Further, if some prey types are only available during certain seasons, one could devise ‘seasonal constraints’ (similar to area constraints) ensuring that some prey taxa are present for every season. Finally, one could consider contributions from preys that do not appear in the food web (e.g. preys consumed outside the spatial area covered by the food web data) by crediting these predators with some proportion of their prey intake regardless of the taxon set selected. Such additional constraints can be easily included in the ILP framework.

The set of taxa returned by the optimization procedure is a starting point for conservation planning, but should be followed by consideration of the biology of the selected taxa. A food web is a simplified representation of a community or meta-community and lacks information that might bear on the suitability of the taxon set. For example, it should be confirmed that the prey taxa predicted to support each predator are sufficiently abundant and widespread to do so, or that they can reasonably be expected to become more common as a result of conservation action. If the food web contains errors, such as a link between taxa that no longer co-occur or the omission of an important link, it might lead to suboptimal taxon selection. Further, taxa may be subject to additional constraints that may be difficult to capture in the ILP, so at times it may be necessary to reconsider the taxa targeted for conservation action in light of additional biological or societal information.

We note that the ILP framework is extensible to other diversity measures provided that the measures can be expressed as a linear function, for example the number of segregating sites (Watterson 1975; Bryant & Klaere ²⁰¹²). Moreover, the spatial reserve selection under SD (Problem 1) can be extended to take into account abundance data (e.g. the population size of plant species). The constraint is then to preserve at least the minimum abundance required for the persistence of each taxon. Another extension to the viable taxon selection problems 2, 3 and 4 is to choose species under budgetary constraints. Here, each species has a conservation cost and the inclusion of the taxon is constraint by the budget. Close collaboration between conservation biologists and mathematicians is recommended to convert complex conservation problems into an ILP framework (see also Underhill ¹⁹⁹⁴).

The importance of preserving the diversity of life is widely recognized and understood. In an ideal world, we could ensure the persistence of all levels of biodiversity, but with limited resources the prioritization of some taxa or ecosystems is unavoidable. We thus need good criteria with which to apply triage, to prioritize the allocation of these resources to maximize conservation return under budget constraints (Bottrill et al. ²⁰⁰⁸). We have demonstrated the utility of the ILP approach to show how sensible and objective conservation decisions can be made in a world of limited resources, numerous economical and ecological constraints. The evaluation of different future scenarios with the aid of the ILP approach presented here will certainly prove to be a valuable contribution to conservation planning in a changing world.

Data accessibility

All data used in this manuscript are present in the manuscript and its supporting information.

Supporting Information

Additional Supporting Information may be found in the online version of this article.

Data S1

Reserve Selection Problems Revisited.

Data S2. Data description.

Data S3. Additional results and analysis.

Table S1. Diet composition matrix for 250 Caribbean species.

Table S2. NCBI accession numbers of six genes for Caribbean case study.

Table S3. Sequence data collected for Caribbean case study.

Table S4. List of taxa in optimal sets S_PD, S_SD, S₁, S₂ for Caribbean case study.

Fig. S1. QDS chosen by the minimum representation problem and the spatial reserve selection for the Cape of South Africa.

Fig. S2. QDS determined by Marxan for the minimum representation problem.

Fig. S3. QDS for W₂, W₃, W₄.

Fig. S4. QDS that host the threatened genera Polhillia, Clivia, Daubenya, and Marasmodes.

Fig. S5. Food web restricted to only those taxa present in S_PD or S_SD.

Fig. S6. Dependence of SD on subset size, k, and diet portion, d.

Fig. S7. Gene trees for 12S rRNA, 16S rRNA, 18S rRNA, 28S rRNA, COI, CYTB.

Fig. S8. Tree for supermatrix of six genes.

Fig. S9. Super split network of six gene trees.