Riboswitch Conformations Revealed by Small-Angle X-Ray Scattering

Summary

Riboswitches are functional RNA molecules that control gene expression through conformational changes in response to small-molecule ligand binding. In addition, riboswitch 3D structure, like that of other RNA molecules, is dependent on cation–RNA interactions as the RNA backbone is highly negatively charged. Here, we show how small-angle X-ray scattering (SAXS) can be used to probe RNA conformations as a function of ligand and ion concentration. In a recent study of a glycine-binding tandem aptamer from Vibrio cholerae, we have used SAXS data and thermodynamic modeling to investigate how Mg²⁺-dependent folding and glycine binding are energetically coupled. In addition, we have employed ab initio shape reconstruction algorithms to obtain low-resolution models of the riboswitch structure from SAXS data under different solution conditions.

1. Introduction

Since the discovery of catalytic RNA by Cech and Altman in the early 1980s it has become increasingly clear that RNA, like proteins, can fold into intricate 3D structures to carry out cellular functions. The RNA backbone, unlike proteins, is highly negatively charged and RNA folding and interactions are therefore dependent on the presence of positively charged cations (1, 2). Ion-dependent RNA folding has been studied by a number of techniques, including footprinting methods (3, 4), gel mobility, NMR spectroscopy (5), and fluorescence resonance energy transfer (6, 7).

SAXS has been an important technique to monitor ion-induced RNA folding (8–15). In particular, SAXS measurements have shown that RNA molecules undergo rapid compaction on the millisecond time scale upon addition of ions, driven primarily by electrostatic shielding. Formation of native tertiary interactions and folding to the catalytically active conformation, in contrast, can be much slower.

Recently, the discovery of riboswitches has further increased the interest in RNA structure and conformations. Riboswitches are RNA molecules located in the 5′-UTR of mRNA that are capable of binding small-molecule metabolites. Small-molecule binding to the aptamer domain causes conformational changes that directly regulate gene expression, at the transcriptional or translational level, without the need for protein cofactors. For recent reviews of riboswitch mechanisms and structures see refs. 16–22.

The glycine-binding VCI-II aptamer from Vibrio choleraeis part of a particular intriguing riboswitch (23). It features two glycine-binding sites that bind glycine cooperatively (23). We have used SAXS in combination with hydroxyl radical footprinting to follow the conformations of the VCI-II tandem aptamer as a function of glycine and Mg²⁺ concentration (24). The results show that, on going from low salt concentrations to high Mg²⁺ (10 mM) conditions, the molecule undergoes a partial folding transition characterized by significant conformational changes and compaction. Addition of glycine in the presence of millimolar Mg²⁺ leads to a further conformational change and compaction upon glycine binding. Thermodynamic modeling has indicated that the second transition from the conformation in high Mg²⁺ alone to the glycine-bound state requires the association of additional Mg²⁺ ions (24).

In a follow-up study, we have probed the structure of the VCI-II tandem aptamer in the absence and presence of glycine for a range of different mono- and divalent ions. The results indicate that partial folding in the absence of glycine can be induced by any of the tested ions and is likely dominated by unspecific electrostatic contributions of the ion atmosphere. Glycine binding, in contrast, is not observed in monovalent and certain divalent ions (Sr²⁺, Ba²⁺) and likely requires specific ion binding (Jan Lipfert, Adelene Y.-L. Sim, Daniel Herschlag, and Sebastian Doniach, in preparation).

In this chapter, we describe in detail how SAXS measurements can be used to study the conformations of functional RNAs as a function of salt and ligand concentration by using the VCI-II tandem aptamer as a representative example. Particular emphasis is given to the use of ab initio 3D structure reconstruction algorithms. Programs to obtain low-resolution shapes from SAXS data have first been developed for applications to proteins and protein complexes (25–27). Recently, we have shown that these programs can be successfully applied to nucleic acids (28). In the case of the VCI-II tandem aptamer, we have obtained low-resolution reconstructions of all three thermodynamic states (the low salt or unfolded state, the compact intermediate, and the fully folded and glycine-bound state) by using the 3D reconstruction algorithm DAMMIN (24).

2. Materials

All chemicals are purchased from Sigma-Aldrich, Co., unless otherwise noted. Chemicals are dissolved in deionized, RNase-free Milli-Q water; stocks are prepared every 1–3 months and stored at −20°C.

2.1. In Vitro RNA Transcription

1. 10× Transcription buffer (quantities for 50 mL stock): 20 mL 1 M Tris–HCl, pH 8.1, 12.5 mL 1 M magnesium chloride, 1 mL 1 M spermidine, 0.5 mL 10% Triton X-100, 16 mL deionized, RNase-free Milli-Q water.

2. 1 M Dithiothreitol (DTT).

3. 10 mM NTP stock: 10 mM each of ATP, CTP, GTP, and UTP. Stocks are adjusted to pH 7.0 by addition of sodium hydroxide. Concentrations are determined from the absorbance at 259, 272, 252, and 262 nm, respectively. The absorption coefficients are α₂₅₉(ATP) = 15.3 × 10³ (M cm)⁻¹, α₂₇₂(CTP) = 9.6 × 10³ (M cm)⁻¹, α₂₅₂(GTP) = 13.7 × 10³(M cm)⁻¹, and α₂₆₂(UTP) = 9.9 × 10³(M cm)⁻¹.

4. T7 RNA polymerase, ≈50,000 U/mL.

5. DNA template with T7 promoter (T7 promoter sequence: GCGCTTAATACGACTCACTATA). Short DNA templates (up to 100 bp) can be purchased from Integrated DNA Technologies (http://www.idtdna.com). The DNA template for the VCI-II riboswitch was created by PCR ligation (29).

6. 0.5 M Sodium ethylenediamine tetraacetic acid (EDTA), adjusted to pH 8.

7. 3 M Na-acetate, pH 5.4.

8. Cold ethanol, stored at −20°C.

9. Oakridge 50-mL centrifuge tubes.

2.2. RNA Gel Purification

1. 10× Tris–borate–EDTA (TBE) buffer. For 2 L stock, use 242 g Tris base (1 M final concentration), 102.7 g boric acid (0.83 M final concentration), and 7.44 g EDTA. Adjust volume to 2 L with RNase-free Milli-Q water and autoclave. Final 1× TBE buffer has pH ~8.0.

2. 8% Acrylamide gel mix. For 1 L stock, dissolve 420 g urea in 800 mL water (for 7 M urea final concentration). Add 200 mL 40% acrylamide (29:1 acrylamide:bis-acrylamide) solution.

3. Tetramethylethylenediamine (TEMED).

4. 10% Ammonium persulfate (APS).

5. Loading dye solution for gel purification. For 10 mL stock, add 0.4 mL 0.5 M EDTA solution to 9.6 mL formamide (for a final EDTA concentration of 20 mM). Add ≈2 mg/mL xylene cyanol and bromophenol blue.

6. Tris–EDTA–NaCl (TEN) buffer. For 250 mL stock, use 2.5 mL 1 M Tris–HCl (final concentration: 10 mM), pH 8, 417 μL 600 mM EDTA (final concentration: 1 mM), and 25 mL 3 M NaCl (final concentration: 300 mM). Add water to 250 mL final volume and filter through a 0.2-μm pore size syringe filter.

7. 50-mL Falcon tubes (BD Biosciences, San Jose, CA).

2.3. SAXS Measurements

1. 10× (500 mM) Na–MOPS buffer, pH 7.0.

2. 10× (100 mM) glycine stock.

3. 10× MgCl₂ stocks: 0.01, 0.02, 0.05, 0.1, 0.2, 0.5, 1.0, 2.0, 5.0, 10.0, 20.0, 50.0, 100.0, and 200.0 mM.

4. 50 kDa Cut-off microcone centrifuge filters (Millipore).

2.4. SAXS Molecular Weight Standard

1. 100 mM Na-acetate buffer, pH 5.4.

2. Guanidine hydrochloride (GdnHCl).

3. Horse heart cytochrome c, lyophilized.

4. 0.2-μm Pore size syringe filters and sterile syringes.

3. Methods

3.1. How Much RNA Is Required for a SAXS Measurement?

3.1.1. RNA Concentration Requirements

The forward scattering I(0) from an RNA or protein sample in solution in a SAXS experiment is given by

$$I(0)=K\mathrm{c}{(v\mathrm{\Delta }\rho )}^2{(\text{MW})}^2,$$ (1)

where c is the concentration, MW is the molecular weight of the macromolecule, Δρ is the average electron contrast of the molecule, ν the partial specific volume, and K is a constant that depends on parameters of the measurement setup and is typically determined from comparison with a molecular weight standard. Eqn. 1 is valid only if interparticle interference effects are negligible, which is typically the case in SAXS measurements of biological samples (see later). Equation 1 provides a useful guideline to determine appropriate sample concentrations. The scattering contrast (Δρ)² is approximately constant for all RNA molecules (and about five times larger for RNA compared to proteins (12)). The expected scattering signal is therefore linear in the (molar) concentration and increases quadratically with the molecular weight of the sample. The VCI-II tandem aptamer comprises 226 residues and has a molecular weight of ≈70 kDa. With the SAXS set up at beam line 12-ID at the Advanced Photon Source, high-quality scattering profiles can be obtained with an RNA concentration of 20 μM for this construct. For smaller (larger) RNA constructs, the concentration should be increased (decreased) according to the ~(MW)² proportionality. Control measurements should be carried out with at least twofold higher and twofold lower concentrations to check for aggregation or interparticle interference effects (see later). In the case of the VCI-II glycine-aptamer, we have obtained scattering profiles with RNA concentrations in the range of 5–50 μM and observed no systematic dependence of the profile shape on RNA concentration (24).

3.1.2. Sample Volume Requirements

The intense X-ray radiation used in SAXS measurements at state-of-the-art synchrotron sources generates radicals that quickly degrade biological samples (see later). RNA samples for SAXS measurements should therefore be used only for one measurement. The sample requirement per measurement is determined by the sample cell used in the setup. We have developed a sample cell and cell holder for biological SAXS measurements with 16 μL sample volume (30). Allowing for pipetting and loading losses, this corresponds to ≈20 μL per measurement. The number of measurements required depends, naturally, on the purpose of the study. Obtaining high-quality scattering profiles for an RNA under particular solution conditions typically requires triplicate repeat measurements at different RNA concentrations, i.e., about ten individual measurements. A thorough investigation of an RNA construct, which includes characterization under different solution conditions and Mg²⁺ and ligand titrations, requires at least similar to 50 individual measurements or about 1 mL RNA solution at the desired measurement concentration. This corresponds to ≈1–2 mg RNA for RNA constructs with a few hundred residues.

3.2. In Vitro RNA Transcription

Production of milligram quantities of RNA requires transcription reactions with ≥10 mL final volume. As the amount of reagents required represents a significant cost, it is advisable to test reagents first by running test reaction with 50–100 μL final volume and to check reaction products on a denaturing gel. In all steps of RNA transcription, purification, and preparation for the measurements great care must be taken to avoid contamination with RNases.

1. For a 10-mL transcription reaction, mix 1 mL 10× transcription buffer, 0.4 mL 1 M DTT, 1 mL 10 mM NTP stock, 0.1 mL DNA template (100 μg/mL), 7.4 mL water, and 0.1 mL ≈ 50,000 units/mL T7 polymerase in an Oakridge 50-mL centrifuge tube.

2. Vortex the transcription solution and incubate for 3–4 h in a 37°C waterbath.

3. Add 1 mL 0.5 M EDTA, 1 mL 3 M Na-acetate, pH 5.4, and 30 mL cold ethanol. Precipitate RNA for at least 4 h at −20°C.

4. Centrifuge for 40 min at 16,000 rpm (24,000 × g). Carefully pour out the supernatant; a translucent RNA pellet should be visible. Dry and resuspend the RNA pellet in 0.5 mL water.

3.3. RNA Gel Purification

1. Add 75 μL TEMED and 750 μL 10% APS to 100 mL 8% denaturing acrylamide gel mix to initiate the polymerization reaction. Immediately pour gels using large spacers to make 1–2 large wells per gel for loading. Let the acrylamide polymerize for at least 1 h.

2. Run gels with 1× TBE buffer and use a metal plate attached to the glass gel plates to avoid temperature gradients. Before loading the RNA constructs, prerun the gel at 55 W for at least 30 min.

3. Add 1/2 volume loading dye to the resuspended RNA solution and load the gel. Run the purification gel at 55 W for 3 h (adjust the time for shorter or longer RNA constructs).

4. Take down the gel and wrap in Saran wrap. Image gel bands by UV shadowing and mark desired bands. Excise gel bands with a sterile scalpel. Crush gel pieces with a pestle in a 50-mL Falcon tube (BD Biosciences), add ≈5 mL of TEN buffer.

5. Freeze gel pieces on dry ice and thaw at room temperature. Repeat three freeze–thaw cycles. Agitate for at least 4 h at 4°C.

6. Spin in swinging bucket centrifuge for 20 min at 4,000 rpm (1,500 × g). Pour out supernatant and filter solution through a 0.2-μm syringe filter.

7. Add 1/10 volume 3 M Na-acetate, pH 5.4, and 3 volumes cold ethanol. Precipitate RNA for at least 4 h at −20°C.

8. Centrifuge for 40 min at 16,000 rpm (24,000 × g). Carefully pour out the supernatant; a translucent RNA pellet should be visible. Wash pellet with 200 μL of 70% ethanol/30% water solution and air dry the pellet. Resuspend RNA in 100–400 μL water (see Note 1).

Determine the RNA concentration photospectrometrically by absorbance at 260 nm. A typical absorption coefficient for RNA is α₂₆₀ ≈ 2.2 × 10⁶ (M cm)⁻¹ (i.e., a reading of 1 absorption unit with a 1-cm cuvette corresponds to an RNA concentration of 0.45 μM or 32 μg/mL VCI-II RNA) (see Note 2).

3.4. SAXS Measurements

3.4.1. Sample Preparation for SAXS Measurements

RNA Sample Preparation

Buffer subtraction for background correction is essential for SAXS measurements of biological samples. As the scattering signal from RNA samples is comparable in strength to the buffer signal, especially at high momentum transfer q (cf. the sample and buffer profiles in Fig. 1), it is crucial to match the buffer closely to the sample. One strategy to achieve good agreement between buffer and sample conditions is to prepare a stock solution of buffer, to take aliquots for the sample and buffer measurements, and to add the same relative volume of RNA solution and water to the sample and buffer aliquots, respectively. Another possibility is to exchange the buffer repeatedly (3–4 times) using centrifuge spin columns. As the RNA concentration in a typical SAXS measurement is relatively high, it is important to take into account finite concentration effects. For example, 100 μM of a 100-residue RNA can be associated with up to approximately 5 mM of Mg²⁺ ions. For accurate Mg²⁺ titrations, it is, therefore, necessary to prepare the samples by buffer exchange. Similarly, titrations for ligands with micromolar- or submicromolar-binding affinities require buffer exchange.

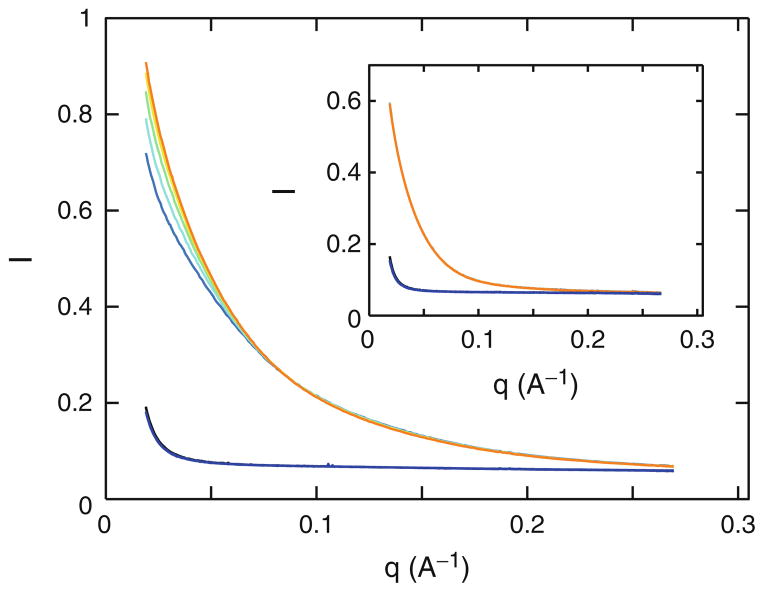
Fig. 1.

The effect of radiation damage on scattering profiles. Raw scattering profiles for a 24-bp DNA duplex (main graph) and for the VCI-II glycine riboswitch construct (inset). Scattering profiles from five subsequent 1.0-s exposures of the DNA/RNA samples are shown for each nucleic acid. Corresponding buffer profiles measured immediately before and after the DNA/RNA samples are virtually identical and shown in the bottom part of the graphs. The 24-bp DNA duplex sample was prepared as described (31, 32) and measured at a DNA concentration of 0.52 mM in 1 mM Na–MOPS buffer, pH 7.0, with 10 mM MgCl₂. The VCI-II RNA was prepared as described in Subheading 3 and measured at an RNA concentration of 20 μM in 50 mM Na– MOPS, pH 7.0, with 10 mM MgCl₂ and 10 mM glycine. The effect of radiation damage is clearly visible as an increase in forward scattering for subsequent exposures in the 24-bp DNA duplex data set. All five profiles were found identical in the experiments with riboswitch RNA Note that both samples were exposed to the same radiation dose. The fact that the DNA duplex measurement, but not the VCI-II RNA, shows strong signs of radiation damage is due to the high DNA and low buffer concentration used. Measurements of the same DNA sample in 50 instead of 1 mM Na–MOPS show no signs of radiation damage (data not shown).

For the VCI-II tandem aptamer, Mg²⁺ titrations in the absence and presence of 10 mM glycine are prepared as follows:

1. Prepare 1 mL buffer aliquots for different Mg²⁺ concentrations. Mix 0.1 mL 500 mM Na–MOPS buffer, 0.1 mL 100 mM glycine stock, 0.1 mL 10× MgCl₂ stock at the desired concentration, and 0.7 mL water. For the titration in the absence of glycine, omit the glycine stock and use 0.8 mL water.

2. Prepare RNA aliquots with 0.8 nmols of RNA (to obtain 40-μL aliquots of 20 μM RNA solutions) in 50-kDa cut-off microcone centrifuge filters. Exchange ≥ 100 μL buffer at least three times in the microcone filters.

3. Elute the RNA aliquots into 40 μL final volume. This sample volume is sufficient for two measurements. Equilibrate RNA samples for 20 min in a 50°C water bath.

4. Spin buffer and RNA sample solutions for 10 min at 13,000 rpm (16,000 × g) immediately before the SAXS measurement.

As wet lab equipment and time are limited during synchrotron beam times, it can be advantageous to prepare aliquots in advance. In this case, Eppendorf tubes with the RNA aliquots should be flash frozen by immersion in liquid nitrogen and stored and shipped on dry ice (see Note 3).

Sample Preparation for a SAXS Molecular Weight Standard

1. Dissolve 2.38 g GdnHCl in 50 mL Na-acetate buffer (for a final concentration of 0.5 M GdnHCl). Filter buffer solution through 0.2-μm pore size syringe filter.

2. Weight out 8 mg of cytochrome c and dissolve in 1 mL buffer. Filter protein solution through 0.2-μm pore size syringe filter.

3. Prior to the SAXS measurement, spin buffer and protein sample solutions for 10 min at 13,000 rpm (16,000 × g).

Cytochrome c is a 11.7-kDa globular protein, its radius of gyration is 13.8 Å, and in solution it has an intense brown color. It serves as a convenient measurement and molecular weight standard. The buffer used for the cytochrome c standard with its Gdn-HCl content is also useful to wet new sample cells by repeated loading.

3.4.2. SAXS Measurements of Riboswitch RNA

We use a sample cell specifically designed for biological SAXS measurements (30) and a Hamilton syringe for rinsing and loading the cell. We recommend measuring a matching buffer profile before and after each RNA sample measurement.

1. Rinse the cell with deionized, RNase-free water.

2. Rinse the cell three times with the desired buffer. Load the cell with buffer solution.

3. Measure buffer scattering profile.

4. Load cell with the RNA solution in the same buffer.

5. Measure RNA scattering profile.

6. Repeat from step 1.

The exposure time needs to be adjusted to achieve a good signal-to-noise ratio without causing radiation damage (see later).

3.5. Data Analysis

3.5.1. SAXS Data Reduction

The raw data from the X-ray detector have to be processed to obtain a one-dimensional scattering profile. The details of this procedure depend on the detector and measurement setup. Most SAXS beam lines make efficient procedures for circular averaging of the detector signal (in the case of 2D CCD detectors) available to their users. We calibrate the scattering angle by comparison to silver behenate, a scattering standard (33), and correct for incident beam intensity.

3.5.2. Radiation Damage

The intense X-ray beams available at synchrotrons generate radicals that degrade biological samples such as RNA. One particular effect of ionizing radiation is the formation of intermolecular crosslinks that cause aggregation. It is important to limit the exposure time such that radiation-induced changes of the sample are negligible, as otherwise the signal becomes uninterpretable. The standard procedure to gauge the effects of radiation exposure on the sample is to record several scattering profiles in short succession and to compare the subsequent measurements of the same sample. Systematic changes of the SAXS profile in a series of exposures are a sign of radiation damage. As crosslinked and aggregated species scatter strongly in the forward direction (due to the ~(MW)² dependence in Eq. 1), radiation damage typically leads to an increase in the forward scattering (Fig. 1).

RNA samples are more resistant to radiation damage than proteins. At beam line 12-ID of the Advanced Photon Source, we routinely expose protein samples for 2 × 0.5 s and RNA samples 4–5 × 1.0 s without incurring significant radiation damage. However, the acceptable radiation dose will vary depending on sample and buffer conditions, and we compare subsequent exposure on the same sample routinely for all our SAXS measurements. In general, higher RNA concentration increases the probability of intermolecular crosslinks and therefore increases the effects of radiation damage. In contrast, we have observed that higher buffer concentrations (MOPS or Tris) tend to confer some protection from radiation damage (Fig. 1).

3.5.3. Buffer Subtraction

If the scattering profiles obtained from subsequent exposures of the same sample show no systematic differences, they can be averaged to improve signal quality. The next step is then to subtract the buffer scattering signal for background correction. We recommend comparing buffer profiles measured before and after the RNA sample measurement (see, e.g., the buffer profiles in Fig. 1). If the two buffer profiles show no systematic differences, their average is subtracted from the RNA sample scattering profile. If the two buffer profiles exhibit systematic differences, it is useful to compare to similar buffer profiles to decide which measurements should be discarded as outliers.

3.5.4. Concentration Dependence

Equation 1 predicts a linear dependence of the scattering profile on RNA concentration for a monodisperse and dilute sample. An important test of sample quality is therefore to compare measurements at different RNA concentrations after rescaling of the scattering profiles by RNA concentration. Changes in the shape of the scattering profile with increasing RNA concentration can have several reasons. An increase in the scattering at low q with increasing concentration (in addition to the linear dependence predicted from Eq. 1) is often a result of sample aggregation and radiation damage. However, even monodisperse samples in the absence of radiation damage exhibit a nontrivial concentration dependence at high concentrations, as the measured scattering profile is a product of the particle form factor P(q) (which describes the scattering pattern of an ideal infinite dilute mono-disperse solution of the particles) and the solution structure factor S(q,c) (34).

$$I(q,c)=cP(q)S(q,c).$$ (2)

The structure factor S(q,c) describes the interactions of RNA molecules in solution. S(q,c) deviates from 1 most strongly at low q. S(q,c) < 1 at low q is indicative of repulsive interactions, a situation frequently observed for measurements of RNA samples under low salt conditions where strong electrostatic repulsion dominates the interparticle potential. S(q,c) > 1 at low q is characteristic of attractive interparticle interactions (but in practice very difficult to distinguish from aggregation and radiation damage). For sufficiently dilute solutions S(q,c) ≈ 1 for all values of q. For most purposes it is preferable to measure in this dilute solution regime, even though it is in principle possible to compute S(q,c) from solution theory (34).

3.5.5. Guinier Analysis

The scattering intensity at low q in the dilute limit behaves as (34, 35).

$$\underset{q\to 0}{lim}I(q)=I(0)exp(-R_g^2{q}^2/3).$$ (3)

Equation 3 is called the Guinier approximation (see Note 4). R_g is the radius of gyration and I(0) is the forward scattering intensity. R_g and I(0) are determined from a linear fit to a plot of ln(I(q)) as a function of q². It is important to choose an appropriate q range for the Guinier fits. For the lowest q values, a beam stop obscures the detector and blocks the transmitted beam. In close vicinity to the beam stop strong X-ray reflections, so called parasitic scattering, will dominate the signal and it is best to discard data points below a certain value q_min. The value of q_min specific to a particular setup and can be determined from repeated Guinier analysis of a scattering standard with different choices of q_min. Equation 3 is only valid for small q. The upper limit of the range of q values used in the Guinier fit, q_max, should be chosen adaptively such that q_maxR_g < 1.3 for approximately spherical objects and smaller for elongated shapes (34).

The value of I(0) obtained from Guinier fits (Eq. 3) can be related to the molecular weight of the sample (Eq. 1) by comparison with a molecular weight standard of known concentration c and molecular weight MW_S:

$$\text{MW}=\sqrt{\frac{I(0)}{I_{\mathrm{S}}(0)}\frac{c_{\mathrm{S}}}{c}{\left(\frac{v_{\mathrm{S}}\mathrm{\Delta }{\rho }_{\mathrm{S}}}{v\mathrm{\Delta }\rho }\right)}^2{\text{MW}}_{\mathrm{S}}^2}.$$ (4)

If a nucleic acid weight standard is used (e.g., a short DNA duplex (24)) (ν_SΔρ_S/νΔρ)² ≈ 1.0, if a protein weight standard is used (ν_SΔρ_S/νΔρ)² ≈ 0.4 for RNA samples. In practice, the molecular weight determination by Eq. 4 is often limited by the accuracy of the concentration measurements (36). Use of Eq. 4 provides, nonetheless, a good check on sample quality.

3.5.6. Thermodynamic Modeling of Scattering Data

SAXS profiles provide a powerful tool to follow structural transitions of RNA molecules as a function of solution conditions. It is often desirable to describe transitions, at least as a first pass, by simple thermodynamic models. In such models, the measured scattering profiles are decomposed into linear combinations of scattering profiles representing contributions from different structural states. In the case of the VCI-II glycine-riboswitch construct, for example, we have modeled the SAXS data using a three-state model with an unfolded state, a partially folded state in the absence of glycine, and a glycine-bound conformation.

In general, models can be fit either to the R_g data, using the relationship

$$R_{\mathrm{g},k}^2=\sum _{i=1}^N{f}_{i,k}{R}_{\mathrm{g},i}^2$$ (5)

or to the full scattering profiles using

$$I_k(q)=\sum _{i=1}^N{f}_{i,k}{I}_i(q).$$ (6)

where R_g,k and I_k(q) are the radius of gyration and scattering profile obtained for solution condition k (where different solution conditions can correspond to different concentrations of Mg²⁺, glycine, to different time points, etc.) and R_g,i and I_i(q) are the radius of gyration and scattering profile of the thermodynamic state i, which are properties of the state and do not depend on the solution conditions. For example, if an RNA exhibits two-state folding behavior as a function of Mg²⁺ concentration with an unfolded state U and a folded state F, Eq. 5 reads $R_{\mathrm{g}}^2([{\text{Mg}}^{2+}])=f_U([{\text{Mg}}^{2+}])R_{\mathrm{g},U}^2+f_F([{\text{Mg}}^{2+}])R_{\mathrm{g},F}^2$ and Eq. 6 simplifies to I(q)([Mg²⁺]) = f_U([Mg²⁺])I_U(q)+ f_F ([Mg²⁺])I_F(q). The f_i,k are the fractional occupancies of the states i under condition k. The dependence of the f_i on solution conditions can be modeled using simple empirical relationships, such as the Hill equation. Often it is possible to determine I_i(q) and R_g,i directly, e.g., by considering the highest and lowest Mg²⁺ points in a two-state RNA folding transition. Analysis of SAXS profiles by singular value decomposition can be very useful to determine whether a two-state model is sufficient and to model partially populated intermediates (see later).

3.5.7. Analysis of Scattering Profiles by Singular Value Decomposition

In analyzing titration series, e.g., series of scattering profiles obtained as a function of salt or ligand concentration or time, two problems commonly arise: how to determine the minimum number of states that are required to fit the data; and, if there are intermediate states present, how to determine the scattering profiles and fractional occupancies of intermediates that cannot be observed in isolation. Analysis of the scattering profiles by singular value decomposition (SVD) can help to address both these questions (37). SVD constructs an optimal and orthogonal basis for the space of scattering profiles. Inspection of the singular values and basis functions using the criteria of Henry and Hofrichter (38) permits to determine the number of state required to fit the data. Furthermore, determination of the scattering profiles of intermediates states is greatly facilitated by fitting the experimental data in the space of SVD basis functions (rather than by treating each q channel as an independent fitting parameter). Several articles provide excellent introductions to the details of SVD analysis and fitting (38–40).

3.5.8. Graphical Representation of Scattering Profiles

At first sight, SAXS profiles appear relatively featureless. To aid the comparison of scattering profiles, it is useful to consider several representations of the scattering data that visually emphasize particular aspects of the data. Figure 2 presents SAXS profiles for the VCI-II tandem aptamer under different solution conditions. A linear I(q) plot (Fig. 2a) emphasizes the low q region, where the scattering intensity is largest. This representation is useful to discern radiation damage (Fig. 1) or concentration dependencies. Features at intermediate or high q that are related to the shape of the molecule are, however, difficult to distinguish in the I(q) plot. A logarithmic plot (Fig. 2b) emphasized the low and high q data about equally and is a useful representation to provide an overview of scattering data. The so-called Kratky representation of q² × I(q) as a function of q (Fig. 2c) emphasized intermediate to high values of q and is particularly useful to distinguish different conformations of the same construct. Folding transitions are best monitored in the Kratky representation (37, 41). In the case of the VCI-II construct the unfolded, partially folded, and glycine-bound conformations are most readily compared in the Kratky plots (Fig. 2c). In some cases representation of the data as q × I(q) as a function of q, a so-called Holtzer plot, has been proven to be most useful (31).

Fig. 2.

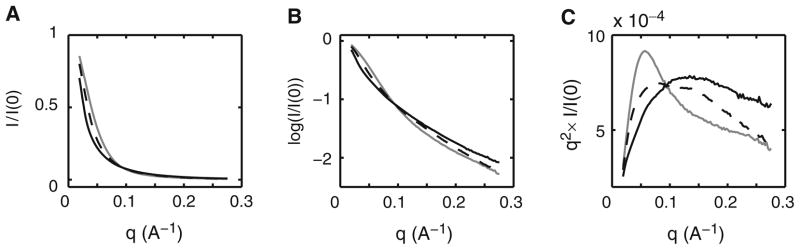
Scattering profiles for the unfolded (thin solid line), high Mg²⁺ and no glycine (thin dashed line), and glycine-bound (thick gray line) conformations of the VCI-II tandem glycine aptamer. Data are shown in (a) as linear I(q) plots, (b) as logarithmic log(I(q)) plots, and (c) in Kratky representation [q² × I(q) as a function of q].

3.6. Ab Initio Structure Reconstructions

3.6.1. Indirect Fourier Transforms

The distribution function of intramolecular distances P(r) can be obtained from a regularized Fourier transform of the scattering profile I(q). A number of software packages are available for calculation of the P(r) function. We use the program GNOM (42) with default parameters to compute P(r) distributions. The value of the input parameter D_max, the maximum intramolecular distance, is determined by varying D_max in steps of 2–5 Å. The appropriate value of D_max yields a solution that (a) fits the experimental scattering profile I(q) with a (b) smooth and (c) strictly positive P(r) distribution. The output files of the program GNOM can serve as input to a suite of programs developed by Svergun and coworkers, see later. A perl script to run series of GNOM transformations with different values for D_max is available online at http://drizzle.stanford.edu/scripts.html or can be obtained from the authors upon request.

3.6.2. Structure Reconstruction

Early SAXS work on RNA was primarily limited to the use of R_g and D_max to follow structural transitions and to manual model building by considering the calculated P(r) functions (43). However, it is possible to determine the low-resolution shape of RNA molecules from SAXS data by using ab initio structure reconstruction algorithms (28). The basic principle behind these algorithms is to represent the molecular shape by a set of dummy atoms or beads (25–27). For each configuration of beads a theoretical scattering profiles is computed and compared to the experimentally measured I(q). The programs use nonlinear optimization strategies to iteratively update the bead models by adding, removing, and translating beads to improve the fit to the experimental data. Here, we describe use of the software DAM-MIN (26), which uses simulated annealing to update the model and imposes a compactness criterion. DAMMIN uses the output of the program GNOM (see earlier), the default model search volume is a sphere with a diameter given by D_max in the GNOM file. We use DAMMIN with default parameters and a D_max value that is 10–20 Å larger than the optimal value determined in the GNOM analysis, to ensure a sufficiently large search volume. As RNA molecules tend to adopt elongated shapes (44), it can in some cases increase the model resolution to run additional reconstructions starting from a cylindrical search volume. DAM-MIN computes the fit of the model to the data and it is advisable to inspect the agreement between the scattering profile of the reconstruction and the experimental I(q).

As the relationship between 1D scattering profiles and 3D models is not unique, it is advantageous to test the robustness of the shape reconstructions for a particular scattering profile by running 10–15 reconstructions with different initial random seeds. We compare the resulting models by computing pairwise Normalized Spatial Discrepancy (NSD) values with the program SUPCOMB (45). Models that have NSD values ≤1 are considered similar and indicate repeatable reconstruction runs. In this case, SUPCOMB can be used to generate an averaged model from the individual reconstructions that corresponds to the union of all models and a “filtered” model that corresponds to the consensus model from all runs.

Finally, we recommend to compute series of reconstructions and to compare the consensus models for several repeat measurements of the same sample. In the study of the VCI-II glycine-riboswitch construct, we have obtained NSD values <1 both for the comparison of models from repeat DAMMIN runs against the same scattering profile and for reconstructions using different experimental profiles for the same solution condition (24). The resulting models provide low-resolution electron densities maps for all three thermodynamic states of the riboswitch (Fig. 3).

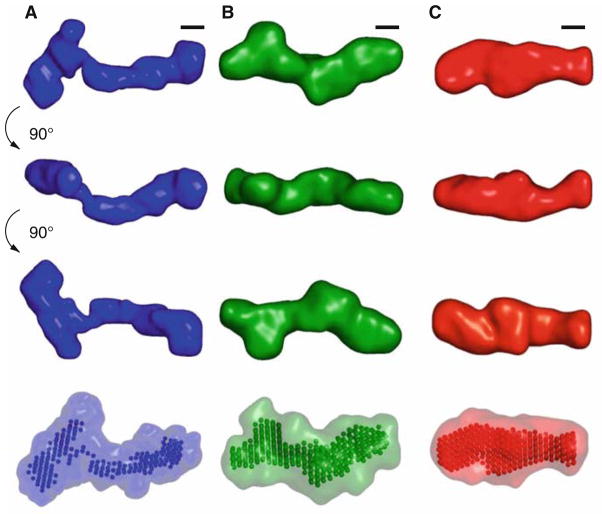
Fig. 3.

Low-resolution structural models for the VCI-II riboswitch tandem aptamer under different solution conditions. Average unfolded conformation (column A), conformation in the presence of 10 mM magnesium and absence of glycine (column B), and glycine-bound structure (column C). The first three rows show the “filtered” structure (see Subheading 3.6 for details of the reconstruction procedure) for each of the conformations in three different orientations. Black scale bars in each column correspond to 20 Å, the diameter of an A-form RNA helix. The rendered densities were generated by convoluting the bead models with a Gaussian kernel using the program Situs (46, 47). The last row shows the “filtered” models as beads and the convex hull of all bead models for a given conformation as a transparent surface. Reproduced from ref. 24 with permission from Elsevier Limited.

The programs GNOM, DAMMIN, and SUPCOMB are available from the website of the Svergun group in Hamburg (http://www.embl-hamburg.de/ExternalInfo/Research/Sax/software.html). Perl scripts to conveniently run series of DAM MIN reconstructions and to average the results are available online at http://drizzle.stanford.edu/scripts.html or can be obtained from the authors upon request.

3.6.3. Electrostatic Calculations Using Bead Models as Input

Recently, there has been substantial progress in describing ion-RNA interactions and ion-dependent RNA folding transitions from first principles using electrostatic theories such as Poisson–Boltzmann (PB) (1, 48–51). Electrostatic modeling requires a representation of the molecular geometry of the RNA molecule of interest. Most often, atomic resolution models derived from crystallography are used (48–51). However, this approach is problematic for molecules that have not been crystallized or for conformations for which no high-resolution structure is available.

An attractive alternative approach is to use the bead models derived from ab initio SAXS shape reconstructions to define the molecular geometry for electrostatic calculations. We have recently shown that SAXS-derived bead models with uniformly assigned charges can be used in PB calculations to predict ion association to nucleic acids (28). The accuracy of predictions based on bead models is similar to those obtained with atomic resolution models (28). Application of bead model electrostatic calculations to the modeling of the salt dependence of RNA folding is currently under way (Jan Lipfert, Adelene Y.-L. Sim, Daniel Herschlag, and Sebastian Doniach, in preparation). A script to convert DAMMIN models to the PQR format appropriate for PB calculations with the Adaptive Poisson Boltzmann Solver (52) is available online at http://drizzle.stanford.edu/scripts.html or can be obtained from the authors upon request.