An adaptive filtered back-projection for photoacoustic image reconstruction

Abstract

Purpose:

The purpose of this study is to develop an improved filtered-back-projection (FBP) algorithm for photoacoustic tomography (PAT), which allows image reconstruction with higher quality compared to images reconstructed through traditional algorithms.

Methods:

A rigorous expression of a weighting function has been derived directly from a photoacoustic wave equation and used as a ramp filter in Fourier domain. The authors’ new algorithm utilizes this weighting function to precisely calculate each photoacoustic signal’s contribution and then reconstructs the image based on the retarded potential generated from the photoacoustic sources. In addition, an adaptive criterion has been derived for selecting the cutoff frequency of a low pass filter. Two computational phantoms were created to test the algorithm. The first phantom contained five spheres with each sphere having different absorbances. The phantom was used to test the capability for correctly representing both the geometry and the relative absorbed energy in a planar measurement system. The authors also used another phantom containing absorbers of different sizes with overlapping geometry to evaluate the performance of the new method for complicated geometry. In addition, random noise background was added to the simulated data, which were obtained by using an arc-shaped array of 50 evenly distributed transducers that spanned 160° over a circle with a radius of 65 mm. A normalized factor between the neighbored transducers was applied for correcting measurement signals in PAT simulations. The authors assumed that the scanned object was mounted on a holder that rotated over the full 360° and the scans were set to a sampling rate of 20.48 MHz.

Results:

The authors have obtained reconstructed images of the computerized phantoms by utilizing the new FBP algorithm. From the reconstructed image of the first phantom, one can see that this new approach allows not only obtaining a sharp image but also showing the correct signal strength of the absorbers. The reconstructed image of the second phantom further demonstrates the capability to form clear images of the spheres with sharp borders in the overlapping geometry. The smallest sphere is clearly visible and distinguishable, even though it is surrounded by two big spheres. In addition, image reconstructions were conducted with randomized noise added to the observed signals to mimic realistic experimental conditions.

Conclusions:

The authors have developed a new FBP algorithm that is capable for reconstructing high quality images with correct relative intensities and sharp borders for PAT. The results demonstrate that the weighting function serves as a precise ramp filter for processing the observed signals in the Fourier domain. In addition, this algorithm allows an adaptive determination of the cutoff frequency for the applied low pass filter.

1. INTRODUCTION

Optical imaging techniques have been widely used in a number of important biomedical applications, but they face a serious challenge for deep tissue imaging due to the difficulty of recovering scattered photons in turbid media. Photoacoustic tomography (PAT), also termed as optoacoustic tomography (OAT), is a noninvasive imaging method for high-resolution mapping of optical-absorption energy in deep tissue. PAT is based on a hybrid technology that combines rich optical contrast mechanisms and superior ultrasonic penetration depth and resolution. In recent years, PAT technology has successfully addressed some of the most challenging issues in conventional optical and ultrasound imaging methods and is now attracting growing interest in preclinical and clinical research.^1–18 For PAT, photons from a short-laser pulse are absorbed by certain tissues, causing impulsive heating and acoustic stress in the tissue. The tissue then re-emits the absorbed energy as broadband ultrasonic pressure waves, which propagate to the outside of the tissue and are detected by a mechanically scanned ultrasound receiver or an array of receivers. In the process of photoacoustic imaging formation, the kernel is the algorithm of imaging reconstruction (AIR). From a technical point of view, photoacoustic imaging remains challenging with a multitude of approaches under development for imaging method improvement, such as signal acquisition, algorithmic processing, and image quantification capacities,^19–25 as well as for hardware performance, such as laser delivery and ultrasound detection technologies.^26–30 As a fast reconstruction method, current back-projection (BP) algorithms are able to produce good images for spherical,^31,32 cylindrical,³³ and planar geometries³⁴ in simulations and have widely been applied in volumetric image reconstruction for PAT applications.^14,35–38 As reviewed by Beard,¹⁰ Kuchment, and Kunyansky,^39,40 the recent developments of BP algorithms lead to improved image quality,^41,42 which has increased the capabilities of PAT toward important new studies in the biomedical settings.^1–10,38,43 BP formulas are implemented either in the spatiotemporal domain or in the Fourier domain.^36,38 In BP algorithms, one of the representative works³⁶ is based on a closed-form inversion formulas (a modified back-projection formula),

$${\displaystyle p_0\left(\mathbf{r}\right)\approx {\int }_{{\mathrm{\Omega }}_0}{\left.\frac{d\mathrm{\Omega }}{{\mathrm{\Omega }}_0}\left[2p\left({\mathbf{r}}_0,t\right)-2t\frac{\partial p\left({\mathbf{r}}_0,t\right)}{\partial t}\right]\right|}_{ct=r-r_0}.}$$ (1)

This well-known algorithm is very successful in detecting the position and shape of absorbing objects in turbid media.¹¹

While filtered back-projection (FBP) techniques have proven to be useful when solving for time-dependent partial differential equations through Fourier spectral methods, there are still several critical issues that need to be addressed to further improve the quality of FBP-reconstructed images. A disadvantage of conventional back-projection algorithms is that they are not exact in experimental settings²⁵ and may lead to the appearance of substantial artifacts in the reconstructed image, such as the accentuation of fast variations in the image, which is accompanied by negative optical-absorption values that otherwise have no physical interpretation.²⁵ Although these artifacts have not prevented the use of BP algorithms for structural imaging,¹¹ they may limit the quantification capacity, the image fidelity, and the accurate use of the method for functional and molecular imaging applications,⁴⁴ including multispectral imaging applications, since these imaging modes require high quantification ability. Up to now, the kernel for FBP algorithm used in PAT, i.e., the choice of the negative wing around the back-projected data which originated from the raw data modified in the frequency domain, does not contain a general expression that can indicate to what extent the restrictions are on spectrum leakage by using window functions in Fourier domain for different sampling frequencies. In addition, there is no criterion about the limit of the low-pass filter’s cutoff frequency in the frequency domain. A fast method is also needed to simulate the photoacoustic pressure signal of complex tissues.

In this paper, we report a novel and robust FBP algorithm that improves the image fidelity through calculations in the Fourier domain with a rigorous expression of a weighting function that precisely counts the contribution of each photoacoustic signal and an adaptive criterion that sets a cutoff frequency of filtering. Also we introduce a fast calculation method to generate the model of photoacoustic pressure signals. This paper is organized as follows: In Sec. 2, we derive a precise expression for a new FBP algorithm, which is started from fundamental formulae of PAT. In Sec. 3, we propose using the ACE method, which is based on the fast multipole method (FMM), to create the photoacoustic pressure model. Section 4 presents numerical simulation results of phantom samples based on our new algorithm. Section 5 concludes the paper with the main ideas and our contributions to image reconstruction for PAT.

2. MATHEMATICS FOR PHOTOACOUSTIC TOMOGRAPHY

In PAT, acoustic stresses are created inside a tissue after it absorbs energy from a short-laser pulse. The acoustic stresses relax by launching ultrasound waves (i.e., photoacoustic emission), which act as instantaneous acoustic sources. The detection of the ultrasound waves that propagate to the outside of the tissue can be used to reconstruct three-dimensional (3D) images of the tissue. The basic physics background and mathematical formula for the photoacoustic wave generation and propagation are described below.

2.A. Photoacoustic wave equations

When a short-laser pulse irradiates on a sample with certain absorbers, the incident light is absorbed [the absorbed energy is H(r, t)] before the sample density (ρ) changes.⁴⁵ For the case that laser pulse duration is much shorter than the thermal diffusion time, the thermal diffusion can be neglected, and then one has the pressure field $p\left(\text{r},t\right)$ corresponding to an ultrasonic wave,

$${\displaystyle \left({\nabla }^2-\frac{1}{c^2}\frac{{\partial }^2}{\partial t^2}\right)p\left(\mathbf{r},t\right)=-\frac{\alpha }{C_p}\frac{\partial H\left(\mathbf{r},t\right)}{\partial t},}$$ (2)

where C_p is the constant pressure specific heat capacity, c is acoustic speed, and α is the volume thermal expansion-index.

2.B. Heating function

It is applicable in most experimental conditions to consider the incident laser pulse having a Gaussian profile

$${\displaystyle H\left(\mathbf{r},t\right)=H\left(\mathbf{r}\right)\cdot \frac{exp\left(t^2/2{\tau }^2\right)}{\tau },}$$ (3)

where τ is a characteristic time. Based on the definition of a Dirac function that $\delta \left(x\right)=\underset{n\to \infty }{lim}\sqrt{n/\pi }{e}^{-n{x}^2}$, the heating function can be modeled as a Dirac delta function if c ⋅ τ is much shorter than the scale across the “heating” area,

$${\displaystyle H\left(\mathbf{r},t\right)=H\left(\mathbf{r}\right)\delta \left(t\right).}$$ (4)

For photoacoustic effect, this is satisfied when the duration of the laser pulse is much shorter than the time it takes for the sound to travel across the heated region, a condition known as stress confinement. This means that the laser pulse is short enough; the density of the sample has no time to change during the heating process. Under this condition, the photoacoustic wave equation can be written as

$${\displaystyle \left({\nabla }^2-\frac{1}{c^2}\frac{{\partial }^2}{\partial t^2}\right)p=-\frac{\alpha }{C_p}H\left(\mathbf{r}\right)\frac{\partial \delta \left(t\right)}{\partial t}.}$$ (5)

2.C. Weighting function in Fourier space

The source pressure p₀(r) can be expressed as

$${\displaystyle p_0\left(\mathbf{r}\right)=\frac{1}{{\left(2\pi \right)}^3}\underset{\mathbf{k}}{\int }p\left(\mathbf{k},t\right)W\left(\mathbf{k},\mathbf{r},t\right)e^{-i\mathbf{k}\cdot \mathbf{r}}{\text{d}}^3\mathbf{k},=\frac{1}{{\left(2\pi \right)}^3}{\int }_{\mathbf{k}}{p}_f\left(\mathbf{k},t\right)e^{-i\mathbf{k}\cdot \mathbf{r}}{\text{d}}^3\mathbf{k},}$$ (6)

where $W\left(\mathbf{k},\mathbf{r},t\right)=e^{-2i\mathbf{k}\cdot \mathbf{r}}/cos\left(ckt\right)$ is a weighting function and $p_f\left(\mathbf{k},t\right)=p\left(\mathbf{k},t\right)W(\mathbf{k},\mathbf{r},t)$.⁴⁶

The weighting function has a rigorous form directly derived from the photoacoustic wave equation (see Appendix A). It is seen that weighting function represents the amount of contributions from a signal p(k, t) in the Fourier domain. As demonstrated in our numerical simulations shown in Sec. 4, the weighting function plays a critical role for determining the image quality in the process of photoacoustic image reconstruction. The weighting function has a series of singular points when $ckt=\pm \left(n+1/2\right)$, therefore, in Fourier domain for a sampling period (T), one should, naturally, choose the cutoff frequency f_cutoff using ckt < π/2 or 2πf_cutoffT < π/2 to avoid singular points. This allows us to obtain an objective upper limit for setting the cutoff frequency f_cutoff for a low pass filter. We obtain that $f_{\text{cutoff}}<\left(f_{\text{sampling}}/4\right)$, where f_sampling is the sampling rate.

2.D. Image of retarded potential

From the photoacoustic wave equation, Landau and Lifshitz introduced the result⁴⁷

$${\displaystyle p\left(\mathbf{r},t\right)=\frac{1}{4\pi c}\frac{\partial }{\partial t}{\int }_{\left|\mathrm{\Delta }\mathbf{r}\right|=ct}\frac{p_0\left(\mathbf{r}-\mathrm{\Delta }\mathbf{r}\right)}{ct}\text{d}S.}$$ (7)

Considering the first-order approximation of (7), Kruger³ and Liu⁴⁸ obtained the following expression (8) for a spherical measurement geometry

$${\displaystyle \prod _0\left({\mathbf{r}}_0\right)\approx -K\int {\int }_{2\pi }{\left.\text{d}\mathbf{n}\left[t\frac{\partial p\left(\mathbf{r},t\right)}{\partial t}+2p\left(\mathit{r},t\right)\right]\right|}_{t=\left|\text{r}-{\text{r}}_0\right|/c},}$$ (8)

where K is a constant and $\prod _0\left(\mathbf{r}\right)$ represents the image of retarded potential which is generated by the optically absorbed parts of the samples.⁴⁸

For an object located near the center of the spherical (or circular) detection geometry, Eq. (8) can provide a good reconstructed configuration, but it does not hold when the object deviates from the center of the spherical geometry.⁴⁹ In addition, the reconstruction artifacts occur when the integration spherical shells are different from the planar surfaces. Therefore, based on the result in the spherical geometry given by Finch et al.,³¹ Xu and Wang studied Fourier domain reconstruction method and further wrote a back-projection form as Eq. (1). In their algorithm, instead of using measured signals, they used filtered pressure signals to reconstruct the absorbers and reduced the reconstruction artifacts to some extent.

We consider that there are a total number of transducers, N, which are evenly distributed in a 2π-solid angle and each transducer occupies a solid angle of ΔΩ. Evaluating the contribution of measured signals via Eq. (6) for the discretized space, we can replace Eq. (8) with the following expression:

$${\displaystyle \prod _0\left({\mathbf{r}}_0\right)=-K\mathrm{\Delta }\mathrm{\Omega }\sum _{i=1}^N{\left[t\frac{\partial p_f\left({\mathbf{r}}_i,t\right)}{\partial t}+2p_f\left({\mathbf{r}}_i,t\right)\right]}_{t=\left|{\mathbf{r}}_i-{\mathbf{r}}_0\right|/c},}$$ (9)

where p_f represents the filtered signal.

If the transducers are not evenly distributed, a normalization factor, A_i, which also depends on measurement configuration, needs to be introduced and Eq. (9) becomes

$${\displaystyle \prod _0\left({\mathbf{r}}_0\right)=-\sum _{i=1}^N{A}_i\mathrm{\Delta }\mathrm{\Omega }{\left[t\frac{\partial p_f\left({\mathbf{r}}_i,t\right)}{\partial t}+2p_f\left({\mathbf{r}}_i,t\right)\right]}_{t=\left|{\mathbf{r}}_i-{\mathbf{r}}_0\right|/c},}$$ (10)

where $\prod \left({\mathbf{r}}_0\right)=\prod _0\left(\mathbf{r}\right)/K$ represents the relative intensity of reconstructed image.

3. MODELING AND NUMERICAL COMPUTATION

For more complex configurations of absorbers, the cost of generating measurement data for numerical modeling simulation is huge. To address this challenging issue, our previous research demonstrated that the FMM based algorithmic structure of ACE could perform the computations in an optimal manner.^50–53

Under stress and thermal confinements in a homogeneous acoustic medium, the pressure of the acoustic signals generated by a short-laser pulse is given by Poisson’s solution of Eq. (4),

$${\displaystyle p\left(\mathbf{r},t\right)=\frac{\mathrm{\Gamma }}{4\pi c}\frac{\partial }{\partial t}{\int }_{S^{\prime }}\frac{H({\mathbf{r}}^{\prime },t)}{|\mathbf{r}-{\mathbf{r}}^{\prime }|}\text{d}{S}^{\prime },}$$ (11)

where Γ is the Gruneisen coefficient, a dimensionless constant that represents the efficiency of the conversion of heat to pressure, and S′ is a time-dependent surface for which |r − r′| = ct.

Equation (11) states that the pressure signal in a homogeneous acoustic medium is solely due to the optical absorption at locations r′ so that the generated acoustic signals require time t to reach the detector r. In practice, a discrete version of (11) is used to simulate the signals collected with a finite number of transducers,

$${\displaystyle p\left(\mathbf{r},t\right)={\mathrm{\Gamma }}_A\frac{\partial }{\partial t}\mathrm{\Phi }(\mathbf{r},t),}$$ (12)

where Γ_A = Γ/4πc can be treated as a constant and

$${\displaystyle \mathrm{\Phi }\left(\mathbf{r},t\right)=\sum _i\frac{H(\mathbf{r},t)}{|\mathbf{r}-{\mathbf{r}}_i|}.}$$ (13)

Consider a source domain Ω_S ∈ R³ and a sensing domain Ω_O ∈ R³. Centers of Ω_S and Ω_O are denoted by r_S and r_O. It is also assumed that Ω_S ⊂ Ω^S and Ω_S ∈ Ω^S and Ω^S ∈ Ω^O = Ø. In what follows, the domains Ω^S and Ω^O are called parents of Ω_S and Ω_O, respectively. The parent domains centered at r^S and r^O, respectively, with r^S ∉ Ω_S and r^O ∉ Ω^O.

The potential Φ(r, t) at time t due to sources ∀r_i ∈ Ω_S observed at r is given by

$${\displaystyle \mathrm{\Phi }\left(\mathbf{r},t\right)=\sum _{n=0}^{\infty }\sum _i^k{\left(-1\right)}^n\frac{H({\mathbf{r}}_i,t)}{n!}{\mathbf{r}}_i^n\cdot n\cdot {\nabla }^n\frac{1}{\mathbf{r}},}$$ (14)

where ⋅n ⋅ means n contraction of two tensors.

We finally calculate Φ(r, t) in a local area via

$${\displaystyle \mathrm{\Phi }\left(\mathbf{r},t\right)=\sum _{n=0}^T{L}^{\left(n\right)}\cdot n\cdot {\left({\rho }_{oi}\right)}^n,}$$ (15)

where r − r_o = ρ_oi and T is a truncation number. Detailed formulations and derivations omitted here are given in Appendix B.

The following expression can be used to generate complex models:

$${\displaystyle p\left({\mathbf{r}}_i,t\right)={\mathrm{\Gamma }}_A\frac{\partial }{\partial t}\sum _{n=0}^T{L}^{\left(n\right)}\cdot n\cdot {\left({\rho }_{oi}\right)}^n.}$$ (16)

Besides the significant improvement in model simulation speed, the error analysis for the potential parts of Eq. (12) is calculated in order to make our study more complete. The absolute error in making the multipole approximation can be obtained using

$${\displaystyle {\epsilon }_m=\left|\mathrm{\Phi }\left(\mathbf{r},t\right)-\sum _{n=0}^T{M}^{\left(n\right)}\cdot n\cdot {\nabla }^n\frac{1}{r}\right|\le \sum _{n=T+1}^{\infty }{C}_m{d}_a^n{r}^{-n-1}\sum _{l=0}^{\infty }\frac{{\left(-1\right)}^l}{l}{r}^l\le \frac{C_m}{\left(r-d_a\right)}{\left(\frac{d_a}{r}\right)}^{T+1},}$$ (17)

where d_a denotes the size of the smallest subdomain in ACE scheme and C_m can be treated as a constant.⁵²

For a uniform sample spherical absorber, one can adopt the approximate model suggested in^36,48

$${\displaystyle p(\mathbf{r},t)=A_{0}U\left(a-|R-ct|\right)(R-ct)/2R,}$$ (18)

where A₀ is a constant, U(a − |R − ct|) is Heaviside function, a is radius of sphere, and R denotes the distance between the center of absorber and detector.

4. NUMERICAL SIMULATIONS AND RESULTS

In order to test the new FBP algorithm, we have conducted numerical simulations on different phantom samples, which are comprised of several spherical absorbers arranged in different configurations and suspended in a nonabsorbing medium. In the simulations, we treated the transducer as an ideal point detector.

Two sampling geometries were used in these simulations. First, we consider a planar measurement configuration, where an acoustic detector scanned on a plane to receive the photoacoustic emission signals from the absorbers. The new algorithm requires multiplying Fourier signals with the weighting function defined in Eq. (6) before back-projection. The treated signals are then projected back via Eq. (10) in time domain. This signal processing will greatly reduce the blurring effect and background noise of measurement signals.

In the following simulations, we assume that the data-sampling rate is set to be 20.48 MHz and the sound of speed is 1500 m/s. Based on the discussion in Sec. 2, our cutoff frequency will be set adaptively; in this case, the cutoff frequency for the low-pass filter is set to 5.0 MHz.

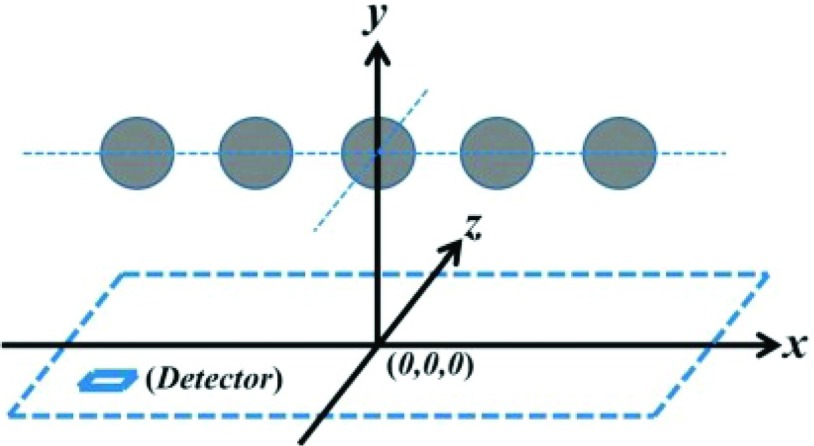
Our first numerical simulation is designed to test the geometry and the contour of cross sectional images. The phantom sample contains five uniform spherical absorbers, which are arranged on a plane with a distance of 15.0 mm to the detection plane (Fig. 1). Each spherical absorber has a radius of 1.5 mm. The center positions of the absorbers are at (−18.0, 0.0, 15.0), (−9.0, 0.0, 15.0), (0.0, 0.0, 15.0), (9.0, 0.0, 15.0), and (18.0, 0.0, 15.0) in a unit of mm, respectively. The relative intensities per unit volume are 1.0, 2.0, 3.0, 4.0, and 5.0 for the absorbers counted from left to right, respectively. In this simulation, we assume that a rectangular-shaped detector moves in a plane along both x- and y-axis from −30.0 to 30.0 mm with a spatial sampling period of 2/3 mm. Therefore, the photoacoustic signals are collected at 8281 (91 × 91) total positions. We also chose a small number of pixels (i.e., only 91 pixels × 91 pixels) for the cross-sectional reconstructed image in our numerical simulation to test if our FBP algorithm can still generate a high quality image even under poor measurement conditions. The detected area of 45.0 × 45.0 mm for the total pixel numbers used corresponds to a spatial resolution of 0.495 mm/pixel.

FIG. 1.

Geometry of the phantom sample used for the first simulation. Details can be found in the text.

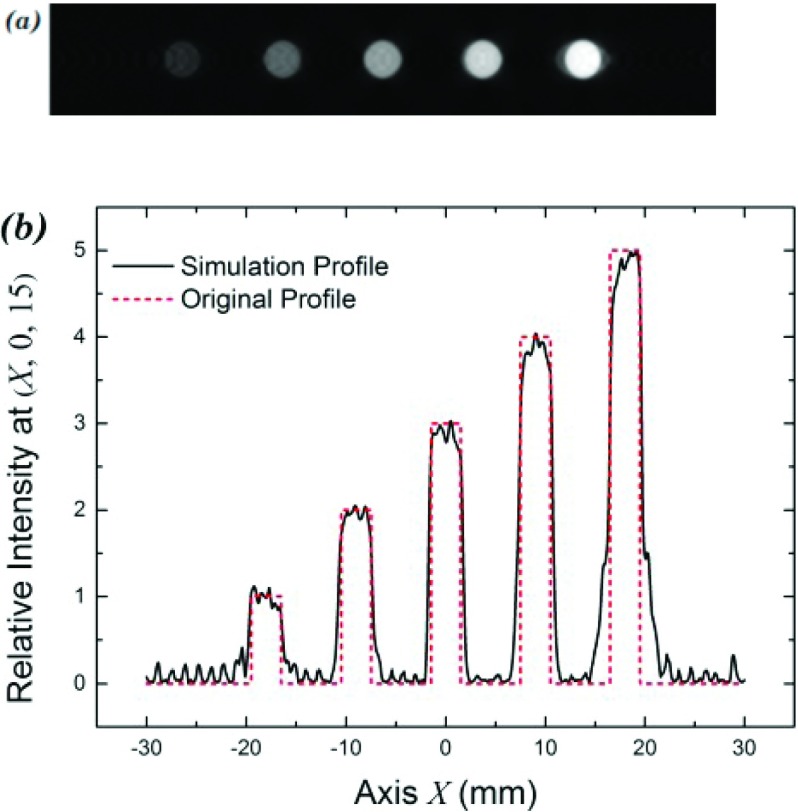
A cross section of a reconstructed image is shown in Fig. 2(a). We can see that this new approach allows us obtaining not only a sharp image [Fig. 2(a)] but also correct signal strength from the absorbers that well matches with the values of the absorption assumed for each absorber [Fig. 2(b)].

FIG. 2.

The first simulation for our back-projection algorithm. (a) Reconstructed image at the plane z = 15.0 mm; (b) relative intensities of the absorbers in the reconstructed image at a cross section plan (x,0,15).

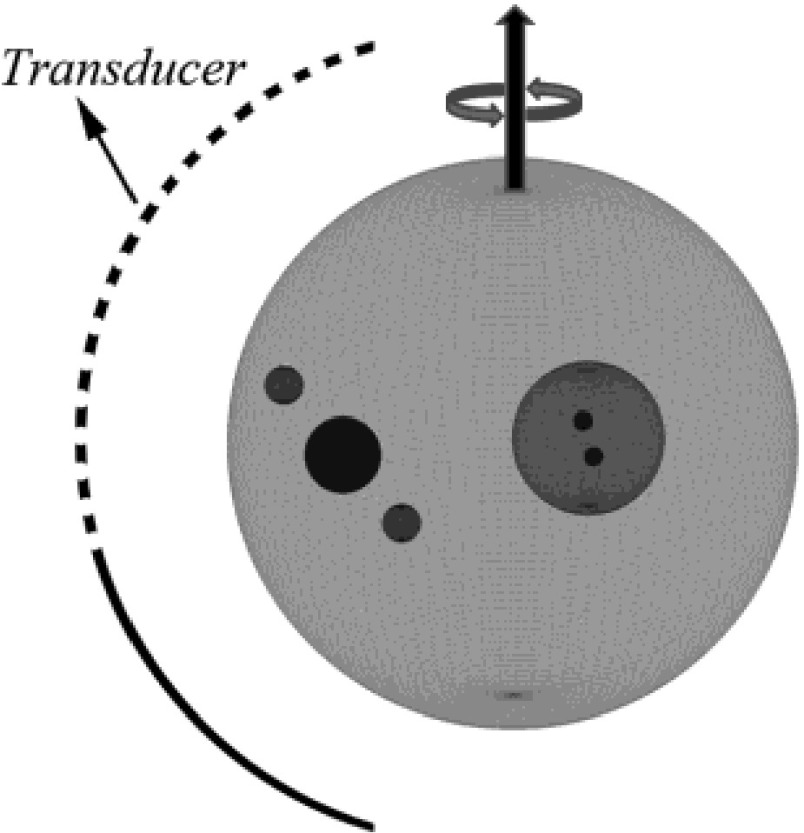
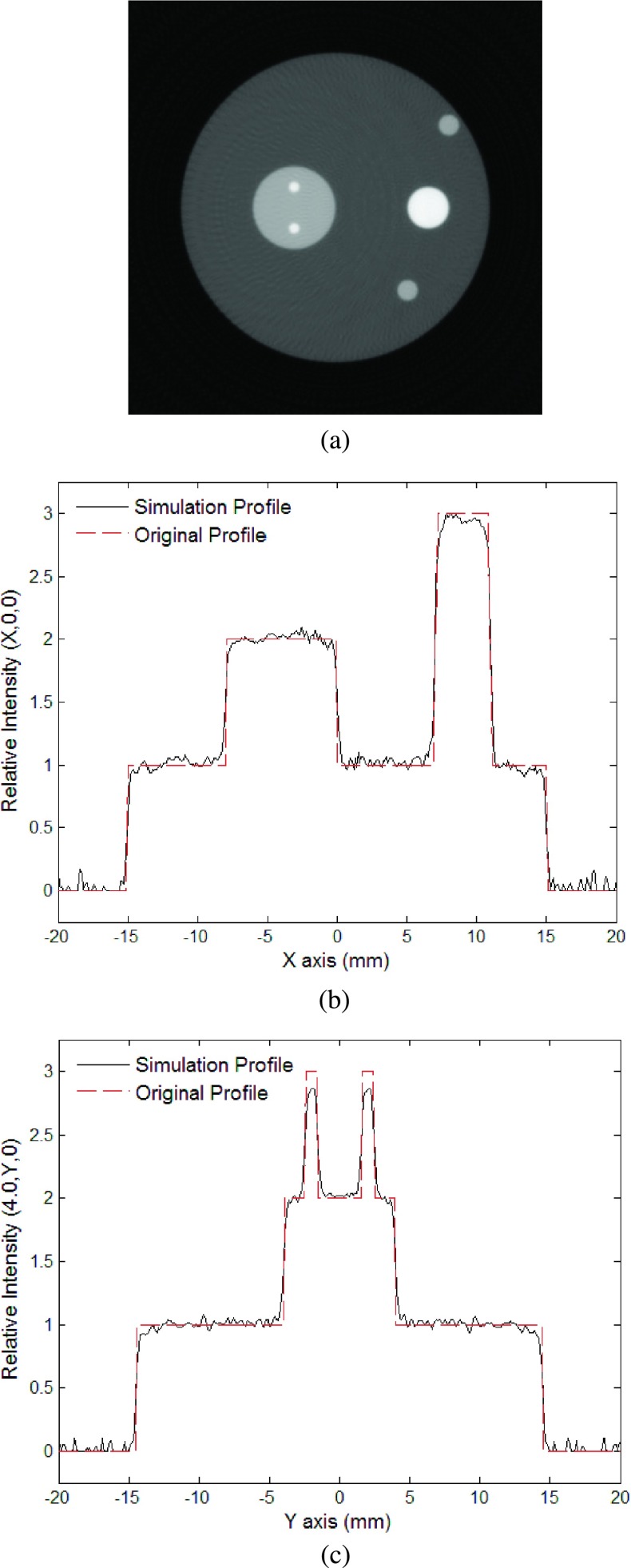
In our second numerical simulation, we designed a phantom sample containing absorbers with different sizes and overlapping areas, as shown in Fig. 3. We want to evaluate the performance of the new FBP algorithm for this complicated geometry. In addition, we also add a noise source to the observed signals to mimic more realistic experimental conditions. In details, the configuration of the second model is as follows: seven spherical absorbers are arranged in a way as shown in Fig. 3. Their center positions are at (0.0, 0.0, 0.0), (−4.0, 0.0, 0.0), (−4.0, 2.0, 0.0), (−4.0, −2.0, 0.0), (9.0, 0.0, 0.0), (11.0, −8.0, 0.0), and (7.0, 8.0, 0.0), respectively, where the coordinate unit is millimeter. Sphere 1 contains the other six spherical absorbers, while sphere 2 further contains spheres 3 and 4. The seven spherical absorbers have a radius of 15.0, 4.0, 0.5, 0.5, 2.0, 1.0, and 1.0 mm, respectively. For sphere 1, the intensity per unit volume is 1.0 except for the overlapping area. Sphere 2 has intensity per unit volume of 2.0 except for the overlapping area. For spheres 3, 4, 5, 6, and 7, the intensity per unit volume is 3.0, 3.0, 3.0, 2.0, and 2.0, respectively.

FIG. 3.

Geometry of absorbers for second simulation (details can be found in text).

The second measurement configuration is an arc-shaped detector array composed of 50-point detectors, evenly spaced over a span of 160°, with a radius of 65 mm. The detector array rotates in 2° steps over 360°, giving 9000 (50 × 180) detection points (see Fig. 3).

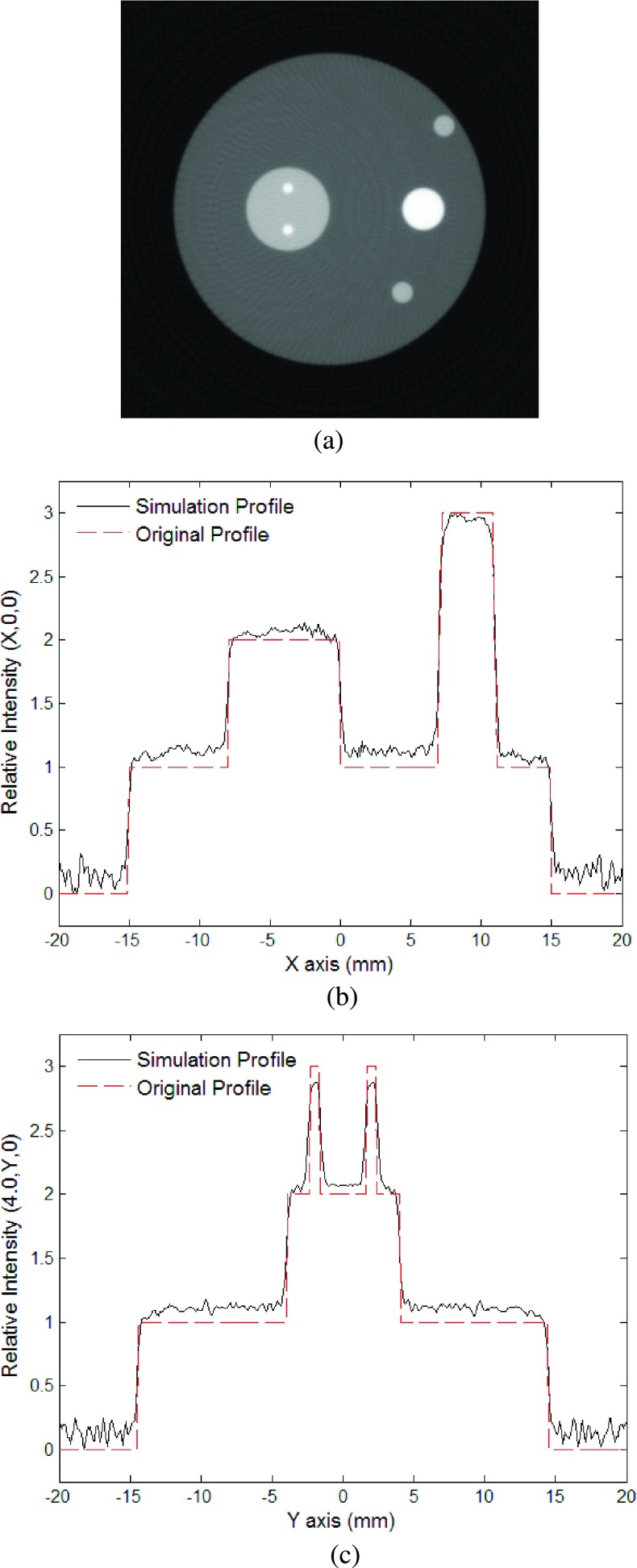
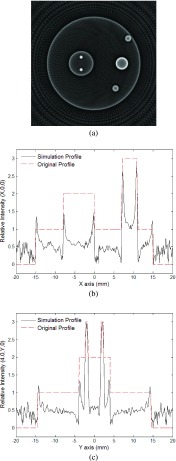
For the second model, we first performed the simulation of the phantom sample without noise. Figure 4(a) is a gray scale image of the reconstructed cross sectional image in the z = 0 mm plane. The reconstructed image is sharp enough and well represents the geometry of the absorbers. Although some small artificial structures can be seen around the reconstructed images of the absorbers, they are minimal and are mainly due to the limited detection angle and bandwidth. Figures 4(b) and 4(c) show a comparison of the intensities between the original and the reconstructed distributions along the lines at (x, 0, 0) and (−4, y, 0), respectively. The reconstructed intensity profiles are sharp and the values closely match with the original ones. Due to surrounding artifacts caused by the ringing effect, the intensity of the largest sphere was slightly higher than the initial intensity. This was mended by subtracting the average of the background from the image (Fig. 5). The high quality of the reconstructed images demonstrates the advantages of the new FBP algorithm, which benefits from the rigorously derived weighting function in the Fourier domain and an adaptive cutoff frequency, which differs from the usage of the filter functions in conventional FBP.

FIG. 4.

The second simulation without noise: (a) Reconstructed image using the new algorithm at plane z = 15.0 mm; (b) relative intensity of reconstructed image at (x, 0, 15); (c) relative intensity of reconstructed image at (−4, y, 15).

FIG. 5.

The second simulation without noise. After subtracting the background, the intensity well matches the original values of the model. (a) Reconstructed image using the new algorithm at plane z = 15.0 mm; (b) relative intensity of reconstructed image at (x, 0, 15); (c) relative intensity of reconstructed image at (−4, y, 15).

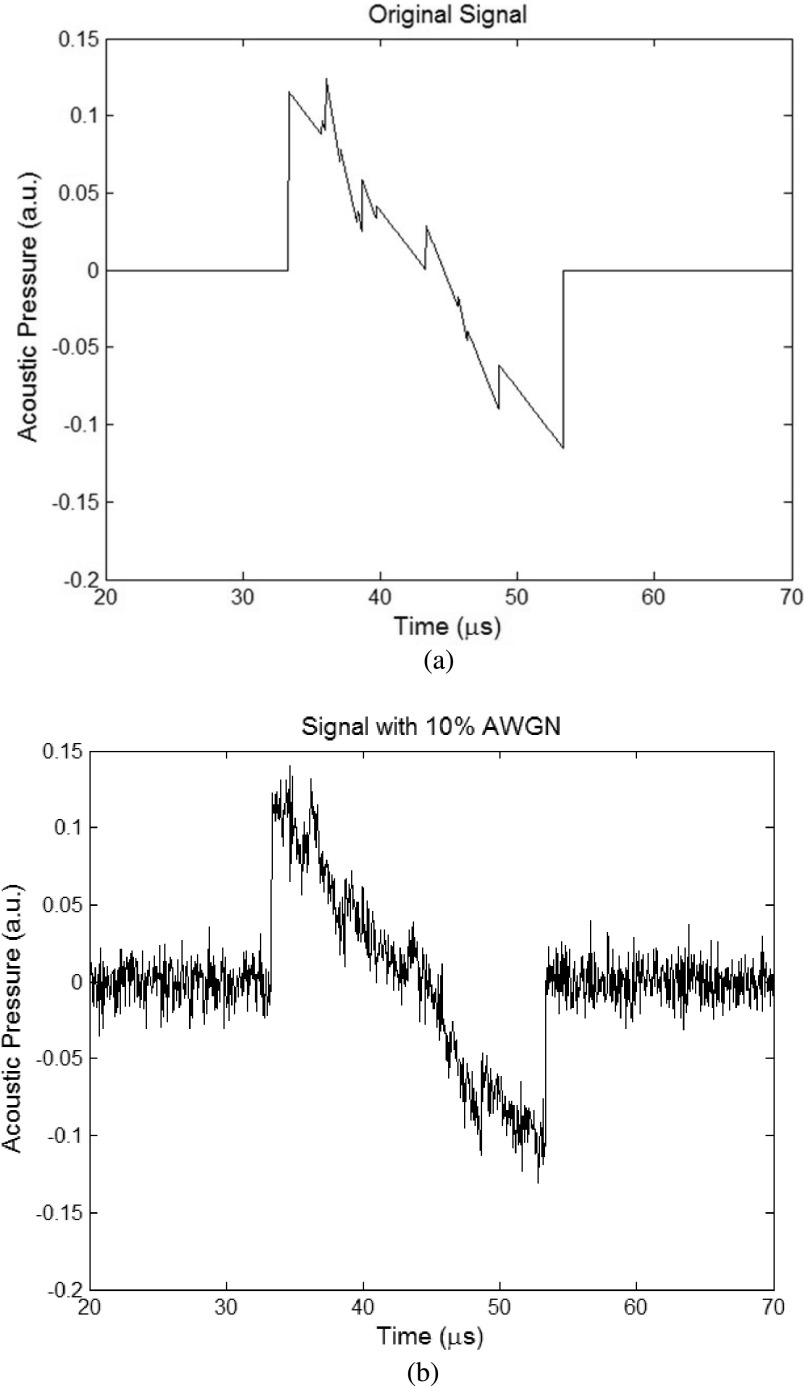
Next, we consider the case with additional noise in the measurements for the second model. From Eq. (16), we have (19), where the noise is 10% additive white Gaussian noise (AWGN), relative to maximum of each signal. Figure 6 gives an example of the time domain signal from a detector used for the simulations, where Fig. 6(a) shows an ideal signal without noise and Fig. 6(b) shows the signal with noise added,

$${\displaystyle p\left(\mathbf{r},t\right)={\mathrm{\Gamma }}_A\frac{\partial }{\partial t}\sum _{n=0}^T{L}^{\left(n\right)}\cdot n\cdot {\left({\rho }_{oi}\right)}^n+\text{noise}.}$$ (19)

FIG. 6.

An example of time domain signals from a detector used for the simulation. (a) Noiseless signal and (b) signal with 10% AWGN relative to the signal’s maximum.

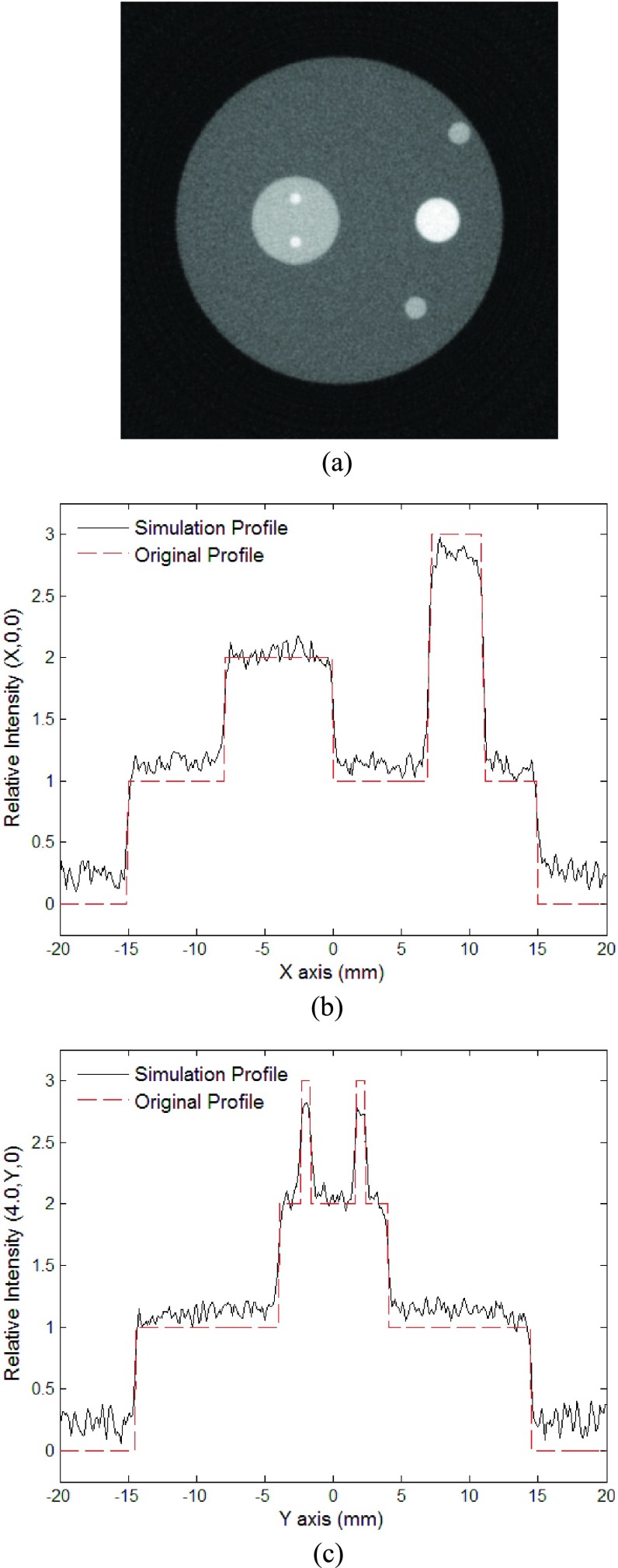
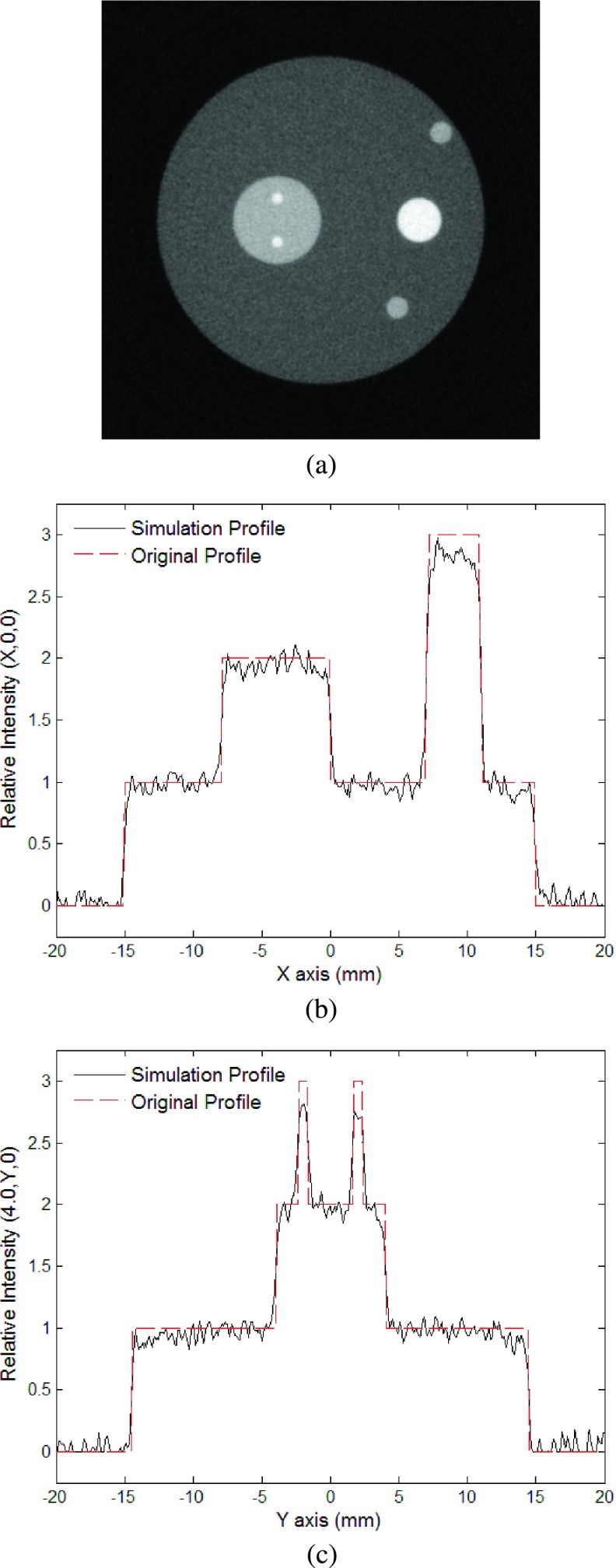
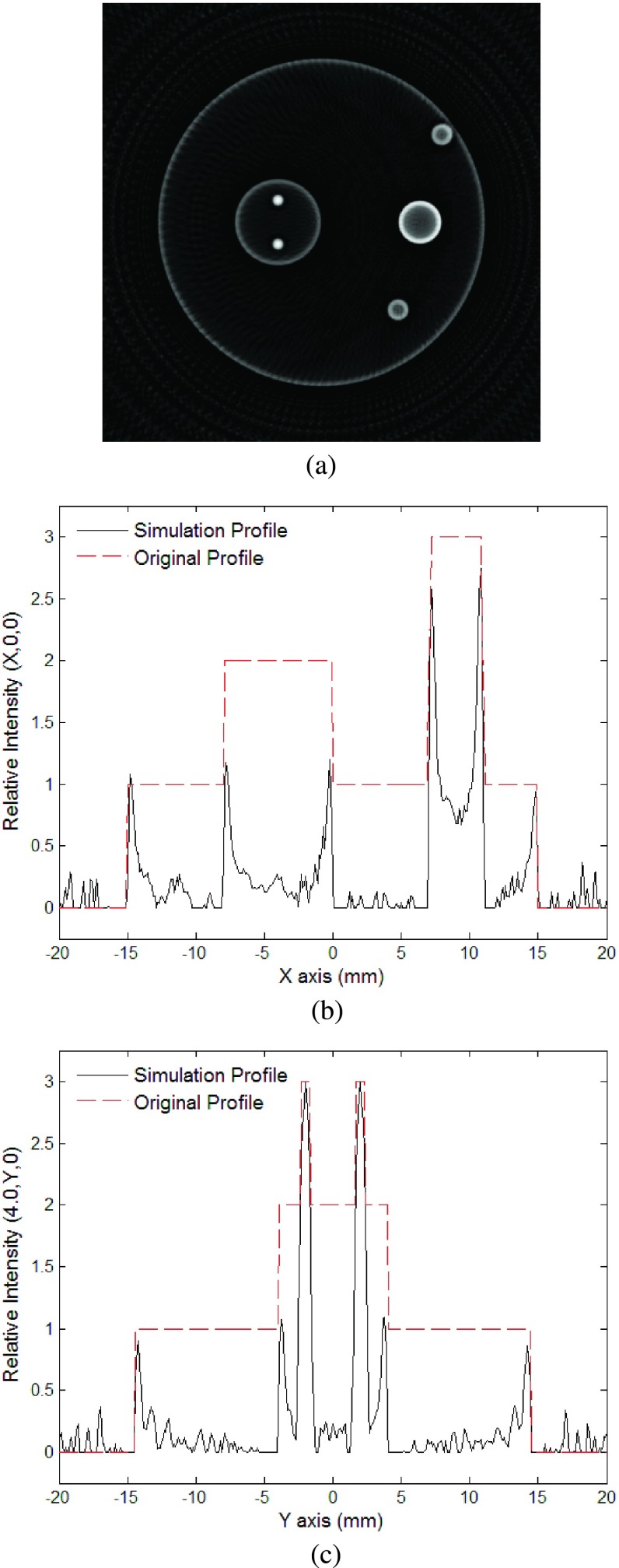
Figures 7(a) and 8(a) are reconstructed gray-scale images of the cross section of the absorbers in the z = 0 mm plane with noise introduced to the observed signals, where Fig. 8(a) is with the background subtracted. Although noise appears in the images, they are still clear enough to well present the geometry of the absorbers. Figures 7(b), 7(c), 8(b), and 8(c) show a comparison of the intensities between the original and the reconstructed intensity distributions along the lines (x, 0, 0) and (−4, y, 0). Despite the significant amount of noise, the reconstructed intensity profiles are still in good agreement with the original ones. The fact that the noise remains at a minimal level demonstrates the robustness of the new FBP algorithm for reconstructing PAT images of complicated structures with reasonable amount of detection noise.

FIG. 7.

The second simulation with noise added to the observed signals: (a) Reconstructed image using the new algorithm at plane z = 15.0 mm; (b) relative intensity of reconstructed image at (x, 0, 15); (c) relative intensity of reconstructed image at (−4, y, 15).

FIG. 8.

The second simulation with noise added to the observed signals and the background subtracted: (a) Reconstructed image using the new algorithm at plane z = 15.0 mm; (b) relative intensity of reconstructed image at (x, 0, 15); (c) relative intensity of reconstructed image at (−4, y, 15).

It is worth noticing that even under the assumed poor detection condition with a spatial resolution of 0.495 mm/pixel, the reconstructed image still well reproduces the geometry of the smallest absorbers, i.e., sphere 3 and sphere 4 with a radius of 0.5 mm for the cases either without (Figs. 4 and 5) or with detection noise (Figs. 7 and 8). In comparison, the results of utilizing a Hanning Window, with a cutoff frequency of 4 MHz, indicate that the image boundaries are well displayed but information of intensity is lost within the spheres (Figs. 9 and 10).

FIG. 9.

Simulation with Hanning window applied to noiseless signals: (a) Reconstructed image using the new algorithm at plane z = 15.0 mm; (b) relative intensity of reconstructed image at (x, 0, 15); (c) relative intensity of reconstructed image at (−4, y, 15).

FIG. 10.

Simulation with Hanning window applied to noiseless signals and the background subtracted: (a) Reconstructed image using the new algorithm at plane z = 15.0 mm; (b) relative intensity of reconstructed image at (x, 0, 15); (c) relative intensity of reconstructed image at (−4, y, 15).

5. CONCLUSIONS

In this paper, we have developed an improved FBP algorithm for PAT image reconstruction. We obtained an exact form of a weighting function from the basic photoacoustic wave equation. The weighting function serves as a precise ramp filter for processing the observed signals in the Fourier domain. Utilizing the weighting function, one can precisely calculate the contribution of the measured signals in Fourier domain. In addition, we also obtained an adaptive criterion to determine the cutoff frequency for the low-pass filter in Fourier domain. These new approaches allow us to obtain a sharper image. For fast numerical modeling, based on traceless, totally symmetric Cartesian tensors, we have introduced the ACE method to create the pressure model for simulating photoacoustic signals. In addition, our image reconstruction method utilizes the retarded potential generated by photoacoustic sources. We conducted numerical simulations on different phantom samples and demonstrated the effectiveness and robustness of our new FBP image reconstruction method. High quality reconstructed images were achieved using this algorithm, which have sharp borders and precise relative absorbed energy, even for complicated sample structures and with introduced noise in the observed signals.

APPENDIX A: WEIGHTING FUNCTION

Photoacoustic wave Eq. (2) has a general solution that can be expressed as,²⁶

$${\displaystyle p\left(\mathbf{r},t\right)=\frac{\alpha }{C_p}{\int }_{t^{\prime }=0}^{t^{\prime }=\infty }{\int }_{V}G\left(\mathbf{r},{\mathbf{r}}^{\prime },t,t^{\prime }\right)H\left({\mathbf{r}}^{\prime }\right){\delta }^{\prime }\left(t^{\prime }\right){\text{d}}^3{\mathbf{r}}^{\prime }\text{d}{t}^{\prime },}$$ (A1)

where $G\left(\mathbf{r},{\mathbf{r}}^{\prime },t,t^{\prime }\right)=\delta \left(\left|\mathbf{r}-{\mathbf{r}}^{\prime }\right|-c\left(t-t^{\prime }\right)\right)/4\pi |\mathbf{r}-{\mathbf{r}}^{\prime }|$, i.e., Green’s function.

In order to further derive the solution for the photoacoustic wave equation, we first utilize the following mathematics substitution: $\int {\delta }^{\prime }\left(t-t_0\right)f\left(t\right)\text{d}t=f^{\prime }\left(t_0\right)$ and $\partial G/\partial t^{\prime }=-\left(\partial G/\partial t\right)$.

We then obtain

$${\displaystyle p\left(\mathbf{r},t\right)=\frac{\alpha }{C_p}{\int }_{V}H\left({\mathbf{r}}^{\prime }\right)\frac{\partial G(\mathbf{r},{\mathbf{r}}^{\prime },t)}{\partial t}{\text{d}}^3{\mathbf{r}}^{\prime }.}$$ (A2)

From the inverse Fourier transform of Green’s function, we also have

$${\displaystyle G\left(\mathbf{r},{\mathbf{r}}^{\prime },t,t\right)=\frac{1}{{\left(2\pi \right)}^4}\int \int \frac{e^{-i\mathbf{k}\cdot \left(\mathbf{r}-{\mathbf{r}}^{\prime }\right)}{e}^{i\omega \left(t-t^{\prime }\right)}}{k^2-{\left(\omega /c\right)}^2}d\omega {\text{d}}^3\mathbf{k}.}$$ (A3)

For the frequency axis, we can see that there are two simple poles when ω = ± ck because

$${\displaystyle \frac{e^{-i\mathbf{k}\cdot \left(\mathbf{r}-{\mathbf{r}}^{\prime }\right)}{e}^{i\omega \left(t-t^{\prime }\right)}}{k^2-{\left(\omega /c\right)}^2}=\frac{e^{-i\mathbf{k}\cdot \left(\mathbf{r}-{\mathbf{r}}^{\prime }\right)}{e}^{i\omega \left(t-t^{\prime }\right)}}{(k+\omega /c)(k-\omega /c)}.}$$ (A4)

For t > 0, we can calculate the integration based on Cauchy’s residue theorem,⁵⁴

$${\displaystyle G\left(\mathbf{r},{\mathbf{r}}^{\prime },t\right)=\frac{c}{{\left(2\pi \right)}^3}\int \frac{sin\left(ckt\right)}{k}{e}^{i\mathbf{k}\cdot \left(\mathbf{r}-{\mathbf{r}}^{\prime }\right)}{\text{d}}^3\mathbf{k}.}$$ (A5)

Hence, we have

$${\displaystyle \frac{\partial G(\mathbf{r},{\mathbf{r}}^{\prime },t)}{\partial t}=\frac{c^2}{{\left(2\pi \right)}^3}\int cos\left(ckt\right)e^{i\mathbf{k}\cdot \left(\mathbf{r}-{\mathbf{r}}^{\prime }\right)}{\text{d}}^3\mathbf{k}.}$$ (A6)

The pressure distribution function p(r, t) can be further derived by utilizing the above equation. We have

$${\displaystyle p\left(\mathbf{r},t\right)=\frac{1}{{\left(2\pi \right)}^3}\int p_0\left(\mathbf{k}\right)cos\left(ckt\right)e^{i\mathbf{k}\cdot \mathbf{r}}{\text{d}}^3\mathbf{k}.}$$ (A7)

We know that

$${\displaystyle p\left(\mathbf{r},t\right)=\frac{1}{{\left(2\pi \right)}^3}\int p\left(k,t\right)e^{-i\mathbf{k}\cdot \mathbf{r}}{\text{d}}^{3}k.}$$ (A8)

Comparing Eqs. (A7) and (A8), we obtain in Fourier space that

$${\displaystyle p_0\left(\mathbf{k}\right)=\frac{p(\mathbf{k},t)}{cos\left(ckt\right)}{e}^{-2i\mathbf{k}\cdot \mathbf{r}}.}$$ (A9)

Therefore, the initial pressure source function in time domain can be expressed as

$${\displaystyle p_0\left(\mathbf{r}\right)=\frac{1}{{\left(2\pi \right)}^3}{\int }_{k}p\left(\mathbf{k},t\right)W\left(\mathbf{k},\mathbf{r},t\right)e^{-i\mathbf{k}\cdot \mathbf{r}}{\text{d}}^3\mathbf{k},}$$ (A10)

where $W\left(\mathbf{k},\mathbf{r},t\right)=e^{-2i\mathbf{k}\cdot \mathbf{r}}/cos\left(ckt\right)$ is the weighting function, which represents the amount of contributions from a signal $p\left(\mathbf{k},t\right)$ for the image reconstruction in the Fourier domain.

APPENDIX B: ACCELERATED CARTESIAN EXPANSIONS

1. Multipole expansion

The total potential at any point r ∈ Ω_O due to k sources q_i, i = 1, …, k located at points r_i ∈ Ω_S is given as

$${\displaystyle \mathrm{\Phi }\left(\mathbf{r}\right)=\sum _{n=0}^{\infty }{\mathbf{M}}^{\left(n\right)}\cdot n\cdot {\nabla }^n\frac{1}{\mathbf{r}},}$$

$${\displaystyle {\mathbf{M}}^{\left(n\right)}=\sum _{i=1}^k\left(-1\right)\frac{q_i}{n!}\underset{i}{\overset{n}{\mathbf{r}}},}$$ (B1)

where M⁽ⁿ⁾ is the totally symmetric multipole tensor about the origin r_S = {0, 0, 0}.

2. Multipole-to-multipole expansion

Given a multipole expansion of k sources about the r_S = {0, 0, 0},

$${\displaystyle {\mathbf{M}}^{\left(n\right)}=\sum _{m=0}^n\hspace{0.17em}\sum _{p\left(m,n\right)}\frac{m!}{n!}{\left({\mathbf{r}}_s^P\right)}^{n-m}{\mathbf{O}}^m,}$$ (B2)

where O⁽ⁿ⁾ is old multipole tensor and P(m, n) is the permutation of all partitions of n into sets n − m and m.

3. Multipole to local translation

Assume that the domains Ω^S and Ω^O are sufficiently separated, and the distance between their centers r^OS = |r^S − r^O| is greater that diam {Ω^S} and diamf {Ω^O}. If a multipole expansion M⁽ⁿ⁾ is located at r^S, then another expansion L⁽ⁿ⁾ that produces the same field ∀r ∈ Ω^O is given by

$${\displaystyle \mathrm{\Phi }\left(\mathbf{r}\right)=\sum _{n=0}^{\infty }{\rho }^{\left(n\right)}\cdot n\cdot {\mathbf{L}}^{\left(n\right)},}$$

$${\displaystyle L^{\left(n\right)}=\sum _{m=n}^{\infty }\frac{1}{n!}{\mathbf{M}}^{\left(m-n\right)}\cdot \left(m-n\right)\cdot {\tilde{\nabla }}^m\frac{1}{r^{\mathit{os}}},}$$ (B3)

where ρ = r − r^O.

4. Local to local expansion

A local expansion O⁽ⁿ⁾ that exists in the domain Ω^O centered around r^O can be shifted to the domain Ω_O centered at r_O using

$${\displaystyle {\mathbf{L}}^{\left(n\right)}=\sum _{m=0}^n\left(\begin{array}{c}\hfill m\hfill \\ \hfill m-n\hfill \end{array}\right){\mathbf{O}}^{\left(m\right)}\cdot \left(m-n\right)\cdot {\left({\mathbf{r}}^C\right)}^{m-n},}$$ (B4)

where r^C = r_O − r^O.

5. Local to source

Finally, the potential at any point in the Ω_O can be obtained using

$${\displaystyle \mathrm{\Phi }\left(\mathbf{r},t\right)=\sum _{n=0}^{\infty }{L}^{\left(n\right)}\cdot n\cdot {\left({\rho }_{oi}\right)}^n,}$$ (B5)

where ρ_oi = r − r_O.