A multistage mathematical approach to automated clustering of high-dimensional noisy data

Significance

Organizing large, multidimensional datasets by subgrouping data as clusters is a major challenge in many fields, including neuroscience, in which the spike activity of large numbers of neurons is recorded simultaneously. We present a mathematical approach for clustering such multidimensional datasets in a relatively high-dimensional space using as a prototype datasets characterized by high background spike activity. Our method incorporates features allowing reliable clustering in the presence of such strong background activity and, to deal with large size of datasets, incorporates automated implementation of clustering. Our approach effectively identifies individual neurons in spike data recorded with multiple tetrodes, and opens the way to use this method in other domains in which clustering of complex datasets is needed.

Abstract

A critical problem faced in many scientific fields is the adequate separation of data derived from individual sources. Often, such datasets require analysis of multiple features in a highly multidimensional space, with overlap of features and sources. The datasets generated by simultaneous recording from hundreds of neurons emitting phasic action potentials have produced the challenge of separating the recorded signals into independent data subsets (clusters) corresponding to individual signal-generating neurons. Mathematical methods have been developed over the past three decades to achieve such spike clustering, but a complete solution with fully automated cluster identification has not been achieved. We propose here a fully automated mathematical approach that identifies clusters in multidimensional space through recursion, which combats the multidimensionality of the data. Recursion is paired with an approach to dimensional evaluation, in which each dimension of a dataset is examined for its informational importance for clustering. The dimensions offering greater informational importance are given added weight during recursive clustering. To combat strong background activity, our algorithm takes an iterative approach of data filtering according to a signal-to-noise ratio metric. The algorithm finds cluster cores, which are thereafter expanded to include complete clusters. This mathematical approach can be extended from its prototype context of spike sorting to other datasets that suffer from high dimensionality and background activity.

Cluster analysis is important in many fields, ranging from biochemistry (1) to genetics (2) to neuroscience (3, 4). In neuroscience, improved sensors (4) have permitted large increases in the size and dimensionality of recorded datasets. An essential problem remains that the brain contains millions of simultaneously active neurons, emitting action potentials (spikes) with varying frequencies and patterns related to ongoing behavior and brain state (3, 5). The identification of signals from individual neurons, in a sea of brain action potential, is critical. Commonly used four-sensor electrodes (tetrodes) (6, 7) and array recording methods (4) produce large, multidimensional datasets, which then require cluster analysis to separate signals from individual neurons. These expansive datasets present the need for fully automated methods for spike sorting (3, 4) with mathematical calculations and algorithms capable of analyzing multidimensional recordings (8). In particular, there is a need for algorithms than can process data containing overlapping clusters with unclear borders in the persistence of strong background signals.

Due to its great complexity, spike sorting currently lacks a well-developed solution (3, 9). The recordings made from many neurons with varying proximity to probes provide no knowledge as to the number of clusters present (6). Also, there are often no clear boundaries between the signals of the different neurons recorded, and the density of neurons varies widely across different regions of the brain and across different recording methods (10). Overlapping clusters and strong background activity, produced by neighboring neurons, as well as the similarity of spike waveforms in given classes of neurons, present different problems for algorithms that rely on matching spike waveforms to templates, principal component analysis (PCA), density, and distance metrics (5). Compounding the complexity of the spike-sorting problem, recordings can involve 10–20 “useful” dimensions, especially those that use tetrodes or multisensor probes (8).

Our approach individually solves the three primary challenges of spike sorting: space complexity, cluster overlap, and differing cluster densities, all in the presence of background activity. To combat feature space complexity, our algorithm employs a method of space evaluation, whereby each dimension in the feature space is independently evaluated based on its contribution to the goal of clustering. To overcome the challenge of cluster overlap and bridges, our algorithm includes a system of extensive preprocessing that removes all data except for cluster cores, which are identified by larger spike density relative to their surroundings. Later, during postprocessing, clusters are rebuilt around these cores. Finally, to take into account differing clustering densities and a wide range of signal-to-noise ratio (SNR) in regions of the data spaces, our algorithm introduces a multipass clustering method. Upon each iteration, the algorithm changes its threshold for SNR and removes successful clusters from the data space, thereby simplifying the space and making it more likely to find clusters that are typically difficult to find.

Results

We analyzed neuronal data recorded with tetrodes, represented as 32 voltage readings per tetrode channel over the interval of 1 ms (Fig. 1A). Tetrode recordings often have slightly misaligned data streams from the four sensors. Waveforms are interpolated and aligned (Fig. S1; Materials and Methods) by shifting signal waveforms from the different channels horizontally along the time axis. Obvious noise, introduced as a malfunction of system components, is removed from the recorded data (Fig. S2; Materials and Methods). Sometimes more than one spike is recorded during the 1 ms of data capture typically used, and these nearly simultaneous spikes must be separated into two independent spikes (Fig. S1D).

Fig. 1.

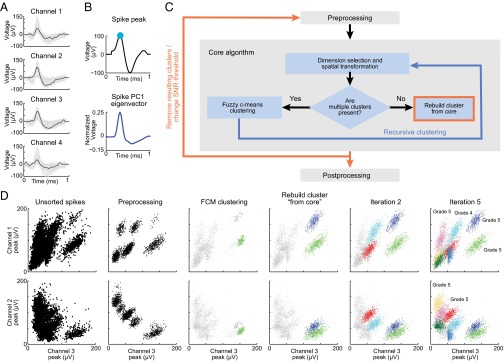
Algorithm flowchart and feature extraction. (A) Raw spikes recorded by four channels of a tetrode measured over 1 ms. Black traces represent a spike simultaneously recorded by four tetrode channels, and gray traces show all spikes recorded during the session. (B) Features extracted from the spikes measured by each channel. Each spike recorded on a channel is decomposed into voltage peak (Upper) and projected into PC1 eigenvector (Lower). (C) Algorithm flowchart. High density cluster cores are isolated (preprocessing), and the modality of each dimension is identified and weighted according to importance for clustering (dimension selection and spatial transformation). The dataset is clustered by FCM. If the resulting cluster remains multimodal, then it is recursively clustered (blue arrow). Surrounding points are then reattributed to cluster cores (rebuild cluster from core), which terminates the core algorithm (red frame). After each iteration of the algorithm, the SNR level is adjusted, and the clustering algorithm repeats (red arrow). Each cluster identified by this algorithm is examined and graded (postprocessing). (D) An example of spike sorting of data recorded with tetrodes and processed by the algorithm. Space bins with low density and spikes with low SNR are temporarily removed (preprocessing). Cluster centers are identified (FCM clustering), and points around the cluster center are attributed to that cluster (rebuild cluster from core). Using lower SNR, additional clusters are found (iteration 2), and eventually, the entire data space is clustered, and the optimality of each cluster can be rated (iteration 5).

Algorithm Design.

For the spikes of individual neurons to be clustered by the algorithm, the recorded spike waveforms must be featurized. Each feature of a spike wave, which will hereafter be termed a “dimension,” corresponds to an attribute of the waveform. Attributes must be chosen so as to maximize the power of identification, while avoiding unnecessary complexity. The algorithm that we developed includes a feature space consisting of 11 dimensions: four peak voltage dimensions, each corresponding to each tetrode channel (example of one channel peak voltage dimension shown in Fig. 1B, Upper); four PC dimensions, including PC1 of each waveform (example of eigenvectors used for PC spike projections shown in Fig. 1B, Lower); and three peak PC dimensions. PC dimensions are calculated by means of a modified PC technique (Materials and Methods).

The algorithm attempts to identify a cluster for spikes of one neuron in the presence of the background activity of other neurons. The algorithm presented overcomes these challenges through three processes. The initial “cleaning” temporarily removes background and overlapping activity through SNR and density filters (Fig. 1 C and D). Without background and overlapping activity, a simple algorithm can be used to find cluster centers. The second process, rebuilding clusters from cores, occurs after cluster core identification. The removed spikes are assigned to correct clusters based on the removed spikes’ similarity to the spikes in the cluster cores. The third process, iteration with different SNRs, involves the repetition of the main clustering process. The algorithm begins by identifying clusters with a high SNR, and once identified, these clusters are removed from the dataset (Fig. 1C and Fig. S3). On each iteration, the SNR and density filters are decreased until the clusters with low SNR are identified (Fig. 1 C and D). Once clusters are finalized, the identified clusters are graded (Fig. 1 C and D).

Recursive Clustering Paired with Dimensional Evaluation.

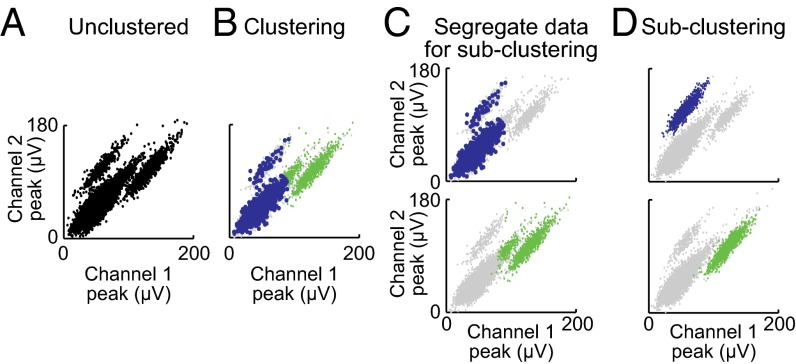
Clustering is difficult in a multidimensional environment due to the “curse of dimensionality” and the fact that some clusters are only visible in a specific dimensional set. To solve these problems, the algorithm uses recursive clustering (Fig. 2) combined with dimension selection and evaluation (Fig. 3). Clustering is performed using fuzzy c-means (FCM) clustering (Fig. S4). In each step of recursive clustering, the initial dataset is prepared for clustering by dimensional evaluation and selection. Dimensional evaluation also provides criteria for ending the recursive clustering. The resulting clusters from the first iteration of recursive clustering (Fig. 2 A and B) are separated and are individually clustered (Fig. 2C). This process continues recursively until each cluster has been evaluated (Fig. 2D).

Fig. 2.

Recursive clustering based on dimensional selection and evaluation. (A) Data before clustering. (B) The dataset is clustered by FCM. (C) The two clusters are separated for independent processing. (D) The original clusters are subclustered. The resulting clusters are found to be unimodal, and the process completes.

Fig. 3.

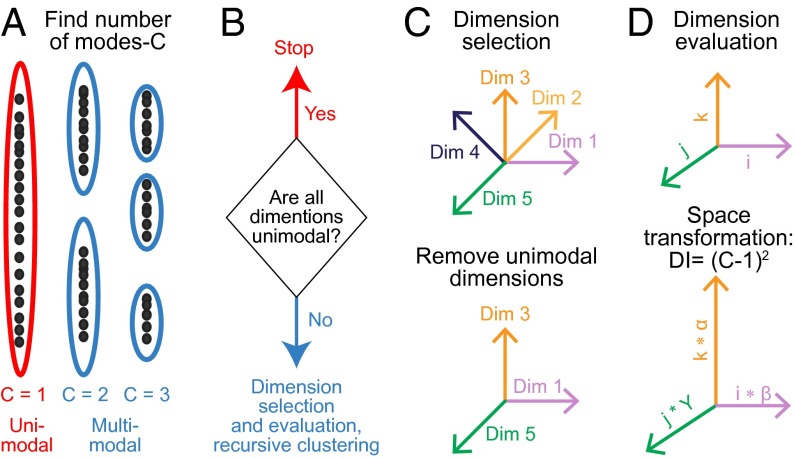
Dimensional selection and evaluation. (A) Using FCM paired with MPC, the number of potential clusters is evaluated. The dimension's dataset is sorted into different numbers of clusters, and then MPC chooses the optimal number of clusters. (B) If all dimensions are unimodal, the recursive clustering process ends. (C) If at least one dimension is multimodal, the space is constructed from the dimensions that have two or more modes (Upper). All unimodal dimensions are then removed from the space (Lower). (D) Each dimension is examined for number of modes (“C”). Dimensional importance (DI) is calculated for each of the dimensions. Feature space is transformed by weighting (scaling) each dimension by dimensional importance.

Dimensional Importance.

The cluster configuration is represented in a multidimensional space. Each dimension likely has a different contribution to an algorithm's ability to find different clusters in the configuration. This contribution can be termed as its “dimensional importance.” Dimensional importance is a function of the number of clearly separable data density peaks across a dimension, known as modes (Fig. 3A). Unimodal dimensions have a clustering value of zero according to this metric. As the modality of a dimension increases, its dimensional importance also increases. The number of clearly separable modes is identified by first projecting the data onto the dimension of interest. Then cluster analysis is performed on the one-dimensional projection of the data using FCM with different numbers of clusters. The number of well-separable clusters is found by modified partition coefficient (MPC) analysis (11) (Fig. 3A; Materials and Methods). If each dimension of the configuration is unimodal, then the configuration does not require further clustering. This criterion is used as the stop-condition for recursive subclustering (Fig. 3B). If one or more dimensions of the configuration are not unimodal, dimensional selection prepares for another recursive clustering step (Fig. 3B). A space for clustering is constructed from the multimodal dimensions (Fig. 3C). Dimensions with higher modality are given more weight during clustering to account for increased value (Fig. 3D and Fig. S4).

Rebuilding of Clusters from Identified Cores.

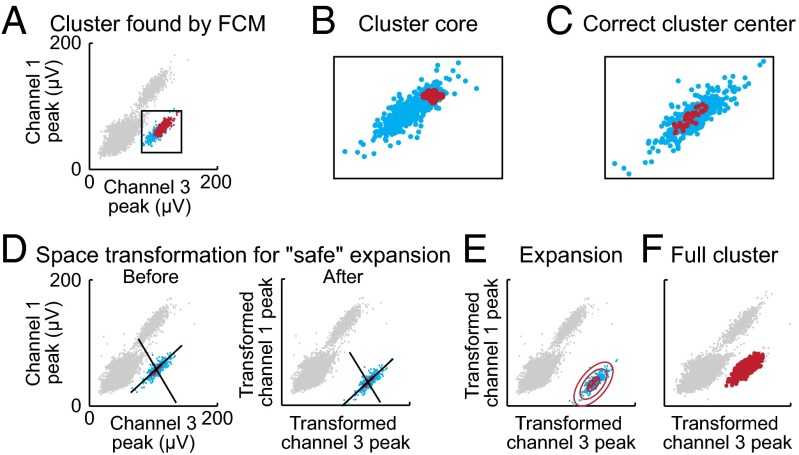
In the initial stages of the algorithm, low SNR spikes and background activity are removed. After the identification of cluster cores by the recursive clustering process, each spike must be properly assigned to its core (Fig. 4A; Materials and Methods). However, several challenges arise during spike assignment. The central challenge is the fact that cluster cores found by FCM during recursive clustering usually do not coincide with true cluster centers (centers of mass of the cores; Fig. 4B). To find full clusters, clusters must be rebuilt around the cores (Fig. 4B). Further, during the process of rebuilding a cluster from cluster centers, the algorithm must avoid mistakenly attributing spikes from neighboring clusters to that cluster. In addition, cluster cores that are detected by FCM can be found inside multiunit activity or very far away from the true cluster center (Fig. S5A). To address these challenges, our cluster-rebuilding algorithm includes a three-step process. First, the algorithm iteratively finds correct cluster centers (Fig. 4C). To find a center, the algorithm uses a process of expansion and contraction that iteratively moves the identified cluster core toward the cluster’s center of mass. Second, the algorithm measures and transforms the space between neighboring clusters. The distance from the cluster core to the rest of the spikes is independently measured in each dimension. For dimensions along which the cluster is close to the rest of the spikes, distance is elongated (Fig. 4D; Materials and Methods). Then clusters are rebuilt from cores (Fig. 4 E and F). Third, the modality of the density functions of the resulting clusters is analyzed (Fig. S5 B and C). Two types of density functions are attributed to “bad” clusters: clusters with fat-tailed distributions (Fig. S5B) or multi-modal distributions (Fig. S5C). When such bad clusters are identified, the assignments of spikes to those clusters are discarded, and those spikes, reintegrated with the rest of data, continue to the next iteration of the algorithm.

Fig. 4.

Rebuilding clusters from cores. (A) Spikes clustered by the FCM algorithm (red) and those that should be assigned to the cluster (blue). (B) The location of the cluster core found by FCM (red) does not match with the cluster center. (C) The “correct” core (red) of the cluster (blue) is identified. (D) The distance between the cluster and its neighbors is calculated. (E) The space between the cluster and its neighbors is transformed, so that the cluster (blue) can be rebuilt from its core (red) without stepping on neighboring clusters (gray). Previously removed spikes are attributed to the cluster core. (F) Finally, the full cluster (red) is rebuilt from the core.

Assignment of Cluster Quality.

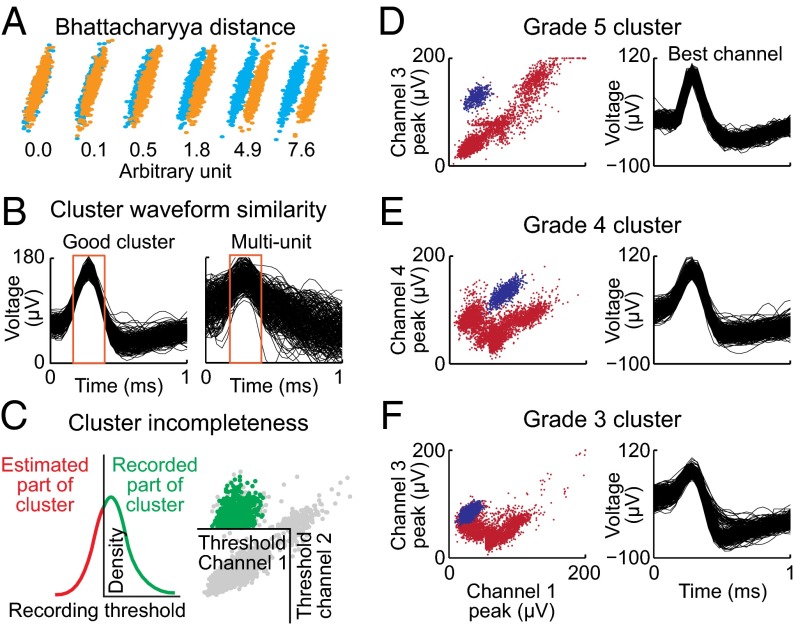
Identified clusters have different quality, reflecting many factors, including the intrinsic properties of the given neuron, properties of the recording tetrode, recording distance, quality of the recording system, and levels of nearby background activity (10, 12). To create an accurate measure of quality, the algorithm evaluates the assigned clusters through a series of four methods. First, the separation of the cluster from the remainder of the data is measured as the Bhattacharyya distance (13) between clusters (Fig. 5A) and the L-ratio (10). Second, the similarity of raw waveforms to the cluster mean waveform is calculated (Fig. 5B). Third, cluster incompleteness is measured using the symmetry of distribution (Fig. 5C). Fourth, the stationarity of the recordings through all recording periods is examined. Outputs from these four methods are combined in the calculation of the final grade (Fig. S6). Clusters are graded on a scale from −9 to +5. Clusters with grades of 3, 4, and 5 are separable neurons that can be used for data analysis (Fig. 5 D–F). Clusters with grades of 1 and 2 are strongly contaminated with multiunit activity. Clusters with negative grades are classified as different types of artifact.

Fig. 5.

Grading of cluster quality. (A) Two overlapping, normally distributed clusters are shown (blue and orange dots). Bhattacharyya distance accurately measures the level of overlap between the clusters. (B) The analysis was performed with time window corresponding to the widths at half peak (red rectangles). Spikes are normalized, and the error of projection to the mean waveform is calculated. (C) The level of cluster incompleteness is quantified, identifying asymmetrical clusters that result from inappropriate thresholds for spike detection. (D–F) Three examples of final cluster grades (blue clusters): an excellent (grade 5) cluster (D), a mediocre (grade 4) cluster (E), and a separable (grade 3) cluster (F).

Estimates of the Algorithm’s Success.

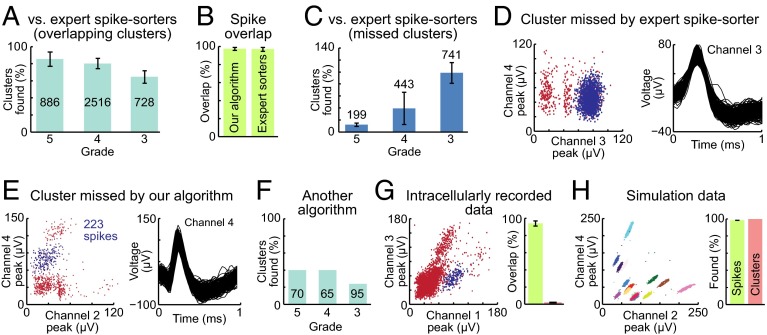
To measure the success of our algorithm, we made comparisons to three baselines. First, we created a baseline of clusters identified by eight expert spike-sorters, using spikes recorded in the neocortex and dorsal striatum. We rated clusters found by these spike-sorters by the method described above (Figs. S6 and S7). Then, considering only the clusters useful for data analysis (886 clusters with grade 5, 2,516 clusters with grade 4, and 728 clusters with grade 3), we counted the number of these clusters found by the algorithm. A cluster was considered found only if it was also graded 3, 4, or 5. Our algorithm successfully found more than 80% of clusters identified by expert spike-sorters (Fig. 6A). We calculated the percentage of spikes found by both spike-sorters and our algorithm in well-isolated clusters (grade 5), and we found 97.4% of overlap (Fig. 6B). Additionally, the algorithm found clusters that the expert spike-sorters missed, often as a result of human error (Fig. 6 C and D). Hence, we conclude that the algorithm is in good agreement with expert spike-sorters. However, our algorithm also occasionally missed small clusters (Fig. 6E). To evaluate our algorithm’s performance against existing software, we compared the number of clusters found by KlustaKwik (8) (Fig. 6F) and by our algorithm (Fig. 6A), against clusters identified by expert spike-sorters in a set of real tetrode recordings. The number of clusters found was significantly higher for our algorithm (Fig. 6 A and F). We next tested data from experiments in which extracellular recordings were performed simultaneously with intracellular recordings (14, 15), and the percentage of correctly attributed spikes was calculated. The proportion of spikes correctly attributed by our algorithm was greater than 90%, and the proportion of misidentified spikes was ∼2% (Fig. 6G). An additional comparison involved the use of simulation data (16). We generated different datasets with waveforms resembling those of striatal neurons in which the correct spikes per cluster were known (Fig. 6H and Fig. S8). These data were generated with different levels of background noise and neuronal firing rates, and waveforms were sampled with the same probability as observed in actual cortical and striatal recordings. The number of correctly attributed spikes per cluster and the number of correct clusters found by the algorithm were counted. Our algorithm successfully found all clusters in the simulation-generated spike data with the degree of overlap that we typically encounter in real tetrode recordings, and over 98% of spikes belonging to those clusters were correctly identified (Fig. 6H).

Fig. 6.

Algorithm performance. (A) The percentage of clusters with acceptable grades that were identified by our algorithm relative to those identified by expert spike-sorters. Error bars represent SDs across eight separate datasets. (B) The intersection of spikes found by our algorithm and expert spike-sorters in clusters having grade 5. (Left) The percent of overlapping spikes in the spikes found by our algorithm. (Right) The percent of overlapping spikes in the spikes found by expert spike-sorters. (C) The percentage of clusters that were not found by spike-sorters, but were identified by our algorithm, relative to the number of clusters identified by spike-sorters. (D) An example of a cluster (spike waveform at right) that was identified by our algorithm (blue) but not found by spike-sorters. Red dots show other clusters including multiunit clusters. (E) An example of a cluster that was identified by spike-sorters (blue), but not found by our algorithm (due to the small size and sparseness of spikes). (F) Performance of an existing algorithm. Number of clusters with acceptable grades that were correctly identified by KlustaKwik compared with the expert spike-sorter baseline. The number of clusters found was significantly higher for our algorithm (P < 0.001, χ² test). (G) Performance on data from experiments in which extracellular recordings were performed with simultaneous intracellular recordings. (Left) A cluster identified by intracellular recording (blue) is shown among the remaining units recorded only extracellularly (red). (Right) The percentage of extracellularly recorded spikes correctly assigned to intracellularly identified clusters by the algorithm (green) and the percentage of spikes found by the algorithm that were not recorded intracellularly (red). (H) Performance on simulation data. (Left) An example of simulation data in which 16 clusters were successfully identified by the algorithm. (Right) The percentage of simulation spikes assigned to correct clusters by the algorithm (green) and percentage of simulation clusters accurately identified by the algorithm (red). Error bars represents SDs across simulation clusters.

Discussion

Our approach suggests a reliable mathematical method for cluster identification, implemented and tested for the prototype problem of neuronal spike sorting. As increasing numbers of hardware systems allow for the recording of spike activity from thousands of neurons simultaneously, manual clustering of the data becomes impossible even for trained experts, and a fully automated method becomes a requirement (4). We have developed a mathematical approach for the identification of clusters, and demonstrate that this algorithm involving iterative cleaning and dimension-sensitive rebuilding of clusters effectively sorts spikes in the presence of this multidimensionality and high background activity, an environment with which clustering struggles in general. The success of our algorithm in the spike-sorting context suggests that our approach to data separation could be harnessed for clustering in similarly challenging environments, including classifications of proteins, genes (2), and pattern recognition (17).

There have been many prior attempts to solve spike-sorting problems. One approach uses algorithms that cluster by minimizing distance between points, such as k-means and FCM algorithms (17). These algorithms combine classic distance minimization techniques with other intricate algorithms. All algorithms that use distance minimization must contain methods that combat the natural weaknesses of distance minimization algorithms, which are especially prevalent in spike sorting: overlapping clusters, background noise, and lack of knowledge of the number of clusters (3, 6, 10). Another approach uses density algorithms (18). This approach, which clusters together points that stem from a density nucleus, can provide reliable sorting in difficult cases (18). However, density algorithms are challenged by certain problems, including density and background variability between clusters.

An additional approach, which searches for similarity between spike shapes, includes PCA (19) and template library matching (20). PCA can successfully cluster overlapping points (19), but it faces the challenge of similarity in spike shape between neurons. A fourth approach uses advanced algorithms to match the shapes of measured waveforms to the shapes of waveforms in a template library (20). These algorithms encounter difficulties when a waveform does not match with template library, defaulting either to an incorrect match or missing neurons. Increasing these challenges, neurons have many different, although similar, shapes. Template-matching algorithms also present the task of preparing a template library of each of these neuron shapes. Independent component analysis (ICA) can successfully identify independent sources by decomposing a signal into multiple independent signals (5, 21). However, ICA techniques operate under the assumption that the number of neurons is equal to or less than the number of electrodes, so ICA is not a good fit for spike sorting in the brain, where multiunit activity recorded by four channels of a tetrode often contains 5–10 neurons.

Our objective and subjective methods of rating algorithms allows us to compare our algorithm against the success of these several clustering techniques. In an environment where many algorithms lack a relevant baseline, and each is less than optimal in general (9), finding relevant grading criteria is essential (10, 12). Our approach is to test spikes sorted by our algorithm against several baselines, including a human cluster database, a neuron simulation database, and intracellular recordings combined with extracellular recordings. These methodologies are essential for grading and rating our algorithm, and can be translated to other similar cases. Our ability to find a relevant baseline for comparison of our algorithm, however, is limited. A human-clustered baseline provides a very good baseline, but humans struggle to find exact borders of clusters on a 2D projection, introducing up to 10–20% variability.

High levels of background activity and high levels of overlap between clusters limit clustering effectiveness. The ratio between background activity and overlap between the clusters must remain under a certain ratio, with respect to cluster size and the level of similarity of the cluster waveforms. Given that all of these variables compoundly contributed to the effectiveness of the algorithm, it was difficult to isolate the key cases when testing with simulation data. We ultimately simulated a similar configuration of 16 neurons with highly overlapping clusters (Fig. 6H), and encountered some clustering errors. Many clusters were found, but some were merged, and some had a significant number of spikes misclassified (Fig. S8).

Several other factors, when combined, limit the effectiveness of our algorithm and clustering in general. Small clusters (100–250 spikes) may be missed by our algorithm (Fig. 6E). Analysis may also be impacted by small cluster sizes. Our algorithm assumes that clusters must have Gaussian distributions, an assumption without which FCM and rebuilding clusters from cores will not function. A possible source of non-Gaussian distributions is tetrode drift, in which a tetrode moves slightly during recordings.

Another limitation is overlap between nearly simultaneous spikes. Our algorithm assumes a consistent spike shape for each recorded neuron, but spike shape may actually vary within a burst of activity. The bursts that we observed in our cortical and striatal training sets did not impact the algorithm’s clustering ability. However, if the problem occurs, a possible solution would involve measuring several clusters for each spike shape at the burst, and later, based on the constant time between the clusters, merging the clusters.

In summary, the full automation of this algorithm, combined with its successful performance in sets of test data, recommend this approach for spike clustering of neuronal data as well as other datasets.

Materials and Methods

Additional description of study materials and methods is provided in SI Materials and Methods.

Spike Alignment.

Spike waveforms are interpolated before alignment. For our striatal and cortical data, we use cubic spline interpolation. Our algorithm converts a 32-point waveform into a 120-point waveform. For each channel, the 1-ms recording window is expanded to 1.25 ms, by adding 18.75 ms to the beginning and 6.25 ms to the end. This expansion gives room to shift waveforms horizontally within the 1.25-ms window to achieve peak alignment (Fig. S1 A–C) while avoiding excessive truncation. The shifted waveforms are padded with zeros and are sometimes truncated at the edge of the 1.25-ms window. This spike alignment prevents the generation of misleading results in PCA.

Spike Amplitude SNR Filter.

To compute spike amplitude SNR, the algorithm first calculates amplitude = peak – valley for the candidate spike waveform on each of the four tetrode channels, where peak and valley are the maximum and minimum voltage values, respectively (Fig. S3A). To normalize the amplitudes of differences among tetrode channels (in particular, those resulting from differences in impedance and proximity of the wire to the neuron), the algorithm calculates the z-scores of the amplitudes for each channel individually. For each spike, it then finds the best channel, i.e., the channel having the maximum z-score over the four channels; finally, it normalizes these maximum values through computation of z-scores. Each spike’s SNR is defined as its final z-score. Thus, each spike has a single SNR value. A candidate spike is retained only if its SNR is greater than a criterion level. In each iteration of the algorithm, as described below, this level is decreased. In the final iteration, the filter is removed. For the examples given here, the level begins at 2 and decreases to 1.5, 1.0, and 0 (Fig. 3B).

Local Density Filter.

To enhance the separability of clusters, this filter aims to remove background spikes that are not part of clusters. The algorithm partitions the 4D peak space into bins. If the density of a bin is less than the density of the bins in its neighborhood (multiplied by a constant), the algorithm removes the spikes in the bin. Bins not containing spikes are omitted from the analysis; this promotes the removal of spikes from bins containing edges of clusters (Fig. S3 C–E).

Multiple Iterations.

Repetition of the core algorithm often yields additional clusters (Fig. 1 C and D and Fig. S3B). The number of iterations is specified in the configuration file and is five for the examples given here. The stationarity filter is applied in every iteration. SNR and local density filters are omitted only in the final iteration to look for valid clusters that may have been filtered out. In each iteration, the SNR criterion level is decreased.

PCA of the Waveforms.

In most cases, when performing PCA, we apply to the waveform in each channel a mean subtraction that focuses on the variability in the shape of the waveform rather than on vertical shifts of the whole waveform. The waveform in each channel is subtracted by the mean of the points within that waveform. This mean subtraction is intended to reduce the impact of variability due to background multiunit activity. By contrast, when computing peak PCs, the waveform in each channel is subtracted by the mean of all waveforms over time in that channel.

Dimensional Evaluation.

Dimensional importance, used in weighting the dimensions via the spatial transformation described below, is calculated for each dimension (Fig. 3). Dimensional importance is based on the number of valid clusters in the projection of the distribution of candidate spike data points onto a 1D subspace. The evaluation of clusters is performed by a combination of FCM clustering (to find the clusters) and a MPC (to assess cluster validity) (11).

FCM requires the number of clusters, c, as one of its inputs. To find the number of clusters that optimizes the cluster validity, the algorithm performs FCM clustering on the projection of the distribution multiple times, varying c. Each time FCM clustering is performed, the MPC value m is recalculated. MPC ranges between 0 and 1. The maximum value of m and corresponding number of clusters c are used in dimension evaluation as follows: If m < 0.75, then the partitioning as a result of FCM describes the data poorly, so we set dimensional importance = 0, and the dimension is removed. Otherwise, dimensional importance = (c − 1)², thereby giving dimensions with more identifiable clusters more weight.

Spatial Transformation.

In preparation for FCM clustering of the multidimensional distribution of candidate spike data points, a transformed feature space is constructed by weighting (scaling) each dimension by its dimensional importance as determined in the dimension evaluation step (Fig. 3D). Before this transformation, the projection of the distribution onto each dimension is normalized independently using a z-score.

Computing Cluster Quality Measures.

We evaluate cluster quality based on several criteria (Fig. S6): (i) Bhattacharyya distance to other identified clusters is calculated (13). (ii) Bhattacharyya distance is calculated to multiunit activity. (iii) L-ratio, the distance from the cluster and the rest of the data, is calculated (10). (iv) Cluster waveform similarity is computed to measure spike waveform consistency. Each waveform is compared with the normalized mean cluster waveform. The total projection error is summed. (v) Cluster incompleteness is estimated as the fraction of the cluster truncated by the spike recording threshold. Our measure of cluster incompleteness assumes that the cluster has a normal distribution. (vi) Cluster consistency in time is found to ensure that the neuron is consistently active during the recording session. (vii) Cluster multimodality is measured using FCM with MPC. (viii) The number of active tetrode channels is identified.

For each cluster, based on a combination of the criteria listed above, we evaluated cluster quality. Clusters are rated as good, mediocre, separable, multiunit activity, or unacceptable (Fig. S6).