Abnormal cortical growth in schizophrenia targets normative modules of synchronized development

Abstract

Background

Schizophrenia is a disorder of brain connectivity and altered neurodevelopmental processes. Cross-sectional case-control studies in different age groups have suggested that deficits in cortical thickness in childhood-onset schizophrenia may normalize over time, suggesting a disorder-related difference in cortical growth trajectories.

Methods

We acquired MRI scans repeated over several years for each subject, in a sample of 106 patients with childhood-onset schizophrenia and 102 age-matched healthy volunteers. Using semiparametric regression, we modeled the effect of schizophrenia on the growth curve of cortical thickness in ~80,000 locations across the cortex, in the age range 8–30. In addition, we derived normative developmental modules, composed of cortical regions with similar maturational trajectories for cortical thickness in typical brain development.

Results

We found abnormal non-linear growth processes in prefrontal and temporal areas that have previously been implicated in schizophrenia, distinguishing for the first time between cortical areas with age-constant deficits in cortical thickness and areas whose maturational trajectories are altered in schizophrenia. In addition, we showed that when the brain is divided into five normative developmental modules, the areas with abnormal cortical growth overlap significantly only with the cingulo-fronto-temporal module.

Conclusions

These findings suggest that abnormal cortical development in schizophrenia may be modularized, or constrained by the normal community structure of developmental modules of the human brain connectome.

Introduction

Schizophrenia is increasingly understood to emerge from the abnormal development of relationships or connectivity between functional or anatomical areas of the brain. Magnetic resonance imaging (MRI) has demonstrated a wide range of disruptions in gray matter and white matter in schizophrenia (1–5). Disrupted structural and functional connectivity between brain regions has also been found with many imaging modalities(6–9). One hypothesis is that these disruptions reflect a pathology of neurodevelopment(1–5; 10; 11), with particular vulnerability in adolescence(12).

Childhood-onset schizophrenia (COS), a rare and severe form of schizophrenia that begins before age 13, provides a unique opportunity to explicitly test hypotheses about alterations in brain development. The cellular substrates of developmental change in MRI measures of cortical thickness are not known with certainty; but there is reason to think that processes of synaptic pruning and axonal myelination, which are ongoing during adolescence, could contribute to macroscopic shrinkage of cortical thickness during this time period(13). Previous studies of COS patients have demonstrated that cortical thickness of frontal and temporal lobe regions is reduced most severely in early adolescence and may partially “normalize” in early adulthood(14; 15). These cross-sectional data imply, but do not directly demonstrate, that schizophrenia may be associated with abnormal maturational trajectories for frontal and temporal cortical thickness.

Human brain networks can be studied at the scale of MRI by estimating the structural covariance between cortical regions as a measure of anatomical connectivity(16). It has recently been shown that brain regions that have strong structural covariance also tend to have synchronized rates of maturational change over the course of adolescence(17). Specifically, graph analysis of longitudinal MRI data has demonstrated a community structure of developmental modules, each module comprising a group of cortical areas with growth curves that are similar to each other and different to the growth curves of areas in other modules(18). These developmental modules correspond quite closely to the modules of adult anatomical networks, implying that synchronized growth processes in adolescence are important to the formation or consolidation of the normal adult connectome. It is important to note that the overlap between structural covariance and white matter connectivity, while substantial, is also incomplete(19). It is plausible that shared genetic and environmental influences lead to inter-regional correlations in brain anatomy even in the absence of a direct white matter connection between the areas(16). New data on modular development of human cortex during normal adolescence have not yet been translated to inform the analysis of hypothetically abnormal cortical development in people with schizophrenia.

Here we studied a large sample of MRI data from patients with COS (N=102; 7–32 years) and age-matched healthy volunteers (N=106; 7–32 years). Participants were scanned on average 2.6 times, with at least 2 years between consecutive scans (range=1–6 longitudinal scans per participant). We used semiparametric regression based on penalized splines(20; 21) to model the non-linear growth curves, or relationships between age and mean cortical thickness, at each of 80,000 locations (vertices) of the cortex. This analysis allowed us to test directly the hypothesis that schizophrenia is associated specifically with abnormal cortical thickness maturation during adolescence. We were also able to locate these regions of abnormal cortical maturation in the context of the normal community structure of developmental modules. This allowed us to test the hypothesis that abnormal cortical maturation in schizophrenia is modularized, or constrained by the normative community structure of developmental modules.

Methods and Materials

Sample and image processing

The sample included 525 longitudinal structural MRI scans from 208 subjects including 103 people with COS (age range 7–32; see Supplementary Table S1 for demographic information). All scans were acquired on the same 1.5T GE scanner located at the National Institutes of Health (NIH) Clinical Center in Bethesda, MD, using a T1-weighted fast spoiled gradient echo sequence: TE 5ms; TR 24ms; flip angle 45 degrees; matrix 256x256x124; field of view 24cm. The Montreal Neurological Institute’s CIVET pipeline estimated cortical thickness at ~40,000 vertices per hemisphere, as previously described(22–24). This study was approved by the NIH Institutional Review Board.

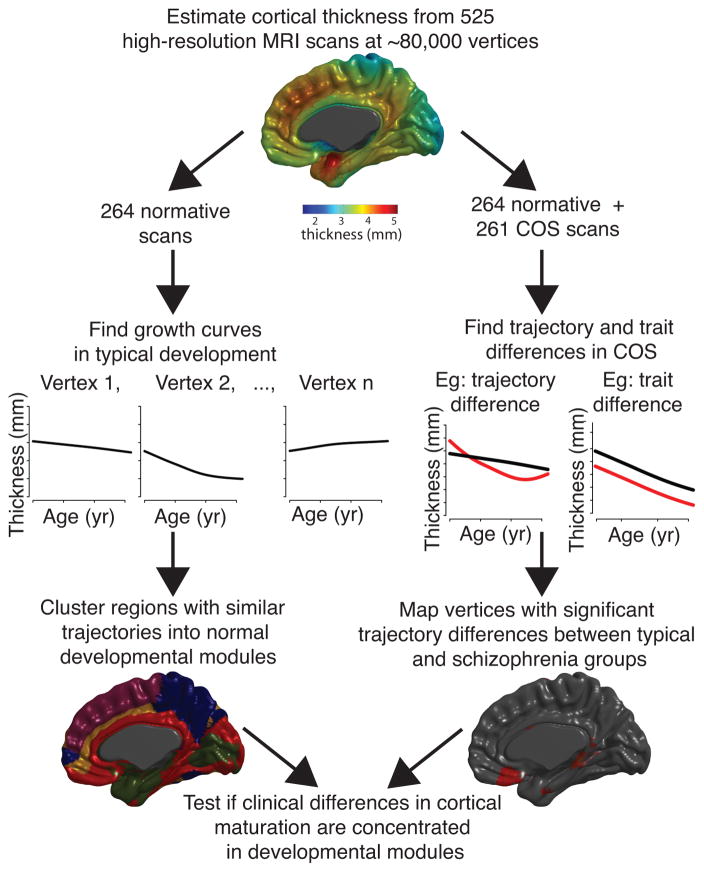
We conducted two main streams of analysis, using penalized cubic splines to estimate the non-linear relationship between age and cortical thickness at each cortical vertex (Figure 1), where the resulting curves represent group-level averages over subjects. We first tested the null hypothesis that there is zero between-group difference (COS versus healthy volunteers) in mean cortical growth curves. Since the spline-based model was specified to differentiate age-invariant (“trait”) from age-dependent (“trajectory”) effects of diagnosis on mean cortical thickness, we could distinguish group differences in these two aspects of cortical thickness. Having thus identified vertices where cortical thickness trajectories were significantly different between groups, we then explored the secondary hypothesis that regions of abnormal growth might be concentrated in one or a few developmental modules of the normal human brain connectome. To address this hypothesis, we used longitudinal MRI data from the healthy volunteers to define topological modules of vertices that shared distinctively similar growth trajectories. We then aligned the vertices of abnormal cortical growth with the normative developmental modules and tested the null hypothesis that vertices of abnormal growth were uniformly distributed over normative developmental modules.

Figure 1. Schematic of streams of analysis.

As part of the intramural NIMH study of typical development and childhood-onset schizophrenia (COS), 525 high-resolution magnetic resonance imaging scans were acquired on 208 subjects, 102 with COS. For each scan, thickness was estimated at ~80,000 cortical vertices via MNI’s CIVET pipeline, and penalized splines were used to estimate maturational trajectories (thickness as a function of age). Using only healthy subjects, developmental modules were derived by clustering vertices with similarly shaped maturational trajectories. Using both healthy subjects and subjects with COS, schizophrenia-related alterations in cortical maturation were tested for all cortical vertices. Finally, it was determined whether schizophrenia-related alterations in maturational trajectories were influenced by the organization of normative developmental modules.

Statistical analysis was performed in R (www.cran.r-project.org) using packages gamm4(25), mgcv(21; 26–29), vows(30), cluster(31) and clue(32; 33).

Penalized spline models

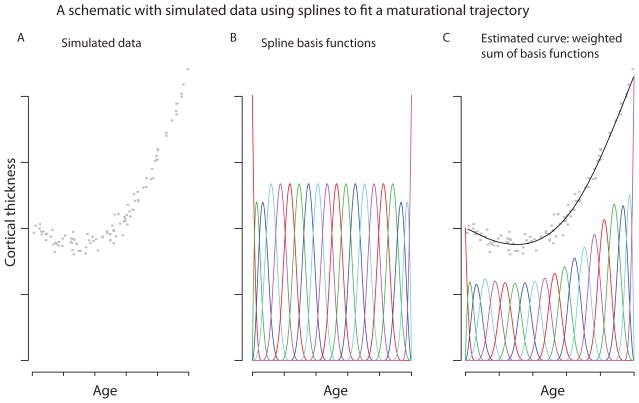
Penalized spline mixed-effect models were used to fit maturational trajectories at every vertex. Rather than specifying a polynomial form for the maturational trajectory (linear, quadratic, etc.), we allow much greater flexibility by taking it to be a linear combination of spline basis functions (Figure 2). Essentially, the fitted growth curve is a weighted sum of these basis functions. It is crucial to find a balance between the curve’s smoothness and its goodness of fit. For example in Figure 2, a bumpy enough curve could pass through all of the points, but this would not be biologically plausible. Here, we use restricted maximum likelihood to choose both the appropriate degree of smoothness and the random effect variance (20; 26; 34; 35).

Figure 2. Spline models.

A) For purposes of illustration, we used 100 simulated data points, to represent the cortical thickness of 100 subjects at different ages. B) Cubic B-spline basis functions, each in a different color. C) A weighted sum of the basis functions was used to fit a smooth curve to the simulated data.

More formally, let age_ij denote the age of the i^th individual at the time of his/her j^th scan. The thickness measured at the v^th vertex is modeled as a smooth function g_v of age plus a random person effect u_iv plus error:

$${\text{thickness}}_{\text{ijv}}=g_v({\text{age}}_{ij})+u_{\text{iv}}+{\text{error}}_{\text{ijv}}$$ (1)

where g_v is the essentially arbitrary smooth function, defined as the linear combination of 10 piecewise cubic B-spline functions (36). Technical details regarding the degree of smoothness of this function are provided in the Supplement.

Group differences in maturational trajectories

To test for group differences in maturational trajectories for each of the ~80,000 cortical vertices, we consider varying coefficient models(37). The idea is to express the mean trajectory g_v of equation (1) as

$$g_v(\text{age})=\{\begin{array}{cc}{f}_v(\text{age})& \text{for}\text{typical}\text{development};\\ f_v(\text{age})+{\beta }_v(\text{age})& \text{for}\text{COS}.\end{array}$$ (2)

Here, f_v is a “baseline” developmental trajectory, and β_v represents the difference between the groups, which may vary with age (hence the term “varying coefficient”). Thus testing for a group difference reduces to testing the null hypothesis, H₀, that β_v(age) is identically zero, which can be done by a modified Wald statistic(38).

If this null hypothesis is rejected, we can further ask whether the group difference is constant or age-varying. Formally this works by decomposing the COS effect β_v(age) of (2) into constant and age-varying components,

$${\beta }_v(\text{age})={\beta }_v^{(1)}+{\beta }_v^{(2)}(\text{age}).$$ (3)

Here, ${\beta }_v^{(1)}$ models the age-constant difference, leaving ${\beta }_v^{(2)}$ (age) (which is constrained to sum to zero) to model age-varying differences exclusively. Thus, group differences are tested via two null hypotheses: H_0a, that ${\beta }_v^{(1)}=0$, and H_0b, that ${\beta }_v^{(2)}$ (age) is identically zero. Both can again be tested by Wald-type tests(38). By and large, H_0a is rejected when H₀ is rejected. When H_0a is rejected but H_0b is not, there appears to be a “trait-like” difference in cortical thickness between groups that is constant across the age range; when H_0b is rejected, there is a group difference in the shape of the trajectory itself(38). In all models, an additional (age-invariant) term was included for gender. All brain-wide statistical maps were corrected for multiple comparisons using false discovery rate (FDR)-adjusted P-values(39).

Modules of synchronized maturational change in typical development

Using only the typically developing subjects’ data, we partitioned the cortex into developmental “modules” consisting of brain regions that showed synchronized maturational change. Because the spline-based estimates of maturation are entire curves defined along a continuum of points, traditional clustering methods for multivariate data cannot be directly applied. This problem is overcome by using a “functional principal component” basis to reduce the curves to a finite number of orthogonal features(40). After this transformation, k-medoids clustering(41) was applied to the principal component scores(42). k-medoids clustering minimizes the sum of distances from the cluster centers; this is more robust to noise and outliers than k-means clustering, which minimizes the sum of squared distances.

This procedure, if applied directly to the estimated spline parameters, results in clusters differentiated by absolute differences in cortical thickness (Supplemental Figure S1). To focus on synchronous neurodevelopment -- i.e., similarly shaped trajectories, or similar changes in thickness over time -- we instead performed clustering on the first derivatives of the fitted curves, i.e. $g_v^{\prime }$ (age) for each vertex v. This procedure was performed for a range of numbers of clusters, from k=2 to k=10.

Overlap between altered maturational trajectories in COS and modules of synchronized maturational change in typical development

Two methods were employed to determine whether there was a significant overlap between, on the one hand, modules of synchronized maturational change in typical development, and on the other hand, cortical regions with abnormal maturational trajectories in COS. First, for each module, the number of regions of group differences (sets of spatially contiguous vertices with FDR < .05) within the module was calculated. Chi-squared tests were used to compare the distribution of these regions to what would be expected based simply on the sizes of the modules. To account for spatial autocorrelation, each region was assigned to the module with which it had the most overlap, and the statistical test was performed based on the distribution of these regions rather than the distribution of the individual vertices.

Second, the overlap between the brain areas of group difference and the modules of cortical maturation was assessed by a randomization test. For each of 5000 simulations, surrogate areas matching the real brain areas of group difference in number and in size were placed in random positions on the cortical surface. The overlap between these surrogate areas and the modules of synchronized maturational change was calculated. Each module’s P-value was calculated as the proportion of randomized-data overlap values that exceeded the real-data overlap (Supplementary Figure S2).

Results

Cortical growth curves in healthy adolescents

The dominant form of the curves was a monotonically decreasing function of age. On average, cortical thickness decreased in a roughly linear fashion from about 3.6mm at 10 years to about 3.3mm at 26 years (Figure 3). However, there was considerable variation in the form of the curves. Many vertices showed monotonic but non-linear decreases over time; some had no evident change in cortical thickness over time (flatline); at some vertices cortical thickness increased monotonically with age, or there was a U- or inverted U-relationship between age and cortical thickness (Figure 4).

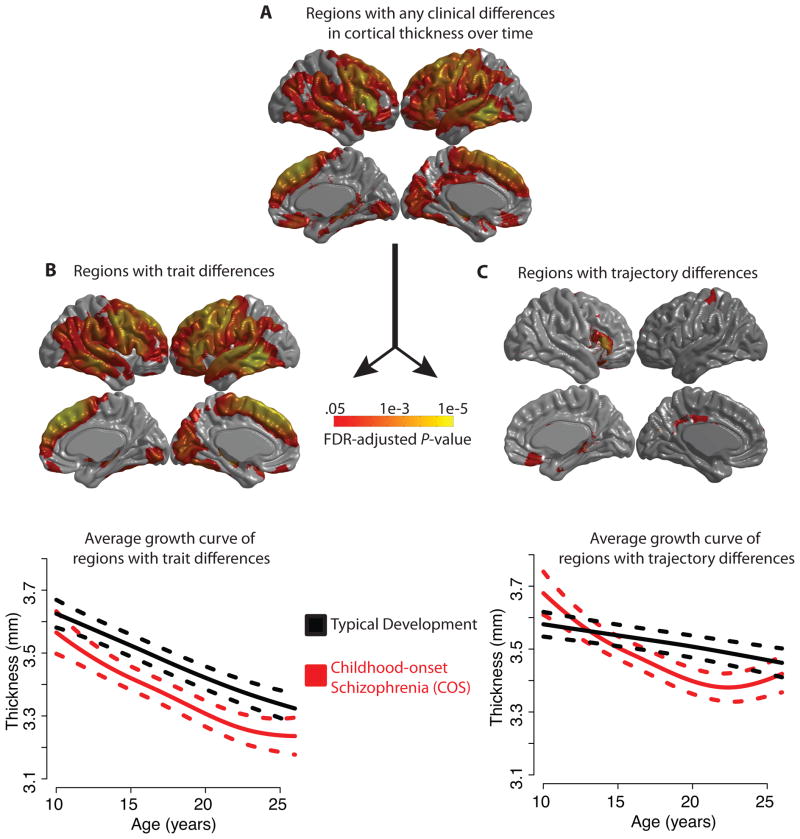
Figure 3. Abnormalities of growth curves in childhood-onset schizophrenia (COS) for each of the ~80,000 cortical vertices, using penalized spline models and FDR-adjusted p-values.

A) Cortical regions with any difference in the maturational trajectory in COS, either a constant trait difference or an age-varying trajectory difference. In other words, the null hypothesis H₀, that β_v (age) in equation (2) is identically zero, is rejected. B) Regions for which the null hypothesis H_0a that ${\beta }_v^{(1)}=0$ in equation (3) is rejected. All of these regions are in fact thinner in COS. The plot below shows the average maturational trajectory of these regions with 95% confidence intervals. C) Regions with significant group differences in trajectory, i.e., the null hypothesis H_0b that ${\beta }_v^{(2)}$ (age) is identically zero in equation (3) is rejected. The plot below shows the average maturational trajectory of these regions with 95% confidence intervals.

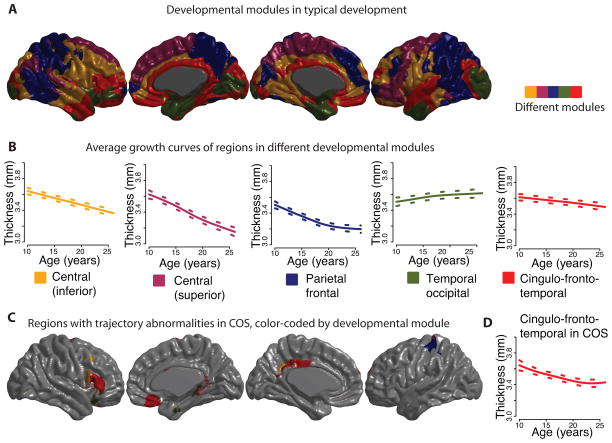
Figure 4. Developmental modules comprised of regions with similar maturational trajectories for cortical thickness during childhood and adolescence.

A k-medoids algorithm was applied to the set of estimated maturational trajectories to explore patterns of coordinated maturation across the cortex. A) As an illustration we present a map of the set of 5 developmental modules, which can be differentiated into an inferior central module (yellow), a superior central module (purple), a parietal frontal module (blue), a temporal occipital module (green), and finally a cingulo-fronto-temporal module composed of cingulate, temporal and prefrontal areas (red). B) The growth trajectory for each module is shown, averaged over all of the vertices in the module, for the typical development group of subjects. C) The cingulo-fronto-temporal module has a particularly high concentration of areas whose maturational trajectories are altered in COS (Figure 3C), although the developmental modules were calculated using only the typically developing sample. D) The growth trajectory averaged over all vertices in the cingulo-fronto-temporal module, in the COS group of subjects.

People with COS have altered cortical maturational trajectories

There were group differences in the maturational trajectories of specific cortical areas. For the large majority of the ~80,000 cortical vertices, the null hypothesis H₀ could be rejected: a single maturational curve did not suffice to model the data of both diagnostic groups (Figure 3A). The largest between-group differences were located in bilateral inferior frontal gyrus, left precentral gyrus and supplementary motor area, right medial frontal areas and left lateral temporal areas (Supplementary Table S2).

These group differences could be subdivided into trait differences in cortical thickness that did not change over developmental time, rejecting the null that hypothesis H_0a that ${\beta }_v^{(1)}=0$ in (3) but not the null hypothesis H_0b that ${\beta }_v^{(2)}$ (age) is identically zero; and trajectory differences in age-dependent change in cortical thickness, rejecting H_0b.

Most of the statistically significant group differences were in trait thickness (Figure 3B). Patients with COS had thinner cortex than healthy volunteers at many locations and these thickness deficits did not change as a function of age(15). The largest differences were located in the left hemisphere, including inferior frontal gyrus, precentral gyrus and superior temporal gyrus. But there were many large areas of group difference in the right hemisphere, including medial frontal, inferior frontal and temporal regions (Supplementary Table S3).

There was also strong evidence for group differences in the trajectories of cortical thickness (Figure 3C). The most significant differences were located in right inferior frontal gyrus in the triangular part (MNI coordinates of peak vertex, X=52.1, Y=28.6, Z=−1.4) and the opercular part (X=50.3, Y=21.1, Z=11.5), right orbital cortex (X=3.1, Y=23.8, Z=−18.9), left posterior cingulate (X=−8.1, Y=−42.7, Z=33.5) and left post-central gyrus (X=−27.3, Y=−30.3, Z=74.2) (Supplementary Table S4). In these areas, the normal curves were typically linearly decreasing functions of age. In the patients with COS, the maturational trajectory was different: there was faster-than-normal reduction of cortical thickness in the adolescent period (age 10–18 years, approximately) followed by a plateau or even a slight increase in cortical thickness in the young adult period (age 18–26, approximately). Note that some (but not all) of the areas of abnormal cortical thickness growth also have trait differences in cortical thickness. The exceptions are left posterior cingulate and right orbital cortex, which have significant trajectory differences but not trait differences in COS (Supplementary Table S5).

Normative developmental modules

In typical development, communities of cortical areas with similar growth trajectories of cortical thickness are discernible across the brain (Figure 4A; Supplementary Figure S3). For illustrative purposes, we focus on the decomposition into k=5 clusters or modules, although the main results were consistent across resolutions from k=2 to k=10.

In general, contralateral homologous regions in left and right cortical hemispheres tend to appear in the same developmental modules, with certain exceptions such as inferior frontal gyrus. The modules are to a large extent spatially contiguous, but also distributed across the cortex. At a high spatial resolution, nearby vertices tend to belong to the same modules. At the finest resolution available, equal to 1.53mm on average, 81% of vertices are in the same topological module all neighboring vertices in physical space; and an additional 18% are in the same module as all but one of their immediate spatial neighbors. In contrast, at the centimeter scale of brain macroanatomy, each module is composed of a small number of relatively large spatially-distinct components (mean across modules=12.4 distinct components greater than 10 vertices in size). This preponderance of short-distance synchronized growth balanced by significant spatially distant synchronized growth is reminiscent of functional(43; 44) and structural(45) brain networks, as well as economical small-world networks in general(46).

Most of the modules tend to decrease in cortical thickness over the observed age range. The cortical modules are differentiated by their rates of decline: for example, vertices in the cingulo-fronto-temporal module demonstrated relatively gradual decrease in cortical thickness across adolescence and early adulthood, whereas the central modules demonstrated faster reductions of cortical thickness that was completed earlier in adolescence. A plateau appearing to occur around age 20 further distinguishes the parietal frontal module. The apparent exception to these trends is the occipito/temporal pole cluster, which appears to increase in thickness across the age range (Figure 4B).

Abnormal growth in COS is concentrated in specific modules of typical development

Finally, regions with differently shaped trajectories in COS were disproportionately found within specific maturational modules (which were estimated using the normative data only) (Figure 4C). In particular, the cingulo-fronto-temporal module had a high concentration of regions with abnormal trajectories in schizophrenia, including right inferior frontal gyrus, right orbital cortex, right gyrus rectus, and left posterior cingulate (Supplementary Table S6). If the regions with abnormal trajectories were randomly distributed across the cortex, this module would be expected to include only 25% of the regions with abnormal trajectories, simply because of its size. In fact, this module contains 50% of the regions with abnormal trajectories, twice that expected by chance. The superior central module contained the second largest proportion of the abnormal cortical maturation, mostly within left postcentral gyrus. The other three developmental modules, despite collectively accounting for 65% of the cortex, contained only 25% of the cortical area with abnormal trajectories in COS.

For all of the modular resolutions tested (k=2–10), the trajectory differences in COS were not proportionally distributed among the modules (Chi-squared test, FDR-adjusted P≪.001, in all cases) (Supplementary Figures S2 and S3). Figure 4C illustrates the case of 5 maturational modules, where only the cingulo-fronto-temporal module overlaps significantly with the group differences (FDR-adjusted P<.009).

Discussion

Here we present new evidence of age-specific, non-linear alterations in cortical development in people with schizophrenia. While a large fraction of cortical regions shows an age-invariant or trait-like deficit in cortical thickness, a smaller set of regions shows alterations in the shapes of maturational trajectories, in particular right inferior frontal gyrus, right medial orbital cortex and left posterior cingulate. In addition, altered maturational trajectories may be concentrated within a single module of normative brain development. The developmental modules consisted of brain areas with similar maturational trajectories for cortical thickness in typical development. When the brain is divided into five developmental modules, which were derived using the typically developing sample only, a single one of these modules – the cingulo-fronto-temporal module - contains a disproportionate number of the cortical areas with altered maturational trajectories in COS.

Normative cortical thickness trajectories and developmental modules

The cellular or molecular underpinnings of neuroimaging features cannot be directly inferred, but decreases in cortical thickness and gray matter during adolescence may reflect synaptic pruning(12; 47). A recent rodent study found that gray matter alterations visible in structural MRI were correlated with markers of synaptic remodeling from post-mortem immunohistochemistry, indicating that synaptic remodeling can affect structural MRI phenotypes(48). In humans, the maturational trajectories of decreasing cortical thickness during adolescence also correlates with neuropathological evidence showing decreasing numbers of synapses in human cortex during adolescence(49).

Previous evidence suggests that most cortical areas have an “inverted U” maturational trajectory. Different anatomical areas peak in their gray matter volume and cortical thickness during different developmental windows(47; 50), and there is a posterior-to-anterior wave in the timing of these peaks(51). The peak cortical thickness in most brain areas has been suggested to occur before age 10(47; 50; 51), consistent with our findings of largely decreasing cortical thickness, since younger children were not included in our sample. Like any curve, however, a maturational trajectory is distinguished by many features other than its maximum, as rates of growth or reduction in size may vary in a complex fashion across development (1–5; 52).

Developmental modules, composed of brain anatomical areas that grow or decrease in size in a coordinated fashion, remain to be fully explored. Inter-regional covariance of morphological properties such as cortical thickness across subjects possesses a modular community structure partly analogous to white-matter and functional connectivity networks (15; 19; 53; 54). Moreover, this cross-sectional structural covariance network at least partially reflects patterns of synchronized maturation between brain areas(17; 18).

Abnormal cortical growth curves in schizophrenia

Decreased cortical thickness may reflect synaptic overpruning (22; 23; 55; 56), neurodegeneration, changes in myelination, development of neurotransmitter systems(24; 57; 58), and regional disruptions of gene expression(39; 59; 60). Overall, there is a vast and sometimes contradictory literature on specific regional alterations in brain regional volume, thickness, surface area and other morphological properties in schizophrenia(1–3; 40; 61). One explanation for this constellation of findings – in addition to the heterogeneity of the disorder itself and the constantly changing nature of neuroimaging methodologies -- is that the neuroanatomy of the disease is age-variant, affecting a developmental process rather than part(s) of the brain per se(10; 14; 15; 42). It is important to note that our finding of accelerated reductions in cortical thickness is theoretically consistent with a process of neurodegeneration that occurs after the onset of the disease, as opposed to a developmental process that begins before the start of symptoms. These alternative hypotheses will hopefully be tested by large population-based cohort studies in the future(62). The relationship between clinical metrics and this pattern of neuroanatomical alterations is another critical issue, which should be addressed by future studies.

The network context of neuroanatomical alterations is critical. Resting-state fMRI studies (measuring “functional connections” based on synchronized fluctuations in intrinsic brain activity) have demonstrated abnormal network connectivity in schizophrenia(63), as have diffusion MRI studies of networks of white-matter connections(8; 64). It is not surprising that schizophrenia-related alterations in brain anatomy exist at the level of connected systems, rather than individual brain regions. In fact, population-wide patterns of interregional correlations in brain anatomy are themselves altered in schizophrenia(16).

The maturation of brain anatomy, including the relationships between the growth curves of different cortical regions, is relevant to the study of brain connectivity in health and schizophrenia. Brain areas that grow together may have more similar patterns of gene expression compared to the rest of the brain(65–67), and neuroanatomical modularity may reflect and contribute to modularization in the development of cognitive functions(68; 69). It is plausible that different biological mechanisms impact growth curves in different parts of the brain and some, but not all, of these mechanisms are associated with schizophrenia. Our finding of convergence between, on the one hand, brain areas with COS-alterations in thickness-trajectories and, on the other hand, the composition of specific developmental modules (derived from the normative data only) suggests that neurodevelopmental abnormalities in schizophrenia target specific modular systems: in particular a cingulo-fronto-temporal module was most strongly associated with abnormal cortical growth curves in these data. The disruption of these neuroanatomical modules could reflect alterations in genetic systems that disproportionately impact these areas of the brain, developmental insults that occur at a critical ontogenetic time period for these areas, and/or or disruptions in cognitive functions subsumed by distributed neural circuitry.

Methodological issues

Polynomial models have been the basis for most work to date analyzing the growth curves of brain regions(47; 51; 70). However, accurate modeling of neurodevelopment is severely limited by the assumption that regional brain growth must correspond to linear, quadratic or cubic functions(52; 71). As discussed further in Supplementary Materials, penalized spline models are more flexible, more robust to demographic variability, and allow greater refinement in hypothesis testing (21; 52; 72).

Patients with COS had lower IQs and greater exposure to psychiatric medication than typically developing children, on average. The IQ deficit is expected as cognitive deficits are a major symptom of schizophrenia(73). Most patients in our sample were being treated with clozapine at the time of scan, due to the severity of their illness. Previous reports of cortical thickness abnormalities in the nonpsychotic siblings of these patients suggest that neuroanatomical alterations have genetic or shared environmental origins rather than being a consequence of drug treatments(74). However, we cannot rule out the possibility that demographic confounds contribute to our results. In addition, patients were more likely to be non-right-handed, which has been reported many times(75–77) but is unlikely to account for the pattern of neuroanatomical alterations observed in schizophrenia(78).

In case-control studies of brain anatomy, controversy remains regarding whether, and how, to control for group differences in brain volume. A supplementary analysis demonstrated that the trajectory differences between groups are unchanged if total brain gray matter volume is included as a covariate in the spline models (Supplementary Figure S4). Interestingly, the addition of this term to the model results in fewer brain areas with statistically significant age-invariant trait differences in local cortical thickness, for example there are no residual differences in the occipital lobe, but the age-varying differences in trajectory are robust to including this additional covariate. Therefore, some of the trait differences in local cortical thickness could be the result of a global insult, but the differences in the shape of maturational trajectories are not due simply to a global difference in brain volume. Even when including total gray matter volume as a covariate, there is significant overlap between these brain areas with maturational trajectory differences in COS and the cingulo-fronto-temporal module of typical development.