Cophylogeny Reconstruction via an Approximate Bayesian Computation

Abstract

Despite an increasingly vast literature on cophylogenetic reconstructions for studying host–parasite associations, understanding the common evolutionary history of such systems remains a problem that is far from being solved. Most algorithms for host–parasite reconciliation use an event-based model, where the events include in general (a subset of) cospeciation, duplication, loss, and host switch. All known parsimonious event-based methods then assign a cost to each type of event in order to find a reconstruction of minimum cost. The main problem with this approach is that the cost of the events strongly influences the reconciliation obtained. Some earlier approaches attempt to avoid this problem by finding a Pareto set of solutions and hence by considering event costs under some minimization constraints. To deal with this problem, we developed an algorithm, called Coala, for estimating the frequency of the events based on an approximate Bayesian computation approach. The benefits of this method are 2-fold: (i) it provides more confidence in the set of costs to be used in a reconciliation, and (ii) it allows estimation of the frequency of the events in cases where the data set consists of trees with a large number of taxa. We evaluate our method on simulated and on biological data sets. We show that in both cases, for the same pair of host and parasite trees, different sets of frequencies for the events lead to equally probable solutions. Moreover, often these solutions differ greatly in terms of the number of inferred events. It appears crucial to take this into account before attempting any further biological interpretation of such reconciliations. More generally, we also show that the set of frequencies can vary widely depending on the input host and parasite trees. Indiscriminately applying a standard vector of costs may thus not be a good strategy.

Cophylogeny is the reconstruction of ancient relationships among ecologically linked groups of organisms from their phylogenetic information. The study of host–parasite systems has a long history and has been already well addressed in the literature (e.g., Charleston 1998; Conow et al. 2010; Huelsenbeck et al. 1997; Merkle and Middendorf 2005; Page 1994b; Paterson and Banks 2001). It also has broad applications throughout biology. For instance, the same mathematical model can be applied to gene–species associations (Bansal et al. 2012; Doyon et al. 2011a,b; Hallett and Lagergren 2001; Tofigh et al. 2011). Hence, any single method for host/parasite associations that is developed could be applicable to both situations. Lately indeed, there have been attempts to introduce a general framework that incorporates all existing models (Wieseke et al. 2013).

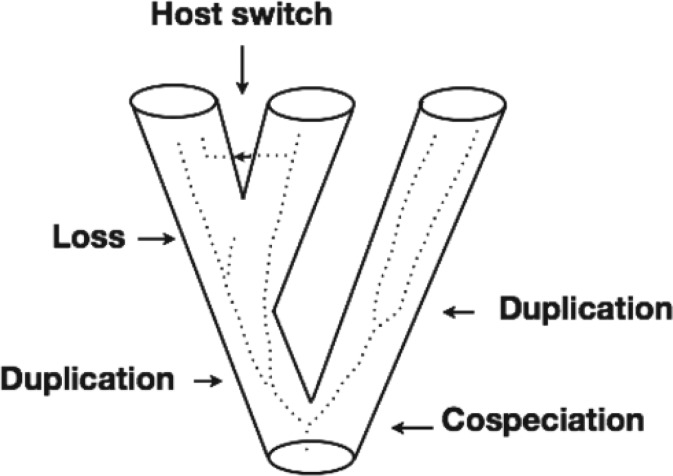
Our work is particularly focused on reconstructing the coevolutionary history of host–parasite systems. Specifically, we are given a host tree $H$, a parasite tree $P$, and a function $\varphi$ mapping the leaves of $P$ to the leaves of $H$. In general, four main macro-evolutionary events are assumed to be recovered: (i) cospeciation, when the parasite diverges in correspondence to the divergence of a host species; (ii) duplication, when the parasite diverges “without the stimulus of host speciation” (Paterson and Banks 2001); (iii) host-switching, when a parasite switches, or jumps from one host species to another independent of any host divergence; and (iv) loss, which can describe three different and undistinguishable situations: (a) speciation of the host species independently of the parasite, which then follows just one of the new host species due to factors such as, for instance, geographical isolation; (b) cospeciation of host and parasite, followed by extinction of one of the new parasite species and; (c) same as (b) with failure to detect the parasite in one of the two new host species. These events are depicted in Figure 1.

Figure 1.

Recoverable events for a coevolutionary reconstruction. The tube represents the host tree and the dotted lines the parasite tree.

A parsimonious solution for reconciling the phylogenetic trees for hosts on one side, and parasites on the other, simply assigns a cost to each of the four types of events and then seeks to minimize the total cost of the mapping. If host switches are forbidden, exact solutions can be found in time linear in the size of the trees (e.g., Goodman et al. 1979; Guigó et al. 1996; Mirkin et al. 1995; Page 1994a). If timing information is available, for example, if we happen to know the order in which speciation events occurred in the host phylogeny, then any proposed reconciliation must also respect the temporal constraints imposed by the available timing information. Host switches are thus restricted to occur only between coexisting species. When coexistence relationships are known for all host species, the reconciliation problem can again easily be solved using dynamic programming, this time polynomially in the size of the trees (Conow et al. 2010; Drinkwater and Charleston 2014; Libeskind-Hadas and Charleston 2009). However, when timing information is not available, the difficulty of separating between compatible and incompatible switches makes the reconciliation problem NP-hard (Ovadia et al. 2011; Tofigh et al. 2011). A number of algorithms have been developed that allow for solutions that are biologically unfeasible, that is, solutions where some of the switches induce a contradictory timing ordering for the internal vertices of the host tree (Doyon et al. 2011). In this case, the algorithms are able to generate optimal solutions in polynomial time. For the fastest existing ones, see for example Bansal et al. (2012).

Clearly in all situations, the choice for the cost values is crucial in the solution(s) found. Indeed, arbitrarily choosing a cost vector may lead to solutions where the events in the optimal solutions do not necessary reflect the reality (Charleston 2003, e.g. describes a study on the distribution of the events in optimal reconciliations). From a biological point of view, reasonable cost values for an event-based reconciliation are not easily chosen. It is also natural to think that the frequency of the events is not constant across data sets. Thus, different pairs of host/parasite phylogenies might be associated with different cost events. Moreover, our results show that for the same pair of host and parasite trees, different reconciliations—in the sense of presenting a different set of frequencies for the events—may constitute equally probable solutions. It is thus crucial to take this into account before attempting any further biological interpretation of such reconciliations.

Some approaches (Charleston 2012; Libeskind-Hadas et al. 2014) attempt to choose the costs of the events by adopting some minimization constraints and by focusing on Pareto optimal solutions. As indicated in Ronquist (2003), if each event is associated with a cost that is inversely related to its likelihood (the more likely is the event, the smaller its cost), then the most parsimonious reconstruction will also, in some sense, be the most likely explanation of the observed data. Likelihood-based approaches should in general be preferred to parsimony-based methods as they remove the subjective step of cost parameter choice and rely instead on a simultaneous inference of parameter values and events. Some work has been done along these lines, for instance in testing for coevolution (Huelsenbeck et al. 1997,2000. This, however, excluded duplications and tended to over-estimate the number of host switches. Instead, in Szöllősi et al. (2013) all four types of events are considered, but the method was developed with the objective of reconstructing a species tree starting from multiple gene trees. The aim is similar in Arvestad et al. (2003) but the type of approach is different and the model again incomplete as in Huelsenbeck et al. (1997, 2000), this time not allowing for host switches. The likelihood approach adopted in Huelsenbeck et al. (1997, 2000) and Szöllősi et al. (2013) moreover presents the inconvenience of being computationally intensive.

The huge space of possible solutions is also an issue, for instance, in population genetics for reconstructing the evolutionary history of a set of individuals. Since the early work of Pritchard et al. (1999), the literature from this domain has seen classical Monte Carlo methods and their variants being replaced by Approximate Bayesian Computation (ABC), a set of more efficient statistical techniques (Beaumont et al. 2002). In complex models, likelihood calculation is often unfeasible or computationally prohibitive. ABC methods, also called likelihood-free inference methods, bypass this issue while remaining statistically well-founded. For more details, we refer to the review of Marin et al. (2012) as well as the convergence results in Fearnhead and Prangle (2012).

Following these ideas, we developed an algorithm, called Coala (Coala stands for “COevolution Assessment by a Likelihood-free Approach”, and is also the Portuguese spelling for Koala, the arboreal herbivorous marsupial native to Australia), for estimating the frequency of the events based on a likelihood-free approach. Given a pair of “known” host and parasite trees and a prior probability distribution associated with the events, Coala simulates the temporal evolution of a set of species (the parasites) following the evolution of another set (the hosts) as represented by the latter's known phylogenetic tree. In this way, it generates under different parameter values a number of simulated multilabeled parasite trees which are then compared with the known parasite tree. The ABC principle is to keep the parameter values (event probabilities) giving rise to parasite trees that are “close” to the known one. The output of the algorithm is then a distribution on such parameter values that is a surrogate of the posterior probability for the events which would best explain the observed data.

To the best of our knowledge, the only other method that might be compared with ours is the parameter adaptive approach CoRe-Pa (Merkle et al. 2010). In this case, the space of cost vectors is explored either by sampling such vectors at random assuming a uniform distribution model or by using a more sophisticated approach, the so-called Nelder–Mead simplex method (Nelder and Mead 1965). The first appears to be the option by default in CoRe-Pa. In both cases, the function to minimize is the difference between the probabilities directly computed from the cost vector chosen and the actual relative frequencies observed during the reconstruction using such vector. This choice may appear somewhat circular as one would expect that, because reconstruction is driven by the cost vector, the frequency of the events thus reconstructed not only would, but indeed should agree with it.

Method

General Framework

The method we propose relies on an ABC. This belongs to a family of likelihood-free Bayesian inference algorithms that attempt to estimate posterior densities for problems where the likelihood is unknown a priori. Given a set of observed data $D_0$ and starting with a prior distribution $\pi$ on the parameter space $\Theta$ of the model, the objective is to estimate the parameter values $\theta \in \Theta$ that could lead to the observed data using a Bayesian framework. More precisely, the Bayesian paradigm consists in finding the posterior given $D_0$ defined as:

$$p(\theta |D_0)=\frac{p(D_0|\theta )\pi (\theta )}{p(D_0)}.$$

If the likelihood function $p(D_0|\theta )$ cannot be derived, then a likelihood-free approximation can be used to estimate this posterior distribution and thus the parameter values. In general, a likelihood-free computation involves a chain of parameter proposals and only accepts a set of parameter values on condition that the model with these values generates data that satisfy a performance criterion with respect to the observed data (Sisson et al. 2007, 2009). Strict acceptance (or inversely rejection) is based on whether the generated data $D_S$ perfectly matches the observed data $D_0$. In cases where the probability of perfectly matching the data is very small, a tolerance $d(D_s,D_0)\le ϵ$ is adopted to relax the rejection policy, where $d$ is a distance measure. In either case, this is called the fitting criterion. Note that this fitting criterion often relies only on a summary statistic instead of the full data sets $D_S$ and $D_0$. Moreover, for complex models where the prior and posterior densities are believed to be sufficiently different, the acceptance rate is very low and then the use of a likelihood-free Sequential Monte Carlo (SMC) search that involves many iterations leads to a more appropriate strategy. SMC is also preferred among other possible methods as it is flexible, easy to implement, parallelisable, and applicable to general settings (Del Moral et al. 2012).

The ABC–SMC algorithms approximate the posterior distribution by using a large set of randomly chosen parameter values. Over sufficiently many iterations and under suitable conditions, the stationary distribution of the Markov chain will approach the distribution of $p(\theta |d(D_S,D_0)\le ϵ)$, which will converge to the posterior density $p(\theta |D_0)$ if the statistics used to compare the generated data with the real one are sufficient and $ϵ$ is small enough. In our case, the observed data are a pair of host and parasite trees, denoted by $H$ and $P$ respectively, and a list of associations between parasite and host leaves. The parameter vector of the model is composed of the probabilities of each one of four events corresponding to respectively: speciation of the parasite together with a speciation of its host (called cospeciation); speciation of the parasite without concomittant speciation of the host (called duplication); switch (also known as jump) of the parasite to another host (called host switch, which is further assumed to be without loss on the original host); and speciation of the host without concomitant speciation of the parasite, and thus loss of the parasite for one of the new host species (called loss). We thus have that $\theta$ stands for a vector of four probabilities $\langle p_c,p_d,p_s,p_l\rangle$. Note that each node in the host tree either matches a node in the parasite tree or represents a loss, giving rise to the four possible events. For this reason, the parameter $\theta$ is constrained such that $p_c+p_d+p_s+p_l=1$ (see Section “Parasite tree generation algorithm” for more details).

Starting from the host and respecting the probabilities of the events specified in a given parameter vector ${\theta }_i$, we generate $M$ parasite trees, where $M\ge 1$.

Once a parasite tree $\tilde{P}$ is thus simulated, it can be compared with the real parasite tree $P$ by computing a distance between the two. For a given parameter vector ${\theta }_i$, we can then produce a distance summary of the generated trees, and use this as a criterion in the ABC rejection method. The latter selects the parameter vector(s) that approximate the observed data within a given tolerance threshold.

The ABC–SMC procedure allows us to refine the list of accepted probability vectors by sampling a vector ${\theta }_i$, introducing a small perturbation to it to produce a vector ${{\theta }^{\prime }}_i$, and then collecting a new distance summary for ${{\theta }^{\prime }}_i$.

The list of vectors output in the final step of the algorithm defines the posterior distribution of the coevolutionary event probabilities for the given pair $H$ and $P$. Table 1 shows a summary of the notation used throughout this work.

Table 1.

Notation

Notation	Description
$H$	Host tree.
$P$	Parasite tree.
$\varphi$	Function from the leaves of $P$ to the leaves of $H$. It represents the associations between currently living host species and parasites.
$\gamma$	Function from the vertices of $P$ to the vertices of $H$. It represents the reconciliation between $H$ and $P$ and extends $\varphi$.
$\Sigma ,\Delta ,\Gamma$	Sets of parasite vertices associated with, respectively, cospeciation, duplication, and host switch events.
$\Xi$	Set containing arcs of the parasite tree that are associated to host switch events.
$\Lambda$	Multiset containing all vertices $h\in V(H)$ that are associated to loss events.
$D_0$	Observed data.
$D_S$	Generated data.
$\Theta$	Parameter space.
$\theta$	Parameter value.
$\tilde{P}$	Simulated parasite tree.
$p_i$	Probability of the event $i$, where $i\in \{c,d,s,l\}$.
$c_i$	Cost of the event $i$, where $i\in \{c,d,s,l\}$.
$o_i$	Number of observed events of the type $i$, where $i\in \{c,d,s,l\}$.

Note: $c=$ cospeciation, $d=$ duplication, $s=$ host switch, and $l=$ loss.

Parasite Tree Generation Algorithm

The Duplication–Transfer–Loss (DTL) model

To simulate the coevolutionary history of the two input phylogenies, we rely on the event-based model presented in Tofigh et al. (2011), and later further analyzed in Bansal et al. (2012).

A rooted phylogenetic tree is a leaf-labeled tree that models the evolution of a set of taxa from their most recent common ancestor (placed at the root). The internal vertices of the tree correspond to the speciation events. The tree is rooted so a direction is intrinsically assumed that corresponds to the direction of increasing evolutionary time. Henceforth, by a phylogenetic tree $T$, we mean a rooted tree with labeled leaves where every vertex has in-degree 1 and out-degree 2 except for the leaves, which have out-degree 0. For such a tree $T$, the set of vertices is denoted by $V(T)$, the set of arcs by $A(T)$, and the set of leaves by $L(T)$. The root of $T$ is denoted by $r(T)$. Given an arc $a=(v,w)\in A(T)$, going from $v$ to $w$, we call its head, denoted by $h(a)$, the vertex $w$ and its tail, denoted by $t(a)$, the vertex $v$. For a vertex $v\in V(T)$, we define the set of descendants of $v$, denoted by $Des(v)$, as the set of vertices in the subtree of $T$ rooted at $v$ (including $v$). Similarly, the set of ancestors of $v$, denoted by $Anc(v)$, is the set of vertices in the unique path from the root of $T$ to $v$ (including the end points). For a vertex $v\in V(T)$ different from the root, we call its parent, denoted by $par(v)$, the vertex $x$ for which there is the arc $(x,v)\in A(T)$. We denote by 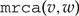the most recent common ancestor of $v,w$ in $T$. Finally, we denote by $\ge$ the partial order induced by the ancestry relation in the tree. Formally, for $x,y\in V(T)$, we say that $x\ge y$ if $x\in Anc(y)$. If neither $x\in Anc(y)$ nor $y\in Anc(x)$, the vertices are said to be incomparable.

Let $H,P$ be the phylogenetic trees for the host and parasite species respectively. We define $\varphi$ as a function from the leaves of $P$ to the leaves of $H$ that represents the association between currently living host species and parasites. These associations are part of the input of our algorithm, together with the trees themselves. In our model, we allow each parasite to be related to one and only one host, whereas a host can be related to zero, one, or more than one parasite. More formally, $\varphi$ is thus a function which needs not be surjective nor injective.

A reconciliation $\gamma$ is a function $\gamma :V(P)\to V(H)$ that is an extension of $\varphi$. In particular $\gamma$ partitions the set $V(P)$ into three sets $\Sigma$, $\Delta$, and $\Gamma$ which correspond to the vertices of $P$ associated with, respectively, cospeciations, duplications, and host switches. The reconciliation $\gamma$ also defines a subset $\Xi$ of $A(P)$ which corresponds to the arcs associated with host switches.

Given a reconciliation $\gamma$, the following holds (Tofigh et al. 2011; Charleston 2002):

1. For any $p\in L(P)$, $\gamma (p)=\varphi (p)$ ($\gamma$ extends $\varphi$).

2. For any internal vertex $p\in V(P)-L(P)$ with children $p_1$ and $p_2$:

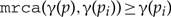   • (a) , for $i=1,2$ (a child cannot be mapped to an ancestor of the parent).
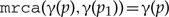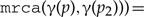
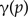   • (b) or (one of the two children is mapped to the subtree rooted at the parent).

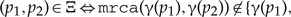
3. For any 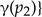(the arc $(p_1,p_2)$ is an arc denoting a host switch).

4. For any $p\in V(P)-L(P)$ with children $p_1$ and $p_2$:

   • (a) $p\in \Gamma \iff (p,p_1)\in \Xi$ or $(p,p_2)\in \Xi$ ($p$ is associated with a host switch).
   • (b) 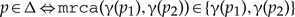(the children are mapped to comparable vertices and $p$ is associated with a duplication event).
   • (c) 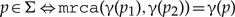and $\gamma (p_1)$ and $\gamma (p_2)$ are incomparable ($p$ is associated with a cospeciation event).

The losses are identified by a multiset (generalization of a set where the elements are allowed to appear more than once) $\Lambda$ whose elements are in $V(H)$ containing all the vertices $h\in V(H)$ that are in the path between the image of a vertex $p\in V(P)$ and the image of one of its children. The images themselves are not included in the count, except for the duplication event, where one of the images is included.

The triple $S=\langle H,P,\gamma \rangle$ is said to be a reconciliation. Given a vector $\langle c_c,c_d,c_s,c_l\rangle$ of nonnegative real values that correspond to the cost of each type of event, the cost of a reconciliation is equal to $c_c|\Sigma |+c_d|\Delta |+c_s|\Gamma |+c_l|\Lambda |$.

Finally, a reconciliation is said to be acyclic or time feasible if there exists a total order on $V(H)\cup V(P)$ that is consistent with the two partial orders induced by $H$ and $P$ and respects all temporal constraints imposed by both tree topologies and by the set of host switch events. For a detailed definition of a time-feasible scenario, we refer to Stolzer et al. (2012).

Evolution of parasites

The evolution of the parasites is simulated by following the evolution of the hosts traversing the phylogenetic tree $H$ from the root to the leaves, and progressively constructing the phylogenetic tree for the parasites. During this process, a single parasite vertex can be in two different states: mapped or unmapped. At the moment of its creation, a new vertex $v$ is unmapped and is assigned a temporary position on an arc $a$ of the host tree $H$. We denote this position by $\langle v,a\rangle$. From this position, we can decide to map $v$ to a vertex $w$ of $H$ (all coevolutionary events except for loss), or, in the case of a loss, to move $v$ to another position. In the first case, $v$ is always mapped to the vertex $h(a)$ that is the head of the arc $a$. We denote this mapping by $[v:w]$ with $w=h(a)$.

Because in all three nonloss cases (cospeciation, duplication, and host switch), the parasite is supposed to speciate and two children are created for $v$, denoted by $v_1$ and $v_2$. Their positioning along arcs of the host then depends on which of the three events took place. In the case of a loss, no child for $v$ is created (at this step) because there is no parasite speciation, and $v$ is just moved to one of the two arcs outgoing from $h(a)$ chosen randomly. Notice however that, in order to avoid confusing a loss with another event (for instance, a cospeciation), some precautions must be taken, as explained more specifically in the next paragraph concerning the simulation of a loss event.

These choices, together with the general framework for our parasite tree generation method, are provided next.

Starting the generation

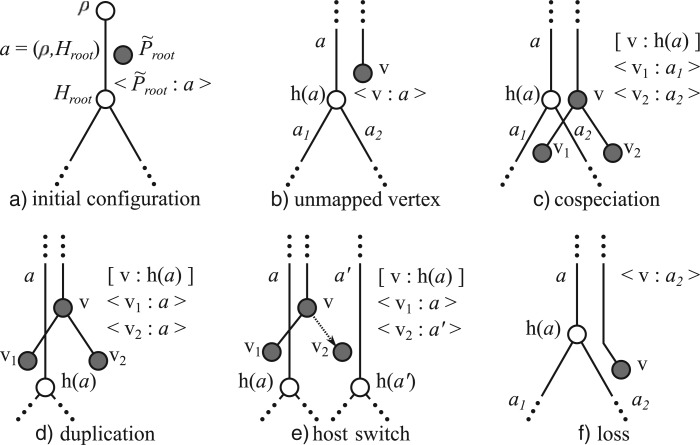
The generation of the simulated parasite tree $\tilde{P}$ starts with the creation of its root vertex ${\tilde{P}}_{\text{root}}$. This vertex is positioned before the root of $H$ on the arc $a=(\rho ,H_{\text{root}})$. This allows the simulation of events that happened in the parasite tree before the most recent common ancestor of all host species in $H$. Figure 2a depicts this initial configuration.

Figure 2.

Events during the generation of the parasite tree $\tilde{P}$. The host tree has white vertices and the parasite tree gray vertices. The association $\langle v:a\rangle$ indicates that an unmapped parasite vertex $v$ is positioned on the arc $a$ of the host tree. The association $[v:w]$ indicates that the parasite vertex $v$ is mapped to the host vertex $w$. a) initial configuration; b) unmapped vertex; c) cospeciation; d) duplication; e) host switch; f) loss.

The evolutionary events

For any vertex $v$ of $\tilde{P}$ that is not yet mapped and whose position is $\langle v,a\rangle$ (Fig. 2b), we choose to apply one among the four allowed operations, depending on the probability of each event. In what follows, we denote by $a_1,a_2$ the arcs outgoing from the head $h(a)$ of the arc $a$.

• Cospeciation (Fig. 2c): we apply the mapping $[v:h(a)]$ and we create the vertices $v_1$ and $v_2$ as children of $v$. We position them as follows: $\langle v_1,a_1\rangle$ and $\langle v_2,a_2\rangle$. This operation is executed with probability $p_c$.

• Duplication (Fig. 2d): We apply the mapping $[v:h(a)]$ and we create the vertices $v_1$ and $v_2$ as children of $v$. Both $v_1$ and $v_2$ are positioned on $a$. This operation is executed with probability $p_d$.

• Host switch (Fig. 2e): We apply the mapping $[v:h(a)]$ and we create the vertices $v_1$ and $v_2$ as children of $v$. We then randomly choose one of the two children and position it on $a$. Finally, we randomly choose an arc $a^{\prime }$ that does not violate the time feasibility of the reconstruction so far Stolzer et al. 2012. If such an arc does not exist, it is not possible for a host switch to take place. In this case, we choose between the three remaining events with probability $p_i/(p_c+p_d+p_l)$ with $i\in \{c,d,l\}$. Otherwise, we position $v_2$ on $a^{\prime }$. This operation is executed with probability $p_s$.

• Loss (Fig. 2f): This operation is executed with probability $p_l$ and consists of randomly choosing an arc outgoing from the head $h(a)$ of $a$ and positioning $v$ on it. Observe that we are considering only losses resulting from lineage sorting. It would be interesting to incorporate extinction or failure to detect infection but this would require the addition of new parameters, thus making the model more complex to analyze. However, if $v$ was created by a duplication event and is being processed for the first time, we have to verify if its sibling vertex $v^{\prime }$ was already processed and also suffered a loss. In this case, $v$ must be positioned on the same arc $a^{\prime }$ where $v^{\prime }$ was positioned. This procedure is adopted to avoid later mappings where a duplication followed by two losses would be confused with a cospeciation.

We also assume that no evolutionary event takes place whenever a leaf of $H$ is reached. This means that, if $v$ is positioned on an arc incoming to a leaf, then $v$ is mapped to the leaf and no further operation is executed. Hence, the generation of $\tilde{P}$ terminates when all the created vertices are mapped (i.e., have reached a leaf of the host tree). Finally, the leaves of the parasite tree $\tilde{P}$ are labeled according to their mapping to the leaves of the host tree. Observe that as more than one parasite can be mapped to the same host, $\tilde{P}$ is a multilabeled tree (i.e. trees whose leaf labels need not be unique). Finally, some combinations of host switches can introduce an incompatibility due to the temporal constraints imposed by the host and parasite trees, as well as by the reconciliation itself. During the generation of the parasite tree, we always allow only for host switches that do not violate the time-feasibility constraints. For the criteria enabling to assess time-feasibility, we refer to Stolzer et al. (2012).

Note that in this model, we do not use information about edge lengths. This is a positive aspect of the method in the sense that branch lengths are not always easy to determine with accuracy. In contrast, we cannot simulate the “null events” (parasite doing nothing in the host tree). Moreover, for now, we do not simulate “failure to diverge” which describes a situation where a host speciates whereas the parasite does not but continues to inhabit both of the two new species of hosts. Despite the importance of this event, mathematically speaking it is not clear how to include it in the cophylogenetic reconciliation model because we have to allow the association of a parasite to multiple hosts. The ideas presented by Drinkwater and Charleston (2014) for the improvement of node mapping algorithms may help on the simulation of the “failure to diverge” event in future work.

Because the simulation model is restricted to the events of cospeciation, duplication, host switch, and loss, the probabilities of these four events sum up to one.

Cophylogeny Parameter Estimation Algorithm

Prior distribution $\pi$

The parameter $\theta =\langle p_c,p_d,p_s,p_l\rangle$ lives in the simplex ${\mathcal{S}}_3$ (the $p$'s are positive and sum to one). It is then standard to sample $\theta$ from a Dirichlet distribution which is a family of continuous multivariate probability distributions parameterized by a vector $\alpha$ of positive real numbers that determine the shape of the distribution (Gelman et al. 2003).

In our simulations, we adopt a uniform Dirichlet distribution (namely $\alpha =(1,1,1,1)$) that corresponds to sampling uniformly from the simplex ${\mathcal{S}}_3$. This is often used when there is no previous knowledge favoring one component (e.g., coevolutionary event) of $\theta$ over another. However, the method we implemented allows the user to specify other prior distributions when such knowledge is available.

Choice of summary statistic and fitting criterion

The ABC inference method is based on the choice of a summary statistic that describes the data while performing a dimension reduction task. The latter is used to evaluate the quality of agreement (similarity) between the simulated data sets (the generated parasite trees) and the observed (the real parasite tree). In our case, the summary statistic will be based on the measured distances between the generated parasite trees and the real one.

The distance of each simulated tree to the real parasite tree is therefore informative about the quality of the vector that generated it. Hence, the distance that will be used must take into account: (i) how well does the simulated tree represent the set of trees generated by a given vector, and (ii) how topologically similar is the simulated tree to the real parasite tree.

Concerning the first point, the intuition is as follows. In our model, when generating a parasite tree, the expected frequency of an event should be close to the corresponding probability value of the parameter vector used to generate the tree. To this purpose, for a given vector $\theta =\langle p_c,p_d,p_s,p_l\rangle$ and for each simulated tree $P_{\theta }$ that was generated according to this vector, we kept track of the number of events $obs=\langle o_c,o_d,o_s,o_l\rangle$ associated with this simulation. We compared the observed number of events to the expected $exp=\langle e_c,e_d,e_s,e_l\rangle$. Observe that the expected number of events can be easily calculated using the size of the parasite tree $P$ and the vector $\theta$. A tree is a good representative if the observed number of events is near to the expected. More formally, for a real parasite tree $P$, a vector $\theta =\langle p_c,p_d,p_s,p_l\rangle$, and a simulated parasite tree $P_{\theta }$ for which the observed number of events are $obs=\langle o_c,o_d,o_s,o_l\rangle$, we define a measure $D_1(P,P_{\theta })$ as follows:

$$D_1(P,P_{\theta })=\frac{1}{4}\times {\displaystyle \sum _{i\in \{c,d,s,l\}}\frac{|e_i-o_i|}{\max \{e_i,o_i\}}}.$$

As concerns point (ii), we use a metric for comparing phylogenetic trees. There is a wide literature on distances for phylogenetic trees (Felsenstein 2003). Our choice was driven by the need to have one that can be computed efficiently and accurately. Unfortunately, many of the distances used in biology are also NP-hard to compute (Baroni et al. 2005; Hein 1990; Waterman and Smith 1978), whereas some of the fastest, like for instance, the Robinson–Foulds distance (Robinson and Foulds 1981) which can be calculated in linear time (Day 1985), are poorly distributed and thus not good enough discriminators (Bryant and Steel 2009; Steel and Penny 1993). Moreover, many efficient-to-compute distances are not robust to small changes (such as in the position of a single leaf) in one of the two trees.

Recall that in our method the leaves of the parasite tree $\tilde{P}$ are labeled according to their mapping to the leaves of the host tree and that more than one parasite can be mapped to the same host. Hence, we are interested in distances between multilabeled trees.

In our context, the distance that best meets the requirement of efficiency and accuracy appears for now to be the maximum agreement area cladogram (MAAC) (Ganapathy et al. 2006). This is a generalization for multi-labeled trees of the well-known maximum agreement subtree (Finden and Gordon 1985; Farach-Colton et al. 1995) and it corresponds to the number of leaves in the largest isomorphic subtree that is common to two (multilabeled) trees. Clearly this isomorphism takes into account the labels of the trees. The MAAC distance can be calculated in $O(n^2)$ time where $n$ is the size of the largest input tree (Ganapathy et al. 2006).

We use a normalized version of MAAC that takes into account also the number of leaves in common between the two trees. More formally, for two trees $P$ and $P^{\prime }$ with leaf sets $L(P)$ and $L(P^{\prime })$ respectively, we define the measure $D_2(P,P^{\prime })$ as follows:

$$D_2(P,P^{\prime })=\{\begin{array}{ll}1-\frac{MAAC(P,P^{\prime })}{|L(P)\cap L(P^{\prime })|}\hfill & \text{if }L(P)\cap L(P^{\prime })\ne \varnothing \hfill \\ 1\hfill & \text{otherwise.}\hfill \end{array}$$

Observe that the intersection operation involves multisets. We recall that a multiset is a generalization of a set where the elements are allowed to appear more than once, hence the operations take into account their multiplicity in the following way: if the multiplicity of an element $e$ in a multiset $A$ is given by $[e](A)$, then $[e](A\cap B)$ is given by $\min \{[e](A),[e](B)\}$.

Finally, we propose a distance that is based on these two components $D_1$ and $D_2$. For a real parasite $P$, a vector $\theta =\langle p_c,p_d,p_s,p_l\rangle$, and a simulated parasite tree $P_{\theta }$, we define the distance $d(P,P_{\theta })$ as follows:

$$d(P,P_{\theta })={\beta }_1{D}_1(P,P_{\theta })+{\beta }_2{D}_2(P,P_{\theta }), \text{with} {\beta }_1+{\beta }_2=1.$$

According to our experiments (see Supplementary Material available at, http://dx.doi.org/10.5061/dryad.9g5fp), the most appropriate values are ${\beta }_1=0.7$ and ${\beta }_2=0.3$ but this can be set by the user. The main drawback of this distance is that it is not a metric; however, it achieves good results with respect to discriminating the trees as observed in our experiments.

In Coala, we implemented two other distances, both of which are variations of the MAAC. A user can choose the most appropriate one depending on the case. In this article, we show only the results for the two-component distance, as this had the most discriminating power (data not shown).

Given a parameter vector $\theta =\langle p_c,p_d,p_s,p_l\rangle$, we generate $M$ trees and for each of them we consider the distance of $\tilde{P}$ from the real parasite tree $P$. From this set of distances, $D$, we produce a summary, denoted by $S(\theta )$, that characterizes the set of trees generated with the parameter vector. In our experiments, we choose $S(\theta )$ as the average of all the produced distances.

The summary $S(\theta )$ is the value that is used in the rejection/acceptance step of the ABC method.

Finally, it is worth noting that although the choice of a summary statistic (or equivalently here a summary tree distance) is independent from the generation process (coevolution model), such a choice may have a deep impact on the performance and the results of the method. This is one of the main issues with ABC-related methods. Some recent works have attempted to improve this step (Fearnhead and Prangle 2012). From the experiments done however, we can already see that the two-component distance seems to be a good enough discriminator.

ABC–SMC Procedure

The ABC–SMC procedure is composed of a sequence of $R>1$ rounds. For each of these rounds, we define a tolerance value ${\tau }_r$ ($1\le r\le R$) which determines the percentage of parameter vectors to be accepted. Associated with a tolerance value ${\tau }_r$, we have a threshold ${ϵ}_r$ which is the largest value of the summary statistic associated with the accepted parameter vectors.

• Initial round ($r=1$):

  • Draw an initial set of $N$ parameter vectors ${\left\{{\theta }_1^i\right\}}_{(1\le i\le N)}$ from the prior $\pi$. Then, for each ${\theta }_1^i$ generate $M$ trees ${\{{\tilde{P}}_j({\theta }_1^i)\}}_{(1\le j\le M)}$. Select $Q={\tau }_1\times N$ parameter vectors ${\theta }_1$ that have the smallest $S({\theta }_1)$, thus defining the threshold ${ϵ}_1$ and the set $A_1$ of accepted parameter vectors.
• Following rounds ($2\le r\le R$):

  1. Sample a parameter vector ${\theta }^{\star }$ from the set $A_{(r-1)}$. Create a parameter vector ${\theta }^{\star \star }$ by perturbing ${\theta }^{\star }$. The perturbation is performed by adding to each coordinate of ${\theta }^{\star }$ a randomly chosen value in $[-0.01,+0.01]$ and normalising it.
  2. Generate $M$ trees ${\{{\tilde{P}}_j({\theta }^{\star \star })\}}_{(1\le j\le M)}$ and compute $S({\theta }^{\star \star })$. If $S({\theta }^{\star \star })\le {ϵ}_{(r-1)}$, add ${\theta }^{\star \star }$ into the quantile set $S_r$. If $|S_r|<Q$, return to Step 1.
  3. Based on the set $S_r$, select ${\tau }_r\times Q$ parameter vectors ${\theta }_r$ that have the smallest $S({\theta }_r)$, thus defining the threshold ${ϵ}_r$ and the set $A_r$ of accepted parameters.

The final set $A_R$ of accepted parameter vectors is the result of the ABC–SMC procedure and characterizes the list of parameter vectors that may explain the evolution of the pair of host and parasite trees given as input.

Let us observe that, because in all our experiments we are assuming a uniform prior distribution and also are performing the perturbations in a uniform way, the weights induced by the proposals appear to be uniform (Beaumont et al. 2009). However, in the case of a different prior, weights should be used in the process in order to correct the posterior distribution according to the perturbation made.

Clustering the Results

Coala implements a hierarchical clustering procedure to group the final list of accepted parameter vectors. The basic process of a hierarchical clustering is as follows. At the beginning, each parameter vector forms a single cluster. Then at each step, the pair of clusters that have the smallest distance to each other are merged to form a new cluster. The distance that we use between the vectors $\theta =\langle p_c,p_d,p_s,p_l\rangle$ and ${\theta }^{\prime }=\langle q_c,q_d,q_s,q_l\rangle$ is the ${\chi }^2$ distance, which is a weighted Euclidean distance defined as follows:

$$d(\theta ,{\theta }^{\prime })=\sqrt{{\displaystyle \sum _{i\in \{c,d,s,l\}}2}\times \frac{{(p_i-q_i)}^2}{(p_i+q_i)}}.$$

At the end of this process, we have a single cluster containing all the items represented as a tree (hierarchical cluster tree or dendrogram) showing the relationship among all the original items. As we make no assumptions concerning the space of the vectors we are dealing with, we chose to apply a more general but still efficient method, introduced in Langfelder et al. (2007), to select the branches to be cut in the dendrogram. The method proceeds in two steps. Starting with the complete dendrogram, it first identifies preliminary clusters that satisfy some criteria: for example, they contain a certain minimum number of objects (to avoid spurious divisions), any two clusters are at least some distance apart, etc. (Langfelder et al. 2007, for more details). In a second step, all the items that have not been assigned to any cluster are tested for sufficient proximity to preliminary clusters; if the nearest cluster is close enough, the item is assigned to that cluster, otherwise the item remains clustered according to the complete dendrogram.

Finally, once the vectors are split into clusters, we associate to each one a representative parameter vector. To define each coordinate of the “consensus” parameter vector, we take the mean value of the respective coordinate in all the parameter vectors which are inside the cluster. We then normalize the “consensus” coordinates to sum to one.

Experimental Results and Discussion

We evaluated our method in two different ways. First we designed a self-test to show that the principle underlying it is sound and to test it on simulated data sets.

We then extended the evaluation to four real examples that correspond to biological data sets from the literature. This choice was dictated by: (i) the availability of the trees and of their leaf mapping; and (ii) the desire to, again, cover for situations as widely different as possible in terms of the events supposed to have taken place during the host–parasite coevolution. As a matter of fact, the first point drove the choice more than the second: there are not so many examples available from which it is easy to extract the tree and/or leaf mapping and that are big enough to represent meaningful data sets on which to test Coala. All four examples were also analyzed in the original paper from which they were extracted by one or more of the existing algorithms that search for a most parsimonious (possibly cyclic) reconciliation (i.e., for a reconciliation of minimum cost). Except in one case, which is a heuristic strategy and therefore does not guarantee optimality of the solution, all existing algorithms need to receive as input the cost of the events, which is thus established a priori and drives the conclusions on the results obtained.

Finally, we applied Coala to a biological data set of our own, representing the coevolution of bacteria from the Wolbachia genus and the various arthropods that host them. This data set was selected because of its size: the trees have each 387 leaves.

Experimental Parameters

All data sets were processed by Coala configured with the same parameters. For each data set, we generated $N=2000$ parameter vectors in the first round. For each of the vectors, we generated $M=1000$ parasite trees using our method. We required these trees to have a size at most twice the one of the real parasite tree, otherwise the tree was discarded as being too different from the original. If a given vector did not generate $M$ such trees in 5000 trials, then the vector was immediately associated with a distance equal to 1 which indicated that it represented the real data badly.

We used the average of all the 1000 distances produced as a fitting criterion in the rejection/acceptance step of the ABC method. The tolerance value used in the first round was ${\tau }_1=0.1$. For the remaining rounds $2\le i\le R$, we defined ${\tau }_i=0.25$. Notice that ${\tau }_1\times N=200$ defines the size $Q$ of the quantile set which must be produced in each new round. Thus, after the last round, we have ${\tau }_R\times Q=50$ accepted vectors. These vectors are grouped into clusters and a representative vector is associated with each cluster as explained in the Section “Clustering the results.”

We ran the experiments using $R=3$ and $R=5$ rounds. The number of rounds is an important parameter, which defines the characteristics of the list of accepted parameter vectors.

However, observe that a high number of rounds will tend to overfit the data and thus hide a possible variability in the list of accepted vectors that could provide significant alternatives for explaining the studied pair of trees.

Because, we are interested in exploring different alternatives for each data set, we present only the results which were obtained after running Coala for 3 rounds. The results involving 5 rounds may be found in the Supplementary Material available at http://dx.doi.org/10.5061/dryad.9g5fp.

Simulated Data sets

We first evaluated our model on simulated data. Clearly, in order to do this, we have to generate the phylogenies for the hosts and parasites whose coevolution is being studied in such a way that the probability of each event is known. The basic idea is that if we are able to select a “typical” (or representative) parasite tree $P_{\theta }$ that is generated starting from a host tree $H$ and a given probability vector $\theta$, Coala should be able to list values close to $\theta$ among the vectors accepted in the last round.

It is important to observe that many different probability vectors can explain the same pair of trees. We will therefore consider it acceptable if Coala produces clusters that are relatively close to $\theta$.

Generating simulated data sets

Due to the high variability of the parasite trees which can be simulated given a host tree $H$ and a vector $\theta$, the task of choosing the most “typical” tree can be hard. To simplify this task and select a typical tree, we impose two conditions which must be observed by the simulated tree. The first one requires that the candidate tree should have a size close to the median for all the trees which are simulated using $H$ and $\theta$. The second condition requires that the observed number of events of a candidate tree should be very close to the expected number given $\theta$.

In practical terms, we execute the following procedure: in order to get realistic data sets we choose a real host tree $H$ (see Supplementary Material available at http://dx.doi.org/10.5061/dryad.9g5fp, for more information). Then, given a probability vector $\theta$ and $H$, we generate 2000 parasite trees using our model, without imposing any limit on the size of the generated trees. We then compute the median size of all generated trees and we filter out those whose size is far from this value (difference greater than 1 or 2 leaves from the median value). Finally, we select as typical tree $P_{\theta }$ the one that shows the smallest ${\chi }^2$ distance between the vector $\theta$ and the vector of observed frequencies of events.

We generated in this way 9 data sets ($H$,$P$) associated with the following 9 probability vectors: ${\theta }_1=\langle 0.70,0.10,0.10,0.10\rangle$, ${\theta }_2=\langle 0.80,0.15,0.01,0.04\rangle$, ${\theta }_3=\langle 0.75,0.01,0.16,0.08\rangle$, ${\theta }_4=\langle 0.70,0.05,0.02,0.23\rangle$, ${\theta }_5=\langle 0.60,0.20,0.00,0.20\rangle$, ${\theta }_6=\langle 0.55,0.00,0.20,0.25\rangle$, ${\theta }_7=\langle 0.45,0.10,0.15,0.30\rangle$, ${\theta }_8=\langle 0.40,0.20,0.10,0.30\rangle$, and ${\theta }_9=\langle 0.30,0.20,0.40,0.10\rangle$ (see the Supplementary Material available athttp://dx.doi.org/10.5061/dryad.9g5fp, for more details). The choice of vectors was done with the aim to cover different patterns of probability. All data sets were generated with the same host tree $H$ of 36 leaves.

Self-test

As concerns the self-test, we designed the following procedure. Let $P_{\theta }$ denote the simulated parasite tree chosen in correspondence of the probability vector $\theta$, as explained in the previous section. We recall that the host tree $H$ remains the same during all the self-test experiments. For a pair of host and parasite trees ($H,P_{\theta }$), we ran Coala 50 times. In each run $j$, we computed the quality $q_j$ that corresponded to how well the method was able to recover the target vector $\theta$ used for generating the data set $P_{\theta }$. To do this, for each run $j$, we considered the representative vectors of the clusters produced as output. We computed the ${\chi }^2$ distance for each of the representative vectors to the target vector $\theta$ and set $q_j$ to the smallest value among them.

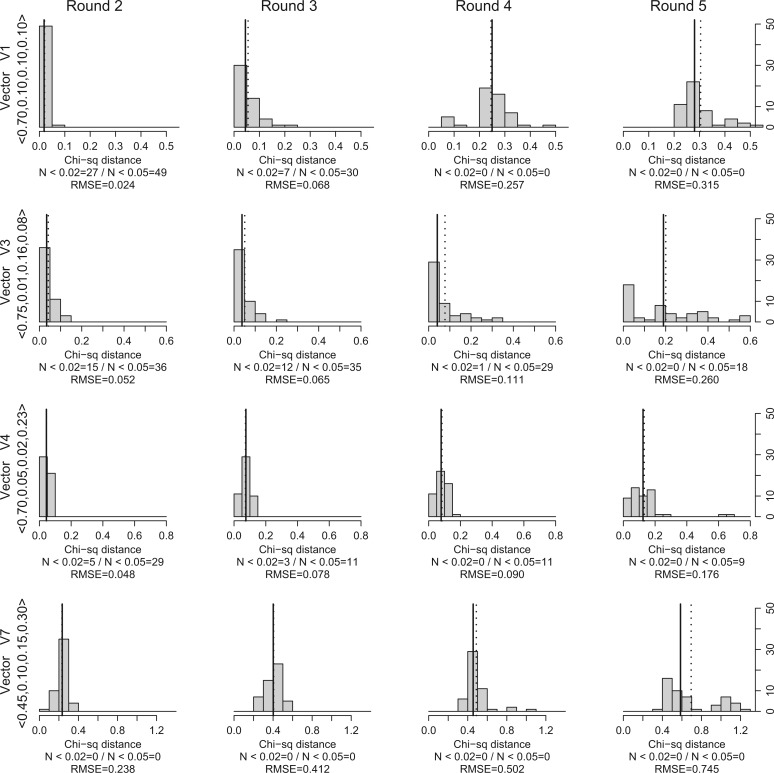
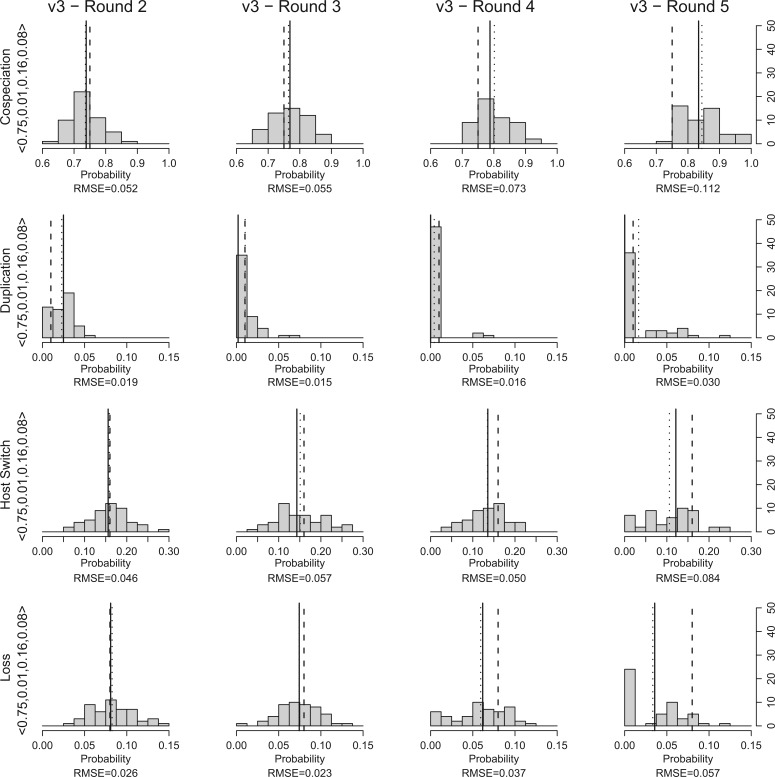
Figure 3 shows the distribution of the quality values which were obtained at the end of each round (from 2 to 5) for the simulated data sets ${\theta }_1$, ${\theta }_3$, ${\theta }_4$, and ${\theta }_7$ (the results for the remaining data sets can be found in the Supplementary Material available at http://dx.doi.org/10.5061/dryad.9g5fp). Figure 4 shows the histograms of the event probabilities observed for the 50 parameter vectors with smallest ${\chi }^2$ distance at the end of each round for data set ${\theta }_3$ (again, the results for the remaining data sets are available in the Supplementary Material available at http://dx.doi.org/10.5061/dryad.9g5fp).

Figure 3.

For each simulated data set, we ran Coala 50 times and, at the end of each round (from 2 to 5), we took note of the cluster whose representative parameter vector had the smallest ${\chi }^2$ distance to the probability vector used to generate the simulated data set. The histograms show the distribution of the smallest ${\chi }^2$ distance observed on each one of the 50 runs at the end of each round (for the simulated data sets $v_1={\theta }_1$, $v_3={\theta }_3$, $v_4={\theta }_4$, and $v_7={\theta }_7$.). The solid and dotted vertical lines indicate median and mean values, respectively.

Figure 4.

For each simulated data set, we ran Coala 50 times and, at the end of each round (from 2 to 5), we took note of the cluster whose representative parameter vector had the smallest ${\chi }^2$ distance to the probability vector used to generate the simulated data set. The histograms show the distribution of the event probabilities observed on the list of parameter vectors which have the smallest ${\chi }^2$ distance on each run for the data set $v_3={\theta }_3$. The solid and dotted vertical lines indicate median and mean values, respectively. The dashed vertical line indicates the “target” value.

Up to a certain level of cospeciation probability (≥0.50), our results (Fig. 3) show that in the rounds 2 and 3, Coala is able to select parameter vectors that are close to the target probability vector. Looking to the histograms of these two rounds, we can observe that in most of the runs, the closest parameter vector has low ${\chi }^2$ distance to the target. After the third round, this tendency changes and the closest parameter vectors show high ${\chi }^2$ distances indicating that Coala is mainly selecting vectors which are far from the target one.

Because Coala is based on an ABC–SMC approach, the accepted vectors in one round have summary statistics (i.e., average distance) smaller than the $ϵ$ defined in the previous round. This means that at each new round, Coala is selecting parameter vectors that have more probability of explaining the pair of trees given as input because their simulated parasite trees are, on average, closer to the real one.

Although we try to choose the best representative parasite tree $P$ for each pair ($H$, $\theta$), we cannot guarantee that $\theta$ is the best explanation for the association between $H$ and $P$. Even so, Coala was able to select parameter vectors that are close to the target probability vector in the first rounds. Figure 4 shows the histograms of the event probabilities observed among the 50 parameter vectors with smallest ${\chi }^2$ distance at the end of each round for data set ${\theta }_3$, and confirms these observations. We can see that at round 2, the median and mean event probabilities (solid and dotted vertical lines respectively) are very close to the target value (dashed vertical line). When we increase the number of rounds, the distance between the median/mean probabilities and the target values increases.

When we decrease the cospeciation probability to values smaller than 0.50, Coala selects very few vectors which are close to the target vector. When the cospeciation probability decreases while the duplication and host switch probabilities increase, the variability of the tree topologies observed increases exponentially. Due to this, selecting a typical tree becomes an almost impossible task and this may explain the obtained results. Increasing the number of simulated trees to compute the summary statistic might enable us to improve the quality of the results. However, this would require a much longer execution time.

Biological Data sets Extracted from the Literature

To evaluate Coala on biological data sets, we extracted four pairs of host and parasite trees from the literature. However, due to space issues, in this work we present only two of them. A description and the results obtained on the additional biological data sets can be found in the Supplementary Material available at http://dx.doi.org/10.5061/dryad.9g5fp. Before presenting and discussing the data sets, we provide details on how we performed the analyses.

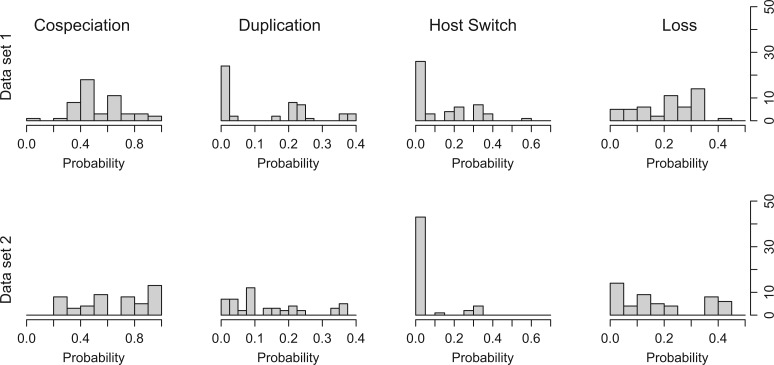
Each data set was processed by Coala as described in the Section “Experimental parameters.” Table 2 shows the representative parameter vectors obtained for each one of the data sets and Figure 5 the histograms of the event probabilities of the list of accepted vectors obtained at the end of the third round.

Table 2.

Representative probability vectors produced by Coala at Round 3

Data set	Cluster	$p_c$	$p_d$	$p_s$	$p_l$	No. of vectors
	0	0.030	0.000	0.557	0.413	1
1	1	0.461	0.258	0.000	0.281	24
	2	0.554	0.000	0.270	0.176	20
	3	0.910	0.016	0.058	0.016	5
	1	0.851	0.082	0.000	0.066	25
2	2	0.473	0.204	0.000	0.323	10
	3	0.238	0.349	0.000	0.413	8
	4	0.580	0.002	0.282	0.136	7

Figure 5.

Distribution of the probability values for each event type observed on the parameter values accepted on the third round while processing the biological data sets 1 and 2.

In order to compare our results to the existing literature, we transformed each one of the representative parameter vectors $\langle p_c,p_d,p_s,p_l\rangle$ into a vector of costs that was then used to compute optimal reconciliations between the host and the parasite trees given as input. The transformation was done by defining $c_i=-\ln p_i$, with $i\in \{c,d,s,l\}$, which is based on a commonly accepted idea that the cost of an event is inversely related to its probability (e.g., Charleston 1998; Ronquist 2003; Huelsenbeck et al. 1997). Indeed, if $p_i$ is equal to 1, then we expect all the events to be of type $i$, thus the cost of the corresponding event must be 0. Similarly, if $p_i$ is equal to 0, we expect that event $i$ never happens, and thus the cost must be assigned to $+\infty$.

To the best of our knowledge, the only methods that enumerate all optimal reconciliations are CoRe-Pa (Merkle et al. 2010), Notung (Stolzer et al. 2012), and Eucalypt (Donati et al. 2014). However CoRe-Pa in some cases misses solutions, probably because it considers some additional constraints. Notung does not allow cospeciation costs different from zero and the remaining event costs must be described by integer values. We thus present the results of Eucalypt which allows the configuration of all event costs and accepts real numbers.

Table 3 shows, for each data set, the vector of costs ($c_c$, $c_d$, $c_s$, $c_l$) produced by transforming the representative parameter vectors obtained after the third round (Table 2). Column $Opt$ indicates the cost of the optimal solution and columns $\#c$, $\#d$, $\#s$, $\#l$ the numbers of each event type which are observed among the enumerated scenarios. Finally, columns $\#A$ and $\#C$ indicate, respectively, the total number of acyclic and cyclic scenarios.

Table 3.

Event vectors obtained by transforming the probability vectors (Table 2) into cost vectors

Data set	Cluster	$c_c$	$c_d$	$c_s$	$c_l$	$Opt$	$\#c$	$\#d$	$\#s$	$\#l$	$\#A$	$\#C$
	0	3.517	13.816	0.584	0.885	14.044	1	0	15	2	2944	0
1	1	0.775	1.355	7.824	1.270	48.664	11	2	3	11	2	0
	2	0.591	8.517	1.310	1.736	16.217	9	0	7	1	1	0
	3	0.094	4.160	2.844	4.154	24.892	9	0	7	1	1	0
	1	0.161	2.496	9.210	2.717	153.544	22	11	8	18	0	12
2	2	0.748	1.592	9.210	1.130	105.393	22	19	0	52	1	0
	3	1.436	1.053	8.112	0.884	97.548	22	19	0	52	1	0
	4	0.545	6.266	1.265	1.996	72.588	17	5	19	4	4	0

Note: $\#c,\#d,\#s$, and $\#l$ denote the number of each event type which are observed among the enumerated scenarios. $\#A$ and $\#C$ indicate, respectively, the total number of acyclic and cyclic scenarios.

Data set 1: flavobacterial endosymbionts and their insect hosts

This data set was extracted from the work of Rosenblueth et al. (2012) and is composed of a pair of host and parasite trees which have each 17 species (see Supplementary Material available at http://dx.doi.org/10.5061/dryad.9g5fp). The parameter adaptive approach of CoRe-Pa (Merkle et al. 2010) was used to infer the more appropriate cost vectors for analyzing this data set. Nine such vectors were produced. However, only one, $\langle c_c=0.088,c_d=0.325,c_s=0.339,c_l=0.248\rangle$, was associated with a feasible reconciliation in the sense that host switches happened between contemporary species only (the branch length was used to infer this information). Because CoRe-Pa can produce unfeasible (i.e., cyclic) solutions during the parameter adaptive approach, Rosenblueth et al. decided to complement their study with Jane 3 (Conow et al. 2010), which uses a genetic algorithm approach to produce only acyclic reconciliations. They thus started with the only cost vector obtained by CoRe-Pa associated with a feasible reconciliation, however transforming it into integer numbers (a requirement of the software), and then gradually changed the costs until a feasible reconciliation was produced (again using branch-length information). This procedure resulted in the cost vector $\langle c_c=1,c_d=1,c_s=1,c_l=2\rangle$ and a reconciliation with 9 cospeciations, 0 duplication, 7 host switches and 1 loss, the same as obtained by CoRe-Pa.

Running Coala on this data set, we obtain 3 nonsingleton clusters which are quite different from each other (Table 2). Cluster 0 is formed by a single accepted vector which did not cluster with any other because it is too far apart. Cluster 1 shows probabilities of 0.46, 0.26, and 0.28, respectively, for cospeciation, duplication, and loss. After transforming these into costs (Table 3), the obtained reconciliation scenarios have 11 cospeciations, 2 duplications, 3 host switches, and 11 losses. Clusters 2 and 3 show very low duplication probability. Although Cluster 2 exhibits intermediate values for the remaining probabilities, Cluster 3 has a very high cospeciation probability value (0.91) and low host switch (0.06) and loss (0.02). Due to the low duplication value, these clusters show the same reconciliation scenario: 9 cospeciations, 0 duplications, 7 host switches, and 1 loss, which is identical to the one proposed by Rosenblueth et al. (2012).

Dataset 2: Rodents and Hantaviruses

This data set is taken from Ramsden et al. (2009, Fig. 2) and considers the coevolution of hantaviruses with their insectivore and rodent hosts. The host tree consists of a total of 34 hosts (28 rodents and 6 insectivores) and the parasite tree includes 42 hantaviruses. It was strongly believed that hantaviruses cospeciated with rodents becuase their phylogenetic trees have topological similarities with three consistently well-defined clades (Hughes and Friedman 2000; Jackson and Charleston 2004; Nemirov et al. 2004; Plyusnin and Morzunov 2001). The authors show that to support this hypothesis, the evolutionary rate of the RNA sequences of the hantaviruses should be several orders of magnitude smaller than the rates which are normally observed in RNA viruses that replicate with RNA-dependent RNA polymerase (Hanada et al. 2004). By analyzing the cophylogenetic reconciliations, the authors show that scenarios with more than 20 cospeciations are statistically nonsignificant. To explain the topological congruences, the authors point to the fact that host-switching followed by pathogen speciation can generate congruence between trees, particularly when pathogens preferentially switch among closely related hosts. Based on this fact and on the observed patterns of amino acid replacement observed in these viruses (compatible with host-specific adaptation), the authors conclude that the coevolutionary history of these hosts and parasites is the result of a recent history of preferential host-switching and local adaptation.

Looking at Table 2, we can observe that Clusters 1, 2, and 3 have representative vectors with zero probability for host switch events: Cluster 1 has a very high cospeciation probability (0.85), whereas Clusters 2 and 3 have probability values which are almost equally distributed among cospeciation, duplication, and loss events. After transforming these vectors into costs (Table 3), we obtain scenarios with a high number of cospeciations which is considered nonsignificant by Ramsden et al. (2009).

Differently from the others, Cluster 4 shows a vector with host switch probability higher than the probabilities of duplication and loss. When converted into costs (Table 3), this generates time-consistent scenarios with 17 cospeciations, 5 duplications, 19 host switches, and 4 losses, a result much closer to the explanation given by Ramsden et al. (2009). These results reinforce the idea that, although Coala is able to identify vectors which can explain a pair of trees, having a prior knowledge of the dynamics of the interactions of the two groups of species is important to identify the clusters that better explain their coevolution.

Wolbachia and their Arthropod Hosts Data set

Wolbachia is a large, phylogenetically diverse monophyletic genus of intracellular bacteria that are currently considered the most abundant endosymbionts in arthropods. In insects alone, it is estimated that over 65% of the species are infected by Wolbachia. The data set used in this artcile corresponds to Wolbachia species that were detected in an extensive set of arthropods collected from 4 young, isolated islands (less than 5 Myr old) (Simões et al. 2011; Simões 2012). The trees are a subset of those discussed in (Simões et al. 2011; Simões 2012), where we retained only those parasites which were associated with a unique host, the hosts diverge by at least 2% at the level of the CO1 genes that were used for reconstructing their phylogenetic tree and the Wolbachia sequences (corresponding to the fbpA gene) differ by at least one SNP. Each resulting tree is composed of 387 leaves. The initial results presented in Simões (2012) seemed to indicate that host switches might be quite frequent even among hosts that are physiologically and molecularly very distinct and thus phylogenetically distant.

The Wolbachia-arthropods data set was also processed by Coala as described in the Section “Experimental parameters.” Table 4 shows the three clusters which were obtained at the end of the third round. All these clusters have significantly high cospeciation probabilities (>0.77). The first cluster has a very low duplication probability and a host switch probability around 0.5. The two other clusters point to a relatively high duplication probability and low level of host switches. The difference between them is related to the probability of losses, which is around 0.14 for Cluster 2 and zero for Cluster 3.

Table 4.

Representative probability vectors produced by Coala, at the end of the third round, while processing the Wolbachia-arthropods data sets

Cluster	$p_c$	$p_d$	$p_s$	$p_l$	No. of vectors
1	0.866	0.006	0.055	0.073	26
2	0.771	0.078	0.010	0.141	22
3	0.964	0.022	0.014	0.000	2

Cluster 1 goes in the direction of what was presented in Simões (2012) where the author suggested that in the last 3 Ma, there were many transfers of Wolbachia, including between different arthropod orders, that is over large phylogenetic distances. Clusters 2 and 3 point to an opposite scenario.

Similarly to the analysis performed for the small biological data sets, we transformed each one of the representative parameter vectors into a vector of costs that was then used to compute optimal reconciliations between the host and the parasite trees given as input.

What is most striking with the results obtained for this data set is the absolutely huge number of optimal reconciliations that can be derived for all clusters. Because the total number of solutions makes impossible the enumeration of all the results, for this data set, we therefore only computed the costs of the optimal solutions and the total number of solutions. Additionally, for each cluster, we sampled 10,000 solutions and we checked for the presence of acyclic solutions. Table 5 summarizes the results obtained.

Table 5.

Total number of solutions obtained by transforming the probability vectors (Table 4) into cost vectors for Wolbachia-arthropods data sets

Cluster	$c_c$	$c_d$	$c_s$	$c_l$	$Opt$	Solutions	Acyclic solutions
1	0.144	5.116	2.899	2.623	917.475	$5.4\times {10}^{43}$	No
2	0.260	2.551	4.595	1.961	1407.877	$9.8\times {10}^{40}$	No
3	0.037	3.817	4.269	13.816	1375.725	$1.6\times {10}^{51}$	Yes

For the small sampling that we performed, we were able to find feasible (acyclic) solutions only with the cost vector produced with the event probabilities of Cluster 3. However, the results obtained with all the other four data sets used here lead us to suggest that the number of feasible solutions might quite possibly remain large.

Conclusions

We have developed an automated method that, starting from two phylogenies representing sets of host and parasite species, allows extraction of information about the costs of the events in a most probable reconciliation. It is clear that within a parsimony-based approach, an optimal solution strictly depends on the specific values attributed to these costs. However, there seldom is enough information for assigning those values a priori. Indeed, we observe in the results we obtained on a diverse selection of data sets that the costs inferred by our simulations may be very different across data sets, thus motivating the use of estimated instead of fixed costs. Such costs may even differ widely for a same pair of host–parasite trees, as is observed for the Wolbachia-arthropods data set.

These costs are inversely related to their likelihood, and so to their expected frequency. For this reason, providing information on the frequencies of the events is an important issue, in particular in the cases where the reconciliation methods fail to find a solution. The latter can happen, for instance, if all the optimal solutions that are identified by the existing reconciliation algorithms are biologically unfeasible due to the presence of cycles, becuase finding an acyclic reconciliation is an NP-hard problem. In addition, if the host and parasite trees are large (for instance, on the order of hundreds of taxa), these cases cannot be handled by the existing reconciliation algorithms in the sense that there are too many solutions to test for acyclicity.

As a future work, we first plan to refine the model used for the reconciliation problem, including more biological information and making it more realistic. In particular, we could include information about the distance of the allowed host switches (for instance if we expect a host switch to rarely happen between species that are too far from each other), or allow the mapping of the leaves to be an association instead of a function (thus addressing the cases where a parasite can be found in more than one host species). Moreover, we should also consider the case where the input phylogenies are not fully resolved, meaning that the trees are not binary.

A more efficient exploration of the parameter space is another important future issue that would significantly increase the efficiency of our procedure and also allow to handle larger trees.

It is important to observe that most studies on cophylogeny assume that the phylogenies of the organisms are correct. Clearly, this may affect the results observed. It would therefore be interesting to be able to infer the cophylogenetic reconciliation directly from sequence data.

Finally, the accuracy of the results obtained by our method depends on the choice of the metric used for comparing trees. Designing new metrics that can be computed efficiently while still capturing the similarity for multilabeled, not fully resolved trees is therefore another important future issue which we believe is also interesting per se.

Availability

The Coala program is available at http://coala.gforge.inria.fr/ and runs on any machine with Java 1.6 or higher. The Eucalypt program is available at http://eucalypt.gforge.inria.fr/.

Running Time

The experiments were executed at the IN2P3 Computing Center (http://cc.in2p3.fr/). For the simulated data sets, each pair of trees was processed with 3 threads for speeding up the simulation process. The time necessary to complete 5 rounds for all 50 runs varied from 1 to 2 days depending on the size of the trees. For the biological data sets 1 to 4, we also used 3 threads. The observed execution times for 5 rounds were between a couple of hours for the smallest data set (Data set 1) and 1 day for Data set 4. Due to its size, the data set Wolbachia-arthropods was processed with 150 threads and it required approximately 8 days to complete 5 rounds.

Supplementary Material

Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.9g5fp.

Funding

The research leading to these results was funded by the European Research Council under the European Community's Seventh Framework Programme (FP7/2007-2013) / ERC grant agreement no. [247073]10, and by the French National Research Agency (ANR) / Project ANR MIRI BLAN08-1335497. It was supported by the ANR funded LabEx ECOFECT.