Spatial scales of interactions among bacteria and between bacteria and the leaf surface

Abstract

Microbial life on plant leaves is characterized by a multitude of interactions between leaf colonizers and their environment. While the existence of many of these interactions has been confirmed, their spatial scale or reach often remained unknown. In this study, we applied spatial point pattern analysis to 244 distribution patterns of Pantoea agglomerans and Pseudomonas syringae on bean leaves. The results showed that bacterial colonizers of leaves interact with their environment at different spatial scales. Interactions among bacteria were often confined to small spatial scales up to 5–20 μm, compared to interactions between bacteria and leaf surface structures such as trichomes which could be observed in excess of 100 μm. Spatial point-pattern analyses prove a comprehensive tool to determine the different spatial scales of bacterial interactions on plant leaves and will help microbiologists to better understand the interplay between these interactions.

For the first time, we quantified the spatial scales of interactions among leaf-colonizing bacteria and between these bacteria and plant leaf surface structures.

Graphical Abstract Figure.

For the first time, we quantified the spatial scales of interactions among leaf-colonizing bacteria and between these bacteria and plant leaf surface structures.

INTRODUCTION

The plant leaf surface as a microbial habitat, also known as the phyllosphere (Last 1955), is an important arena for plant–microbe interactions. Many of these interactions are in principle well understood biologically (Meyer and Leveau 2011), physically (Hirano and Upper 2000), chemically (Beattie 2011) or genetically (Bailey, Lilley and Diaper 1996; Espinosa-Urgel 2004; Pontiroli et al., 2009). The phyllosphere is a complex and heterogeneous environment where microbial colonizers experience temporally and spatially variable competition for resources, facilitative interactions with other microbes, exposure to environmental stresses such as UV radiation, rapidly changing temperatures, and desiccation (Leveau 2006). Furthermore, the leaf surface exhibits a pronounced topography and a variety of structural elements, such as stomata, trichomes, or veins which influence microbial fitness in the phyllosphere in various ways (Timmer, Marois and Achor 1987; Leveau 2001; Monier and Lindow 2004; Yadav, Karamanoli and Vokou 2005).

One of the most difficult questions to answer is how all these factors interact with each other and how they rule microbial life in the phyllosphere. Some factors may be more locally confined than others. For example, the competition of microbes for a carbon source may be spatially confined within a few micrometers around the individuals, whereas environmental factors such as temperature will only change along larger distances, e.g. several millimeters or more. This means that different interactions of bacteria with their environment operate at different spatial scales and a good understanding of these scales is a prerequisite for a thorough interpretation of microbial colonization patterns in the phyllosphere. Numerous studies have looked at the spatial distribution of bacteria in the phyllosphere but often stopped at a general description of observed patterns (Blakeman 1985; Mansvelt and Hattingh 1989; Morris, Monier and Jacques 1998; Fett and Cooke 2003; Hong et al., 2010; Yu et al., 2014). These studies all confirmed the non-random association of microbial colonizers with leaf structures such as stomata or leaf veins and the aggregated character of bacterial colonization patterns on leaves in general. Other studies applied various statistical methods to correlate bacterial success in the phyllosphere to leaf morphological features or to interactions between microbes (Monier and Lindow 2004; Yadav, Karamanoli and Vokou 2005; Hunter et al., 2010). None of these studies, however, was spatially explicit in the sense that it quantified the spatial scale (or reach) of the underlying processes. For instance, the aggregation of Pseudomonas syringae near bean leaf trichomes of the glandular type was noted (Monier and Lindow 2004) but the radius around the trichomes within which this process was significant, i.e. the spatial scale of the process remained undefined. Knowing this spatial scale would be very useful towards conceiving (or rejecting) mechanistic explanations for microbial colonization patterns.

Spatial point-pattern analysis (Illian et al., 2008; Wiegand and Moloney 2014) provides tools to identify and evaluate interactions between the points in a point pattern, e.g. between individuals in a population. The results can help to understand the processes that formed the pattern and to assess the spatial scale at which these processes operate. In the most basic case, point-pattern analysis is used to test if points in a pattern are randomly distributed. More particularly, the case of complete spatial randomness (CSR) is used as a null model against which the observed patterns are compared. Under CSR, the location of each point is random and independent from the location of other points. The alternative hypothesis (point distribution does not follow CSR) can be differentiated as points being aggregated or scarce at certain spatial scales. Latter case usually leads to a regularity in the pattern. The aggregation of points can indicate facilitative interactions between individuals, whereas regular patterns often arise from inhibitory interactions. Both patterns, however, also may have been formed by an unobserved external factor such as heterogeneous nutrient availability—a fact that requires careful consideration when discussing results.

The pair correlation function g(r) (Ripley 1977; Fig. 1) is currently the preferred method to study the distribution of points in a pattern, if fully mapped location data for all points, e.g. all individuals of a species in an area, are available (Illian et al., 2008; Wiegand, He and Hubbell 2013). It uses all inter-point distances in a pattern to determine the probability to find points at a certain distance r around a typical point of the pattern. If the points, e.g. bacteria on a leaf surface, are randomly distributed in space, the pair correlation function takes the value 1 at all spatial scales r. Values g(r) > 1 indicate an aggregation of points at scale r, whereas values g(r) < 1 indicate a scarcity of points (cf. Fig. 1). For example, a pattern of randomly placed (circular) clusters of points, where the typical diameter of a cluster is 5 μm, will (ideally) result in a pair correlation function with g(r) > 1 for radii r smaller than or equal to 5 μm and g(r) = 1 for r > 5 μm.

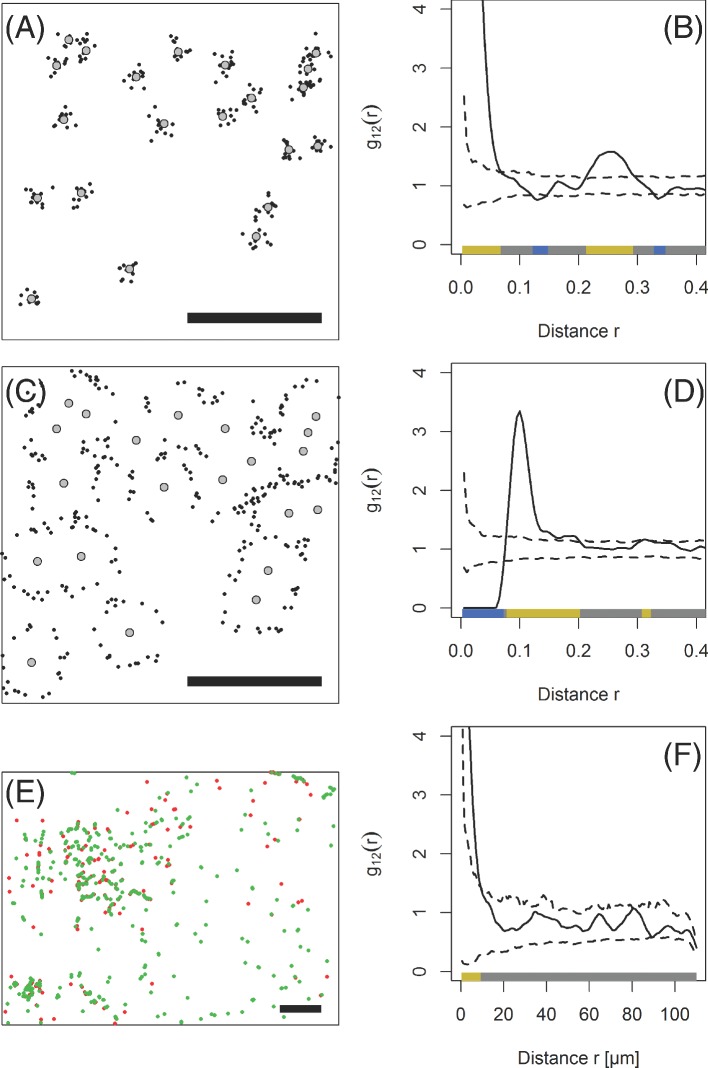
Figure 1.

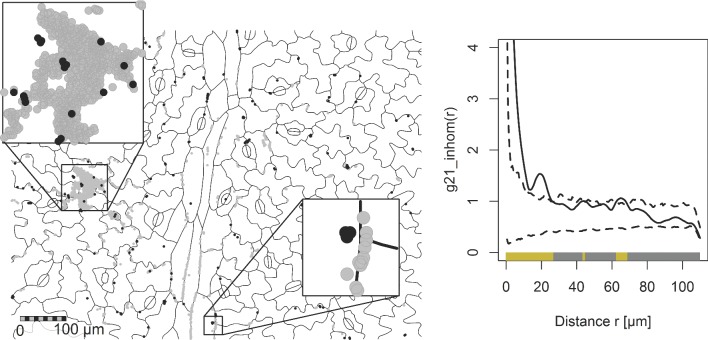
Cross-type pair correlation functions [(B), (D) and (F), solid lines] of artificial and observed point patterns (A), (C) and (E). (A), (C): artificial point patterns in a unit square (scale bars are 0.4 units), (E): pattern of DsRed-labeled P. syringae (red) and GFP-labeled P. agglomerans (green) on a bean leaf (scale bar is 110 μm). If the function exceeds the simulation envelopes [(B), (D) and (F), broken lines] at scale r, the points are significantly aggregated at scale r. Values for g₁₂(r) smaller than the lower bound of the simulation envelopes indicate a significant scarcity of points of pattern 2 at distance r of an arbitrary point of pattern 1. The colored bands (‘quantum plots’) at the bottom of the graphs depict the spatial scales at which the pair correlation functions deviate from the simulation envelopes. In pattern A, the black points were aggregated around the gray points up to a scale of 0.07 units. A second maximum around r = 0.25 units suggest a periodicity in the pattern that could arise from a typical distance of 0.25 units between clusters. In pattern C, the black points aggregated 0.1 units from the gray points but avoided coming closer than this. The P. agglomerans cells in E aggregated around P. syringae cells but no significant patterns were found at scales larger than 10 μm.

Two important extensions of the pair correlation function exist. Firstly, the cross-type pair correlation function g₁₂(r) (Lotwick and Silverman 1982) is used to study the interactions between points from two different point patterns, e.g. between individuals of two different species. Secondly, the inhomogeneous pair correlation function g_inhom(r) (Baddeley, Moller and Waagepetersen 2000) was developed to study the interactions between point patterns where the distribution of points is inhomogeneous, e.g. when the point density increases along an unobserved environmental gradient. Both extensions to the pair correlation function can be combined to analyze the interactions between two point patterns of which at least one pattern is inhomogeneous.

Pair correlation functions can exhibit complex behavior, especially when the distribution of points was formed by more than one process. The pattern of black points in Fig. 1C for example was produced by two competing processes, one of which attracts the black points towards the grey points, whereas the second process forbids the black points to come closer than 0.1 units to the grey points. One may think of moths being attracted by the light of campfires and repulsed by the intense heat at the same time. Both processes are represented in the corresponding cross-type pair correlation function g₁₂(r) (Fig. 1D).

Pair correlation functions are usually evaluated by their deviations from Monte Carlo simulation envelopes (Kenkel 1988). These envelopes are based on a series of simulated point patterns that were generated according to a suitable null model, e.g. CSR. But also more complex null models such as a parameterized cluster process are possible (Wiegand and Moloney 2014). By calculating the pair correlation function for a number m of these simulated patterns, one can derive simulation envelopes which delineate the range of values that g(r) takes if the observed points were distributed by the process in the null model. Observed values of g(r) greater than the upper bound of the envelope at scale r indicate a significant aggregation of points at scale r, whereas values of g(r) below the lower bound of the envelope at scale r indicate a scarcity of points at scale r (cf. Fig. 1). The level of significance α attached to such a simulation envelope is approximately 2/(m+1). However, note that this level of significance is a guideline only, due to type I error inflation in these simulation envelopes (Loosmore and Ford 2006; Baddeley et al., 2014). Nevertheless, for the purposes of exploratory analysis, Monte Carlo simulation envelopes can yield important insights into the point pattern under study (Baddeley et al., 2014).

In microbiology, the potential of spatial point-pattern analysis has not yet been fully explored. The majority of studies represent landscape-scale epidemiology (Jonsson et al., 2010; Rao, Kitron and Weigel 2010; Lin et al., 2011). However, at the landscape scale, geostatistical methods are more common (Dandurand, Schotzko and Knudsen 1997; Franklin et al., 2002; Franklin and Mills 2003; Brown et al., 2004; Gosme and Lucas 2009). The difference between point-pattern analysis and geostatistics is that the former studies the spatial associations between objects (points) in an area that is completely mapped, while the latter studies continuous processes at selected sampling locations. In spatial point-pattern analysis, the location of a finite number of spatially discrete entities such as individuals or colonies is studied. This requires a complete survey of all individuals (colonies, entities) within the observation window and yields information about the spatial relationship between the entities. In geostatistical methodology, a (potentially infinite) number of samples at different locations are considered and values for a spatially continuous variable, e.g. soil moisture or relative abundances in a microbial community, are measured. From that, conclusions about the spatial properties of these variables are drawn. Only few studies have applied point-pattern analysis on an individual cell level, for example to quantify micro-scale clustering of bacteria in soils (Nunan et al., 2002; Raynaud and Nunan 2014) or the micro-scale inhibition of bacteria and algae in stream biofilms (Augspurger et al., 2010). Our study is the first to perform spatial point-pattern analysis of bacterial colonization patterns on plant leaves including the interactions between bacteria and leaf structures. The phyllosphere represents an excellent microbial habitat to test the usefulness of point-pattern analyses in surface-based colonization. In this study, we analyzed the colonization patterns of the bacteria P. agglomerans and P. syringae on leaves of common bean. The aim of our study was to reveal how and on which spatial scales these patterns were influenced by the presence of other bacteria and by plant features such as stomata, trichomes, vein cells or the grooves between epidermal cells and to give an outlook on probable processes that formed the observed patterns.

METHODS

Experimental setup

We inoculated cut sections from primary leaves of two-week old green bean plants (Phaseolus vulgaris cv. Blue Lake Bush) with either single or mixed suspensions of the bacterial species P. agglomerans 299R and P. syringae B728a. Our study therefore included two lines of experiments, (a) single-species experiments where leaves were inoculated with one strain (P. agglomerans) and (b) mixed-species experiments where both strains were co-inoculated in equal quantities. The single-species experiments were used to study spatial patterns of P. agglomerans. Mixed inoculation with both strains was used 2-fold to study the changes in the colonization patterns of P. agglomerans when competing with a second species, and to study the interactions between both strains. Single-species and mixed-species setups were further processed the same way. We chose members of Pseudomonas and Pantoea as they are among the best-studied genera in the phyllosphere. The Pseudomonas genus is of special economic interest because of its wide variety of plant pathogenic strains (Hirano and Upper 2000; Espinosa-Urgel 2004; Monier and Lindow 2004; Masák et al., 2014). Much is known already about the biology of P. agglomerans, its interactions with Pseudomonas species and its importance as a bio-control agent (Kempf 1989; Marchi et al., 2006; Yu et al., 2014).

In our study, single-species experiments featured P. agglomerans strains 299R (pFRU48) and 299R (pFRU97) (Tecon and Leveau 2012). Plasmids pFRU48 and pFRU97 drive the constitutive expression of fluorescent proteins GFP (green) and DsRed (red), respectively. In two-species experiments, we used GFP-producing 299R::JBA28 (Leveau and Lindow 2001) with P. syringae B728a (pFRU97) (Monier and Lindow 2004). We cultivated the bacteria separately in 5 ml of Lysogeny broth liquid medium with 50 mg kanamycin per liter at 30°C. Cells were harvested during mid-exponential phase by centrifugation for 10 min at 2500 g, washed twice in M9 minimal medium (Sambrook, Fritsch and Maniatis 2001) without carbon source and diluted in M9 (no carbon) to an approximate concentration of 10⁷ individuals/ml.

Sections of 15 mm × 15 mm were cut from bean leaves (mid leaf, about 5 mm off the central vein) and edge-sealed by dipping briefly into 90–100°C paraffin wax. Two leaf sections each were placed on agarose gel in a petri dish with the adaxial side facing up. Inoculation with 50 μl of a 10⁷ cells per ml suspension was performed using an Airbrush Iwata Eclipse HP-CS (ANEST IWATA Corporation, Yokohama, Japan) at 100 kPa pressure. We either inoculated a mixture of red and green P. agglomerans or a mixture of red P. syringae and green P. agglomerans cells. We chose to use mixtures of red and green P. agglomerans cells to have more information on a posteriori mixing processes also in the single-species experiments (Tecon and Leveau 2012). Inoculation was performed through a hole in the lid of a plastic container 170 mm above the leaf surface. The nozzle of the airbrush was slightly swirled during inoculation to assure a good spread across the petri dish. The sections were either observed under the microscope directly (time t = 0) or the petri dishes were sealed to maintain a 100% relative humidity environment and put in an incubator at 28°C. Incubation times ranged between 10 and 72 h to cover many stages of early leaf colonization.

Additionally, we inoculated a series of leaves with DsRed-labeled P. syringae B728a only, incubated them for 92 h at room temperature and high humidity. We then cut sections from these leaves, sealed the edges with wax and inoculated these sections with green P. agglomerans 299R and incubated for another 0–72 h at 28°C.

A full record of incubation times for all samples is given with further information in the Table S1 (Supporting Information).

Sample preparation and image acquisition

After incubation, leaf sections were transferred to a microscope slide with the adaxial side facing up and covered with 10–50 μl Aqua Poly/Mount (Polyscience Inc., Warrington PA, USA) medium to ensure a good coverage of the sample. We then carefully added a cover slip which we fixed with strips of adhesive tape to all sides. From each leaf section, we typically took 10 micrographs at random positions using an Axio Imager.M2 fluorescence microscope (Carl Zeiss AG, Oberkochem, Germany) equipped with EC Plan-Neofluar10x/0.3, 20x/0.5 and 40x/0.6 (Zeiss) objectives and an AxioCAM MRn monochrome camera. Image sizes were 895.3 μm × 670.8 μm, 447.6 μm × 335.4 μm and 223.8 μm × 167.7 μm for the 10×, 20× and 40× objective, respectively, but in few instances smaller, when out-of-focus areas had to be cropped. For the fluorescence images, we used a GFP filter cube (exciter: 470; emitter: 525/50; beam splitter: 495) and a rhodamine filter cube (exciter: 546/12; emitter: 607/80; beam splitter 560). We also took phase-contrast images of all samples to visualize the leaf surface structure. To account for the topography of the leaf surface, we took all images as 3D ‘z-stacks’, i.e. several shots of the same area at different planes of focus. These were saved in the native Zeiss .zvi format.

Image processing

The .zvi images were processed using the open-source ImageJ software package (Rasband, W.S., ImageJ, U. S. National Institutes of Health, Bethesda, Maryland, USA, http://imagej.nih.gov/ij/, 1997–2012). We extracted the location (x-/y-coordinates) of all bacterial individuals and all structural elements of the leaf surface, i.e. stomata, trichomes, veins, grooves. The location of stomata was represented by a point within each guard cell; for the location of trichomes, we used the center of each base cell, and veins were represented by a point at the center of each vein cell. For the grooves between epidermal cells, we marked the intersections where at least three grooves come together. If grooves have an effect on the distribution of bacterial leaf colonizers, these intersections will be of special importance as they represent locations of high-groove density.

Spatial statistics

Our study consists of three groups of analyses: (a) the analysis of interactions between the individuals of the same bacterial species = intraspecific interactions, (b) the interactions between the two bacterial species = interspecific interactions and (c) the interactions between bacteria (not considering species identity) and the different structural elements of the leaf surface such as stomata or vein cells. The quality and scale of the patterns observed in these analyses can be used to develop hypotheses about the underlying processes/interactions that contributed to the observed distributions. This procedure has to be performed cautiously depending on the null model against which the observed pair correlation function is tested (Baddeley et al., 2014).

To study the spatial distribution of P. agglomerans, we calculated the inhomogeneous pair correlation function from the location data of the bacterial cells (intraspecific analysis, P. agglomerans only, not considering different colors). We also calculated intraspecific inhomogeneous pair correlation functions of P. agglomerans growing with P. syringae and vice versa and also for the pattern of ‘pooled’ bacteria, i.e. patterns of all bacterial individuals regardless of their color or species.

To explore the interactions between P. agglomerans and P. syringae, we calculated the inhomogeneous version of the cross-type pair correlation function g₁₂(r). This was performed separately for the data sets in which both strains were inoculated together at the same time and for the data sets in which P. agglomerans was inoculated after P. syringae had already grown on the leaf for 92 h.

For all inhomogeneous pair correlation functions, intraspecific and interspecific, we used a Gaussian smoothing kernel with standard deviation σ = 110 μm to estimate the local densities λ(x, y). We found that σ = 110 μm gave the most stable results for the pair correlation functions across our whole data set. Moreover, this scale is above the maximum expected interaction distance: based on work by Jeff Chanat, Frankin and Mills estimated the interaction distances between bacterial individuals in a solution to be around 10 times their cell size (Franklin and Mills 2007) which translates to about 10 μm in our study. Interactions between bacteria in the rhizoplane were found to steeply decay at scales greater than 5 μm and have not been observed beyond 78 μm (Gantner et al., 2006). For the phyllosphere, for which such measurements did not exist until now, we would not expect longer ‘calling distances’.

To study the interactions between the bacterial colonizers and the leaf surface structures (stomata, trichomes, veins and grooves), we used the cross-type pair correlation function. For stomata, trichomes and groove nodes, we assumed a homogeneous distribution. Vein cells, however, are distributed heterogeneously along linear structures (the veins), and we additionally calculated the inhomogeneous cross-type pair correlation function, again with σ = 110 μm.

All pair correlation functions g(r) for each sample were tested for significant clumping or scarcity of points using Monte Carlo simulation envelopes. Throughout our study, we estimated 95% simulation envelopes from 199 simulations of the null model. At each spatial scale r, we selected the fifth highest and fifth lowest values of g(r) for the upper and lower bound of the envelope, respectively.

The null models used in the analyses reflect the biological hypotheses to be tested. For the intraspecific analyses (studying only one bacterial species), we applied the CSR null model where the location of a point is independent from the location of other points. Therefore, we generated random point patterns of the same point density as the observed pattern. For the analyses of cross-type pair correlation functions (interaction between bacterial species, and interactions between bacteria and leaf surface structures), we applied the independence null model, i.e. we performed 199 toroidal shifts (Wiegand and Moloney 2014). Here, a bacterial pattern is shifted a random distance into a random direction and points that exit the (rectangular) observation window reappear at the opposite edge of the window. The location of the other observed point pattern (either the other bacterial strain or a leaf structure) stayed unchanged. This approach preserves the internal structure of both point patterns (here, the structure of the bacterial pattern and the structure of e.g. the stomatal pattern). This way, the independence null model exclusively tests for independence between the patterns and is unaffected by patterns (e.g. clustering) that may be present within the individual point patterns. Thus, the toroidal shift null model is especially well suited to study the interactions between two different point patterns as it preserves all other interactions within the first pattern and only considers differences that arise from the dependence (interaction) of the first pattern on the second pattern. Also, it only relies on random shifts of one of the patterns and therefore is not subject to the limitations with respect to interaction distances discussed in Baddeley et al. (2014).

All calculations were performed using the ‘spatstat’ package (Baddeley and Turner 2005) in the statistics software R (R Core Team 2013).

Data presentation

The results from our analyses using pair correlation functions were summarized in frequency plots (Figs 3, 4 and 6). For each of these frequency plots, we looked at the pair correlation functions of all samples and plotted the relative frequencies of significant aggregation and scarcity. These were represented as stacked bars for every distance class r at which the pair correlation function was evaluated. Since each pair correlation function was evaluated up to a maximum distance r depending on the size of the observation window of the respective sample, sample size typically decreases with increasing spatial scale r. Not all data sets had stomata, trichomes or veins in them. This resulted in a reduced number of samples used in the respective analyses.

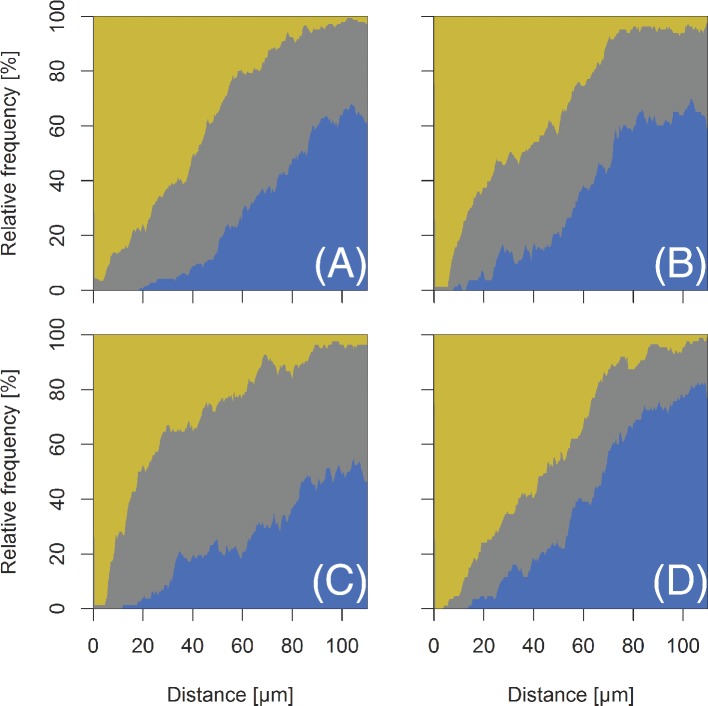
Figure 3.

Intraspecific interactions of bacteria in the bean phyllosphere. The graphs give the relative frequency of significant aggregation (yellow/light gray), randomness (medium gray) and scarcity (blue/dark gray) at different scales up to 110 μm as determined by inhomogeneous pair correlation functions. (A): interactions between individuals of P. agglomerans when growing as the sole species on the leaf. (B): interactions between individuals of P. agglomerans when growing in competition with P. syringae. (C): interactions between individuals of P. syringae when growing in competition with P. agglomerans. (D): interactions between bacterial individuals not considering species identity (both species growing together). Numbers of samples were 145 in A, 82 in B, 83 in C and 87 in D.

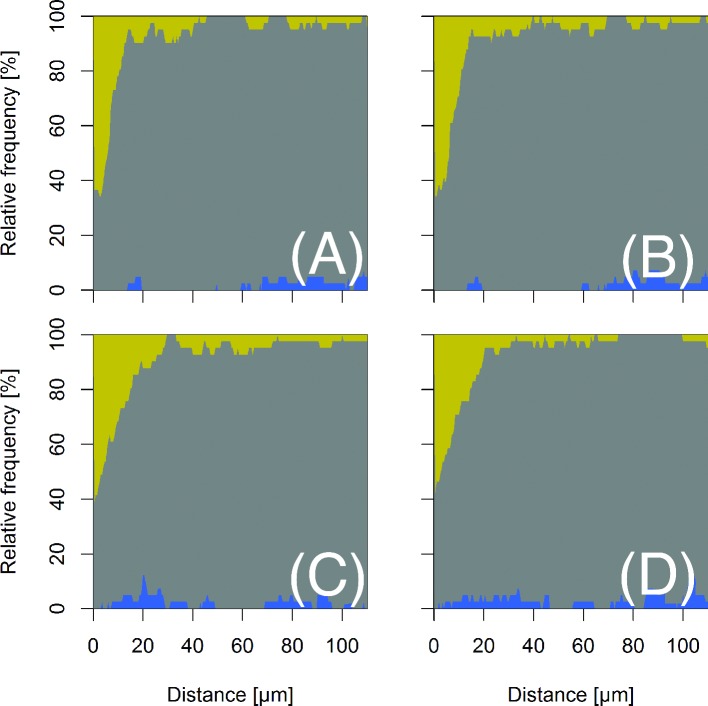
Figure 4.

Interspecific interactions of bacteria in the bean phyllosphere. The graphs give the relative frequency of significant aggregation (yellow/light gray), randomness (medium gray) and scarcity (blue/dark gray) at different scales as determined by inhomogeneous cross-type pair correlation functions using random toroidal shifts as a null model. (A), (C): aggregation of individuals of P. agglomerans around individuals of P. syringae. (B), (D): aggregation of P. syringae around P. agglomerans. In (A) and (B), both strains were inoculated jointly and incubated for 0–72 h. In (C) and (D), P. syringae was inoculated first and incubated for 92 h before P. agglomerans was inoculated. After inoculation with P. agglomerans, these samples were incubated for another 0–72 h. Number of samples was 41 in all four analyses.

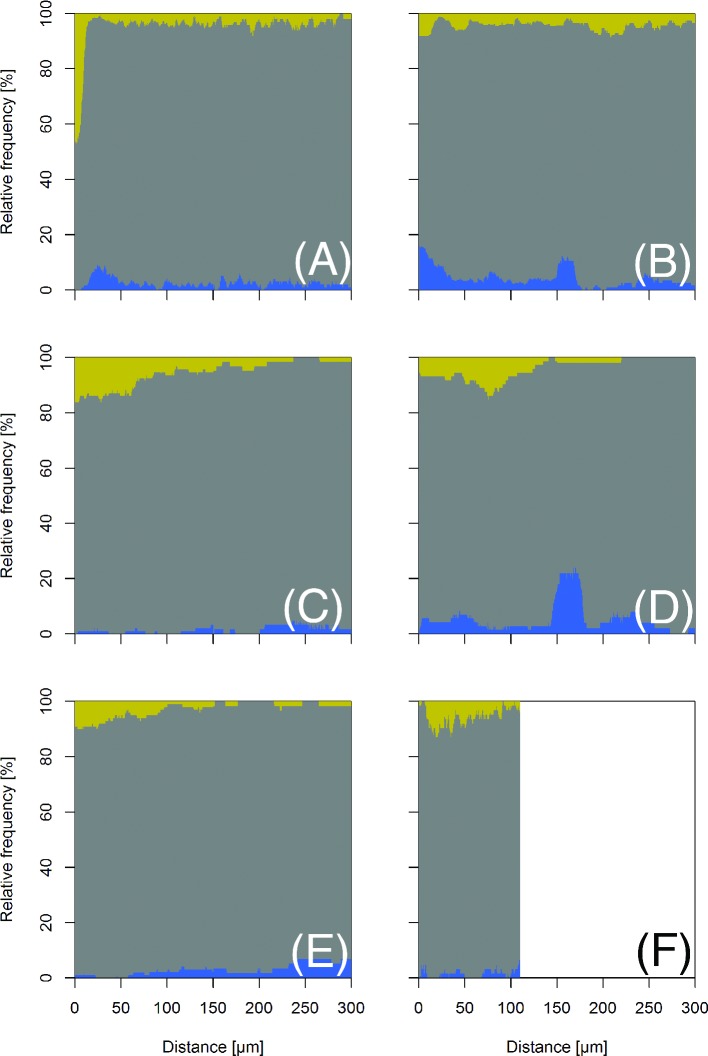
Figure 6.

Interactions of bacteria with structural elements of the bean phyllosphere. The graphs give the relative frequency of significant aggregation (yellow/light gray), randomness (medium gray) and scarcity (blue/dark gray) at different scales as determined by cross-type pair correlation functions (g₁₂) using random toroidal shifts (cf. main text) as a null model. (A)–(E): homogeneous g₁₂, (F): inhomogeneous g₁₂. In (F), the local point density was estimated using a moving Gaussian smoothing kernel of bandwidth 110 μm, which limited our analysis up to this scale. (A): interaction of bacteria with grooves between epidermal cells. (B): interaction with stomata. (C): interaction with glandular trichomes. (D): interaction with hooked trichomes. (E)–(F): interactions with vein cells. Number of samples were 244 in (A) and (B), 93 in (C), 72 in (D), 99 in (E) and 62 in (F).

RESULTS AND DISCUSSION

In total, we analyzed point patterns from 244 samples (i.e. images of fields of view under the microscope) from 42 different adaxial leaf sections from 23 independent spray experiments. A rather typical pattern is depicted in Fig. 1E. The total area of all observation windows was approximately 75.63 mm² and contained 131 429 bacterial individuals, 2192 stomata, 135 glandular trichomes, 74 hooked trichomes and 819 vein cells. We found 43 674 nodes at which three or more grooves between epidermal cells came together. Bacterial population sizes on leaves increased within the first 20 h after inoculation and remained constant thereafter (Fig. 2).

Figure 2.

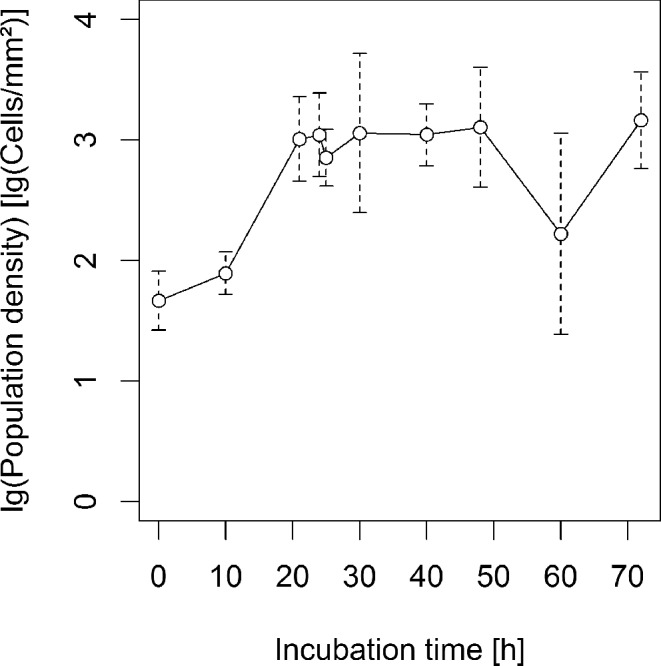
Mean bacterial population density (open circles) and standard deviation (broken lines) over time from all samples excluding samples where P. agglomerans was inoculated 92 h after P. syringae.

Interactions between bacterial individuals of the same species

When P. agglomerans was the only colonizer of the bean leaves, bacterial cells clustered at scales up to 7 μm in 90% of our samples (Fig. 3A). This means that within a 7 μm radius around a typical individual we found significantly more bacterial cells than expected if the cells were randomly distributed. The percentage of significant clustering gradually decayed at scales larger than 7 μm and disappeared into a background noise around 85 μm away from a typical P. agglomerans cell. This small-scale aggregation of bacteria is in agreement with most published studies on the general spatial distribution of bacteria on leaves (Kinkel 1997; Beattie and Lindow 1999; Leveau 2001; Monier and Lindow 2004) but none of these studies were able to report statistically verified information on the scale of the aggregation. Our results are also consistent with the concept of heterogeneously distributed but highly localized availability of resources (Leveau 2001; Kinkel, Newton and Leonard 2002) and with the concept of clonal ‘staying-together’ growth behavior (Tecon and Leveau 2012).

When P. agglomerans was inoculated in combination with P. syringae, small-scale aggregation of P. agglomerans cells was observed for more than 98% of our samples, while the noise distance was reduced to about 75 μm (Fig. 3B). Comparison of Fig. 3A and B suggests that the interaction with P. syringae increases the level of clustering of P. agglomerans. Garbeva et al. (2011) showed that the shape of colonies of P. fluorescens changes from irregular shapes in isolation to spherical when exposed to Pedobacter-born signaling molecules, thereby suggesting an interspecific interaction. Because of the reduced surface-to-volume ratio, cells in a spherical colony will be more spatially aggregated than the same cells in an irregular-shaped colony of comparable packing density. Similar mechanisms may explain the increase in small-scale aggregation of our P. agglomerans cells when exposed to compete with P. syringae cells. Alternatively to the active response mechanism suggested by Garbeva et al. (2011), the increase in small-scale aggregation prevalence could be the result of steric constraints that colonies of the one species impose on the development of colonies of the other species.

Aggregation of P. syringae competing with P. agglomerans was found at scales up to at least 5 μm in the majority of the sample images (Fig 3C). At scales larger than 5 μm, prevalence of significant aggregation rapidly decayed such that aggregation up to 28 μm was found in every third sample and disappeared in a background noise around 90 μm. Compared to P. agglomerans cells in Fig. 3B, the P. syringae cells were clustered at smaller scales, i.e. more compact than P. agglomerans. If we considered local resource availability as the most important determinant of bacterial colonization patterns, the tendency of P. syringae being more clustered than P. agglomerans could be the result of P. syringae using other, more spatially confined resources compared to P. agglomerans. Alternatively, if both strains were to use similar resources, P. syringae would require higher concentrations of some key resources. Such ideas could be pursued in a future study that combines spatial point-pattern analysis with data from bacterial bioreporters for nutrient availability (Leveau 2001) or micrometer-scale metabolic profiling (Fang and Dorrestein 2014) of the phyllosphere, both of which would provide high-resolution spatial information on nutrient availability along the leaf surface.

The spatial distribution of bacteria not considering their species exhibited small-scale aggregation of cells in all samples up to 4 μm followed by an almost linear decay in prevalence that disappeared in a background noise at almost 90 μm (Fig. 3D).

The general pattern of scarcity of cells towards larger scales (above 50 μm, Fig. 3A–D) is more difficult to explain. A classical interpretation would be a regularity in the environment, e.g. the undifferentiated epidermal cells in our experiments. This is, however, difficult to verify given their complex shape and the probable multitude of additional interfering interactions of bacteria with their environment. A non-biological explanation is that a bias arose from the bandwidth of the Gaussian smoothing kernel used for the inhomogeneous pair correlation functions. The inhomogeneous method applied here is known to be biased downwards and can give unexpected results especially for regular patterns (Baddeley, Moller and Waagepetersen 2000). Although our choice of 110 μm for the bandwidth gave the most stable results for 50 randomly chosen images from our data set, it is possible that it worked better for the sparser P. syringae patterns than for the denser P. agglomerans patterns. Additionally, the inhomogeneous pair correlation function requires the points to be ‘second-order intensity reweighed stationary’ (Baddeley, Moller and Waagepetersen 2000), an assumption probably violated by our complex bacterial colonization patterns on bean leaves (Baddeley, pers. comm.). Nevertheless, we recommend the use of the inhomogeneous pair correlation. Given (a) its non-cumulative nature which puts it ahead of other methods such as the Ripley's K-function (Ripley 1976; Wiegand and Moloney 2014), (b) its ability to look at distance beyond the nearest neighbor of a point and (c) its ability to (within limits) account for heterogeneity in the point pattern, it is the best available method for the data at hand in our study.

Interactions between bacterial individuals of different species

The interspecific analyses of mix-inoculated P. agglomerans and P. syringae cells revealed a clustering of P. agglomerans cells within 10 μm around individuals of P. syringae and vice versa (Fig. 4A and B). Clustering was found in more than 60% of our samples. A typical pattern that exhibited this clustering is shown in Fig. 1E. In the example pattern of P. syringae near P. agglomerans pictured in Fig. 5, the inhomogeneous pair correlation was very similar to the overall results in Fig. 4B. In this particular sample, P. syringae was less abundant than P. agglomerans (176 P. syringae cells against 1380 of P. agglomerans) and the P. syringae clusters were small (10 μm in diameter and less, Fig. 5). Similar patterns were found in many other samples. From the pair correlation function (Fig. 5), we can see that P. syringae typically aggregated up to 11 μm near P. agglomerans cells, for example in the large P. agglomerans colony (left inset in Fig. 5). The aggregation from 18 to 23 μm is only very weak and probably mostly due to two colonies at the left edge of the large P. agglomerans colony and maybe a colony surrounded by a half moon-shaped P. agglomerans colony (right inset in Fig. 5). In summary, the pattern observed in this particular sample captures important aspects of the interactions between the two species that seem to be typical for bean leaves in our experiments.

Figure 5.

Left: spatial pattern of P. agglomerans (gray points) and P. syringae (black points) on a bean leaf surface. Right: the inhomogeneous pair correlation function (PCF, solid line) and 95% simulation envelope (broken lines) for P. syringae cells near P. agglomerans cells derived from the pattern (interpretation of the PCF same as in Fig. 1). The spatial pattern is typical in the sense that the PCF result well resembles the general results for this interaction shown in Fig. 4B.

In experiments where P. syringae had the opportunity to develop on the bean leaves for 92 h under 100% humidity at room temperature prior to the arrival of P. agglomerans, P. syringae was much more abundant than P. agglomerans. The late-arriving GFP-labeled P. agglomerans cells only developed poorly (84.2% P. syringae versus 15.8% P. agglomerans, averaged over all samples). Here, P. syringae probably was able to exclude P. agglomerans from successful establishment by depleting patches rich in resources prior to the arrival of P. agglomerans. Such processes have recently been shown in a study on the reproductive success of P. agglomerans on pre-colonized bean leaves (Remus-Emsermann, Kowalchuk and Leveau 2013). In this setting, aggregation of P. agglomerans around P. syringae was observed in 60% of our samples and up to 20–30 μm from a typical P. syringae individual and vice versa (Fig. 4C and D).

Summarizing the results from our interspecific studies, the two strains settle in the same regions of a leaf and do not seem to avoid each other. The maximum range of interactions leading to a co-aggregation of the two species lies around 20–30 μm. In the majority of our samples, however, we found no significant interspecific aggregation at scales larger than 10 μm, a value that evidently fits well the value of 10 times the bacterial cell diameter suggested by Frankling and Mills (2007).

Bi-variate analyses of bacteria near bean leaf surface features

Due to the heterogeneous distribution of suitable sites on the leaf surface, interactions between bacteria are usually not the only determinant of bacterial distribution in the phyllosphere.

In our study, the grooves, or more precisely the intersection points of grooves between epidermal cells of the bean leaf were frequently attracting bacteria on a small scale up to 12 μm (Fig. 6A). Attraction of bacteria to grooves was apparent in about 45% of our samples. This aggregation of microbial colonizers of the phyllosphere has been frequently reported (Diem 1974; Blakeman 1985; Davis and Brlansky 1991; Leveau 2001; Monier and Lindow 2004). The grooves between epidermal cells have been hypothesized to retain water longest during periods of evaporation (Kinkel 1997; Leveau 2001). Considering that the presence of water on leaf surfaces can stimulate leaching of substances from inside the leaf (Tukey 1970) and that nutrients in solution will accumulate in regions that retain evaporating water the longest, it becomes obvious why plant leaf surface features such as the grooves could be a good proxy for explaining microbial success and therefore colonization patterns in the phyllosphere. Nevertheless, it remained unclear how much of the bacterial aggregation on small scales can be accounted to accumulation of nutrients in the grooves and how much is due to other processes such as a physical or gravitational groove effect.

We found no strong signs of bacterial aggregation near stomata which is in line with the study of Monier and Lindow (2004) who studied P. syringae on bean leaves. In fact, we rather detected a slight tendency of bacteria to avoid stomata which lasted up to 35 μm (Fig. 6B). Then again, stomata have been reported for a long time to be positively correlated with high densities of leaf colonizers (Miles, Daines and Rue 1977; Blakeman 1985; Mew and Vera 1986; Timmer, Marois and Achor 1987; Mansvelt and Hattingh 1989). In these studies, incubation time was longer (3–30 days) and in the studies of Miles, Daines and Rue (1977), Timmer, Marois and Achor (1987) and Mansvelt and Hattingh (1989) incubation was performed under less humid conditions. We conclude that interactions with stomata may occur on bean leaves but they are less important under the conditions tested in our experiments and that these interactions are more important in less humid environments. Under such conditions, stomatal transpiration has been shown to produce highly localized zones of elevated humidity (Burkhardt et al., 1999) which will facilitate bacterial growth under otherwise dry conditions. Further studies of the spatial distribution of bacteria on dry leaves could reveal the spatial scale up to which this localized increase in humidity is effective.

On a larger scale, we observed an aggregation of bacteria within a 0–60 μm (less often 100 μm) neighborhood around glandular trichomes in up to 16% of our samples (Fig. 6C). This interaction has also been reported before (Blakeman 1985; Leveau 2001; Monier and Lindow 2004; Yadav, Karamanoli and Vokou 2005), but here we can for the first time quantify the range of this interaction. In the literature, the effect is usually explained by nutritious exudates of the glandular trichomes (Ascensão and Pais 1998; Monier and Lindow 2004) or their ability to retain water droplets (Brewer, Smith and Vogelmann 1991) which also could increase nutrient leaching from the leaf interior (Schönherr and Baur 1996).

We also found significant aggregation of bacteria within up to 120 μm around hooked trichomes but at any spatial scale aggregation was not observed in more than about 15% of our samples (Fig. 6D). Interestingly, aggregation was most prevalent between 60–100 μm around hooked trichomes, suggesting an interplay between an attracting (e.g. increased water availability) and a repulsing process (e.g. gravitational, away from elevated trichomes on veins). Aggregation of bacteria near hooked trichomes has been reported before on bean leaves (Leveau 2001; Monier and Lindow 2004). These studies mention a thinner cuticle and the presence of more nutrients compared to undifferentiated epidermal cells as probable properties that facilitate bacterial growth near hooked trichomes.

Bacteria were significantly aggregated around vein cells but usually in not more than 10% of our samples that had vein cells in them (Fig. 6E and F). Both the homogeneous and the inhomogeneous pair correlation functions detected aggregation at scales up to 100 μm. The most obvious difference between the two functions was that the inhomogeneous pair correlation function (Fig. 6F) found no clear signs of aggregation of bacteria within 8 μm around the centers of vein cells. This small-scale randomness could be explained by a process in which the large-scale attraction of bacteria towards veins is locally overruled by the small-scale aggregation of cells in the grooves between vein cells. However, it remained unclear why this effect is not also visible in Fig. 6E. The association of bacterial colonizers of leaves with leaf veins has been reported frequently and has usually been attributed to veins being regions of increased water availability, leakage and nutrient availability (Canny 1990; Leveau and Lindow 2001; Axtell and Beattie 2002; Monier and Lindow 2004). Glandular trichomes, which also caused attraction of bacteria, were often located on veins and may thus be sufficient to explain the attraction of bacteria towards veins. Disentangling such facilitative processes not directly related to the veins should be subject of further studies.

CONCLUSIONS

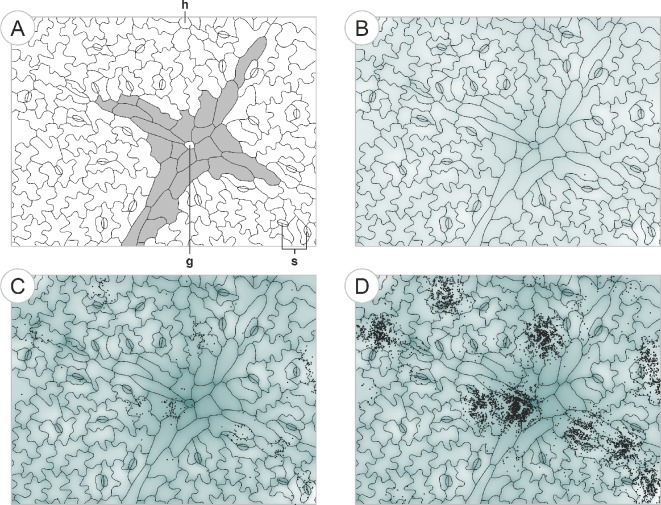
In this study, we showed how point-pattern analysis can improve our understanding of micro-ecological processes in the phyllosphere. Most importantly, we determined spatial scales or distances of major importance to processes that shape the spatial distribution of bacteria on bean leaves. Where the uni-variate analysis (Fig. 3) mostly informed about the spatial structure of bacterial colonization patterns, the bi-variate analyses (Figs 4 and 6) allowed for an estimation of the operational range of interactions between two co-occurrent bacterial strains or between bacteria and structural elements of the leaf surface. Our study is the first to report such interaction distances for bacteria and plant leaves. These interactions are not static but may develop in time as discussed for example for bacterial interactions with stomata. The strength of the underlying processes ranged from weak effects, such as the tendency of bacteria to avoid stomata, to strong effects such as the aggregation of bacteria in the grooves between epidermal cells. The co-aggregation of individuals of P. agglomerans and P. syringae suggests that these two strains facilitate each other or at least exploit resources in the phyllosphere in similar ways during early phases of colonization. It is important to consider how all these processes interact with each other, facilitating or canceling each other out, thereby leading to the complex colonization patterns of bacteria observed in the phyllosphere. Based on the results of this study, we developed a conceptual model that gives an impression of how all these processes might come together to create the bacterial colonization patterns observable in the bean phyllosphere (Fig. 7). We assert that our findings are primarily valid for P. agglomerans and P. syringae on bean leaves and that the interaction regime of other microbial colonizers on different hosts may differ from our results. This may be especially true for bacterial development under less humid conditions than in our experiments. In conclusion, our study is a starting point of a series of future experiments that will use spatial point-pattern analysis to unravel the significance of the different spatial interactions between microbial leaf colonizers and their environment.

Figure 7.

A conceptual model of bacterial development based on the findings of this study. We used a simple simulation model based on the strength and range of bacterial interactions on bean leaves determined in our study in order to determine if these processes were sufficient to generate colonization patterns similar to the observed ones. The simulated colonization pattern in (D) suggests that the concert of many different interactions at different spatial scales is able to explain the complex bacterial colonization patterns observed on bean leaves. (A): the starting ‘landscape’. Epidermal structure of a young bean leaf. An x-shaped leaf vein (shaded in grey) locally approaches the leaf surface from the leaf interior with a glandular trichome (g) at the intersection. The vein is surrounded by stomata (s) and undifferentiated epidermal cells (‘puzzle pieces’). The base of a hooked trichome (h) can be seen near the middle of the upper boundary. (B): prior to colonization by microbes, resources (shaded areas) gathered on the leaf surface by processes such as epidermal leaching, especially near veins grooves between epidermal cells, and excretion by glandular trichomes. Single bacterial colonizers arrive on the leaf. (C): in the course of time, bacterial colonizers reproduce more successfully at locations rich in resources. Additionally, bacterial cells tend to get trapped near the grooves either by gravitational processes or by the increased density of leaf surface area that decreases cell motility. (D): further bacterial growth. After 20 h, growth stops in locations where the resource requirements reach the level of leaching of new resources from the leaf interior. Colonization of new resource-rich regions allows further growth of the bacterial population.

SUPPLEMENTARY DATA

Supplementary data is available at FEMSEC online.

FUNDING

This research was part of the Research Training Group 1644—Scaling Problems in Statistics funded by the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG).

Conflict of interest statement: None declared.