A hybrid model for combining case-control and cohort studies in systematic reviews of diagnostic tests

Abstract

Systematic reviews of diagnostic tests often involve a mixture of case-control and cohort studies. The standard methods for evaluating diagnostic accuracy only focus on sensitivity and specificity and ignore the information on disease prevalence contained in cohort studies. Consequently, such methods cannot provide estimates of measures related to disease prevalence, such as population averaged or overall positive and negative predictive values, which reflect the clinical utility of a diagnostic test. In this paper, we propose a hybrid approach that jointly models the disease prevalence along with the diagnostic test sensitivity and specificity in cohort studies, and the sensitivity and specificity in case-control studies. In order to overcome the potential computational difficulties in the standard full likelihood inference of the proposed hybrid model, we propose an alternative inference procedure based on the composite likelihood. Such composite likelihood based inference does not suffer computational problems and maintains high relative efficiency. In addition, it is more robust to model mis-specifications compared to the standard full likelihood inference. We apply our approach to a review of the performance of contemporary diagnostic imaging modalities for detecting metastases in patients with melanoma.

1 Introduction

Comparative effectiveness research relies fundamentally on the accurate assessment of clinical outcomes. Rapid escalations in the cost of medical diagnostic tests, together with growth in the number of available instruments have generated an increasing need for scientifically rigorous methods for comparing diagnostic tests in clinical practice. Many quantitative comparisons of diagnostic tests are based on systematic reviews of diagnostic accuracy. In such reviews, the performance of a diagnostic test is often summarized by paired indices, such as sensitivity and specificity, or positive and negative predictive values (PPV and NPV)^1,2.

The procedure of pooling paired indices is not straightforward because of three important characteristics of such data. The first is that the estimated sensitivities and specificities are typically negatively correlated between studies³. A possible cause of this negative correlation is that studies may have used different thresholds to define positive and negative test results. The second important characteristic is the substantial between-study heterogeneity in paired indices^4,5,6. Such heterogeneity may arise due to differences in study population characteristics, variability of assessment, and other factors. The third characteristic is that some prevalence-dependent indices, such as predictive values, i.e., PPV and NPV, require knowledge about disease prevalence that is not estimable in case-control studies. In addition, it has been suggested that sensitivity and specificity can be correlated with disease prevalence. One of the reasons is that the classification of disease status is typically based on a continuum of measurable traits. For classification of disease status based on continuous traits, the underlying distribution of the continuous traits not only determines disease prevalence, but also determines misclassification rates (i.e., sensitivity and specificity), because subjects with true levels close to the cut-point are more likely to be misclassified^7,8. If the underlying distributions of continuous traits are heterogeneous across studies, the sensitivities and specificities are likely to be correlated with the prevalence.

A variety of methods have been proposed to account for the first two characteristics of data encountered in systematic reviews of diagnostic test accuracy, see a recent review by Ma et al.⁹. The current methods can be classified into two categories. The first category consists of methods based on a summary receiver operating characteristic curve generated from the study data^10,4 and hierarchical summary receiver operating characteristic model^11,6,12,13. The second category consists of methods that use bivariate general mixed-effects model and bivariate generalized linear mixed-effects model (GLMM) to describe sensitivity and specificity simultaneously^{14,15,3,16,13,17,18}. Interestingly, the hierarchical summary receiver operating characteristic model and the bivariate GLMM have been found to be very closely related, and even identical in the absence of covariates^19,20.

More recently, a trivariate GLMM has been proposed that can simultaneously account for all three aforementioned characteristics of the data in systematic review of diagnostic test accuracy⁸. The trivariate GLMM jointly models disease prevalence with diagnostic test sensitivity and specificity based on the data from the cohort studies. Based on the estimated disease prevalence, the clinically meaningful indices, such as PPV and NPV, are immediately available. However, the trivariate GLMM also has a few limitations. First, systematic reviews often involve a mixture of case-control and cohort studies; whereas trivariate GLMM is restricted to cohort studies. In this situation, discarding all of the case-control studies can lead to a substantial loss of efficiency. Secondly, the correlations among disease prevalence, sensitivity and specificity need to be estimated, and three-dimensional integrals has to be evaluated in the likelihood. In this case, non-convergence problems and singular information matrices have been reported when maximizing the likelihood, especially when the number of studies is relatively small¹⁷. Although modern computational techniques such as Laplace or adaptive Gaussian quadrature approximation are available in software, such as NLMIXED in SAS (SAS Institute Inc., Cary, NC) and ADMB (Automatic Differentiation Model Builder), these approximations may still have non-negligible approximation errors and the estimates may be sensitive to initial values, leading to unstable or unreproducible results. To the best of our knowledge, there is currently no satisfactory solution to these limitations.

Our motivating study is a systematic review of modern diagnostic imaging modalities for surveil-lance of melanoma patients. Melanoma is the least common but most deadly type of skin cancer and occurs in melanocytes, which are cells that produce the skin pigment melanin. Melanoma accounts for more than 75% of deaths related to skin cancer²¹. Sentinel lymph node biopsy is the gold standard for pathological staging of metastasis in melanoma. Diagnostic imaging is often utilized following the surgical treatment of melanoma in patients who are at high risk of disease recurrence. The type of imaging and the interval of testing which is the most effective and cost-effective have not been defined. The goal of surveillance imaging is to detect melanoma recurrence in regional lymph nodes and/or distant sites at a point when it remains treatable and/or possible surgically resectable. Current diagnostic imaging modalities for the surveillance of melanoma patients include ultrasonography (US), computed tomography (CT), positron emission tomography (PET) and a combination of both (PET-CT). It is critical to assess and compare the performance of these contemporary diagnostic imaging modalities to compare accuracy in various clinical settings and to support clinical decision making. A systematic review of published studies has examined diagnostic modality characteristics and identified 98 studies from 10, 528 patients with melanoma between January 1, 1990 and June, 30, 2009²². Out of 98 studies, 57 were cohort studies and the numbers of case-control and cohort studies stratified by type of cancer and type of imaging modality are summarized in Table S1 in the supplementary materials. The original analysis in Xing et al.²² treated the case-control studies and cohorts equivalently, and ignored the information on prevalence of melanoma. Consequently, clinically more relevant measures, such as the overall PPV and NPV, cannot be obtained. In this paper, we propose a hybrid multivariate random effects model to combine case-control and cohort studies. Such a strategy of joint modeling fully utilizes the data and can provide estimates of measures related to disease prevalence (e.g., PPV and NPV). However, the standard likelihood-based inference of the proposed hybrid model is still subject to the aforementioned non-convergence problem and computational difficulty. Motivated by the fact that the commonly used measures of diagnostic tests (e.g., sensitivity, specificity, PPV and NPV) do not involve correlation parameters, we propose an alternative inference procedure based on the composite likelihood^23,24 where a working independence assumption is adopted. Simulation studies suggest that the composite likelihood, which avoids an explicit modeling of the dependence structure, does not lead to a substantial efficiency loss. Therefore, the composite likelihood inference is a practical solution to the non-convergence problem and computational difficulty. Furthermore, the inference based on the composite likelihood only relies on the marginal normality of logit prevalence, sensitivity and specificity. Hence the composite likelihood method can be more robust than the standard full likelihood inference to mis-specifications of the joint distribution. In fact, the composite likelihood has been widely applied to applications such as longitudinal data analysis and multivariate survival data analysis^25,26,27,28. However, to the best of our knowledge, the present paper is the first application of composite likelihood in systematic reviews of diagnostic tests.

This paper is organized as follows. In Section 2, we describe the proposed hybrid model and two inference procedures, namely the full likelihood and composite likelihood methods. In Section 3, we conduct simulation studies to compare these two inference procedures. We apply our method in Section 4 to a systematic review of the accuracy of contemporary diagnostic imaging modalities for detecting metastases in patients with melanoma. We provide a brief discussion in Section 5.

2 Statistical Methodology

Denote D and T as the respective disease status ascertained by a gold standard and the result from a diagnostic test under investigation (1: positive; 0: negative). Sensitivity (Se) and specificity (Sp) are respectively the probability of a positive test result in a subject with the disease and the probability of a negative test result in a subject who does not have the disease, i.e., Se = Pr(T = 1|D = 1) and Sp = Pr(T = 0|D = 0). The positive predictive value (PPV) and negative predictive value (NPV) are the probability of having the disease given a positive test result and the probability of not having the disease given a negative test result, i.e., PPV = Pr(D = 1|T = 1) and NPV = Pr(D = 0|T = 0), respectively.

We consider a systematic review of diagnostic test accuracy with m studies. For simplicity of notations, assume that the first m₁ studies are case-control studies and the remaining m₂ studies are cohort studies (m = m₁ + m₂). Table 1 summarizes typical data from the ith study by a 2 × 2 table²⁹. Specifically, denote n_i11, n_i00, n_i01, and n_i10 as the number of true positives, true negatives, false negatives, and false positives, respectively, and denote n_i1 = n_i11 + n_i01 and n_i0 = n_i10 + n_i00 as the numbers of subjects with and without the disease, respectively. Let π_i, Se_i and Sp_i be the study-specific disease prevalence, and diagnostic test sensitivity and specificity, respectively. Note that π_i is estimable only in cohort studies, i.e., i = m₁ + 1, . . . , m.

Table 1.

Possible data outcomes and probabilities for study i (i=1, . . ., m). In each cell, the first row shows the observed count, the second row shows the corresponding conditional probability of test outcome given disease status in case-control studies, or the corresponding probability of cell memberships in cohort studies.

	Disease Status by a Gold Standard Test (D)
Diagnostic test (T)	1a. Case-control studies (i=1, 2, . . ., m1)		1b. Cohort studies (i=m1+1, m1+2, . . ., m)
	Disease (+)	Non-disease (−)	Disease (+)	Non-disease (−)
Positive (T+)	ni11 Sei	ni10 1 – Spi	ni11 πiSei	ni10 (1 – πi) (1 – Spi)
Negative (T−)	ni01 1 – Sei	ni00 Spi	ni01 πi (1 – Sei)	ni00 (1 – πi)Spi
Total	ni1 1	ni0 1	n i1 π i	ni0 1 – πi

In practice, there is often significant heterogeneity in the study-specific disease prevalence, and test sensitivity and specificity across studies due to differences in study population characteristics, assessment methods and intervals, and other related factors. Additionally, in practice, diagnostic test sensitivity and specificity are often negatively correlated, and such sensitivity and specificity can be correlated with disease prevalence in cohort studies^7,8. To account for these characteristics and to effectively combine case-control and cohort studies, we propose the following hybrid generalized linear mixed-effects model (referred to as the hybrid model hereafter). This model can be formulated in two stages. The first stage specifies the probability of observing the data described in Table 1 for a given study-specific disease prevalence (for a cohort study only), and diagnostic test sensitivity and specificity,

$$\begin{array}{cc}\hfill & \text{for}i=1,\dots ,m_1,(\mathrm{i}.\mathrm{e}.,\text{case-control studies})\hfill \\ \hfill & (n_{i11},n_{i00})\mid ({\mathrm{Se}}_i,{\mathrm{Sp}}_i)\sim \text{Binomial}(n_{i1};{\mathrm{Se}}_i)\times \text{Binomial}(n_{i0};{\mathrm{Sp}}_i);\hfill \\ \hfill & \text{for}i=m_1+1,\dots ,m,(\mathrm{i}.\mathrm{e}.,\text{cohort studies})\hfill \\ \hfill & (n_{i11},n_{i10},n_{i01},n_{i00})\mid ({\pi }_i,{\mathrm{Se}}_i,{\mathrm{Sp}}_i)\sim \text{Multinomial}(n_i;{\pi }_i{\mathrm{Se}}_i,(1-{\pi }_i)(1-{\mathrm{Sp}}_i),{\pi }_i(1-{\mathrm{Se}}_i),(1-{\pi }_i){\mathrm{Sp}}_i),\hfill \end{array}$$ (1)

where n_i is the number of subjects in the ith study, and Binomial(·; ·) and Multinomial(·; ·) are defined as

$$\begin{array}{c}\hfill \text{Binomial}(y;n,p)=\left(\begin{array}{c}\hfill n\hfill \\ \hfill y\hfill \end{array}\right)p^y{(1-p)}^{n-y}\text{and}\hfill \\ \hfill \text{Multinomial}(y_1,y_2,y_3,y_4;n,p_1,p_2,p_3,p_4)=\left(\begin{array}{c}\hfill n\hfill \\ \hfill y_1,y_2,y_3,y_4\hfill \end{array}\right)p_1^{y_1}{p}_2^{y_2}{p}_3^{y_3}{p}_4^{y_4},\hfill \end{array}$$

where p₁ + p₂ + p₃ + p₄ = 1 and y₁ + y₂ + y₃ + y₄ = n. At the second stage, a random effects model is assumed to take into consideration the heterogeneity between studies, the correlation between (Se_i, Sp_i) for i = 1, . . . , m₁ and the correlations among (π_i, Se_i, Sp_i) for i = m₁ + 1, . . . , m,

$$\begin{array}{cc}\hfill & \text{for}i=1,\dots ,m_1,(\mathrm{i}.\mathrm{e}.,\text{case-control studies})\hfill \\ \hfill & \mathrm{g}\left({\mathrm{Se}}_i\right)={\mathbf{X}}_{\mathbf{i}}^T{\beta }_1{+}_{i1},\mathrm{g}\left({\mathrm{Sp}}_i\right)={\mathbf{Z}}_{\mathbf{i}}^T{\beta }_2+{\mu }_{i2};\hfill \\ \hfill & \text{for}i=m_1+1,\dots ,m,(\mathrm{i}.\mathrm{e}.,\text{cohort studies})\hfill \\ \hfill & \mathrm{g}\left({\pi }_i\right)={\mathbf{W}}_{\mathbf{i}}^T{\beta }_0{+}_{i0},\mathrm{g}\left({\mathrm{Se}}_i\right)={\mathbf{X}}_{\mathbf{i}}^T{\beta }_1+{\mu }_{i1},\mathrm{g}\left({\mathrm{Sp}}_i\right)={\mathbf{Z}}_{\mathbf{i}}^T{\beta }_2+{\mu }_{i2},\hfill \end{array}$$ (2)

where g(·) is a known link function such as a logit function, W_i, X_i, Z_i are vectors of study-level covariates, possibly overlapping, related to π_i, Se_i and Sp_i respectively. Examples of such study-level covariates include type of disease (e.g., regional cancer versus distant cancer), and the Quality Assessment of Diagnostic Accuracy Studies (QUADAS) scale³⁰. Here we model specificity (i.e., Pr(T = 0|D = 0)) instead of the probability Pr(T = 1|D = 0) because correctly identifying the disease status (i.e., T = 0) given a patient without disease (i.e., D = 0) is considered as a “success event”. The random intercepts (μ_i1, μ_i2) for a case-control study and (μ_i0, μ_i1, μ_i2) for a cohort study are assumed to respectively follow a bivariate normal distribution with mean zero and covariance matrix Σ₁ for i = 1, . . . , m₁, and a trivariate normal distribution with mean zero and covariance matrix Σ₂ for i = m₁ + 1, . . . , m, defined as

$${\Sigma }_1=\left(\begin{array}{cc}\hfill {\tau }_1^2\hfill & \hfill {\rho }_{12}{\tau }_1{\tau }_2\hfill \\ \hfill \hfill & \hfill {\tau }_2^2\hfill \end{array}\right)\text{and}{\Sigma }_2=\left(\begin{array}{ccc}\hfill {\tau }_0^2\hfill & \hfill {\rho }_{01}{\tau }_0{\tau }_1\hfill & \hfill {\rho }_{02}{\tau }_0{\tau }_2\hfill \\ \hfill \hfill & \hfill {\tau }_1^2\hfill & \hfill {\rho }_{12}{\tau }_1{\tau }_2\hfill \\ \hfill \hfill & \hfill \hfill & \hfill {\tau }_2^2\hfill \end{array}\right).$$

The parameters ${\tau }_0^2$, ${\tau }_1^2$ and ${\tau }_2^2$ capture the between-study heterogeneity in disease prevalence, and test sensitivities and specificities, respectively, and the parameters ρ₀₁, ρ₀₂ and ρ₁₂ describe the correlations between the respective random effects (π_i, Se_i), (π_i, Sp_i) and (Se_i, Sp_i) in the transformed scale, respectively.

To simplify the notations and make our discussion concrete, we assume W_i = X_i = Z_i = 1 and choose a logit link function. In this case, β₀, β₁ and β₂ specify the overall disease prevalence, and diagnostic test sensitivity and specificity (in logit scale), respectively. Besides sensitivity and specificity, other clinically relevant measures, e.g. the overall PPV and NPV, can be calculated as

$$\mathrm{PPV}=\frac{e^{{\beta }_0+{\beta }_1}(1+e^{{\beta }_2})}{e^{{\beta }_0+{\beta }_1}(1+e^{{\beta }_2})+(1+e^{{\beta }_1})}\text{and}\mathrm{NPV}=\frac{e^{{\beta }_2}(1+e^{{\beta }_1})}{e^{{\beta }_2}(1+e^{{\beta }_1})+e^{{\beta }_0}(1+e^{{\beta }_2})}.$$ (3)

In practice, a high NPV is required for a diagnostic test to be useful in ruling out disease, and a high PPV is required for a diagnostic test to be useful in detecting disease.

For simplicity of notation, denote ${\theta }_0={({\beta }_0,{\tau }_0^2)}^T$, ${\theta }_1={({\beta }_1,{\tau }_1^2)}^T$, ${\theta }_2={({\beta }_2,{\tau }_2^2)}^T$ and ρ = (ρ₀₁, ρ₀₂, ρ₁₂)^T Under the hybrid model assumption, the log likelihood function is

$$\begin{array}{cc}\hfill & \log L({\theta }_0,{\theta }_1,{\theta }_2,\rho )\hfill \\ \hfill =& \sum _{i=1}^{m_1}\log \mathrm{Pr}(n_{i00},n_{i11};{\theta }_1,{\theta }_2,{\rho }_{12})+\sum _{i=m_1+1}^m\log \mathrm{Pr}(n_{i00},n_{i01},n_{i11};{\theta }_0,{\theta }_1,{\theta }_2,\rho )\hfill \\ \hfill =& \sum _{i=1}^{m_1}\log \int \int \text{Binomial}(n_{i00},{\mathrm{Se}}_i)\times \text{Binomial}(n_{i1};{\mathrm{Se}}_i){\varphi }_1({\mathrm{Se}}_i,{\mathrm{Sp}}_i;{\theta }_1,{\theta }_2,\rho {\zeta }_{12})d{\mathrm{Se}}_{i}d{\mathrm{Sp}}_i+\sum _{i=m_1+1}^m\log \int \int \int \text{Multinomial}(n_{i11},n_{i10},n_{i01};{\pi }_i\mathrm{Se}{\zeta }_i,(1-{\pi }_i)(1-{\mathrm{Sp}}_i),{\pi }_i(1-{\mathrm{Se}}_i))\times {\varphi }_2({\pi }_i,{\mathrm{Se}}_i,{\mathrm{Sp}}_i;{\theta }_0,{\theta }_1,{\theta }_2,\rho )d{\pi }_{i}d{\mathrm{Se}}_{i}d{\mathrm{Sp}}_i,\hfill \end{array}$$ (4)

where ϕ₁(·, ·; θ₁, θ₂, ρ₁₂) is the bivariate logit normal density with mean (β₁, β₂)^T and covariance matrix Σ₁ and ϕ₂(·, ·, ·; ₀, θ₁, θ₂,ρ) is the trivariate logit normal density with mean (β₀, β₁,β₂)^T and covariance matrix Σ₂ at the logit scale. The integrals in equation (4) do not have a closed-form and have to be calculated using numerical methods such as adaptive Gaussian quadrature³¹. In practice, the package NLMIXED in SAS version 9.3 (SAS Institute Inc., Cary, NC) can be used to maximize the approximation to the log likelihood function in equation (4). Other methods such as automatic differentiation model builder (ADMB; http://admb-project.org) can also be used to approximate this likelihood.

Although conceptually straightforward, the standard maximum full likelihood method (hereafter referred to as the FL method) faces the non-convergence and computational problems as described in the introduction section. These problems are due to the two- and three-dimensional integrals in the likelihood function L(θ₀, θ₁, θ₂,ρ) and the need of estimating correlation parameters ρ¹⁷. In fact, the FL method encounters the issues of non-convergence and a singular covariance matrix when used to analyze the motivating study on metastases. Specifically, for the subgroup of the PET-CT test with a total of 8 studies, we failed to obtain the maximum likelihood estimates as the likelihood in equation (4) contains 9 parameters. For the subgroup of the CT test with a total of 12 studies, the convergence of the FL method heavily depends on the choice of the initial values: the FL method leads to non-convergent results for some default choice of initial values. For the subgroup of the PET test with a total of 29 studies, a “poor” choice of initial value results in a singular covariance matrix. These results are summarized in Table S2 in the supplemental material.

As suggested in equation (3), the commonly used measures of diagnostic tests are functions of (β₀, β₁, β₂) only and do not involve the correlation parameters. Therefore, we propose an alternative inference procedure that focuses on (β₀, β₁, β₂) without inferring ρ. The key of the proposed procedure is the factorization of the multinomial likelihood function as a product of three independent binomial likelihoods. Specifically, the likelihood function based on a cohort study for given (π_i, Se_i, Sp_i) can be factored as

$$\text{Multinomial}(n_{i11},n_{i10},n_{i01},n_{i00};{\pi }_i{\mathrm{Se}}_i,(1-{\pi }_i)(1-{\mathrm{Sp}}_i),{\pi }_i(1-{\mathrm{Se}}_i),(1-{\pi }_i){\mathrm{Sp}}_i)\propto \text{Binomial}(n_{i1}\mid n_i;{\pi }_i)\times \text{Binomial}(n_{i11}\mid n_{i1};{\mathrm{Se}}_i)\times \text{Binomial}(n_{i00}\mid n_{i0};{\mathrm{Sp}}_i),$$

where i = m₁ + 1, . . . , m. Given the above factorization, we can construct a composite likelihood function under a working independence assumption. Mathematically, by letting ρ₀₁ = ρ₀₂ = ρ₁₂ = 0 in equation (4), we obtain the following composite likelihood function

$$\log L_c({\theta }_0,{\theta }_1,{\theta }_2)=\log L_0\left({\theta }_0\right)+\log L_1\left({\theta }_1\right)+\log L_2\left({\theta }_2\right)$$ (5)

where

$$\begin{array}{cc}\hfill \log L_0\left({\theta }_0\right)=& \sum _{i=m_1+1}^m\log \mathrm{Pr}(n_{i1}\mid n_i;{\theta }_0)=\sum _{i=m_1+1}^m\left\{\log \int \text{Binomial}(n_{i1}\mid n_i,{\pi }_i)\varphi ({\pi }_i;{\theta }_0)d{\pi }_i\right\},\hfill \\ \hfill \log L_1\left({\theta }_0\right)=& \sum _{i=1}^m\log \mathrm{Pr}(n_{i11}\mid n_{i1};{\theta }_1)=\sum _{i=1}^m\left\{\log \int \text{Binomial}(n_{i11}\mid n_{i1},{\mathrm{Se}}_i)\varphi ({\mathrm{Se}}_i;{\theta }_1)d{\mathrm{Se}}_i\right\},\hfill \\ \hfill \log L_2\left({\theta }_2\right)=& \sum _{i=1}^m\log \mathrm{Pr}(n_{i00}\mid n_{i0};{\theta }_2)=\sum _{i=1}^m\left\{\log \int \text{Binomial}(n_{i00}\mid n_{i0},{\mathrm{Sp}}_i)\varphi ({\mathrm{Sp}}_i;{\theta }_2)d{\mathrm{Sp}}_i\right\},\hfill \end{array}$$

and ϕ(·; θ_j) is the univariate logit normal distribution with mean β_j and variance ${\tau }_j^2$ in logit scale, and is indexed by θ_j (j = 0, 1, 2).

Since each component of the composite likelihood function, log L_j(θ_j) (j = 0, 1, 2), is a true log marginal likelihood, the score equation of composite likelihood is unbiased. Consequently, the estimator $({\tilde{\theta }}_0,{\tilde{\theta }}_1,{\tilde{\theta }}_2)$ defined as a solution of the score equation, is consistent and asymptotically normal. However, the conventional covariance matrix estimator ${{\mathcal{I}}_c({\tilde{\theta }}_0,{\tilde{\theta }}_1,{\tilde{\theta }}_2)\}}^{-1}$, where ${\mathcal{I}}_c({\theta }_0,{\theta }_1,{\theta }_2)=-{\partial }^2\log L_c({\theta }_0,{\theta }_1,{\theta }_2)∕\partial {({\theta }_0,{\theta }_1,{\theta }_2)}^2$, is no longer valid because $E\left\{{\mathcal{I}}_c({\theta }_0,{\theta }_1,{\theta }_2)\right\}$ is not the covariance matrix of ∂L_c(θ₀, θ₁, θ₂)/∂(θ₀, θ₁, θ₂) in the presence of correlations among (π_i, Se_i, Sp_i).

Assume m₂/m → r > 0 as m → ∞. As shown in Section 1 of the supplementary material, the estimator $({\tilde{\theta }}_0,{\tilde{\theta }}_1,{\tilde{\theta }}_2)$ is asymptotically normal with mean zero and symmetric covariance matrix

$$\Sigma =\left(\begin{array}{ccc}\hfill r^{-1}{{\mathbf{I}}_{00}}^{-1}\hfill & \hfill r^{-1∕2}{{\mathbf{I}}_{00}}^{-1}{\mathbf{I}}_{01}{{\mathbf{I}}_{11}}^{-1}\hfill & \hfill r^{-1∕2}{{\mathbf{I}}_{00}}^{-1}{\mathbf{I}}_{02}{{\mathbf{I}}_{22}}^{-1}\hfill \\ \hfill \hfill & \hfill {{\mathbf{I}}_{11}}^{-1}\hfill & \hfill {{\mathbf{I}}_{11}}^{-1}{\mathbf{I}}_{12}{{\mathbf{I}}_{22}}^{-1}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill {{\mathbf{I}}_{22}}^{-1}\hfill \end{array}\right),$$

where

$${\mathbf{I}}_{00}=E\left\{-\frac{1}{m_2}\frac{{\pi }^2\log L_0\left({\theta }_0\right)}{\partial {{\theta }_0}^2}\right\},{\mathbf{I}}_{\mathbf{jj}}=E\left\{-\frac{1}{m}\frac{{\partial }^2\log L_j\left({\theta }_{\mathbf{j}}\right)}{\partial {{\theta }_{\mathbf{j}}}^2}\right\},$$

$${\mathbf{I}}_{12}=E\left[\frac{1}{m}\left\{\frac{\partial \log L_1\left({\theta }_1\right)}{\partial {\theta }_1}\right\}{\left\{\frac{\partial \log L_2\left({\theta }_2\right)}{\partial {\theta }_2}\right\}}^T\right]\text{and}{\mathbf{I}}_{0\mathbf{j}}=E\left[\frac{1}{m_2}\left\{\frac{\partial \log L_0\left({\theta }_0\right)}{\partial {\theta }_0}\right\}{\left\{\frac{\partial \log L_j\left({\theta }_{\mathbf{j}}\right)}{\partial {\theta }_{\mathbf{j}}}\right\}}^T\right]$$

for j = 1, 2. In practice, the asymptotic covariance matrix Σ can be consistently estimated by its empirical counterpart $\tilde{\Sigma }$ as follows.

$$\tilde{\Sigma }=\left(\begin{array}{ccc}\hfill {\tilde{r}}^{-1}{\tilde{\mathbf{I}}}_{00}^{-1}\hfill & \hfill r^{-1∕2}{\tilde{\mathbf{I}}}_{00}^{-1}{\tilde{\mathbf{I}}}_{01}{\tilde{\mathbf{I}}}_{11}^{-1}\hfill & \hfill r^{-1∕2}{\tilde{\mathbf{I}}}_{00}^{-1}{\tilde{\mathbf{I}}}_{02}{\mathbf{I}}_{22}^{-1}\hfill \\ \hfill \hfill & \hfill {\tilde{\mathbf{I}}}_{11}^{-1}\hfill & \hfill {\tilde{\mathbf{I}}}_{11}^{-1}{\tilde{\mathbf{I}}}_{12}{\tilde{\mathbf{I}}}_{22}^{-1}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill {\tilde{\mathbf{I}}}_{22}^{-1}\hfill \end{array}\right),$$

where r̃ = m₂/m,

$$\begin{array}{c}\hfill {\tilde{\mathbf{I}}}_{00}=-\frac{1}{m_2}\sum _{i=m_1+1}^m\frac{{\partial }^2\log \mathrm{Pr}(n_{i1}\mid n_i;{\tilde{\theta }}_0)}{\partial {\theta }_0^2},{\tilde{\mathbf{I}}}_{11}=-\frac{1}{m}\sum _{i=1}^m\frac{{\partial }^2\log \mathrm{Pr}(n_{i11}\mid n_{i1};{\tilde{\theta }}_1)}{\partial {\theta }_1^2},\hfill \\ \hfill {\tilde{\mathbf{I}}}_{22}=-\frac{1}{m}\sum _{i=1}^m\frac{{\partial }^2\log \mathrm{Pr}(n_{i00}\mid n_{i0};{\tilde{\theta }}_2)}{\partial {\theta }_2^2},\hfill \\ \hfill {\tilde{\mathbf{I}}}_{01}=-\frac{1}{m_2}\sum _{i=m_1+1}^m\left\{\frac{\partial \log \mathrm{Pr}(n_{i1}\mid n_i;{\tilde{\theta }}_0)}{\partial {\theta }_0}\right\}{\left\{\frac{\partial \log \mathrm{Pr}(n_{i11}\mid n_{i1};{\tilde{\theta }}_1)}{\partial {\theta }_1}\right\}}^T,\hfill \\ \hfill {\tilde{\mathbf{I}}}_{02}=-\frac{1}{m_2}\sum _{i=m_1+1}^m\left\{\frac{\partial \log \mathrm{Pr}(n_{i1}\mid n_i;{\tilde{\theta }}_0)}{\partial {\theta }_0}\right\}{\left\{\frac{\partial \log \mathrm{Pr}(n_{i00}\mid n_{i0};{\tilde{\theta }}_2)}{\partial {\theta }_2}\right\}}^T,\hfill \end{array}$$

and

$${\tilde{\mathbf{I}}}_{12}=\frac{1}{m}\sum _{i=1}^m\left\{\frac{\partial \log \mathrm{Pr}(n_{i11}\mid n_{i1};{\tilde{\theta }}_1)}{\partial {\theta }_1}\right\}{\left\{\frac{\partial \log \mathrm{Pr}(n_{i00}\mid n_{i0};{\tilde{\theta }}_2)}{\partial {\theta }_1}\right\}}^T.$$

The composite likelihood method (hereafter referred to as CL method) reduces the computationally demanding three-dimensional integrals in the full likelihood to computationally much simpler one-dimensional integrals. More importantly, the non-convergence problem of FL method is alleviated since no correlation parameter (i.e., ρ₀₁, ρ₀₂ or ρ₁₂) is involved in the composite likelihood. The maximum composite likelihood estimate ${\tilde{\beta }}_j$ can be obtained by conducting a univariate meta-analysis with a random effects model, which is available in most statistical software. The covariance matrix of $({\tilde{\theta }}_0,{\tilde{\theta }}_1,{\tilde{\theta }}_2)$ can be easily calculated using the above formulas, which involve only one-dimensional integrals. Note that the off-diagonal matrices in Σ properly account for the covariance between the estimated overall disease prevalence and diagnostic test sensitivity and specificity, which is not possible if investigators conduct meta-analysis by univariate meta-analysis. We consider the CL method as a method between multivariate and univariate meta-analyses, inheriting the ability of multivariate meta-analysis to infer functions of overall parameters such as PPV and NPV (i.e., functions of β₀, β₁ and β₂) while not suffering from its limitations.

The asymptotic results of $({\tilde{\theta }}_0,{\tilde{\theta }}_1,{\tilde{\theta }}_2)$ can be used to construct approximate Wald-type confidence intervals/regions for diagnostic measures of interest. Alternatively, composite likelihood ratio based inference is available. In general, the composite likelihood ratio test statistic converges to a nonstandard asymptotic distribution as a weighted sum of independent ${\chi }_1^2$ distributions, which can be derived as a special case of results on misspecified likelihoods^32,33. Several adjustments of composite likelihood have been proposed in order to have an approximate or asymptotic χ² distribution^{34,35,36,37,24,38}.

3 Simulation Study

To evaluate and compare the finite sample performance of the FL and CL methods, we conduct simulation studies. The data are generated from a two-stage procedure, as specified by equations (1) and (2). Two settings of covariates are considered. In the first setting, there is no study-level covariate except the intercept, i.e., W_i = X_i = Z_i = 1. In the second setting, we consider two covariates: a binary covariate (e.g. 1 for regional cancer and 0 for distant cancer), and a continuous covariate sampled from a uniform distribution (e.g., QUADAS score with range of 1 ~ 14). We consider a moderate size meta-analysis with m = 30 studies, and a relatively large meta-analysis with m = 50 studies. We assume equal numbers of case-control and cohort studies. The numbers of subjects in each study (i.e., (n_i0, n_i1) in case-control studies and n_i in cohort studies) are randomly drawn from the studies on metastases described in Introduction Section. Specifically, in the case-control study, the range of the number of subjects per study is 10 to 100 for patients with metastasis, and 10 to 124 for patients without metastasis. In the cohort studies, the number of subjects per study ranges from 20 to 220. For the setting without study-level covariate, two configurations of overall disease prevalence, and test sensitivity and specificity are considered, namely, β₀ = logit(0.2), β₁ = logit(0.6) or logit(0.9) and β₂ = logit(0.9). For the setting with study-level covariates, the values of regression coefficients are set at the estimates from fitting the model on the studies on metastases. We let the between-study variances in disease prevalence and test sensitivity and specificity be ${\tau }_0^2={\tau }_1^2={\tau }_2^2=1$. To evaluate the impact of the correlation structure on the inference, we let the correlation parameters (ρ₀₁, ρ₀₂, ρ₁₂) take values of (0, 0, 0), (0, 0, −0.6), (0.2, −0.2, −0.6), (0.6, −0.6, −0.6) or (0.8, −0.8, −0.8) to represent different levels of correlation among disease prevalence and test sensitivity and specificity (in logit scale).We also consider the heterogeneity in correlation where the correlation parameters (ρ₀₁, ρ₀₂, ρ₁₂) take the values of (0, 0, −0.6) in half of the studies and take different values of (0.6, −0.6, −0.6) in the remaining half. Under this setting, the likelihood of the FL method is mis-specified, whereas the likelihood of the CL method is not because the CL method does not assume homogeneous correlation across studies. For each simulation setting, we generate 1, 000 samples. The samples are simulated in R (R Development Core Team, Version 2.14.1). The CL method is implemented in R by using the glmmML package³⁹. The FL method is implemented in SAS where adaptive Gaussian quadrature method in the NLMIXED procedure is used to maximize the full likelihood. Programming codes are provided in Section 6 of the supplementary material.

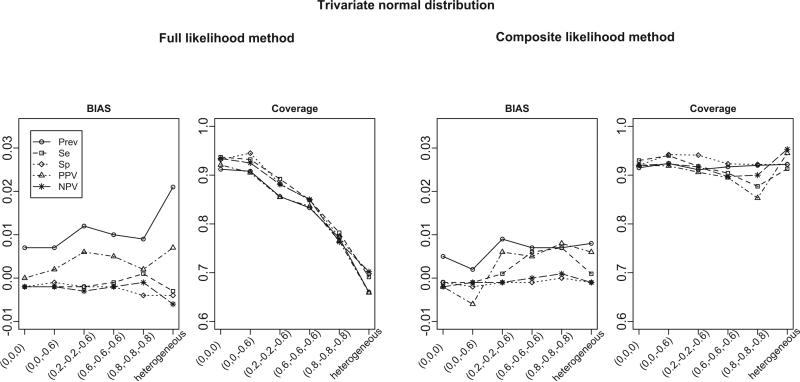
Figure 1 summarizes the empirical bias and the coverage of the 95% Wald-based confidence intervals of estimates from the FL and CL methods based on 1, 000 samples when the number of studies is 30. The parameters of interest are the overall disease prevalence (Prev), test sensitivity (Se) and specificity (Sp), and positive and negative predicted values (PPV and NPV). We note that PPV and NPV are functions of parameters (β₀, β₁, β₂) as described by equation (3). Delta method is used to derive their standard errors. From the left two panels of Figure 1, the FL method gives approximately unbiased estimates and its coverage is close to the nominal level when the correlations are zero, i.e., (ρ₀₁, ρ₀₂, ρ₁₂) = (0, 0, 0). When the correlations become stronger, the estimates from the FL method are still approximately unbiased, but the coverage of the confidence intervals deteriorates (range of coverage: 76.3 ~ 95.1%). Furthermore, when the correlation structures are heterogeneous across studies (denoted as “heterogeneous”), the bias of the FL method becomes larger and its coverage is below 70%. In contrast, the CL method provides approximately unbiased estimates and confidence intervals with better coverage under all correlation structures considered (range of coverage: 85.3 ~ 95.3%), including the scenario with heterogeneous correlation structures. We note that the non-convergence rate (i.e., number of iterations reaches the default number of 200 iterations while the relative gradient convergence criterion < 10⁻¹⁰ is not satisfied) for the FL method increases as the degree of correlation increases, and varies from 10.9% to a substantial proportion of 47.6%, whereas the non-convergence rate for the CL method is less than 1.5% under all settings considered. We also calculate the relative efficiency (RE) of CL method, defined as the square of the empirical standard error of the estimates from the CL method, divided by that of the FL method. The range of RE under all correlation structures except the heterogeneous one is 76.6% to 122.2%. The efficiency loss is expected because the FL method is asymptotically the most efficient method, while the efficiency gain can be explained by the advantage of not estimating the correlation parameters in the CL method. There is a 82 to 109% efficiency gain in the CL method under heterogeneous correlation structure setting due to the better fit of the CL method compared to the FL method. We also conducted simulations for scenarios with m = 8 and 50 studies, and similar findings are obtained in that the CL method has better coverage, avoids the non-convergence problem and is robust to the heterogeneous correlation structures. We note that when the number of studies is small (e.g., m = 8), although the CL method has substantially better coverage than the FL method (range of coverage: 77.5 ~ 89.4% versus 29.3 ~ 88.7%), bootstrap standard errors from the CL method should be used for more satisfactory coverage. The detailed simulation results are summarized in Tables S3 ~S8 in the supplementary material.

Figure 1.

Bias and coverage for estimated disease prevalence, sensitivity, specificity, PPV and NPV from the full likelihood (FL) and the composite likelihood (CL) methods. The true overall disease prevalence is 0.2, sensitivity is 0.9, and specificity is 0.9. The data are generated from bivariate GLMM (for case-control studies) and trivariate GLMM (for cohort studies). Results are summarized from 1000 simulations. The x-axis represents for the different settings of pairwise correlations among study-specific prevalence, sensitivity and specificity (in logit scale).

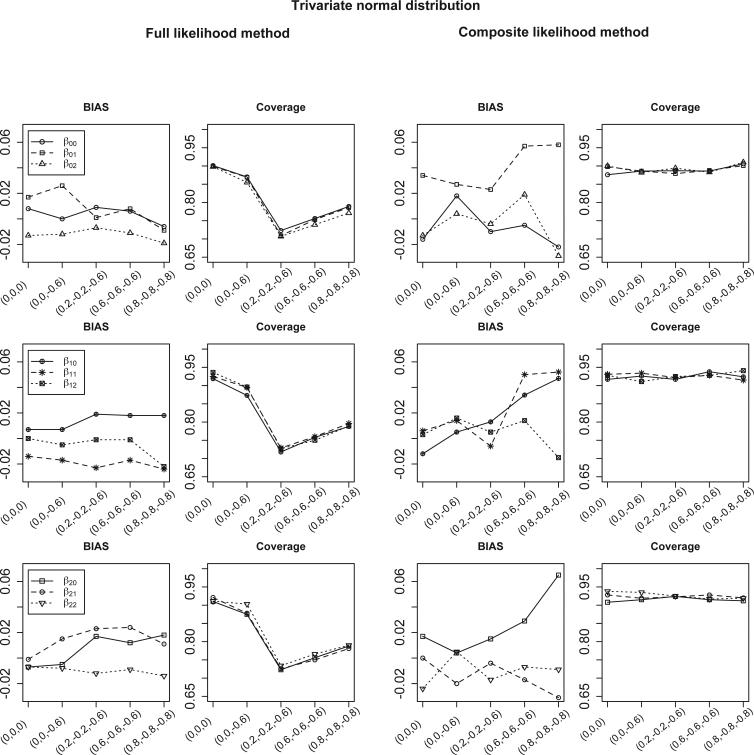
Figure 2 summarizes the simulation results when study-level covariates are available and the number of studies is 30. In this case, the regression coefficients are parameters of interest. The CL method has slightly larger bias but much better coverage than the FL method. The range of the non-convergence rate of the FL method is 10.1 to 12.7%; whereas the non-convergence rate of the CL method is less than 1.5%. The range of the RE of the CL method is 55.9 to 116.6%. There is a substantial loss of efficiency for the CL method when the correlations are high (i.e., ρ₀₁ = 0.8, ρ₀₂ = −0.8 and ρ₁₂ = −0.8). However, the corresponding coverage of β₀₀ is 90.6% for the CL method and 78.9% for the FL method when the RE is 56.0%. This suggests that choosing the FL method over the CL method in this setting to achieve better efficiency comes at the cost of a much lower coverage. A similar finding is obtained when the number of studies is 50; these results are summarized in Tables S9 ~S10 in the supplementary material.

Figure 2.

Bias and coverage for estimated meta-regression parameters in equation (2) from the full likelihood (FL) and the composite likelihood (CL) methods. The true values of regression parameters are (β₀₀, β₀₁, β₀₂) = (0.173, −1.295, 0), (β₁₀, β₁₁, β₁₂) = (1.712, −1.266, 0) and (β₂₀, β₂₁, β₂₂) = (1.912, 1.263, 0). The data are generated from bivariate GLMM (for case-control studies) and trivariate GLMM (for cohort studies). Results are summarized from 1000 simulations. The x-axis represents for the different settings of pairwise correlations among study-specific prevalence, sensitivity and specificity (in logit scale).

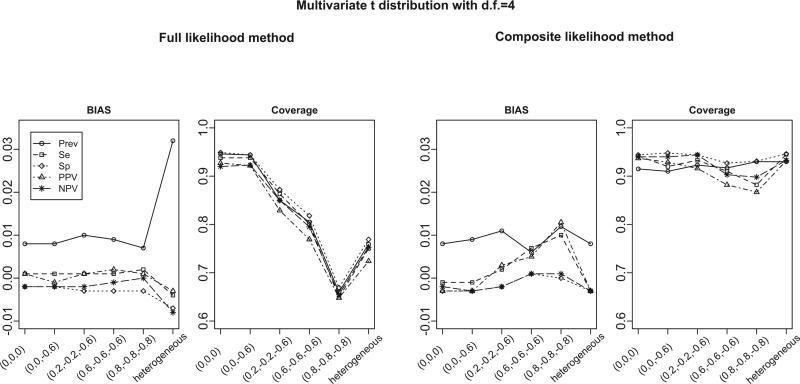
To investigate the robustness of both methods to mis-specifications of the model, we generate study-specific prevalence, sensitivity and specificity from a trivariate t-distribution with 4 degrees of freedom. This setting mimics the situation in which the distributions have heavier tails than those of the normal distributions. Under this setting, both the likelihood of the FL method and the likelihood of the CL method are mis-specified. Figure 3 summarizes the bias and coverage from 1, 000 simulations for various correlation structures when the number of studies is 30. The simulation results suggest that despite the mis-specification, the bias of both methods is in a reasonable range. The only exception is that the FL method has relatively large biases under heterogeneous correlation structures. The coverage of the FL method is close to the nominal level only when the correlations are small, and deteriorates quickly as the correlation increases. In contrast, the CL method has better coverage in all settings considered. Similar findings are obtained when the number of studies is 8 or 50. These results are summarized in Tables S11 through S16 in the supplementary material.

Figure 3.

Bias and coverage for estimated disease prevalence, sensitivity, specificity, PPV and NPV from the full likelihood (FL) and the composite likelihood (CL) methods. The true overall disease prevalence is 0.2, sensitivity is 0.9, and specificity is 0.9. The data are generated from bivariate t-distribution (for case-control studies) and trivariate t-distribution (for cohort studies). Results are summarized from 1000 simulations. The x-axis represents for the different settings of pairwise correlations among study-specific prevalence, sensitivity and specificity (in logit scale).

In summary, both FL and CL methods perform well when the number of studies is relatively large and the correlations are relatively small, and the CL method outperforms the FL method when the number of studies is relatively small, or when the correlations are relatively large. In addition, the CL method has certain robustness to heterogeneous correlation structures, and model mis-specifications. The CL method maintains relatively high efficiency except that the correlations are exceptionally high, which is consistent with the previous findings in settings of longitudinal data analyses^40,41,42,25. Considering these performances of the CL method, and its computational advantages, we recommend the use of the CL method for practical investigators.

4 A systematic review of modern diagnostic imaging modalities for surveillance of melanoma patients

We apply the proposed model and the CL method to a systematic review of published studies which examined diagnostic modality characteristics for melanoma. This systematic review contains 98 studies that had obtained data from 10, 528 patients with melanoma between January 1, 1990 and June 30, 2009²². As mentioned, the available studies includes 41 case-control studies and 57 cohort studies. To effectively combine the case-control and cohort studies, we fit the model described by equations (1) and (2). A sequence of nested models are fitted where the smallest model (referred to as the baseline model) includes a variable for stage of cancer (i.e., 1 for regional and 0 for distant), and three dummy variables for types of imaging modalities with PET-CT as the reference group. Larger models were considered by including interaction terms between type of cancer and imaging modalities. For the CL method, modifications of Akaike's information criterion (AIC) and Bayesian information criterion (BIC) have been proposed in the literature^43,44. Specifically, the composite likelihood version of AIC is defined as⁴³

$$\text{CL-AIC}=-2\log L_c+2d_s^{\ast }$$ (6)

where $d_s^{\ast }=\mathrm{trace}\left\{\widehat{J}{\left(\widehat{H}\right)}^{-1}\right\}$, Ĵ is the estimated covariance matrix of ∂L_c(θ₀, θ₁, θ₂)/∂(θ₀, θ₁, θ₂) evaluated at $({\tilde{\theta }}_0,{\tilde{\theta }}_1,{\tilde{\theta }}_2)$ and Ĥ is −∂² log L_c(θ₀, θ₁, θ₂)/∂(θ₀, θ₁, θ₂)² evaluated at $({\tilde{\theta }}_0,{\tilde{\theta }}_1,{\tilde{\theta }}_2)$. In Section 2 of the supplementary materials, we show that for our model $d_s^{\ast }$ converges with increasing m to the number of parameters in the model. The composite likelihood version of BIC is defined as⁴⁴

$$\text{CL-BIC}=-2\log L_c+d_s^{\ast }\log \left(m\right)+2\gamma d_s^{\ast }\log \left(P\right)$$

where P is the number of model parameters, and γ is a tuning parameter and is taken as 0 when P is relatively small compared to the number of studies as suggested in Gao and Song⁴⁴. The results of fitting the sequence of nested models are summarized in Table 2. Both composite likelihood versions of AIC and BIC suggest the use of the baseline model with 18 model parameters. To investigate the model assumptions, we start with checking the normality assumption on the logit prevalence, sensitivity and specificity. QQ-plots are provided in Figure S3 of the supplementary material. Test of normality is conducted by Shapiro-Wilk test⁴⁵ for each subgroup and the p-values are all greater than 0.05, suggesting that the normality assumption is appropriate. The sequence of models in Table 2 implicitly assume equal variance in logit prevalence, sensitivity and specificity for different subgroups. To check such assumption, we apply the Bartlett's test⁴⁶ for the homogeneity in variances across subgroups. The test suggests that homogeneity assumption is appropriate for logit prevalence and specificity, but not for logit sensitivity (p < 0.001). To study the sensitivity of the results from the baseline model (as recommended by both CL-AIC and CL-BIC) to the equal variance assumption, we conduct an alternative analysis within each of the subgroups (stratified by stage of cancer, and type of imaging modality). And we found that the results from the subgroup analyses are generally similar to those from the baseline model. There are only 2 case-control studies and 1 cohort study in the subgroup of CT for regional cancer. In this subgroup, the CL method cannot be applied since the model for the metastasis prevalence contains two parameters and the estimation requires at least two cohort studies. Instead, the bivariate GLMM was fitted to obtain estimates of diagnostic sensitivity and specificity, but not metastasis prevalence, PPV, nor NPV.

Table 2.

Model selection using the CL-AIC and CL-BIC when analyzing the data in Xing et al. (2011).

Model	$d_s^{\ast }$	−2logCL	CL-AIC	CL-BIC
baseline	18	1537	1573	1620
+ I(Regional)*I(US)	21	1534	1576	1632
+ I(Regional)*I(CT)	21	1535	1577	1632
+ I(Regional)*I(PET)	21	1534	1576	1632
+ I(Regional)*I(US) + I(Regional)*I(CT)	24	1532	1580	1643
+ I(Regional)*I(US) + I(Regional)*I(PET)	24	1529	1577	1641
+ I(Regional)*I(CT) + I(Regional)*I(PET)	24	1533	1581	1644
+ I(Regional)*I(US) + I(Regional)*I(CT) + I(Regional)*I(PET)	27	1525	1579	1650

baseline: meta-analysis model with study-level covariates of I(Regional) + I(US) + I(CT) + I(PET).

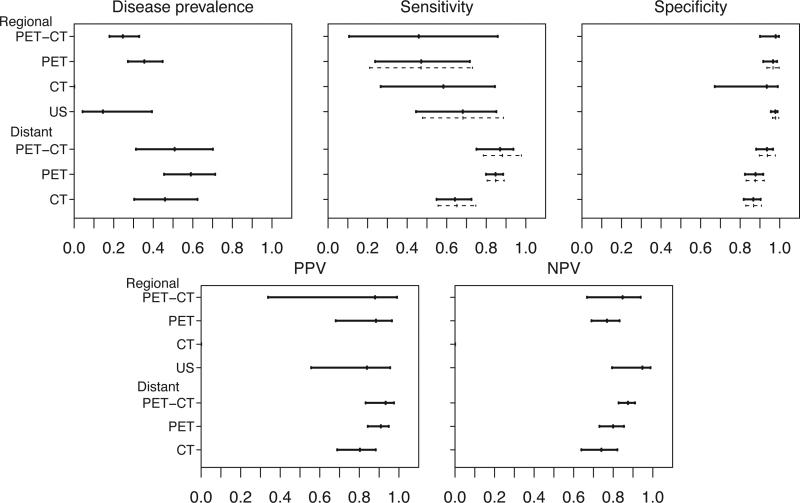
Figure 4 presents the results from the subgroup analyses with CL method on the overall metastasis prevalence, diagnostic sensitivity and specificity, PPV and NPV, and the associated 95% confidence intervals for the four diagnostic imaging modalities. The confidence intervals are symmetric around the estimates in the logit scale and asymmetric in the original scale. The results from fitting bivariate GLMM are displayed as the dashed lines in Figure 4 for comparison. In general, our results are consistent with those from bivariate GLMM, with respect to sensitivity and specificity. Here we highlight selected results of diagnostic sensitivities and specificities, and the PPV and NPV. For the surveillance of regional lymph node metastasis, US has the highest sensitivity (68%; 95% CI = 44% to 85%) and specificity (98%; 95%CI = 96% to 99%) among all four imaging modalities. On the other hand, patients diagnosed by PET-CT or PET have higher estimated metastasis prevalence and hence higher estimated PPV, compared to patients diagnosed by US. For the surveillance of distant lymph node metastasis, PET-CT has the highest sensitivity (87%; 95% CI = 75% to 94%), specificity (94%; 95% CI = 88% to 97%), PPV (93%; 95% CI = 83% to 97%) and NPV (87%; 95% CI = 83% to 91%). There is a significant heterogeneity in prevalence of metastasis across different imaging modalities and stage of metastasis (regional vs distant). These differences are potentially meaningful in practice. Patients with distant metastasis have higher PPV than patients with metastasis that is confined to regional lymph nodes. The results of this systematic review of imaging modalities used to stage melanoma suggest that US is a more accurate imaging modality for diagnosing lymph node involvement and PET-CT is the preferred imaging modality to diagnose distant metastasis. In addition, due to the low metastasis prevalence among patients for whom lymph node metastasis is diagnosed by US, a positive test result from US yields the lowest PPV among all imaging modalities.

Figure 4.

Upper panels: estimated metastasis prevalence, sensitivities and specificities and 95% confidence intervals of four diagnostic imaging modalities using the composite likelihood method; Lower panels: estimated PPVs and NPVs and 95% confidence intervals of four diagnostic imaging modalities using the composite likelihood method. Solid lines: confidence intervals estimated from the CL method. Dashed lines: confidence intervals estimated from the bivariate GLMM method.

As we know, a univariate summary measure of diagnostic tests may not be su cient, and the use of bivariate summary measures is preferred when describing diagnostic tests such as (sensitivity, specificity) or (PPV, NPV). Additionally, estimates of these bivariate summary measures are often correlated. Therefore, separate confidence intervals that do not account for such a correlation may be misleading¹⁹, and confidence regions should be used. Figure 5 shows the summary points and 95% confidence regions for sensitivity versus 1 minus specificity (upper left panel), PPV versus NPV (upper right panel), sensitivity and specificity versus metastasis prevalence (middle panels), and predictive values versus metastasis prevalence (lower panels) without stratification on stages of metastasis (i.e. regional or distant). These regions are calculated as Wald-based confidence regions and are not elliptical because they are in the original scale. The elliptical confidence regions in the logit scale are displayed in Figure S4 in the supplementary material. Specifically, following Douglas⁴⁷, the parametric representation of the boundary of the elliptical Wald-type confidence region for sensitivity and specificity (in logit scale) is

$$S_1={\widehat{S}}_1+s_{S_1}\sqrt{\left(2f_{2,n-2;\alpha }\right)}\cos \varphi \text{and}{C}_1={\widehat{C}}_1+s_{C_1}\sqrt{\left(2f_{2,n-2;\alpha }\right)}\cos (\varphi +\arccos r),$$

where s_S1 and s_C1 are the estimated standard errors ofŜ₁ andĈ₁ , r is the estimate of their correlation, ϕ runs from 0 to 2π, and f_2,n−2;α is the upper 100 % point of the F distribution with degrees of freedom 2 and n − 2, and n is the number of studies. For joint confidence regions of PPV and NPV (or pairs of other measures), delta method is used to obtain the covariance matrix.

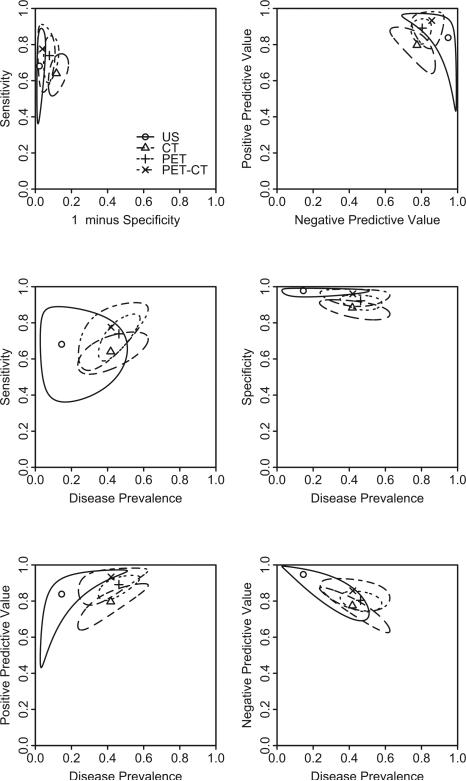
Figure 5.

Summary points and 95% confidence regions of sensitivity versus 1-minus-specificity (up per left panel), PPV versus NPV (upper right panel), sensitivity and specificity versus metastasis prevalence (middle panels), predictive values versus metastasis prevalence (lower panels) for four diagnostic imaging modalities. Filled circle: summary point; solid line: boundary of 95% confidence region for the summary point.

As suggested by the upper left panel, there is more variation in sensitivity than in specificity. This is because the number of true positives is much less than the number of true negatives. The PPV and NPV tend to have similar variations as seen in the upper right panel. The middle panels suggest that the confidence region covers a larger range of prevalence than specificity, which suggests more variation in estimated prevalence than specificity. Such a finding is consistent with that from the upper left panel of Figure 4, where a significant heterogeneity in the estimated metastasis prevalence is found. As seen in the lower panels, the PPV and NPV tend to have similar variation as compared to the prevalence. In summary, given the wide ranges of those confidence regions, it suggests that more studies are needed to increase the precision of those estimates, and to reach definitive conclusions comparing those imaging modalities.

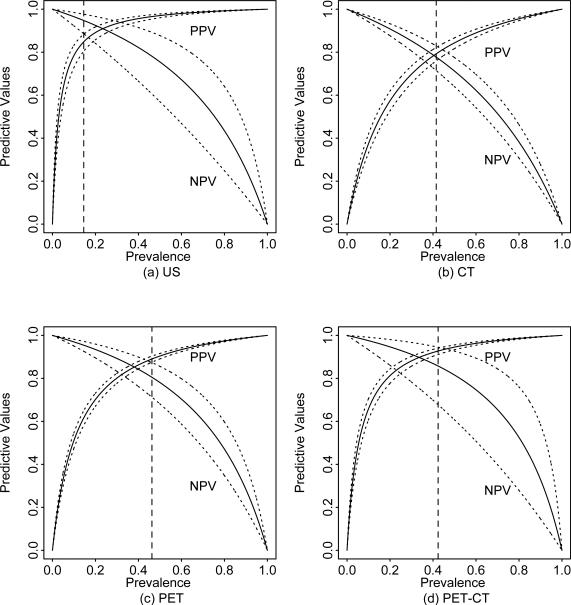
Figure 6 shows the estimated PPV and NPV with their pointwise 95% confidence intervals based on the overall estimates of sensitivity and specificity for each of imaging modalities. This figure is particularly useful for clinicians who want to obtain the PPV and NPV for a different cohort of patients under investigation. The solid vertical dashed lines indicate the estimated prevalence of metastasis for patients diagnosed by the imaging modality. For example, the estimated prevalence for patients diagnosed by US is 15%, and the estimated overall PPV and NPV are 85% (95% CI: 80%, 88%) and 95% (95% CI: 89%, 98%) respectively. In contrast, the estimated overall PPV and NPV for patients diagnosed by CT are 79% (95% CI: 76%, 82%) and 78% (95% CI: 71%, 83%) with estimated prevalence being 42%. This suggests that US is more useful than CT in ruling out disease and detecting disease for patients diagnosed by the corresponding imaging modality. We note that we did not stratify by stage of cancer in this analysis as the number of studies stratified by both stage of cancer and type of imaging modality is very limited.

Figure 6.

The overall PPV and NPV plot for a given prevalence based on the meta-analysis without study-level covariate using CL method. Solid and dotted lines denote the estimate and 95% confidence interval. Dashed vertical lines denote the estimated overall prevalence.

5 Discussion

Multivariate meta-analysis gains its popularity recently, especially in systematic review of diagnostic tests⁴⁸. In this paper, we proposed a hybrid multivariate random effects model for study of diagnostic test accuracy. There are two major advantages of multivariate meta-analysis over univariate meta-analysis. First, unlike univariate meta-analysis, multivariate meta-analysis can provide valid inference on functions of overall population parameters, such as PPV and NPV. Secondly, by jointly modeling the study-specific effects, multivariate meta-analysis is expected to have more efficiency than univariate meta-analysis in terms of parameter estimation. On the other hand, multivariate meta-analysis may suffer the non-convergence problem and computational difficulties, especially when the number of studies is relatively small, a common situation in practical meta-analysis.

In this paper, we propose the composite likelihood inference procedure, which can be thought as a procedure between multivariate and univariate meta-analyses, inheriting the ability of multivariate meta-analysis to infer functions of overall parameters while not suffering from their limitations. Through simulation studies, we find that the composite likelihood inference does not suffer severe efficiency loss except the situations with exceptionally high correlations. The composite likelihood inference is also more robust than the full likelihood inference to model mis-specifications. Therefore, the composite likelihood method can serve as a useful alternative in multivariate meta-analysis of diagnostic tests.