Abstract
Linear Dynamical System (LDS) is an elegant mathematical framework for modeling and learning Multivariate Time Series (MTS). However, in general, it is difficult to set the dimension of an LDS’s hidden state space. A small number of hidden states may not be able to model the complexities of a MTS, while a large number of hidden states can lead to overfitting. In this paper, we study learning methods that impose various regularization penalties on the transition matrix of the LDS model and propose a regularized LDS learning framework (rLDS) which aims to (1) automatically shut down LDSs’ spurious and unnecessary dimensions, and consequently, address the problem of choosing the optimal number of hidden states; (2) prevent the overfitting problem given a small amount of MTS data; and (3) support accurate MTS forecasting. To learn the regularized LDS from data we incorporate a second order cone program and a generalized gradient descent method into the Maximum a Posteriori framework and use Expectation Maximization to obtain a low-rank transition matrix of the LDS model. We propose two priors for modeling the matrix which lead to two instances of our rLDS. We show that our rLDS is able to recover well the intrinsic dimensionality of the time series dynamics and it improves the predictive performance when compared to baselines on both synthetic and real-world MTS datasets.
Introduction
Multivariate time series (MTS) analysis is an important statistical tool to study the behavior of time dependent data and to forecast its future values depending on the history of variations in the data (Reinsel 2003). MTS modeling takes into account the sequences of values of several contemporaneous variables changing with time. By analyzing the influence of other observable variables known or suspected to be related to the time series of interest, better understanding and forecasting are usually obtained. For example, in economics, forecasting consumer price index usually depends on the time series of money supply, the index of industrial production and treasury bill rates (Kling and Bessler 1985). In clinical domain, in order to get accurate sequential predictions of the patients’ parameters, such as platelets counts, time series of hemoglobin, hematocrit and red blood cell measurements should be considered (Batal et al. 2013). Developing and learning accurate models of MTS are critical for their successful applications in outcome prediction, decision support, and optimal control.
A large spectrum of models have been developed and successfully applied in MTS modeling and forecasting (Du Preez and Witt 2003; Ljung and Glad 1994). However, MTS modeling of real-world data poses numerous challenges. First, a large number of MTS collected in the real-world problems have a relatively short span (Bence 1995). For example, in biology, more than 80% of all time series in gene expression datasets are short (less than 80 data points) (Ernst, Nau, and Bar-Joseph 2005). In economics, econometric MTS, such as gross domestic product, consumer price index, etc, are measured quarterly or yearly which leads to MTS’ lengths of less than 200 (Data 2014). In the clinical domain, patients’ clinical MTS are usually less than 50 due to the fact that the majority of patients’ hospitalizations is less than two weeks (Liu, Wu, and Hauskrecht 2013). A short-span complex MTS undoubtedly poses a hard modeling problem since the existing well-developed models and algorithms may easily overfit the data when they are applied to such time series. Second, while in some cases the problem of short-span MTS may be alleviated by learning the models from multiple short-span MTS instances, the number of MTS instances available in the datasets is often limited and for many problems it is restricted to just one time series we want to learn from (e.g. various time series in economics or business) and the model overfitting remains a big concern.
In this paper we study and develop solutions that are applicable and can learn models from short-span MTS. Our work focuses on the refinements of a popular model for MTS analysis: the Linear Dynamical System (LDS) (a.k.a Kalman filter) (Kalman 1960) and its application to MTS forecasting. We aim to develop an algorithm to automatically learn an LDS that performs better forecasting when learned from a small amount of complex MTS data.
Briefly, the LDS is a classical and widely used model for real-valued sequence analysis, that is applicable to many real-world domains, such as engineering, astronautics, bioinformatics, economics, etc (Lunze 1994; Liu and Hauskrecht 2013). This is due to its relative simplicity, mathematically predictable behavior, and the fact that exact inference and predictions for the model can be done efficiently. The LDS is Markovian and assumes the dynamic behavior of the system is captured well using a small set of real-valued hidden-state variables and linear state transitions corrupted by a Gaussian noise. The LDS can be learned from observation data. Standard LDS learning approaches use the Expectation-Maximization (EM) (Ghahramani and Hinton 1996) or spectral learning (Katayama 2005; Van Overschee and De Moor 1996) algorithms. However, learning an LDS model from short-span low-sample MTS datasets gives rise to numerous important questions: (1) Since the observational sequences in MTS data may exhibit strong interactions and co-movements, given the MTS sequences, how many hidden states are needed to represent the system dynamics well?; (2) Due to the fact that the number of parameters representing transitions among hidden state components (a.k.a transition matrix) is quadratic in the dimensionality of the hidden space, how do we prevent the overfit of the model parameters when the training size is small?
In this work we address the above issues by presenting a regularized LDS framework (rLDS) which
recovers the intrinsic dimensionality of MTS by minimizing the rank of the transition matrix rather than the state space size.
prevents model overfitting given short MTS datasets.
supports accurate MTS forecasting.
Our framework builds upon the probabilistic formulation of the LDS model, and casts its parameters optimization as a maximum a posteriori (MAP) problem, where the choice of parameter priors biases the model towards a low-rank solution. We propose two strategies for choosing the parameter priors that lead to two instances of our rLDS. The first strategy, rLDS𝒢, assumes a multivariate Laplacian prior over each row of the LDS’s transition matrix. This enforces a row-level sparsity on the transition matrix (Garrigues and Olshausen 2010; Raman et al. 2009). The second strategy, rLDSℛ, relies on a nuclear norm prior on the entire transition matrix to induce the low-rank matrix property (Alquier et al. 2014). Experiments show that our regularized framework can recover very well the underlying dynamical model in a variety of synthetic domains. We also show that rLDS gives a better accuracy than alternative methods when predicting future time series values on several real-world datasets.
The reminder of the paper is organized as follows: the Background and Related Work section introduces the LDS and provides a detailed review of existing regularized methods related to LDSs. In the The Regularized LDS Framework section, we describe the inference and learning procedures for rLDS and the two regularization strategies with their corresponding optimizations. The Experiment section focuses on two problems: (1) recovery of the intrinsic MTS dimensionality, and (2) MTS forecasting on a variety of synthetic and real-world datasets and comparison of the proposed approach to alternatives. We summarize our work and outline potential future extensions in the Conclusion section.
Background and Related Work
Linear Dynamical System
The Linear Dynamical System (LDS) models real-valued MTS using hidden states :
| (1) |
Briefly, {zt} is generated via the transition matrix A ∈ ℝd × d. Observations {yt} are generated from zt via the emission matrix C ∈ Rn × d (see eq.(1)). and are i.i.d. multivariate normal distributions with mean 0 and covariance matrices Q and R respectively. The initial state (z1) distribution is also multivariate normal with mean ξ and covariance matrix Ψ. The complete set of the LDS parameters is Ω = {A, C, Q, R, ξ, Ψ}. While in some LDS applications the model parameters are known a priori, in the majority of real-world applications the model parameters are unknown, and we need to learn them from MTS data. This can be done using standard LDS learning approaches such as the Expectation-Maximization (EM) (Ghahramani and Hinton 1996) or spectral learning (Katayama 2005; Van Overschee and De Moor 1996) algorithms.
Related Work
Recently, various regularization methods have been incorporated into LDSs for both time series modeling and prediction tasks. These can be divided into five categories: C1: state regularization; C2: innovation regularization; C3: combination regularization; C4: parameter regularization; and C5: regularization on other related models.
C1: State Regularization
In the state regularization approach (Carmi, Gurfil, and Kanevsky 2010; Angelosante, Roumeliotis, and Giannakis 2009; Charles et al. 2011) the hidden states are sparsified during the Kalman filter inference step. (Charles et al. 2011) formulates the traditional Kalman filter as a one-step update optimization procedure and incorporates sparsity constraints to achieve a sparse state estimate ẑt at each time stamp t. (Angelosante, Roumeliotis, and Giannakis 2009) treats all the state estimates as a state estimate matrix and enforces a row-level group lasso on the state estimate matrix.
C2: Innovation Regularization
In signal processing, “innovation” is referred to as the error of state estimation, i.e., ‖ẑt − Aẑt−1‖. Both (Asif et al. 2011) and (Charles et al. 2011) incorporate ℓ1 regularization on innovation during the state estimation procedures to balance fidelity to the measurements against the sparsity of the innovations.
C3: Combination Regularization
The basic idea underlying the combination regularization is to find a representation of the LDS which is sparse in terms of a given dictionary of LDSs. Given multiple MTS sequences, (Ghanem and Ahuja 2010) trains an LDS for each MTS and obtains the final LDS by using a weighted combination of the individual LDSs such that each weight is regularized by an ℓ1 penalty.
C4: Parameter Regularization (★)
Parameter regularization introduces regularization penalties on the parameters of an LDS during the learning process. (Boots, Gordon, and Siddiqi 2007) develops a spectral algorithm that is able to learn a stable LDS by limiting the largest eigenvalue of transition matrix A to be less than 1. Our rLDS also belongs to this category due to the fact that we develop a Maximum a Posteriori learning framework and apply low-rank priors on the A to implicitly shut down spurious and unnecessary dimensions and prevent overfitting problem simultaneously.
C5: Regularization on Other Related Models
There are various approaches that incorporate regularizations into MTS models that are alternatives to LDSs. For example, (Chiuso and Pillonetto 2010) introduces a Bayesian nonparametric approach to the identification of observation-only linear systems. (Städler and Mukherjee 2013) considers a hidden Markov model with d multivariate normal emission matrices and applies an ℓ1-penalization on the inverse covariance matrix of every state-specific emission matrix.
Our rLDS is different from C1 and C2 methods since both of them try to learn a sparse representation for the hidden-state estimation problem by assuming that all parameters of the LDS are known a priori. Hence they are not directly applicable to the problem of learning MTS models from data. The combination approach in C3 requires an extensive training process since it has to build a dictionary of multiple LDSs trained on the different time series. Also, the combination approach does not attempt to solve the overfitting problem and it does not attempt to determine the correct number of hidden states. Compared with (Chiuso and Pillonetto 2010) in C5 category, our rLDS utilizes hidden states to capture the variations behind MTS while (Chiuso and Pillonetto 2010) relies on an observation-only linear system where no hidden states are involved. The underlining assumption of this approach is that the observations are obtained from linear combinations of previous observations and additional system inputs, which may be too restrictive to model complex MTS and makes the model more sensitive to noisy observations and outliers. Another method in C5 (Städler and Mukherjee 2013) uses a hidden Markov model with discrete hidden states and entries in the transition matrix describe the transition probabilities between these discrete states. LDSs and HMMs are under different underlying assumptions. The LDS is often preferred to HMM in modeling real-value MTS since it is able to model better smooth state evolution. Similarly to LDSs, in HMMs we usually don’t have a prior knowledge about the discrete states and their number. Finally, even though our rLDS belongs to the same category (C4) as the stable LDS proposed by (Boots, Gordon, and Siddiqi 2007), the two methods focus on the different aspects of the problem. (Boots, Gordon, and Siddiqi 2007) attempts to achieve stability in a learned LDS while our rLDS tries to find an appropriate state space and prevent overfitting given a small amount of MTS data.
The Regularized LDS Framework
In this section, we propose a regularized LDS framework that is able to (1) automatically shut down unnecessary and spurious dimensions of a LDS’ hidden state space, and consequently, determine its optimal dimensionality; (2) prevent the model overfitting problem for short-span low-sample MTS datasets; (3) support accurate MTS forecasting.
rLDS Framework
In rLDS, the LDS has a large implicit state space but a low-rank transition matrix. The rLDS recovers the intrinsic dimensionality of MTS by using the rank of transition matrix rather than the state space size. In order to achieve the low-rank property, we introduce a prior, i.e., p(A) (The choice of p(A) is discussed in the Learning section) for the hidden state transition matrix A. The log joint probability distribution for our rLDS is: , where and .
Learning
We develop an Expectation-Maximization (EM) algorithm for the MAP estimation of the rLDS. In the following, we use ‖·‖F, ‖·‖* and ‖·‖2 to represent the matrix Frobenius norm, matrix nuclear norm and vector Euclidean norm. vec(·) denotes the vector form of a matrix; and ⊗ represents the Kronecker product. Id is the d × d identity matrix.
E-step(Inference)
Since the Markov chain z defined by the LDS is unobserved, we cannot learn our rLDS directly. Instead, we infer the hidden state expectations. The E-step infers a posterior distribution of latent states z given the observation sequences y, p(z|y, Ω). In the following, we omit the explicit conditioning on Ω for notational brevity.
The E-step requires computing the expected log likelihood of the log joint probability with respect to the hidden state distribution, i.e., 𝒬 = 𝔼z[log p(z, y, A|Ω)], which depends on 3 sufficient statistics 𝔼[zt|y], and . Here we follow the backward algorithm in (Ghahramani and Hinton 1996) to compute them. The backward algorithm is presented in the supplemental material.
| (2) |
M-step(Learning)
In the M-step, we try to find Ω that maximizes the likelihood lower bound 𝒬 (eq.(2)). As we can see, 𝒬 function’s differentiability with respect to A depends on the choice of A’s prior, i.e., p(A), while it is differentiable with respect to (C, R, Q, ξ, Ψ). Therefore, we separate the optimization into two parts, i.e., O1 and O2.
O1: Optimization of A
In each iteration in the M-step, we need to maximize with respect to A, which is equivalent to minA g(A) − log p(A), where .
In order to recover the intrinsic dimensionality from MTS datasets through the rank of transition matrix A rather than the state space size d, we need to choose specific priors which can induce the desired low-rank property. Here we have two choices of inducing a low-rank A: (1) a multivariate Laplacian prior and (2) a nuclear norm prior as shown in Table 1. Ai represents each row (or column)1 of A. The prior choices lead to two instances of our rLDS framework, I1 (rLDS𝒢) and I2 (rLDSℛ).
Table 1.
Prior choices for rLDS.
| Prior Name | Prior Form | Regularization |
|---|---|---|
| Multivariate Laplacian | ∝ exp(−λ1‖Ai‖2) | λ1‖Ai‖2 |
| Nuclear norm | ∝ exp(−λ2‖A‖*) | λ2‖A‖* |
I1: rLDS𝒢 with multivariate Laplacian priors
In rLDS𝒢, we assume every row Ai is independent of each other and has the multivariate Laplacian density. Also in order to avoid overfitting, we add a multivariate Gaussian prior to each Ai, which leads to the ridge regularization. Therefore, we combine the multivariate Laplacian prior and Gaussian prior to get a new prior for transition matrix A. Its log probability is:
| (3) |
and the objective function we want to optimize becomes:
| (4) |
| (5) |
where a = vec(A), is the row membership indicator, and Q−1 = LL′. Mathematical transformation from eq.(4) to eq.(5) is listed in the supplemental material.
Since eq.(5) consists of a quadratic form and a non-smooth Euclidean norm, it can be easily casted into a second order cone program (SOCP) (eq.(6)), which can be solved efficiently by any existing SOCP solvers. Various algorithms can be used to solve eq.(5), such as (Yuan, Liu, and Ye 2011; Qin, Scheinberg, and Goldfarb 2013), however, the second order optimization methods, like SOCP, always get solutions with high precision (low duality gap) (Bach et al. 2011). If the state size stays moderate (<50) which is the case in our experiments, the SOCP solver should be a reasonable choice.
| (6) |
I2: rLDSℛ with a nuclear norm prior
In rLDSℛ, we directly assume A has a nuclear norm density and similarly to rLDS𝒢, we also assume a multivariate Gaussian prior for each Ai. In this case our objective function is:
| (7) |
Since h(A) is convex and differentiable with respect to A, we can adopt the generalized gradient descent algorithm to minimize eq.(7). The update rule is
| (8) |
where ρk is the step size at iteration k and the proximal function proxρk (A) is defined as the singular value soft-thresholding operator,
| (9) |
where A = Udiag(σ1, ⋯, σd)V′ is the singular value decomposition (SVD) of A.
An important open question here is how to set the step size of the generalized gradient method to assure it is well behaved. Theorem 1 gives us a simple way to select the step size while also assuring its fast convergence rate.
Theorem 1
Generalized gradient descent with a fixed step size for minimizing eq.(7) has convergence rate O(1/k), where k is the number of iterations.
Proof
The proof appears in the supplemental material.
O2: Optimization of Ω\A = {C, R, Q, ξ, Ψ}
Each of these parameters is estimated similarly to (Ghahramani and Hinton 1996) by taking the corresponding derivative of the eq.(2), setting it to zero, and by solving it analytically. Update rules for Ω\A = {C, R, Q, ξ, Ψ} are as follows:
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
Algorithm 1.
Parameter estimation in rLDS
| INPUT: Initialization Ω(0) = {A(0), C(0), Q(0), R(0), ξ(0), Ψ(0)}. | |
| PROCEDURE: | |
| 1: | repeat |
| 2: | E-step: estimate 𝔼[zt|y], and . |
| 3: | M-step: M1:estimate C, R, Q, ξ, Ψ by eq.(10) – eq.(14) |
| 4: | if rLDS𝒢 then |
| 5: | M2:estimate A by SOCP solvers. |
| 6: | end if |
| 7: | if rLDSℛ then |
| 8: | M2:estimate A by generalized gradient descent algorithm. |
| 9: | end if |
| 10: | until Convergence |
| OUTPUT: Learned LDS parameters: Ω̂ = {Â, Ĉ, Q̂, R̂, ξ̂, Ψ̂}. | |
Summary of the learning algorithm
The entire parameter estimation procedure for rLDS is summarized by Algorithm 1.
Experiment
In this section, we will (1) verify that our regularized LDS approach indeed results in a low-rank solution and (2) show that our rLDS models are able to alleviate model overfitting by starting the learning process from a large initial hidden state space and by working with small amounts of training data. Experiments are conducted on both synthetic and real-world datasets. We would also like to note that the hyper parameters (λ1, λ2 and λ3) used in our methods are selected (in all experiments) by the internal cross validation approach while optimizing models’ predictive performances.
Baselines
We compare the two instances of our rLDS framework, i.e., rLDS𝒢 and rLDSℛ to the following LDS learning baselines:
LDS learned using the standard EM learning algorithm (EM) (Ghahramani and Hinton 1996) that iteratively finds the maximum likelihood solution.
Subspace identification algorithm (SubspaceID) (Van Overschee and De Moor 1996). SubspaceID computes an asymptotically unbiased solution in closed form by using oblique projection and SVD.
Stable linear dynamical system (StableLDS) (Boots, Gordon, and Siddiqi 2007). StableLDS constrains the largest singular value of the transition matrix to ensure the stability of LDS models.
Evaluation Metrics
We evaluate and compare the performance of the different methods by calculating the average Mean Absolute Percentage Error (Average-MAPE) of models’ predictions. Average MAPE measures the prediction deviation proportion in terms of the true values:
where |·| denotes the absolute value; yij and ŷij are the jth true and predicted observations from time series i. n is the number of time series and T is the length of a MTS.
Datasets
Synthetic Data
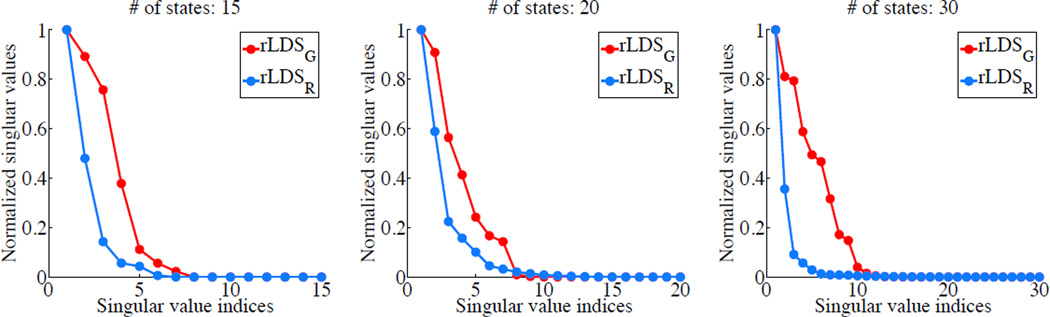
To get a good understanding of our approach, we first test it on synthetic data. We generate our synthetic MTS dataset of length T = 200 using a 20-state LDS with zero-mean, 0.01 variance Gaussian innovations. A uniform random emission matrix C is used to generate 20 measurements at each time stamp t with i.i.d. zero mean variance 0.01 measurement noise. We uniformly and randomly generate a 20 × 20 matrix, normalize its SVD decomposition by its largest singular value to ensure its stability and truncate its 10 smallest singular values to obtain an exact 10-rank matrix A. We train both rLDS𝒢 and rLDSℛ with the different state sizes, i.e., d = 15, 20 and 30. The results of rLDS𝒢 and rLDSℛ for recovering MTS intrinsic dimensionality are shown in Figure 1. Figure 1 shows the shrinkage changes of 20 singular values from A. We can see that both the multivariate Laplacian prior and the nuclear norm prior lead us to a low-rank transition matrix and that our rLDS framework is able to recover the correct dimension even if the dimensionality of the initial state space is large.
Figure 1.
State space recovery on a synthetic dataset.
Production and Billing Data
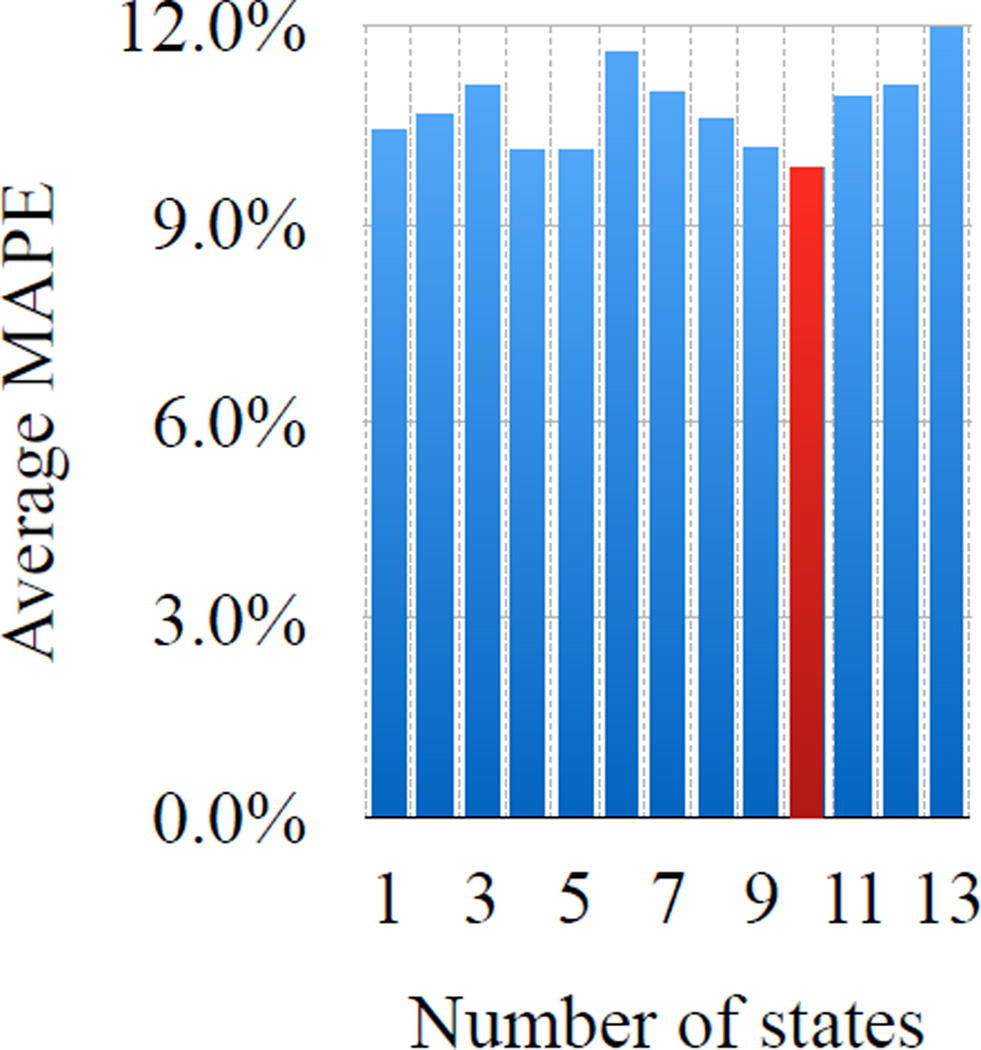
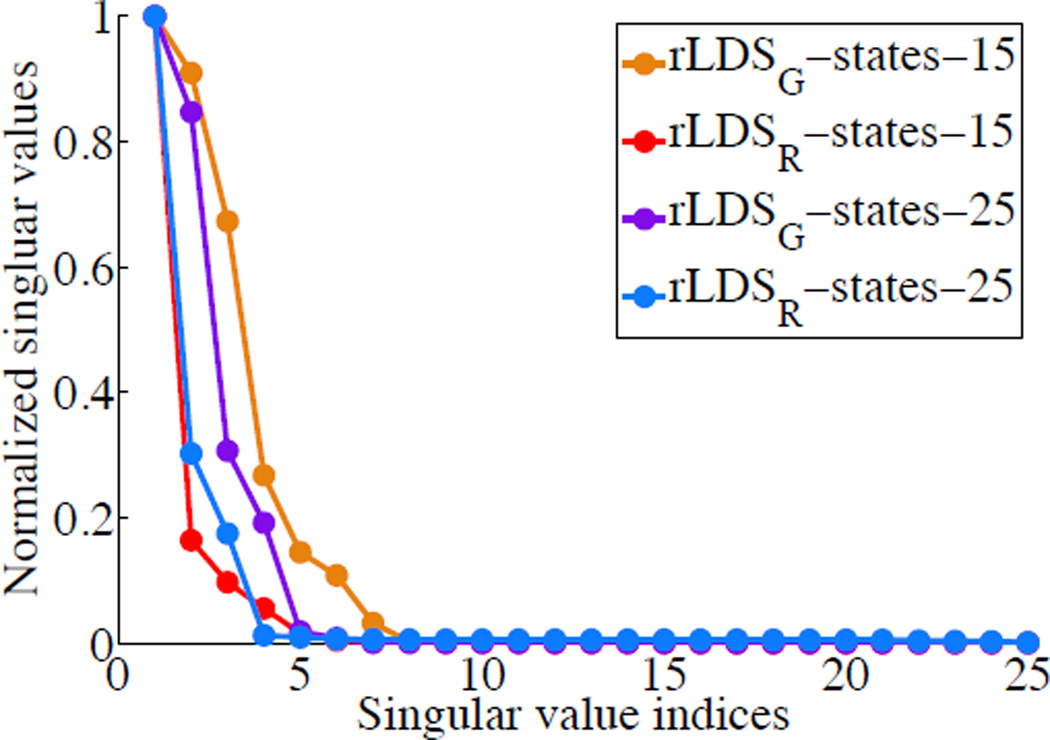
We use production and billing figures data (Reinsel 2003) as a benchmark data set2 for the time series prediction experiments. The data is a bivariate time series of length T = 100. We run various LDS learning baselines on the first 60 observations of this data and use the remaining 40 for testing. First we train the LDS models with the standard EM algorithm and vary the state space size of the LDS from 1 to 13. The prediction results are shown in Figure 3. As we can see, the prediction performance varies a lot with the different number of hidden states we use in the model and the LDS model tends to overfit the data when the state space becomes large. For example, an LDS with 13 states that shows significant prediction performance deterioration uses a 13 × 13 transition matrix. However, its is trained on only 60 × 2 = 120 data points. In contrast to this, our rLDS approach was run on 15 and 25 initial states and the results show that the approach is able to shut down unnecessary dimensions and capture the dynamics using a lower-dimensional hidden state space representation (See Figure 4). In order to gain a more comprehensive insight into rLDS’s prediction abilities, we explored numerous initial state space sizes (We also varied the training size: 90 for training and 10 for testing, due to the space limit, we put the results in the supplement material.) The results of these experiments are summarized in Table 2 which show that our rLDS methods is able to outperform all the baselines in terms of their prediction performance.
Figure 3.
LDS EM overfitting in benchmark data.
Figure 4.
rLDS state size recovery.
Table 2.
Average-MAPE results on Production and Billing dataset with 60 training and 40 testing.
| # of hidden states | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 30 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EM | 5.3373 | 5.5524 | 5.0509 | 5.0554 | 5.7982 | 5.4934 | 5.2820 | 4.9238 | 5.5338 | 5.3662 | 5.2434 | 5.6036 | 5.3460 | 5.6191 |
| SubspaceID | 6.2172 | 5.9854 | 4.6016 | 4.8212 | 4.9923 | 4.8569 | 5.4445 | 5.3183 | 5.2360 | 5.3034 | 5.3023 | 5.8577 | 5.7320 | 5.6683 |
| StableLDS | 6.2172 | 5.9854 | 4.6016 | 4.8212 | 4.9923 | 4.8569 | 5.4445 | 5.3183 | 5.2360 | 5.3034 | 5.3023 | 5.8577 | 5.7320 | 5.6683 |
| rLDS𝒢 | 6.2172 | 5.9854 | 4.6016 | 4.8212 | 4.9923 | 4.8569 | 5.1989 | 5.1876 | 5.2016 | 5.3034 | 5.1499 | 5.1792 | 5.1588 | 5.2175 |
| rLDSℛ | 5.2210 | 5.2065 | 4.6016 | 4.8212 | 4.9923 | 4.8569 | 5.2031 | 4.9005 | 4.8618 | 5.0249 | 5.0135 | 5.0169 | 4.9559 | 5.2235 |
Clinical Data
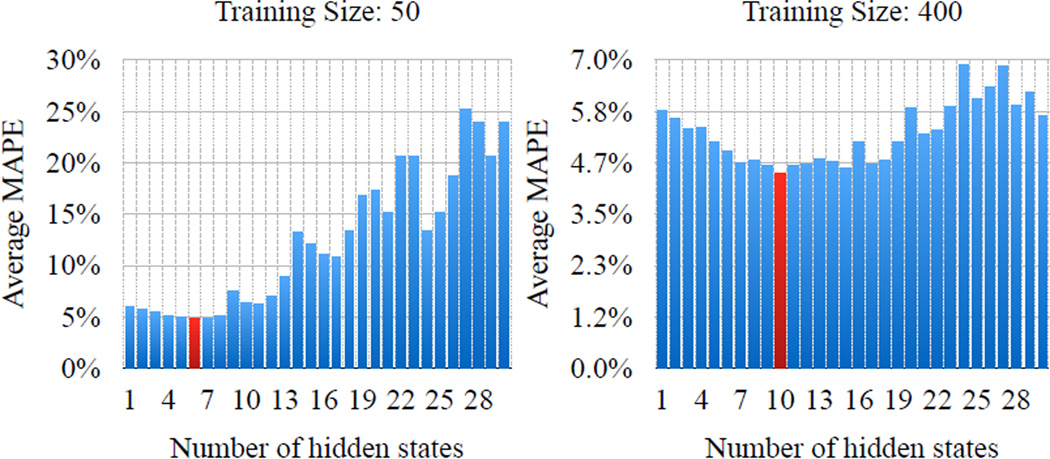
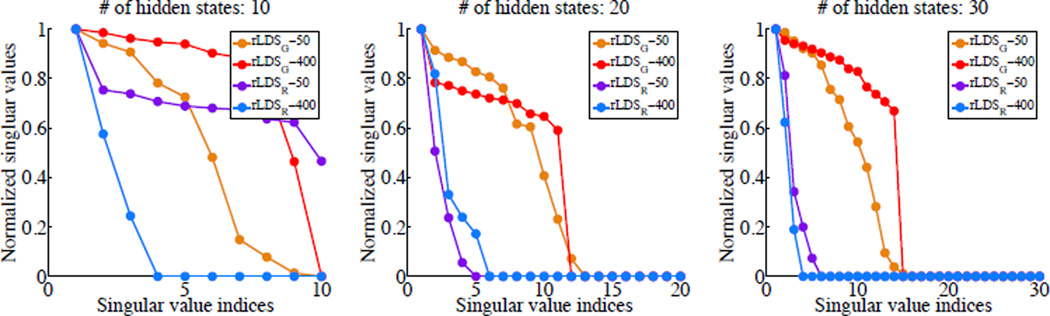
We also test our rLDS on a MTS clinical data obtained from electronic health records of post-surgical cardiac patients in PCP database (Hauskrecht et al. 2010; Valko and Hauskrecht 2010; Hauskrecht et al. 2013). We take 500 patients from the database who had their Complete Blood Count (CBC) tests3 done during their hospitalization. The MTS data consists of 6 individual CBC lab time series: mean corpuscular hemoglobin concentration, mean corpuscular hemoglobin, mean corpuscular volume, mean platelet volume, red blood cell and red cell distribution width. We have randomly selected 100 patients out of 500 as a test set and used the remaining 400 patients for training the models. We first run standard EM to learn an LDS from the training data and varied the initial hidden state space sizes from 1 to 30. The results showing the average MAPE on the test set are summarized in Figure 5. The results show an overfitting pattern very similar to the pattern seen in Figure 3 for the production data. After that we applied our rLDS approach using models with 10, 20 and 30 initial states and the same train/test data splits. The results are listed in Figure 2 and Table 3. Once again the results show that our rLDS methods are very robust and lead to better prediction performance in the majority of the experiments.
Figure 5.
LDS EM overfitting with different training sizes in clinical data.
Figure 2.
State space recovery on a clinical dataset.
Table 3.
Average-MAPE results on Clinical dataset with different training sizes.
| Training Size: 50 | Training Size: 400 | |||||
|---|---|---|---|---|---|---|
| # of states | 10 | 20 | 30 | 10 | 20 | 30 |
|
|
||||||
| EM | 6.28 | 17.24 | 23.98 | 4.43 | 5.91 | 5.72 |
| SubspaceID | 6.55 | 6.99 | 7.44 | 6.10 | 6.16 | 6.27 |
| StableLDS | 6.54 | 6.99 | 7.40 | 6.10 | 6.16 | 6.27 |
| rLDS𝒢 | 4.98 | 4.97 | 4.86 | 4.51 | 4.25 | 4.35 |
| rLDSℛ | 4.65 | 4.95 | 5.01 | 4.65 | 4.46 | 4.67 |
Conclusion
In this paper, we presented a regularized LDS learning framework for MTS modeling. Comparing with the traditional LDS learning algorithms, the advantages of our rLDS are: (1) it automatically seeks the intrinsic state dimensionality; (2) it is robust in preventing model overfitting even for a small amount of MTS data; and (3) it is able to make accurate MTS prediction. Experiment results on both synthetic and two real-world datasets demonstrated that rLDS outperforms other state-of-the-art LDS learning approaches in terms of MAPE and effectively prevent LDSs from overfitting the data even with a large initial state space. In the future, we plan to study a combination of our regularized framework with spectral learning algorithms for LDS.
Supplementary Material
Acknowledgment
The work in this paper was supported by grants R01GM088224 and R01LM010019 from the NIH. Its content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH.
Footnotes
Without loss of generality, we will use Ai to represent the row in the following text.
CBC panel is used as a broad screening test to check for such disorders as anemia, infection, and other diseases.
References
- Alquier P, Cottet V, Chopin N, Rousseau J. Bayesian matrix completion: prior specification and consistency. 2014 arXiv preprint arXiv: 1406.1440. [Google Scholar]
- Angelosante D, Roumeliotis SI, Giannakis GB. Lasso-kalman smoother for tracking sparse signals. 2009 Conference Record of the Forty-Third Asilomar Conference on Signals, Systems and Computers; IEEE; 2009. pp. 181–185. [Google Scholar]
- Asif MS, Charles A, Romberg J, Rozell C. ICASSP. IEEE; 2011. Estimation and dynamic updating of time-varying signals with sparse variations; pp. 3908–3911. [Google Scholar]
- Bach F, Jenatton R, Mairal J, Obozinski G. Convex optimization with sparsity-inducing norms. Optimization for Machine Learning. 2011:19–53. [Google Scholar]
- Batal I, Valizadegan H, Cooper GF, Hauskrecht M. A temporal pattern mining approach for classifying electronic health record data. ACM Transactions on Intelligent Systems and Technology. 2013;4(4):63. doi: 10.1145/2508037.2508044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bence JR. Analysis of short time series: correcting for autocorrelation. Ecology. 1995:628–639. [Google Scholar]
- Boots B, Gordon GJ, Siddiqi SM. A constraint generation approach to learning stable linear dynamical systems. Advances in Neural Information Processing Systems. 2007:1329–1336. [Google Scholar]
- Carmi A, Gurfil P, Kanevsky D. Methods for sparse signal recovery using kalman filtering with embedded pseudo-measurement norms and quasi-norms. IEEE Transactions on Signal Processing. 2010;58(4):2405–2409. [Google Scholar]
- Charles A, Asif MS, Romberg J, Rozell C. Sparsity penalties in dynamical system estimation. 2011 45th Annual Conference on Information Sciences and Systems; IEEE; 2011. pp. 1–6. [Google Scholar]
- Chiuso A, Pillonetto G. Learning sparse dynamic linear systems using stable spline kernels and exponential hyperpriors. Advances in Neural Information Processing Systems. 2010:397–405. [Google Scholar]
- Data FRE. Federal reserve economic data. 2014 http://research.stlouisfed.org/fred2/. [Google Scholar]
- Du Preez J, Witt SF. Univariate versus multivariate time series forecasting: an application to international tourism demand. International Journal of Forecasting. 2003;19(3):435–451. [Google Scholar]
- Ernst J, Nau GJ, Bar-Joseph Z. Clustering short time series gene expression data. Bioinformatics. 2005;21(suppl 1):i159–i168. doi: 10.1093/bioinformatics/bti1022. [DOI] [PubMed] [Google Scholar]
- Garrigues P, Olshausen BA. Group sparse coding with a laplacian scale mixture prior. Advances in Neural Information Processing Systems. 2010:676–684. [Google Scholar]
- Ghahramani Z, Hinton GE. Technical report, Technical Report CRG-TR-96-2. University of Totronto; 1996. Parameter estimation for linear dynamical systems. [Google Scholar]
- Ghanem B, Ahuja N. Sparse coding of linear dynamical systems with an application to dynamic texture recognition. 2010 20th International Conference on Pattern Recognition; IEEE; 2010. pp. 987–990. [Google Scholar]
- Hauskrecht M, Valko M, Batal I, Clermont G, Visweswaran S, Cooper GF. Conditional outlier detection for clinical alerting. AMIA Annual Symposium Proceedings; American Medical Informatics Association; 2010. p. 286. [PMC free article] [PubMed] [Google Scholar]
- Hauskrecht M, Batal I, Valko M, Visweswaran S, Cooper GF, Clermont G. Outlier detection for patient monitoring and alerting. Journal of Biomedical Informatics. 2013;46(1):47–55. doi: 10.1016/j.jbi.2012.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalman RE. A new approach to linear filtering and prediction problems. Journal of basic Engineering. 1960;82(1):35–45. [Google Scholar]
- Katayama T. Subspace methods for system identification. Springer; 2005. [Google Scholar]
- Kling JL, Bessler DA. A comparison of multivariate forecasting procedures for economic time series. International Journal of Forecasting. 1985;1(1):5–24. [Google Scholar]
- Liu Z, Hauskrecht M. Artificial Intelligence in Medicine. Springer; 2013. Clinical time series prediction with a hierarchical dynamical system; pp. 227–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Z, Wu L, Hauskrecht M. Modeling clinical time series using gaussian process sequences. SIAM International Conference on Data Mining; SIAM; 2013. pp. 623–631. [Google Scholar]
- Ljung L, Glad T. Modeling of dynamic systems. 1994 [Google Scholar]
- Lunze J. Qualitative modelling of linear dynamical systems with quantized state measurements. automatica. 1994;30(3):417–431. [Google Scholar]
- Qin Z, Scheinberg K, Goldfarb D. Efficient block-coordinate descent algorithms for the group lasso. Mathematical Programming Computation. 2013;5(2):143–169. [Google Scholar]
- Raman S, Fuchs TJ, Wild PJ, Dahl E, Roth V. The bayesian group-lasso for analyzing contingency tables. International Conference on Machine Learning; ACM; 2009. pp. 881–888. [Google Scholar]
- Reinsel GC. Elements of multivariate time series analysis. Springer; 2003. [Google Scholar]
- Städler N, Mukherjee S. Penalized estimation in high-dimensional hidden markov models with state-specific graphical models. The Annals of Applied Statistics. 2013;7(4):2157–2179. [Google Scholar]
- Valko M, Hauskrecht M. Feature importance analysis for patient management decisions; 13th International Congress on Medical Informatics MEDINFO 2010; 2010. pp. 861–865. [PMC free article] [PubMed] [Google Scholar]
- Van Overschee P, De Moor B. Subspace identification for linear systems: Theory, implementation. Methods. 1996 [Google Scholar]
- Yuan L, Liu J, Ye J. Efficient methods for overlapping group lasso. Advances in Neural Information Processing Systems. 2011:352–360. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.