Neural Mechanisms of Human Perceptual Choice Under Focused and Divided Attention

Abstract

Perceptual decisions occur after the evaluation and integration of momentary sensory inputs, and dividing attention between spatially disparate sources of information impairs decision performance. However, it remains unknown whether dividing attention degrades the precision of sensory signals, precludes their conversion into decision signals, or dampens the integration of decision information toward an appropriate response. Here we recorded human electroencephalographic (EEG) activity while participants categorized one of two simultaneous and independent streams of visual gratings according to their average tilt. By analyzing trial-by-trial correlations between EEG activity and the information offered by each sample, we obtained converging behavioral and neural evidence that dividing attention between left and right visual fields does not dampen the encoding of sensory or decision information. Under divided attention, momentary decision information from both visual streams was encoded in slow parietal signals without interference but was lost downstream during their integration as reflected in motor mu- and beta-band (10–30 Hz) signals, resulting in a “leaky” accumulation process that conferred greater behavioral influence to more recent samples. By contrast, sensory inputs that were explicitly cued as irrelevant were not converted into decision signals. These findings reveal that a late cognitive bottleneck on information integration limits decision performance under divided attention, and places new capacity constraints on decision-theoretic models of information integration under cognitive load.

Introduction

Decisions based on noisy information can be optimized by repeated sampling and integration over space and time (Wald and Wolfowitz, 1949; Bogacz et al., 2006). In the primate, parietal and prefrontal neurons with long time constants of integration contribute to near-optimal discrimination of psychophysical stimuli, such as the random dot kinematogram, by accumulating reliability-weighted momentary inputs from sensory regions up to a decision threshold (Roitman and Shadlen, 2002; Gold and Shadlen, 2007; Beck et al., 2008). However, cognitive psychologists have traditionally argued that decisions are limited not just by noise but by capacity, a constraint that emerges most clearly when a target (to-be-judged) item is presented alongside one or more distracters (Posner et al., 1980; Carrasco, 2011; Summerfield and Egner, 2014). Traditional models attribute such capacity limits to an information bottleneck that gates entry into central decision systems, either at an early or a late perceptual stage (Cherry, 1953; Broadbent, 1958; Treisman, 1969; Duncan, 1980; Pashler, 1984; Lavie and Tsal, 1994). More recent accounts have emphasized the dynamic biasing of resource allocation according to the number of items or tasks that occur in parallel (Desimone and Duncan, 1995; Reynolds and Chelazzi, 2004), but have continued to debate the stage (or stages) at which filtering occurs (Lachter et al., 2004; Benoni and Tsal, 2013).

A standard tool for investigating capacity limits in perception involves presenting two or more potential targets at different spatial locations and varying advance information about which will be probed (Posner et al., 1980; Carrasco, 2011). Focusing attention on one spatial location enhances contralateral neural responses at early sensory stages (Hillyard and Mangun, 1987; Hopfinger et al., 2000), so resulting performance advantages have been primarily attributed to top-down biasing mechanisms that divert limited cognitive resources to the cued item at the expense of its competitors (Desimone and Duncan, 1995; Reynolds and Chelazzi, 2004). Performance suffers substantially when advance cues are unavailable or ambiguous, but it is unknown how dividing attention impacts the decision mechanisms that promote accurate discrimination of noisy sensory inputs. For example, dividing attention across spatial locations could impair decision making by the following means: (1) limiting the precision (i.e., the signal-to-noise ratio) of sensory processing; (2) precluding the conversion of sensory inputs into decision signals; or (3) attenuating the accumulation of decision information toward an appropriate response.

Here, we arbitrated among these possibilities using computational modeling and human electroencephalographic (EEG) recordings, in combination with a visual spatial attention task in which two streams of information needed to be integrated simultaneously and independently over time before making a category judgment about one of them. Building on recent findings obtained in a single-stream version of the task (Wyart et al., 2012), we asked specifically whether dividing attention leads information to be lost during (1) perceptual encoding in sensory signals, (2) conversion to associative decision signals, or (3) accumulation toward a motor response.

Materials and Methods

Participants.

Seventeen students were recruited from the University of Oxford (age range, 19–29 years; nine females). All had normal or corrected-to-normal vision, and reported no history of neurologic or psychiatric disorders. They provided written consent before the experiment and received £30 in compensation for their participation, in addition to bonuses depending on their categorization performance (approximately £6). The experiment followed local ethics guidelines.

Stimuli.

Visual stimulation was delivered using the Psychophysics-3 Toolbox (Brainard, 1997; Pelli, 1997) and additional custom scripts written in MATLAB (MathWorks). The display CRT monitor had a resolution of 1024 × 768 pixels and a refresh rate of 60 Hz, and was gamma corrected using a decoding exponent of 2.2. Participants viewed the stimuli from a distance of ∼80 cm, their head placed on a chin rest in a darkened, quiet room.

Each trial comprised two streams of eight Gabor patterns presented every 333 ms (i.e., 3 Hz) at ∼4° of visual angle to the left and right of a fixation point, preceded by two visual masks and followed by one visual mask presented at the same presentation rate. All Gabor patterns had identical parameters (contrast, 50%; diameter, 4° of visual angle; spatial frequency, two cycles per degree of visual angle; Gaussian envelope with an SD of 1° of visual angle), except for their angular tilt. Premasks and postmasks were created from the linear superposition of the four prototypical cardinal and diagonal Gabor patterns. Each stimulus was presented on the screen for 317 ms (19 frames) and followed by a blank period of 17 ms (1 frame) to avoid visual “tearing” artifacts across successive elements, thus resulting in a stimulus onset asynchrony of 333 ms.

Experimental design.

In all trials, participants were asked to make a binary category judgment about one of two streams of oriented Gabor patterns; whether the tilt of the patterns in the stream fell closer to the cardinal or diagonal axes. Each pattern, located at position k in the stream, could thus be described by the following two quantities: its “perceptual update” (PU_k), corresponding to its angular distance from sample k − 1, and its “decision update” (DU_k), corresponding to its projection on the cardinal–diagonal decision axis, which mapped nonmonotonically onto tilt, following a w-shaped profile depicted in Figure 1c. Positive or negative feedback was provided as a function of whether the given response (cardinal or diagonal) matched the sign of the sum of presented decision updates (DU_1…8). In half of the trials (the “focused attention” condition), participants were attending to one stream and ignoring the other stream according to a fully predictive cue, corresponding to a transient color change in the fixation point chosen among the following three highly discernable colors: pink, blue, or orange (e.g., pink for the left stream, blue for the right stream for participant 1), occurring 1333 ms before the onset of the first element (i.e., 667 ms before the onset of the first premask). In the focused attention condition, each trial ended with a second, identical color flash in the fixation point 667 ms after the postmask, probing the stream that participants should respond to. In the other half of the trials (the “divided attention” condition), participants were provided with an uninformative color change in the fixation point before the onset of the first element (orange for participant 1), and the stream that participants should respond to was revealed only at probe onset, using the same color-side mapping as in the focused attention condition (i.e., pink for the left stream, blue for the right stream for participant 1). Therefore, the only difference between the two conditions was that the color cue was fully predictive of which stream would be later probed in the focused attention condition and fully uninformative in the divided attention condition. The meaning of the three color changes was counterbalanced across participants.

Figure 1.

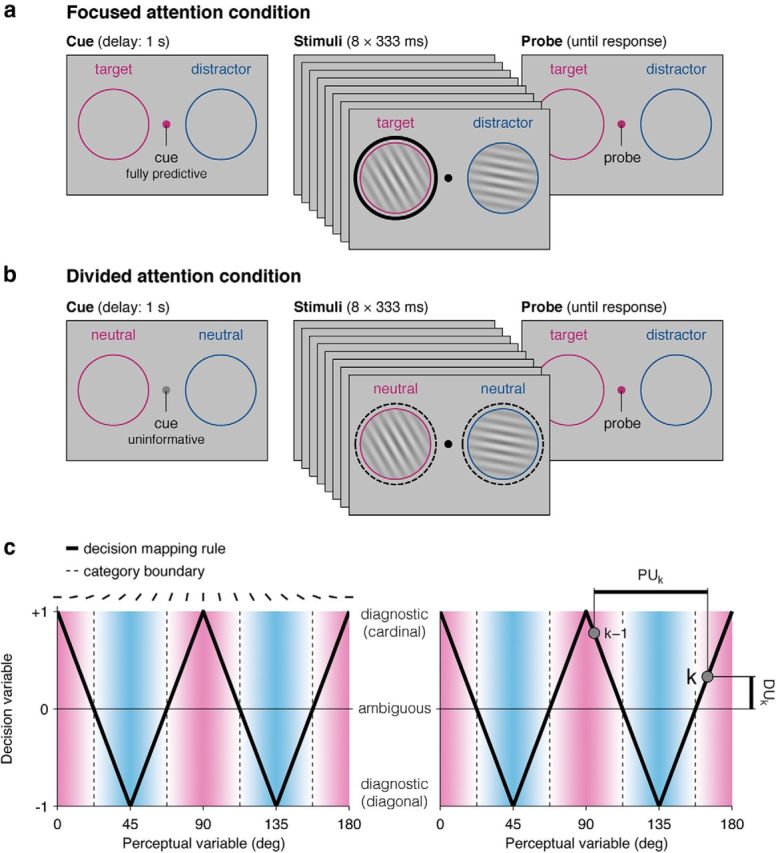
Experimental design. Human participants viewed streams of eight visual gratings presented simultaneously at 3 Hz in their left and right visual fields, before being probed to make a category judgment about one of the two streams. a, In the focused attention condition, participants were cued (left) as to which stream would be probed. b, In the divided attention condition, which stream would be probed was revealed only after offset of the final sample (right). c, Folded decision-mapping rule relating the tilt of sample k (perceptual variable, x-axis) to the cardinal–diagonal decision axis (decision variable, y-axis). Left, The decision-mapping rule follows a w-shaped profile (thick black line) and crosses four category boundaries (dashed lines) in [0, π]. Right, Geometric representation of PU_k and DU_k. PU_k is defined as the absolute angular difference between sample k and the previous sample k − 1, shown as the thick horizontal line. By contrast, DU_k is defined by the amount of category evidence provided by sample k, shown as the thick vertical line.

In each trial, the tilt of each Gabor pattern (sample) was drawn randomly from a probability density function whose generating parameters were titrated for each participant before the experiment (see below). Importantly, the generative categories of the left and right streams were manipulated orthogonally, such that participants could not infer the category of one stream by attending to the other stream. This was made explicit to the participants before the experiment. Across trials, the tilt of each Gabor pattern followed a circular uniform distribution. Participants responded by pressing either of two response buttons with the left or right index finger (DirectIN high-speed button box, Empirisoft), using a cardinal/diagonal response mapping (e.g., cardinal, left hand; diagonal, right hand) fully counterbalanced across participants. Auditory feedback was given at the end of each trial, 250 ms following each response, depending on the agreement between the response and the sign of the decision value across the eight samples. Increasing pairs of tones (440–880 Hz) followed correct responses, whereas decreasing ones (880–440 Hz) followed errors.

Each participant took part in two experimental sessions, taking place on different days. Both sessions were identical in terms of instructions and task (except that they used different pseudorandom sequences), but the first one served as a training session without EEG recordings, whereas the second one corresponds to the test session whose behavioral and EEG data are described here. At the beginning of each session, each participant undertook a short practice block followed by a titration block, during which his or her psychophysical threshold (i.e., the absolute decision value corresponding to a categorization accuracy of 75%) was estimated using an adaptive staircase procedure (Kaernbach, 1991), resulting in a category sensitivity of 1.48 ± 0.05 (group-level mean ± SEM). The experiment consisted of 400 trials, delivered in eight blocks of 50 trials (25 trials in the focused attention condition, 25 trials in the divided attention condition). After each block, participants were presented with a wheel of fortune that randomly selected one trial from the block. Participants won an additional £1 bonus if their response on that trial was correct. The titration procedure targeting 75% accuracy ensured that participants typically won £6 in additional bonuses across the eight experimental blocks.

Computational modeling of human choice.

We performed model-based analyses of choice behavior to (1) identify a model that predicts choice and (2) characterize the observed difference between focused and divided attention conditions via selective changes in model parameters. All analyses rely on a multivariate logistic regression of choice from a linear combination of the decision information provided by the eight successive samples (Wyart et al., 2012). More precisely, this regression estimates the eight decision weights (w_ks) associated with each sample k, defined as the multiplicative contribution of the corresponding decision update DU_k to the subsequent binary (cardinal–diagonal) choice, as follows:

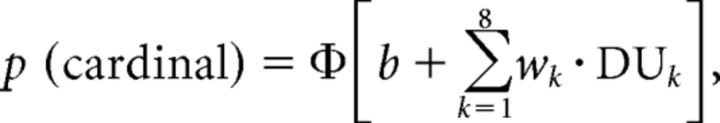where P (cardinal) corresponds to the probability of judging the stream as cardinal, Φ to the cumulative normal function, and b to an idiosyncratic bias toward one of the two responses.

This first model, including nine free parameters, was outperformed during Bayesian model selection by the following leaky accumulator model, which includes only three free parameters by postulating that the successive decision weights are not independent but are related by an exponential function parameterized by a single free parameter or “leak” α, as follows:

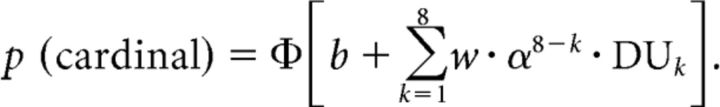This leaky accumulator model provided the most parsimonious fit to the human data. The two key parameters in the model are the sensitivity to decision updates, parameterized by w, and the leak on the accumulated decision value following each new sample, parameterized by α. The model was fitted to the human choice data separately in the focused and divided attention conditions using maximum likelihood estimation—implemented in practice by minimizing its negative value using the interior-point algorithm of the fmincon function in MATLAB.

Bayesian model selection was based on the model evidence (approximated by the Bayesian information criterion) using both fixed-effects and random-effects approaches previously described in the literature. The model evidence adequately takes into account the model complexity by penalizing models with an overly large number of parameters. The fixed-effects comparison assumes all participants to have used the same underlying model to generate their behavior, such that the overall model evidence for a given model is proportional to the product of model evidence for the model for all participants. Based on this model evidence, we compared different models by computing their Bayes factor as the ratio of model evidence of the compared model (Jeffreys, 1961; Kass and Raftery, 1995). The random-effects comparison is more conservative in allowing different participants to use different models to generate their behavior, and aims at inferring the distribution over models that participants draw from (Penny et al., 2010). For this comparison, we computed support for the leaky accumulator model by the exceedance probability (p_exc), which is the (second-order) probability that participants were more likely to choose this model to generate behavior than any alternative model.

EEG acquisition and preprocessing.

A Compumedics Neuroscan EEG system with NuAmps digital amplifiers was used to record EEG signals from 35 Ag/AgCl electrodes, located at FP1, FP2, F7, F3, Fz, F4, F8, FT7, FC3, FCz, FC4, FT8, T7, C3, Cz, C4, T8, TP7, CP3, CPz, CP4, TP8, P7, P3, Pz, P4, P8, PO7, PO3, POz, PO4, PO8, O1, Oz, and O₂; plus four additional electrodes used in a bipolar montage as horizontal and vertical electro-oculograms (EOGs), and two electrodes located at the mastoids used as a reference. All electrode impedances were kept below 5 kΩ. EEG signals were recorded at a sampling rate of 1 kHz and high-pass filtered on-line at 0.1 Hz. Fixation at the center of the screen was monitored on-line using an EyeLink-1000 system sampling binocularly at 500 Hz to ensure that participants did not make overt saccades toward the cued stream in the focused attention condition, or toward either stream in the divided attention condition.

Preprocessing was performed using the EEGLAB toolbox for MATLAB (Delorme and Makeig, 2004). The data were down-sampled to 250 Hz, bandpass filtered between 1 and 40 Hz, and then epoched from 500 ms before the onset of the color cue to 1 s following the offset of the probe. We visually inspected these epochs (1) to remove trials containing nonstereotypical artifacts (such as transient muscular activity) and (2) to identify visually “bad” electrodes showing frequent amplifier “jumps” or other electrical artifacts (e.g., spikes), which were interpolated to the weighted average of neighboring electrodes (maximum, one bad electrode per participant). Independent component analysis (ICA) was then performed on the epoched data—excluding the EOG, reference, and interpolated electrodes from the analysis—and ICA components were visually inspected to reject the ones capturing stereotypical artifacts (in particular, eye blinks and sustained high-frequency noise). Last, single epochs were reinspected visually to ensure that no artifact remained. The simultaneously acquired eye-tracking data from the second (test) session was epoched and screened off-line to ensure that none of our subjects made overt saccades (>2° of visual angle) toward the direction of the cued stream in the focused condition, or toward either stream in the divided condition. Rejected trials were excluded from all further analyses, resulting in an average of 370 ± 5 trials per participant (mean ± SEM).

The 1 Hz high-pass cutoff was applied as an “implicit” baseline to correct for slow drifts in the single-trial EEG data, which are particularly detrimental for the correlation-based approach adopted throughout the study. Importantly, while slow drifts in single-trial EEG data do not affect the shape of the average (i.e., the event-related potentials), they destroy the correlations between the same single-trial signals and stimulus-dependent quantities due to the 1/f property of the EEG spectrum. This implicit baselining approach has the advantage of not requiring to baseline explicitly the data, which would have required the definition of an extra baselining window before each sample—something that is difficult in the context of the present task due to the large amount of overlap between event-related responses to successive samples as a result of the rapid serial visual presentation procedure used (Capilla et al., 2011).

Spectral analyses were performed using the FieldTrip toolbox for MATLAB (Oostenveld et al., 2011). The spectral power of band-limited EEG oscillations between 8 and 32 Hz was estimated using a “multitapering” time–frequency transform (Mitra and Pesaran, 1999; Pesaran et al., 2002; Slepian tapers; frequency range, 8–32 Hz; five cycles; and three tapers per window). The purpose of this multitapering approach is to obtain more precise power estimates by smoothing across frequencies. Note that this time–frequency transform uses a constant number of cycles per window across frequencies, hence a time window whose duration decreases inversely with increasing frequency. When averaged, the alpha frequency band used to measure focusing-related lateralization at occipital electrodes corresponds to 8–16 Hz. For the lateralized choice preparatory signals recorded at central electrodes, the mu frequency band corresponds to 8–16 Hz, whereas the beta frequency band corresponds to 16–32 Hz. In most cases, both the mu and beta bands showed similar patterns and profiles, and were subsequently pooled.

For simplicity, we report statistical tests on EEG data averaged across electrode sites. Lateral occipital electrodes correspond to electrodes O1, PO7, and P7 in left hemisphere, and electrodes O₂, PO8 and P8 in right hemisphere. Lateral parietal electrodes correspond to electrodes PO3, P3 and CP3 in left hemisphere, and electrodes PO4, P4, and CP4 in right hemisphere. Centroparietal midline electrodes correspond to electrodes PO3, POz, PO4, P3, Pz, P4, CP3, CPz, CP4, C3, Cz, and C4. Central/motor electrodes correspond to electrodes C3 and CP3 in left hemisphere, and electrodes C4 and CP4 in right hemisphere, which were analyzed for their difference in calculating an interhemispheric asymmetry (or lateralization) index in log-power decibel units.

EEG analyses—encoding of parametric information.

We regressed single-trial EEG signals against several parametric quantities associated with individual samples at successive time points following corresponding onsets (Wyart et al., 2012). These analyses were performed separately for each of the eight samples in the streams, averaged across samples per participant, and finally averaged across participants to produce a group-level, second-level grand average. For each sample k, a general linear regression model was used in which we included the perceptual updates PU_k (i.e., the tilt between sample k and k − 1) and the unsigned (absolute) value of decision updates DU_k (i.e., the amount of decision-relevant information provided by sample k) for the left and right streams (or, similarly, for the later probed and unprobed streams) as four parametric regressors to predict the trial-to-trial, z-scored variability in EEG signals at a given time t following sample k. This parametric regression was performed separately at successive time points from 0 to 800 ms following sample k. The time course of the corresponding parameter estimates (i.e., the normalized best-fitting regression coefficients) measured the sensitivity of single-trial EEG signals to perceptual and decision updates for each stream, under both focused and divided attention. Because these time courses are time series of the between-trial correlation between the EEG and sample k, we refer to them as describing the “encoding” of perceptual and decision updates provided by sample k. No baselining was applied to the EEG data before the regression. We used this single-trial parametric approach in a previous publication in which participants performed the cardinal–diagonal task on a single stream of gratings (Wyart et al., 2012).

A comparable approach was adopted to assess how signed decision updates were encoded in interhemispheric mu- and beta-band activity at lateral central electrodes. For each participant, we subtracted the spectral log-power between these electrodes, C3 + CP3 − C4 + CP4 or vice versa, depending on the cardinal–diagonal response mapping used for each participant. The hemisphere associated with “cardinal” responses (right if the participant responded cardinal with his or her left index finger, or left otherwise) was counted positively, whereas the motor electrode associated with “diagonal” responses was counted negatively.

EEG analyses—decoding of decision parameters.

We used an analytic approach analogous to a psychophysiological interaction analysis (Friston et al., 1997) to assess the following: (1) the relationship between the encoding of the absolute DU_k and the w_k assigned to that sample in the subsequent categorical choice; and (2) the time course of choice preparatory signals in the last hundreds of milliseconds preceding response execution. We refer to this analysis scheme as a “decoding” approach, because it quantifies the following: (1) how trial-to-trial variability in the encoding of sample k in the EEG (i.e., residuals from the encoding regression described above) covaried with its contribution to choice across trials; and (2) how trial-to-trial variability in choice preparatory signals predicted choice behavior over and above extrinsic fluctuations in decision value (Wyart et al., 2012).

To do so, we quantified whether and how much trial-to-trial fluctuations in EEG signals exerted a modulatory influence on the relationship between the eight decision updates and choice via multivariate parametric regression. In other words, we determined whether EEG-informed regressions of choice led to a significant increase in prediction accuracy. This type of approach is often called “psychophysiological,” because it assesses how trial-to-trial variability in the EEG (i.e., a physiological variable) influences (i.e., interacts with) the subsequent categorical choice (i.e., a psychological variable). Here we contrasted the following two forms of psychophysiological influences: (1) an additive influence, whereby trial-to-trial EEG variability biases the subsequent choice; or (2) a multiplicative influence, whereby the same neural variability modulates the weight assigned to the sample evidence in the subsequent choice. In practice, we estimated the parameters b_k,t and w_k,t of these psychophysiological terms at each time point following each sample k via an EEG-informed regression of choice for which the neural residuals r_k,t from the regression against each DU_k were entered either alone (additive influence, parameter b_k,t) or as their interaction with the corresponding decision update (multiplicative influence, parameter w_k,t) as an additional predictor of the subsequent categorical choice, as follows:

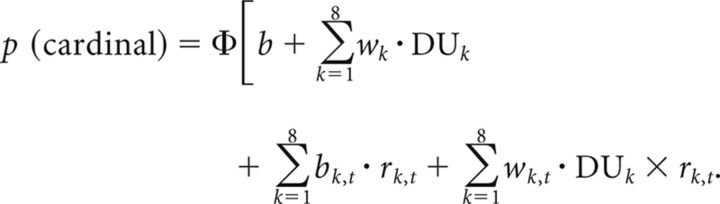More details about this procedure are found in the study by Wyart et al. (2012), where it was applied to a single-stream version of the task. In contrast to conventional “choice probability” measures (Britten et al., 1996), this general procedure allows the determination of not only whether, but also how trial-to-trial fluctuations in brain signals predict variability in the subsequent choice behavior. Here we replicated the qualitative dissociation between the influence of the following two types of neural residuals on choice (Wyart et al., 2012): (1) slow parietal EEG signals at 500–600 ms following each sample; and (2) lateralized motor mu- and beta-band activity in the last 500 ms preceding choice onset. For slow parietal residual and across-attention conditions, Bayesian model selection among additive and multiplicative influences gave a fixed-effects Bayes factor of 10^5.6, and a random-effects p_exc of 0.98 in favor of the multiplicative (weight modulation) account. The same result was obtained separately under focused attention (Bayes factor ≈ 10^4.5, p_exc = 0.96) and divided attention (Bayes factor ≈ 10^3.1, p_exc = 0.88). By contrast, lateralized motor mu- and beta-band residuals yielded a fixed-effects Bayes factor of 10^17.0, and a random-effects p_exc of 0.999 in favor of the additive (bias) account. As for slow parietal residuals, this pattern held separately for the two attention conditions (focused attention: Bayes factor ≈ 10^11.9, p_exc = 0.995; divided attention: Bayes factor ≈ 10^3.7, p_exc = 0.92). These control analyses confirm that residuals in slow parietal signals predict the strength of sample-by-sample weighting, whereas residuals in motor mu- and beta-band lateralization predict fluctuations in response bias in favor of either response (Wyart et al., 2012).

Statistical procedures.

The EEG encoding and decoding analyses described above were performed separately for each participant and each sample. At the population (group) level, we used standard parametric tests (e.g., paired t tests and repeated-measures ANOVA) to assess the statistical significance of observed effects across the group. The type 1 error rate arising from multiple comparisons was appropriately controlled for using nonparametric cluster-level statistics (Maris and Oostenveld, 2007) computed across electrodes, time points, and frequencies.

When reporting nonsignificant differences, we complemented standard “frequentist” tests with Bayes factors to distinguish between an insensitive test (not providing evidence in favor or against the null hypothesis) and a genuine absence of difference (Dienes, 2011). For this purpose, we compute a group-level, random-effects Bayes factor under the exact same assumptions as a standard t test: that the distribution of the observed effect across individuals can be approximated by a normal distribution of the mean (μ) and SD (σ). To compute the Bayes factor, we computed the maximum log-likelihood of the following two models: the “null” hypothesis, which assumes that μ = 0 and has therefore one less parameter than the “effect” hypothesis, for which both μ and σ can be adjusted freely to the observed data. We then used the Bayesian information criterion to compare the two models and compute the corresponding Bayes factor. Note that the maximum attainable evidence in favor of the “null” hypothesis grows with the degrees of freedom of the test (here, the number of participants). While Bayesian statistics are usually not considered in terms of thresholds, it is generally assumed that a Bayes factor below 1 of 3 corresponds to substantial evidence in favor of the null hypothesis, whereas a Bayes factor >3 corresponds to substantial evidence in favor of the effect hypothesis (Jeffreys, 1961; Kass and Raftery, 1995).

Results

Scalp EEG activity was recorded from 17 healthy human participants while they viewed streams of eight visual gratings presented simultaneously at 3 Hz in their left and right visual fields, before being probed to make a category judgment about one of the two streams. In the focused attention condition, participants were cued in advance as to which stream would be probed (Fig. 1a). In the divided attention condition, which stream would be probed was revealed only after offset of the final sample (Fig. 1b). Participants were required to respond with their left or right index finger according to whether the tilt of the gratings in the probed stream fell closer, on average, to the cardinal or diagonal axes. Each grating pattern or “sample,” located at position k in the stream, could thus be described by the following two scalar quantities: its PU_k value, reflecting its angular distance from sample k − 1; and its DU_k value, corresponding to its projection on the cardinal–diagonal decision axis, which mapped nonmonotonically onto sample tilt (Fig. 1c; see Materials and Methods). Decisions were made according to whether the sum of DUs 1–8 (DU_1…8) for the probed, “target” stream favored the cardinal or diagonal category, regardless of the information available in the competing “distractor” stream.

Behavior

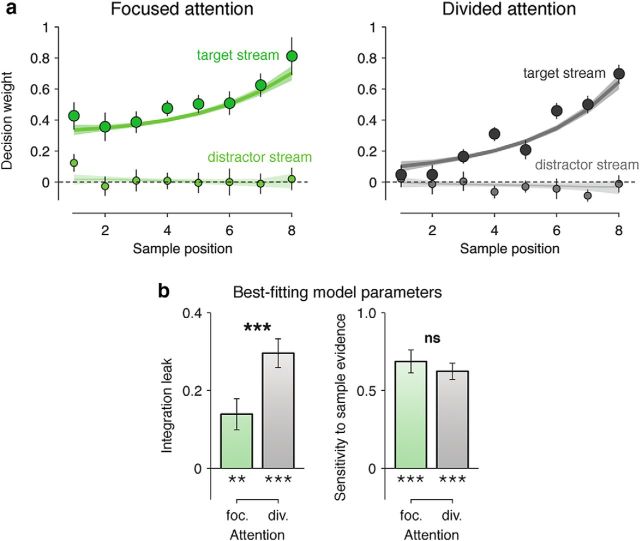
Categorization performance suffered in the divided relative to the focused attention condition (focused attention, 76.1 ± 0.8%; divided attention, 67.7 ± 1.0%; F_(1,16) = 49.2, p < 0.001). We used multivariate logistic regression to estimate the impact (weight) that each sample carried over the subsequent choice (see Materials and Methods). Regression coefficients indexing the eight sample weights for the probed and unprobed streams are depicted in Figure 2a. As can be seen, sample weights for the unprobed stream were not significantly greater than zero, indicating that participants based their decisions solely on the relevant (probed) information, even in the divided attention condition (focused: t₍₁₆₎ = 0.9, p > 0.2, divided: t₍₁₆₎ < 0, p > 0.5). For the probed stream, sample weights were smaller in the divided relative to the focused attention condition (F_(1,16) = 55.9, p < 0.001), but also smaller for earlier samples 1–4 than later samples 5–8 (F_(1,16) = 28.2, p < 0.001).

Figure 2.

Human behavior. a, Decision weighting profiles across the eight samples, sorted by their position in the stream, for target (large dots) and distractor (small dots) streams in the focused (left) and divided (right) attention conditions. Dots and attached error bars indicate the human data (mean ± SEM). Lines and shaded error bars indicate the predictions of the best-fitting model. b, Best-fitting model parameters in the focused (left bar) and divided (right bar) attention conditions. Left, Integration leak. Right, Sensitivity to sample information. Conventions are the same as in a. **p < 0.01, ***p < 0.001. ns, Nonsignificant effect.

This “recency bias” could be captured by a simple leaky accumulator model in which the DU_k provided by each sample k is added to a running sum from which part of the information leaks away exponentially before sample k + 1 (see Materials and Methods). This model, which has two free parameters (the sensitivity to sample information and the magnitude of the integration leak) provided a more accurate description of human choice behavior than a leak-free accumulator model in terms of Bayesian information criterion (focused: Bayes factor ≈ 10⁵², p_exc > 0.999; divided: Bayes factor ≈ 10⁶⁶, p_exc > 0.999), and a more parsimonious description than the full logistic regression model, including eight independent samples weights (focused: Bayes factor ≈ 10⁹¹, p_exc > 0.999; divided: Bayes factor ≈ 10⁸³, p_exc > 0.999), in both attention conditions. Comparing best-fitting parameters across participants (Fig. 2b) revealed that where the sensitivity to sample information did not differ between the focused and divided attention conditions (focused attention, 0.66 ± 0.07; divided attention, 0.61 ± 0.05; t₍₁₆₎ = 0.7, p > 0.5, familywise p_exc = 0.06), the integration leak was significantly greater under divided attention (focused attention, 0.14 ± 0.04; divided attention, 0.30 ± 0.04; t₍₁₆₎ = 4.2, p < 0.001, familywise p_exc = 0.95). Accordingly, a selective increase in integration leak under divided attention accounted for substantially more choice variability than a reduced sensitivity to sample information (Bayes factor ≈ 10¹³, p_exc = 0.92).

We conducted additional behavioral analyses to ensure that the differences observed between focused and divided conditions—in particular the increased integration leak under divided attention—could not be driven indirectly by the congruence or incongruence between decision information provided by the two streams. First, we observed no effect of between-stream congruency on categorization performance under divided attention (t₍₁₆₎ = 0.5, p > 0.5). We also refitted our computational model separately for trials in which the two streams were congruent and incongruent, and found that neither the sensitivity to sample information nor the integration leak depended on between-stream congruency (sensitivity: F_(1,16) = 1.8, p > 0.2; integration leak: F_(1,16) = 2.6, p = 0.12). Moreover, congruency did not modulate the effect of attention (F_(1,16) = 13.8, p = 0.001) on the integration leak (interaction, F_(1,16) = 0.9, p > 0.2). Even taken in isolation, the best-fitting integration leak did not differ significantly between congruent and incongruent streams under divided attention (t₍₁₆₎ = 1.7, p > 0.1). Together, these control analyses support the observation that it is the dividing of attention which increases the integration leak, not the congruence or incongruence between the decision information provided by the two streams.

EEG data

Encoding of perceptual updates

Next, we investigated how perceptual information in both streams modulated electrical brain activity. Instead of computing event-related averages, we used a parametric single-trial approach (Philiastides and Sajda, 2006; Philiastides et al., 2006; Ratcliff et al., 2009; Wyart et al., 2012) in which the momentary PU_k value was regressed against EEG data at each electrode and time point following the onset of sample k (see Materials and Methods), separately for the left and right streams. Plotting the time course of the resulting regression coefficients under focused and divided attention revealed contralateral encoding of perceptual information at occipital electrodes in both conditions (Fig. 3a, top), with a first positive deflection peaking at 120 ms followed by a second negative deflection at ∼260 ms (both clusterwise p < 0.001; see Materials and Methods). In the focused attention condition, contralateral encoding of perceptual information for the target (cued) stream at 120 ms (Fig. 3b, top) was stronger than the distractor (uncued) stream (F_(1,16) = 7.2, p = 0.01). However, contralateral encoding of perceptual information for both streams in the divided attention condition was also stronger than that for the distractor stream (F_(1,16) = 6.5, p = 0.02) and was not attenuated relative to the target stream (F_(1,16) < 1, p > 0.2). Here (and in subsequent analyses), we tested whether an absence of significant difference is due to a genuine absence of effect (rather than a lack of sensitivity) by computing Bayes factors under the same parametric assumptions as conventional statistics (see Materials and Methods). For the current comparison, we obtained a Bayes factor of 0.32, suggesting no loss in the precision of sensory processing under divided attention (Fig. 3c). Interestingly, encoding of perceptual information at ipsilateral occipital electrodes was significant only for the target stream in the focused attention condition (Fig. 3a,b, bottom panels), with a 30 ms delay in peak correlation relative to the contralateral hemisphere (ipsilateral, 157 ms; contralateral, 123 ms; bootstrapped t₍₁₆₎ = 4.8, p < 0.001), as if additional cortical territory was being flexibly recruited to facilitate the perceptual encoding of information unambiguously cued as relevant.

Figure 3.

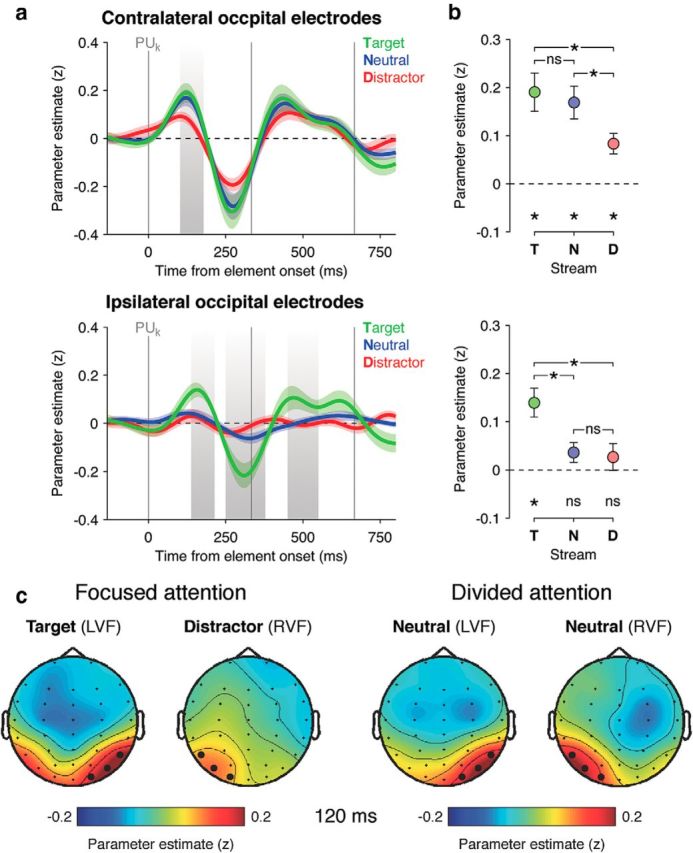
Encoding of perceptual updates. a, Neural encoding of PU_k in lateral occipital EEG signals, expressed as parameter estimate in z-units. Top, Encoding time courses at contralateral occipital electrodes for target (green) and distractor (red) streams in the focused attention condition, and neutral (blue) streams in the divided attention condition. Bottom, Encoding time courses at ipsilateral occipital electrodes for the same streams. Shaded error bars indicate SEM. b, Differences in encoding strength among target (T), neutral (N), and distractor (D) streams at the first peak of ∼120 ms. Top, Contralateral occipital electrodes. Bottom, Ipsilateral occipital electrodes. *p < 0.05. c, Encoding scalp topographies at 120 ms following sample k in the focused (left) and divided (right) attention conditions. LVF, Left visual field; RVF, right visual field. Topographies were flipped across the midline in the focused attention condition such that the target stream appears in the left visual field, and the distractor stream appears in the right visual field. Thick dots indicate the lateral occipital electrodes of interest.

Encoding of decision updates

We then turned to the encoding of momentary decision information provided by individual samples in both streams. For this purpose, we measured the extent to which EEG signals covaried with the “diagnosticity” of each sample (i.e., the absolute value of DU_k, at each electrode and time point following the onset of sample k). Previously, we have demonstrated that decision information in this task is encoded by slow parietal signals with a characteristic profile peaking negatively at 300 ms and followed by a second positive deflection peaking at ∼500 ms (Wyart et al., 2012). Beginning with the focused attention condition (Fig. 4a, left), we replicated this encoding profile for the target stream (both clusterwise p < 0.01; note that data from the target stream are also reported in the supplementary materials in the article by Wyart et al., 2012). However, no such profile was observed for the distractor stream (i.e., no significant cluster was identified at p < 0.05). This suggests that under focused attention, although distracting perceptual information explicitly cued as irrelevant is encoded in early occipital signals (Fig. 3a), the corresponding decision information has been fully filtered out in late parietal signals 200 ms later. Interestingly, while the first negative component peaked contralaterally to the corresponding stream (Fig. 4b, left; F_(1,16) = 5.8, p = 0.02) and concomitantly with the second perceptual component (Fig. 3a), the second positive component was symmetrical over midline centroparietal electrodes (F_(1,16) = 1.1, p > 0.2, Bayes factor = 0.44), which is consistent with the idea of a gradual transition from spatially selective sensory representations to a supramodal, associative decision code (O'Connell et al., 2012; Kelly and O'Connell, 2013).

Figure 4.

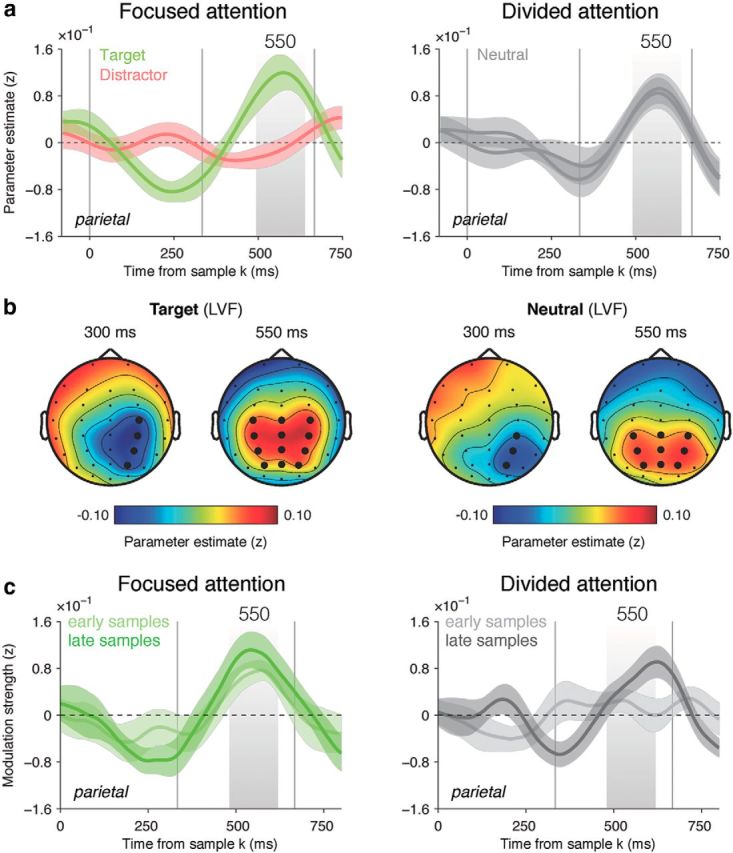
Encoding of decision updates and decoding of decision weights. a, Neural encoding of DU_k in bilateral centroparietal signals, expressed as parameter estimate in z-units, in the focused (left) and divided (right) attention conditions. Conventions are the same as in Figure 3. b, Encoding scalp topographies at 300 and 550 ms following sample k for target (left) and neutral (right) streams. Topographies were flipped horizontally across the midline such that the corresponding stream appears in the left visual field. Conventions are the same as in Figure 3. c, Neural decoding of decision weight assigned to sample k in bilateral centroparietal signals following its onset, expressed as modulation strength in z-units, in the focused (left) and divided (right) attention conditions. Lighter curves indicate decoding strength for earlier samples 1–4, whereas darker curves indicate decoding strength for later samples 5–8. Conventions are the same as in a.

In the light of this, we next tested whether the decision information encoded transiently by late parietal signals at 500–600 ms corresponded with (1) the absolute value of the momentary decision update provided by the latest sample (in other words, the size of the current evidence accumulation step; Wyart et al., 2012) or (2) the absolute value of the cumulative sum of decision updates up to the latest sample (i.e., the amount of accumulated evidence; O'Connell et al., 2012). For this purpose, we compared the log-likelihood of the following two regression models: (1) a model in which late parietal signals were regressed against momentary decision updates; and (2) a model in which the same neural signals were regressed against the cumulative sum of decision updates. Bayesian model selection confirmed that late parietal signals in our discrete multisample categorization task covaried more tightly with momentary decision updates than their cumulative sum (Bayes factor ≈ 10^7.6, p_exc = 0.90).

Next, we turned to our key question of how the encoding of decision information was modulated by dividing attention. In the divided attention condition (Fig. 4a, right), decision information from both “neutral” streams (that were subsequently probed or unprobed with equal probability) at 500–600 ms was encoded with equal strength (F_(1,16) < 1, p > 0.5, Bayes factor = 0.25) and thus differed from the pattern observed in the focused attention condition (interaction, F_(1,16) = 6.9, p = 0.01). Remarkably, the encoding of decision signals under divided attention was as strong as for the target stream under focused attention (F_(1,16) = 1.7, p > 0.2, Bayes factor = 0.57). Using the distractor stream in the focused attention condition as the baseline, decision encoding was significantly stronger for both streams in the divided attention condition (F_(1,16) = 7.4, p = 0.01). Furthermore, the encoding profile measured under divided attention showed the same early lateralization and late symmetry as the profile for the target stream under focused attention (Fig. 4b, right; early negative component: F_(1,16) = 8.2, p = 0.01; late positive component: F_(1,16) < 1, p > 0.5; Bayes factor = 0.26). Together, these findings indicate that momentary decision information can be encoded in parallel in slow parietal signals for two spatially distinct sources of information. This is particularly surprising given that the cardinal-diagonal judgment was rendered highly demanding by the use of a nonmonotonic mapping from features (i.e., the orientations of individual samples) to categories (cardinal or diagonal; Fig. 1c).

Decoding of decision weights

Behavioral data clearly demonstrate a performance loss in the divided attention condition, and computational modeling suggests that this results from an increased integration leak occurring over successive samples, not from a reduced sensitivity to sample information (Fig. 2). Consistently with this account, the preceding analysis indicates that slow parietal signals can encode momentary decision information from two simultaneous streams without significant loss (Fig. 4a,b). It follows that the behavioral impairment observed under divided attention should be reflected not in the encoding of decision information per se, but in the relationship between the strength of encoding and the impact that the corresponding sample wielded over the subsequent choice (decision “weight”). To test this prediction, we extracted residual fluctuations in slow parietal signals from their parametric regression against the decision update triggered by each sample k, and estimated the extent to which these fluctuations covaried with the w_k value assigned to sample k using logistic regression (Wyart et al., 2012; see Materials and Methods). Plotting the strength of this psychophysiological interaction for the probed stream in the focused and divided attention conditions (Fig. 4c), we observed that the decoding of decision weights in slow parietal signals was indeed dampened at 500–600 ms under divided attention (F_(1,16) = 6.8, p = 0.01).

Our computational model further predicted that the attenuated decoding of decision weights in the divided attention condition should be selectively driven by earlier samples (i.e., those from which more information leaks away). In other words, the encoding strength of decision information under divided attention should predict its subsequent influence on choice for later samples 5–8, not for earlier samples 1–4. This prediction was also confirmed by the neural data (Fig. 4c, right), at 500–600 ms in the divided attention condition (samples 5–8: t₍₁₆₎ = 3.6, p = 0.002; samples 1–4: t₍₁₆₎ = 0.4, p > 0.5; Bayes factor = 0.27). The decoding of decision weights for earlier samples under divided attention was dampened compared with both later samples from the same trials (F_(1,16) = 4.8, p < 0.05), and earlier samples under focused attention (F_(1,16) = 4.6, p < 0.05). This finding converges with behavioral modeling analyses suggesting that the impaired decision performance observed under divided attention results from a leak of information during sequential integration.

Focusing of spatial attention

Building on previous work (Wyart et al., 2012), these findings demonstrate that momentary decision information can be encoded simultaneously with no sign of interference in slow parietal signals for two streams of evidence, unless one of them is explicitly cued as irrelevant. This result suggests that the impairment observed under divided attention is not due to rapid switches of a single focus of attention between the two spatial locations. To further substantiate this claim, we analyzed specific spectral bands of EEG signals that have been assigned unique functional significance in attention and decision making. Specifically, the orientation of covert attention to a given spatial location has been associated with a contralateral suppression of EEG signals in the alpha (8–12 Hz) frequency band over the visual cortex (Thut et al., 2006; Siegel et al., 2008; Foxe and Snyder, 2011). By contrast, the integration of decision information up to a hand response has been associated with a progressive lateralization of EEG signals in the mu and beta (8–32 Hz) frequency bands over the motor cortex (Donner et al., 2009; Gould et al., 2012). Our subsequent analyses thus targeted these two frequency bands to pinpoint the stage at which decision information is lost under divided attention.

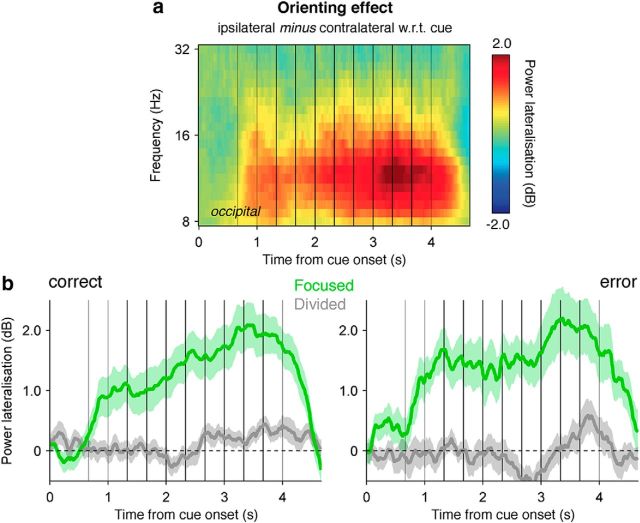
We began by plotting lateralized alpha-band activity (with respect to the cue) at lateral occipital electrodes in the focused attention condition (Fig. 5a). Consistent with previous findings, alpha-band activity was strongly suppressed contralaterally to the target stream in the focused attention condition, and this effect was sustained across the integration period (F_(1,16) = 29.3, p < 0.001). Importantly, the strength of alpha-band lateralization did not differ according to whether the subsequent choice was successful or not (Fig. 5b) in either attention condition (focused: F_(1,16) < 1, p > 0.2, Bayes factor = 0.32; divided: F_(1,16) < 1, p > 0.5, Bayes factor = 0.26). In other words, successful choices were not accompanied by stronger alpha-band suppression toward the stream that was later identified as being relevant. Consistent with this finding, logistic regression of categorization accuracy on the basis of the sum of decision updates and the lateralization of occipital alpha-band activity toward the stream subsequently probed did not reveal any significant cluster at p < 0.1, from the onset of the cue until choice onset. These observations are in agreement with the view that performance under divided attention is limited by information integration and not by rapid switches in the focus of attention between the two streams. The fact that the bilateral desynchronization of alpha-band activity under divided attention was as strong as the contralateral desynchronization observed under focused attention (F_(1,16) < 1, p > 0.5, Bayes factor = 0.24), and was stronger than the ipsilateral desynchronization (F_(1,16) = 27.4, p < 0.001), further supports the absence of spatial competition for sensory processing resources between the two streams in the divided attention condition.

Figure 5.

Focusing of spatial attention. a, Lateralization of alpha-band activity (8–16 Hz) with respect to the cued location at lateral occipital electrodes throughout stream presentation in the focused attention condition. Gray vertical lines indicate the onsets of the premask and postmasks, and black vertical lines indicate the onsets of the eight evidence samples. b, Temporal profile of orienting-related alpha-band lateralization in the focused (green lines) and divided (gray lines) attention conditions, separately for correct choices (left) and errors (right). Conventions are the same as in a. Shaded error bars indicate SEM.

Decoding of choice preparatory signals

Previous findings, including those obtained using a single-stream version of this task (Wyart et al., 2012), have shown that lateralized beta-band activity at central electrodes encodes the integrated tally of information during the last hundreds of milliseconds preceding choice (Donner et al., 2009; Gould et al., 2012). Under focused attention, we observed that the DU_k value covaried with the strength of mu- and beta-band lateralization at lateral central electrodes overlying the motor cortex (Fig. 6a, top left), from 500 ms following the onset of sample k (mu band: t₍₁₆₎ = 3.4, p = 0.003; beta band: t₍₁₆₎ = 3.8, p = 0.001). By contrast, this correlation was entirely absent in the divided attention condition (mu band: t₍₁₆₎ = 0.1, p > 0.5, Bayes factor = 0.24; beta band: t₍₁₆₎ = 0.8, p > 0.2, Bayes factor = 0.32), up until the onset of the probe (Fig. 6a, bottom left).

Figure 6.

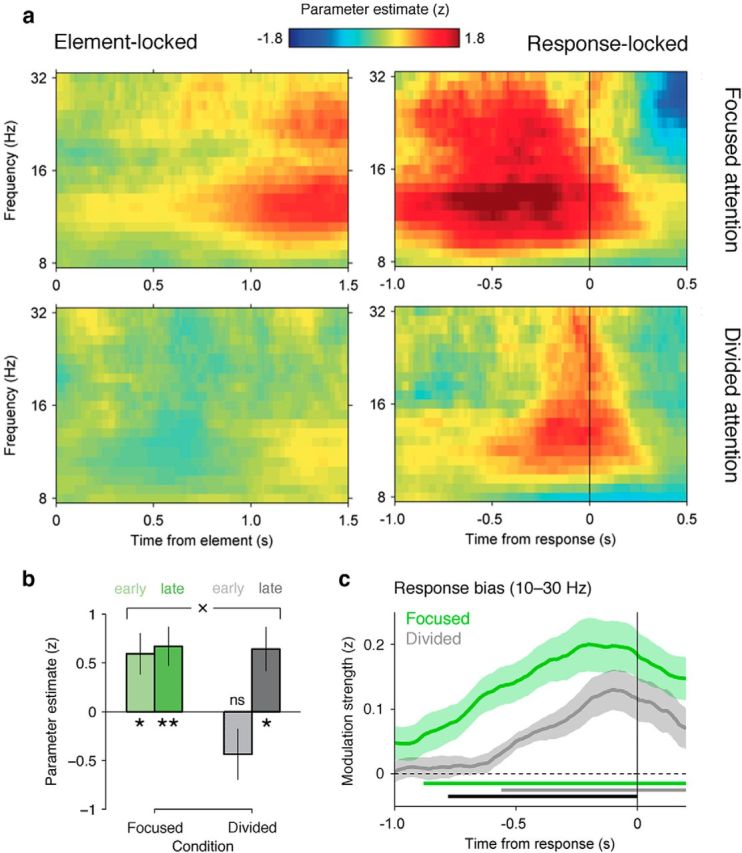
Decoding of choice preparatory signals. a, Neural encoding of DU_k in lateralized mu- and beta-band activity (8–32 Hz) at lateral central electrodes, expressed as parameter estimate in z-units, in the focused (top) and divided (bottom) attention conditions. Left, Neural encoding locked to the onset of sample k. Right, Neural encoding locked to response. b, Encoding strength for earliest samples 1–2 (lighter bars) and latest samples 7–8 (darker bars), in the focused (left) and divided (right) attention conditions. Conventions are the same as in Figure 2. c, Neural decoding of response from lateralized choice preparatory signals in the last second preceding response execution. The thick bars under the curves indicate cluster-level significance for the focused (green) and divided (gray) attention conditions, and their difference (black). Shaded error bars indicate SEM.

Even in the last 200 ms preceding choice onset (Fig. 6a, right panels), the encoding of the summed decision information in response preparation signals was attenuated under divided attention (F_(1,16) = 6.9, p = 0.01). To investigate whether this effect was the result of an integration leak, we regressed separately the earliest samples 1–2 and the latest samples 7–8 against mu- and beta-band lateralization signals (Fig. 6b), allowing us to estimate the contribution of these samples to choice preparatory signals. Note that we included reaction times (signed by choice) as a nuisance covariate to partial out the main effect of response vigor on response preparation (although comparable results were obtained without this extra regressor). In addition to a main effect of attention (F_(1,16) = 5.9, p < 0.03), a factorial analysis revealed a significant interaction between attention and sample position (F_(1,16) = 5.8, p < 0.03), indicating that early samples did not influence choice preparation under divided attention. This neural “leak” parallels the recency effect observed in the behavioral data (Fig. 2) and the attenuated decoding of decision weights for earlier samples (Fig. 4c) observed under divided attention.

Reaction times were not a focus of interest in this study, because responses could be prepared during information integration only in the focused attention condition, resulting in faster correct responses (focused attention, 353 ± 24 ms; divided attention, 625 ± 31 ms; F_(1,16) = 141.5, p < 0.001). Accordingly, responses could be decoded significantly earlier from residual fluctuations in response preparation signals under focused attention (Fig. 6c; focused attention, 815 ms; divided attention, 320 ms; bootstrapped t₍₁₆₎ = 5.7, p < 0.001; see Materials and Methods). Behaviorally, the delaying of response preparation until probe onset under divided attention resulted in a modulation of response times by the aggregate level of conflict between the decision information provided by the two streams, congruent if the two streams favored the same category, and incongruent otherwise (divided attention: F_(1,16) = 26.8, p < 0.001; focused attention: F_(1,16) = 0.1, p > 0.5; interaction: F_(1,16) = 19.4, p < 0.001). Within the divided attention condition, however, responses could not be decoded significantly earlier from fluctuations in motor mu- and beta-band lateralization when the two streams were congruent rather than incongruent (congruent, 325 ms; incongruent, 275 ms; bootstrapped t₍₁₆₎ = 0.3, p > 0.5). In both cases, responses could not be decoded in the last 200 ms preceding the onset of the probe (congruent: t₍₁₆₎ = 1.1, p > 0.2; incongruent: t₍₁₆₎ = 1.6, p = 0.12). This pattern of results further indicates that, although decision information was encoded in parallel and independently under divided attention, resolving the interference between conflicting information provided by the two streams following probe onset contributed to the slowing of response times observed in this condition.

Discussion

The neural and computational mechanisms underpinning attention and decision making have been extensively investigated in isolation. However, a theoretical framework for understanding their interaction has yet to be firmly established. Here, we built upon previous work that has dissociated distinct sensory (visual), decision (parietal), and response (premotor) processing stages that occur en route to a binary category judgment about sequentially occurring information (Smith et al., 2004; de Lafuente and Romo, 2006; Gold and Shadlen, 2007; O'Connell et al., 2012; Wyart et al., 2012). Our findings reveal two distinct attentional filters during decision formation. The first filter occurs as information is passed from feature-selective sensory cortices to a centroparietal signal (O'Connell et al., 2012), at which time it is incorporated into the frame of reference of the category judgment (here, cardinal–diagonal). At this stage, evidence that is unequivocally cued as decision irrelevant (i.e., the uncued stream in the focused attention condition) is eliminated. However, when multiple sources of information need to be integrated simultaneously and independently, a second filter allows only a subset of information to flow from parietal decision signals to effector-selective cortices where it is integrated into a response. This second filter results in an integration leak whereby information proximal to a decision carries greater sway over choices. These two attentional filters map respectively onto the two major experimental manipulations that are typically (and often, interchangeably) used to understand the capacity limits of human information processing, namely directing and dividing attention. Together, these results imply that information can be selected at both an early or a late processing stage, and, as previously hypothesized, that the balance between early and late selection may depend on the level of resources available to perform the task (Lavie and Tsal, 1994).

The facilitatory influence of spatial precueing on the precision of sensory signals has been known for several decades (Hillyard and Mangun, 1987; Hopfinger et al., 2000). However, by dissociating the perceptual and decision information provided by discrete evidence samples, we were able to pinpoint the precise computational stage at which this selection occurs. Perceptual information (i.e., the angular tilt between current and previous samples) was encoded for both cued and uncued streams in contralateral visual cortex, albeit with lower precision for the uncued, distractor stream. However, the most substantial filtering occurred as perceptual information was transformed into the frame of reference of the decision: no reliable encoding of decision updates was observed for the uncued stream in slow parietal signals, as previously reported for gradually changing signals (O'Connell et al., 2012; Kelly and O'Connell, 2013). Interestingly, cued perceptual information was also encoded in ipsilateral visual cortex (Di Russo et al., 2003; Ester et al., 2009), as if additional cortical tissue was recruited to facilitate the processing of decision-relevant locations of space. This is in accord with the view that processing capacity is limited by the cortical territory that can be devoted to the competing contents of perception (Franconeri et al., 2013). However, we note that this additional recruitment of ipsilateral visual cortex observed for the attended stream did not appear critical for performance, in terms of later encoding of decision information in parietal signals. We can only speculate that this ipsilateral encoding of perceptual information would be beneficial to task performance under tight perceptual constraints, using either low-contrast or noisy stimuli. Together, these findings are consistent with theories emphasizing the early filtering of sensory signals under focused attention, but further indicate that selection occurs during the conversion of sensory signals into associative decision signals.

Category judgments can be described by decision-theoretical models in which information is sampled sequentially, but the mathematical formulation that best describes information integration still remains controversial (Wald and Wolfowitz, 1949; Usher and McClelland, 2001; Rouder and Ratcliff, 2004; Ratcliff and McKoon, 2008; Teodorescu and Usher, 2013). Normative models, such as the serial probability ratio test (Wald and Wolfowitz, 1949) and the drift-diffusion model (Ratcliff and McKoon, 2008), assume that integration occurs without loss, whereas other models incorporate a leak parameter that allows information to decay back exponentially to baseline across time (Usher and McClelland, 2001; Ossmy et al., 2013). Leaky integration may describe performance particularly well in extended judgment tasks such as the one used here, where decisions follow evidence provided in discrete samples (Smith and Vickers, 1989). In such tasks, human decisions are often better predicted by information that occurs closer in time to the choice, termed a recency bias. Our behavioral data suggest that the integration leak increases substantially when attention is spread over multiple potentially relevant sources of information. Neurally, this effect is expressed in a muted relationship between the neural processing of early samples and their contribution to choice, and later by a failure to encode early samples in response preparation signals overlying motor cortex in the last hundreds of milliseconds preceding unilateral manual responses (Donner et al., 2009; de Lange et al., 2013). In our study, where the information remains stationary over the course of the trial, this integration leak should be seen as a suboptimal constraint on information processing, not an adaptive process. In other words, an ideal observer performing our task would exhibit no leak, as human participants in the single-stream version of the task (Wyart et al., 2012), unlike in conditions where the state of the environment (here, the category of the stream) can change unexpectedly within each trial (Ossmy et al., 2013).

Our finding that a late processing bottleneck impairs information integration under divided attention might at first glance appear to contradict the findings reported in earlier studies (Luck et al., 1994; Müller et al., 2003), where dividing attention leads to a global dampening of early sensory signals. Moreover, other studies (Thut et al., 2006; Kelly et al., 2009) have reported that attention modulates the link between hemispheric alpha-band lateralization and performance, an effect that we failed to observe. However, some crucial differences exist between the current study and earlier work. First, previous studies manipulated task difficulty at an early sensory or perceptual level, by presenting stimuli at low contrast, or asking participants to perform fine-grained visual discriminations. This manipulation makes it hard to separate the influences of uncertainty at the perceptual and decision stages on performance, or to isolate whether dividing attention operates by attenuating sensory processing, or precluding the conversion of sensory information into a decision signal. By contrast, our task allows us to measure the neural encoding of perceptual and decision information in a dissociable fashion, and to assess how they are respectively influenced by attention. Second, our analyses did not focus on the global influence of attention on the average amplitude of event-related potentials, but instead on the degree of correlation between brain activity and perceptual or decision information at the single-trial level. This provides a more nuanced estimate of how the brain processes each sample during sequential integration.

Nevertheless, considering our work alongside these earlier studies offers some more general insights into the influence of dividing attention on perceptual choice. Notably, whereas the main source of uncertainty in previous studies was at the level of detecting or discriminating the stimuli, in our task the major difficulty faced by participants was in integrating decision information across samples. Together with our findings, these observations might suggest that dividing attention impairs the stage of processing that is the most demanding in the context of the task at hand. However, our paradigm and approach differ in a number of ways from those used previously; it will thus be important for future work to validate our findings and interpretation using other paradigms that can distinguish between perceptual and decision stages of processing.

We reported previously that during serial integration, decision information is weighted according to slow fluctuations in parietal signals with a characteristic time constant of 500 ms (Wyart et al., 2012). When two salient events occur in close proximity (e.g., within half a second), then the second may be underweighted or even “blinked.” This occurs because it falls in a trough of excitability that is maximal at ∼250 ms following the first salient event, and thereby fails to enter the integration process that ultimately leads to choice. Here we extend these initial findings by showing that this serial constraint on momentary information processing occurs upstream from a second capacity constraint on information integration when attention is divided between multiple competing sources of information in space. This highlights the dissociation between the serial processing of decision-relevant evidence (which can occur in parallel at two spatial locations) and integration toward an appropriate response (which breaks down selectively under divided attention), and suggests a general capacity limit on human decision making under cognitive load.