Chiral structures from achiral liquid crystals in cylindrical capillaries

Significance

Nematic liquid crystals (LCs) are arguably the simplest examples of partially ordered condensed matter, and they are core materials in many commercial products. Our experiments explore fundamental questions about how chiral configurations of LCs can arise from achiral building blocks. Left- and right-handed chiral structures are produced by a delicate balance of LC bulk elasticity and surface conditions in confinement. The key experimental ingredients are biocompatible aqueous lyotropic chromonic LCs that twist easily. Combined with the new constraints, this class of achiral LC exhibits chiral structures and a rich assortment of defects, which hint at applications in sensing and optics.

Abstract

We study chiral symmetry-broken configurations of nematic liquid crystals (LCs) confined to cylindrical capillaries with homeotropic anchoring on the cylinder walls (i.e., perpendicular surface alignment). Interestingly, achiral nematic LCs with comparatively small twist elastic moduli relieve bend and splay deformations by introducing twist deformations. In the resulting twisted and escaped radial (TER) configuration, LC directors are parallel to the cylindrical axis near the center, but to attain radial orientation near the capillary wall, they escape along the radius through bend and twist distortions. Chiral symmetry-breaking experiments in polymer-coated capillaries are carried out using Sunset Yellow FCF, a lyotropic chromonic LC with a small twist elastic constant. Its director configurations are investigated by polarized optical microscopy and explained theoretically with numerical calculations. A rich phenomenology of defects also arises from the degenerate bend/twist deformations of the TER configuration, including a nonsingular domain wall separating domains of opposite twist handedness but the same escape direction and singular point defects (hedgehogs) separating domains of opposite escape direction. We show the energetic preference for singular defects separating domains of opposite twist handedness compared with those of the same handedness, and we report remarkable chiral configurations with a double helix of disclination lines along the cylindrical axis. These findings show archetypally how simple boundary conditions and elastic anisotropy of confined materials lead to multiple symmetry breaking and how these broken symmetries combine to create a variety of defects.

The emergence of chirality from achiral systems poses fundamental questions about which we have limited mechanistic understanding (1–11). When the chiral symmetry of an achiral system is broken, a handedness is established, and materials with different handedness commonly exhibit distinct and useful properties (10–14) relevant for applications ranging from chemical sensors (15, 16) to photonics (17–19). To date, considerable effort has been expended to control handedness in materials (for example, by chiral separation of racemic mixtures or chiral amplification of small enantiomeric imbalances) (1, 8, 20–22). Recently and in a different vein, identification and elucidation of pathways by which achiral building blocks spontaneously organize to create chiral structures have become an area of active study. Examples of these pathways include packing with multiple competing length scales (8–10, 23, 24), reconfiguration through mechanical instabilities of periodic structures (20, 25, 26), and helix formation of flexible cylinders through inter- and intracylinder interactions (27, 28). In addition, the system of a broken chiral symmetry often consists of domains of opposite handedness with defects separating the domains.

Liquid crystals (LCs) are soft materials composed of anisotropic mesogens that provide remarkable examples of chiral symmetry breaking arising from elastic anisotropy (29–42). In essence, an LC can minimize elastic free energy by organizing its achiral units into chiral structures, such as helices and chiral layers, that incorporate twist deformation (7, 8). The elastic free energy describing nematic LC deformations depends on so-called splay, twist, bend, and saddle-splay elastic moduli, and when twist deformation is comparatively easy, twisting can relieve strong splay and/or bend deformation and lead to production of equilibrium chiral structures (29, 32, 35–38). Similarly, saddle-splay deformation can stabilize chiral structures (43–46).

Elasticity-driven chiral symmetry breaking is perhaps most readily manifested in confined LCs (31–43), wherein surface anchoring imposes a preferred angle for LC mesogens at the interface of the confining boundary. Topological defects enforced by boundary conditions can play a key role in the symmetry breaking as well, because energetically costly deformations are often concentrated in the vicinity of the defects (35–37). A simple example of this phenomenon is found in spherical LC droplets with planar anchoring; here, two surface point defects, called Boojums, cause the director to adopt a twisted bipolar configuration, in which energetically cheap twist deformations relieve strong splay deformation near the Boojums.

In this paper, we introduce chiral symmetry-broken configurations of nematic LCs in a cylindrical confinement geometry, and we explore the energetics of the configurations and their defects. This general class of configuration has been investigated in cylinders (47–52). However, this system differs significantly from earlier work. The configurations that we report on have homeotropic boundary conditions, and their chirality is not of molecular origin (i.e., handedness is not derived from chiral mesogens or dopants). Our chiral symmetry-breaking experiments use Sunset Yellow FCF (SSY), a lyotropic chromonic LC (LCLC) with small twist elastic constant, in polymer-coated capillaries. SSY is composed of columnar aggregates of organic, plank-like molecules in water. The conformal polymer coating is prepared through chemical vapor deposition. The coating induces homeotropic anchoring of the aggregates on the cylinder surfaces through noncovalent interactions (53) thereby enabling the experimental studies of LCLCs confined in curved geometries with homeotropic alignment. Other than for their biocompatibility (54, 55), LCLCs are known for their very small twist modulus compared with splay and bend moduli; this property renders LCLCs susceptible to spontaneous chiral symmetry breaking (56, 57).

Nematic SSY was found to exhibit two different configurations in the cylinder: one twisted and escaped radial (TER) and one with a double helix of disclinations. The samples also contained a variety of chiral defects originating from symmetry breaking. We investigate their structure and energetics using polarized optical microscopy (POM), numerical calculations of director configurations based on elastic free energies, and Jones matrix-simulated optical textures. The chiral director configurations and defects provide a fascinating example of chiral symmetry breaking arising from elastic anisotropy and show the consequences of a delicate interplay between anisotropic elasticity, boundary conditions, chirality, and topological defects.

Results and Discussion

TER Director Configuration.

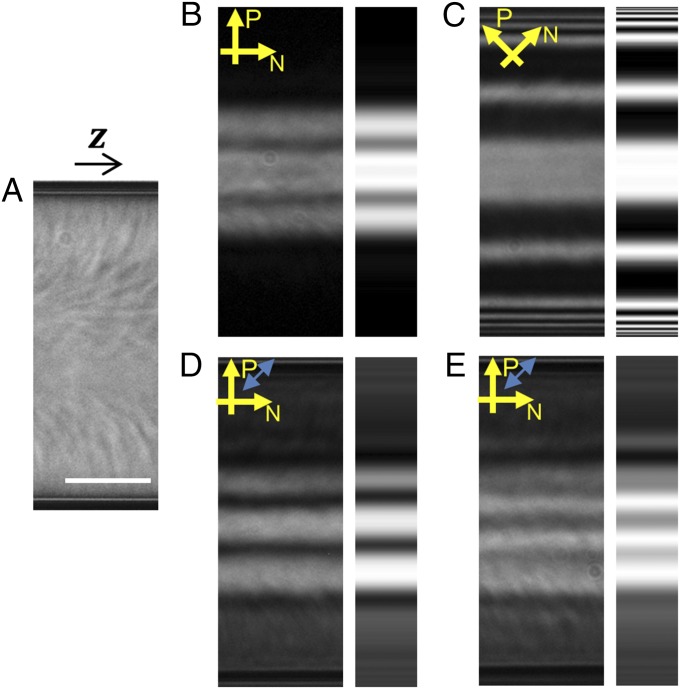
POM images of nematic SSY in capillaries with homeotropic boundary conditions exhibit features that are subtly different from those in the POM images of samples in the well-known escaped radial configuration (58–60). In the bright-field microscopy image in Fig. 1A, a flickering speckle pattern follows the LC director field of the escaped radial configuration; such anisotropic speckle patterns result from thermal fluctuations of the LC directors and accompanying fluctuations of the local extraordinary index of refraction (59, 60). The LC directors are radial near the capillary wall and bend along the radius to be parallel to the cylindrical axis near the sample center; the choice between two degenerate directions of bend deformation determines the escape direction. The center of the escaped radial configuration appears extinguished under perpendicularly crossed polarizers when either a polarizer or an analyzer is oriented parallel to the cylindrical axis. The extinguished intensity arises in this case because all LC directors along the central beam path lack an azimuthal component [α(r, ϕ, z) = 0] (Fig. 2A shows angle definitions). In Fig. 2A, β(r, ϕ, z) is the angle between the z unit vector ($\widehat{z}$) and an LC director (n) at (r, ϕ, z); α(r, ϕ, z) is the angle between the r unit vector ($\widehat{r}$) and the x–y projection (n_xy) of the director at (r, ϕ, z). Thus, the bright central region of the nematic SSY shown in Fig. 1B indicates that the director configuration is different from common escaped radial configurations. Furthermore, in Fig. 1 D and E, POM images with a full-wave plate inserted into the beam path reveal the existence of two different director configurations with the same escape direction.

Fig. 1.

Optical microscopy images and simulated patterns of nematic SSY in a cylinder between crossed polarizers with and without a full-wave plate; z is parallel to the cylindrical axis of the capillary. The concentration and temperature of SSY are 31.5% (wt/wt) and 25.0 °C, respectively. (A) A bright-field microscopy image of nematic SSY with a TER director configuration escaping toward z < 0. Notice the directional texture resulting from thermal fluctuations of the LC directors. In B–E, (Left) POM images of the TER director configuration under monochromatic illumination (wavelength = 650 nm) and (Right) corresponding POM patterns simulated by Jones matrix calculations of a director-field model between a polarizer (P) and an analyzer (N) with and without a full-wave plate are shown; the pass axis directions of the polarizers are shown as single-headed yellow arrows, and the slow axis of the wave plate is shown as a double-headed blue arrow. Materials and Methods has details about the calculation of director configurations and the Jones matrix calculation. The escape directions are identical, and the twists in D and E are left- and right-handed, respectively. (Scale bar: 25 μm.)

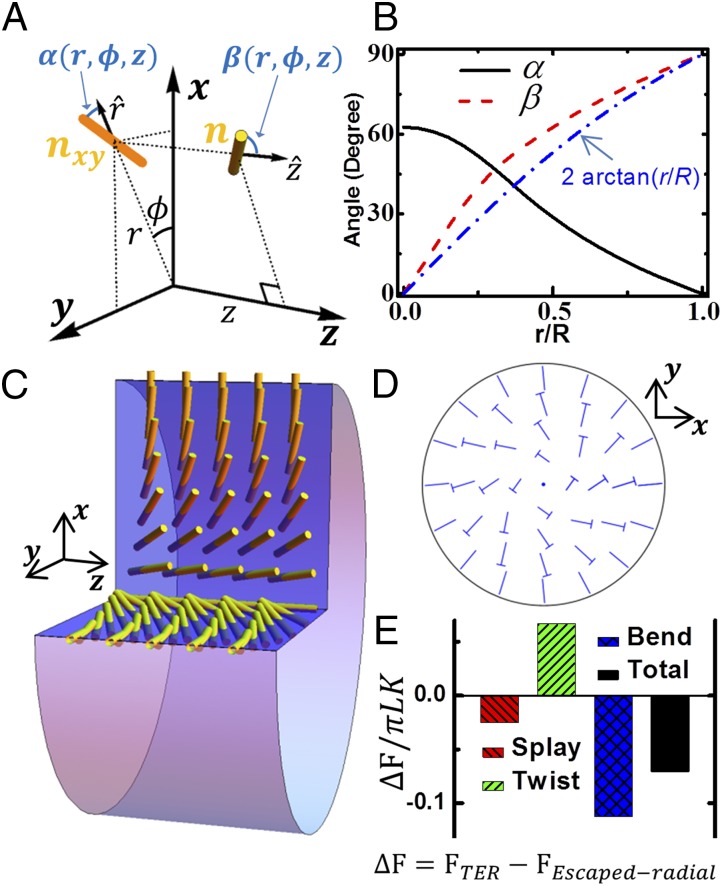
Fig. 2.

A TER director configuration. (A) A cylindrical coordinate system (r, ϕ, z) is used to describe the TER director configuration, where z is parallel to the cylindrical axis; β(r, ϕ, z) is defined by the angle between the z unit vector ($\widehat{z}$) and an LC director (n; an orange rod) at (r, ϕ, z), and α(r, ϕ, z) is defined by the angle between the r unit vector ($\widehat{r}$) and the x–y projection (n_xy) of the director at (r, ϕ, z) (Eq. 2). (B) Numerically calculated profiles of α and β in the TER director configuration as a function of r/R when K₁:K₂:K₃ = 1:0.09:0.94 [i.e., the elastic moduli values for 31.5% (wt/wt) SSY at 25.0 °C]. R is the radius of the cylindrical confinement. The blue dash–dot curve corresponds to 2arctan(r/R), which is the dependence of β on r/R of the escaped radial configuration without twist (α = 0) when K₁ = K₃ = K and K₂ is greater than the critical value$\hspace{0.17em}{K}_2^c\approx 0.27K$. C and D provide schematic diagrams of a right-handed TER director configuration. In C (the perspective view), yellow rods represent LC directors. Here, the directors escape to the west. In D (the cross-sectional view), the directors are shown as nails with heads that come out of the page. (E) ΔF represents the splay, twist, and bend elastic energies and their sum in the TER configuration (F_TER) minus the corresponding parameters in the twistless escaped radial director configuration (F_{Escaped-radial}). (ΔF is the energy difference between configurations for each parameter and their sum.) L is the cylinder length.

Because nematic SSY has a small twist elastic modulus compared with splay and bend moduli, it adopts a TER configuration in cylinders with homeotropic boundary conditions. In contrast to the escaped radial configuration with no azimuthal component [α(r, ϕ, z) = 0], the TER configuration has both nonzero α(r) and β(r) with azimuthal symmetry. For example, Fig. 2B shows numerically calculated α(r/R) and β(r/R) for 31.5% (wt/wt) SSY at 25.0 °C; here, R is the cylinder radius, and the ratio between splay, twist, and bend moduli is K₁:K₂:K₃ = 1:0.09:0.94 (Materials and Methods discusses numerical calculations of director configuration) (56). Notice that β(r/R) exhibits considerable deviation from 2arctan(r/R), the analytic solution of the escaped radial configuration, when K₁ = K₃. [Note also that the conditions α(r/R = 1) = 0° and β(r/R = 1) = 90° indicate that the directors satisfy the homeotropic boundary condition, and the condition β(r/R = 0) = 0° corresponds to directors pointing parallel to the cylindrical axis at the center of the cylinder.]

The TER configuration is depicted in Fig. 2 C and D. Because of the nonzero twist encoded by nonzero α(r), the configuration is chiral and can be either right- or left-handed. For instance, the configuration in Fig. 2 C and D is right-handed according to the convention of the handedness of helices (i.e., the streamlines formed by the directors trace out right-handed helices). Finally, note that the simulated optical textures based on these numerically calculated profiles shown in Fig. 1 match the experiments quite well (details in Materials and Methods and Fig. S1 shows comparisons at other concentrations and temperatures).

The TER configuration lowers the elastic free energies of the escaped radial configuration by introducing a twist deformation with degenerate right- or left-handedness. Specifically, our numerical calculations suggest that, with K₁ = K₃ = K, the total elastic free energy of the TER configuration becomes smaller than that of the escaped radial configuration when $K_2<K_2^c\approx 0.27K$ (details in Fig. S2). Thus, as shown in Fig. 2E, the TER configuration has less splay, bend, and total elastic free energy than corresponding energies in the escaped radial configuration at the expense of increased twist elastic free energy. The two different directions of the twist deformation (i.e., the handedness) have the same elastic free energy and have been observed experimentally with no noticeable preference for either handedness. In other words, the chiral symmetry of the confined achiral nematic SSY is spontaneously broken because of its very small twist modulus compared with the other moduli. Chiral structures are, thus, generated from an LC with achiral mesogens.

We note that the energetics of chiral symmetry breaking in cylinders with homeotropic anchoring are different from the energetics in recently reported spherical droplets of nematic LCLCs with planar anchoring (37). In the spherical droplets, two topological point defects called Boojums play a critical role in the chiral symmetry breaking. Energetically cheap twist deformation cancels out strong splay elastic free energy near the defects to achieve the well-known twisted bipolar configuration; twist deformation, however, increases bend elastic free energy. In this work, singular defects do not play a role in the formation of TER configurations. Moreover, as shown in Fig. 2E, the twist deformation cancels both splay and bend elastic free energies, and the contribution from bend cancellation is much greater than the one from splay cancellation. For instance, if the bend modulus increases while the other moduli are fixed, the twist angle in the TER configuration increases; in the spherical droplet, by contrast, the twist angle in the twisted bipolar configuration would decrease.

Chiral Defects in the TER Director Configuration.

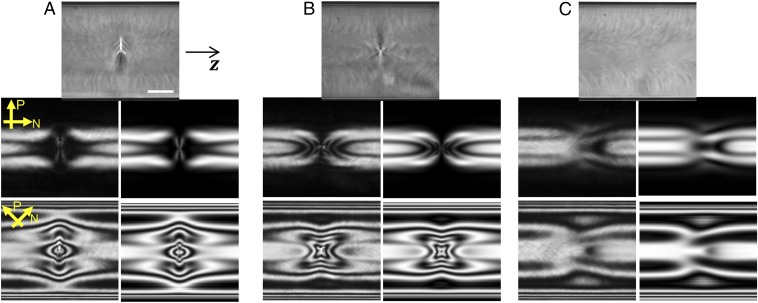
The two degenerate escape directions and the two degenerate senses of handedness (right/left) in the TER configuration lead to three possible types of defects for these systems: radial point defects, hyperbolic point defects, and domain walls of opposite handedness. Singular point defects (hedgehogs) have been observed previously in the common escaped radial configuration without twist, and they are located in regions where the escape direction changes (58–63). Fig. 3 shows experimental and simulated images of our system, which possesses twist. In Fig. 3 A and B, a singular radial (hyperbolic) defect is found to arise when the two opposite escape directions (e.g., toward z > 0 or z < 0) of the TER configuration converge (diverge). The flickering speckle patterns in the bright-field images in Fig. 3 provide clues that help us identify the type of defect. The radial and hyperbolic defects always appear in pairs because of the conservation of topological charge enforced by the boundary condition; indeed, annihilation of defects by merging of adjacent pairs was occasionally observed. In addition to these singular defects, we observed a nonsingular defect with no change in the escape direction, which is shown in Fig. 3C; it is a domain wall across which the handedness of the twist changes (e.g., from left to right). In Fig. 3, the POM images and corresponding simulation images clearly show a modulation of the LC directors as a result of handedness inversion. A POM image with a full-wave plate is shown in Fig. 4C, and it shows the handedness inversion; notice that the right- and left-end regions in Fig. 4C differ, despite the same escape direction, and they match Fig. 1 D and E, respectively. A pair of domain walls will also undergo annihilation by merging, and such annihilations were often observed experimentally.

Fig. 3.

Optical microscopy (bright-field and POM) images of defects and simulated patterns of corresponding defects that arise when nematic SSY is placed in the cylinder; z is parallel to the cylindrical axis of the capillary. The concentration and the temperature of the SSY are 31.5% (wt/wt) and 25.0 °C, respectively. The pass axis directions of the polarizer (P) and analyzer (N) are shown as yellow arrows. (Top) Bright-field microscopy images and (Middle and Bottom) POM images with two different directions of crossed polarizers of (A) a radial defect, (B) a hyperbolic defect, and (C) a twist domain wall. Middle Left and Bottom Left show the experimental images taken under monochromatic illumination (wavelength = 650 nm), and Middle Right and Bottom Right correspond to POM patterns simulated by Jones matrix calculations of director-field models. (Scale bar: 25 μm.)

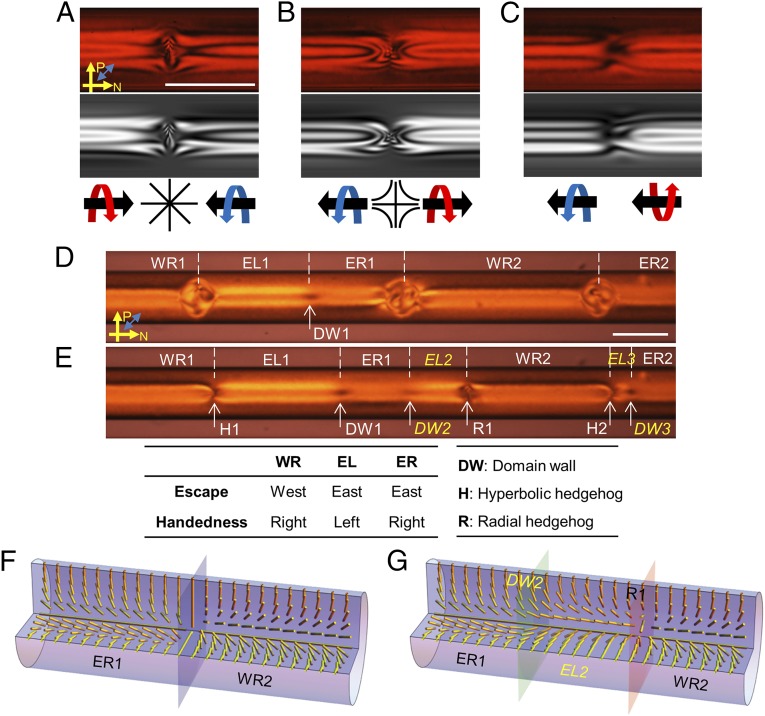
Fig. 4.

Chirality of nematic SSY defects in a cylinder. The pass axis directions of a polarizer (P) and an analyzer (N) are shown as single-headed yellow arrows, and the slow axis of the wave plate is shown as a double-headed blue arrow. (Top) POM images taken between crossed polarizers and a full-wave plate under monochromatic illumination (wavelength = 650 nm), (Middle) the corresponding simulated POM patterns, and (Bottom) schematic diagrams of (A) a radial defect, (B) a hyperbolic defect, and (C) a domain wall. The concentration and temperature of the SSY are 31.5% (wt/wt) and 25.0 °C, respectively. In the schematic diagrams, thin black lines depict director configurations around the singular defects. Thick straight arrows and rotating arrows represent escape directions and handedness, respectively (blue, left-handedness; red, right-handedness). (D and E) POM images of 31% (wt/wt) SSY in a capillary at (D) 40 °C and (E) 38 °C under polychromatic illumination. White dashed lines separate nematic domains, and each nematic domain is labeled with the escape direction of the LC directors [i.e., to the east (E) or west (W)], the handedness of the twist is labeled right-handed (R) or left-handed (L), and the number indicates whether the domain is first, second, third, etc. for each type of domain starting from the left. East (west) corresponds to a direction toward z > 0 (z < 0) (Fig. 1). For example, the WR1 domain is the first (i.e., 1; starting from the left) right-handed domain for which LC directors escape toward the west direction. Hyperbolic defects (Hs), radial defects (Rs), and domain walls (DWs) are labeled in a similar way and marked by white single-headed arrows. The table specifies the meanings of the abbreviations. Note that three isotropic-phase droplets separate the nematic domains in D, where SSY is in a nematic–isotropic coexistence phase. (F and G) Schematic diagrams of (F) a radial defect of the same handedness and (G) a radial defect of the opposite handedness with a domain wall. Yellow rods represent LC directors, and the labels correspond to those in D and E. (Scale bar: 100 μm.)

The escape direction changes sign in passing from one side of a hedgehog to the other in the common escaped radial configuration without twist. In TER configurations, the twist direction can change as well. All of the hedgehogs that we observed in the TER system were heterochiral (i.e., they exhibited a handedness inversion in which twist direction changed from one side of the defect to the other). Interestingly, we never observed a homochiral hedgehog bounded by domains of the same handedness. This absence was surprising, especially considering the degeneracy of both the handedness and escape direction in the TER configuration. Fig. 4 A and B shows representative images of the observed radial and hyperbolic defects under crossed polarizers and a full-wave plate. Notice that their right- and left-end regions do not match after a 180° rotation of either region, which indicates that the regions have the opposite handedness.

Why are singular defects of the same handedness absent? To explore this question, we studied how defects form in response to changes in temperature and thermodynamic phase of SSY in the capillary. To this end, the temperature of 31% (wt/wt) nematic SSY in the capillary was increased to 52 °C to melt the LC into the fully isotropic phase. Then, the temperature was slowly decreased, and the sample evolved through the isotropic–nematic coexistence phase to 38 °C, the point at which the SSY became a fully nematic phase. The coexistence phase is shown in Fig. 4D, wherein we observe cylindrical nematic LC domains of finite length separated by spherical domains of isotropic phase. By applying a slow cooling rate of ∼0.5 °C/min and providing enough relaxation time (∼5 min) for the sample at each measurement temperature, we ensured that each separated nematic domain adopted its own equilibrium configuration. (When the cooling rate was fast, thermally induced flow aligned the nematic SSY and initially led to formation of a single nematic domain without twist and without singular defects. Thereafter, the chiral symmetry of the domain was broken, and many domain walls at random positions were created but still no singular defects; in this case, the sample had only one escape direction.) As a result, the nematic domains in Fig. 4D have TER configurations with independent escape directions and independent twisting handedness. For clarity, we label each nematic domain with the escape direction of the LC directors [i.e., to the east (E) or the west (W)]; we label the handedness of the twist as right-handed (R) or left-handed (L), and we use a numerical index as an identifier. East (west) corresponds to the escape direction toward z > 0 (z < 0) in Fig. 2 A and C. The WR1 domain, for example, is the first (i.e., 1; starting from the left) right-handed domain for which LC directors escape toward the west. Hyperbolic defects (Hs), radial defects (Rs), and domain walls (DWs) are labeled in a similar way.

Our observations of defect formation show that heterochiral hedgehogs are favored over homochiral ones. As the temperature was decreased into the coexistence regime, the nematic domains grew to replace the isotropic domains. Eventually, as shown in Fig. 4E, when the isotropic domains disappeared, the nematic domains merged and formed defects according to the escape directions and twisting handedness of the merging domains. For example, the WR1 and EL1 domains in Fig. 4E formed a hyperbolic defect H1, because the WR1 domain escaped toward the west and the EL1 domain escaped toward the east. Additionally, the handedness of the twist deformation changed across the H1 defect; the WR1 domain is right-handed, and the EL1 domain is left-handed; this handedness inversion is consistent with observations in Fig. 4B. By contrast, the ER1 and WR2 domains did not create a radial defect of the same handedness, shown as Fig. 4F; rather, they created a heterochiral radial defect (R1) and a domain wall (DW2) shown in Fig. 4 E and G. This domain wall creation also arose between WR2 and ER2 domains as shown in Fig. 4E.

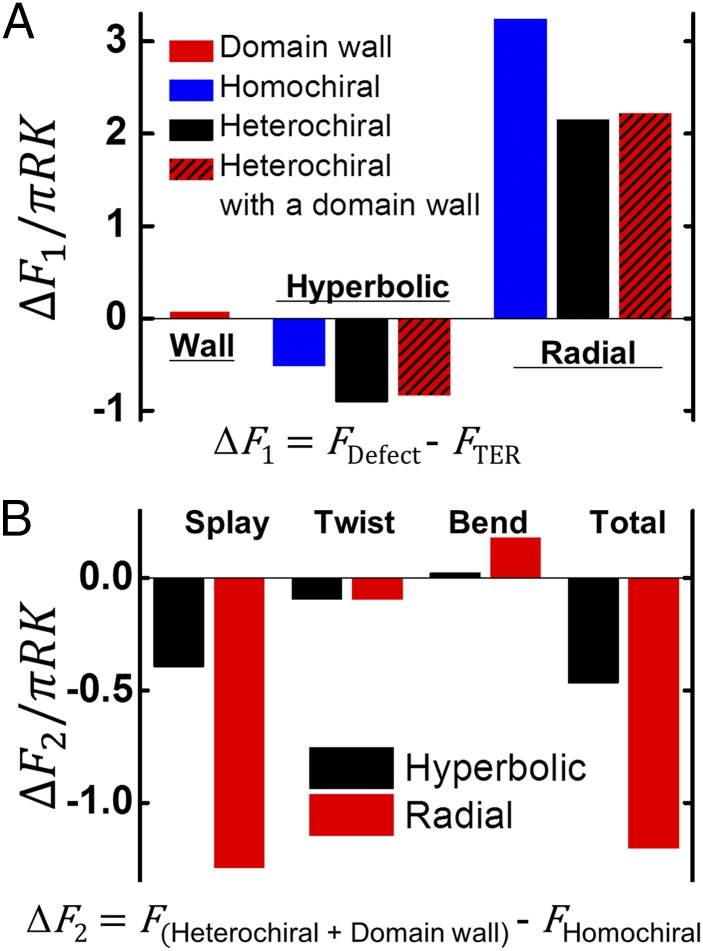
Numerical calculations of chiral defects’ equilibrium director configurations and their elastic free energies reveal that the heterochiral singular defects are energetically favored over homochiral ones. In Figs. 3 and 4 A–C, these numerically computed director configurations and their associated optical textures calculated by Jones matrices successfully reproduced optical textures of all three types of defects (details in Materials and Methods). Furthermore, the numerical calculations enabled us to compare the elastic free energies of the defects in Fig. 5A. Specifically, we calculated differences (ΔF₁ in Fig. 5A) between the total elastic free energy of each defect (F_Defect) and that of the TER configuration (F_TER); these free energy differences are normalized by πRK, where R is the radius of the cylinder and K is the splay modulus. In addition, we calculated the difference in energy (ΔF₂ = F_{Heterochiral + Domain wall} − F_Homochiral) between the combination of a heterochiral defect and a domain wall and an isolated homochiral defect. Fig. 5B illustrates the results of this calculation along with the individual contributions to this energy difference from splay, twist, and bend distortions.

Fig. 5.

Energetics of the chiral defects. Elastic free energies (F) are normalized by πRK to be unitless; R is the radius of the cylinder. K = K₁ with K₁:K₂:K₃ = 1:0.09:1, which approximates the elastic constants of 31.5% (wt/wt) SSY at 25.0 °C. (A) Differences (ΔF₁) between the normalized total elastic free energy of each defect (F_Defect) and the TER configuration (F_TER). (B) Differences (ΔF₂) between the normalized splay, twist, bend elastic free energies, and their sum of a heterochiral hyperbolic (radial) defect with a domain wall (F_{Heterochiral + Domain wall}) and a homochiral hyperbolic (radial) defect (F_Homochiral).

Notice that the combined energy of a heterochiral defect and a domain wall is lower than the energy of an isolated homochiral defect. Thus, an isolated homochiral radial (hyperbolic) defect can lower its energy by splitting into a heterochiral radial (hyperbolic) defect and a domain wall; in the process, it lowers its splay elastic free energy, with only a slight decrease in its twist energy and a slight increase in its bend energy. As shown in Fig. S3, this splay energy cancellation can be understood visually by studying the director in the planes of the singular defects. These results explain why singular defects choose to be heterochiral, creating an additional domain wall if necessary to satisfy the boundary conditions, and why a domain wall between two heterochiral defects is energetically stable and does not combine with either of the defects to create a homochiral one. Note also that, although the hyperbolic defect costs less energy than the TER configuration does, the sum of the energies of a radial–hyperbolic defect pair is always greater than the energy of the TER configuration as expected.

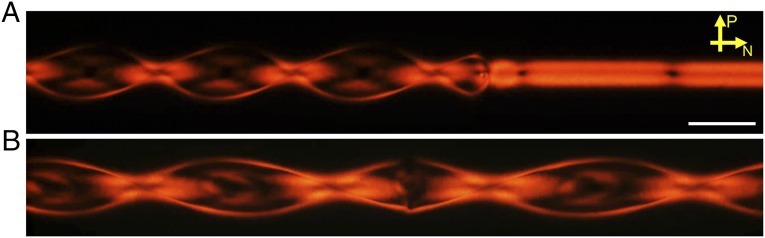
Lastly, we report on an exotic chiral director configuration with a double helix of disclinations. These configurations were observed in the same nematic SSY LC samples confined to the cylinder. As shown in Fig. 6A, the TER configuration on the right side is replaced by a double helix of disclinations slowly growing from the left side at an approximate speed of 500 μm/h (a growing helix is shown in Movie S1). After injection of nematic SSY into capillaries, all nematic SSY samples had the TER configuration at 25 °C (with or without heating and cooling through the isotropic phase). This TER configuration was stable at least for 1 d in most capillaries. Although the sealed capillaries were stored at room temperature, the double helices nucleated at arbitrary positions in the capillaries, albeit often at their ends, and they then started to grow. Because both right- and left-handed helices are allowed, the domain wall-like defects shown in Fig. 6B sometimes formed. The approximate range of the pitch of the helices was from 5 to 10 times the cylinder diameter. Because the pitch varied considerably, even within a single capillary, it was difficult to characterize the pitch and find a relation to its capillary size and the properties of nematic SSY.

Fig. 6.

POM images of nematic SSY with a double helix of disclinations in a cylinder under polychromatic illumination. The concentration and temperature of the SSY are 30.0% (wt/wt) and 23 °C, respectively. Yellow arrows correspond to the pass axis directions of the polarizer (P) and the analyzer (N). (A) A twisted planar–polar configuration (left side) replacing the TER configuration (right side). Two dark spots in the TER configuration correspond to domain walls. (B) A domain wall (center of the image) between two double helices with opposite chirality. (Scale bar: 100 μm.)

We suggest that this configuration with a double helix is a twisted planar–polar configuration schematically shown in Fig. S4. We hypothesize that a planar–polar configuration with homeotropic boundary conditions and two straight surface disclinations parallel to the cylindrical axis can twist to lower its elastic free energy (again because of the small twist modulus of nematic SSY). Note that a similar configuration was reported in a chiral nematic phase near its transition to the smectic-A phase (52); the former situation differs from this case, wherein the double helix of disclinations exists in an achiral nematic phase far from any phase transition. It seems implausible that changes in SSY took place during storage to cause these transitions (e.g., a slight increase in concentration despite sealing of the capillaries or a degradation of the homeotropic alignment layer). Indeed, heating and cooling of all of the nematic SSY samples recovered the TER configuration, but this was eventually followed by another conversion to the twisted planar–polar configuration with a double helix.

Although suggestive, at this time, we cannot determine whether this configuration with a double helix is a true ground state for nematic SSY in a cylinder; additional investigation is required. According to Crawford et al. (64), the energetics of this transition could be related to the saddle-splay modulus (K₂₄) of nematic SSY and a finite anchoring strength of the alignment layer. For instance, a weak anchoring strength permits considerable deviation from a radial orientation near the cylindrical capillary wall and can, therefore, facilitate formation of surface disclinations as we see in the twisted planar–polar configuration with a double helix. The saddle-splay modulus of nematic SSY and the anchoring strength at the SSY–parylene interface are not known, and we expect that characterization of these properties will be essential for understanding the twisted planar–polar configuration with a double helix.

Conclusion

We have explored spontaneous chiral symmetry breaking and rich phenomena involving chiral defects in the achiral nematic LCLC (SSY) confined to cylindrical capillaries with homeotropic anchoring. Despite the absence of intrinsic chirality, nematic SSY produces TER configurations with two degenerate directions for both twisting and escape. These configurations were explained theoretically using elastic free energy models that include the giant elastic anisotropy of nematic SSY. Furthermore, these degeneracies lead to chiral defects: domain walls separating domains of opposite twist handedness and radial and hyperbolic hedgehogs. Interestingly, the radial and hyperbolic defects separate only domains of opposite handedness, and our numerical calculations of elastic free energies reveal their energetic selection. Lastly, in the same system, we report an extraordinary chiral symmetry-broken configuration with a double helix of disclinations, which could be the true ground state of the system. We presume that the helix formation also results from the very small twist elastic modulus compared with the other moduli and that the energetics of the transition from the TER configuration to the twisted planar–polar configuration are closely related to the saddle-splay modulus and a finite anchoring strength, but more investigation is needed.

Additional study of LCLCs in a cylindrical geometry will enable us to investigate unexplored properties of LCLCs, such as the saddle-splay modulus (65, 66), and also, develop applications using chiral structures. For example, we should be able to study chiral amplification by splitting the chiral degeneracy or imprinting a certain handedness (67, 68). In a different vein, application of various classes of external fields or addition of a small amount of chiral dopant might induce a “sergeants and soldiers” type of behavior, wherein a small energetic preference for one handedness over another tips the balance (1, 8, 21, 22). Finally, defect-free configurations of a single handedness may have applications for reconfigurable optical components and devices with optical rotatory power. (As proven in our fast cooling experiment of the SSY from isotropic to nematic phase, flow-induced alignment in a capillary can impose a uniform escape direction that prevents the formation of singular defects.)

Materials and Methods

Preparation of Nematic SSY Confined in Parylene-Coated Capillaries.

All borosilicate glass capillaries were obtained from Vitrocom, and their inner diameters ranged from 50 to 200 μm. Parylene-N films were deposited by chemical vapor deposition using a commercial parylene coater (PDS2010; Specialty Coating Systems) (53). In this process, 0.5–2 g [2.2]paracyclophane was deposited under vacuum conditions (∼55 mtorr) onto every exposed surface of the capillary. The temperatures for vaporization, pyrolysis, and deposition of parylene-N were 160 °C, 650 °C, and 20 °C, respectively.

SSY was purchased from Sigma-Aldrich at a purity of 90%, and it was then further purified using a published method (69–71). The purified SSY was then dissolved in deionized water (18.2 MΩ cm) to make nematic SSY solutions with concentrations that ranged from 29.0% (wt/wt) to 31.5% (wt/wt). Vacuum suction was applied to one end of the capillary to fill the interiors of the parylene-coated capillaries with the nematic SSY solutions (LC was introduced into the system from the other end of the capillary). The capillaries were then placed on glass microscope slides and sealed with epoxy glue to prevent water evaporation. We covered the sample with an indium tin oxide (ITO) coated glass, and the gap between the ITO-coated glass slide and the glass substrate was filled with index matching oil (n = 1.474 at wavelength = 589.3 nm). The oil and the capillaries therein could be electrically heated by the ITO-coated glass; its temperature was measured by a thermocouple submerged in the oil. A proportional-integral-derivative (PID) controller (CNi32; Omega) controlled the sample temperature between 23 °C and 65 °C, with a stability of ±0.1 °C.

Optical Microscopy.

We collected bright-field and POM images using a Leica DM IRB Inverted Microscope with a 63× dry objective that had coverslip-thickness correction and an N.A. = 0.7. Occasionally, we used a 10× dry objective with an N.A. = 0.25 for large field-of-view images. Images were collected either with a black/white CCD (UP-680CL; UNIQ Vision Inc.) or a color CCD (UC-1800DS-CL; UNIQ Vision Inc.) camera under quasimonochromatic illumination (center wavelength = 650 ± 2 nm; FWHM = 10 ± 2 nm) derived from a halogen lamp (using a band-pass filter; P10-650; Orion). For SSY, the transmittance at 650 nm was greater than 95%, and no fluorescence was observed for 650-nm excitation (37). The samples were rotated on a circular stage located between a polarizer and an analyzer. Additionally, for phase retardation experiments, a full-wave plate (optical path difference ∼ 550 nm; Analyzer IC/P; Leica) was placed in front of the analyzer.

Jones Matrix Calculations.

To characterize the LC director configurations, the experimental POM images of samples under monochromatic illumination were compared with simulated 2D transmittance profiles; the latter were computed using models of LC director fields and known optical components (polarizers and a full-wave plate) using 2 × 2 Jones matrices (72). Briefly, simulated plane waves were projected through the optical components and the volume elements (voxels) of the model LC director field. The model LC was placed on a 3D grid. Then, the corresponding Jones matrices of the optical components and the voxels along the beam path were multiplied sequentially to derive transmitted intensities at each output pixel. Note that, for this calculation, the effects of refraction, reflection, and diffraction were assumed to be negligible. The resulting approximate calculations can provide reasonable simulations, because the birefringence of SSY is small [Δn ∼ −0.07 at 633 nm in ∼31% (wt/wt) at room temperature], and the differences in the refractive indices of the glass capillary (n = 1.474 at 589.3 nm) and the SSY (n = 1.42 at 589 nm in isotropic 0.8 M SSY solution at room temperature) (69) are modest. Additionally, the glass capillaries were surrounded by index matching oil (n = 1.474 at 589.3 nm). Per the work by Horowitz et al. (69), we found best values of the birefringence of SSY to match experimental data at each concentration and temperature (Fig. S1).

Numerical Calculation of Director Configurations.

The Frank elastic free energy describing LC deformations is given by Eq. 1:

$$F=\hspace{0.17em}{\displaystyle \int d^3\mathit{x}\hspace{0.17em}\left[\frac{1}{2}{K}_1{\left(\mathit{\nabla }\cdot \mathit{n}\right)}^2+\frac{1}{2}{K}_2{\left(\mathit{n}\cdot \mathit{\nabla }\times \mathit{n}\right)}^2+\frac{1}{2}{K}_3{\left(\mathit{n}\times \mathit{\nabla }\times \mathit{n}\right)}^2\right]}.$$ [1]

Here, n is the nematic director, and K₁, K₂, and K₃ are the splay, twist, and bend elastic moduli, respectively (73, 74). We use the elastic moduli reported by Zhou et al. (56) for numerical calculation of director configurations at each concentration and temperature. Using cylindrical coordinates and the parameterization illustrated in Fig. 2, the director is

$$\mathit{n}=\cos \alpha \sin \beta \widehat{\mathit{r}}+\sin \alpha \sin \beta \widehat{\varphi }+\cos \beta \widehat{\mathit{z}}\mathrm{.}$$ [2]

We first investigate the TER configuration when permitting only an r dependence for α and β. The boundary conditions given by homeotropic anchoring are α(r = R) = 0 and β(r = R) = π/2. The TER configuration requires β(r = 0) = 0 or π corresponding to escape toward the west or east, respectively; here, west (east) corresponds to the direction toward z < 0 (z > 0) in Fig. 2 A and C; α is a free parameter at r = 0, but stationarity of the free energy functional enforces a condition on its derivative: ${\partial }_r\alpha \left(r=0\right)=0$. With these boundary conditions, we can cast energy minimization as a relaxational problem. To this end, we introduce a time coordinate, t, on which the director angles α(r, t) and β(r, t) now depend; we then provide initial guesses of α(r, t = 0) and β(r, t = 0) and numerically solve

$${\partial }_t\alpha =-{\mathit{\Gamma }}_{\alpha }\frac{\delta F}{\delta \alpha }\hspace{1em}\text{and}\hspace{1em}{\partial }_t\beta =-{\mathit{\Gamma }}_{\beta }\frac{\delta F}{\delta \beta }$$ [3]

using the method of lines up to some t_max when α and β converge to solutions of the Euler–Lagrange equations for this system. The Γ factors are relaxation rates. The resultant TER configuration director angles are α_TER(r) = α(r, t_max) and β_TER(r) = β(r, t_max).

We investigate domain walls and singular defects by letting the director angles depend on both r and z, where z ranges from −z_max to z_max. In this case, we apply the same relaxational method as above but with different boundary conditions. For all domain walls and defects, homeotropic boundary conditions again require α(r = R, z) = 0 and β(r = R, z) = π/2; the TER configuration requires β(r = 0, z) = 0 or π, and stationarity of the free energy functional enforces ${\partial }_r\alpha \left(r=0,z\right)=0$. The identity of the domain wall or defect will depend on the boundary conditions at $\pm z_{\text{max}}$.

To obtain a domain wall, we can impose the conditions $\alpha \left(r,z=\pm z_{\text{max}}\right)=\pm {\alpha }_{\text{TER}}\left(r\right)$ and $\hspace{0.17em}\beta \left(r,z=\pm z_{\text{max}}\right)={\beta }_{\text{TER}}\left(r\right)$.

To obtain a radial defect, we impose the conditions $\beta \left(r,z=-z_{\text{max}}\right)=\pi -{\beta }_{\text{TER}}\left(r\right)$ and $\hspace{0.17em}\beta \left(r,z=z_{\text{max}}\right)={\beta }_{\text{TER}}\left(r\right)$.

The hyperbolic defect has $\beta \left(r,z=-z_{\text{max}}\right)={\beta }_{\text{TER}}\left(r\right)$ and $\hspace{0.17em}\beta \left(r,z=z_{\text{max}}\right)=\pi -{\beta }_{\text{TER}}\left(r\right)$.

For these singular defects, choosing $\alpha \left(r,z=\pm z_{\text{max}}\right)=\pm {\alpha }_{\text{TER}}\left(r\right)$ will lead to a same-handedness defect, and choosing $\alpha \left(r,z=\pm z_{\text{max}}\right)={\alpha }_{\text{TER}}\left(r\right)$ will lead to an opposite-handedness defect. For all configurations, we can change the handedness everywhere with $\hspace{0.17em}\alpha \left(r,z\right)\to -\alpha \left(r,z\right)$, and we can change the escape direction everywhere with $\hspace{0.17em}\beta \left(r,z\right)\to \pi -\beta \left(r,z\right)$.

After we have the defect configurations, we can substitute them into the Frank free energy functional (Eq. 1) and integrate numerically to obtain free energies. Although the directors are not well-defined at the defect, the integrals are still convergent. We use an extremely small cutoff distance (∼10⁻¹⁶ R) near r = 0 to perform the numerical integration.

We also investigated the role of saddle-splay deformation, which corresponds to an elastic free energy contribution of

$$F_{24}=-\frac{1}{2}{K}_{24}{\displaystyle \int d^3\mathit{x}\nabla \cdot \left[\mathit{n}\nabla \cdot \mathit{n}+\mathit{n}\times \nabla \times \mathit{n}\right]},$$ [4]

where K₂₄ is the saddle-splay elastic modulus (73, 75). It can be integrated to the boundaries of a bulk system. Here, our boundaries are the capillary wall, the capillary ends, and potentially, the singular defects contained in the capillary. The director orientation at the capillary wall is fixed by homeotropic anchoring for all configurations, and therefore, this surface will not contribute to relative free energy differences among the configurations. Note that different escape directions at the capillary ends do lead to saddle-splay energy differences; however, these differences do not scale with the capillary length, whereas bulk energy differences do scale with capillary length. Hence, saddle-splay effects are negligible in the limit of a long capillary. Finally, we have calculated analytically and numerically that the singular defects do not contribute to the saddle-splay free energy. Thus, we conclude that F₂₄ does not play a role in our system and can be ignored.