Abstract
Optogenetics provides an alternative to electrical stimulation to manipulate membrane voltage, and trigger or modify action potentials (APs) in excitable cells. We compare biophysically and energetically the cellular responses to direct electrical current injection versus optical stimulation mediated by genetically expressed light-sensitive ion channels, e.g., Channelrhodopsin-2 (ChR2). Using a computational model of ChR2(H134R mutant), we show that both stimulation modalities produce similar-in-morphology APs in human cardiomyocytes, and that electrical and optical excitability vary with cell type in a similar fashion. However, whereas the strength-duration curves for electrical excitation in ventricular and atrial cardiomyocytes closely follow the theoretical exponential relationship for an equivalent RC circuit, the respective optical strength-duration curves significantly deviate, exhibiting higher nonlinearity. We trace the origin of this deviation to the waveform of the excitatory current—a nonrectangular self-terminating inward current produced in optical stimulation due to ChR2 kinetics and voltage-dependent rectification. Using a unifying charge measure to compare energy needed for electrical and optical stimulation, we reveal that direct electrical current injection (rectangular pulse) is more efficient at short pulses, whereas voltage-mediated negative feedback leads to self-termination of ChR2 current and renders optical stimulation more efficient for long low-intensity pulses. This applies to cardiomyocytes but not to neuronal cells (with much shorter APs). Furthermore, we demonstrate the cell-specific use of ChR2 current as a unique modulator of intrinsic activity, allowing for optical control of AP duration in atrial and, to a lesser degree, in ventricular myocytes. For self-oscillatory cells, such as Purkinje, constant light at extremely low irradiance can be used for fine control of oscillatory frequency, whereas constant electrical stimulation is not feasible due to electrochemical limitations. Our analysis offers insights for designing future new energy-efficient stimulation strategies in heart or brain.
Introduction
Optogenetics is the combined use of genetic and optical techniques for functional actuation, sensing, and control in biological tissue (1–4). Using genetically introduced light-gated ion channels and pumps, optogenetics offers alternatives to traditional methods of excitation and suppression, i.e., contactless optical control of action potentials (APs) in excitable cells and tissues in vitro and in vivo. Advantages of optogenetic actuation over traditional electrical or chemical manipulations have been widely discussed in recent literature (1,2,5–17); these include features intrinsically born out of the marriage of optical and genetic manipulations including cell-specific targeting and excellent spatiotemporal resolution. In particular, Channelrodopsin-2 (ChR2) and its variants have enjoyed widespread application as optical actuators in neuroscience (1,2,5–9), and more recently in experimental cardiac research (10,11,14,16–23).
Direct electrical stimulation involves the injection of an external current with a predefined waveform and without a specific ionic identity, which brings the membrane potential above threshold to trigger an AP. As part of the history of electronic pacemakers and defibrillators, vast literature exists on waveform optimization for such electrical stimulation, searching for waveforms that are most efficient at minimum charge, for both neuroscience (24,25) and cardiac applications (26–30). Because the electrical stimulus is superimposed on the ongoing membrane potential dynamics, but insensitive to it, there is no built-in feedback.
In contrast, stimulation by opsins such as ChR2 results in a cellular-level, light-controllable transmembrane ion flux of known identity that is mechanistically distinct from electrical stimulation. Significantly, current mediated by ChR2 responds instantly to changes in transmembrane voltage during an AP, with a reversal potential at ∼0 mV, resulting in a real-time negative feedback control (14,15). Therefore, unlike electrical stimulation, the waveform of the light-induced excitatory current, experienced by the cell, will be a function of the AP morphology and thus will vary with cellular phenotype, in addition to the variations due to the strength and duration of the optical stimulus. The result is a dynamic ChR2 current during an AP that is qualitatively and quantitatively distinct from both optically induced currents observed under a voltage-clamp and from traditional electrical current injections (15,16). As such, the theoretical efficiency, or otherwise optimality, of a particular optogenetic stimulation modality must be evaluated per cell type and over a wide range of stimulation protocols. Recent progress has been made to develop in silico tools for such analysis of optical stimulation in the contexts of neuroscience (31–35) and cardiac research (13,16,19,36).
In this report, using computational modeling and analysis, we focus on comparing and contrasting optogenetic and electrical stimulation of excitable cells to address the following subjects.
-
1.
Implications for physiological relevance in cardiac stimulation. Do both stimulations engage inherent currents in a similar manner, and generate similar AP waveforms?
-
2.
Energetic considerations. Are there any energetic benefits to one or the other type of stimulation, and under what conditions?
-
3.
Unique new capabilities in controlling electrical activity. What can optogenetic stimulation offer that is not feasible or made practicable by direct electrical stimulation?
We address these questions at the single-cell level using a model of ChR2 variant H134R and analyzing its performance across human cardiac (and other) cell types and for different stimulation protocols.
Materials and Methods
Cardiomyocyte models—electrical and optical stimulation
To our knowledge, we recently developed and experimentally validated a new mathematical model of ChR2(H134R) (Eq. 1), where gChR2 is the scaling conductance, G(V) is the voltage rectification function, O1 and O2 are the ChR2 open state probabilities, γ is the ratio O1/O2, and EChR2 is the reversal potential for ChR2 (16). The modular form of the ChR2 current model allowed for direct plug-in into various cell-type models, all implemented in the software MATLAB (The MathWorks, Natick, MA). Integration for the cell models was done using a built-in integration algorithm (ode15s) with a variable time step, which was suitable for stiff systems of ordinary differential equations at absolute and relative error tolerances of 10−10. Cardiac cell models used in this study included the 2006 version of the human ventricular cell model by ten Tusscher and Panfilov (37), the human ventricular cell model by O’Hara et al. (38) that allowed modeling of transmural variations, the human atrial models by Courtemanche et al. (39), and the human Purkinje fiber model by Sampson et al. (40). Additionally, we used a single-compartment giant squid axon model by Hodgkin and Huxley, modified to describe experimentally observed excitability characteristics (41). The voltage output for all cell models has a general form (Eq. 2). For pure electrical stimulation, IChR2 was zero, and stimulation was through current injection (Iel). For optical stimulation, Iel was set to zero, and IChR2 corresponding to an applied light pulse was calculated and used. The total ionic current due to other inherent components was computed as described in the original references for ventricular cells (IiV), atrial cells (IiA), Purkinje cells (IiP), ventricular cells with transmural variation as in the O’Hara model (IiVT) (39), and the modified Hodgkin-Huxley model (IiHH) (Eqs. 3–7).
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
During simulations, the response was examined after a 2000-s equilibration period without optical and electrical stimulation for each cell; for Purkinje fibers, the unstimulated condition was used as determined by Sampson et al. (40). Simulations of IChR2 without voltage sensitivity (no-V condition) were performed by setting ChR2 parameters to their values at −80 mV regardless of changing membrane voltage.
Construction of strength-duration curves
Electrical and optical strength-duration (S-D) curves were defined, respectively, as the minimum electrical (pA/pF) and optical (mW/mm2) strength required to generate an AP for a given stimulus duration (ms). APs were defined as an increase in transmembrane voltage to >−20 mV within 400 ms of the start of stimulation, leading to the error function
| (8) |
where Vmax is the maximum voltage within 400 ms of stimulus onset (mV); S is stimulus strength (current amplitude, pA/pF, and irradiance, mW/mm2, for electrical and optical stimulation respectively); and D is stimulus duration (ms). The time interval was chosen to generously accommodate late activations triggered by the stimuli but not interfere with slow endogenous pacemaking in Purkinje. Required strength for each duration was determined numerically to find threshold stimulus amplitude Sth by finding the zero-crossing of the error function with respect to S with constant D.
Calculation of stimulus charge and average current
Threshold charge per unit capacitance Qth (nC/μF) was defined as the integral with respect to time of the inward (depolarizing) stimulating current (Ith, pA/pF) at each point on the S-D curve,
| (9) |
where Tend was defined as 1 s after the onset of stimulation to ensure sufficient time for complete poststimulation closure of ChR2, and thus termination of IChR2 in the case of optical stimulation. Threshold average current was defined as the total stimulating charge divided by the stimulus duration:
| (10) |
Analysis and curve fitting of threshold membrane characteristics
Electrical and optical S-D curves were fit to the classic monoexponential relation, sometimes referred to as the Hill-Lapicque equation (42), with threshold strength, Sth and free parameters rheobase, Srheo (pA/pF or mW/mm2), and chronaxie, τchron (ms) (log refers to natural logarithm):
| (11) |
For optical stimulation, alternative to using irradiance, average current versus duration curves were fit similarly, i.e.:
| (12) |
Curves of irradiance versus average IChR2 (Ith,avg) at threshold conditions were empirically fit to the power series:
| (13) |
All best fits were computed using a nonlinear least-squares algorithm in the software MATLAB. The segments of the S-D curves used for fitting were in the regions 0.7–40 ms and 0–35 pA/pF for electrical stimulation, and 0.30–240 ms and 0–50 mW/mm2 for optical stimulation, with convergence at tolerances of 10−12.
Computational probing of membrane resistance
Membrane resistance Rm was defined as the inverse of the slope of the current-voltage relationship, and it was determined using a small change in membrane voltage and the resultant change in transmembrane current (43,44). Rm during an AP at time t (with membrane voltage Vm) was determined by separately clamping the voltage 10 mV above and below Vm (Vm,+10 and Vm,−10, respectively) and measuring the resulting net transmembrane currents (Im,+10 and Im,−10), as in Eq. 14 (45). Values for the net current were taken 5 ms after clamping to avoid the transient response. Diastolic Rm was defined as Rm at 500 ms after the onset of AP-triggering stimulation (44).
| (14) |
Optical modulation of AP duration
APD at 80% repolarization (APD80) was the interval between reaching 20% of maximum amplitude during depolarization (upstroke) and falling to the same level during repolarization. Baseline APD80 (0% change) was defined as that from a 0.5 ms, 50 pA/pF rectangular electrical pulse for both atrial and ventricular cardiomyocytes. Percent change in APD80 was calculated after applying a 0.1 mW/mm2 or 5 mW/mm2 optical stimuli at varying optical pulse delay (time after the start of electrical stimulation) and pulse duration, both in 1-ms intervals. Phase maps of delay versus duration were constructed using contour plots.
Optical modulation of pacemaking in Purkinje fibers
We characterized long-duration low-irradiance optical modulation of intrinsic pacemaking activity in the Purkinje fiber model with 100-s simulations of constant-irradiance optical stimulation. The pacemaking frequency for each irradiance was evaluated during the final 30 s of the simulation as the inverse of the average cycle length.
Results
We analyzed the response of different excitable cells to direct electrical current injection versus optogenetic stimulation. These included optically excitable models of human atrial (39), ventricular (37,38), and Purkinje (40) cardiomyocytes; in some simulations, a modified model of a giant squid axon (41) (modified Hodgkin-Huxley) was used. Optogenetic stimulation was represented by light-induced ChR2(H134R) current (IChR2) through the introduction of an experimentally validated ChR2 model (16).
Similarities in electrical and optogenetic stimulation of cardiomyocytes
Our simulation results reveal that upon short triggering pulses (electrical or optical), AP morphology is preserved between electrical and optical stimulation for different cell types; furthermore, both stimulation modalities engage very similar contributions by the innate ionic currents (Fig. 1 and Figs. S1–S3 in the Supporting Material). Comparing the response of human ventricular (V), atrial (A), and Purkinje (P) myocytes using S-D curves, we find that their optical excitability qualitatively mimics their electrical excitability, with V requiring the highest energy to excite, followed by A, and P being most excitable (Fig. 2, A and B).
Figure 1.
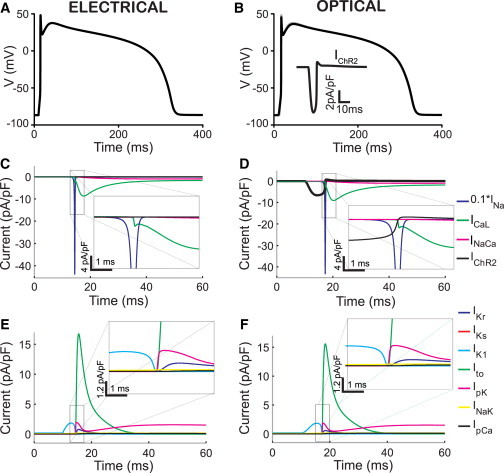
Electrical (left) and optical (right) stimulation produce similar AP morphology in human ventricular cardiomyocytes. (A and B) Triggered APs by injection of electrical current (5 ms, 8 pA/pF), and an optical pulse (10 ms, 0.5 mW/mm2, 470 nm), respectively. Note that the optical trace is overlaid on the electrically triggered AP but practically indistinguishable. (Inset in B) Time course of the resultant ChR2 current. (C and D) Underlying inward currents during electrical (C) and optical (D) stimulation. (E and F) Underlying outward currents during electrical (E) and optical stimulation (F). (Insets) Zoomed-in versions of the area of interest. To see this figure in color, go online.
Figure 2.
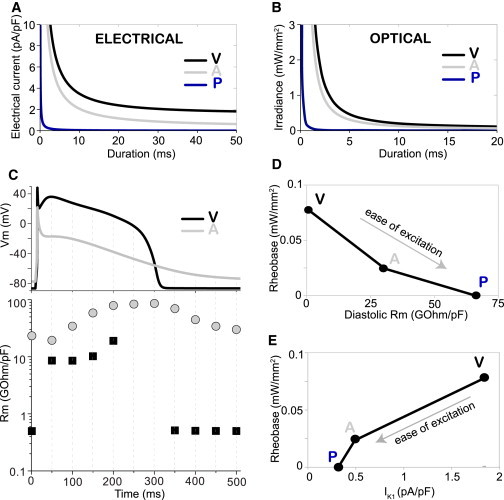
Differential optogenetic excitability of human ventricular, atrial, and Purkinje cardiomyocytes tracks their response to electrical stimulation and is linked to differential membrane resistance Rm and IK1 strength. (A) Strength-duration curves for electrical stimulation by direct current injection (rectangular pulse) in human cardiomyocytes (V, ventricular; A, atrial; P, Purkinje cells). (B) S-D curves for optical stimulation by a light pulse (470 nm) in cardiomyocytes. (C) Membrane resistance (Rm) quantification is shown (bottom) at selected time points during ventricular and atrial APs (top). (D) Threshold irradiance for excitation (rheobase) varies inversely with diastolic Rm determined for V, A, and P myocytes. (E) Rheobase varies proportionally to the peak inward rectifier current, IK1, determined for optically elicited APs in P, A, and V myocytes. To see this figure in color, go online.
From an electrical circuit perspective, the relative ease of cell excitation by a given injected current depends on the cell’s membrane impedance: the larger the impedance, the bigger the voltage changes induced in the cell by the current, i.e., the easier it will be to excite the cell. The resistive component of the membrane impedance, Rm, is a combination of the equivalent resistances of all ion channels in the membrane; it varies during the phases of the AP, and it varies with cell type. At rest (diastole), one of the key determinants of Rm is the actively conducting inward rectifier current, IK1—the larger it is, the more hyperpolarized the resting membrane potential and the lower the Rm will be (i.e., difficult to excite). Neither Rm nor IK1 are perfect measures of excitability, but they both can be predictive of the ease with which cells and tissues can be excited electrically.
Here we show that both of these measures are also related to (predictive of) optogenetic excitability (Fig. 2, D and E, and Williams et al. (16)), i.e., higher Rm (quantified by the Zaniboni empirical method of small perturbations (43,44)) and/or lower IK1 are indeed associated with easier optical excitation, which is seen across cardiac cell types (V, A, P). Furthermore, within the ventricles, regional differences in electrical excitability are matched by a qualitatively similar pattern of optical excitability, where endocardial cells are more excitable than epicardial and midmyocardial cells (Fig. S3, A–D), and such differences can be explained in part by differential expression of IK1 across the ventricular wall (38), although the existence and identity of midmyocardial cells has been controversial.
Waveform differences in the triggering current between electrical and optogenetic stimulation due to negative voltage feedback
Although similar determinants of excitability are at play for electrical and optical stimulation, and both modalities yield similar AP morphology, a closer examination of the S-D curves reveals some differences (Figs. 3, A and B, and S4, A and B). A monoexponential curve fits very well (r2 = 1) the excitation threshold (S-D curve) for electrical stimulation of a ventricular cardiomyocyte, but such a theoretical curve, assuming a simple RC equivalent circuit and a rectangular stimulation pulse (Eq. 11) (46,47), is a poor fit for optical stimulation data in the same cells, when we use irradiance and pulse duration.
Figure 3.
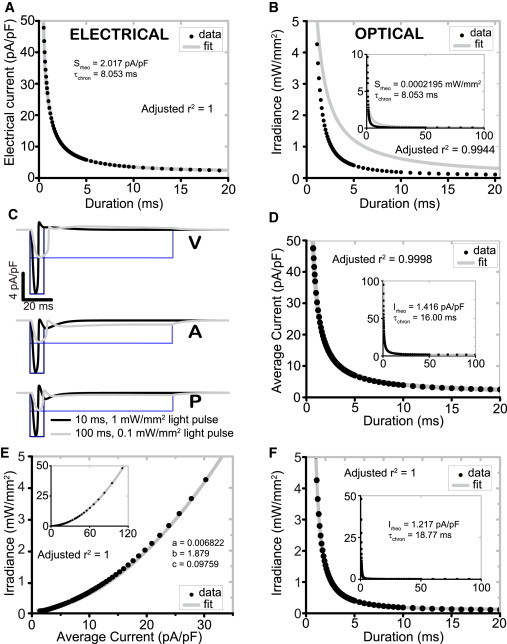
Waveform differences in the optical stimulating current produce a correctable change in the shape of S-D curve for human cardiomyocytes. (A) Electrical S-D curves in human ventricular cardiomyocytes fit well a theoretical monoexponential relationship assuming simple equivalent RC-circuit behavior. (B) Optical S-D curves (using irradiance) deviate from the theoretical monoexponential curve. (C) Differences in current waveform for electrical and optical stimulation: ChR2 current waveforms from optical stimuli of 10 ms and 1 mW/mm2 (black) and 100 ms and 0.1 mW/mm2 (gray). Corresponding rectangular pulses of electrical current injection of equivalent amplitude and duration shown for comparison (blue). (D) Optical S-D curves using average ChR2 current offer a good monoexponential fit. (E) Empirical mapping of irradiance to the average inward stimulating current, using a power series model. (F) Corrected optical S-D curve according to Eq. 15 (correction using the mapping in E) fits the theoretical monoexponential relationship for irradiance versus pulse duration. (All insets) Experimental fit of optical data over extended range. To see this figure in color, go online.
To explain these differences, we compare short and long pulses of electrical and optical stimulation and the resultant inward (depolarizing) currents introduced by both modalities in ventricular, atrial, and Purkinje cardiomyocytes (Fig. 3 C). Light-induced IChR2 experiences instant negative feedback through the changing membrane voltage during a triggered AP, i.e., IChR2 is promptly reduced due to strong inward rectification (16) as the voltage reaches positive values (15). Such waveform differences between the rectangular pulse in ideal direct electrical current injection and the feedback-controlled IChR2 are especially apparent for longer pulses and/or APs with longer plateau phase, where the voltage is around or above the reversal potential for IChR2. Therefore, ChR2 current throughout an AP is heavily dependent on AP morphology (and thus cell type), which in turn is influenced by the stimulus duration.
To prove causal effect of the IChR2 waveform in the modified optical S-D curve, we examined the average ChR2 current at threshold Ith,avg, determined for each point on the optical S-D curve (Eq. 10). Indeed, if Ith,avg is used instead of irradiance, the resultant new S-D curve follows the classical monoexponential relationship with stimulus duration (Eq. 12) (Fig. 3 D). Further, we show a cell-type-specific empirical mapping from threshold average current to irradiance for optical stimulation, i.e., Sth versus Ith,avg, and produce a good fit from a three-term power series (Eq. 13) (Figs. 3 E and S4 C). This mapping simultaneously compensates for the kinetics and voltage- and light-sensitivity of IChR2, and thus allows for the modification of the classic monoexponential S-D equation (Eq. 15) to produce an excellent fit for optical stimulation (Figs. 3 F and S4 D)
| (15) |
with a, b, and c from the previous fit of irradiance versus Ith,avg, and free parameters Irheo and τchron.
Charge needed to excite optically versus electrically reveals optimal settings for different modes of stimulation
To compare directly electrical and optical stimulation, we quantified the total charge (in nC/μF) delivered by a depolarizing stimulus, i.e., the time-integrated current under a depolarizing pulse waveform (Figs. 4 and S3, E and F). The results reveal that the feedback-controlled ChR2 current waveform is beneficial for longer duration (low-irradiance) pulses applied to cardiomyocytes. However, due to the slower ChR2 onset kinetics (compared to the instantaneous electrical current injection considered here), optical stimulation is less efficient for short pulses, i.e., it requires higher charge to reach threshold. For nonoscillatory cardiomyocytes (atrial and ventricular cells), the charge needed for optical stimulation becomes lower than that needed for electrical current injection for pulses longer than 70 ms (Fig. 4 A). These benefits for long-pulse optical stimulation are eliminated if we abolish the voltage sensitivity of ChR2 (no-V in Fig. 4, B and C), and hence the negative voltage feedback. For such a voltage-insensitive optical actuator, the optical charge curves become very similar to the ones for electrical stimulation (Fig. 4 A).
Figure 4.
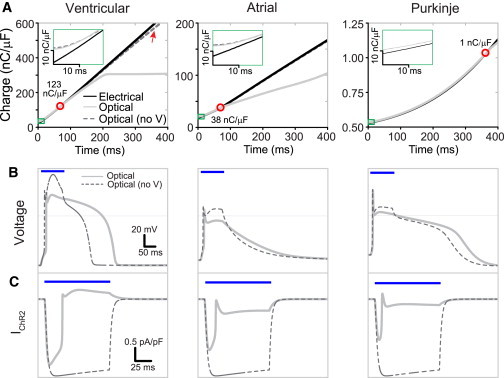
Minimum charge (nC/μF) to excite human cardiomyocytes: direct comparison of electrical and optical stimulation. (A) Charge is calculated for the electrical and optical pulses with and without voltage sensitivity at the S-D curves for V, A, and P myocytes, as described in the text. Optical no-V curves (dashed line) are generated with ChR2 voltage sensitivity removed, i.e., parameters fixed at values corresponding to those at −80 mV. (Red circles and displayed values) Cross-over point between the electrical and optical charge curves. (Insets) Zoomed view of the charge for short-duration pulses (green rectangle) where efficiency of optical stimulation is limited by channel activation kinetics. (B and C) Comparison of AP (B) and IChR2 (C) morphology with (solid line) and with eliminated voltage-dependent magnitude and kinetics (no-V, dashed line) from a 100 ms, 0.1 mW/mm2 pulse. (Blue bars) Time of optical stimulation. Note the lack of voltage-dependent negative feedback in the current traces (in C), which translates to very similar optical-charge curves to electrical stimulation (in A). To see this figure in color, go online.
Waveform-driven energy benefits for optical stimulation do not extend to application in neural cells, represented here with a modified Hodgkin-Huxley model of an axon (Fig. S5). In this cell type, optical stimulation requires a greater charge than electrical stimulation for all stimulus durations. This is due to the mismatch in kinetics: the slower kinetics of ChR2 (exaggerated in these simulations due to the lower temperature for the squid axon (6°C)) causes the channel to remain open for some time after the termination of the light pulse. The shorter neuronal AP and thus much faster return to negative voltages (facilitating ChR2 opening), combined with the slower ChR2 kinetics, results in reactivation of IChR2 and the generation of post-AP depolarizing current. In cardiomyocytes, this current would otherwise be intrinsically terminated or become outward (hyperpolarizing) due to the significantly longer maintenance of depolarization. This effect is shown in Fig. S6, B and C, where even short optical pulses produce a significant depolarizing current after the completion of the neuronal AP.
Unique modulation of ongoing electrical activity in cardiomyocytes by optogenetic stimulation
Due to electrochemical limitations, electrical stimulation is usually applied as brief pulses. In contrast, optical stimulation permits longer stimuli without undesirable side effects. When intrinsically self-oscillatory cells, such as Purkinje or sino-atrial cells, are subjected to such long optical pulses, the resultant frequency of pacemaking can be tuned. Fig. 5 shows a monotonic increase in the pacemaking frequency of human Purkinje cells with irradiance under constant illumination. A large dynamic range is observed, showing >250% increase in pacemaking frequency with very low irradiances (≤20 μW/mm2) when persistent illumination is applied.
Figure 5.
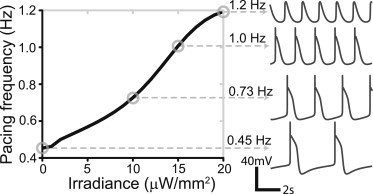
Constant low-level optical stimulation (via ChR2) can fine-tune pacing rate in Purkinje fibers. Oscillatory AP traces and corresponding pacing frequencies are shown on the right for selected points (circles) at 0, 10, 15, and 20 μW/mm2 constant illumination.
Furthermore, one can consider optical stimulation not just for triggering APs, but also for modulating ongoing excitation, i.e., reshaping the APs (15). During ongoing electrical activity and propagating waves of excitation through cardiac tissue, the applied optical stimulation would fall on different phases of the AP of the underlying cells. In such cases, IChR2 can modify the AP morphology depending on the duration, strength, and timing of the optical stimuli. Fig. 6 presents full phase portraits of the resultant modifications of the APD as a function of stimulus duration and the phase or delay of application. The effect is stronger in atrial myocytes due to the faster return to negative voltages, at which substantial inward ChR2 current is generated. Optogenetic stimulation of atrial myocytes with longer pulses applied at sufficient delay with respect to the upstroke can result in substantial AP prolongation and early afterdepolarization (EAD)-like responses. The modulation of human ventricular AP duration (APD) by light-induced IChR2 is much more subtle, especially for short pulses delivered during the plateau; long pulses that extend to the final repolarization phase of the AP, can result in ventricular APD prolongation, which can be enhanced by increasing light levels.
Figure 6.
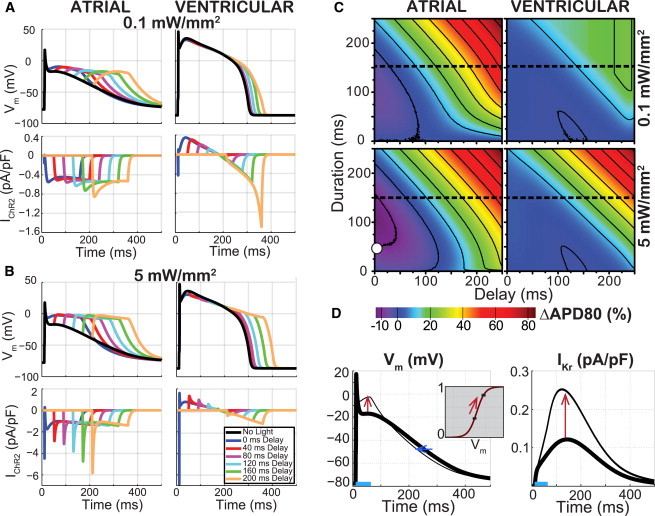
Optogenetic perturbation of ongoing electrical activity produces timing-, duration-, irradiance-, and cell-specific modulation of APD. Activity was triggered by electrical current injection (0.5 ms, 50 pA/pF). (A and B) Example traces of transmembrane voltage in human atrial and ventricular cardiomyocytes and the corresponding ChR2 current resulting from a 150 ms, 0.1 mW/mm2 optical stimulus (A) and 5 mW/mm2 (B), applied at variable delay after the electrical stimulation. (C) Phase maps of APD modulation showing percent change from electrical-only APDs at 80% repolarization (APD80) in human atrial and ventricular cardiomyocytes resulting from a 0.1 mW/mm2 (top) and 5 mW/mm2 (bottom) optical stimulus. (Dashed line) Cross-section corresponding to traces in (A) and (B). (D) Illustration of the mechanism of paradoxical APD shortening for atrial cells. (White circle) For the condition indicated in (C), with 50 ms, 5 mW/mm2 pulse at 0 ms delay, the optically triggered AP (left, thin line), overlaid with the electrically triggered AP (left, thick line), is shown. The early plateau elevation (red arrow) increases the activation of IKr (inset) and doubles the corresponding outward current after the optical pulse (right, red arrow), leading to APD shortening (left, blue arrow). To see this figure in color, go online.
Additionally, relatively short optical pulses delivered close to the time of the upstroke can produce paradoxical APD shortening in atrial cells—an effect that becomes more pronounced with increasing irradiance (Fig. 6 C). This APD shortening is not due to a hyperpolarizing current contributed by ChR2—no such current is present at the respective voltages (Fig. 6, A and B). Instead, the depolarizing ChR2 current, triggered by the optical pulse, elevates the early plateau potential in atrial cells, which sets the mechanism for APD shortening via the delayed rectifier, IKr (Fig. 6 D). Specifically, the ChR2-mediated change in plateau voltage (from −17 mV to −4 mV for the case shown in Fig. 6 D) occurs in the steepest portion of the steady-state activation curve for IKr (see inset), thus leading to a substantial increase in the channel’s open probability (from 39 to 83%), and to a doubling of the repolarizing IKr current after the termination of the optical pulse. Even though other currents are also affected through their dependence on the membrane voltage, the unexpected boost of IKr dominates the response and results in net APD shortening.
As seen in Fig. 6, the effects of optogenetic stimulation during an ongoing cardiac electrical activity depend on the AP waveform because the latter determines the amplitude of the underlying ChR2 current through voltage feedback; in turn, the ChR2 contribution can alter the membrane potential and engage other currents in shaping the AP.
Discussion
Choosing an excitatory opsin with well-quantified behavior over physiological voltages and irradiances, ChR2(H134R), we evaluated its role as a driver and modulator of APs within different cell human cardiomyocytes in silico. We show that due to ChR2’s voltage dependence, the optically triggered IChR2 waveform during an AP across different cell types (Fig. 3 C, also Figs. 1, S1–S3, and S6) ceases by completion of the AP upstroke, before producing a small outward current as the cell depolarizes to potentials >0 mV. In ventricular cardiomyocytes and other cells with AP plateaus >0 mV, this minimal outward current is sustained until termination of either the AP (i.e., repolarization) or the stimulating light pulse. Regardless, AP morphology and recruitment of underlying currents is indistinguishable between electrical and optical stimulation for sufficiently brief optical stimuli (Figs. 1, S1–S3, and S6). Similarly, we show a preserved differential order of excitability between cardiac cell types (Fig. 2) and further, for ventricular cells from different regions (endocardial, midmyocardial, or epicardial) (Fig. S3), subjected to electrical or optical stimulation. In other words, the rates of electrical and optical excitability are guided by the same cellular properties, notably membrane resistance Rm and inward rectifier current IK1 (Fig. 2). Thus, in addition to the use of cell-type specific promoters for selective ChR2 expression (8), a layer of specificity for targeting cell types can be achieved via selective dosing of optical energy based on prior knowledge of differential excitation thresholds (16). These single cell findings can be further leveraged by using tissue- and organ-level models (13,19,36) to identify optimal targets for pacemaking, cardioversion, and arrhythmia suppression, as we have shown for energy-reduction in cardiac pacing through the His bundle (and the Purkinje system) in a whole heart (13).
Theoretical limits of performance/efficiency of optogenetic AP initiation
The dynamic IChR2 waveform causes differences in performance between optical stimulation and electrical current injection with a rectangular waveform. Electrical stimulation produced S-D curves of cardiomyocytes that are well described by a traditional monoexponential equation that assumes a constant AP threshold (i.e., no accommodation) (46,47), whereas optical curves fit poorly for stimulus durations <20 ms (Figs. 3, A and B, and S4, A and B). Light-triggered activation of ChR2 is a kinetic process with a voltage- and irradiance-dependent time constant >1 ms at physiological temperatures (16,48). Therefore, for short pulses, the delay in the full opening of the opsin channel leads to attenuated current, i.e., greater required stimulus amplitude compared to direct electrical current injection. This disadvantage can be at least partly mitigated when using faster opsins with accelerated activation kinetics, such as ChETA (E123T) (49) and ET/TC (E123T/T159C) (50). If instead of irradiance, we consider the average current involved in optogenetic stimulation, then a good match is achieved to the theoretical S-D curve (Fig. 3 D). With knowledge of an empirically determined relationship between average IChR2 and irradiance at excitation threshold for a given cell type (Eq. 13) (Figs. 3 E and S4 C), it is possible to produce a cell type-specific modification to the S-D equation (Eq. 15), and allow an excellent fit for optical S-D curves (Figs. 3 F and S4 D).
To directly compare efficiency between electrical and optical stimulation, we used the measure of threshold total depolarizing (inward) charge (i.e., the integral of IChR2 or Iel with respect to time) needed to generate an AP. In atrial and ventricular cardiomyocytes, with sufficiently long APs, we find that for longer-duration stimuli (>70 ms), optical stimulation requires less charge than electrical stimulation (Fig. 4). This is a direct result of the negative voltage feedback control of the ChR2 waveform during an AP. Such instantaneous feedback prevents the flow of extraneous inward current after reaching an AP threshold. Faster opsins, including ChETA and ET/TC, would be expected to expand the region over which optical stimulation is superior to electrical stimulation to shorter pulse durations. When voltage dependence of ChR2 is eliminated, the light-triggered inward current persists, akin to a low-pass-filtered version of electrical current injection (Fig. 4 C), and therefore charge curves for electrical and optical stimulation become very similar (Fig. 4 A).
Interestingly, we observe this charge/energy benefit for initiating single APs by light to be potentially unique to cardiomyocytes by virtue of their longer APDs. Implementation into a modified Hodgkin-Huxley neuron model (41) reveals a greater charge requirement for optical stimulation for all pulse durations (Fig. S5). The combined effects of the short neuronal AP duration and slower ChR2 kinetics result in an incomplete closing of the ChR2 channel before repolarization (Fig. S6). The result is a significant inward current after an AP and thus an undesired increase in the total carried charge.
Optogenetic control of automaticity/intrinsic pacemaking
Purkinje fibers exhibit automaticity (for the model used here, the intrinsic rate is ∼0.45 Hz in the absence of stimulation). Continuous subthreshold depolarizations in Purkinje fibers can accelerate this self-oscillation by complementing the effect of the pacemaking current, IHCN/If, resulting in a faster depolarization to the AP threshold thereby reducing cycle length.
Persistent electrical current injection is electrochemically unsuitable. The limitation in extending the typically used short electrical stimulation pulses (under 1 ms) stems from the irreversible Faradaic processes that occur at the electrode-solution interface during prolonged monophasic current injections. Such electrochemical reactions, i.e., transfer of electrons between the metal electrode surface and the solution (reduction and oxidation reactions), can yield potentially harmful chemical species, including reactive oxygen species at the cathode, that diffuse into the tissue; they can also damage the electrode itself by corrosion during anode stimulation (47). The electrical charge delivered during a current injection is directly proportional to the mass of the chemical product formed at the electrode-solution interface and released into the tissue. Shortening the pulse duration is the simplest and most commonly used measure to minimize the contribution of irreversible Faradaic reactions and damage during electrical stimulation.
In contrast, optical stimulation can employ much longer pulses without undesirable side effects. However, at high light levels, ChR2 operation and the operation of some hyperpolarizing opsins, e.g., H+ pumps, may result in local change in pH. For low-to-intermediate light levels, this is not a concern (51). Therefore, light-gated ion channels can be used to produce persistent depolarizing current without such limitations, and can be applied in a multicellular and in vivo setting. Using the example of Purkinje fibers, we find that constant illumination of endogenous pacemakers expressing ChR2 allows for tuning of pacemaking frequency with a large dynamic range (250% increase in frequency) with very low irradiances (≤20 μW/mm2) (Fig. 5), which presents an attractive new application of cardiac optogenetics.
Hyperpolarizing opsins, such as eNpHR3.0 (52) (chloride pump) or ArchT (H+ pump) (53), have previously been shown to suppress activity across a variety of neurons in vitro and in vivo. In the same way, these optogenetic suppressors can allow for variable light-controlled suppression of cardiac automaticity, as shown in the zebrafish heart (22). However, the produced outward pump currents are small (one photon = one ion transported) and high light levels are needed, raising concerns about potential heating, especially when red-shifted wavelengths are used (see Supplement in Williams et al. (16) for light-induced thermal effects). Many of these hyperpolarizing opsin pumps are rather simple in their electrophysiological signatures, and therefore can be represented mathematically with simple three- or two-state models (34). They produce an outward current throughout the relevant voltage range, with relatively fast on- and off-kinetics (<10 ms) and negligible inactivation. They exhibit very mild voltage dependence and slight decrease in outward current at more negative potentials (21,51). Coexpression of both depolarizing (e.g., ChR2) and hyperpolarizing opsins has previously been shown to facilitate bidirectional control of neuronal spiking using multiple (54,55) or single (56) constructs. In the heart, suitable targets for such light modulation of endogenous pacemaking include the sinoatrial node, atrioventricular node, and the aforementioned Purkinje fibers.
Cell-dependent optogenetic control of AP morphology
Applying optical stimulation during ongoing APs can produce cell-type specific modifications of APD, dependent on the duration, strength, and timing of the optical stimulus (Fig. 6). Atrial cardiomyocytes are more sensitive than ventricular cardiomyocytes to optical AP modulation via ChR2. Because of their less depolarized plateau, ChR2 in atrial cardiomyocytes can continue to produce inward current mid-AP, potentially leading to EAD-like responses. Conversely, hyperpolarizing opsins will have a suppressive effect on EADs and APD-shortening effects, as shown in vitro using eNpHR3.0 (21). Recent advances, such as the development of Cl−-conducting ChR2, iC1C2 (57), make it possible to achieve larger outward currents than the first-generation (pump) opsins, and therefore employ lower light levels. These hyperpolarizing tools can be used to modify AP shape over time and space, including countering EADs. However, it should be noted that due to anode-break phenomena and hyperpolarization-induced enabling/reopening of sodium channels, inhibitory action on excitation by hyperpolarizing currents is much more complex in nature. This is especially so in spatially extended systems (see variable outcomes in Park et al. (21)) than induction of excitation and AP modulation by depolarizing currents, as we have discussed.
Optogenetics provides a platform for bidirectional control of AP morphology, with application to control of electrical instabilities, e.g., alternans and related arrhythmias. Furthermore, arbitrary waveform stimulation can be easily imposed by light, which together with knowledge of the proper irradiance-to-current mapping (as shown in Eq. 13 and Fig. 3 E) can be used to perturb voltage in a predictable manner and to probe cardiac dynamics. Such robustness and precision of controlling membrane voltage bidirectionally is not affordable by traditional electrical or chemical stimulation.
Considering the phase-dependent effects of optical stimulation in modulating the AP duration in ventricular and especially in atrial single cells (Fig. 6), it is expected that uniform global illumination will result in repolarization gradients at the tissue level due to propagating APs and therefore inherent underlying phase differences. Depending on tissue coupling and the conduction velocity of propagation, such repolarization gradients can be large enough to be relevant to arrhythmia induction. Thus, optical stimulation can be deliberately used as a tool to study the induction of arrhythmias by modifying the AP waveform over space, i.e., applying space-specific graded light irradiance to produce designer repolarization gradients or to correct/cancel existing repolarization gradients by dosing the light over space. Such manipulations are not possible using electrical stimulation as a research tool. Further simulations, using spatially extended models, can aid in revealing the full potential of optogenetic perturbation in cardiac tissue.
Limitations
The goal of this study was to reveal the fundamental cell-level behavior of optogenetic stimulation. Organ-level simulations (13,19,36) are needed to fully consider the anatomical and spatial aspects, neglected here, including tissue-level coupling and light-tissue interactions, e.g., absorption and scattering for in vivo use of cardiac optogenetics (17,58–60). Similarly, the idealized perfectly rectangular electrical current injection, assumed here, will be modified in the actual tissue setting due to electrode and tissue impedances as well as spatial variability of the stimulating electric field. In this work, we ignore the actual efficiency of the sources and the losses (of applied light and applied electric fields) that will occur due to such tissue-level interactions; instead, we use the calculated charge (time-integrated current pulse) at the cell level as a surrogate for energy needed to stimulate. While such a simplistic approach helps us compare directly electrical and optical stimulation, clearly the actual energy in both cases will be influenced in a significant way by the omitted losses. Therefore, our analysis reflects only a brink (the cell level response) in the complex light-tissue (or electric field-tissue) interactions, and spatially extended modeling is needed for full evaluation of the energy performance of the two modalities. Nevertheless, our findings provide basic guidance in understanding electrical versus optogenetic stimulation.
Author Contributions
E.E. initiated the project. E.E. and J.C.W. designed the experiments; J.C.W. ran the simulations; and E.E. and J.C.W. analyzed the results, prepared figures, and wrote the article.
Acknowledgments
We thank Xuxin Chen and Jianjin Xu for early help in implementation of different cell models, and Kevin J. Sampson for help with the implementation of the Purkinje cell model.
This work was supported by National Institutes of Health National Heart, Lung, and Blood Institute grant No. R01HL111649 to E.E.
Supporting Material
References
- 1.Deisseroth K. Optogenetics. Nat. Methods. 2011;8:26–29. doi: 10.1038/nmeth.f.324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Boyden E.S. A history of optogenetics: the development of tools for controlling brain circuits with light. F1000 Biol. Rep. 2011;3:11. doi: 10.3410/B3-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Miesenböck G. The optogenetic catechism. Science. 2009;326:395–399. doi: 10.1126/science.1174520. [DOI] [PubMed] [Google Scholar]
- 4.Dugué G.P., Akemann W., Knöpfel T. A comprehensive concept of optogenetics. Prog. Brain Res. 2012;196:1–28. doi: 10.1016/B978-0-444-59426-6.00001-X. [DOI] [PubMed] [Google Scholar]
- 5.Deisseroth K. Optogenetics and psychiatry: applications, challenges, and opportunities. Biol. Psychiatry. 2012;71:1030–1032. doi: 10.1016/j.biopsych.2011.12.021. [DOI] [PubMed] [Google Scholar]
- 6.Bernstein J.G., Garrity P.A., Boyden E.S. Optogenetics and thermogenetics: technologies for controlling the activity of targeted cells within intact neural circuits. Curr. Opin. Neurobiol. 2012;22:61–71. doi: 10.1016/j.conb.2011.10.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Boyden E.S., Zhang F., Deisseroth K. Millisecond-timescale, genetically targeted optical control of neural activity. Nat. Neurosci. 2005;8:1263–1268. doi: 10.1038/nn1525. [DOI] [PubMed] [Google Scholar]
- 8.Yizhar O., Fenno L.E., Deisseroth K. Optogenetics in neural systems. Neuron. 2011;71:9–34. doi: 10.1016/j.neuron.2011.06.004. [DOI] [PubMed] [Google Scholar]
- 9.Nagel G., Szellas T., Bamberg E. Channelrhodopsin-2, a directly light-gated cation-selective membrane channel. Proc. Natl. Acad. Sci. USA. 2003;100:13940–13945. doi: 10.1073/pnas.1936192100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jia Z., Valiunas V., Entcheva E. Stimulating cardiac muscle by light: cardiac optogenetics by cell delivery. Circ. Arrhythm. Electrophysiol. 2011;4:753–760. doi: 10.1161/CIRCEP.111.964247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bruegmann T., Malan D., Sasse P. Optogenetic control of heart muscle in vitro and in vivo. Nat. Methods. 2010;7:897–900. doi: 10.1038/nmeth.1512. [DOI] [PubMed] [Google Scholar]
- 12.Ambrosi C.M., Entcheva E. Optogenetics’ promise: pacing and cardioversion by light? Future Cardiol. 2014;10:1–4. doi: 10.2217/fca.13.89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Boyle P.M., Williams J.C., Trayanova N.A. A comprehensive multiscale framework for simulating optogenetics in the heart. Nat. Commun. 2013;4:2370. doi: 10.1038/ncomms3370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Entcheva E. Cardiac optogenetics. Am. J. Physiol. Heart Circ. Physiol. 2013;304:H1179–H1191. doi: 10.1152/ajpheart.00432.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Entcheva E., Williams J.C. Channelrhodopsin2 current during the action potential: “optical AP clamp” and approximation. Sci. Rep. 2014;4:5838. doi: 10.1038/srep05838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Williams J.C., Xu J., Entcheva E. Computational optogenetics: empirically derived voltage- and light-sensitive channelrhodopsin-2 model. PLOS Comput. Biol. 2013;9:e1003220. doi: 10.1371/journal.pcbi.1003220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ambrosi C.M., Klimas A., Entcheva E. Cardiac applications of optogenetics. Prog. Biophys. Mol. Biol. 2014;115:294–304. doi: 10.1016/j.pbiomolbio.2014.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hofmann B., Maybeck V., Offenhäusser A. Light induced stimulation and delay of cardiac activity. Lab Chip. 2010;10:2588–2596. doi: 10.1039/c003091k. [DOI] [PubMed] [Google Scholar]
- 19.Abilez O.J., Wong J., Kuhl E. Multiscale computational models for optogenetic control of cardiac function. Biophys. J. 2011;101:1326–1334. doi: 10.1016/j.bpj.2011.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bingen B.O., Engels M.C., de Vries A.A. Light-induced termination of spiral wave arrhythmias by optogenetic engineering of atrial cardiomyocytes. Cardiovasc. Res. 2014;104:194–205. doi: 10.1093/cvr/cvu179. [DOI] [PubMed] [Google Scholar]
- 21.Park S.A., Lee S.R., Yue D.T. Optical mapping of optogenetically shaped cardiac action potentials. Sci. Rep. 2014;4:6125. doi: 10.1038/srep06125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Arrenberg A.B., Stainier D.Y., Huisken J. Optogenetic control of cardiac function. Science. 2010;330:971–974. doi: 10.1126/science.1195929. [DOI] [PubMed] [Google Scholar]
- 23.Nussinovitch U., Shinnawi R., Gepstein L. Modulation of cardiac tissue electrophysiological properties with light-sensitive proteins. Cardiovasc. Res. 2014;102:176–187. doi: 10.1093/cvr/cvu037. [DOI] [PubMed] [Google Scholar]
- 24.Foutz T.J., Ackermann D.M., Jr., McIntyre C.C. Energy efficient neural stimulation: coupling circuit design and membrane biophysics. PLoS ONE. 2012;7:e51901. doi: 10.1371/journal.pone.0051901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sahin M., Tie Y. Non-rectangular waveforms for neural stimulation with practical electrodes. J. Neural Eng. 2007;4:227–233. doi: 10.1088/1741-2560/4/3/008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Walcott G.P., Melnick S.B., Ideker R.E. Relative efficacy of monophasic and biphasic waveforms for transthoracic defibrillation after short and long durations of ventricular fibrillation. Circulation. 1998;98:2210–2215. doi: 10.1161/01.cir.98.20.2210. [DOI] [PubMed] [Google Scholar]
- 27.Fishler M.G. Theoretical predictions of the optimal monophasic and biphasic defibrillation waveshapes. IEEE Trans. Biomed. Eng. 2000;47:59–67. doi: 10.1109/10.817620. [DOI] [PubMed] [Google Scholar]
- 28.Qu F., Li L., Efimov I.R. Mechanisms of superiority of ascending ramp waveforms: new insights into mechanisms of shock-induced vulnerability and defibrillation. Am. J. Physiol. Heart Circ. Physiol. 2005;289:H569–H577. doi: 10.1152/ajpheart.01117.2004. [DOI] [PubMed] [Google Scholar]
- 29.Jones J.L., Jones R.E. Improved defibrillator waveform safety factor with biphasic waveforms. Am. J. Physiol. 1983;245:H60–H65. doi: 10.1152/ajpheart.1983.245.1.H60. [DOI] [PubMed] [Google Scholar]
- 30.Roy O.Z., Wehnert R.W. A more efficient waveform for cardiac stimulation. Med. Biol. Eng. 1971;9:495–501. doi: 10.1007/BF02474706. [DOI] [PubMed] [Google Scholar]
- 31.Foutz T.J., Arlow R.L., McIntyre C.C. Theoretical principles underlying optical stimulation of a channelrhodopsin-2 positive pyramidal neuron. J. Neurophysiol. 2012;107:3235–3245. doi: 10.1152/jn.00501.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Arlow R.L., Foutz T.J., McIntyre C.C. Theoretical principles underlying optical stimulation of myelinated axons expressing channelrhodopsin-2. Neuroscience. 2013;248:541–551. doi: 10.1016/j.neuroscience.2013.06.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Talathi S.S., Carney P.R., Khargonekar P.P. Control of neural synchrony using channelrhodopsin-2: a computational study. J. Comput. Neurosci. 2011;31:87–103. doi: 10.1007/s10827-010-0296-6. [DOI] [PubMed] [Google Scholar]
- 34.Nikolic K., Jarvis S., Schultz S. Computational models of optogenetic tools for controlling neural circuits with light. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2013;2013:5934–5937. doi: 10.1109/EMBC.2013.6610903. [DOI] [PubMed] [Google Scholar]
- 35.Grossman N., Nikolic K., Degenaar P. Modeling study of the light stimulation of a neuron cell with channelrhodopsin-2 mutants. IEEE Trans. Biomed. Eng. 2011;58:1742–1751. doi: 10.1109/TBME.2011.2114883. [DOI] [PubMed] [Google Scholar]
- 36.Wong J., Abilez O.J., Kuhl E. Computational optogenetics: a novel continuum framework for the photoelectrochemistry of living systems. J. Mech. Phys. Solids. 2012;60:1158–1178. doi: 10.1016/j.jmps.2012.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.ten Tusscher K.H., Panfilov A.V. Alternans and spiral breakup in a human ventricular tissue model. Am. J. Physiol. Heart Circ. Physiol. 2006;291:H1088–H1100. doi: 10.1152/ajpheart.00109.2006. [DOI] [PubMed] [Google Scholar]
- 38.O’Hara T., Virág L., Rudy Y. Simulation of the undiseased human cardiac ventricular action potential: model formulation and experimental validation. PLOS Comput. Biol. 2011;7:e1002061. doi: 10.1371/journal.pcbi.1002061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Courtemanche M., Ramirez R.J., Nattel S. Ionic mechanisms underlying human atrial action potential properties: insights from a mathematical model. Am. J. Physiol. 1998;275:H301–H321. doi: 10.1152/ajpheart.1998.275.1.H301. [DOI] [PubMed] [Google Scholar]
- 40.Sampson K.J., Iyer V., Kass R.S. A computational model of Purkinje fiber single cell electrophysiology: implications for the long QT syndrome. J. Physiol. 2010;588:2643–2655. doi: 10.1113/jphysiol.2010.187328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Clay J.R., Paydarfar D., Forger D.B. A simple modification of the Hodgkin and Huxley equations explains type 3 excitability in squid giant axons. J. R. Soc. Interface. 2008;5:1421–1428. doi: 10.1098/rsif.2008.0166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Fozzard H.A., Schoenberg M. Strength-duration curves in cardiac Purkinje fibers: effects of liminal length and charge distribution. J. Physiol. 1972;226:593–618. doi: 10.1113/jphysiol.1972.sp009999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Zaniboni M., Cacciani F., Groppi M. Effect of input resistance voltage-dependency on DC estimate of membrane capacitance in cardiac myocytes. Biophys. J. 2005;89:2170–2181. doi: 10.1529/biophysj.105.062828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Zaniboni M., Pollard A.E., Spitzer K.W. Beat-to-beat repolarization variability in ventricular myocytes and its suppression by electrical coupling. Am. J. Physiol. Heart Circ. Physiol. 2000;278:H677–H687. doi: 10.1152/ajpheart.2000.278.3.H677. [DOI] [PubMed] [Google Scholar]
- 45.Kaur J., Nygren A., Vigmond E.J. Fitting membrane resistance along with action potential shape in cardiac myocytes improves convergence: application of a multi-objective parallel genetic algorithm. PLoS ONE. 2014;9:e107984. doi: 10.1371/journal.pone.0107984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Noble D., Stein R.B. The threshold conditions for initiation of action potentials by excitable cells. J. Physiol. 1966;187:129–162. doi: 10.1113/jphysiol.1966.sp008079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Merrill D.R., Bikson M., Jefferys J.G. Electrical stimulation of excitable tissue: design of efficacious and safe protocols. J. Neurosci. Methods. 2005;141:171–198. doi: 10.1016/j.jneumeth.2004.10.020. [DOI] [PubMed] [Google Scholar]
- 48.Chater T.E., Henley J.M., Randall A.D. Voltage- and temperature-dependent gating of heterologously expressed channelrhodopsin-2. J. Neurosci. Methods. 2010;193:7–13. doi: 10.1016/j.jneumeth.2010.07.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Gunaydin L.A., Yizhar O., Hegemann P. Ultrafast optogenetic control. Nat. Neurosci. 2010;13:387–392. doi: 10.1038/nn.2495. [DOI] [PubMed] [Google Scholar]
- 50.Berndt A., Schoenenberger P., Oertner T.G. High-efficiency channelrhodopsins for fast neuronal stimulation at low light levels. Proc. Natl. Acad. Sci. USA. 2011;108:7595–7600. doi: 10.1073/pnas.1017210108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Chow B.Y., Han X., Boyden E.S. High-performance genetically targetable optical neural silencing by light-driven proton pumps. Nature. 2010;463:98–102. doi: 10.1038/nature08652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Gradinaru V., Zhang F., Deisseroth K. Molecular and cellular approaches for diversifying and extending optogenetics. Cell. 2010;141:154–165. doi: 10.1016/j.cell.2010.02.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Han X., Chow B.Y., Boyden E.S. A high-light sensitivity optical neural silencer: development and application to optogenetic control of non-human primate cortex. Front. Syst. Neurosci. 2011;5:18. doi: 10.3389/fnsys.2011.00018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Han X., Boyden E.S. Multiple-color optical activation, silencing, and desynchronization of neural activity, with single-spike temporal resolution. PLoS ONE. 2007;2:e299. doi: 10.1371/journal.pone.0000299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Zhang F., Wang L.P., Deisseroth K. Multimodal fast optical interrogation of neural circuitry. Nature. 2007;446:633–639. doi: 10.1038/nature05744. [DOI] [PubMed] [Google Scholar]
- 56.Han X., Qian X., Boyden E.S. Informational lesions: optical perturbation of spike timing and neural synchrony via microbial opsin gene fusions. Front. Mol. Neurosci. 2009;2:12. doi: 10.3389/neuro.02.012.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Berndt A., Lee S.Y., Deisseroth K. Structure-guided transformation of channelrhodopsin into a light-activated chloride channel. Science. 2014;344:420–424. doi: 10.1126/science.1252367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Klimas A., Entcheva E. Toward microendoscopy-inspired cardiac optogenetics in vivo: technical overview and perspective. J. Biomed. Opt. 2014;19:080701. doi: 10.1117/1.JBO.19.8.080701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Bishop M.J., Plank G. Simulating photon scattering effects in structurally detailed ventricular models using a Monte Carlo approach. Front. Physiol. 2014;5:338. doi: 10.3389/fphys.2014.00338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Bishop M.J., Rowley A., Bub G. The role of photon scattering in voltage-calcium fluorescent recordings of ventricular fibrillation. Biophys. J. 2011;101:307–318. doi: 10.1016/j.bpj.2011.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


