Abstract
Increased risk of infectious disease is assumed to be a major cost of group living, yet empirical evidence for this effect is mixed. We studied whether larger social groups are more subdivided structurally. If so, the social subdivisions that form in larger groups may act as barriers to the spread of infection, weakening the association between group size and infectious disease. To investigate this ‘social bottleneck’ hypothesis, we examined the association between group size and four network structure metrics in 43 vertebrate and invertebrate species. We focused on metrics involving modularity, clustering, distance and centralization. In a meta-analysis of intraspecific variation in social networks, modularity showed positive associations with network size, with a weaker but still positive effect in cross-species analyses. Network distance also showed a positive association with group size when using intraspecific variation. We then used a theoretical model to explore the effects of subgrouping relative to other effects that influence disease spread in socially structured populations. Outbreaks reached higher prevalence when groups were larger, but subgrouping reduced prevalence. Subgrouping also acted as a ‘brake’ on disease spread between groups. We suggest research directions to understand the conditions under which larger groups become more subdivided, and to devise new metrics that account for subgrouping when investigating the links between sociality and infectious disease risk.
Keywords: sociality, infectious disease, social structure, social network, meta-analysis, comparative analysis
1. Introduction
The social transmission of infectious agents is widely expected to increase with group size in animal societies [1–4]. Some empirical evidence supports this prediction. For example, Whiteman & Parker [5] found higher louse abundance in larger aggregations of Galapagos hawks (Buteo galapagoensis), while Ezenwa [6] discovered a positive association between prevalence of intestinal parasites and group size in African artiodactyls. Across primates, malaria prevalence increases with group size in comparative tests [7,8], and a recent study found evidence for positive selection on genes related to immunity in species living in larger groups [9]. Despite the intuitive appeal of the ‘group size–infectious disease effect’, some studies have failed to discover the expected positive association. For example, Arnold & Lichtenstein [10] did not find significantly higher levels of ectoparasite infection in an intraspecific study of alpine marmots (Marmota marmota) living in larger groups, and in comparative studies of primates, group size showed no significant associations with immune system parameters that are expected to proxy disease risk [11–13].
Similarly, complex relationships exist between disease risk, group size and social organization in insect societies [14], whose evolution also has been strongly influenced by infectious disease [15–17]. For example, pathogen infection rates in bumblebee colonies increase with interindividual contact rates [18], which should increase with colony network density and size. However, in an infection study, termite nymphs had higher fungal infection rates when reared in smaller groups or alone, versus in groups of moderate size [19]. Increased susceptibility to socially transmitted infectious agents has been reported in smaller and larger honeybee colonies relative to those of moderate size [20,21].
In some cases, a negative association between group size and infectious disease makes sense. For example, an individual living in a larger group may obtain relief from vectors that actively search for their hosts, such as biting flies and the infectious diseases that they transmit (e.g. yellow fever virus and filarial nematodes). This may arise through the encounter-dilution effect, where detection of a group by a searching parasite increases more slowly than group size and the probability that an individual is attacked decreases with group size [22,23]. Overall, these effects can result in a lower per capita biting rate, and thus a negative association between group size and infection risk. Evidence for the encounter-dilution effect has been proposed for several systems, including biting flies on horses [24] and ectoparasites on rodents [25].
To make sense of these diverse patterns and potential effects, researchers have turned to meta-analyses to assess the linkage between group size and infectious disease risk across taxa [23,26,27]. In one recent meta-analysis, Rifkin et al. [26] found that 19 of 69 studies showed a negative association between group size and infectious disease (not all significant). Across all parasite and pathogen types, the average effect size was only r = 0.141, which is considered a ‘weak’ effect [28]. Counter to predictions of the encounter-dilution effect, the authors found that vector-borne infectious diseases and parasitoids showed the highest (positive) effect sizes among five subsets of parasites. In another recent meta-analysis, Patterson & Ruckstuhl [27] found larger effect sizes for some subsets of parasite and pathogen types, and a negative association between group size and parasitism for mobile parasites, but weak (non-significant) effect sizes involving parasite richness.
In this paper, we investigate the hypothesis that social network structure modulates the association between group size and infectious disease risk: larger groups may be more subdivided structurally, resulting in social subgroups that act as transmission bottlenecks within the group [29]. If so, these social barriers would offset the increased potential for an infectious agent to spread in larger groups, and thus reduce the overall association between group size and infectious disease risk (although it need not eliminate the association completely). Several studies have investigated aspects of this ‘social bottleneck hypothesis’ [30–32]. In a study that directly investigated network structure in non-human primates, Griffin & Nunn [29] found a positive association between group size and social network subdivision (community modularity), and negative associations between modularity and parasite richness (including micro- and macroparasites). However, several issues with this study suggest that further research is needed: sample sizes were small, the metric of community modularity used may show a mathematical relationship with network size, and data on parasite richness and network structure for each species were obtained from different social groups (owing to lack of information on the same social groups).
To investigate the social bottleneck hypothesis, we combined empirical and theoretical approaches to examine the links between group size, group subdivision and disease spread. Empirically, we expanded the taxonomic scope of the analysis to include a broader array of organisms (including social insects), and included additional measures of network structure. We used meta-analysis and phylogenetic comparative methods [33,34] to investigate whether group size covaries with these network metrics within and across species. We also developed a theoretical model that simulates the spread of a socially transmitted infection in social groups varying in size and degree of subdivision. We compare disease prevalence and spread in relation to subgrouping and other variables relevant to social disease transmission, predicting that greater subgrouping will limit outbreak size, because infections will tend to be more contained within subgroups. Importantly, our model enabled us to assess how the effect of substructure within groups compares with other epidemiologically important drivers of outbreak size, such as mortality rates and per contact probability of transmission.
2. Material and methods
(a). Social networks and network structure
We obtained data on social networks from 102 social groups in 43 species of animals. Network data were gathered by surveying the literature for published association matrices and by contacting authors for permission to use data for matrices not directly published, but for which network analyses had been performed. To generate networks [35], we generally preferred social behaviours involving affiliative associations, although some agonistic interactions were also used. For 11 species, data were available for more than one social group, meaning that we had intraspecific variation recorded in the database; for seven of these species, we obtained four or more networks, allowing us to examine the association between group size and network characteristics within species (and to combine these intraspecific analyses in a meta-analysis of different species). Network sizes ranged from 3 to 143, with a mean of 23.9; 36 of the 102 networks had fewer than 10 nodes. Details are provided in the electronic supplementary material, including information on sources of data, type of interaction used and whether the animals were from wild or captive populations.
We generated weighted social networks, with symmetric ties (assuming no difference between ij and ji interactions) in undirected networks to allow for the greatest inclusion of networks; when provided, ij and ji weights were summed, and then all ties were normalized, so that the average tie strength was equal to 1. We chose network metrics that we expected to be mathematically independent of, but empirically associated with, network (group) size, and that capture different aspects of network structure: modularity, clustering, distance and centrality.
The first metric is Newman's [36] leading-eigenvector measure of community modularity, hereafter called Newman's modularity. This is one of multiple measures of modularity that gauge how divided a given graph is into subgroups, with higher values indicating greater subdivision into distinct subgroups. Newman's algorithm was designed to be mathematically independent of network (group) size. As such, it has been used to investigate associations between network size and modularity in metabolic networks [37], although we acknowledge that constraints exist on the number of modules at extremely small group sizes. As a measure of network substructure, Newman's modularity offers the best test of the social bottleneck hypothesis; in this context, we predicted that modularity shows a positive association with group size. Newman's modularity was calculated using the R [38] package ‘igraph’ [39].
As a second metric, we calculated the clustering coefficient, which quantifies how densely direct neighbours are connected to one other (i.e. the number of links between neighbours divided by the maximum number of links that could exist between them). Clustering measures variation in connectivity among nodes at a more local level than does modularity. It evaluates the prevalence of those cases in which a node is connected to two other nodes, and those are also connected to each other (forming a triangle), in essence capturing the redundancy of ties. This binary measure uses presences or absences of ties, rather than their weights, to provide a more readily intelligible metric. Predictions are less clear-cut for the clustering coefficient than for Newman's modularity and will depend on the specifics of the network and the initially infected individual. While we generally expect that disease transmission will typically increase in networks with higher clustering owing to increased redundancy of ties, and therefore greater opportunity for transmission [40,41], these patterns are likely to be weaker and may be more complex than for Newman's modularity. Clustering coefficients were calculated using UCINET 6 [42].
For a third metric, we calculated a weight-normalized distance between nodes, using Opsahl's [43] updated algorithm for Dijkstra's [44] cost-corrected shortest distances from one node to another. In this measure, distances are represented as the number of ‘normalized’ ties (a tie of the average weight of all ties in the network) that compose the shortest path between two nodes. We used the mean of all shortest paths within a network to represent the average shortest distance between nodes in the network, with larger distances representing a less traversable network. Weight-normalized distances were calculated using the R package ‘tnet’ [45]. We checked for the effect of weighting by comparing the same network measures for the binary (a more common measure of shortest distances) and weighted versions of all networks, and the difference was negligible. Increased internodal distance may increase with group size, and could delay the rate of disease transmission across the entire network. However, in social networks, distance can be shortened by modularity in network structure [40].
A fourth measure, eigenvector centralization, captured variation in connectedness across nodes in the graph. Eigenvector centrality, the nodal metric that corresponds to and composes the network-level metric of centralization, is the measure of the influence of a node in a network [46,47]. Euclidean-normalized eigenvector centralities of all nodes are used in calculating a single eigenvector index for the entire network, called eigenvector centralization. All centralities are compared with that of the most central node, such that lower eigenvector centralization values denote a less centralized network in general, where ties are more egalitarian in their distribution. Higher eigenvector centralization values denote a more centralized network, where one or a few nodes efficiently connect the highest-degree nodes of the network. Eigenvector centralization was calculated using the R package ‘igraph’ [39]. While the social bottleneck hypothesis does not explicitly predict the relationship between eigenvector centralization and group size, this measure quantifies the evenness of the relative importance of individuals in the group. From the viewpoint of disease spread within groups, one might expect that an infectious agent would move more rapidly across a more centralized network. However, because removal of highly central nodes can fragment a centralized network, this effect would depend, in part, on pathogen attributes such as disease latency, case fatality rates and the degree of immunity after clearing infection.
In summary, we provide analyses using four measures of network structure, some of which are weighted and some of which are not. Newman's modularity provides the clearest prediction of the social bottleneck hypothesis, and thus is the one we focus on for testing that hypothesis.
(b). Statistical analysis of comparative data
For species with four or more networks available, we calculated correlation coefficients between network structure and network size for each of the measures of network structure separately, and then conducted a meta-analysis in the software Comprehensive Meta-Analysis, v. 2 [48]. We also conducted a phylogenetic meta-analysis of the resulting effect sizes using the methods described by Lajeunesse [49], as implemented in PhyloMeta [50].
We also ran phylogenetic comparative analyses involving phylogenetic generalized least-squares (PGLS) in R using the package caper [51], with a statistical model of ‘network structure ∼ group size’. For species with more than one network, we avoided taking an average of the network metric, and instead used only a single network for each species, with data on network size and the network metrics thus obtained from the same network. To deal with this intraspecific variation, we randomly chose one network for each species (if more than one was available), and then ran a standard PGLS on the resulting dataset, including estimation of the branch scaling coefficient λ, which is a measure of phylogenetic signal [52,53]. This was repeated 1000 times for each analysis, and mean and distributions of resulting statistical output were compiled. We assessed significance as having a mean p-value less than 0.05.
For both the meta-analysis and the comparative analysis, we compiled a phylogeny for the mammalian species in the final dataset by pruning the published, revised mammalian supertree from Bininda-Emonds et al. [54], and by manually grafting additional branches as needed, using node estimates from Time-Tree for splits among vertebrates, between vertebrates and arthropods, and between wasps and bees [55]. Additional branches were added for the split between the ant genera Pogonomyrmex and Camponotus (at 104.7 Ma) from Brady et al. [56], and for the recent split between the two wasp species of Ropalidia, arbitrarily estimated at 1 Ma, based on their status as congeneric species (no genetic estimates were available for these species). The tree is provided in the electronic supplementary material. To isolate the effects of deep branches in the trees (i.e. between invertebrates and vertebrates), we ran comparative analyses with both the full phylogeny and with a phylogeny composed only of the mammals.
(c). Theoretical model of disease spread
Our theoretical model was constructed as a modification of a meta-population model used previously to study the spread of socially transmitted infections [57] and cultural traits [58]. The model was implemented in MATLAB version R2013b. Simulations took place on a 10 × 10 square lattice, where each cell represented a distinct social group that was formed based on user-specified values for group size (g) by drawing a random number from a Poisson distribution (with mean of g for number of females, which was doubled to give the total group of males and females). Individuals were characterized by infection status, including number of days in an incubation period (c, i.e. exposed but not yet infectious) and, following host incubation, number of days in a host infectious period (f). All individuals in the population were initially uninfected.
Individuals were randomly assigned to one of s subgroups within each social group; setting s equal to 1 resulted in no subgroup structure. We assumed that disease spread was higher among individuals within the same subgroup than among individuals in different subgroups, with subgroup affiliation representing the only source of heterogeneity in the edges of the network (although an actual network was not generated). By assuming only two kinds of ties—those within subgroups (modules) and those between subgroups—our model deals with important types of nodal heterogeneity in real-world systems that may affect disease spread (e.g. super-spreaders), which may obscure the effect we were most interested in (subgrouping).
Model dynamics proceeded in discrete time steps, which represented single days in the lives of host individuals. In each time step, the following processes took place sequentially: (i) infection of hosts through exposure to other infected individuals in the same social group; (ii) deaths due to the intrinsic mortality rate and/or disease-related mortality; (iii) stochastic dispersal of individuals to neighbouring groups; and (iv) stochastic births of individuals in groups to replace individuals lost to background (but not disease-related) mortality.
More specifically, infection occurred with transmission probability β1 through contact with an infectious individual in its subgroup, and β2 through contact with an infectious individual in a different subgroup (but within the same social group). In all simulations, β1 > β2. We assumed that after clearing infection, individuals lacked immunity to the infectious agent and therefore could be re-infected (i.e. a susceptible–exposed–infected–susceptible (SEIS) model); this assumption is especially reasonable for macroparasites, which are common in animal social groups and generally do not elicit lifelong or complete immunity. Each individual experienced a baseline probability of death (mb), and infected individuals had an additional source of mortality due to disease (md), where md was a multiplier of mb (range of values is given in table 1).
Table 1.
Simulation parameters and range of values used (Latin hypercube sample).
| parameter | minimum | maximum |
|---|---|---|
| group size: females (g) | 8 | 60 |
| number of subgroups (s) | 2 | 6 |
| mortality ratea (mb) | 0.000055 | 0.0055 |
| disease mortality (md) | 1 | 11 |
| transmission within subgroups (β1) | 0.01 | 0.03 |
| transmission between subgroups (β2) | 0.001 | 0.01 |
| dispersal rate (i) | 0.001 | 0.01 |
| incubation period (c) | 1 | 41 |
| infectious period (f) | 1 | 41 |
aBased on life span range of 0.5–50 years and time step of 1 day in the simulations.
Births occurred for groups with at least one individual present. We assumed that the population was at carrying capacity when the simulation was initiated, and we implemented extra calculations to help maintain the initial demographic context throughout a simulation run. To achieve this, we recorded the initial sizes of each group. Groups that were smaller in the current time step relative to their initial values—but that still had at least one individual in the group—had a higher probability of receiving a birth. Specifically, they were twice as likely to be assigned a birth as other groups that matched or exceeded initial group sizes. It is worth repeating, however, that disease-related mortality resulted in overall reductions in population size, as these individuals were not replaced.
Dispersal of individuals to neighbouring groups occurred with probability i. The new group was selected randomly from among those on the border or corners of the origination cell, and thus not determined based on group size, although dispersal was not allowed to cells where the group had disappeared owing to deaths of all individuals. The lattice was bounded spatially and was not reflective; thus, a dispersing individual that hit a boundary did not move in that time step. Dispersal was completed in one time step. We assumed that dispersal was more likely for groups in which the number of individuals of a particular sex was above the initial values for the number of individuals for that sex, thus using a procedure similar to that described above for mortality to maintain the initial population structure.
(d). Model parametrization and analysis of output
To explore how multiple parameters influence disease dynamics, we undertook multivariate analyses using random sampling via Latin hypercube sampling, which is a type of stratified Monte Carlo sampling that is more efficient than random sampling or assessing all possible parameter values [58–61]. As summarized in table 1, nine parameters were varied across flat distributions in the Latin hypercube sample: group size (g), number of subgroups (s), transmission probability within subgroups (β1), transmission probability between subgroups (β2), intrinsic (mb) and disease-related mortality (md), rate of dispersal (i), incubation period (c) and infectious period (f). For parameters that required integer or discrete values (s, i, c and f), we sampled them as continuously varying traits in the Latin hypercube design and then averaged to units required by the simulation model (group size, g, was drawn from a Poisson function, resulting in an integer value for the number of individuals of one sex in a group, and doubled to represent both sexes).
With this approach, we generated N = 500 parameter sets for the simulation. For simulation Ni, we ran the model with the Latin hypercube sample Ni, and then re-ran the model for sample Ni with number of subgroups (s) set to 1 to simulate transmission in groups without substructure, resulting in a total of 1000 simulations (one-half of which had no subgrouping within groups). This produced a paired-design simulated dataset that enabled us to test whether prevalence was lower when subgroups were present, independently of variation in other parameters. In addition to simply comparing output from simulations with and without subgrouping, we investigated output variables (average prevalence and number of groups infected, i.e. disease spread) in a statistical model that included all the predictor variables, but with subgrouping set to a binary variable, to indicate whether the simulation had subgroups. Among the output samples with subgrouping, we also tested whether the number of subgroups had a negative effect on prevalence and number of groups infected, and how the effect size for s compared with effect sizes of other variables in the model, particularly female group size (g).
For statistical testing, we used an information theoretic framework based on model averaging [62]. Specifically, we obtained an Akaike information criterion (AIC) weight for each of the possible models, and then averaged the subset of models with Akaike weights greater than 0.001. We implemented full-model averaging, in which means and variances of parameters that were not included in a model were set to 0 for that model and included when averaging the coefficient estimates. We standardized coefficients so that larger coefficients indicated larger effects. We assessed ‘significance’ via the ‘importance’ measure for each variable, which indicates the cumulative Akaike weights in the models that included that variable (and thus ranges from 0 to 1).
Analyses were conducted in R [38] with the packages MuMIn [63] and QuantPsyc [64]. To obtain the Latin hypercube sample, we used the R package tgp [65,66].
3. Results
(a). Network structure and group size: meta-analysis
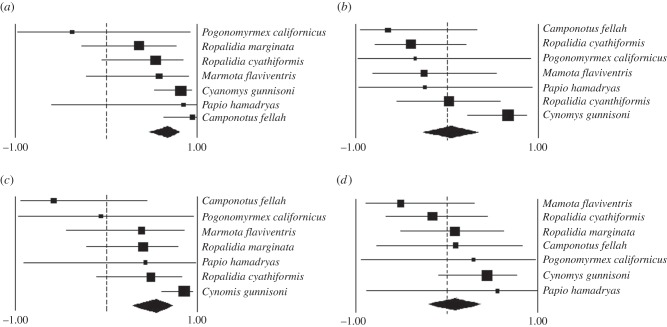
We first conducted a meta-analysis of associations between group size and network metrics using data on seven species with intraspecific variation. We tested whether there was phylogenetic signal in the meta-analysis [49], and found no evidence for such an effect (e.g. for Newman's modularity, AICnon-phylo-model = 21.97, AICphylo-model = 30.44, favouring the non-phylogenetic model). Thus, we used standard (non-phylogenetic) meta-analysis techniques. Results are summarized in figure 1. Newman's modularity and weight-normalized distance both showed a strong positive relationship with group size within species (Newman's modularity: Z = 5.052, p < 0.001; weight-normalized distance: Z = 3.821, p < 0.001). The results involving Newman's modularity support predictions of the social bottleneck hypothesis, whereas the results involving distance indicate that networks are less traversable when groups are larger. In contrast, the clustering coefficient and eigenvector centralization showed no discernible relationships with group size (clustering coefficient: Z = 0.258, p = 0.797; eigenvector centralization: Z = 0.560, p = 0.575).
Figure 1.
Results of meta-analysis. Panels show forest plots depicting the effect size and 95% confidence limits for individual studies in analyses of (a) Newman's modularity, (b) clustering coefficient, (c) weight-normalized distance and (d) eigenvector centralization. The diamond symbol shows the overall effect size and confidence limits.
(b). Network structure and group size: phylogenetic generalized least-squares
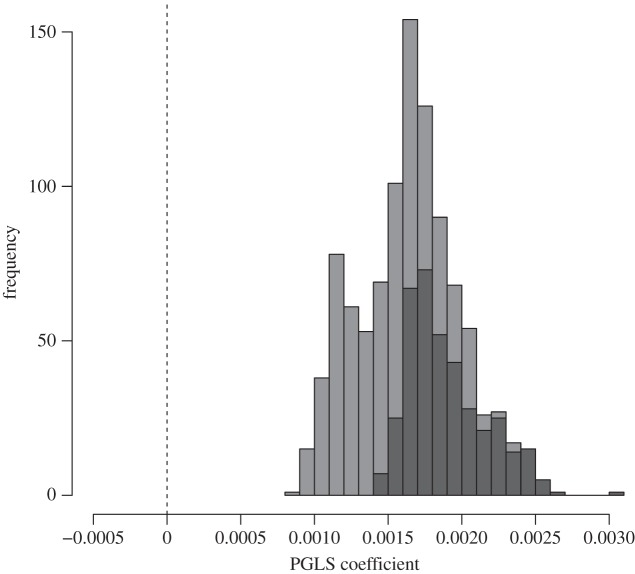
We next conducted phylogenetic comparative analyses of correlated evolution using PGLS across species, using a resampling procedure to deal with intraspecific variation when it existed. Results are provided in tables 2 (all animals) and 3 (mammals only). For Newman's modularity using the full dataset, the association with group size was always positive across randomized datasets (figure 2), but not consistently significant (mean p-value of 0.079). Statistical significance was on average weaker when only mammals were analysed, although all estimated regression coefficients remained positive (table 3). The positive trend across species is weaker than in meta-analysis of within-species associations of network structure and group size (figure 1). We used matched data on network metrics and size from the same social groups rather than averaging intraspecific data for a ‘species-specific’ network. Thus, weaker results in the cross-species analyses are likely to arise because additional interspecies differences account for network modularity independently of group size.
Table 2.
PGLS results, examining the full dataset of vertebrates and invertebrates. Sample size was N = 43 (number of analysed species) in all analyses. Aside from ‘% coefficients >0’, all entries in this table are means across 1000 random subsets of data to account for intraspecific variation.
| model | % coefficients >0 (%) | PGLS coefficient | standard error | p-value | R2 | lambda |
|---|---|---|---|---|---|---|
| Newman's modularity | 100 | 0.002 | 0.001 | 0.079 | 0.081 | <0.001 |
| clustering coefficient | <1 | −0.004 | 0.003 | 0.207 | 0.042 | <0.001 |
| weight-normalized distance | 94.7 | 0.011 | 0.019 | 0.549 | 0.012 | 0.344 |
| eigenvector centralization | 0.5 | −0.001 | 0.001 | 0.404 | 0.026 | 0.231 |
Table 3.
PGLS results, examining mammals only. Sample size was N = 38 in all analyses. Aside from ‘% coefficients >0’, all entries in this table are means across 1000 random subsets of data to account for intraspecific variation.
| model | % coefficients >0 (%) | PGLS coefficient | standard error | p-value | R2 | lambda |
|---|---|---|---|---|---|---|
| Newman's modularity | 100 | 0.005 | 0.003 | 0.210 | 0.061 | <0.001 |
| clustering coefficient | 21.9 | −0.006 | 0.011 | 0.594 | 0.015 | <0.001 |
| weight-normalized distance | 5.7 | −0.029 | 0.050 | 0.566 | 0.012 | <0.001 |
| eigenvector centralization | 17.4 | −0.001 | 0.003 | 0.621 | 0.011 | 0.005 |
Figure 2.
Distribution of regression coefficients for the association between group size and modularity in comparative analyses. The distribution is based on random selection of a single value per species in the comparative analysis to account for intraspecific variation. Darker bars indicate proportions of statistical results that were significant at p < 0.05.
The clustering coefficient tended to show a negative association with group size based on the regression coefficient, but again, the mean p-value was above our significance threshold when all species were examined (table 2) and when focusing on mammals (table 3). Similarly, weight-normalized distance and eigenvector centralization showed no significant associations with group size. Based on the signs of the estimated regression coefficients, weight-normalized distance tended to show consistent positive associations with group size across all species, and eigenvector centralization showed consistent negative associations with group size, yet this consistency disappeared when investigating only mammals (tables 2 and 3). The consistency in the sign of the regression coefficients was not matched with compelling levels of statistical significance.
(c). Theoretical model of disease spread
Across 1000 simulations, maximum prevalence showed a bimodal distribution, reflecting that the simulation failed to take off in many simulation runs (figure 3a); maximum prevalence was less than 5% in 253 of the simulations. In most simulations, the disease went extinct (figure 3b), as expected given that disease-induced mortality was greater than background mortality and individuals that died from the disease were not replaced. However, in 45 of the simulations, a peak was reached and the prevalence was still declining when the simulation ended (figure 3c). To control for variation in disease dynamics of different simulation runs, we based our analyses on results involving maximum prevalence, rather than final or average prevalence.
Figure 3.
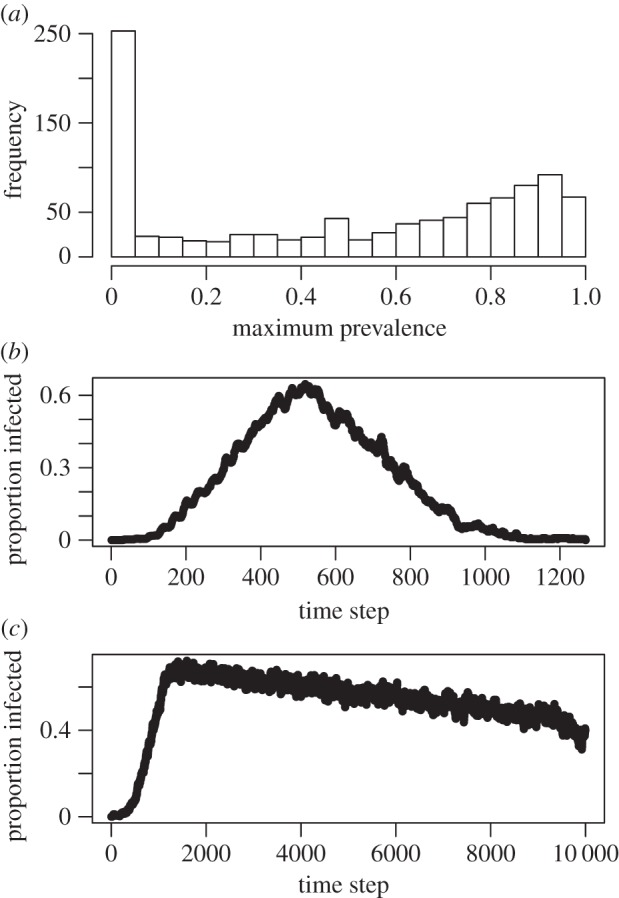
Example simulation output. (a) The distribution of maximum prevalence at the end of the full 1000 simulations, combining results of simulations with and without social substructure. (b) Example of prevalence over time for a run in which the simulated infectious disease went extinct. (c) Example of prevalence over time for a run in which the simulated infectious agent was heading toward extinction, but had not yet reached that point. On the basis of the patterns in b and c, we focused on maximum prevalence over the course of a simulation as one of our two outcome measures from the simulation (with number of groups infected as the other outcome measure).
We also examined the number of groups infected in a simulation run. In 183 of the 1000 simulations, the disease never left the starting group (i.e. only one group was infected), whereas in 595 cases, all 100 groups were infected at least once during the simulation run. The mean number of groups infected (out of 100 on the lattice) was 73.1, reflecting that the disease was very effective in spreading across the lattice in most simulations. Overall, initial indications are that the simulation parameters used in the Latin hypercube sample captured substantial variation in outbreak success.
We found that maximum prevalence was substantially higher in the 500 simulations without subgrouping (median of 73.4%, standard deviation = 0.353) than in the 500 simulations with subgrouping (median of 39.1%, standard deviation = 0.355). As shown in figure 4, the patterns were consistent in the vast majority of simulations, with subgrouping resulting in lower peak prevalence in all but 45 simulations (given the very low prevalence for ‘no subgroups' in most of these cases, they typically represent stochastic early extinctions). A similar pattern was found when examining the number of groups infected, with higher numbers of social groups infected on the 100-group lattice without subgrouping (mean = 81.1 groups), when compared with cases when individuals within social groups showed structured interactions (mean = 65.0). In only 41 paired comparisons (out of 500) did the number of groups infected come out higher in simulations with subgroups present than with subgroups absent (and most of these again probably represent stochastic extinctions). Thus, we find clear evidence that subgrouping resulted in fewer groups becoming infected.
Figure 4.
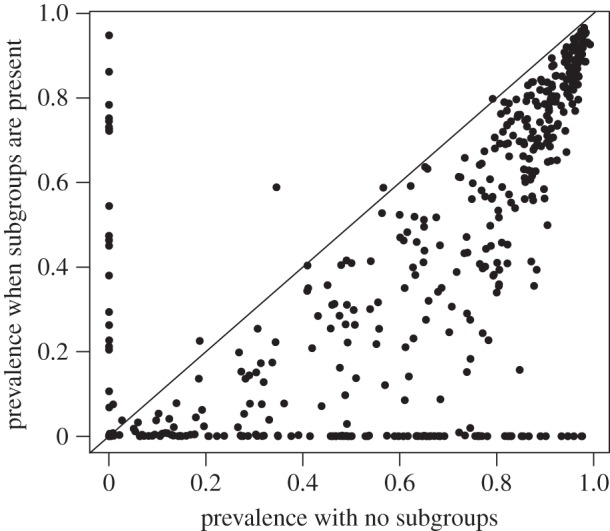
Prevalence of infection in paired simulations with and without social structure. Points below the line of equality indicate cases where prevalence was higher in simulations without subgrouping, when compared with simulations under identical conditions with subgrouping. In total, 500 such paired comparisons were conducted. The vast majority of these comparisons exhibited greater maximum prevalence in simulation runs without subgrouping.
We also used the simulations to assess the effects of subgrouping relative to other epidemiologically important variables, such as mortality resulting from infection. First, we examined predictors of maximum prevalence across all simulations, with predictors involving the variables shown in table 1 and subgrouping coded as a binary factor (0 indicated no subgrouping, whereas 1 indicated subgrouping was present). These analyses revealed clear positive effects of group size on maximum prevalence, and clear negative effects of subgrouping on maximum prevalence (table 4). Thus, individuals in larger groups had more risk, but an independent negative effect existed owing to subgrouping. These effects are comparable in size to other key variables, such as mortality rates and infectious period, and somewhat larger than the effects of transmission probability. Similar results were obtained when using the number of subgroups as a predictor (rather than using the binary codes), and when examining patterns only within the subset of simulations that involved subgrouping (2 < s < 6).
Table 4.
Effect of group subdivision and other simulation parameters on ‘maximum prevalence’.
| variable | estimate | lower CI | upper CI | importance |
|---|---|---|---|---|
| intercept | 0.000 | −0.038 | 0.038 | n.a. |
| female group size (g) | 0.461 | 0.423 | 0.499 | 1.00 |
| presence of subgroups (binary factor) | −0.259 | −0.297 | −0.222 | 1.00 |
| transmission within subgroups (β1) | 0.124 | 0.086 | 0.162 | 1.00 |
| transmission between subgroups (β2) | 0.060 | 0.021 | 0.098 | 0.98 |
| dispersal rate (i) | 0.085 | 0.047 | 0.123 | 1.00 |
| mortality rate (mb) | −0.313 | −0.351 | −0.275 | 1.00 |
| disease mortality (md) | −0.256 | −0.294 | −0.218 | 1.00 |
| infectious period (f) | 0.333 | 0.295 | 0.371 | 1.00 |
| incubation period (c) | 0.009 | −0.029 | 0.046 | 0.28 |
We also investigated a linear model predicting the number of groups infected. We again found strong positive effects of group size, with g having the largest effect size in the model (table 5). Subgrouping—coded as a binary factor—showed a negative effect, and was present in all models retained, with importance of 1.0. Only infectious period and group size had a larger standardized regression coefficient (in absolute magnitude) than subgrouping in this statistical model. We also found that probability of transmission within subgroups (β1) was more important than transmission of infection across subgroups (β2) in accounting for the number of groups infected.
Table 5:
Effects of group subdivision and other simulation parameters on ‘number of groups infected’.
| variable | estimate | lower CI | upper CI | importance |
|---|---|---|---|---|
| intercept | 0.000 | −0.050 | 0.050 | n.a. |
| group size (g) | 0.366 | 0.315 | 0.416 | 1.00 |
| presence of subgroups (binary factor) | −0.192 | −0.242 | −0.142 | 1.00 |
| transmission within subgroups (β1) | 0.087 | 0.037 | 0.138 | 0.99 |
| transmission between subgroups (β2) | 0.036 | −0.015 | 0.087 | 0.49 |
| dispersal rate (i) | 0.038 | −0.013 | 0.088 | 0.51 |
| mortality rate (mb) | −0.178 | −0.229 | −0.128 | 1.00 |
| disease mortality (md) | −0.092 | −0.143 | −0.042 | 1.00 |
| infectious period (f) | 0.329 | 0.279 | 0.379 | 1.00 |
| incubation period (c) | −0.037 | −0.088 | 0.013 | 0.51 |
4. Discussion
One of the intrinsic costs of social life is increased risk of acquiring socially transmitted infectious agents. Disease transmission is theoretically expected to increase with group size. However, the individuals in social groups are not randomly connected; a benefit of this social structure may be the mitigation of disease impact as group size becomes larger. We call this the social bottleneck hypothesis.
We used empirical comparative and meta-analyses to determine whether measures of social network structure covary with group size, and we coupled these tests with a simulation model of disease spread in relation to group structure and other variables. Our empirical analyses focused on potential links between network structure and size, expanding on a previous analysis of primates [29]. The data indicate that network substructure, as measured by Newman's modularity, increases in larger social groups, supporting the social bottleneck hypothesis. In a meta-analysis of variation in group size and modularity in seven species, we found consistently positive associations between these variables. Although weaker in comparative analyses, indications of a positive effect of network size on modularity remained. Differences between within-species and cross-species analyses do not reflect issues with treating group size and network properties as characteristic of a species in the comparative tests, because our comparative analyses actually use paired data on network characteristics and network size rather than averaging to the species level. Instead, weaker results in comparative tests suggest that biological differences across the wide range of species in our comparative analysis affect the network measures. Other network parameters also covaried with group size, especially weight-normalized distance in the meta-analyses.
Our theoretical model investigated the effects of subgrouping on disease spread. As expected, greater subgrouping slowed the spread of disease and reduced maximum prevalence in the simulation model. The statistical analyses revealed that the effect of subgrouping was as important as some other key epidemiological parameters in accounting for the spread of disease. Of course, these conclusions are only valid in the context of the simulation design and range of parameters used here. While it is plausible that similarly strong effects of subgrouping exist in real-world systems, we presently lack the data to assess this possibility directly.
We focused on how subgrouping may covary with group size and potentially mitigate the spread of a socially transmitted disease, partly as an explanation for the weakness of the group size–infectious disease effect in one recent meta-analysis [26]. Several other explanations for a weak group size–infectious disease effect should also be considered. First, it could be that the relevant level of analysis is the meta-population, and that living in groups—regardless of how big—acts to ‘quarantine’ infectious agents at the population level. Indeed, it is useful to consider subgrouping at multiple levels: individuals within groups, groups within populations and even different populations. Rates of contact between these subdivisions are likely to play important roles in disease dynamics.
Second, animals in larger groups may invest more in immune defences, as suggested in a recent study of primate molecular evolution [67]. However, other studies of primates have failed to find support for this possibility in comparative analyses of leucocytes [11–13] or spleen size [68]. These mixed findings suggest—at least in primates—that individual immune responses are unlikely to be a major response to increased disease risk in larger groups, although more research is clearly needed to rule out such effects. A negative relationship between sociality and individual immunity may actually be found in some taxonomic groups where group level defences occur [16]. Honeybees, for example, have reduced numbers of immunity and detoxification genes [69,70], suggesting that highly social systems may shift from individual physiological immunity to effects at the social group level [15,71]. This ‘social immunity’ can be enhanced by behavioural strategies, such as social grooming [17] and/or isolation or removal of infected individuals. These behaviours, in turn, can be influenced by group size. In ants, for example, allogrooming rates [15] and the relative performance of maintenance behaviours, such as waste removal [72], have been shown to increase with group size.
A third possibility is that only a minority of the infectious agents in wild populations spread from host to host through social contact; instead, parasites and pathogens of wildlife may show a proportionally greater occurrence of routes involving faecal–oral transmission and vector transmission, and the strength of these transmission pathways may correlate more weakly with group size. However, theoretical models indicate that group size covaries with the spread of faecally transmitted pathogens [73], and a recent meta-analysis found the strongest effect sizes among vector-transmitted parasites and pathogens [26]. Hence, this explanation also appears to fall short, although more research is needed in a wider array of biological systems.
Finally, social structuring may provide other mechanisms to generate heterogeneity beyond the measures of network structure examined here. Genetic variation can theoretically provide a barrier to disease spread if a subset of related individuals express immunity, leading to the suggestion that parasitism may have favoured the evolution of multiple mating by queens in highly eusocial ant and bee colonies [15]. In mammalian societies, relatedness could provide substructure if individuals within family groups are more likely to contact each other, or if dominance rank affects social interactions. Substructuring may similarly be generated by differences in behavioural roles and spatial separation [14,41]. Groups could also substructure by age, as found in the network structure of honeybee colonies. Older bees, which are more likely to forage and thus to be exposed to pathogens in the environment, are more likely to contact one another than younger bees, and this provides a buffer against pathogen exposure for younger bees in the hive [41].
Our findings also suggest that research is needed to identify alternative metrics of group size that account for network structure. In essence, we need a measure of effective group size, from the standpoint of disease transmission in a group. Just as effective population size can be estimated as the harmonic mean of population size over time, effective group size could be the harmonic mean of module sizes in a group. Or, simulation approaches could be used to estimate mean and variance of outbreak size for groups with different substructuring characteristics. This was essentially the approach taken by Griffin & Nunn [29], and it could be extended to parametrize for a specific infectious agent, including for agents that elicit lasting immunity. Indeed, a single measure of effective group size may be impossible to obtain, given that different infectious agents will perceive a group and population differently based on incubation period, transmissibility, dispersal, immunity and transmission mode.
A related issue involves development of additional network structure metrics of modularity, and ideally metrics that are independent of group size. We focused on a measure—Newman's modularity—that is proposed to be independent of group size [36]. However, group size itself is an important aspect of subgrouping because, for example, many more possibilities for forming subgroups exist among 30 individuals than among four. Larger groups can also have more subgroups than smaller groups.
In conclusion, our combined empirical and theoretical analysis reveals real and potential links between group size, substructuring and socially transmitted infectious diseases. Of the network measures we investigated, modularity—i.e. subgrouping—is one that covaries with group size. It could be that increased subgrouping is a counterstrategy to infectious disease risk in larger groups that is shaped by natural selection, or greater subgrouping could be a simple by-product of limited amounts of time for interaction in larger groups. Understanding the mechanisms that generate this pattern is important for many aspects of sociality, and for understanding disease dynamics in wildlife populations.
Supplementary Material
Supplementary Material
Acknowledgements
We thank Daniel Blumstein and Raghavendra Gadagkar for providing data, Alexander Vining for help with formatting the figures, two anonymous referees and Peter Kappeler for comments on the manuscript.
Data accessibility
Data used for the comparative and meta-analyses are provided in the electronic supplementary material.
Funding statement
This research was initiated through a working group supported by the National Evolutionary Synthesis Center (NESCent), NSF no. EF-0423641. Training in phylogenetic comparative methods was provided by the AnthroTree Workshop, which was supported by the NSF (BCS-0923791) and NESCent. C.M.M. was supported by Harvard University and the NSF Graduate Research Fellowship Programme (DGE-1144152).
Authors' contributions
C.L.N. initiated and guided the research and crafted the initial manuscript. Network analyses were led by F.J. and C.M.M., with data compilation by C.M.M., F.J., J.L.V. and J.H.F. Comparative and meta-analyses were led by C.M.M. Epidemiological simulations were led by C.L.N. All authors contributed to the writing of the manuscript and approved its submission.
Conflict of interests
We have no competing interests.
References
- 1.Freeland WJ. 1979. Primate social groups as biological islands. Ecology 60, 719–728. ( 10.2307/1936609) [DOI] [Google Scholar]
- 2.Møller AP, Dufva R, Allander K. 1993. Parasites and the evolution of host social behavior. Adv. Stud. Behav. 22, 65–102. ( 10.1016/S0065-3454(08)60405-2) [DOI] [Google Scholar]
- 3.Loehle C. 1995. Social barriers to pathogen transmission in wild animal populations. Ecology 76, 326–335. ( 10.2307/1941192) [DOI] [Google Scholar]
- 4.Altizer S, et al. 2003. Social organization and parasite risk in mammals: integrating theory and empirical studies. Annu. Rev. Ecol. Evol. Syst. 34, 517–547. ( 10.1146/annurev.ecolsys.34.030102.151725) [DOI] [Google Scholar]
- 5.Whiteman NK, Parker PG. 2004. Effects of host sociality on ectoparasite population biology. J. Parasitol. 90, 939–947. ( 10.1645/GE-310R) [DOI] [PubMed] [Google Scholar]
- 6.Ezenwa VO. 2004. Host social behavior and parasitic infection: a multifactorial approach. Behav. Ecol. 15, 446–454. ( 10.1093/beheco/arh028) [DOI] [Google Scholar]
- 7.Davies CR, Ayres JM, Dye C, Deane LM. 1991. Malaria infection rate of Amazonian primates increases with body weight and group size. Funct. Ecol. 5, 655–662. ( 10.2307/2389485) [DOI] [Google Scholar]
- 8.Nunn CL, Heymann EW. 2005. Malaria infection and host behaviour: a comparative study of Neotropical primates. Behav. Ecol. Sociobiol. 59, 30–37. ( 10.1007/s00265-005-0005-z) [DOI] [Google Scholar]
- 9.Wlasiuk G, Khan S, Switzer W, Nachman M. 2010. A history of recurrent positive selection at the toll-like receptor 5 in primates. Mol. Biol. Evol. 26, 937–949. ( 10.1093/molbev/msp018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Arnold W, Lichtenstein AV. 1993. Ectoparasite loads decrease the fitness of alpine marmots (Marmota marmota) but are not a cost of sociality. Behav. Ecol. 4, 36–39. ( 10.1093/beheco/4.1.36) [DOI] [Google Scholar]
- 11.Nunn CL, Gittleman JL, Antonovics J. 2000. Promiscuity and the primate immune system. Science 290, 1168–1170. ( 10.1126/science.290.5494.1168) [DOI] [PubMed] [Google Scholar]
- 12.Nunn CL. 2002. A comparative study of leukocyte counts and disease risk in primates. Evolution 56, 177–190. ( 10.1111/j.0014-3820.2002.tb00859.x) [DOI] [PubMed] [Google Scholar]
- 13.Semple S, Cowlishaw G, Bennett PM. 2002. Immune system evolution among anthropoid primates: parasites, injuries and predators. Proc. R. Soc. Lond. B 269, 1031–1037. ( 10.1098/rspb.2001.1950) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Naug D, Camazine S. 2002. The role of colony organization on pathogen transmission in social insects. J. Theor. Biol. 215, 427–439. ( 10.1006/jtbi.2001.2524) [DOI] [PubMed] [Google Scholar]
- 15.Schmid-Hempel P. 1998. Parasites in social insects. Princeton, NJ: Princeton University Press. [Google Scholar]
- 16.Meunier J. 2015. Social immunity and the evolution of group living in insects. Phil. Trans. R. Soc. B 370, 20140102 ( 10.1098/rstb.2014.0102) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Theis FJ, Ugelvig LV, Marr C, Cremer S. 2015. Opposing effects of allogrooming on disease transmission in ant societies. Phil. Trans. R. Soc. B 370, 20140108 ( 10.1098/rstb.2014.0108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Otterstatter MC, Thomson JD. 2007. Contact networks and transmission of an intestinal pathogen in bumble bee (Bombus impatiens) colonies. Oecologia 154, 411–421. ( 10.1007/s00442-007-0834-8) [DOI] [PubMed] [Google Scholar]
- 19.Rosengaus RB, Maxmen AB, Coates LE, Traniello JF. 1998. Disease resistance: a benefit of sociality in the dampwood termite Zootermopsis angusticollis (Isoptera: Termopsidae). Behav. Ecol. Sociobiol. 44, 125–134. ( 10.1007/s002650050523) [DOI] [Google Scholar]
- 20.Eischen FA. 1987. Overwintering performance of honey bee colonies heavily infested with Acarapis woodi (Rennie). Apidologie 18, 293–304. ( 10.1051/apido:19870401) [DOI] [Google Scholar]
- 21.Jeffree E, Allen D. 1956. The influence of colony size and of nosema disease on the rate of population loss in honey bee colonies in winter 1. J. Econ. Entomol. 49, 831–834. ( 10.1093/jee/49.6.831) [DOI] [Google Scholar]
- 22.Mooring MS, Hart BL. 1992. Animal grouping for protection from parasites: selfish herd and encounter-dilution effects. Behaviour 123, 173–193. ( 10.1163/156853992X00011) [DOI] [Google Scholar]
- 23.Côté IM, Poulin R. 1995. Parasitism and group size in social animals: a meta-analysis. Behav. Ecol. 6, 159–165. ( 10.1093/beheco/6.2.159) [DOI] [Google Scholar]
- 24.Rubenstein DI, Hohmann ME. 1989. Parasites and social behavior of island feral horses. Oikos 55, 312–320. ( 10.2307/3565589) [DOI] [Google Scholar]
- 25.Bordes F, Blumstein DT, Morand S. 2007. Rodent sociality and parasite diversity. Biol. Lett. 3, 692–694. ( 10.1098/rsbl.2007.0393) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rifkin J, Nunn CL, Garamszegi LZ. 2012. Do animals living in larger groups experience greater parasitism? A meta-analysis. Am. Nat. 180, 70–82. ( 10.1086/666081) [DOI] [PubMed] [Google Scholar]
- 27.Patterson JEH, Ruckstuhl KE. 2013. Parasite infection and host group size: a meta-analytical review. Parasitology 140, 803–813. ( 10.1017/S0031182012002259) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cohen J. 1988. Statistical power analysis for the behavioral sciences, 2nd edn Hillsdale, NJ: Erlbaum Associates. [Google Scholar]
- 29.Griffin R, Nunn CL. 2011. Community structure and the spread of infectious disease in primate social networks. Evol. Ecol. 26, 779–800. ( 10.1007/s10682-011-9526-2) [DOI] [Google Scholar]
- 30.Salathe M, Jones JH. 2010. Dynamics and control of diseases in networks with community structure. PLoS Comput. Biol. 6, e1000736 ( 10.1371/journal.pcbi.1000736) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rushmore J, Caillaud D, Hall RJ, Stumpf RM, Meyers LA, Altizer S. 2014. Network-based vaccination improves prospects for disease control in wild chimpanzees. J. R. Soc. Interface 11, 20140349 ( 10.1098/rsif.2014.0349) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Carne C, Semple S, Morrogh-Bernard H, Zuberbühler K, Lehmann J. 2014. the risk of disease to great apes: simulating disease spread in orang-utan (Pongo pygmaeus wurmbii) and chimpanzee (Pan troglodytes schweinfurthii) association networks. PLoS ONE 9, e95039 ( 10.1371/journal.pone.0095039) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nunn CL. 2011. The comparative approach in evolutionary anthropology and biology. Chicago, IL: University of Chicago Press. [Google Scholar]
- 34.Garamszegi LZ. 2014. Modern phylogenetic comparative methods and their application in evolutionary biology. Berlin, Germany: Springer. [Google Scholar]
- 35.Craft ME. 2015. Infectious disease transmission and contact networks in wildlife and livestock. Phil. Trans. R. Soc. B 370, 20140107 ( 10.1098/rstb.2014.0107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Newman ME. 2006. Modularity and community structure in networks. Proc. Natl Acad. Sci. USA 103, 8577–8582. ( 10.1073/pnas.0601602103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kreimer A, Borenstein E, Gophna U, Ruppin E. 2008. The evolution of modularity in bacterial metabolic networks. Proc. Natl Acad. Sci. USA 105, 6976–6981. ( 10.1073/pnas.0712149105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.R Development Core Team. 2014. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. [Google Scholar]
- 39.Csardi G, Nepusz T. 2006. The igraph software package for complex network research. InterJournal Complex Syst. 1695. [Google Scholar]
- 40.Newman ME, Watts DJ. 1999. Scaling and percolation in the small-world network model. Phys. Rev. E 60, 7332 ( 10.1103/PhysRevE.60.7332) [DOI] [PubMed] [Google Scholar]
- 41.Naug D. 2008. Structure of the social network and its influence on transmission dynamics in a honeybee colony. Behav. Ecol. Sociobiol. 62, 1719–1725. ( 10.1007/s00265-008-0600-x) [DOI] [Google Scholar]
- 42.Borgatti SP, Everett MG, Freeman LC. 2002. UCINET for Windows: software for social network analysis. Lexington, KY: Analytic Technologies. [Google Scholar]
- 43.Opsahl T, Agneessens F, Skvoretz J. 2010. Node centrality in weighted networks: Generalizing degree and shortest paths. Soc. Netw. 32, 245–251. ( 10.1016/j.socnet.2010.03.006) [DOI] [Google Scholar]
- 44.Dijkstra EW. 1959. A note on two problems in connexion with graphs. Numer. Math. 1, 269–271. ( 10.1007/BF01386390) [DOI] [Google Scholar]
- 45.Opsahl T. 2009. Structure and evolution of weighted networks. London, UK: Queen Mary: University of London. [Google Scholar]
- 46.Bonabeau E, Dagorn L, Freon P. 1999. Scaling in animal group-size distributions. Proc. Natl Acad. Sci. USA 96, 4472–4477. ( 10.1073/pnas.96.8.4472) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kasper C, Voelkl B. 2009. A social network analysis of primate groups. Primates 50, 343–356. ( 10.1007/s10329-009-0153-2) [DOI] [PubMed] [Google Scholar]
- 48.Borenstein M, Hedges L, Higgins J, Rothstein H. 2005. Comprehensive meta-analysis, 2nd edn Englewood, NJ: Biostat. [Google Scholar]
- 49.Lajeunesse M. 2009. Meta Analysis and the Comparative Phylogenetic Method. Am. Nat. 174, 369–381. ( 10.1086/603628) [DOI] [PubMed] [Google Scholar]
- 50.Lajeunesse MJ. 2011. phyloMeta: a program for phylogenetic comparative analyses with meta-analysis. Bioinformatics 27, 2603–2604. ( 10.1093/bioinformatics/btr438) [DOI] [PubMed] [Google Scholar]
- 51.Orme D, Freckleton R, Thomas G, Petzoldt T, Fritz S, Isaac N. 2011. caper: comparative analyses of phylogenetics and evolution in R. See http://R-Forge.R-project.org/projects/caper/.
- 52.Pagel M. 1999. Inferring the historical patterns of biological evolution. Nature 401, 877–884. ( 10.1038/44766) [DOI] [PubMed] [Google Scholar]
- 53.Freckleton RP, Harvey PH, Pagel M. 2002. Phylogenetic analysis and comparative data: a test and review of evidence. Am. Nat. 160, 712–726. ( 10.1086/343873) [DOI] [PubMed] [Google Scholar]
- 54.Bininda-Emonds ORP, et al. 2007. The delayed rise of present-day mammals. Nature 446, 507–512. ( 10.1038/nature05634) [DOI] [PubMed] [Google Scholar]
- 55.Hedges SB, Dudley J, Kumar S. 2006. TimeTree: a public knowledge-base of divergence times among organisms. Bioinformatics 22, 2971–2972. ( 10.1093/bioinformatics/btl505) [DOI] [PubMed] [Google Scholar]
- 56.Brady SG, Schultz TR, Fisher BL, Ward PS. 2006. Evaluating alternative hypotheses for the early evolution and diversification of ants. Proc. Natl Acad. Sci. USA 103, 18 172–18 177. ( 10.1073/pnas.0605858103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Nunn CL, Thrall PH, Stewart K, Harcourt AH. 2008. Emerging infectious diseases and animal social systems. Evol. Ecol. 22, 519–543. ( 10.1007/s10682-007-9180-x) [DOI] [Google Scholar]
- 58.Nunn CL, Thrall PH, Bartz K, Dasgupta T, Boesch C. 2009. Do transmission mechanisms or social systems drive cultural dynamics in socially structured populations? Anim. Behav. 77, 1515–1524. ( 10.1016/j.anbehav.2009.02.023) [DOI] [Google Scholar]
- 59.Seaholm SK, Ackerman E, Wu SC. 1988. Latin hypercube sampling and the sensitivity analysis of a Monte-Carlo epidemic model. Int. J. Bio-Med. Comput. 23, 97–112. ( 10.1016/0020-7101(88)90067-0) [DOI] [PubMed] [Google Scholar]
- 60.Blower SM, Dowlatabadi H. 1994. Sensitivity and uncertainty analysis of complex-models of disease transmission—an HIV model, as an example. Int. Stat. Rev. 62, 229–243. ( 10.2307/1403510) [DOI] [Google Scholar]
- 61.Rushton SP, Lurz PWW, Gurnell J, Fuller R. 2000. Modelling the spatial dynamics of parapoxvirus disease in red and grey squirrels: a possible cause of the decline in the red squirrel in the UK? J. Appl. Ecol. 37, 997–1012. ( 10.1046/j.1365-2664.2000.00553.x) [DOI] [Google Scholar]
- 62.Burnham KP, Anderson DR. 2002. Model selection and multimodel inference: a practical information-theoretic approach. Berlin, Germany: Springer [Google Scholar]
- 63.Barton K. 2011. MuMIn: Multi-model inference. R package version 1.6.5. Vienna, Austria: R Foundation for Statistical Computing. [Google Scholar]
- 64.Fletcher TD. 2012. QuantPsyc: quantitative psychology tools. R package version 1.5. Vienna, Austria: R Foundation for Statistical Computing. [Google Scholar]
- 65.Gramacy RB. 2007. tgp: an R package for Bayesian nonstationary, semiparametric nonlinear regression and design by treed Gaussian process models. J. Stat. Soft. 19, 6. [Google Scholar]
- 66.Gramacy RB, Taddy M. 2012. Categorical inputs, sensitivity analysis, optimization and importance tempering with tgp version 2, an R package for treed Gaussian process models. J. Stat. Soft. 33, 1–48. [Google Scholar]
- 67.Wlasiuk G, Nachman M. 2010. Promiscuity and the rate of molecular evolution at primate immunity genes. Evolution 64, 2204–2220. ( 10.1111/j.1558-5646.2010.00989.x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Nunn CL. 2002. Spleen size, disease risk and sexual selection: a comparative study in primates. Evol. Ecol. Res. 4, 91–107. [Google Scholar]
- 69.Weinstock GM, et al. 2006. Insights into social insects from the genome of the honeybee Apis mellifera. Nature 443, 931–949. ( 10.1038/nature05260) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Evans J, et al. 2006. Immune pathways and defence mechanisms in honey bees Apis mellifera. Insect Mol. Biol. 15, 645–656. ( 10.1111/j.1365-2583.2006.00682.x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Cremer S, Armitage SA, Schmid-Hempel P. 2007. Social immunity. Curr. Biol. 17, R693–R702. ( 10.1016/j.cub.2007.06.008) [DOI] [PubMed] [Google Scholar]
- 72.Holbrook C, Eriksson T, Overson R, Gadau J, Fewell J. 2013. Colony-size effects on task organization in the harvester ant Pogonomyrmex californicus. Insect. Soc. 60, 191–201. ( 10.1007/s00040-013-0282-x) [DOI] [Google Scholar]
- 73.Nunn CL, Thrall PH, Leendertz FH, Boesch C. 2011. The spread of fecally transmitted parasites in socially-structured populations. PLoS ONE 6, e21677 ( 10.1371/journal.pone.0021677) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data used for the comparative and meta-analyses are provided in the electronic supplementary material.