In vivo coincidence detection in mammalian sound localization generates phase delays

Abstract

Sound localization critically depends on detection of differences in arrival time of sounds at the two ears (acoustic delay). The fundamental mechanisms are debated, but all proposals include a process of coincidence detection and a separate source of internal delay which offsets the acoustic delay and determines neural tuning. We obtained in vivo patch clamp recordings of binaural neurons in the Mongolian gerbil, combined with pharmacological manipulations, to directly compare neuronal input to output and to separate excitation from inhibition. The results cannot be accounted for by existing models and reveal that coincidence detection is not an instantaneous process but is shaped by the interaction of intrinsic conductances with preceding synaptic activity. This interaction generates an internal delay as an intrinsic part of the process of coincidence detection. The multiplication and time-shifting stages thought to extract synchronous activity in many brain areas can thus be combined in a single operation.

Spatial hearing is the premier model system to study temporal processing in the brain^{1, 2}. Because there is no explicit representation of space at the level of the receptor organ, spatial sound attributes have to be computed in the brain. In humans, the dominant cue is the difference in arrival time of sounds at the two ears: the interaural time difference or ITD. Extraction of this cue is performed by neurons in the medial superior olive (MSO) in mammals and in the nucleus laminaris (NL) in birds^{1, 3}. MSO neurons receive excitatory input from both ears relayed from the cochlea through the ipsi- and contralateral cochlear nuclei (Fig. 1a). In addition, inhibition is provided through the medial and lateral nuclei of the trapezoid body⁴.

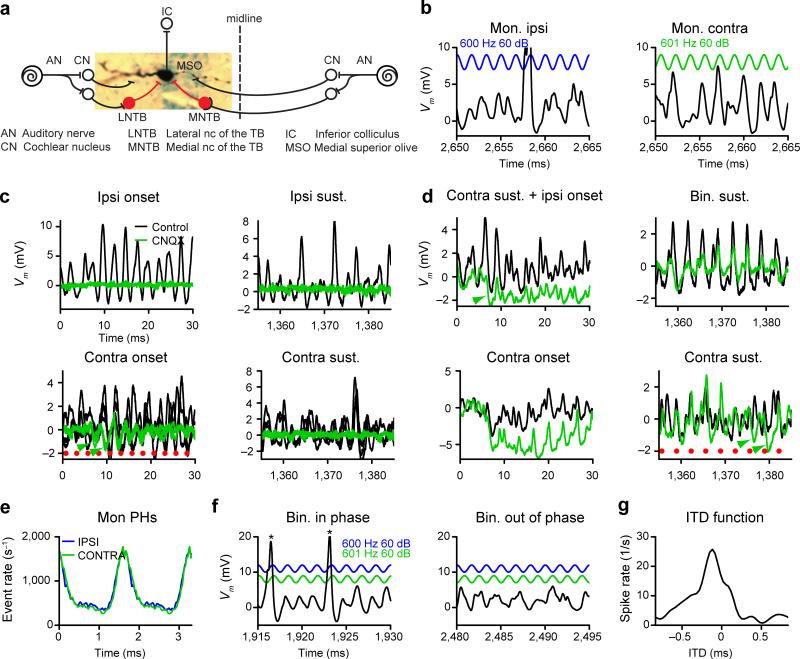
Figure 1.

EPSPs, IPSPs and spikes of MSO neurons in vivo. (a) Labeled MSO neuron (characteristic frequency = 1015 Hz) with schematic circuit. Excitatory neurons in black and inhibitory neurons in red. (b) Whole-cell recording during monaural stimulation with a sinusoidal tone. V_m (relative to V_rest) in black, stimulus in blue (ipsi) or green (contra). Characteristic frequency = 923 Hz. Across cycles, EPSPs tended to occur at a similar phase of the stimulus, showing that the excitatory inputs are phase-locked. IPSPs were hard to identify due to the large number of EPSPs and associated afterhyperpolarizations. (c,d), Onset and sustained parts of the monaural responses with (green) or without (black) CNQX for two neurons. (c): stimulus 400/401 Hz 70 dB. Characteristic frequency = 1625 Hz. (d): stimulus 300/301 Hz 70 dB. Red dots indicate start of sound cycles. Green arrowheads indicate examples of IPSPs. For the neuron in d, EPSPs were not completely suppressed. Characteristic frequency = 653 Hz. (e) EPSP monaural period histograms, for the same dataset as in b. (f) Response of the neuron in b to in-phase and out-of-phase portions of a binaural beat, where each ear receives the same stimulus as in b. Asterisks indicate spikes. Colors as in b. (g) ITD function calculated from the binaural beat spiking response for the neuron in b.

The relatively simple organization of the MSO circuit makes it a powerful system to study coincidence detection, a canonical neural operation important for the extraction of synchronous activity present in many brain areas^{2, 5, 6}. Afferent inputs can be controlled independently by playing sound to either ear, and extensive behavioral data document the capabilities and limitations of this binaural system⁷.

The paucity of in vivo recordings has caused vigorous debate regarding the nature of ITD computation in mammals^{1, 8-10}. In 1948, Jeffress hypothesized that MSO neurons act as instantaneous coincidence detectors, firing when excitatory inputs from each ear are in temporal register. These neurons would be tuned to ITD by virtue of different axonal conduction delays between the excitatory inputs from both ears¹¹, and this difference causes an “internal delay” i.e. a difference in the latency of the ipsi- versus contralateral ear to excite MSO neurons. A maximal number of coincidences occurs at the ITD that compensates for this internal delay: this ITD is defined as the best delay. Furthermore, Jeffress postulated that best delays are topographically mapped due to systematic delay lines.

While Jeffress’ model is thought to be consistent with ITD computation in NL in birds^{3, 12}, there is much debate regarding its applicability to mammals. Extracellular and juxtacellular studies suggest that ITD tuning in MSO neurons reflects instantaneous coincidence detection of excitatory postsynaptic potentials (EPSPs)^{8, 13, 14}. Also, anatomical delay line configurations and a gradient of best delays have been described^{13, 15, 16}. However, these features do not explain the population distribution of best delays^{17, 18}. Other factors have been proposed to provide internal delay, such as fast phase-locked inhibition^{10, 19}, asymmetric rise times of EPSPs²⁰, an asymmetric origin of the axon²¹, and disparities in the frequency tuning of the inputs from the two ears^{22, 23}. In all of these models, however, the basic premise of instantaneous coincidence detection has never been questioned.

We studied coincidence detection by obtaining the first in vivo whole-cell recordings from verified MSO neurons, visualizing spikes as well as excitatory and inhibitory synaptic inputs. Our results are difficult to reconcile with the dominant proposals and show that ITD tuning is not well predicted on the population level by a linear summation of monaural inputs. Instead, recent input history shapes coincidence detection through small changes in the membrane potential that dynamically alter action potential threshold. The interplay between synaptic inputs and the intrinsic conductances of MSO neurons strongly affects the best delay and effectively contributes to internal delay.

RESULTS

Input and output of MSO neurons in vivo

We obtained whole-cell recordings from 59 MSO neurons in vivo in Mongolian gerbils under general anesthesia, using the blind in vivo patch-clamp technique. The identity of half of these neurons was anatomically confirmed by labeling with biocytin (Fig. 1a; Fig. 2a). Intracellular responses were dominated by excitatory events (Fig. 1b), as suggested by extra- and juxtacellular studies^{8, 13}. EPSP shape and size were similar to in vitro recordings (Fig.1; Fig. 5c,g)^{9, 24}. EPSPs appeared as discrete events (Fig. 1b), confirming in vivo juxtacellular recordings⁸.

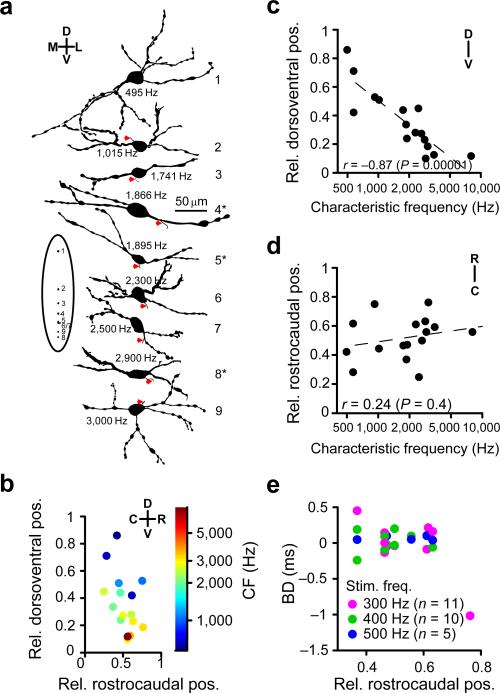
Figure 2.

Anatomical location of MSO neurons. (a) Camera lucida drawings (made by Dr. P.H. Smith). CF is indicated with each neuron. Inset on the left shows position of the cell bodies on a schematic dorsoventral MSO outline. Red arrowheads indicate axonal origin. Asterisks indicate the neurons with shifts of 200 μs or more. (b) Projection of retrieved cell bodies on a normalized side view of the MSO. Abscissa is the normalized rostrocaudal location for the coronal section in which the cell body was localized (0 corresponds to caudal pole and 1 to rostral pole of the MSO). Ordinate is the normalized dorsoventral distance for the coronal section in which the cell body was located (0 corresponds to ventral border and 1 to dorsal border of the MSO). Colors indicate characteristic frequency. (n = 16) (c,d) Normalized dorsoventral (c) and rostrocaudal (e) positions of MSO neurons as a function of characteristic frequency. Dashed lines are linear fits (n = 16). c: linear correlation t(14) = –6.47 (n = 16). d: linear correlation t(14) = 0.92 (n = 16). (e) Best delay as a function of normalized rostrocaudal position. Color indicates stimulus frequency. There is no evidence for a rostrocaudal map of best delays.

Figure 5.

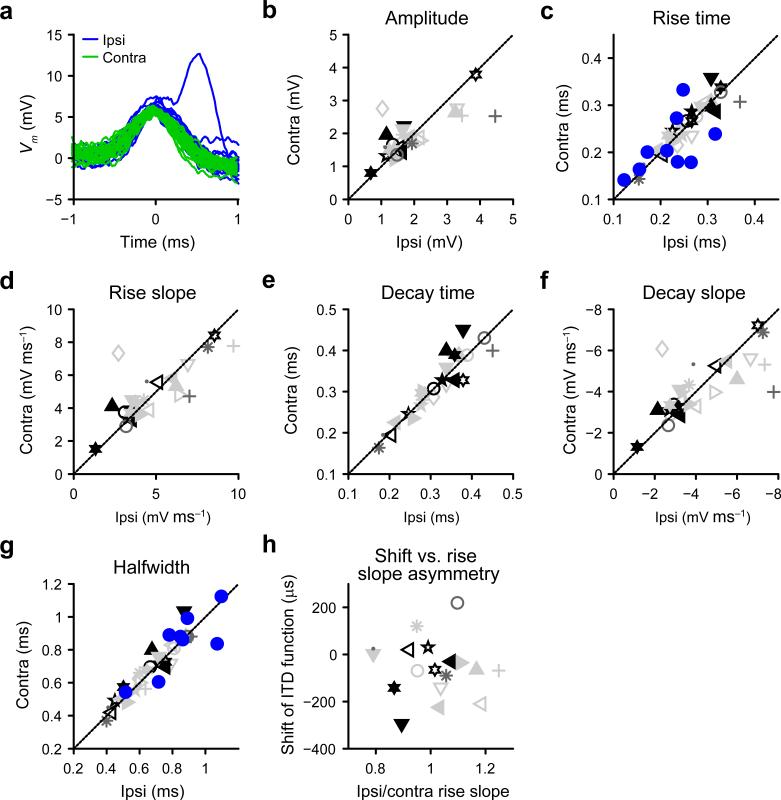
Symmetry of monaural excitatory inputs. (a) Superposition of the 20 largest EPSPs during monaural ipsilateral (blue) and monaural contralateral (green) stimulation, for a neuron with characteristic frequency = 1000 Hz. (b)-(g), Scatter plots of several EPSP metrics for the population of MSO neurons, to monaural stimulation with 300 or 301 Hz tones at 70 dB SPL (n = 26). Symbols as in Figure 3b. For each dataset, the median value of the metric during monaural contralateral stimulation is shown relative to its ipsilateral equivalent. Diagonal line indicates identity. For rise time (c) and halfwidth (g), blue filled circles show the same data for in vitro thick slice recordings (n = 9). (h) Scatter plot of shift of rITDf relative to predITDf as a function of the relative size of ipsilateral EPSP rise slope (rise slope ipsi / rise slope contra). Correlation is not significant (linear correlation r = –0.075, t(16) = -0.30, P = 0.77 (18 datasets from 18 neurons)).

Discrete IPSPs were small and scarce, possibly because EPSPs mask the presence of IPSPs (Fig. 1b,c,d,f). To better visualize IPSPs, we blocked EPSPs with local pressure application of the AMPA receptor antagonist CNQX (220 or 440 μM). Under these conditions IPSPs were clearly identified, but were not always present (Fig. 1c,d). For the neuron shown in Figure 1c, IPSPs were only seen at the onset of contralateral stimulation. Another neuron showed strong IPSP summation at the stimulus onset, as has been recently observed in vitro⁹, as well as phase-locked IPSPs in the sustained response, particularly for contralateral stimulation (Fig. 1d). The paucity, small size, and temporal summation of IPSPs are difficult to reconcile with the hypothesis that IPSPs set the ITD-tuning of MSO neurons^{10, 19, 25}. This conclusion is strengthened by results from blocking inhibition (Fig. 4, below).

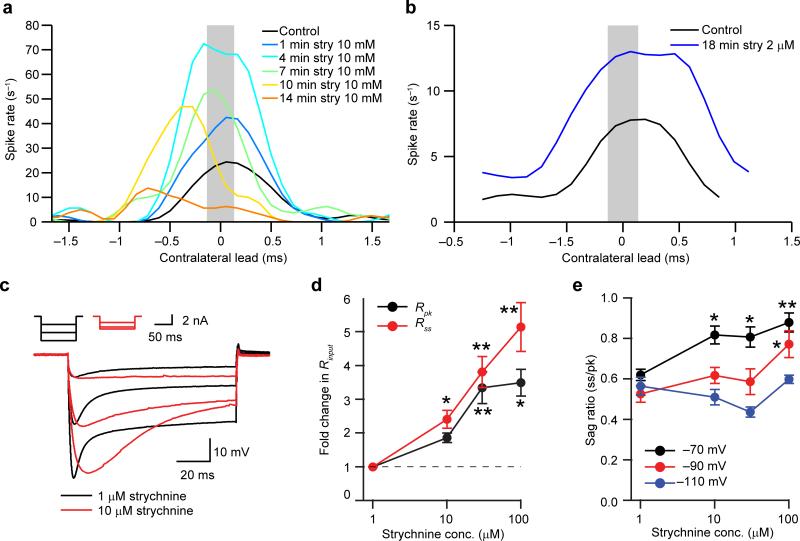
Figure 4.

Concentration dependent effects of strychnine on ITD functions and intrinsic physiology. (a) ITD function of one neuron before and during strychnine iontophoresis (10 mM). ITD functions progressively changed, suggesting concentration dependent effects. Stimulus: 300 Hz/80 dB SPL. Characteristic frequency = 1149 Hz. (b) ITD functions before and during strychnine (2 μM) application by pressure. The increased spike rate demonstrates that the dose effectively antagonized inhibition, but there was no leftward shift in the position of the ITD function. Stimulus: 400 Hz/70 dB SPL. ITD functions are static ITD functions. Characteristic frequency = 538 Hz. (c) In vitro responses of an MSO neuron to hyperpolarizing current steps delivered in the presence of 1 μM (black) or 10 μM (red) strychnine. Inset shows current steps used to elicit responses. (d) Peak (R_pk) and steady state (R_ss) input resistances increased with increasing strychnine concentrations. Data are normalized to resistances measured in 1 μM strychnine. (e) Increasing strychnine concentrations increased the sag ratios of current steps that elicited peak hyperpolarizations to –70 mV but not –110 mV, suggesting a shift in I_h activation to more hyperpolarized potentials. (d,e) One-way two-tailed ANOVA with Tukey's post-hoc. R_pk: F(3,19) = 7.459; n = 7, 7, 5, 4; P = n.a., 0.221, 0.002, 0.012. R_ss: F(3,19) = 12.731; n = 7, 7, 5, 4; P = n.a., 0.049, 0.001, 0.0001. Sag ratio at –70 mV: F(3,17) = 7.144; n = 6, 6, 5, 4; P = n.a., 0.013, 0.026, 0.004. Sag ratio at –90 mV: F(3,17) = 3.704, n = 6, 6, 5, 4; P = n.a., 0.535, 0.822, 0.021. Sag ratio –110 mV: F(3,17) = 3.340, n = 6, 6, 5, 4; P = n.a., 0.681, 0.096, 0.922. n and P values listed for 1, 10, 30, 100 μM, respectively. * P < 0.05, ** P < 0.01. Data in d and e represent mean ± s.e.m.

Measurement of the timing of the EPSPs in responses to monaural stimulation, relative to the stimulus cycle, showed clear phase-locking of the inputs to stimulation of either ear (Fig. 1e). MSO neurons thus receive excitatory inputs from both sides with preserved stimulus timing information, which allows them to compare the timing of the sound at the two ears during binaural stimulation. When the inputs are in phase, events will sum and larger depolarizations increase the probability of firing (Fig. 1f, left panel). When the inputs are out of phase, depolarization and spiking decrease. Counting the number of spikes for different ITDs results in an ITD function (Fig. 1g).

Mapping physiology to anatomy

Biocytin labeling allowed linking of the physiological and anatomical properties of individual neurons. Retrieved neurons showed the stereotyped bipolar morphology of MSO principal neurons^{26, 27} (Fig. 1a; Fig. 2a). We plotted the location of cell bodies on a normalized dorsoventral and rostrocaudal axis, and observed that neurons with a higher characteristic frequency were localized more ventrally than neurons with a lower characteristic frequency (Fig. 2b,c), confirming the tonotopy deduced from extracellular recordings²⁸ and labeled afferents¹⁸, while there was no significant frequency tuning trend rostrocaudally (Fig. 2d).

The rostrocaudal axis, orthogonal to the tonotopic map, is the dimension along which a map of best delays has been proposed in accordance with the Jeffress model^{11, 13, 15}. We did not find evidence for systematic changes in BD along the rostrocaudal dimension of the MSO (Fig. 2e), contrary to the systematic axonal conduction delays predicted by the Jeffress model.

Relation of ITD tuning to subthreshold inputs

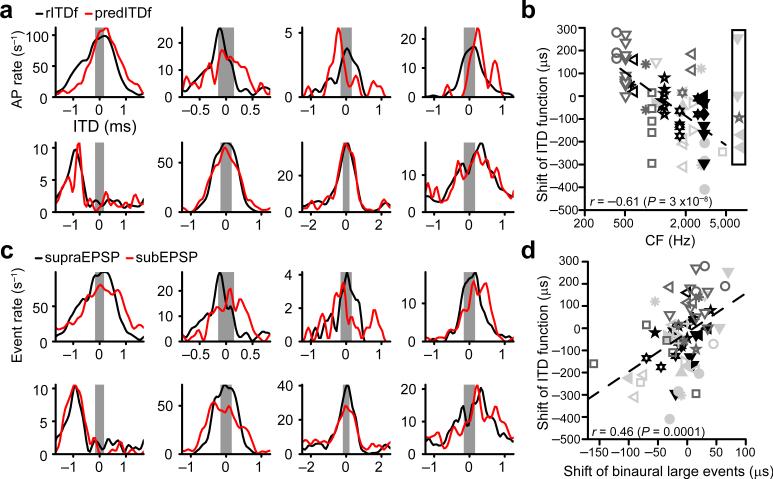
Intracellular in vivo recordings capture the subthreshold inputs as well as the suprathreshold output, providing powerful data to test the hypothesis of instantaneous coincidence detection by comparing the binaural output of a MSO neuron to its monaural inputs. For the neuron in Figure 1e-g, the incoming EPSPs from each side overlapped most in time when ITD = 0 ms. Therefore, in the framework of instantaneous coincidence detection, the expected best delay of this neuron is 0 ms. Surprisingly, the ITD function indicated a best delay for which, on average, the ipsilateral EPSPs led the contralateral EPSPs (negative delay, by convention; Fig. 1g). We tested the plausibility of instantaneous coincidence detection more rigorously on the population of MSO neurons. Figure 3a shows ITD functions for eight neurons obtained to a binaural beat. To predict the result of instantaneous coincidence detection, we summed the responses obtained to monaural ipsilateral and contralateral stimuli and generated predicted spikes whenever the sum crossed a threshold. Predicted spike times were transformed into predicted ITD functions (predITDfs; Fig. 3a). In several cases, predITDfs and real binaural ITD functions (rITDfs) corresponded well (Fig. 3a, bottom row). But similar to the case in Figure 1e-g, we often observed mismatches in ITD (Fig. 3a, top row). The shift of rITDf relative to predITDf was similar for a reversed binaural beat, for different values of threshold used to predict spikes and for a prediction based on crosscorrelation of the monaural period histograms (Supplementary Fig. 1).

Figure 3.

ITD tuning of MSO neurons often deviates from instantaneous coincidence detection. (a) rITDf (black lines) and predITDf (red lines) for 8 datasets. Grey rectangles indicate the approximate physiological ITD range (± 130 μs²⁹). Respective stimuli (left to right, top to bottom, ipsi/contra): 300/301 Hz 70 dB; 600/601 Hz 60 dB; 400/401 Hz 70 dB; 400/401 Hz 70 dB; 300/301 Hz 90 dB; 400/401 Hz 70 dB; 200/201 Hz 90 dB; 400/401 Hz 60 dB. Respective characteristic frequencies: 1895 Hz; 923 Hz; unknown; 1741 Hz; 3031 Hz; 3031 Hz; 1154 Hz; 2639 Hz. Top row shows neurons with a mismatch between rITDf/predITDf, whereas the neurons in the bottom row show good correspondence. (b) Shift between rITDf and predITDf as a function of characteristic frequency for 72 datasets (28 neurons) with significant suprathreshold ITD tuning (Rayleigh test α < 0.001). Rectangle indicates datasets with unknown characteristic frequency. Different symbols correspond to different neurons. Linear correlation: t(65) = –6.26 (67 datasets from 25 neurons). (c) ITD tuning of subEPSPs (black lines) and supraEPSPs (red lines) for the datasets in a. (d) Shift between rITDf and predITDf (as in b) relative to the shift between subEPSPs/supraEPSPs ITD tuning (from c). Same symbols as in b (one outlying data point is not shown but included in the correlation). Linear correlation: t(70) = 4.31 (72 datasets from 28 neurons).

We quantified the shift by crosscorrelating rITDf and predITDf. The lag of maximal correlation is the shift value (y axis in Fig. 3b). At the population level the shift value was correlated with the characteristic frequency of the neurons. At low characteristic frequencies the real best delay was often at larger positive ITDs than expected; at high characteristic frequencies the shift was usually towards more negative ITDs. For 36/72 datasets where enough spikes were recorded to make significant rITDfs (17/28 neurons), the absolute value of this shift was larger than 100 μs, and for the entire population the shifts covered > 500 μs: these values are large relative to the gerbil physiological ITD range (roughly ±130 μs²⁹).

Shift is not explained by dominant proposals of ITD tuning

The shift between rITDfs and predITDfs is not compatible with instantaneous coincidence detection. We examined whether alternative hypotheses for ITD-tuning may explain it. Phase-locked inhibition has been proposed to shift the ITD function^{10, 19}. Previous studies using strychnine iontophoresis to block glycine receptor-mediated inhibition during extracellular MSO recordings, showed a shift of best delay to 0 ms ^{10, 19}, presumably reflecting distortions in EPSP timing by IPSPs. By combining strychnine (10 mM) iontophoresis with whole-cell recordings, we observed shifts in ITD functions (Fig. 4a). However, this effect continually evolved over time: after an initial increase, spike rate progressively decreased until ITD tuning was insignificant (Fig. 4a). Because strychnine binds to glycine receptors at relatively low concentrations (strychnine K_d ≈ 2 – 14 nM)³⁰, we hypothesized that iontophoresis generated high levels of drug that might cause nonspecific effects. Therefore, we switched to pressure application to ensure that the maximal drug concentration in the brain could not exceed, and was probably below, that in the puffer pipette (2 μM). Pressure application did not cause a shift in ITD tuning (Fig. 4b). At the population level, strychnine 2 μM applied by pressure (7 datasets from 5 neurons) resulted in a similar increase in spike rate as 10 mM applied by iontophoresis (5 datasets from 3 neurons), respectively 57.8 ± 18.0 spikes/s and 55.2 ± 21.7 spikes/s (mean ± s.e.m.; two-sample one-tailed t-test t(10) = 0.092; P = 0.5), and was therefore equally effective in blocking inhibition. The change in best IPD (interaural phase difference) was significantly larger during iontophoresis (10 mM;–0.087 ± 0.044 cycles) compared to pressure application (2 μM; –0.0015 ± 0.021 cycles; mean ± s.e.m.; two-sample one-tailed t-test t(10) = 1.95 (P = 0.04)). Pressure application of strychnine did not cause a significant change in ITD tuning (paired sample one-tailed t-test t(6) = –0.070 (P = 0.47)). These experiments suggest that the best delay shift observed with strychnine iontophoresis^{10, 19} is due to nonspecific effects of strychnine at high concentrations and not to the removal of inhibition.

In vitro slice experiments revealed that the intrinsic electrical properties of MSO neurons are altered by strychnine at concentrations as low as 10 μM (Fig. 4c-e). Steady state input resistance more than doubled in 10 μM strychnine (Fig. 4d) and the sag ratio, reflecting the activation of hyperpolarization activated cation current (I_h), increased with current steps to –70 mV but not –90 or –110 mV, possibly reflecting a shift in the activation range of I_h towards more hyperpolarized potentials (Fig. 4e)³¹. In addition, 10 μM strychnine increased EPSP halfwidths in 5 out of 7 cells (paired-sample t-tests were performed for each cell; t(99) < –8.33; P < 0.001; data not shown). Similarly, strychnine iontophoresis increased monaural EPSP halfwidths in vivo (ipsi: paired sample one-tailed test t(3) = 2.67; P = 0.04; contra: t(3) = 3.83; P = 0.02, 5 datasets from 3 neurons) but pressure application of strychnine did not (ipsi: paired sample one-tailed test t(5) = –0.26; P = 0.6; contra: t(5) = –0.82; P = 0.8; 6 datasets from 4 neurons; data not shown). Taken together, these results do not support the hypothesis that glycinergic inhibition systematically shifts ITD tuning.

One study that used electrical stimulation in vitro to activate MSO inputs suggested that steeper ipsilateral than contralateral EPSPs resulted in more negative best delays²⁰, although stimulation of auditory nerve roots did not lead to asymmetric EPSPs⁹. In vivo, the shape of EPSPs elicited by ipsilateral or contralateral monaural acoustic stimulation was usually strikingly symmetrical (Fig. 5a). This was confirmed when we measured median EPSP amplitudes and kinetics to monaural acoustic stimulation (Fig. 5b-g). This result confirms juxtacellular measurements of cycle-averaged EPSPs⁸. Individual neurons sometimes did show asymmetries, especially in terms of amplitude (e.g. Fig. 5b, +), which could translate into an asymmetrical EPSP slope (Fig. 5d), but this could not explain the shift of the ITD function at the population level (Fig. 5h).

Finally, asymmetric placement of the axon, which sometimes originates from a dendrite rather than the soma, has been proposed as a factor in ITD-tuning^{21, 27}. Because the final comparison between inputs from both sides occurs at the axon initial segment, such an asymmetrical position could treat incoming events from opposing sides differently²¹. Figure 2a shows eight MSO neurons for which the axonal origin was identified. In 2/8 neurons the axon originated from a dendrite (cases 4 and 7). However, the neurons with a large shift (|shift| > 200 μs) did not systematically show this feature (asterisks in Fig. 2a).

Shift in ITD tuning relates to recent input history

To explore why the largest number of output spikes is not always generated at the predicted best delay, we compared ITD tuning of suprathreshold EPSPs to that of the largest subthreshold EPSPs (respectively supraEPSPs and subEPSPs), both obtained from the same responses to binaural stimulation. For N suprathreshold EPSPs, the N largest subthreshold EPSPs were selected for this analysis: the ITD tuning for both types of events is graphed in Figure 3c (same cases as in Figure 3a). Interestingly, datasets with a shift between rITDf and predITDf (Fig. 3a, top row) tended to have a corresponding mismatch between ITD tuning of supraEPSPs and subEPSPs (Fig. 3c, top row), unlike datasets without a shift (Fig. 3a,c bottom row). At the population level, there was a significant correlation between the shift of rITDf vs. predITDf and the shift of supraEPSP vs. subEPSP ITD tuning (Fig. 3d). Thus, the mismatch between actual and predicted ITD tuning is also seen within the binaural responses, and relates to a factor that makes equal sized EPSPs successful at some but not other ITDs.

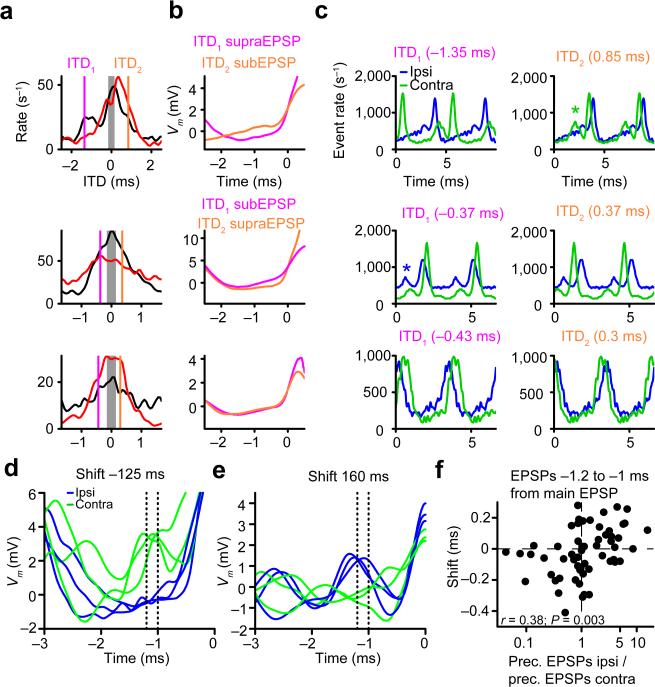
To identify this factor, we examined a case with a clear negative shift (Fig. 6a, top panel), and compared the membrane potential (V_m) preceding subEPSPs or supraEPSPs at two ITDs (ITD_1,2), for which the supraEPSP rate was equal, but the difference in subEPSP rate was maximal. At these 2 ITDs the output spike rate was identical, but there were more large EPSPs that failed to trigger spikes for ITD₂ than for ITD₁. We observed that the average V_m preceding subEPSPs at ITD₂ was depolarized compared to that preceding supraEPSPs at ITD₁ (Fig. 6b, top panel). Examination of individual cycles revealed that this depolarization reflected small EPSPs preceding the main EPSP (Supplementary Fig. 2, top row). For a case with a positive shift (Fig. 6a,b, middle panels; Supplementary Fig. 2), the opposite was true: now ITD₁ generated more subEPSPs than ITD₂, and was preceded by relative depolarization compared to ITD₂. A completely different stimulus (broadband noise) and analysis showed the same association between leading depolarization and absence of spiking (Supplementary Fig. 3). For a case without a shift, there was no difference in the preceding V_m (Fig. 6a,b, bottom panels). Therefore, the shift in ITD function can be linked to differences in V_m history.

Figure 6.

Deviation from instantaneous coincidence detection is related to variation in preceding V_m. (a) ITD tuning for supraEPSPs (black line) and subEPSPs (red line) for example datasets with a negative shift (top), a positive shift (middle) and no shift (bottom). Magenta/orange vertical lines indicate ITDs with equal spike rate but a large difference in subEPSP rate (ITD₁, ITD₂). Respective stimuli: 200/201 Hz 70 dB; 200/201 Hz 70 dB; 300/301 Hz 70 dB. Respective characteristic frequency: 1895 Hz; 508 Hz; 1231 Hz. (b) Average supraEPSPs and subEPSPs for ITD₁ and ITD₂ indicated in a. (c) Monaural EPSP period histograms (2 cycles) arranged for ITD₁ (left column) and ITD₂ (right column). Despite the different degrees of “coincidence” between ipsi- and contralateral inputs for these two ITDs, they generate the same number of spikes. Green and blue asterisks indicate a small group of respectively contralateral and ipsilateral EPSPs that lead the main group of EPSPs. (d,e) Example monaural ipsi- and contralaterally evoked traces leading up to large EPSPs (peak at 0 ms). Dotted lines indicate an interval 1.2 ms to 1 ms before the main EPSP peak. Respective stimuli (CF): 350/351 Hz, 70 dB SPL (characteristic frequency = 1741 Hz); 200/201 Hz, 70 dB SPL (characteristic frequency = 616 Hz). (f) Shift is plotted relative to the ratio (ipsi/contra) of the number of preceding depolarizations 1.2 to 1 ms before the main EPSP peak (linear correlation; t(56) = 3.07; 64 datasets from 26 neurons).

We explored whether the difference in preceding V_m was related to features of the monaural inputs. Figure 6c shows the ipsilateral and contralateral monaural EPSP period histograms for the same neurons as in Figure 6a,b, ordered to correspond to ITD₁/ITD₂. Note that the main peak in the EPSP distribution for the contralateral response) was preceded by a smaller peak. At ITD₂, this early group of EPSPs generated the early depolarizations observed in the binaural responses associated with many spike failures (Supplementary Fig. 2, top row). By contrast, at ITD₁, at which fewer spike failures occurred, the ipsilateral inputs lead in time and early “mistimed” depolarizations were less prominent. Note that even though the inputs were less coincident for ITD₁ than for ITD₂, the number of output spikes generated was equal. For the case with a positive shift, the situation is inverted: now preceding EPSPs were more prominent in the ipsilateral response (blue asterisk). The histograms for the dataset without shift (Fig. 5c, bottom row) were more symmetrical, resulting in similar voltage traces for ITD₁ and ITD₂ (Fig. 5b, bottom row).

These observations suggest that subtle asymmetries in the temporal patterns of ipsilateral versus contralateral EPSPs shift ITD tuning by generating ITD dependent differences in the V_m preceding a coincidence. To explore whether those asymmetries are also associated with the shift at the population level, we identified the 5% largest EPSPs in the monaural responses, and counted the cases preceded by depolarization as large as the median EPSP. We observed that, for a case with a negative shift, large contralateral EPSPs were more often preceded by depolarization than ipsilateral EPSPs (Fig. 6d), confirming the results in Figure 6c. For a case with a positive shift, the opposite was true (Fig. 6e). At the population level, there was a significant correlation between the ratio of ipsilateral versus contralateral preceding EPSPs (occurring 1.2 to 1 ms before the main EPSP), and the shift of the ITD function (Fig. 6f).

Preceding V_m modifies spiking by Kv1 channel activation

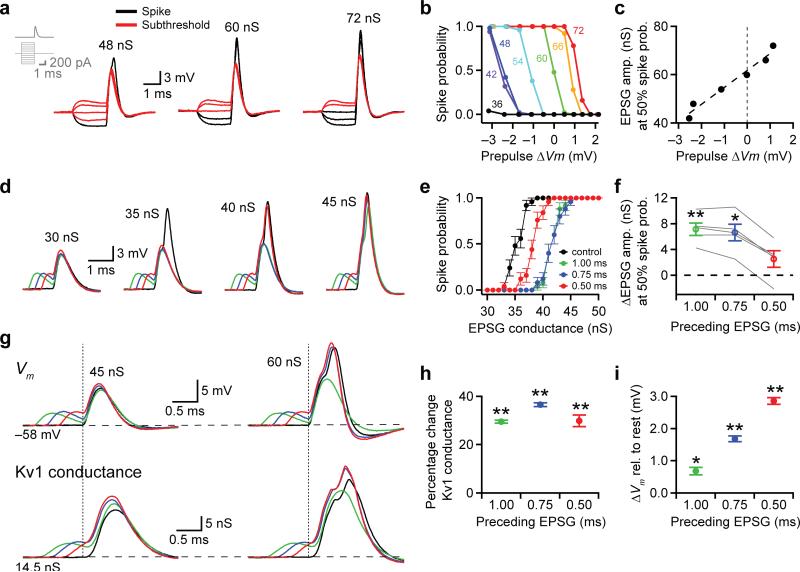
To examine under tightly controlled conditions whether small differences in preceding V_m affect spike probability, we made dual somatic whole-cell recordings from MSO neurons in gerbil brainstem slices and simulated excitatory postsynaptic conductances (EPSGs) with dynamic clamp (Fig. 7). Currents were injected through one electrode while V_m was measured without bridge balance artifacts with the other. First, we simulated a single EPSG and used current steps to manipulate the V_m for the 2 ms preceding EPSG onset (Fig. 7a, inset). EPSG amplitudes were varied to yield EPSPs that were subthreshold (Fig. 7a, left and middle) or suprathreshold (Fig. 7a, right) in the absence of a current step. Preceding hyperpolarizing current steps strongly reduced the EPSG amplitude required to evoke a spike, whereas preceding depolarizing steps had the opposite effect (Fig. 7a). The preceding V_m strongly influenced spike probability (Fig. 7b) and the EPSG amplitude required to elicit a spike (Fig. 7c). Across the population of neurons, the relationship between the EPSG amplitude needed to elicit spikes in 50% of trials and the preceding V_m had a slope of 6.61 ± 0.69 nS/mV (mean ± s.e.m., linear fit, r = 0.96 – 0.99, P < 0.01, n = 5 cells), indicating that a 1 mV change in preceding V_m can alter the conductance threshold for a spike by nearly 7 nS.

Figure 7.

Preceding V_m influences spike probability and Kv1 channel activation. (a) EPSGs were simulated using dynamic clamp while the preceding V_m was manipulated with 2 ms current steps (inset). EPSGs of different amplitudes elicited spikes (black) or subEPSPs (red) depending on the preceding V_m. (b) Spike probability as a function of preceding V_m. Numbers indicate EPSG amplitudes (nS) for correspondingly colored curves. (c) The EPSG amplitude required to reach 50% spike probability was correlated with the preceding V_m (linear fit, r = 0.98, P = 0.0005, t(4) = 10.552). (d) Pairs of EPSGs were simulated with the preceding EPSG starting 1.00 (green), 0.75 (blue), or 0.50 ms (red) before the main EPSG. Amplitudes of the main EPSGs are indicated. (e) Small preceding EPSGs raised the conductance needed for the main EPSG to elicit a spike. Same cell as d. (f) Across cells, preceding EPSGs that led by 1.00 and 0.75 ms significantly increased the conductance required to reach 50% spike probability. Gray lines show data from individual cells. Repeated measures ANOVA with Tukey's post-hoc: F(3,12) = 29.702; n = 5, 5, 5; P = 0.006, 0.023, 0.332. (g) Measurement of V_m (top row) and Kv1 conductance (bottom row) in experiments where Kv1 was simulated by dynamic clamp after pharmacological block with 4-aminopyridine. EPSGs of two amplitudes are shown with and without small (~3 mV) preceding EPSGs. Vertical dashed lines indicate the onset of the main EPSG. Horizontal dashed lines indicate the –58 mV resting membrane potential (top) and the 14.5 nS resting Kv1 conductance (bottom). (h,i) Preceding EPSGs significantly increased the Kv1 conductance (h) and membrane potential (i) measured at the onset of the main EPSG. Repeated measures two-tailed ANOVA with Tukey's post-hoc: Kv1 conductance, F(3,12) = 100.394; n = 5, 5, 5; P = 3.7 × 10⁻⁵, 0.0003, 0.004 . Membrane potential, F(3,12) = 171.414; n = 5, 5, 5; P = 0.013, 0.0003, 8.1 × 10⁻⁵. n and P values listed for 1.00, 0.75, 0.50 ms, respectively. * P < 0.05, ** P < 0.01. Data in e,f,h,i represent mean ± s.e.m.

Second, we examined how a small preceding EPSG affected the probability that an EPSG would elicit a spike. Preceding EPSGs were set to start 1.00, 0.75, or 0.50 ms before the onset of the main EPSG and to generate ~3 mV EPSPs. Varying the amplitude of the main EPSG showed that preceding EPSGs increased the conductance needed for the main EPSG to elicit a spike (Fig. 7d,e). On average, preceding EPSGs that led by 1.00 and 0.75 ms increased the main EPSG amplitude needed to reach 50% spike probability by 7.2 ± 1.0 and 6.6 ± 1.3 nS, respectively (mean ± s.e.m. Fig. 7f; repeated measures ANOVA with Tukey's post-hoc, P < 0.05).

Third, we hypothesized that preceding EPSPs influence subsequent EPSPs by activating low-voltage activated Kv1 potassium channels. Kv1 channels constitute ~90% of the low-voltage activated K⁺ current in MSO neurons²⁴ and are situated at a steep portion of their activation curve at the resting V ³²_m. In order to visualize how Kv1 channels respond to preceding EPSPs without significantly altering the normal integrative properties of MSO neurons, we blocked intrinsic potassium channels by including 5 mM 4-aminopyridine in the recording electrodes and then replaced them by simulating Kv1 conductances with dynamic clamp⁹. When pairs of EPSGs were simulated as before (Fig. 7d-f), the depolarization induced by preceding EPSGs (Fig. 7g top) increased the simulated Kv1 conductance above resting levels (Fig. 7g bottom). This additional Kv1 conductance remained active at the onset of the main EPSG (vertical dashed lines, Fig. 7g). Across five cells, preceding EPSGs that led by 1.00, 0.75, and 0.50 ms increased the Kv1 conductance active at the onset of the main EPSG by ~30–37% over the control condition (Fig. 7h; control mean ± s.e.m. = 14.97 ± 0.73 nS; repeated measures ANOVA with Tukey's post-hoc, P < 0.001) and increased the V_m by ~0.7 – 3 mV above rest (Fig. 7i; repeated measures ANOVA with Tukey's post-hoc, P < 0.05). Despite the fact that the preceding EPSP is mostly complete by the onset of the main EPSP (green trace in Fig. 7g) the Kv1 conductance is delayed relative to the preceding EPSP, and is well placed to reduce spike probability during the main EPSP. Conversely, when a preceding EPSP leads by a smaller time (red trace in Fig. 7g), the depolarization remaining from that EPSP can partially or completely counteract the additional Kv1 conductance activated by the EPSP, explaining the inability of 0.50 ms preceding EPSPs to consistently shift spike probabilities (Fig. 6f). Interestingly, we found a similar effect of timing in vivo: preceding EPSPs 1.2 to 1.0 ms before the main EPSP were correlated with an ITD function shift (Fig. 6f) but EPSPs leading by 0.7 to 0.5 ms were not (Supplementary Fig. 4). Together, these data show that even small fluctuations in preceding membrane potential can have a large effect on spike probability, due, at least in part, to increased activation of Kv1 channels.

DISCUSSION

The current work provides the first systematic in vivo intracellular study of identified MSO neurons. We showed that ITD tuning is inadequately explained by instantaneous coincidence detection of afferent inputs. Instantaneous coincidence detection is a process that is modeled by the mathematical operation of crosscorrelation³³ and that evaluates the degree of coincidence of events during a narrow time window (the coincidence window). In this scheme, the output is insensitive to events occurring before the coincidence window (Supplementary Fig. 5a), and the best delay is simply the ITD that corresponds to maximally coinciding inputs. However, we found that recent input history affects spiking probability (Supplementary Fig. 5b). The interaction between intrinsic properties and temporal input patterns constitutes a new form of internal delay. Previous models (axonal, inhibitory, or cochlear delays) focus on the relative timing of events in monaural channels. In contrast, we found that “coincidence” does not equate to a simple temporal alignment of EPSPs: instead, the interaction of intrinsic properties and temporal input patterns can shift the interaural phase at which maximal spiking is obtained. Because this shift inherently occupies a fraction of the stimulus cycle, it is more appropriately described as a phase delay.

The deviation from instantaneous coincidence detection seems to contradict conclusions from previous extracellular work that compared binaural tuning to monaural input timings derived from spikes evoked by monaural sounds^{13, 14, 34}. These spikes represent only a fraction of the incoming excitatory events, as MSO neurons respond poorly to monaural sounds. Furthermore, these studies used differences in monaural best phases to predict binaural tuning, which is a less stringent prediction of binaural tuning than our methods of summing and thresholding monaural inputs or crosscorrelating the entire subthreshold monaural period histograms. Although in this previous work the difference in monaural best phases was clearly correlated to the binaural interaural best phase (ref. 18, their Fig. 6B), there is scatter around the diagonal, of up to 0.2 cycles. For a tone of 300 Hz, this difference represents 667 μs, which is larger than the shifts we have found (Fig. 3b). A recent study with mainly juxtacellular recordings compared cycle-averaged binaural responses (averaged separately to the ipsi- and contralateral stimulus frequency) with binaural spikes⁸. A relatively good match was found, although, again, in several of the reported functions there may be a shift relative to the prediction (their Figs. 3A, 4B), as revealed by the population scatter plot (their Fig. 3E).

What mechanisms underlie the mismatch between monaural inputs and best delay? Our data suggest that preceding synaptic activity shifts best delay by altering the activation of intrinsic Kv1 channels and thereby adjusting spike threshold. We suspect that preceding EPSPs also inactivate voltage-gated Na⁺ channels. Prior in vitro experimental and modeling studies have shown that action potential initiation in MSO neurons is tightly controlled both by Kv1 channels^{9, 20, 24, 35} and voltage-gated Na⁺ channels^{36, 37}. Kv1 channels regulate firing in other auditory neurons as well, e.g. octopus cells where they contribute to exceptional temporal precision³⁸. Together, the activation of Kv1 channels and inactivation of Na⁺ channels reduce spike probability by decreasing the ratio of Na/K currents.

The combination of in vivo intracellular recording, pharmacology and anatomy provides a powerful means to address most mechanisms previously proposed for ITD-tuning (excluding the proposal of cochlear disparities^{22, 23}). First, we confirmed the frequency tuning map in the MSO^{13, 18, 28}. Data of MSO frequency tuning is extremely limited, as most studies report suprathreshold best frequency, which is generally poorly correlated with characteristic frequency. Characteristic frequencies were >400 Hz (Fig. 3b), similar to the lower limit in the gerbil auditory nerve³⁹. We did not find evidence for a spatial map of best delay (Fig. 2e), a central tenet of the Jeffress model¹¹.This is in contrast to the avian NL, where a map of ITD is thought to exist³. Our observation of discrete EPSPs supports the low number of excitatory inputs estimated in vitro⁴⁰, consistent with a process in which MSO neurons require only a small number of inputs to generate output⁴¹. This is in stark contrast to NL neurons in the barn owl, where massive convergence of inputs creates a stimulus analogue potential⁴².

Second, the inhibitory hypothesis of ITD tuning states that phase-locked IPSPs shift the best delay to positive ITDs^{10, 19, 25}. Our data directly demonstrate that removing inhibition does not systematically shift the ITD function towards negative ITDs, contradicting the primary evidence for the inhibitory hypothesis^{10, 19}. Both our in vitro and in vivo data suggest that the previously reported effects of strychnine on best delay are probably mainly due to nonspecific effects on intrinsic conductances. It is still possible that individual IPSPs modify the timing of individual EPSPs, but our results contradict the general occurrence of this phenomenon as envisioned before^{10, 19}. By restricting the strychnine concentration to ≤ 2 μM with pressure application, we observed that inhibition decreased spike rate across ITDs and could narrow the ITD function without introducing systematic shifts (Fig. 4b), confirming earlier in vitro results⁹.Finally, our data do not suggest important roles for two other mechanisms proposed: asymmetric rise times of EPSPs²⁰ and an asymmetric origin of the axon²¹.

The ‘two-channel hypothesis’ of auditory space representation⁴³ proposes that azimuth is coded via two broad hemispheric spatial channels, based on the finding that the steepest slope of the ITD functions is localized in the physiological range^10,19. The viability of this model has been questioned^44,45, and in agreement with others^23,46,47, we found a best delay distribution with several small and even negative values (Fig. 2e). ITD functions with such best delays (e.g. Fig. 1g) do not fit the two-channel hypothesis.

We conclude that neural coincidence detection in a physiologically intact preparation is not a simple summation and thresholding operation, but is adaptive in the sense that it is strongly affected by recent input history. Thus, the binaural interaction itself effectively contributes an internal delay. Intriguingly, this contribution is dependent on characteristic frequency (Fig. 3b). That best delay tends to decrease with characteristic frequency and is better characterized as a phase than a time shift was first pointed out in guinea pig⁴⁸ and subsequently confirmed in other mammals, including gerbil^{10, 19, 46}. The frequency dependence of the phase-shift we discovered is in line with the best delay distributions in mammals: towards larger positive ITDs at low characteristic frequencies and towards negative ITDs at higher characteristic frequencies. Thus, our results suggest that two key properties of best delay – phase delay and dependence on characteristic frequency - are at least partly based on the delay associated with coincidence detection discovered here.

Coincidence detection is a general mechanism to extract the temporal information in neural firing that is present across many brain areas^{5, 6}. In neocortical pyramidal neurons, for example, studies have highlighted the role of active dendritic properties in amplifying coincident synaptic excitation^{49, 50}. In these studies, the role of voltage-gated channels is solely to adjust the probability of action potential output arising from the summation of populations of excitatory inputs. Our study stands apart in that we show a role for voltage-gated ion channels in changing the timing requirements for coincidence detection away from the timing dictated by synaptic inputs. In slower (e.g. cortical) neurons, delays induced by the interaction of synaptic events with intrinsic voltage-gated ion channels may last many milliseconds and could critically shape the decoding of phase or time relationships.

ONLINE METHODS

Animals

All procedures were approved by the KU Leuven Ethics Committee for Animal Experiments and The University of Texas at Austin IACUC and were in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals. Young (postnatal age 29.4 ± 0.34 day) and adult male and female wildtype Mongolian gerbils, without previous experimental history, were used for the in vivo experiments. At both ages, MSO neurons are mature both physiologically (in vitro)²⁴ and anatomically⁵¹. The gerbils used in the in vivo experiments were housed with 6 or fewer per cage, with a 10 hour light/dark cycle (lights turn on at 7 AM, and off at 9 PM).

Preparation

The animals were anesthetized with ketamine (80-120 mg/kg)/xylazine (8-10 mg/kg) in NaCl 0.9% i.p. followed by maintenance anesthesia with ketamine (30-60 mg/kg) / diazepam (0.8-1.5 mg/kg) in aqua, or ketamine (60 mg/kg) / acepromazine (0.6 mg/kg) in NaCl 0.9% i.m. Depth of anesthesia was judged using the toe pinch reflex. To minimize respiratory secretions, atropine (0.02 mg/kg) was administered i.m. when necessary. Body temperature was kept at 37° C using a homeothermic blanket (Harvard Apparatus). A tracheotomy and an ipsilateral carotidectomy were performed. A metal head bar was glued to the skull with dental composite. Pinna folds around the external meatus were removed. The bulla was opened on both sides in most animals in order to maintain acoustic symmetry. After making a craniotomy on the medial bulla wall, the meningeal layers were carefully removed.

In vivo patch-clamp recordings

Patch clamp electrodes with resistance between 5 and 8 MΩ were made with a horizontal puller (Model P-87, Sutter Instrument Co.) using borosilicate glass capillaries with filament (1B120F-4, World Precision Instruments, Inc., Sarasota, FL). Electrodes were filled with intracellular solution containing 115 mM K gluconate (Sigma), 4.42 mM KCl (Fisher), 10 mM Na₂ phosphocreatine (Sigma), 10 mM HEPES (Sigma), 0.5 mM EGTA (Sigma), 4 mM Mg-ATP (Sigma), 0.3 mM Na-GTP (Sigma) and 0.1 or 0.2% biocytin (Invitrogen). The pH was adjusted to 7.30 with KOH (Sigma) and osmolality was brought to 300 mOsm with sucrose. The chloride concentration was chosen to set the E_Cl near the physiological value as measured in vitro by Magnusson et al⁵². In vivo whole cell recordings were made using the blind patch technique⁵³, using a patch clamp amplifier (BVC-700A; Dagan, Minneapolis, MN). Positive pressure on the electrode was 4-5.5 psi when crossing the brain surface and lowered to 1 psi at 200 μm below the surface, and further to 0.5–0.6 psi at 250–350 μm below the surface. The electrode was then advanced in steps of 1–2 μm while monitoring the current response to 2–3 mV voltage steps (in voltage-clamp mode). When the electrode resistance increased together with a pulsation of the current response at heartbeat frequency, the electrode was advanced 4–8 μm further before pressure was dropped to 0 psi. The command voltage was stepped to –70 mV and slight suction applied if needed to obtain a GΩ seal. Slow suction allowed us to rupture the cell membrane and achieve the whole-cell configuration. After gaining access to the neuron, the amplifier was switched to current clamp mode, capacitance compensation was applied and the bridge balanced. Series resistance was 64.5 ± 3.4 MΩ for in vivo recordings. Initial resting membrane potential was –53.0 ± 1.1 mV (corrected for a liquid junction potential of 10 mV). The neural signal was low-pass filtered at 5 kHz, sampled at 50–100 kHz, and acquired using custom algorithms in IgorPro (WaveMetrics) or MATLAB (The Mathworks).

Pharmacology

To apply CNQX, two patch clamp electrodes were paired in a piggyback construction. The distance between the tips was ~30–150 μm. One electrode was filled with intracellular solution, and the other with CNQX 440 μM in 0.25 mM NaCl or 220 μM in 0.125 mM NaCl (pH adjusted to 8.2 with NaOH). CNQX was applied using positive pressure (0.3 – 0.5 psi). Similar piggyback electrodes were used for application of 2 μM strychnine with positive pressure. In a few neurons, strychnine was applied using iontophoresis, as in earlier extracellular experiments^{10, 19}. For these experiments, a two-barrel electrode (pulled from Septum theta glass, World Precision Instruments, Inc., Sarasota, FL) was paired to a patch clamp electrode in a piggyback construction. One channel of the theta glass was filled with strychnine (10 mM in distilled water, pH adjusted to 3.5 with HCl), and the other channel was filled with NaCl (1M in distilled water, pH adjusted to 3.5 with HCl). Holding current was –30 nA, ejection current was +30 nA, applied using an iontophoresis system (MVCS-01C-45, NPI Electronic, Stuttgart, Germany). The decision to apply CNQX or strychnine, whether using iontophoresis or pressure, was made before contact with the neuron was established and therefore randomized to its properties.

Acoustic stimuli

Experiments were performed in a double-walled sound proof room (IAC, Niederkrüchten, Germany). Sound stimuli were generated using TDT System II hardware and custom MATLAB software and delivered to the ears using Etymotic speakers attached to hollow ear bars. The stimulus system was acoustically calibrated at each ear, using a probe microphone (Bruel and Kjaer, Nærum, Denmark).

When intracellular access was obtained, a frequency-tuning curve was collected using an automatic threshold-tracking algorithm, typically using binaural short tones. The characteristic frequency (CF) was defined as the frequency of the tuning curve yielding the lowest threshold. Triggering was set for APs or large EPSPs. Responses were then obtained to long tones producing a 1 Hz binaural beat. Stimulus carrier frequency was generally set at the binaural best frequency (BF: frequency of maximal spike output), which was usually lower than the CF. Typical settings were: stimulus duration 5 s with an interstimulus interval of 1 s, the contralateral ear 1Hz higher than the ipsilateral ear, SPL 70 dB SPL at both ears. Monaural responses to the same stimuli were obtained interleaved with binaural stimulation. In some experiments an ipsilateral and contralateral stimulus, each of 10 s, were played with an offset of 5 s, so that binaural as well as monaural responses to the same stimuli were obtained in one repetition. The parameters varied were carrier frequency and SPL. The collection of monaural and binaural responses to tones of the same frequency and intensity for one neuron is referred to as a dataset. If time allowed, responses were also obtained to broadband noise (typical bandwidth 50-8000 Hz).

Analysis

No statistical methods were used to pre-determine sample sizes but our sample sizes are similar to those reported in previous publications^{8, 10, 13, 19}. In the analysis of the pharmacological and in vitro experiments, each neuron served as its own control by comparing the responses before and during drug application or across experimental manipulations. Similarly, monaural and binaural in vivo responses to tones were compared within datasets. No blinding was performed during experiments or analysis.

Neurons that were not successfully retrieved for histology were classified as MSO neurons by the similarity of their physiological responses to those of neurons that were retrieved. Criteria included mainly excitatory responses to sound from either ear, sensitivity to binaural beat stimuli in subthreshold or suprathreshold responses, and narrow EPSPs (halfwidths < 1.5 ms)^{11, 18, 19, 35}.

Event detection, phase-locking and ITD tuning

For some datasets, voltage traces were high-pass filtered before analysis because of heartbeat or breathing artifacts. A digital FIR filter was applied in MATLAB, using an upper cut-off frequency of 20-70 Hz (MATLAB built-in functions fir1 and filtfilt). To identify the resting membrane potential and to timestamp events, data were wavelet denoised using the MATLAB built-in function wden⁵⁴. Resting membrane potential (V_rest) was determined for each denoised response by analyzing spontaneous activity preceding the start of the first stimulus repetition. Intervals of 1 ms duration where the voltage standard deviation was ≤ 0.05 mV were identified. V_rest was defined as the median of the average voltage of these intervals. If there were no such ‘resting’ intervals present, V_rest was defined as the median voltage of the spontaneous activity. For a few recordings, there was insufficient spontaneous activity recorded just before the stimulus. In those cases V_rest was defined as the median voltage of the driven response.

Excitatory events were separated into spikes and EPSPs using criteria for amplitude, repolarizing slope and/or afterhyperpolarization, tailored for each recording. Events identified as spikes had to be separated by at least 1 ms, and events labeled as EPSPs had to be separated by at least 0.1 ms. For each neuron, events were stacked onto each other to verify visually that separation into two discrete groups by these criteria was adequate. Spikes and EPSPs were timed at the peak of the wavelet denoised waveform. Amplitude of EPSPs and spikes is expressed relative to V_rest.

Phase-locking was studied by determining the stimulus phase for EPSP and spike peaks. These values were tallied in period histograms. The onset response was discarded and the analysis was restricted to the ongoing response, beyond 1 s.

Binaural beat stimuli with a 1 Hz beat frequency were used to evaluate ITD sensitivity, again discarding the initial 1 s. By convention positive ITD refers to the contralateral stimulus leading the ipsilateral stimulus in phase. Best delay was defined by treating spikes as unit length vectors with the angle defined by the phase of the stimulus at the peak of the spike, and calculating the vector average. ITD functions were generated by graphing spike rate as a function of interaural phase (50 bins, triangular 3-point smoothing).

Prediction of binaural ITD tuning from monaural responses (Fig. 3a,b,d; Supplementary Fig. 1)

ITD sensitivity for spike output was compared to the timing of the inputs by generating a predicted ITD function (predITDf) from the input events. For this analysis, monaural responses were obtained to the same stimuli as were used during the binaural beat. After subtraction of V_rest, the monaural responses were summed (ipsilateral response + contralateral response), and thresholded to predict the occurrence of spikes. The threshold was changed in an iterative loop until the predicted spike rate differed by less than 1% from the binaural spike rate or 20 iterations were reached. A predicted ITD function was then constructed from the timing of the predicted spikes relative to the phase of the ipsilateral and contralateral stimulus. Alternatively, ITD tuning was predicted by comparing the timing of monaural EPSPs using the monaural EPSP period histograms (PHs; Supplementary Fig. 1d-f). For this analysis, the ipsi- and contralateral PHs to monaural stimulation were crosscorrelated to obtain predITDf. In contrast to the analysis where monaural responses are summed directly, this analysis takes only EPSP timing into account, not amplitude and shape. To quantify the relative position (“shift”) on the ITD-axis of the predicted and real ITD function (rITDf), these functions were crosscorrelated and the lag for maximal correlation was determined (Fig. 3b,d;Supplementary Fig. 1f). A negative shift between rITDf and predITDf refers by convention to rITDf being tuned towards more negative ITDs (less contralateral lead) than predITDf.

ITD tuning of binaural output vs. binaural input events (Fig. 3c,d; Fig.6a)

ITD tuning of spikes (supraEPSPs) was compared to ITD tuning of the largest subthreshold EPSPs (subEPSPs), both obtained during the binaural beat response. For this analysis, the n largest subEPSPs were selected where n was the number of spikes. The mismatch of the supraEPSP ITD function and the subEPSP ITD function was obtained as the lag of the maximum in their crosscorrelation function (Fig. 3d).

To gain insight into the mechanism that generated the difference in ITD tuning between supraEPSPs and subEPSPs, we selected two ITDs (ITD₁, ITD₂) for which there was no difference in supraEPSP rate (in the interval ITD_1,2 ± 0.1 ms), and the difference in subEPSP rate was maximal (Fig. 6a). We then isolated all supraEPSPs and subEPSPs occurring within 0.05 to 0.2 ms of ITD₁ and ITD₂. These events were aligned at the maximum of the first derivative leading up to the EPSP peak (Supplementary Fig. 2) and the average was calculated for supraEPSPs and subEPSPs separately (Fig. 6b). To compare the binaural V_m with the monaural input timing, monaural EPSP PHs for ITD₁ and ITD₂ are shown in Fig. 6c.

Quantification of asymmetries in the temporal pattern of monaural inputs (Fig. 6f; Supplementary Fig. 4)

We identified the 5% largest EPSPs in the monaural responses. For those events, we looked at the maximal depolarization 1.2 – 1 ms and 0.7 – 0.5 ms before the EPSP peak. We divided the number of times this depolarization exceeded the median EPSP amplitude during ipsilateral stimulation by that during contralateral stimulation. If this ratio was > 1, more large depolarizations occurred during ipsilateral stimulation than during contralateral stimulation.

Binaural output vs. binaural input during broadband stimulation (Supplementary Fig. 3)

Binaural supraEPSPs and subEPSPs during stimulation with binaural broadband noise were studied similarly as for the tone responses. Again the n largest subEPSPs were selected, where n equals the number of supraEPSPs, and without regard for the stimulus (correlated or uncorrelated broadband noise, different ITDs). Events were aligned at the maximum of the first derivative leading up to the EPSP peak and the average was calculated for supraEPSPs and subEPSPs separately.

Histology

At the end of the experiment, animals were overdosed with pentobarbital and perfused using saline followed by either 4% paraformaldehyde (PFA) in 0.1M PO₄ buffer or a sequence of 1% PFA/1% glutaraldehyde/0.004% CaCl₂ and 1% PFA/1% glutaraldehyde/0.004% CaCl₂. Coronal sections of 70 μm thickness were made through the brainstem with a vibratome (Leica VT1200). Sections were processed with commercial kits (VECTASTAIN Elite ABC Kit (Standard) and Peroxidase substrate kit DAB SK-4100, Vector Laboratories, Inc. Burlingame, CA 94010) to visualize the biocytin. A background Nissl stain was performed using thionin 0.2%. The tissue was mounted, cleared and coverslipped. For each isolated MSO neuron, the rostrocaudal location of the cell body was expressed relative to the most rostral and most caudal poles of the nucleus, and the dorsoventral location was expressed relative to the dorsal and ventral border of the nucleus in the same slice as the cell body (Fig. 2b-e).

In vitro slice experiments

In vitro recordings were made from brainstem slices prepared from 23.9 ± 0.7 day old wildtype male and female Mongolian gerbils, without previous experimental history, following previously described protocols⁹. The gerbils used in the in vitro experiments were housed with 10 or fewer per cage before weaning and 4 or fewer per cage after weaning, with a 12 hour light/dark cycle (lights turn on at 7 AM, and off at 7 PM). Gerbils were deeply anesthetized with isoflurane, the brain removed and rapidly dissected to isolate the brainstem, and 200 μm horizontal slices containing the MSO were cut on a vibratome (Leica). Slices were prepared in 32°C ACSF, incubated for 30 minutes in 35°C ACSF, then stored at room temperature. ACSF was bubbled with 95% O₂/5% CO₂ and contained (in mM): 125 NaCl, 25 glucose, 25 NaHCO₃, 2.5 KCl, 1.25 NaH₂PO₄, 1.5 CaCl₂, 1.5 MgSO₄. Recordings from visually identified MSO neurons were made at 37°C using a MultiClamp 700B amplifier (Molecular Devices) in current clamp mode. Electrodes were filled with the same intracellular solution used for in vivo recordings. For the strychnine experiments (Fig. 4c-e), the starting ACSF contained 1 μM strychnine, and 10, 30, and 100 μM strychnine solutions were each washed-in for at least 10 minutes before measurements were made. For the dynamic clamp experiments (Fig. 7), dual somatic whole cell recordings were used to allow one electrode to record the membrane potential while the other injected currents as commanded by the dynamic clamp. The dynamic clamp consisted of SM2 software (Cambridge Conductance) controlling a Toro 8 DSP operating at 33-50 kHz. Dynamic clamp-simulated EPSGs followed a double exponential time course (time constants = 0.1 ms rise, 0.18 ms decay) with a reversal potential of 0 mV. In the preceding EPSG experiments (Fig. 7d-i), spontaneous EPSPs and IPSPs were blocked by including 10 μM NBQX and 1 μM strychnine in the ACSF. In one experiment (Fig. 7g-i), endogenous K⁺ channels were blocked by including 5 mM 4-aminopyridine in the intracellular solution, and the Kv1 conductance simulated by the dynamic clamp using a Hodgkin-Huxley model as previously described⁹. Bridge balance was maintained and series resistance (<20 MΩ) routinely monitored throughout all recordings. V_m was corrected for a 10 mV liquid junction potential. Data were acquired and analyzed using custom algorithms in IgorPro (Wavemetrics).

Statistics

Data are presented as mean ± s.e.m. Data distribution was assumed to be normal but this was not formally tested. Correlation values of scatter plots are linear correlation coefficients. The correlation P-value was calculated with the MATLAB function corrcoef, which uses a t-statistic. Paired-sample t-tests were used to study the effect of strychnine on ITD tuning and EPSP halfwidth in vivo, and the relation between preceding membrane potential and sub/suprathreshold EPSPs. Two-sample t tests were used to compare strychnine application using positive pressure and iontophoresis. ANOVA tests were used to test the significance of the changes in input resistance and sag ratio with strychnine in vitro, and the effect of preceding EPSGs in vitro. Statistical significance was defined as P < 0.05. Significant suprathreshold ITD tuning was defined by Rayleigh test for circular uniformity, α ≤ 0.001.