Robustness in the fitting of Molecular Mechanics parameters

Abstract

Automated methods for force field parametrization have attracted renewed interest of the community, but the robustness issues associated with the often ill-conditioned nature of parameter optimization have been vastly underappreciated in the recent literature. For this reason, the present paper offers a detailed description of the origin and nature of these issues. This includes a discussion of the RESP charge-fitting model, which does contain explicit robustness-enhancing measures albeit not in the context of bonded parameters, and which forms an inspiration for the present work. It is also discussed how all the bonded parameters in a Class I force field can be simultanteously fit using the Linear Least Squares (LLS) procedure, and a novel restraining strategy is presented that overcomes robustness issues in the LLS fitting of bonded parameters while minimally impacting the fitted values of well-behaved parameters. Two variants of this methodology are then validated through a number of case studies, including the fitting of bond-charge increments, which illustrates the method’s potential for robustly solving general LLS problems beyond force field parametrization.

1 INTRODUCTION

Mathematical optimization problems are ubiquitous in science and engineering. The design of empirical force fields for molecular mechanics is an example of a discipline where optimization plays a central role. Specifically, a force field is the sum of a potential energy function and a parameter set, the latter typically comprising hundreds of numerical parameters all of which require optimization. In the case of the popular Class I additive force fields, the parameters can be classified by the type of parameter optimization effort required, which is different for van der Waals parameters, partial charges and bonded parameters. ^1–3 For condensed phase force fields, optimizing van der Waals parameters involves reproducing bulk phase properties through bulk phase simulations, which is laborious, computationally intensive and hard to automate. Fortunately, these van der Waals parameters also exhibit a high degree of transferability, so once a sufficiently wide palette is available for a given force field, little van der Waals parameter optimization is required to add large numbers of arbitrary molecules to the force field. ² The same cannot be said of the charges and bonded parameters.³ Over the last few decades, increases in computer power and improvements in Quantum Chemistry software have made it possible to generate acceptable Molecular Mechanics models using solely Quantum Mechanical (QM) target data for the optimization of these parameters. This has spurred a wave of renewed interest in automatic optimization of force field parameters, with efforts to automate the setup of the required QM calculations as well as the actual optimization of the charges and bonded parameters. ^4–6 While QM-derived charges have seen considerable success, ^7,8 the use of automatically optimized bonded parameters is less widespread and not routine. This is at least partially due to robustness problems in the optimization, which are scarcely documented in the literature and usually not considered in the development of automatic optimization programs. The present paper tries to rectify this situation, by which we hope to facilitate routine and automatic optimization of force fields for organic molecules. Additional introductory information about optimization problems and multi-objective optimization is respectively provided in sections S1.1 and S1.2 of the Supporting Information.

1.1 Linear Least Squares

Simply spoken, an optimization involves finding values for n parameters such that a merit function that depends on these parameters attains an optimal value. This can be generalized to multi-objective optimization problems, where the goal is to find values for n parameters such that m ensuing numerical properties (henceforward called “observables”) each approach respective target values. Although force field parametrization in principle falls into the latter category, for the sake of mathematical tractability, it is often reduced to a single-objective optimization with a merit function that is the sum (or mean) of the squares of the differences between the observables and their respective target values, i.e. the squared distance between the observable vector and target vector. In the case of linear equations, this is called the Linear Least Squares (LLS) approach, which will be the focus of the present paper. To facilitate the discussion, we will express the system of linear equation in terms of matrices and vectors throughout this paper. As such, the LLS approach consists of finding an approximate solution in X of the generally inconsistent system AX = B, where the parameter vector X is the vector of unknown parameters K₁ … K_n, the target vector B is the vector of target data points T₁ … T_m, and each column i of m × n response matrix A is a response vector R_i with elements R_1i … R_mi.

$${\mathbf{R}}_i=\left[\begin{array}{c}{R}_{1i}\\ R_{2i}\\ ⋮\\ R_{mi}\end{array}\right],\mathbf{A}=\left[\begin{array}{cccc}{R}_{11}& R_{12}& \cdots & R_{1n}\\ R_{21}& R_{22}& \cdots & R_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ R_{m1}& R_{m2}& \cdots & R_{mn}\end{array}\right],\mathbf{X}=\left[\begin{array}{c}{K}_1\\ K_2\\ ⋮\\ K_n\end{array}\right],\mathbf{B}=\left[\begin{array}{c}{T}_1\\ T_2\\ ⋮\\ T_m\end{array}\right]$$

Using these definitions, the least-squares solution is the value of the vector X that minimizes merit function S = ||B′ − B||², where the observable vector B′= AX, and each response vector R_i determines the change in B′ in response to a change in parameter $K_i:{\mathbf{R}}_i=\frac{\partial {\mathbf{B}}^{\prime }}{\partial K_i}$. Any response vector can have a large norm or be close to zero, and any two response vectors can be orthogonal, nearly orthogonal, parallel, or nearly parallel, which greatly influences the behavior of the system, as discussed in more detail in the next sections. How to obtain the least-squares solution X is a historically well-studied problem, and algorithms for doing so (e.g. QR factorization and Singular Value Decomposition) are commonly part of mathematical software libraries. For example, the program developed as part of the present work performs a QR factorization by calling of LAPACK’s DGELS routine. ⁹

1.2 Ill-conditionedness and robustness

It has been mentioned in the previous paragraph that the problem is only nontrivial if the system of equations is mathematically inconsistent. This statement and its implications merit a more detailed discussion. Any two equations may be inconsistent, necessitating an approximate solution, but this does not imply that all parameters are defined. Thus, from a least-squares point of view, a system can be inconsistent and underdetermined at the same time. For example, the following system:

$$\begin{array}{l}1K_1+0K_2=10\\ 1K_1+0K_2=11\end{array}$$

is inconsistent in K₁ and undetermined in K₂; in the least-squares solution, K₂ can have any value (one would likely choose 0) as long as K₁ = 10.5. A more insidious problem is ill-conditionedness. Consider the very similar system:

$$\begin{array}{l}0.999K_1+0.001K_2=10\\ 1.001K_1+0.001K_2=11\end{array}$$

This system is exactly solvable; the solution is X = (500, −489500). Thus, adding only the slightest numerical noise in the coefficients results in a completely different solution. Furthermore, it should be noted that the approximate solution (10.5, 0) produces an observable vector B′ that deviates only 5% from the target vector B, which would be acceptable for some practical purposes. Perturbing both elements of B′ by 5% requires a change of 500 in K₂ as opposed to a change in K₁ of only 0.5; accordingly, if a fixed perturbation is applied to K₁, the least-squares optimal solution in K₂ is perturbed 1000-fold. The system is almost underdetermined, or more formally ill-conditioned (with K₂ being “poorly determined” according to Bayly et al.’s terminology¹⁰). Using the definitions from section 1.1, parallel response vectors R_i lead to underdetermination, while nearly parallel response vectors cause ill-conditionedness. Indeed, in the first example above, R₂ is the null vector, which is parallel to any other vector, while in the second example, R₁ = (0.999, 1.001) and R₂ = (0.001, 0.001) are almost parallel. This situation can be readily identified and quantified by performing a Singular Value Decomposition (SVD) and calculating the condition number from the singular values. However, the pragmatic interest of the present paper is not so much to quantify the problem, as to find an approximate fitting methodology for linear systems that avoids this lack of robustness altogether.

1.3 The RESP Model

A prominent example of an LLS problem in the field of Molecular Mechanics is electrostatic potential-based charge fitting. Lack of robustness because of ill-conditionedness is commonly observed when solving the associated system of linear equations, which led Bayly et al. to propose the RESP model in which restraints are added to the system. ¹⁰ As discussed in depth in section S1.3 of the Supporting Information, this has provided a strong inspiration for the present work. Specifically, we undertake a similar effort to find a set of workarounds to make the derivation of bonded parameters from a Potential Energy Surface (PES) robust enough to be widely useful to non-expert users. We furthermore endeavor to choose our workarounds carefully so that they can be generalized to other linear optimization problems without having to abandon the algebraically convenient LLS functional form.

2 METHODOLOGY

2.1 The dihedral fitting problem

The dihedral portion of an empirical force field’s potential energy function is commonly determined by

$$\sum _{\mathit{dihedral}\mathit{terms}i}^n{K}_i^{\varphi }(1+cos(n_i\varphi -{\delta }_i))$$ (1)

where ϕ is the dihedral angle and $K_i^{\varphi }$, n_i and δ_i are respectively the amplitude, multiplicity and phase associated with a given dihedral term. A dihedral parameter, defined by a sequence of 4 atom types, can consist of multiple such dihedral terms with different n_i, which are strictly positive integers no larger than 6 and are typically chosen based on the symmetry of the rotatable bond in question. It should be noted that a δ_i other than 0° or 180° gives rise to an asymmetric potential, which is unphysical for a symmetric molecule and non-transferable between molecules of different symmetry, and therefore often undesirable. Also, changing δ_i from 0° to 180° or vice versa is equivalent to inverting the sign of $K_i^{\varphi }$, except for a constant offset of $2K_i^{\varphi }$ that is physically irrelevant because MM energies are only meaningful in a relative sense. Therefore, δ_i can be set to 0 in (1), leaving only $K_i^{\varphi }$ to be fit (programmatically, a negative $K_i^{\varphi }$ in the solution vector X can be translated back to a δ_i of 180° a posteriori). As first implemented by Halgren et al. ¹¹ and further discussed by Guvench et al. ¹², this reduces the dihedral fitting problem to a system of linear equations that can be solved using the LLS approach. Specifically, consider m conformations of a molecule. For each conformation j, a target (typically QM) energy $E_j^{QM}$ is available, along with a corresponding initial MM energy $E_j^{M{M}_0}$ in which all force field terms are present except the dihedrals being fitted. Using the notation from section 1.1, let $T_j=E_j^{QM}-E_j^{M{M}_0}-c^T$ and $R_{ji}=cos(n_i{\varphi }_j)-c_i^R$ (which can be precomputed from the dihedral angle ϕ_j in conformation j). The constant offsets $c^T=\frac{1}{m}{\displaystyle \sum _{j=1}^m}{E}_j^{QM}-E_j^{M{M}_0}$ and $c_i^R=\frac{1}{m}{\displaystyle \sum _{j=1}^m}cos(n_i{\varphi }_j)$ ensure that ${\displaystyle \sum _{j=1}^m}{T}_j=0$ and ${\displaystyle \sum _{j=1}^m}{R}_{ji}=0$ for all values of i, and don’t impact the physics as explained above. Note that the constant 1 in (1) is absorbed into $c_i^R$. The least-squares optimal amplitudes $K_i^{\varphi }$ for the dihedral terms i are now given by the elements of the solution vector K_i. By virtue of the offsets c^T and $c_i^R,{\displaystyle \sum _{j=1}^m}{T}_j^{\prime }={\displaystyle \sum _{j=1}^m}{\displaystyle \sum _{i=1}^n}{K}_i{R}_{ji}=0$, guaranteeing that B′ and B are always aligned in a way that minimizes merit function S, which therefore is equal to the square of the figure of merit “RMSE” in ¹².

2.2 Extension to variable phases

In the rare cases where fitting of the phase δ_i is desirable, the above scheme is no longer applicable because the response of the energy to δ_i is not linear. This limitation can be overcome by expressing a variable-phase dihedral term as the sum of two terms with independently variable amplitudes and fixed, predetermined phases δ_x and δ_y:

$$K_i^{\varphi }(1+cos(n_i\varphi -{\delta }_i))=K_{x,i}^{\varphi }(1+cos(n_i\varphi -{\delta }_x))+K_{y,i}^{\varphi }(1+cos(n_i\varphi -{\delta }_y))$$

Indeed, for a fixed δ_x ≠ δ_y, any ( $K_{x,i}^{\varphi },K_{y,i}^{\varphi }$) corresponds to a single ( $K_i^{\varphi }$, δ_i) and vice versa, as expressed by the phasor addition rule. However, an angle of 90° between δ_x and δ_y is a prerequisite for the corresponding response vectors R to be orthogonal, which improves robustness as explained in section 1.2. For mathematic and computational convenience, it is appealing to choose δ_x = 0 and δ_y = π/2, so that ${K_i^{\varphi }}^2={K_{x,i}^{\varphi }}^2+{K_{y,i}^{\varphi }}^2,{\delta }_i=arctan\frac{K_{y,i}^{\varphi }}{K_{x,i}^{\varphi }}$ and cos(n_iϕ − δ_y) = sin(n_iϕ). Although the same decomposition is commonly used in MD software such as CHARMM to improve performance by limiting the number of computationally expensive trigonometric functions to be evaluated,^* Hopkins and Roitberg independently noted that it can also be of utility in the fitting of asymmetric dihedrals. ¹³ However, we show in section 2.10 that in combination with restraints (sections 2.5 and 2.6), this choice imposes a small spurious asymmetric bias on the solution, and that in these circumstances, a more correct choice is δ_x = −π/4 and δ_y = π/4, which retains the advantage of being orthogonal and is mathematically not substantially more complicated.

It should be repeated that variable phases are not commonly desirable, and the remainder of this paper will assume fixed phases as discussed in section 2.1, unless explicitly noted otherwise.

2.3 Extension to other bonded parameters

All other bonded parameters in a Class I force field, specifically bonds, angles, improper dihedrals and optional Urey-Bradley (UB) terms, correspond to harmonic terms in the potential energy function of the form $K_i{(x-x_i^0)}^2$, where K_i is the force constant and $x_i^0$ the reference value (distance for bond and UB, angle for angle and improper dihedral). Traditionally, parameters for these terms were obtained by analysis of the (experimental or QM) vibrational spectrum, but this is a somewhat complex procedure that is not trivial to automate, and it was observed during the parametrization of the CHARMM General Force Field (CGenFF) to commonly suffer from severe robustness problems related to the fact that many contributions of different parameters are mixed into one vibrational frequency, with substantial differences in mixing between the MM and target spectra. ^2,14 Instead, we propose to perform QM potential energy scans along these Degrees of Freedom (DF), ideally consisting of the minimum energy conformation and at least two other conformations at both sides of the minimum. This can readily be automated, and its higher computational cost is mostly rendered irrelevant by advances in QM software and computer power.

Just as for the dihedrals in section 2.1, ${(x-x_i^0)}^2$ can be precomputed if $x_i^0$ is known before-hand, making LLS fitting of K_i trivial. This is almost always the case for improper dihedrals, where $x_i^0$ is generally 0, but rarely for the other bonded parameters such as bonds and angles. For these cases, we can express the harmonic function with variable reference value as the sum of two harmonic functions with fixed reference values, analogous to section 2.2:

$$K_i{(x-x_i^0)}^2=K_{x,i}{(x-x_x^0)}^2+K_{y,i}{(x-x_y^0)}^2$$ (2)

in which case K_i = K_x,i + K_y,i and $x_i^0=\frac{K_{x,i}{x}_x^0+K_{y,i}{x}_y^0}{K_{x,i}+K_{y,i}}$, or the weighted mean of $x_x^0$ and $x_y^0$, weighted by K_x,i and K_y,i, respectively. The choice of $x_x^0$ and $x_y^0$ is less clear-cut than that of δ_x and δ_y in section 2.2; choosing them too close together would clearly lead to illconditionedness due to the vectors R being near-parallel, but choosing them too far apart may also cause numerical precision issues, with small changes in K_x,i and K_y,i causing big shifts in $x_i^0$. In our current implementation, we simply use the lower and upper limit of the input scan range for this purpose, as the scan range necessarily needs to be wide enough to produce a significant energy difference but small enough to stay within the thermally accessible region and to avoid artifacts such as chemical rearrangements in the QM calculations.

2.4 Sources of ill-conditionedness in bonded parameter fitting

Just like in the case of charge fitting (section S1.3), there are some inherent sources of illconditionedness in the fitting of bonded parameters in general and dihedrals in particular. An avoidable yet oft-overlooked class of these problems is the case where the fitting algorithm is tasked to fit dihedral multiplicities that are forbidden by the molecule’s symmetry, as elaborated in section S2.1.1 of the Supporting Information. Conversely, the present discussion will be limited to giving an example of a closely related phenomenon that is not avoidable. Specifically, in the example of the ψ protein backbone rotation, the two carbonyl carbon substituents with 180° offset each have their own combinations of atom types (i.e. ${\mathrm{N}}_i-{\mathrm{C}}_i^{\alpha }-{\mathrm{C}}_i-{\mathrm{N}}_{i+1}$ and ${\mathrm{N}}_i-{\mathrm{C}}_i^{\alpha }-{\mathrm{C}}_i={\mathrm{O}}_i$) and own parameter, which we will henceforward call a and b. Assume that the same set of dihedral multiplicities is used for both of these parameters, and that the target PES can be exactly fitted using the same multiplicities. In this case, the equation $\mathbf{AX}=\mathbf{B}$ is exactly satisfied as long as $K_a^{\varphi }-K_b^{\varphi }=K_{\mathit{target}}^{\varphi }$ and $K_a^{\varphi }+K_b^{\varphi }=K_{\mathit{target}}^{\varphi }$ for n_i = 1, 3 and n_i = 2, 4, 6, respectively^* (assuming the phases are both 0 and allowing for negative amplitudes, as discussed in section 2.1). In other words, the system has an undetermined DF in the form of an arbitrary constant offset that can be simultaneously applied to $K_a^{\varphi }$ and $K_b^{\varphi }$. In terms of vectors, R_a and R_b are parallel. For non-idealized geometries, the vectors are almost parallel, the constant offset has a small residual impact on B′, the algorithm will try to exploit this to fit arbitrary features in B, and undesirably large, mostly compensatory $K_i^{\varphi }$ values will ensue, as illustrated by the example in section 4.1.2 below. From this, it can easily be seen that ill-conditioned dihedral fitting problems are ubiquitous and cannot generally be avoided by a knowledgeable choice of multiplicities. The issue is not limited to dihedral parameters either; an example involving valence angles is worked out in section S2.1.2 of the Supporting Information.

On a more general level, the number of parameters in a molecule with no recurrent atom types is equal to the number of redundant internal coordinates, while the number of DF along which perturbations can be performed is 3N – 6. While actual molecules more often than not have recurrent atom types, the fact remains that the bonded parametrization of a single molecule is almost always underdetermined/ill-conditioned. Therefore, any fitting algorithm that is to be generally useful for this purpose must forcefully include a mechanism to mitigate this problem. Past efforts have often included implicit or even unintentional features to this effect, as elaborated in section S2.1.3 of the Supporting Information. In the present paper, we formally analyze the problem and propose a general solution.

2.5 Limitations of constant restraint

The most straightforward measure against overfitting is to weakly restrain the parameters towards approximate but reasonable “initial guess” ^* values, as successfully implemented in the RESP charge model (sections 1.3 and S1.3). In the case of bonded parameters, these initial guess values will depend on the type of parameter. Specifically, because of the symmetry of sigma bonds, dihedral parameters around single bonds that are not subject to conjugation are mostly correction terms for imperfections in the 1–4 and longer-range non-bonded interactions. ³ In a force field where these imperfections are not systematic errors, the average amplitude for this type of bonds should approach 0, so it seems reasonable to pull their restraints towards 0, like in the RESP model. Of all bonded parameters, this class of dihedral parameters is the most critical for correct conformational behavior. For dihedral parameters around (hyper)conjugative single bonds and (partial) double bonds, as well as bond, angle and improper dihedral parameters, reasonable initial guess values different from 0 could be proposed on a case-by-case basis, but this exceeds the scope of the present paper. As the algorithms proposed in this paper limit sensitivity to the restraints’ initial guesses (see section 2.9), they allow the case-by-case assignment of these guesses to be performed in a very approximate fashion.

Once the initial guess (i.e. target of a restraint) is determined, and assuming a harmonic functional form is chosen for its computationally convenient properties, the remaining question is its force constant. The most naive choice is to use a constant value, as used in the RESP model. However, this was found to be problematic in practice. Indeed, as discussed in section S1.3, Bayly et al. observed that larger parameters experience a stronger restraining force, which they overcame by sacrificing computational convenience in favor of a hyperbolic restraint. While this ad hoc measure was empirically shown to largely overcome the observed disproportionate restraining bias, it can be seen from the discussion in section S2.2 of the Supporting Information that the problem is fundamentally not due to the harmonic functional form of the restraint, and as such, changing the functional form to a hyperbolic one is not expected to produce the intended results for all LLS problems. Additionally, it does not yield direct control over the factor by which independent/orthogonal parameters are scaled down due to the restraints. Given such control, it would become possible to multiply the resulting parameters by the same factor after the fitting, and thus eliminate the effect of the bias on well-behaved parameters altogether. The next section discusses a proposal to attain this goal.

2.6 General expression for variable restraints

Similar as in section 1.1, the harmonically restrained LSS problem discussed in section 2.5 can generally be defined as the solution to the system A_resX_res = B_res, with X_res being the vector of restrained parameters $K_1^{\mathit{res}}\dots K_n^{\mathit{res}}$, and A_res and B_res being A and B with extra lines added as follows:

$${\mathbf{A}}_{\mathit{res}}=\left[\begin{array}{cccc}{R}_{11}& R_{12}& \cdots & R_{1n}\\ ⋮& ⋮& \ddots & ⋮\\ R_{m1}& R_{m2}& \cdots & R_{mn}\\ b_1& 0& \cdots & 0\\ 0& b_2& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & b_n\end{array}\right],\mathbf{X}=\left[\begin{array}{c}{K}_1^{\mathit{res}}\\ K_2^{\mathit{res}}\\ ⋮\\ K_n^{\mathit{res}}\end{array}\right],{\mathbf{B}}_{\mathit{res}}=\left[\begin{array}{c}{T}_1\\ ⋮\\ T_m\\ 0\\ 0\\ ⋮\\ 0\end{array}\right]$$

where b₁ … b_n are the force constants of the restraints (henceforward referred to as biases) associated with parameters $K_1^{\mathit{res}}\dots K_n^{\mathit{res}}$ and the n zeroes that are appended to the original target vector B are the initial guess values for the restraints; the case of nonzero initial guess values is discussed separately in section 2.10. Finding the LLS solution of this system involves minimizing the merit function $S_{\mathit{res}}={\Vert {\mathbf{B}}_{\mathit{res}}^{\prime }-{\mathbf{B}}_{\mathit{res}}\Vert }^2$, or in other words, finding the value of the vector X_res for which

$$\frac{\partial S_{\mathit{res}}}{\partial {\mathbf{X}}_{\mathit{res}}}=0\iff \forall k\in \{1,\dots ,n\}:\frac{\partial S_{\mathit{res}}}{\partial K_k^{\mathit{res}}}=0\iff \sum _{j=1}^m{R}_{jk}\left(\left(\sum _{i=1}^n{R}_{ji}{K}_i^{\mathit{res}}\right)-T_j\right)+b_k^2{K}_k^{\mathit{res}}=0$$ (3)

Consider the case where the unrestrained system as described in section 1.1 is exactly solvable, i.e.

$$\forall j\in \{1,\dots ,m\}:\left(\sum _{i=1}^n{R}_{ji}{K}_i\right)-T_j=0$$ (4)

Per section 2.5, we want the restraining bias to scale each parameter K_i that makes up this perfect solution by a chosen fraction (henceforward referred to as the bias fraction) σ_i:

$$K_i^{\mathit{res}}=(1-{\sigma }_i)K_i$$ (5)

Substituting (5) in (3) yields

$$\begin{array}{l}{b}_k=\sqrt{-\frac{{\displaystyle \sum _{j=1}^m}{R}_{jk}\left(\left({\displaystyle \sum _{i=1}^n}{R}_{ji}(1-{\sigma }_i)K_i\right)-T_j\right)}{(1-{\sigma }_k)K_k}}\\ =\sqrt{-\frac{{\displaystyle \sum _{j=1}^m}{R}_{jk}\left(\left(\left({\displaystyle \sum _{i=1}^n}{R}_{ji}{K}_i\right)-T_j\right)-{\displaystyle \sum _{i=1}^n}{R}_{ji}{\sigma }_i{K}_i\right)}{(1-{\sigma }_k)K_k}}\end{array}$$ (6)

Per (4), this simplifies to:

$$\begin{array}{ll}\hfill b_k& =\sqrt{\frac{{\displaystyle \sum _{j=1}^m}{R}_{jk}{\displaystyle \sum _{i=1}^n}{R}_{ji}{\sigma }_i{K}_i}{(1-{\sigma }_k)K_k}}\\ \hfill \iff b_k& =\sqrt{\frac{1}{1-{\sigma }_k}\sum _{i=1}^n{\sigma }_i\langle {\mathbf{R}}_k\mid {\mathbf{R}}_i\rangle \frac{K_i}{K_k}}\end{array}$$ (7)

where the notation 〈R_k|R_i〉 denotes the dot product R_k · R_i to reflect the fact that the m elements of the vectors R_i are generally discrete samples of a continuous function.

Calculating b_k using equation 7 before performing the restrained LLS fit would be straightforward, except that the factor K_i/K_k is a priori unknown, and its introduction is based on the assumption that the unrestrained system is exactly solvable, which is generally not the case. A natural solution would be to perform an unrestrained LLS to obtain this factor and calculate the biases b_k prior to the restrained LLS, but even assuming that the original system is never truly underdetermined, this will simply lead to a restrained solution that is equal to the unrestrained – and often ill-conditioned – solution, scaled down exactly by the fraction σ_i. Therefore, this will do nothing to improve robustness. A similar proposal would be to calculate the biases from the restrained solutions $K_i^{\mathit{res}}/K_k^{\mathit{res}}$ in an iterative self-consistent fashion, but this is neither guaranteed to converge quickly nor to yield more reasonable results. Indeed, the main lesson from this thought experiment is that a solution that approximates the exact K_i/K_k is undesirable from the point of view of robustness.

Before discussing how to resolve this problem, a closer understanding of the functional form of (7) is in order. Specifically, the expression under the square root can be broken down into a self-term and a sum of cross-terms:

$$b_k=\sqrt{\frac{{\sigma }_k}{1-{\sigma }_k}\langle {\mathbf{R}}_k\mid {\mathbf{R}}_k\rangle +\frac{1}{1-{\sigma }_k}\sum _{i\ne k}{\sigma }_i\langle {\mathbf{R}}_k\mid {\mathbf{R}}_i\rangle \frac{K_i}{K_k}}$$ (8)

If all the response vectors are orthogonal, 〈R_k|R_i〉 will always be zero for i ≠ k, and only the self-term remains for each k. This term is not dependent on any K value, and $\sqrt{\langle {\mathbf{R}}_k\mid {\mathbf{R}}_k\rangle }$ is simply the norm of the vector R_k, so that

$$b_k^{\mathit{self}}=\sqrt{\frac{{\sigma }_k}{1-{\sigma }_k}}\Vert {\mathbf{R}}_k\Vert$$ (9)

In other words, if all the response vectors are orthogonal, the bias b_k required for pulling K_k down by a fraction σ_k is trivially dependent on σ_k and ||R_k|| only. This makes it clear that the cross-terms express the coupling between non-orthogonal DF. Specifically, 〈R_k|R_i〉 is proportional to the cosine of the angle (in m-dimensional Euclidean space) between the two vectors: 〈R_k|R_i〉 = ||R_k|| ||R_i|| cos θ. Consider an unrestrained system where these vectors are almost parallel, which is a common occurrence as discussed in section 2.4. Introducing a single bias b_i that makes $K_i^{\mathit{res}}$ lower than K_i by a fraction σ_i into this system will make $K_k^{\mathit{res}}$ higher than K_k by an almost-equivalent magnitude, so that B′ is almost unchanged. To further rationalize this observation, (8) can be rewritten in the following form:

$$b_k=\sqrt{\frac{1}{1-{\sigma }_k}\langle {\mathbf{R}}_k\mid {\mathbf{R}}_k\rangle \left({\sigma }_k+\sum _{i\ne k}{\sigma }_i\frac{K_i}{K_k}\frac{\langle {\mathbf{R}}_k\mid {\mathbf{R}}_i\rangle }{\langle {\mathbf{R}}_k\mid {\mathbf{R}}_k\rangle }\right)}$$

This shows $\frac{\langle {\mathbf{R}}_k\mid {\mathbf{R}}_i\rangle }{\langle {\mathbf{R}}_k\mid {\mathbf{R}}_k\rangle }$ is a quantitative measure for how strongly a perturbation in K_i influences K_k. For parallel vectors R_k and R_i, swapping i and k inverts this factor: $\frac{\langle {\mathbf{R}}_k\mid {\mathbf{R}}_i\rangle }{\langle {\mathbf{R}}_k\mid {\mathbf{R}}_k\rangle }={\left(\frac{\langle {\mathbf{R}}_i\mid {\mathbf{R}}_k\rangle }{\langle {\mathbf{R}}_i\mid {\mathbf{R}}_i\rangle }\right)}^{-1}$. In this respect, K_i and K_k behave as if they were the vertical positions of the opposite ends of a lever with mechanical advantage $\frac{\langle {\mathbf{R}}_k\mid {\mathbf{R}}_i\rangle }{\langle {\mathbf{R}}_k\mid {\mathbf{R}}_k\rangle }$.^* Similarly, σ_iK_i is the absolute magnitude of the perturbation in K_i. Multiplying this by $\frac{\langle {\mathbf{R}}_k\mid {\mathbf{R}}_i\rangle }{\langle {\mathbf{R}}_k\mid {\mathbf{R}}_k\rangle }$ yields the negative of the absolute magnitude of the corresponding perturbation in K_k in the absence of any other influences, and dividing this by K_k translates this to a relative value, which is added to the relative perturbation σ_k directly imposed on K_k, as to annul the effect of σ_i.

It should be noted that the mechanical analogy of a lever is not a perfect one. To illustrate this, consider the exactly solvable but underdetermined system consisting of two identical response vectors a and b discussed in section 2.4, with an infinite number of unrestrained solutions subject to the condition K_a+K_b = K_target. If this system is restrained by the biases $b_a^{\mathit{self}}$ and $b_b^{\mathit{self}}$ given in (9), with σ_a = σ_b = σ, the restrained LLS solution will approach the unrestrained solution for which $K_a=K_b=\frac{1}{2}{K}_{\mathit{target}}$ (because this minimizes the merit function), but $K_a^{\mathit{res}}=(1-\frac{1}{2}\sigma )K_a$ and $K_b^{\mathit{res}}=(1-\frac{1}{2}\sigma )K_b$, in disagreement with (5). This violates the analogy of a rigid lever, and can be rationalized by observing that the two biases work at cross-purposes. The analogy could partially be recovered by assuming a flexible lever with a rigidity proportional to the aformenetioned factor cos θ; indeed, the parameters K associated with perpendicular vectors do not couple at all. However, this analogy is still not perfect and should be thought of as an intuitive rationalization tool rather than a rigorous alternative description.

While the unrestrained system has no single solution (K_a, K_b) due to the underdetermination, arbitrarily choosing K_a = K_b in (7) or (8) for the purpose of calculating the cross-terms yields $b_a=b_b=\sqrt{2}{b}_a^{\mathit{self}}=\sqrt{2}{b}_b^{\mathit{self}}$. Using these biases, the restrained LLS solutions is $K_a^{\mathit{res}}=K_b^{\mathit{res}}=(1-\sigma )K_a=(1-\sigma )K_b=(1-\sigma )\frac{1}{2}{K}_{\mathit{target}}$, so the cross-terms potentiates the biases as to bring the solution in agreement with (5). Interestingly, arbitrarily setting K_a = 2K_b in (7) or (8) instead so that $b_a=\sqrt{\frac{3}{2}}{b}_a^{\mathit{self}}$ and $b_b=\sqrt{3}{b}_b^{\mathit{self}}$ yields $K_a^{\mathit{res}}=(1-\sigma )\frac{2}{3}{K}_{\mathit{target}}$ and $K_b^{\mathit{res}}=(1-\sigma )\frac{1}{3}{K}_{\mathit{target}}$, and (5) is now satisfied for the solution $K_a=\frac{2}{3}{K}_{\mathit{target}}$ and $K_b=\frac{1}{3}{K}_{\mathit{target}}$. Thus, it can be seen that in a truly underdetermined system, the arbitrary choice of the relative magnitudes of K_i and K_k in (7) and (8) directly determines relative magnitudes of $K_i^{\mathit{res}}$ and $K_k^{\mathit{res}}$. A similar relationship exists for ill-conditioned systems, albeit in a more approximate fashion. This knowledge confirms the earlier observation that using the exact K_i/K_k from the unrestrained solution of an ill-conditioned system for the purpose of calculating the biases will yield restrained solutions that are similarly affected by the ill-conditionedness, and raises further doubt on whether a hypothetical self-consistent calculation of these factors would convergence towards a robust solution. However, the same knowledge can be exploited to propose values that can be used in (7) and (8) in lieu of K_i/K_k in order to robustly obtain desirable results.

2.7 Uniform bias

The discussion in the previous paragraph makes it tempting to propose to set K_i/K_k = 1 in (7) and (8). In a truly underdetermined fit of multiple equivalent parameters K_i (ie. with perfectly parallel R_i), this would result in the parameters being given the same value, and in an ill-conditioned system that approaches this situation, the parameters values would tend to be similar. This would be desirable in common cases such as 3 equivalent dihedral parameters around the same rotatable bond (illustrated in subsection 4.1.1) or 2 angle parameters around a trigonal planar center (discussed in section S2.1.2), where it is the authors’ experience that similar values improve transferability. However, this naive proposal fails when the vectors R_k and R_i are antiparallel (see the discussion in section 2.4 for odd n_i values). In that case, parameters K_i with the same sign will counteract each other, and restraining them to be similar substantially decreases the robustness of already ill-conditioned systems. To obtain the same balance and transferability as discussed above, the parameters would need to be restrained to be of similar magnitude but opposite sign, i.e. K_i/K_k = −1. This can be accomplished by observing that for antiparallel vectors, the factor 〈R_k|R_i〉 in (7) and (8) is negative as well, so that the behavior will be as desired in the cases discussed so far if we change (7) to:

$$b_k=\sqrt{\frac{1}{1-{\sigma }_k}\sum _{i=1}^n{\sigma }_i\mid \langle {\mathbf{R}}_k\mid {\mathbf{R}}_i\rangle \mid }$$ (10)

This, however, poses another problem. In section 2.3, we expressed harmonic parameters with variable reference value as a sum of two harmonic functions with fixed reference values, which we proposed to set equal to the lower and upper limit of the input scan range. It can be shown that under these circumstances, the 〈R_x,i|R_y,i〉 of the component harmonic functions will generally be negative; however, for an $x_i^0$ that lies between $x_x^0$ and $x_y^0$ (as will commonly be the case), the fitted K_x,i and K_y,i need to have the same sign, which would be disfavored by (10), again decreasing the robustness. Similar situations may arise for variable phase dihedral parameters for certain scan ranges. The solution here is to apply the absolute value in (10) only when k and i are not components of the same compound parameter; if they are, the sign is retained, i.e.

$$b_k=\sqrt{\frac{1}{1-{\sigma }_k}\left(\left(\sum _{i\ne k^{\prime }}{\sigma }_i\mid \langle {\mathbf{R}}_k\mid {\mathbf{R}}_i\rangle \mid \right)+{\sigma }_{k^{\prime }}\langle {\mathbf{R}}_k\mid {\mathbf{R}}_{k^{\prime }}\rangle \right)}$$

where k′ is k’s counterpart in a compound parameter. It should finally be noted that setting K_k′/K_k = 1 biases the two components towards having equal values, so that the resultant reference value or phase is biased towards the middle between the reference values or phases of the components, i.e. the middle of the scan range for bonds and angles. In practice, the impact of this effect was observed to be small. As we did not find a way to compensate or otherwise eliminate any restraint-induced bias on the reference values and phases, a small bias towards the center of the scan range seems relatively benign, justifiable, and an acceptable limitation of the methodology.

2.8 Target-adapted bias

It is the authors’ experience that for response vectors that are roughly parallel, non-compound parameters (or more precisely, parameters that are not components of the same compound parameter) that have the same sign usually lead to the most favorable fit, both in terms of reproducing the target vector and preventing overfitting and the associated large, mostly mutually compensating parameter values. Similarly, non-compound parameters with opposite sign are usually the most favorable for response vectors that are roughly antiparallel. While the rationale for this has been demonstrated in section 1.2 for the asymptotic case where the response vectors are almost exactly parallel or antiparallel, the considerations for compound parameters in section 2.7 demonstrate that this cannot be held as a general rule in more complex cases, which is the main limitation of the uniform bias. Additionally, it would appear desirable to employ the properties of the factor K_i/K_k discussed in section 2.6 to make the fitting procedure favor the parameters that have the greatest impact on how well B′ reproduces B for the smallest change in parameter.^* Both of these concerns could tentatively be addressed by proposing to set

$$K_i/K_k=\langle {\mathbf{R}}_i\mid \mathbf{B}\rangle /\langle {\mathbf{R}}_k\mid \mathbf{B}\rangle$$ (11)

in (7) and (8), which will henceforward be referred to as “target-adapted bias”. Per the discussion in section 2.6, the resulting restraint would indeed favor low K_k values for parameters whose response vector is close to orthogonal to the target vector. It should be noted that the uniform bias formula presented in section 2.7 (or even a simple LLS procedure with constant b_k as discussed in section 2.5) already has an inherent tendency to this effect, so that the target-adapted bias disproportionally favors parameters k with high 〈R_k|B〉. As for the sign, two perfectly antiparallel vectors (R_i and R_k) by definition have opposite dot products with a third vector (B). While this is not necessarily true for roughly antiparallel vectors, the treatment is asymptotically correct and the chance of an incorrect sign increases as the angle between the vectors becomes greater and 〈R_k|R_i〉 in (7) and (8) decreases in absolute value, so that the numerical impact of K_i/K_k on the total b_k becomes smaller as its “precision” decreases. Compound harmonics are again an exception; as explained in section 2.7, a positive K_y,i/K_x,i would usually be desirable, while (11) is likely to be negative owing to the response vectors typically being roughly antiparallel (〈R_x,i|R_y,i〉 < 0). In light of the discussion in section 2.7, it would appear logical to use an absolute value in these cases, but it was empirically observed that differences in the magnitudes of K_k′/K_k values had unpredictable effects on the reference values obtained from equation 2 (data not shown). Better results were obtained by using the uniform bias approach for K_k′/K_k for all compound functions, so that the final target-adapted bias becomes

$$\begin{array}{l}{b}_k=\sqrt{\frac{1}{1-{\sigma }_k}\left(\left({\displaystyle \sum _{i\ne k^{\prime }}}{\sigma }_i\langle {\mathbf{R}}_k\mid {\mathbf{R}}_i\rangle \frac{\langle {\mathbf{R}}_i\mid \mathbf{B}\rangle }{\langle {\mathbf{R}}_k\mid \mathbf{B}\rangle }\right)+{\sigma }_{k^{\prime }}\langle {\mathbf{R}}_k\mid {\mathbf{R}}_{k^{\prime }}\rangle \right)}\\ =\sqrt{\frac{1}{(1-{\sigma }_k)\langle {\mathbf{R}}_k\mid \mathbf{B}\rangle }\left(\left({\displaystyle \sum _{i\ne k^{\prime }}}{\sigma }_i\langle {\mathbf{R}}_k\mid {\mathbf{R}}_i\rangle \langle {\mathbf{R}}_i\mid \mathbf{B}\rangle \right)+{\sigma }_{k^{\prime }}\langle {\mathbf{R}}_k\mid {\mathbf{R}}_{k^{\prime }}\rangle \langle {\mathbf{R}}_k\mid \mathbf{B}\rangle \right)}\end{array}$$

using the same notation as in section 2.7. The limitation of having a small bias on the reference values and phases of compound parameters remains the same as in the uniform bias.

2.9 Bias compensation

Both the uniform and target-adapted bias functions reliably decrease all well-behaved fitted force constants and amplitudes by a fraction σ_k. This makes it possible to scale these values up by a same amount after fitting, so that the final force constants and amplitudes for well-behaved DF have exactly the same value as they would have without biasing restraint. We will henceforward refer to this operation as “bias compensation”, and apply it to all results of restrained fits unless explicitly stated otherwise. It should be noted that this does not nullify the advantages that led us to introduce the biasing restraint in the first place, because the ill-conditioned DF are impacted far stronger by said biasing restraints.

2.10 Restraints with nonzero target

All restraints discussed up to this point pull the fitted K_k values towards zero. As discussed in section 2.5, this is particularly appropriate for dihedral parameters around rotatable bonds, and as demonstrated in the case studies below, it yielded excellent results when applied to dihedral fitting problems in general. However, it was found to be far less appropriate for bonds and angles, which not only cannot reasonably expected to approach zero, but in practice very often turn out to be non-orthogonal and/or ill-conditioned to some degree, causing their force constants to be pulled down far more than σ_k and rendering the bias compensation ineffective. An appealing solution would be to construct B_ref in section 2.6 by adding nonzero values to B, but unfortunately, the corresponding expression for b_k (equivalent to to equation (7)) is not of practical use. Rather, we opted to subtract the energy contribution associated with the initial guess parameter (i.e. $K_k^{\mathit{initguess}}{\mathbf{R}}_k$) from B prior to the fitting, and combine the fitted K_k with the initial guess parameter before outputting the result, so that pulling K_k towards 0 is equivalent to pulling the final result towards $K_k^{\mathit{initguess}}$. As mentioned before, this scheme is most often applied to bond and angle parameters which, as discussed in section 2.3, generally are expressed as a combination of two harmonic functions, the resultant of which is now a correction term to be applied on top of $K_k^{\mathit{initguess}}$ by means of equation (2). Per the discussion in section 2.7, this correction term contains a slight bias towards the middle of the scan range because K_k′/K_k is set to 1 both in the uniform and the target-adapted bias, causing a small but artificial distortion in the final reference value. As it would be more ideal to bias the reference value towards its corresponding value in the initial guess parameter, this was attempted by choosing K_k′/K_k such that the resultant reference value of 2 component parameters with ratio K_k′/K_k would equal the initial guess reference value. However, similar as in section 2.8, K_k′/K_k values other than 1 gave rise to unpredictable results in practice. This was worked around by leaving K_k′/K_k = 1 and shifting both $x_x^0$ and $x_y^0$ such that they are centered around the initial guess reference value without changing their mutual distance. This shift was also straightforward to apply in the cyclic phase space of variable-phase dihedrals and improper dihedrals. As discussed in section 2.2, it is even advantageous to shift the δ_x and δ_y of dihedrals with no initial guess phase to −π/4 and π/4. Doing so applies a slight bias towards a symmetric potential and thereby improves transferability, whereas the more naive choice of δ_x = 0 and δ_y = π/2 imposes a small spurious bias towards π/4 and 5π/4.

2.11 Group fitting and weighting of data points and parameters

As discussed by Guvench et al. ¹², it is often desirable to assign different importance to different data points in the LLS fit (i.e. elements to the target vector B). This can straightforwardly be accomplished by multiplying each row j of A and B by the square root of a user-defined weight factor w_j, which results in an intuitive weighting consistent with reference ¹². Perhaps somewhat less trivial is the possibility of applying per-parameter weight factors by multiplying each column of B (i.e. each response vector R_i) and each output parameter K_i by a weight factor w_i. This proved crucial to bring the bond, angle and dihedral parameters on the same footing. Specifically, these different types of parameters are expressed in different units and have different magnitudes, and mixing them in the same restrained LLS fit (with either uniform or target-adapted bias) only gives reasonable results when applying a w_i of 200 to the bonds and 40 to the angles and improper dihedrals. In the program developed as part of the present work, this basic weighting scheme is applied by default. Finally, to make it possible to fit a parameter to target data sets calculated on chemically different molecules containing that parameter, it is necessary to have the ability to calculate independent offsets c^T and $c_i^R$ (as defined in section 2.1) for each set of data points.¹⁵ In other words, the conformational energies associated with different chemical entities need to be aligned independently, as it is often meaningless to try to capture the energy difference between different compounds. This feature, henceforward referred to as “group fitting“, also found unexpected use for routinely fitting bond and angle parameters in a robust fashion, as discussed in section 2.12.

2.12 Potential Energy Scanning considerations

It is generally accepted that for a given potential energy function, the scope and quality of a force field is largely defined by the target data used in its parametrization. A variant of this rule holds true even at the level of optimizing a modest number of bonded parameters to conformational energy differences, in that even the most robust fitting algorithm cannot be expected to yield reasonable results if the target data does not unambiguously define the parameters to be fitted. Therefore, when generating target data in the form of QM potential energy scans, the details of these calculations should be chosen carefully. While a substantial body of knowledge regarding the scanning of dihedral DF for this purpose, there has been much less previous work on the scanning of bond and angle DF. Our experiences and the ensuing recommendations in this respect can be found in section S2.3 of the Supporting Information. In summary, bond and angle scans consisting of 3 points in principle suffice to approximate the associated force constant. In our proposal, one of the scan points is the minimum energy conformation and for the two others, the DF of interest is respectively incremented and decremented by a constant. The best results were obtained if this constant was chose such that the outer points are between 1 and 3 kcal/mol above the middle (minimum energy) point. This typically corresponded to step sizes of ~0.05Å and ~5° for bonds and angles, respectively. Importantly, it was found that in contrast with dihedral scans, degrees of freedom that are not directly involved in bond, angle and improper scans should not be allowed to relax. However, performing a concerted fit of dihedral and other parameters in this fashion gives rise to an energetic discrepancy between the set of constrained and the set of relaxed scan points. This was solved by using the group fitting discussed in section 2.11 to independently align these two sets.

As an alternative to Potential Energy Scans, Burger et al. recently proposed MC sampling of molecular conformations. ¹⁶ While, as argued in section S2.3, this may not be practical when the number of DF is large, a lot of parameter fitting problems involve small model compounds and modest numbers of parameters, making MC sampling an interesting prospect. While a systematic evaluation of this option within the current framework is outside the scope of the present paper, it may become the subject of future work.

3 COMPUTATIONAL DETAILS

All relaxed QM potential energy scans were performed at the MP2/6-31G(d) level of theory using the “ModRedundant” feature of the Gaussian 03 program. ¹⁷ The program’s defaults were used for all other options, except that the “NoSymm” keyword is often required when starting a scan from a symmetric geometry. As discussed in section 4.2.2 and reference ¹⁸, in the case of THF, MP2/6-31G(d) is not sufficient to quantitatively capture the potential energy surfaces that result from higher-level calculations or experiment. However, the aim is to provide a proof-of-concept for the present parameter fitting methodology, not to provide an updated force field, which would involve many other considerations. Conversely, the hexopyranose scans in section 4.2.3 are aimed at future release to the community, and were therefore performed at the MP2/cc-pVQZ//MP2/6-31G(d) level. Specifically, after performing a relaxed potential energy scan at MP2/6-31G(d) level using Gaussian 03, single point energies of all the resulting conformations were calculated at the MP2/cc-pVQZ using PSI4.¹⁹ Where applicable, constrained QM potential energy scans were performed at MP2/6-31G(d) level, using Gaussian 03’s “Scan” feature with a Z-matrix representation of an MP2/6-31G(d) optimized structure.

Where applicable, version 2b8 and 0.9.7 of the CGenFF force field and program were used, respectively. All MM scans were performed using the CHARMM program ²⁰ by reading the QM geometry for each scan point into CHARMM. As discussed in section 2.12, the constrained MM scans that are indicated for bonds and angles are performed by simply computing single-point energies on these QM geometries; for the relaxed dihedral scans, energy minimizations (gradient tolerance = 10⁻⁴ kcal mol⁻¹ Å⁻¹) are performed while constraining all DF associated with all parameters being fit, including non-dihedral DF and DF that are not explicitly being scanned (e.g. in case a dihedral parameter applies to two separate chemically equivalent bonds out of which only one is scanned). For practical reasons, this constraining scheme is implemented using restraints with high force constants (99999 kcal mol⁻¹ Å⁻² for bonds and 9999 kcal mol⁻¹ radian⁻² for all other types of degrees of freedom), which are removed after the minimization to yield the MM energy. This is in line with the procedure employed in reference ¹², which contains more details. Sample CHARMM scripts are provided with the program to facilitate reproducing the current procedure. The parameter fitting was performed using the “lsfitpar” program that will be made available under an open-source license. Its interface is similar but not identical to the “fit_dihedral.py” program from reference ¹²; usage examples are provided with the program. Unless stated otherwise, the uniform bias (section 2.7) was used with σ_i = 0.001.

4 CASE STUDIES

4.1 Toy systems

In this subsection, two case studies are presented that consists of mathematical functions rather than real molecules, but are representative of phenomena that commonly occur in real molecules. This allows the study of said phenomena in a controlled environment devoid of any considerations other than the one of interest.

4.1.1 2+1 dihedrals around the same rotatable bond

To illustrate the difference between the uniform and the target-adapted bias, this case study consists of three dihedral angles a, b and c around the same rotatable bond, with the same parameter applying to b and c. This case is ubiquitous; for example, a might represent the O-C-C-C dihedral in 1-propanol (compound 6 in figure 1), while b and c represent its two O-C-C-H dihedrals. In this example, the rotatable bond is scanned from 0 to 345° in steps of 15°, a, b and c are each offset by 120° and the target potential consists of a single cosine function with $K_3^{\varphi }=3\text{kcal}/\text{mol}$, n = 3 and δ₃ = 0°. As the unrestrained system for this idealized situation is underdetermined, any solution for which $K_{a,3}^{\varphi }+2K_{b,3}^{\varphi }=3\text{kcal}/\text{mol}$ is exact. On this system, the uniform bias yields $K_{a,3}^{\varphi }=K_{b,3}^{\varphi }=1\text{kcal}/\text{mol}$ while the adaptive bias results in $K_{a,3}^{\varphi }=0.6$ and $K_{b,3}^{\varphi }=1.2$ after applying the bias compensation discussed in 2.9 in both cases. Since a perturbation in $K_{b,3}^{\varphi }$ has twice the impact on how well B′ reproduces B as the same perturbation in $K_{a,3}^{\varphi }$, the adaptive bias as intended gave $K_{b,3}^{\varphi }$ twice the magnitude, minimizing ||X|| in the process. While emphasizing the parameter with the highest response and minimizing the parameter vector are important objectives during parameter optimization, in this (unfortunately very common) case, it leads to higher amplitudes on the dihedrals associated with the hydrogens, which is both unphysical and poorly transferable. In contrast, the uniform bias as intended equalized the amplitudes $K_3^{\varphi }$, which minimizes max(X) and yields parameters that are more physical and transferable. While it should be noted that in an actual parameter optimization, dihedral parameters involving hydrogen atoms are typically transferred from existing parameter in the force field, similar situations can arise with non-hydrogen atoms, and since one of the stated goals of this work is to be useful to non-expert users, the uniform bias was chosen to be the default in the lsfitpar program, even though expert user may occasionally be able to improve the general quality of the parameters by choosing the adaptive bias option.

Figure 1.

Skeletal formulas of compounds discussed in the manuscript, with representation chosen to highlight attributes of interest. Compounds 1-5 can be found in Figure S1 in the Supporting Information. 6: 1-propanol, with the rotatable bond discussed in section 4.1.1 marked. 7 and 8: N-sec-butylformamide and N-propylformamide, respectively. As discussed in section 4.1.2, a PES of the right (C-C-N-C) dihedral in the latter compound may display spurious asymmetry if the left (C-C-C-N) dihedral is sampled asymmetrically. 9 and 10: N-ethylsulfamate (NESM) and tetrahydrofuran (THF), as discussed as case studies in sections 4.2.1 and 4.2.2, respectively. 11: a representative hexopyranose monosaccharide. CHARMM atom names are given in the figures for NESM 9 and the hexopyranose monosaccharide 11 in order to facilitate the discussion.

4.1.2 A typical ill-conditioned pair of dihedrals

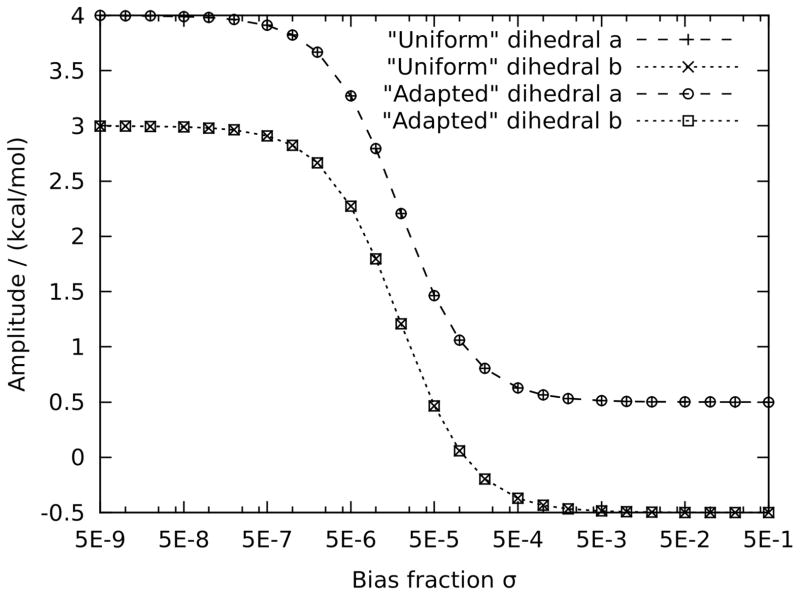
This case study consists of two dihedral angles a and b around an idealized rotatable bond that contains a subtly nonplanar sp² atom. The rotatable bond is scanned from −180° to 179° in steps of 1° driven by a, and b is offset by 179.5° to mimic a 0.5° deviation from planarity. The target potential consists of a single cosine function with $K_1^{\varphi }=1\text{kcal}/\text{mol}$, n = 1 and δ₁ = 2°, the latter to simulate a slight asymmetry in the target data that can be either an artefact or caused by the presence of an asymmetric center. This is an ubiquitous occurrence in real-life force field studies as well; to name just two examples, the C-C-N-C and C-C-N-H dihedral angles in the asymmetric molecule N-sec-butylformamide (compound 7 in figure 1) exhibit this type of behavior, as do the same dihedrals in its symmetric counterpart N-propylformamide (compound 8 in figure 1) if the C-C-C-N dihedral is accidentally sampled slightly asymmetrically in the target conformational ensemble. As demonstrated in Hopkins et al.’s case studies, ¹³ avoiding this kind of subtle asymmetry is difficult, and it can safely be assumed to be present in the majority of nontrivial dihedral parametrization studies, underlining the importance of the method performing well in this case study. Indeed, although the exact solution to the unrestrained least-squares problem is $K_{a,1}^{\varphi }=4\text{kcal}/\text{mol}$ and $K_{b,1}^{\varphi }=3\text{kcal}/\text{mol}$, it would be preferable for the fitting algorithm to ignore the asymmetry and output $K_{a,1}^{\varphi }=0.5\text{kcal}/\text{mol}$ and $K_{b,1}^{\varphi }=-0.5\text{kcal}/\text{mol}$, as this would be more physical in the case of a symmetric molecule and (vastly) more transferable in the presence of an asymmetric center, at the cost of an insignificant 2° error in reproducing the target data. As can be seen in figure 2, the solution is within 2% of the above unrestrained solution when the bias fraction is ≤ 2 × 10⁻⁷, but within 2% of the desired solution when the bias fraction is ≥ 10⁻³, with a sigmoid (on the present logarithmic scale) transition in-between. Even for bias factors σ up to 0.5, the bias compensation (section 2.9) gives rise to the correct solution, although this is not generally the case on more complex real-life problems; in this context, bias factors between 0.001 and 0.03 produce the best results in the authors’ experience.

Figure 2.

Dihedral amplitude as a function of bias fraction σ for case study 4.1.2: a typical ill-conditioned pair of dihedrals. “Uniform” and “Adapted” stand for uniform and target-adapted bias, respectively; there is no perceptible difference between the two because 〈R_a|B〉 and 〈R_b|B〉 differ by only 0.03%.

4.2 Model compounds

While the lsfitpar program was internally validated on a significant number of compounds, the qualities of interest, i.e. robustness in the hands of a non-expert user and the generation of parameters that are “physical” and transferable, are not trivial to quantify, and are not problematic for all molecules. Therefore, two model compounds are discussed in detail to illustrate the use and behavior of the present algorithm.

4.2.1 N-ethylsulfamate

N-ethylsulfamate (NESM; compound 9 in figure 1) was selected because it exhibited significant coupling between different types of parameters as well as issues associated with the scan range for bonds and angles, thus presenting a good case study for the present algorithm as well as the practical considerations discussed in sections 2.12 and S2.3. Relaxed Potential Energy Scans were performed on the three dihedral angles C3-N2-S1-O11, C4-C3-N2-S1, and C4-C3-N2-H21 from −180° to 180° in steps of 5° (see figure 1, compound 9 for a key of the atom names). This small step size was chosen for cosmetic reasons, i.e. to get a smoother plot in figure 3; a step size of 15° is more common in practical studies as it produces more than enough target data to fit any sensible combination of multiplicities in the vast majority of cases, with cyclic structures being an important exception (see sections 4.2.2 and S3.1). As discussed in section 2.12, fully constrained 3-point scans were performed on the valence angles and bonds of interest. Specifically, the angles C3-N2-H21, H31-C3-N2 and H32-C3-N2 were each decremented and incremented by 10° in the QM optimized structure. Conversely, step sizes of 5° and 0.05 Å were used for the C4-C3-N2 angle and the C3-N2 bond, respectively. As the different scans had widely differing numbers of points, weight factors inversely proportional to the number of scan points were applied in order to give both the bond scan and the set of four angle scans the same weight as the set of three dihedral scans.

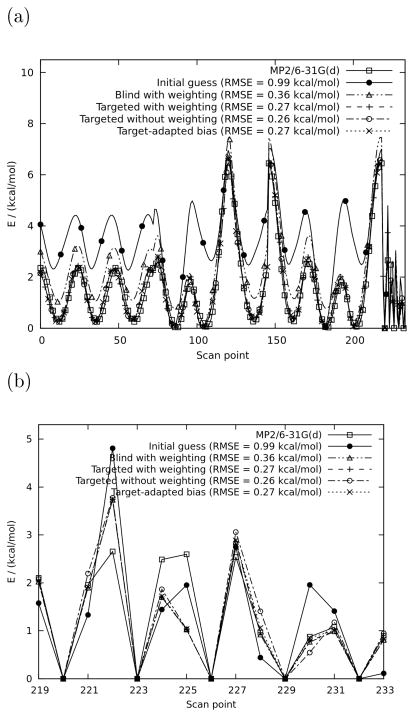
Figure 3.

PES of N-ethylsulfamate (NESM; see compound 9 in figure 1 for a key of the atom names used in this study). Points 0-72, 73-145 and 146-218 are respectively scans of the dihedrals C3-N2-S1-O11, C4-C3-N2-H21 and C4-C3-N2-S1. The angles C3-N2-H21, H31-C3-N2, H32-C3-N2 and C4-C3-N2 were scanned in scan points 219-221, 222-224, 225-227 and 228-230, respectively, whereas scan points 231-233 represent the C3-N2 bond. In agreement with the methodology discussed in section 2.12, the set of (relaxed) dihedral scan points (0-218) was aligned separately from the set of (constrained) bond and angle scans (219-233). RMSEs were calculated without weighting. Figure 3b zooms in on the bond and angle scans in order to bring differences to light that cannot be seen in figure 3a.

An initial guess parameter set was put together manually by combining parameters assigned by analogy by the CGenFF program ²¹ with manual adjustments and relevant parameters transferred from an earlier parametrization study on N-methylsulfamate. ²² As shown by figure 3, while this initial guess might be qualitatively acceptable for some purposes, it shows large quantitative deviations. The LLS solution with uniform bias and no restraints on bonds and angles (labeled “blind” in the figure) reproduces the bonds and angles well (figure 3b), but performs poorly on the dihedrals (figure 3a) compared to the other fits. On closer inspection (table 1), this appears to be caused by a somewhat unrealistic value for the C-N-S angle parameter compared to its initial guess value, which is highly trustworthy because it was optimized on the closely related model compound N-methylsulfamate. The observation that this angle significantly worsens the dihedral profiles despite the algorithm being given ample freedom in terms of multiplicities illustrates that dihedrals can strongly depend on other parameters, underlining the relevance of the present work. Furthermore, the fact that this angle is relatively sensitive to the presence or absence of an initial guess indicates that it is ill-defined; indeed, the geometric degree of freedom associated with this parameter was not explicitly scanned, forcing the algorithm to derive its value from energetic information that is implicitly present in the relaxed dihedral scans. This was done for the sake of illustration and while the result is encouraging, it is obviously safer in practical applications to either improve conformational sampling or use a high-quality transferred parameter, if available.

Table 1.

Parameters for fitted N-ethylsulfamate (NESM; compound 9 in figure 1) compared to the initial guess (see section 4.2.1). RMSE values were calculated as in reference ¹² but without weighting.

Parameter definition		“Blind”a fit; RMSE = 0.36 kcal/mol		“Targeted”a fit; RMSE = 0.27 kcal/mol		“Adapted”a fit; RMSE = 0.27 kcal/mol		Initial guess; RMSE = 0.99 kcal/mol
BOND
Atom types		Force constantb	Reference lengthb	Force constantb	Reference lengthb	Force constantb	Reference lengthb	Force constantb	Reference lengthb
CG321 NG2S3		318.7	1.443	322.4	1.443	329.2	1.444	266.0	1.460
ANGLES
Atom types		Force constantb	Reference angleb	Force constantb	Reference angleb	Force constantb	Reference angleb	Force constantb	Reference angleb
CG331 CG321 NG2S3		23.0	108.4	27.3	109.7	37.7	111.6	70.0	109.5
NG2S3 CG321 HGA2		38.0	105.2	38.3	105.2	38.7	105.2	51.5	107.5
CG321 NG2S3 SG3O1		76.5	107.9	58.7	104.9	54.2	104.0	39.5	103.1
CG321 NG2S3 HGP1		51.5	109.5	51.8	109.5	52.2	109.5	35.0	109.0
DIHEDRALS
Atom types	Multiplicity	Amplitudeb	Phaseb	Amplitudeb	Phaseb	Amplitudeb	Phaseb	Amplitudeb	Phaseb
CG331 CG321 NG2S3 SG3O1	1	0.453	180	0.755	180	0.653	180	1.500	180
CG331 CG321 NG2S3 SG3O1	2	1.137	0	0.866	0	0.885	0	0.650	180
CG331 CG321 NG2S3 SG3O1	3	0.391	0	0.628	0	0.667	0	1.000	0
CG331 CG321 NG2S3 SG3O1	4	0.190	180	0.151	180	0.142	180	N/A	N/A
CG331 CG321 NG2S3 SG3O1	6	0.107	0	0.113	0	0.111	0	N/A	N/A
CG331 CG321 NG2S3 HGP1	1	1.110	0	0.741	0	0.790	0	0.000	0
CG331 CG321 NG2S3 HGP1	2	0.477	0	0.321	0	0.325	0	N/A	N/A
CG331 CG321 NG2S3 HGP1	3	0.052	180	0.235	180	0.266	180	N/A	N/A
CG321 NG2S3 SG3O1 OG2P1	3	0.545	0	0.552	0	0.556	0	0.537	0

^aIn the blind fit, bonds and angles are unrestrained, while in the targeted fit, they are restrained towards their initial guess values, as discussed in section 2.10. Dihedrals are restrained towards 0 in all cases. Both the blind and targeted fit were obtained using the uniform bias; conversely, the adapted fit is the same as the targeted fit but using the target-adapted bias.

^bConform CHARMM conventions, bond force constants are in kcal mol⁻¹ Å⁻², bond reference lengths in Å, angle force constants in kcal mol⁻¹ radian⁻², reference angles and dihedral phases in degrees, and dihedral amplitudes in kcal mol⁻¹.

While the fit without weighting has the lowest RMSE, it performs significantly worse than others on the angles (figure 3b), which can trivially be explained by the fact that the weighting strongly emphasizes the angles and bonds. Combined with the observation that the weighting doesn’t make the dihedrals observably worse, this justifies its routine application in concerted fitting. It should also be noted that the RMSEs in the figure and table were calculated without weighting, thus inherently favoring parameters that were fit without weighting because an LLS fit that uses a given weighting scheme minimizes the correspondingly weighted RMSE. Finally, although a small but significant difference in the value for the C-C-N angle parameter can be observed between the uniform and target-adapted bias, their PES and RMSE are not significantly different, underlining the somewhat ill-conditioned nature of even this seemingly straightforward and innocuous problem. While in this case study, the RMSE for the uniform bias is lower than that for the target-adapted bias by an insignificant amount, preliminary data indicate that the former’s advantage becomes stronger when given more ill-conditioned problems.

4.2.2 Tetrahydrofuran

Tetrahydrofuran (THF; compound 10 in figure 1) was chosen as a less trivial example of concerted bond, angle and dihedral fitting. Indeed, its pseudorotational energy surface is complex and subtle, and qualitative disagreement exists between different levels of correlated ab initio QM calculations as well as experiment. ¹⁸ From a Molecular Mechanics point of view, while ring strain often dominates the conformational energetics of small rings, in the case of all-sp³ 5-membered rings, the effect of the ring strain is subtle because the idealized tetrahedral angle (109.5°) is only subtly larger than the inner angle in an ideal planar pentagon (108°), thus exerting only a small in-plane force. Competing with this is an out-of-plane dihedral force caused by 1–4 repulsion, which is strong enough to induce a set of nonplanar minima, but not to impose high barriers between them. Therefore, all-sp³ 5-membered rings such as THF are a prime example of molecules that would benefit from concerted angle and dihedral fitting. However, this is complicated by the fact that the relationship between the parameters and the conformational energetics is less straightforward than for noncyclic molecules and that it is not trivial to obtain a set of target data that is not ill-conditioned, as discussed in depth in section S3.1 of the Supporting Information. Therefore, previous efforts have involved alternating adjustments to angle and dihedral parameters ² in an empirical fashion using a target data set that contained QM energies for only a limited number of conformations.²³ Another factor that makes THF an attractive case study is that it is the scaffold for the furanose carbohydrates, ²⁴ which include the ribose moiety in the RNA and DNA backbone.

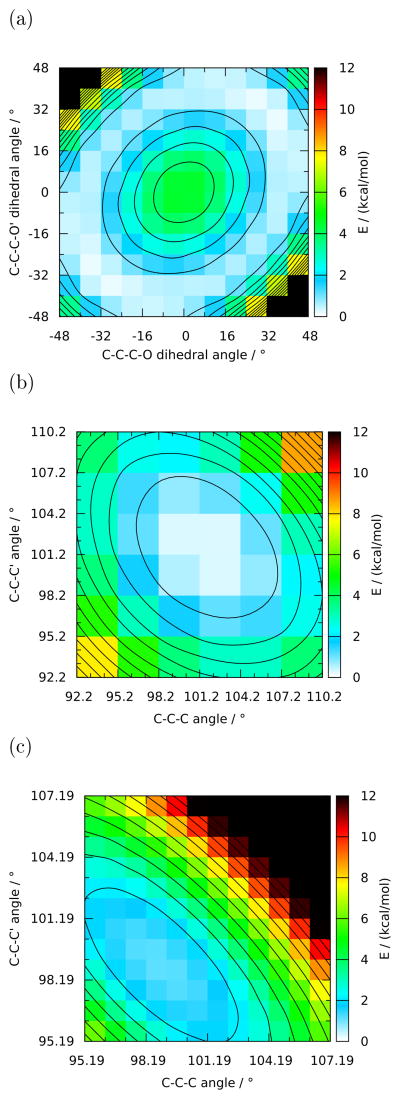
In agreement with the analysis in section S3.1, a relaxed 2D scan was conducted on the pair of C-C-C-O dihedral angles (figure 4a), which neatly shows an annular minimum-energy basin corresponding to the ring’s pseudorotational surface. A second relaxed 2D scan was performed on the pair of C-C-C valence angles (figure 4b), and the latter scan was repeated while constraining both C-C-C-O dihedral angles at −39.72 ° (figure 4c). In the fully relaxed angle PES, both angles were scanned from 92.19° to 110.19° in steps of 3° (figure 4b). This (somewhat unexpectedly) brought a case of the aforementioned hysteresis to light in one of the scan points, underlining the prevalence of this problem as discussed in section S3.1. Conversely, the angle PES with constrained dihedrals was scanned from 95.19 ° to 107.19° in steps of 1° (figure 4c) because of geometrical convergence issues associated with the constraints. Finally, these three 2D scans were followed by three relaxed 3-point scans on the three chemically distinct bonds in the molecule. This implies that the C-C bond parameter is scanned twice in chemically different environments. Doing so leads to a fitted parameter that is a compromise between the two environments, which is generally desirable². Moreover, the availability of a higher diversity of target data can typically only improve the quality of the fit. ¹⁶ The bonds were scanned by decrementing and incrementing their respective MP2 equilibrium distances by 0.06 Å. These were relaxed scans as well because performing fully constrained scans on a single bond or angle as recommended in section 2.12 is not possible in a cyclic structure.^* As the different scans had widely differing numbers of points, weight factors inversely proportional to the number of scan points were applied in order to give the two 2D angle scans equal weight in the fit. Similarly, the set of three bonds scans and the 2D dihedral scan were given equal weight to the sum of the two angle scans.

Figure 4.

2-Dimensional QM PES of Tetrahydrofuran (THF; compound 10 in figure 1). 4a: relaxed PES around the two C-C-C-O dihedral angles; 4b: relaxed PES around the two C-C-C valence angles; 4c: PES around the two C-C-C valence angles while constraining both C-C-C-O dihedral angles at −39.72° and relaxing all other DF. The quantities in each plot are relative to that plot’s absolute minimum (b) (as opposed to the global minimum.)

Fitting the parameters in THF to the QM profiles resulting from the above scans gave excellent results to the extent that that a graphical representation of the fitted PES is indistinguishable from the corresponding QM data. Therefore, we will limit ourselves to discussing the data in table 2. As can be seen from the RMSEs, both of the fitted parameter sets appear to outperform the original CGenFF model; inspection of the PES (not shown) reveals that the discrepancies in the latter are mainly in the dihedral profile. This is no surprise, as the dihedral parameters in CGenFF were not only fitted to a different set of target data at a different level of theory and with less freedom in the multiplicities (i.e. we introduced a 4-fold term because this gave a substantial improvement in the reproduction of the shape of the PES), but also and more importantly represent a compromise between different model compounds, including compounds such as cyclopentane and pyrrolidine. For these reasons and because they were fit “on top of” different bond and angle parameters, the dihedral parameters cannot be compared between CGenFF and the fitted model; the only significant observation that can be made is that the amplitudes are of very similar magnitude. As discussed in section 2.5, the dihedral term can be considered a correction term for the remainder of the potential energy function; thus, the fact that these corrections are of similar magnitude indicates that the fitted bond and angle parameters are physically at least equally relevant as the CGenFF values. Indeed, all the parameter associated with the bonds and angles are very similar, enforcing the validity of both the present work and the (more laborious) established methodology that contains a component of chemical intuition. The only nontrivial difference in the parameters is the reference C-O-C angle, where the CGenFF and the fitted values bracket the angle measured in the QM minimized conformation, which is very close to the ideal tetrahedral angle. It can be speculated that the smaller reference value in the fitted parameter set helps reproduce certain details of the PES (see below), but given the highly coupled nature of the 5-membered ring, no reliable statements can be made in this respect. Of note is the observation that the different level of theory does not result in radically different parameters, in line with the fact that, while reference ¹⁸ does show different sets of minima depending on the level of theory, the differences are small purely in energetic terms, as the barriers between the minima are low in all cases.

Table 2.

Parameters for fitted Tetrahydrofuran (THF; compound 10 in figure 1) compared to CGenFF. RMSE values were calcualted as in reference ¹² but without weighting. The CGenFF values were copied from the work in reference ²³, exept that the CG3C52 CG3C52 reference length was increased from 1.518 to 1.530 because the former value was based on surveys of X-ray crystallographic data and was found to be incompatible with the CGenFF’s QM-based parametrization philosophy. ² The latter value is a compromise between the X-ray and QM data; a pure QM-fitted reference length would be expected to be even higher.

Parameter definition		“Blind”a fit; RMSE = 0.28 kcal/mol		“Targeted”a fit; RMSE = 0.16 kcal/mol		“Adapted”a fit; RMSE = 0.15 kcal/mol		CGenFF; RMSE = 0.73 kcal/mol
BONDS
Atom types		Force constantb	Reference lengthb	Force constantb	Reference lengthb	Force constantb	Reference lengthb	Force constantb	Reference lengthb
CG3C52 CG3C52		209.8	1.553	215.5	1.554	217.1	1.553	195.0	1.530
CG3C52 OG3C51		284.6	1.429	308.1	1.428	308.5	1.428	350.0	1.425
ANGLES
Atom types		Force constantb	Reference angleb	Force constantb	Reference angleb	Force constantb	Reference angleb	Force constantb	Reference angleb
CG3C52 CG3C52 CG3C52		93.7	107.6	98.6	107.6	98.6	107.7	58.0c	109.5c
CG3C52 CG3C52 OG3C51		46.9	112.2	53.7	111.4	52.3	111.7	45.0	111.1
CG3C52 OG3C51 CG3C52		69.6	107.0	81.1	106.0	80.3	106.3	95.0	111.0
DIHEDRALS
Atom types	Multiplicity	Amplitudeb	Phaseb	Amplitudeb	Phaseb	Amplitudeb	Phaseb	Amplitudeb	Phaseb
CG3C52 CG3C52 CG3C52 CG3C52	3	0.056	180	0.023	180	0.038	0	0.410	180
CG3C52 CG3C52 CG3C52 CG3C52	4	0.490	0	0.434	0	0.401	0	N/A	N/A
CG3C52 CG3C52 CG3C52 OG3C51	3	0.381	180	0.144	180	0.098	180	0.000	0
CG3C52 CG3C52 CG3C52 OG3C51	4	0.198	0	0.072	0	0.053	0	N/A	N/A
CG3C52 CG3C52 OG3C51 CG3C52	3	0.647	0	0.530	0	0.623	0	0.500	0
CG3C52 CG3C52 OG3C51 CG3C52	4	0.048	180	0.037	180	0.080	180	N/A	N/A

^aIn the blind fit, bonds and angles are unrestrained, while in the targeted fit, they are restrained towards their respective CGenFF values, as discussed in section 2.10. Dihedrals are restrained towards 0 in all cases. Both the blind and targeted fit were obtained using the uniform bias; conversely, the adapted fit is the same as the targeted fit but using the target-adapted bias.

^bConform CHARMM conventions, bond force constants are in kcal mol⁻¹ Å⁻², bond reference lengths in Å, angle force constants in kcal mol⁻¹ radian⁻², reference angles and dihedral phases in degrees, and dihedral amplitudes in kcal mol⁻¹.

^cThe CG3C52 CG3C52 CG3C52 parameter has an additional Urey-Bradley term, i.e. a harmonic potential as a function of the distance between the outer atoms with force constant 11.16 kcal mol⁻¹ Å⁻² and reference distance 2.561 Å. Since this term is not included in the fit, the fitted angle force constant is expected to be significantly higher than in CGenFF to make up for its lack, and the fitted reference length ^b may also differ.

Introducing nonzero target values for the bonds and angles only yielded a small change in the parameters and a modest improvement in the fit, with very small gains in the high-energy regions of the angle scan with constrained dihedrals. This indicates that the bond and angle parameters are not underdetermined; it appears that even though the conformational ensemble was not explicitly aimed at avoiding correlation, the target data was diverse enough for the LSS algorithm to deconvolute the inevitable correlation in the relaxed scans. This picture is corroborated by the observation that the target-adapted bias gives almost identical results. The present case study thus illustrates that relaxed scans are in fact a viable option when the model compound’s potential energy surface is scanned exhaustively enough, allowing for convenient routine parametrization of rings. The fact that the target-adapted bias yields a very slightly (albeit not significantly) lower RMSD and minute improvements in the PES demonstrates that in the less common cases where robustness is not an issue, the target-adapted bias sometimes performs better - on rare occasions significantly so. ¹⁴ Finally, it should be noted that in the more common cases where the degree of underdetermination is higher, a greater dependence on sensible target values is expected as discussed above and illustrated in section 4.2.1.

4.2.3 Hexopyranose monosaccharides

To demonstrate that the present methodology is applicable for fitting larger sets of parameters, it was used to refit the dihedral parameters of the hexapyranose monosaccharides in the CHARMM Drude polarizabile force field; see figure 1, compound 11 for a representative structure. The bonded part of this force field uses the same energy terms and fitting schemes as its additive (i.e. non-polarizable) counterpart. For the reparametrization of the hexapyranose monosaccharides, the electrostatic description (consisting of atom-centered and lone pair charges, atomic polarizabilities and Thole damping parameters) in the current Drude force field for pyranose ²⁵ was first updated to reproduce a new set of dipole moments and sugar-water interactions at MP2/cc-pVQZ level; this work will be described elsewhere. Then, the dihedral parameters were refit, targeting several pyranose diasteromers (table 3) in order to provide sufficient target data. Potential energy scans with step sizes of 15° were performed, including all the possible dihedrals consisting of the hydroxyl hydrogen and heavy atoms in the different diastereomers. In order to better reproduce the statistically important low-energy states, only the points with a potential energy less than 12 kcal/mol above the global minimum were retained as target data, resulting in a total of 1887 points (table 3). A uniform set of 26 dihedral parameters were fitted to maintain transferability across all 16 different hexapyranose diasteromers. In addition to the reasons discussed in previous sections, the fact that parameters obtained in this fashion need to be valid for different chiralities provides justification for fixing the dihedral phases. Multiplicities of 1, 2, 3 and 4 were fit for the intra-ring dihedrals (C1-C2-C3-C4, C2-C3-C4-C5, C3-C4-C5-O5, C4-C5-O5-C1, C5-O5-C1-C2, and O5-C1-C2-C3), using 1, 2 and 3 for all other dihedrals.

Table 3.

Overview of Pyranose monosaccharide conformations used as target data for dihedral parameter fitting.

monosaccharide	type of conformational scana	# conformations
α-altrose	exocyclic + ring + C1, C2, C3, C4, C6 hydroxyl	417
β-altrose	exocyclic + ring + C1, C2, C3, C4, C6 hydroxyl	440
α-glucose	exocyclic + ring + C1, C2, C3, C4, C6 hydroxyl	343
β-glucose	exocyclic + ring + C1, C2, C3, C4, C6 hydroxyl	320
α-galactose	exocyclic + ring	130
β-galactose	exocylic + ring	76
α-talose	C3, C4 hydroxyl	43
β-gulose	exocyclic + C4 hydroxyl	47
β-manose	C2, C3 hydroxyl	47
β-idose	C3 hydroxyl	24
total		18887

^aexocyclic = O5-C5-C6-O6 torsion, ring = O1-C1-O5-C5, O2-C2-C1-O5, and O4-C4-C5-O5 torsions, hydroxyl = the torsion of hydroxyl group connected to a given carbon atom. The atom numbering is clarified in figure 1, compound 11.

While the hexapyranose diasteromers in this study are chemically distinct, they have the same connectivity. Accordingly, arguments can be made both in favor of and against applying the group fitting discussed in section 2.11. In this work, we performed uniform-bias LSS fits (1) considering every different diastereomer as a different group, (2) considering all monosaccharides that are chemically distinct in aqueous solution on macroscopic time scales as different groups, but anomers of the same monosaccharide as the same group, ¹⁵ and (3) without group fitting. The resulting RMSEs were respectively 0.52, 0.54 and 0.56 kcal/mol, and visual inspection of the energy profiles revealed no significant differences. This indicates that, in contrast to the additive CHARMM force field for carbohydrates, ²⁶ the nonbonded interactions (to which the dihedrals are a correction term) in the Drude polarizabile force field are accurate enough to capture the energy differences between the different diastereomers. The lower RMSE values further underline the increased accuracy of the nonbonded description in the Drude polarizabile force field compared to its additive counterpart (RMSE = 1.69 kcal/mol) as well as the previous iteration of the same polarizable force field (RMSE = 1.18 kcal/mol). ²⁵ As the non-group fitted parameters are thought to be more transferable because they include the energy differences between the diastereomers as target data, these parameters will be released in an upcoming update of the CHARMM Drude polarizabile force field. This also enables free energy perturbation studies between any two diastereomers, which was not possible with any of the previous CHARMM force fields. The PES resulting from the selected parameter set is shown in figure 5. Only one dihedral term, the 1-fold term on O4-C4-C5-C6, has an amplitude of 2.51 kcal/mol, with amplitudes lower than 1.10 for all other terms (see supporting information), again confirming the enhanced description of the nonbonded interactions in the Drude polarizabile force field. Very similar observations were made for the furanose parameter set, which will be discussed in an upcoming paper. ²⁷ As for validating the restrained LSS procedure, the results from this case study demonstrate that the present method is applicable on larger numbers of parameters and that its improvements not only benefit the parametrization of class I additive, but also polarizable force fields.

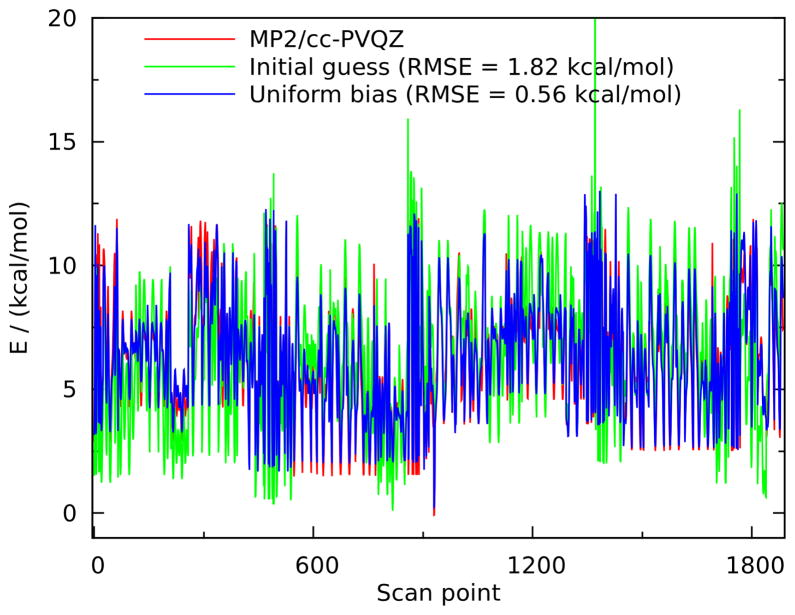
Figure 5.

PES for all the hexopyranose monosaccharides, as summarized in table 3 and discussed in section 4.2.3. The different PES are aligned as discussed in section 2.1. The initial guess data was taken from reference ²⁵, including the “old” electrostatic parameters for a fair comparison. Nevertheless, the initial guess RMSE is significantly higher than in the reference (1.18 kcal/mol); this is to a small extent because of the different QM level of theory and to a bigger extent due to the fact that group fitting was used in the reference. Accordingly, it can clearly be seen in the picture that the initial guess poorly reproduces the energy difference between some groups of points.

4.3 CGenFF bond-charge increments

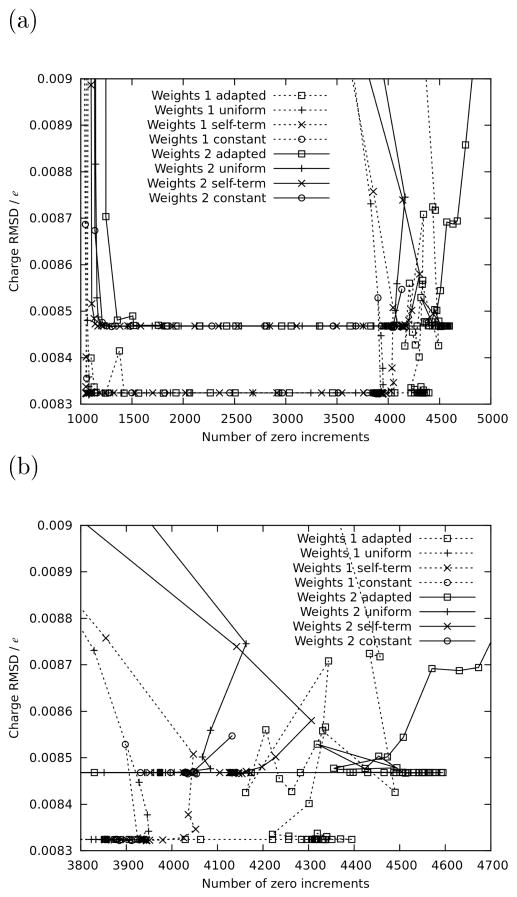
To demonstrate the current restraining scheme’s usefulness beyond bonded parameters, we used it to fit the bond-charge increments that are used by the CGenFF program for the assignment of charges by analogy. ²¹ As discussed in the cited reference, the underdetermined nature of this fit was originally overcome using the same constant restraints that are the subject of sections 2.5. Also, some of the fitted increments were empirically adjusted a posteriori in order to rigorously satisfy a number of preexisting charge assignment rules in the CHARMM force field. As the fit was later redone for each subsequent new release of the force field, it was found that the resulting bond-charge increments underwent small but significant changes in a seemingly random fashion, each time necessitating a slightly different variation of the set of empirical adjustments, which made the process laborious. This relative lack of robustness presented an opportunity to compare the performance of the constant restraints (b_k = b) with the uniform and target-adapted biases on a completely different problem than bonded parameters. Also included in the comparison was a bias consisting of the self-term only, i.e. $b_k=b_k^{\mathit{self}}$ as defined in equation (9).

As this optimization contains large numbers of DF that are poorly determined, ²¹ the number of increments that are rounded to zero after fitting is used as a measure for the effectiveness of the restraints. The rounding is explained in more detail in the caption of Figure 6. In this figure, the charge RMSD is plotted against the aforementioned measure of effectiveness for a wide, logarithmically scaled range of restraint fractions σ, or the restraints b in the case of the constant restraint. This is repeated for two different weighting schemes: “weights 1” in the figure denotes the wighting scheme from the reference, where the charges on all hydrogen atoms are weighted by a factor 10, while for “weights 2”, all non-hydrogen terminal atoms are weighted by a factor 10 and the hydrogen atoms are weighted by a factor 100. On the left side of figure 6a, the restraints are numerically insignificant and the LSS calculation fails because of the underdetermined character associated with cyclic moieties²¹; arbitrary results are produced due to numerical imprecision. For stronger restraints (~2 × 10⁻²¹ < σ < ~2 × 10⁻¹⁵ for the adaptive bias with weights 2), the RMSD rapidly reaches a plateau at an “optimal” value, while the number of zero increments increases roughly proportional to the logarithm of the bias, reflecting improvements in the relevance/transferability of the parameter vector that do not affect the quality of the fit. Figure 6b zooms in on the lower right corner, where the most desirable solutions are located. Here, a concentration of data points can be observed, reflecting the fact that a change of the bias within this region (~5 × 10⁻¹⁵ < σ < ~1 × 10⁻⁹ for the adaptive bias with weights 2) will have little effect on the solution. This demonstrates that the present method indeed is capable of finding the most desirable solution in a robust fashion. Finally, when increasing the bias beyond this range, it starts dominating the solution, causing a somewhat chaotic transition into a region where the RMSD increases steeply for a comparably small increase in the number of near-zero solutions.

Figure 6.

Charge RMSD versus the number of zero increments for the following series of bias fractions σ (or restraints b for the constant bias): 1 × 10⁻²², 2 × 10⁻²², 5 × 10⁻²², 1 × 10⁻²¹, 2 × 10⁻²¹, 5 × 10⁻²¹, …, 5 × 10⁻¹. Consecutive points in this series are connected by lines. In this context, a zero increment is defined as an increment that is rounded to zero by the rounding scheme described reference ²¹; essentially, increments on hydrogen atoms are rounded to zero if they are smaller than 0.0025 e in absolute value, while increments involving only nonhydrogen atoms need to be smaller than 0.0005 e. As described in the reference, additional rounding is performed on select parameters, but this is of little consequence to the relative locations of the points. Figure 6b is a magnification of the lower right corner of figure 6a.

Comparing the different weighting schemes, it is apparent from figure 6b that “weights 2” performs better when keeping in mind that the vertical axis has a very narrow range compared to the horizontal one. Within the same weighting scheme, the RMSD plateau is at the same location for all restraining methods, including the constant bias. Conversely, in terms of numbers of zeroes, the target-adapted bias clearly performs best for this particular application, followed by a significant margin by the “self-term only” bias, which in turn performs slightly better than the uniform and constant biases. The latter two perform similarly, except that the “desirable σ or b range” is twice as large (on a logarithmic scale) for the uniform bias. In fact, the self-term and uniform biases both feature a larger desirable range than the adaptive and constant biases. Keeping in mind that the cross-terms are required for the fitting of bonded parameters, ruling out the self-term and constant biases, this observation appears to support our previous hypothesis that the uniform bias performs slightly worse than the adaptive bias on well-behaved problems but is more robust. While the fact that the self-term performs better than the uniform bias is surprising, it should be stressed that this case study concerns a very specific niche application and serves to demonstrate the viability of the present biasing scheme’s basic principles for applications other than bonded parameter optimization, rather than providing solid conclusions regarding the relative performance of its different variants; if anything can be concluded in this respect, it is that the most optimal variant depends on the application.

5 SUMMARY

A detailed overview of the origin and nature of robustness issues in optimization problems in general and the fitting of bonded parameters in particular was presented in terms of matrices and vectors, allowing for degrees of freedom in the fitting procedure to be qualified as orthogonal, parallel or nearly parallel. It is also discussed how all the bonded parameters in a Class I force field can be fit using the Linear Least Squares (LLS) procedure. A novel restraining strategy was proposed that overcomes the robustness issues associated with doing so in a single, non-iterative LLS fit, with minimal impact on the fitted values of well-behaved parameters. It should be stressed that while this method effectively overcomes inherent robustness issues, it is no substitute for target data of sufficient quality and quantity. The methodology in question harmonically restrains the parameters so that the restraints can readily be integrated into the matrices that form the input for LLS functions in mathematical software libraries. Its novel aspect lies in a careful choice of the restraint force constants, which are calculated such that well-behaved parameters are scaled down by the restraint by an exact factor that can be applied to the output of the LLS procedure to annihilate the impact of the restrains on these well-behaved parameters. The formula (8) for determining these restraints contains terms that describe the crosstalk between the restraints on different non-orthogonal parameters. These terms in turn each contain a factor that cannot be known a priori. Two approximation strategies for these factors were presented, each with its strong and weak points. Both of these strategies were validated through a number of case studies, which also serve to establish a standard methodology for potential energy scanning and concerted fitting of bond, angle and dihedral parameters. Of special note is the inclusion of the fitting of bond-charge increments in the case studies, which illustrates the method’s potential for robustly solving general LLS problems beyond bonded parameters or even beyond force field parametrization. The fitting part of the methodology was implemented in a C program named “lsfitpar” that will be made available to the community under an open-source license alongside the necessary documentation at http://mackerell.umaryland.edu/~kenno/lsfitpar/. It is therefore hoped it will become an important part of the sprawling ecosystem of automatic parametrization interfaces. Future directions include validating the methodology for the purpose of charge fitting and extending the program’s feature set.