Simple versus complex models of trait evolution and stasis as a response to environmental change

Significance

Paleontologists have long argued about what the fossil record call tell us about how species evolve over long periods. Simple models such as stasis and random walks have been used to explore evolutionary patterns, but these have not always adequately captured the ways in which traits change over time in fossil species. Here we find that models with complex evolutionary dynamics are often favored, especially for fossil series that sample many populations, suggesting that the underlying evolutionary reality is likely more complex than represented by simplified—though still useful—models of trait change.

Abstract

Previous analyses of evolutionary patterns, or modes, in fossil lineages have focused overwhelmingly on three simple models: stasis, random walks, and directional evolution. Here we use likelihood methods to fit an expanded set of evolutionary models to a large compilation of ancestor–descendant series of populations from the fossil record. In addition to the standard three models, we assess more complex models with punctuations and shifts from one evolutionary mode to another. As in previous studies, we find that stasis is common in the fossil record, as is a strict version of stasis that entails no real evolutionary changes. Incidence of directional evolution is relatively low (13%), but higher than in previous studies because our analytical approach can more sensitively detect noisy trends. Complex evolutionary models are often favored, overwhelmingly so for sequences comprising many samples. This finding is consistent with evolutionary dynamics that are, in reality, more complex than any of the models we consider. Furthermore, the timing of shifts in evolutionary dynamics varies among traits measured from the same series. Finally, we use our empirical collection of evolutionary sequences and a long and highly resolved proxy for global climate to inform simulations in which traits adaptively track temperature changes over time. When realistically calibrated, we find that this simple model can reproduce important aspects of our paleontological results. We conclude that observed paleontological patterns, including the prevalence of stasis, need not be inconsistent with adaptive evolution, even in the face of unstable physical environments.

Paleontologists have long sought to document patterns of trait change within fossil species and to infer from these patterns their underlying evolutionary drivers (1–3). However, only recently have sufficient case studies accumulated to assess what the aggregated fossil record has to say about phenotypic evolution occurring on the 10⁵- to 10⁷-y timescales routinely captured in paleontological sequences. Several factors have contributed to this cumulative increase, including advances in geochronology that more readily permit time-calibrating evolutionary sequences, better morphometric practices for documenting trait change, and new analytical tools to examine the resulting data. Perhaps most important, however, is that paleontologists were motivated to capture many additional examples of trait evolution in fossil lineages in response to the intense debate centered around punctuated equilibrium (4–6)—the notion that species do not usually evolve gradually over long periods of time but instead emerge in a discontinuous pattern, in bursts of change associated with cladogenesis followed by longer intervals of morphological stasis.

Punctuated equilibrium proponents and critics disagreed about how best to interpret the same patterns of trait evolution, and thus early reviews (7, 8) did little to resolve the debate. Newly developed statistical approaches (9–11), particularly likelihood-based methods (12, 13), helped by providing objective means to determine which interpretations are most strongly justified by data. Method development focused on three canonical models germane to punctuated equilibrium: stasis, directional or sustained gradual change, and an intermediate model of a random walk. Two recent compilations found much more support for stasis than gradual evolution on paleontological timescales; in only 5% of cases was directional evolution the best supported model, with the remaining sequences divided almost equally between random walks and stasis (14, 15).

These compilations helped to resolve some lingering issues, but they have an important limitation in that they applied a rather restricted set of models. Stasis, random walks, and directional change are simple models in the sense that they require few parameters to specify, and also in that they each imply uniform evolutionary dynamics within fossil sequences (16). When a sequence is modeled as a directional trend, for example, it is assumed that the trend holds with the same strength over the entire temporal span of measured fossil populations. Paleontologists have long explored explanations that violate this kind of uniformity (10, 17, 18), and several have warned of the limitations of trying to coerce a broad variety of evolutionary phenomena into a few, too-simplified models (16, 19–21).

Here we present a database of case studies of trait evolution compiled from the published paleontological literature that expands upon recent efforts (14, 15) to total 709 sequences of trait evolution from nearly 200 different lineages. Our main goal is to examine evolutionary patterns by fitting these sequences to a wider set of models including ones with complex (nonuniform) evolutionary dynamics. We consider models with punctuated change (16), as well as those characterized by a shift from one evolutionary mode to another (e.g., directional change followed by stasis). Including such mode-shift models should result in a fairer test of the frequency of directional evolution because this strategy can recognize directionality that occurs but does not persist throughout an entire time-series. Compared with previous compilations, we also use a different algorithmic approach that is better able to detect noisy trends when they are present (22). Taken together, our procedures should increase the sensitivity with which directional evolution can be recognized.

One previous finding that we confirm here is that stasis is common in fossil sequences. Paradoxically, stasis prevails even though rapid evolutionary shifts are well documented within living populations and geological proxies suggest a continually dynamic environmental milieu (23, 24). For some paleontologists, this paradox is inconsistent with neo-Darwinian interpretations of stasis that emphasize stabilizing selection and trait adaptedness (25–27). We explore this suggestion by comparing our empirical results with evolutionary series simulated under a scenario in which traits adaptively track environmental change, using a long-term and highly resolved climate record as a proxy. The goal of these simulations is to test whether this simple environmental/adaptive model, when calibrated realistically, is able to reproduce pertinent aspects of the empirical fossil record.

Results

The compiled stratigraphic sequences range in length from 7 to 114 samples (median, 14) and in duration from 5 ky to more than 50 My, with most between 100 ky and 10 My (SI Appendix, Fig. S1). As in our previous quantitative analyses, purely directional evolution is rarely (9%) the best-supported model, although this total increases to 13% when all models with a directional component are combined (Table 1). Random walks (28%) and stasis (38%) are common, with nearly half of the latter category best accounted for by a strict version of stasis that implies no true evolutionary differences among samples in a sequence. These percentages are even higher when complex models that feature these models in part are included: 39.4% of best-supported models include a random walk, and 62.9% include stasis. In total, 175 sequences are best described by one of the complex evolutionary models; punctuations and shifts from a random walk to stasis are particularly well represented (Table 1). This tally represents 25% of sequences overall but 45% of those long enough (≥14 samples) to be fit by complex models.

Table 1.

Frequency with which each model is the best supported

Model category	Model	Frequency	Percentage
Simple	Strict stasis (1)	124	17
	Stasis (2)	147	21
	Random walk (2)	201	28
	Directional (3)	62	9
Complex	Punctuation (4)	67	9
	Stasis-RW (4)	19	3
	Stasis-Dir (5)	16	2
	RW-Stasis (5)	59	8
	Dir-Stasis (6)	14	2

Models are listed in order of increasing numbers of parameters (in parentheses). Complex models imply nonuniform dynamics, either as a punctuation or a shift in evolutionary mode within a sequence. RW, random walk; Dir, directional evolution.

Complex models tend to receive increasing support as sequences include more and more samples (Fig. 1). For example, 94% of sequences (58 of 62) with >40 samples are best supported by a model that implies complex evolutionary dynamics. The small-sample modified Akaike Information Criterion (AICc) has some tendency to overfit in this context (Methods); to address this potential bias in favor of complex models, we also implemented a more stringent parametric bootstrapping test. Results indicate that complex models favored by AICc are usually also significantly better than the best simple model according to the bootstrap test (Fig. 1).

Fig. 1.

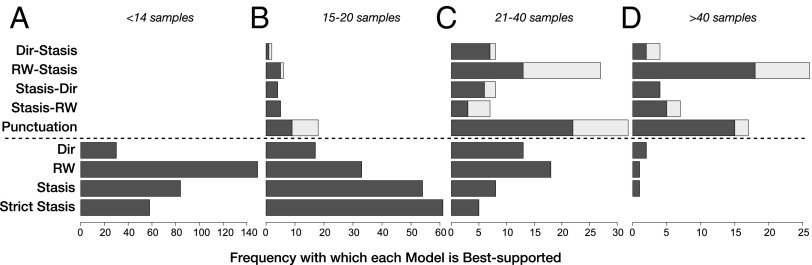
Frequencies with which each model is best supported with sequences divided into four categories on the basis of sequence length: (A) sequences with fewer than 14 samples (n = 321), (B) with 14–20 samples (n = 200), (C) with 21–40 samples (n = 126), and (D) >40 samples (n = 62). Models are listed in order of increasing numbers of parameters from bottom to top, with the dotted horizontal line separating the simple (uniform) models below from the complex (nonuniform) models above. Model names follow Table 1. Total bars indicate models favored by AICc; dark gray represent portion in which a complex model is also significantly favored by a more conservative parametric bootstrapping test.

Several factors contribute to the propensity for different models to be favored (Table 2). Strict stasis is less probable with increasing temporal duration of sequences, and the broad version of stasis is also less likely to be best supported as the number of samples increases. Both kinds of stasis are more prevalent in marine compared with terrestrial or lacustrine environments, and in macroinvertebrates and vertebrates compared with microfossils (SI Appendix, Tables S1 and S2). Purely directional evolution is more likely to be favored in sequences of longer temporal duration (Table 2), but strong correlates of directionality are not evident otherwise (SI Appendix, Table S3). Complex models are substantially more likely to be favored with increasing numbers of samples, but not with increasing temporal duration (Table 2); this class of model is also less prevalent among benthic microfossil sequences (SI Appendix, Table S4). In addition, age model error that is caused by undetected variation in sedimentation rate has a tendency to spuriously favor complex evolutionary models, but the effect is not large enough to account for these patterns (SI Appendix, SI Text).

Table 2.

Factors that predict whether certain models are the best supported

Model(s)	Retained variables in logistic regression
Strict stasis	dur (−), env, taxon
Strict stasis + stasis	ns (−), dur (−), env, taxon
Directional	dur (+), taxon
Complex*	ns (+), env, taxon

Right column summarizes the multiple logistic regression model retained from a stepwise AIC procedure. The independent variables are sequence length (number of samples, ns), sequence temporal duration (dur), and broad categories for the environment (env) and fossil taxon (taxon). A positive sign after ns and dur indicates that an increase in that independent variable increases the probability of favoring that model.

^*Regression performed only for those sequences with 14 or more samples (n = 388) because complex models were only fit for these sequences.

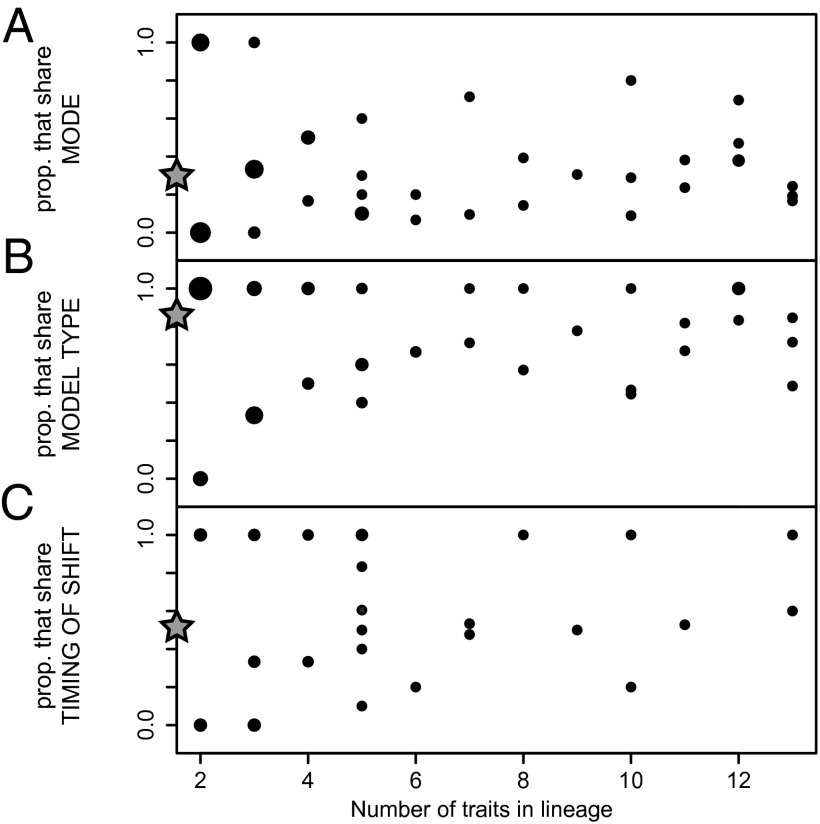
Rarely do all traits within a species lineage show the same evolutionary mode, although pairwise comparison of traits within species lineages shows that modes may be shared among a few or the majority of traits (Fig. 2A). It is, however, very common for traits within a species lineage to show the same type of evolutionary model (either simple or complex; Fig. 2B). The timings of mode shifts among traits best fit by complex models are coordinated as frequently as they are not (Fig. 2C).

Fig. 2.

Coordination of results among traits within species lineages in which more than one trait was measured. Proportion of pairwise comparisons in which (A) the specific model of evolutionary mode is shared, (B) the type of evolutionary mode (either simple or complex; Methods) is shared, and (C) the timing of the mode shift is shared (for comparisons in which both traits are best accounted for by a complex model). Size of points corresponds to the relative number of comparisons at those coordinates. Stars on y axes represent median values.

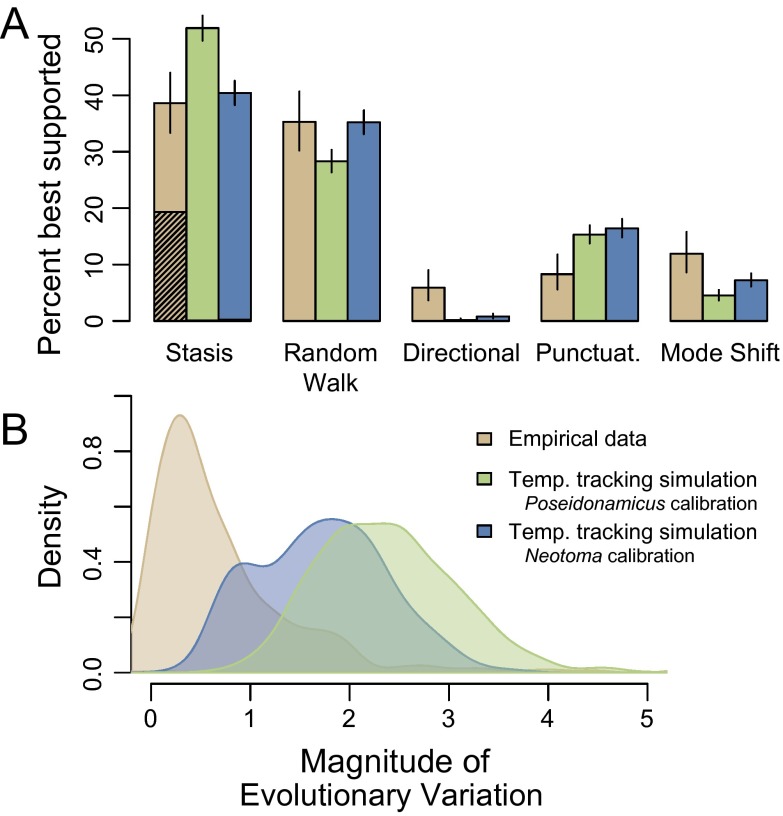
When simulated evolutionary sequences are generated according to a model in which traits track a long-term global climate curve (Fig. 3), these artificial sequences match patterns found in empirical paleontological data in several important ways. The overall distribution of how often each model is best supported is remarkably similar between simulated and real data sets (Fig. 4A). Both simulated and empirical data are most often accounted for by stasis, followed closely by the random walk model. Directional evolution is rare in the empirical data and even more so in the simulated datasets. In both real and simulated data, punctuations and mode-shift models are best supported in approximately 20% of sequences. The temperature-tracking model was calibrated with two empirical examples of a trait, body size, showing temperature-dependences among living and fossil populations. Both of these calibrations produce similar results.

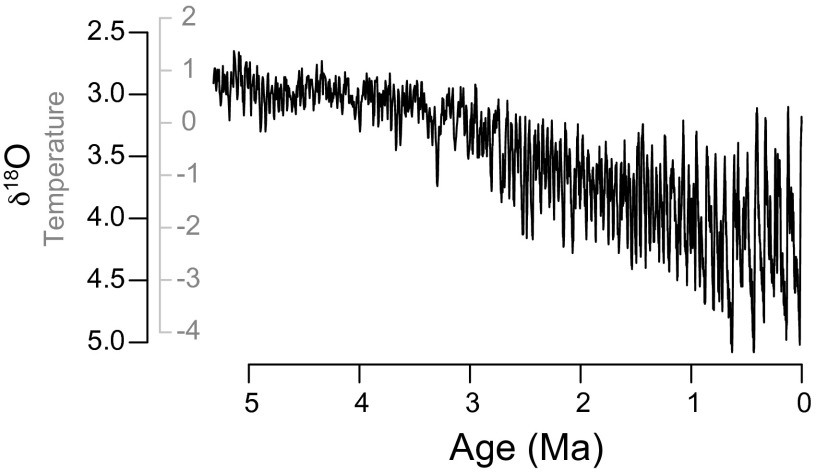
Fig. 3.

Composite deep-sea oxygen isotope curve (50) showing fluctuations in global climate over the past 5.32 My. Original isotopic scale (black axis) was scaled to temperature (gray axis) as described in Methods, expressed as °C deviations from the present day. The temperature version of this curve was used to simulate trait evolution that tracks temperature.

Fig. 4.

Comparison of temperature-tracking simulations to empirical results. (A) Best-fitting models for simulations in which trait evolution tracks temperature compared with that for the subset of empirical sequences (n = 337) of the appropriate duration and resolution to be compared with the global temperature curve. The empirical results are in tan next to two different calibrations of the temperature-tracking model: for the deep-sea ostracode P. major (green) and the packrat N. cinerea (blue). Bar heights indicate the proportion of empirical or simulated outcomes (2,000 replications) that resulted in that model or set of models being best supported according to AICc. Stasis includes the broad sense model and strict stasis, with the contribution of the latter shown as hatching (too limited to see in the simulated datasets). Mode shift includes the four models involving a shift from stasis to a random walk or directional change, or vice versa. Black lines at the top of the bars span 95% binomial confidence limits on the proportions. (B) Density plots showing the distribution of magnitudes of evolutionary change across empirical and simulated data sets. Evolutionary variation was measured as the SD of sample means, with the contribution of sampling error removed (Methods).

The strict version of stasis is common in the empirical data but rare in the simulations (Fig. 4A). Indeed, compared with the distribution from the simulated sequences, evolutionary changes are generally smaller in magnitude in the empirical dataset (Fig. 4B).

Discussion

Our expanded survey is consistent with its predecessors in finding that stasis and random walk modes are prevalent in paleontological sequences, and in suggesting that sustained directional evolution is infrequently observed. The total incidence of directionality, 13%, is higher compared with the 5% found in previous studies (14, 15). Part of this increase comes from allowing mode-shift models in which directional change operates for only a portion of the observational window; the remainder stems from a methodological shift from restricted maximum likelihood (REML) to a more sensitive maximum-likelihood approach. Analyzing the present data using REML does result in lower frequencies of directional change, but the distribution of winning models is otherwise very similar (SI Appendix, Table S5). Although we favor the directional mode more so than in previous studies, our 13% figure is likely an overestimate because the published literature that we summarize has disproportionately analyzed traits and lineages for which prior evidence exists for directional patterns of trait change (27, 28).

Previous indications that directional trends are more likely to be observed in planktonic microfossils than in other fossil groups (14, 29, 30) are not supported by logistic regression (SI Appendix, Table S3). Similarly, the raw proportion of sequences best fit by directional models is not very different among planktonic microfossils (15.3%), benthic microfossils (19.8%), and vertebrates (14.2%). This proportion is notably lower among macroinvertebrates (7.8%), but this figure may be depressed by two studies (31, 32) that included numerous traits in which stasis dominated.

The propensity of complex models to be favored increases strongly with the number of samples in a sequence. If, in reality, mode shifts or punctuations occur at some rate per unit time, sequences observed over longer temporal windows also should be more likely to exhibit complex dynamics, but this is not evident in our compilation (Table 2). One way to reconcile this finding is to posit that the evolutionary reality that we seek to characterize is usually more complicated than even the most complex models we are likely to entertain. If this were true, duration would not matter because the underlying reality of even short temporal intervals is complex. Instead, the ability of complex models to win is limited only by the information content of a sequence, and therefore its number of samples. Regardless of how complex evolutionary patterns truly are, simple models are still useful as tools for extracting first-order information about the nature (22) and pace (33) of evolutionary divergence, as long as one is mindful of their limitations.

The variation in the timing of shifts in evolutionary dynamics emphasizes the mosaic nature of evolution documented here and elsewhere (15). Although trait evolution may be tightly correlated within a lineage (e.g., SI Appendix, Fig. S2), traits that show the same mode of evolution can still vary in the timing of shifts, and vice versa (e.g., SI Appendix, Figs. S3 and S4), and in some cases there may be no similarity at all (e.g., SI Appendix, Fig. S5). The extent to which evolutionary coordination among traits depends on internal biotic factors (e.g., the degree of integration among traits) versus external pressures (e.g., shared sensitivity to changes in some aspect of the environment) cannot be determined from these data alone. The increasing support for complex models with increasing sequence length may partly account for the tendency for all measured traits within a species lineage to share simple or complex dynamics (Fig. 2B), if not the specific mode (Fig. 2A), because trait time-series measured from the same evolutionary sequence usually have the same number of samples. The same effect may contribute to the similar breakdown of simple versus complex in the empirical data and the climate tracking simulations (Fig. 4A).

Evolutionary sequences simulated under a simple temperature-tracking model provide a surprisingly close match to the empirical distribution of winning evolutionary models (Fig. 4A). Contrary to previous suggestions (25–27), it seems that stasis can be an expected outcome even in the face of dynamic environmental change. Two keys can help to make sense of this result. First, although we develop here a strict version of stasis that implies constancy of form, the broader notion of evolutionary stasis only holds that changes are modest and fluctuating rather than accumulating (23, 27). Thus, evolutionary changes in response to changing environments can be consistent with stasis, as long as environments do not change in an accumulating manner. Second, the temporal structure of climate, at least as measured from our proxy curve, is dominated by fluctuations that are short (100 ky or less) compared with durations of species in our compilation. Although it is true that temperature shows dramatic swings, this variation is strongly bounded by glacial–interglacial limits. Accordingly, most traits that track temperature will also show a bounded, fluctuating pattern that we recognize as stasis.

Our proxy for environmental change is particularly useful here because its exceptional duration and resolution permit realistic evolutionary modeling. In addition, it reflects temperature and correlated environmental variables with clear biological relevance. However, it is still just one proxy climate curve whose magnitudes and frequencies pertain most clearly to the late Cenozoic icehouse world. Its boundedness, however, may apply to other important drivers, such as sea-level fluctuations, or rainfall and seasonality in terrestrial environments. In each of these examples natural limits are reached at both ends of an environmental continuum. These limits can be reached and returned to repeatedly over species’ lifetimes. We suspect that such bounded patterns in environmental proxies are the norm. Characterizing the mode of evolution in response to additional environmental proxies may be important for understanding how physical drivers may broadly influence biological evolution (34).

The main difference in outcomes between the temperature-tracking simulations and the empirical data are that the simulations produce larger evolutionary changes and correspondingly fewer instances of strict stasis. This difference is predictable in that we have only calibrated the model with examples in which body size systematically varies with temperature (Bergmann’s rule). Temperature sensitivity is common for body size (35, 36), but it is not universal, and traits that do not show temperature-related geographic variation are not expected to change particularly when climate does. Moreover, body size is seen as a relatively labile trait, and so it may exhibit ample variation unrelated to temperature, which translates to high residual variance in our model. If we added low-variation and temperature-insensitive traits to these simulations, it would depress the magnitudes of evolutionary change and bring the simulations and empirical data closer into alignment. Nevertheless, we emphasize that we do not view this environmental tracking model as a universal explanation for evolutionary patterns in fossil lineages; metapopulation structure (23, 25), habitat tracking (37), and other processes (38–43) are undoubtedly also important. Rather, we use this model to argue against the suggestion that the paleontological record is inconsistent with well-adapted traits responding to dynamic physical environments.

Recently, Uyeda et al. (40) used a large database of evolutionary changes in body size to demonstrate that differences spanning less than 1 My varied within a bounded interval but that magnitudes of change increased markedly with time beyond this threshold. Their explanation for this pattern combined stasis over short timescales with longer-term accumulation of stochastic jumps resulting from rare shifts in the species’ niches or adaptive zones (2). This account involves two models considered here, stasis and punctuations, and their interpretation implies that the latter should dominate over longer intervals. The Uyeda et al. approach does not include random walks, directional change, or mode-shift models but, from an appropriately broad perspective, there are several ways in which these two analyses are compatible. Our logistic regressions (Table 2) show that the probability of stasis decreases with increasing temporal duration, which is consistent with Uyeda et al.’s finding that bounded evolutionary changes dominate over durations shorter than 1 My. Moreover, the temperature tracking simulations provide a possible microevolutionary mechanism that could account for the bounded component of their model. Finally, we unexpectedly found that the temperature-tracking model can reproduce Uyeda et al.’s marked uptick in evolutionary divergence at ∼1 My (SI Appendix, Fig. S6). This uptick occurs because a long-term trend of intensifying icehouse conditions is slow enough that it exceeds glacial–interglacial fluctuations only after one to several million years of accumulated change. Thus, in addition to breakthroughs in species’ adaptive zones, it is possible for environmental variation to be structured such that it imparts a pattern of bounded change that transitions to one of unconstrained divergence.

Methods

Data Compilation.

We compiled published paleontological studies that track through time one or more measured traits from (in the opinion of the original authors) a single, species-level lineage. We included slightly revised (SI Appendix, SI Text) versions of two recent compilations of time-series (also referred to as “sequences”) of trait evolution from fossil lineages (14, 15) and added additional cases from the literature. Additional data were obtained from published tables or appendixes, by digitizing published figures, or from raw data provided by the authors. Age models were taken from the original publications, if available, or from other references. A summary table of all included sequences is available in Dataset S1, and the raw data have been accessioned into the Dryad data repository (10.5061/dryad.m010p).

Evolutionary Models.

We followed previous treatments of the three canonical models of evolutionary mode (13, 14). Trait increments in the random walk model are independent and equally likely to be increases or decreases. This model is characterized by a parameter, the step variance, that determines the size of the steps and hence the evolutionary rate (33). Directional evolution is a generalization of this process to allow for evolutionary steps that are biased toward increases or decreases. Stasis was modeled as uncorrelated (white noise) variation around a steady mean (44). We also considered a special case of stasis with zero variance around the long-term mean, which we call “strict stasis” because it represents stasis in its narrowest sense of implying no real evolutionary variation in a trait.

In addition to the above four uniform models, we explored a set of models that allowed evolutionary mode to shift once within a sequence, dividing it into two segments with different evolutionary dynamics. These include classic punctuations, in which stasis around one mean instantaneously shifts to stasis around a different mean (16), and four mode-shift models that start in stasis but then shift to directional evolution or a random walk, or vice versa. In total, we considered four simple models (directional evolution, random walk, stasis, and strict stasis) and five complex ones (punctuation, stasis–random walk, stasis–directional, random walk–stasis, directional–stasis). SI Appendix, SI Text discusses further the properties of these models.

Because evolutionary mode cannot be determined robustly from short sequences (16), we required that each segment contain at least seven samples. As a result, complex models were fit only to sequences comprising 14 or more samples. The shift point in punctuational and mode-shift models was estimated as a free parameter, following ref. (16).

Models were fit in the R environment (45), using functions from the paleoTS package, version 0.4-5 (46). Previous analyses used a restricted maximum-likelihood approach that divides a sequence into adjacent, ancestor-to-descendant trait differences, which are evaluated by a likelihood function. Here we use a full maximum-likelihood approach that considers all samples in a sequence jointly as a single draw from a multivariate normal distribution (22). In the paleoTS package, these two options are implemented as the “AD” and “Joint” methods, and simulations show that they perform similarly in most respects (22), except that the “Joint” approach that we use here is better able to detect noisy trends (22).

Model support was measured using AICc. Simulations suggest that AICc may unduly favor complex models in this context, even when simple models are true (SI Appendix, Fig. S7); this effect seems especially pronounced for models that involve a shift to a new stasis mean (punctuations, random walk–stasis, and directional–stasis). Accordingly, for sequences best fit by any complex model, we implemented an additional, more stringent test via parametric bootstrapping (47). This approach simulates trait evolution under the best-supported simple model and then fits that (true) model in addition to the best-supported complex model. The difference in support was measured as the likelihood ratio test statistic, which is equal to twice the difference in log-likelihood between simple and complex models. This process was repeated over 499 replicates to generate a null distribution of the likelihood ratio statistic, with the P value computed as (k + 1)/500, where k is the number of replicates in which the likelihood ratio statistics exceeded the observed value (48).

Logistic regressions were performed to test whether the probability of a sequence being best supported by a particular model or set of models was related to sequence length (number of samples, log-transformed), sequence duration (log-transformed), broad categories of environment (terrestrial, lacustrine, marine-shallow, marine-deep, marine-pelagic), and categories of fossils (planktonic microfossils, benthic microfossils, invertebrate macrofossils, vertebrates). Stepwise AIC was used to choose among regression models, which were run separately to predict the probability of strict stasis, any kind of stasis, directional evolution, and any complex model. Regressions were performed using the glm and stepAIC functions in R, and the glht function from the multcomp package (49) was used to test for post hoc differences among the environmental and taxon categories. Because individual lineages often supplied multiple, potentially correlated traits, sequences are not truly independent and thus these regressions are best considered heuristic (mean pairwise absolute correlation between changes in trait means measured from the same series: 0.403, SD = 0.280).

Coordination of Results Among Traits Within Species Lineages.

For every species lineage for which more than one trait was measured (n = 71), we tallied how frequently pairs of traits showed (i) the same best-fit model of evolutionary mode; (ii) the same type of evolutionary mode (simple or complex); and (iii) the same timing of shifts in evolutionary dynamics, if both traits were best characterized by a complex mode of evolution. We considered all shift points within 1.92 log-likelihood units of the maximum-likelihood solution when comparing pairs of traits. This set of shift points represents all of the solutions within a 95% confidence interval (16).

Simulating Trait Evolution That Tracks Environmental Change.

Simulating a scenario in which traits evolve in response to changing environmental conditions requires (i) a proxy curve capturing temporal change in an environmental variable, (ii) a model and calibration that determines the sensitivity of traits to environmental change, and (iii) realistic sample sizes and chronologies for evolutionary sequences.

We used as our proxy for environmental change a composite curve of deep-sea oxygen isotope values (50) that is commonly used as a surrogate for overall climate state (Fig. 3). This curve is particularly suitable because it is of long duration (5.32 My) and fine temporal resolution (successive points separated by 1–5 ky). Moreover, this curve mostly reflects an aspect of the environment—temperature—that commonly covaries with biological traits. To better relate this curve to traits, we converted it from its original isotopic units to degrees Celsius by scaling it so that the difference between the present day and the last glacial maximum (19–23 K_a) is 4 °C, which is a reasonable global estimate (51).

The temperature-tracking model assumes a simple linear relationship between temperature and trait values: x = b₀ + b₁T + e, where x is the trait, b₀ and b₁ are the intercept and slope of its relationship with temperature (T), and e is a normally distributed residual term. The sensitivity of the trait to temperature is given by b1. Evolutionary changes that are unrelated to temperature are represented by the variance of e. This relationship is consistent with populations adaptively tracking changes in temperature, assuming a response lag that is negligible on paleontological timescales (see refs. 52 and 53). We calibrated this model using empirical examples of Bergmann’s rule, the pattern by which body size tends to be larger in colder parts of a taxon’s geographic range (54). We use two different calibrations based on taxa for which this relationship has been demonstrated in the modern world and in the fossil record: the deep-sea ostracode Poseidonamicus and the packrat Neotoma. The Poseidonamicus regression considered the log of carapace length among modern populations from the species Poseidonamicus major (55). Published body mass versus temperature relationships for Neotoma cinerea were digitized from Smith and Betancourt (56). The resulting body mass data were cube-root transformed to behave similarly to linear size measurements, log-transformed, and regressed against temperature. These particular calibrations bracket a range of Bergmann’s rule patterns from strong in Poseidonamicus to moderate in Neotoma (SI Appendix, Fig. S8).

To simulate sequences with realistic chronologies and sample sizes, we drew randomly with replacement from the subset of the empirical sequences that were of appropriate duration (<3 My) and resolution (>10 ky) to be compared with the climate curve (n = 337). Each sampled chronology was placed randomly within the temporal span of the temperature curve, and the temperatures at that chronology’s sampling times were computed by linear interpolation. From these temperature data, trait values were generated with the formula above using the values from either the Poseidonamicus or Neotoma calibrations. These generated sequences reflect true population means, to which sampling error was added as normally distributed variation with a mean of zero and a variance of s²/n, where s² is the within-population variance and n is the sample size taken from the selected empirical sequence. For Poseidonamicus, the data from reference 55 estimate s² as 0.000467, whereas 0.0025 was used for Neotoma because this corresponds to a coefficient of variation of 5, which is a typical value for linear size dimensions in mammals (57). In this manner, 2,000 evolutionary sequences were generated, each consistent with the assumed model of temperature tracking, but with empirically realistic sample ages and sample sizes.

These simulated sequences were compared with the relevant empirical sequences according to how frequently each of the models was best supported. In addition, we compared simulated versus empirical distributions of magnitudes of evolutionary variation, measured as the square root of the stasis variance parameter. This parameter is essentially equal to the SD of trait values across samples with the contribution of sampling error removed (33). We also tracked how this evolutionary variation accrued over time under this model.