Stoichiometric control of DNA-grafted colloid self-assembly

Significance

Recently, there has been an increased interest in understanding the self-assembly of DNA-grafted colloids into different morphologies. Conventional approaches assume that the critical design parameters are the size and number of DNA grafts on each particle. Stoichiometry is viewed as a secondary variable and its exact role in this context is unresolved. In contrast with these expectations, our experiments show that the equilibrium lattice structure can be tuned through variations in the imposed stoichiometry. These findings are captured through simple extensions of the complementary contact model. Stoichiometry is thus shown to be a powerful handle to control these self-assembled structures.

Abstract

There has been considerable interest in understanding the self-assembly of DNA-grafted nanoparticles into different crystal structures, e.g., CsCl, AlB₂, and Cr₃Si. Although there are important exceptions, a generally accepted view is that the right stoichiometry of the two building block colloids needs to be mixed to form the desired crystal structure. To incisively probe this issue, we combine experiments and theory on a series of DNA-grafted nanoparticles at varying stoichiometries, including noninteger values. We show that stoichiometry can couple with the geometries of the building blocks to tune the resulting equilibrium crystal morphology. As a concrete example, a stoichiometric ratio of 3:1 typically results in the Cr₃Si structure. However, AlB₂ can form when appropriate building blocks are used so that the AlB₂ standard-state free energy is low enough to overcome the entropic preference for Cr₃Si. These situations can also lead to an undesirable phase coexistence between crystal polymorphs. Thus, whereas stoichiometry can be a powerful handle for direct control of lattice formation, care must be taken in its design and selection to avoid polymorph coexistence.

Over the past several decades, there has been increasing interest in programmable self-assembly for materials fabrication. Rather than using traditional methods of shaping bulk materials, the emerging concept is to focus on the design of nanoscale building blocks that self-organize into desired structures. This “design” philosophy has led to the development of novel techniques such as DNA origami, where specific interactions are used to direct the folding of oligonucleotides into a variety of assemblies (1–6). Another vein of research is to focus on the directed assembly of DNA-grafted nanoparticles (DNA-NPs) into superlattices with well-defined crystal morphologies. These systems have unusual photonic and plasmonic properties with applications in spectroscopy, surface imaging, and optical sensors (7, 8).

A large number of theories and simulations have been developed to delineate the hybridization interactions between two interacting DNA-NPs (9–20). Despite the success of these theories in providing insights into the ground-state free energy, they are generally limited to enumerating interactions at the two-particle level. They also ignore any entropic effects relevant to this self-assembly process (9–12, 17–21). Molecular dynamics simulations avoid these difficulties and extend this analysis to superlattice self-assembly so as to provide a detailed understanding of the effects of kinetics (13), DNA sequence (14), and electrostatics (15, 16, 22) on lattice stability. We particularly highlight the work of Li et al. (16), who explicitly considered the role of stoichiometry on the crystal morphology formed. They selected several stoichiometries, i.e., 1:1, 2:1, and 3:1. We focus here on one specific case, 2:1. As the size and linker ratios of the colloids are varied, the only structures formed are ${\text{AlB}}_2$ or an amorphous entity. Here, the linker and size ratios are defined as the ratio of the number of grafted DNA linkers and of the hydrodynamic radii of the complementary particles in the system, respectively. This result reinforces the commonly held view that the desired crystal will only form if the right stoichiometry is used.

Similarly, several coarse-grained models also allow for the rapid determination of the crystal structure formed by binary mixtures of DNA-grafted colloids (23–25). The complementary contact model (CCM) is a canonical example of such a coarse-grained description (23). Inspired by experiments, this theory assumes that only attractive energetics (derived from DNA base pairing) determine the standard-state free energy. Thus, the CCM ignores any repulsive interactions. With this ansatz, the model further assumes that any DNA linkers that are within the overlap area between two DNA-NPs hybridize with any available complementary linkers. This reduces the complex many-particle interaction problem to a simple binary NP problem. The ground-state morphology is found by first assuming a variety of known crystal structures. Because each morphology defines the number of nearest neighbors that a given NP can interact with, we can calculate the lattice energy and from there locate the global energy minimum. This coarse-graining approach is able to successfully predict the regimes of phase space where four experimentally observed lattice structures, i.e., $\text{CsCl}$, ${\text{AlB}}_2$, ${\text{Cr}}_3\text{Si}$, and ${\text{Cs}}_6{\text{C}}_{60}$, form.

Results and Discussion

Repulsion and an Effective Interaction Parameter.

Despite its successes, the CCM still has several deficiencies that need to be addressed. As Srinivasan et al. (26) noted, this model does not take into account entropic repulsions due to the chain compression of noncomplementary DNA strands (that cannot base-pair). In the original CCM, the definition of the nearest neighbor(s) is the shortest distance to the colloid with cDNA strands. Thus, any potential shorter distance noncomplementary interactions are ignored. For simple structures such as a body-centered cubic or a simple cubic lattice, this definition does not ignore any nearest-neighbor noncomplementary interactions. In the case of more complicated structures, such as the face-centered cubic or the ${\text{AlB}}_2$ structure, this generalization fails. Consider the ${\text{AlB}}_2$ structure. Based on CCM assumptions, the first nearest-neighbor interaction shell for the B colloids would contain six Al colloids. However, there exists a closer inner shell containing three noncomplementary B colloids that are ignored by the CCM. This inner shell provides repulsive interactions that make the ${\text{AlB}}_2$ lattice energetically less stable relative to the current version of the CCM (SI Appendix D).

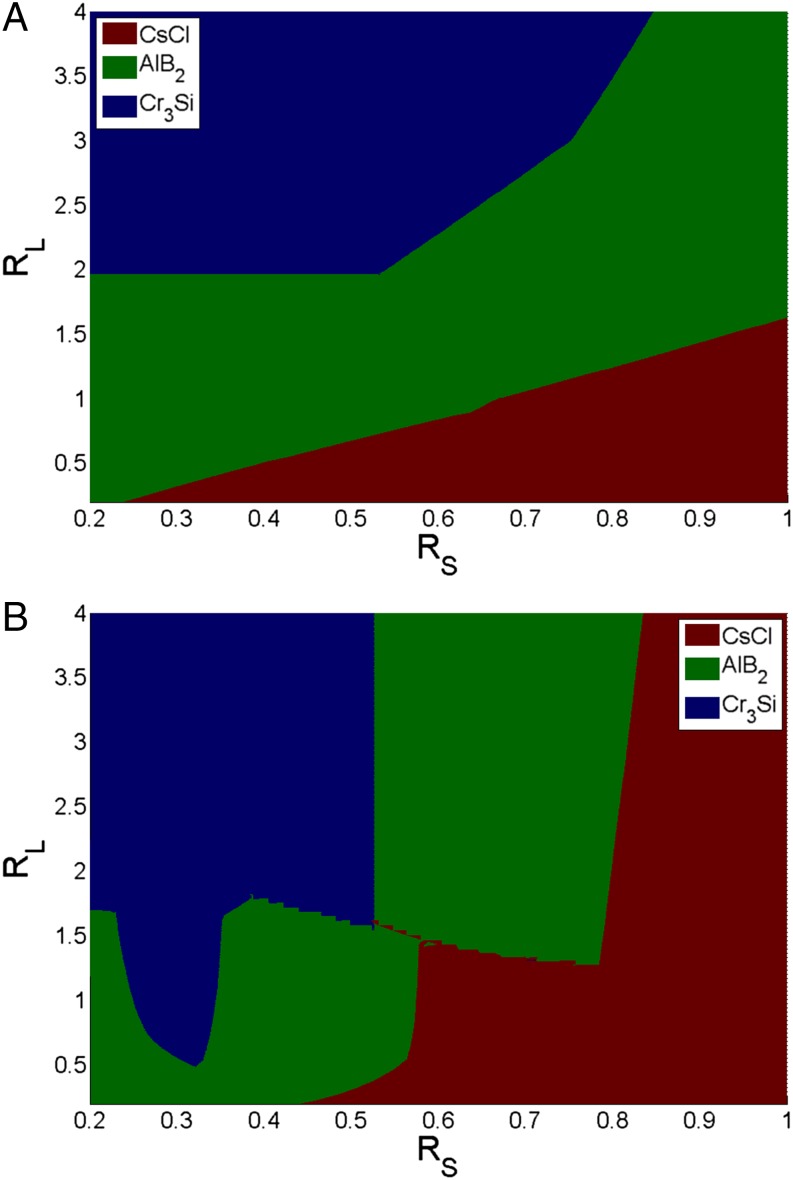
To incorporate this effect we must extend the CCM to consider both complementary and noncomplementary interactions. Again, consider ${\text{AlB}}_2$. The simplest approach would be to redefine the Al layer as the second interaction shell. Because the CCM only considers nearest-neighbor interactions, this shift would place the Al atoms outside the interaction range of the central B atom. The model would thus predict no attractive interactions and hence no crystal formation. To remedy this problem and to account for both the repulsive and attractive interactions self-consistently, we introduce a scaling argument for the number of Al nearest neighbors. That is, we “shift” the Al particles such that they are the same distance away from the central B particle as the inner repulsive B particle shell. This shift is accompanied by a “reduction” in the total number of interacting Al particles, so that the Al particles in this shell still attain the same solid angle at the central B colloid as in the unshifted analog. This procedure ensures that the total Al–B attractions are unaffected by rescaling. Thus, we define the effective number of complementary nearest neighbors as $N{N}_{ij,eff}={\alpha }^{2}N{N}_{ij}$, where $N{N}_{ij}$ indicates the number of nearest-neighbor $ij$ pairs in the unshifted case. α is a scaling factor that is purely defined by the ratio of the $i-j$ crystallographic distance from its original to its “rescaled” value. For ${\text{AlB}}_2$ and ${\text{Cr}}_3\text{Si}$, $\alpha =$ 0.729 and 0.894, respectively. With this ansatz, the (free) energy of the system becomes $F=-L_{total}D\sigma +L_{free}$, where σ is the ratio of the attractive energy gain to repulsive energy lost per pair, D is the percent of DNAs that are duplexed (derived from the original CCM), $L_{total}$ is the total number of DNA strands on the particle, and $L_{free}$ is the number of free, unpaired linkers per particle in the unit cell. Whereas the exact value of σ can vary depending on the types of DNA bases used and length of the interacting linkers, its typical range is 5–10. Sensitivity tests performed for varying values of σ in this range do not change model predictions. As Fig. 1 shows, the addition of repulsive interactions causes significant changes to the predicted morphology diagram. The most significant change relative to the Macfarlane predictions is a clear increase in the “area” occupied by the CsCl structure and a significant reduction in the ${\text{AlB}}_2$ regime. This clearly follows from the destabilization of the ${\text{AlB}}_2$ lattice by the introduction of repulsive interactions into the CCM.

Fig. 1.

CCM predictions for structures based on the minimum of the standard chemical potentials. (A) The original CCM model as presented by Macfarlane et al. (23). (B) Model predictions after the inclusion of repulsion effects.

Incorporating Stoichiometry into the CCM.

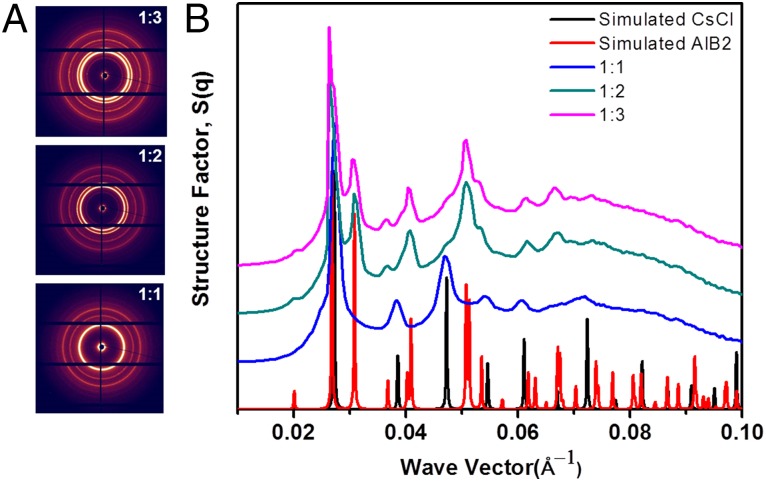
Whereas including repulsive interactions is an important change to the CCM, our focus is relaxing the assumption that only the right stoichiometric mix will yield a desired crystal lattice. To investigate the effect of stoichiometry we performed experiments where different amounts of the two types of particles were mixed (SI Appendix B). At a size ratio of 0.75 and linker ratio of 2.0, the CCM predictions for the standard-state free energies suggest that CsCl is the ground-state structure. Indeed, when we mix the two colloids in a 1:1 ratio, the CsCl lattice results (Fig. 2). For stoichiometries of 1:2 and 1:3, however, small angle X-ray scattering (SAXS) measurements suggest that the ${\text{AlB}}_2$ lattice forms preferentially (Fig. 2). These results emphasize that the crystal formed depends on the geometries of the particles and the stoichiometry. A more complete summary of our experimental findings and those of Macfarlane et al. are reported in Fig. 3 (23).

Fig. 2.

SAXS scattering results. (A) Experimental SAXS pattern for size ratio 0.75, linker ratio 2.0, and three different stoichiometries, namely 1:1, 1:2, and 1:3, respectively. (B) Structure factor S(q) derived from the SAXS pattern superimposed with simulated CsCl (black) and AlB₂ (red) traces. The traces are shifted in the y direction for clarity.

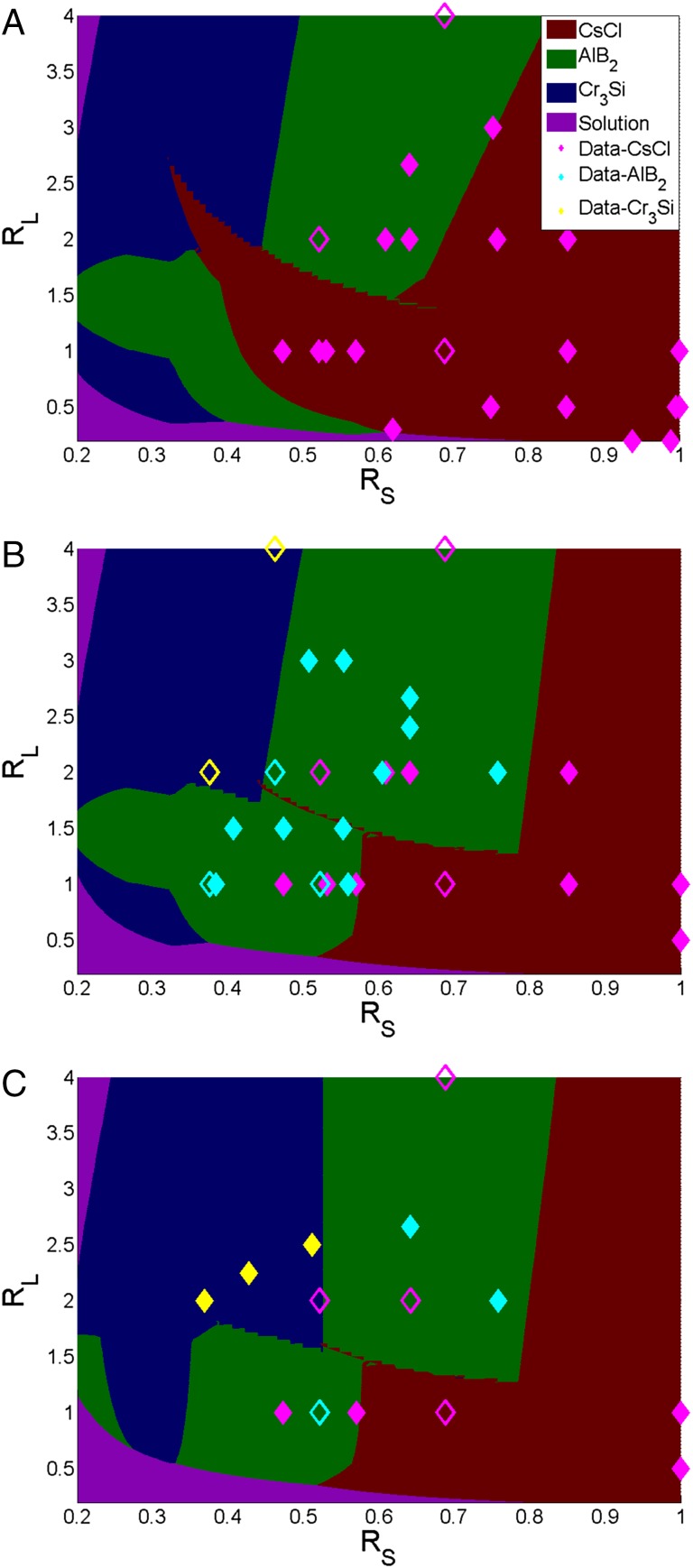
Fig. 3.

Morphology phase diagram in the $K\to \infty$ limit. Stoichiometric ratios: (A) 1:1, (B) 2:1, (C) 3:1. “Solution” implies that no crystal lattice forms. Scatter points represent experimental data: filled symbols represent pure morphology whereas open symbols represent polymorphs or disordered structures. A mixed CsCl implies that it is the dominant phase with traces of others crystals also being formed. Majority of experimental data are now correctly predicted.

To incorporate stoichiometry into the model, we cast the self-assembly process as a series of parallel chemical reactions of the form $aA+bB\rightleftharpoons cC$. Minimizing the free energy of this multireaction system under the constraints of constant T and P yields $a{\mu }_A+b{\mu }_B=c{\mu }_C$, where ${\mu }_i$ is the chemical potential of component i. We now assume that the solution of A, B, C … (including all reactants and products) is ideal. ${\chi }_i$ is the mole fraction of component i. It then follows that ${\mu }_i={\mu }_i^o+kT\hspace{0.5em}\text{ln}\left({\chi }_i\right)$. The standard-state chemical potential (or free energy) ${\mu }_i^o$ is determined from the CCM, discussed above. Experimental stoichiometry is introduced into the model through the ratio $R_N$:1, where $R_N$ is the initial number of moles of type A and 1 is the number of moles of type B. Thus, we can define a set of mole balances $R_N=N_{A,free}+{\displaystyle {\sum }_i{P}_{i,A}{N}_i}$ for component A, and $1=N_{B,free}+{\displaystyle {\sum }_i{P}_{i,B}{N}_i}$ for B, where $N_i$ is the number of moles of each particle–lattice type, $N_{i,free}$ is the number of moles of unhybridized particles, and $P_{i,A}$ and $P_{i,B}$ are the crystallographic number of particle A and B in the lattice, respectively. A hybrid genetic algorithm least-squares optimizer coupled with a branch and bound solver was developed to solve this highly nonlinear set of equations (the nonlinearity is attributed to the free energies of the reactions being so favorable that they essentially go to completion––the limiting reactant mole fraction then goes close to zero, causing singularities to appear). The results reveal $R_N$-dependent shifts in the phase boundary (Fig. 3), confirming the role of stoichiometry on lattice formation.

Equilibrium Analysis.

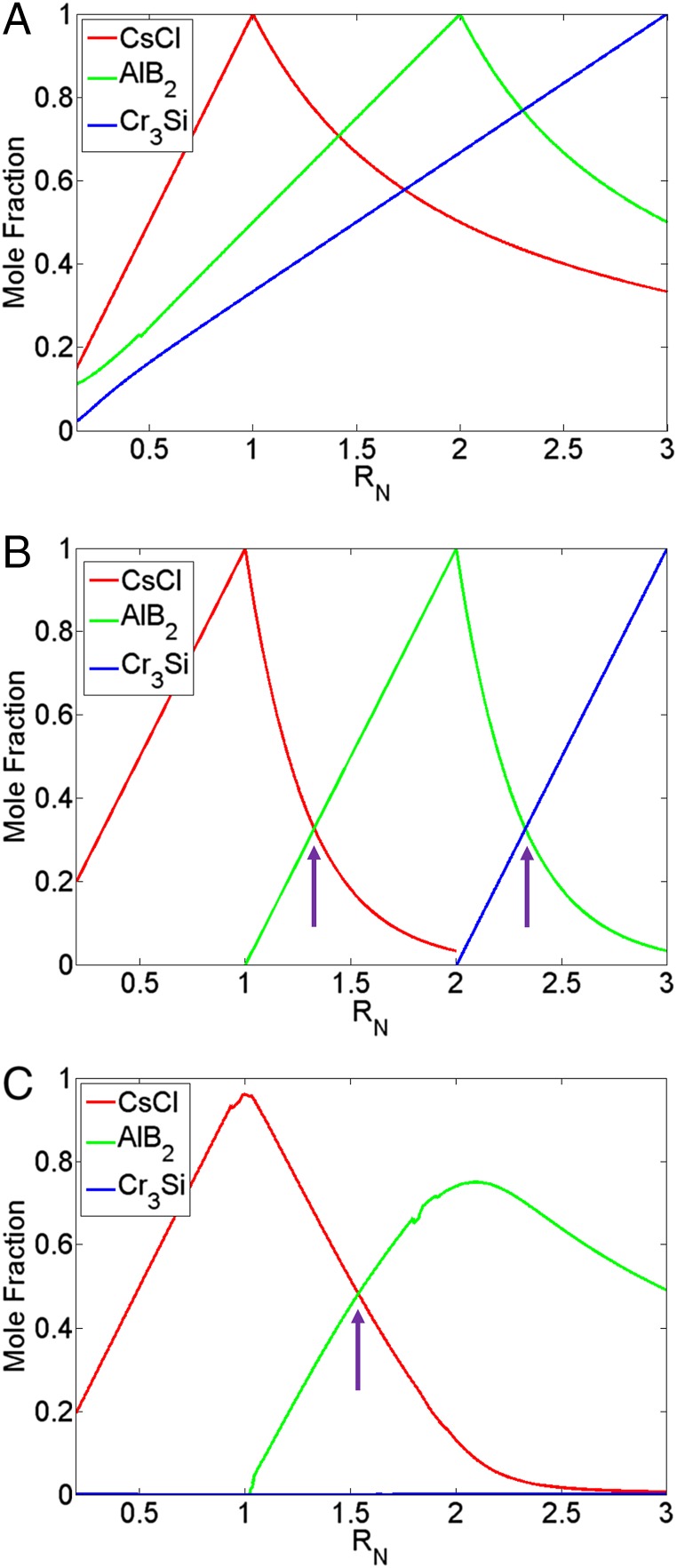
To understand the shifts in the phase boundaries with changes in stoichiometry, we start by performing an equilibrium analysis for a system of uncoupled “reactions.” First, consider the single reaction $a{\mu }_A+{\mu }_B={\mu }_C$. From thermodynamics it follows that the equilibrium constant $K=\exp \left(-{\displaystyle \sum {\nu }_i{\mu }_i^o}/\left(kT\right)\right)$, where ${\nu }_i$ is the stoichiometric coefficient of component i. Under the assumption of an ideal solution $K=N_c{\left(1+R_N-a{N}_c\right)}^a/{\left(R_N-a{N}_c\right)}^a\left(1-N_c\right)$, where $N_c$ is the number of moles of the product that forms. If we evoke the limit $K\to \infty$, it follows that the number of moles of the product is either $N_c$ = 1 (beyond $R_N=a$) or that it varies linearly as $R_N$, i.e., ${\chi }_c=R_N/a$ up until $R_N=a$ (Fig. 4A). However, a more realistic representation is to couple the three possible kinetic equations together, i.e., for CsCl, ${\text{AlB}}_2$, and ${\text{Cr}}_3\text{Si}$. This yields a system of coupled equations that follows the form

$$K_i=\frac{N_{c_i}{\left(1+R_N-{\displaystyle {\sum }_i{a}_i{N}_{c_i}}\right)}^{a_i}}{{\left(R_N-{\displaystyle {\sum }_i{a}_i{N}_{c_i}}\right)}^{a_i}\left(1-{\displaystyle {\sum }_i{N}_{c_i}}\right)}=\exp \left(\frac{-{\displaystyle \sum {\nu }_i{\mu }_i^o}}{kT}\right).$$

Fig. 4.

Dependence of lattice formation on $R_N$. (A) Uncoupled. (B) Coupled: $R_S$ = 0.5, $R_L$ = 1.65. K values: CsCl: 8.70E8, ${\text{AlB}}_2$: 1.32E9, ${\text{Cr}}_3\text{Si}$: 1.15E10. (C) Coupled: $R_S$ = 0.75, $R_L$ = 2.0. K values: CsCl: 1.16E5, ${\text{AlB}}_2$: 3.17E6, ${\text{Cr}}_3\text{Si}$: 5.60E3. Arrows in B and C indicate point of phase transition in the $K\to \infty$ limit. All plots indicate linear dependence of the mole fraction on the stoichiometric ratio up to the correct $R_N$ for the lattice. The coupled systems also reveal a direct $R_N$-dependent transition between competing structures.

Fig. 4B emphasizes the importance of coupling the kinetic systems as it reveals direct transitions between one equilibrium structure to another with changes in the stoichiometric ratio––in this case from CsCl to ${\text{AlB}}_2$ to ${\text{Cr}}_3\text{Si}$ as we increase $R_N$ from 1 to 3, respectively. Note that the mole fractions of the different species in Fig. 4B do not always add to unity––this implies that the remainder represents free “monomer” in solution. Fig. 4C shows predictions of the coupled system at a point in phase space where only CsCl or ${\text{AlB}}_2$ is predicted to form. In agreement with this prediction, we only experimentally observe a transition from CsCl to ${\text{AlB}}_2$ for this choice of size and linker ratios (Fig. 2). Even at the ideal $R_N$ of 2:1 for ${\text{AlB}}_2$, the model predicts a small amount of CsCl, whereas the experiments only see the ${\text{AlB}}_2$. Furthermore, also in agreement with experiments, the ${\text{Cr}}_3\text{Si}$ crystal morphology never forms as we increase $R_N$ toward the 3:1 ratio (where stoichiometry would suggest an equilibrium ${\text{Cr}}_3\text{Si}$ lattice). These results indicate that having the right stoichiometry alone is not sufficient to obtain a desired lattice. Rather, the formation of a specific crystal structure requires a proper combination of size, DNA linker, and stoichiometric ratios.

Here, we note a crucial difference between Figs. 3 and 4. The phase diagrams shown in Fig. 3 are constructed in the hypothetical $K\to \infty$ limit, whereas those in Fig. 4 are for finite K values. In the infinite-K limit, either $R_N={\displaystyle {\sum }_i{a}_i{N}_{c_i}}$ or $1={\displaystyle {\sum }_i{N}_{c_i}}$ are acceptable solutions, but the crystal with the lower standard-state free energy (or the higher number of DNA bases being paired) is infinitely preferred. Thus, there is no coexistence between different solid phases. For finite K, we predict regions of coexistence between two lattice structures, which suggests that pure crystal polymorphs would be hard to create (more on this below).

Knowledge of the equilibrium mole fractions also allows for the calculation of the effective chemical potential for each “product” at equilibrium: ${\mu }_{i,eff}={\displaystyle {\sum }_i{\chi }_i{\mu }_i}$. In the limit $K\to \infty$, the ${\mu }_i^o$ term of the most stable structure dominates (over all other chemical potentials) and the sum reduces to ${\chi }_i{\mu }_i^o$, where i indicates the most energetically favorable lattice. Because ${\chi }_i=R_N/a_i$ under these conditions, the equation for the effective chemical potential becomes

$${\mu }_{i,eff}={\mu }_i^o\frac{R_N}{a_i}.$$ [1]

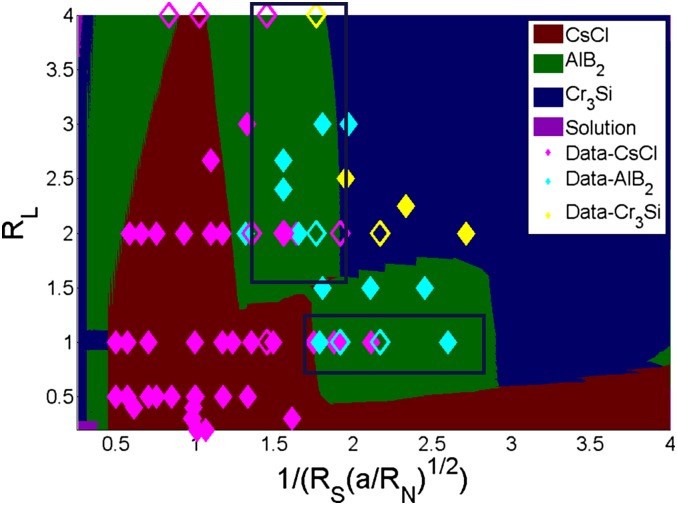
This generalization of the effects of stoichiometry into an effective chemical potential term accurately captures the experimental observations made by Macfarlane et al. (23). We gain further insights into this situation by introducing the size, linker, and stoichiometric ratios into the main expression for the chemical potential to determine the explicit dependence of ${\mu }_{i,eff}$ on these three experimental variables. This results in ${\mu }_{i,eff}\sim \left(R_L{R}_N/R_S^2{a}_i\right)$, where $R_S,$ $R_L$, $R_N$ are the size, linker, and stoichiometric ratios, respectively. This result shows that the chemical potential scales inversely with the square of the size ratio and stoichiometry ratios and linearly with the linker ratio. Consequently, we combine all of the effects of stoichiometry into a single phase diagram by plotting $R_L$ vs. $\left(1/R_S\right){\left(R_N/a_i\right)}^{1/2}$ (Fig. 5).

Fig. 5.

Generalized phase diagram. Scatter points represent experimental data: filled: pure, open: mixed or disordered. Mixed indicates predominantly indicated phase with traces of others. General agreement with experimental data observed at all stoichiometry, size, and linker ratios. Regions within blue boxes show some degree of experimental confusion between CsCl and ${\text{AlB}}_2$.

Relationship to Experiments.

Fig. 5 demonstrates predominantly good agreement between the CCM predictions and experimental data, implying that stoichiometry effects are well understood in the framework of this theory. (There are important exceptions, discussed below.) These results suggest that stoichiometry can be used as a tuning variable to form desired crystal morphologies from DNA-grafted NPs. Thus, deviations away from the ideal size or linker ratios for the formation of a specific lattice can be “corrected” by mixing different ratios of the required building blocks. For example, consider the case where the desired structure is ${\text{AlB}}_2$, the size ratio is 0.5, and the linker ratio is 1. Assuming an ideal case where the correct stoichiometric ratio of the building blocks is introduced into the system ($a/R_N=1$), we obtain $\left(1/R_S\right){\left(R_N/a_i\right)}^{1/2}$ = 2, and the ground-state lattice, i.e., ${\text{AlB}}_2$, is obtained as desired. However, introducing a deficit stoichiometric ratio $R_N$ = 1 would shift the composite x-axis parameter to 1.41. Here, the predicted equilibrium structure becomes CsCl. Thus, a shift in the stoichiometric ratio destabilizes the ground-state ${\text{AlB}}_2$ structure in favor of the CsCl lattice.

There remain, however, two experimental bands of data which are in apparent disagreement with theoretical predictions in the $K\to \infty$ limit. One corresponds to a vertical band with an x-axis value $\sim$ 1, whereas the second comprises a horizontal zone with y-axis value $\sim$ 1. In these regions where the theory in the limit $K\to \infty$ predicts the formation of an ${\text{AlB}}_2$ phase, experiments see confusing trends––either CsCl, ${\text{AlB}}_2$, or a combination of these two structures––possibly suggesting phase coexistence. One possible reason for these bands of “confusion” is clear from the results shown in Fig. 4 B and C, where calculations were performed for finite (but large) values of K. For $R_N$ values less than 1, we only predict pure CsCl, in agreement with experimental data. For $R_N>$ 1, the model calculations suggest coexistence of two (or more) lattice structures, especially in regions where ${\text{AlB}}_2$ is predicted to be the dominant structure. These predictions are clearly reflected in the bands of experimental confusion, implicating phase coexistence in these regions.

From a design perspective, the interplay between stoichiometry, DNA-NP size ratio, and linker ratio opens up a significant window for materials fabrication. Before the incorporation of stoichiometry, it was thought that self-assembly into a desired lattice structure involved precise design of the necessary DNA-NPs parameters (i.e., size and linker ratios) as well as mixing the stoichiometric amounts of the particles as defined by the desired crystal lattice. Our current study reveals that mixing different ratios of the required building blocks can shift the equilibrium lattice structure, although in some cases it can lead to undesired phase coexistence. Thus, the same set of DNA-NPs can be used to obtain different lattice structures by simply altering the stoichiometric mix. This deemphasizes the need for precise experimental control over the size and linker ratios. Furthermore, we note that stoichiometry serves as a “corrective” factor for the calculated chemical potential. Thus, we can define an activity coefficient ${\gamma }_i$ for the effects stoichiometry where ${\gamma }_i=\exp \left(-\left({\mu }_i^o/kT\right)\left(a_i-R_N/a_i\right)\right)$ that can be readily applied to future theories for calculating the lattice free energy.

Conclusion

In summary, the main focus of our work was to examine the effects of stoichiometry on the crystal lattices that can be obtained from the self-assembly of DNA-grafted colloids. Whereas previous works have highlighted examples where stoichiometry can drive shifts in the equilibrium lattice structure formed, there is little understanding as to what serves as the major driving force behind the observed transitions (16, 23). Our analysis reveals that deviations away from the ideal stoichiometry force the system to behave similarly to a series of competing, parallel reactions. We thus emphasize that stoichiometry is an underappreciated handle for controlling DNA-grafted colloidal self-assembly.

Materials and Methods

See SI Appendix for additional details.

Preparation of DNA-Grafted Colloidal Assembly.

The disulfide bond in the thiol-modified oligonucleotides was reduced to a monothiol functionality using tris(2-carboxyethyl)phosphine (TCEP) (1:200 molar ratio of DNA:TCEP, overnight) in water. The oligonucleotides were purified using G-25 size exclusion columns (GE Healthcare). Purified monothiol-modified oligonucleotides were incubated AuNPs in a 30:1 ratio for the 5 nm, 100:1 ratio for the 10 nm, and 200:1 for the 15 nm AuNPs, in 10 mM phosphate buffer (pH 7.4). NaCl concentration was gradually increased to 500 mM over 24 h at room temperature to ensure full coverage. AuNP–DNA conjugates were washed five times using Microcon centrifugal devices (100-kDa molecular weight cut-off membrane filters) in 10 mM phosphate buffer (pH 7.4) and resuspended in 10 mM phosphate buffer with 500 mM NaCl. The required amount of linker strands was then added to fabricate particles of different types and sizes. The linker design is the same as Macfarlane et al. (23). Particles A and B are functionalized with single-stranded thiolated DNA A-SH and B-SH, respectively and cross-linked following the described protocol for crystalline assemblies (23).

SAXS Measurements.

SAXS experiments were performed at the National Synchrotron Light Sources X-9A beam line. Scattering data were collected with a PILATUS CCD area detector and converted to 1D scattering intensity vs. wave vector transfer, q = (4π/λ)sin(θ/2), where λ = 0.918 Å and θ are the wavelength of incident X-rays and the scattering angle, respectively. The structure factor S(q) was obtained as I(q)/F(q), where I(q) and F(q) are background-corrected 1D scattering intensities obtained by azimuthal integration of CCD images for assembled particle superlattices and unaggregated free particles, respectively.

CCM.

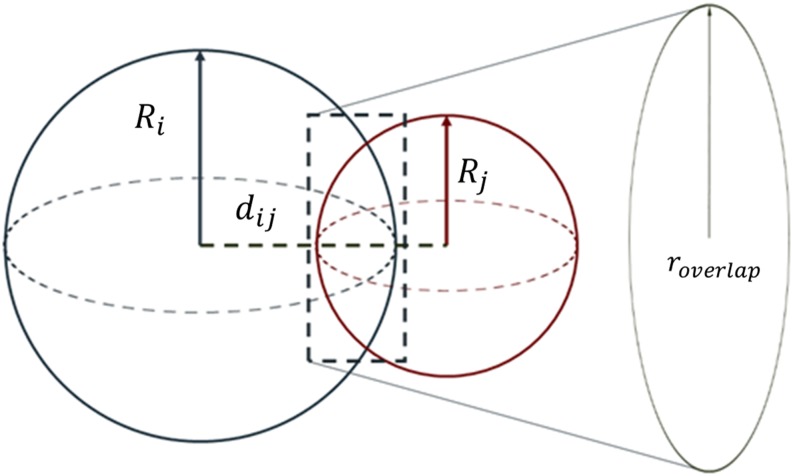
A brief summary of the model is provided. For additional details we refer to both SI Appendix and the original paper (23). The hydrodynamic radius of each DNA-NP is defined as $R_{i,max}=r_{NP,i}+0.34x_i+0.4$, where $r_{NP,i}$ is the nanoparticle radius, $x_i$ is the number of DNA base in the dsDNA regime of the linker, and 0.4 is the length of the thiolated bond connecting the DNA linker to the core NP. The interparticle distance between two interacting DNA-NPs is defined as $d_{ij}=r_{NP,i}+r{+}_{NP,j}+0.255\left(x_i+x_j\right)+0.8$. The 0.255 value indicates a relaxed DNA base-pair length as opposed to 0.34 for the full stretch length. The overlapping surface areas can then be determined using simple geometry (Fig. 6).

Fig. 6.

CCM. $R_i$ and $R_j$ are the hydrodynamic radii, $d_{ij}$ is the interparticle distance, and $r_{overlap}$ is the radius of the overlapping plane between the two spheres. The interacting area is the surface area of the sphere that lies within the other sphere.

Restriction parameters are defined for deficit number of interacting linkers and interaction areas for each particle. The fractional number of duplexed DNA is calculated as $duple{x}_i={\displaystyle {\sum }_j\left(A_{ij}N{N}_{ij}/A_{i,total}\right)r_{i,area}{r}_{ij,linker}}$, where $N{N}_{ij}$ is the number of nearest neighbors, $A_{ij}$ is the interaction area of particle i to particle j, $A_{i,total}$ is the total surface area of particle i, and the $r_i$ and $r_{ij}$ are interaction restrictions terms.

Effective Nearest-Neighbor Parameter.

Define the CCM distances in terms of the crystallographic distances (subscript “o”) such that $R_i=\alpha R_{i,o}$ and $d_{ij}=\alpha d_{ij,o}$, where $R_i$ is the hydrodynamic radius, $d_{ij}$ is the interparticle distance, and α is the scaling factor defined as the ratio of the from the particle’s original shell to its new shell. Via subsequent substitutions and grouping of terms (SI Appendix), the scaling factor α affects the overlap areas ($A_{ij}$) between two interacting spheres as follows: $A_{ij}={\alpha }^2{A}_{ij,o}$. Directly substituting into the relation for the percent duplexed gives $duple{x}_i={\displaystyle {\sum }_j\left({\alpha }^2{A}_{ij,o}N{N}_{ij}/A_{i,total}\right)r_{i,area}{r}_{ij,linker}}$, where $N{N}_{ij}$ is the number of nearest neighbors and the $r_i$ and $r_{ij}$ are restriction terms defined by the contact model (SI Appendix). Grouping α and $N{N}_{ij}$ yields an effective nearest parameter $N{N}_{ij,eff}={\alpha }^{2}N{N}_{ij}$.