Doubly Robust Learning for Estimating Individualized Treatment with Censored Data

Summary

Individualized treatment rules recommend treatments based on individual patient characteristics in order to maximize clinical benefit. When the clinical outcome of interest is survival time, estimation is often complicated by censoring. We develop nonparametric methods for estimating an optimal individualized treatment rule in the presence of censored data. To adjust for censoring, we propose a doubly robust estimator which requires correct specification of either the censoring model or survival model, but not both; the method is shown to be Fisher consistent when either model is correct. Furthermore, we establish the convergence rate of the expected survival under the estimated optimal individualized treatment rule to the expected survival under the optimal individualized treatment rule. We illustrate the proposed methods using simulation study and data from a Phase III clinical trial on non-small cell lung cancer.

1. Introduction

Clinicians routinely tailor treatment to the individual characteristics of each patient. Individualized treatment rules formalize this practice by mapping patient characteristics to a recommended treatment. There is a large body work on estimation of optimal individualized treatment rules, using data from clinical trials or observational studies (Murphy, 2003; Robins, 2004; Zhao et al., 2009, 2011; Qian & Murphy, 2011; Zhang et al., 2012b). Regression-based approaches model the regression of outcome on patient covariates and treatment and infer the optimal individualized treatment rule from the modeled regression. The performance of regression-based methods depends critically on the predictive performance of the estimated regression model. In addition, because regression-based approaches require the modeling of treatment-covariate interactions, the number of terms can be large with high-dimensional covariates. An alternative class of procedures, known as classification-based methods, maximize an estimator of the marginal mean outcome over a pre-specified class of individualized treatment rules. These methods typically rely on fewer modeling assumptions about the conditional distribution of the outcome given covariates and treatment and so are potentially more robust to model misspecification; furthermore, they avoid inversion of a predictive model, which can be computationally expensive in some settings. Zhao et al. (2012) and Zhang et al. (2012a) showed that maximization of the estimated marginal mean outcome is equivalent to minimizing a weighted misclassification error with weights that are proportional to the observed clinical outcomes. Classification-based approaches have been shown to work well in settings without censoring (Zhao et al., 2012; Zhang et al., 2012a; Kang et al., 2014; Zhao et al., 2014). However, heretofore both regression-based and classification-based methods were restricted to use with non-censored data.

When the primary outcome of interest is survival time, the observations are commonly subject to right censoring because of subject dropout or administrative censoring. One approach is to fit a parametric or semiparametric survival model, including patient covariates and treatments to infer the optimal decision rule from the fitted survival model. Goldberg & Kosorok (2012) model the completely observed survival time and adjust for censoring by inverse probability of censoring weighting. These methods are intended to form high-quality predictions but may not be consistent for the optimal treatment rule (Qian & Murphy, 2011). Furthermore, parametric or semiparametric models can be sensitive to model misspecification and inverse-weighting may suffer from numerical instability when the censoring rate is high.

We extend the outcome weighted learning approach of Zhao et al. (2012) to accommodate censored data. The extension involves maximizing an estimator of the mean survival time under right censoring. The method avoids inversion of a predictive model by recasting the estimated mean survival time as a weighted misclassification rate where the weights involve both the observed outcome and inverse probability of censoring weights. We also introduce a doubly robust version of outcome weighted learning to account for potential bias introduced by a misspecified censoring model. The method is doubly robust in the sense that the obtained individualized treatment rule is consistent for the optimal rule when the model for either survival or censoring times is correct, but not necessarily both. We use a convex relaxation idea from support vector machines (Cortes & Vapnik, 1995) to construct a computationally efficient algorithm.

2. Methodology

2·1. Value function and optimal treatment rule

Let T̃ denote survival time, X = (X₁,…, X_d)^T ∈ 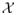denote subject covariates, and A ∈ {−1, 1} denote the binary treatment assigned. Define τ to be the end of the study; because there is no information about survival beyond τ we use T = min(τ, T̃) as the outcome of interest. When we are interested in survival time on the log scale, we can use log(T) as the outcome. We assume that data are collected in a randomized trial so that treatment A is randomly assigned with a randomization probability that is completely determined by X. Thus, there are no unmeasured confounders (Rubin, 1974, 1978; Splawa-Neyman et al., 1990). Furthermore, we assume that π(a; X) = pr(A = a |X) is strictly bounded away from zero with probability 1 for each a. 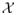A treatment rule, say , is a function from into the space of treatments {−1, 1}; under , a patient with covariates X = x is assigned treatment (x). The value of a regime , denoted V( ), is the expected outcome under . Let E denote expectation with respect to the distribution of (T, A, X) in the observed data, and 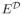denote expectation under the restriction that A = (X), then it can be shown (Qian and Murphy, 2011) that

$$V(\mathcal{D})=E^{\mathcal{D}}(T)=E\{T\mid X,A=\mathcal{D}(X)\}=E\left[\frac{TI\{A=\mathcal{D}(X)\}}{\pi (A;X)}\right],$$ (1)

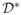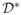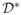where I(·) is an indicator function. A treatment rule, say , is said to be optimal if V ( ) ≥ V( ) for all rules . To characterize , write the last term in (1) as E {[I{ (X) = 1}E(T | A = 1, X) + I{ (X) = −1}E(T | A = −1, X)]} which implies

$${\mathcal{D}}^{\ast }(x)=\text{sign}\{E(T\mid A=1,X=x)-E(T\mid A=-1,X=x)\}.$$ (2)

Thus, 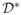(x) is the maximizer of E(T|X = x, A = a) with respect to a.

2·2. Outcome weighted learning with censored data

Censoring due to patient dropout is commonly seen in studies of survival time. Let C denote the potential censoring time, which could exceed τ, and assume that C and T are independent given (A, X). We observe data comprising n independent identically distributed subjects, {Y_i = T_i ∧ C_i, Δ_i = I(T_i ≤ C_i), X_i, A_i}, i = 1, …, n, where Δ = I(T ≤ C) denotes the censoring indicator. Our goal is to estimate the optimal treatment rule 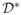using the censored data.

Maximizing V ( ) is equivalent to minimizing E [TI{A ≠ (X)}/π(A; X)] according to (1). This is a weighted classification problem, where misclassification corresponds to A ≠ (X), and the weights are T/π(A; X). This point of view motivated the development of outcome weighted learning for noncensored outcomes (Zhao et al., 2012). We generalize this approach to censored outcomes. Hereafter, we assume that event times and censoring times are continuous. Let $S_C^{\ast }(t\mid A,X)=\text{pr}(C>t\mid A=a,X=x)$ be the conditional treatment specific survival function for the censoring time given covariates x. Recall that T = min(T̃, τ). Then,

$$\begin{array}{l}E\left\{\frac{\mathrm{\Delta }Y}{S_C^{\ast }(Y\mid A,X)}\mid A,X\right\}=E\left\{\frac{\stackrel{\sim }{T}I(\stackrel{\sim }{T}<\tau )I(C>\stackrel{\sim }{T})}{S_C^{\ast }(\stackrel{\sim }{T}\mid A,X)}+\frac{\tau I(\stackrel{\sim }{T}\ge \tau )I(C>\tau )}{S_C^{\ast }(\tau \mid A,X)}\mid A,X\right\}\\ =E\{\stackrel{\sim }{T}I(\stackrel{\sim }{T}<\tau )+\tau I(\stackrel{\sim }{T}\ge \tau )\mid A,X\}=E(T\mid A,X),\end{array}$$

where we have used the conditional independence of T and C given X, A. Therefore,

$$V(\mathcal{D})=E\left[\frac{E(T\mid A,X)}{\pi (A;X)}I\{A=\mathcal{D}(X)\}\right]=E\left[\frac{\mathrm{\Delta }Y}{S_C^{\ast }(Y\mid A,X)\pi (A;X)}I\{A=\mathcal{D}(X)\}\right].$$ (3)

To obtain an estimator of 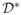one could attempt to maximize an empirical estimate of the right-hand-side of (3). This is equivalent to minimizing

$$n^{-1}\sum _{i=1}^n\frac{{\mathrm{\Delta }}_i{Y}_i}{{\widehat{S}}_C(Y_i\mid A_i,X_i)}\frac{I\{A_i\ne \mathcal{D}(X_i)\}}{\pi (A_i;X_i)},$$ (4)

where Ŝ_C is a consistent estimator for $S_C^{\ast }$. However, direct optimization is intractable because of the discontinuous indicator functions; instead, we minimize a convex relaxation of (4). Because the objective function can be viewed as a weighted misclassification rate, we base our relaxation on support vector machines (Cortes & Vapnik, 1995). We replace I{A ≠ (x)} with a convex surrogate ϕ{Af(x)}, where (x) = sign{f(x)} and ϕ(t) = max(1 − t, 0) denotes the hinge loss. Details for estimating 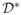are at the end of this section.

In the above formulation, a misspecified model for C given (A, X) can lead to biased estimation. Thus, we also propose a doubly robust estimator which protects against such misspecification. Let $E_{\stackrel{\sim }{T}}^m(T\mid T>t,A,X)$ denote a working model for the conditional mean residual life-time given (A, X) derived from a working survival model for S_T̃ (t | A, X), and let $S_C^m(t\mid A,X)$ denote a working model for S_C(t | A, X). Then, using the construction given in Section 2.3.2 of van der Laan & Robins (2003), we define the augmented value function,

$$V^m(\mathcal{D})=E\left(\right[\frac{\mathrm{\Delta }Y}{S_C^m(Y\mid A,X)}-\int E_{\stackrel{\sim }{T}}^m(T\mid T>t,A,X)\left\{\frac{{dN}_C(t)}{S_C^m(t\mid A,X)}+I(Y\ge t)\frac{{dS}_C^m(t\mid A,X)}{S_C^m{(t\mid A,X)}^2}\right\}\left]\frac{I\{A=\mathcal{D}(X)\}}{\pi (A;X)}\right),$$

where N_C(t) = (1 − Δ)I(Y ≤ t). In addition to the inverse probability of censoring weighting, there is an augmentation term in the weights for I{A = (X)}. The following lemma shows that V^m( ) is equivalent to V( ) when either working model is correct; the proof is deferred to the Supplementary Material.

Lemma 1

If either $E_{\stackrel{\sim }{T}}^m(T\mid T>t,A,X)=E(T\mid T>t,A,X)$ or $S_C^m(t\mid A,X)=S_C^{\ast }(t\mid A,X)$, then V^m( ) = V( ).

Define

$$R(Y,\mathrm{\Delta },S_C,E_{\stackrel{\sim }{T}})=\frac{\mathrm{\Delta }Y}{S_C(Y\mid A,X)}-\int E_{\stackrel{\sim }{T}}(T\mid T>t,A,X)\left\{\frac{{dN}_C(t)}{S_C(t\mid A,X)}+I(Y\ge t)\frac{{dS}_C(t\mid A,X)}{S_C{(t\mid A,X)}^2}\right\},$$ (5)

Lemma 1 shows that if either working model is correct then $V(\mathcal{D})=E[R(Y,\mathrm{\Delta },S_C^m,E_{\stackrel{\sim }{T}}^m)I\{A=\mathcal{D}(X)\}/\pi (A;X)]$. Thus, we can apply the weighted classification approach to estimate the optimal treatment rule using weights $R(Y,\mathrm{\Delta },S_C^m,E_{\stackrel{\sim }{T}}^m)/\pi (A;X)$.

To distinguish the two learning approaches, we call the first approach inverse censoring weighted outcome weighted learning and the second approach doubly robust outcome weighted learning. Estimation is implemented as follows:

• Step 1. Fit a model for T̃ given (A, X) to construct estimate Ŝ_T̃ (T | A, X) of S_T̃ (T |, A, X). Estimate E_T̃ (T | T > t, A, X) for t ∈ [0, τ) by

  $${\widehat{E}}_{\stackrel{\sim }{T}}(T\mid T>t,A,X)=\frac{\tau {\widehat{S}}_{\stackrel{\sim }{T}}(\tau \mid A,X)}{{\widehat{S}}_{\stackrel{\sim }{T}}(T\mid A,X)}-{\int }_t^{\tau -}ud{\widehat{S}}_{\stackrel{\sim }{T}}(u\mid A,X).$$

• Step 2. Fit a model for C given (A, X) to form estimate Ŝ_C(t | A, X) of S_C(t | A, X).

• Step 3. Calculate W_i = Δ_iY_i/Ŝ_C(Y_i | A_i, X_i) for the first approach and W_i = R(Y_i, Δ_i, Ŝ_C, Ê_T̃) for the second approach. If negative weights occur with the doubly robust methods we can subtract min_i W_i from all the weights.

• Step 4. Use the algorithm outlined below to obtain f̂(x) by minimizing

  $$\sum _{i=1}^n{W}_i\frac{\varphi \{A_{i}f(X_i)\}}{\pi (A_i;X_i)}+{\lambda }_n{\Vert f\Vert }^2.$$ (6)

• Step 5. The decision rule is 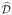(x) = sign{f̂(x)}.

We have added a regularization term λ_n||f||² to avoid overfitting in Step 4. Here, ||f|| is a norm defined on the space that f belongs to, and λ_n is a tuning parameter that controls the severity of penalization. We use a linear decision function f(x) = θ₀ + θ^T x, to illustrate the algorithm utilized in this step. In this case, ||f|| is the Euclidean norm of θ. Let W denote a generic weight constructed in Step 3 using one of the proposed methods. The optimization problem in Step 4 can be written as $min\gamma {\sum }_{i=1}^n{W}_i{\xi }_i+{\Vert \theta \Vert }^2$ subject to ξ ≥ 0 and A_i(θ^T X_i + θ₀) ≥ (1− ξ_i). By introducing Lagrange multipliers, we obtain the Lagrangian

$$\frac{1}{2}{\Vert \theta \Vert }^2+\gamma \sum _{i=1}^n{W}_i{\xi }_i-\sum _{i=1}^n{\alpha }_i\{A_i({\theta }^T{X}_i+{\theta }_0)-(1-{\xi }_i)\}-\sum _{i=1}^n{\mu }_i{\xi }_i,{\alpha }_i,{\mu }_i\ge 0.$$

By taking derivatives with respect to θ, θ₀ and ξ_i, we have $0={\sum }_{i=1}^n{\alpha }_i{A}_i,\theta ={\sum }_{i=1}^n{\alpha }_i{A}_i{X}_i$ and α_i = γW_i − μ_i. It follows that the dual problem is

$$\underset{\alpha }{max}\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{A}_i{A}_j{X}_i^T{X}_j$$ (7)

subject to 0 ≤ α_i ≤ γW_i and ${\sum }_{i=1}^n{\alpha }_i{A}_i=0$. The dual problem can be solved using quadratic programming. Estimates θ̂ = Σ_α̂i0α̂_iA_iX_i and θ̂₀ follow from the Karush–Kuhn–Tucker conditions. When a linear decision rule is not sufficient, the procedure can be generalized using nonlinear kernel functions. For every positive definite kernel k : 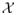× 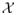→ ℝ, there is a unique reproducing kernel Hilbert space 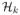, which is the completion of the linear span of all functions {k(·, x), x ∈ 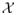}. The norm in 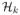, denoted by ||·||_k, is induced by the inner product, ${\langle f,g\rangle }_k={\sum }_{i=1}^n{\sum }_{j=1}^m{\alpha }_i{\beta }_{j}k(x_i,x_j)$, for $f(·)={\sum }_{i=1}^n{\alpha }_{i}k(·,x_i)$ and $g(·)={\sum }_{j=1}^m{\beta }_{j}k(·,x_j)$. A general nonlinear function f(x) can be used instead of a linear function. By the representer theorem (Kimeldorf & Wahba, 1971), the minimizer must admit a representation of the form $f(·)={\sum }_{i=1}^n{\alpha }_{i}k(·,X_i)$. In addition, to solve the optimization problem, we only need to compute the kernel matrix, where the inner product $X_i^T{X}_j$ in the dual objective function (7) is replaced by k(X_i, X_j). Quadratic programming can still be applied to obtain α̂_i (i = 1,…, n). The resulting decision rule is 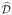(X) = sign{Σ_α̂i0α̂_ik(X_i, X) + θ̂₀}.

2·3. Working models for estimating S_C(t | A, X) and E_T̃ (T | T > t, A, X)

In our simulated experiments we used the Cox proportional hazards model for the requisite survival functions (Cox, 1972). Let Z_T and Z_C denote regressors constructed from X and A used in the Cox proportional hazards models for T and C respectively. Let λ_Ci(t) and λ_Ti(t) denote the hazard functions of censoring and failure times for subject i respectively. Under the Cox model, ${\lambda }_{Ci}(t)={\lambda }_{C0}(t)exp({\beta }_C^T{Z}_{C_i})$ and ${\lambda }_{Ti}(t)={\lambda }_{T0}(t)exp({\beta }_T^T{Z}_{Ti})$, where λ_C0(t) and λ_T0(t) are baseline hazard functions for censoring and failure times, respectively. The estimator for β_C, say β̂_C, maximizes the partial likelihood

$$\prod _{i=1}^n{\left\{\frac{exp({\beta }_C^T{Z}_{Ci})}{{\sum }_{Y_j\le Y_i}exp({\beta }_C^T{Z}_{Cj})}\right\}}^{1-{\mathrm{\Delta }}_i}.$$

We use the Breslow estimator

$${\widehat{\mathrm{\Lambda }}}_{C0}(t)={\int }_0^t\frac{{\sum }_{k=1}^n{dN}_{Ck}(u)}{{\sum }_{j=1}^{n}I(Y_j\ge u)e^{{\widehat{\beta }}_C^T{Z}_{Cj}}}$$

for the cumulative baseline hazard function Λ_C0(t). An estimator of Λ_C(t|A_i, X_i), the cumulative hazard function of censoring time for subject i, is $exp({\widehat{\beta }}_C^T{Z}_{Ci}){\widehat{\mathrm{\Lambda }}}_{C0}(t)$. An estimator for S_C(t|A_i, X_i) is ${\widehat{S}}_C(t\mid A_i,X_i)=exp{\{-{\widehat{\mathrm{\Lambda }}}_{C0}(t)\}}^{exp({\widehat{\beta }}_C^T{Z}_{Ci})}$. Estimates β̂_T and Λ̂_T̃0(t) are obtained similarly. Details for estimating E_T̃(T|T > t, A, X) are in the Supplementary Material.

3. Theoretical Results

Let f(x) be the decision function with the decision rule given by (x) = sign{f(x)}, and write V (f) to denote the value function V ( ). We define the pseudo value as

$$V_R(f,S_C,E_{\stackrel{\sim }{T}})=E\left(\frac{R(Y,\mathrm{\Delta },S_C,E_{\stackrel{\sim }{T}})I[A=\text{sign}\{f(X)\}]}{\pi (A;X)}\right).$$

Therefore, Lemma 1 can be restated as $V(f)=V_R(f,S_C^{\ast },E_{\stackrel{\sim }{T}})=V_R(f,S_C,E_{\stackrel{\sim }{T}}^{\ast })$, where $S_C^{\ast }(t\mid A,X)$ is the true conditional survival function of C given (A, X), and $E_{\stackrel{\sim }{T}}^{\ast }(T\mid T>t,A,X)$ is the true conditional mean residual lifetime given (A, X). Define convex surrogate loss function

$$L_{\varphi }(f,S_C,E_{\stackrel{\sim }{T}})=\frac{R(Y,\mathrm{\Delta },S_C,E_{\stackrel{\sim }{T}})\varphi \{Af(X)\}}{\pi (A;X)},$$ (8)

where ϕ(t) = max(1 − t, 0). Define 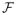to be the set of all measurable functions from 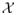into ℝ. Our first result states that the decision function obtained by minimizing the expectation of this surrogate loss over 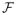maximizes V_R for any S_C and E_T̃. Furthermore, we quantify the differences using the hinge loss versus zero-one loss. The proofs are essentially the same as Theorems 3.1 and 3.2 in Zhao et al. (2012) and are thus omitted.

Lemma 2

If f̃ minimizes E{L_ϕ(f, S_C, E_T̃)) over 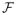with any models for S_C and E_T̃, then

1. V_R(f̃, S_C, E_T̃) = 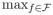V_R(f, S_C, E_T̃), that is, f̃ yields the maximum value of V_R;

2. for any f ∈ ,

   $$V_R(\stackrel{\sim }{f},S_C,E_{\stackrel{\sim }{T}})-V_R(f,S_C,E_{\stackrel{\sim }{T}})\le E\{L_{\varphi }(f,S_C,E_{\stackrel{\sim }{T}})\}-E\{L_{\varphi }(\stackrel{\sim }{f},S_C,E_{\stackrel{\sim }{T}})\},$$

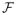   that is, the value lost due to using a suboptimal decision function f is bounded by the expected surrogate loss.

Our main result establishes the convergence rates for value of the estimated decision rule f̂. As described in Section 2, we use weights that depend on the estimated survival functions, and hinge loss as a surrogate loss function. To bound the difference between the true and the empirical expectation of the surrogate, which involves random quantities, that is, estimates for survival and censoring times, we use the following assumptions:

Assumption 1

Both Ê_T̃(T|A = a, X = x) and Ŝ_C(t|A = a, X = x) converge in probability to $E_{\stackrel{\sim }{T}}^m(t\mid A,X)$ and $S_C^m(t\mid A,X)$ uniformly in t ∈ (0, τ] for every (x, a). Moreover, for some constant γ > 0,

$$E\{\mid R(Y,\mathrm{\Delta },{\widehat{S}}_C,{\widehat{E}}_{\stackrel{\sim }{T}})-R(Y,\mathrm{\Delta },S_C^m,E_{\stackrel{\sim }{T}}^m)\mid \}=O_p(n^{-\gamma }).$$ (9)

Assumption 2

For some η > 0, $S_C^m(\tau \mid A,X)>\eta$ with probability 1.

Assumption 1 implies that Ê_T̃(T|A, X) and Ŝ_C(t|A, X) converge to fixed functions, even if the imposed working models are wrong. Moreover, it imposes an assumption on the variance of the survival function estimators. The constant γ depends on the working models used for estimating S_C and E_T̃. If we assume parametric or semiparametric models, including the Cox proportional hazards model and transformation models, then γ = 1/2 in (9). Assumption 2 ensures that some subjects do not fail at the end of the study and thus have observation time τ.

In addition, we restrict the choice of reproducing kernel Hilbert space to the space associated with Gaussian radial basis function kernels, $k(x,x^{\prime })=exp(-{\sigma }_n^2{\Vert x-x^{\prime }\Vert }^2)$, x, x′ ∈ 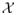, where σ_n > 0 is the kernel bandwidth parameter varying with n controlling the spread of the kernel. We can determine the complexity of 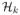in terms of capacity bounds with respect to the empirical L₂-norm, defined as ${\Vert f-g\Vert }_{L_2(P_n)}={(n^{-1}{\sum }_{i=1}^n{\mid f(X_i)-g(X_i)\mid }^2)}^{1/2}$, f, g ∈ 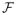for functional class 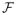. For any ε > 0, the covering number of 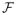with respect to L₂(P_n), N{ 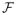, ε, L₂(P_n)}, is the smallest number of L₂(P_n) ε-balls needed to cover 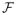, where an L₂(P_n) ε-ball around a function g ∈ 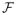is the set {f ∈ 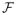:||f − g||_L2(Pn) < ε}. It has been shown in Theorem 2.1 of Steinwart & Scovel (2007) that for any ε > 0,

$$\underset{P_n}{sup}logN\{B_{{\mathcal{H}}_k},\epsilon ,L_2(P_n)\}\le c_n{\epsilon }^{-p},$$ (10)

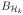where $c_n=c_{p,\delta ,d}{\sigma }_n^{(1-p/2)(1+\delta )d}$, is the closed unit ball of 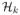, p and δ are any numbers satisfying 0 < p ≤ 2 and δ > 0, c_p,δ,d is a constant depending only on p, δ and d, and the supremum is taken over finitely discrete probability measures P_n.

Let $f^m={\text{argmin}}_{f\in \mathcal{F}}E\{L_{\varphi }(f,S_C^m,E_T^m)\}$. According to Lemma 2, f^m also maximizes $V_R(f,S_C^m,E_T^m)$, and $\mid V_R(f^m,S_C^m,E_T^m-V_R(f,S_C^m,E_T^m))\mid \le \mid E\{L_{\varphi }(f,S_C^m,E_T^m)\}-E\{L_{\varphi }(f^m,S_C^m,E_T^m)\}\mid$ for any function f. Hence, the convergence rate of the value using the estimated rule under the hinge loss will dominate the rate under the 0–1 loss. Define the approximation error function

$$a(\lambda )=\underset{f\in {\mathcal{H}}_k}{inf}[E\{L_{\varphi }(f,S_C^m,E_{\stackrel{\sim }{T}}^m)\}+\lambda {\Vert f\Vert }_k^2-E\{L_{\varphi }(f^m,S_C^m,E_{\stackrel{\sim }{T}}^m)\}].$$

The following theorem bounds the excess value optimal treatment rule relative to the doubly robust estimator of the optimal treatment rule. Its proof can be found in the Appendix.

Theorem 1

Assume Assumptions 1 and 2 hold and that λ_n → 0 and λ_nn^min(2γ,1) → ∞ as n → ∞. If we estimate f̂ within a reproducing kernel Hilbert space 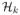associated with Gaussian radial basis function kernels, then with probability greater than 1 − 2e^−b,

$$\begin{array}{l}V(f^{\ast })-V(\widehat{f})\le 2\underset{f\in \mathcal{F}}{sup}\mid V_R(f,S_C^{\ast },E_{\stackrel{\sim }{T}}^{\ast })-V_R(f,S_C^m,E_{\stackrel{\sim }{T}}^m)\mid +a({\lambda }_n)\\ +M_p{c_n}^{2/(p+2)}{(n{\lambda }_n)}^{-2/(p+2)}+M_p{\lambda }_n^{-1/2}{c_n}^{2/(p+2)}{n}^{-2/(p+2)}\\ +Kb{(n{\lambda }_n)}^{-1}+2{\mathit{Kbn}}^{-1}{\lambda }_n^{-1/2}+O_p(n^{-\gamma }{\lambda }_n^{-1/2}),\end{array}$$ (11)

where M_p is a constant depending on p and K is a sufficiently large positive constant.

In this theorem, f^*(x) = E(T|A = 1, X = x) − E(T|A = −1, X = x) gives the optimal treatment rule. On the right-hand-side of (11), the first term reflects the estimation bias from the working models for T and C. The second term is the approximation error due to using the 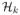space. The last term is the stochastic variability of estimating $S_C^m$ and $E_{\stackrel{\sim }{T}}^m$. The rest of the terms contain the empirical loss function for estimation of the optimal treatment rule. In particular, the convergence rate γ depends on the estimating procedure applied to the two working models.

A corollary is that when either the model for survival time or the model for censoring time is correctly specified, with probability greater than 1 − 2e^−b, we have

$$V(f^{\ast })-V(\widehat{f})\le a({\lambda }_n)+M_p{c_n}^{2/(p+2)}{(n{\lambda }_n)}^{-2/(p+2)}+M_p{\lambda }_n^{-1/2}{c_n}^{2/(p+2)}{n}^{-2/(p+2)}+Kb{(n{\lambda }_n)}^{-1}+2{\mathit{Kbn}}^{-1}{\lambda }_n^{-1/2}+O_p(n^{-\gamma }{\lambda }_n^{-1/2}).$$

Remark 1

With the hinge loss, it has been shown that if the reproducing kernel Hilbert space is rich enough, the optimizer within the reproducing kernel Hilbert space approaches the optimal treatment decision rule as the sample size goes to ∞ for appropriately chosen tuning parameters. The Gaussian kernel is one such kernel, which can induce a reproducing kernel Hilbert space that is flexible enough to approximate the optimal decision rule. While the approximation error term usually goes to zero as λ_n → 0, the other term controlling the stochastic error will increase. The optimal bandwidth λ_n can be obtained by setting the orders of a(λ_n) and $max\{c_n^{2/(p+2)}{(n{\lambda }_n)}^{-2/(p+2)},n^{-\gamma }{\lambda }_n^{-1/2}\}$ equal to each other. The approximation error function a(λ_n) is usually related to the data-generating distribution, especially the behavior close to the decision boundary, which is the true optimal decision rule if either working model is correct. Intuitively, we should be able to learn the treatment rule more rapidly for well-separated optimal treatment classes, that is, distributions that have low density near the boundary.

This behavior can be characterized in terms of the size of the set of points that are close to boundary f^*(x) = 0 (Tsybakov, 2004; Steinwart & Scovel, 2007). There exist a constant c₁ such that $a({\lambda }_n)\le c_1{\lambda }_n^{q/q+1}$, when using a Gaussian kernel with its kernel band-width σ_n varying with λ_n as ${\sigma }_n={\lambda }_n^{-1/\{(q+1)d\}}$ and $c_n={\lambda }_n^{-(1-p/2)(1+\delta )/(q+1)}$. Here, q > 0 is the noise exponent that characterizes the distribution close to the boundary (Steinwart & Scovel, 2007), and a larger q indicates a better separation between two treatment classes. More details on q are provided in the Appendix. An optimal choice of λ_n that balances bias and variance is λ_n = max{n^{−2(q+1)/{(4+p)q+2+(2−p)(2+δ)}}, n^{−2(q+1)γ/(2q+1)}}. The achieved convergence rate of the value due to the estimated rule versus the optimal value is thus max[n^{−2q/{(4+p)q+2+(2−p)(2+δ)}}, n^{−2qγ/(2q+1)}].

The rate consists of two parts: the first part reflects the rate of convergence in estimating the optimal decision rule, which is consistent with the results without censoring (Zhao et al., 2012); the second part is related to survival function estimation. When q is sufficiently large and δ and p are close to zero, the convergence rate is close to n^−γ, where γ is determined by the survival function estimator. A Cox model for the survival function estimates leads to γ = 1/2. Other working models can also be applied, such as transformation models (Zeng & Lin, 2007), nonparametric methods based on kernel type estimators (Dabrowska, 1989), or machine learning techniques (Zhu & Kosorok, 2012). However, the rate n^−γ can be slower than O_p(n^−1/2) for certain estimators.

Remark 2

Although the theoretical results are derived only for doubly robust estimators, inverse censoring weighted estimators enjoy the property stated in Theorem 1, as it is a special case obtained by setting the augmentation term to zero. However, the first term on the right-hand-side of (11) will change unless the censoring model is correctly specified.

4. Simulation Studies

4·1. Preliminaries

We aim to maximize the value function in terms of the survival time on the log scale. We compare the inverse censoring weighted and the doubly robust methods for selecting optimal individualized treatment with Cox regression and Q-learning adjusted with censoring weights (Goldberg & Kosorok, 2012). For Cox regression, we fit a proportional hazards model with treatment-by-covariate interactions, and identify the optimal individualized treatment based on the predicted outcomes. To apply Q-learning, we fit Q(X, A) = Φ(X, A)θ, where Φ(X, A) = (1, X, A, XA), to the log of the failure time. We also apply a regularized version of Q-learning, called L₂ Q-learning, where an L₂ penalty is used for regularization. The estimator is obtained as

$${\text{argmin}}_{\theta }\sum _{i=1}^n{\{log(Y_i)-\mathrm{\Phi }(X_i,A_i)\theta \}}^2\frac{{\mathrm{\Delta }}_i}{{\widehat{S}}_C(Y_i\mid A_i,X_i)}+{\lambda }_n{\Vert \theta \Vert }^2,$$

where λ_n is a tuning parameter to be selected using cross-validation, and Ŝ_C(Y|A, X) is the estimated conditional survival function of C given (A, X) that can be obtained using Cox regression. The estimated optimal decision rule is 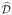(x) = argmax_a∈{−1,1}Φ(x, a)θ̂.

4·2. Simulation study

Ten independent covariates, X₁, …, X₁₀, were generated from the uniform distribution on [0, 1]. Treatments were generated from {−1, 1} with equal probabilities 0·5. Four different scenarios are presented, corresponding to different combinations of correct or incorrect survival time and censoring time models. Specifically, we generated T̃ or C from the accelerated failure time or Cox models in different scenarios, while we always used a proportional hazards model as a working model for both T̃ and C given (A, X). Regarding the specification of the model basis, we include treatment covariate interaction terms in the survival function modeling since we are interested in whether certain characteristics moderate treatment effects. Conversely, we do not model the censoring time with interaction terms unless we have full knowledge of the data, because it is not typical to posit a complex model for the censoring mechanism in practice. Details for calculating the doubly robust weights using Cox working models are given in the Supplementary Material.

For each scenario, a test data set of size 10,000 is generated to evaluate the estimated rules. The decision rules are estimated from training data using the proposed methods as described in Section 2 and the competitors. The sample sizes for the training data sets were taken to equal to 100, 200 and 400, and the simulations were repeated 1000 runs for each sample size. A linear basis is applied for model fitting in Q-learning. Linear kernels were used for both the implementation of inverse censoring weighted and doubly robust outcome weighted learning. We also explored the use of Gaussian kernels, and found that the performances were comparable to the linear kernel. The learning procedure was implemented using a Library for Support Vector Machines developed in Chang & Lin (2011). The tuning parameter λ_n in (6) was chosen using 5-fold cross validation over a pre-specified grid, with the criterion being the empirical pseudo value function. Specifically, for each tuning parameter, we partitioned the training data into 5 parts, each of which serves as the validation set once while the other 4 parts of the data are utilized for estimation. We sum up the empirical pseudo values calculated across the validation sets from the corresponding trained decision rules, and choose the optimal tuning parameter as the one maximizing the summed value.

In the following, we consider four generative models.

Case 1: The true models are Cox models for both T̃ and C. The survival time T is the minimum of τ = 1.5 and T̃, where T̃ is generated with hazard rate function

$${\lambda }_{\stackrel{\sim }{T}}(t\mid A,X)={\lambda }_{\stackrel{\sim }{T}0}(t)exp\{0·6X_1-0·8X_2+(0·6-0·4X_1-0·2X_2-0·4X_3)A\},$$

and λ_T̃0(t) = 2t. The censoring time C is generated with hazard rate function

$${\lambda }_C(t\mid A,X)={\lambda }_{C0}(t)exp\{0·5X_1+0·5X_2+(-1+0·4X_1-0·6X_2)A\},$$

where λ_C0(t) = 2t. The censoring percentage is around 56%. The optimal decision boundary is linear with 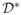(X) = −sign(0·6 − 0·4X₁ − 0·2X₂ − 0·4X₃). We use the Cox regression model with covariates (X₁, X₂, X₃, A, X₁A, X₂A, X₃A) to model survival and censoring times respectively. Therefore, both models are correctly specified.

Case 2: The true model for T̃ is a Cox model, and the true model for C is an accelerated failure time model. The survival time T is the minimum of τ = 2 and T̃, where

$${\lambda }_{\stackrel{\sim }{T}}(t\mid A,X)={\lambda }_{\stackrel{\sim }{T}0}(t)exp\{-1·5X_1+0·5X_2+(1-0·7X_1-1·2X_2)A\}.$$

We let censoring time C be generated from an accelerated failure time model with

$$log(C)=-0·3+0·6X_1-0·1X_2+0·3X_3+(0·2-X_1-2X_2+0·5X_3)A+\epsilon ,$$

where ε is generated from N(0, 1). The censoring percentage is around 34%. The optimal decision boundary is 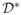(X) = −sign(0·5 − 0·1X₁ − 0·6X₂). We use the Cox model as the working model for both T̃ and C given (A, X). Specifically, we use (X₁, X₂, A, X₁A, X₂A) as covariates to model survival time, and (X₁, X₂, X₃) to model censoring time. Therefore, the working model is correctly specified for T but incorrect for C.

Case 3: The true model for T̃ is an accelerated failure time model, and the true model for C is a Cox model. The survival time T is the minimum of τ = 2 and T̃, which is generated with

$$log(\stackrel{\sim }{T})=-0·5-0·8X_1+0·7X_2+0·2X_3+(0·6-0·4X_1-0·1X_2-0·4X_3)A+\epsilon .$$

The censoring time C is generated from the Cox proportional hazards model, where

$${\lambda }_C(t\mid A,X)={\lambda }_{C0}(t)exp\{-0·5X_1-0·5X_2+0·2X_3-(1-0·5X_1+0·3X_2-0·5X_3)A\},$$

and λ_C0(t) = 2t. The censoring percentage is around 45%. The optimal decision boundary is linear with 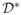(X) = sign(0·6 − 0·4X₁ − 0·1X₂ − 0·4X₃). We use the Cox model for both T̃ and C given (A, X). Specifically, we use (X, A, XA) to model survival time, and (X₁, X₂, X₃, A, X₁A, X₂A, X₃A) to model censoring time. Therefore, the working model is correctly specified for C but incorrect for T.

Case 4: The true models are accelerated failure time models for both T and C. The survival time T is the minimum of τ = 2.5 and T̃, where

$$log(\stackrel{\sim }{T})=-0·2-0·5X_1+0·5X_2+0·3X_3+(0·5-0·1X_1-0·6X_2+0·1X_3)A+\epsilon .$$

The censoring time C is generated from an accelerated failure time model with

$$log(C^{\ast })=0·5-0·8X_1+0·4X_2+0·4X_3+(0·5-0·1X_1-0·6X_2+0·3X_3)A+\epsilon ,$$

and ε is generated from N(0, 1). The censoring percentage is around 31%. The optimal decision boundary is linear with 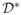(X) = sign(0·5 − 0·1X₁ − 0·6X₂ + 0·1X₃). We use (X, A, XA) to model survival time, and X to model censoring time. Therefore, both working models are incorrectly specified.

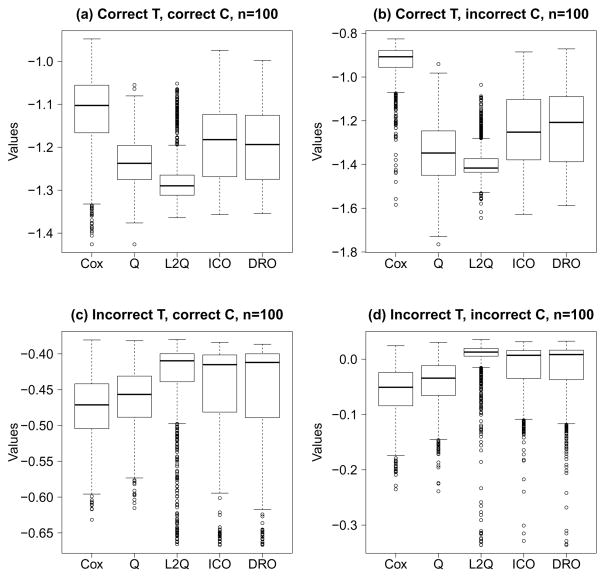
Since we know the true data generating mechanism under every scenario, for each of 1000 replicates, we calculate the values based on the logarithm of the survival time using the constructed rule from different methods. Figure 1 shows these values when n = 100, where larger values indicate longer survival. Additional results using other sample sizes are provided in the Supplementary Material.

Fig. 1.

Boxplots of values of estimated rules using different methods, representing the logarithm of the survival time with higher values being more preferable. Cox, Cox model; Q, inverse censoring weighted Q-learning; L2Q, inverse censoring weighted L₂ Q-learning; ICO, inverse censoring weighted outcome weighted learning with linear kernel; DRO, doubly robust outcome weighted learning with linear kernel.

In general, inverse censoring weighted and doubly robust outcome weighted learning have satisfactory performances. Inverse censoring weighted outcome weighted learning performs better when the censoring model is correctly specified, see Fig. 1(a) and 1(c). Indeed, doubly robust outcome weighted learning requires estimating both censoring and survival probabilities, which yield a higher variability compared with that of the inverse censoring weighted outcome weighted learning. The strength of doubly robust approach can be seen when the censoring model is mis-specified but the survival model is correct, since it can correct the bias from using only inverse censoring weighting, see Fig. 1(b). When the survival data are truly generated from the Cox model, Cox regression with correct basis results in the best performances, see Fig. 1(a) and 1(b). However, the strength is lost when the survival time is generated from an accelerated failure time model. Although Q-learning is improved by L₂-regularization, possibly by reducing overfitting, Q-learning based methods can have suboptimal performances even when the censoring model is correctly specified but survival time is generated from a Cox model, see Fig. 1(a). This is due to model misspecification when inverse censoring weighted Q-learning models the logarithm of the survival time.

We also consider a nonlinear example of possible model misspecification in the Supplementary Material. The number of covariates is increased to 30, and T̃ and C are generated from Cox models with complex effects. When the censoring or survival model is correctly specified, we use the true sets of covariates for model fitting. If the model is incorrect for survival time or censoring time, we use a linear basis. In addition to a linear kernel, we apply both methods with a Gaussian kernel. We can see that the gain from using a Gaussian kernel is pronounced, since it may better approximate the nonlinear treatment decision rules.

5. Application

We illustrate the proposed methods using advanced non-small-cell lung cancer data (Socinski et al., 2002), which is collected in a two-arm randomized trial with survival time as the primary endpoint. Non-small-cell lung cancer is the leading cause of cancer-related mortality, and approximately 30% to 40% of all new cases present with stage IV or stage IIIB disease. To investigate the optimal duration of therapy that maximizes survival, a prospective randomized phase III trial was initiated in 1998. Patients with advanced non-small-cell lung cancer were recruited and randomized to either four cycles of carboplatin/paclitaxel or continuous therapy with carboplatin/pactaxel until disease progression. The study enrolled 230 subjects; however, we restrict our analysis to the 224 subjects with complete information. In the analysis sample, 112 subjects were assigned to each treatment. The censoring rate was 32%. The baseline covariates include age ranging from 32 to 82 with median 63, sex with 138 male and 86 female, race with 162 white, 54 black and 8 other, performance status with 117 Karnofsky performance status 90% to 100% and 97 70% to 80%, and stage with 30 Stage IIIB and 194 Stage IV.

In addition to the proposed methods, we apply Cox regression, inverse censoring weighted Q-learning and L₂ Q-learning with a linear basis. We consider two sets of working models: we first use Cox regression with basis (X, A, XA) for both survival time and censoring time, and then use the Kaplan–Meier estimator for censoring time as an alternative. A treatment decision rule is evaluated based on its empirical value adjusted for censoring. The empirical value is calculated by ${\sum }_{i=1}^n{\stackrel{\sim }{R}}_{i}I\{A_i=\mathcal{D}(X_i)\}/{\sum }_{i=1}^{n}I\{A_i=\mathcal{D}(X_i)\}$, with R̃ equal to

$$\frac{\mathrm{\Delta }log(Y)}{{\widehat{S}}_C(Y\mid A,X)}-\int {\widehat{E}}_{\stackrel{\sim }{T}}\{log(T)\mid T>t,A,X\}\left\{\frac{{dN}_C(t)}{{\widehat{S}}_C(t\mid A,X)}+I(Y_i\ge t)\frac{d{\widehat{S}}_C(t\mid A,X)}{{\widehat{S}}_C{(t\mid A,X)}^2}\right\},$$

where Ŝ_C(t | A, X) and Ê_T̃ (T | T > t, A, X) are the estimated censoring probability and residual life conditional on patients characteristics. To avoid overfitting, we employ a cross-validated analysis. At each run, we partition the whole data set into 5 pieces, where 4 parts of the data are used as training data to estimate the individualized treatment rules, and the remaining part is the validation set for implementing the estimated rules, with empirical values stored for each method respectively. The cross-validated values are obtained by averaging the empirical values on all 5 validation subsets. The procedure is repeated 100 times. The averages and standard errors of these values are reported in Table 1, where larger values correspond to longer survival time.

Table 1.

Mean (s.e.) cross-validated days on log sale using different working models for C, with working model for T being a Cox regression model with basis (X, A, XA)

Working model for C	Mean (s.e.) Cross-validated Values
	Cox	Q	L2Q	ICO	DRO
Cox model, basis (X, A, XA)	5·061 (0·381)	5·234 (0·578)	5·258 (0·575)	5·339 (0·404)	5·257 (0·526)
Kaplan–Meier	5·061 (0·381)	5·002 (0·621)	5·000 (0·632)	5·473 (0·166)	5·446 (0·273)

s.e., standard errors; Cox, Cox model; Q: inverse censoring weighted Q-learning; L₂Q, inverse censoring weighted L₂ Q-learning; ICO, inverse censoring weighted outcome weighted learning with linear kernel; DRO, doubly robust outcome weighted learning with linear kernel.

Both inverse censoring weighted and doubly robust outcome weighted learning methods lead to higher values more frequently. We see a comparable performance between the two proposed approaches, which is reasonable if the censoring distribution is correctly specified, although doubly robust outcome weighted learning may have a larger variance. Since the number of covariates is not large, the performances of inverse censoring weighted Q-learning and L₂ Q-learning are similar. They could have difficulties in identifying the optimal treatment rules if the model for survival time does not fit well, even if the censoring weight is correctly specified. Also, when we apply Cox regression to model the censoring time, none of the covariates has a significant effect. Thus, working models with either Kaplan–Meier estimators or Cox regression estimators yield similar results. We then apply the proposed methods to the whole data set using Cox regression working models for both T and C. The treatment recommendations from inverse censoring weighted outcome weighted learning recommends that 119 patients be assigned to continuous therapy with carboplatin/pactaxel, while by using doubly robust outcome weighted learning, 122 out of 224 patients should be given the continuous therapy. By checking the empirical value, we find that both strategies yield close values: 5·301 for inverse censoring weighted outcome weighted learning and 5·567 for doubly robust outcome weighted learning. In fact, sometimes we may have equivalent treatment strategies if there are no differential treatment effects on a subset of the patients. The treatment decision rule produced by inverse censoring weighted Q-learning and L₂ Q-learning however, only leads to an empirical value of 4·756, and an empirical value of 4·744 by using Cox regression.

6. Discussion

As one reviewer pointed out, the proposed method is only one possible reduction of optimizing treatment rules to a weighted classification problem. Alternative choices have been proposed for continuous outcomes (Zhang et al., 2012b; Rubin & van der Lann, 2012), which can be generalized to the censoring data setup.

There may exist multiple treatments for comparison. One approach for extending the proposed framework to handle this case is to incorporate techniques developed in multicategory classification (Lee et al., 2004; Liu & Yuan, 2011). Another important extension is to settings in which there are a large number of variables. In this setting, penalized methods in classification by using sparse penalties could be adapted (Zhu et al., 2004).

Effective management of a chronic illness requires individualized treatment recommendations that are responsive to a patient’s changing health status. Dynamic treatment regimens formalize a dynamic treatment plan as a sequence of treatment rules, one per stage of clinical intervention, that map current patient information to a recommended treatment. Longer life expectancy and an aging population have created a surge in the rate of chronic illness related death. Thus, there is increasing interest in dynamic treatment regimens (Thall et al., 2002; Murphy, 2003; Robins, 2004; Moodie et al., 2007; Zhao et al., 2011; Goldberg & Kosorok, 2012; Huang et al., 2014). Extension of the proposed approach for survival data to the dynamic setting is of great interest.

Appendix

Proof of Theorem 1

First, it can be established that

$$V(f^{\ast })-V(\widehat{f})\le \underset{f\in \mathcal{F}}{sup}{V}_R(f,S_C^m,E_{\stackrel{\sim }{T}}^m)-V_R(\widehat{f},S_C^m,E_{\stackrel{\sim }{T}}^m)+2\underset{f\in \mathcal{F}}{sup}\mid V_R(f,S_C^{\ast },E_{\stackrel{\sim }{T}}^{\ast })-V_R(f,S_C^m,E_{\stackrel{\sim }{T}}^m)\mid .$$

According to Lemma 2(a), $V_R(f^m,S_C^m,E_{\stackrel{\sim }{T}}^m)={sup}_{f\in \mathcal{F}}{V}_R(f,S_C^m,E_{\stackrel{\sim }{T}}^m)$, where $f^m={\text{argmin}}_{f\in \mathcal{F}}E\{L_{\varphi }(f,S_C^m,E_T^m)\}$. Hence, it suffices to derive the convergence rate of $V_R(f^m,S_C^m,E_{\stackrel{\sim }{T}}^m)-V_R(\widehat{f},S_C^m,E_{\stackrel{\sim }{T}}^m)$.

Let $f_{{\lambda }_n}^m={\text{argmin}}_{f\in {\mathcal{H}}_k}[E\{R(Y,\mathrm{\Delta },S_C^m,E_{\stackrel{\sim }{T}}^m)\varphi \{Af(X)\}/\pi (A;X)\}+{\lambda }_n{\Vert f\Vert }_k^2]$. Then,

$$\begin{array}{l}{V}_R(f^m,S_C^m,E_{\stackrel{\sim }{T}}^m)-V_R(\widehat{f},S_C^m,E_{\stackrel{\sim }{T}}^m)\\ \le a({\lambda }_n)+(n^{-1}\sum _{i=1}^n[{\lambda }_n{\Vert \widehat{f}\Vert }_k^2\\ +\frac{R(Y_i,{\mathrm{\Delta }}_i,{\widehat{S}}_C,{\widehat{E}}_{\stackrel{\sim }{T}})\varphi \{A_i\widehat{f}(X_i)\}}{\pi (A_i;X_i)}-{\lambda }_n{\Vert f_{{\lambda }_n}^m\Vert }_k^2-\frac{R(Y_i,{\mathrm{\Delta }}_i,{\widehat{S}}_C,{\widehat{E}}_{\stackrel{\sim }{T}})\varphi \{A_i{f}_{{\lambda }_n}^m(X_i)\}}{\pi (A_i;X_i)}]\\ -E[{\lambda }_n{\Vert \widehat{f}\Vert }_k^2+\frac{R(Y,\mathrm{\Delta },{\widehat{S}}_C,{\widehat{E}}_{\stackrel{\sim }{T}})\varphi \{A\widehat{f}(X)\}}{\pi (A;X)}-{\lambda }_n{\Vert f_{{\lambda }_n}^m\Vert }_k^2-\frac{R(Y,\mathrm{\Delta },{\widehat{S}}_C,{\widehat{E}}_{\stackrel{\sim }{T}})\varphi \{A{f}_{{\lambda }_n}^m(X)\}}{\pi (A;X)}])\\ +E\left[\frac{R(Y,\mathrm{\Delta },S_C^m,E_{\stackrel{\sim }{T}}^m)\varphi \{A\widehat{f}(X)\}}{\pi (A;X)}-\frac{R(Y,\mathrm{\Delta },{\widehat{S}}_C,{\widehat{E}}_{\stackrel{\sim }{T}})\varphi \{A\widehat{f}(X)\}}{\pi (A;X)}\right]\\ +E\left[\frac{R(Y,\mathrm{\Delta },{\widehat{S}}_C,{\widehat{E}}_{\stackrel{\sim }{T}})\varphi \{A{f}_{{\lambda }_n}^m(X)\}}{\pi (A;X)}-\frac{R(Y,\mathrm{\Delta },S_C^m,E_{\stackrel{\sim }{T}}^m)\varphi \{A{f}_{{\lambda }_n}^m(X)\}}{\pi (A;X)}\right]\\ =a({\lambda }_n)+(I)+(II)+(\mathit{III}).\end{array}$$

To bound (II) and (III), we consider the class of functions

$$\begin{array}{l}\mathcal{B}=\{R\{Y,\mathrm{\Delta },S_C({\beta }_C,{\mathrm{\Lambda }}_{C0}),E_{\stackrel{\sim }{T}}({\beta }_T,{\mathrm{\Lambda }}_{T0})\}:{\beta }_C\in {ℝ}^d,\Vert {\beta }_C-{\beta }_C^m\Vert <{\delta }_0,{\beta }_T\in {ℝ}^d,\\ \Vert {\beta }_T-{\beta }_T^m\Vert <{\delta }_0,{\mathrm{\Lambda }}_{C0},{\mathrm{\Lambda }}_{T0}\text{are}\text{bounded}\text{monotone}\text{functions}\text{in}[0,\tau ],\\ \underset{t}{sup}\mid {\mathrm{\Lambda }}_{C0}(t)-{\mathrm{\Lambda }}_{C0}^m(t)\mid <{\delta }_0,\underset{t}{sup}\mid {\mathrm{\Lambda }}_{T0}(t)-{\mathrm{\Lambda }}_{T0}^m(t)\mid <{\delta }_0\},\end{array}$$

where δ₀ is a small constant, and ${\beta }_T^m,{\beta }_C^m,{\mathrm{\Lambda }}_{C0}^m(t),{\mathrm{\Lambda }}_{T0}^m(t)$ are the limits of β̂_T, β̂_C, Λ̂_C0 and Λ̂_T0 based on the Cox models. Then |R{Y, Δ, S_C(β_C, Λ_C0), E_T̃ (β_C, Λ_C0)}|/π(A, X) can be bounded from above by a constant, say M.

Trivial bounds for ||f̂||_k and ${\Vert f_{{\lambda }_n}^m\Vert }_k$ are obtained as ${\Vert \widehat{f}\Vert }_k\le M{\lambda }_n^{-1/2}$ and ${\Vert f_{{\lambda }_n}^m\Vert }_k\le M{\lambda }_n^{-1/2}$. For every $f\in M{\lambda }_n^{-1/2}{B}_{{\mathcal{H}}_k},\mid {(1-Af)}^{+}\mid \le 1+M{\lambda }_n^{-1/2}=B$. Thus,

$$\left|E\left[\frac{R(Y,\mathrm{\Delta },S_C^m,E_{\stackrel{\sim }{T}}^m)\varphi \{Af(X)\}}{\pi (A;X)}-\frac{R(Y,\mathrm{\Delta },{\widehat{S}}_C,{\widehat{E}}_{\stackrel{\sim }{T}})\varphi \{Af(X)\}}{\pi (A;X)}\right]\right|=O_p(n^{-\gamma }{\lambda }_n^{-1/2}).$$

We use empirical process theory to bound (I). Define the functional class

$$\begin{array}{l}\mathcal{L}=\{{\lambda }_n{\Vert f\Vert }_k^2+\frac{R(Y,\mathrm{\Delta },S_C,E_{\stackrel{\sim }{T}})\varphi \{Af(X)\}}{\pi (A;X)}-\frac{R(Y,\mathrm{\Delta },S_C,E_{\stackrel{\sim }{T}})\varphi \{A{f}_{{\lambda }_n}^m(X)\}}{\pi (A;X)}-{\lambda }_n{\Vert f_{{\lambda }_n}^m\Vert }_k^2,\\ f\in M{\lambda }_n^{-1/2}{B}_{{\mathcal{H}}_k},R(Y,\mathrm{\Delta },S_C,E_{\stackrel{\sim }{T}})\in \mathcal{B}\},\end{array}$$

and 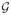= {E(l) − l : E(l) = ε, l ∈ 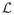}. Let $Z={sup}_{g\in \mathcal{G}}{n}^{-1}{\sum }_{i=1}^{n}g(X_i)$. Since E(g) = 0, g ∈ 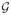, it follows from Lemma S.1 in the Supplementary Material, by setting ρ = 1, that pr{Z ≥ 2E(Z) + σ(Kb)^1/2n^−1/2 + 2KBbn⁻¹} ≤ e^−b, where $B=O({\lambda }_n^{-1/2})$. Furthermore, ${\sigma }^2\le c_n^{\prime }\epsilon$ following the arguments for proving Theorem 3.4 in Zhao et al. (2012), given that $E(l^2)\le c_n^{\prime }E(l)$, where $c_n^{\prime }=O({\lambda }_n^{-1})$. In addition, for $f\in M{\lambda }_n^{-1/2}{B}_{{\mathcal{H}}_k}$,

$$E(Z)=E\left\{\underset{g\in \mathcal{G}}{sup}{n}^{-1}\sum _{i=1}^{n}g(X_i)\right\}=E\left[\underset{E(l^2)\le c_n^{\prime }\epsilon }{sup}\left|E\{l(X)\}-n^{-1}\sum _{i=1}^{n}l(X_i)\right|\right].$$

Since | ${\beta }_C-{\beta }_C^m$| and | ${\beta }_T-{\beta }_T^m$| are bounded by δ₀, they lie in a hypercube of ℝ^2d. Moreover, { ${\mathrm{\Lambda }}_{C0}:{sup}_t\mid {\mathrm{\Lambda }}_{C0}(t)-{\mathrm{\Lambda }}_{C0}^m(t)\mid <{\delta }_0$} is a class of monotone functions, so is { ${\mathrm{\Lambda }}_{T0}:{sup}_t\mid {\mathrm{\Lambda }}_{T0}(t)-{\mathrm{\Lambda }}_{T0}^m(t)\mid <{\delta }_0$}. The function in 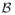is Lipschitz continuous with respect to all these parameters and the Lipschitz constant is less than a constant W. There exists a constant K, depending on d, such that the bracketing number for 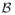satisfies N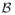_[·]{ , εW, L₂(P)} ≤ K(δ₀/ε)^2d+2. According to (10), sup_Pn log N { 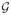, ε, L₂(P_n)} ≤ c_nε^−p, and therefore

$$E(Z)\le c_{p}M{\lambda }_n^{-\frac{1}{2}}max\left\{{(M^2{\lambda }_n{c}_n^{\prime }\epsilon )}^{(2-p)/4}{c_n}^{1/2}{n}^{-1/2},{c_n}^{2/(2+p)}{n}^{-2/(2+p)}\right\},$$

where c_p is a constant depending on p. See Proposition 5.5 in Steinwart & Scovel (2007) and references therein. Consequently,

$$\begin{array}{l}\text{pr}(\left|n^{1/2}\left[n^{-1}\sum _{i=1}^{n}l(X_i)-E\{l(X)\}\right]\right|>{\left(c_n^{\prime }\epsilon Kb\right)}^{1/2}{n}^{-1/2}+2K{\mathit{Bbn}}^{-1}\\ +2c_{p}M{\lambda }_n^{-1/2}max\left\{{(M^2{\lambda }_n{c}_n^{\prime }\epsilon )}^{(2-p)/4}{c_n}^{1/2}{n}^{-1/2},{c_n}^{2/(2+p)}{n}^{-2/(2+p)}\right\})\le e^{-b}.\end{array}$$

Given that 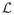is convex, if l ∈ 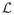satisfies $n^{-1}{\sum }_{i=1}^{n}l(X_i)\le \alpha \epsilon$ and E{l(X)} ≥ ε, there exists l′ ∈ 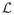such that $n^{-1}{\sum }_{i=1}^n{l}^{\prime }(X_i)\le \alpha \epsilon$ and E{l′(X)} = ε. Thus, with probability at least 1 − e^−b, every l ∈ 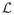with $n^{-1}{\sum }_{i=1}^{n}l(X_i)\le \alpha \epsilon$ satisfies El ∈ ε (Bartlett et al., 2006; Steinwart & Scovel, 2007). Since

$$n^{-1}\sum _{i=1}^n\left[{\lambda }_n{\Vert \widehat{f}\Vert }_k^2+\frac{R(Y_i,{\mathrm{\Delta }}_i,{\widehat{S}}_C,{\widehat{E}}_{\stackrel{\sim }{T}})\varphi \{A_i\widehat{f}(X_i)\}}{\pi (A_i;X_i)}-{\lambda }_n{\Vert f_{{\lambda }_n}^m\Vert }_k^2-\frac{R(Y_i,{\mathrm{\Delta }}_i,{\widehat{S}}_C,{\widehat{E}}_{\stackrel{\sim }{T}})\varphi \{A_i{f}_{{\lambda }_n}^m(X_i)\}}{\pi (A_i;X_i)}\right]\le 0<\alpha \epsilon ,$$

with probability at least 1 − e^−b,

$$E\left[{\lambda }_n{\Vert \widehat{f}\Vert }_k^2+\frac{R(Y,\mathrm{\Delta },{\widehat{S}}_C,{\widehat{E}}_{\stackrel{\sim }{T}})\varphi \{A\widehat{f}(X)\}}{\pi (A;X)}-{\lambda }_n{\Vert f_{{\lambda }_n}^m\Vert }_k^2-\frac{R(Y,\mathrm{\Delta },{\widehat{S}}_C,{\widehat{E}}_{\stackrel{\sim }{T}})\varphi \{A{f}_{{\lambda }_n}^m(X)\}}{\pi (A;X)}\right]\le \epsilon .$$

It follows that,

$$\text{pr}[\mid (I)\mid >{\left\{4c_{p}M{\lambda }_n^{-1/2}{(M^2{\lambda }_n{c}_n^{\prime })}^{(2-p)/4}{c_n}^{1/2}{n}^{-1/2}\right\}}^{4/(p+2)}+c_{p}M{\lambda }_n^{-1/2}{c_n}^{2/(2+p)}{n}^{-2/2+p}+c_n^{\prime }{\mathit{Kbn}}^{-1}+2K{\mathit{Bbn}}^{-1}]\le 2e^{-b},$$

with $c_n^{\prime }=O({\lambda }_n^{-1})$ and $B=O({\lambda }_n^{-1/2})$. Using M_p as a new constant depending on p, we subsequently obtain the desired results.

Geometric noise exponent

The approximation error depends on the noise component q, called the geometric noise exponent (Steinwart & Scovel, 2007). Let

$$\eta (x)=\frac{E\{R(Y,\mathrm{\Delta },S_C^m,E_{\stackrel{\sim }{T}}^m)\mid X=x,A=1\}-E\{R(Y,\mathrm{\Delta },S_C^m,E_{\stackrel{\sim }{T}}^m)\mid X=x,A=-1\}}{E\{R(Y,\mathrm{\Delta },S_C^m,E_{\stackrel{\sim }{T}}^m)\mid X=x,A=1\}+E\{R(Y,\mathrm{\Delta },S_C^m,E_{\stackrel{\sim }{T}}^m)\mid X=x,A=-1\}}+1/2.$$

Hence, 2η(x) − 1 is the decision boundary for the optimal treatment decision rules when we use the pseudo-outcomes. We further define 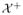= {x ∈ 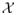: 2η(x) − 1 > 0}, and 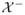= {x ∈ 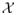: 2η(x) − 1 < 0}. A distance function to the boundary between 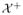and 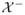is Δ(x) = d̃(x, 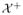) if x ∈ 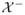, Δ(x) = d̃(x, 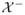) if x ∈ 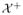and Δ(x) = 0 otherwise, where d̃(x, 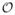) denotes the distance of x to a set with respect to the Euclidean norm. Then the distribution P is said to have geometric noise exponent 0 < q < ∞, if there exists a constant C > 0 such that

$$E\left[exp\left\{-\frac{\mathrm{\Delta }{(X)}^2}{t}\right\}\mid 2\eta (X)-1\mid \right]\le {Ct}^{qd/2},t>0.$$

Δ(X) actually measures the size of the set of points that are close to the opposite class. Indeed, if the data are distinctly separable, that is, when |2η(x) − 1| > δ > 0, for some constant δ, and η is continuous, q can be very large. If either model for the survival time or the censoring time is correctly specified, 2η(x) − 1 is the optimal treatment decision rule, where sign{2η(x) − 1} = sign{f^*(X)}.