Nanoparticle self-assembly at the interface of liquid crystal droplets

Significance

Controlled assembly of nanoparticles at liquid crystal interfaces could lead to easily manufacturable building blocks for assembly of materials with tunable mechanical, optical, and electronic properties. Past work has examined nanoparticle assembly at planar liquid crystal interfaces. In this work, we show that nanoparticle assembly on curved interfaces is drastically different and arises for conditions under which assembly is too weak to occur on planar interfaces. We also demonstrate that liquid crystal-mediated nanoparticle interactions are strong, are remarkably sensitive to surface anchoring, and lead to hexagonal arrangements that do not arise in bulk systems. All of these elements form the basis for a highly tunable, predictable, and versatile platform for hierarchical materials assembly.

Abstract

Nanoparticles adsorbed at the interface of nematic liquid crystals are known to form ordered structures whose morphology depends on the orientation of the underlying nematic field. The origin of such structures is believed to result from an interplay between the liquid crystal orientation at the particles’ surface, the orientation at the liquid crystal’s air interface, and the bulk elasticity of the underlying liquid crystal. In this work, we consider nanoparticle assembly at the interface of nematic droplets. We present a systematic study of the free energy of nanoparticle-laden droplets in terms of experiments and a Landau–de Gennes formalism. The results of that study indicate that, even for conditions under which particles interact only weakly at flat interfaces, particles aggregate at the poles of bipolar droplets and assemble into robust, quantized arrangements that can be mapped onto hexagonal lattices. The contributions of elasticity and interfacial energy corresponding to different arrangements are used to explain the resulting morphologies, and the predictions of the model are shown to be consistent with experimental observations. The findings presented here suggest that particle-laden liquid crystal droplets could provide a unique and versatile route toward building blocks for hierarchical materials assembly.

A growing body of theoretical and experimental work has sought to direct the assembly of molecules and nanoparticles at interfaces by exploiting the elastic forces that arise in liquid crystals (LCs) (1–5). Nematic LCs possess orientational order along a unit vector, the so-called nematic director. They also exhibit defects—regions of low order whose morphology and position depends on a delicate balance between elastic, enthalpic, and interfacial contributions to the free energy. The orientation of nematic LCs and any corresponding defects can be perturbed by introducing particles. The symmetry and structure of the director field around a particle also depends on the interaction between the LC and the particle, often referred to as anchoring. Particles with perpendicular (homeotropic) anchoring induce either dipolar or quadrupolar symmetry in the LC, leading to formation of point defects or Saturn-ring defects, respectively (6). Particles with planar anchoring induce quadrupolar symmetry, which is accompanied by two surface defects, generally referred to as boojums (6). Distortions of the nematic field cost elastic energy and therefore give rise to anisotropic, long-range interactions between particles. Indeed, particles in nematic LCs aggregate and “bind,” thereby minimizing the volume of defects and the large free energy that is associated with their elastic strain. Equilibrium particle arrangements in nematic LCs depend strongly on the topology of the underlying defects. Homeotropic particles with point, dipolar defects form chains along the nematic director, whereas quadrupolar, Saturn-ring defects form kinked chains that are perpendicular to the nematic director (7). Particles with planar anchoring form chains whose main axis forms a 30° angle with the nematic director (8). Recent work has also shown that particles can be trapped in topological defects (9, 10) and in chiral defects (11, 12). Particles localized at a planar LC interface also exhibit LC-induced interactions. For the particular case of perpendicular anchoring, it has been shown that particles aggregate into ordered structures whose morphology can be controlled by addition of surfactants (13). Recently, a robust mechanism has been reported to direct assembly of homeotropic particles trapped at the LC interface into reconfigurable structures by controlling surface anchoring and bulk defect structure (14).

This work considers the aggregation of nanoparticles at LC droplet interfaces. Past studies from our own groups have shown that LCs confined in small droplets can be used to induce formation of intriguing surfactant nanophases at their interfaces (15). Experiments and simulations have also shown that the defects that arise in LC droplets can be used to localize individual nanoparticles or pairs of nanoparticles with considerable precision (16, 17). More generally, droplets offer an effective, yet simple means for confining LCs, thereby controlling the balance of interfacial and elastic contributions to the free energy and the response of LCs to external cues (18, 19). Depending on surface anchoring, LC droplets can exhibit two primary morphologies (20). Homeotropic anchoring leads to radial LC droplets, with a single ring or point defect in the center, whereas planar anchoring leads to bipolar droplets having two surface point (or boojum) defects. The localization of particles at boojums reduces the splay elastic free energy significantly. Remarkably, the trapping of particles into the boojums is independent of the type of anchoring of LC at the particle surfaces (16). A recent study examined the self-assembly of homeotropic particles at the surface of a bipolar droplet and observed formation of star-like patterns (21). Dipole–dipole interactions between particles led to formation of linear chains along the longitudinal orientation of the director field that, upon finding the boojums, organized into stars.

Our focus is to examine and understand the behavior of planar particles located at the surface of micrometer-sized bipolar droplets. We restrict our attention to degenerate planar anchoring and planar droplets because such conditions are much more permissive than homeotropic anchoring, and it is therefore difficult to anticipate the types of arrangements that may arise on the basis of symmetry arguments. By examining the structures and LC morphologies that arise as a function of particle number, we are able to provide a systematic view of nanoparticle assembly in such systems. Our past experiments have shown that a single polystyrene (PS) particle with planar anchoring and radius of 0.5 µm adsorbed at the surface of a bipolar 5CB droplet diffuses into a boojum defect (16). Here, we show that when more particles are adsorbed at the droplet surface, they migrate to the poles and assemble into arrangements that can be mapped into hexagonal arrays around the boojum. The predictions of our theoretical calculations are shown to be consistent with experimental observations (22).

Results and Discussion

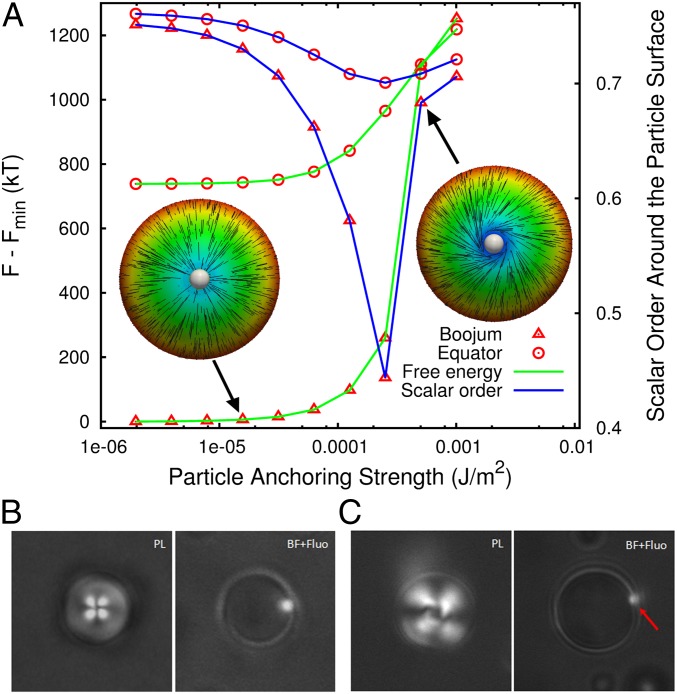
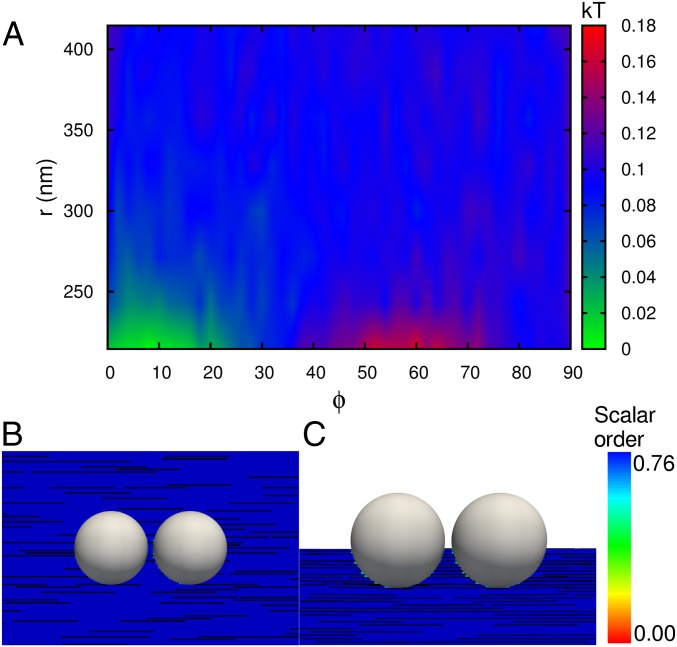
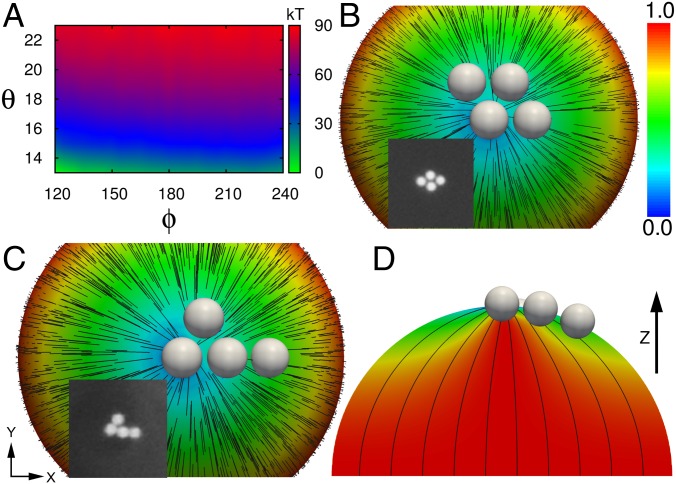
For reference, our analysis begins with a single particle at the surface of a bipolar droplet, where anchoring strength plays an important role in localizing the particle at the boojums. Two competing contributions to the free energy must be considered. On the one hand, when a particle is placed at a pole, effectively removing the boojum, the defect’s high splay elastic energy is reduced. On the other hand, the conflict between the nematic field at the poles and the particle’s planar anchoring increases the surface energy and, therefore, the total free energy. To better understand this trade-off, two types of configurations with a range of anchoring strengths are considered: a polar placement (where the particle is located at a pole, along the z axis at the boojum), and equatorial placement (in the XY plane). Fig. 1A shows the free energy of these two configurations as a function of particle anchoring strength. The difference in the free energy between them indicates that a strong preference exists for adsorbing the particle at the boojum. For polar placement, the nematic field in the pole is stronger than the anchoring contribution, and it reorients the nematic field at the particle’s surface from planar to homeotropic. The scalar order around the particle’s surface for both configurations is shown in Fig. 1A. In both cases, the free energy is minimized not only by orienting the field at the particle’s surface but also by reducing the scalar order. Note that, for a particle in the boojum, the scalar order at the surface is reduced, whereas for a particle in the equator the scalar order is only reduced at two points along the nematic director and close to the surface of the droplet. We have found a critical anchoring strength for polar placement, after which the system experiences rapid changes in the free energy and the scalar order. At that point, the anchoring strength is too large and cannot be overcome by reorientation of the nematic field at the particle’s surface, causing the nematic field to twist and stand along the planar anchoring at the particle’s surface. Twisting the nematic field modifies the interior morphology of the droplet and increases the twist elastic energy by a factor of 4. These results are consistent with our experimental observations. For PS particles, where anchoring is believed to be in the vicinity of 10⁻⁵ to 10⁻⁴ J⋅m⁻² (23), some of the droplets exhibit a bipolar morphology with the particle at the boojum (Fig. 1B), whereas the others exhibit a twisted morphology (Fig. 1C). We attribute the fact that not all droplets adopt a twisted or a bipolar state to the inhomogeneity of the particles, and the fact that the experimental anchoring strength lies exactly in the range where droplets undergo a pronounced change from bipolar to twisted (Fig. 1A). On the basis of these results, we conclude that the elimination of a high splay elastic region (defect) by the particles dominates the increase of surface energy. Note that adsorbing a particle with anchoring 10⁻⁵ J⋅m⁻² at the boojum reduces the contribution of splay elastic energy to the total elastic energy from 60.6% to 59.6%, whereas it increases the contribution of bend elastic energy to the total elastic energy from 38.7% to 39.6%. We have also performed simulations with particle anchorings in the range of 10⁻⁵ to 10⁻⁴ J⋅m⁻² and observed similar behavior. For concreteness, and unless otherwise noted, in the majority of our calculations with more than one particle we fix the particle anchoring strength at W_particle = 1 × 10⁻⁵ J⋅m⁻²; for this anchoring strength, the ratio of Kleman–de Gennes length (24) (L/W) to particle radius, L/WR_p, is 6, and therefore the effect of surface anchoring is nonnegligible. It is important to emphasize that, for such anchoring conditions, our simulations of particles at a planar interface show that the magnitude of quadrupole–quadrupole elastic interaction between adsorbed particles is extremely small. Fig. 2A shows the free energy of two adsorbed particles at the interface as a function of r and φ in polar coordinates; one particle is fixed at the origin. The nematic director is along the x axis. The depth of the minimum in Fig. 2A is smaller than kT; for such small quadrupole–quadrupole interactions, thermal fluctuation should overcome any tendency to aggregate. This observation is consistent with experimental observations of PS particles at planar aqueous–LC interfaces (22). Note, however, that in experiments PS particles might exhibit a weak charge that may lead to additional repulsive effects that are not included in our calculations. Also, note that, as alluded to earlier, the anchoring strength used in experiments is not known with a high degree of precision and might be slightly different from that used in our simulations. Fig. 2 B and C show that the existence of the particle does not perturb the nematic director.

Fig. 1.

(A) Free energy of one particle at the droplet surface as a function of particle anchoring strength for two types of configurations: the particle located at the boojum, and the particle placed in the equator. The difference of free energies indicates that there is a strong tendency to adsorb particles at the boojum. The scalar order around the particle’s surface for both configurations is shown. There is a critical anchoring strength when the particle is located at the boojum, after which the free energy and the local scalar order suddenly increase. At that point, the nematic field twists and stands along the planar anchoring. Insets in the plot correspond to the top view of weak and strong anchoring. The director field is illustrated with black lines, and the color represents the z component of director field. (B and C) Polarized-light, bright-field, and fluorescence images of a 5CB droplet with a PS particle localized at the boojum. (C) Polarized-light image shows the twisting of the nematic field near the boojum.

Fig. 2.

(A) Free energy as a function of r and φ for two particles at a planar LC interface. One particle is located at the origin of a polar coordinate system, and the other is driven around the origin. The nematic director is along the x axis. (B and C) Top view and side view of two particles at closest distance, r = 215 nm, and angle φ = 0°, respectively. The anchoring strength is 10⁻⁵ J/m².

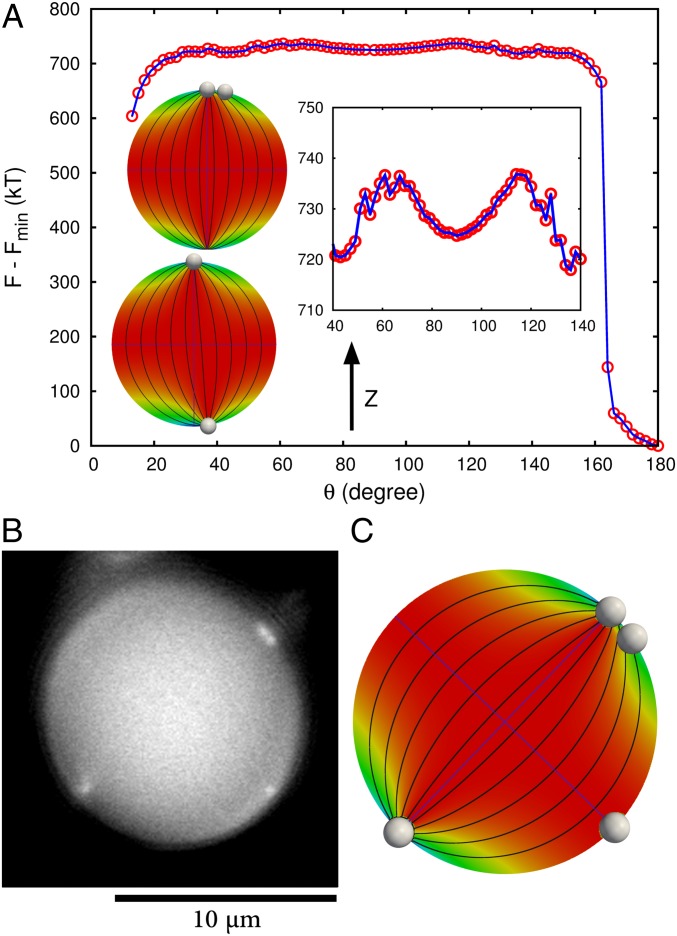
In what follows, we examine the sequential addition of particles to the droplet. For the case of two particles, one is located at the pole along the z axis at the boojum, and the other is driven along the droplet surface from the other pole. The polar angle θ is defined by the particle position vector (relative to the droplet center) and the z axis. Fig. 3A shows the free energy of the system as a function of that angle. The first minimum in the systems, at θ = 13°, occurs when two particles are close to each other. It has a depth of 130 kT relative to the maximum free energy. This strong binding energy should be contrasted with that observed at the planar interface, which is only a fraction of kT. The spherical confinement of the LC by the droplet induces a strong interaction that is not there in the absence of curvature. The second minimum corresponds to two particles located at opposing boojums, and is 600 kT deeper than the first minimum. In the central region (40° < θ < 140°), where the elastic energy is small, one can observe a plateau in the free energy. As shown in the Inset, another minimum is observed at θ = 90° (the equator), with a depth of 10 kT relative to the maximum free energy. This local minimum was not seen in previous many-particle simulations of smaller droplets with Gay–Berne ellipsoids (17). However, our experiments (also shown in Fig. 3B) do confirm that particles are observed to be localized at the equator, consistent with our predictions. Another significant difference is that, in previous work, when two particles were close they shared the boojum. Here, the boojum absorbs only one particle. Note that, in Gay–Berne simulations, the ratio of particle radius to droplet radius was four times larger than that considered here. When the particle is close to the opposite boojum, θ > 160°, the boojum moves away from the z axis and absorbs the particle. As shown in Fig. 3A, this effect reduces the elastic free energy significantly.

Fig. 3.

(A) Free energy for two particles, one of which is located at the boojum along the z axis, and the other is driven along the droplet surface. The polar angle θ controls particle separation. Inset pictures in the plot correspond to the final phase of systems at θ = 13° and θ = 170°. The field lines and color that represents the z component of director field show the position of two boojums. In the first minimum, at θ = 13°, the boojum adsorbs only one particle. At the angle 170° the opposite boojum diffuses to the particle to reduce the elastic free energy. Inset plot shows a local minimum at θ = 90°, which corresponds to the equator of the droplet. (B) Fluorescent micrographs of a 5CB droplet in water with four PS particles. Particles are localized at the positions predicted by simulations. (C) Localization of four particles at the droplet surface corresponding to the minimum free energy, in agreement with the experimental observation of B.

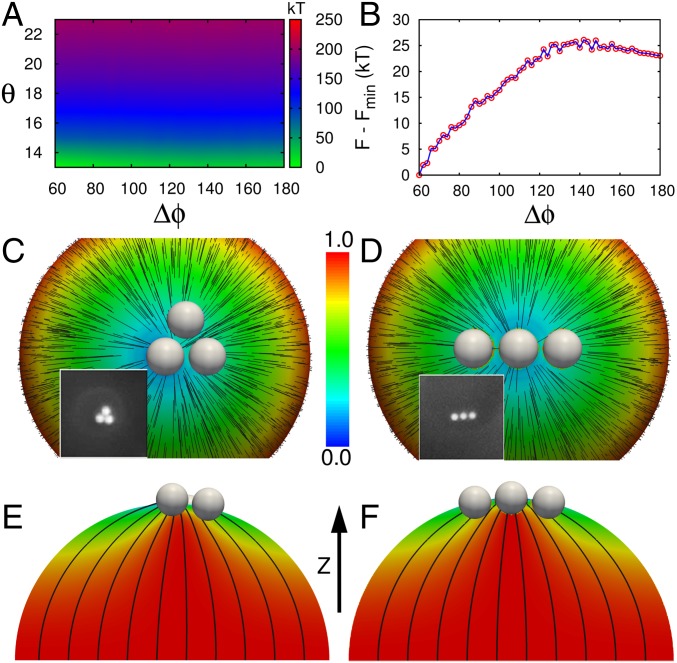
For the case with three particles, one of them is fixed along the z axis at the position of the boojum, and the other two particles are driven along the droplet surface to find the arrangement with the minimum free energy. The position of the particles is given by a polar angle, θ, and the azimuthal angle, φ. Two particles are constrained to have the same polar angle, and their separation is defined by the difference between their corresponding azimuthal angles, Δφ. Fig. 4A shows the free-energy profile for three particles as a function of θ and Δφ. As indicated in Fig. 4A, and consistent with results from previous simulations with two particles (see above), there is a strong tendency for particles to aggregate at the pole where θ is a minimum, namely θ = 13. At the minimum distance from the boojum, there are two minima, at Δφ = 60 and 180 (Fig. 4B), which correspond to an equilateral triangle and a line arrangement of the three particles, respectively. The equilateral triangle arrangement corresponds to the global minimum; the ratio between the triangle edges and the radius of the particles is 1.12, which is consistent with experiments (which yield a value of 1.17; SI Text). The line arrangement is metastable, with a free energy that is higher than that of the equilateral triangle arrangement by 23 kT. The contribution of splay elastic energy for the equilateral triangle arrangement is 59.7%, which is higher than that for the line arrangement and the droplet with one particle at the boojum by 0.4% and 0.1%, respectively. That result shows that the splay elastic energy is high only at the boojum, and in the pole both splay and bend energy contribute by the same amount. Therefore, the first particle eliminates the high splay energy at the boojum, and the others aggregate to the pole to reduce the total elastic energy. At the pole, interactions between particle defects cause them to assemble into different arrangements, which we discuss in what follows.

Fig. 4.

Arrangement of three particles at the droplet surface, one of which is located at the boojum; the other two particles are driven along the droplet surface. Two particles are constrained to have the same polar angle from the boojum. The polar angle θ controls the distance of the two particles with the last particle fixed at the boojum, and the difference of corresponding azimuthal angles Δϕ monitors the separation of two particles. (A) The free-energy profile indicates that the boojum strongly adsorbs particles to reduce the free energy. (B) Free energy as a function of Δϕ at θ = 13°, closest distance to the boojum. Two minima are observed at θ = 60 and 180, which correspond to an equilateral triangle and a line arrangement of the three particles, respectively. (C and D) Top view of two stable particle arrangements. The director field is illustrated with black lines, and color represents the z component of the director field. Insets in the figures correspond to fluorescence micrographs of 5CB droplets in water emulsions with three PS particles. (E and F) Field lines within the droplet for equilateral triangle and a line arrangement, respectively.

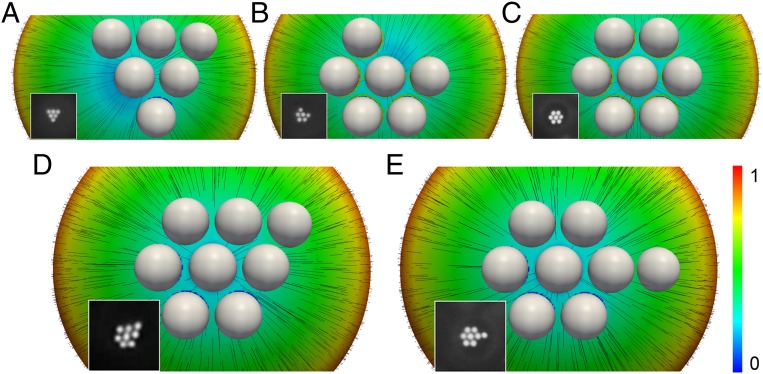
As a next step, we consider three fixed particles in a stable, equilateral triangle arrangement, and add a fourth additional particle to the droplet surface. As shown in the free-energy profile of Fig. 5A, there is a minimum at θ = 13 and φ = 120, corresponding to a diamond arrangement (Fig. 5B). We can see in Fig. 5A that the diamond arrangement is the only stable arrangement for four particles. However, as shown in Fig. 5C, one can alternatively locate the fourth particle far away from the particles in the boojum and behind the two other particles. In that case, the quadrupolar defects organize them into a line along the direction of the nematic field (Fig. 5C) (25). The particle arrangement in Fig. 5C is also metastable, and has a free energy that is 70 kT higher than that of the diamond arrangement. The strength of the interactions between particle defects decreases significantly when they move away from the boojum, and becomes negligible at the equator, on the order of 1 kT. This is consistent with results from previous simulations with two particles at the flat interface (see above). Both arrangements exhibit the same splay and bend contributions to the total elastic energy, namely 59.6% and 39.6%, respectively. Those contributions are equal to the contributions in a droplet with one particle at the boojum.

Fig. 5.

(A) Free-energy profile for four particles as a function of θ and ϕ. Three particles are fixed in a stable equilateral triangle arrangement, and the other one is driven along the droplet surface. (B and C) Top view of particle arrangements at the droplet surface. The director field is illustrated with black lines, and color represents the z component of the director field. (B) Diamond arrangement of four particles with minimum free energy. (C) A metastable arrangement for four particles. (D) Field lines within the droplet for the metastable arrangement. Insets correspond to fluorescent micrographs of 5CB droplets in water emulsions with four PS particles.

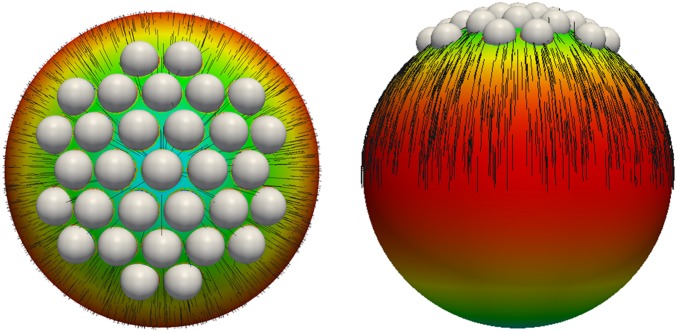
When the number of particles is increased in a sequential manner, we find that all stable multiparticle arrangements correspond to a hexagonal array (Fig. 6 A–C). Note that the multiparticle arrangement shown in Fig. 6C reduces the splay elastic energy contribution to the total elastic energy by 1.4% compared with the droplet with one particle at the boojum. With eight particles, we can examine the arrangement of a second layer of particles around the boojum. We first consider a hexagonal arrangement with one particle in the center located at the pole of the droplet. The boojum is placed at the center, and the eighth particle is driven around the hexagonal structure. We find two arrangements having a low free energy: a diamond and a line (Fig. 6 D and E). The diamond arrangement has a minimum free energy because the particle is closer to the boojum. The difference of free energy between these two arrangements is 11 kT. By moving away from the boojum, the depth of the free-energy minimum becomes shallower, as was shown in Fig. 3A. There is also a plateau in the free energy. Both arrangements exhibit the same splay and bend contributions to the total elastic energy—58.5% and 40.7%, respectively. Due to the curvature of the surface of the droplet, for large particle coverages, the particles cannot assemble into a perfect uniform hexagonal lattice; in that case, the hexagonal lattice transforms into a lattice that also includes five-coordinated sites, reminiscent of those observed in curved colloidal crystals (26). However, as shown in Fig. 7, for the coverages considered in this work, particles can form hexagonal lattices that cover the pole completely. For the arrangement of Fig. 7, with 31 particles, the contributions of elastic splay and bend to the total elastic energy are 56.4% and 42.6%, respectively.

Fig. 6.

(A–C) Multiparticle arrangements at the pole of bipolar droplet. Insets in the figures correspond to fluorescence micrographs of 5CB droplets in water emulsions. (D and E) Two arrangements for eight particles: a diamond and a line arrangement. The diamond arrangement has 11 kT lower free energy than the line arrangement.

Fig. 7.

Hexagonal lattices arrangement of multiparticle at the pole of bipolar droplet, which covers the pole.

It is important to point out that there is a precedent for observing hexagonal assemblies at planar interfaces; in particular, past work has shown that elastic LC-mediated interactions between a pair of planar particles at the interface of a hybrid channel can induce particles to arrange into hexagonal shapes (27, 28). A central difference between past observations and the results presented here is that, on planar interfaces, the particles used in our simulations do not exhibit attractions, and in experiments, they actually exhibit weak electrostatic repulsions. We propose the following argument, based on different elastic contributions to the free energy, to explain the origin of attractions in the droplet, but their absence on a flat interface. A bipolar droplet has two poles, each having a large elastic energy. The size of the pole can be estimated from the results in Fig. 3A, as the region where the free-energy profile reaches a plateau θ = 13°. In a bipolar droplet, 45% of the total elastic energy is localized in the two poles; these regions, however, only represent 4% of the droplet’s volume. The elastic-energy density is therefore large at the poles. The presence of particles at the poles reduces or eliminates that high elastic energy. The contributions of splay, twist, and bend elastic energy to the total elastic energy in a pole are 76%, 0.4%, and 23%, respectively. Particles in a pole therefore assemble into arrangements that can reduce splay and bend elastic energy. For example, for the three particles shown in Fig. 4 C and D, the triangular arrangement reduces the bend elastic energy, whereas the line arrangement reduces splay energy. The contribution of splay elastic energy to the total elastic energy in a pole for the line arrangement is 74%, which is lower than that for a triangular arrangement by 2%. In contrast to the polar region, at the center of the droplet the elastic energy density is small, and particle clusters do not appear there (or in a flat surface) because they have little effect on lowering the free energy.

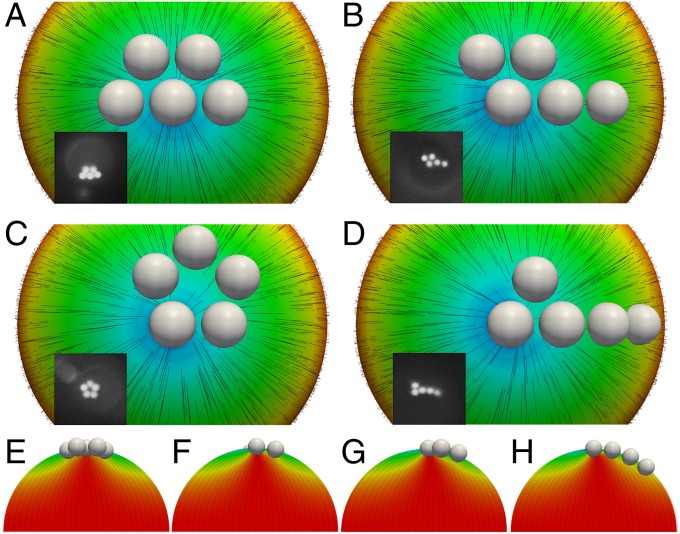
In addition to a hexagonal arrangement, we also considered a pentameric ring pattern. Fig. 8 A–D shows results for different arrangements of five particles, organized in order of increasing free energy. As expected, the hexagonal arrangement, which covers a larger fraction of the pole, is the most stable arrangement (Fig. 8A). Other arrangements shown in Fig. 8 B–D are metastable and have free energies that are 66, 142, and 153 kT higher than that of the hexagon, respectively. Another possibility for a pentamer ring pattern is to locate the boojum at the center of the ring. Our results indicate that this configuration is completely unstable, and the boojum absorbs the particle.

Fig. 8.

Top view of five particle arrangements at the pole of bipolar droplet. (A) Stable arrangement with minimum free energy. (B–D) Metastable arrangements have free energies that are 66, 142, and 153 kT higher than that of the stable arrangement, respectively. The director field is illustrated with black lines, and color represents the z component of director field. Insets in the figures correspond to the fluorescent micrographs of 5CB droplets in water emulsions. (E) Field lines within the droplet for arrangement in A. (F and G) Field lines within the droplet for pentameric ring pattern. (H) Field lines within the droplet for arrangement in D.

The result reported in this paper demonstrates the arrangement of planar particles at the surface of bipolar droplet. We show that bipolar droplets that possess two boojums can be used to assembly of planar particles to the poles and create dipolar droplets. The presence of particles at the poles eliminates the high splay elastic energy and therefore reduces the free energy. Our calculations also indicate that, when the same particles are placed at a planar interface, the interaction between them is much weaker than the thermal energy. The confinement induced by the droplet therefore serves to increase the interactions between particles by at least three orders of magnitude, thereby providing a powerful and potentially useful means for controlling or modulating nanoparticle assembly into ordered structures through manipulation of droplet size. Particles at the poles assemble into different packing arrangements that can be mapped onto hexagonal lattices. We show that, among all of packing arrangements at the pole, the one that covers a larger fraction of the pole is the most stable and exhibits the lowest free energy. The results of our theoretical description have been shown to be in remarkable agreement with experimental observations, particularly when we consider that a simple model with only one elastic constant was used to describe the LC. Past work has shown that the use of two elastic constants can influence the interaction of two planar particles (25), and introducing additional elastic constants could lead to improved predictions for subsequent studies. As noted earlier, the PS particles used in experiments are slightly charged and exhibit an electrostatic repulsion that is evident in assembly experiments at planar interfaces. At droplet interfaces, the attractions mediated by the LC can easily overcome electrostatic repulsions. In future work, it will be interesting to examine the effects of charge and salt concentration on the assembly processes outlined here.

Simulation and Experimental Details

The LC–nanoparticle system is described at the level of a Landau–de Gennes free-energy model for the Q tensor. The total free energy is given as follows:

$$F={\displaystyle \underset{bulk}{\int }\left\{\frac{A}{2}\left(1-\frac{U}{3}\right)Q_{ij}{Q}_{ji}-\frac{AU}{3}{Q}_{ij}{Q}_{jk}{Q}_{ki}+\frac{AU}{4}{\left(Q_{ij}{Q}_{ji}\right)}^2\right\}dV}+{\displaystyle \underset{bulk}{\int }\left\{\frac{L}{2}\frac{\partial Q_{ij}}{\partial x_k}\frac{\partial Q_{ij}}{\partial x_k}\right\}dV}+{\displaystyle \underset{surface}{\int }\left\{W_{droplet}{\left({\tilde{Q}}_{ij}-{\tilde{Q}}_{ij}^{\perp }\right)}^2\right\}dS}+{\displaystyle \underset{surface}{\int }\left\{W_{particle}{\left({\tilde{Q}}_{ij}-{\tilde{Q}}_{ij}^{\perp }\right)}^2\right\}dS},$$

where A and U are material parameters that capture the thermodynamics of the LC, L is the elastic constant in the one-constant approximation, and W_particle and W_droplet denote the strength of particle and droplet surface anchoring, respectively. The first term represents the short-range free energy by a Landau–de Gennes expression (29). The bulk scalar order parameter is controlled by the dimensionless parameter U. The second term characterizes the elastic long-range free energy that arises from distortions of the nematic field (30). The last two terms describe degenerate-planar anchoring at the droplet and particle surface, respectively (31). The total free energy is calculated by using a finite-difference scheme on a uniform cubic grid, with a resolution of 7.15 nm, equal to the nematic coherence length of 5CB. The total free energy is minimized by an Euler finite difference relaxation algorithm (32). The following numerical parameters are used: the droplet radius is R_d = 1 µm, the particles’ radius is R_p = 0.1 µm, A = 1.17 × 10⁵ J⋅m³, U = 5, corresponding to a bulk scalar order S = 0.76, L = 6 × 10⁻¹² J⋅m⁻¹, W_droplet = 1 × 10⁻³ J⋅m⁻², and W_particle = 2 × 10⁻⁶ - 1 × 10⁻³ J⋅m⁻².

Additional details pertaining to the calculations and the experimental systems are provided in SI Text. Note that the size of the droplet and particles considered in simulations are smaller than those considered in experiments, but the ratio between them is the same. As explained in SI Text, consistent with experimental observations in our simulations, one-half of the particles is inside the droplet.