On the Bayesian Derivation of a Treatment-based Cancer Ontology

Abstract

Traditional cancer classifications are primarily based on anatomical locations. As knowledge is heavily compartmentalized in the oncological specialties, discovering new targets for existing drugs (drug inference) can take years. Furthermore, our lack of understanding of the mechanisms underlying drug efficacy sometimes undercuts the effectiveness of genetic approaches to drug inference. This study tackles the twin problems of cancer reclassification and drug inference by constructing a global cancer ontology inductively from treatment regimens. A topological abstraction algorithm was performed on the bipartite graph of drugs and cancers to highlight important edges, and a Bayesian algorithm was then applied to determine a new treatment-based classification of cancer, producing 6 highly significant clusters (p < 0.05), confirmed by Fisher’s exact test and enrichment analyses. Edge probabilities derived from its drug inference routine matched real edge frequencies (R2 ≈ 0.96). Drug inference results were reinforced by the identification of relevant published Phase II and III clinical trials, and the drug inference routine differentiated between high- and low-likelihood targets (p < 0.05). This novel treatment-based ontology has the potential to reorganize cancer research and provide powerful tools for drug inference using global patterns of drug efficacy.

2 Introduction

Two major issues in oncology are rational cancer reclassification and the efficient inference of the effectiveness of drugs against cancers other than their initial target, which we will refer to henceforth as the drug inference problem.

Throughout the history of oncology, the discipline has been split into subfields based primarily on the anatomic location of cancer. The current partitioning of the field of oncology has led to the compartmentalization of knowledge. Even within the same subfield, there is a tendency to split between the study of untreated patients and of relapsed patients, driven primarily by the exacting needs of clinical drug testing and approval.

Currently, many drugs are studied for one specific cancer and one specific context only immediately after their development, decreasing their impact considerably. As a result, discovering additional treatment contexts for a new drug can take a long time. For example, the drug imatinib was first found effective in chronic myelogenous leukemia (CML) and gastrointestinal stromal tumors (GISTs) in 2002 [1, 2]. Despite the fact that the drug was known to target c-KIT and that it has been known that certain melanomas harbor c-KIT mutations since 2005 [3], imatinib was not shown to be effective for c-KIT mutated melanoma until 2011 [4]. This long process demonstrates the need for a global solution for drug inference.

The development of large-scale biological databases has enabled researchers to explore patterns shared by cancer subtypes and target certain protein pathways crucial to the development of cancer for treatment via inhibitors. The ontological methods developed in recent years in computational genomics provide new tools for such an analysis. In a bioinformatics context, ontology is defined as the study of hierarchical classifications generated from biological data that can be used to test biological hypotheses. Recent developments in bioinformatics sustained by genomic sequencing and ontological methods have attempted to provide computational solutions to the above two problems. These solutions have adopted an approach involving the construction of models for cancers based on specific biological mechanisms such as oncogenes, protein pathways, or gene functionality [5, 6, 7].

Such an approach based on biological mechanisms is powerful in directing future cancer research, but further investigations following its guidance sometimes cannot find supportive empirical outcomes. For example, after a highly significant single nucleotide polymorphism (SNP) was found in the v-Raf murine sarcoma viral oncogene homolog B1 (BRAF) gene in melanoma patients, the drug vemurafenib was developed to target the relevant protein and led to great improvements in the treatment of melanoma [8]. The BRAF SNP was later found to be present in a significant proportion of colorectal cancers, but the use of vemurafenib in colorectal contexts has largely failed [9, 10]. Since the current literature still cannot explain many common phenomena that have a high impact on treatment efficacy, including tumor-host interactions [11], drug efflux mechanisms [12], and other indirect mediators of drug resistance, approaches to drug inference that focus on a limited range of biological mechanisms are vulnerable to such challenges.

This study provides a unified solution to the problems of insufficient cross-specialty communication and of drug inference in cancer research by developing a novel cancer-context and drug ontology. Differently from previous approaches that attempt to pinpoint the biological causes of cancer, this approach is defined by a systematic, large-scale, quantitative analysis of the existing database of cancer treatment regimens. In contrast to previous cancer studies which build a biological model of cancer first and then infer drug efficacy accordingly, this study takes an inductive approach using data mining techniques to form a standardized cancer treatment database, then constructing the aggregate pattern of cancer subtypes. Furthermore, previous approaches consider a few key biological mechanisms that lead to cancer, whereas we black-box the currently unknown, complicated biological processes underlying cancer by using the effectiveness of existing treatment regimens as an indicator of their joint impact. An additional contribution of our approach is the global nature of the meta-analysis. Instead of comparing the mutations of only a few cancer subtypes at a time to infer drug efficacy on new targets, we compute the likelihood that any existing drug can be applied to any new target in the sorted clusters of cancers, allowing a more global drug inference study. Thus, our drug inference algorithm is capable of magnifying the effectiveness of existing cancer treatments.

To cluster cancers in a clinically meaningful way, the clustering algorithm needs to meet several criteria. We need a hypergraph to represent the relationships between cancer contexts and drugs, with edges corresponding to the set of cancer contexts treated by each drug. An effective algorithm needs to use edge weights, as certain treatments have more evidence of efficacy than others. The algorithm should determine the optimal number of clusters if the clustering is not hierarchical. Furthermore, the clusters should contribute to a probabilistic framework for drug inference, and each cluster should have an associated treatment profile. A soft clustering algorithm is optimal, as we should be able to capture uncertainty about whether a certain cancer should be assigned to one cluster or another. And finally, the algorithm should devalue unlikely treatment profiles in order to find the most plausible clustering.

Bayesian hypergraph clustering methods have addressed each of these concerns. The algorithm can incorporate edge weights by linearly weighting each edge-wise calculation, ensuring that high-evidence treatments have more impact on the clustering. A Bayesian method naturally eliminates nodes from extraneous clusters, inferring the optimal number of clusters as a byproduct of maximizing the information score (negative log likelihood) of the clustering [13]. Bayesian methods also provide probabilities for cluster assignments and edge generation between clusters and nodes, enabling a probabilistic solution to the drug inference problem using a soft clustering approach. Additionally, some Bayesian algorithms calculate rational priors for the parameters, discounting unlikely treatment profiles [14].

By supporting such a cluster analysis, a Bayesian algorithm can provide a novel treatment-based ontology of cancers that addresses both the cancer reclassification problem and the drug inference problem simultaneously. We can then test the accuracy of the drug inference results against the existing literature and use this accuracy as a metric to confirm the quality of the reclassification.

3 Methods

The dataset used in this study is from the cancer regimen online knowledge management system of HemOnc.org (http://www.hemonc.org), developed by Warner and Yang. It contains over 160 drugs, 480 regimens, and 50 cancers that are linked in a network. Some medications included in this dataset were excluded from this analysis as they are supportive. These included growth factors, bone modifying agents, and other supportive medications. Steroids were retained if and only if they were an integral part of a chemotherapy regimen.

Cancers themselves are mainly classified by anatomic location and treatment context in this dataset. We reclassified treatment regimens, when possible, between the previously treated and untreated contexts. When regimens were a mixture of first-line and second-line treatments, they were split into treated and untreated sub-contexts.

Most regimens in this dataset had already been classified into primary and secondary contexts, but a minority required further classification. One method used to distinguish primary treatments from second-line treatments was a naive classification algorithm run on the abstracts of PubMed papers associated with the treatments. For example, if “adjuvant” was found in the title of a paper, the associated treatment was considered a treatment for the untreated (primary) context. Slightly under 50% of all PubMed papers referenced by the database that were not already classified in the metadata were successfully classified using this algorithm.

Edges are key in determining the optimal clustering of a network. The important edges in the network are first separated out by using the Alterovitz principal component analysis-based (PCA) algorithm [15]. This provides the function of preserving the most important treatments for each cancer, and thus increasing the specificity of the treatment database. The Vazquez Bayesian clustering algorithm [13] was then applied to the hypergraph generated by the adjacency sets of vertices in the abstracted graph. Details of the computational process are provided in the Appendix. Clinical interpretations were assigned to clusters based on commonalities in treatment strategy, and then Fisher’s exact test was applied to determine the treatment information enrichment provided by the Bayesian clustering algorithm.

4 Results

The extraction of the most important features of G_DDs resulted in a reduction from 936 edges to 589 edges. As each cancer has many minor treatments that interfere with optimal clustering, the extraction of important features by the topological abstraction algorithm directly enabled the Bayesian clustering.

After abstraction, from the Bayesian algorithm, 19 clusters were found. The clusters ranged in size from 1 to 21; the 14 clusters with at least two cancers are shown in Table 1, in which r/r diseases represent second-line treatment contexts, or cases in which patients had previously been treated.

Table 1:

Computed cancer classification and its clinical relevance.

No.	Shared treatment	Members of cancer cluster	p-value
1	Nucleoside analogs	CML r/r, AML r/r, APL, CNS NHL untreated, ALL untreated, T-NHL untreated	5.95 · 10−6
2	Platinums	Ovarian r/r, HL r/r, SCLC r/r, Sarcoma untreated, NSCLC untreated	8.21 · 10−2
3	Platinums / taxanes	Breast r/r, Bladder untreated, Cervical untreated, H&N untreated, Esophagus untreated, Breast HER2+ untreated	1.63 · 10−3
4	Immunotherapy	Melanoma untreated, Renal r/r	3.93 · 10−5
5	5FU / Folinic acid	Pancreatic untreated, Esophagus r/r, Gastric untreated, Colon r/r, Cervical r/r, Rectal untreated, HCC r/r	1.22 · 10−4
6	R-CHOP	HIV NHL untreated, MCL untreated, Aggressive NHL, FL r/r, Thymoma untreated	7.81 · 10−9
7	MTOR inhibitors	Renal untreated, ALL r/r, MCL r/r	1.60 · 10−2
8	–	CML untreated, Brain, NET r/r	–
9	–	AML untreated, CLL	–
10	–	FL untreated, HL untreated	–
11	–	CNS NHL r/r, T-NHL r/r	–
12	–	MDS untreated, Melanoma r/r	–
13	–	Anal untreated, Bone r/r, NET untreated, MPD untreated, HCC untreated	–
14	–	Thymoma r/r, Amyloid, MZL r/r	–

With the confidences calculated for these cluster assignments and the θ-values calculated by the clustering algorithm for hyperedge incidence probabilities, extrapolated confidence in treatment efficacy was calculated using Equation (1). These clusters could generally be qualitatively characterized by a set of shared treatments without any consideration of the hyperparameters, confirming their clinical value. These treatments are briefly characterized in Table 1.

Clinical interpretations were then assigned to these clusters by finding commonalities in the treatment strategies of the cancers. The principal treatment patterns found in these interpretations were then tested for statistical significance, using the Fisher’s exact test calculation of treatment information enrichment. Six of the 14 clusters that had more than one cancer were found to have high statistical significance (p < 0.05), with the lowest having p < 10⁻⁸, as shown in Table 1. A clinical interpretation was found for one other cluster. Treatment strategies for other clusters were not evaluated due to the lack of data in the treatment database about those clusters. This significance demonstrates that the algorithm not only constructed clinically meaningful clusters, but was able to optimally partition the set of cancers among clusters to maximize clinical information across all clusters.

Our clustering technique also provides a powerful solution to the drug inference problem. Ranking cancer-treatment pairs according to descending order of computed likelihoods, we found that input edges, edges that had already been placed in the database, represented the bulk of the high-likelihood edges, as shown in Figure 1, demonstrating that our Bayesian model achieved a reasonably close fit to the existing data.

Figure 1:

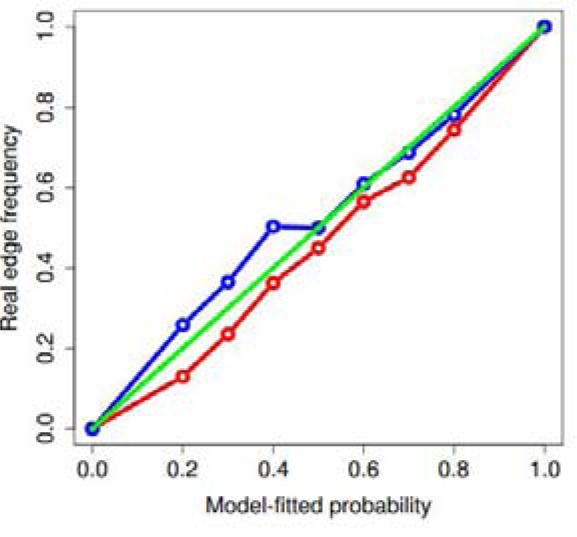
Model-fitted probability vs. real edge frequency

The lower bound curve, at point 0.1k, denotes the real occurrence frequency of edges with computed confidence between 0.1(k−1) and 0.1k, whereas the upper bound curve represents that of edges with confidence between 0.1k − 0.05 and 0.1k + 0.05. Taking the points (0.1, 0.1), (0.2, 0.2),…, (1.0, 1.0) as predicted values, we obtained R2 = 0.958 for the lower bound line and R2 = 0.960 for the upper bound line. The figure thus demonstrates that the Bayesian computed probabilities correspond quite clearly to the database’s edge incidence probabilities, showing that our clustering-derived incidence model closely approximates the original hypergraph, passing a basic sanity test.

For each possible edge, the probability of the edge occurring according to the Bayesian model was calculated. To measure the probabilistic approach’s performance on the drug inference problem, we took its ten highest-confidence newly inferred edges and reviewed the literature. These edges, their model-derived probabilities, and associated clinical trial references are shown in Table 2.

Table 2:

Inferred treatment recommendations and confidence levels

Drug	Cancer subtype	Probability	Reference
Fluorouracil	HCC r/r	0.88	[16]
Dexamethasone	Bladder untreated	0.83	[17]
Carboplatin	Sarcoma untreated	0.79	[18]
Cisplatin	Sarcoma untreated	0.79	[19]
Gemcitabine	Sarcoma untreated	0.79	[20]
Folinic acid	HCC r/r	0.74	[21]
Temozolomide	CML untreated	0.72
Methotrexate	APL r/r	0.70	[22]
Cytarabine	T-NHL untreated	0.70	[23]
Cytarabine	CML r/r	0.70	[24]

As a control group, the bottom ten inferred edges, picked from above 1% confidence, were also considered in the literature review. As shown in the last column of Table 2, we found that while eight of the ten high-confidence edges had mentions in Phase II/III literature and the other two were being studied in non-clinical contexts, only two of the ten low-confidence edges had mentions in Phase II/III literature. Indeed, one of the low-confidence pairs was found to have a negative instead of positive relationship between treatment and cancer. A significant difference (p = 0.023) therefore exists between the high-confidence and low-confidence edges inferred by the clustering algorithm, and this demonstrates that our algorithm is capable of differentiating between promising treatments and treatments that are likely to fail. In short, although these treatments had already been discovered by other investigators, we were able to infer them from a database that did not contain them.

Thus, our algorithm was able to discern the hidden structure of G_DDs and has contributed both to the solution of the drug inference problem and the cancer reclassification problem, with the latter being confirmed both quantitatively by the drug inference results and qualitatively by inspection of common treatments by cluster and by inspection of the relationships between cancers in the same cluster.

5 Discussion and Conclusion

The results demonstrate the strength of the treatment-based Bayesian clustering algorithm and provide a simultaneous solution to the cancer reclassification problem and the drug inference problem. While previous works represent the biologically-motivated approach to oncology, this study represents a new direction of global network meta-analysis on existing treatment regimen data.

Aside from the traditional anatomical classification of cancer, recent reclassification studies have been performed on a local scale. For example, breast cancer was split into many different subtypes [25].

Our meta-analysis takes a holistic, inductive approach, using clinical efficacy data as its main variable, which reflects the entirety of all biological mechanisms behind cancer. Our treatment-based ontology sheds light on several rational cancer reclassifications. For example, in the traditional anatomy-based model, renal cancer and melanoma are deemed to be unrelated. According to our treatment-based ontology, however, they belong to the same cluster because they are similarly treated diseases, commonly found to coexist [26], and commonly treated by the same specialists. Such a reclassification will reorganize oncological knowledge, as the traditional divisions among anatomical locations will be replaced by the patterns of shared treatment efficacies.

Although our approach does not open the black box of the biology behind cancer, it does consider these mechanisms indirectly, through treatment efficacy. Instead of considering etiology directly, we first reclassify cancers based on treatment efficacy, and then suggest further investigations into similarities in the underlying biology. For example, in the case of renal and melanoma cancers (cluster 5), our new reclassification suggests that specialists working on the two cancers may jointly investigate new approaches to immunotherapy. Similarly, thymoma, which is treated primarily by CHOP regimens, unexpectedly occurred in the B-cell non-Hodgkin’s lymphoma clusters, which shares those regimens but is not related anatomically. Thus, similarities in the underlying etiologies of cancers in this cluster may be jointly investigated by their respective specialists. All of these examples had high statistical significance for treatment information enrichment, as shown by Table 1. The significance of these biological validations is three-fold. These similarities represent a preliminary biomedical validation of our reclassification of cancers, and the statistical significance of the information enrichment lends credibility to our approach to drug inference. Furthermore, our findings suggest that the Bayesian algorithm, applied to a more complete database and augmented with further biological information, may be capable of quickly identifying new commonalities between the etiologies of cancers, which would merit further investigation.

Previous efforts at drug inference have focused on SNPs and oncogenes, among other genetics-motivated biological mechanisms. As the development of drugs such as vemurafenib has shown, the challenge to this approach is that it considers only a small number of the biological mechanisms that jointly determine drug efficacy and is therefore often ineffective as a solution to the drug inference problem. As a result, the potential impact of new chemotherapy drugs is limited to one cancer until oncologists slowly begin to experimentally apply them to other cancers.

Though drug inference has often been performed on a local scale, comparing the genetic and molecular profiles of two cancers at a time, we take a global approach to the problem of drug inference, unifying it with a cancer reclassification model. Our focus on treatment efficacy rather than its main causal factors enabled this study to map global similarities between cancer subtypes by first finding clusters, then computing probabilities for the efficacy of repurposed drugs in a unified model. The effectiveness of the Bayesian algorithm at the drug inference problem is demonstrated by its differentiation between likely and unlikely treatment recommendations. As the last column of Table 2 demonstrates, likely treatment candidates had a high correlation with appearances of Phase II/III clinical trials in the literature. Unlikely treatment candidates, in contrast, had a much lower frequency of mentions in the literature. Thus, the drug inference extrapolations were clinically relevant. This suggests that a global model for cancer reclassification may be able to simultaneously address the drug inference problem.

The inductive statistical method of treatment efficacy analysis adopted by this study suggests a new way of discovering cancer knowledge by analyzing the rapidly accruing digital data on cancer treatments. At one level, it offers an alternative to models built on key genetic profiles and biological mechanisms. At another level, however, it also complements these biological models by providing a new way to organize cancer specialties and infer drug efficacy according to the treatment-based clusters identified by our statistical algorithm.

However, this paper represents only the preliminary step in exploiting our Bayesian network analysis approach in drug inference. Though we have confirmed the efficacy of the Bayesian approach in analyzing incomplete cancer-drug databases, the next step is applying the approach to a more complete database, which would allow us to make novel treatment recommendations.

In our work towards solving the cancer reclassification and drug inference problems, we have identified several important questions that must be addressed to perfect the power of our clustering algorithms and to extend the impact of our findings.

One of the potential improvements to our approach is the inclusion of more data in our meta-analysis. One possible approach is to adjust the Bayesian model; new hyperpriors can be designed for the distribution of treatment effectiveness. Another way to make more information available to the clustering algorithm would be to provide more information on absolute efficacy, in the form of negative edges. If a certain drug was found in a study to be completely ineffective against a particular cancer, a separate ineffective hyperedge should be created to include this information in clustering considerations. Although hemonc.org did not have negative information as it was meant to be a treatment guideline database, a more comprehensive database would yield better clusters. In addition to efficacy data, the inclusion of direct biological mechanisms in our inductive approach could provide a powerful syncretic method that may solve the problem of discovering new subtypes of cancer as well.

Furthermore, the possibility remains that the unit of our clustering, the cancer treatment context, is not the best disease unit to use. For example, gastrointestinal stromal tumors are included in the sarcoma contexts, but are treated differently from most sarcomas. Dividing cancers into contexts in some other way may provide more information or better clusters.

In addition to addressing these problems in clinical oncology, cancer treatment network analysis can also yield better ways to organize other processes relating to cancer care, such as drug production. Cancer drug shortages are a major problem in cancer treatment [27]. We can track sudden bursts in publications in particular clusters using a network analysis algorithm running on a cancer treatment network. Thus, it may be possible to predict drug shortages in the future, ensuring that production can be increased before the demand spike.

Analytical models of cancers based on biological etiologies have characterized cancer meta-analysis and drug inference thus far. The inductive, global, treatment-based approach outlined in this paper directly analyzes treatment efficacy data to provide a unified solution to both cancer reclassification and drug inference. Our combination of topological abstraction and Bayesian techniques was effective at elucidating the structure of the cancer treatment network provided by the regimen database, discovering hidden commonalities between cancers whose validity is confirmed by our Fisher’s exact test p-values (p < 0.05), and suggesting new directions of research using treatment patterns found in the database. Its drug inference extrapolation routine, which black-boxes biological mechanisms by considering final treatment efficacy instead of partial sets of biological data, also yielded positive results (p < 0.05) in drug inference, as shown by our review of clinical literature. This Bayesian approach is also flexible enough to accept new forms of treatment efficacy data to further improve its impact.

A Appendix

A.1 Algorithms

Let the shortest distance matrix of graph G_DDs, the bipartite graph consisting of edges between chemotherapeutic drugs and cancers they treat, be D. We perform PCA on the set of row vectors of D, and project all vectors into the vector space defined by the principal components. We then discard all but the 20 principal components that contribute the highest variance, and then project all vectors back into the original vector space. We form a modified matrix D′ with these vectors as row vectors. We then redraw G to form G′, in which an edge between i and j exists if and only if $D_{\mathit{ij}}^{\prime }\le 1.5$.

A Bayesian clustering algorithm due to Vazquez [13] was then applied to the modified hypergraph. From G′, we defined a hypergraph H, with hyperedges corresponding to the disease adjacency sets of the drugs in the database. Then define a to be the adjacency matrix of H; that is, a_ij = 1 if and only if vertex i belongs to edge j.

Let B denote the Beta function. We define:

$$B(p;\alpha ,\beta )=\frac{1}{B(\alpha ,\beta )}{p}^{\alpha -1}{(1-p)}^{\beta -1};D(\mathrm{\pi };\gamma )=\frac{1}{B(\gamma )}{\displaystyle \prod _{k=1}^K{\mathrm{\pi }}_k^{{\gamma }_k-1}}$$

A similar limit applies for γ in this case.

We apply a Variational Bayes expectation-maximization (EM) algorithm. We minimize an upper bound F on the negative log likelihood of the data by performing a convergent algorithm that converges at the most likely cluster assignment probability matrix and adjacency probability matrix. Variational approximations for probabilities and parameters are first computed, followed by cluster probabilities, at every step of the convergent algorithm.

Let K be an initial upper bound for the appropriate number of clusters. Let θ_kj be the probability that a vertex in cluster k will belong to hyperedge j. Let p be a matrix of probabilities of cluster assignments. Let π denote the hidden frequency vector describing cluster sizes. This frequency vector is relevant because it allows us to define a prior D(π; γ) that punishes uneven clusterings. Let γ denote a vector, indexed by group indices k, where γ_k refers to the sum of the probabilities of each node falling in cluster k. In all of our equations, R(θ), R(π) denote likelihood estimates for θ, π, respectively. Also, define

$$\langle A(\varphi )\rangle ={\displaystyle \int d\varphi P(\varphi |D)A(\varphi ),}$$

for any function A on the parameters ϕ.

To ensure convergence at a global minimum of Kullback-Leibler (KL) divergence, we seed the vector π with a large number (1000) of random sets of probabilities, and the following algorithm is applied to each π, after which the parameters corresponding to the lowest KL divergence are chosen as the final parameters for our model.

Until F varies by less than a certain threshold ϵ, the following steps are iterated (we chose 10⁻6):

$$\begin{array}{ll}{m}_{ik}=\langle \ln {\pi }_k\rangle +{\displaystyle \sum _j{a}_{ij}}\langle \ln {\theta }_{kj}\rangle +(1-a_{ij})\langle \ln (1-{\theta }_{kj})\rangle & {\alpha }_{kj}=\in +{\displaystyle \sum _{ij}{p}_{ik}{a}_{ij}}\\ p_{ik}=\frac{e^{m_{ik}}}{{\displaystyle {\sum }_s{e}^{m_{is}}}}& R(\pi )=D(\pi ;\gamma )\\ R(\theta )={\displaystyle \prod _{kj}B({\theta }_{kj};{\alpha }_{kj},{\beta }_{kj})}& \langle \ln ({\pi }_k)\rangle =\psi ({\gamma }_k)-\psi \left({\displaystyle \sum _k{\gamma }_k}\right)\\ \langle \ln ({\theta }_{kj})\rangle =\psi ({\alpha }_{kj})-\psi (\in +{\gamma }_k)& {\gamma }_k=\in +{\displaystyle \sum _i{p}_{ik}}\\ \langle \ln (1-{\theta }_{kj})\rangle =\psi (\in -{\gamma }_k-{\alpha }_{kj})-\psi (\in +{\gamma }_k)& F={\displaystyle \sum _{ik}{p}_{ik}}\ln p_{ik}-{\displaystyle \sum _{kj}\ln B({\alpha }_{kj},{\beta }_{kj})-\ln B(\gamma )}\end{array}$$

Similar equations are defined for β.

After the algorithm finishes, the elements of p are the desired probabilities. Summing over all potential cluster assignments, we can then estimate the likelihood that a certain drug works on a certain disease.

To determine the quality of the clusters derived from the Bayesian algorithm, Fisher’s exact test was applied in an enrichment analysis of treatment information. Clinical interpretations were assigned to each cluster, consisting of treatments shared among the diseases in the cluster. The frequency of the occurrence of these shared drug hyperedges in that cluster was then compared to the frequency in G_DDs, from which p-values were derived.

As the Bayesian algorithm calculates ${\varphi }_{\mathit{kj}}^{\prime }=\log {\theta }_{kj}$ and p_ik, we can determine the exact model-derived likelihood

$$P(i\in G_j|\varphi )={\displaystyle \sum _k{e}^{{\theta }_{\mathit{kj}}^{\prime }}{p}_{ik},}$$ (1)

where G_j represents the neighborhood of treatment j. Clusters resulting from the Bayesian hypergraph clustering algorithm were filtered by confidence, and only cluster assignments with confidences higher than 0.95 were retained.

The PCA-based topological abstraction algorithm was run using 20 principal components. After topological abstraction was complete, the Bayesian hypergraph clustering algorithm was applied to the resulting graph, excluding edges between pairs of drugs and pairs of diseases. Likelihoods were calculated using Equation (1).

A.2 Glossary

• 5-FU: 5-fluorouracil

• ALL: Acute lymphocytic leukemia

• AML: Acute myelogenous leukemia

• APL: Acute promyelocytic leukemia

• CLL: Chronic lymphocytic leukemia

• CML: Chronic myelogenous leukemia

• FL: Follicular lymphoma

• HCC: Hepatocellular carcinoma

• HIV NHL: Human immunodeficiency virus-related non-Hodgkin lymphoma

• HL: Hodgkin lymphoma

• H&N: Head and neck carcinoma

• MCL: Mantle cell lymphoma

• MDS: Myelodysplastic syndrome

• MPD: Myeloproliferative disorders

• MTOR: Mammalian target of rapamycin

• MZL: Marginal zone lymphoma

• NET: Neuroendocrine tumor

• NHL: Non-Hodgkin lymphoma

• NSCLC: Non-small cell lung cancer

• PCNSL: Primary central nervous system lymphoma

• R-CHOP: Rituximab, cyclophosphamide, hydroxydaunorubicin, Oncovin, prednisone

• SCLC: Small-cell lung cancer

• T-NHL: T-cell non-Hodgkin lymphoma